Abstract
We investigate the topology of sectoral returns in the US stock market using minimum spanning tree (MST) analysis. We examine four distinct time periods: the full period, the Global Financial Crisis (GFC), the COVID-19 pandemic, and the Russia-Ukraine war period. By comparing the static results across these periods, we identify differences in the network structure. Additionally, a rolling window analysis is conducted to explore the time-varying nature of the MST. We employ a TVP-VAR based connectedness framework to ensure a robust analysis of the sectoral return linkages. Our main findings are summarized as follows: First, the structure of the MST varies in different periods, with distinct crisis period structures. During the GFC, the industrial sector dominated clustering, whereas COVID-19 affected the financial, IT, and industrial sectors. The Russia-Ukraine war period showed clustering centered on materials, except in the industrial sector. These varying structures may explain the different characteristics of each crisis. Second, both static and rolling window analyses highlight the significance of the industrial sector in the US stock market. Third, the utilities sector exhibits the lowest centrality measures, indicating its minimal importance and lack of relationships with other industries. These findings provide valuable insights into the interrelationships among industries in the US stock market. Market participants can leverage these findings to enhance their understanding and improve their portfolio management. By utilizing this information, investors can develop optimal diversification strategies to maximize returns and minimize risk.
Keywords: Dynamic network, Sectoral return, Minimum spanning tree, 2008 global financial crisis, COVID-19 pandemic, Russia-Ukraine war
1. Introduction
The global financial market has interconnected for several decades. Information technology and communication are gradually strengthening this degree of connection. Therefore, global market participants closely monitor their own financial markets, as well as other global financial markets. Even in academia, numerous studies have investigated the interactions between global financial markets of equity, oil, agriculture, and metals [1], [2], [3], [4], [5], [6], [7], [8], [9], [10].
However, the inter-industrial relationship within a financial market, is also significant for market participants, with instances of different industries reacting to the same external shock. For example, industries like communication services experienced temporary steep growth, due to the COVID-19 pandemic, while the consumer discretionary industry incurred huge losses. Therefore, several studies examine the relationships between various industries [11], [12], [13], [14], [15].
The COVID-19 pandemic has significantly impacted financial markets, resulting in both positive and negative outcomes across industries. Furthermore, the crude oil market exhibits considerable volatility, leading to diverse responses in different sectors. Moreover, the Russia-Ukraine war has once again sent financial markets under heavy external shocks [16], [17], [18], [19], [20]. In response to these shocks, the interactions among industries within the financial market have undergone notable changes, influenced by varying interests. Understanding these industry-specific relationships is crucial for market participants because they inform portfolio management, risk hedging, and policymaking. Therefore, this study examines the transformations in interrelationships within the financial market resulting from these shocks.
Consequently, we investigate the network topological return connectedness among industries of the United States (US) in this study. After calculating each sectoral return, we use the minimum spanning tree (MST) to construct a return network. Accordingly, we also examine the interdependency structure and integration of the US stock market. We proceed to conduct a static and dynamic analysis of their topological features, during three crises: the 2008 global financial crisis (GFC), the COVID-19 pandemic, and the Russia-Ukraine (RU) war. Furthermore, we provide the robustness test results to enhance the credibility and robustness of our research.
MST has been widely used as a network configuration due to its ability to simplify complicated networks and provide a robust network structure. As a result, it has found broad application in understanding the topology of stock markets, bond markets, crude oil markets, overnight index swap rate markets, and energy future markets [21], [22], [23], [24], [25], [26], [27], [28], [29]. The detailed introduction of these studies are given in Section 2.1.
We present two theoretical frameworks to support our research. The first framework is rooted in herding behavior, which explains investors' tendencies to follow others' trading actions. Several studies have explored the cross-sectional stock linkages in relation to herding behavior [30], [31], [32], [33]. Notably, [33] observed that market-wide herding is not commonly observed in the US market, but they found evidence of herding behavior at the sectoral level.
The second theoretical background justifying our research is based on the concept of information flow within the stock market. This perspective considers the interaction between different components in a network and utilizes information flow measures to analyze linkages across sectors. Previous studies have examined the information flow between sectors in the stock market and use this as a basis for investigating the relationships between sectors [34], [35], [36].
Our study contributes to the existing body of literature in three significant ways. First, we address a notable gap in research by examining the dynamic return networks among industries. Prior to our study, there has been a lack of extensive investigation in this area. By filling this gap, we provide valuable insights into the interrelationships and connections between industries in financial markets.
Second, our study contributes to previous research by analyzing the changing network topology during three major crises: the Global Financial Crisis (GFC), the COVID-19 pandemic, and the Russia-Ukraine war. While there have been several studies comparing the GFC and the COVID-19 pandemic [29], [37], [38], [39], [40], [41], [42], only a few have examined the network topology during both the GFC and the COVID-19 pandemic [29], [42]. Furthermore, to the best of our knowledge, no study has comprehensively analyzed all sectors in the US stock market during the Russia-Ukraine war in terms of network topology. Our study aims to bridge these gaps and shed light on the evolving relationships among industries during these critical periods. We review several recent studies on the impact of the GFC, the COVID-19 pandemic, and the RU-war on equity sector market connectedness in Section 2.2.
Finally, the empirical results have practical implications for portfolio managers. By understanding the changes in industry-specific relationships within the financial market, portfolio managers can effectively rebalance the weight of each industry in their portfolios. This information enables them to make informed decisions that optimize their portfolio performance and manage risk. Additionally, our findings can assist policymakers in monitoring and addressing potential financial market risks.
The remainder of this paper is organized as follows. In the following section, we review the previous studies analyzing financial markets using MST and the relationship between the equity sector during a crisis. Section 3 provides a preliminary statistical analysis of the sectoral returns, apart from introducing a sectoral return network. Section 4 presents the empirical results and the data analysis. We provide the robustness check results in Section 5. Finally, section 6 presents the summary and concluding remarks.
2. Literature review
2.1. Financial market and MST
In this subsection, we briefly review the previous literature analyzing financial markets using network topology.
Many studies have analyzed the network topology of equity markets using MST. [22] examined the network topology of individual stocks and global stock indices. They showed that a correlation-based network is a useful method for extracting economic information from a set of financial time series. Similarly, [23] constructed the MST for a portfolio of stocks from the London Stock Exchange FTSE100 index. They found that some stocks from the same sector cluster together. Similarly, [24] used the MST structured by the stocks in the Shanghai-Shenzhen 300 Index. They mentioned that a classification based on the topology structure can provide more information than a simple division by industry. Recently, [29] examined the dynamic interrelationship between Islamic and conventional equity sectors using network analysis during the COVID-19 pandemic. Their findings show that Islamic and conventional equities exhibit different patterns of industry-level dependence during normal and crisis periods.
Some studies have applied the MST to financial markets other than equity markets. [26] analyzed the comovement patterns of twenty government bond market indices based on the concept of MST. In addition, they examined the dynamic evolution of bond market linkages. Similarly, [27] investigate changes in world crude oil markets by constructing the MST for them. According to the MST, crude oil markets in geographically adjacent countries or regions are interconnected. Recently, [28] investigate the centrality structure of overnight index swap networks. Based on their centrality structure, they analyze how financial crises affect the global interest rate market centralization.
2.2. Industries and crisis
This subsection introduces various studies that have explored the changes in the interrelationships between different equity sectors during the crisis. [43] examined the dynamic relationships between the components of the sovereign yield curve (level, slope, curvature) and sectoral equity indices in China during the Chinese stock market crisis periods. They empirically provided not only the intra-connectedness among sectors, but also the impact of each yield curve component on the equity sectors. [44] investigated the interrelationships between gold and oil commodity futures and 22 European equity sectors during crises such as the 2011–12 European debt crisis, 2014–15 oil crisis, 2016 Brexit referendum, and the COVID-19 pandemic. They showed that the COVID-19 pandemic has had the greatest impact on the relationships among them. [45] examined the connectedness between the COVID vaccination and sectoral equity markets in the US. According to their findings, vaccination has positively affected the sector indices. In particular, the relationship was strong in the communication services, financial, health care, industrial, information technology, and real estate equity sectors, but weak in the utility sector. Similarly, [46] examine the dynamic relationships between Defi assets and sector stock markets during the COVID-19 pandemic crisis. They also showed that their relationship varies over time, and that the COVID-19 pandemic has greatly affected this relationship. Recently, [47] analyzed the impact of the Silicon Valley Bank (SVB) bankruptcy on the US stock market from a sectoral perspective and found that the financial sector was the most affected.
Some studies have analyzed the impact of crises on non-equity markets. [48] investigated how global supply chain pressure affects commodity market sectors (energy, non-energy, agriculture, food, raw materials, and precious metals) under extreme market conditions. [49] examined the dependence structure among carbon emissions prices, crude oil prices, natural gas prices, and geopolitical risks in Brazil, China, India, Russia, and South Africa from January 2003 to September 2019 including the 2008 Global Financial Crisis and Brexit.
3. Data and methodology
3.1. Sectoral return data description
We use 11 sectors1 of the S&P 500 index, including approximately 500 companies. Since its market cap is 70–80% of the total US stock market capitalization, the S&P 500 index has been widely used as a benchmark for US economic conditions. Following [50], we calculate the average log return of the i-th sector, at time t, as follows:
where N is the total number of stocks2 in the sector at time t, and is the closing price of the j-th stock in the sector at time t. Accordingly, we employ all stock closing prices in the S&P 500 index, from January 2002 to June 2022,3 to calculate the sectoral return. We provide the summary statistics for the average log returns for all sectors, in Table 1. Based on this table, all sectoral return distributions are left-skewed and high-peaked. In addition, the Jarque-Bera test results indicated that, they were not normally distributed.
Table 1.
Summary statistics for the average log return of sectors in the S&P 500 index. The Jarque-Bera test statistic tests for the null hypothesis of normality in sample returns. † indicates a rejection of the null hypothesis at the 1% significance level.
| Sectors | Mean | Std. Dev. | Skewness | Kurtosis | Jarque-Bera |
|---|---|---|---|---|---|
| Communication Service(CS) | 2.32e-05 | 0.0138 | -0.4373 | 7.0809 | 10942.55† |
| Consumer DiscretionaryCD | 4.74e-05 | 0.0148 | -0.3199 | 9.808 | 20766.61† |
| Consumer Staples(CST) | 2.68e-05 | 0.0091 | -0.3206 | 11.1113 | 26627.64† |
| Energy(ENG) | 2.59e-05 | 0.0201 | -0.9183 | 17.4125 | 65900.04† |
| Financials(FIN) | 1.15e-05 | 0.0167 | -0.3569 | 12.3832 | 33072.31† |
| Health Care(HC) | 4.02e-05 | 0.0118 | -0.4229 | 6.7519 | 9953.45† |
| Industrials(IND) | 3.19e-05 | 0.0136 | -0.4591 | 8.1898 | 14599.12† |
| Information Technology(IT) | 3.83e-05 | 0.0155 | -0.2106 | 5.3099 | 6099.12† |
| Materials(MAT) | 2.94e-05 | 0.0149 | -0.5302 | 8.1666 | 14578.22† |
| Real Estate(RE) | 2.97e-05 | 0.0168 | -0.4188 | 18.2297 | 71586.4† |
| Utilities(UTI) | 2.02e-05 | 0.012 | -0.0632 | 14.8896 | 47660.35† |
In addition, Fig. 1 displays the correlation matrix for the sectoral return series, implying their strong positive correlation. This result indicates the requirement to investigate the relationship between sectoral returns and their topological characteristics. Therefore, the following section showcases the construction of a correlation-based network.
Figure 1.
Correlation coefficient of the sectoral returns.
3.2. Sectoral return correlation network construction
We establish return correlation networks based on previous studies [51], [52], [53], [54], by primarily estimating the Pearson correlation coefficient between the daily sectoral returns i and j:
| (1) |
where denotes the average over a given period. According to [55], the distance matrix D is derived from the elements in (2) using the defined in (1),
| (2) |
Given the distance matrix, we can construct the MST by using Kruskal's algorithm [56]. Using the MST approach, we capture the correlation properties among sectoral returns, and analyze the clustering behaviors and dominant sectors in the US stock market. We also investigated the centrality structure of the network in terms of several measures: degree centrality, closeness centrality, betweenness centrality, and eigenvalue centrality. These are useful for identifying the influence of each node in the network. These measures are defined as follows:
| (3) |
| (4) |
| (5) |
| (6) |
where N is the number of nodes and , if and only if i and j sectors have an edge in the MST, and zero otherwise. is the minimum path distance from i to j in the MST. is the number of shortest paths between sectors j and k, and is the number of shortest paths between sectors j and k, passing through sector i. is the largest eigenvalue of adjacency matrix A, and is the eigenvector corresponding to .
According to the definitions in (3)–(6), degree centrality indicates the influence of node i in the network. The closeness centrality measures the average distance between nodes i and all other network nodes. The betweenness centrality demonstrates the frequency of node i passing through the shortest path between other nodes. The eigenvector centrality determines the influence of node i on its neighbor. In other words, it measures the relative importance of node i, thus reflecting its neighbor's importance.
In addition, we calculated the degree of integration [27], [57], [58] as follows:
| (7) |
where is the total number of edges in the MST, and is the edge of the MST. The smaller the value of in (7), the higher the integration. For convenience of interpretation, we employed the inverse integration degree ().
4. Centrality network analysis
4.1. Static network analysis
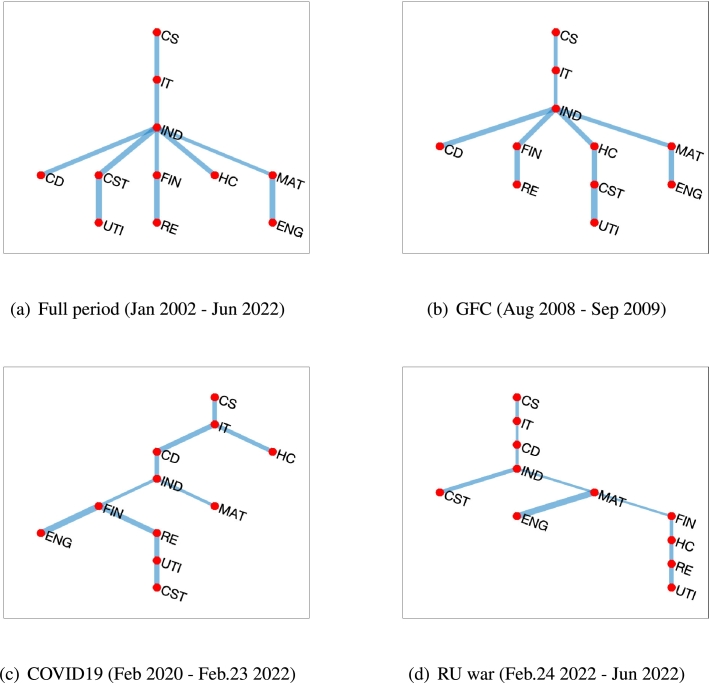
First, we present a static analysis of the sectoral return network for four periods: the whole period, the GFC period (August 2007-March 2009), the COVID-19 pandemic (February 2020-February 23, 2022), and the RU war period (February 24, 2022-June 2022). The static analysis results are displayed for the four centrality measures and inverse integration degree.
Table 2 lists the sectors with the four centrality measures, and degree of integration in the four periods. In addition, we display the MST of the sectoral return network for four periods in Fig. 2. In the figure, node indicates sector, and the width of the edge is the distance between two nodes. A summary of the static analysis results is as follows.
Table 2.
The four centrality measures of all sectors and the inverse integration degree during the four periods. The highest value of each measure is indicated in bold. Notes: Degree = Degree centrality in (3), Closeness = Closeness centrality in (4), Betweeness = Betweeness centrality in (5), Eigenvector = Eigenvector centrality in (6).
| Panel A : Full period (inverse integration degree = 1.6033) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sectors | CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI |
| Degree | 1 | 1 | 2 | 1 | 2 | 1 | 6 | 2 | 2 | 1 | 1 |
| Closeness | 0.0333 | 0.0435 | 0.0476 | 0.0333 | 0.0476 | 0.0435 | 0.0714 | 0.0476 | 0.0476 | 0.0333 | 0.0333 |
| Betweeness | 0 | 0 | 9 | 0 | 9 | 0 | 41 | 9 | 9 | 0 | 0 |
| Eigenvector | 0.0409 | 0.09 | 0.1058 | 0.0409 | 0.1058 | 0.09 | 0.2331 | 0.1058 | 0.1058 | 0.0409 | 0.0409 |
| Panel B : GFC period (inverse integration degree = 2.0477) | |||||||||||
| Sectors | CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI |
| Degree | 1 | 1 | 2 | 1 | 2 | 2 | 5 | 2 | 2 | 1 | 1 |
| Closeness | 0.0312 | 0.04 | 0.0357 | 0.0312 | 0.0435 | 0.0476 | 0.0625 | 0.0435 | 0.0435 | 0.0312 | 0.027 |
| Betweeness | 0 | 0 | 9 | 0 | 9 | 16 | 39 | 9 | 9 | 0 | 0 |
| Eigenvector | 0.0466 | 0.0937 | 0.0586 | 0.0466 | 0.1129 | 0.1179 | 0.2271 | 0.1129 | 0.1129 | 0.0466 | 0.0242 |
| Panel C : COVID-19 pandemic period (inverse integration degree = 1.8800) | |||||||||||
| Sectors | CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI |
| Degree | 1 | 2 | 1 | 1 | 3 | 1 | 3 | 3 | 1 | 2 | 2 |
| Closeness | 0.0256 | 0.04 | 0.0227 | 0.0312 | 0.0435 | 0.0256 | 0.0455 | 0.0333 | 0.0323 | 0.0357 | 0.0286 |
| Betweeness | 0 | 21 | 0 | 0 | 27 | 0 | 29 | 17 | 0 | 16 | 9 |
| Eigenvector | 0.0477 | 0.1263 | 0.0281 | 0.0746 | 0.1609 | 0.0477 | 0.1697 | 0.1028 | 0.0787 | 0.1028 | 0.0607 |
| Panel D : RU war period (inverse integration degree = 1.7043) | |||||||||||
| Sectors | CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI |
| Degree | 1 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 | 2 | 1 |
| Closeness | 0.0222 | 0.0345 | 0.0303 | 0.0312 | 0.0385 | 0.0323 | 0.0417 | 0.0278 | 0.0435 | 0.0263 | 0.0213 |
| Betweeness | 0 | 16 | 0 | 0 | 21 | 16 | 27 | 9 | 29 | 9 | 0 |
| Eigenvector | 0.0322 | 0.1144 | 0.0822 | 0.0831 | 0.1197 | 0.0782 | 0.1752 | 0.0687 | 0.1773 | 0.047 | 0.022 |
Figure 2.
MST for the three complete crisis periods of GFC, COVID-19 pandemic, and RU war. The width on the lines denotes the distance between the corresponding two nodes (sectors).
First, throughout the entire period, the industrials sector remained the most important industry in the network, forming a hub (Fig. 2-(a)) supported by Table 2-(A). The industrials sector was also the most important one during the GFC and the COVID-19 pandemic (see Fig. 2-(b),(c) and Table 2-(B),(C)). Despite the existence of different stock markets, few studies have reported identical results, indicating the major role of industrials sector in linking other sectors [29], [59].
Second, the materials sector during the RU war, had the highest centrality measures. The Russian-Ukraine war has increased global supply chain turmoil, especially in the raw material market.4 This is consistent with the results of the network analysis (see Fig. 2-(d) and Table 2-(D)).
Third, the MST plot revealed clustering characteristics in each network. In the sectoral return network of the US stock market, all period saw clustering centered on industries. Similarly, during the COVID-19 pandemic, clustering was centered on the IT and financial sectors. The cluster centered on the IT sector is likely due to the tech boom during the pandemic. The linkage of the energy sector with the financial sector cluster, may be due to the unstable crude oil market during the pandemic, causing financial market turmoil. In addition, during the RU-war, additional clustering centered on the materials sector, presumably due to the aforementioned global supply chain disruption.
Finally, based on the inverse integration degree, the GFC network had the strongest integration among the four periods. The COVID-19 and RU War epochs were also more integrated than the complete period. In other words, when financial markets are in crisis, the US stock market tends to be more integrated at the industry level. The same results are supported by other studies [13], [15].
4.2. Dynamic network analysis
We further analyze the dynamic relations among sectors using a monthly non-overlapping rolling window analysis. This involves constructing the sectoral return network for each month, to estimate the four centrality measures and the inverse integration degree, based on the network.5
Figure 3, Figure 4, Figure 5, Figure 6 depict the trends of the four centrality measures (degree, closeness, betweenness, and eigenvector centrality) from January 2007 to June 2022. We chose this time span to focus on the characteristics of the sectoral return network, during the crisis period. In each figure, the three shaded areas indicate the crisis periods. The solid red line represents the statistical average value over the entire period. Following previous studies [51], [53], [60], [61], we interpret the rolling window analysis results as follows:
Figure 3.
Time-varying degree centrality in the MST. M. = Mean.
Figure 4.
Time-varying closeness centrality in the MST.
Figure 5.
Time-varying betweenness centrality in the MST.
Figure 6.
Time-varying eigenvector centrality in the MST.
First, the industrials sector has the highest average value for all four measures, indicating that it is the most dominant sector in the sectoral return network of the rolling data sample. On the other hand, the energy sector has the smallest average value in the degree and betweenness centrality measures, and the utilities sector has the smallest average value in the closeness and eigenvector centrality measures. That is, they have a less intensive relationship with other industries, in terms of sectoral returns.
Second, each sectoral maximum and minimum average value the betweenness centrality measure portrayed the largest difference between the maximum and minimum average values for each sector. In this measure, the industrials sector has the maximum and the energy sector has the minimum. This indicates that the industrials sector has a more powerful intermediary influence in the network, whereas the role of information delivery in the energy sector is quite weak.
Third, there were several notable changes in centrality measures during the crisis. During the GFC period, changes were apparent for these measures in the IT sector, with a probable relation to the IT sector's higher rebounding performance than other industries at that time.6 Prominence also increased in the early days of COVID-19, with the increase in the energy sector's betweenness central measurement. This may reflect the shock to the US stock market, caused by the sharp drop in crude oil prices [15]. On the other hand, RU-war period saw rising consumer staples and financial sectors, without a significant increase.
Finally, note the difference between the static analysis and rolling window analysis, due to the differing data periods used to create the network.
Furthermore, we plot the time-varying inverse integration degree in Fig. 7. Based on the plot, during the GFC period (November 2008) and early COVID-19 period (March 2020), the integration of the sector return network increased. We also found that network integration has been gradually increasing since the outbreak of the Russian-Ukraine War. These results are consistent with the static analysis results. On the other hand, there were more peaks of integration in March 2010, August and November 2011. This may be due to the flash crash [62] and the 2010 European sovereign debt crisis. At this time, the level of integration was high. Research on this topic is left for future research.
Figure 7.
Time-varying inverse integration degree in the MST.
5. Robustness check
We conducted robustness checks to ensure the reliability and validity of our findings. To achieve this, we employed a time-varying parameter vector autoregression (TVP-VAR) based connectedness approach, as proposed by [63], to measure the linkages among sectoral returns. The TVP-VAR based connectedness approach offers several advantages over the traditional spillover framework [64]. These advantages include more precise parameter estimation, increased robustness to outliers, and the elimination of the need for a rolling window size. Moreover, this methodology has been widely used in numerous studies to investigate the relationships among various financial assets [16], [65], [66], [67], [68], [69], [70], [71]
We briefly review the TVP-VAR based connectedness method. The TVP-VAR(p) model, represented by Equations (8) and (9), plays a central role in our framework. Equation (8) describes the relationship between the observed variables, denoted as , and their lagged values, denoted as .
| (8) |
| (9) |
The time-varying parameter vector captures the evolving relationships, with representing the error term, conditional on the information set , following a normal distribution with mean zero and covariance matrix . Similarly, Equation (9) describes the evolution of the time-varying parameters, where follows a normal distribution with mean zero and covariance matrix .
By applying the world representation theorem, the TVP-VAR(p) model can be transformed into a vector moving average (VMA) representation, as shown in Equation (10). This representation expresses as a linear combination of lagged error terms , with as the corresponding -dimensional matrix.
| (10) |
To examine the dynamic connectedness between different variables, we incorporate time-varying parameters and variance-covariance matrices into the measure of connectedness developed by Diebold and Yilmaz. According to [72], we calculate the elements of the dynamic H-step generalized variance decomposition matrix , as formulated by
| (11) |
where denotes the diagonal element of . These elements quantify the contribution of each variable i to the forecast error variance of variable j by considering a horizon of H periods.
Normalized terms are then derived by dividing each element in (11) by the sum of all elements in the same row, i.e. . These normalized terms enable us to calculate dynamic total directional connectedness, net total directional connectedness, and total connectedness, which capture the interdependence among the variables.
The total connectedness index (TCI) measures overall interconnectedness and is obtained using Equation (12). This represents the sum of the normalized elements in the matrix, reflecting the percentage of total connectedness.
| (12) |
Moreover, we compute the directional connectedness received by variable i from all other variables j (denoted as ) using Equation (13). This is calculated by summing the normalized elements in each row, excluding the diagonal element, and dividing it by the sum of the corresponding column.
| (13) |
Similarly, the directional connectedness transmitted by variable i to all other variables j (denoted as ) is determined using Equation (14). It is obtained by summing the normalized elements in each column, excluding the diagonal element, and dividing it by the sum of the corresponding row.
| (14) |
Furthermore, we estimate the net connectedness from variable i to all other variables j by subtracting the directional connectedness received () from the directional connectedness transmitted (), as shown in Equation (15). This net connectedness value represents the difference between the two directional connectedness measures, and provides insights into the direction and magnitude of the net flow of information or shocks between variables.
| (15) |
The spillover effects among sectoral returns are examined for the full period, the GFC, the COVID-19 pandemic, and the Russia-Ukraine war. The findings are presented in Table 3 for the full period, and Table 4, Table 5, Table 6 for the respective crisis periods.
Table 3.
Summary of return spillovers in all sectors during the full period. Notes: TCI = total return connectedness index in (12); FROM = in (13), total return connectedness received by the i-th sector from all other sectors; TO = in (14), total return connectedness transmitted by the i-th sectors to all other sectors; TO (own) = total return connectedness generated by the i-th sector, including the contribution of its own; NET = in (15), net return connectedness.
| CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI | FROM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 21.04 | 8.74 | 6.88 | 5 | 9.16 | 9.28 | 9.98 | 11.75 | 8.2 | 5.84 | 4.15 | 78.96 |
| CD | 8.6 | 20.03 | 7.21 | 4.81 | 9.59 | 8.58 | 11.28 | 10.03 | 9.49 | 6.56 | 3.81 | 79.97 |
| CST | 7.43 | 7.87 | 22.64 | 4.16 | 8.61 | 8.83 | 9.61 | 7.43 | 8.01 | 7.57 | 7.85 | 77.36 |
| ENG | 6.29 | 6.19 | 4.68 | 31.1 | 8.05 | 6.35 | 9.54 | 6.8 | 11.24 | 4.45 | 5.31 | 68.9 |
| FIN | 8.32 | 8.89 | 7.33 | 5.7 | 18.37 | 8.95 | 12.14 | 9.66 | 10.04 | 6.25 | 4.33 | 81.63 |
| HC | 8.93 | 8.35 | 7.86 | 4.88 | 9.38 | 19.58 | 10.5 | 10.82 | 8.82 | 6.31 | 4.57 | 80.42 |
| IND | 8.34 | 9.5 | 7.38 | 6.15 | 11.07 | 9.07 | 16.43 | 10.23 | 11.65 | 5.87 | 4.31 | 83.57 |
| IT | 10.69 | 9.38 | 6.39 | 5.08 | 9.77 | 10.35 | 11.36 | 18.44 | 9.17 | 5.87 | 3.5 | 81.56 |
| MAT | 7.66 | 8.83 | 6.79 | 7.58 | 10.09 | 8.36 | 12.94 | 9.17 | 18.49 | 5.81 | 4.27 | 81.51 |
| RE | 6.85 | 7.72 | 8.45 | 4.12 | 7.88 | 7.67 | 8.1 | 7.33 | 7.39 | 25.37 | 9.1 | 74.63 |
| UTI | 5.6 | 5.16 | 10.7 | 5.18 | 6.36 | 6.45 | 6.92 | 5.03 | 6.28 | 11.03 | 31.3 | 68.7 |
| TO | 78.72 | 80.64 | 73.68 | 52.65 | 89.97 | 83.9 | 102.37 | 88.25 | 90.29 | 65.55 | 51.2 | 857.22 |
| TO(own) | 99.75 | 100.66 | 96.32 | 83.76 | 108.33 | 103.48 | 118.8 | 106.69 | 108.78 | 90.92 | 82.5 | TCI |
| NET | -0.25 | 0.66 | -3.68 | -16.24 | 8.33 | 3.48 | 18.8 | 6.69 | 8.78 | -9.08 | -17.5 | 77.93 |
Table 4.
Summary of return spillovers in all sectors during the GFC period.
| CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI | FROM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 14.68 | 7.89 | 8.5 | 5.77 | 9.13 | 9.22 | 11.06 | 11.07 | 8.01 | 8.18 | 6.49 | 85.32 |
| CD | 8.46 | 15.9 | 8.42 | 4.46 | 10.67 | 8.19 | 10.68 | 9.32 | 7.82 | 10.97 | 5.13 | 84.1 |
| CST | 9.04 | 8.32 | 15.96 | 5.62 | 9.01 | 10.07 | 10.23 | 9.08 | 7.36 | 7.79 | 7.52 | 84.04 |
| ENG | 6.85 | 5 | 6.26 | 25.65 | 5.67 | 6.58 | 8.6 | 7.67 | 14.47 | 4.81 | 8.44 | 74.35 |
| FIN | 9.27 | 10.02 | 8.5 | 4.85 | 14.76 | 8.73 | 10.57 | 9.48 | 7.48 | 10.58 | 5.76 | 85.24 |
| HC | 9.5 | 7.9 | 9.71 | 5.84 | 8.87 | 15.24 | 10.36 | 10.09 | 7.91 | 7.51 | 7.06 | 84.76 |
| IND | 9.88 | 8.86 | 8.56 | 6.2 | 9.35 | 8.98 | 13.05 | 10.36 | 9.64 | 8.63 | 6.5 | 86.95 |
| IT | 10.71 | 8.36 | 8.1 | 6.21 | 9.03 | 9.48 | 11.23 | 14.2 | 8.5 | 8.54 | 5.63 | 85.8 |
| MAT | 8.48 | 7.56 | 7.06 | 10.13 | 7.61 | 7.84 | 11.47 | 9.13 | 16.45 | 7.38 | 6.9 | 83.55 |
| RE | 8.82 | 10.88 | 7.82 | 4.44 | 11.28 | 7.86 | 10.36 | 9.48 | 7.63 | 15.7 | 5.73 | 84.3 |
| UTI | 8.2 | 5.96 | 9.25 | 7.73 | 7.38 | 9.01 | 9.32 | 7.62 | 8.51 | 6.61 | 20.41 | 79.59 |
| TO | 89.21 | 80.75 | 82.18 | 61.25 | 88 | 85.95 | 103.87 | 93.29 | 87.33 | 81.01 | 65.15 | 917.99 |
| TO(own) | 103.89 | 96.65 | 98.14 | 86.9 | 102.76 | 101.19 | 116.93 | 107.49 | 103.78 | 96.71 | 85.56 | TCI |
| NET | 3.89 | -3.35 | -1.86 | -13.1 | 2.76 | 1.19 | 16.93 | 7.49 | 3.78 | -3.29 | -14.44 | 83.45 |
Table 5.
Summary of return spillovers in all sectors during the COVID-19 pandemic period.
| CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI | FROM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 25.7 | 9.56 | 7.55 | 2.96 | 8.31 | 9.23 | 7.11 | 14.09 | 6.26 | 6.09 | 3.15 | 74.3 |
| CD | 7.64 | 19.97 | 6.72 | 5.14 | 10.91 | 7.31 | 12.03 | 10.37 | 9.96 | 6.34 | 3.62 | 80.03 |
| CST | 6.74 | 7.59 | 23.33 | 2.8 | 8.31 | 7.53 | 9.35 | 6.4 | 8.09 | 9.35 | 10.51 | 76.67 |
| ENG | 3.55 | 7.57 | 3.62 | 33.97 | 13.71 | 3.12 | 12.2 | 4.3 | 11.55 | 3.67 | 2.74 | 66.03 |
| FIN | 6.15 | 9.89 | 6.81 | 7.9 | 17.91 | 6.79 | 13.61 | 8.31 | 12.27 | 5.85 | 4.51 | 82.09 |
| HC | 8.35 | 8.23 | 7.81 | 2.48 | 8.3 | 23.97 | 8.18 | 13.1 | 6.97 | 7.53 | 5.07 | 76.03 |
| IND | 5.25 | 10.77 | 7.42 | 7.09 | 13.39 | 6.59 | 17.56 | 7.76 | 13.55 | 5.97 | 4.64 | 82.44 |
| IT | 11.7 | 10.83 | 6.13 | 3.31 | 9.57 | 11.87 | 9.02 | 21.08 | 7.65 | 6.18 | 2.65 | 78.92 |
| MAT | 5.01 | 9.76 | 7.02 | 7.36 | 13.33 | 6.3 | 14.99 | 7.17 | 19.54 | 5.16 | 4.35 | 80.46 |
| RE | 6 | 7.68 | 10.34 | 2.91 | 7.45 | 7.97 | 7.79 | 7.08 | 6.16 | 26.13 | 10.49 | 73.87 |
| UTI | 3.71 | 5.08 | 14.01 | 2.64 | 6.88 | 6.3 | 7.25 | 3.37 | 6.23 | 12.63 | 31.91 | 68.09 |
| TO | 64.09 | 86.97 | 77.43 | 44.6 | 100.16 | 73.01 | 101.52 | 81.95 | 88.7 | 68.77 | 51.73 | 838.91 |
| TO(own) | 89.8 | 106.94 | 100.75 | 78.57 | 118.07 | 96.98 | 119.08 | 103.03 | 108.25 | 94.9 | 83.63 | TCI |
| NET | -10.2 | 6.94 | 0.75 | -21.43 | 18.07 | -3.02 | 19.08 | 3.03 | 8.25 | -5.1 | -16.37 | 76.26 |
Table 6.
Summary of return spillovers in all sectors during the RU war period.
| CS | CD | CST | ENG | FIN | HC | IND | IT | MAT | RE | UTI | FROM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CS | 20.02 | 12.4 | 3.75 | 1.2 | 10.91 | 9.85 | 10.53 | 14.61 | 9.56 | 5.86 | 1.3 | 79.98 |
| CD | 10.23 | 16.29 | 6.21 | 1.42 | 11.53 | 9.87 | 12.53 | 12.8 | 11.43 | 6.1 | 1.6 | 83.71 |
| CST | 4.37 | 8.35 | 21.32 | 1.28 | 9.7 | 10.25 | 10.6 | 6.17 | 9.83 | 9.13 | 9.01 | 78.68 |
| ENG | 3.78 | 4.63 | 2.38 | 53.19 | 4.91 | 5.23 | 6.16 | 5.63 | 5.83 | 3.24 | 5.01 | 46.81 |
| FIN | 8.87 | 11.33 | 7.01 | 1.66 | 15.61 | 10.19 | 11.94 | 11.3 | 12.62 | 6.69 | 2.79 | 84.39 |
| HC | 8.38 | 9.96 | 7.7 | 1.87 | 10.61 | 16.21 | 10.85 | 11.54 | 10.21 | 9.33 | 3.35 | 83.79 |
| IND | 8.33 | 11.93 | 7.26 | 1.97 | 11.47 | 10.09 | 15.03 | 11.23 | 11.87 | 7.29 | 3.53 | 84.97 |
| IT | 11.87 | 12.61 | 4.51 | 1.67 | 11.36 | 11.27 | 11.62 | 16.07 | 10.46 | 7.07 | 1.49 | 83.93 |
| MAT | 7.97 | 11.46 | 7 | 2.27 | 12.62 | 9.88 | 12.53 | 10.79 | 15.74 | 6.58 | 3.15 | 84.26 |
| RE | 6.46 | 7.81 | 8.43 | 1.78 | 8.58 | 11.52 | 9.82 | 9.04 | 8.48 | 19.42 | 8.66 | 80.58 |
| UTI | 2.99 | 3.54 | 13.59 | 3.26 | 5.58 | 6.55 | 7.62 | 3.2 | 6.74 | 14.23 | 32.71 | 67.29 |
| TO | 73.24 | 94.03 | 67.83 | 18.37 | 97.26 | 94.71 | 104.21 | 96.3 | 97.03 | 75.52 | 39.89 | 858.4 |
| TO(own) | 93.26 | 110.32 | 89.15 | 71.56 | 112.87 | 110.92 | 119.23 | 112.37 | 112.77 | 94.94 | 72.6 | TCI |
| NET | -6.74 | 10.32 | -10.85 | -28.44 | 12.87 | 10.92 | 19.23 | 12.37 | 12.77 | -5.06 | -27.4 | 78.04 |
The analysis reveals that the industrial sector consistently exhibits the highest level of connectedness to the return network across all periods, with a value of 102.37% for the full sample. This result aligns with the dominance of the industrial sector in the sectoral return network observed throughout the study period.
During the GFC, the industrial sector demonstrated the highest connectedness with the returns network, with a value of 103.87%. This further supports the finding that the industrial sector was the most influential within the sectoral return network during the GFC. In the context of the COVID-19 pandemic, the industrial and finance sectors display substantial connectivity with the return network, with values of 101.52% and 100.16%, respectively. These results are consistent with the outcomes of static network analysis conducted during the COVID-19 pandemic (see Table 5). Similarly, during the Russia-Ukraine war period, the industries, financial, and materials sectors exhibited significant connectedness with the return network, with values of 104.21%, 97.26%, and 97.03%, respectively. These findings align with the results obtained from the static analysis of the RU-war.
Overall, the industrial sector provides high connectedness to the return network during the full and crisis periods, corroborating the results obtained from both static and dynamic network analyses. Additionally, throughout the entire period, and during the crisis period, the energy and utilities sectors exhibited low connectedness to the return network. This further supports the findings presented in the previous section, which indicate a weaker relationship between these sectors and returns from other sectors.
Additionally, the dynamic TCI is illustrated in Fig. 8. By comparing the inverse integration degree depicted in Fig. 7, it becomes evident that the timing of the increase in the inverse integration degree and the rise in TCI align during crisis periods (the GFC, the COVID-19 pandemic, and the RU-war).
Figure 8.
Dynamic total connectedness index.
6. Discuss and concluding remarks
In this study, we explore the topology of sectoral returns in the US stock market using a minimum spanning tree. In particular, we consider four time periods in detail: the full, GFC, COVID-19, and RU-war periods. By comparing the static results from the four periods, we discovered differences among the periods in terms of the network. Furthermore, using rolling window analysis, we investigated the time-varying structure of the MST. By adopting the TVP-VAR based connectedness framework, we ensure a more robust analysis of the sectoral return linkages in our study. Our main findings are summarized as follows:
First, the structure of MST differs for each period, with clearly differing crisis period structures. During the GFC, clustering was centered on the industrials sector. However, during the COVID-19 pandemic, there were clusters centered on financial and IT sectors, as well as industrials sectors. In addition, during the RU-war period, clustering centered on materials was found, except in the industrials sector. This different structure of MSTs may have caused the different characteristics of each crisis period.
Second, according to both static and rolling window analyses, the industrials sector is of primary importance in the US stock market. The sector includes a wide range of airlines, construction, engineering, and railroad companies. In light of the characteristics of these industrials sectors, they may play the most important role in the sectoral return network, in terms of linkage between other sectors.
Third, the utilities sector has the lowest overall centrality measures. This implies a significantly low importance of utilities in the sectoral return network, further indicating the lack of relationships between the utilities sector and other industries, and the return of utilities is independent. One of the reasons being, the utilities sector has been considered defensive and low-risk due to stable returns of utility companies [38], [73], [74].
Our findings have several important implications for future studies. First, the observed changes in the structure of the MST during the crisis indicate significant transformations in the organization and relationships of the network of sectoral returns under different economic circumstances. This aligns with previous research that demonstrates the dynamic nature of the network's topological properties over time [26], [28], [29].
Specifically, the centrality of the IT and financial sectors during the COVID-19 pandemic period can be attributed to two key factors. First, the boom in the IT industry is the result of an increased reliance on non-face-to-face activities and digital services due to the pandemic [75]. Second, the centrality of the financial sector is closely linked to US financial policies implemented to mitigate the economic downturn caused by the pandemic [76], [77].
Furthermore, the clustering observed around the materials sector during the period of the Russia-Ukraine war suggests that global supply chain disruptions in the raw material market have had widespread effects on the overall US economy ([78], [79]).
Second, our results indicate the important role played by the industrial sector in the US stock market network, which is consistent with the findings of [80]. Moreover, our results suggest that the industrial sector has transmitted numerous shocks to other sectors within a spillover framework [81].
Third, the utilities sector exhibits the lowest overall centrality measures within the sectoral return network. Additionally, the lack of strong relationships between the utility sector and other industries within the network indicates the relatively isolated nature of utility returns. Therefore, investors and analysts should recognize the potential diversification benefits of utility stocks, particularly during periods of high market volatility or economic uncertainty.
Our empirical findings help market participants better understand the interrelationships among industries in the US stock market. Hence, these findings can be used for portfolio management, through the process of building an optimal diversification strategy.
For instance, different sectors play significant roles in driving market dynamics and interconnections during crises. Understanding these structural changes can help investors and policymakers anticipate sector-specific vulnerabilities, and modify their strategies accordingly. Furthermore, the industrial sector has served as a key connector, influencing the overall network structure. Therefore, recognizing the influential role of the industrial sector can guide investment decisions and risk management strategies, because changes in this sector may have cascading effects on other sectors and the entire stock market. Similarly, the low overall centrality measures of the utilities sector imply that investors seeking diversified exposure should consider its relatively isolated nature.
Funding statement
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2021R1F1A1046138).
CRediT authorship contribution statement
Sun-Yong Choi: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Global Industry Classification Standard.
The total number of shares (N) changes, as the incorporated stock changes in the sector.
We collect the data from finance.yahoo.com.
“How a Russian invasion of Ukraine, the ‘breadbasket of Europe,’ could hit supply chains”, CNBC, https://www.cnbc.com/2022/02/23/impact-of-russia-ukraine-on-supply-chains-food-metals-commodities.html.
In order to reflect the RU-war period, one-month was assumed from February 1 to 21, and February 22 to March 31, 2022, respectively.
“Confronting the Crisis: Its impact on the ICT industry. https://www.itu.int/osg/csd/emerging_trends/crisis/fc01.html.
Data availability
Data will be made available on request.
References
- 1.Booth G.G., Martikainen T., Tse Y. Price and volatility spillovers in Scandinavian stock markets. J. Bank. Finance. 1997;21(6):811–823. [Google Scholar]
- 2.Lin S.X., Tamvakis M.N. Spillover effects in energy futures markets. Energy Econ. 2001;23(1):43–56. [Google Scholar]
- 3.Apergis N., Rezitis A. Agricultural price volatility spillover effects: the case of Greece. Eur. Rev. Agric. Econ. 2003;30(3):389–406. [Google Scholar]
- 4.Baele L. Volatility spillover effects in European equity markets. J. Financ. Quant. Anal. 2005;40(2):373–401. [Google Scholar]
- 5.Chang C.-L., McAleer M., Tansuchat R. Analyzing and forecasting volatility spillovers, asymmetries and hedging in major oil markets. Energy Econ. 2010;32(6):1445–1455. [Google Scholar]
- 6.Du X., Cindy L.Y., Hayes D.J. Speculation and volatility spillover in the crude oil and agricultural commodity markets: a bayesian analysis. Energy Econ. 2011;33(3):497–503. [Google Scholar]
- 7.Musunuru N. Modeling price volatility linkages between corn and wheat: a multivariate garch estimation. Int. Adv. Econ. Res. 2014;20(3):269–280. [Google Scholar]
- 8.Li Y., Giles D.E. Modelling volatility spillover effects between developed stock markets and Asian emerging stock markets. Int. J. Econ. Finance. 2015;20(2):155–177. [Google Scholar]
- 9.Shahzad S.J.H., Ferrer R., Ballester L., Umar Z. Risk transmission between Islamic and conventional stock markets: a return and volatility spillover analysis. Int. Rev. Financ. Anal. 2017;52:9–26. [Google Scholar]
- 10.Choi S.-Y., Hong C. Relationship between uncertainty in the oil and stock markets before and after the shale gas revolution: evidence from the ovx, vix, and vkospi volatility indices. PLoS ONE. 2020;15(5) doi: 10.1371/journal.pone.0232508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hassan S.A., Malik F. Multivariate garch modeling of sector volatility transmission. Q. Rev. Econ. Finance. 2007;47(3):470–480. [Google Scholar]
- 12.Buccheri G., Marmi S., Mantegna R.N. Evolution of correlation structure of industrial indices of us equity markets. Phys. Rev. E. 2013;88(1) doi: 10.1103/PhysRevE.88.012806. [DOI] [PubMed] [Google Scholar]
- 13.Yang R., Li X., Zhang T. Analysis of linkage effects among industry sectors in China's stock market before and after the financial crisis. Phys. A, Stat. Mech. Appl. 2014;411:12–20. [Google Scholar]
- 14.Collet J., Ielpo F. Sector spillovers in credit markets. J. Bank. Finance. 2018;94:267–278. [Google Scholar]
- 15.Choi S.-Y. Dynamic volatility spillovers between industries in the us stock market: evidence from the Covid-19 pandemic and black monday. N. Am. J. Econ. Finance. 2022;59 [Google Scholar]
- 16.Umar Z., Polat O., Choi S.-Y., Teplova T. The impact of the Russia-Ukraine conflict on the connectedness of financial markets. Finance Res. Lett. 2022 [Google Scholar]
- 17.Umar Z., Bossman A., Choi S.-Y., Teplova T. Does geopolitical risk matter for global asset returns? Evidence from quantile-on-quantile regression. Finance Res. Lett. 2022 [Google Scholar]
- 18.Qureshi A., Rizwan M.S., Ahmad G., Ashraf D. Russia-Ukraine war and systemic risk: who is taking the heat? Finance Res. Lett. 2022 [Google Scholar]
- 19.Yousaf I., Patel R., Yarovaya L. The reaction of g20+ stock markets to the Russia–Ukraine conflict “black-swan” event: evidence from event study approach. J. Behav. Exp. Finance. 2022;35 [Google Scholar]
- 20.Singh A., Patel R., Singh H. Recalibration of priorities: investor preference and Russia-Ukraine conflict. Finance Res. Lett. 2022;50 [Google Scholar]
- 21.Miccichè S., Bonanno G., Lillo F., Mantegna R.N. Degree stability of a minimum spanning tree of price return and volatility. Phys. A, Stat. Mech. Appl. 2003;324(1–2):66–73. [Google Scholar]
- 22.Bonanno G., Caldarelli G., Lillo F., Micciche S., Vandewalle N., Mantegna R.N. Networks of equities in financial markets. Eur. Phys. J. B. 2004;38(2):363–371. [Google Scholar]
- 23.Coelho R., Hutzler S., Repetowicz P., Richmond P. Sector analysis for a ftse portfolio of stocks. Phys. A, Stat. Mech. Appl. 2007;373:615–626. [Google Scholar]
- 24.Zhuang R., Hu B., Ye Z. 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence) IEEE; 2008. Minimal spanning tree for Shanghai-Shenzhen 300 stock index; pp. 1417–1424. [Google Scholar]
- 25.Birch J., Pantelous A.A., Soramäki K. Analysis of correlation based networks representing dax 30 stock price returns. Comput. Econ. 2016;47(4):501–525. [Google Scholar]
- 26.Gilmore C.G., Lucey B.M., Boscia M.W. Comovements in government bond markets: a minimum spanning tree analysis. Phys. A, Stat. Mech. Appl. 2010;389(21):4875–4886. [Google Scholar]
- 27.Ji Q., Fan Y. Evolution of the world crude oil market integration: a graph theory analysis. Energy Econ. 2016;53:90–100. [Google Scholar]
- 28.Fang M., Taylor S., Uddin A. The network structure of overnight index swap rates. Finance Res. Lett. 2021 [Google Scholar]
- 29.Shahzad S.J.H., Naifar N. Dependence dynamics of Islamic and conventional equity sectors: what do we learn from the decoupling hypothesis and Covid-19 pandemic? N. Am. J. Econ. Finance. 2022;59 [Google Scholar]
- 30.Litimi H., BenSaïda A., Bouraoui O. Herding and excessive risk in the American stock market: a sectoral analysis. Res. Int. Bus. Finance. 2016;38:6–21. [Google Scholar]
- 31.Zheng D., Li H., Chiang T.C. Herding within industries: evidence from Asian stock markets. Int. Rev. Econ. Finance. 2017;51:487–509. [Google Scholar]
- 32.BenMabrouk H., Litimi H. Cross herding between American industries and the oil market. N. Am. J. Econ. Finance. 2018;45:196–205. [Google Scholar]
- 33.Ukpong I., Tan H., Yarovaya L. Determinants of industry herding in the us stock market. Finance Res. Lett. 2021;43 [Google Scholar]
- 34.Wang Z., Kutan A.M., Yang J. Information flows within and across sectors in Chinese stock markets. Q. Rev. Econ. Finance. 2005;45(4–5):767–780. [Google Scholar]
- 35.Aromi D., Clements A. Spillovers between the oil sector and the s&p500: the impact of information flow about crude oil. Energy Econ. 2019;81:187–196. [Google Scholar]
- 36.Yue P., Cai Q., Yan W., Zhou W.-X. Information flow networks of Chinese stock market sectors. IEEE Access. 2020;8:13066–13077. [Google Scholar]
- 37.Kinateder H., Campbell R., Choudhury T. Safe haven in gfc versus Covid-19: 100 turbulent days in the financial markets. Finance Res. Lett. 2021;43 [Google Scholar]
- 38.Choi S.-Y. Analysis of stock market efficiency during crisis periods in the us stock market: differences between the global financial crisis and Covid-19 pandemic. Phys. A, Stat. Mech. Appl. 2021;574 [Google Scholar]
- 39.Choi S.-Y. Volatility spillovers among northeast Asia and the us: evidence from the global financial crisis and the Covid-19 pandemic. Econ. Anal. Policy. 2022;73:179–193. [Google Scholar]
- 40.Gunay S. Comparing Covid-19 with the gfc: a shockwave analysis of currency markets. Res. Int. Bus. Finance. 2021;56 doi: 10.1016/j.ribaf.2020.101377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gunay S., Can G. The source of financial contagion and spillovers: an evaluation of the Covid-19 pandemic and the global financial crisis. PLoS ONE. 2022;17(1) doi: 10.1371/journal.pone.0261835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rehman M.U., Ahmed N., Shahzad S.J.H., Vo X.V. Dependence dynamics of stock markets during Covid-19. Emerg. Mark. Rev. 2022 [Google Scholar]
- 43.Umar Z., Yousaf I., Aharon D.Y. The relationship between yield curve components and equity sectorial indices: evidence from China. Pac.-Basin Finance J. 2021;68 [Google Scholar]
- 44.Mensi W., Yousaf I., Vo X.V., Kang S.H. Asymmetric spillover and network connectedness between gold, brent oil and eu subsector markets. J. Int. Financ. Mark. Inst. Money. 2022;76 [Google Scholar]
- 45.Yousaf I., Qureshi S., Qureshi F., Gubareva M. Connectedness of covid vaccination with economic policy uncertainty, oil, bonds, and sectoral equity markets: evidence from the us. Ann. Oper. Res. 2023:1–27. doi: 10.1007/s10479-023-05267-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yousaf I., Jareño F., Tolentino M. Connectedness between defi assets and equity markets during Covid-19: a sector analysis. Technol. Forecast. Soc. Change. 2023;187 doi: 10.1016/j.techfore.2022.122174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yousaf I., Goodell J.W. Responses of us equity market sectors to the silicon valley bank implosion. Finance Res. Lett. 2023 [Google Scholar]
- 48.Lau C.K., Soliman A.M., Albasu J., Gozgor G. Dependence structures among geopolitical risks, energy prices, and carbon emissions prices. Resour. Policy. 2023;83 [Google Scholar]
- 49.Gozgor G., Khalfaoui R., Yarovaya L. Global supply chain pressure and commodity markets: evidence from multiple wavelet and quantile connectedness analyses. Finance Res. Lett. 2023;54 [Google Scholar]
- 50.Choi S.-Y. The influence of shock signals on the change in volatility term structure. Econ. Lett. 2019;183 [Google Scholar]
- 51.Sensoy A., Tabak B.M. Dynamic spanning trees in stock market networks: the case of Asia-Pacific. Phys. A, Stat. Mech. Appl. 2014;414:387–402. [Google Scholar]
- 52.Hu S., Gu Z., Wang Y., Zhang X. An analysis of the clustering effect of a jump risk complex network in the Chinese stock market. Phys. A, Stat. Mech. Appl. 2019;523:622–630. [Google Scholar]
- 53.Moghadam H.E., Mohammadi T., Kashani M.F., Shakeri A. Complex networks analysis in Iran stock market: the application of centrality. Phys. A, Stat. Mech. Appl. 2019;531 [Google Scholar]
- 54.Wang D., Huang W.-Q. Centrality-based measures of financial institutions' systemic importance: a tail dependence network view. Phys. A, Stat. Mech. Appl. 2021;562 [Google Scholar]
- 55.Mantegna R.N. Hierarchical structure in financial markets. Eur. Phys. J. B, Condens. Matter Phys. 1999;11(1):193–197. [Google Scholar]
- 56.Kruskal J.B. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 1956;7(1):48–50. [Google Scholar]
- 57.Ji Q., Bouri E., Roubaud D. Dynamic network of implied volatility transmission among us equities, strategic commodities, and brics equities. Int. Rev. Financ. Anal. 2018;57:1–12. [Google Scholar]
- 58.Onnela J.-P., Chakraborti A., Kaski K., Kertesz J., Kanto A. Dynamics of market correlations: taxonomy and portfolio analysis. Phys. Rev. E. 2003;68(5) doi: 10.1103/PhysRevE.68.056110. [DOI] [PubMed] [Google Scholar]
- 59.Wu F., Zhang D., Zhang Z. Connectedness and risk spillovers in China's stock market: a sectoral analysis. Econ. Syst. 2019;43(3–4) [Google Scholar]
- 60.Dimitrios K., Vasileios O. A network analysis of the Greek stock market. Proc. Econ. Finance. 2015;33:340–349. [Google Scholar]
- 61.Wang Z., Gao X., An H., Tang R., Sun Q. Identifying influential energy stocks based on spillover network. Int. Rev. Financ. Anal. 2020;68 [Google Scholar]
- 62.Demirer R., Leggio K.B., Lien D. Herding and flash events: evidence from the 2010 flash crash. Finance Res. Lett. 2019;31 [Google Scholar]
- 63.Antonakakis N., Chatziantoniou I., Gabauer D. Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. J. Financ. Risk Manag. 2020;13(4):84. [Google Scholar]
- 64.Diebold F.X., Yılmaz K. On the network topology of variance decompositions: measuring the connectedness of financial firms. J. Econom. 2014;182(1):119–134. [Google Scholar]
- 65.Gabauer D., Gupta R. On the transmission mechanism of country-specific and international economic uncertainty spillovers: evidence from a tvp-var connectedness decomposition approach. Econ. Lett. 2018;171:63–71. [Google Scholar]
- 66.Aharon D.Y., Demir E. Nfts and asset class spillovers: lessons from the period around the Covid-19 pandemic. Finance Res. Lett. 2022;47 doi: 10.1016/j.frl.2021.102515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wang Y., Bouri E., Fareed Z., Dai Y. Geopolitical risk and the systemic risk in the commodity markets under the war in Ukraine. Finance Res. Lett. 2022;49 [Google Scholar]
- 68.Raza S.A., Shah N., Guesmi K., Msolli B. How does Covid-19 influence dynamic spillover connectedness between cryptocurrencies? Evidence from non-parametric causality-in-quantiles techniques. Finance Res. Lett. 2022;47 doi: 10.1016/j.frl.2021.102569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Younis I., Shah W.U., Yousaf I. Static and dynamic linkages between oil, gold and global equity markets in various crisis episodes: evidence from the wavelet tvp-var. Resour. Policy. 2023;80 [Google Scholar]
- 70.Yousaf I., Riaz Y., Goodell J.W. Energy cryptocurrencies: assessing connectedness with other asset classes. Finance Res. Lett. 2023;52 [Google Scholar]
- 71.Patel R., Kumar S., Bouri E., Iqbal N. Spillovers between green and dirty cryptocurrencies and socially responsible investments around the war in Ukraine. Int. Rev. Econ. Finance. 2023;87:143–162. [Google Scholar]
- 72.Koop G., Pesaran M.H., Potter S.M. Impulse response analysis in nonlinear multivariate models. J. Econom. 1996;74(1):119–147. [Google Scholar]
- 73.Grout P.A., Zalewska A. Stock market risk in the financial crisis. Int. Rev. Financ. Anal. 2016;46:326–345. [Google Scholar]
- 74.Biancone P.P., Radwan M. Sharia-compliant financing for public utility infrastructure. Util. Policy. 2018;52:88–94. [Google Scholar]
- 75.Ben-Ahmed K., Ayadi I., Hamad S.B. Covid-19 impact on digital companies' stock return: a dynamic data analysis. Finance Res. Lett. 2022;46 doi: 10.1016/j.frl.2021.102340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Bhar R., Malliaris A.G. Modeling us monetary policy during the global financial crisis and lessons for Covid-19. J. Policy Model. 2021;43(1):15–33. doi: 10.1016/j.jpolmod.2020.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Feldkircher M., Huber F., Pfarrhofer M. Measuring the effectiveness of us monetary policy during the Covid-19 recession. Scott. J. Polit. Econ. 2021;68(3):287–297. doi: 10.1111/sjpe.12275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Orhan E. The effects of the Russia-Ukraine war on global trade. J. Int. Trade, Logist. Law. 2022;8(1):141–146. [Google Scholar]
- 79.Cui L., Yue S., Nghiem X.-H., Duan M. Exploring the risk and economic vulnerability of global energy supply chain interruption in the context of Russo-Ukrainian war. Resour. Policy. 2023;81 [Google Scholar]
- 80.Millington T., Niranjan M. Construction of minimum spanning trees from financial returns using rank correlation. Phys. A, Stat. Mech. Appl. 2021;566 [Google Scholar]
- 81.Umar Z., Yousaf I., Gubareva M., Vo X.V. Spillover and risk transmission between the term structure of the us interest rates and Islamic equities. Pac.-Basin Finance J. 2022;72 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.