Abstract
Wind energy has gained prominence over the past few decades because of its environment-friendly nature and abundant availability. However, the exploration of wind energy requires adequate knowledge of the wind distribution parameters before installing the wind turbine. This study assessed the potential of harvesting wind energy at two Gambian locations by fitting the best model comparing Weibull and Raleigh Distributions. A novel approach combining the energy pattern factor and standard deviation methods in estimating the distribution parameters of the characteristics of wind in the Gambian locations of Yundum and Basse has been presented and statistically analyzed using the Weibull and Raleigh distribution functions. The results showed that the shape parameters ranged from 4.88 to 6.98 and 3.87–6.15 for Yundum and Basse locations, the Weibull scale parameter ranged from 6.60 to 10.58 m/s and 4.51–8.69 m/s for Yundum and Basse while the calculated wind power densities ranged from 139 to 718 W/m2 and 46–390 W/m2 for Yundum and Basse respectively. These results clearly show a high potential for generating electricity with wind in the study areas. The statistical analysis revealed that the Weibull models perform better at Yundum in terms of = 0.33, and 1.57 while the Raleigh distribution gives a better fit for Basse in terms of and only making it more suitable for calculating the wind power potentials.
Keywords: Wind energy, Raleigh distribution, Weibull distribution, Statistical tools, The Gambian locations
1. Introduction
Fossil fuels are the most widely used in many countries around the world today. However, these fossil resources used for meeting the energy needs of most of these countries shall surely run out sooner or later; hence, they are non-renewable. Moreover, their harmful nature to the environment and human health conditions has called for research in search of renewable energy and environment-friendly sources worldwide [1]. The use of wind energy as one of the oldest renewable energy sources dates back to BC 2800 [2]. Wind energy has been consistently used in North America and Europe for over six decades. On the other, African countries have utilized less than 1% of the world's total wind power capacity, with a few installations found mainly in Egypt and South Africa [3,4].
Wind energy resources are got from the motion of particles of air across the surface of the Earth. The differences in air pressure between any defined two regions produce wind. Chiras [5] reported that uneven heating of the Earth's surface is responsible for these pressure differences. Hence, a conscious exploration of the wind system over a geographical location helps determine the accruable energy that can be harnessed from the wind to energy systems. A description of how the wind is created is essential to examine this. Air particles are being acted upon by several atmospheric forces such as the pressure gradient force, the Coriolis force, gravitational force, centrifugal force, and friction, which set it into motion and produce wind [6,7].
Water and electricity, which are the much-needed vital essentials of life, can be provided by Wind energy resources using suitable mechanical power and electricity generation technologies. However, unlike the sun, which is global in nature, winds are more peculiar to specific areas and locations rather than being distributed evenly and widespread like The Gambia and many other countries of the world [8].
The operation of wind energy systems largely depends on the wind shaft position, the size of the power generating system, and the wind regime [9]. Despite the numerous advantages of using wind energy and its high potential globally, it has been reported that wind only accounts for 1.4% of the total world electric power [7,10]. Implementing wind power over large scales can be affected by two main difficulties which are: the identification of suitable decent wind locations and potential, and the apparent nature of the intermittency of winds, especially in developing countries of the world like The Gambia. Worldwide, scientific research in this area is in top gear to surmount these challenges.
Mentis et al. [11] assessed wind energy potential for entire African countries using Geographic Information System (GIS) based approach for handling existing wind data and their results showed that The Gambia has a technical wind power potential of 43.3 TWh/year for both grided and non grided restrictions. Since this potential is taken based on grid criteria, regions outside the major cities will certainly not be accounted for. Flores [8] proposed a master plan for renewable energy generation in The Gambia, he reported that the mean wind speed are moderate for the Gambia, with wind speed ranging from 2.8 to 4.2 m/s across all stations studied and vary significantly with location and regions. However, the overall variations were not explicitly accounted for. Furthermore, he suggested that implementing wind energy projects in The Gambia could be economical only in coastal areas like Kanuma and Jambanjelly because of low wind speed. However, linking multiple wind farms together can counter the difficulty he claimed by eliminating low wind speed events and reducing the intermittency of wind power [12]. This approach reduces the spatial and temporal dependence of wind speed substantially and is more beneficial for larger wind power installation areas.
In The Gambia, power is inaccessible, unreliable, and unaffordable for the citizenry and even the little is dominance of petroleum resources. Diversification of power supply patterns and mitigation of environmental nuisance requires the determination of the wind energy potential for use as an alternative source of power for a particular location. Wind speed Frequency distribution can be analyzed in terms of lognormal, Gamma, Weibull, and Rayleigh distributions. Recent studies have shown that the Weibull distribution model parameters give the best-fit wind distribution for most regions of the world [1,13,14].
Most researchers have deployed different methods to calculate the Weibull and Raleigh distribution parameters. The majority suggested that the energy pattern factor and standard deviation methods are better. Hence, this work technically analyzed the wind energy potential for siting of wind farms in two Gambian locations by fitting the best model comparing Weibull and Raleigh Distribution. To achieve this, a novel approach combining the energy pattern factor and standard deviation methods in estimating the distribution parameters of the Weibull and Raleigh distribution model parameters, using thirty-two (1990–2021) years’ data of wind speed measured by the Yundum and Basse Meteorological stations was adopted.
2. Materials and methods
2.1. The study area and data source description
The Gambia is located on the coast of West Africa. It is known to be a relatively small country with a total land area of only 11,300 km2. Surrounded by the neighboring Senegal, it is dominated mainly by the Gambia River shores. The Population of the inhabitants was counted to be 1,882,450 according to the 2013 Population and Housing Census report [15].
The Gambia relies entirely on petroleum to meet its energy demand. Presently, its Energy Ministry takes on the entire energy sector's responsibility, which comprises two divisions, i.e., the Energy Division and the Petroleum Commission. Energy Policy formulation and supervision of the Gambia Renewable Energy Centre are carried out by the Energy Division; the Energy Ministry also monitors the duties of the National Water and Electricity Company (NAWEC), an establishment responsible for electricity generation, transmission, and distribution.
Thirty-two years of data on wind speed measured by the Yundum and Basse meteorological stations were used for this study. In these stations, anemometers are installed, which can measure wind speed hourly, monthly, and even in the long term by inserting a memory card based on the need of the local meteorologist. The study stations are shown in Table 1. Fig. 1 is the Google live wind map of The Gambia showing these locations.
Table 1.
Study stations and location.
| S/N | Site | Location |
Elevation Z (m) |
Duration | |
|---|---|---|---|---|---|
| Latitude | Longitude | ||||
| 1 | Basse | 13 N | 14 W | 18.10 | 1990–2021 |
| 2 | Yundum | 13.21 | 16.39 | 29.00 | 1990–2021 |
Fig. 1.
Google wind map of The Gambia showing the study locations.
2.2. Theoretical calculations of the wind basics and frequency distribution model parameters
Thirty-two years (1990–2021) of data obtained from the Yundum and Basse Meteorological stations were analyzed using Mat Lab and Microsoft Excel computer tools. The data was taken at 31.0 m above sea level in units of knots and then transformed into the wind speed unit of meters per second using equation (1).
| (1) |
where W is the wind speed and ζ is the conversion factor, which in the application is taken to be 0.51444. We also investigated the wind speed variation measured as a function of altitude. This was possible using the power law profile expression presented by Jaramillo and Borja [16] and Ahmed-Shata and Hanitsch [17], which estimates the wind speed at a given height in terms of the wind speed measured at another height as in Equation (2).
| (2) |
where and are the mean wind speed taken at the heights and respectively. While depends on factors like atmospheric stability class and surface roughness of the terrain where the measurement is taken and in practice takes values from 0.05 .
Now, the Weibull and Raleigh distribution functions are the most commonly used in the fitting of wind speed data over a defined area and time. These functions are widely applied in the analysis of wind energy data, identification of wind distribution function parameters, and the economics of wind energy [18,19]. The Weibull Probability density function was used to evaluate the reliability of the wind energy potential and it is given as:
| (3) |
where is the wind speed probability observed, c is the scaling parameter of the Weibull function, and L is a dimensionless shape parameter of the Weibull distribution [20].
The cumulative density function corresponding to the Weibull probability density function is defined as:
| (4) |
Supposing that the dimensionless shape parameter L, of the Weibull function as in Equation (3) takes the value 2.0, then Equation (3) reads:
| (5) |
Equation (5) is the Raleigh distribution function, which is a special case of Equation (3) when the overall magnitude of a vector (wind speed) relates to its directional components [21].
Following the work of Al Buhari [19], the mean and standard deviation of the Weibull probability function requires the mean and standard deviation parameters which can be determined using equations (6), (7)), respectively:
| (6) |
| (7) |
where denotes the gamma function which depends on the shape parameter L or the width of the distribution.
The ratio of the total amount of power available in the wind to the power calculated by the mean cube speed gives the Energy Pattern Factor (EPF). EPF refers to the wind power density and wind speed variation of an area within a given period and it is mathematically represented as shown in equation (8):
| (8) |
Combining the methods of Energy Pattern Factor (EPFM) and Standard Deviation (STDM) presented by Azad et al. [22], Mohammadi and Mostafaeipour [23] and Shaban et al. [24] the shape L, and scale c, parameters of the Weibull distribution were computed using our novel equations (9), (10)):
| (9) |
| (10) |
where are the mean and standard deviation of the wind speed.
Al Buhairi [19] and Shu et al. [25] theoretically reported that the wind power P, at speed W, through an area A, swept by the rotor blades varies as the cube or third power of the wind speed (W) as given in Equation (11):
| (11) |
where is the mean air density usually taken as 1.225 .
A more reliable formula for calculating the air density regarding the height above sea level of a particular location is given as in equation (12):
| (12) |
where z is the elevation of the location against sea level [1,6].
However, wind, unlike other meteorological factors, always shows variability spatially and temporally and so cannot be precisely determined. Therefore, developing wind power at any given location for use by specialists and engineers involved in the wind power industry is better in terms of a probability distribution function, which gives the likely hood of a certain wind speed occurring [26]. Thus, the wind power density can be computed with equation (14), using the Weibull Parameters in equations (4), (8), (9), (10), (13) as:
| (13) |
| (14) |
Celik [21] showed that if we apply equation (5) in the middle term of equation (13), then we get our cumulative Raleigh wind power density function as equation (15):
| (15) |
Equations (14), (15)) and relevant statistical techniques are used to evaluate the wind energy potential of the Yundum and Basse locations of The Gambia.
2.3. Statistical analysis of the Weibull and Raleigh distribution parameters
Statistical tools of Root Mean Square Deviation Correlation determination coefficient , The Nash-Sutcliffe coefficient of efficiency , Mean absolute error , and Chi Square of goodness of fit are applied in determining the performances of the Raleigh and Weibull distributions. These statistical tools can be defined in equations (16), (17), (18), (19), (20), respectively:
| (16) |
where are the i-th measured and predicted values of the Raleigh and Weibull distributions, respectively, and N is the total number of data points. A good model estimates should have close to zero.
| (17) |
value approaching unity shows a best model fit with less scatter or deviations [27].
| (18) |
where are the measured and predicted ith values and is mean of the measured data, respectively. values usually range from and a perfect model has a NSCOE = 1. Negative values of NSCOE signify that the model is less effective in predicting the variation of the mean observations and NSCOE = 0.0 means that the model can no longer estimate the measured data than does the measured mean which is a major limitation [27,28].
| (19) |
As in Equation (19), the least values of shows higher accuracy of a mathematical model [29].
| (20) |
where N is the sum of the frequencies of the observations taken [18,25].
3. Results and discussions
The monthly average wind speed data for the study period of thirty-two years was calculated with the corresponding Weibull and Raleigh Distribution parameters and presented in Table 2, Table 3. Also presented are the monthly mean wind and directions at Yundum and Base in Fig. 2, Fig. 3. While the wind speed probabilities are computed using equations (4), (5)) for the study locations and presented in Table 4 and Fig. 4, Fig. 5, respectively.
Table 2.
Mean Monthly wind speed data and Distribution Parameters of Yundum station for the period 1990–2021.
| Months |
|
Weibull |
|
Raleigh |
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (m/s) | L | C | (W/m2) | L | C | (W/m2) | |||||
| Jan. | 7.76 | 5.80 | 8.37 | 9.45 | 4.62 | 274.99 | 2.00 | 8.76 | 6.66 | 5.69 | 345.52 |
| Feb. | 8.09 | 5.98 | 8.71 | 9.39 | 4.82 | 308.50 | 2.00 | 9.13 | 6.94 | 5.93 | 390.96 |
| Mar. | 7.82 | 5.83 | 8.44 | 9.44 | 4.65 | 280.91 | 2.00 | 8.83 | 6.71 | 5.74 | 353.36 |
| Apr. | 7.79 | 5.82 | 8.41 | 9.44 | 4.63 | 277.94 | 2.00 | 8.80 | 6.68 | 5.71 | 348.64 |
| May | 7.48 | 5.65 | 8.10 | 9.50 | 4.44 | 248.48 | 2.00 | 8.45 | 6.42 | 5.49 | 309.50 |
| Jun. | 9.59 | 6.81 | 10.26 | 9.10 | 5.76 | 493.69 | 2.00 | 10.83 | 8.23 | 7.03 | 652.00 |
| Jul. | 9.14 | 6.56 | 9.80 | 9.09 | 5.48 | 432.24 | 2.00 | 10.32 | 7.84 | 6.70 | 563.64 |
| Aug. | 9.90 | 6.98 | 10.58 | 9.19 | 5.96 | 539.13 | 2.00 | 11.18 | 8.50 | 7.26 | 718.30 |
| Sep. | 9.79 | 6.92 | 10.46 | 9.03 | 5.89 | 522.71 | 2.00 | 11.05 | 8.40 | 7.18 | 693.25 |
| Oct. | 8.13 | 6.00 | 8.76 | 9.05 | 4.85 | 312.73 | 2.00 | 9.18 | 6.97 | 5.96 | 396.05 |
| Nov. | 6.06 | 4.88 | 6.61 | 9.38 | 3.57 | 139.16 | 2.00 | 6.84 | 5.20 | 4.44 | 164.46 |
| Dec. | 7.14 | 5.46 | 7.73 | 9.55 | 4.23 | 218.57 | 2.00 | 8.06 | 6.13 | 5.24 | 269.42 |
Table 3.
Mean Monthly wind speed data and Distribution Parameters of Basse station for the period 1990–2021.
| Months |
|
Weibull |
|
Raleigh |
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (m/s) | L | C | (W/m2) | L | C | (W/m2) | |||||
| Jan. | 5.27 | 4.54 | 5.77 | 9.41 | 3.10 | 94.15 | 2.00 | 5.95 | 4.52 | 3.87 | 108.01 |
| Feb. | 5.54 | 4.69 | 6.05 | 9.40 | 3.26 | 107.95 | 2.00 | 6.25 | 4.75 | 4.06 | 125.35 |
| Mar. | 4.95 | 4.36 | 5.43 | 9.41 | 2.91 | 79.32 | 2.00 | 5.59 | 4.25 | 3.63 | 89.79 |
| Apr. | 5.42 | 4.62 | 5.92 | 9.40 | 3.19 | 101.67 | 2.00 | 6.12 | 4.65 | 3.98 | 117.60 |
| May | 6.41 | 5.18 | 6.96 | 9.30 | 3.79 | 161.07 | 2.00 | 7.23 | 5.50 | 4.70 | 194.60 |
| Jun. | 8.08 | 6.15 | 8.69 | 8.99 | 4.82 | 304.69 | 2.00 | 9.12 | 6.93 | 5.92 | 389.27 |
| Jul. | 6.58 | 5.28 | 7.14 | 9.27 | 3.89 | 173.07 | 2.00 | 7.42 | 5.64 | 4.83 | 209.84 |
| Aug. | 5.80 | 4.84 | 6.32 | 9.38 | 3.42 | 122.41 | 2.00 | 6.54 | 4.97 | 4.25 | 143.59 |
| Sep. | 7.01 | 5.53 | 7.59 | 9.20 | 4.16 | 206.00 | 2.00 | 7.91 | 6.01 | 5.14 | 209.84 |
| Oct. | 4.83 | 4.29 | 5.30 | 9.41 | 2.84 | 74.18 | 2.00 | 5.45 | 4.14 | 3.54 | 143.59 |
| Nov. | 4.08 | 3.87 | 4.51 | 9.32 | 2.40 | 46.80 | 2.00 | 4.60 | 3.50 | 2.99 | 253.91 |
| Dec. | 4.96 | 4.36 | 5.44 | 9.41 | 2.92 | 79.76 | 2.00 | 5.60 | 4.25 | 3.64 | 82.99 |
Fig. 2.
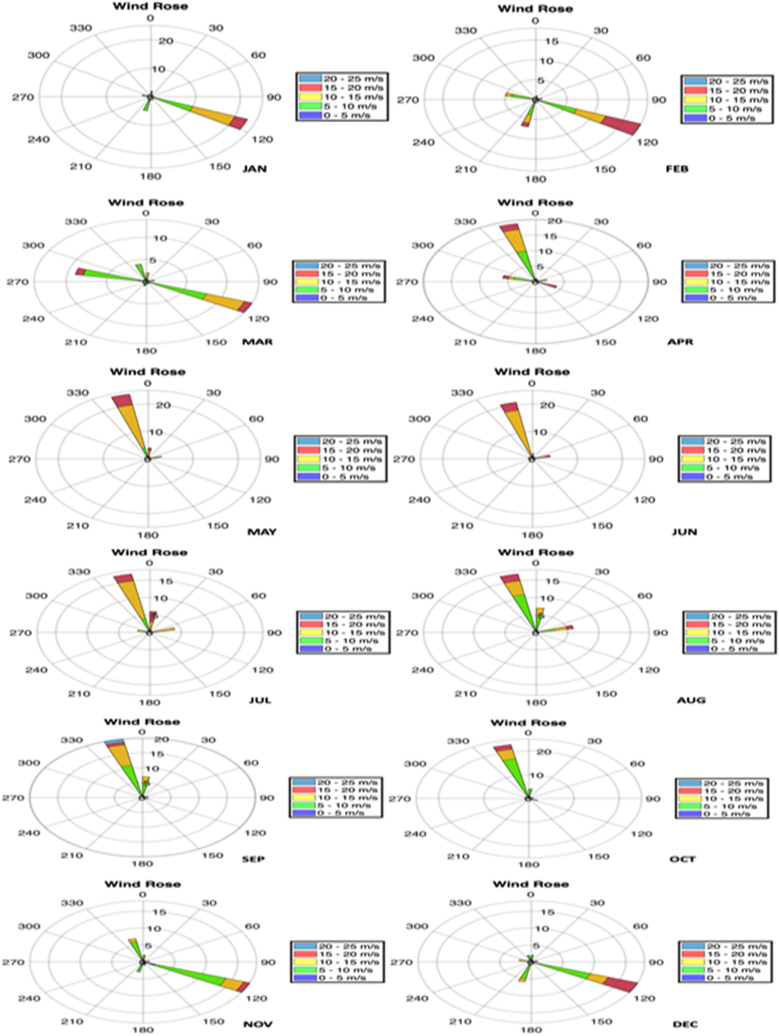
Monthly wind speed and direction at Yundum from (1990–2021).
Fig. 3.
Monthly wind speed and direction at Basse from (1990–2021).
Table 4.
The Battelle-Pacific North-west Laboratory (PNL) wind power classification source.
| Wind |
10 m wind |
10 m wind |
30 m wind |
30 m wind |
50 m wind |
50 m wind |
|---|---|---|---|---|---|---|
| power |
power |
speed |
power |
speed |
power |
speed |
| class | (W/m2) | (m/s)/mph | (W/m2) | (m/s)/mph | (W/m2) | (m/s)/mph |
| 1 | /9.8 | /11.5 | /12.5 | |||
| 2 | /11.5 | /13.4 | /14.3 | |||
| 3 | /12.5 | /14.5 | /15.7 | |||
| 4 | /13.4 | /15.7 | /16.8 | |||
| 5 | /14.3 | /16.8 | /17.9 | |||
| 6 | /15.7 | /18.3 | /19.7 | |||
| 7 | /21.1 | /24.5 | /26.6 |
Source:http://rredc.nrel.gov/wind/pubs/atlas/tables/l - I T.html; Saeidi et al. (2011)
Fig. 4.
Weibull and Raleigh probability distribution of wind at Yundum (1990–2021).
Fig. 5.
Weibull and Raleigh probability distribution of wind at Basse (1990–2021).
In Table 2, Table 3 and Fig. 2, Fig. 3, the monthly variability of the mean wind speed and direction, the Weibull and Raleigh distribution parameters, and the potential wind power densities are presented for the study locations. It is observed that at Yundum the highest wind speed was recorded during August, followed by September, June, and July in that order. While the least mean wind speed occurred in November. For Basse, the highest mean wind speed where recorded in June, followed by September and then July, respectively. While the least wind speed was captured in November. The annual mean wind speeds computed over 32 years presented in Fig. 2, Fig. 3 show the mean annual wind speed of 8.2 m/s and 5.8 m/s captured at Yundum and Basse stations. The monthly variability of the wind speed can be as a result of the uneven distribution of pressure over these stations since the atmosphere attempts to balance the uneven distribution of pressure over the earth's surface by means of winds. Besides the climatic conditions of Yundum and Basse, the bare nature of the two cities with few windbreaks, low and erratic rainfall, and high temperatures can also contribute to the variability of the winds. Interestingly, it is worth noting that on average, Yundum presents the highest wind speed than Basse with corresponding higher values of the dimensionless shape L, scale parameter C, and the wind power density of the Weibull and Raleigh distributions. The reason for this may not be farfetched from the temperature gradient of these locations, which plays an important role in the location's strong winds and the fact that the wind speed increases with elevation above ground and the elevation of Yundum is 29.0 m while that of Basse is 18.1 m; among other climatic factors. The parameters C, L, and power density are the determinant factors for the examination of the wind energy potential of any given location. Where the scale factor C gives the stretched out of the distribution and indicates where the majority of the distribution is concentrated. The shape factor L defines the average width of the wind speed distribution of the terrain. Smaller values of L mean a relatively wider distribution of wind speed, while larger values of L show a limited distribution.
A careful observation of Table 1, Table 2 also shows that the shape parameters ranged from 4.88 to 6.98 and 3.87–6.15 for Yundum and Basse locations, the Weibull scale parameters or factors ranged from 6.60 to 10.58 m/s and 4.51–8.69 m/s for Yundum and Basse while the calculated wind power densities from the Weibull and Raleigh functions ranged from 139 to 718 W/m2 and 46–390 W/m2 for Yundum and Basse respectively. These values of wind speed and wind power density presented are within the wind power density classification classes of the first – sixth, at an altitude range of 10 m as recommended by The Battelle-Pacific North-west Laboratory (PNL) wind power classification source and presented in Table 4. More so, an ideal wind turbine requires a minimum wind speed of 3.3–7.3 m/s and a wind power density of 100–200 W/m2 to start turning to generate electricity and strong wind range of 13.8–16.7 m/s to full capacity generation. While a wind speed of 25.0 m/s should not be allowed to operate a turbine to prevent it from damage [30]. Thus, the values presented by both the Weibull and Raleigh models have clearly shown high potential for generating electricity from wind in the Yundum and Basse locations of the Gambia except for November and March in Basse where the wind power density was slightly less than these ratings. Nevertheless, even for these months, the potential is yet appropriate for operating rural and small community with low capacity wind turbines.
Table 4 presents a standard wind speed and power density classification for comparison purposes, while in Table 5, the mean monthly probability density distributions as measured and calculated using the Weibull and Raleigh distributions for the two stations studied are presented. And in Fig. 4, Fig. 5, the Weibul density function of Yundum and Basse is shown.
Table 5.
Monthly probability distribution of wind speed from the measured and calculated Weibull and Raleigh Distributions in Yundum and Basse for the period 1990–2021.
| Months | Yundum |
Basse |
|||||
|---|---|---|---|---|---|---|---|
| MYPD | WCYPD | RCYPD | MBPD | WCBPD | RCBPD | MYPD | |
| Jan. | 0.4752 | 0.8676 | 0.0923 | 0.4845 | 0.9989 | 0.0951 | |
| Feb. | 0.4743 | 0.7915 | 0.0885 | 0.4840 | 0.9979 | 0.0920 | |
| Mar. | 0.4732 | 0.8535 | 0.0916 | 0.4872 | 0.9980 | 0.0984 | |
| Apr. | 0.4729 | 0.8590 | 0.0919 | 0.4858 | 0.9994 | 0.0954 | |
| May | 0.4715 | 0.9147 | 0.0957 | 0.4794 | 0.9886 | 0.0818 | |
| Jun. | 0.4681 | 0.3571 | 0.0747 | 0.4723 | 0.7083 | 0.0767 | |
| Jul. | 0.4690 | 0.4569 | 0.0783 | 0.4778 | 0.9811 | 0.0776 | |
| Aug. | 0.4669 | 0.3121 | 0.0723 | 0.4831 | 0.9988 | 0.0923 | |
| Sep. | 0.4687 | 0.3934 | 0.0731 | 0.4750 | 0.9448 | 0.0768 | |
| Oct. | 0.4722 | 0.7035 | 0.0881 | 0.4870 | 0.9999 | 0.1039 | |
| Nov. | 0.4803 | 0.9960 | 0.1182 | 0.4927 | 1.0000 | 0.1222 | |
| Dec. | 0.4770 | 0.9581 | 0.1003 | 0.4875 | 0.9999 | 0.0938 | |
Table 4 presents the power density and wind speed classification schemes, the wind classification is vital in evaluating the possibility of utilizing wind turbines for a given region. Our study adopts the wind power classification scheme presented by the Battelle-Pacific North-west Laboratory (PNL) for reference purposes in Table 4. The classification is based on seven classes and depends on three heights of 10 m, 30 m, and 50 m, respectively. From the classification in Table 4, the average wind power densities in the Yundum and Basse locations determined from the Weibull distribution can be fitted into the first to the sixth class with a range of 135–539 W/m2 and 46–304 W/m2 for Yundum and Basse. While the mean power densities calculated with the Raleigh distribution can be fitted into the second to seventh classes with a range of 164–718 for Yundum and first to sixth classes with a range of 82–389 W/m2 for Basse all on the base of 10 m and 30 m height respectively. However, Saeidi et al. [31] opined that Classes 1 and 2 are limited and less efficient for wind energy harvesting at full capacity. Their potential is useful for generating low-capacity wind turbines for use on small scales, especially in villages and semi-urban areas.
Table 5 shows the monthly probability distribution of wind speed measured and calculated with the Weibull and Raleigh distributions using Equations (3), (5)). It is observed that the measured probabilities are similar for all the months, revolving around 0.46–0.48. The Weibull probabilities calculated ranged from 0.3 to 1.0 and 0.7–1.0 for Yundum and Basse. While the Raleigh probabilities presented low values ranging from 0.10 to 0.30 and 0.00–0.07 for Yundum and Basse. Furthermore, it is observed that the probabilities followed a trend with the highest probabilities being reported for November and then December for the measured and all models except for November in Basse where the trend was observed to be unsustainable by the Raleigh formula. These probabilities indicate the level of certainty of the monthly wind speed occurring at defined locations and must be determined before the installation of a wind turbine by engineers [32].
To assess the Weibull distribution of Yundum and Basse, the mean monthly probability density distributions of Weibull for all of the thirty-two years depicted in Table 5 are shown in Fig. 4, Fig. 5. These distributions are similar for the two locations studied with a narrow peak wind speed of 9.9 m/s and 8.1 m/s for Yundum and Basse respectively. Furthermore, statistical tools were employed to study the monthly probability density distributions computed from the Rayleigh and Weibull distributions in comparison to the measured distributions to evaluate the suitability of the two distributions and the results are depicted in Table 6.
Table 6.
Statistical test results of the Weibull and Raleigh probability distributions.
| Statistical tool |
Location site |
|||
|---|---|---|---|---|
| Yundum |
Basse |
|||
| S/N | Weibull | Raleigh | Weibull | Raleigh |
| 1. | 0.333882 | 0.383801 | 0.390686 | 0.390933 |
| 2. | 0.787094 | 0.888439 | 0.474294 | 0.864604 |
| 3. | 1.572994 | 20.42977 | 2.934881 | 20.34309 |
| 4. | 0.45460792 | 0.2793352 | −2.3858717 | −2.79678598 |
| 5. | 0.291708 | 0.383692 | 0.484942 | 0.390858 |
Table 6 depicts the statistical evaluation of the Weibull and Raleigh distributions used in estimating the wind energy potentials at the Yundum and Basse locations of the Gambia. The best estimating technique will show the highest values of and and the least values of , and . Thus, from the results, Weibull models perform better at Yundum in terms of , and while Raleigh distribution gives a better fit in Yundum for . For Basse, the Weibull distribution gives a better distribution in terms of the , and while Raleigh distribution predicts better in terms of However, on average of the overall five statistical tests, the Weibull probability density function performed best for both Yundum and Basse, making it more suitable method for calculating wind power potentials. The variations of the Weibull and Raleigh distributions results from the measured results can be attributed to the different numerical coefficients and parameters involved in the calculations of the EPFM and STDM, c and L, among others. This is in agreement with the results of Teimourian et al. [33] on assessing wind energy distribution models.
4. Conclusions
A novel approach combining the EPFM and STDM in estimating the distribution parameters of the characteristics of wind in the Gambian locations of Yundum and Basse has been studied and analyzed statistically using the Weibull and Raleigh distribution function. The study aimed to technically determine the potential of harvesting wind energy at the studied locations by fitting the best model comparing Weibull and Raleigh Distributions.
The wind speed data of thirty-two years (1990–2021) was used. Wind power density and probability density distributions were calculated from the wind speed data, the dimensionless shape L, and scale parameter C, which were evaluated. The mean monthly wind speed, L, C, and wind power density values presented generally show slight variations. A comparison of the monthly probability distribution of wind speed measured with the Weibull and Raleigh models showed that the Weibull presents higher results followed by the measured probabilities.
The statistical testing revealed that the Weibull distribution gives better results for the power density distribution than the Rayleigh distribution, in agreement with the work of Al-Buhari [19] and Mostafaeipour et al. [34]. The average wind speed and power densities measured and computed with the two models when compared with the wind power classification source showed a good potential across the two cities and hence encourages the utilization of wind energy to generate power in these locations. However, the power densities recorded for October and November in Basse are classified under classes 1 and 2 and may be limited and less efficient for wind energy harvesting at full capacity. Their potential is still useful for generating low-capacity wind turbines for use on small scales, especially in villages and semi-urban areas. The availability of data has limited us to carry out this study in only two locations. It is recommended to repeat and extend a similar study to other areas of the country using different calculation approaches for the generalization of results.
Author contribution statement
Tyoyima John Ayua: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Moses Eterigho Emetere: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Data availability statement
Data will be made available on request.
Additional information
No additional information is available for this paper.
Declaration of competing interest
The corresponding author on behalf of all the authors declared that no conflicts of interest exist. All the authors read and approved the manuscript.
Acknowledgements
We acknowledged the contributions of the staff of Yundum and Basse meteorological stations for collecting the data we used for this assessment, and would sincerely like to thank Mr. Mamadou A. R. Jallow of The Meteorological Service Department for his tireless effort in securing the meteorological data set that was needed for this study.
Nomenclature
- W
wind speed (m/s)
- ζ
conversion factor of wind speed in knot unit to m/s (0.51444)
- c
scale parameter (m/s)
- L:
dimensionless shape parameter (width of the distribution)
mean wind speed (m/s)
standard deviation of the wind speed (m/s)
the gamma function
- EPF
Energy Pattern Factor
- EPFM
Energy Pattern Factor Method
- STDM
Standard Deviation Method
- :
mean air density kg/m3
- Z
height above sea level (m)
- P(W)
wind power (W)
- A
area (m2)
- W
wind power density by Weibull distribution (W/m2)
- R
wind power density by Weibull distribution (W/m2)
Root Mean Square Deviation
Correlation coefficient of determination
The Nash-Sutcliffe coefficient of efficiency
- :
Mean absolute error
Chi Square of the goodness of fit
predicted or modeled values
- MYPD
Monthly probability distribution of wind speed measured at Yundum
- WCYPD
Monthly Weibull probability distribution of wind speed calculated at Yundum
- RCYPD
Monthly Raleigh probability distribution of wind speed calculated at Yundum
- MBPD
Monthly probability distribution of wind speed measured at Basse
- WCBP
Monthly Weibull probability distribution of wind speed calculated at Basse
- RCBPD
Monthly Raleigh probability distribution of wind speed calculated at Basse
References
- 1.Dokur E., Kurban M. Wind speed potential analysis based on Weibull Distribution. Balkan Journal of Electrical and Computer engineering. 2015;3(4):231–235. doi: 10.17694/bajece.72748. [DOI] [Google Scholar]
- 2.Genc A., Erisoglu M., Pekgor A., Oturanc G., Hepbasli A., Ulgen K. Estimation of wind power potential using Weibull distribution. Energy Sources. 2005;27(9):809–822. doi: 10.1080/00908310490450647. [DOI] [Google Scholar]
- 3.Kaldellis J.K., Zafirakis D. The wind energy (R)evolution: a short review of a long history. Renew. Energy. 2011;36(7):1887–1901. doi: 10.1016/j.renene.2011.01.002. [DOI] [Google Scholar]
- 4.Negash T., Möllerström E., Ottermo F. An assessment of wind energy potential for the three topographic regions of Eritrea. Energies. 2020;13:1846. doi: 10.3390/en13071846. [DOI] [Google Scholar]
- 5.Chiras D.D. eighth ed. Jones and Bartlett Publishers; 2010. Environmental Science: Action for a Sustainable Future; p. 632. [Google Scholar]
- 6.Patel M.R. CRC press; 2005. Wind and Solar Power Systems: Design, Analysis, and Operation. [Google Scholar]
- 7.Mentis D. KTH School of Industrial Engineering and Management, Energy Technology EGI-2013 Division of Energy Systems Analysis; 2013. Wind Energy Assessment in Africa. A GIS-Based Approach. Published M. Sc Thesis. [Google Scholar]
- 8.Flores E.R. Department of Electrical Engineering, University of Kassel; 2010. Master Plan for Renewable Energy Based Electricity Generation in the Gambia. Published doctoral dissertation. [Google Scholar]
- 9.Kurban M., Hocaoğlu F.O., Kantar Y.M. Comparative analysis of two different statistical distributions used in estimation of wind energy potential. Pamukkale University Journal of Engineering Sciences. 2011;13(1) [Google Scholar]
- 10.IEA International energy agency. 2009. http://www.iea.org/stats/electricitydata.asp?COUNTRY_CODE=29 [Online]Available at:
- 11.Mentis D., Hermann S., Howells M., Welsch M., Siyal S.H. Assessing the technical wind energy potential in Africa a GIS-based approach. Renew. Energy. 2015;83(C):110–125. doi: 10.1016/j.renene.2015.03.072. [DOI] [Google Scholar]
- 12.Archer C.L., Jacobson M.Z. Evaluation of global wind power. J. Geophys. Res. 2005;110 doi: 10.1029/2004JD005462. [DOI] [Google Scholar]
- 13.Shu Z.R., Jesson M. Estimation of Weibull parameters for wind energy analysis across the UK. J. Renew. Sustain. Energy. 2021;13 doi: 10.1063/5.0038001. [DOI] [Google Scholar]
- 14.Akdag S.A., Guler O. UTES'2008; Istanbul: 2008. Weibull Distribution Parameters Comparison of Determination Methods. VII. National Clean Energy Symposium; pp. 707–714. 17-19 December 2008. [Google Scholar]
- 15.GBOS . 2013. Gambia Bureau of Statistics Report on the Gambia 2013 Population and Housing Census Preliminary Results. [Google Scholar]
- 16.Jaramillo O.A., Borja M.A. Wind speed analysis in La Ventosa, Mexico: a bimodal probability distribution case. Renew. Energy. 2004;29:1613–1630. doi: 10.1016/j.renene.2004.02.001. [DOI] [Google Scholar]
- 17.Ahmed Shata A.S., Hanitsch R. Evaluation of wind energy potential and electricity generation on the coast of Mediterranean Sea in Egypt. Renew. Energy. 2006:1183–1202. doi: 10.1016/j.renene.2005.06.015. [DOI] [Google Scholar]
- 18.Akpinar E.K., Akpinar S. An assessment on seasonal analysis of wind energy characteristics and wind turbine characteristics. Energy Convers. Manag. 2005;46:1848–1867. doi: 10.1016/j.enconman.2004.08.012. [DOI] [Google Scholar]
- 19.Al Buhari M.H. A statistical analysis of wind speed data and an assessment of wind energy potential in Taiz-Yemen. Assiut University Bulletin for Environmental Researches. 2006;9(2):21–32. [Google Scholar]
- 20.Egbert B., Rienk V.G. second ed. John Wiley & SONS, LTD; 1999. Environmental Physics. [Google Scholar]
- 21.Celik A.N. A statistical analysis of wind power density based on the Weibull and Rayleigh models at the southern region of Turkey. Renew. Energy. 2004;29(4):593–604. doi: 10.1016/j.renene.2003.07.002. [DOI] [Google Scholar]
- 22.Azad A.K., Rasul M.G., Yusaf T. Statistical diagnosis of the best Weibull methods for wind power assessment for agricultural applications. Energies. 2014;7:3056–3085. doi: 10.3390/en7053056. [DOI] [Google Scholar]
- 23.Mohammadi A., Mostafaeipour A. Using different methods for comprehensive study of wind turbine utilization in Zarrineh, Iran. Energy Conversation and Management. 2013;65:463–470. [Google Scholar]
- 24.Shaban A.H., Resen A.K., Bassil N. Weibull parameters evaluation by different methods for wind mills farms. Energy Rep. 2020;6:188–199. doi: 10.1016/j.egyr.2019.10.037. [DOI] [Google Scholar]
- 25.Shu Z.R., Li Q.S., Chan P.W. Investigation of offshore wind energy potential in Hong Kong based on Weibull distribution function. Appl. Energy. 2015;156:362–373. [Google Scholar]
- 26.Chang T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Appl. Energy. 2011;88(1):272–282. [Google Scholar]
- 27.Aukitino T., Khan M.G.M., Ahmed M.R. Wind energy resource assessment for Kiribati with a comparison of different methods of determining Weibull parameters. Energy Convers. Manag. 2017;151:641–660. doi: 10.1016/j.enconman.2017.09.027. [DOI] [Google Scholar]
- 28.Krause P., Boyle D.P., Base F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005;5:89–97. doi: 10.5194/adgeo-5-89-2005. [DOI] [Google Scholar]
- 29.Prema V., Rao K.U., Jnaneswar B.S., Badarish C.A., Ashok P.S., Agarwal S. In: Intelligent Systems Technologies and Applications. Berretti S., Thampi S.M., Srivastava P.R., editors. Springer; Switzerland: 2016. Application of hybrid neuro-wavelet models for effective prediction of wind speed. [DOI] [Google Scholar]
- 30.Quebec Hydro. 2022. Overview of Hydro-Québec’s Energy Resources: Wind Power and Other Sources of Energy.https://news.hydroquebec.com/media/filer_private/2023/01/20/overview_of_hydro-quebecs_energy_resources.pdf Retrieved from. [Google Scholar]
- 31.Saeidi M., Mirhosseini M., Sedaghat A., Mostafaeipour A. Feasibility study of wind energy potential in two provinces of Iran: North and South Khorasan. Renew. Sustain. Energy Rev. 2011;18(8):3558–3569. doi: 10.1016/j.rser.2011.05.011. [DOI] [Google Scholar]
- 32.Kang S., Khanjari A., You S., Lee J. Comparison of different statistical methods used to estimate Weibull parameters for wind speed contribution in nearby an offshore site, Republic of Korea. Energy Rep. 2021;7:7358–7373. doi: 10.1016/j.egyr.2021.10.078. [DOI] [Google Scholar]
- 33.Teimourian H., Abubakar M., Yildiz M., Teimourian A. A comparative study on wind energy assessment distribution models: a case study on Weibull distribution. Energies. 2022;15(15):5684. doi: 10.3390/en15155684. [DOI] [Google Scholar]
- 34.Mostafaeipour A., Jadidi M., Mohammadi K., Sedaghat A. 2014. An Analysis of Wind Energy Potential and Economic Evaluation in Zahedan. Iran. 30: 641-650. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.