Assisted-GNSS positioning algorithm based on one-way fuzzy time information

Abstract

In order to solve the problem that the accuracy of approximate position and approximate time information is limited by the traditional auxiliary positioning algorithm, this paper analyzes the problem that the calculation amount may increase and fail when these auxiliary information exceeds the precision requirement range and puts forward a positioning algorithm based on one-way fuzzy time assistance that is suitable for the positioning solution of GNSS satellite navigation receivers under the condition of fuzzy time information, such as the rotation condition. Methods using the reference information in the ephemeris information, the relatively accurate approximate time information can be reasonably searched and verified so as to achieve the effect of obtaining the positioning result with less calculation. The experimental results show that this method can accurately calculate the exact position even if there is an error in the approximate position information under the condition of one-way time assistance, which not only solves the problem that it cannot be positioned under the conditions of rotation but also does not increase the additional calculation amount and has practical engineering value.

1. Introduction

Global navigation satellite system (GNSS) signals have low landing power and are vulnerable to interference. Small-power interference can affect satellite navigation signals within several kilometers [1]. To eliminate GNSS interference sources, GNSS interference should be detected, identified, and located first [2]. In the traditional GPS positioning solution [[3], [4], [5], [6]] process, it is necessary to obtain observations from at least four satellites to obtain the user's 3D coordinates and local clock differences [7]. However, in environments such as occlusion and weak signals [8], due to the interruption of the signal [9] and other effects, it is impossible to complete the synchronization of satellite navigation message frames and obtain the time information of the signal according to the traditional method, and it is also impossible to locate the target by solving the pseudo-range observation equation (there is ambiguity in the pseudo-range value). In this case, even if multiple satellites can be received, the positioning solution cannot be completed because the signal time of each satellite is incomplete.

The exploration of the assisted GPS positioning method [10] started earlier [[11], [12], [13]]. Initially, this method has many challenges in practical application, and it needs to rely on relevant auxiliary conditions to implement it [14,15]. However, with the development of social science and technology, all kinds of communication infrastructure, such as cellular networks, Wi-Fi networks [16] and related hardware devices such as portable high-precision clock devices, have become convenient sources for the algorithm to obtain information. In the research direction of this project, that is, under the condition of rotation, the signal received by the receiver is in a discontinuous state. This makes the receiver often unable to completely receive the message information for bit synchronization and frame synchronization [17,18] to obtain the millisecond integer part of the satellite signal transmission time, so it is impossible to complete the receiver positioning calculation by traditional methods [19,20].

The A-GPS (Assisted-GPS) positioning algorithm addresses this issue by setting the receiver's millisecond time as an unknown to be solved and introducing a fifth satellite observation equation for solving [[21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31]]. A-GPS receivers have the following characteristics: (1) They employ large-scale parallel correlation technology to simultaneously process multiple correlation signals to enhance reception sensitivity and achieve long-term accumulation of input signals, enabling accurate measurement of pseudo-code phase. (2) The receivers have the ability to receive signals from base stations, especially cellular network terminal base stations, to obtain essential auxiliary information. This information includes GPS satellite ephemeris and satellite clock deviation parameters required for GPS positioning. (3) They use the technique of resolving the ambiguity of the pseudorange observation to achieve precise receiver positioning. By solving and processing the ambiguity of the pseudorange observation, accurate positioning results can be obtained. The receiver utilizes these auxiliary methods to obtain the user's approximate location, time, navigation data, etc. After obtaining the receiver's complete millisecond time, the positioning result is determined. This method is particularly suitable for cases with only one-way ambiguous information. However, the traditional research in the early stages mainly focused on low-dynamic environmental requirements, and thus it had some limitations.

In recent years, scholars have proposed techniques to address the positioning problem of non-continuous satellite signals by circumventing the issue of signal discontinuity caused by rotation conditions using methods such as A-GPS without demodulating navigation messages [32,33]. Specifically, literature [34] demonstrated that the receiver can determine the satellite time in milliseconds integer from the pseudocode phase measurements of five satellites to complete the positioning calculation, but all need to satisfy the condition that the clock difference is known and the probable position error is within 150 km, or equivalently, the position is known and the receiver equivalent clock difference error is within 187.5s; Literature [35] further investigated the search range when the approximate position was not determined and quantified the computation volume when the position error exceeded the limit. The study also analyzed the impact of the number of satellites involved in the solution on the search times, proving that the fewer the number of satellites, the faster the search speed; Literature [36] analyzed the situation where the A-GPS algorithm calculates the initial setting of the satellite signal's whole-millisecond time error and proposed some identification methods to solve it. However, the root cause of this problem, i.e., the fractional initial value problem within the receiver clock difference milliseconds, has not been analyzed. Literature [37] proposed a method to eliminate pseudo-range ambiguity by using the lambda-fraction function, but the calculation amount is too large and the algorithm complexity is too high.

Assisted positioning algorithm is based on approximate location and time information before positioning to enable satellite navigation receiver positioning. In the literature [38], a novel assisted enhanced positioning algorithm based on a mathematical model of geodetic height extrapolation is proposed. This algorithm can assist in incomplete positioning and find three-dimensional positioning even in the case of temporary satellite signal loss. However, the limitations of the extrapolation model can affect positioning accuracy. One specific application scenario is when a rotating carrier requires information injection before launch. However, due to operational constraints or mismatched device selection and application requirements, it is often not feasible to install a timing chip on the receiver equipment. Especially, timing chips, which typically rely on battery power to maintain time accuracy even after the device is powered off. However, issues related to battery selection and installation arise. In some cases, after the device receives time information through a serial communication link, it must rely on the local hardware crystal oscillator for timing, meaning that the device cannot be turned off, limiting its usage and response time.

Therefore, when designing or improving assisted positioning algorithms with relatively high positioning accuracy but large time ambiguity, specific design requirements need to be considered. Firstly, the information injection process before the launch of the rotating carrier requires high positioning accuracy, so the algorithm should focus on improving positioning accuracy in its design. Secondly, due to the significant time ambiguity, i.e., the low accuracy of time information, special attention needs to be given to the handling and utilization of time information in the positioning algorithm. It may be necessary to utilize other environmental features or auxiliary information, such as surrounding landmarks or signal strength variations, to assist in positioning.

So in this application scenario, only use the millisecond-time, one-way time information obtained at the signal level to position the receiver. For this problem, where the hardware condition caused only one-directional time assist or in the rotation condition, the satellite signal non-continuously caused assisted time error is large and cannot be limited. This article proposes an algorithm for achieving receiver positioning based on the above situation to reduce a series of problems, such as a hardware component in the application scene (punctuality chip) and the accompanying design inspection. At the same time, the positioning accuracy can be increased, and it is suitable for limited conditions such as a lack of time information.

The application scheme of this algorithm is shown in Fig. 1. When the above situation is detected in hardware, the algorithm proposed in this paper is used to locate the receiver. That is, this algorithm can be applied to the practical application environment of rotating carrier navigation; that is, the message, approximate time, and approximate position can only be added by the A-GPS method. For launch products, there is often high approximate location information, but due to design and other factors, it is impossible to rely on batteries and other modules for time synchronization and punctuality, so this paper discusses the specific laws and solutions to such problems.

Fig. 1.

Flowchart of the algorithm for hardware problem solutions.

2. Receiver time recovery method

In the process of satellite navigation receiver solution, the residual of pseudorange $P_i$ can be expressed as

$$P_i\left(u,t_d^r,{\phi }^{chip}\right)={\rho }_i-\parallel s_i\left(t_i^s\right)-u\parallel -c{t}_d^r{\epsilon }_i=D_i-c{t}_i^{s,ms}-\parallel s_i\left(t^r-t_d^r-{\tau }_i\right)-\Delta u\parallel -c\left(t_d^{r,ms}+t_d^{r,chip}\right)+{\epsilon }_i=D_i-c\left(t_i^{s,ms}+t_d^{r,ms}\right)-\parallel s_i\left(t^r-t_d^r-{\tau }_i\right)-u\parallel -c{t}_d^{r,chip}+{\epsilon }_i=D_i-c{t}_i^{ms}-\parallel s_i\left(t^r-t_d^r-{\tau }_i\right)-u\parallel -{\phi }^{chip}+{\epsilon }_i$$ (1)

The above formula states that, $c$ represents the speed of light, $d=0.001\times c$. $u$ represents the approximate position of the receiver, which is obtained through auxiliary means, such as mobile cellular networks or WLAN. $t_d^r$ is the receiver's local clock bias. $t_d^{r,ms}$ and $t_d^{r,chip}$ correspond to the millisecond-level and sub-millisecond-level parts, respectively. ${\phi }^{chip}$ is the pseudorange measurement error caused by the millisecond-level internal portion of the receiver clock bias, denoted as ${\phi }^{chip}={ct}_d^{r,chip}$, $\Delta {\phi }^{chip}\in \left[-\mathrm{d}/2,\mathrm{d}/2\right]$. ${\rho }_i$ represents the pseudorange of satellite $i$. $s_i\left(t_i^s\right)$ represents the position of satellite $i$ at time $t_i^s$. $t_i^s$ corresponds to the signal transmission time, while $t_i^{s,ms}$ and $t_i^{s,chip}$ correspond to the millisecond and sub-millisecond parts, respectively. $t_i^{s,chip}$ can be obtained from the phase measurement information of the receiver. ${\tau }_i$ corresponds to the signal propagation delay of satellite $i$. $D_i$ represents $c\left(t^r-t_i^{s,chip}\right)$. $t^r$ is the local approximate time of receiver, which can be obtained either directly from the timing information of the receiver or through auxiliary means. ${\epsilon }_i$ represents observation noise.

From the corresponding equation, it can be found that the approximate position of the receiver $u$ and the approximate local time of the receiver ${\tau }_i$ have a direct impact on the pseudorange residual. However, due to limitations such as signal reception conditions, the value of $t_i^{s,ms}$ cannot be directly obtained. Nevertheless, $t_i^{s,ms}$ has a discrete characteristic and can be solved by reverse calculation using information such as $u$ and ${\tau }_i$, resulting in a floating-point number $t_i^{s,ms}$, which can then be rounded to the nearest integer to avoid the problem of unsolvable calculations caused by the inability to obtain $t_i^{s,ms}$.

In the process of solving for $t_i^{s,ms}$, the influence of the initial values of ${\tau }_i$ and ${\phi }^{chip}$ for satellite delay estimation are considered. They are expanded in Taylor series at the approximate position and estimated clock bias, neglecting components of order two and higher, which yields:

$$\begin{array}{c}{P}_i\left(u,t_d^r,{\tau }_i,{\phi }^{chip}\right)=P_i\left(u^{\left(0\right)},t_d^{r\left(0\right)},{\tau }_i^{\left(0\right)},{\phi }^{chip\left(0\right)}\right)+v_i\left(t_i^{s\left(0\right)}\right){\theta }_i^{\left(0\right)}\left(t_i^{s\left(0\right)}\right)\left(\Delta t_d^r+\Delta {\tau }_i\right)+{\theta }_i^{\left(0\right)}\left(t_i^{s\left(0\right)}\right)\Delta u-\Delta {\phi }^{chip}+{\epsilon }_i\end{array}$$ (2)

where ${\theta }_i^{\left(0\right)}\left(t_i^{s\left(0\right)}\right)=s_i\left(t_i^{s\left(0\right)}\right)-u^{\left(0\right)}/\Vert s_i\left(t_i^{s\left(0\right)}\right)-u^{\left(0\right)}\Vert$, is the satellite line-of-sight vector for the approximate position, $v_i\left(t_i^{s\left(0\right)}\right)$ is the maximum relative ground-receiver velocity of the satellite at time $t_i^{s\left(0\right)}$, at a velocity of 800 m/s, $\Delta {\tau }_i$ represents the satellite position error caused by the estimated satellite delay.

Substituting ${{\rm P}}_i\left(u^{\left(0\right)},t_d^{r\left(0\right)},{{\tau }_i}^{\left(0\right)},{\phi }^{chip\left(0\right)}\right)=D_i-c{t}_i^{ms}-\Vert s_i\left(t_i^{S\left(0\right)}\right)-u^{\left(0\right)}\Vert -{\phi }^{chip\left(0\right)}+{\epsilon }_i$, we have

$$\begin{array}{c}{D}_i-c{t}_i^{ms}-\Vert s_i\left(t_i^{S\left(0\right)}\right)-u^{\left(0\right)}\Vert -{\phi }^{chip\left(0\right)}+{\epsilon }_i=-v_i\left(t_i^{s\left(0\right)}\right){\theta }_i^{\left(0\right)}\left(t_i^{s\left(0\right)}\right)\left(\Delta t_d^r\right)-{\theta }_i^{\left(0\right)}\left(t_i^{s\left(0\right)}\right)\Delta u+\Delta {\phi }^{chip}\end{array}$$ (3)

to determine the solution conditions of the equation. Then, the satellite transmission time in milliseconds can be expressed as

$$\begin{array}{c}{N}_i^{ms}=\frac{1}{d}\left(\begin{array}{c}{D}_i-\parallel s_i\left(t_i^{S\left(0\right)}\right)-u^{\left(0\right)}\parallel -{\phi }^{chip\left(0\right)}+{\epsilon }_i+v_i\left(t_i^{s\left(0\right)}\right){\theta }_i^{\left(0\right)}\left(t_i^{s\left(0\right)}\right)\left(\Delta t_d^r\right)+{\theta }_i^{\left(0\right)}\left(t_i^{s\left(0\right)}\right)\Delta u-\Delta {\phi }^{chip}\end{array}\right)\end{array}$$ (4)

To complete the positioning calculation, it is necessary to obtain the complete integer millisecond result through the above formula calculation.

However, in practical applications, the approximate position and time cannot simultaneously meet the accuracy requirements, especially when the accuracy range increases to a certain extent. The above calculation may lead to multiple possible values of $N_i^{ms}$ for each satellite with the corresponding number $i\text{.}$ This will greatly increase the range of combinations for multiple satellites. Literature [32] has pointed out that when time information is completely unavailable, the calculation amount can increase by 1.5 × 10⁷ times.

There are a lot of challenges to the carrier positioning algorithm for a certain type of carrier with high positioning requirements, such as sounding rockets. In this case, especially when it is blocked before launch, the signal cannot be effectively captured. However, after the launch, due to the carrier itself and environmental factors, the received signal also becomes incomplete. Therefore, we need an auxiliary positioning method to solve this problem. Before the sounding rocket is launched, we can improve the accuracy of the approximate position by adding information such as position. However, the traditional method is limited by the device workflow; the process level does not meet the platform requirements in terms of cost, volume, and so on, and it is impossible to obtain time information by adding a punctual module to the receiver. In this case, we need to optimize the design based on the existing algorithm. When the approximate location information is accurate, new ideas and methods to simplify the traditional location method are sought by trying to change the algorithm's search mode.

3. One-way fuzzy time-assisted approximate time search algorithm

In scenarios where the receiver has no external timing and can only obtain time within milliseconds, without being able to obtain complete millisecond time information from the signal, traditional methods cannot complete the positioning solution. The solution is to use existing time information, such as the reference time $Toe$ in the navigation message, according to the discrete characteristics in equation (Eq. 1) and (Eq. (2)), and sequentially calculate $n$ discrete time units $N$, assuming a time range of ($Toe+f\left(\omega \right))$ (When $n=1$, search range of $f\left(\omega \right)$ is conducted in a time unit of one time. If the search result is unreasonable, it means failure. Increase the value of n to continue the search (Fig. 6). When $n=2$, search range of $f\left(\omega \right)$ is conducted in a time unit of two time, and so on.), as a new approximate time to recalculate the positioning result. When the positioning result and the approximate position, approximate time, and other information are consistent, it can be determined that the assumed approximate time ($Toe+f\left(\omega \right))$ is the true value, and the positioning result at this time can be taken. The value of $N$ cannot exceed the theoretical upper limit error of 187.5s for the assisted positioning method, otherwise all solutions may fail.

Fig. 6.

Schematic diagram of the change in search space range after the improved algorithm. (A) shows the traditional method of searching and the scope of the search. (B) shows the change in search method and search scope after changing the dimension. (C) shows the change in search method and search scope after using the strategy in this paper.

Note: The darker the color, the more overlapping the search space.

The specific implementation steps are as follows:

First, calculate the corrected pseudorange values for all satellites ${\rho }_c^{\left(i\right)}$.

$$\begin{array}{c}{\rho }_c^{\left(i\right)}={\rho }^{\left(i\right)}-I-T-S+\delta t^{\left(s\right)}\end{array}$$ (5)

In this equation, ${\rho }_c^{\left(i\right)}$ represents the measured pseudorange of satellite $i$, $I$ represents the ionospheric delay correction value, $T$ represents the tropospheric delay correction, $S$ represents the Earth rotation correction value, and $\delta t^{\left(s\right)}$ represents the satellite clock bias.

Assuming the approximate time $t_0$ is completely unknown, take $t_0=Toe$ time and calculate the satellite-earth distance $D^{\left(i\right)}\left(t_0+f\left(\omega \right)\right)$ at the time $\left(t_0+f\left(\omega \right)\right)$ with an interval of $N$ s. Based on this time, calculate the distance between the satellite position and the approximate position, and then calculate the difference between this distance and the corrected pseudorange. Sum up this difference for all satellites at a certain time:

$$\begin{array}{c}d\left(n\right)=\sum _{i=1}^m\left|D^{\left(i\right)}\left(t_0+n*N\right)-{\rho }_c^{\left(i\right)}\right|\end{array}$$ (6)

Where $m$ represents the number of satellites.

Solve the value of $n_{\min }$ corresponding to the minimum value of $d\left(n\right)$ among all time intervals. And obtain the time interval closest to the current time $t_{now}$, which is

$$\begin{array}{c}{t}_{now}=t_0+n_{\mathit{min}}*N\end{array}$$ (7)

Then, according to the auxiliary positioning equation, substitute $t_{now}$ into the calculation to obtain the positioning result, including the receiver's position coordinates, clock bias, and absolute deviation value, and perform iterative calculations. According to the least square principle, the least square equation can be obtained

$$\begin{array}{c}\{\begin{array}{c}\Delta X^{\left(k\right)}={\left[H^{\mathrm{T}}\left(X^{\left(k\right)}\right)H\left(X^{\left(k\right)}\right)\right]}^{-1}·H^{\mathrm{T}}\left(X^{\left(k\right)}\right)\Delta \rho \left(X^{\left(k\right)}\right)\\ X^{\left(k+1\right)}=X^{\left(k\right)}+\Delta X^{\left(k\right)}\end{array}\end{array}$$ (8)

where $k$ represents the $k$-th iteration,

$$\begin{array}{c}\Delta X^{\left(k\right)}=\left[\Delta u,\Delta t_{\mathrm{d}}^{\mathrm{r}},\Delta {\phi }^{chip}\right]\end{array}$$ (9)

initial value $X^{\left(0\right)}=\left[u^{\left(0\right)},t_{\mathrm{d}}^{\mathrm{r}\left(0\right)},{\phi }^{chip\left(0\right)}\right]$,

$$\begin{array}{c}H\left(X^{\left(k\right)}\right)=\left[\begin{array}{ccc}{v}_1^{\left(k\right)}\left(t_1^{\mathrm{s}\left(k\right)}\right)& -v_1\left(t_1^{\mathrm{s}\left(k\right)}\right)v_1^{\left(k\right)}\left(t_1^{\mathrm{s}\left(k\right)}\right)& 1\\ v_2^{\left(k\right)}\left(t_2^{s\left(k\right)}\right)& -v_2\left(t_2^{s\left(k\right)}\right)v_2^{\left(k\right)}\left(t_2^{s\left(k\right)}\right)& 1\\ ⋮& ⋮& ⋮\\ -v_n^{\left(k\right)}\left(t_n^{\mathrm{s}\left(k\right)}\right)& -v_n\left(t_n^{\mathrm{s}\left(k\right)}\right)v_n^{\left(k\right)}\left(t_n^{\mathrm{s}\left(k\right)}\right)& 1\end{array}\right]\end{array}$$ (10)

$$\begin{array}{c}\Delta \rho \left(X^{\left(k\right)}\right)=\left[\begin{array}{c}{D}_1-c{t}_1^{\text{ms}}-\parallel s_1\left(t_1^{\mathrm{s}\left(k\right)}\right)-u^{\left(k\right)}\parallel {\phi }^{\text{chip}}+{\epsilon }_1^{\left(k\right)}\\ D_2-c{t}_2^{\text{ms}}-\parallel s_2\left(t_2^{\mathrm{s}\left(k\right)}\right)-u^{\left(k\right)}\parallel {\phi }^{\text{chip}}+{\epsilon }_2^{\left(k\right)}\\ D_n-c{t}_n^{\text{ms}}-\parallel s_n\left(t_n^{\mathrm{s}\left(k\right)}\right)-u^{\left(k\right)}\parallel {\phi }^{\text{chip}}+{\epsilon }_n^{\left(k\right)}\end{array}\right]\end{array}$$ (11)

until $X^{\left(k+1\right)}-X^{\left(k\right)}\le \Delta t$, and $\Delta t$ is the approximate time precision, the success rate of the algorithm is calculated. Among them, Fig. 2 shows the core processing flow of the algorithm.

Fig. 2.

The algorithm processing flowchart.

Among them, the judgment basis for the rationality of the results is as follows.

• •Unreasonable when $\left|{u-u}^{\left(0\right)}\right|>d/2$.
• •Convert the position coordinates of the receiver into geodetic coordinates, and judge whether the result is reasonable according to the rationality of the height.

If all the search spaces of time ambiguity are calculated and no suitable results are obtained, it is proved that the algorithm has failed to locate.

4. Experimental verification

In order to further verify the feasibility of the positioning method proposed in this paper, the experimental verification is carried out with the help of the experimental equipment and application environment provided by the rotating carrier test platform, as shown in Fig. 3.

Fig. 3.

Experimental application scenario.

Among them, the experimental black box provides a safe environment without signal interference. Through the software, the program-controlled motor can be controlled to drive the rotating carrier to rotate, so as to simulate the rotating environment. The receiver board is placed in the rotating carrier, and the signal source transmits analog signals to the receiver through the antenna.

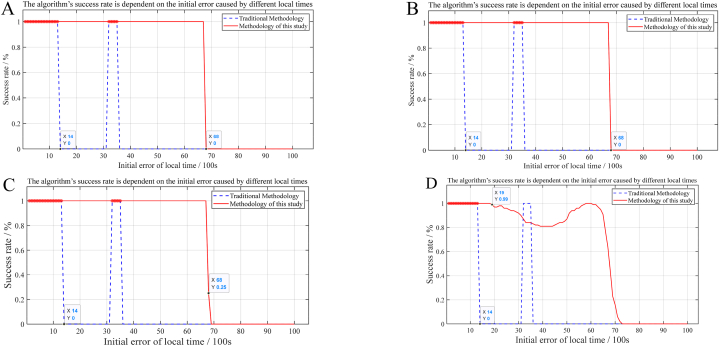
Based on this experimental scenario, carry out the general verification of the algorithm based on conservative principles. When solving, the whole millisecond time of the signal in the original signal data is set to be unknown, and the traditional method and the method in this paper are used to solve the positioning at intervals of 100s, in which the approximate position is the accurate position, and the measured values are used for other pseudo-range information. The reason for choosing 100s is that there is an error between the actual approximate position and the theoretical approximate position, so it is necessary to choose a time interval that is half smaller than the maximum time error of 187.5s, and the time interval of 100s is chosen according to the conservative principle, which is conducive to observing the results of the algorithm and verifying the generality of the algorithm. The result is shown in Fig. 4.

Fig. 4.

Comparison of success rates with traditional algorithms under different approximate localization errors of (A) 10 m, (B) 100 m, (C) 1 km, and (D) 10 km.

As shown in Fig. 4A–D, in the experiment, the success rate of the traditional method drops to 0 after the time error exceeds 1400s, which is in line with the situation that the calculation error will occur after the time error exceeds 187.5s in theory. The time search method in this paper is improved and can theoretically adapt to any time error. In this case, the maximum time error reaches 6000s, which shows that the condition limitation of the original algorithm is extended. When the error ranges are 10 m, 100 m, 1 km, etc., the success rate of the receiver is almost the same, and it starts to decline when the time error exceeds 6800s, which also shows that when the position error is relatively small, the influence on the algorithm success rate, that is, the whole millisecond time, is also small, mainly due to the approximate time error.

In the case that there is no approximate location information at all, the elevation error range can be set to 10 km by using the law of the elevation range of surface accessories, as shown in Fig. 4D. According to the results of the simulation calculation, the success rate of the receiver begins to decrease when the time error exceeds 1900s, and the performance is only slightly improved compared with the traditional method. It shows that when the approximate position error is large, it will also affect the sensitivity of the algorithm to the approximate time error. This phenomenon can also show that the feature that the approximate position and approximate time accuracy jointly affect the success rate of the algorithm still exists.

In the traditional method, due to the uncertainty of time error, direct iterative calculation can lead to error amplification. Although similar attempts can be made, the traditional iterative calculation process requires re-calculation of satellite positions and re-solving the least squares positioning solution each time a new time is attempted. The matrix operation calculation amount will increase rapidly with the increase of calculation times. However, the method proposed in this paper only needs to quickly estimate the approximate time range. When searching with an interval of 100s, it can stop as long as it can search for a small sum of absolute values of pseudorange residuals, without performing positioning calculation every time. Therefore, it has obvious advantages in calculation speed and efficiency.

In order to further verify the applicability of the algorithm, with the experimental method of 4.1, modify the time interval and repeat the experiment many times. The experimental data are shown in Table 1. Obviously, it can be found that when the algorithm is applied in practice, the time interval of 60s is more conducive to the positioning and calculation of the receiver. As shown in Fig. 5, the analysis of the experimental results is similar to that in 4.1.

Table 1.

The change of solution success rate at different time intervals.

Time span N	The number of samples when the success rate continuously drops from 100%/0%
	Traditional method	This method (10m–100 m)	This method (1 km)	This method (10 km)
30	45/46	100/-	100/-	–
40	33/34	100/-	100/-	16/-
50	27/28	100/-	100/-	12/-
60	22/23	100/-	100/-	30/-
70	19/20	96/97	96/98	29/-
80	16/17	84/85	84/86	24/91
90	15/16	75/76	75/77	22/81
100	13/14	67/68	67/69	18/73
110	12/13	61/62	61/63	18/66
120	11/12	56/57	56/58	–
130	10/11	52/53	52/54	–
140	9/10	48/49	48/50	6/7
150	9/10	45/46	45/47	6/7

Fig. 5.

At the time interval of 60s, the success rates of the traditional method and this method are compared under different approximate position errors of (A) 10 m, 100 m, 1 km, and (B) 10 km.

Statistic the experimental results. Table 1 shows the corresponding changes in the success rate when the time interval changes. As can be seen from Table 1, when the approximate error ranges are 10 m, 100 m and 1 km, this method is obviously due to the traditional method in terms of the number of successful samples. When the approximate error range is 10 km, this method has obvious advantages in the time interval of 60s-110s, but it is not high for the traditional algorithm, which accords with the conclusion that the value of n should be slightly less than half of 187.5s.

From the overall comparison of the experiment, the effect of using the time interval of 60s is better in practical application, while the time interval of 100s accords with the generality of the algorithm. Choose a reasonable time interval is conducive to obtaining better experimental results.

This method can also set a threshold value. After searching for a value smaller than the threshold, positioning calculation can be performed. When the positioning result error exceeds the approximate position error, it indicates that it may be due to large pseudorange observation error or too loose threshold setting, and the correct time range can be searched further. The additional calculations caused by this are few and linearly increasing, and can be almost ignored according to the current processing power of embedded processors. Therefore, this method not only solves the problem of whether it can be positioned, but also has good engineering practical value.

By setting a reasonable approximate position error for repeated experiments, it can be found that since the whole millisecond value of the approximate time to be solved is discrete, the approximate position error within a reasonable range cannot directly affect the whole millisecond value of the solution and the final positioning error.

To sum up, this algorithm can improve the success rate of the algorithm under various approximate position errors without reducing its performance.

5. Computational complexity evaluation

In this example, the accuracy of the approximate position information is relatively accurate, and only the influence brought by the uncertainty of the time dimension needs to be considered. As shown in Fig. 6A–B, when $u_n$ approaches $0$, it essentially reduces the original two-dimensional uncertainty in time and position to one-dimensional search, as shown in Fig. 6C. The algorithm in this paper is further simplified, only considering the case of $t_n>0$, and the original circular search is changed into segmented search, which can have less calculation under the condition of large search space and large number of satellites, simplify the complexity of the original algorithm and improve the operation speed.

In the positioning calculation, the fewer observed satellite data selected, the smaller the computational complexity. Therefore, the conditions when using five satellites are compared. When the uncertainty of the auxiliary approximate time information exceeds ± 187.5s, it is necessary to consider increasing the search range and re-solving. The search dimension of $n$ satellites is $\omega$, which is

$$\begin{array}{c}\omega =\lceil \frac{\Vert \Delta u\Vert +v_i\left|\Delta t_d^r\right|+\left|\Delta {\phi }^{chip}\right|}{d}-\frac{1}{2}\rceil \end{array}$$ (12)

and the maximum number of searches is $L$, which is

$$\begin{array}{c}L={\omega }^n\end{array}$$ (13)

Calculate the maximum number of computations required by the conventional method and the method proposed in this paper, respectively, as the search space varies, as shown in Table 2.

Table 2.

Comparison of the maximum number of calculations.

Approximate time accuracy $\Delta t$/s	Search space $\omega$	Traditional method	This method
0 ≤ $\Delta t$ ≤187.5	1	1	1
187.5＜ $\Delta t$ ≤562.5	2	32	3
562.5＜ $\Delta t$ ≤937.5	3	243	5
937.5＜ $\Delta t$ ≤1312.5	4	1024	7

From the comparison of Tables 2 and it can be seen that according to the traditional algorithm, each satellite should consider a separate whole millisecond search range, and even under the condition of five satellites, it still has a high amount of calculation. As can be seen from Table 3, when the number of satellites increases, the amount of calculation increases exponentially due to the algorithm, and with the increase of search space, the number of calculations becomes too large. However, this method is not affected by this because it reduces the search dimension and changes the search mode. What's more, as shown in the above two tables, the calculation amount of this method increases linearly. This also echoes the results of using segmented search in Fig. 6C.

Table 3.

The increase in the number of satellites is the comparison of the maximum number of calculations.

Search space $\omega$	Traditional method				This method
	n = 5	n = 6	n = 7	n = 8	n
1	1	1	1	1	1
2	32	96	288	864	3
3	243	729	2187	6561	5
4	1024	3072	9216	27648	7

Note: n is the number of satellites.

Through practical calculation, we find that the experimental results of the algorithm (Fig. 4) and the speed of the algorithm (Table 2) are far better than expected. The reason may be that the speed of the algorithm is faster than the theoretical one due to various reasons such as the change of the satellite speed to the earth, the change of the satellite geometric distribution, and the least square iteration method. In order to ensure the robustness of the algorithm, this algorithm conservatively adopts twice the theoretical maximum time error (350s) as the size of the segmented search space, which makes the whole algorithm.

6. Conclusion

In this study, we deeply explore and analyze the rotating carrier A-GPS method and related algorithms. The research shows that these methods are of practical value under specific conditions, and it is found that the formula of the classical algorithm is possible to be simplified for solving the problem under specific demand scenarios. Although certain conditions need to be met, they can be achieved with the requirements analyzed in this paper, which is of great help in improving the efficiency of solving. In order to verify the feasibility of the new solution method, we use the hardware object of the rotary navigation receiver to collect data and carry out the algorithm simulation experiment. The experimental results show that our method still has good performance under the condition of increasing the approximate position error, which verifies the effectiveness of the one-way fuzzy time information positioning algorithm.

When the algorithm encounters extreme conditions, such as a large time precision error, compared with the problem that the traditional method may fail to calculate, which leads to a sharp increase in the amount of calculation, this method can obtain better control over the amount of calculation, and at the same time, the reason why this method is superior is explained by a schematic diagram. However, when there is no approximate position information at all, the elevation error is too large, and there is only one-way fuzzy time information, the solution method in this paper has not achieved a more obvious performance improvement. Under this more complicated condition, if we can further improve the algorithm to solve this limitation, it will make the application scope of the algorithm wider.

Author contribution statement

Rundong Li, Peng Wu: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper. Lu Feng, Haibo Tong, Zhipeng Ren: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.