Abstract
Motivation
Efficient assessment of the blood–brain barrier (BBB) penetration ability of a drug compound is one of the major hurdles in central nervous system drug discovery since experimental methods are costly and time-consuming. To advance and elevate the success rate of neurotherapeutic drug discovery, it is essential to develop an accurate computational quantitative model to determine the absolute logBB value (a logarithmic ratio of the concentration of a drug in the brain to its concentration in the blood) of a drug candidate.
Results
Here, we developed a quantitative model (LogBB_Pred) capable of predicting a logBB value of a query compound. The model achieved an R2 of 0.61 on an independent test dataset and outperformed other publicly available quantitative models. When compared with the available qualitative (classification) models that only classified whether a compound is BBB-permeable or not, our model achieved the same accuracy (0.85) with the best qualitative model and far-outperformed other qualitative models (accuracies between 0.64 and 0.70). For further evaluation, our model, quantitative models, and the qualitative models were evaluated on a real-world central nervous system drug screening library. Our model showed an accuracy of 0.97 while the other models showed an accuracy in the range of 0.29–0.83. Consequently, our model can accurately classify BBB-permeable compounds as well as predict the absolute logBB values of drug candidates.
Availability and implementation
Web server is freely available on the web at http://ssbio.cau.ac.kr/software/logbb_pred/. The data used in this study are available to download at http://ssbio.cau.ac.kr/software/logbb_pred/dataset.zip.
Graphical Abstract
Graphical Abstract.
1 Introduction
The blood–brain barrier (BBB) is a highly selective semi-permeable membrane composed of endothelial cells. The BBB regulates the transport of molecules from blood vessels to the central nervous system (CNS) (Bradbury 1993), and the tightly selective permeability enables to maintain homeostasis of the brain microenvironment, and protects the CNS from damage by harmful substances (Abbott et al. 2010).
CNS diseases are the second most common following cardiovascular diseases (Vilella et al. 2015). The lower success rate of the CNS drugs (8%) than that of the cardiovascular drugs (20%) is mainly due to the BBB since most small-molecule and macromolecule drugs are not able to cross through the BBB into the brain (Chen and Liu 2012, Gao et al. 2013, Valentini et al. 2019). Therefore, BBB permeability of CNS drugs should be improved to elevate the success rate in CNS drug discovery (Di et al. 2013).
Various in vivo and in vitro experimental assays have been developed to measure the BBB permeability of molecules: a logarithmic ratio of the concentration of a drug in the brain to its concentration in the blood (logBB) (Abbott 2004, Carpenter et al. 2014, Ciura and Dziomba 2020). In vitro methods such as parallel artificial membrane permeability assay (PAMPA) and immobilized artificial membrane (IAM) typically use cultured brain tissue cells or artificial membranes to measure a drug concentration on each side (Reichel et al. 2003, Carrara et al. 2007, Mensch et al. 2009). Though in vitro methods have advantages in performing experiments in parallel and are suitable for drug screening, none of the methods can reproduce in vivo environments and, thus, in vitro logBB values are often not consistent with in vivo logBB values (Colquitt et al. 2011). On the contrary, in vivo methods using living animals are appropriate to obtain real logBB values, but they are more difficult to conduct as well as time-consuming and laborious, and thus are not suitable for large-scale experiments (Srinivasan et al. 2015, Valentini et al. 2019).
Due to the experimental difficulties, computational methods have been introduced to estimate the BBB permeability of drug candidates (Kumar et al. 2013; Radan et al. 2022). Early prediction models were mainly qualitative and predicted whether a query compound was BBB-permeable or nonpermeable (Muehlbacher et al. 2011). Several machine learning algorithms including random forest (RF) (Svetnik et al. 2003), support vector machine (SVM) (Ghorbanzad’e and Fatemi 2012), genetic algorithm (Shen et al. 2008), and artificial neural network (ANN) (Jung et al. 2007) have been used to develop BBB permeability classification models (Gerebtzoff and Seelig 2006, Guerra et al. 2008, Mehdipour and Hamidi 2009, Martins et al. 2012, Suenderhauf et al. 2012, Wang et al. 2018, Singh et al. 2020, Tang et al. 2022). In a recent study, a BBB classification model was developed based on Light Gradient Boosting Machine (LightGBM), a gradient-boosting framework based on decision tree algorithms, with 7162 compounds and achieved a high area under the curve (AUC) value of 0.94 (Shaker et al. 2021).
Recently, the demand for quantitative BBB permeability models has been increasing to predict the permeability of drug candidates to cross BBB (Muehlbacher et al. 2011). Several quantitative models have been developed with the logBB values of compounds. However, since the publicly available logBB dataset is very limited, it is difficult to develop a high-performance quantitative model using a small dataset. Therefore, out of several published quantitative models, only few are publicly accessible (Platts et al. 2001, Bayat et al. 2011, Muehlbacher et al. 2011, Shin et al. 2021). One of the publicly accessible models for quantitative prediction is PreADMET (Lee et al. 2004). It is an online web server for the quantitative prediction of drug properties, developed by Lee et al., in 2004 based on ANN trained with the 2D descriptors calculated by TOPOMOL (Lee et al. 2004, Polyakova et al. 2006). Another available model is ADMET Prediction Service developed by Dyabina et al. (2016). It was trained based on ANN with the logBB values of 529 compounds. In a recent study by Ciura et al. (2020), multi-linear regression (MLR) and SVM were developed with known logBB values of only 45 marketed drugs. They used 30 of the drugs for model training and 11 for testing. The models achieved an R2 score of 0.69 by SVM model and 0.76 by MLR model on the training dataset. When applied to the test dataset, R2 was over > 0.9. The abnormally high R2 score on the test dataset might be due to the extremely small amount of data. Wang et al., assembled a dataset of 439 logBB values (341 for training and 98 for validation) and developed three machine learning models based on RF, SVM, and k-nearest neighbor (kNN) using 192 2D descriptors calculated by Molecular Operating Environment (MOE) (Wang et al. 2015). Then, they developed a consensus model that averages the predicted scores generated from the three machine learning models. The consensus model attained an R2 of 0.52 on validation dataset. Liu et al. (2001) developed a quantitative structure activity relationship (QSPR) models to evaluate the BBB penetration. The authors used a dataset of 112 compounds with experimentally determined BBB penetration and calculated various molecular descriptors using Dragon software. They used MLR and partial least squares regression to develop QSPR models. The best model achieved an R2 of 0.70 on validation dataset. Wu et al., proposed an ANN model to predict the BBB permeability of drug-like compounds (Wu et al. 2021). The model used a group contribution method to estimate the molecular descriptors and was trained on a dataset of experimentally measured logBB values of 255 compounds. The model achieved a prediction accuracy with a relative error of 0.810 and root mean square error (RMSE) of 0.236 on an external validation dataset (40 compounds).
Here, we aimed at developing a quantitative BBB permeability prediction model with a larger dataset and thereby having a higher accuracy. To the best of our knowledge, we compiled the largest logBB dataset from various literature (Platts et al. 2001, Fu et al. 2005, Bayat et al. 2011, Muehlbacher et al. 2011, Carpenter et al. 2014, Shin et al. 2021, Tang et al. 2022) and used a gradient boosting machine learning algorithm (LightGBM) for model construction (Zhang et al. 2019). Our constructed model (LogBB_Pred) showed an R2 of 0.61 and mean square error (MSE) of 0.36, which were better than publicly available quantitative BBB models when evaluated on a test dataset. Our model is freely accessible via http://ssbio.cau.ac.kr/software/logbb_pred/ for practical use and we believe that our model would be useful in early high-throughput screening of CNS drugs and would increase the success rate in CNS drug development.
2 Materials and methods
2.1 Dataset collection and preprocessing
The size and quality of datasets greatly impact the performance of the prediction models trained by machine learning algorithms (Chen et al. 2021). For a better performance, we compiled the largest dataset, to the best of our knowledge, of the experimentally measured 1276 logBB values from the literature (Platts et al. 2001, Fu et al. 2005, Bayat et al. 2011, Muehlbacher et al. 2011, Carpenter et al. 2014, Shin et al. 2021, Tang et al. 2022). To avoid bias in the dataset leading to a biased or overfitted prediction model, similar chemical compounds were discarded based on Tanimoto similarity with a cutoff of 0.85 (Bajusz et al. 2015, Macomber et al. 2015). For the similarity calculation, chemical compounds were represented in the format of simplified molecular-input line-entry system (SMILES) (Weininger 1988) and their fingerprints were calculated by Dragon software (Mauri et al. 2006). Tanimoto similarity was calculated based on the fingerprints of compounds. Consequently, the final dataset contained 913 logBB values ranging from −2.69 to 1.7. The equation for Tanimoto similarity is:
| (1) |
T denotes Tanimoto similarity between molecules a and b, where Na and Nb represent the numbers of on bits in the molecules a and b, and Nc denotes the number of bits that are on in both molecules.
For feature preparation, the physical and chemical properties of chemical compounds were calculated from the chemical structures represented in the SMILES format. Specifically, the properties (1650 2D/3D molecular descriptors) including eccentric connectivity index (Sharma et al. 1997) and charged partial surface area (Stanton and Jurs 1990) were calculated using a publicly available tool, Mordred, which is a recently published molecular descriptor calculator (Grisoni et al. 2018, Moriwaki et al. 2018).
After removing descriptors with missing values, the resulting dataset contained 1164 informative molecular descriptors for each compound. Since there might be redundant features, we filtered out such features by Pearson’s correlation coefficient (PCC) between features (Thakkar et al. 2021). If two features are redundant, only one with lower PCC with logBB was discarded. To find an optimal feature set, different training datasets were constructed with different coefficient thresholds from 0.1 to 0.9. After filtering, features were normalized using standard scaling technique (Raju et al. 2020). The datasets were used for cross-validation and an optimal threshold was determined.
In order to validate model performance, we collected additional 109 compounds (Hou and Xu 2003). Compounds that showed a Tanimoto similarity >0.85 with those in the training dataset were discarded, which resulted in a total of 27 unique compounds. These compounds were used as an independent test dataset for external validation. For the evaluation of our model as a classification model, we also collected binary data of compounds (BBB-permeable and BBB-nonpermeable) from MedChemExpress (https://www.medchemexpress.com/).
2.2 Model construction and evaluation
In this study, we used LightGBM algorithm to develop a regression model to predict BBB permeability (logBB value) (Zhang et al. 2019). LightGBM is an advanced method of gradient boosting decision tree and is known to perform better than other decision tree learning algorithms (Friedman 2001, Al Daoud 2019). LightGBM also implements sparse optimization, multiple loss functions, regularization, bagging, early stopping, and efficient parallel training.
For comparison, we also developed prediction models based on other machine learning algorithms: RF (Svetnik et al. 2003), kNN (Song et al. 2017), ANN (Tadeusiewicz 2015), MLR (Vieira et al. 2016), AdaBoost (CAO et al. 2014), XGBoost (Ogunleye and Wang 2020), and SVM (Ben-Hur et al. 2008). RF is an ensemble learning method that combines multiple decision trees to improve model accuracy and generalization. It has been widely applied for classification as well as regression (Svetnik et al. 2003). kNN is another simple and efficient algorithm for both classification and regression tasks. kNN algorithm finds the k-nearest data points in a training dataset close to a given input data point, and then predict an output based on the majority vote or the average of the k-nearest neighbors (Song et al. 2017). ANN is an algorithm mimicking human brain learning and is composed of nodes and connections (Lancashire et al. 2009). The learning process of ANN is to find the best interconnections (weights) between nodes constituting the network topology. MLR is a statistical method used to model a linear relationship between a dependent variable and one or more independent variables. The objective of MLR is to find the best-fit line that represents the relationship between variables (Vieira et al. 2016). SVM is a supervised learning algorithm used for classification and regression analysis. Its fundamental concept is to identify a hyperplane that most effectively divides data points into distinct classes. The objective of the algorithm is to locate the decision boundary that optimizes the margin between the classes, which is defined as the gap between the hyperplane and the closest data points from each class (Ben-Hur et al. 2008). AdaBoost, known as Adaptive Boosting, is an ensemble method in machine learning. This algorithm initially assigns equal weights to all data points and constructs a model. It then increases the weights of misclassified points, emphasizing their importance in the subsequent model. This process continues until a lower error rate is achieved, leading to the training of multiple models (Cao et al. 2014). XGBoost (Extreme Gradient Boosting) uses gradient boosting, which adjusts the weights of misclassified data points to prioritize difficult-to-predict instances. This process leads to the creation of a strong ensemble model that provides accurate predictions for various tasks, such as classification and regression (Ogunleye and Wang 2020).
The 913 compounds were utilized as a training dataset. For evaluation, we conducted a 10-fold cross-validation with the training dataset. For model optimization, we performed parameter optimization since parameters often impact the accuracy of prediction models (Yang and Shami 2020). Parameters were optimized on the basis of their impact on model performance, GridSearchCV method was applied for parameters optimization and selected parameters and their range values investigated are listed in Supplementary Table S1 (Belete and Huchaiah 2022). An optimized model was evaluated on the independent dataset of 27 unique compounds.
2.3 Performance metrics
The quantitative model performance was measured based on two statistical criteria namely coefficient of determination (R2) and mean square error (MSE). They are defined as below:
| (2) |
| (3) |
denotes a predicted logBB value, denotes an actual logBB value, is the mean of the actual values, and n is the amount of data. The R2 score close to +1 and MSE score close to 0 represent a higher accuracy and better performance. These metrics were used to evaluate our model and to compare the performances of publicly available models.
The qualitative model performance was calculated based on Matthew’s correlation coefficient (MCC), sensitivity, and specificity. They are defined as below:
| (4) |
| (5) |
| (6) |
where TP represents the number of true positives, TN represents the number of true negatives, FP represents the number of false positives, and FN denotes the number of false negatives.
3 Results and discussion
To advance the CNS drug discovery, it is essential to develop a cheap, fast, and accurate method to assess the BBB permeability of drug candidates. Computational prediction of BBB permeability would be an alternative method to the in vitro and in vivo methods. Though computational predictions are not perfect yet, they can reduce the number of drug candidates enough to afford experimental testing and allow high-throughput screening of a huge number of chemical compounds at a much faster speed. Thus, the challenge in CNS drug discovery is the development of an accurate BBB permeability prediction model.
In this study, we compiled the largest logBB dataset, to our knowledge, and used an efficient machine learning algorithm to build a more accurate quantitative model. Currently, most published BBB permeability prediction models are classification models that just determine whether a query compound is BBB-permeable or not (Castillo-Garit et al. 2017, Wang et al. 2018, Plisson and Piggott 2019, Singh et al. 2020). In CNS drug discovery, it is essential to predict the quantitative BBB permeability of chemical compounds, such as logBB since certain BBB-less-permeable drugs are still effective at low concentrations enough to be used as drug candidates. However, due to the limited data size of available logBB values, there are several quantitative BBB permeability prediction models (Sun 2004, Bayat et al. 2011, Wu et al. 2021) and only few of them are publicly available to access (Lee et al. 2004, Dyabina et al. 2016).
3.1 Overall flow of model construction
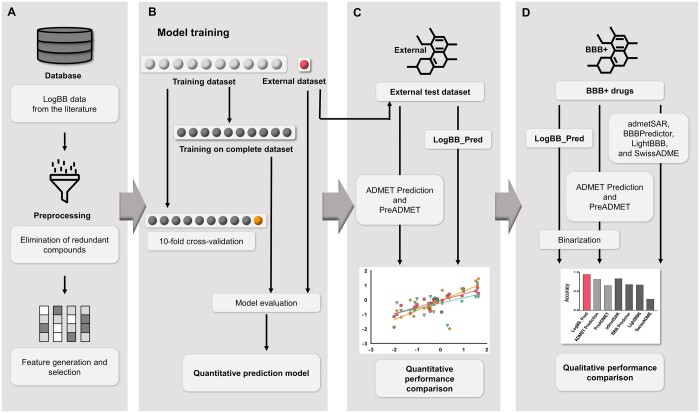
The overall scheme to construct a quantitative logBB prediction model is illustrated in Fig. 1. Firstly, we collected the logBB values of chemical compounds from the various published literature and removed redundant chemicals to avoid biased or overfitted learning (Fig. 1A). To prepare features, we calculated the physical and chemical properties (descriptors) of the chemical compounds and discarded the descriptors with missing values. Redundant features were also removed based on PCC threshold. An optimal PCC threshold was determined by testing models built on various feature numbers, i.e. PCC threshold. Prediction models were developed based on various learning algorithms including LightGBM and trained models were cross validated (Fig. 1B). The final optimized model trained using LightGBM algorithm with different parameters were evaluated quantitatively on a test dataset and its performance was compared with other quantitative models (Fig. 1C). To investigate whether our model performs well as a classification model, the compounds in the test dataset were binarized into BBB-permeable and nonpermeable by a logBB threshold of −1 (Gao et al. 2017). The performance as a qualitative model was also compared with other qualitative models (Fig. 1D).
Figure 1.
Schematic diagram of logBB prediction model construction. (A) LogBB dataset collection and features preprocessing. (B) Model was trained on a complete dataset and further evaluated on external dataset, and average model performance was also measured by applying 10-fold cross-validation. (C) Independent test dataset was used to compare the performance of our model with other publicly available quantitative models. (D) Binarized test dataset and additional BBB-permeable drug library were used to compare the performance of our model as a qualitative model with publicly available qualitative models.
3.2 Data collection
In this study, as data size is one of the critical factors affecting the performance of machine learning models, we compiled 1276 logBB values of chemical compounds from the literature (Platts et al. 2001, Fu et al. 2005, Bayat et al. 2011, Muehlbacher et al. 2011, Carpenter et al. 2014, Shin et al. 2021, Tang et al. 2022), which is the largest logBB dataset, to our knowledge. Although we collected the largest dataset, it should be noted that logBB values were determined by different experimental methods or under different conditions, and, thus, the quality of the dataset can still be improved. However, this issue could be resolved only when a robust and high-throughput experimental method is used.
3.3 Data preprocessing
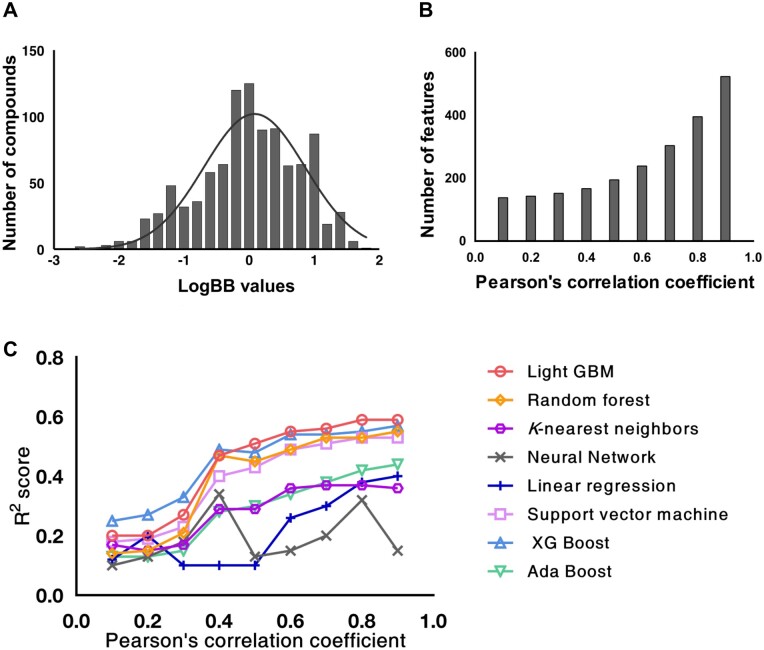
Since there might be similar chemical compounds in the collected logBB dataset, similar compounds were discarded based on Tanimoto similarity between chemicals to maintain the uniqueness of the compounds. Otherwise, the dataset may lead to a biased and overfitted model with abundant similar compounds. To calculate Tanimoto similarity, chemical compounds were firstly represented in SMILES format and then proceeded to Extended connectivity fingerprints (ECFPs) calculation using Dragon software (Mauri et al. 2006). The fingerprints, represented as 1024 bits of 0 or 1, were then used to calculate the similarity of two chemical compounds. The compounds with a similarity of over 0.85 were discarded from the dataset, which was a commonly accepted threshold to determine whether the two chemical compounds are similar or not (Macomber et al. 2015). Finally, 913 compounds were left in the logBB dataset and the distribution of these logBB values is shown in Fig. 2A.
Figure 2.
LogBB value distribution of collected data, and number of features, and performances with respect to the threshold of Pearson’s correlation coefficient. (A) Distribution of logBB values compiled in our dataset. (B) The number of selected features (y axis) when redundant features were removed based on a given threshold of Pearson’s correlation coefficient (x axis). (C) Ten-fold cross-validation results of the models trained using various learning algorithms with respect to various selected features based on Pearson’s correlation coefficient.
In machine learning, numerical values (features) are required for training. Mordred was used to calculate the physical and chemical properties (descriptors), and those numerical values were used as features for machine learning. Mordred calculated 1650 2D and 3D molecular descriptors including molecular weight, lipophilicity (logP), number of rings, number of bonds, and number of atoms. Molecular descriptors are mathematical representation of molecular properties: 2D descriptors provide information regarding size, shape, and electronic distribution, and 3D descriptors describe the 3D conformation of a molecule, such as intramolecular bonding (Nettles et al. 2006). A total of 1650 descriptors were initially considered for the analysis. Those with missing values were removed from the dataset, leaving a subset of informative descriptors.
Like the similarity between chemicals, there may be similar features that have similar impact on model performance. We calculated pairwise PCC values between features, and between feature and logBB. If a pair of features has a greater correlation than a threshold, one with lower correlation with logBB was discarded. The optimal PCC threshold was 0.8 when we evaluated the effect of various PCC thresholds on performance.
3.4 Cross-validation with training dataset
We constructed models based on different learning algorithms (LightGBM, RF, kNN, MLR, SVM, AdaBoost, XGBoost, and ANN) and cross-validated them in 10-fold. Firstly, we set a PCC threshold and selected features. The number of features with respect to PCC threshold is shown in Fig. 2B. Once features were selected, six different models using different learning algorithms were constructed using 90% of the training dataset and then evaluated on the remaining 10% of the data. This model construction and evaluation were iterated 10 times and averaged performance values were obtained. The cross-validation results with respect to various feature numbers, i.e. PCC threshold, are shown in Fig. 2C. LightGBM outperformed other algorithms in terms of R2 score when trained with the features extracted using a PCC threshold of 0.8 (Fig. 2C).
LightGBM has many advantages such as faster training speed, higher efficiency, and better accuracy, and, thus, it outperforms existing boosting frameworks in terms of accuracy (Al Daoud 2019). Another advantage is the employment of Gradient-Based One-Side Sampling and Exclusive Feature Bundling techniques, which allows handling a large number of data instances and data features, respectively, and therefore avoiding overfitting problems (Zhang et al. 2019). In addition, the algorithm supports an exclusive feature bundling to reduce the dimensionality of a dataset, and thereby making it faster and more efficient (Al Daoud 2019).
The evaluation revealed that the model trained using LightGBM algorithm with 396 informative features selected with a PCC threshold of 0.8 demonstrated better prediction performance in terms of R2 score compared with other algorithms and other numbers of features. The resulting average MSE of LightGBM model was 0.22 and its R2 score was 0.59 (Table 1). During the cross-validation, parameters of the algorithms were investigated to optimize the models since parameter optimization can improve model accuracy (Huang 2020). The investigated parameters of LightGBM are listed in Supplementary Table S1 along with their searched value ranges and selected optimal parameter values.
Table 1.
Performance comparison of our model with publicly available quantitative models.
| Model | R 2 | MSE | Reference | |
|---|---|---|---|---|
| Cross-validation | Our model (LogBB_Pred) | 0.59 | 0.22 | This study |
| Independent evaluation | Our model (LogBB_Pred) | 0.61 | 0.36 | This study |
| ADMET prediction service | 0.56 | 0.41 | Dyabina et al. (2016) | |
| PreADMET | 0.3 | 0.66 | Lee et al. (2004) |
3.5 Performance comparison with other quantitative models
The LightGBM model was further evaluated using an independent dataset collected separately for an unbiased model validation. The model achieved an R2 score was 0.61 and MSE of 0.36 (Table 1 and Fig. 3), indicating that our model can be used as a highly accurate tool for predicting the potential blood–brain barrier permeability of query compounds. Therefore, it can also be used for screening large chemical compounds for CNS drug candidates.
Figure 3.
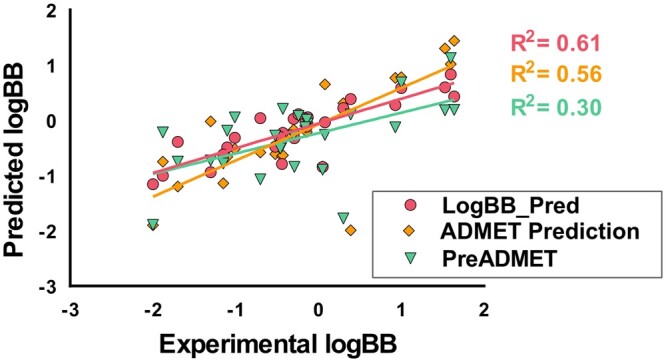
Performance comparison with other quantitative models. The predicted logBB values on an independent test dataset by our model and by other publicly available quantitative models. The predicted logBB values by our model are marked in red circles, those predicted by ADMET Prediction Service are marked in orange squares, and those predicted by PreADMET are marked in green triangles.
The performance of our model was compared with those of publicly available quantitative BBB prediction models: ADMET Prediction Service (Dyabina et al. 2016) and PreADMET (Lee et al. 2004). As publicly available quantitative models are few, we could compare ours with only those two models. The compounds included in the test dataset were queried to the public models to predict their logBB values, and the predicted values are shown in Fig. 3 and their performances are shown in Table 1. It should be noted that the compounds used to train the model served at ADMET Prediction Service and PreADMET were not known, the compounds included in the test dataset might be used for the training of the models. Nonetheless, our model had a higher R2 score and smaller MSE than other models. The R2 scores of ADMET Prediction Service and PreADMET were 0.56 and 0.30, respectively. The MSE scores of the two models were 0.41 and 0.66, respectively. Consequently, our model can predict logBB values of query compounds more accurately and reliably.
3.6 Performance comparison with other qualitative models
To date, many BBB qualitative (classification) models, that predict whether a query molecule is BBB-permeable or not, have been published and some of them are publicly available to access. Thus, we compared the performance of our model with those of the available BBB qualitative models to investigate whether our quantitative model can also operate as a qualitative model and outperform conventional qualitative models.
The test dataset used to compare the performance of quantitative models was also used to compare the performances of qualitative models. To make our quantitative model operate as a qualitative model, compounds with a predicted logBB over the cutoff of −1.0 was categorized as BBB-permeable while those below the cutoff were classified as BBB-nonpermeable (Kunwittaya et al. 2013, Dyabina et al. 2016).
Our model achieved an accuracy of 85%, MCC of 0.60, and a positive predictive value (PPV) of 1.0, when it was used as a qualitative model on the independent test dataset (Table 2). The high MCC value represents that our model can accurately classify both BBB-permeable compounds and BBB-nonpermeable compounds. In addition, the high PPV value represents that our model can accurately identify compounds capable of crossing through BBB. The performance of our model was comparable with the best qualitative model (admetSAR) investigated in this study (Table 2), even though our model was developed as a quantitative model. In addition, the PPV of admetSAR was only 0.66, which means that only 66% of the admetSAR-suggested compounds are BBB permeable, while our model was 100%. This is important in drug discovery to find potential drug candidates and to avoid unnecessary experiments. Other qualitative models did not show better performance results than ours. Consequently, our model can be used not only to predict absolute logBB values but also to efficiently classify drug compounds into BBB-permeable or BBB-nonpermeable based on conventional logBB cutoff.
Table 2.
Performance comparison of our model with publicly available qualitative models.
| Dataset |
Independent test dataseta |
||||
|---|---|---|---|---|---|
| Model | Our model (LogBB_Pred) | admetSAR | LightBBB | SwissADME | BBB predictor |
| Accuracy (%) | 0.85 | 0.85 | 0.70 | 0.70 | 0.70 |
| MCC | 0.6 | 0.65 | 0.42 | 0.29 | 0.15 |
| Sensitivity | 0.42 | 0.85 | 0.70 | 0.57 | 0.28 |
| Specificity | 0.99 | 0.66 | 0.74 | 0.75 | 0.85 |
| NPVb | 0.83 | 0.94 | 0.45 | 0.44 | 0.80 |
| PPVc | 1 | 0.66 | 0.89 | 0.22 | 0.77 |
| URL | http://ssbio.cau.ac.kr/software/logbb_pred | http://lmmd.ecust.edu.cn/admetsar2 | http://ssbio.cau.ac.kr/software/BBB | http://www.swissadme.ch/ | https://www.cbligand.org/BBB/index.php |
| Reference | This study | Yang et al. (2019) | Shaker et al. (2021) | Daina et al. (2017) | Liu et al. (2014) |
The independent test dataset used for the comparison of quantitative models was also used for qualitative model evaluation.
Negative predictive value: (number of true negatives)/(number of true negatives + number of false negatives).
Positive predictive value: (number of true positives)/(number of true positives + number of false positives).
For further comparison, we also evaluated the qualitative models on the CNS drug screening library containing only BBB-permeable chemical compounds, obtained from MedChemExpress (https://www.medchemexpress.com/). The compounds included in our dataset or those similar to the compounds included in our dataset in terms of Tanimoto similarity were discarded. As a result, we obtained 396 BBB-permeable compounds. Our model outperformed the other qualitative models (Fig. 4). Our model achieved an accuracy of 97% while admetSAR achieved 83%, LightBBB achieved 67%, BBB Predictor achieved 67%, and SwissADME achieved 29%. We also evaluated the quantitative models (ADMET Prediction Server and PreADMET) on the CNS drug screening library with the same binarization of predicted logBB values as ours. They achieved accuracies of 81% and 65%, respectively. Comparing a quantitative model with a qualitative model poses inherent challenges. Notably, to our knowledge, we complied the largest logBB dataset and which was used to develop our quantitative model (LogBB_Pred). The larger dataset could be one of the factors for the improved performance of our model. These results indicate that our model is able to accurately predict BBB-permeable compounds even in a real-world drug screening library and would be practically used for CNS drug screening.
Figure 4.
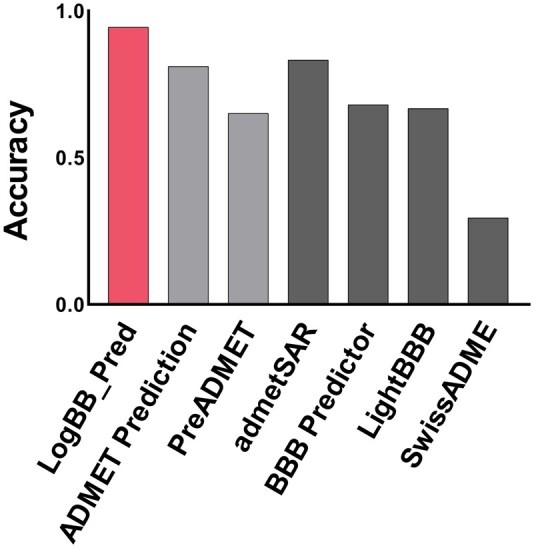
Performance comparison of qualitative models with a real-world CNS drug screening library. Three hundred and ninety-six compounds available from MCE company were used for model performance comparison. It should be noted that all the compounds in the library were BBB-permeable. The prediction accuracies of the quantitative models are shown in light gray color, and those of qualitative models are shown in dark gray color.
3.7 Web server construction
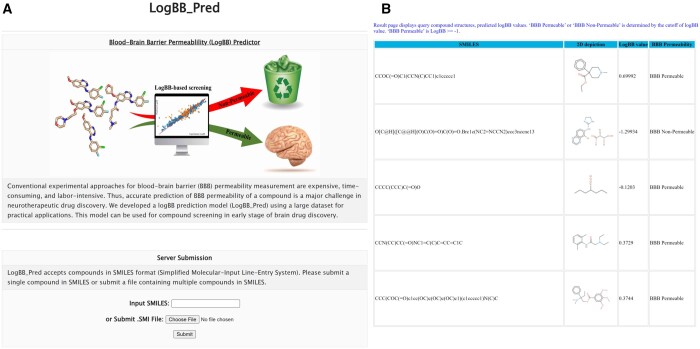
Developed prediction models should be freely accessible to drug developers, medicinal chemists, and other researchers to advance CNS drug discovery. To share our model, we constructed a web server that accepts a compound, or a list of compounds represented in a SMILES format and returns predicted logBB values (Fig. 5). The server is accessible via http://ssbio.cau.ac.kr/software/logbb_pred/.
Figure 5.
User interface of our LogBB_Pred web server. (A) Input interface where a user can submit a query compound in SMILES format or upload a file containing multiple compounds in the format of SMILES. (B) Prediction result page. The structure and predicted logBB value are displayed. “BBB Permeable” means its predicted logBB ≥ −1.
4 Conclusion
Experimental methods to measure logBB values are costly and low throughput, thus making BBB permeability assessment a bottleneck in CNS drug discovery. In this study, we developed a quantitative model (LogBB_Pred) to predict an absolute logBB value of a query molecule, which showed superior performance over conventional prediction models. Our model can accurately identify which molecules are potentially BBB-permeable, and accurately predict what their logBB values are. Therefore, our model can be used for practical virtual screening of a large number of chemical compounds to find CNS drug candidates as an alternative to experimental methods and consequently facilitate the advance of CNS drug discovery.
Supplementary Material
Contributor Information
Bilal Shaker, Department of Biomedical Engineering, Chung-Ang University, Seoul 06974, Republic of Korea.
Jingyu Lee, Department of Biomedical Engineering, Chung-Ang University, Seoul 06974, Republic of Korea.
Yunhyeok Lee, Department of Biomedical Engineering, Chung-Ang University, Seoul 06974, Republic of Korea.
Myeong-Sang Yu, Department of Biomedical Engineering, Chung-Ang University, Seoul 06974, Republic of Korea.
Hyang-Mi Lee, Department of Biomedical Engineering, Chung-Ang University, Seoul 06974, Republic of Korea.
Eunee Lee, Division of Pediatric Neurology, Department of Pediatrics, Severance Children’s Hospital, Yonsei University College of Medicine, Epilepsy Research Institute, Seoul 03722, Republic of Korea.
Hoon-Chul Kang, Department of Anatomy College of Medicine, Yonsei University, Seoul 03722, Republic of Korea.
Kwang-Seok Oh, Convergence Drug Research Center, Korea Research Institute of Chemical Technology, Daejeon 34114, Republic of Korea.
Hyung Wook Kim, Department of Bio-integrated Science and Technology, College of Life Sciences, Sejong University, Seoul 05006, Republic of Korea.
Dokyun Na, Department of Biomedical Engineering, Chung-Ang University, Seoul 06974, Republic of Korea.
Supplementary data
Supplementary data are available at Bioinformatics online.
Conflict of interest
None declared.
Funding
This work was supported by the Bio & Medical Technology Development Program of the National Research Foundation (NRF) funded by the Korean government (MSIT) [NRF-2022M3E5F3081268, 2022M3A9B6082687]; and a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health and Welfare, Republic of Korea [HI21C1659].
References
- Abbott NJ. Prediction of blood–brain barrier permeation in drug discovery from in vivo, in vitro and in silico models. Drug Discov Today Technol 2004;1:407–16. [DOI] [PubMed] [Google Scholar]
- Abbott NJ, Patabendige AAK, Dolman DEM et al. Structure and function of the blood–brain barrier. Neurobiol Dis 2010;37:13–25. [DOI] [PubMed] [Google Scholar]
- Al Daoud E. Comparison between xgboost lightgbm and catboost using a home credit dataset. Int J Comput Inf Eng 2019;13:6–10. [Google Scholar]
- Bajusz D, Rácz A, Héberger K et al. Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations? J Cheminform 2015;7:20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayat Z, Movaffagh J, Noruzi S et al. Development of a computational approach to predict blood–brain permeability on anti-viral nucleoside analogues. Russ J Phys Chem 2011;85:1923–30. [Google Scholar]
- Belete DM, Huchaiah MD. Grid search in hyperparameter optimization of machine learning models for prediction of HIV/AIDS test results. Int J Comput Appl 2022;44:875–86. [Google Scholar]
- Ben-Hur A, Ong CS, Sonnenburg S et al. Support vector machines and kernels for computational biology. PLoS Comput Biol 2008;4:e1000173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradbury MWB. The blood–brain barrier. Exp Physiol 1993;78:453–72. [DOI] [PubMed] [Google Scholar]
- Cao Y, Miao Q-G, Liu J-C et al. Advance and prospects of AdaBoost algorithm. Acta Autom Sin 2014;39:745–58. [Google Scholar]
- Carpenter TS, Kirshner DA, Lau EY et al. A method to predict blood–brain barrier permeability of drug-like compounds using molecular dynamics simulations. Biophys J 2014;107:630–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrara S, Reali V, Misiano P et al. Evaluation of in vitro brain penetration: optimized PAMPA and MDCKII-MDR1 assay comparison. Int J Pharm 2007;345:125–33. [DOI] [PubMed] [Google Scholar]
- Castillo-Garit JA, Casanola-Martin GM, Le-Thi-Thu H et al. A simple method to predict blood–brain barrier bermeability of drug-like compounds using classification trees. Med Chem 2017;13:664–9. [DOI] [PubMed] [Google Scholar]
- Chen H, Chen J, Ding J et al. Data evaluation and enhancement for quality improvement of machine learning. IEEE Trans Rel 2021;70:831–47. [Google Scholar]
- Chen Y, Liu L. Modern methods for delivery of drugs across the blood–brain barrier. Adv Drug Deliv Rev 2012;64:640–65. [DOI] [PubMed] [Google Scholar]
- Ciura K, Dziomba S. Application of separation methods for in vitro prediction of blood–brain barrier permeability—the state of the art. J Pharm Biomed Anal 2020;177:112891. [DOI] [PubMed] [Google Scholar]
- Ciura K, Ulenberg S, Kapica H et al. Assessment of blood–brain barrier permeability using micellar electrokinetic chromatography and P_VSA-like descriptors. Microchem J 2020;158:105236. [Google Scholar]
- Colquitt RB, Colquhoun DA, Thiele RH et al. In silico modelling of physiologic systems. Best Pract Res Clin Anaesthesiol 2011;25:499–510. [DOI] [PubMed] [Google Scholar]
- Daina A, Michielin O, Zoete V et al. SwissADME: a free web tool to evaluate pharmacokinetics, drug-likeness and medicinal chemistry friendliness of small molecules. Sci Rep 2017;7:42717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di L, Rong H, Feng B et al. Demystifying brain penetration in Central nervous system drug discovery. J Med Chem 2013;56:2–12. [DOI] [PubMed] [Google Scholar]
- Dyabina AS, Radchenko EV, Palyulin VA et al. Prediction of blood–brain barrier permeability of organic compounds. Dokl Biochem Biophys 2016;470:371–4. [DOI] [PubMed] [Google Scholar]
- Friedman J. Greedy function approximation: a gradient boosting machine. Ann Stat 2001;29:1189–232. [Google Scholar]
- Fu X, Song ZF, Fu CY et al. A simple predictive model for blood–brain barrier penetration. Pharmazie 2005;60:354–8. [PubMed] [Google Scholar]
- Gao H, Pang Z, Jiang X et al. Targeted delivery of nano-therapeutics for major disorders of the Central nervous system. Pharm Res 2013;30:2485–98. [DOI] [PubMed] [Google Scholar]
- Gao Z, Chen Y, Cai X et al. Predict drug permeability to blood–brain–barrier from clinical phenotypes: drug side effects and drug indications. Bioinformatics 2017;33:901–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerebtzoff G, Seelig A. In silico prediction of blood–brain barrier permeation using the calculated molecular cross-sectional area as main parameter. J Chem Inf Model 2006;46:2638–50. [DOI] [PubMed] [Google Scholar]
- Ghorbanzad'e M, Fatemi MH. Classification of central nervous system agents by least squares support vector machine based on their structural descriptors: a comparative study. Chemom Intell Lab Syst 2012;110:102–7. [Google Scholar]
- Grisoni F, Consonni V, Todeschini R. Impact of molecular descriptors on computational models. Methods Mol Biol 2018;1825:171–209. [DOI] [PubMed] [Google Scholar]
- Guerra A, Páez J, Campillo N. Artificial neural networks in ADMET modeling: prediction of blood–brain barrier permeation. QSAR Comb Sci 2008;27:586–94. [Google Scholar]
- Hou TJ, Xu XJ. ADME evaluation in drug discovery. 3. Modeling blood–brain barrier partitioning using simple molecular descriptors. J Chem Inf Comput Sci 2003;43:2137–52. [DOI] [PubMed] [Google Scholar]
- Huang K. An optimized LightGBM model for fraud detection. J Phys Conf Ser 2020;1651:012111. [Google Scholar]
- Jung E, Kim J, Kim M et al. Artificial neural network models for prediction of intestinal permeability of oligopeptides. BMC Bioinformatics 2007;8:9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar R, Sharma A, Tiwari RK et al. Can we predict blood brain barrier permeability of ligands using computational approaches? Interdiscip Sci 2013;5:95–101. [DOI] [PubMed] [Google Scholar]
- Kunwittaya S, Nantasenamat C, Treeratanapiboon L et al. Influence of logBB cut-off on the prediction of blood–brain barrier permeability. Biomed Appl Technol J 2013;1:16–34. [Google Scholar]
- Lancashire LJ, Lemetre C, Ball GR et al. An introduction to artificial neural networks in bioinformatics – application to complex microarray and mass spectrometry datasets in cancer studies. Brief Bioinform 2009;10:315–29. [DOI] [PubMed] [Google Scholar]
- Lee S, Chang GS, Lee IH et al. The PreADME: PC-based program for batch prediction of ADME properties. EuroQSAR 2004;9:5–10. [Google Scholar]
- Liu H, Wang L, Lv M et al. AlzPlatform: an Alzheimer’s disease domain-specific chemogenomics knowledgebase for polypharmacology and target identification research. J Chem Inf Model 2014;54:1050–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu R, Sun H, So SS. Development of quantitative structure – property relationship models for early ADME evaluation in drug discovery. 2. Blood–brain barrier permeabilty. J Chem Inf Comput Sci 2001;41:1623–32. [DOI] [PubMed] [Google Scholar]
- Macomber L, Minkara MS, Hausinger RP et al. Reduction of urease activity by interaction with the flap covering the active site. J Chem Inf Model 2015;55:354–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martins IF, Teixeira AL, Pinheiro L et al. A Bayesian approach to in silico blood–brain barrier penetration modeling. J Chem Inf Model 2012;52:1686–97. [DOI] [PubMed] [Google Scholar]
- Mauri A, Consonni V, Pavan M et al. DRAGON software: an easy approach to molecular descriptor calculations. Match 2006;56:237–48. [Google Scholar]
- Mehdipour AR, Hamidi M. Brain drug targeting: a computational approach for overcoming blood–brain barrier. Drug Discov Today 2009;14:1030–6. [DOI] [PubMed] [Google Scholar]
- Mensch J, Oyarzabal J, Mackie C et al. In vivo, in vitro and in silico methods for small molecule transfer across the BBB. J Pharm Sci 2009;98:4429–68. [DOI] [PubMed] [Google Scholar]
- Moriwaki H, Tian Y-S, Kawashita N et al. Mordred: a molecular descriptor calculator. J Cheminform 2018;10:14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muehlbacher M, Spitzer GM, Liedl KR et al. Qualitative prediction of blood–brain barrier permeability on a large and refined dataset. J Comput Aided Mol Des 2011;25:1095–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nettles JH, Jenkins JL, Bender A et al. Bridging chemical and biological space: ‘target fishing’ using 2D and 3D molecular descriptors. J Med Chem 2006;49:6802–10. [DOI] [PubMed] [Google Scholar]
- Ogunleye A, Wang QG. XGBoost model for chronic kidney disease diagnosis. IEEE/ACM Trans Comput Biol and Bioinf 2020;17:2131–40. [DOI] [PubMed] [Google Scholar]
- Platts JA, Abraham MH, Zhao YH et al. Correlation and prediction of a large blood–brain distribution data set – an LFER study. Eur J Med Chem 2001;36:719–30. [DOI] [PubMed] [Google Scholar]
- Plisson F, Piggott AM. Predicting blood–brain barrier permeability of marine-derived kinase inhibitors using ensemble classifiers reveals potential hits for neurodegenerative disorders. Mar Drugs 2019;17:81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polyakova Y, Mei Jin L, Ho Row K et al. Linear regression based QSPR models for the prediction of the retention mechanism of some nitrogen containing heterocycles. J Liq Chromatogr Relat Technol 2006;29:533–52. [Google Scholar]
- Radan M, Djikic T, Obradovic D et al. Application of in vitro PAMPA technique and in silico computational methods for blood–brain barrier permeability prediction of novel CNS drug candidates. Eur J Pharm Sci 2022;168:106056. [DOI] [PubMed] [Google Scholar]
- Raju VNG, Lakshmi KP, Jain VM et al. Study the influence of normalization/transformation process on the accuracy of supervised classification. In: Proceedings of the 3rd International Conference on Smart Systems Inventive Technology (ICSSIT), India: IEEE, 2020. 729–35.
- Reichel A, Begley DJ, Abbott NJ et al. An overview of in vitro techniques for blood–brain barrier studies. Methods Mol Med 2003;89:307–24. [DOI] [PubMed] [Google Scholar]
- Shaker B, Yu M-S, Song JS et al. LightBBB: computational prediction model of blood–brain-barrier penetration based on LightGBM. Bioinformatics 2021;37:1135–9. [DOI] [PubMed] [Google Scholar]
- Sharma V, Goswami R, Madan AK et al. Eccentric connectivity index: a novel highly discriminating topological descriptor for structure-property and structure-activity studies. J Chem Inf Comput Sci 1997;37:273–82. [Google Scholar]
- Shen J, Du Y, Zhao Y et al. In silico prediction of blood–brain partitioning using a chemometric method called genetic algorithm based variable selection. QSAR Comb Sci 2008;27:704–17. [Google Scholar]
- Shin HK, Lee S, Oh H-N et al. Development of blood–brain barrier permeation prediction models for organic and inorganic biocidal active substances. Chemosphere 2021;277:130330. [DOI] [PubMed] [Google Scholar]
- Singh M, Divakaran R, Konda LSK et al. A classification model for blood brain barrier penetration. J Mol Graph Model 2020;96:107516. [DOI] [PubMed] [Google Scholar]
- Song Y, Liang J, Lu J et al. An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017;251:26–34. [Google Scholar]
- Srinivasan B, Kolli AR, Esch MB et al. TEER measurement techniques for in vitro barrier model systems. J Lab Autom 2015;20:107–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanton DT, Jurs PC. Development and use of charged partial surface area structural descriptors in computer-assisted quantitative structure-property relationship studies. Anal Chem 1990;62:2323–9. [DOI] [PubMed] [Google Scholar]
- Suenderhauf C, Hammann F, Huwyler J et al. Computational prediction of blood–brain barrier permeability using decision tree induction. Molecules 2012;17:10429–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H. A universal molecular descriptor system for prediction of LogP, LogS, LogBB, and absorption. J Chem Inf Comput Sci 2004;44:748–57. [DOI] [PubMed] [Google Scholar]
- Svetnik V, Liaw A, Tong C et al. Random Forest: a classification and regression tool for compound classification and QSAR modeling. J Chem Inf Comput Sci 2003;43:1947–58. [DOI] [PubMed] [Google Scholar]
- Tadeusiewicz R. Neural networks as a tool for modeling of biological systems. Bio-Algorithms Med-Syst 2015;11:135–44. [Google Scholar]
- Tang Q, Nie F, Zhao Q et al. A merged molecular representation deep learning method for blood–brain barrier permeability prediction. Brief Bioinform 2022;23:1–10. [DOI] [PubMed] [Google Scholar]
- Thakkar A, Patel D, Shah P et al. Pearson correlation coefficient-based performance enhancement of vanilla neural network for stock trend prediction. Neural Comput Appl 2021;33:16985–7000. [Google Scholar]
- Valentini S, Santoro G, Baffetta F et al. Monocyte-activation test to reliably measure the pyrogenic content of a vaccine: an in vitro pyrogen test to overcome in vivo limitations. Vaccine 2019;37:3754–60. [DOI] [PubMed] [Google Scholar]
- Vieira V, Creed J, Scrosati R et al. On the choice of linear regression algorithms for biological and ecological applications. ARRB 2016;10:1–9. [Google Scholar]
- Vilella A, Ruozi B, Belletti D et al. Endocytosis of nanomedicines: the case of glycopeptide engineered PLGA nanoparticles. Pharmaceutics 2015;7:74–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Kim MT, Sedykh A et al. Developing enhanced blood–brain barrier permeability models: integrating external bio-assay data in QSAR modeling. Pharm Res 2015;32:3055–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Yang H, Wu Z et al. In silico prediction of blood–brain barrier permeability of compounds by machine learning and resampling methods. ChemMedChem 2018;13:2189–201. [DOI] [PubMed] [Google Scholar]
- Weininger D. SMILES, a chemical language and information system: 1: introduction to methodology and encoding rules. J Chem Inf Comput Sci 1988;28:31–6. [Google Scholar]
- Wu Z, Xian Z, Ma W et al. Artificial neural network approach for predicting blood brain barrier permeability based on a group contribution method. Comput Methods Programs Biomed 2021;200:105943. [DOI] [PubMed] [Google Scholar]
- Yang H, Lou C, Sun L et al. AdmetSAR 2.0: web-service for prediction and optimization of chemical ADMET properties. Bioinformatics 2019;35:1067–9. [DOI] [PubMed] [Google Scholar]
- Yang L, Shami A. On hyperparameter optimization of machine learning algorithms: theory and practice. Neurocomputing 2020;415:295–316. [Google Scholar]
- Zhang J, Mucs D, Norinder U et al. LightGBM: an effective and scalable algorithm for prediction of chemical toxicity-application to the Tox21 and mutagenicity data sets. J Chem Inf Model 2019;59:4150–8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.