Predicting speech intelligibility in hearing-impaired listeners using a physiologically inspired auditory model

Abstract

This study presents a major update and full evaluation of a speech intelligibility (SI) prediction model previously introduced by Scheidiger, Carney, Dau, and Zaar [(2018), Acta Acust. United Ac. 104, 914–917]. The model predicts SI in speech-in-noise conditions via comparison of the noisy speech and the noise-alone reference. The two signals are processed through a physiologically inspired nonlinear model of the auditory periphery, for a range of characteristic frequencies (CFs), followed by a modulation analysis in the range of the fundamental frequency of speech. The decision metric of the model is the mean of a series of short-term, across-CF correlations between population responses to noisy speech and noise alone, with a sensitivity-limitation process imposed. The decision metric is assumed to be inversely related to SI and is converted to a percent-correct score using a single data-based fitting function. The model performance was evaluated in conditions of stationary, fluctuating, and speech-like interferers using sentence-based speech-reception thresholds (SRTs) previously obtained in 5 normal-hearing (NH) and 13 hearing-impaired (HI) listeners. For the NH listener group, the model accurately predicted SRTs across the different acoustic conditions (apart from a slight overestimation of the masking release observed for fluctuating maskers), as well as plausible effects in response to changes in presentation level. For HI listeners, the model was adjusted to account for the individual audiograms using standard assumptions concerning the amount of HI attributed to inner-hair-cell (IHC) and outer-hair-cell (OHC) impairment. HI model results accounted remarkably well for elevated individual SRTs and reduced masking release. Furthermore, plausible predictions of worsened SI were obtained when the relative contribution of IHC impairment to HI was increased. Overall, the present model provides a useful tool to accurately predict speech-in-noise outcomes in NH and HI listeners, and may yield important insights into auditory processes that are crucial for speech understanding.

1. Introduction

A large number of speech intelligibility (SI) prediction models have been proposed over the past decades, usually with the aim to provide tools for assessing transmission channels (e.g., in telecommunications and room acoustics) and signal-enhancement algorithms and/or to better understand the healthy human auditory system in terms of speech processing in various conditions. Most of these models rely on a simplistic linear representation of the peripheral stages of the human auditory system, employing a linear filterbank to simulate the frequency selectivity of the auditory system (e.g., ANSI, 1997; Rhebergen et al., 2006; Taal et al., 2011). Some of the most powerful and versatile linear models combine the initial filterbank stage with a subband envelope extraction followed by another filterbank that analyses the slower level fluctuations in the subband signals (e.g., Houtgast et al., 1980; Elhilali et al., 2003; Jørgensen and Dau, 2011; Jørgensen et al., 2013; Relaño-Iborra et al., 2016; review: Relaño-Iborra and Dau, 2022, this issue). The model predictions are obtained by comparing the noisy or processed speech signal with a reference signal, usually the clean speech or the noise alone, and obtaining either a type of signal-to-noise ratio (SNR, e.g., ANSI, 1997; Rhebergen et al., 2006; Houtgast et al., 1980; Jørgensen and Dau, 2011; Jørgensen et al., 2013) or a correlation-type metric (Taal et al., 2011; Relaño-Iborra et al., 2016). The decision metric can then be transformed to SI in percent correct based on data and predictions from a given fitting condition, e.g., speech in stationary speech-shaped noise (SSN).

The SI models mentioned above have been created using simplistic linear pre-processing with a focus on accounting for as many acoustic conditions as possible in a population of normal-hearing (NH) listeners. However, the healthy auditory system is strongly nonlinear due to cochlear amplification attributed to outer hair cells (OHCs) and the saturating nonlinear nature of the inner hair cells (IHCs). Hearing impairment, on the other hand, which is far from being fully understood in all its complexity, typically induces a partial linearization of the system due to an OHC-loss-induced reduction in cochlear amplification (review: Heinz, 2010). Therefore, linear models provide a suboptimal starting point for accounting for effects of hearing impairment, as they may already be considered “impaired” in a sense and thus are functionally limited in accounting for (supra-threshold) effects of hearing impairment beyond audibility limitations. Only a few researchers have attempted to incorporate more sophisticated nonlinear models of the auditory periphery in an SI-prediction framework. Relaño-Iborra et al. (2019) adapted the computational auditory signal processing and perception model (CASP; Jepsen et al., 2011), an auditory model with nonlinear OHC (but not IHC) behavior that contains an envelope-frequency analysis stage, for predicting SI using a processed-speech vs. clean-speech correlation approach. The resulting speech-based CASP (sCASP) model showed accurate predictions across many acoustic conditions and plausible trends across different presentation levels for NH listeners, while its predictive power regarding effects of hearing impairment on SI has not been fully explored yet (Relaño-Iborra and Dau, 2022, this issue). Another nonlinear model of the auditory periphery is the auditory-nerve model (ANM), which has been developed to describe the temporal properties of auditory-nerve rate functions and spike trains in cats and other species (Carney, 1993; Zilany et al., 2009; Zilany et al., 2014). The ANM simulates the nonlinear behavior of both OHCs and IHCs and can thus can functionally account for level effects as well as for OHC and IHC impairment. Zilany and Bruce (2007) incorporated the ANM in the framework of Elhilali et al. (2003) and showed promising predictions for word recognition across different presentation levels in NH and hearing-impaired (HI) listeners. Hines and Harte (2012) used the ANM in combination with their image-processing based Neurogram Similarity Index Measure (NSIM) to predict phoneme identification scores across different presentation levels in NH listeners. Bruce et al. (2013) used an ANM-based model framework to predict effects of masking release on consonant identification in NH and HI listeners. Hossain et al. (2016) conceived a reference-free model using a bispectrum analysis of the ANM-based neurogram to predict phoneme identification scores for groups of NH and HI listeners.

Carney et al. (2015) proposed a model of vowel coding in the midbrain, which was shown to be robust over a wide range of sound levels as well as background noise. The model is heavily based on the interaction of sound level, basilar membrane nonlinearities controlled by the OHCs, and the saturating nonlinearity of the IHCs in the ANM, which yield very flat responses at characteristic frequencies (CFs) close to vowel formant frequencies, whereas responses that fluctuate strongly at the fundamental frequency (F₀) are found at CFs in between vowel formants. As also argued in Carney (2018), these fluctuation profiles can be revealed by a bandpass (or band-enhanced) filter centered around F₀, which is a simplistic representation of responses of inferior-colliculus (IC) neurons, many of which exhibit band-pass tuning to amplitude modulations. Inspired by these observations, Scheidiger et al. (2018) proposed a modeling framework that mimics the above process using the ANM followed by a bandpass modulation filter. The processing was applied to the noisy speech and the noise-alone signals, and the decision metric was based on the across-CF correlation between the internal representations of the two signals. Scheidiger et al. (2018) showed accurate predictions for NH listeners across different noise types and promising predictions for some, but not all, of the considered HI listeners.

The current study proposes a matured version of the modeling approach conceived by Scheidiger et al. (2018), removing some of the unnecessary complexity of the original model and adding a crucial component that limits the sensitivity of the across-CF correlation metric used for predicting SI. The study furthermore systematically investigated the predictive power of the updated SI model, simulating SRTs measured in NH listeners (Jørgensen et al., 2013) and in HI listeners (Christiansen and Dau, 2012) using sentences in SSN, 8-Hz sinusoidally amplitude-modulated noise (SAM), and the speech-like international speech test signal (ISTS; Holube et al., 2010). This evaluation was conducted by comparing measured and predicted NH and HI group SRTs, as well as by comparing individual HI listener SRTs with the corresponding model predictions. Similarly, the measured and predicted masking release (MR), i.e., the SI benefit induced by fluctuating interferers (SAM, ISTS) as compared to a stationary interferer (SSN), was explicitly compared. In addition to predicting the measured data, the model’s reaction to a number of presentation levels (in NH configuration) and the effect of interpreting the hearing losses with different proportions of IHC and OHC impairment were also analyzed.

2. Method

2.1. Model description

A flowchart of the proposed model is shown in Fig. 1. The inputs to the model are the noisy speech stimulus (SN) and the noise alone (N), which serves as a reference signal. The two signals are processed through the ANM (Zilany et al., 2014), which represents the auditory periphery in terms of peripheral frequency tuning and various non-linear aspects of the cochlear mechanics and the hair cell responses. The ANM also receives a spline-interpolated version of the audiogram at the considered characteristic frequencies (CFs), which determines the model’s internal configuration in terms OHC and IHC impairment. Thirteen logarithmically spaced CFs between 0.5¹ and 8 kHz were considered here. For each CF, 18 fibers were simulated using 13 high-, 3 medium-, and 2 low-spontaneous-rate fibers (HSR, MSR, and LSR, respectively; Liberman, 1978). The instantaneous firing rates at the output of the IHC-AN synapse model were averaged across the simulated fibers, down-sampled from a sampling rate of 100 kHz to 1 kHz, and considered for further processing as the auditory-nerve signals sn_AN (cf, t) and n_AN (cf, t), with cf representing the CF number and t denoting the discrete time sample.

Figure 1.

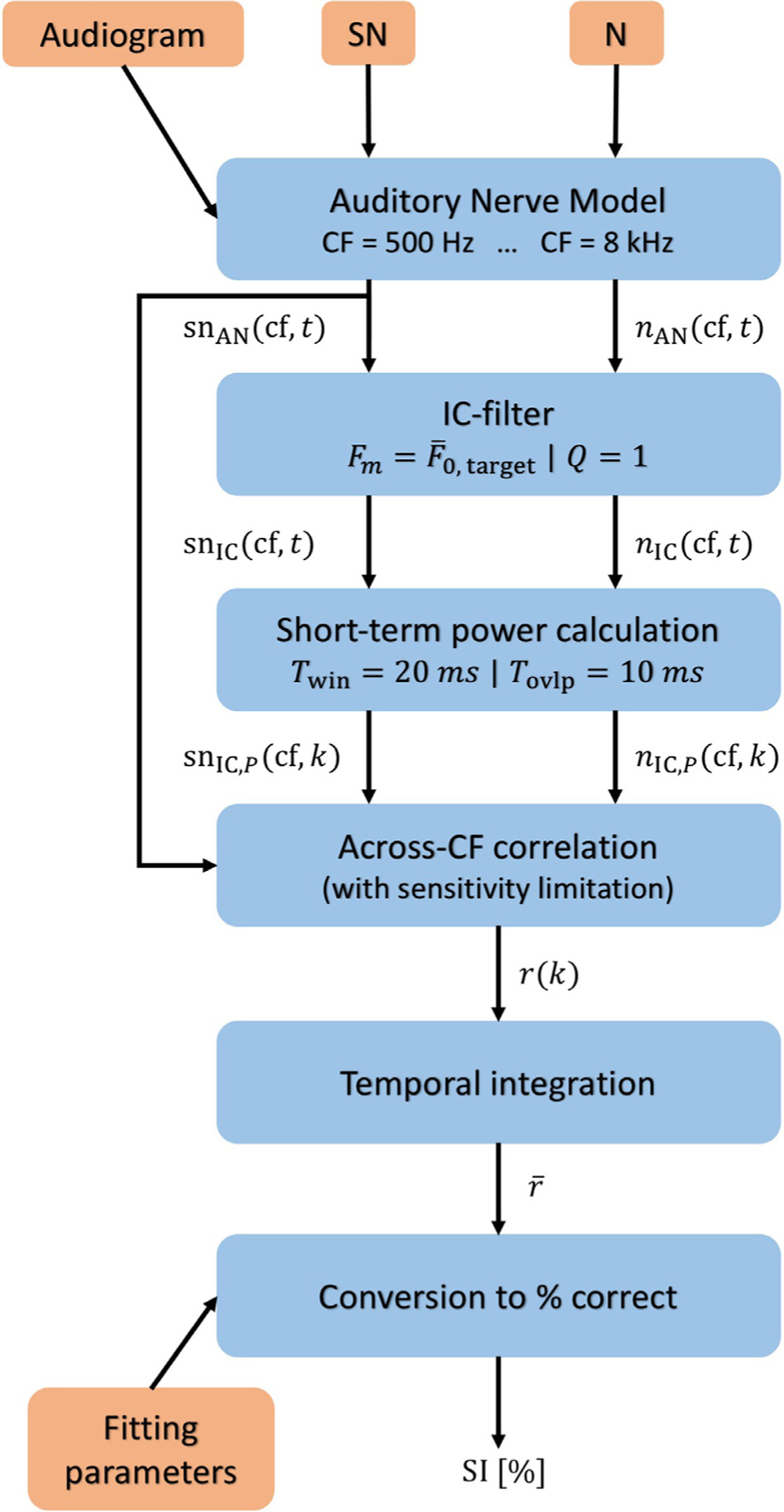
Flowchart of the model.

To simulate the IC neurons, sn_AN (cf, t) and n_AN (cf, t) were processed through a 6^th-order bandpass filter with a Q-factor of 1, centered at the average F₀ of the target speech (here: 119 Hz, see below), resulting in sn_IC (cf, t) and n_IC(cf, t). Next, a short-term power calculation was performed by segmenting the filter outputs into 20-ms time frames in 10-ms steps (i.e., using 50% overlap) and averaging the squared values within each segment k, resulting in the short-term IC power representations sn_IC,P (cf, k) and n_IC,P (cf, k).

The noisy-speech and noise-alone signals were then compared by means of an across-CF short-term correlation with a sensitivity-limitation term, defined as

$$r(k)=\mathrm{corr}\left({\text{SN}}_{\text{profile }}(k)+L,N_{\text{profile }}(k)+L\right),$$ (eq. 1)

where the vectors SN_profile (k) = [sn_IC,P (1, k), sn_IC,P (2, k), … , sn_IC,P (N cf, k)] and N_profile (k) = [n_IC,P (1, k), n_IC,P (2, k), … , n_IC,P (N cf, k)] represent the across-CF fluctuation profiles described in Carney et al. (2015) and Carney (2018), with N_cf denoting the number of CFs, and the vector $L=\text{max}\left(\frac{1}{T}{\displaystyle {\sum }_{t=1}^T{\mathrm{sn}}_{\text{AN}}}(\text{cf},t)\right)\cdot \left[1,2,\dots ,N_{\text{cf}}\right]$ with T denoting the number of samples, represents the sensitivity-limitation term. The role of L in eq. 1 is to ensure a convergence to r(k) = 1 when the noisy-speech and noise-alone fluctuation profiles are zero (no fluctuations). The larger the magnitude of the fluctuation profiles in relation to the maximum long-term spike rate of the noisy speech (sn_AN), the more the correlation between the noisy-speech and noise-alone fluctuation profiles determines r(k). The resulting across-CF correlation values r(k), obtained for each segment, are then simply averaged to yield the decision metric of the model, a single value $\overline{r}=\frac{1}{K}\sum _{k=1}^{K}r(k)$ with K denoting the number of segments.

Assuming an inverse relationship between $\overline{r}$ and SI, as a high correlation between noisy speech and noise alone implies little access to target-speech information, and vice versa, the decision metric $\overline{r}$ is converted to SI (in percent) according to

$$\text{SI}=\frac{100\%}{1+e^{a\cdot \overline{r}+b}},$$ (eq. 2)

where a and b are freely adjustable parameters that were estimated once based on a fitting condition with known SI scores, obtained in SSN for NH listeners, using nonlinear regression (see below).

2.2. Reference data

Data collected from five NH listeners (between 24 and 33 years old) were taken from Jørgensen et al. (2013). Data collected from 13 HI listeners (between 51 and 73 years, 63.8 years on average) with largely symmetric sensorineural hearing losses ranging from mild to severe (see Fig. 2) were taken from Christiansen and Dau (2012). Both studies used natural, meaningful, Danish fiveword sentences, spoken by a male speaker with an average F₀ of 119 Hz (Nielsen and Dau, 2009). Three interferers were considered here: (i) Speech-shaped noise (SSN), a stationary masker with a long-term spectrum identical to the average spectrum of all sentences, (ii) an 8-Hz sinusoidally amplitude-modulated (SAM) SSN, and (iii) the international speech test signal (ISTS, Holube et al., 2010), a largely unintelligible signal that consists of randomly con-catenated syllables taken from multiple recordings spoken by different female speakers in various languages (average F₀: 207 Hz). SRTs were measured using an adaptive procedure with the target speech presented at 60 dB sound pressure level (SPL) to the NH listeners and at 80 dB SPL to the HI listeners, whereas the level of the interferers was adapted. All stimuli were presented diotically via headphones.

Figure 2.

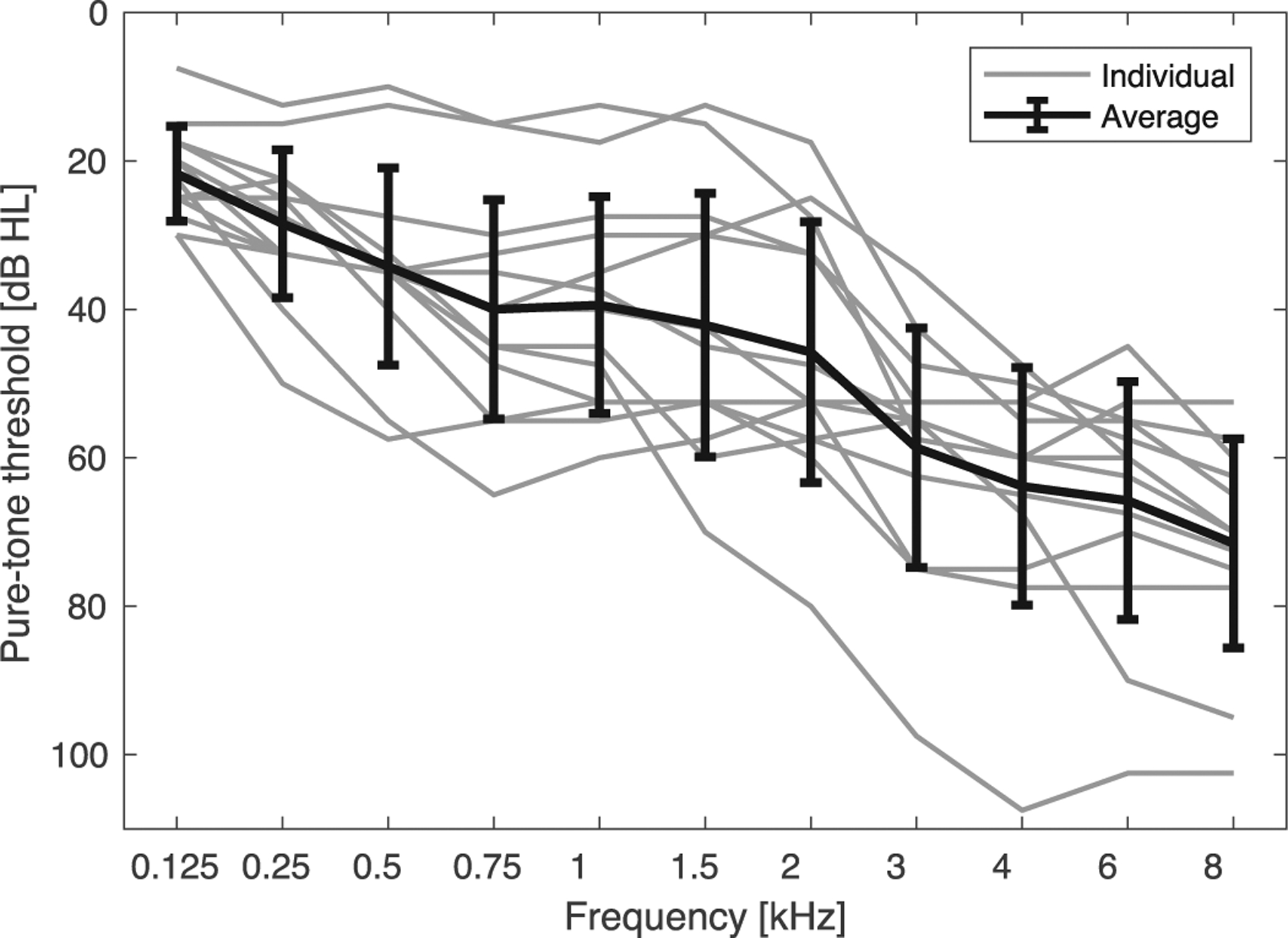
Audiograms of the 13 HI listeners measured by Christiansen and Dau (2012), averaged across left and right ears. The thin gray lines show the individual audiograms; the thick black line shows the across-listener average. Error bars represent ±1 standard deviation from the mean.

2.3. Model simulations

All model simulations were run using MATLAB (MathWorks, Natick, MA), with the help of a computer cluster for the ANM simulations. Ten sentences of the speech corpus were chosen for the model simulations. All simulation results were averaged across these ten sentences in order to obtain a stable decision metric before converting it to SI (see eq. 2). The simulated input SNRs ranged from −21 dB to 12 dB in 3-dB steps, covering the measured SRTs obtained for all listeners and conditions. The level of the noise-alone reference signal was adjusted to be identical to the overall level of the noisy speech, thus approximating the noise level for negative SNRs and the speech level for positive SNRs. The maximal difference between the level of the noise in the mixture and the level of the noise-alone reference signal was about 12 dB and occurred at the highest considered SNR of 12 dB. The overall level was selected instead of the actual level of the noise in the mixture to ensure that the (nonlinear) ANM processing applied to the noise-alone reference signal was as similar as possible to the ANM processing applied to the mixture.

2.3.1. Normal-hearing configuration

The standard configuration of the ANM (in “human” mode, see Ibrahim and Bruce, 2010) was used to predict SRTs measured in NH listeners and to probe the model with respect to effects of changes in presentation level. Model predictions were obtained for target speech levels of 0, 20, 40, 60, 80, and 100 dB SPL, with 60 dB SPL corresponding to the speech level used in the experiment. The decision metric was converted to SI as described in Sec. 2.1. (eq. 2), with parameters fit based on the SSN condition and a speech level of 60 dB SPL in the NH ANM configuration. The fitting parameters were calculated using a nonlinear regression between percent-correct data measured for a range of SNRs (−8, −6, −4, −2, 0, and 2 dB) in young NH listeners (see sentence-correct scores in Fig. 7 in Nielsen and Dau, 2009) and the corresponding model decision metrics. Finally, SRTs were calculated for all conditions as the 50%-correct points on the predicted psychometric functions.

Figure 7.

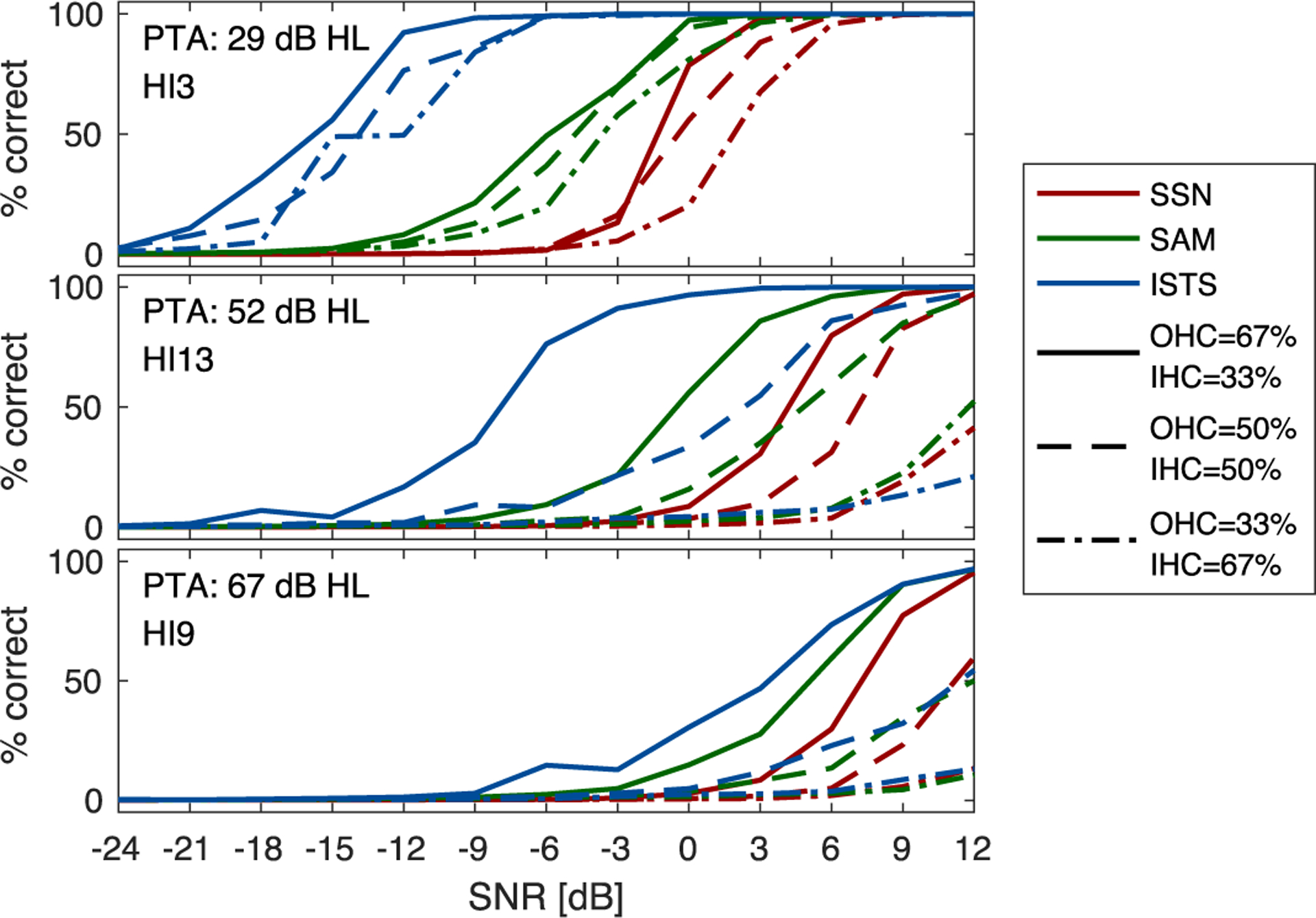
Simulated psychometric functions for three selected HI listeners using different relative contributions of OHC and IHC impairment. The noise conditions are color-coded (red: SSN; green: SAM; blue: ISTS). The relative contributions of the OHC/IHC impairment were 67% / 33% (solid lines), 50% / 50% (dashed lines) and 33% / 67% (dash-dotted lines).

2.3.2. Hearing-impaired configuration

The configuration of the ANM (in “human” mode, see Ibrahim and Bruce, 2010) was adapted according to the across-ear average audiograms of the individual HI listeners (as the hearing losses were largely symmetric). To this end, the audiogram was spline-interpolated at the considered CFs and the ANM’s OHC and IHC impairment parameters (C_ohc and C_ihc) were found based on the “fitaudiogram2” MATLAB function provided with the ANM. As the relative contributions of OHC and IHC impairment to the total hearing loss cannot be determined based on the audiogram alone, it was assumed that 67% of the total hearing loss was related to OHC impairment and 33% to IHC impairment (Zilany et al., 2007; Bruce et al., 2013). However, to probe the model’s behavior for different combinations of OHC and IHC impairment, two additional cases were considered, with (i) OHC impairment accounting for 33% and IHC impairment for 67% and (ii) OHC impairment and IHC impairment each accounting for 50% of the total hearing loss. As in the corresponding experiment (Christiansen and Dau, 2012), the target speech level was set at 80 dB SPL. The decision metric was converted to SI scores and then to SRTs using the same procedure and the same fitting parameters as for the NH case, see Sec. 2.3.1.

3. Results

3.1. Model predictions for the NH and HI groups

This section compares the measured data with the model predictions for the two groups of NH and HI listeners. The comparison is conducted in terms of (i) SRTs as a function of the SSN, SAM, and ISTS conditions and (ii) in terms of MR, defined as MR _SAM = SRT_SSN − SRT_SAM and MR_ISTS = SRT_SSN − SRT_ISTS. The left panel of Fig. 3 demonstrates that the NH group (open squares) performed better and thus reached lower SRTs than the HI group (open diamonds). For both groups, the highest SRTs were observed for SSN, followed by SAM with lower SRTs, and ISTS with the lowest SRTs. However, the differences in SRTs across conditions were substantially larger in the NH group than in the HI group, which is also reflected in a substantially higher MR observed for the NH than for the HI listeners (right panel of Fig. 3). The SRTs predicted by the model² (filled symbols in the left panel of Fig. 3) were in line with the NH and HI group data, capturing both the effect of the different noise conditions per group and the differences between groups, even in terms of the standard deviations across HI listeners. However, the predicted SRTs for the SAM and ISTS interferers tended to be slightly lower than the measured SRTs, which was consistent across groups. Therefore, while the MR for the SAM and ISTS conditions and its reduction due to hearing loss (squares vs. diamonds in the right panel of Fig. 3) was well captured, the predicted MR was generally somewhat too high.

Figure 3.

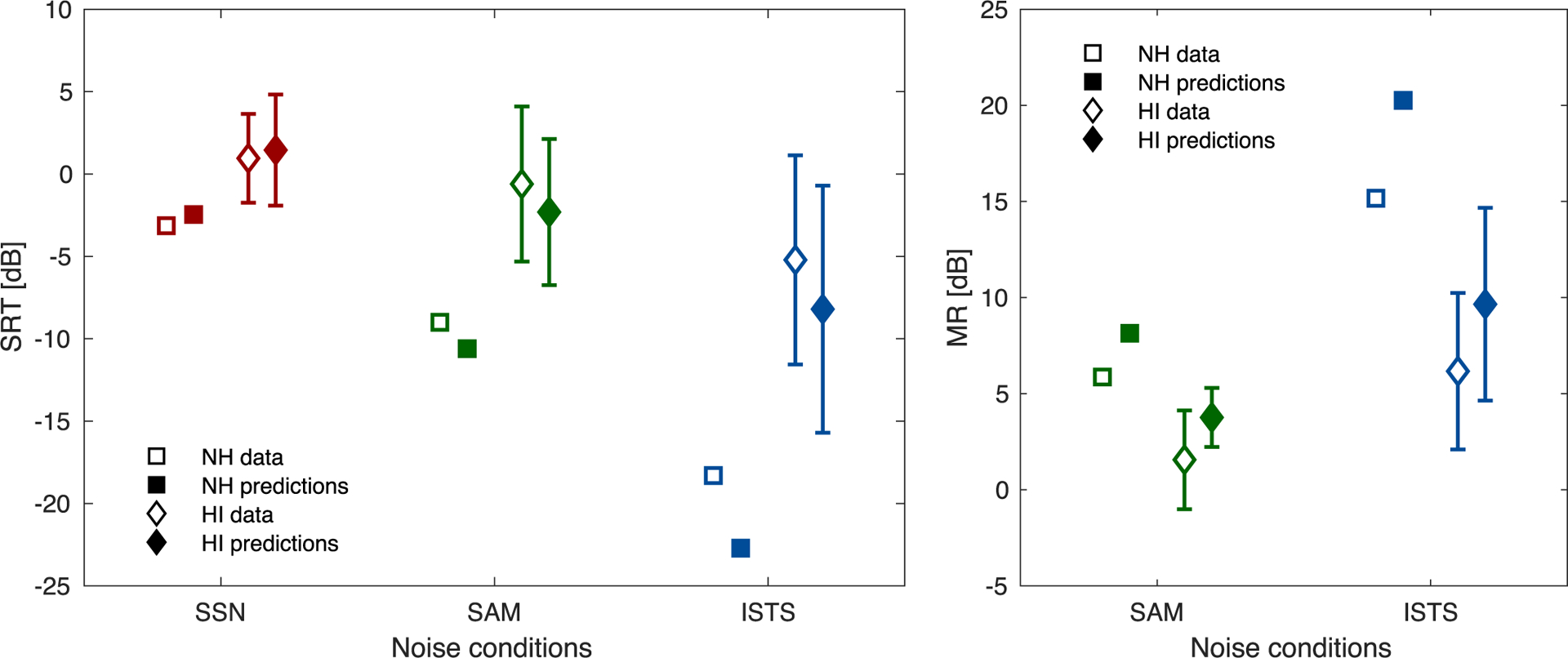
Group-level SRT and MR data and predictions. Left panel: Measured and predicted SRTs for NH and HI listeners as a function of noise condition. Right panel: Measured and predicted MRs obtained with SAM and ISTS interferers for NH and HI listeners. NH data and predictions are represented by open/filled squares, HI data and predictions by open/filled diamonds. Error bars indicate ±1 standard deviation across HI listeners.

3.2. Model predictions for individual HI listeners

As seen in Fig. 3, there was a large variability across individual listeners’ SRTs within the HI group, the extent of which was also reflected in the model predictions. To determine whether the model predictions merely reflect the group variability by coincidence or whether they indeed account for individual listener data, Fig. 4 shows the SRTs (left panel) and MRs (right panel) predicted for the individual HI listeners as a function of their measured counterparts. As can be seen in the left panel of Fig. 4, the individual HI listeners’ SRTs cover wide ranges of 10, 15, and 20 dB for the SSN (red), SAM (green), and ISTS (blue) condition, respectively. The predicted SRTs show a similar picture, with high condition-specific correlations of 0.67 (SSN, p=0.01) and 0.8 (SAM, ISTS; p=0.001) and an even higher across-condition correlation of 0.84 (p < 0.0001). For comparison, the original model version showed condition-specific correlations between 0.3 and 0.5 (p > 0.05) and an across-condition correlation of 0.58 (p < 0.001), cf. Scheidiger et al. (2018). The mean absolute error (MAE), which was calculated as the average of the absolute values of the differences between measured and predicted SRTs to quantify the average deviation from a perfect prediction in dB, indicated the best predictions for SSN (1.9 dB), followed by SAM (2.8 dB) and ISTS (4.7 dB), with an across-condition MAE of 3.1 dB. For comparison, the original model version showed MAEs of 2.17 (SSN), 5.48 (SAM), and 7.12 dB (ISTS), cf. Scheidiger et al. (2018). It should be noted that the condition-specific MAEs are directly proportional to the SRT ranges induced by the three conditions. The qualitative agreement between model predictions and measured data was slightly better when looking at the predicted and measured MR for the individual HI listeners, shown in the right panel of Fig. 4. Here, the specific correlations were 0.83 (SAM, p=0.0005) and 0.85 (ISTS, p=0.0002) and the across-condition correlation was 0.88 (p < 0.0001). However, the general overestimation of the MR in the model (cf. Sec. 3.1) can also be observed here, as almost all data points are above to the diagonal, indicating that predicted MR values were higher than measured values, and leading to MAEs of 2.2 dB (SAM), 3.7 dB (ISTS), and 3 dB (combined).

Figure 4.

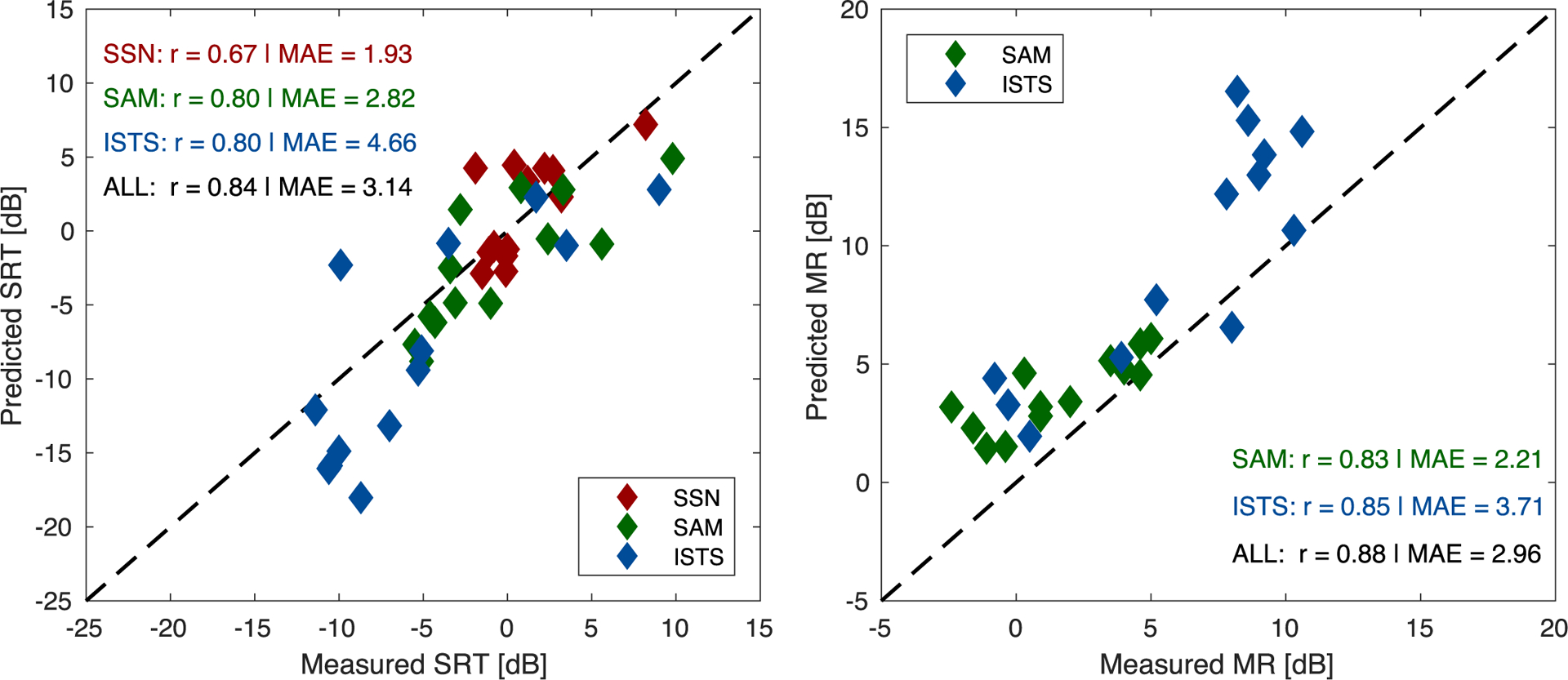
Measured vs. predicted SRTs (left panel) and MRs (right panel) for the 13 individual HI listeners. The different noise conditions are shown in color (red: SSN; green: SAM; blue: ISTS). Condition-specific and across-condition correlation coefficients (r) and mean absolute errors (MAE) are shown in the respective panels to quantify the model performance. The dashed diagonal line represents perfect agreement between measured in predicted values.

For reference, Fig. 5 depicts the SRTs measured for the individual HI listeners as a function of their average hearing loss, as represented by their pure-tone threshold average (PTA) across all audiometric frequencies between 125 and 8000 Hz. It can be observed that, for values above roughly 40 dB HL, the PTA is directly related to an elevation in SRTs and a reduction in MR. This relation is reflected in correlations between PTA and SRTs (between 0.62 and 0.85, 0.0229>p> 0.0002) that are in the range of the correlations observed between the model predictions and the measured SRTs (cf. Fig. 4). However, because the PTA is independent of the speech-test condition, the across-condition correlation between PTA and SRTs is non-existent (r = −0.04, p=0.83), whereas the model correctly predicts the effects of individual hearing loss on the different speech-test conditions.

Figure 5.

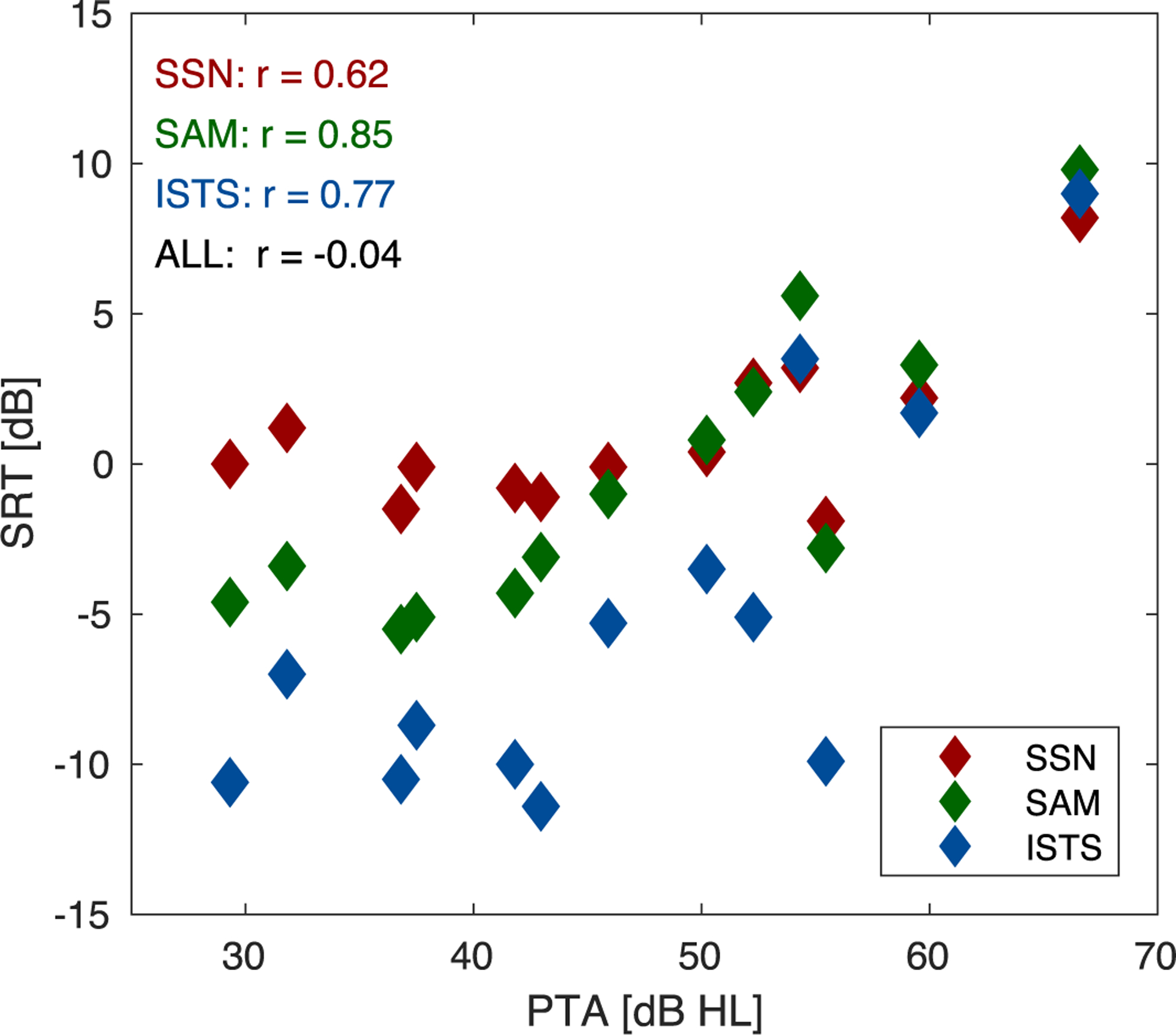
Pure-tone threshold average (PTA) vs. measured SRTs for HI listeners. The different noise conditions are shown in color (red: SSN; green: SAM; blue: ISTS). Condition-specific and across-condition correlation coefficients (r) are shown in the respective panels to quantify the relationship between PTA and SRTs.

3.3. Effect of presentation level in NH configuration

To probe the model’s reaction to variations in presentation level, model predictions were also obtained in the NH configuration for a range of speech levels. This range of levels was not included in the experimental reference data; however, it has been demonstrated that speech intelligibility breaks down at low broadband levels somewhat above 20 dB SPL, due to insufficient audibility (e.g., Nilsson et al., 1994). Furthermore, a so-called “roll-over” effect has been shown at high speech levels, between 80 and 100 dB SPL, resulting in elevated SRTs as compared to medium speech levels (e.g., French and Steinberg, 1947; Speaks et al., 1967; Festen, 1993). Figure 6 depicts the predicted SRTs (squares) for speech levels between 0 and 100 dB SPL (in 20-dB steps) along with the reference SRTs measured at a speech level of 60 dB SPL (dashed lines, cf. Fig. 3). Triangles indicate that the predicted SRT was either very high or not applicable due to very low predicted SI scores. For speech levels of 0 and 20 dB SPL, no SRTs were obtained in any of the noise conditions, as the predicted SI scores were around 0% at all tested SNRs (with a slight increase at positive SNRs in all noise conditions for a speech level of 20 dB SPL). For speech levels of 40 and 60 dB SPL the predicted SRTs were well aligned with the SRTs measured at 60 dB SPL. For speech levels of 80 dB SPL a slight trend toward elevated predicted SRTs was observed, which differed across noise conditions. For speech presented at 100 dB SPL, a significant elevation of the predicted SRTs was observed in all noise conditions. Overall, the predictions obtained for the different speech levels therefore matched the expectations derived from literature.

Figure 6.

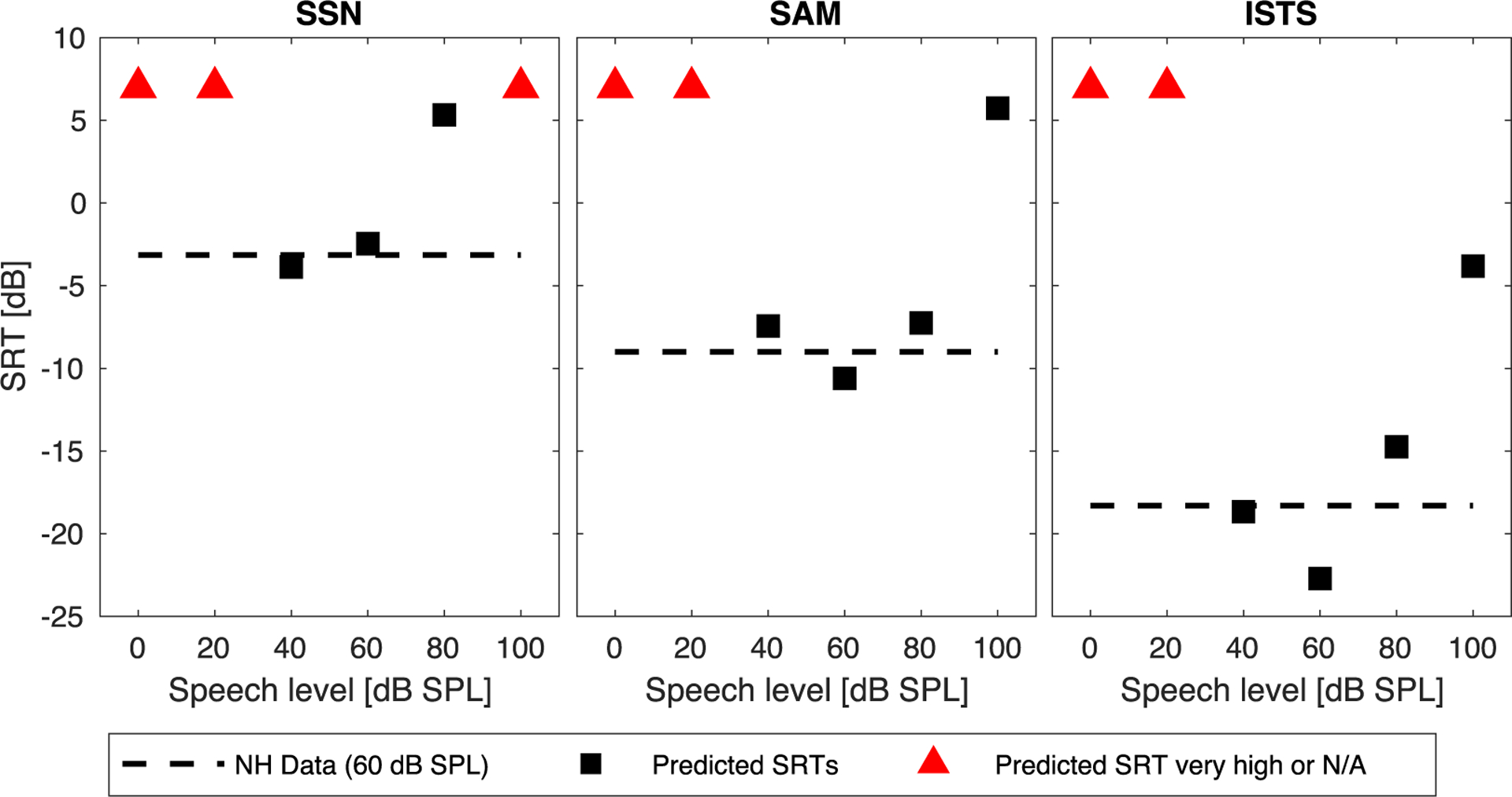
SRTs predicted in NH configuration as a function of target speech level for SSN (left), SAM (middle), and ISTS (right) conditions. The black dashed lines indicate the SRTs measured in NH listeners (at a speech level of 60 dB SPL). The black squares represent predicted SRTs, whereas the red triangles indicate SRTs that were either very high or not applicable because predicted SI scores were too low.

3.4. Effect of different hearing-threshold interpretations

The predictions shown for HI listeners in Sec. 3.1 and 3.2 were based on the commonly used assumption that 67% of the total hearing loss is due to OHC impairment and 33% due to IHC impairment. Here, the effect of using three different configurations of OHC and IHC impairment, namely 67% / 33%, 50% / 50%, and 33% / 67%, is demonstrated. Figure 7 shows the effects of these different configurations using three examples of predictions obtained for individual HI listeners with a range of hearing losses (HI3, top: PTA = 29 dB HL; HI13, middle: PTA = 52 dB HL; HI9, bottom: PTA = 67 dB HL). For all listeners and noise conditions, the predictions obtained with the default configuration 67% / 33% (shown as solid lines) indicate the highest SI scores, followed by the 50% / 50% condition (dashed lines), while the lowest SI scores were predicted for the 33% / 67% configuration (dash-dotted lines). These results suggest that when the relative contribution of IHC impairment increases (and that of OHC impairment decreases), the model predicts a reduction in SI. When comparing the three panels in Fig. 7, the magnitude of the effect depends on the severity of the hearing loss, which increases from top to bottom.

The best of the three mentioned OHC/IHC impairment configurations was picked for each HI listener by finding the configuration that yielded the smallest absolute difference between measured and predicted SRTs, averaged across noise conditions. For six listeners, the standard configuration of 67% OHC and 33% IHC impairment was most suitable; for another six listeners, the configuration with 50% / 50% IHC impairment provided the best SRT match; for a single listener, the configuration of 33% OHC and 67% IHC impairment was selected. Figure 8 depicts a re-plot of the scatter plot shown in the left panel of Fig. 4, using the model predictions obtained with the best-fitting OHC/IHC impairment configuration for each HI listener. It can be seen that all correlations (condition-specific and across condition) increased as compared to Fig. 4. The mean absolute error decreased overall as well as for the SAM and ISTS conditions, but increased slightly for the SSN condition.

Figure 8.

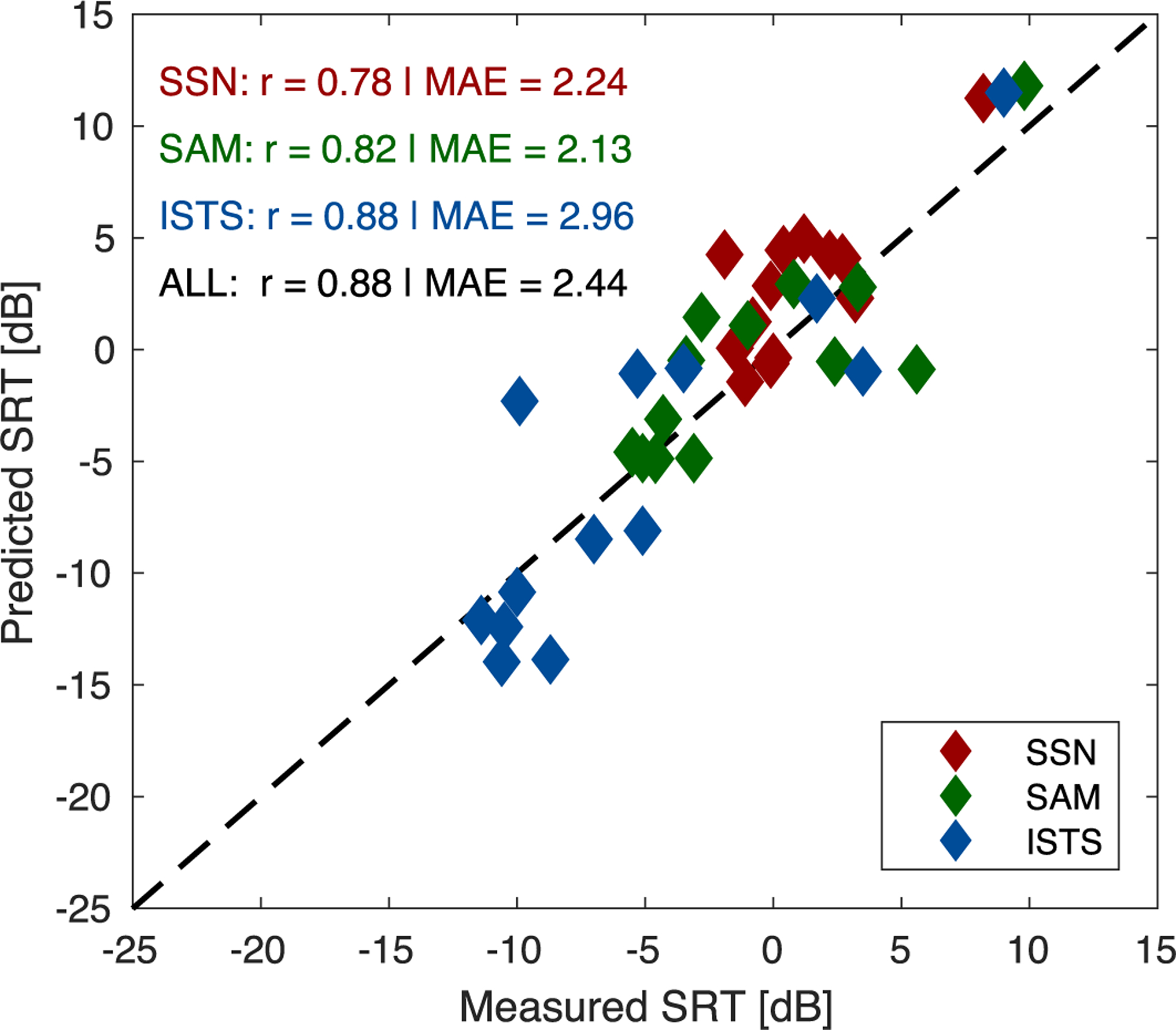
Measured vs. predicted SRTs using the best fitting OHC/IHC impairment configuration in the model for each of the 13 HI listeners. The different noise conditions are shown in color (red: SSN; green: SAM; blue: ISTS). Condition-specific and across-condition correlation coefficients (r) and mean absolute errors (MAE) are shown in the respective panels to quantify the model performance. The dashed diagonal line represents perfect agreement between measured and predicted values.

4. Discussion

4.1. Model performance and behavior

The proposed SI model, which is based on Scheidiger et al. (2018) and Carney et al. (2015), was evaluated based on NH data (Jørgensen et al., 2013) and HI data (Christiansen and Dau, 2012) in three different noise conditions. Based only on a single conversion function (“fitting”), obtained using NH listener data collected in SSN, and incorporating the HI listeners’ audiograms in the front-end processing, the model accounted very well for (i) NH group SRTs across SAM and ISTS interferers and thus for MR, (ii) generally elevated SRTs in the HI group, and (iii) HI group SRTs across SSN, SAM, and ISTS interferers and thus for the hearing-loss-induced reduction in MR. The model furthermore captured the large across-listener variability in SRTs within the HI group in terms of the standard deviation, and indeed predicted individual SRTs as well as individual MRs with good precision. However, the model globally showed a slight overestimation of the MR for both NH and HI listeners, especially in the case of the ISTS interferer. Overall, these results represent a major improvement over the predictive power shown by Scheidiger et al. (2018) for the same data using a predecessor of the proposed model, especially when it comes to predictions of HI listeners’ SRTs.

In addition to the described predictions of experimental data, the responses of the model to changes in presentation level was assessed (in the NH configuration). The model predicted floor-level SI scores for target speech levels of 0 and 20 dB SPL, largely stable SRTs for 40 and 60 dB SPL in the range of the NH listeners’ SRTs (collected at 60 dB SPL), somewhat elevated SRTs for 80 dB SPL and substantially elevated SRTs for 100 dB SPL. This modeling result is well in line with experimental results from the literature, showing SRTs in quiet of about 24 dB(A) (Nilsson et al., 1994) and elevated SRTs at high speech levels, between 80 and 100 dB SPL (i.e., the “roll-over” effect, e.g., French and Steinberg, 1947; Speaks et al., 1967; Festen, 1993). Furthermore, while the default interpretation of the HI listeners’ audiograms was based on the commonly used assumption that 67% of the total hearing loss is caused by OHC impairment and 33% by IHC impairment (Zilany et al., 2007; Bruce et al., 2013), the effect of modifying this assumption was also assessed. The model predicted a detrimental effect on SI for increasing HI due to IHC impairment, and a suitable listener-specific selection of the hearing-loss interpretation was shown to further improve the correspondence between simulated and measured SRTs. As the underlying principle of stable rate patterns considered here is heavily based on IHC transduction (cf. Zilany et al., 2014; Carney et al., 2015; Carney, 2018), this model behavior was already hypothesized in Scheidiger et al. (2018). The model might thus also be interesting for investigating the effects of damaged IHCs and synapses (for reviews see Lopez-Poveda, 2014; Carney, 2018).

4.2. Model design in relation to other studies

The design of the model differs substantially from most other established SI prediction models due to its use of a sophisticated nonlinear auditory model as a front end. Some comparable efforts have been published (Zilany et al., 2007; Hines and Harte, 2012; Bruce et al., 2013; Hossain et al., 2016; Relaño-Iborra et al., 2019) but not yet fully evaluated for sentence recognition in different maskers. The use of the noise alone as a reference signal is reminiscent of various SI prediction models that derive an SNR-type decision metric (e.g., ANSI, 1997; Rhebergen et al., 2006; Jørgensen and Dau. 2011; Jørgensen et al., 2013). However, other correlation-based SI prediction models typically use the clean speech as a reference (e.g., Taal et al., 2011; Relaño-Iborra et al., 2016; Relaño-Iborra et al., 2019), such that the decision metric describes the qualitative similarity between responses to the noisy/processed speech and to the clean speech and is thus directly related to SI. These models have the advantage of being applicable in conditions beyond additive interference, such as various signal distortions (see Relaño-Iborra et al., 2016). The proposed model instead adopts the somewhat unusual strategy of combining the noise-alone reference with a correlation-based decision metric, thus computing the qualitative similarity between noisy speech and noise alone, which is inversely related to SI. This approach has the advantage that both noisy speech and noise alone may be processed through the front end in the same HI configuration, as no assumption about the intelligibility of the reference signal has to be made. In contrast, a clean-speech reference signal would always have to be processed through the front end in NH configuration, as it acts as an “ideal” reference and the HI configuration would potentially compromise this assumption. However, a correlation between two signals that were processed by the model in different configurations is at risk of trivially representing the difference between the two configurations.

The decision metric of the proposed model, which was inspired by the observation of stable across-CF rate patterns in the IC (Carney et al., 2015; Carney 2018), explicitly compares the fluctuation strength around F₀ across CF. This approach is in contrast with other SI models that have a modulation-analysis stage, which typically apply a channel-by-channel analysis and consider only/mainly the “classical” lower speech-modulation rates using a modulation filterbank approach (e.g., Houtgast et al., 1980; Jørgensen and Dau., 2011; Jørgensen et al., 2013; Relaño-Iborra et al., 2016; review: Relaño-Iborra and Dau, 2022, this issue). Some powerful SI models do analyze the spectral variations of their internal representations, such as the sCASP (Relaño-Iborra et al., 2019) and the spectro-temporal modulation index (STMI; Elhilali et al., 2003). However, their across-frequency analyses differ strongly from the approach proposed here, as the sCASP correlates time-frequency representations of processed and clean speech at the output of each considered modulation filter and the STMI compares the power of the processed and clean speech after spectro-temporal modulation analysis. A noteworthy aspect of the model design is its implicit use of periodicity cues, represented by the IC filter around the F₀ of speech. Several studies have attempted to disentangle the relative contributions of temporal envelope (ENV) and temporal fine structure (TFS) cues to speech intelligibility by separating the ANM outputs into different frequency ranges to represent (low-frequency) ENV and (high-frequency) TFS cues (e.g., Hines and Harte, 2012; Swaminathan and Heinz, 2012; Wirtzfeld et al., 2017). The results of Hines and Harte (2012) and Swaminathan and Heinz (2012) suggested that the ENV representation was sufficient in many conditions, whereas Wirtzfeld et al. (2017) demonstrated that the addition of TFS information contributed substantially to predicting phoneme identification in suitable processing conditions (speech chimaeras). The proposed model does not explicitly consider TFS cues in its analysis of fluctuation profiles: the considered IC bandpass filter around 119 Hz operates only on ANM outputs for CFs of 500 Hz and above, such that there is no overlap between the TFS passing through the peripheral filter (i.e., components near the AN-fiber CF) and the IC filter. Instead, the phase-locking occurring at the selected range of CFs analyzed by the IC filter is generally F₀ phase-locking, following the beating pattern that results from the interaction between individual (harmonic) components within a given peripheral filter. This temporal response falls in the ENV category in principle; however, the IC filter frequency is substantially higher than commonly used for ENV processing (e.g., Wirtzfeld et al., 2017). If there is one dominant harmonic component within the peripheral filter’s frequency range, the AN-fibers instead tend to phase-lock mainly to the TFS of that component, such that the otherwise observed F₀ phase-locking disappears, i.e., the dominant component “captures” the AN-fiber (Leong et al., 2020; Maxwell et al., 2020; Carney 2018; Carney et al. 2015). It should be noted that TFS-based SI models may take advantage of some of the information contained in the fluctuation profiles considered by the proposed model. However, the availability of these cues in a classical TFS sense would be limited to the phase-locking range, whereas the fluctuation profiles are not limited by the roll-off in TFS phase-locking and are thus expected to work across a wider range of CFs. Furthermore, the fluctuation profiles do not require a dedicated “decoding” mechanism, whereas it has yet to be clarified how a TFS-based code would be decoded.

Finally, the sensitivity-limitation term included in the decisionmetric calculation is a crucial addition to the model as compared to Scheidiger et al. (2018), which adds substantial predictive power to the model regarding effects of low presentation levels and severe hearing losses by essentially imposing a noise floor on the across-CF correlation. This noise floor was defined based on the maximum long-term auditory-nerve spike rate and was thus driven by the individual stimulus. However, an alternative simulation approach with a fixed sensitivity-limitation term yielded comparable results (with some loss of predictive power). Additional modifications relative to the previous model version by Scheidiger et al. (2018) had only minor effects and were related (i) to the numbers and proportions of simulated HSR, MSR, and LSR fibers (previous version: 30/10/10; current version: 13/3/2) with the aim to save computation time and improve the physiological plausibility (Liberman, 1978) and (ii) to the number of ears considered in the model (previous version: binaural with long-term better-ear selection; current version: monaural using average audiograms), aiming to simplify the approach as the present data set was collected using diotic headphone presentation and the HI listeners had symmetric hearing losses.

4.3. Future considerations

Several improvements and future investigations of the proposed model should be considered. While the model has been evaluated here in a range of conditions and for various hearing losses, the stimuli differed only in broadband level between the NH and HI groups (60 vs. 80 dB SPL), while there was no difference whatsoever in the stimuli across HI listeners. To challenge the model with different stimuli and to minimize potential effects of audibility, the model should in a next study be evaluated using HI data measured with individualized amplification. A potentially limiting factor when predicting other data sets could be the current monaural design of the model. It may therefore be worthwhile to define a binaural version of the model that can exploit a short-term better-ear advantage in dichotic listening conditions.

The present study used a standard interpretation of the audiogram in terms of the contributions of OHCs and IHCs to hearing loss, which may be appropriate for many listeners according to Johannesen et al. (2014). However, this study also demonstrated substantial predicted effects of adjusting the OHC and IHC contributions to hearing loss, and indicated that the model predictions could potentially be further improved by individually adjusting the OHC and IHC impairment parameters. It may thus be beneficial to fine-tune the model using measures beyond the audiogram (e.g. Sanchez-Lopez et al., 2020) to define OHC and IHC status rather than making simplistic assumptions. As synaptopathy (Henry, 2022; Bramhall et al., 2019; Carney, 2018) has been a much discussed potential aspect of supra-threshold hearing loss recently, it should be noted that the proposed model does not predict a noteworthy difference between the mix of HSR, MSR, and LSR fibers reported here and a simple HSR-based version (not shown here), suggesting that loss of MSR and LSR fibers typically associated with synaptopathy would not influence the responses of this model.

Lastly, due to its explicit analysis of fluctuations in the range of the target-speech F₀, the model may have the potential to predict different levels of difficulty in segregating the target speech from speech interferers that may be induced by different amounts of overlap in F₀. While the male target speaker vs. female-speaker-based ISTS interferer condition simulated in the present study represents a case of almost perfect perceptual separability in this sense and is thus well captured by several models (e.g., Jørgensen et al., 2013; Relaño-Iborra et al., 2016), it has been proven difficult to account for more fine-grained differences in periodicity between target and masker with established SI-prediction models (e.g., Steinmetzger et al., 2019; Relaño-Iborra, 2019).

5. Conclusions

The present study presented a matured version of a speech-intelligibility prediction model previously proposed by Scheidiger et al. (2018). The model is based on a sophisticated nonlinear auditory model that allows incorporation of hearing loss, combined with a back end that quantifies the similarity between across-frequency fluctuation profiles of noisy speech and noise alone. The model showed accurate predictions of speech reception thresholds (SRTs) measured in normal-hearing listeners across a number of speech-in-noise conditions as well as plausible effects in response to changes in presentation level. Furthermore, the model accounted accurately for SRTs measured in hearing-impaired (HI) listeners solely by incorporating the listeners’ audiograms in the front-end processing. Additional simulations indicate that a fine-tuning of the hearing-loss representation in the model using measures beyond the audiogram may allow investigation of effects of inner- and outer-hair-cell impairment on speech intelligibility in detail. Further investigations are required to (i) assess the model’s predictive power with respect to speech-intelligibility data collected with hearing-loss-based individualized amplification, (ii) extend the model toward a binaural version, (iii) incorporate supra-threshold hearing-loss measures, and (iv) test the model’s predictive power in conditions that are challenging in terms of speech-stream segregation.