A Model for Gastrointestinal Tract Motility in a 4D Imaging Phantom of Human Anatomy

Abstract

Background:

Gastrointestinal (GI) tract motility is one of the main sources for intra/inter-fraction variability and uncertainty in radiation therapy for abdominal targets. Models for GI motility can improve the assessment of delivered dose and contribute to the development, testing, and validation of deformable image registration (DIR) and dose-accumulation algorithms.

Purpose:

To implement GI tract motion in the 4D extended cardiac-torso (XCAT) digital phantom of human anatomy.

Materials and Methods:

Motility modes that exhibit large amplitude changes in the diameter of the GI tract and may persist over timescales comparable to online adaptive planning and radiotherapy delivery were identified based on literature research. Search criteria included amplitude changes larger than planning risk volume expansions and durations of the order of tens of minutes. The following modes were identified: peristalsis, rhythmic segmentation, high amplitude propagating contractions (HAPCs), and tonic contractions. Peristalsis and rhythmic segmentations were modeled by traveling and standing sinusoidal waves. HAPCs and tonic contractions were modeled by traveling and stationary Gaussian waves. Wave dispersion in the temporal and spatial domain was implemented by linear, exponential, and inverse power law functions. Modeling functions were applied to the control points of the nonuniform rational B-spline surfaces defined in the reference XCAT library. GI motility was combined with the cardiac and respiratory motions available in the standard 4D-XCAT phantom. Default model parameters were estimated based on the analysis of cine MRI acquisitions in 10 patients treated in a 1.5T MR-linac.

Results:

We demonstrate the ability to generate realistic 4D multimodal images that simulate GI motility combined with respiratory and cardiac motion. All modes of motility, except tonic contractions, were observed in the analysis of our cine MRI acquisitions. Peristalsis was the most common. Default parameters estimated from cine MRI were used as initial values for simulation experiments. It is shown that in patients undergoing stereotactic body radiotherapy for abdominal targets, the effects of GI motility can be comparable or larger than the effects of respiratory motion.

Conclusion:

The digital phantom provides realistic models to aid in medical imaging and radiation therapy research. The addition of GI motility will further contribute to the development, testing, and validation of DIR and dose accumulation algorithms for MR-guided radiotherapy.

I. INTRODUCTION

The accuracy and precision of radiation therapy is dependent on the characterization of target motion.¹ Gastrointestinal (GI) tract motility is one of the main sources for intra/inter-fraction variability and uncertainty in the treatment of abdominal targets. The integrated MR-linac^2–5 provides a novel platform for the delivery of precision radiotherapy and may enable improvements in therapeutic response by increasing dose to the target while sparing organs-at-risk (OARs).^6–9 Broadly, the sources of uncertainty in MRI-guided radiotherapy can be categorized into delivery- and patient-specific factors. Recent work on the longitudinal assessment of quality assurance measurements has identified delivery-specific factors related to performance, stability, safety, and machine tolerance levels.^10,11

The uncertainties that arise from variations in patient anatomy and physiology remain the most challenging to quantify and mitigate. This is particularly challenging in the abdomen where respiratory, cardiac, and GI motion are often simultaneously present during delivery. Although the presence of periodic (respiratory or cardiac) motion increases the complexity of radiation therapy, it is possible to devise clinically acceptable treatment plans by exploiting the cyclical changes in anatomical features.

Previous research has found that the effect of intrafraction GI motility is patient-specific and can be of the same magnitude or larger than the effect of respiratory motion.^12–14 Furthermore, movements in the GI tract can appear spontaneously, in response to biomechanical or biochemical stimuli, of varying amplitude and frequency, and develop over a wide range of timescales.^15–21 Such complex changes in anatomy, especially when close to the target, necessitate constant monitoring of radiotherapy delivery and, if needed, plan adaptation or revision.

Accurate computational models of human anatomy have become an indispensable tool in medical imaging and radiation therapy research.^22–28 When combined with measurement, models for GI motility can improve the assessment of delivered dose to target/OARs and contribute to the development, testing, and validation of deformable image registration and dose-accumulation algorithms. Furthermore, physiological modeling parameters can inform the selection of patient-specific planning risk volume (PRV) margins to increase safety and quality in radiotherapy. To the best of our knowledge, computational phantoms that provide a realistic model of GI motion are not available. In this work we present an implementation of GI motility in the widely used 4D extended cardiac-torso (XCAT) phantom. Cine MRI from patients undergoing treatment in a 1.5T MR-linac were analyzed to estimate default parameters for the model and to provide examples describing the effect of GI motility combined with respiratory and cardiac motion.

II. MATERIALS AND METHODS

II.A. Modeling framework

This study considers motility modes that exhibit large amplitude changes in the diameter of the GI tract and may persist over timescales comparable to online adaptive planning and radiotherapy delivery. The modes were selected based on literature review using search criteria for identifying amplitude changes larger than typical safety OAR expansions and durations in the order of several minutes.^{15–21,29,30} The following modes were modeled: peristalsis, rhythmic segmentation, high amplitude propagating contractions (HAPC), and tonic contractions. The models are intended for the organ of origin (i.e., peristalsis in esophagus and small intestine, HAPCs in colon) but can be applied to any user-specified GI tract organ.

The overall modeling framework is given by:

$$r(\overrightarrow{x},t)=r_0(\overrightarrow{x})+ℱ(\overrightarrow{x},t)\cdot {𝒟}_s(\overrightarrow{x})\cdot {𝒟}_t(t)$$ Eqn. (1)

where $r\left(\overrightarrow{x},t\right)$ represents the radius of the organ cross-section, $r_0\left(\overrightarrow{x}\right)$ represents the radius of the organ at $t=0sec,ℱ(\overrightarrow{x},t)$ is the function modeling the non-dispersive component of the wave, and ${𝒟}_s\left(\overrightarrow{x}\right),{𝒟}_t(t)$ represent functions modeling dispersion in the spatial $(\overrightarrow{x})$ and temporal $(t)$ domain, respectively. This approach allows for the implementation of several modeling functions for motility and dispersion, without loss of generality.

Peristalsis (PS) is modeled with sinusoidal traveling waves:

$${ℱ}_{PS}(\overrightarrow{x},t)=A\cdot \text{sin}\left(2\cdot \pi \cdot \left(\frac{\overrightarrow{x}-c\cdot t}{\lambda }\right)\right)$$ Eqn. (2)

where A, c, and $\lambda$ are the amplitude, speed, and wavelength of the peristaltic wave, respectively.

Rhythmic segmentations (RS) are modeled with sinusoidal standing waves:

$${ℱ}_{RS}(\overrightarrow{x},t)=A\cdot \text{sin}\left(\frac{\pi \cdot \overrightarrow{x}}{L}\cdot n\right)\cdot cos\left(\frac{\pi \cdot c\cdot t}{L}\cdot n\right)$$ Eqn. (3)

where A, c, L, and n are the amplitude, speed, organ length, and number of nodal points for the segmentation wave, respectively. This model assumes that the endpoints of the organ are stationary and counted as nodes.

High amplitude propagating contractions (HAPC) are modeled with Gaussian traveling waves:

$${ℱ}_{HAPC}(\overrightarrow{x},t)=A\cdot e^{-\frac{4\cdot \text{ln}(10)\cdot {(\overrightarrow{x}-c\cdot t)}^2}{s_b^2}}$$ Eqn. (4)

where A, c, and $s_b$ are the amplitude, speed, and bolus size of HAPC wave, respectively. Note that the bolus size $(s_b)$ specifies the dimension of the contraction along the length of the organ while the amplitude (A) specifies the dimension orthogonal to the direction of wave velocity. The bolus size is defined by the full-width at tenth-maximum of the propagating Gaussian wave.

Tonic contractions (TC) are modeled with an inverted stationary Gaussian function:

$${ℱ}_{TC}(\overrightarrow{x},t)=\{\begin{array}{cc}0,\hfill & t<t_c\hfill \\ -A\cdot e^{-{\left(\frac{\overrightarrow{x}-{\overrightarrow{x}}_0}{s_c}\right)}^2},\hfill & t>t_c\hfill \end{array}$$ Eqn. (5)

where $A,{\overrightarrow{x}}_0,s_c,t_c$ are the amplitude, location, size, and time of appearance of contraction, respectively. The size $(s_c)$ specifies the dimension of the contraction along the length of the organ while the amplitude (A) specifies the dimension orthogonal to length of organ. For ease of implementation, the amplitude and location of tonic contractions may also be described as a fraction of the organ cross section and organ length. While Eqn. (5) implies that tonic contractions appear instantaneously, a gradual appearance of this motility pattern can be generated by varying the amplitude (A) as a function of time. Figure 1 presents a simulation of GI motility patterns for all modes considered in our work.

Figure 1.

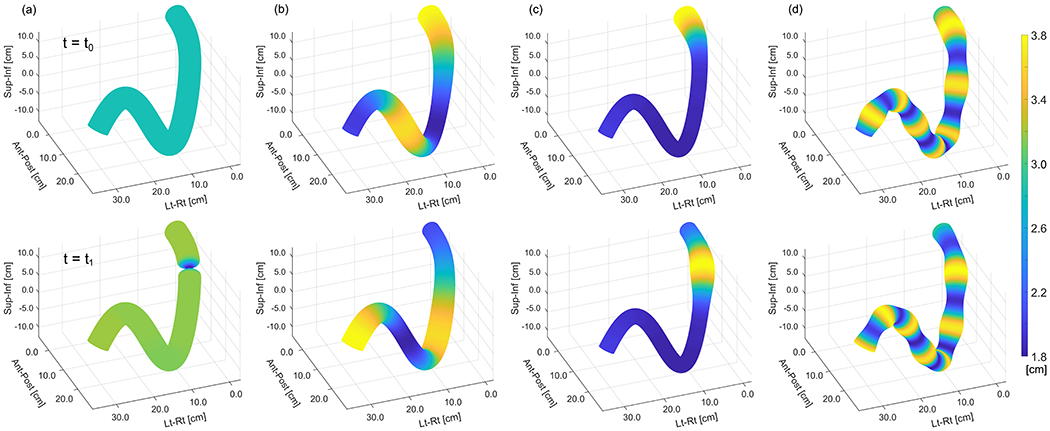
Hypothetical section of GI tract simulating motility for (a) tonic contractions, (b) peristalsis, (c) HAPCs, (d) rhythmic segmentation. Top and bottom rows show the wave at two different timepoints.

Phase shifts are not explicitly included in our modeling equations since they amount to a shift in the time axis. A phase shift can be implemented by changing the start and endpoint of the temporal axis in the simulation parameters.

Wave dispersion is designed by analogy to known dispersion models in physiological and experimental systems.^31–35 The amplitude of the wave is attenuated by processes in the spatial and/or temporal domain using one of three user-selected functions:

$$(\text{Linear}){𝒟}_i(𝓊)=\text{max}(0,1-\alpha \cdot 𝓊)$$ Eqn. (6)

$$(\text{Exponential}){𝒟}_i(𝓊)=e^{-\alpha \cdot 𝓊}$$ Eqn. (7)

$$(\text{Inverse Power Law}){𝒟}_i(𝓊)={(1+\alpha \cdot {𝓊}^2)}^{-1/2}$$ Eqn. (8)

where the generalized variable $𝓊$ stands for either $\overrightarrow{x}$ or t, and i is an index identifying the spatial (s) or temporal (t) dispersion shown in Eqn. (1). The variable $(\alpha )$ is a parameter that defines the amount of amplitude attenuation in either the spatial or temporal domain. Figure 2 presents examples of the dispersion models for several attenuation parameters.

Figure 2.

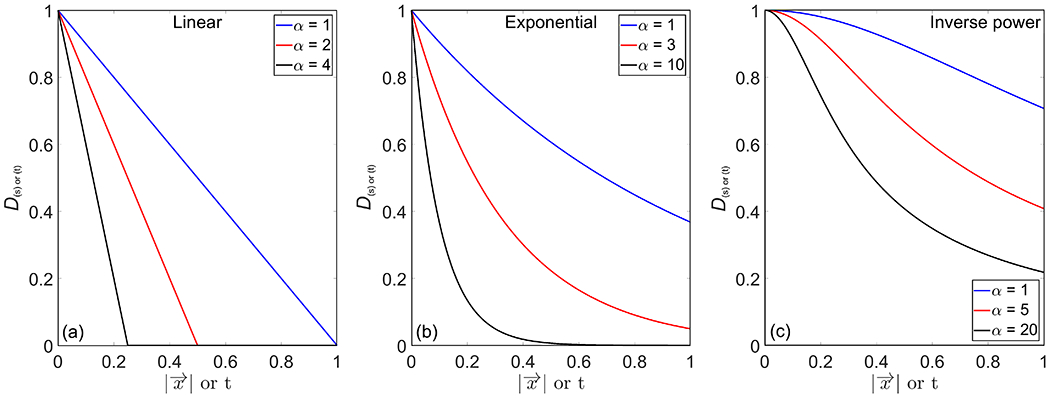
Examples of temporal and spatial dispersion modeled with (a) linear, (b) exponential, and (c) inverse power functions with varying attenuation parameters.

The organs in the XCAT phantom are modeled using cubic nonuniform rational B-spline (NURBS) surfaces.²⁴ To implement GI motility, the wave equation is applied at the control points of the NURBS surfaces defined in the reference XCAT phantom. The reference surfaces are dynamically updated at each timepoint based on user-specified parameters that describe the motility wave. The control points are displaced radially from the centroid of the cross section of the organ. This approach is consistent with measurements of organ distention resulting from luminal transmural pressure.¹⁵

Finally, GI motility is combined with respiratory and cardiac motion after constraining the displacement vector field to avoid artificial organ dislocation, overlap, and deformation, as described in previous work.²⁴

II.B. Measurements

Default parameters for the GI motility model were estimated from cine MRI acquisitions of patients planned and treated in a 1.5T MR-linac (Elekta AB, Stockholm, Sweden). The study was conducted under an IRB approved retrospective protocol number 21-129. Ten patients were included in our analysis. Appendix Table A1 lists relevant patient characteristics. The details of the workflow including simulation, planning, online adaptation, and delivery are described elsewhere.³⁶ Of note, abdominal compression was used for immobilization and motion management. Cine MRI data were acquired at simulation in a 3T MRI scanner (Philips Medical Systems, Best, Netherlands), at the beginning of each treatment fraction to verify setup reproducibility, and during each fraction of radiotherapy delivery in the 1.5T MR-linac. Table 1 lists the MRI acquisition parameters. The cine imaging planes for simulation and verification were centered on the GTV. For beam-on cine, the imaging planes were centered on the GTV or an abdominal organ-at-risk, at the discretion of prescribing physician.

Table 1.

Acquisition parameters for cine MRI datasets used to estimate default parameters for the GI motility model. Simulation cine was acquired in a 3T MR-simulator, setup and beam-on cine were acquired in a 1.5T MR-linac. For beam-on cine, the reported acquisition time is the median and range (min-max).

	Simulation Cine	Setup Verification Cine	Beam-on Cine
Imaging sequence	bFFE (2D)
Imaging planes	Axial / Coronal / Sagittal (interleaved)
FOV [mm]	420 x 420
Voxel size [mm]	3 x 3 x 5
Frame rate [Hz]	5
FA	40°
TR / TE [ms]	2.6 / 1.3	3.4 / 1.7
Acquisition time [min]	~1	~1	11.6 (4.6-15.1)

bFFE=balanced fast field echo, FOV=field of view, TR=repetition time, TE=echo time, FA=flip angle

A motility event was counted if it (a) was observed in esophagus, stomach, small bowel, large bowel, or rectum; (b) had a measurable displacement of the GI tract wall by at least 3.0 mm; (c) travelled along or perpendicular to the length of the tract. Initially, the diameter of the non-distended organ was estimated while no motility was observed. A peristaltic wave was identified by periodic propagating movement while HAPCs were identified by movements that extend over distances greater than 10-20 cm in the large bowel.²⁰ If antegrade (or retrograde) propagating movement was followed by retrograde (or antegrade) movement, the event was considered to be rhythmic segmentation. A tonic contraction was identified if a large stationary contraction was observed at any point of the GI tract. The wave speed was estimated as the distance/time traveled along the direction of motion. The amplitude of the wave was measured in the direction orthogonal to wave velocity. Bolus size was estimated by measurements in the same direction as wave velocity. If large air pockets were present in the tract, motility was noted but measurements were discarded due to susceptibility artifacts. A similar approach was followed when measurements were confounded by through-plane respiratory motion that was comparable to the magnitude of GI motility. In general, GI motility occurs at much larger timescales when compared to respiratory motion and they can easily be decoupled. When possible, propagating motion was cross-checked with the orthogonal cine MRI planes for consistency. A total of 330 cine MRI datasets (10 patients, simulation + pre + delivery, 5 fractions, 3 orthogonal planes) were manually analyzed using ImageJ (National Institutes of Health, Bethesda, MD).³⁷ The review and analysis of cine MRI datasets was performed by a board-certified medical physicist with seven years of experience in the planning and delivery of adaptive radiotherapy to GI targets.

For the generation of T2-weighted images in XCAT, signal intensities were derived from representative 3D acquisitions (3D T2w: TR/TE = 1300/87 ms, voxel size = 1 × 1 × 2 mm, FOV = 400 × 450 × 250 mm) used for online plan adaptation in the 1.5T MR-linac.

III. RESULTS

Figure 3 presents a surface rendering of the small and large bowel at two timepoints of GI motility implemented in the reference XCAT phantom. The rendering is created by using the control points of the NURBS surface for each organ and the motion model presented in this work. This example demonstrates peristalsis in the small bowel and HAPCs in the colon. Arrows point to the location of the wave starting point. The movie (SurfaceRendering.avi) included in the Appendix shows the waves propagating in their respective organ.

Figure 3.

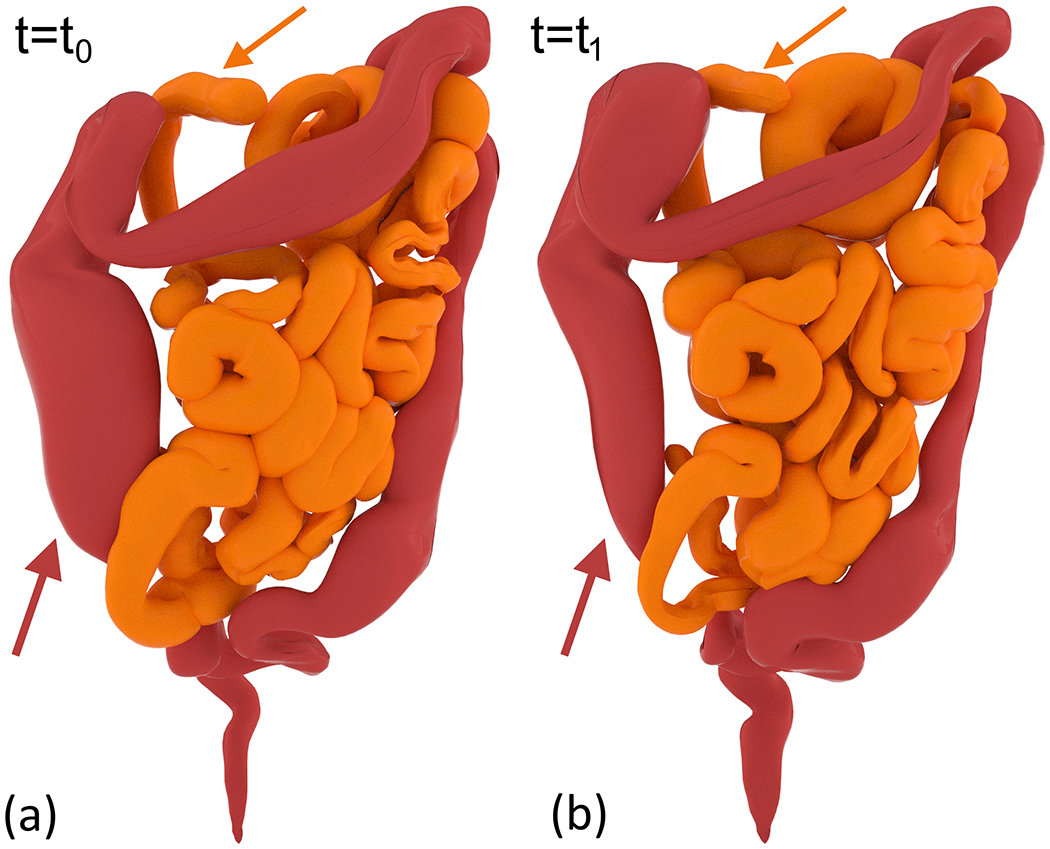
Surface rendering of small and large bowel demonstrating peristalsis and HAPCs. (a) and (b) show the wave at two separate timepoints. Arrows point to the location of the wave origin in each organ.

The effect of the interaction between GI motion and organ volume is provided in Figure 4. A peristaltic wave propagating in the small intestine was simulated using the parameters listed in Table 2. The model parameters for respiratory motion represent the median amplitude of tumor displacement, reported in our previous work.³⁶ The model parameters for the peristaltic wave represent the median values reported in Table A2 in the Appendix. The domain of the simulation timespan is over the period of respiration (if no GI motion) or over the period of the peristaltic wave. Figure 4(a) demonstrates the variation of organ volume when only respiratory and cardiac motion is present in the phantom. The relative impact of cardiac or respiratory motion combined with peristaltic motion is shown in Figure 4(b) and Figure 4(c), respectively. Figure 4(d) combines all motion modes. Given that the effect of cardiac motion on the volume of abdominal GI organs is negligible, Figure 4(b) demonstrates the effect of peristalsis alone. In this case, cardiac motion primarily modulates lung and esophagus volume. Changes in stomach, pancreas, and large intestine volumes are driven by peristaltic motion. Finally, when all motion modes are combined, we find that the effect of peristaltic motion is comparable or larger than the effect of respiratory motion in all abdominal GI organs.

Figure 4.

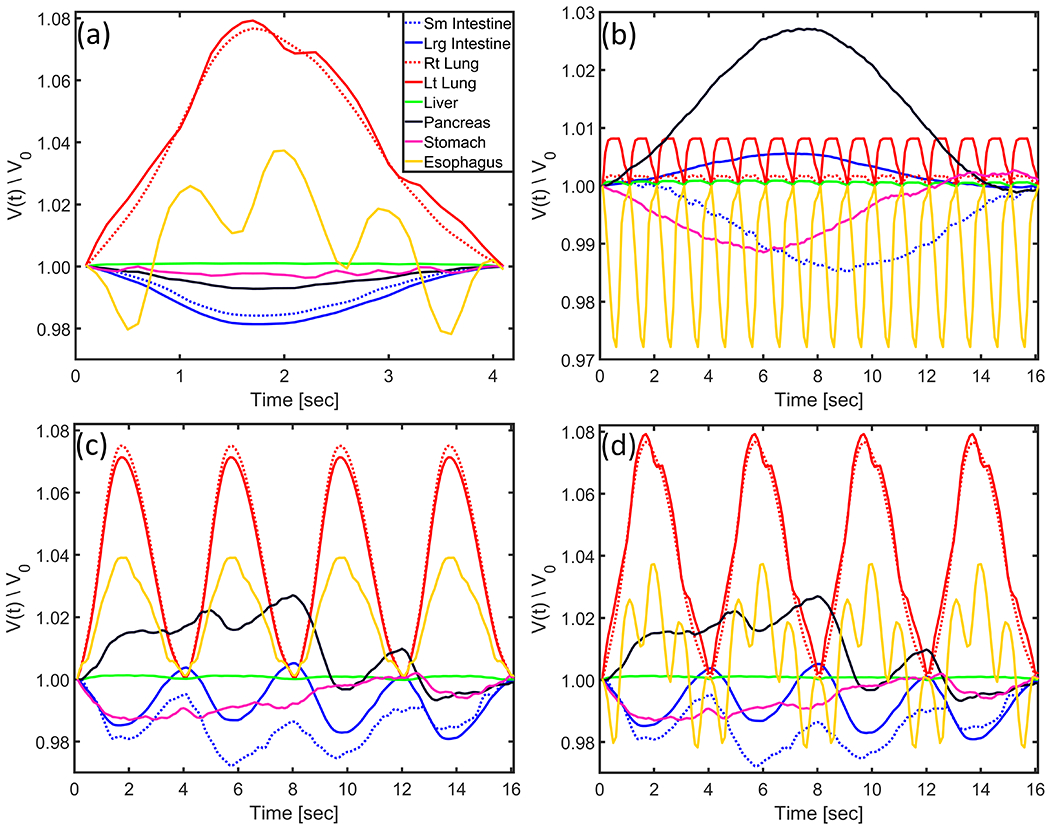
Example of the effect of peristaltic wave propagation on surrounding organ volume. A peristaltic wave was simulated using the parameters listed in Table 2. Change in organ volume in the presence of (a) only respiratory and cardiac motion, (b) only peristaltic and cardiac motion, (c) only peristaltic and respiratory motion, (d) peristaltic, respiratory, and cardiac motion. Organ volume is normalized to volume at first timepoint.

Table 2.

Timing and wave parameters for simulation of peristaltic wave in the small intestine. The respiratory amplitude represents the median value of target displacement reported in our previous work.³⁶ ΔV represents the change in left ventricle volume (i.e. the ratio of volumes) from diastole to systole.

Respiratory Period [sec]	4.0
Respiratory Amplitude (SI / AP / LR) [cm]	0.4 / 0.2 / 0.0
Heart Period [sec]	1.0
Heart LV ΔV (diastole/systole)	2.6
Peristalsis Amplitude [cm]	0.4
Peristalsis Wavelength [cm]	9.6
Peristalsis Wave Speed [cm/sec]	0.6

The magnitude of the deformation field between two timepoints of GI motility is presented in Figure 5. In this example, a simulated 4D T2-weighted MRI dataset incorporates peristalsis in the small intestine and HAPC in the large intestine. The timing and wave parameters for this simulation are listed in Table 3. The arrows in Figure 5(a,b) point to the location of the wave origin in each organ. The deformation field relates the displacement from the timepoint in panel (a) to that in panel (b). For clarity, the wavelength and bolus size of the peristaltic and HAPC waves are multiplied by a factor of 10 from the median values in Table A2. In order to highlight displacements arising primarily from GI motility, the two timepoints are chosen such that they are approximately in the same cardiac and respiratory phase.

Figure 5.

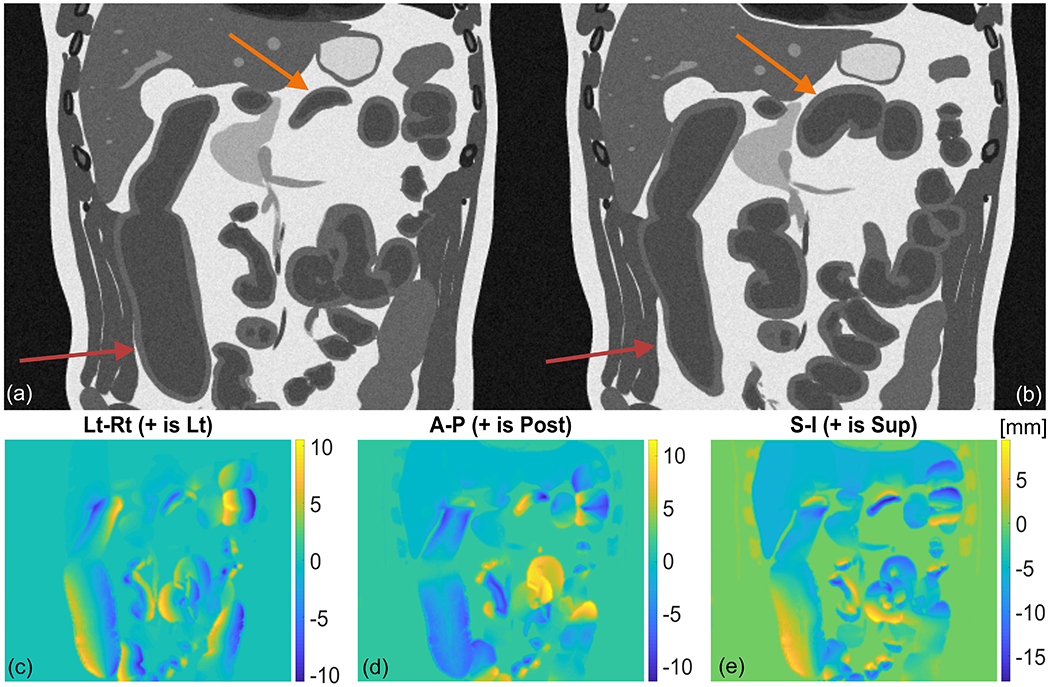
Gastrointestinal motility in a simulated 4D T2-weighted MRI dataset demonstrating peristalsis and HAPC in the small and large bowel. Panel (a) and (b) show the wave at two separate timepoints. Arrows point to the location of the wave origin in each organ. Panels (c,d,e) show magnitude of displacement in the Lt-Rt, Ant-Post, and Sup-Inf direction, respectively. The deformation field relates displacement from motion state in panel (a) to motion state in panel (b).

Table 3.

Timing and wave parameters for simulation of peristaltic wave in the small intestine and HAPC in large intestine. ΔV represents the change in left ventricle volume (i.e. the ratio of volumes) from diastole to systole.

	Peristalsis	HAPC
Respiratory Period [sec]	4
Respiratory Amplitude (SI / AP / LR) [cm]	1.0 / 0.4 / 0.0
Heart Period [sec]	1
Heart LV ΔV (diastole/systole)	2.6
Amplitude [cm]	1
Wave Speed [cm/sec]	1
Wavelength [cm]	96	NA
Bolus Size [cm]	NA	16

In the analysis of the imaging data, peristalsis was observed in 19/50 fractions (10 in small bowel, 9 in stomach), rhythmic segmentation was observed in 7/50 fractions (6 in small bowel, 1 in stomach), and HAPCs in 3/50 fractions (in large bowel). Tonic contractions were not observed. Additionally, GI motility was present in 22/50 fractions but could not be classified either due to through-plane respiratory motion or susceptibility artifacts from large air pockets. Table A2 lists the median (range) values for the modeling parameters estimated from our patient population. Note that different modes of GI motion could be simultaneously observed in the same patient and imaging session. Due to the location of the imaging planes used for cine acquisition, the esophagus and rectum were rarely visible. A representative example of peristaltic motion observed in one of our patients is shown in Figure 6.

Figure 6.

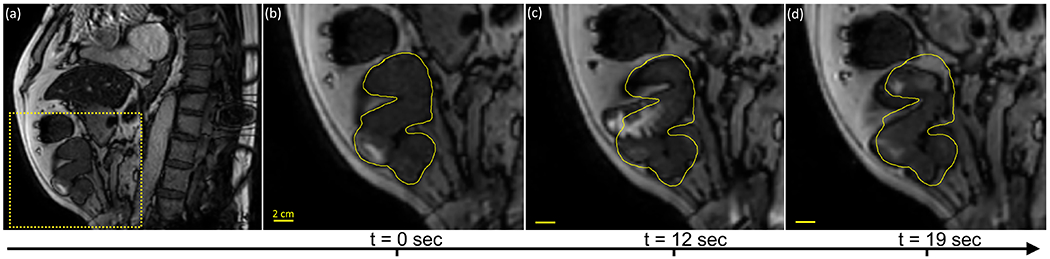
Representative example of peristalsis observed in the small bowel. (a) Sagittal slice of first timepoint in cine acquisition. Dashed box represents zoom-in area for panels (b,c,d) showing the peristaltic wave at three subsequent timepoints. The yellow contour represents the position of the small bowel at the first timepoint.

Figure 7 shows an example of peristalsis implemented in the 4D-XCAT phantom. The model displays a simulated 4D T2-weighted MRI dataset combining GI motility with cardiac and respiratory motion. For clarity, the timepoints shown in the figure are at matched respiratory and cardiac phases. The parameters used to generate this model were estimated from the analysis of the cine data for the patient shown in Figure 6. Note that the effect of abdominal compression can be approximated in the XCAT phantom by scaling the long and short axis of the torso and abdomen. The example in Figure 7 uses a factor of 1.15 scaling for the torso long/short axis and a factor of 0.9 scaling for the abdomen long/short axis. A simulation of a set of multimodal acquisitions for CT and T1/T2-weighted images is provided in Appendix Figure A1.

Figure 7.

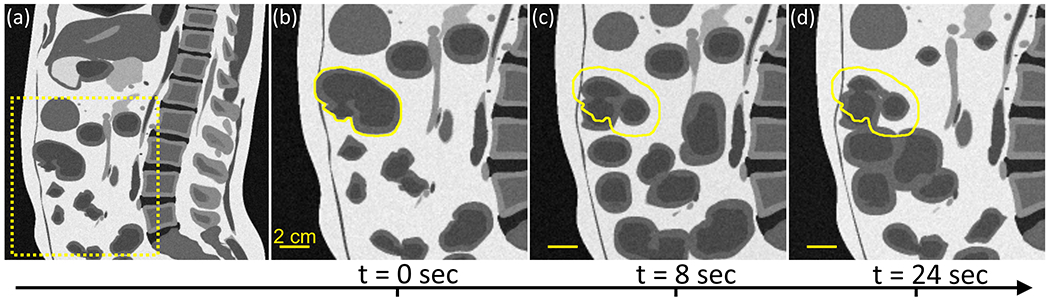
Representative example of peristalsis implemented in the small bowel. (a) Sagittal slice of first time-point in simulation. Dashed box represents zoom-in area for panels (b,c,d) showing the peristaltic wave at three subsequent time-points. The yellow contour represents the position of the small bowel at the first time-point.

IV. DISCUSSION

This work presents an implementation of gastrointestinal tract motility in the 4D-XCAT digital phantom of human anatomy. The phantom provides a generalized model for multimodality imaging research enabling development, testing, and validation of deformable image registration and dose accumulation algorithms. Figure A1 in the Appendix presents an example of T1-weighted, T2-weighted, and CT images. Such datasets can be used in investigating within/cross-modality image registration by comparing with the analytical deformation field computed in XCAT, as seen in Figure 5. Recent work has demonstrated the feasibility of a unified multi-domain image transformation that allows for realistic image generation and segmentation for CT and T1/T2-weighted MRI datasets.^38,39 We hypothesize that the application of motility models to these datasets will accelerate development in DIR algorithms, which in turn may enable applications to 4D dose planning. Furthermore, simulated CT images can be incorporated in a clinical dose-calculation algorithm to provide the ground truth dose for investigating accumulation methods.

The phantom provides the means for studying the effect of the interaction between modes of physiological motion and target/OAR volume changes. As demonstrated in Figure 4, the effect of intrafraction GI tract motility can be of the same magnitude or larger than the effect of respiratory motion. Other studies report similar findings.^12–14 The effect of physiological motion on target/OAR volumes is dependent on the relative amplitude and frequency of the various modes of motility. To further demonstrate the interaction between respiratory and GI motion, Figure A2 in the Appendix shows an example of the effect of the peristaltic wave when the amplitude of the respiratory motion is larger (also see Appendix movie Peristaltis_Only.avi and Peristalsis_Cardiac_Respiratory.avi showing a simulation in the presence of peristalsis only and with all motion modes, respectively). The peristaltic wave propagating in the small intestine was simulated using the parameters listed in Table A3 in the Appendix. In context, initial organ volumes are listed in Table A4 in the Appendix. Knowledge of modeling parameters for GI tract motility, particularly the wave speed and amplitude, will inform the selection of patient-specific PRV margins and improve treatment planning for radiotherapy. Note that GI motion is typically a slow process and the interplay effect between target/OAR location and MLC opening may not always be negligible, especially for low dose-rate delivery.⁴⁰

Gastrointestinal tract motility is not fully understood.^16–20 In our study, the empirical equations of motion are presented as part of a phenomenological modeling framework. A similar approach has been followed for other physiological processes.^41–44 Our models can be applied to the esophagus, stomach, small/large intestine, and rectum. While sinusoidal and Gaussian functions may not capture all aspects of GI tract motility, the proposed equations produce similar motion patterns when compared to observations in patient images, as seen in Figure 6 and Figure 7. We recognize there are other modes of GI track motion not discussed in our work. Besides HAPCs and tonic contractions, colon motility events include short/long single motor events, retrograde motor patterns, cyclic propagating motor patterns, and intrahaustral activity.²⁰ Nevertheless, depending on user parameters and the spatiotemporal domain of the simulation, our equations of motion can be used to describe several motility modes. For example, the cyclic propagating motor patterns of the colon exhibit similar properties to peristalsis and rhythmic segmentation.²⁰ To first approximation, other events may be modeled as a superposition of the functions described here.

Dispersion equations are also presented as part of a phenomenological modeling framework by analogy to known models in physiological and experimental systems.^31–35 Improvements in cine MRI spatial resolution and coverage will enable accurate measurements of dispersion. Currently, the characterization of dispersion from single-slice cine acquisitions is confounded primarily by lack in coverage. In 2D imaging, dispersion and large-wavelength motility waves can appear identical. Therefore, dispersion measurements were intentionally omitted. However, we often observe changes in GI tract motion that could be interpreted as dispersion. For instance, stomach peristalsis may temporarily fade then re-appear after a certain amount of time. Such events can be modeled by temporal dispersion. An example of this observation is provided in Appendix movie Dispersion.avi (the frame rate has been increased by a factor of 5 to highlight stomach motion). Finally, note that some motility patterns can occur spontaneously or in response to biochemical or biomechanical stimuli,²¹ reinforcing the need for including a model for dispersion in the GI motility equations. Future work will allow XCAT users to input any function for modeling spatial and temporal dispersion.

The analysis of the patient data included in this work is intended to provide a set of parameters that serve as a starting point for the equations describing GI motility. The validation of any model for GI motility necessitates cine MRI data with sufficient coverage of the entire tract. Such acquisitions will also allow for automatic analysis of changes in the GI tract, obviating the need for manual measurements of wave parameters.^14,45

CONCLUSION

We demonstrate the ability to generate realistic 4D medical images that simulate four modes of GI motility combined with respiratory and cardiac motion. All modes of motility, except tonic contractions, were observed in the analysis of our cine MRI acquisitions of patients undergoing radiotherapy. Peristalsis was the most common. Default parameters estimated from cine MRI data are used as initial values for simulation experiments. The digital phantom provides realistic models to aid in imaging and radiation therapy research.