Evaluating the resolution of conventional optical microscopes through point spread function measurement

Summary

In the imaging process of conventional optical microscopy, the primary factor hindering microscope resolution is the energy diffusion of incident light, most directly described by the point spread function (PSF). Therefore, accurate calculation and measurement of PSF are essential for evaluating and enhancing imaging resolution. Currently, there are various methods to obtain PSFs, each with different advantages and disadvantages suitable for different scenarios. To provide a comprehensive analysis of PSF-obtaining methods, this study classifies them into four categories based on different acquisition principles and analyzes their advantages and disadvantages, starting from the propagation property of light in optical physics. Finally, two PSF-obtaining methods are proposed based on mathematical modeling and deep learning, demonstrating their effectiveness through experimental results. This study compares and analyzes these results, highlighting the practical applications of image deblurring.

Graphical abstract

Physics; Optics; Optical imaging

Introduction

Various types of microscopes, including fluorescence,^1,2,3 electron,^4,5 and scanning microscopes,^6,7,8,9 are currently available for micro/nanoscale observations. However, conventional optical microscopes are nondestructive, fast, and dynamic; therefore, they remain important observation tools in biomedicine, microelectronics, chemistry, and precision instrument manufacturing.^10,11,12

The first practical optical microscope was invented by Antonio van Leeuwenhoek in 1673 with a magnification of approximately 270×. This was the first time visible light and lens sets were used to capture images of samples that are difficult to observe with the naked eye. However, the ability of an optical microscope to distinguish the details of an observed target has an upper limit because of incident light diffraction, defined as the resolution of the microscope. A series of studies have been conducted to calculate the resolution of optical microscopes because it is related to the properties of light distribution. George Airy proposed a method to calculate the distribution of the bright and dark spots caused by the fluctuations of incident light that passes through a diffraction-limited system.¹³ Ernst Abbe calculated the resolution of optical microscopes based on the numerical aperture of the lenses and the wavelength of incident light.¹⁴ John Strutt gave a quantitative relationship between the distribution of Airy disks and resolution based on Abbe’s theory; the Rayleigh criterion was then proposed to quantitatively evaluate the resolution of optical microscopes using the intensity distributions of adjacent diffraction disks.¹⁵ Fresnel further expressed the wavefront intensity as a superposition of the waves of multiple points’ vibrations and established an analytical mathematical expression for the phenomenon of circular hole diffraction.¹⁶ Based on the mathematical description of diffraction provided by Fresnel, examined the properties of intensity distribution under different boundary conditions were examined by Kirchhoff, Fraunhofer, and Sommerfeld, which formed the basis of diffraction theory in physical optics.^17,18

In sum, to study the influence of energy diffusion caused by light diffraction on imaging resolution during the microscope imaging process, establishing a quantitative relationship between diffraction-induced energy diffusion and the degree of blurring in complex optical systems based on diffraction theory is essential. Therefore, a series of study have been conducted to research it in recent years based on the diffraction theories in physical optics.

Diffraction theories in physical optics

Keller established the geometric theory of diffraction (GTD), formulating simple rules for calculating diffraction fields.¹⁹ Borovikov refined the GTD and established rules for distinguishing the regions where geometric optics and diffraction fields are applied.²⁰ The GTD connected the applicable ranges of geometric optics and diffraction fields through transition regions and provided models of wave propagation in these regions.^21,22 Bouwkamp proposed several three-dimensional diffraction field expressions based on the Kirchhoff integral.²³ Based on the study by Bouwkamp, which considered that the amplitude at any point in space originates from the interference created at that location by a converging spherical wave propagating along the optical axis, Born and Wolf established a three-dimensional diffraction field expression with its origin at the intersection of the optical axis and the plane of the aperture.²⁴ Hopkins contributed to the expression of a three-dimensional diffraction field by introducing the difference between the distances from the aperture plane to receiving plane and from the spherical wave focus point to the receiving plane (i.e., the defocus distance).²⁵ Li and Wolf improved the three-dimensional diffraction field equation reported by Hopkins to obtain more accurate results for diffraction states with different Fresnel numbers.²⁶ Meanwhile, Frieden and Pederson described the three-dimensional diffraction field of off-axis spherical waves.^27,28 Although these researchers analyzed the diffraction properties through experiments or simulations, their models for calculating the intensity distribution mostly comprised complicated non-analytical functions, even approximate integral solutions. Therefore, analyzing the diffraction properties of a practical diffraction system simply and rapidly is difficult.

To solve this problem, Wang proposed a three-dimensional diffraction field model for circular-hole Fresnel diffraction and calculated expressions for divergent and convergent spherical wave models.²⁹ In contrast to previous research that focused on divergent waves, he put forth a mathematical relationship between divergent and convergent waves and extended his method to calculate the intensity distribution of the convergent waves, which is an important theoretical basis for intensity analysis during imaging.

Alongside the continuous improvement of diffraction theory, these theories were also applied to optical imaging and gradually formed diffraction imaging theory. These theories are also gradually being applied to the assessment and calibration of practical optical systems. Duffieux was the first to propose an imaging theory based on diffraction.³⁰ Blanchard used diffraction theory to design diffraction gratings and applied the improved gratings to camera lenses for aberration correction.³¹ These gratings were also applied to wavefront sensing systems. Stefan gave a method to calculate the optical transfer function (OTF) of a large-aperture imaging system under different medium refractive index conditions based on the diffraction model reported by Frieden and applied the OTF model to the description of confocal microscopes and partially coherent imaging systems.³² Diffraction theory imaging applications generally rely on measuring the degree of energy diffusion in blurred images when diffraction occurs and on establishing an OTF. However, accurate descriptions of the degree of energy diffusion are difficult to achieve using simple methods, such as gratings, and the results contain unknown aberrations from the systems.

Therefore, analyzing the mechanisms of light-intensity diffusion in optical imaging systems based on diffraction theory is necessary. In optical microscope systems, the mechanism of light-intensity diffusion is generally expressed as a point spread function (PSF). Therefore, the accurate acquisition of PSFs is important for the calibration and resolution enhancement of optical microscopes. Four main methods are currently available for obtaining more accurate PSFs of optical microscopes: mathematical, experimental, analytical, and deep learning.

Common methods of PSF acquisition

Mathematical methods

For the development of an accurate mathematical model of PSFs, the two main factors of PSF formation must be analyzed: the light source and the microscope system. To study the light source, Durnin proposed a model for the light intensity distribution of diffraction-free Gaussian beams of different orders under different conditions.^33,34 Sprangle compared the variation of the light intensity distribution of Gaussian and Bessel beams for different parameters.³⁵ Ruschin proposed a modified Bessel beam model with reduced diffraction phenomena and long-distance propagation.³⁶ Overfelt compared the propagation capabilities and light-intensity model variations of Bessel, Gaussian, and Bessel-Gaussian beams under the single-hole Fresnel and Fraunhofer diffraction conditions.³⁷ The aforementioned studies provided the propagation laws for different types of light sources when diffraction occurs.

For practical optical microscope systems, Gibson and Lanni summarized the existing models and proposed a three-dimensional convergent spherical wave diffraction field model with a more accurate representation of the defocus distance and provided a detailed model of the PSFs of the oil-immersion objective lens.³⁸ Agard collected and analyzed images of fluorescent objects using oil- and water-immersion objective lenses, confirming the PSF model reported by Gibson and Lanni.³⁹ Lalaoui introduced an effective medium approximation based on the study by Gibson and Lanni, creating a PSF model with more accurate refractive index parameters, thus significantly improving the accuracy of the PSF estimation.⁴⁰ Török found that the conventional scalar diffraction field cannot accurately describe the propagation law of electromagnetic waves when the diffraction field passes through two media with a large difference in the refractive index, thus proposing a vector field model to describe circular hole diffraction based on the theory of Li and Wolf.⁴¹ Building on the study by Török, Haeberlé combined the diffraction field model put forth by Gibson and Lanni and proposed a point-diffusion function model for high-numerical-aperture lenses.⁴² In addition, some scholars have established mathematical models to theoretically calculate PSFs by describing the response of the imaging system through the pupil functions of the objective lens in Fourier optics.^43,44,45

Overall, the advantage of mathematical methods is that the PSFs of optical microscopes can be calculated rapidly, and the trends of PSFs can be predicted. Simultaneously, if the optical microscope system is more complex, the construction of the corresponding mathematical model becomes more challenging.

Experimental methods

The PSF of an optical microscope system is not a regular point-like pattern and varies with spatial location during actual microscopic observation. Therefore, an experimental method is used to obtain the PSF for optical microscopes. Researchers have generally used subresolution fluorescent microbeads embedded in optical cements or tilted surfaces at different locations to measure the PSF of optical microscopes. This is particularly true for some self-made fluorescence imaging systems, which are mostly calibrated using morphological image measurements of fixed-size microbeads. Gibson and Lanni analyzed the images of fluorescent microbeads collected using an oil-immersion objective lens and produced an expression for the corresponding PSF.⁴⁶ However, this method poses two major challenges: first, precisely controlling the position of a microbead in optical cement is challenging, which leads to inaccurate measurement results; second, human interaction with optical cement can disrupt the local refractive index of the cement, resulting in an inconsistent refractive index in the optical medium, leading to measurement errors. Therefore, obtaining PSFs from fluorescent microbeads embedded at different depths in the observed samples is more complicated. To solve this problem, Bruno proposed a method based on finding PSFs in the observed images and then reconstructing the images.⁴⁷ With the development of single-molecule localization and tracking techniques, researchers can rely on controlled fluorescent molecules to determine the PSF of optical microscope systems.⁴⁸ The advantage of this method is that the accuracy of the PSFs obtained from single fluorescent molecules is much higher than that of fluorescent microbeads. However, the localization and tracking of single molecules are more susceptible to Brownian motion, introducing observation lag and affecting the accuracy of the obtained PSFs.⁴⁹

In contrast, knife-edge methods are also significant for measuring PSF in optical microscopes. These methods can obtain the corresponding PSF by differentiation from the well-defined edge part of the microscopic image.⁵⁰ To measure the PSF precisely, the knife edge in the observed image must be perpendicular or parallel to the sampling direction. Although some knife-edge methods are robust to the angle of the knife edge, several constraints still exist on the selection of large-angle knife edges for optical imaging.⁵¹ For example, edge selection at different positions may lead to significant differences in the PSF measurements.⁵²

The PSFs obtained using these measurement methods provide features that incorporate aberrations in the entire optical system; thus, the effect of the entire optical system on the imaging can be described more accurately. However, the accuracy of these experimental methods is influenced by the characteristics of the observed samples, such as morphology, location, material, and luminous characteristics.

Analytical methods

Since both mathematical and experimental methods have their apparent disadvantages, researchers have devised analytical methods that do not require complex mathematical modeling and collection of a larger number of samples simultaneously to obtain PSFs.

The analytical method is an estimation of the PSF based on an iterative approach. Nagy and Leary proposed a sub-block two-dimensional convolution method based on the fast Fourier transform and a linear interpolation technique for PSFs to reduce the mosaic effect.⁵³ Preza and Conchello applied the layered deconvolution method used in astronomical image processing to microscopic image processing and proposed a Maximum Likelihood-Expectation Maximization deconvolution algorithm.⁵⁴ Maalouf used the Zernike moment expansion of the measured depth-dependent PSFs as an initial condition to provide a theoretical basis for deconvolution.⁵⁵ The measured PSFs were further optimized during the deconvolution process to approximate the true values. Kim extracted a rough PSF from images of the observed samples by performing an intensity analysis and corrected them in iterations using the Lucy-Richardson algorithm, thereby reducing computational complexity.⁵⁶ Chen used images of fluorescent particles obtained from measurements to perform weighted averaging, proposed a method to estimate PSFs with spatial variation, and used deconvolution to obtain more accurate PSFs.⁵⁷

Analytical methods can provide a better approximation of real PSFs using an iterative approach and can reduce the interference of human operations on the observation environment using interpolation techniques. However, analytical methods, which include blind deconvolution and interpolation, consume more computation time and have poorer real-time performance compared to mathematical and experimental methods.

Deep learning methods

Deep learning has become an effective tool for complex tasks. Over the last ten years, a series of networks have been applied to image processing, including convolutional neural networks (CNNs) and deep CNNs.^58,59,60,61 In 2018, Herbel estimated the parameters of a PSF model for astronomically observed images using a CNN.⁶² Elias used a CNN based on a single-molecule localization technique to achieve densely overlapping PSF images over a large axial range, extracted the optimal PSFs from them, output their spatial locations, and used the extracted PSFs for the super-resolution reconstruction of microscopic images.⁶³ Hershko extracted and optimized PSFs at different wavelengths from microscope images using a CNN.⁶⁴ Vasu designed a CNN-based method for the extraction of image blur kernels and effectively applied it to the nonblind deblurring of images.⁶⁵ CNNs and their improved models have been widely used for the blur kernel and PSF estimation of images.

In 2014, based on the idea of allowing two networks (the discriminator and generator) to compete with each other, generative adversarial networks (GANs) were proposed by Goodfellow.⁶⁶ Huang used a GAN to train low-resolution microscope image sets and used the generated PSFs to restore high-resolution images.⁶⁷ Baniukiewicz trained a GAN using microscopic cell image sets and used the generated PSFs to predict the degree of blurring of images located at different defocus depths.⁶⁸ Lim proposed a cycle-consistent GAN (CycleGAN) and used it to generate blur kernels for microscope images.⁶⁹ Serin used a CycleGAN and adaptive instance normalization (AdaIN) to achieve blur kernel transformation under different system conditions and applied it to CT image quality improvement.⁷⁰ In 2022, Philip trained a GAN using microscope image sets with PSFs, effectively applied the generated PSFs to an embryo, and deblurring of the excised brain tissue microscope image.⁷¹

In addition to CNN and GAN, other types of networks have been used for PSF extraction and research. In 2019, Gao proposed a back-propagation quantum neural network and applied it to PSF estimation in Gaussian degradation imaging systems.⁷² Gray used the DEEPLOOP toolbox to train a large number of optical images to estimate and reconstruct PSFs.⁷³ Yang trained the W-Net model using measured PSF image sets and used the generated PSFs to refocus defocused blurred microscope images.⁷⁴

In recent years, deep learning methods have developed rapidly, relying on the powerful computing capability of graphics processing units (GPU), allowing researchers to avoid complex mathematical models of PSFs and obtain more optimal results. However, deep learning methods cannot obtain analytic expressions for PSFs, and a large number of collected images are required as datasets for network training. Moreover, deep learning methods are more sensitive to changes in system parameters such that a small change in any of the camera parameters results in the reacquisition of the datasets in order to accommodate the new parameters.

PSF measurement examples and results

In this study, we propose a PSF acquisition method based on an improved style GAN (StyleGAN) and a PSF modeling method based on the theoretical model in ref.²⁹

First, the ideal image generation module based on the improved StyleGAN is trained using the collected Gaussian beam image sets, and a series of diffraction images of a Gaussian light source containing Airy disks is obtained, where the light intensity distributions in the Airy disks are closer to the theoretical distributions. Second, blur kernels are extracted from the centers of the generated ideal diffraction images with different depth information to replace the PSFs, thus avoiding the noise that occurs during the representation of PSFs using parameter identification or curve fitting. Finally, based on the learnable convolutional half-quadratic splitting and convolutional preconditioned Richardson (LCHQS-CPCR) model, the extracted blur kernels were used to deblur microbead-blurred images located at different depths under visible illumination.

The PSF generation module based on the improved StyleGAN is illustrated in Figure 1.

Figure 1.

Ideal images generation module based on improved StyleGAN⁷⁵

(A and B) (A) The schematic diagram of the ideal images generation module, (B) The structure of the generator in the ideal images generation module.

We input the collected images into the ideal image generation module and set the parameter kimg to 280. kimg is the time required by the StyleGAN discriminator to recognize one thousand real images. The training process for ideal Gaussian light-source diffraction images in the ideal image generation module is shown in Figure 2, which shows that the generated images become closer to the real images as the number of iterations increases. Figure 2A shows the initial images generated by the generator at the beginning of each iteration. Figure 2B shows the generated images when kimg = 40; the color of the generated images gradually approaches the real images. Figure 2C shows the generated images when kimg = 80, the contours of the diffraction rings gradually begin to form. Figure 2D shows the generated images when kimg = 120; StyleGAN inaccurately generated colorful band patterns around the diffraction rings. Figure 2E shows the generated images when kimg = 240, where StyleGAN corrected the generated incorrect patterns by learning more samples, and the diffraction rings in the centers of the images can be clearly observed. Figure 2F shows the generated images when kimg = 280; the diffraction rings have realistic textures and details, and the shapes of the Airy disks are regular and clearly visible.

Figure 2.

Training process in ideal image generation module

(A–F) are the Gaussian light-source diffraction images generated by the generation module when kimg is 10, 40, 80, 120, 240, and 280, respectively.

The loss curves of the generator and discriminator networks during the training process are shown in Figure 3. Figure 3A shows that the loss of the discriminator gradually stabilizes when kimg = 150. In Figure 3B, the loss curve of the generator exhibits a downward trend, and the loss gradually stabilizes at kimg = 160.

Figure 3.

Loss curves of the generator network and discriminator network

(A and B) (A) is the loss curve of the discriminator network, (B) is the loss curve of the generator network.

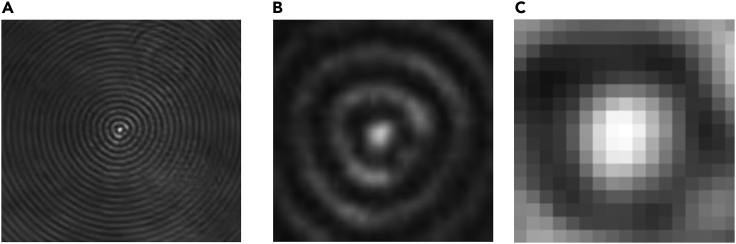
After obtaining the generated ideal diffraction images, we selected images located at different depths from the image set, grayscaled them, and then intercepted the central positions of the Airy disks as the blur kernels of the images. The grayscale image at Δd = 0 μm is shown in Figure 4A, and its central part that includes the Airy disk, is shown in Figure 4B, where Δd is the defocus distance of observed object; in Figure 4C, the central part of the Airy disk in Figure 4B was accurately extracted as the blurring kernel.

Figure 4.

Extraction of the blurring kernel from a generated image

(A–C) (A) is the diffraction image of an ideal Gaussian light source, (B) is the central part of diffraction image (A) that contains the Airy disk, and (C) is the blurring kernel extracted from (B).

The second method for obtaining the PSF is the theoretical modeling method. Our theoretical PSF model is as follows:

$$\begin{array}{l}{{\rm I}}_P={\left(e-1\right)}^2·\frac{1-J_0\left(2N\pi \frac{\rho }{Ka}\right)e_k^{-}-J_0\left(2N\pi \frac{\rho }{Ka}\right)e_k^{+}+J_0^2\left(2N\pi \frac{\rho }{Ka}\right)}{{\left(\exp \left(\frac{{\rho }^2}{C^2{K}^2{a}^2}\right)+e-2\right)}^2}\\ e_k^{-}=\exp \left[-iCN\pi \left(1+\frac{{\rho }^2}{K^2{C}^2{a}^2}\right)\right],e_k^{+}=\exp \left[iCN\pi \left(1+\frac{{\rho }^2}{K^2{C}^2{a}^2}\right)\right]\end{array}$$ (Equation 1)

where J_n is the nth-order Bessel function, ρ is the distance from a point on the imaging surface to the optical axis, e is the natural constant, I_p is light intensity distribution at a point on the imaging surface, K is a set of constants, N = a²/λδ; δ = b₀(1-(ξ²Δd/f(b₀f+ξfΔd))); C = ξ²Δd/(b₀f²+ξfΔd); ξ = b₀-f; Δd = d-d₀; a is the effective radius of the objective lens, λ is the wavelength of the light source, b₀ is the ideal image distance of a microscope, d is the object distance, d₀ is the ideal object distance of a microscope, and f is the focal length of a microscope.

To compare the aforementioned two methods, we extracted the blurring kernels from the original image at Δd = 0 μm and its corresponding generated image, calculated their average intensity curves through the center of the intensity peak, and compared it with our proposed theoretical modeling method. The results are shown in Figure 5. Compared to the light-intensity distribution curve of the original image, the intensity distribution curve of our image generated by StyleGAN is closer to the theoretical PSF curve. In addition, the obtained curve is smoother and possesses stronger symmetry of the optical axis.

Figure 5.

The comparison between the generated image, the original image, and the theoretical PSF model we proposed, where x is the imaging plane coordinate

After an accurate PSF model has been established, the resolution of optical microscope can be evaluated based on the Rayleigh criterion in Figure 6. According to the definition of the Rayleigh criterion, when the overlapping position intensity of the light intensity curves of two adjacent light sources accounts for 73.5% of the peak intensity of a single curve, the distance between their centers is the minimum resolution. The results in Figure 6 show that, when the Rayleigh criterion was met, the distance between the two centers was 1100 nm. To further validate the intensity distribution model, a simplified formula to estimate the minimum resolution of a practical optical system is used,

$${\psi }_{\min }=\frac{0.61\lambda }{NA}$$ (Equation 2)

where ψ_min is the resolution; NA is the numerical aperture of the objective lens. The calculated resolution using Equation 2 was 1159 nm, which was 59 nm different from the resolution calculated by our model, the error is about 5%, so it is believed that the light intensity distribution model we proposed is basically accurate.

Figure 6.

Schematic diagram of resolution evaluating based on Rayleigh criterion

Finally, the blur kernels extracted from the generated ideal diffraction images are used to deblur the images of microbeads under visual light illumination at different depths based on the LCHQS-CPCR model. It is an end-to-end model, that is, it performs pre-training, extraction of image prior features, image deconvolution and deblurring independently. In LCHQS-CPCR, firstly, the deconvolution module performs the deconvolution operation on the input blurred images. Secondly, the network further convolves the results of the initial deconvolution with the gradients in both horizontal and vertical directions to denoise. Finally, the denoised gradient images are subjected to further deconvolution to obtain the clear images. The gradients of the clear images are inputs of the convolutional layer in next iteration. In our deblurring experiment, the images of dynamic microbeads in solution were collected by the optical microscope, where the diameter of the microbeads was 10.08 μm; the images at different depths are as shown in Figure 7. The image-deblurring method based on the LCHQS-CPCR model is shown in Figure 8, where the outline of the microbeads is observed to become clearer, and that the noise between the microbeads is effectively removed.

Figure 7.

Original microbead images at different depths

(A–F) are the images of microbeads when Δd are 0 μm, 2 μm, 4 μm, 6 μm, 8 μm, and 10 μm, respectively.

Figure 8.

Clear images after reconstruction using our method

(A–F) are clear images of microbeads after reconstruction when Δd are 0 μm, 2 μm, 4 μm, 6 μm, 8 μm, and 10 μm, respectively.

Discussion

In summary, the PSF is an important factor for characterizing the properties of image blurring in optical systems and is the most direct way to enhance the resolution of microscopes. Therefore, the accurate measurement of PSF is a crucial issue in optical microscopy. In this study, we presented the advantages and disadvantages of each of the four methods for obtaining PSFs, because of which these four methods are often applied in different scenarios. Mathematical methods based on spatial diffraction field theory were the first to be proposed and belonged to the most traditional methods. However, owing to the development of microscope technology, the hardware structure has become increasingly complex, leading to increased difficulty in accurately modeling specific microscope systems. Therefore, mathematical methods are often aimed at optical systems in which the structures are relatively simple and easy to model. Although experimental methods can express complete system aberrations, obtaining an analytical expression of the PSF is challenging; therefore, researchers tend to choose a variety of well-established PSF models and then use various PSF models to fit the experimental results separately to determine the most accurate PSF representation. The analytical method is based on experiment and uses an interpolation technique to further reduce the number of samples required and improve the accuracy of the results. Deep learning methods are a future trend with strong generality but with high hardware requirements. For PSF measurements, the use of multiple methods, both combined and cross-validated, will be a future trend. For example, the powerful ability of deep learning can be used to generate PSF sets with specific properties that complement experimental methods. The fast and precise features of mathematical methods can also provide real-time validation of the accuracy of other methods.

Limitations of the study

Due to the complexity of PSF genesis and the coupling of multiple system parameters in advanced optical imaging, researchers may not be able to acquire an accurate PSF using a single PSF obtaining method. Therefore, it is difficult for some composite PSF obtaining methods in practical situations to be accurately categorized in this review.

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Weihan Hou (ihwhlr@126.com).

Materials availability

This study did not generate new unique reagents.

Data and code availability

Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Instructions for section 1: Data

All data reported in this paper will be shared by the lead contact upon request.

Instructions for section 2: Code

This paper does not report original code.

Instructions for section 3

Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Appendix

The derivation process of Equation 1 is shown below.

In Ref.,²⁹ the distance r from the light source to a point on spherical wave when Fresnel diffraction occurs can be expressed as,

$$r\approx b+\frac{M}{2b}{q}^2+\frac{{\rho }^2}{2b}-\frac{q\rho }{b}\cos \alpha$$ (Equation 3)

where cosα and M can be expressed as,

$$\cos \alpha =\frac{q^2+{\rho }^2-g^2}{2q\rho },M=\frac{d\pm b}{d}$$ (Equation 4)

where d is the distance from the light source to the circular hole; b is the distance from the circular hole to the receiving plane; a is the radius of the circular hole, ρ is the distance from a point on the receiving plane to the optical axis, q is the distance from any point on the wave front to the center of the wave front, and α is the angle between q and ρ. Introducing Equation 3 into the expression for the amplitude E_p of Fresnel diffraction in Equation 5 yields Equations 6 and 7,

$$E_P=\frac{-i}{\lambda }{E}_0\underset{\mathrm{\Sigma }}{\iint }\frac{\exp \left(ikr\right)}{r}d\Phi$$ (Equation 5)

$$E_P=E_0\exp \left[\frac{ik}{2b}\left({\rho }^2+M{a}^2\right)\right]\times {\sum _{n=1}^{\infty }\left(-i\frac{Ma}{\rho }\right)}^n{J}_n\left(\frac{kqa}{b}\right)$$ (Equation 6)

$$E_0=\frac{\exp \left(ik\left(d\pm b\right)\right)}{d\pm b}$$ (Equation 7)

where dΦ is the infinitesimal element of spherical wave, k = 2π/λ is the wavenumber, λ is the wavelength of light source, a is the effective radius of lens, J_n is n-th order Bessel function.

In the process of lens imaging, the variation of object distance Δd and the variation of image distance Δb are related as follows,

$$\Delta b=\frac{\Delta d{\xi }^2{b}_0}{b_0{f}^2+\xi f\Delta d}$$ (Equation 8)

where ξ = b₀-f, f denotes the focal length, b₀ is the ideal image distance. Substituting Equation 8 into Equation 3 yields Equation 9,

$$r=\delta +\frac{\Delta d{\xi }^2}{2b_0\delta f\left(f+\delta \Delta d\right)}{q}^2+\frac{{\rho }^2}{2\delta }-\frac{q\rho \cos \alpha }{\delta }$$ (Equation 9)

where,

$$\delta =b_0-\Delta b=b_0\left(1-\frac{\Delta d{\xi }^2}{f\left(b_{0}f+\xi \Delta d\right)}\right)$$ (Equation 10)

Therefore, combining Equations 9 and 6 yields Equation 11,

$$E_P=E_0\exp \left[iCN\pi \left(1+\frac{{\rho }^2}{C{a}^2}\right)\right]\times {\sum _{n=1}^{\infty }\left(-\frac{iCa}{\rho }\right)}^n{J}_n\left(\frac{k\rho a}{\delta }\right)$$ (Equation 11)

where N = a²/λδ; C = ξ²Δd/(b₀f²+ξfΔd), and E₀ is denoted as,

$$E_0=\frac{\exp \left(ikC{b}_0\right)}{C{b}_0}$$ (Equation 12)

Then, light intensity I_p can be calculated as,

$$I_p=E_P·{E_P}^{\ast }={\sum _{n=1}^{\infty }\left(-i\frac{Ca}{\rho }\right)}^n{J}_n\left(2N\pi \frac{\rho }{a}\right)·{\sum _{n=1}^{\infty }\left(i\frac{Ca}{\rho }\right)}^n{J}_n\left(2N\pi \frac{\rho }{a}\right)$$ (Equation 13)

According to the property of Bessel function, there are Equations 14 and 15 that hold true,

$$J_{-n}\left(x\right)={\left(-1\right)}^n{J}_n\left(x\right)$$ (Equation 14)

$$\sum _{n=-\infty }^{\infty }{J}_n\left(x\right)y^n=J_0\left(x\right)+\sum _{n=1}^{\infty }{\left(-y\right)}^n{J}_n\left(x\right)+\sum _{n=1}^{\infty }{y}^n{J}_n\left(x\right)$$ (Equation 15)

The summation of the n-th Bessel functions can be transformed into,

$$\sum _{n=-\infty }^{\infty }{y}^n{J}_n\left(x\right)=\exp \left[\frac{x}{2}\left(y-\frac{1}{y}\right)\right]$$ (Equation 16)

With the property of orthogonal polynomial,²⁹ we obtain,

$$\frac{{\sum _{n=1}^{\infty }\left(-\frac{1}{y}\right)}^n{J}_n\left(x\right)}{{\sum _{n=1}^{\infty }\left(y\right)}^n{J}_n\left(x\right)}=\frac{\exp \left(-\frac{1}{y^2}\right)-1}{e-1}$$ (Equation 17)

where e is the natural constant.

Therefore, Equation 15 can be transformed into,

$$\sum _{n=-\infty }^{\infty }{y}^n{J}_n\left(x\right)=J_0\left(x\right)+\left(1+\frac{\exp \left(-\frac{1}{y^2}\right)-1}{e-1}\right)\sum _{n=1}^{\infty }{y}^n{J}_n\left(x\right)$$ (Equation 18)

Combining Equation 18 with Equation 13 yields Equation 19,

$${{\rm I}}_P={\left(e-1\right)}^2\frac{1-J_0\left(x\right)\exp \left[\frac{x}{2}\left(y-\frac{1}{y}\right)\right]-J_0\left(x\right)\exp \left[-\frac{x}{2}\left(y-\frac{1}{y}\right)\right]+J_0^2\left(x\right)}{{\left(\exp \left(-\frac{1}{y^2}\right)+e-2\right)}^2}$$ (Equation 19)

Replace x and y in Equation 19 with the parameters as follows,

$$x=2N\pi \frac{\rho }{a},y=\frac{Ca}{\rho }$$ (Equation 20)

Then, the light intensity I_P can be denoted as,

$$\begin{array}{l}{{\rm I}}_P={\left(e-1\right)}^2·\left(\frac{1-J_0\left(2N\pi \frac{\rho }{a}\right)e^{-}-J_0\left(2N\pi \frac{\rho }{a}\right)e^{+}+J_0^2\left(2N\pi \frac{\rho }{a}\right)}{{\left(\exp \left(\frac{{\rho }^2}{C^2{a}^2}\right)+e-2\right)}^2}\right)\\ e^{-}=\exp \left[-iCN\pi \left(1+\frac{{\rho }^2}{C^2{a}^2}\right)\right],e^{+}=\exp \left[iCN\pi \left(1+\frac{{\rho }^2}{C^2{a}^2}\right)\right]\end{array}$$ (Equation 21)

Introducing a set of constants K to Equation 21 makes the simplification based on the orthogonal polynomial property more accurate, so that Equation 1 can be obtained.