Compositional functional regression and isotemporal substitution analysis: Methods and application in time-use epidemiology

Abstract

The distribution of time that people spend in physical activity of various intensities has important health implications. Physical activity (commonly categorised by the intensity into light, moderate and vigorous physical activity), sedentary behaviour and sleep, should not be analysed separately, because they are parts of a time-use composition with a natural constraint of $24$ h/day. To find out how are relative reallocations of time between physical activity of various intensities associated with health, herewith we describe compositional scalar-on-function regression and a newly developed compositional functional isotemporal substitution analysis. Physical activity intensity data can be considered as probability density functions, which better reflects the continuous character of their measurement using accelerometers. These probability density functions are characterised by specific properties, such as scale invariance and relative scale, and they are geometrically represented using Bayes spaces with the Hilbert space structure. This makes possible to process them using standard methods of functional data analysis in the $L^2$ space, via centred logratio (clr) transformation. The scalar-on-function regression with clr transformation of the explanatory probability density functions and compositional functional isotemporal substitution analysis were applied to a dataset from a cross-sectional study on adiposity conducted among school-aged children in the Czech Republic. Theoretical reallocations of time to physical activity of higher intensities were found to be associated with larger and more progressive expected decreases in adiposity. We obtained a detailed insight into the dose–response relationship between physical activity intensity and adiposity, which was enabled by using the compositional functional approach.

1. Introduction

How people spend their daily time in physical activity (PA) of various intensities has important health implications. Researchers have sought to measure people’s time-use behaviours using accelerometers. Accelerometers measure proper acceleration (units mg) which is then used to estimate the intensity of PA a person is engaging in at any given time window, usually spanning $15$ s to $1$ min.^1,2 These time windows are then aggregated to produce a daily summary of time spent across a continuum of PA intensities.

For ease of interpretation, the PA continuum is commonly categorised into discrete energy expenditure bands of light, moderate and vigorous PA. When also considering daily time spent in sedentary behaviour (SB) and sleep, the whole $24$ -h day is usually split into five mutually exclusive and exhaustive parts (sleep, SB and light PA (LPA), moderate PA (MPA) and vigorous PA (VPA)). It is now well accepted that these parts should not be analysed separately because they are co-dependent parts of a time-use composition with a natural constraint of $24$ h/day.^5,3,6,4 Indeed, such a constraint plays an important role even when only a subcomposition is of interest; for example, if only activities during waking hours are analysed. The constraint imposes a relative data structure, in that all relevant information is contained in ratios between time-use components. The absolute raw values of the time-use components and their total sum are irrelevant. Accordingly, any statistical approach for time-use data should satisfy scale invariance – that is, that the results will be identical for any possible representation of the input data (proportions, percentages or similar). Scale invariance is satisfied by compositional data analysis methods, specifically, the log-ratio methodology.^7,9,8

A shift towards the compositional data approach is underway in the field of time-use epidemiology, with increasing number of studies employing this methodology. Moreover, a common analysis in time-use epidemiology is isotemporal substitution analysis, ¹⁰ which quantifies the effect of reallocating a given (absolute) amount of time (e.g. $10$ min/day) between PA intensity zones (e.g. from LPA to VPA). Defining reallocations of time in absolute units enables a straightforward and simple interpretation, which is important for public health messaging. However, to achieve scale invariance, a preferred approach should be to define reallocations in a relative sense. That is, time spent in a given behaviour is increased (or decreased) by applying a positive multiple (e.g. by doubling it), at the expense (or in favour) of one or more remaining behaviours, so that the given total (e.g. $100\mathrm{\%}$ , $24$ h/day) remains unchanged. This can be termed compositional isotemporal substitution analysis.

As noted above, to date most time-use epidemiology studies have categorised the raw continuous PA data obtained from accelerometry into energy expenditure bands. However, such categorisation is somewhat artificial and might lead to the loss of relevant information. Raw accelerometer data can in fact be understood as functional data, that is, data representing the variables or units of interest which could be naturally viewed as a smooth curve or function. ¹¹ Note that, in moving from the usual discretisation into PA intensity categories to the fine-grain distribution provided by raw accelerometer data, we are still primarily interested in the relative structure of the data distribution; that is, we are still interested in scale invariance. Thus, the compositional conceptualisation is extended to this functional, continuous case (equivalent to dealing with infinitely many PA categories). From a probabilistic perspective, such data distributions can be characterised as probability density functions (PDFs) of continuous variables. PDFs are functions of relative nature which are subject to a unit integral constraint; however, due to their relative scale property, a PDF is just one representative of a class of functions carrying the same relative information. PDFs can be characterised as infinite-dimensional compositional data.^12,13 In time-use epidemiology, there have already been several attempts to capture the local effects of time-use distributions by splitting PA into a larger number of intensity categories.^14,15 Several authors also suggested that accelerometer data could be analysed using functional data analysis (FDA).^16–18 However, none of these papers consider systematically how to achieve scale invariance. According to the GRANADA consensus statement, the FDA is considered as one of adequate analytical approaches to examine associations between accelerometer – determined movement behaviours and health outcomes. ¹⁵ Moreover, experts call for efforts to translate findings from FDA into meaningful and useful information for public health messaging.

Therefore, the aim of this article is to make an important methodological step forward by generalising the ordinary compositional approach to deal with entire accelerometer data distributions, characterised as PDFs, while considering their compositional properties based on the theory of Bayes spaces. ¹³ In Section 2, compositional data, PDFs and their geometrical representation using Bayes spaces with Hilbert space structure are reviewed. An isometric mapping from the Bayes space into the standard $L^2$ space is introduced, which enables preprocessing of PDFs and their analysis using ordinary method in FDA. Specifically, preprocessing of PDFs is done using a spline representation, as usually conducted in FDA, and scalar-on-function regression is presented for further analysis. Section 3 proposes a functional counterpart to isotemporal substitution analysis which adequately addresses the relative scale of PDFs. In Section 4, the proposed methodology is applied to empirical accelerometer data collected from Czech adolescents, to analyse how adiposity is influenced by their time-use distribution. Finally, Sections 5 and 6 include, respectively, discussion and an example of how results of such analysis can inform public health stakeholders.

2. Methods

In the following, we will provide an overview of the basic ideas underlying Bayes spaces as sample spaces of PDFs. Then we will detail a spline-based representation of PDFs which honours their geometric structure. This machinery is needed to proceed with theoretical and computational aspects of compositional scalar-on-function regression as well as compositional functional isotemporal substitution analysis.

2.1. Bayes spaces

The introduction of Bayes spaces as a generalisation of the Aitchison geometry to infinite-dimensional spaces requires some basic definitions. Let us denote ${\mathcal{B}}^2(I)$ a Bayes space of PDFs of square-integrable logarithm defined on a bounded domain, usually an interval $I=[a,b]\subseteq \mathbb{R}$ for practical reasons. The main aim is to construct an isometric isomorphism between ${\mathcal{B}}^2(I)$ and standard $L^2(I)$ spaces, where the notation reflects the assumed (interval) domain. Two positive functions $f$ and $g$ with the same support are equivalent if $f=c\cdot g$ for $c\in \mathbb{R}$ . A Bayes space ${\mathcal{B}}^2(I)$ then consists of densities $f$ from an equivalence class of proportional densities.

In a Bayes space, we can define mathematical operations corresponding to the sum of two functions and to the multiplication of a function by a constant in the standard $L^2$ space. Given two absolutely integrable PDFs $f,g\in {\mathcal{B}}^2(I)$ and real number $c\in \mathbb{R}$ , the operations perturbation and powering are thus defined as

$$\begin{array}{rl}(f\oplus g)(t)& =\frac{f(t)g(t)}{{\int }_{I}f(s)g(s)\text{d}s},t,s\in I\end{array}$$ (1)

$$\begin{array}{rl}(c\odot f)(t)& =\frac{f{(t)}^c}{{\int }_{I}f{(s)}^c\text{d}s},t,s\in I\end{array}$$ (2)

respectively. The functions resulting from these operations are also PDFs. The perturbation-subtraction between two PDFs $f,g\in {\mathcal{B}}^2(I)$ , denoted by $f\ominus g$ , is defined as

$$(f\ominus g)(t)=(f\oplus [(-1)\odot g])(t),t\in I$$ (3)

The operation $\oplus$ can be interpreted as a Bayesian updating of information and $\ominus$ as a cancellation of information. ¹⁹ To complete the Hilbert space structure of the Bayes space, the inner product

$$⟨f,g{⟩}_B=\frac{1}{2\eta }{\int }_I{\int }_I\ln \frac{f(t)}{f(s)}\ln \frac{g(t)}{g(s)}\text{d}t\text{d}s$$ (4)

is defined, where $\eta =b-a$ , $f,g\in {\mathcal{B}}^2(I)$ and $t,s\in I$ .

To enable statistical processing of PDFs using standard methods of FDA in $L^2$ space (which do not capture geometric properties of PDFs as noted previously), the centred logratio (clr) transformation for PDFs was defined by van den Boogaart et al. ¹³ as a generalisation of its well-known multivariate counterpart. ⁷ By clr transformation, an isometric isomorphism between ${\mathcal{B}}^2(I)$ and $L^2(I)$ is established. This is defined for $f\in {\mathcal{B}}^2(I)$ and $t,s\in I$ as

$$\text{clr}(f)(t):=f_c(t)=\text{ln}f(t)-\frac{1}{\eta }{\int }_I\text{ln}f(s)\text{d}s$$ (5)

The definition of the clr transformation implies that the resulting densities induce a zero integral constraint

$$\begin{array}{rl}{\int }_I\text{clr}(f)(t)\text{d}t& ={\int }_I\text{ln}f(t)\text{d}t-{\int }_I\frac{1}{\eta }{\int }_I\text{ln}f(s)\text{d}s\text{d}t=0,t,s\in I\end{array}$$ (6)

Accordingly, the space of real-valued functions with a zero integral on $I$ is denoted as $L_0^2(I)$ in this contribution. Due to the isometric isomorphism between ${\mathcal{B}}^2(I)$ and $L^2(I)$ spaces, operations and inner product between the elements of ${\mathcal{B}}^2(I)$ can be computed in terms of their counterparts in $L^2(I)$ using the clr transformation. Because the clr transformation is a one-to-one mapping, its inverse also exists and can be defined as

$${\text{clr}}^{-1}[f_c](t)=\frac{\exp (f_c(t))}{{\int }_I\exp (f_c(s))\text{d}s},t,s\in I$$ (7)

2.2. Spline representation of PDFs

FDA relies on approximating of the input data, which are assumed to be realisations of discretised functions, using splines. ²⁰ However, considering PDFs as elements of a Bayes space, it is necessary to perform such a spline representation in the clr space $L_0^2(I)$ . The construction of splines is connected with the formulation of basis functions. A system of basis functions is a set of known functions that are linearly independent and that allow a good approximation of any function as a linear combination of $K$ of them forming a collection $\{{\phi }_1,\dots ,{\phi }_K{\}}^{\mathrm{\top }}$ . Thus, a function $x(t)$ can be expressed by the linear expansion defined as $x(t)=\sum _{k=1}^K{c}_k{\phi }_k$ , where ${\phi }_k$ is a known basis function and $(c_1,\dots ,c_K{)}^{\mathrm{\top }}$ is a vector of their respective unknown real basis coefficients. One well-known basis expansion is the B-spline basis system, which is particularly suitable for capturing the shape of known smooth PDFs. In our case, it is desirable for the basis functions to be elements of the ${\mathcal{B}}^2(I)$ space.

To define a B-spline basis in $L^2(I)$ , let’s call $\mathrm{\Delta }\lambda :=\{{\lambda }_0=a<{\lambda }_1<\cdots <{\lambda }_g<b={\lambda }_{g+1}\}$ a given sequence of knots in $I=[a,b]$ and denote $S_k^{\mathrm{\Delta }\lambda }[a,b]$ the vector space of polynomial splines of degree $k>0$ with a given sequence of knots in $I$ . Note that dim $(S_k^{\mathrm{\Delta }\lambda }[a,b])=g+k+1$ . Then, a B-spline of the basis $B$ of order $k+1$ with $k\in \mathbb{N},$ is defined by

$$\begin{array}{rl}{B}_i^{k+1}(t)& =\frac{t-{\lambda }_i}{{\lambda }_{i+k}-{\lambda }_i}{B}_i^k(t)+\frac{{\lambda }_{i+k+1}-t}{{\lambda }_{i+k+1}-{\lambda }_{i+1}}{B}_{i+1}^k(t)\end{array}$$ (8)

while for $k=0$

$$B_i^1(t)=\{\begin{array}{ll}1,& t\in [{\lambda }_i,{\lambda }_{i+1})\\ 0,& \text{otherwise}\end{array}$$

$i=0,\dots ,g$ .

This way, every spline $s_k\in S_k^{\mathrm{\Delta }\lambda }[a,b]$ in $L^2(I)$ can be uniquely represented by

$$s_k(t)=\sum _{i=-k}^g{b}_i{B}_i^{k+1}(t)={\mathbf{B}}_{k+1}{(t)}^T\mathbf{b},t\in I$$ (9)

where $\mathbf{b}=(b_{-k},\dots ,b_g{)}^T$ is the vector of B-spline basis coefficients of $s_k(t)$ .^21,22 For example, for $k=3$ , a cubic spline is obtained. For an arbitrary $l\in 1,\dots ,k-1,$ the task is to find a spline $s_k(t)\in S_k^{\mathrm{\Delta }\lambda }[a,b]$ ²³ which minimises the functional

$$\begin{array}{rl}{J}_l(s_k)& =(1-\alpha ){\int }_a^b[s_k^{(l)}(t){]}^2\text{d}t+\alpha \sum _{i=1}^n{w}_i[f_i-s_k(t_i){]}^2\end{array}$$ (10)

where $w_i>0$ are weights, $i=1,\dots ,n$ , and $\alpha \in (0,1]$ is given. The resulting spline is called a smoothing spline.

In order to work with PDFs, the so-called compositional splines were introduced. Compositional splines not only respect the zero integral constraint (6), but also enable the definition of basis functions directly in the $L_0^2$ space. For this purpose a new type of spline, called ZB-splines is constructed that allows the definition of the compositional spline directly in terms of operations in ${\mathcal{B}}^2(I)$ , ²⁴ as shown in the following.

Thus, ZB-spline functions are defined as

$$Z_i^{k+1}(t)=\frac{\text{d}}{\text{d}t}{B}_i^{k+2}(t),i=0,\dots ,g$$ (11)

for $k\in {\mathbb{N}}_0$ . It can be shown that $Z_i^{k+1}(t)\in L_0^2(I)$ has properties similar to $B_i^{k+1}(t)$ ; both of them are piecewise polynomials of degree $k$ and have continuous derivatives up to degree $k-1$ .

Additional knots need to be added to involve all functions $B_i^{k+1}(t)$ forming the basis, in this case

$$\begin{array}{c}{\lambda }_{-k}=\cdots ={\lambda }_{-1}={\lambda }_0=a\\ b={\lambda }_{g+1}={\lambda }_{g+2}=\cdots ={\lambda }_{g+k+1}\end{array}$$

Now let us consider the following system of ZB-spline functions $Z_i^{k+1}(t)$ with the zero integral constraint on the relevant vector space $Z_k^{\mathrm{\Delta }\lambda }[a,b]$ , that is,

$$Z_k^{\mathrm{\Delta }\lambda }[a,b]:=\{s_k(t)\in S_k^{\mathrm{\Delta }\lambda }[a,b]:{\int }_I{s}_k(t)\text{d}t=0\}$$ (12)

It is clear that this vector space has dimension $g+k$ and that the corresponding functions $Z_{-k}^{k+1}(t),\dots ,Z_{g-1}^{k+1}(t)$ form its basis.

Furthermore, Machalová et al. ²⁴ showed that every spline $s_k(t)\in {\mathcal{Z}}_k^{\mathrm{\Delta }\lambda }[a,b]$ (with this denoting the vector space of polynomial splines of degree $k>0$ defined on a finite interval $[a,b]$ with the sequence of knots $\mathrm{\Delta }\lambda$ ) can be expressed as

$$s_k(t)=\sum _{i=-k}^{g-1}{z}_i{Z}_i^{k+1}(t)={\mathbf{Z}}_{k+1}{(t)}^T\mathbf{z}$$ (13)

where $\mathbf{z}=(z_{-k},\dots ,z_{g-1}{)}^T$ is a vector of spline coefficients. Note that ${\mathbf{Z}}_{k+1}(t)$ is completely characterised by the degree $k$ and a given sequence of knots. The use of the resulting ZB-spline coefficients will be further explored in Section 2.3 in the context of compositional scalar-on-function regression.

Finally, it is possible to define compositional splines directly in the original Bayes spaces by using inverse clr transformation ( ${\text{clr}}^{-1}$ ) of ZB-splines $Z_i^{k+1}(t)$ into ${\mathcal{B}}^2(I)$ . Every compositional spline ${\xi }_k(t)\in {\mathcal{B}}^2(I)$ then has a unique representation

$${\xi }_k(t)=\underset{i=-k}{\overset{g-1}{⨁}}{z}_i\odot {\zeta }_i^{k+1}(t)$$ (14)

where ${\zeta }_i^{k+1}(t)=\text{exp}[Z_i^{k+1}(t)]$ are called CB-splines. ²⁴

2.3. Compositional scalar-on-function regression

According to the Viable Integrative Research in Time-Use Epidemiology framework, investigating relationships between time-use distributions and health outcomes is one of the key scientific questions in time-use epidemiology. ⁶ This is commonly achieved using regression models. In this section, we introduce a compositional scalar-on-function regression model, ²⁵ which provides an appropriate means of including a time-use distribution as an explanatory or predictive variable in a regression model through its characterisation as a PDF and using a ZB-spline representation as described above.

Let us consider a set of $n$ pairs $(y_1,f_1),\dots ,(y_n,f_n)$ , where $y_i$ denote observations of a response variable and $f_i$ are functional predictors in $L^2(I)$ , $i=1,\dots ,n$ . The functional linear regression model is then formulated as

$$y_i={\beta }_0+{\int }_I{\beta }_1(t)\cdot f_i(t)\text{d}t+{ϵ}_i$$ (15)

where $i=1,\dots ,n$ , $t\in I$ , ${\int }_I{\beta }_1(t)\cdot f_i(t)\text{d}t$ is an inner product $⟨{\beta }_1(t),f_i(t){⟩}_2$ , ${\beta }_0\in \mathbb{R}$ is a scalar intercept, ${\beta }_1(I)\in L^2(I)$ is a functional regression parameter and ${ϵ}_1,\dots ,{ϵ}_n$ are random errors with mean zero, finite variance, and independent of the functional predictor. ²⁰ Note that this is analogous to the standard regression model, where the objective is to find estimators of the regression parameters ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$ which minimise the sum of squared errors (SSEs), where

$$SSE({\beta }_0,{\beta }_1)=\sum _{i=1}^n{(y_i-{\beta }_0-{\int }_I{\beta }_1(t)f_i(t)\text{d}t)}^2$$ (16)

With $f_1,\dots ,f_n$ being a sample of functions forming the functional predictor (PDF) in ${\mathcal{B}}^2(I)$ and $y_1,\dots ,y_n$ real response variable, the functional linear regression model for the $i$ -th observation $y_i$ associated with the $i$ -th function $f_i$ is expressed for $i=1,\dots ,n$ , $t\in I$ , as

$$y_i={\beta }_0+{⟨{\beta }_1(t),f_i(t)⟩}_{\mathcal{B}}+{ϵ}_i$$ (17)

where ${\beta }_0\in \mathbb{R}$ and ${\beta }_1(t)\in {\mathcal{B}}^2(I)$ are unknown regression parameters and $ϵ$ is a vector of independent and identically distributed random errors with mean zero. ²⁵ As mentioned above, the clr transformation can be applied on PDFs so that the regression model is equivalently formulated in clr space as

$$\begin{array}{rl}{y}_i& ={\beta }_0+{⟨\text{clr}({\beta }_1)(t),\text{clr}(f_i)(t)⟩}_2+{ϵ}_i\\ & ={\beta }_0+{\int }_I\text{clr}({\beta }_1)(t)\cdot \text{clr}(f_i)(t)\text{d}t+{ϵ}_i\end{array}$$ (18)

Estimation of the regression parameters can be conducted by minimising

$$SSE({\beta }_0,{\beta }_1)=\sum _{i=1}^N(y_i-{\beta }_0-{⟨\text{clr}({\beta }_1)(t),\text{clr}(f_i)(t)⟩}_2{)}^2$$ (19)

This minimisation problem is solved by using a ZB-spline representation of the clr transforms of $f_i(t)$ and ${\beta }_i(t)$ .

Let us consider basis expansions for $\text{clr}(f_i)(t)$ , $i=1,\dots ,n$ and $\text{clr}({\beta }_1)(t)$ . Following Machalová et al., ²⁴ let us consider

$$\begin{array}{rl}\text{clr}(f_i)(t)& =\sum _{j=-k}^{g-1}{z}_{ij}{Z}_j^{k+1}(t)\end{array}$$ (20)

$$\begin{array}{rl}\text{clr}({\beta }_1)(t)& =\sum _{j=-l}^{h-1}{z}_j{Z}_j^{l+1}(t)\end{array}$$ (21)

with ZB-spline coefficients $\mathbf{Z}=(z_{ij})$ , $i=1,\dots ,n$ , $j=-k,\dots ,g-1$ , $\mathbf{z}=(z_{-l},\dots ,z_{h-1})$ , $k$ the degree of ZB-spline for $\text{clr}(f_i)$ and $l$ being the degree of the ZB-spline for $\text{clr}({\beta }_1)$ .

However, after selecting an adequate ZB-spline basis representation for the estimation of ${\beta }_1$ , a new issue arises. There is the possibility that the total number of basis functions exceeds or closely approaches the number of observations. Hence, the least squares estimation of the associated multiple regression model might fail. In addition, a richer basis system may lead to overfitting of the input discretised function and thus, to poor prediction. To deal with this it is recommended to use some form of regularisation approach, e.g. low-dimensional regression or penalised regression, or to reduce the dimensionality of the explanatory PDF using simplicial functional principal component analysis (SFPCA)^26,20,25 as detailed in the following section.

2.4. Simplicial functional principal component analysis

Principal component analysis (PCA) is a commonly used multivariate statistical method for dimension reduction of a dataset. In the FDA context, there is an analogous technique called functional principal component analysis (FPCA). ²⁰ Hron et al. ²⁶ developed as an extension of FPCA for density functions. A brief description of FPCA and its extension SFPCA is provided in the following.

Consider a centred functional random sample $f_1,\dots ,f_n$ in the $L^2(I)$ space (i.e. the mean $\overline{f}=\frac{1}{n}\sum _{i=1}^n{f}_i$ is subtracted from each observation). The aim of FPCA is to capture the main modes of variability of the data by means of a number $L$ of linear combinations of the original variables $f_i(t)=\sum _{i=1}^L⟨f_i,{\xi }_k{⟩}_2{\xi }_k$ .

Firstly, the main mode of variability, the element ${\xi }_1$ in $L^2(I)$ , called the first functional principal component (FPC), is computed. The function ${\xi }_1$ is obtained by solving the following optimisation problem over $\xi \in L^2(I)$ :

$$\underset{\xi }{max}\frac{1}{n}\sum _{i=1}^n⟨f_i,\xi {⟩}_2^2\text{subject to}||\xi |{|}_2=1$$ (22)

The remaining FPCs, $\{{\xi }_j{\}}_{j\ge 2}$ , capturing the remaining modes of variability, have to be orthogonal with the first FPC and with each other, and are thus obtained by solving the previous maximisation problem with the additional orthogonality constraint $⟨{\xi }_k,{\xi }_j{⟩}_2=0,k<j$ . From a theoretical point of view, it can be shown that the FPCs correspond to the eigenfunctions determined by the covariance operator of the original (centred) dataset. Therefore, outputs of the maximisation problem are both eigenfunctions called harmonics ${\xi }_j$ and scores, expressed in terms of the inner product $⟨f_i,{\xi }_k{⟩}_2$ . Harmonics are interpreted in terms of the original data (functions) and scores are coefficients representing data structure of the original observations. Dealing with FPCA is thus analogous to the well-known PCA for multivariate data. The FPCs $\{{\xi }_j{\}}_{j\ge 1}$ coincide with the eigenfunctions of the sample covariance operator $V:L^2(I)\to L^2(I),$ following on $x\in L^2(I)$ as

$$V_x=\frac{1}{n}\sum _{i=1}^n⟨f_i,x{⟩}_2{f}_i$$ (23)

The $j$ -th FPC ${\xi }_j$ and the associated scores ${\mathrm{\Psi }}_{ij}=⟨f_i,x{⟩}_2$ , $i=1,\dots ,n$ are obtained by solving the eigenvalue equation

$$V{\xi }_j={\rho }_j{\xi }_j$$ (24)

where ${\rho }_j$ denotes the $j$ -th eigenvalue, with ${\rho }_1\ge {\rho }_2\ge \cdots \ge {\rho }_L$ . For each $j$ , the term $\frac{{\rho }_j}{\sum _j{\rho }_j}$ is associated with the proportion of total variability explained by the FPC ${\xi }_j$ . The eigenvalue equation is solved using the basis expansion of each $f_i$ , $i=1,\dots ,n$ , considering $K$ known basis functions ${\varphi }_1,\dots ,{\varphi }_K$ :

$$f_i(\cdot )=\sum _{k=1}^K{c}_{ik}{\varphi }_k(\cdot )$$ (25)

where $c_{ik}=⟨f_i,{\varphi }_k{⟩}_2$ , $k=1,\dots ,K$ , that is used below in the estimation section. Smoothing splines are commonly used for this purpose.

To honour the specifics of PDFs, SFPCA reformulates FPCA in terms of centred $\text{clr}(f_1),\dots ,\text{clr}(f_n)$ in ${\mathcal{B}}^2(I)$ , obtained through perturbation-subtraction by $\text{clr}(\overline{f})=\frac{1}{n}\odot \underset{i=1}{\overset{n}{⨁}}\text{clr}(f_i)$ . ²⁶ A similar maximisation problem as in FPCA is then solved here. The maximisation is performed over $\zeta \in {\mathcal{B}}^2(I)$

$$\begin{array}{r}\underset{\zeta }{max}\frac{1}{n}⟨\text{clr}(f_i),\zeta {⟩}_B^2\\ \text{s.t.}||\zeta |{|}_B=1;⟨{\zeta }_j,{\zeta }_k{⟩}_B=0,k<j\end{array}$$

Note that it is possible to formulate the problem and find the unique solution because ${\mathcal{B}}^2(I)$ is a separable Hilbert space.

In practice, it is preferred to perform SFPCA using the efficient routines available for data in $L^2$ space. This is possible by applying the clr transformation $(5)$ . Obviously the zero integral constraint needs to be incorporated into the basis expansion which leads to the use of compositional splines. In the context of compositional scalar-on-function regression, the interest is in the SFPCA scores which are used to build a multiple regression model for the estimation of the functional regression parameter.

2.5. Estimation of the functional regression parameter and its interpretation

In this section, the ZB-spline basis expansion and SFPCA are used for the estimation of the functional parameter ${\beta }_1$ in the regression model (18). The original basis expansion (21) can be rewritten using SFPCA as

$$\begin{array}{rl}\text{clr}(f_i)(t)& =\sum _{i=1}^L{c}_{ij}{\xi }_j\end{array}$$ (26)

$$\begin{array}{rl}\text{clr}({\beta }_1)(t)& =\sum _{j=1}^L{b}_j{\xi }_j(t)\end{array}$$ (27)

$t\in I$ , $i=1,\dots ,n$ , where $c_{ij}=⟨\text{clr}(f_i),{\xi }_j{⟩}_2$ and $b_j=⟨\text{clr}({\beta }_1),{\xi }_j{⟩}_2$ are scores associated with the $j$ -th simplicial functional principal component ${\xi }_j,j=1,\dots ,L$ . Here $L$ corresponds to the number of eigenvalues that is chosen, for example, by cross-validation. Then, a standard multiple regression model

$$\mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{e}$$ (28)

is formulated, with response vector ${\mathbf{y}}_{n\times 1}$ and $n\times (L+1)$ design matrix $\mathbf{X}$ consisting of ZB-spline coefficients $c_{ij}$ . The first column of $\mathbf{X}$ is reserved for the intercept term, which also absorbs the centreing of clr-transformed PDFs $f_i$ (see next section for details). The resulting least squares estimate $\hat{\mathbf{b}}$ of the vector parameter $\mathbf{b}$ is used for the parameter ${\beta }_1$ in $L_0^2(I)$ space

$$\text{clr}(\widehat{{\beta }_1})(t)=\sum _{j=1}^L{\hat{b}}_j{\xi }_j(t)$$ (29)

Consequently, $\text{clr}(\widehat{{\beta }_1})(t)$ can be mapped to the original ${\mathcal{B}}^2(I)$ space by

$${\hat{\beta }}_1(t)=\underset{j=1}{\overset{L}{⨁}}{\hat{b}}_j\odot {\zeta }_j(t)$$ (30)

where ${\zeta }_j=\text{exp}[{\xi }_j],j=1,\dots ,L$ .

However, for the interpretation of the functional regression parameter, which is of primary interest here, it is preferable to consider ${\beta }_1$ in $L_0^2(I)$ space. Accordingly, the interpretation of $\text{clr}({\beta }_1)$ is that positive functional values of the regression parameter contribute to the growth of the values of the response variable and the opposite for negative values by considering the course (absolute values) of the sampled PDFs. This means that the magnitude of the impact of the functional regression parameter to a given subdomain is amplified by high absolute values of the explanatory clr-transformed PDFs; this follows directly from (18) and corresponds to the amount of mass (area) which is integrated in the given subdomain. Interpretation of the functional parameter will be further discussed in the case study developed in Section 4.

3. Compositional functional isotemporal substitution analysis (CFISA)

It was outlined already in Section 1 that isotemporal substitution analysis plays a central role in the interpretation of regression models in PA and time-use epidemiology. It allows us to formulate concrete health recommendations and PA guidelines for public health. As mentioned earlier, from a methodological point of view, reallocations of time between time-use components should preferably be defined in a relative sense, that is, as multiples of compositional parts. This is even more relevant when a functional approach is adopted, where it would be particularly difficult to enable interpretations in terms of (absolute) time units, such as hours or minutes. Importantly, estimated changes in the response variable associated with relative reallocations of time between compositional parts can still be easily interpretable. Therefore, herewith we propose a CFISA.

CFISA can be used to describe how changes in certain subdomains of a time-use distribution (e.g. corresponding to a given interval of PA intensities as measured by accelerometry) are associated with change in a health outcome (e.g. adiposity). The time-use distribution, characterised as a PDF here, is typically represented by the centre $\tilde{f}=\frac{1}{n}\odot \underset{i=1}{\overset{n}{⨁}}{f}_i$ of the sampled time-use distributions. Unlike in the ordinary multivariate case, the basic idea of CFISA can now be approached from many different perspectives within a functional framework. Here we resort to a simple one which facilitates interpretation.

In particular, the domain of the explanatory PDF representing the time-use distribution is divided into $m$ equidistant subdomains (PA intensity intervals) and the relative influence of the $i$ -th subdomain, $i=1,\dots ,m$ , on the response variable is increased at the expense of the other subdomains. This can be achieved by weighting the domain of $\tilde{f}$ . For this, following, ²⁷ $\tilde{f}$ is perturbed by another PDF $g$ that represents the distribution of weights. Being this weighting PDF initially uniform, sequentially increasing a subsection of it has the effect of weighting corresponding subdomains of $\tilde{f}$ through the perturbation operation $(1)$ (see Figures 1 to 4 for illustration). This enables to increase a given PA intensity interval at the expense of other intervals while respecting the course of $\tilde{f}$ . Specifically, if a certain subdomain $I_0\subset I$ of $g$ is multiplied by a factor $K\in (1,m)$ , the others are necessarily multiplied by $(m-K)/(m-1)$ in order to keep the unit integral constraint. Subsequently, $\tilde{f}$ is multiplied by $g$ which induces a $K$ -time increase of $\tilde{f}$ on $I_0$ ; in other words, the PA interval corresponding to intensities from $I_0$ is $K$ -times more likely now. Hence, CFISA can be described in terms of the basic operations in Bayes spaces as a perturbation of $\tilde{f}$ by a weighting PDF $g$ , which represents a shift of $\tilde{f}$ in the compositional sense. Due to the centreing of the sample $f_1,\dots ,f_n$ in SFPCA, it results from the formulation of the functional regression model (15) that ${\beta }_0={\tilde{\beta }}_0-{\int }_I{\beta }_1(t)\cdot \overline{f}(t)\text{d}t,t\in I$ , ²⁵ where ${\tilde{\beta }}_0$ is the intercept from the regression model with the centred functional covariate. After this re-computation, the CFISA model can be expressed as

$$y={\hat{\beta }}_0+⟨\tilde{f}\oplus g,{\hat{\beta }}_1{⟩}_{\mathcal{B}}$$ (31)

where ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$ are the estimates of the regression parameters from the compositional scalar-on-function regression model (17). This means that the weighting is applied directly to the centre $\tilde{f}$ with previously estimated regression parameters $\widehat{{\beta }_0}$ and $\widehat{{\beta }_1}$ from data. Each choice of $g$ then leads to a prediction of the response corresponding to the specific CFISA.

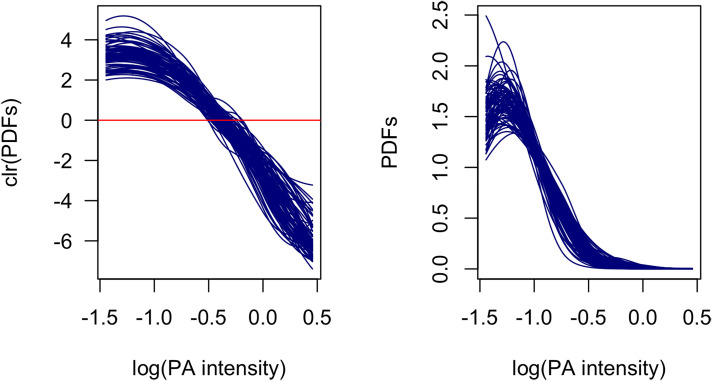
Figure 1.

Sample time-use distributions represented as PDFs after clr transformation (left) and in the original space (right). PA intensity values are presented in a log scale. The red line indicates $\text{clr}(f_i)=0$ . PDFs: probability density functions; clr: centred logratio; PA: physical activity.

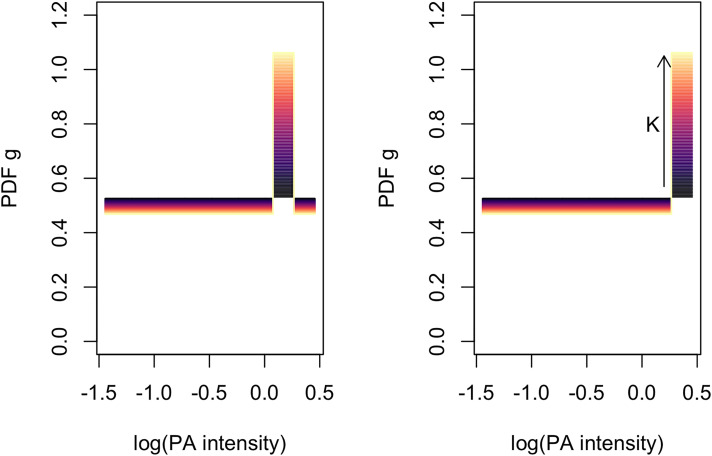
Figure 4.

Weighting probability density functions (PDFs) $g$ according to multiplicative factor $K$ ranging in $[\frac{1}{10},\frac{2}{10}]$ (indicated by colour gradient) for physical activity intensity range (in log scale) split into $10$ subintervals $I_0$ .

4. Application

In this section, we illustrate the use of the proposed compositional functional regression and CFISA to analyse the association of time-use distribution with adiposity among adolescents. Previous studies have found that a higher relative contribution of moderate-to-vigorous PA to the total time and reallocations of time from SB to moderate-to-vigorous PA are associated with a range of health benefits, including better adiposity status.^28,29 The approach we propose in this article can provide a more detailed insight into dose–response relationships, by analysing the entire time-use distribution (i.e. without unnecessary loss of information caused by categorisation of intensities) based on the continuous accelerometer data. A main question asks: how is adiposity associated with reallocations of time from one subdomain of PA intensity to another? For example, what is expected to happen if the actual amount of time spent in one subdomain of PA intensity is multiplied by $K>1$ and the time in other subdomains is decreased proportionally.

The used dataset contains functional observations from a cross-sectional study conducted among school-aged children in the Czech Republic ³⁰ – here, only a subsample of $74$ girls aged between $14$ and $17$ years old was used. The intensity of PA was assessed using tri-axial accelerometers ActiGraph GT9X Link (ActiGraph Corp., Pensacola, FL, USA) – a small device worn on the wrist, based on the Euclidean Norm Minus One (ENMO) metric ¹⁵ and presented on a log scale, since acceleration and force follow a multiplicative process which should be transformed to an additive one prior to further analysis. In this study, we were limited by the dynamic range of the accelerometer. This was equal to $\pm 8000$  mg and the maximum observed intensity was used as a upper limit. A more detailed description of data collection methods can be found elsewhere. ³⁰ The accelerometers provided one intensity value every 5 s, and these values were aggregated over days of the week when the assessment was performed. It is important to stress that our analysis was not focused on the time series of accelerometer values but on their relative structure.

The accelerometer data were aggregated in the form of a histogram, with the log-scaling of the data turning the originally multiplicative process into an additive one. However, there were histogram classes with zero proportions which were assumed to result from undersampling. ³¹ Zero replacement is definitely a critical point of any logratio analysis, especially when it affects a non-negligible fraction of data. Given the relative scale of histogram classes, results based on the logratios may be sensitive to the replacement of zeros by very small values. Among the accelerometry data points we found $180$ zeroes that were imputed by the partial least squares method implemented in the $\mathtt{\text{impRZilr}}$ function from the R-package robCompositions. ³² Alternatively zeroes could be imputed using the R-package zCompositions, ³³ which offers a suite of methods for this purpose. Representative values of the histogram classes, together with the respective proportions of accelerometer values in each one of them, were then used to approximate the histogram by a density function. The proportions were first mapped into clr space where approximation by compositional splines was conducted. In this case, a cubic smoothing spline approach ( $k=3$ ) with six equidistantly spaced knots was used. To fit the splines, the functional from (10) was minimised. The resulting PDFs are displayed in Figure 1, both in the clr space (left) and after back-transformation to the original sample space (right).

4.1. Compositional scalar-on-function regression

A compositional scalar-on-function regression (18) was filled to determine the association between time-use distribution and adiposity. The response variable (adiposity) was expressed as the logit-transformed body fat percentage. Following Sections 2.3 to 2.5, two SFPCs explaining $94$ % of variability were considered sufficient for a reliable approximation of the clr-transformed PDFs. The estimate $\text{clr}({\hat{\beta }}_1)$ of the compositional scalar-on-function regression parameter ${\beta }_1$ is shown in Figure 2.

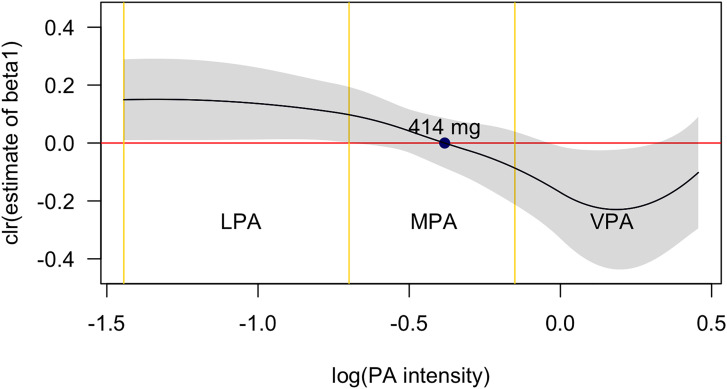
Figure 2.

Estimate of the functional regression parameter ${\beta }_1$ in clr space with approximate $95\mathrm{\%}$ confidence bands. The red line, indicating $\text{clr}(f_i)=0$ , serves as a threshold dividing the parts with positive and negative associations with body fat percentage. The yellow vertical lines are boundaries between PA intensity categories defined using the following thresholds: $36-199$ mg for LPA, $200-706$ mg for MPA and $707-3162$ mg for VPA. clr: centred logratio; PA: physical activity; LPA: light physical activity; MPA: moderate physical activity; VPA: vigorous physical activity.

For the interpretation of the parameter ${\beta }_1$ , it is preferred to stay in the clr space: positive values are associated with a higher body fat percentage, whereas negative values are associated with a lower body fat percentage. In Figure 2, boundaries between PA intensity categories are included: namely, LPA, MPA and VPA corresponding to the ranges 36–199 mg, 200–706 mg and 707–3162 mg, respectively. Uncertainty of the estimation is captured by approximate $95\mathrm{\%}$ confidence bands. By following Kokoszka and Reimherr, ¹¹ these bands were constructed point-wise as $\text{clr}(\widehat{{\beta }_1})\pm 2*\text{sd}(\text{clr}(\widehat{{\beta }_1}))$ , that is, by considering the usual two standard deviations from the estimated expectation. Such standard deviation was computed using exact values of the corresponding B-spline basis functions and the observed variation of the B-spline basis coefficients in $\mathbf{b}$ from equation (9).

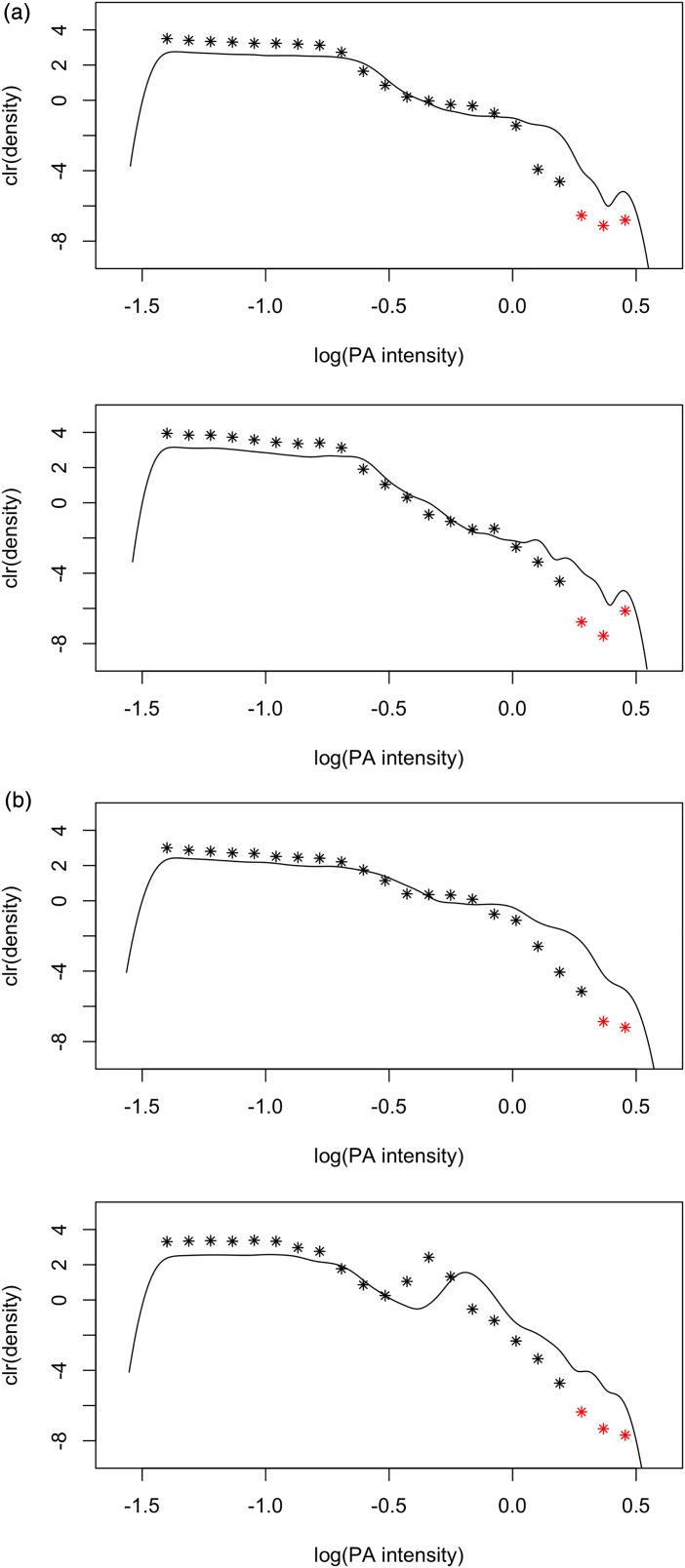
The scale of the PA intensity range in Figure 2 is log-transformed, which was used due to a significant skewness towards the lower values. Due to poor resolution between sleep and SB from the accelerometry only intensities corresponding to PA were considered. We can see that in the LPA subdomain the values of $\text{clr}(\widehat{{\beta }_1})$ are positive, which indicates that a higher body fat percentage is associated with a greater dominance of LPA over other PA intensities. However, the values of the regression parameter decrease with increasing PA intensity and, approximately by the middle of the MPA category ( $414$  mg), they start to be negative with a steadily steeper decreasing trend. On the right-hand end of the curve (starting from $1527$  mg), corresponding to the highest intensities, it is observed that the slope becomes positive. We assume that this is most likely due to artefacts related to the imputation of unobserved intensity data along with the potential misclassification of SB for PA (e.g. arm movement captured by accelerometers while sitting). In Figure 3, evidence to support this explanation is provided by using kernel estimates of the original accelerometer data, which represents another (non-parametric) approximation strategy able to capture local effects. These were turned into clr densities. The graphs in Figure 3 suggest that the issue of positive slope at high PA intensity might be due to misclassifying SB for PA, and not necessarily just caused by the imputation. We observed that the imputation of zeros within histogram classes usually led to a decreasing pattern towards the right-hand end of the domain, if no such misclassifying artefacts have occured. For example, in Figure 3(a), the potential SB for PA misclassification can be observed on the right-hand tail of the clr-transformed kernel estimate, where the density increases and also the imputed values increase accordingly. Moreover, in Figure 3(b), densities without obvious artefacts are depicted, and the imputed values decrease accordingly. Thus, it seems that the problem of the increasing functional regression parameter on the right-hand end of the domain is probably in most cases caused by the nature of the dataset. However, there were also samples where the imputed values did not capture the trend properly and, hence, also contributed to the observed effect. Nevertheless, the function values still remained negative for intensities higher than $1527$  mg (i.e. favourable associations).

Figure 3.

Kernel density estimates visualised via solid lines with stars denoting representatives of histogram classes (red stars correspond to the imputed values). (a) Artefacts of misclassifying SB for PA can be observed on the right-hand tail of the clr-transformed kernel estimates, where the imputed values increase (see points marked in red). (b) Cases without artefacts on the right-hand tail of the distributions (see points marked in red).

The overall conclusion based on Figure 2 is in accordance with previous findings ²⁸ ; a higher intensity of PA is associated with a lower body fat percentage and vice versa. However, considering the PA intensity continuum in relation to adiposity through compositional functional regression provides a more detailed insight into the dose–response shape of this association, beyond just the known general trend.

4.2. Adding sleep and sedentary time

It has been noted before that it is hard to distinguish between sleep and SB from accelerometer data based on the ENMO. Accordingly, there are necessarily weaknesses in subsequent modelling and analysis of such data, both relation to the benefits of sleep and the inability to distinguish SB from low levels of activity. Nevertheless, still information about sleep and SB obtained by self-reporting can be added to a regression model as (non-functional) covariates. For this purpose, an additional three-part composition was defined, where the first two parts corresponded to the relative contributions of sleep and SB, and the remaining part (others) represented the relative contribution of accelerometer values higher than $36$ mg (commonly used upper intensity threshold for SB and sleep behaviour intensities, estimated by Hildebrand et al. ³⁴ ).

Standard compositional data theory establishes that the proper way to add such a composition as an explanatory variable in the regression model is by a log-ratio coordinate representation. A convenient way to do this is using the so-called balances. These balances are associated to an orthonormal basis on the simplex and can be constructed by a sequential binary partition (SBP) of the given composition. ⁹ First step in a SBP is splitting the composition into two groups of parts. In the next steps, each group formed previously is further divided into two groups while possible. Thus, in the $i$ -th step, a balance $z_i$ between two subgroups is defined as a normalised logratio between the geometric means of each group of parts of the form

$$z_i=\sqrt{\frac{r_i{s}_i}{r_i+s_i}}\ln \frac{(\prod _{k=1}^{r_i}{x}_{i_k}^{+}{)}^{1/r_i}}{(\prod _{l=1}^{s_i}{x}_{i_l}^{-}{)}^{1/s_i}},i=1,\dots ,D-1$$

where $x_{i_k}^{+}$ and $x_{i_l}^{-}$ refer to the subsets of $r_i$ and $s_i$ parts going, respectively, into the $+$ (numerator) and $-$ (denominator) groups.

The SBP used by default in our case is depicted in Table 1, and defines the following balances (as we consider two other possible SBPs below, a superscript is used to distinguish them):

$$z_1^{(1)}=\frac{\sqrt{2}}{\sqrt{3}}\text{ln}\frac{\text{others}}{\sqrt{\text{sleep}\cdot \text{SB}}}\text{and}{z}_2^{(1)}=\frac{1}{\sqrt{2}}\text{ln}\frac{\text{sleep}}{\text{SB}}$$

These were added as real-valued covariates into an ordinary multiple regression model to explain body fat percentage (logit transformed), along with the scores of the first two SPFCs obtained in the previous section. By construction, the balance $z_1^{(1)}$ aggregates both logratios $(\text{ln}\frac{\text{others}}{\text{sleep}}$ and $\text{ln}\frac{\text{others}}{\text{SB}})$ with the component others, while $z_2^{(1)}$ is proportional to the pairwise logratio between sleep and SB. The aggregated information contained in $z_1^{(1)}$ , can be further decomposed using the following two alternative SBP-based balance systems,

$$\begin{array}{rl}{z}_1^{(2)}& =\frac{\sqrt{2}}{\sqrt{3}}\text{ln}\frac{\text{SB}}{\sqrt{\text{others}\cdot \text{sleep}}}\text{and}{z}_2^{(2)}=\frac{1}{\sqrt{2}}\text{ln}\frac{\text{others}}{\text{sleep}}\\ z_1^{(3)}& =\frac{\sqrt{2}}{\sqrt{3}}\text{ln}\frac{\text{sleep}}{\sqrt{\text{others}\cdot \text{SB}}}\text{and}{z}_2^{(3)}=\frac{1}{\sqrt{2}}\text{ln}\frac{\text{others}}{\text{SB}}\end{array}$$

where the second coordinates result in the remaining pairwise logratios between behaviours that can be of interest (on top of $z_2^{(1)}$ above). Note that these pairwise logratio coordinates correspond to the so-called backwards pivot coordinates, ³⁵ and orthonormality of all three coordinate systems is essential for the usual interpretation of regression coefficients. ³⁶ Although, according to the regression estimates summarised in Table 2, none of these balances had a statistically significant association with body fat percentage at the usual $5\mathrm{\%}$ significance level ( $p$ -values $0.94$ and $0.21$ , respectively), which might further highlight possible issues with the data discussed at the beginning of the section. However, it may still be worthwhile adding them to the regression model, to obtain a complete picture of how adiposity is associated with the $24$ -h time-use distribution.

Table 1.

Sign matrix used to encode log-ratio balances through a sequential binary partition of the (sleep, sedentary behaviour (SB), others) time-use composition. The columns $r$ and $s$ show the number of parts going into the numerator and denominator of the balance coordinates, respectively.

Order	Sleep	SB	Others	r	s
1	$-$	$-$	$+$	1	2
2	$+$	$-$	0	1	1

Table 2.

Linear regression estimates for log-ratio balances $z_1^{(1)},z_2^{(1)}$ and backwards pivot coordinates $z_2^{(2)},z_2^{(3)}$ in model to explain body fat percentage in terms of time-use distribution including sleep and sedentary behaviour as covariates.

Balances	Estimate	Str. error	T-value	p-value
$z_1^{(1)}$	−0.002533	0.007308	−0.347	0.7299
$z_2^{(1)}$	−0.012234	0.009909	−1.235	0.2211
$z_2^{(2)}$	0.009209	0.012016	0.766	0.4461
$z_2^{(3)}$	−0.005147	0.008608	−0.598	0.5518

4.3. Compositional functional isotemporal substitution analysis

Finally, CFISA is performed to assess how varying the weight of a specific range of PA intensities (at the expense of the remaining ones) influences body fat percentage as response variable. To this end, the domain was divided into $m=10$ equidistant parts and the relative dominance of the respective ranges of intensities was increased. Starting with an uniform distribution of the weighting PDF $g$ (multiplicative factor, proportional weight given to each part of the domain $K=1/10$ ), more time (in relative sense) was gradually given to each of the intervals by increasing the weighting factor up to $K=2/10$ . That is, time devoted to activities of intensities within such part of the domain was doubled at the expense of activities of other intensities. Figure 4 illustrates how the weights are changed in cases where the second-to-last (left) and last interval (right), respectively, are increased (recall that they are also PDFs).

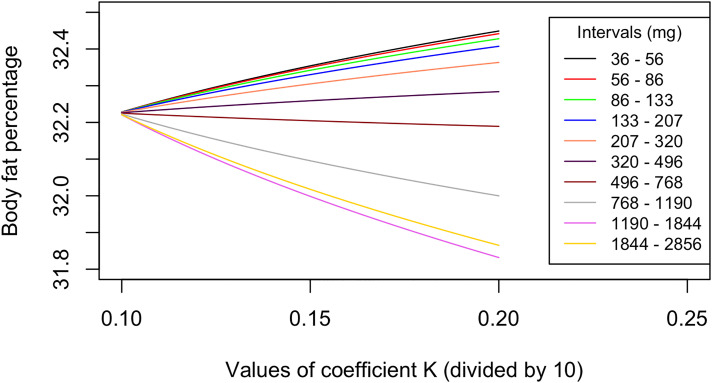
Although doubling ( $K=2$ ) the relative contribution might be rather unrealistic for some intensity ranges, still it is useful to illustrate the effect on body fat percentage of some theoretical reallocations of time between PA intensities. Every curve in Figure 5 represents the expected differences in body fat percentage associated with increasing dominance of the respective PA intensity by the factor $K$ . For example, the yellow curve represents the expected differences in adiposity associated with increases in time spent in PA of intensity between 1844 and 2856 mg; that is, the highest intensity range. The model suggests that doubling the relative time spent in PA of the highest intensity is associated with a $0.4\mathrm{\%}$ reduction in the body fat percentage. It can also be seen that with increasing relative contributions of lower PA intensities which correspond to LPA (i.e. $36--201$  mg), body fat percentage would increase. This role of LPA is in line with recent studies on the effect of daily time-use patterns on mortality. ³⁷ Moreover, these results suggest that the more time is spent in PA of higher intensity, the larger and more progressive decreases in adiposity can be expected.

Figure 5.

Results from compositional functional isotemporal substitution analysis (CFISA) using an uniform distribution of weights with $10$ equidistant subintervals. Each curve corresponds to different physical activity intensity intervals. The lowest curves (magenta and yellow colour) indicate rapid decrease of body fat percentage with increasing weight given to the highest physical activity intensity intervals.

5. Discussion

5.1. Key findings

The compositional functional regression analysis introduced in this article can be used to analyse dose–response relationships between the time spent in different PA intensities, expressed as PDFs derived from accelerometer data, and health outcomes. CFISA that we have also introduced in this article can be used to estimate the expected changes in a health outcome associated with theoretical reallocations of time between different PA intensities. By applying these novel analyses on accelerometer data collected among Czech adolescents, we found that more time spent in higher intensity of PA is associated with a lower body fat percentage. Our findings also suggest that the theoretical reallocations of time to PA of higher intensities are associated with larger expected decreases in body fat percentage.

Novel approaches for analysing time-use data using the compositional functional regression and CFISA may prevent the loss of important information that occurs when the time spent in PA is collapsed into broad intensity categories (e.g. LPA, MPA and VPA). These analyses also enable to adequately address compositional properties of time-use data by respecting the principles of scale invariance and subcompositional coherence.

Analysing changes in health outcomes associated with reallocations of time between time-use components may inform the development of public health messages and recommendations. For example, the current WHO guidelines on PA and SB recommend replacing sedentary time with PA of any intensity. ³⁸ CFISA can be used in future studies to make such recommendations more specific. For example, by using CFISA we may be able to identify the most effective PA intensity for obesity interventions. CFISA also enables us to identify the range of PA intensities that are beneficial for a given health outcome. This may be especially important for populations such as the elderly or chronically ill, where high-intensity PA might be difficult to achieve for a variety of reasons.^40,39 In addition, a change in the intensity of PA within a 24-h daily schedule without changing other components (i.e. SB and sleep) may be an effective strategy to improve some health outcomes. ⁴¹ By using compositional functional regression and CFISA, researchers may gain additional insights into which specific PA intensities should be promoted within such strategies.

5.2. Relationship between PA and adiposity: Findings from the example analysis

We found a curvilinear dose–response relationship between the time spent in PA of different intensities and body fat percentage. Positive (unfavorable) associations were found for lower PA intensities, while negative (favorable) associations were found for higher intensities. The association turned from unfavourable to favourable at $414$  mg which is around the midpoint of the MPA intensity band (i.e. 201–707 mg). In a previous study that used a multivariate pattern analysis to examine the associations of PA and cardiometabolic markers, it turned from unfavourable to favourable at $5000$ counts per minute, which falls into the VPA range. ⁴² Possible reasons for this discrepancy in findings may be differences between the studies in outcome variables, sample characteristics, and analytical approaches.

The fact that the relationship in our study changed from positive to negative around the midpoint of the MPA band should be taken into consideration in future studies. When analysing the overall time spent in MPA in relation to a health outcome, the opposite directions of the relationship below and above the MPA midpoint may cancel each other out and result in no association. This could potentially explain null findings for the relationship between MPA and adiposity among children and adolescents in several previous studies.^30,44,45,43

Our findings also shed new light on the dose–response relationship between VPA and adiposity. While times spent in all vigorous intensities were favourably associated with body fat percentage, the associations were less favourable for intensities above $1527$  mg. Accordingly, by applying CFISA, we found more favourable associations with adiposity for the reallocations of time to the PA intensity range of 1190–1844 mg than to the PA intensity range of 1844–2856 mg. A previous study ¹⁴ found a similar change in the relationship at $8000$ counts per minute. It could be that our finding reflects the true dose–response relationship between PA intensity and adiposity, but it could also be an artefact of the measurement procedure. For example, very high acceleration could have been detected from incidental fast arm movements while being sedentary (e.g. arm and hand gestures). That is, during activities that are typically unfavourably associated with adiposity.

5.3. Strengths and limitations of the study

The key strength of this study is the use of compositional analysis while taking into consideration the entire distribution of accelerometer data, characterised as PDFs.

It is also necessary to mention some limitations of the current study. First, the more narrow the width of a PA band, the higher the likelihood of zero values in the band, especially at higher PA intensities. Given that the presence of zero values prevents expressing the data as log-ratios at the higher end of the VPA spectrum, we had to impute zero values. Attributing some time to these very high intensities of PA among those with zero values may have affected findings of our example analysis. A potential solution to this issue that could be applied in future studies would be to classify PA bands based on equal relative frequencies, rather than using pre-selected PA intensity cut-offs. Second, the strength and shape of the associations between PA and health outcomes may differ on particular days. ⁴⁶ We collected accelerometer data over $7$ days of the week, but we only included their daily averages in the analyses, without considering possible differences across the days of measurement. Third, in our example analysis we focused on PA only. To maintain the daily 24-h time-use constraint, sleep and SB were added in regression models as non-functional covariates. In future studies, similar analyses could also incorporate PDFs for SB.

6. Conclusion

Compositional functional regression can be used to analyse dose–response relationships between time spent in different PA intensities and health outcomes, while CFISA can be used to estimate the expected changes in a health outcome associated with theoretical reallocations of time between different PA intensities. These methods adequately address compositional properties of time-use data, while preventing the loss of important information that occurs when the time spent in PA is collapsed into broad intensity categories. The example analysis of empirical data demonstrated the usefulness of these methods, particularly in providing new insights into the curvilinear relationship between PA intensity and health outcomes. These analyses could be useful not just in time-use epidemiology but also in other fields of study where compositional data can be expressed as PDFs. Future developments of compositional functional regression and CFISA might incorporate time-series aspects into the modelling and extending our proposed approach to longitudinal data.