FEDSLD: FEDERATED LEARNING WITH SHARED LABEL DISTRIBUTION FOR MEDICAL IMAGE CLASSIFICATION

Abstract

Federated learning (FL) enables collaboratively training a joint model for multiple medical centers, while keeping the data decentralized due to privacy concerns. However, federated optimizations often suffer from the heterogeneity of the data distribution across medical centers. In this work, we propose Federated Learning with Shared Label Distribution (FedSLD) for classification tasks, a method that adjusts the contribution of each data sample to the local objective during optimization via knowledge of clients’ label distribution, mitigating the instability brought by data heterogeneity. We conduct extensive experiments on four publicly available image datasets with different types of non-IID data distributions. Our results show that FedSLD achieves better convergence performance than the compared leading FL optimization algorithms, increasing the test accuracy by up to 5.50 percentage points.

1. INTRODUCTION

Deep learning (DL) is well known for requiring a large amount of data for robust training of generalizable models. For DL in medical research [1, 2, 3], large datasets can be difficult to obtain since the data collected by medical centers and hospitals are often privacy-sensitive. Therefore, sharing of the raw data between institutions is usually constrained by the restrictions such as Health Insurance Portability and Accountability Act (HIPAA) in the United States, and General Data Protection Regulation (GDPR) in Europe.

The recent emergence of federated learning (FL) [4, 5, 6] has provided this issue with a feasible solution. FL is a distributed machine learning scenario where only the model weights are shared among the participating clients in the federation, while keeping the data decentralized. In medical research, by bringing different hospitals and medical centers into the federation, researchers can collaboratively train a model utilizing different datasets from siloed institutions besides their own [7, 8, 9].

However, the federated settings generate a new major challenge, namely the statistical data heterogeneity across different participating clients [6, 10, 11, 12, 13]. The data heterogeneity reflects that the data collected by different clients is not identically distributed (non-IID), which often appears in medical datasets from different sites, because of various reasons including different data acquisition protocols and different local demographics. Data heterogeneity may lead to significant increase in communication rounds of the federated training, and inferior performance of the distributed optimization of federated models in certain clients (e.g. medical institutes) [10], which can further cost their incentives to participate in the federation.

In this work, we propose a federated learning algorithm for classification tasks, Federated Learning with Shared Label Distribution (FedSLD), which aims to utilize information regarding the clients’ label distribution, to estimate a general prior label distribution for the entire federation. We claim that FedSLD can mitigate instability of training caused by the statistical heterogeneity of cross-silo FL, such as for medical research. While the algorithm does not access the clients’ data, we assume legitimate for the clients to share the number of samples in each class, which are often the case for cross-silo FL such as in medical applications. More specifically, our contribution in this work is two-fold:

1. We propose a new FL algorithm for medical image classification: Federated Learning with Shared Label Distribution (FedSLD), for robust training with non-IID data.

2. We demonstrate that the proposed FedSLD achieves better performance than the leading FL algorithms by conducting extensive experiments on four publicly available datasets (including two benchmark datasets) under pathological non-IID and practical non-IID data partitions.

2. METHOD

Laws and restrictions in terms of the data privacy constrain the direct access to the raw data. Yet, there are other information regarding the dataset that can be shared in terms of the federated learning. For instance, FedAvg assumes knowledge of the number of samples in each client: after the aggregation step in FedAvg, the algorithm conducts a weighted average of the updated copies for the next round, and the weights used for the averaging, by default, are the normalized number of samples in each client.

In this work, we focus on the classification tasks and assume legitimate to gain knowledge of the label distribution of each client, namely the number of samples from every class. We compute an estimate of the prior label distribution for the entire federation using the gain knowledge on the label distributions. For FL in medical applications, the label distributions from different medical silos can often be drastically different due to the regional demographics. Knowledge of the clients’ label distributions will help us better understand the non-IID data in the federation.

To formulate the process, let us consider a federation with non-IID data. For a given data sample (x, y), where x stand for the data and y represents the label, the probability that it appears in the dataset of client i’s, ${𝒫}_i\left(x,y\right)$, does not necessarily equal to the probability of it to appear in the dataset of client j’s, ${𝒫}_j\left(x,y\right)$. By Bayes’ theorem, we have ${𝒫}_i\left(x|y\right){𝒫}_i\left(y\right)\ne {𝒫}_j\left(x|y\right){𝒫}_j\left(y\right)$. More often than not, especially in medical imaging domain, non-IID data implicitly implies that both the label-conditioned probabilities, $𝒫\left(x|y\right)$, and the marginal label distributions, $𝒫\left(y\right)$, are different for different clients. In this work, we focus on acquiring the information reflecting the marginal label distribution ${𝒫}_i\left(y\right)$ for each client (i = 1, 2, …, N), to compute the estimate of the prior label distribution for the entire federation.

We define the estimate for the prior of class c for the federation, as the sum of the numbers of samples for class c in each client divided by the sum of the total number of samples in each client. This is shown in equation (1), where $\widetilde{𝒫}\left(y=c\right)$ is the estimate prior of class c, n_i,c is the number of samples from class c on client i, n_i is the total number of samples on client i, and N is the number of clients.

$$\widetilde{𝒫}(y=c)=\frac{{\sum }_{i=1}^N{n}_{i,c}}{{\sum }_{i=1}^N{n}_i}$$ (1)

During local update of the current model on a client, given a batch of data ${\left\{\left(x_k,y_k\right)\right\}}_{k=1}^B$, where B is the batch size, we first compute the label distribution in this batch as in equation (2), where the p_b represents the label distribution, $[[\cdot ]]$ means the indicator faction, with its value equal to 1 if the inner part is true, and 0 otherwise. In essence, Equation (2) computes the proportion of class c samples in the batch by normalizing the number of class c samples in this batch.

$$p_b\left(y=c\right)=\frac{{\sum }_{k=1}^B〚y_k=c〛}{B}$$ (2)

$${ℒ}_b\left({\left\{\left(x_k,y_k\right)\right\}}_{k=1}^B\right)=-\sum _{k=1}^B\left(\frac{p_b\left(y=y_k\right)}{\widetilde{𝒫}\left(y=y_k\right)}\cdot \sum _{c=1}^C{y}_{k,c}\text{\hspace{0.17em}log}{\left(f_i\left(x_k\right)\right)}_c\right)$$ (3)

Algorithm 1.

FedSLD.

Input: Initialized model parameter weights w0, number of clients N, number of local epochs E, batch size B, is the batch size, learning rate η, number of rounds R.

1: ∀i ∈ [N], c ∈ [C] acquire ni,c client i’s numbers of samples of each class c.

2: ∀c ∈ [C], $\widetilde{𝒫}(y=c)=\frac{{\sum }_{i=1}^N{n}_{i,c}}{{\sum }_{i=1}^N{n}_i}$// compute estimated prior label distribution.

3: for r ← 1, 2, …, R do

4:  $\forall i\in [N]w_i^r=w^{r-1}$ // broadcast model parameters.

5:  for i ← 1, 2, …, N in parallel do

6:   for ${\left\{x_k,y_k\right\}}_{k=1}^B$ in all minibatches do

7:    ∀c, $p_b(y=c)\leftarrow {\sum }_{k=1}^B〚y_k=c〛/B$

8:    Compute loss ${ℒ}_b$ by Equation 3.

9:    $w_i^r\leftarrow w_i^r-\eta {\nabla }_w{ℒ}_b$

10:   end for

11:  end for

12:  $w^r={\sum }_{i=1}^N\frac{n_i}{n}{w}_I^r$ // aggregate model updates

13: end for

14: return wR

Then, we define the batch loss as a weighted cross-entropy loss, shown in Equation (3), where ${ℒ}_b$ means the batch loss, and f_i represents the copy of the model on client i. By doing this, we can enforce proportional contribution (to the local objective) of each class of the data, with respect to its share of the true underlying distribution across the federation. We follow the aggregation step in a typical FL algorithm, where we compute the weighted average of the updated models from all clients, with the weights being the number of samples in each client. A detailed algorithm is shown in Algorithm 1.

3. EXPERIMENTS AND RESULTS

In this section, we evaluate the performance of the proposed FedSLD through experiments on four publicly available datasets (including two benchmark datasets), and compare it with two leading FL algorithms, FedAvg [4], an algorithm that average the local updates of the global model, and FedProx [11], an algorithm that adds a proximal term on the local objective to enhance performance robustness on non-IID data. To evaluate the general performance of the algorithms, we compute the test accuracies and demonstrate the empirical convergence performance by plotting the training loss and test accuracy curves. In addition, we examine the fairness of the method following recent work [14]. More details on the metrics are in Section 3.1.

3.1. Experiments setup

Datasets.

We conduct experiments on two benchmark image datasets: MNIST and CIFAR10. We further evaluate the methods on two medical image datasets from the MedMNIST dataset collection [15], namely the OrganMNIST(axial) dataset (11-class dataset of liver tumor images) and the PathMNIST dataset (a 9-class dataset of colorectal cancer images). We partition each dataset into a training set and a test set and ensure that they share the same label distribution.

Two non-IID settings.

We set the number of clients to be 12 to mimic a cross-silo FL setting and partition each dataset according to two different non-IID settings: 1) a pathological non-IID setting, where we follow [4] and assign each client with two random classes; 2) a practical non-IID setting, where we randomly partition each class into 12 shards (corresponding to a total of 12 clients): 10 shards of 1%, one shard of 10% and one shard of 80% images in this class. We randomly assign one shard from each class to each client, so that each client will possess images from all classes, with more images from some classes while less images from others. This non-IID setting is more similar to the real-world medical applications, since datasets held at medical centers often contain a variety of classes, and are usually imbalanced with different majority class due to the regional demographics.

Implementation details.

We use the classic four-layer CNN model with two 5×5 convolutional layers and two fully connected layers (hidden layer has 500 units). We use a batch size of 256, 5 local epochs, 0.01 as the learning rate. For the practical non-IID partition, we train the model for 80 rounds, and for the pathological non-IID setting, we train the model for 160 rounds. All experiments are run on an NVIDIA Tesla V100 GPU and implemented in PyTorch and PySyft.

Metrics.

We compute two types of test accuracies for each setting: 1) the Best Mean Client Test Accuracy (BMCTA), computed as the highest mean client test accuracy over all training rounds; 2) the Best Test Accuracy (BTA), computed as the highest test accuracy for the combined test set from each client over all training rounds. We also investigate the methods’ convergence performance by plotting the training loss and test accuracy curves. In addition, we follow [14] and examine the fairness of the methods by using the Gaussian kernel density estimation on the client test accuracies. Higher density at higher accuracy reflects a better result.

3.2. Results

We summarize the numerical results in Table 1. Under the pathological non-IID setting, for MNIST and the two medical datasets, the proposed FedSLD has a better performance with the improvement on the test accuracy of up to 1.57%, and the kernel density estimations in Figure 2 show that FedSLD has slightly higher density which is more concentrated at a higher test accuracy. On CIFAR10, FedSLD reaches competitive performance with FedAvg and FedProx.

Table 1.

The Best Mean Client Test Accuracy (BMCTA) and Best Test Accuracy (BTA) for the pathological and practical non-IID settings. Highest performance are reported in bold.

	BMCTA/BTA under the pathological non-IID			BMCTA/BTA under the practical non-IID
Dataset	FedAvg [4]	FedProx [11]	FedSLD (Ours)	FedAvg [4]	FedProx [11]	FedSLD (Ours)
MNIST	95.60 / 95.92	95.71 / 95.98	95.74 / 96.03	93.41 / 94.15	93.45 / 94.20	95.56 / 95.85
CIFAR10	51.50 / 51.39	51.39 / 51.24	50.81 / 50.71	32.07 / 35.46	31.98 / 35.38	37.48 / 37.79
OrganMNIST(axial)	59.52 / 64.99	59.44 / 65.10	59.70 / 66.13	82.32 / 85.69	81.53 / 85.54	84.75 / 84.75
PathMNIST	56.44 / 57.54	56.62 / 57.56	57.94 / 59.11	52.70 / 57.38	52.77 / 57.72	53.87 / 57.90

Fig. 2.

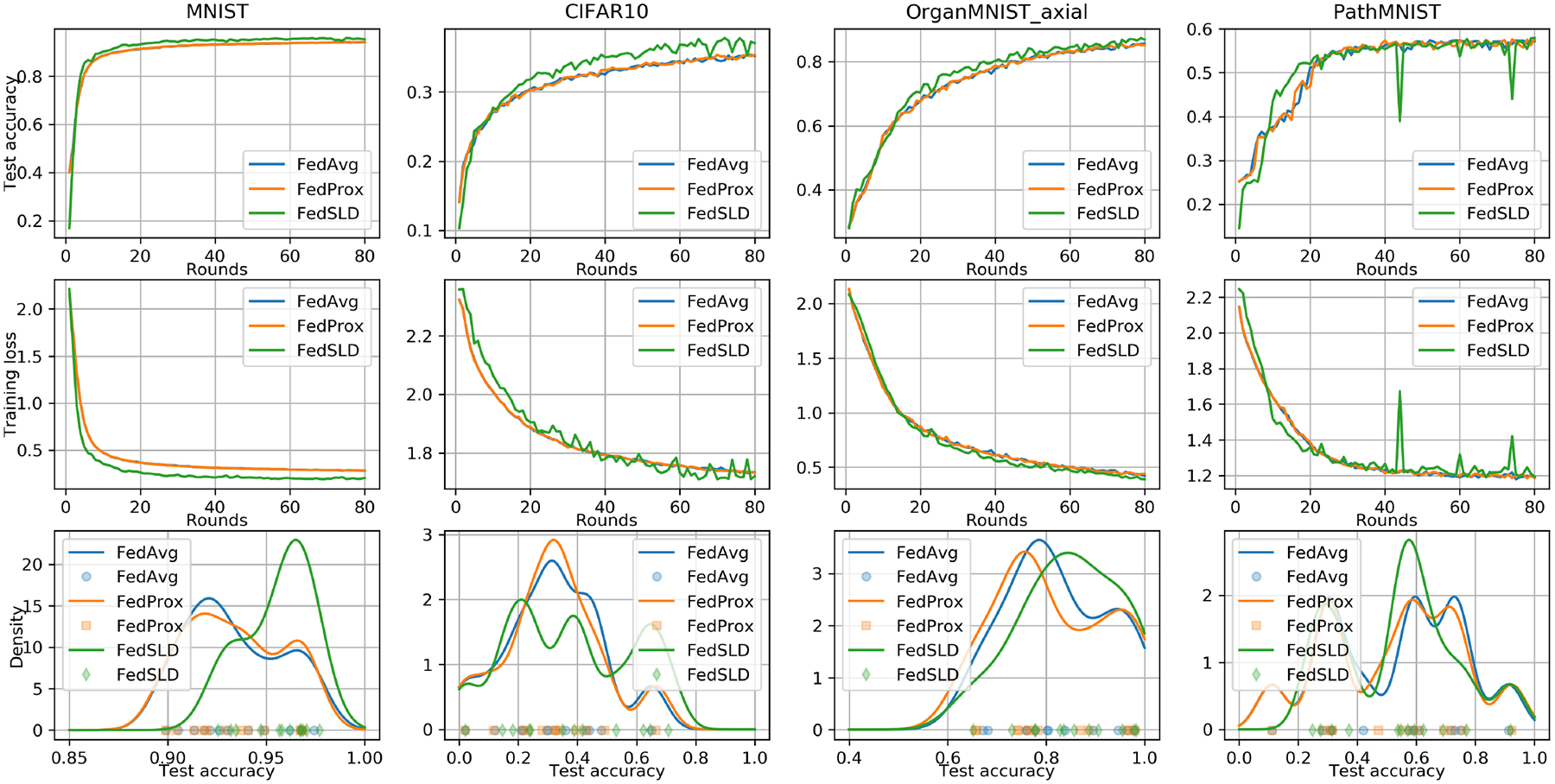
The convergence and fairness performance under the practical non-IID setting. We measure the fairness using Gaussian kernel density estimation. Higher density concentrated at a higher accuracy reflects a better result.

Under the practical non-IID setting, we can see that the proposed FedSLD outperforms the compared FedAvg and FedProx on every dataset, with the improvement of BMCTA ranging from 1.10% to 5.50%, and the improvement of BTA ranging from 0.18% to 2.41%. In addition, Figure 1 shows that FedSLD achieves better convergence behavior on MNIST and OrganMNIST (axial) datasets. The fairness plots reveal that FedSLD not only increases the overall performance with respect to the entire federation, but the variances of the client test accuracies are also reduced on MNIST and PathMNIST datasets, which implies a more fair training. On CIFAR10 and OrganMNIST (axial) datasets, we can see a clear decrease of the density at low accuracy and an increase on the density at high accuracy, which explains the improvement of the BMCTA.

Fig. 1.

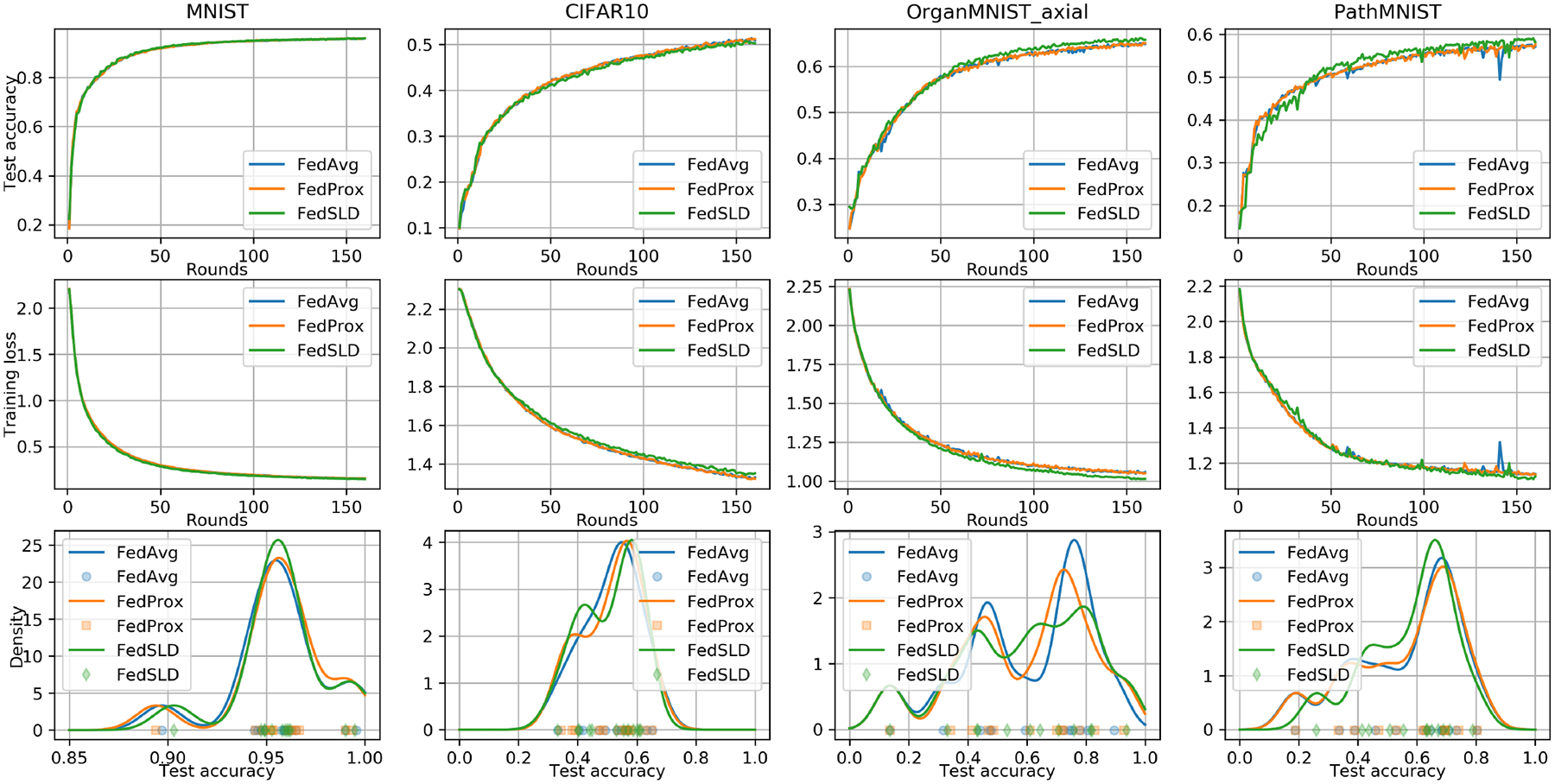
The convergence and fairness performance under the pathological non-IID setting. We measure the fairness using Gaussian kernel density estimation. Higher density concentrated at a higher accuracy reflects a better result.

4. CONCLUSION

In this work, we proposed a new FL algorithm for medical image classification: Federated Learning with Shared Label Distribution (FedSLD). FedSLD aims to mitigate the effect caused by non-IID data by leveraging the clients’ label distribution. We conducted extensive experiments on four publicly available datasets with two types of non-IID setting, and demonstrated that FedSLD outperforms the compared leading FL algorithms, and encourages a more fair performance across all the participating clients.