Skip to main content
PMC home page
Royal Society of Chemistry logoLink to Royal Society of Chemistry
. 2023 Sep 19;23(20):4552–4564. doi: 10.1039/d3lc00512g

Development of a perfusable, hierarchical microvasculature-on-a-chip model†

Sophia W Chen a, Adriana Blazeski a,b, Shun Zhang a,c, Sarah E Shelton a,d,‡,§,✉, Giovanni S Offeddu a,‡,✉, Roger D Kamm a,c,‡,✉
PMCID: PMC10563829  PMID: 37771308

Abstract

Several methods have been developed for generating 3D, in vitro, organ-on-chip models of human vasculature to study vascular function, transport, and tissue engineering. However, many of these existing models lack the hierarchical nature of the arterial-to-capillary-to-venous architecture that is key to capturing a more comprehensive view of the human microvasculature. Here, we present a perfusable, multi-compartmental model that recapitulates the three microvascular compartments to assess various physiological properties such as vessel permeability, vasoconstriction dynamics, and circulating cell arrest and extravasation. Viscous finger patterning and passive pumping create the larger arterial and venular lumens, while the smaller diameter capillary bed vessels are generated through self-assembly. These compartments anastomose and form a perfusable, hierarchical system that portrays the directionality of blood flow through the microvasculature. The addition of collagen channels reduces the apparent permeability of the central capillary region, likely by reducing leakage from the side channels, enabling more accurate measurements of vascular permeability—an important motivation for this study. Furthermore, the model permits modulation of fluid flow and shear stress conditions throughout the system by using hydrostatic pressure heads to apply pressure differentials across either the arteriole or the capillary. This is a pertinent system for modeling circulating tumor or T cell dissemination and extravasation. Circulating cells were found to arrest in areas conducive to physical trapping or areas with the least amount of shear stress, consistent with hemodynamic or mechanical theories of metastasis. Overall, this model captures more features of human microvascular beds and is capable of testing a broad variety of hypotheses.

In this study, we have created a multi-compartmental model replicating a hierarchical vascular bed by combining two methods for vessel-on-chip preparation: viscous finger patterning and self-assembled vascular networks.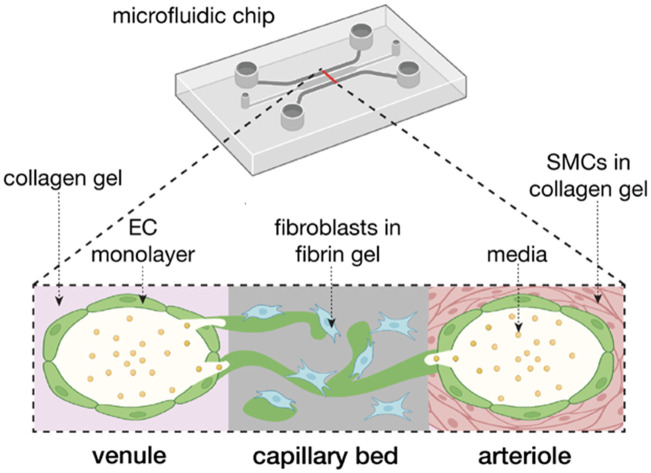graphic file with name d3lc00512g-ga.jpg

Introduction

The circulatory system plays a critical role in the health of every tissue in the body through its functions of gas and nutrient exchange, immune cell transport, endocrine signaling, and tissue repair, among numerous other processes.1 The microvasculature is the interconnected systems of small diameter blood vessels composed of arterioles, capillaries, and venules. These smaller vessels connect to the larger diameter arteries and veins, enabling the circulation of blood by the heart through this hierarchical vascular system.2 One physiologic process dependent on the microvasculature is the dissemination of immune cells, especially to sites of injury or disease. Beyond simply transporting immune cells to sites of inflammation, it has been shown that endothelial cells lining blood vessels also play a role in immune cell signaling and in innate and adaptive immunity.3–5 On the other hand, the circulatory system can also disseminate disease via bacteria or viruses or through the spread of circulating tumor cells (CTCs) from the primary tumor to distant sites via the circulatory system where they can produce metastatic foci. The pathological sequence of hematologic metastasis includes the intravasation of cancer cells, convection to a remote organ or tissue, arrest of CTCs in the microvasculature, and subsequent extravasation and proliferation of these cells. The microvasculature thus plays a complex role in providing routes for cancer cell distribution and spread and understanding the mechanisms that affect the adhesion and extravasation of circulating tumor cells is key to inhibiting metastatic disease.

Since there are limits to what we can learn from human or animal studies, considerable effort has been directed to developing physiologically relevant and simple-to-complex models of the microvasculature to mimic these interactions between cells and tissues in controlled settings. Many of these models in vitro utilize 3D cell culture techniques and microfluidics to recapitulate multicellular architectures more fully than traditional 2D systems.6,7 Among these are “vessel-on-chip” designs that include one or more conduits that can be seeded with cells to produce patterned open-lumen vessels. These employ a variety of engineering techniques and can be used to make more complex microphysiological systems.8,9 Many of these vessel-on-chip systems are fabricated using a small-diameter needle to pattern the extracellular matrix, but these techniques are frequently difficult to perform quickly and at scale, and practical difficulties can include hydrogel breakage or adherence to the needle.10–12 Alternatively, viscous finger patterning (VFP) has also been used to create lumens within a collagen ECM in a process that has been recently used in several vessel-on-chip models.9,19–22 VFP utilizes the property of a less viscous fluid creating finger-like protrusions in more viscous fluids,23 and thus presents an alternative to needle casting methods. Yet, the vessels produced are often hundreds of microns wide and difficult to scale down to the size of typical capillaries.

Another approach to generating vessel-on-chip models is to rely on natural self-assembly to create a self-assembled microvascular network using endothelial cells and fibroblasts suspended in a hydrogel.13 These vessels can have much smaller dimensions, varying from approximately 20 to 200 μm in diameter, and better recapitulate capillary network morphology (including branching) as well as flow and shear stress conditions than 2D systems and straight patterned vessels.14 While both the engineering and self-assembly methods have been used previously, there are relatively few instances in which they have been combined to produce multi-scale networks,15–17 and no study has previously combined VFP with self-assembly. The objective of this study was, therefore, to combine the two vessel-on-chip technologies to create a multi-compartmental model of the microvasculature including microvessels of different sizes. Furthermore, we aimed to recapitulate the hierarchical nature of the arterial-to-capillary-to-venous architecture by applying vascular flow directionally across the system. Previous hierarchical vascular models have lacked self-assembled MVNs that confer physiological relevance to the capillary bed,18 while other models of microvasculature do not present the various compartments together in a hierarchical, fluidically-connected manner.17,19

With the objective of producing a hierarchical endothelial-lined microvascular network, we introduce here a two-step method, combining an established viscous finger patterning (VFP) approach for the larger arteriole and venule and the natural self-assembly method to create the smaller-diameter interconnected vascular network. We use a conventional microfluidic platform with a central gel compartment for the small vessel network, flanked by two side channels in which VFP can be used for the large-diameter patterning. In one side channel, smooth muscle cells are embedded in the collagen gel used for VFP and the inner wall is later coated with an endothelial cell (EC) monolayer to recapitulate the arteriole, in a manner similar to Bulut et al.19 In the opposite channel we form the same VFP-patterned collagen channel and endothelial cell monolayer but lacking smooth muscle cells, representing the venule. The two larger vessel side channels are connected by the microvascular networks in the central compartment, representing the capillary bed. This model preserves the ability to measure vessel permeability, as well as allows for analysis of flow dynamics, arrest, and extravasation of various cell types such as tumor cells and various immune cells. It is simple to construct and produces a connected model of the arteriole-to-capillary-to-venule structure of the microvasculature that can be used for a variety of applications.

Experimental

Cell culture

Human umbilical vein endothelial cells (HUVECs) with or without green fluorescent protein (GFP) from Angio-Proteomie, and normal human lung fibroblasts (NHLFs) from Lonza were cultured on collagen-coated flasks (Corning) with Vasculife VEGF Endothelial Medium and FibroLife S2 Fibroblast Medium (Lifeline Cell Technologies) and cryopreserved at passage 4. HUVECs and NHLFs were then thawed on uncoated flasks (Corning) and grown to 90% confluency before transfer into microfluidic devices. Normal human lung smooth muscle cells (SMCs) from Lifeline Cell Technologies were cultured in VascuLife SMC medium (Lifeline Cell Technologies) and used between passages 3–5. Lung SMCs were chosen for this study to remain consistent with the lung NHLFs used in the microvascular networks and to form a lung MVN model. The breast cancer cell line MDA-MB-231 from ATCC was previously transfected with red fluorescent protein (RFP)24 and cells were cultured in Dulbecco's modified Eagle medium (DMEM) with 10% fetal bovine serum (FBS) and 1% penicillin/streptomycin. Jurkat cells (Clone E6-1, ATCC) were cultured in suspension in Roswell Park Memorial Institute medium (RPMI) supplemented with 10% FBS and 1% penicillin/streptomycin. Jurkat T cells were dyed with Invitrogen CellTracker Red CMTPX Dye one day prior to experiments. Cells were cultured in a humidified incubator at 37 °C and 5% CO2 with media replacement every second day.

Microvascular network formation

Microvascular networks (MVNs) were grown in fibrin gel within microfluidic devices as described previously.25 Fibrinogen (Millipore Sigma) was dissolved in PBS at 6 mg mL−1. Thrombin (Millipore Sigma) was reconstituted in a 0.1% bovine serum albumin (BSA) solution in water to a concentration of 100 U mL−1, then diluted in cold Vasculife VEGF Endothelial Medium to a concentration of 4 U mL−1 for experiments. HUVECs and NHLFs were resuspended in the thrombin solution at 32 million HUVECs per mL and 8 million NHLFs per mL. The HUVECs, NHLFs, and fibrinogen were mixed 1 : 1 : 2 to form a final concentration of 8 million HUVECs per mL, 2 million NHLFs per mL, and 3 mg fibrinogen per mL. This mixture was quickly pipetted into the central gel channel of each device in the idenTx3 Chip (AIM Biotech) and the devices were incubated for 15 minutes to allow the fibrin gel to polymerize. Excess HUVECs were replated and later used to apply the endothelial monolayer to the side channels on day 4 of culture, as described below. Hydraulic resistance of microvascular networks was measured by establishing a pressure head differential across each device and monitoring the flow over time. To accomplish this, reservoirs were attached to each of the media ports of the microfluidic device and filled with media so that one side of the device had a higher media column than the other side, resulting in an initial media height difference of ∼2.5 cm. Changes in the media column heights were recorded for one hour. The height difference in liquid levels h can be shown to decrease exponentially with time t and the resistance to flow RN = dP/Q can be determined by: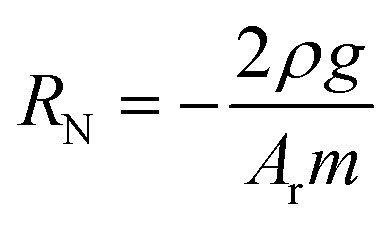graphic file with name d3lc00512g-t1.jpgwhere RN is the network resistance, dP is the change in pressure, Q is the volumetric flow rate, ρ is the density of cell culture media (∼993 kg m−3), Ar is the cross-sectional area of one reservoir, and g is 9.8 m s−2, as previously derived (ESI†). The log slope, m, was calculated by graphing the changing fluid height over time, 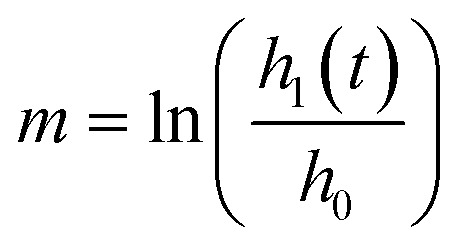Inline graphic. Here, h0 is the initial height difference, and h1 is the height above equilibrium, observed through time, t.

Collagen channel viscous finger patterning

A collagen I gel was formed in the side channels of the microfluidic devices by adapting a previously published protocol from our laboratory.26 Rat tail collagen I (Corning) was diluted on ice to a final concentration of 3 mg mL−1 by combining 162 μL of 3.77 mg mL−1 collagen stock with 20 μL 10× PBS phenol red, 7 μL distilled water, and 11 μL 0.1 N sodium hydroxide for each 200 μL of collagen mixture, adjusted to achieve pH of 7.4. The collagen solution was kept on ice and used within 10 min. For channels containing SMCs, these were resuspended in the collagen solution at 1 million per mL. SMC concentrations of 3 million per mL and 5 million per mL were also tested but yielded less consistent lumen diameters.

We used pressure-assisted VFP of the collagen gel to form lumens in the side channels of the microfluidic devices, similar to what has been previously accomplished for single channels.9 First, the devices were removed from the incubator after polymerization of the fibrin gel in the central channel and allowed to reach room temperature. The side channels of the devices were then filled with cold collagen solution, either with or without SMCs. Immediately after addition of the collagen, 50 μL of cold endothelial medium were added to the bottom media port, and 75 μL were added to top media port, corresponding to a pressure of 12.7 Pa in these devices (schematic shown in Fig. 1). A pipette tip was then used to break any surface tension at either port that would prevent the collagen liquid interface from making direct contact with the cold Vasculife. Devices were then returned to the incubator and media changed daily.

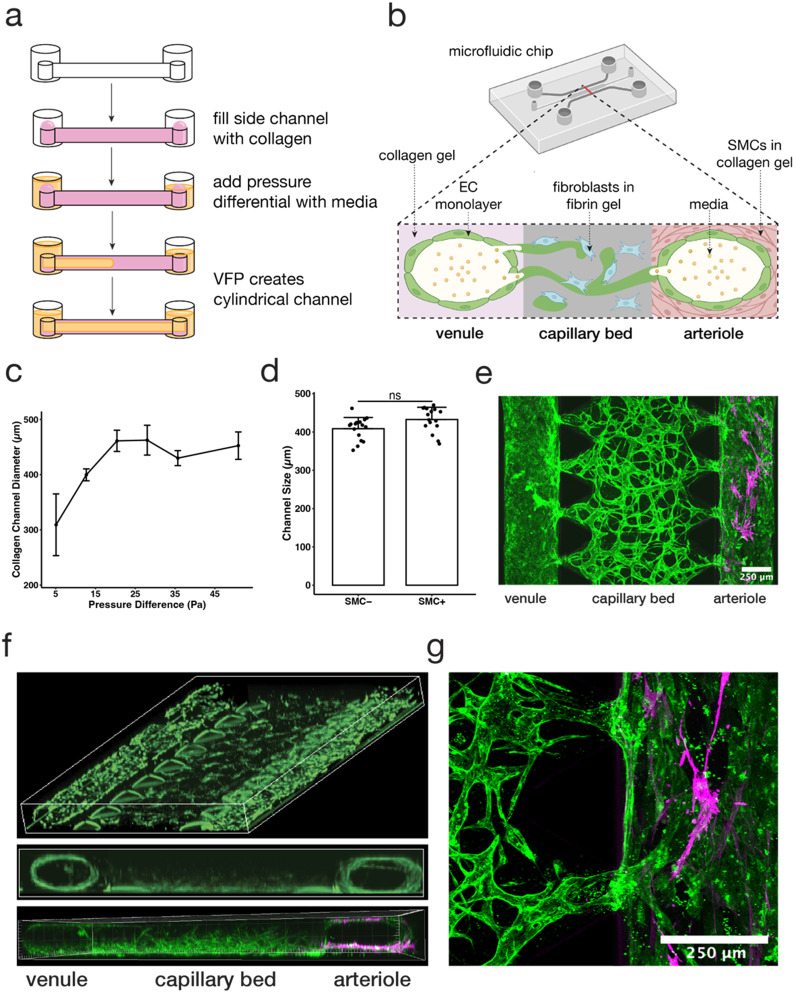
Fig. 1. Viscous finger patterning of collagen gels can be used to create a tricompartmental model of the arteriole-to-capillary-to-venule microvasculature. (a) Schematic diagram of hollow collagen channel formation by pressure-assisted viscous finger patterning (VFP). (b) Schematic cross-sectional diagram of MVNs and collagen channels inside microfluidic device. Partially created with https://BioRender.com. (c) Comparison of collagen channel diameter using various pressure differentials across the channel (data points and error bars indicate average and standard error, respectively; n = 6, 26, 7, 3, 4, 5). (d) Vessel diameters using 12.7 Pa of pressure across the collagen channel with and without SMCs embedded (data points indicate individual channels, bars indicate average, and error bars indicate standard deviation; n = 16; statistical significance by Welch's t-test determined data to be nonsignificant). (e) Confocal z-stack stitched image of aerial view of the device on day 7 of MVN culture; capillaries (middle) modeled by perfusable MVNs made from endothelial cells (EC, green) and fibroblasts (FB) in fibrin gel, venule (left) modeled by collagen channel with EC monolayer, arteriole (right) modeled by collagen channel with smooth muscle cells (SMC, magenta); the scale bar is 250 μm. (f) 3D reconstruction of model depicting view from above (top) and cross-sectional view (middle, bottom; green = GFP HUVECs, magenta = SMCs). (g) Confocal z-stack manually stitched image of junction between capillary bed and arteriole (EC, green; SMC, magenta).

Fig. 1

Open in a new tab

To create an endothelial monolayer on the surface of the collagen gel channels, 100 μL of HUVECs (3 × 106 cells per mL) were introduced on day 4 to the side channels and the devices were slowly rotated at 2 rotations per minute for 15 minutes to achieve a uniformly distributed monolayer. Unattached cells were then aspirated, and fresh media was added to the side channels. To produce interstitial flow across the fibrin gel and the developing MVNs, a pressure difference of 200 Pa was imposed across the gel from day 4 by establishing a hydrostatic pressure difference—old media was aspirated and fresh media was added to a height of 2 cm on the arteriolar side of the device and allowed to flow through to equilibrium each day.

Channel size was determined by imaging the HUVEC GFP monolayer across the length of the vessel using the Nikon Eclipse Ti epifluorescent microscope at 10× magnification and measuring the channel diameter at 25 random locations using ImageJ, FIJI distribution.27

Immunofluorescence staining and imaging

Immunofluorescence staining of SMCs was performed in samples fixed on day 7 of MVN culture with 4% paraformaldehyde28 using a monoclonal antibody against α-smooth muscle actin (α-SMA, Cell Signaling Technologies). Nuclei were stained with DAPI (ThermoFisher) and non-GFP HUVECs were stained with fluorescent Ulex Europaeus Agglutinin I (Vector Technologies). Imaging was performed on an Olympus FV1000 confocal microscope. Stacks were collected using a 10× objective at a resolution of 640 × 640 or 800 × 800 pixels with z-spacing of 5 μm. Image reconstruction was performed with ImageJ, FIJI distribution.27 Manual stitching of images was performed by visual alignment using Adobe Illustrator.

Permeability measurements and quantification

On day 7 of MVN culture, permeability was measured with 70 kDa Texas Red-labeled dextran (ThermoFisher) as described previously.25,28 Dextran was diluted to 0.1 mg mL−1 in endothelial medium and perfused through the MVNs by first emptying one media channel and filling it with the dextran solution, then emptying the other media channel and adding an equal volume of dextran solution. Imaging of the vascular networks was performed on the confocal microscope at 37 °C, microscope settings and image reconstruction technique performed as described above. MVN permeability was determined using automatic segmentation (Trainable Weka Segmentation 3D) of intravascular and extravascular (matrix) compartments, and average intensities of each compartment were used to determine the permeability coefficient, P as described previously.28 Permeability coefficients for the arteriole and venule side channels were determined similarly by comparing average intensities in the large side channel vessel and a small section of the immediately adjacent matrix in the central gel channel.

Tumor cell and immune cell flow and extravasation rate assessment

On day 7, in separate MVN devices, MDA-MB-231 RFP tumor cells or fluorescently labeled Jurkat T cells (using CellTracker Green CMFDA) were perfused through the MVNs to determine cell arrest rates and cancer cell extravasation rates. A pressure difference of 200 Pa (2 cm height difference) was applied across the MVNs using hydrostatic pressure heads producing intravascular flow from the arteriole side to the venule side. Next, 104 tumor cells (10 μL of 1 × 106 cells per mL cell suspension) were added to one inlet of the arteriole vessel, and 100 μL of media were immediately added to the same inlet (approximately 60 Pa pressure differential) so that the tumor cells would become uniformly distributed along the arteriole channel due while simultaneously flowing across the MVNs. Flow velocities produced by these pressure differentials were measured through displacement analysis of 2 μm-diameter fluorescent beads (ThermoFisher), as described previously.29 Devices were incubated for 30 minutes, after which media was changed to wash out cells that did not adhere to the endothelium within the three vascular compartments. Devices with Jurkat T cells were perfused with a UEA-1 endothelial stain (Vector Laboratories) and imaged immediately on the confocal microscope, temperature-controlled at 37 °C. Image reconstruction and cell arrest rate were determined using the ImageJ 3D Objects Counter plugin. Devices with tumor cells were kept in culture for two additional days with interstitial flow restored daily, then fixed. Devices were stained with UEA-1 and DAPI, and confocal microscope was used for imaging as described above. Tumor cell extravasation was determined as described previously24 using IMARIS (Oxford Instruments) to identify extravasated tumor cells.

Smooth muscle cell vasoconstriction

After 7 days of culture, vasoconstricting drugs were applied to stimulate the SMCs in the arteriole side channels, followed by quantification of the magnitude of vessel constriction. Reagents used were 50 mM KCl (ThermoFisher) and 20 nM endothelin-1 (Sigma-Aldrich), both reconstituted in PBS and then diluted to final concentrations in DMEM. To assess channel constriction upon addition of the vasoconstriction drugs, videos of fluorescent endothelial cells were taken using Nikon Eclipse Ti epifluorescent microscope at 10× magnification. Devices were first placed atop the microscope platform and media channels aspirated. Fresh media containing the vasoconstricting drugs were then added into each channel, and AVI videos were recorded at 100 fps for 5 minutes after initial addition of the drug. To quantify vessel constriction, 5 random locations along the vessel were chosen for each movie and the initial diameter was compared to the smallest diameter occurring over the 5 minute timespan.

Statistical analysis

Statistical significance between two groups was assessed using Welch's t-tests. Statistical significance between more than two groups was assessed using ANOVA and Tukey HSD tests. Probability values less than 0.05 were deemed significant (p < 0.05 *, p < 0.01 **, p < 0.001 ***).

Results and discussion

Viscous finger patterning of collagen gels in microfluidic devices produces a more physiological microvasculature network with the ability to recapitulate various flow conditions

Here we generated a three-compartment, hierarchical microfluidic model to better recapitulate the 3D architecture of microvasculature. Previously published microvascular network (MVN) models of microvasculature30,31 have also recapitulated the architecture of human capillaries through interconnected and perfusable lumens with diameters ranging between 10 and 200 μm. These models, generally, do not include additional key components of the microvasculature, such as SMC-lined arterioles upstream and venules downstream of the capillaries. The model presented here extends previous MVN models by introducing these additional compartments.

Specifically, our model design consists of two lumens lined with endothelial cells (ECs) that anastomose with MVNs in the central channel between them, thus creating a connected, perfusable, tricompartmental vascular model. To create the arteriolar- and venular-like compartments, we adapted the viscous finger patterning (VFP) method to generate hollow channels in the collagen gel filling the side channels of the microfluidic device.9,20 This method makes use of the viscosity difference between a hydrogel solution and cell culture medium such that, under an applied pressure difference, the lower viscosity fluid displaces the higher viscosity fluid to form a tubular channel.20 Here, the microfluidic device side channels were filled with a collagen I solution, followed by different media volumes in each outlet to induce pressure-driven channel formation through passive pumping and VFP (Fig. 1a). Our key design parameters were the creation of lumens in the side channels that were i) perfusable along the length of the channel, and ii) connected to the MVN across the microfluidic device to recapitulate the connection between the three microvascular compartments (Fig. 1b). The optimal pressure difference along the side channels was found to be ∼13 Pa producing a diameter of ∼400 μm, which satisfied the desired design parameters above (Fig. 1c). Higher pressures tended to wash out too much of the collagen gel solution, generating lumens with a rectangular cross-section, while lower pressures produced inconsistent lumens with walls that were too thick to permit connections with the MVN in the central channel. In this study, collagen was used instead of fibrin in the VFP-patterned side channels because the fibrin would solidify before a lumen could be formed through VFP, while collagen gelation was slow enough for consistent lumen formation. While recognizing that arterioles in vivo tend to be smaller, in the range of 100 μm, our purpose here is to capture some aspects of the hierarchical network by demonstrating one method by which the larger feeder (“arteriole”) and collector (“venule”) vessels could be incorporated.

A key differentiation in cellular composition between arterioles and venules is the smooth muscle lining surrounding arterioles that is not present in venules.32 To recapitulate the arteriole, smooth muscle cells (SMCs) were mixed with the collagen in one of the side channels prior to VFP,19 allowing the SMCs to reside just outside of the EC monolayer, similar to what is found in vivo33 (Fig. 1e and f). In contrast, the channel on the opposite side of the device was devoid of SMCs, representing a venule. Despite the different cell makeup, no significant difference in the dimension of the arteriole and venule channels was observed (Fig. 1d), indicating that SMCs at this concentration did not affect VFP-driven lumen formation and MVNs self-assembled as before within the fibrin gel in the central channel of the device.9,21–24,34 Future studies can utilize higher SMC concentrations by increasing VFP pressures to reflect a higher cell density within the collagen gel.

The key element of the model was establishing connections between the large lumens in the arteriole and venule channels and the MVN in the central capillary channel. We found that these connections formed spontaneously when channels were size optimized to be around 400 μm, and also when channels were lined with an EC monolayer. Confocal 3D imaging revealed that ECs in the MVN extended between the fibrin and collagen gels, allowing the outer vessel compartments to fuse with the capillary MVN compartment and form an interconnected microvasculature (Fig. 1f and g).

One of the key functional capabilities of the model is the ability to recapitulate circulating cell conditions. Flow conditions were constructed such that fluid flow propagated along the arteriole and across the MVNs to recapitulate the flow directionality within the three compartments: from arteriole to capillary to venule. Hydrostatic pressure heads were used to apply 200 Pa across the capillaries and 60 Pa along the arteriole, as described in the Methods. Using bead displacement tracking to estimate fluid flow velocity, we measured the flow in the arteriole compartment to have an average velocity of 0.34 mm s−1 and a flow rate of approximately 4.3 × 10−11 m3 s−1. At the same time, fluid flow in the capillaries (MVN) compartment had an average velocity of 0.82 mm s−1 and a flow rate of approximately 1.6 × 10−12 m3 s−1. The average speed of beads in the MVN is comparable to in vivo capillary speeds found in the literature, which range from 0.3–1.8 mm s−1.35–39 However, the average bead speed measured in the arteriole was much lower than the 2–3 mm s−1in vivo measured range,35,40,41 due to the low pressure differential applied across the arteriole in this study. The pressure differential across the arteriolar compartment here was a consequence of the design of the experiment – one large-diameter arteriole feeding the entire MVN and the use of hydrostatic pressure heads. Subsequently, whereas the wall shear stress in the capillaries was estimated to be 0.13 Pa, somewhat lower than the 0.5–2 Pa in vivo range,42,43 the arteriolar compartment wall shear stress was estimated to be ∼0.0068 Pa, nowhere near the higher in vivo values of 6–8 Pa or greater found in the literature.42 In future iterations of the model, fluid velocities can be tuned to mimic physiological flow rates of each compartment by using microfluidic pumps that maintain constant pressure differentials and flow rates.29 One important benefit of the tricompartmental model is the ability to regulate the fluid dynamics of the system by tuning the system to achieve different flow velocities across each compartment, which could be used, for example, to model healthy and diseased vascular fluid flow regimes.44

From the bead flow velocity measurements and using Poiseuille's law of resistance, the compartment-specific resistance in the arteriole, R = ΔP/Q, is approximated as 1.4 × 1012 Pa s m−3 in contrast to the much higher resistance of 1.2 × 1014 Pa s m−3 in the capillaries, with R being the resistance, ΔP being the pressure differential applied across the particular compartment, and Q being the flow rate approximated with bead speed measurements and vessel diameter estimations. The aggregate hydraulic resistance of the entire device, determined by driving flow through the entire microfluidic device as detailed above in the Methods, was found to be 3.0 × 1012 Pa s m−3, which is in the same order of magnitude as determined by previous studies using the same microfluidic devices under flow conditions.29 The tricompartmental nature of the model allows for characterization of areas with distinct vascular resistance and geometry that lead to different flow speeds and shear stresses within each compartment. These different stress conditions can affect a variety of different downstream processes, such as tumor cell and immune cell dissemination and extravasation, which we discuss later.

Overall, these results show that while the microfluidic vascular model presented here recapitulates the architecture and hierarchy of three different interconnected microvascular compartments, the flow parameters in the large vessel are far from physiological. In this context, it is important to recognize that since the resistance, shear stress and velocity in a single vessel vary as vessel diameter to the inverse fourth, third and second power, respectively, for a given flow rate, reducing the 400 μm diameter vessel just 4-fold, to 100 μm would produce more realistic values, increasing shear stress, for example, from 0.0068 Pa to 0.43 Pa. However, this method may provide a framework transferable to a variety of different microfluidic device designs.

The tricompartmental model provides lower, more accurate vascular permeability measurements and unimpeded network perfusability

We next assessed vascular barrier function in the model. Microfluidic vascular models are often used to measure the transport of molecules as a way of predicting drug delivery across the endothelium in vivo.14 We compared three conditions: i) devices with EC monolayers but no collagen lining in the side channels, ii) devices with VFP-produced collagen lining and an EC monolayer, and lastly iii) devices with VFP-produced collagen lining, EC monolayer, and embedded SMCs, i.e., the complete tricompartmental model. We measured MVN permeability to 70 kDa dextran to be on the order of 10−7 cm s−1 (Fig. 2a), which is within the range expected from in vivo measurements45–47 and previous studies by our group that report MVN permeabilities of 10−8 and 10−6 cm s−1 depending on device geometry and cell types included.25,28 In the tricompartmental model, the addition of collagen side channels and embedded SMCs did not negatively impact the perfusability of the MVNs as they remained fully perfusable (Fig. 2c), thus maintaining our ability to measure permeability using methodologies developed previously.25

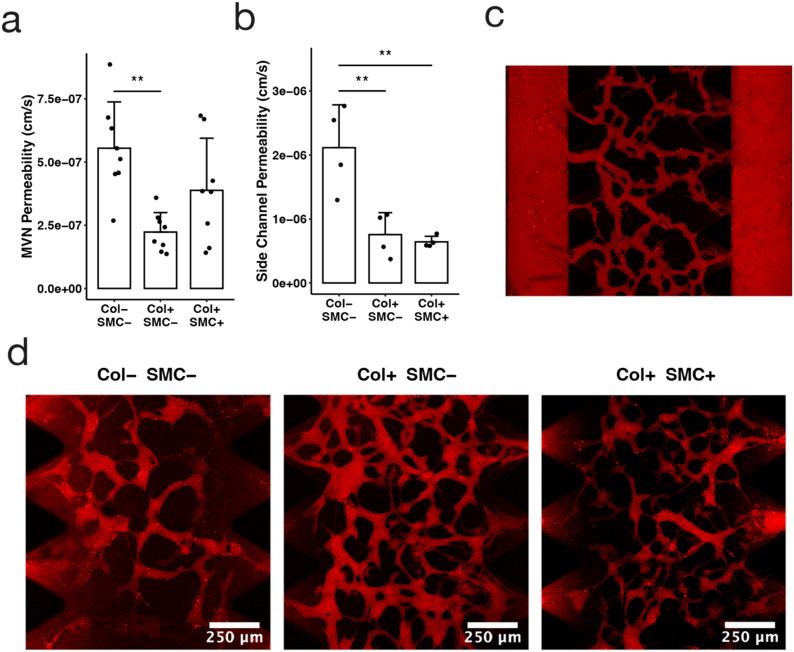
Fig. 2. The tricompartmental model facilitates permeability measurements in small devices. (a) MVN permeability to 70 kDa dextran for each condition: empty side-channels (Col− SMC−), collagen channels without SMCs (Col+ SMC−), and collagen channels with SMCs (Col+ SMC+), with all conditions containing an EC monolayer; data points indicate individual channels, bars indicate average, and error bars indicate standard deviation; n = 8; statistical significance determined by ANOVA and Tukey HSD tests: * p < 0.05, ** p < 0.01, *** p < 0.001). (b) Side channel permeability to 70 kDa dextran as a measure of leakage from side posts; n = 4. (c) Manually-stitched confocal microscopy z-projection image of 70 kDa dextran (red) perfused through fully connected microvasculature. (d) Confocal microscopy z-projection image of MVN section of each condition following the introduction of 70 kDa dextran (red) and incubation for 9 minutes.

Fig. 2

Open in a new tab

A major motivator for adding a collagen lining surrounding the side channel was to reduce the amount of dye leakage interfering with permeability measurements—smaller microfluidic devices tend to be less robust tools for permeability analysis because dextran leakage from the side channels creates false positive signal in the central channel where the MVN resides. Consistent with this hypothesis, we measured lower apparent MVN permeability in devices with collagen channels than in devices without collagen channels: 2.2 × 10−7 ± 0.8 × 10−7 cm s−1 compared to 5.5 × 10−7 ± 1.8 × 10−7 cm s−1 (p < 0.01) (Fig. 2a). We anticipate that this difference is due to a reduction in the dye leakage from the side channels into the central gel region rather than to increased barrier function of MVN vessels in the collagen-lined configuration. This issue had previously been identified in devices with narrow central gel regions28 and the addition of collagen channels lined with ECs appears to reduce dye leakage from the sides.

The capability to independently assess the permeability of each of the three vascular compartments within a single device is another advantage of the tricompartmental model. Previously, permeability was measured only for the MVNs,25 while here we were able to obtain permeability values for the venule and arteriole as well. It should be noted that the permeability values obtained for the arteriole and venule using this method may not be completely accurate for two reasons: dye permeabilizing through the MVNs may erroneously contribute to the side channel signal, and the permeability of the connecting vessel in the arteriole–capillary or venule–capillary junction could differ from the arteriole or venule itself. Nevertheless, we can think of the permeability value obtained for the large side vessels as a proxy for the amount of “leakage” coming in from the sides that could potentially skew MVN permeability measurements—whether the extraneous signal comes from the large vessel itself, the connecting vessel, or simply dextran seeping through the matrix. We found that dextran permeability was lower across collagen channels lined with an EC monolayer, regardless of whether or not smooth muscle cells were included (Fig. 2b). EC-lined collagen channels had average permeability to dextran of 7.6 × 10−7 ± 3.4 × 10−7 and 6.4 × 10−7 ± 0.9 × 10−7 cm s−1, with and without the addition of SMCs, respectively, which is approximately a 3-fold decrease in comparison to the 2.1 × 10−6 ± 0.7 × 10−6 cm s−1 permeability measured in channels with no collagen (p < 0.01) (Fig. 2b). Through confocal microscopy, we observed visibly reduced leakage in collagen-lined devices (Fig. 2d), resulting in more accurate quantification of MVN permeability in our model. Another possible mechanism for reduced leakage in our model could be the formation of tighter junctions when endothelial cells are adhered to the soft collagen gel rather than the stiff plastic, leading to higher barrier function and restricted molecular diffusion.48 Subsequent studies could compare collagen to other hydrogels or examine the effect of gel stiffness or pore size on permeability.49

These large EC-lined collagen channels representing the arteriole and venule (with and without SMCs) exhibited permeabilities (∼7 × 10−7 cm s−1, Fig. 2b), considerably lower than values we and others previously obtained in HUVEC monolayers on stiff membranes25 (10−6 to 10−5 cm s−1). Again, the permeability of the side channels was higher than that of the MVN, aligning with what has been measured in vivo for arteriolar and venular permeabilities compared to capillaries;45–47 however, it should be noted that the low shear stress applied in the arteriole and venule may contribute to the higher permeability of the vessel.13,50 Nevertheless, the system still improves upon 2D transwells and serves as a baseline model estimate for obtaining permeability values of the arteriole and venule.

Vasoconstriction by smooth muscle cells can be measured in the arteriole compartment of the tricompartmental model

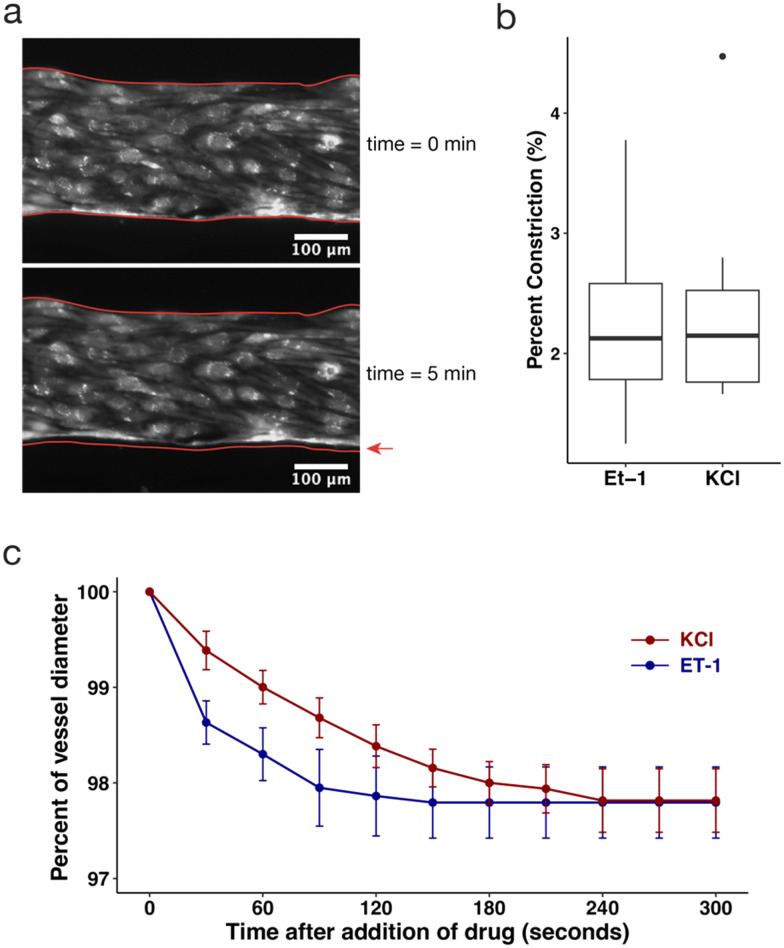
The SMCs embedded in the arteriole compartment add functional capabilities to the model, namely vasoconstriction as a result of exposure to vasoconstricting compounds. We observed a response to the vasoconstricting compounds endothelin-1 (ET-1) and potassium chloride (KCl), indicated by a change in vessel diameter of the arteriole vessels (Fig. 3a). Vessel diameter was measured over a period of 5 minutes after addition of 20 nM ET-1 or 50 mM KCl, using an epifluorescent microscope acquiring images at 100 fps. Vessels stimulated with ET-1 constricted an average of 2.3 ± 0.9%, ranging from 1.2% to 3.8% (Fig. 3b). Similarly, vessels stimulated with KCl constricted an average of 2.4 ± 0.9%, ranging from 1.7% to 4.5% (Fig. 3b). Plotting the average percent of vessel diameter over time over the 5 minute span of each vessel shows that constriction occurred immediately after addition of the drug and plateaued after 4 minutes (Fig. 3c). These results demonstrated smaller constriction than in previous ex vivo and in vivo studies,51,52 which may be due to relatively large lumens used in this in vitro model, as well as the collagen's adherence to the rigid wall of the microfluidic device. Yet, the observed ability to measure vasoconstriction in the tricompartmental model encourages further exploration of this methodology, including through varying the size of the microfluidic device, size of the vessel lumen, stiffness of collagen matrix, or concentration of smooth muscle cells. It would be interesting to observe how vasoconstriction could impact the arrest of disseminating tumor cells, or how constriction affects flow patterns and shear stress through vessels. This model could also aid in testing other metabolic or humoral factors on vasoconstriction and subsequent perfusion as a way to assess the vasoconstricting action of new drugs.1

Fig. 3. The collagen side channel embedded with SMCs demonstrates another functional capability of the model by constricting in response to vasoactive drugs, KCl and ET-1. (a) Microscopy image of representative section of fluorescent endothelial cells lining arteriole channel before drug addition (upper) and 5 minutes after drug addition (lower). Red outlines in both images depict the vessel outline pre-drug treatment, with a red arrow pointing to the gap to show constriction. (b) Boxplots depicting percent change in channel diameter of the arteriole vessel 5 minutes after addition of 20 nM endothelin-1 (ET-1) and 50 mM KCl (box depicts Q1, median, and Q3, and whiskers extend to 1.5 × IQR; outliers represented by individual points; n = 6, 9). (c) Time course experiment tracking vessel constriction over a span of 5 minutes immediately after addition of ET-1 (blue line) and KCl (red line, error bars indicate 95% confidence interval, n = 5 for each drug treatment).

Fig. 3

Open in a new tab

Vascular compartment-specific arrest and extravasation of circulating cells can be quantified in the tricompartmental model

Lastly, we evaluated the use of the tricompartmental model to study circulating cell behavior in the microvasculature. The model design enables the perfusion of various cell types throughout the system to assess where they arrest and how they interact with the surrounding microvasculature (Fig. 4a and b). Microfluidic vascular models have been used before to study the arrest and extravasation of tumor cells to mimic the process of metastasis,15,24 while here, the tricompartmental model design allows for the study of compartment-specific interactions between tumor cells and ECs. We modeled circulating cell conditions using hydrostatic pressure heads as described above to apply a 200 Pa pressure across the capillaries and 60 Pa along the arteriole. However, as discussed above, the shear stresses in the arteriole and venule compartments are far below physiological in vivo values, so we would expect that the rate of adhesion in these compartments may differ widely from physiological values. Therefore, the objective in this study was more to establish the basis of the hierarchical system in which it is possible to study tumor cell and T cell interactions in the arteriole and venule, paving the way for future studies that can more easily apply physiological flow conditions throughout the hierarchical network.

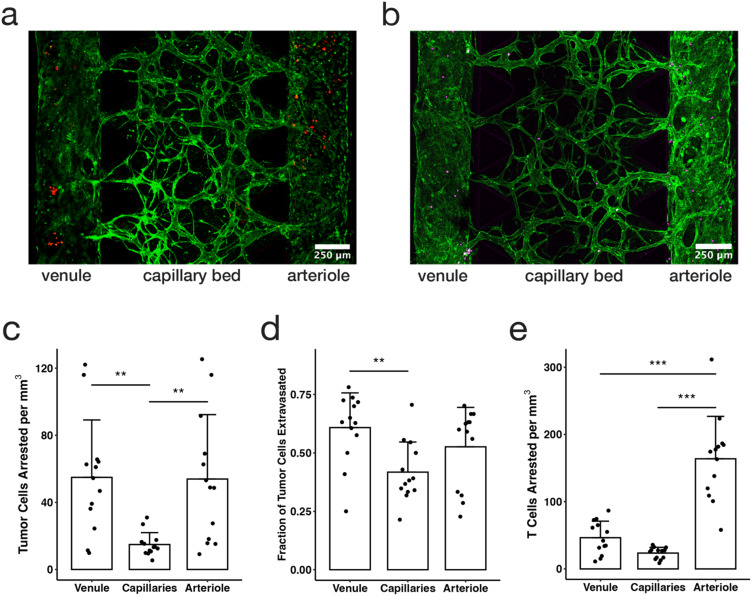
Fig. 4. The hierarchical tricompartmental model can be used to measure arrest and extravasation efficiency of different circulating cells. (a) Fixed confocal image of tricompartmental model 48 hours after tumor cell perfusion (green = ECs, red = MBA-MB-231 tumor cells). (b) Live confocal image taken directly after Jurkat T cell perfusion (green = HUVECs, magenta = Jurkat T cells. (c) Number of tumor cells arrested per mm3 of device volume in each of three compartments (data points indicate measurements from individual devices, bars indicate average, and error bars indicate standard deviation; n = 13; statistical significance determined by ANOVA and Tukey HSD tests: * p < 0.05, ** p < 0.01, *** p < 0.001). (d) Fraction of tumor cells that extravasated within each compartment over a period of 48 hours. (e) Number of T cells arrested per mm3 of device volume in each of three compartments.

Fig. 4

Open in a new tab

A fixed number of tumor cells were injected in the device, where the fluid pressure differential produced flow along the arteriole compartment and across the capillaries compartment to reach the venule compartment. Visually, the cells traveled at a constant speed in the arteriole and slowed down when entering the arterio–capillary junction then sped up considerably as they traversed through each capillary vessel before emerging at the post-capillary venule opening or becoming lodged in narrow capillary vessel segments (Video S1†). This behavior is likely associated with physical trapping and arrest of the circulating cells in the capillaries, as previously observed in vivo and recapitulated in MVN models,24,53 with relatively low adhesive capture in the larger arteriole and venule. Thus, one strength of this model is the ability to observe cell trapping and adhesion in real time in different vascular compartments.

Tumor cell arrest and extravasation were quantified and compared in the three microvascular compartments by applying a 200 Pa pressure difference across the capillary bed to flow tumor cells through the system, and then washing out any cells that did not adhere after 30 minutes. The devices were then incubated for two days to allow cells to extravasate, with the 200 Pa flow across the MVN being applied once per day during a media change and allowed to equilibrate. In this study, we observed that more than three times as many tumor cells arrested in the arteriole and venule compartments (54 ± 34 and 55 ± 38 cells, respectively) than in the capillaries compartment (15 ± 7 cells) (p < 0.01) (Fig. 4c). However, in vivo studies have shown that most tumor cells arrest in the capillaries or in the post-capillary venule due to physical trapping and adhesion effects, and there are fewer reports of tumor cells arresting in the arteriole.54–57 The patterns observed in this study align with the hemodynamic theory of tumor cell behavior in which there are higher arrest and adhesion rates in areas of slower flow speeds and lower shear stresses.58 Here we observed more tumor cells arresting in the arteriole and venule compared to the capillaries, likely due to the higher shear stresses in the capillary compartment than the arteriole or venule. Where flow speed and shear stress are lower, cells are more likely to adhere to the endothelium. In future studies, the pressure differential across each compartment can be tuned to match physiologic values, which may result in cell arrest patterns more closely aligning with in vivo studies. This model would also be well suited to applying continuous flow or recirculation of cells using microfluidic pumps.29

In addition to observing locations and patterns in cell arrest and adhesion, we also quantified extravasation efficiency of cancer cells in each compartment. This is expressed as the fraction of tumor cells that cross the endothelium into the surrounding gel matrix. Tumor cells had higher extravasation efficiency in the venule compartment (0.61 ± 0.15, compared to 0.53 ± 0.17 in the arteriole and 0.42 ± 0.13 in the MVNs over a period of 48 hours, Fig. 4d). Although in vivo studies and in vitro experiments59 show higher tumor cell extravasation rates with higher flow rates, they also emphasize that extravasation occurs only after the tumor cell has securely bound to the vessel wall,60 which is impacted by not only mechanical trapping mechanisms, but also various adhesion interactions between the tumor cell and endothelial cells including integrins and cadherins.61 Our results reinforce the idea that shear stress dominates patterns of cell arrest and adhesion, and therefore extravasation efficiency. The differences in extravasation rate between compartments could also be due to the role of stromal cells and matrix properties, both of which can impede extravasation through mechanical barriers.60 It is possible that SMCs hindered extravasation in the arteriole compartment, while fibroblasts may affect extravasation in the MVN compartment. Overall, our results show that the tricompartmental model can be used to study the effect of different microenvironmental conditions on extravasation in different vascular compartments.

The dissemination and arrest patterns of immune cells can also be studied using microfluidic vascular models.29,62–64 Here, Jurkat cells were used to model T cells and were flowed through the tricompartmental model in a similar method as the tumor cells. However, unlike tumor cells, the Jurkat cells arrested predominantly in the arteriole compartment (164 ± 63 cells), more than three times as many as the venule (46 ± 25 cells, p < 0.001) and six times as many as in the capillaries (24 ± 9 cells, p < 0.001) (Fig. 4e). In vivo studies suggest that immune cells and T lymphocytes mainly arrest in the venules due to a variety of different receptor binding interactions,65 contrary to the findings in this study. There is some evidence that T lymphocytes bind to smooth muscle cells via CD44 and integrins,66 which could result in the increased accumulation of T cells in the arteriole compartment if smooth muscle cells become exposed in the vascular lumen. However, it is more likely that flow-mediated effects, including increased contact time and lower shear stress, are responsible for rapid settling and adhesion of T cells in the arteriole compartment. Overall, arrest patterns for tumor cells and Jurkat T cells were similar, highlighting the utility of the tricompartmental model for studying the dynamics of the arrest and extravasation of different circulating cell types throughout the microvascular compartments under varying flow conditions.

The dissemination of circulating cells can be explained by a combination of mechanical effects and localized interactions between cells.54 Further adaptations of this model could include varying cell types in the central MVN to recapitulate different tissue-specific microenvironments, for example the integration of dermal endothelial cells, dermal fibroblasts, and adipocytes to represent a model of dermal vasculature, or astrocytes and pericytes to model the blood brain barrier.28,67 The work demonstrated here mainly highlights the mechanical aspect to cell dissemination in the microvasculature, and future adaptations with more cell specificity can provide further insight to the importance of cellular makeup in the microenvironment as it relates to cell arrest and extravasation.

Conclusions

The tricompartmental microfluidic model introduced in this work represents the 3D architecture and functionality of the human microvasculature more completely than separate models including either capillary-scale microvascular beds or larger single-channel vessels. The addition of EC-lined collagen channels through viscous finger patterning and of SMCs created an arteriole–capillary–venule architecture without changes in the microfluidic device hardware. The increased functionality of the model allowed for the measurement of compartment-specific permeability and tumor cell and T cell arrest and extravasation, as well as the vasoactive response of the arteriole compartment. This model is a more complete and physiologically relevant vascular platform that can be used for a broader range of hypothesis testing compared to models of single vascular compartments. The key benefits of the hierarchical model are the simultaneous analysis and direct comparison between vascular compartments, as well as the capability to differently tune complex experimental conditions between the three compartments. It also minimizes the potentially non-physiological interactions with device surfaces (e.g., glass, hard plastic or PDMS) and reduces dye leakage artifacts that can lead to elevated estimates of permeability in the capillaries of the central gel region. These capabilities may find application in a broad variety of research efforts, including therapeutic delivery testing, cancer metastasis modeling, and analysis of immune cell behavior.

Author contributions

Conceptualization by SWC, GSO, RDK. Funding acquisition and resources provided by RDK. Investigation by SWC, GSO, and SES. Methodology by SWC, SZ, AB, GSO, and SES. Supervision by SES, GSO, and RDK. Writing-original draft by SWC and SES. Writing-review and editing by SWC, SES, GSO, AB, and RDK.

Conflicts of interest

RDK is a co-founder and a board member of AIM Biotech. He also has current research support from Amgen, Abbvie, Boehringer-Ingelheim, GSK, Novartis, Roche, Takeda, Eisai, EMD Serono, and Visterra.

Supplementary Material

LC-023-D3LC00512G-s001
Download video file (2.5MB, mp4)
LC-023-D3LC00512G-s002

Acknowledgments

This work was supported by the National Institutes of Health and National Cancer Institute through grants U01CA214381 and U54CA261694 to RDK. SES was supported by postdoctoral fellowship K00CA212227. We thank Eunkyung Ko for advice on in vitro vasoconstriction.

†

Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc00512g

References

  1. Yuan S. Y. and Rigor R. R., Regulation of endothelial barrier function, Morgan & Claypool Life Sciences, 2011, vol. 3, pp. 1–146 [PubMed] [Google Scholar]
  2. Loe M. J. Edwards W. D. A light-hearted look at a lion-hearted organ (or, a perspective from three standard deviations beyond the norm) Part 1 (of two parts) Cardiovasc. Pathol. 2004;13(5):282–292. doi: 10.1016/j.carpath.2004.05.001. [DOI] [PubMed] [Google Scholar]
  3. Biedermann B. C. Pober J. S. Human endothelial cells induce and regulate cytolytic T cell differentiation. J. Immunol. 1998;161(9):4679–4687. doi: 10.4049/jimmunol.161.9.4679. [DOI] [PubMed] [Google Scholar]
  4. Rodig N. Ryan T. Allen J. A. et al., Endothelial expression of PD-L1 and PD-L2 down-regulates CD8+ T cell activation and cytolysis. Eur. J. Immunol. 2003;33(11):3117–3126. doi: 10.1002/eji.200324270. [DOI] [PubMed] [Google Scholar]
  5. He J. Baum L. G. Endothelial cell expression of galectin-1 induced by prostate cancer cells inhibits T-cell transendothelial migration. Lab. Invest. 2006;86(6):578–590. doi: 10.1038/labinvest.3700420. [DOI] [PubMed] [Google Scholar]
  6. Low L. A. Mummery C. Berridge B. R. Austin C. P. Tagle D. A. Organs-on-chips: into the next decade. Nat. Rev. Drug Discovery. 2021;20(5):345–361. doi: 10.1038/s41573-020-0079-3. [DOI] [PubMed] [Google Scholar]
  7. Picollet-D'hahan N. Zuchowska A. Lemeunier I. Le Gac S. Multiorgan-on-a-chip: a systemic approach to model and decipher inter-organ communication. Trends Biotechnol. 2021;39(8):788–810. doi: 10.1016/j.tibtech.2020.11.014. [DOI] [PubMed] [Google Scholar]
  8. Ingber D. E. Human organs-on-chips for disease modelling, drug development and personalized medicine. Nat. Rev. Genet. 2022:1–25. doi: 10.1038/s41576-022-00466-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Herland A. van der Meer A. D. FitzGerald E. A. Park T. E. Sleeboom J. J. Ingber D. E. Distinct contributions of astrocytes and pericytes to neuroinflammation identified in a 3D human blood-brain barrier on a chip. PLoS One. 2016;11(3):e0150360. doi: 10.1371/journal.pone.0150360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hasan A. Paul A. Memic A. Khademhosseini A. A multilayered microfluidic blood vessel-like structure. Biomed. Microdevices. 2015;17(5):1–13. doi: 10.1007/s10544-015-9993-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Jiménez-Torres J. A., Beebe D. J. and Sung K. E., A microfluidic method to mimic luminal structures in the tumor microenvironment, in The Tumor Microenvironment, Springer, 2016, pp. 59–69 [DOI] [PubMed] [Google Scholar]
  12. Virumbrales-Muñoz M. Ayuso J. M. Gong M. M. et al., Microfluidic lumen-based systems for advancing tubular organ modeling. Chem. Soc. Rev. 2020;49(17):6402–6442. doi: 10.1039/D0CS00705F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Jeon J. S. Bersini S. Gilardi M. et al., Human 3D vascularized organotypic microfluidic assays to study breast cancer cell extravasation. Proc. Natl. Acad. Sci. U. S. A. 2015;112(1):214–219. doi: 10.1073/pnas.1417115112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Haase K. Kamm R. D. Advances in on-chip vascularization. Regener. Med. 2017;12(3):285–302. doi: 10.2217/rme-2016-0152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Chen M. B. Whisler J. A. Fröse J. Yu C. Shin Y. Kamm R. D. On-chip human microvasculature assay for visualization and quantification of tumor cell extravasation dynamics. Nat. Protoc. 2017;12(5):865–880. doi: 10.1038/nprot.2017.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Osaki T. Sivathanu V. Kamm R. D. Vascularized microfluidic organ-chips for drug screening, disease models and tissue engineering. Curr. Opin. Biotechnol. 2018;52:116–123. doi: 10.1016/j.copbio.2018.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Cuenca M. V. Cochrane A. van den Hil F. E. et al., Engineered 3D vessel-on-chip using hiPSC-derived endothelial-and vascular smooth muscle cells. Stem Cell Rep. 2021;16(9):2159–2168. doi: 10.1016/j.stemcr.2021.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Zhao N. Guo Z. Kulkarni S. et al., Engineering the human blood–brain barrier at the capillary scale using a double-templating technique. Adv. Funct. Mater. 2022;32(30):2110289. doi: 10.1002/adfm.202110289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Bulut M. Vila Cuenca M. de Graaf M. van den Hil F. E. Mummery C. L. Orlova V. V. Three-Dimensional Vessels-on-a-Chip Based on hiPSC-derived Vascular Endothelial and Smooth Muscle Cells. Curr. Protoc. 2022;2(10):e564. doi: 10.1002/cpz1.564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Bischel L. L. Lee S. H. Beebe D. J. A practical method for patterning lumens through ECM hydrogels via viscous finger patterning. J. Lab. Autom. 2012;17(2):96–103. doi: 10.1177/2211068211426694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. de Graaf M. N. Cochrane A. van den Hil F. E. et al., Scalable microphysiological system to model three-dimensional blood vessels. APL Bioeng. 2019;3(2):026105. doi: 10.1063/1.5090986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Delannoy E. Tellier G. Cholet J. Leroy A. M. Treizebré A. Soncin F. Multi-Layered Human Blood Vessels-on-Chip Design Using Double Viscous Finger Patterning. Biomedicines. 2022;10(4):797. doi: 10.3390/biomedicines10040797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Saffman P. G. Taylor G. I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. London, Ser. A. 1958;245(1242):312–329. [Google Scholar]
  24. Offeddu G. S. Hajal C. Foley C. R. et al., The cancer glycocalyx mediates intravascular adhesion and extravasation during metastatic dissemination. Commun. Biol. 2021;4(1):1–10. doi: 10.1038/s42003-020-01566-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Offeddu G. S. Haase K. Gillrie M. R. et al., An on-chip model of protein paracellular and transcellular permeability in the microcirculation. Biomaterials. 2019;212:115–125. doi: 10.1016/j.biomaterials.2019.05.022. [DOI] [PubMed] [Google Scholar]
  26. Shin Y. Han S. Jeon J. S. et al., Microfluidic assay for simultaneous culture of multiple cell types on surfaces or within hydrogels. Nat. Protoc. 2012;7(7):1247–1259. doi: 10.1038/nprot.2012.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Schindelin J. Arganda-Carreras I. Frise E. et al., Fiji: an open-source platform for biological-image analysis. Nat. Methods. 2012;9(7):676–682. doi: 10.1038/nmeth.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hajal C. Offeddu G. S. Shin Y. et al., Engineered human blood–brain barrier microfluidic model for vascular permeability analyses. Nat. Protoc. 2022;17(1):95–128. doi: 10.1038/s41596-021-00635-w. [DOI] [PubMed] [Google Scholar]
  29. Offeddu G. S. Serrano J. C. Chen S. W. et al., Microheart: A microfluidic pump for functional vascular culture in microphysiological systems. J. Biomech. 2021;119:110330. doi: 10.1016/j.jbiomech.2021.110330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kim S. Lee H. Chung M. Jeon N. L. Engineering of functional, perfusable 3D microvascular networks on a chip. Lab Chip. 2013;13(8):1489–1500. doi: 10.1039/C3LC41320A. [DOI] [PubMed] [Google Scholar]
  31. Moya M. L. Hsu Y. H. Lee A. P. Hughes C. C. George S. C. In vitro perfused human capillary networks. Tissue Eng., Part C. 2013;19(9):730–737. doi: 10.1089/ten.tec.2012.0430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Johnson P. C., Overview of the Microcirculation, in Microcirculation, ed. R. F. Tuma, W. N. Durán and K. Ley, Academic Press, 2nd edn, 2008, 10.1016/B978-0-12-374530-9.00022-X [DOI] [Google Scholar]
  33. Hill M. A. Meininger G. A. Arteriolar vascular smooth muscle cells: mechanotransducers in a complex environment. Int. J. Biochem. Cell Biol. 2012;44(9):1505–1510. doi: 10.1016/j.biocel.2012.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Bischel L. L. Young E. W. Mader B. R. Beebe D. J. Tubeless microfluidic angiogenesis assay with three-dimensional endothelial-lined microvessels. Biomaterials. 2013;34(5):1471–1477. doi: 10.1016/j.biomaterials.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ivanov K. Kalinina M. Levkovich Y. I. Blood flow velocity in capillaries of brain and muscles and its physiological significance. Microvasc. Res. 1981;22(2):143–155. doi: 10.1016/0026-2862(81)90084-4. [DOI] [PubMed] [Google Scholar]
  36. Shahidi M. Wanek J. Gaynes B. Wu T. Quantitative assessment of conjunctival microvascular circulation of the human eye. Microvasc. Res. 2010;79(2):109–113. doi: 10.1016/j.mvr.2009.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Intaglietta M. Silverman N. Tompkins W. Capillary flow velocity measurements in vivo and in situ by television methods. Microvasc. Res. 1975;10(2):165–179. doi: 10.1016/0026-2862(75)90004-7. [DOI] [PubMed] [Google Scholar]
  38. Hudetz A. G. Blood flow in the cerebral capillary network: a review emphasizing observations with intravital microscopy. Microcirculation. 1997;4(2):233–252. doi: 10.3109/10739689709146787. [DOI] [PubMed] [Google Scholar]
  39. Fedorovich A. Drapkina O. Pronko K. Sinopalnikov V. Zemskov V. Telemonitoring of capillary blood flow in the human skin: new opportunities and prospects. Clin. Pract. 2018;15(2):561–567. [Google Scholar]
  40. Cheung A. T. Perez R. V. Chen P. C. Improvements in diabetic microangiopathy after successful simultaneous pancreas-kidney transplantation: A computer-assisted Intravital microscopy study on the conjunctival microcirculation. Transplantation. 1999;68(7):927–932. doi: 10.1097/00007890-199910150-00005. [DOI] [PubMed] [Google Scholar]
  41. Wang L. Yuan J. Jiang H. et al., Vessel sampling and blood flow velocity distribution with vessel diameter for characterizing the human bulbar conjunctival microvasculature. Eye & Contact Lens. 2016;42(2):135. doi: 10.1097/ICL.0000000000000146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ballermann B. J. Dardik A. Eng E. Liu A. Shear stress and the endothelium. Kidney Int. 1998;54:S100–S108. doi: 10.1046/j.1523-1755.1998.06720.x. [DOI] [PubMed] [Google Scholar]
  43. Koutsiaris A. G. Tachmitzi S. V. Batis N. et al., Volume flow and wall shear stress quantification in the human conjunctival capillaries and post-capillary venules in vivo. Biorheology. 2007;44(5–6):375–386. [PubMed] [Google Scholar]
  44. Jain R. K. Determinants of tumor blood flow: a review. Cancer Res. 1988;48(10):2641–2658. [PubMed] [Google Scholar]
  45. Renkin E. Multiple pathways of capillary permeability. Circ. Res. 1977;41(6):735–743. doi: 10.1161/01.RES.41.6.735. [DOI] [PubMed] [Google Scholar]
  46. Yuan W. Lv Y. Zeng M. Fu B. M. Non-invasive measurement of solute permeability in cerebral microvessels of the rat. Microvasc. Res. 2009;77(2):166–173. doi: 10.1016/j.mvr.2008.08.004. [DOI] [PubMed] [Google Scholar]
  47. Huxley V. H. Williams D. A. Role of a glycocalyx on coronary arteriole permeability to proteins: evidence from enzyme treatments. Am. J. Physiol. Heart Circ. Physiol. 2000;278(4):H1177–H1185. doi: 10.1152/ajpheart.2000.278.4.H1177. [DOI] [PubMed] [Google Scholar]
  48. Urbano R. L. Furia C. Basehore S. Clyne A. M. Stiff substrates increase inflammation-induced endothelial monolayer tension and permeability. Biophys. J. 2017;113(3):645–655. doi: 10.1016/j.bpj.2017.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. O'Brien F. J. Harley B. A. Waller M. A. Yannas I. V. Gibson L. J. Prendergast P. J. The effect of pore size on permeability and cell attachment in collagen scaffolds for tissue engineering. Technol. Health Care. 2007;15(1):3–17. [PubMed] [Google Scholar]
  50. Polacheck W. J. Kutys M. L. Tefft J. B. Chen C. S. Microfabricated blood vessels for modeling the vascular transport barrier. Nat. Protoc. 2019;14(5):1425–1454. doi: 10.1038/s41596-019-0144-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Welsh D. G. Segal S. S. Endothelial and smooth muscle cell conduction in arterioles controlling blood flow. Am. J. Physiol. Heart Circ. Physiol. 1998;274(1):H178–H186. doi: 10.1152/ajpheart.1998.274.1.H178. [DOI] [PubMed] [Google Scholar]
  52. Motherwell J. M. Azimi M. S. Spicer K. et al., Evaluation of arteriolar smooth muscle cell function in an ex vivo microvascular network model. Sci. Rep. 2017;7(1):1–12. doi: 10.1038/s41598-016-0028-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Scherbarth S. Orr F. W. Intravital videomicroscopic evidence for regulation of metastasis by the hepatic microvasculature: effects of interleukin-1α on metastasis and the location of B16F1 melanoma cell arrest. Cancer Res. 1997;57(18):4105–4110. [PubMed] [Google Scholar]
  54. Guo P. Cai B. Lei M. Liu Y. Fu B. M. Differential arrest and adhesion of tumor cells and microbeads in the microvasculature. Biomech. Model. Mechanobiol. 2014;13(3):537–550. doi: 10.1007/s10237-013-0515-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Morris V. L. MacDonald I. C. Koop S. Schmidt E. E. Chambers A. F. Groom A. C. Early interactions of cancer cells with the microvasculature in mouse liver and muscle during hematogenous metastasis: videomicroscopic analysis. Clin. Exp. Metastasis. 1993;11:377–390. doi: 10.1007/BF00132981. [DOI] [PubMed] [Google Scholar]
  56. Ding L. Sunamura M. Kodama T. et al., In vivo evaluation of the early events associated with liver metastasis of circulating cancer cells. Br. J. Cancer. 2001;85(3):431–438. doi: 10.1054/bjoc.2001.1911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Varotsos Vrynas A. Perea Paizal J. Bakal C. Au S. H. Arresting metastasis within the microcirculation. Clin. Exp. Metastasis. 2021;38(4):337–342. doi: 10.1007/s10585-021-10109-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Follain G. Osmani N. Azevedo A. S. et al., Hemodynamic forces tune the arrest, adhesion, and extravasation of circulating tumor cells. Dev. Cell. 2018;45(1):33–52. doi: 10.1016/j.devcel.2018.02.015. [DOI] [PubMed] [Google Scholar]
  59. Hajal C. Ibrahim L. Serrano J. C. Offeddu G. S. Kamm R. D. The effects of luminal and trans-endothelial fluid flows on the extravasation and tissue invasion of tumor cells in a 3D in vitro microvascular platform. Biomaterials. 2021;265:120470. doi: 10.1016/j.biomaterials.2020.120470. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Azevedo A. S. Follain G. Patthabhiraman S. Harlepp S. Goetz J. G. Metastasis of circulating tumor cells: favorable soil or suitable biomechanics, or both? Cell Adhes. Migr. 2015;9(5):345–356. doi: 10.1080/19336918.2015.1059563. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Strilic B. Offermanns S. Intravascular survival and extravasation of tumor cells. Cancer Cell. 2017;32(3):282–293. doi: 10.1016/j.ccell.2017.07.001. [DOI] [PubMed] [Google Scholar]
  62. Chen M. B. Hajal C. Benjamin D. C. et al., Inflamed neutrophils sequestered at entrapped tumor cells via chemotactic confinement promote tumor cell extravasation. Proc. Natl. Acad. Sci. U. S. A. 2018;115(27):7022–7027. doi: 10.1073/pnas.1715932115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Boussommier-Calleja A. Atiyas Y. Haase K. Headley M. Lewis C. Kamm R. The effects of monocytes on tumor cell extravasation in a 3D vascularized microfluidic model. Biomaterials. 2019;198:180–193. doi: 10.1016/j.biomaterials.2018.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Campisi M. Sundararaman S. K. Shelton S. E. et al., Tumor-derived cGAMP regulates activation of the vasculature. Front. Immunol. 2020;11:2090. doi: 10.3389/fimmu.2020.02090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Masopust D. Schenkel J. M. The integration of T cell migration, differentiation and function. Nat. Rev. Immunol. 2013;13(5):309–320. doi: 10.1038/nri3442. [DOI] [PubMed] [Google Scholar]
  66. Lazaar A. L. Albelda S. M. Pilewski J. M. Brennan B. Puré E. Panettieri Jr. R. T lymphocytes adhere to airway smooth muscle cells via integrins and CD44 and induce smooth muscle cell DNA synthesis. J. Exp. Med. 1994;180(3):807–816. doi: 10.1084/jem.180.3.807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Offeddu G. S. Serrano J. C. Wan Z. et al., Microphysiological endothelial models to characterize subcutaneous drug absorption. ALTEX. 2023;40(2):299–313. doi: 10.14573/altex.2207131. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

LC-023-D3LC00512G-s001
Download video file (2.5MB, mp4)
LC-023-D3LC00512G-s002
LC-023-D3LC00512G-s002.pdf (427.9KB, pdf)

Articles from Lab on a Chip are provided here courtesy of Royal Society of Chemistry

RESOURCES