Population Pharmacokinetics of Ceftizoxime Administered by Continuous Infusion in Clinically Ill Adult Patients

Abstract

Ceftizoxime is a widely used beta-lactam antimicrobial agent, but pharmacokinetic data for use with clinically ill patients are lacking. We studied the population pharmacokinetics of ceftizoxime in 72 clinically ill patients at a community-based, university-affiliated hospital. A population pharmacokinetic model for ceftizoxime was created by using a prospective observational design. Ceftizoxime was administered by continuous infusion to treat patients with proven or suspected bacterial infections. While the patients were receiving infusions of ceftizoxime, serum samples were collected for pharmacokinetic analysis with the nonlinear mixed-effect modeling program NONMEM. In addition to clearance and volume of distribution, various comorbidities were examined for their influence on the kinetics. All 72 subjects completed the study, and 114 serum samples were collected. Several demographic and comorbidity variables, namely, age, weight, serum creatinine levels, congestive heart failure, and long-term ventilator dependency, had a significant impact on the estimate for ceftizoxime clearance. A mixture model, or two populations for estimation of ceftizoxime clearance, was discovered. One population presented with an additive clearance component of 1.6 liters per h. In addition, a maximizer function for serum creatinine levels was found. In summary, two models for ceftizoxime clearance, mixture and nonmixture, were found and are presented. Clearance for ceftizoxime can be estimated with commonly available clinical information and the models presented. From the clearance estimates, the dose of ceftizoxime to maintain the desired concentration in serum can be determined. Work is needed to validate the model for drug clearance and to evaluate its predictive performance.

Ceftizoxime is an aminothiazolyl cephalosporin with an extended spectrum of activity against many gram-negative, nosocomially acquired pathogens (11). This compound has excellent beta-lactamase stability, with good in vitro activity against Haemophilus influenzae, Neisseria gonorrhoeae, members of the family Enterobacteriaceae not carrying a Bush class I beta-lactamase, and Klebsiella pneumoniae (11, 21).

Ceftizoxime is a parenteral cephalosporin that binds poorly to serum proteins (less than 30%) and distributes extensively to extracellular fluid. It is not metabolized, is excreted predominantly by glomerular filtration, and shows linear pharmacokinetics after administration of a single intravenous (i.v.) dose (7, 21). In patients with normal renal function, ceftizoxime has a half-life of approximately 1 to 2 h, with a volume of distribution of about 0.36 liters per kilogram of body weight (7, 21).

Typically, intermittent administration of ceftizoxime has become standard clinical practice in the treatment of bacterial infections (11). However, the most effective method of administration remains controversial (5, 6, 8, 16, 22). The beta-lactam antibiotics, such as ceftizoxime, demonstrate time-dependent, concentration-independent bacterial killing. Combining knowledge of time-dependent bacterial killing with technology for i.v. infusion led to the development of a continuous infusion regimen for ceftizoxime. This study was designed to explore the population pharmacokinetics of ceftizoxime administered by continuous infusion to hospitalized adult patients.

MATERIALS AND METHODS

Subjects.

Patients who were admitted to Metropolitan Hospital, Grand Rapids, Mich., between January and September 1996 and who received continuous infusion of ceftizoxime and for whom one or more serum drug concentrations had been determined were included in the study. Patients younger than 18 years of age, patients who were hypersensitive to cephalosporin, patients who were pregnant or lactating, and patients with central nervous system infections were excluded from the study. This study was approved by the Metropolitan Hospital Institutional Review Board. Informed consent was waived because no additional phlebotomies beyond those needed for routine patient care would be performed during collection of serum for determining ceftizoxime drug concentrations.

Study design.

This study was a prospective clinical observational trial of continuous infusion of ceftizoxime. Patients underwent an initial evaluation for exclusion criteria. Patient monitoring, infusion rate, dose, and serum sampling were coordinated by the therapeutic drug monitoring team of the pharmacy department and the i.v. drug team of the nursing department. Patients received a bolus, or loading dose, followed by a continuous infusion. Continuous infusion began immediately after the loading dose was given. The rate for continuous infusion was calculated by using a relationship between ceftizoxime clearance and creatinine clearance described by Cutler et al. (7). A dose of ceftizoxime (in milligrams) was determined based on the calculated clearance. A continuous infusion rate was calculated to attain a steady-state serum drug concentration equal to 24 μg/ml or two times the highest bacterial MIC of concern for a given patient, whichever was highest. A concentration in serum of 24 μg/ml is three times the National Committee for Clinical Laboratory Standards’ breakpoint for ceftizoxime susceptibility.

Antimicrobial agent and administration.

All patients enrolled in the study received ceftizoxime (Cefizox; Fujisawa Pharmaceutical). Patients received a 1-g loading dose, followed by a continuous infusion of 1 to 6 g per day. The bolus of 1 g, infused over 15 min, was diluted in 50 ml of 5% dextrose in water. The total daily dose for continuous infusion was diluted in 5% dextrose in water. The volume of the dilution varied with the daily quantity of the drug administered; 1-, 1.5-, and 2-g doses were diluted in 250 ml and infused over 24-h periods. Quantities of 3 to 6 g per day were equally divided, diluted in 250 ml of 5% dextrose in water, and infused over 12-h periods. All ceftizoxime infusions were administered via an infusion pump (Flo-Guard 6200; Baxter Co., Deerfield Ill.).

Analytical methods.

Plasma ceftizoxime concentrations were analyzed by the Mayo Clinic biochemical laboratories by a high-pressure liquid chromatography method. Instruments and materials included an LC-10AT pump, an SCL-10A autosampler, an SCL-10A system controller, an SPD-10A UV detector, and a Supelco LC-8-DB column. The mobile phase consisted of 7% acetonitrile in phosphate buffer (pH 7) at a flow rate of 1.5 ml/min. Cefpirome was used as the internal standard. The limit of detection was 5 μg/ml, with results greater than or equal to 5 μg/ml reported as numeric values. Three standards (5, 40, and 200 μg/ml) were used each time an assay was run, to ensure analytical stability. The coefficients of variation (CVs) for the low-, mid-, and high-range controls were 13, 4, and 5.6%, respectively.

Sample collection.

Blood samples for determination of ceftizoxime concentrations were obtained by routine morning phlebotomies after steady-state concentrations had been achieved. The time until a steady-state concentration was reached was estimated to be three to five times the estimated half-life. Blood samples were drawn in a plain, red top tube, spun down, and frozen until time of analysis. From one to five serum drug concentrations were determined for each patient in the study. The serum creatinine level was determined upon the initial evaluation of each patient, with additional values determined as needed according to each patient’s medical status. The serum creatinine level was analyzed by the Jaffe rate method (Synchron CX; Beckman Instruments, Naguabo, Puerto Rico). The interday assay CVs were 5.4 and 1.7% at 0.8 and 3.9 mg/dl, respectively.

Demographic assessment.

Age in years, weight in kilograms, and height in inches were determined from the patients’ admission data. For patients exhibiting large weight fluctuations, a stable preadmission weight was used. The patient’s maximum temperature was recorded daily. A patient was arbitrarily assumed to have a fever when the maximum temperature for the day was greater than 100.6°F. Congestive heart failure, cancer, and diabetes mellitus were each recorded as dichotomous variables. The presence of comorbid diseases was determined from each patient’s medical history. The grading of diseases was not undertaken; only their presence or absence was noted. Residence in the intensive care unit or the ventilator dependency unit was each recorded as a dichotomous variable. The ventilator care unit is unique in that all patients are supported by mechanical ventilation. Long-term mechanical ventilation is necessary due to an underlying condition such as neuromuscular illness, trauma, or cancer. As an indicator of renal function, the serum creatinine level was also coded into the data set for each patient during treatment to reflect the appropriate time interval for collection. When large changes occurred, interpolated values of creatinine level were inserted into the database to emulate a smoothly changing creatinine level. A large change in renal function was defined as a change in serum creatinine of ±2 mg/dl.

Pharmacostatistical model.

The nonlinear mixed-effect modeling program NONMEM V (1) was used for pharmacostatistical analysis. Three significant digits were requested for the estimates. Total serum ceftizoxime concentrations were modeled with a one-compartment open model with first-order elimination kinetics, parameterized in terms of clearance (CL) in liters per hour and volume of distribution (V) in liters. First-order conditional estimation was used (1). Several model-building techniques from the NONMEM reference manual and literature were explored. Two models, mixture and nonmixture, are presented.

Nonmixture model.

The nonmixture model assumes that all patients are sampled from one population. The value of clearance for a typical individual (TVCL) is defined as follows (see Table 3 for definitions of θ):

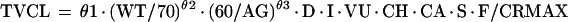1

where WT is weight, AG is age, D is diabetes mellitus, I is residence in the intensive care unit, VU is residence in the ventilator dependency unit, CH is congestive heart failure, CA is cancer, S is sex, and F is fever. The dichotomous factors D, I, VU, CH, CA, S, and F are represented by the indicator variables Z_i (i = 4, 5, 6, 7, 8, 9, 10), respectively. Z_i is defined as 1 if the factor is not present and θ_i if the factor is present. CRMAX is defined as serum creatinine (in milligrams/deciliter) if the serum creatinine level is ≥θ₁₁ and θ₁₁ if the serum creatinine level is <θ₁₁.

TABLE 3.

Parameter estimates for nonmixture and mixture models

Parameter (argument)	Parameter estimate (SE)
	Nonmixturea	Mixture
θ1 (multiplicative constant)	4.82 (0.061)	4.2 (0.089)
θ2 (wt on CL)	0.76 (0.49, 0.99) PL	0.72 (0.098)
θ3 (age)	0.48 (0.12)	0.51 (0.088)
θ6 (long-term ventilator dependency)	0.64 (0.1)	0.62 (0.05)
θ7 (heart failure)	0.86 (0.061)	0.85 (0.066)
θ11 (creatinine)	0.7 (0.088)	0.72 (0.055)
θ12 (wt on V)	0.31 (0.11)	0.29 (0.093)
θ13 (additive constant)	NA	1.59 (0.2)
θ14 (mixing fraction)	NA	0.63 (0.094)
ω2	0.041 (0.014)	0.0084 (0.013)
ς2	0.038 (0.015)	0.032 (0.012)

^aPL, 95% confidence interval constructed by the profile likelihood method; NA, not applicable. 

We model V as follows: V = θ₁₂ · WT, where weight is regarded as time invariant. The serum creatinine level is allowed to vary with time for an individual. Clearance is allowed to vary randomly between patients as follows: CL = TVCL · exp(η), where η is an interindividual random effect of mean 0 and variance ω².

The difference between the jth measured level in the ith patient, C_obsij, and its respective prediction, C_predij, is modeled with an exponential error model as follows: C_obsij = C_predij · exp(ɛ). The random variable ɛ is assumed to be statistically independent of η and to be distributed with mean 0 and variance ς². A fixed effect parameter (θ_i) was considered to be statistically significant (P < 0.05) when its inclusion in the model resulted in a drop in the objective function of 4 or more (based on the change in the NONMEM objective function having an approximate chi-square distribution with 1 degree of freedom when one fixed-effect parameter is added or removed) (1).

Mixture model.

The mixture model, which assumes that the sample is drawn from a population whose clearance is distributed bimodally, uses the same functional form for the typical value of clearance as does the nonmixture model. The two subpopulations differ in that only one of them has an additive clearance component. The typical clearance for one subpopulation is TVCL1, and the typical clearance for the other subpopulation with the additive clearance component is TVCL2; these are expressed as TVCL1 = TVCL and TVCL2 = TVCL + θ₁₃. The proportion of patients belonging to the subpopulation with the additive clearance component (the mixing fraction) is denoted θ₁₄. Clearance is allowed to vary randomly between patients as follows: CL1 = TVCL1 · exp(η₁) and CL2 = TVCL2 · exp(η₂), where CL1 and CL2 are the values of clearance for the two subpopulations, and η₁ and η₂ are interindividual random effects of mean 0 and variance ω². Because of the relatively small sample size, the covariance between η₁ and η₂ was assumed to be zero. For the same reason, the variances of η₁ and η₂ were assumed to be equal. Intraindividual variability was modeled as it was for the nonmixture model. Objective proof of the existence of a mixture model is difficult. In some instances, the chi-square distribution with 2 degrees of freedom can be used when two fixed-effect parameters are simultaneously removed or deleted from a model. This rule cannot be applied here because the two fixed-effect parameters that distinguish the mixture model (θ₁₃ and θ₁₄) cannot be uniquely removed from the model. The default scatterplot of predicted versus observed serum drug concentrations for the mixture model generated by NONMEM is a misleading visual indicator of goodness of fit. Because patients are assigned to their most likely subpopulations, the graphical representation will appear better than it actually is. Therefore, the probability density function of clearance is offered as visual evidence of a mixed population.

RESULTS

A total of 72 patients were enrolled in the study, with a total of 114 serum samples collected. The mean value of ceftizoxime concentration was 25.4 mg/liter. All 72 patients completed the study, with two deaths unrelated to failure of antimicrobial therapy. Table 1 describes the patients studied. A summary of diagnosis of infection, suspected or documented, is as follows: respiratory tract, 45 patients; urinary tract, 11 patients; intraabdominal, 11 patients; skin structure, 2 patients; and septicemia, 3 patients. Severity of illness was assessed with a scale of 0 to 7, with patients receiving a score of 7 being the sickest (10, 12). The mean severity of illness for the current study population was 1.3. Seventeen of the 72 patients participating in the study had a large change in renal function as defined previously in Materials and Methods.

TABLE 1.

Demographics of patients studied

Characteristicb	Mean ± SD	Range
Age	68.6 ± 16.7 yr	21–99 yr
Wt	69.3 ± 18 kg	38–116 kg
Duration	5 ± 3.3 days	1–16 days
CLCRa	59.9 ± 55 ml/min	6–328 ml/min
Ceftizoxime concn	25.4 ± 13.1 mg/liter	8–71 mg/liter

^aCL_CR was estimated by the Cockcroft-Gault method. 

^bThe patients included 29 men and 43 women. 

Table 2 summarizes the dichotomous variables of disease that were recorded for use during analysis (see Materials and Methods for an explanation of the dichotomous variables). Of the variables used in analysis, creatinine, weight, age, heart failure, and ventilator dependency had a significant impact on clearance or volume of distribution (V) estimates. Sex, height, maximum temperature, diabetes, cancer, and intensive care unit status had little or no impact on the estimates of clearance or V.

TABLE 2.

Dichotomous variables of disease

Disease variable	No. of patients in whom disease variable was:
	Present	Not present
Heart failure	31	41
Diabetes	26	46
Cancer	16	56
Residency in:
Intensive care unit	20	52
Ventilator dependent unit	3	69

Treating the sample as if it had been drawn from a single population (nonmixture) resulted in the following relationships for CL and V:

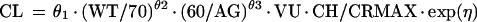2

3

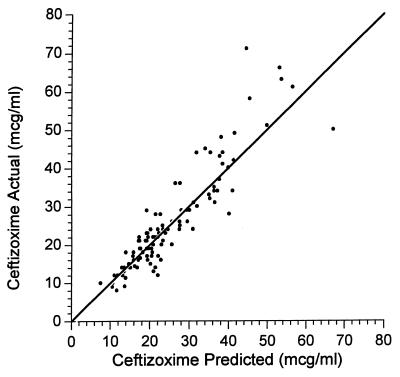
The average value for clearance for the nonmixture model was 2.7 liters per h in the nonventilated, non-congestive-heart-failure patients. A scatterplot representation of the nonmixture model is presented in Fig. 1.

FIG. 1.

Scatterplot of observed versus predicted ceftizoxime concentrations for the nonmixture model. mcg, microgram.

For the mixture model, the following relationships apply:

4

5

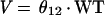6

Due to the ambiguous output of the default scatterplot from NONMEM (see mixture model in pharmacostatistical model), no scatterplot is presented for the mixture model. The average values for clearance for the mixture model were 2.4 and 4.0 liters per h, respectively, for each subpopulation, for nonventilated and non-congestive-heart-failure patients.

Table 3 contains the fixed- and random-effects parameter estimates for both models. With the exception of the additive clearance component and the mixing fraction, the fixed-effects parameter estimates for the two models have numerical values that are quite similar. The presence of congestive heart failure is associated with a decrease in clearance of approximately 15% in both models. Likewise, residence in the ventilator dependency unit is associated with a decrease in clearance of approximately 37%. The CRMAX function indicates that the serum creatinine level should be changed to ≈0.7 mg/dl if it is less than 0.7 mg/dl (θ₁₁) when clearance is estimated. The mixture model approach revealed two subpopulations. Sixty-three percent of the patients were classified as belonging to a subpopulation whose functional form for clearance was very similar to the form used for the nonmixture model. The remaining 37% was distinguished by the presence of an additive clearance component of ≈1.6 liters/h. The estimated V was ≈0.3 liters/kg by a one-compartment model (Table 3).

DISCUSSION

Our initial intent in this study was to explore the population pharmacokinetics of ceftizoxime administered by continuous infusion. We have presented two models that define the clearance of ceftizoxime and express these as equations 2 to 6. Our initial efforts in building a model to describe the kinetics of ceftizoxime were focused on the effects of comorbidities. Upon further exploration, we serendipitously found the mixture model presented here. In previous work (data not shown), we have found mixture modeling to be a powerful tool to identify subpopulations which exist but from which a differentiating variable(s) was omitted during data collection. Mixture modeling has also given us insight into cases of model misspecification (data not shown) and has been utilized by other researchers, notably Ette and Ludden, who showed that cefipime clearance was bimodal (9).

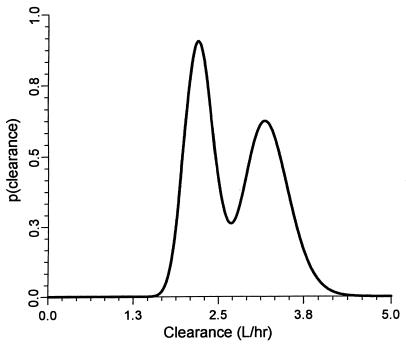
To remove any doubt as to the existence of a mixture model, we plotted a probability density function for clearance (Fig. 2). Figure 2 clearly shows the results for a mixture model of two populations with respect to ceftizoxime clearance from our population. We know that ceftizoxime is eliminated primarily by renal excretion, although we found an additive clearance component for one population of 1.6 liter/h, which we suspect is nonrenal in nature. However, we could not explain the additive clearance component presented, despite further searching and augmentation of the database with the variables tobacco use, race, and liver failure. Tobacco use and race were treated dichotomously, and liver function was rated by the method of Pugh et al. (17). We also tested but could not support the inclusion of an additive clearance component in the nonmixture model. In essence, the discovery of a mixture model is interesting, but the model may be of limited clinical value unless it can identify population to which a patient belongs.

FIG. 2.

Probability density function for ceftizoxime clearance illustrates the presence of two populations for the mixture model.

At the outset, V was not intended to be estimated, due to planned collections of only steady-state concentrations of ceftizoxime. However, as the study progressed, a small number of serum samples were collected under non-steady-state conditions, allowing an estimation of V. The resultant value of 0.3 liter/kg is reasonably close to the steady-state beta-phase estimates of V obtained in other studies (7, 21).

Several dichotomous variables of disease and the time-variant clinical measure serum creatinine (CR_S) were used to build a descriptive model for clearance of ceftizoxime. Of these variables, congestive heart failure and long-term mechanical ventilation have a significant impact. Although the extent of congestive heart failure (n = 31) was not graded, we found a reduced clearance for ceftizoxime of approximately 15% in each model. This finding is most likely due to the impact of congestive heart failure on kidney function (4, 13). Long-term, ventilator-dependent (n = 3) patients presented in this trial show a decrease in clearance of approximately 37%. Statistical significance was reached with ventilator dependency, although the utility of this finding may not have a large clinical application.

Clearance of renally eliminated drugs is often modeled as follows: CL_drug = slope · CL_CR + intercept. While this approach has been widely adopted, it has limitations. A negative intercept could result in a negative drug clearance prediction if the creatinine clearance (CL_CR) is very low. Often the CL_CR value is a measurement of urinary CL_CR, which minimizes the complications of estimating the CL_CR value. An equation arrived at with the urinary CL_CR could present problems in clinical settings, where serum creatinine is more commonly used as an estimator of renal function. Several formulas for CL_CR estimation from serum creatinine are available (3, 14, 18–20). Some of these formulas are optimized for use in obese patients or in patients with low serum creatinine measurements. We chose to avoid estimating CL_CR and instead used the serum creatinine level as a marker of renal function. Our functional form for clearance as expressed in equation 1 allows for flexibility in modeling clearance because weight is treated as a nonlinear function, an approach we have found useful for obese patients.

Our finding that ceftizoxime clearance depends on the patient’s weight and age is in agreement with a previously published report (7) on the relationship between ceftizoxime clearance and measured CL_CR. From the work presented we would like to introduce a maximizer function for the serum creatinine level and its impact on ceftizoxime clearance. We found a maximizer function to be a useful tool for measuring low serum creatinine levels. The idea of adjusting creatinine values to a fixed value if they fall below it in estimations of CL_CR is controversial (2, 20). The referenced cutoff value for serum creatinine levels is 1 mg/dl (2, 23). Values below this cutoff would be changed to 1 mg/dl in evaluations of CL_CR with the Cockcroft-Gault formula. This concept is intuitively appealing, because with certain disease states (i.e., muscle wasting and extensive liver disease), low serum creatinine values can result in erroneously high estimates of CL_CR if no adjustment is made to the serum creatinine. When ceftizoxime clearance was estimated, serum creatinine values below 0.7 mg/dl were changed to 0.7 mg/dl in evaluations of equations 2, 4, and 5. This adjustment resulted in decreases of 14 and 12 points in the NONMEM objective function for the nonmixture and mixture models, respectively. Using this derived maximizer value for serum creatinine in the calculation of ceftizoxime clearance reduces clearance overestimation error from a low serum creatinine value. We have found this maximizer function approach to be useful for estimating both ceftazidime (9a) and aminoglycoside (data not shown) clearance.

In the clinical trial presented here, a kinetic model for estimation of drug clearance has been developed. The method of administration was continuous infusion. A major clinical question is which multiple of the MIC optimizes the patient’s outcome. Optimal ratios of the concentration at steady state (C_SS) to MIC of 2 to 6.6 have been suggested previously (6, 15). The optimal C_SS/MIC ratio for continuous infusion is likely a function of the infecting pathogen’s tolerance and/or ability to adapt, site(s) of infections, concurrent antibiotic therapy, and immune status and/or severity of the patient’s illness.

In summary, we have developed a model to estimate ceftizoxime clearance, using commonly available clinical information. As we proceed with the validation of our model, we cautiously aim for C_SS/MIC ratios of 3 to 4. Ultimately necessary are randomized-outcome trials and pharmacoeconomic trials comparing the intermittent and continuous modes of beta-lactam dosing.