Abstract
The pathological mechanism of attention deficit hyperactivity disorder (ADHD) is incompletely specified, which leads to difficulty in precise diagnosis. Functional magnetic resonance imaging (fMRI) has emerged as a common neuroimaging technique for studying the brain functional connectome. Most existing methods that have either ignored or simply utilized graph structure, do not fully leverage the potentially important topological information which may be useful in characterizing brain disorders. There is a crucial need for designing nove and efficient approaches which can capture such information. To this end, we propose a new dynamic graph convolutional network (dGCN), which is trained with sparse brain regional connections from dynamically calculated graph features. We also develop a novel convolutional readout layer to improve graph representation. Our extensive experimental analysis demonstrates significantly improved performance of dGCN for ADHD diagnosis compared with existing machine learning and deep learning methods. Visualizations of the salient regions of interest (ROIs) and connectivity based on informative features learned by our model show that the identified functional abnormalities mainly involve brain regions in temporal pole, gyrus rectus, and cerebellar gyri from temporal lobe, frontal lobe, and cerebellum, respectively. A positive correlation was further observed between the identified connectomic abnormalities and ADHD symptom severity. The proposed dGCN model shows great promise in providing a functional network-based precision diagnosis of ADHD and is also broadly applicable to brain connectome-based study of mental disorders.
Keywords: Graph convolutional networks, Resting-state fMRI, Brain networks, Precision diagnosis, Attention deficit hyperactivity disorder
1. Introduction
Attention deficit hyperactivity disorder (ADHD) is a common neurodevelopmental disorder characterized by hyperactivity, inattention, and impulsivity. Over five million children in the US are diagnosed with ADHD per year, and 15–65% of them continue to live with the symptoms of ADHD into adulthood (Katzman et al., 2017; Danielson et al., 2018). ADHD impacts self-esteem, interpersonal relationships, and self-regulation (Katzman et al., 2017; Danielson et al., 2018). Despite plentiful research, the pathology and etiology of ADHD are still underexplored. In clinical practice, ADHD patients are diagnosed by assessing their behavior based on well-established guidelines, such as the ADHD clinical practice guideline published by the American Academy of Pediatrics (Wolraich et al., 2019). However, increased literature demonstrated that existing clinical diagnostic categories based on traditional diagnosis methods hinder the discovery of biomarkers in psychiatry (Singh and Rose 2009; Insel and Cuthbert, 2015), because of the neurological and behavioral heterogeneity presented across closely related psychiatric disorders (Hawco et al., 2019). Furthermore, the overlapping symptomology and pathology between ADHD and other mental disorders further complicate precise diagnosis. For example, emotional dysregulation is a common attribute of adult ADHD psychopathology, post-traumatic stress disorder and major depression (Fonzo et al., 2019; Hoogman et al., 2019; Zhu et al., 2020). In addition, some brain regions of high hubness (with more connection to other nodes) are shared between ADHD and autism brain networks (Lake et al., 2019). Due to this, the search for more objective biomarkers is imperative for ADHD diagnosis (Faraone et al., 2014).
Since magnetic resonance imaging (MRI) provides a non-invasive approach with high spatial resolution, it has been widely adopted for neuro-clinical applications (Li et al., 2009). Two main categories of MRI include structural MRI and functional MRI (fMRI). Structural MRI captures morphological changes of brain tissue while fMRI reflects temporal changes related to blood oxygenation and provides insight into the properties of circuit organization (Yeo et al., 2011). Over the past decade, increasing efforts (Vissers et al., 2012; Chen et al., 2015; Fonzo et al., 2019; Khosla et al., 2019; Yan et al., 2019; Chin Fatt et al., 2020) have been dedicated to studying various brain disorders through the functional changes observed by fMRI.
To promote the study of ADHD neuropsychopathology, the ADHD-200 global competition (Consortium, 2012) began in 2011. This competition provided researchers with rich resting-state fMRI (rs-fMRI) data to develop powerful computational tools for neuroimaging-based ADHD-related exploration. In recent years, with advancements in deep learning and artificial intelligence techniques, researchers have deployed various artificial neural network models including multi-layer perceptron (MLP) (Taud and Mas, 2018) and convolutional neural network (CNN) (Simard et al., 2003) to explore informative biomarkers with fMRI data from ADHD-200 database. Mounting evidence has shown that deep learning models outperform traditional machine learning methods for neuroimaging biomarker analysis with increased predictive power albeit with limited interpretability (Abrol et al., 2021). For example, a 3D CNN framework trained on low-level features, such as voxel-mirrored homotopic connectivity extracted from fMRI data and gray matter volume, outperformed several machine learning models with higher accuracy (Zou et al., 2017). Further, a multi-channel MLP was developed to detect ADHD by utilizing functional connectivity features extracted with multiple brain atlases (Chen et al., 2019). This study suggested that the fusion of functional connectome extracted from multi-scale brain parcellations improved ADHD diagnosis precision when compared to a single parcellation.
Though training performance has been promising, existing deep learning methods have encountered challenges in brain connectome analysis. For instance, CNN has been most widely applied to image feature learning since the local neighborhood structures in typical images are defined clearly for convolution and pooling operations in Euclidean space. However, it is hard to effectively extract representative features from brain network graphs due to the irregular Euclidean structures of the graphs (Niepert et al., 2016). Despite this, probing brain network topology may highlight the principles underlying its organizational properties, such as the message transfer pathway through long-range axonal connection from anatomically unconnected nodes (Park and Friston, 2013). Based on the convolution theorem, which states convolution in the graph spatial domain equals the inverse Fourier transform of the multiplication in the graph spectral domain (Zhang et al., 2019), researchers developed a spectral graph convolutional network (GCN) to identify irregular graph information in the spectral domain (Defferrard et al., 2016; Parisot et al., 2017; Levie et al., 2019). Later, the graph convolution operator, which was defined directly in the spatial domain to represent a graph by aggregating neighboring vertex features (Gilmer et al., 2017; Hamilton et al., 2017; Yan et al., 2018; Zhu et al., 2020), became mainstream because of decreased computational complexity.
Recently, there has been increasing interest in building graph neural network models for studying the brain connectome (Bessadok et al., 2021; Isallari and Rekik 2021). Viewing each subject as a node, spectral GCN models have been successfully applied to diagnose Alzheimer’s disease and autism spectrum disorder (Parisot et al., 2017 2018). The researchers explored the influence of different graph modeling strategies on classification performance and reported that different graph edge constructions from various personal phenotypic information significantly affected model performance. Furthermore, integrating both temporal and spatial correlations of rs-fMRI regional time-series signals into a brain-graph adjacency matrix, a spatio-temporal GCN was proposed to predict gender and age, outperforming other approaches such as MLP (Gadgil et al., 2020). Also, the pairwise-learning strategy (Zhang et al., 2018b) has been introduced to train memory-based GCN and has been applied to Parkinson’s disease diagnosis. By utilizing pairs of diffusion MRI-based structural connectivity matrices as input, this learning strategy effectively enlarged the sample size to alleviate model overfitting and enhance diagnosis accuracy.
Despite the promising progress, existing GCN models are limited, as graph edges are fixed during the training process, which is less efficient in capturing the underlying graph representation (Simonovsky and Komodakis 2017; Valsesia et al., 2018; Wang et al., 2019). Additionally, these methods only capture 1-hop neighbor node information in graph convolutional operators, however, recent studies have shown that multi-hop connectivity represents important topological and geometrical properties of the brain connectivity network (Seguin et al., 2018; Wu et al., 2020). To address those limitations, we propose a novel dynamic graph convolutional neural network (dGCN) architecture by exploiting dynamic graph convolution with changing graph structure to characterize the brain functional connectome. Our extensive experimental analysis confirms that the dGCN model outperformed existing methods, demonstrating its efficacy in quantifying brain dysfunctions associated with ADHD. The major contributions of our study are summarized as follows:
We propose a novel approach for incorporating dynamic graph computation and 2-hop neighbor nodes feature aggregation into graph convolution for brain network modeling.
A convolutional pooling strategy is developed to readout the graph, which jointly integrates graph convolutional and readout functions.
With extensive interpretation analyses, our developed model is confirmed to reveal new insights into connectome dysfunctions in ADHD.
2. Methods
2.1. Data acquisition and preprocessing
The rs-fMRI data of the ADHD-200 database were used for our study. This dataset was collected from eight sites including New York University Medical Center (NYU), Peking University (PK), Kennedy Krieger Institute (KKI), NeuroIMAGE Sample, Bradley Hospital/Brown University, Oregon Health & Science University, University of Pittsburgh (UP), and Washington University in St. Louis. In our study, we utilized fMRI data collected from 635 subjects who have complete personal characteristic data (PCD) collected from NYU, PK, KKI, and UP. Participants from the remaining four sites were excluded from our analysis due to incomplete PCD information.
The raw rs-fMRI data were preprocessed using the Athena toolbox (Bellec et al., 2017). The preprocessing steps included (1) removal of the first four echo-planar imaging volumes; (2) slice timing correction; (3) reorientation into right/posterior/inferior orientation; (4) motion correction by realigning echo-planar imaging volumes to the first volume; (5) brain extraction; (6) calculation of mean functional image and co-register of the mean image with the corresponding structural MRI; (7) transforming fMRI data and mean image into 4 × 4 × 4 mm 3 MNI space; (8) estimation of white matter (WM), cerebrospinal fluid (CSF) time signals from down-sampled WM and CSF masks; (9) regressing out WM, CSF, and six motion parameters time series; (10) applying a band-pass filter to exclude frequencies and blurring the data with a 6 mm FWHM Gaussian filter. Although preprocessing has regressed out WM, CSF, and motion time series, brain network modeling may still be affected by head motion confounder that was not fully removed in the preprocessing step. To further mitigate the head motion effects, we applied isolation forest (Liu et al., 2008) to automatically detect outliers and exclude them from the further analysis. As a result, a total number of 603 subjects (including 260 ADHD and 343 healthy controls (HC)) were available for the experimental analysis.
2.2. Proposed approach
All of the variables and notations used in our study are summarized in Table 1.
Table 1.
Summary of notations used in this study.
| Notation | Definition |
|---|---|
| Graph | |
| Vertices set of one graph | |
| Adjacency matrix of one graph | |
| Set of edges linked to node | |
| Set of edges from the top- nearest nodes to node | |
| Edge between node and node | |
| Node features at f convolutional layer after aggregation | |
| Node features at f convolutional layer after update | |
| Weights filter in aggregation operator | |
| Set of all adjacent nodes to node | |
| All node features at layer | |
| Representative features after readout operator at layer | |
| Concatenation operator |
2.2.1. Construction of graphs
In general, graph construction with functional time series can be performed in two different ways, i.e., node-level graph construction and subject-level graph construction. For the node-level graph construction, each subject is treated as a node and the integration of the brain functional connectome and PCD information from each subject is vectorized as node features of the subject. The distances of the nodes’ features are calculated from various similarity measurement methods as the adjacency matrix of this graph (Parisot et al., 2017; Parisot et al., 2018; Kazi et al., 2019; Cao et al., 2021). Eventually, a graph is deployed on a node-level classification, such that the nodes with the same class label cluster closely in one community. Despite its promising performance, this graph construction strategy has a limitation in revealing the topological structure of brain functional connectome since each node (subject) of the graph consists of vectorized connectome features. In addition, the classification model built in this way needs to be re-trained with the entire data for testing a new subject by adding the subject as a new node into the graph (Parisot et al., 2017), which is less flexible for generalizing to unseen subjects.
An alternative strategy is to construct a subject-level graph as an undirected brain network graph as , where is the edge set with denoting the pairwise Pearson’s correlation or other similarity measurements between ROI and , and is a set of nodes contains various node features (Zhang et al., 2018c; Yang et al., 2019; Li and Duncan, 2020). For example, the node features can be gray matter volume, surface area (Yang et al., 2019), or an ROI time series (Gadgil et al., 2020) while each edge typically represents the functional correlation between two nodes (e.g., the time series of two ROIs). In this study, following graph construction in the work (Li and Duncan, 2020), we adopt the subject-level strategy to construct brain network graphs since it provides an elegant way to capture the connectomic topology and uncover more interpretable brain dysfunction patterns. Specifically, we calculate Pearson’s correlation matrix of ROI time series as edge features to form an adjacency matrix and partial correlation coefficients of time series between one ROI and all other ROIs as node features.
2.2.2. Graph convolutional network
GCN aims to learn representative features of each node in a graph by aggregating the features of its neighboring vertices (Xu et al., 2018). For spatial or spectral GCN, a typical convolutional layer contains two operations: aggregation and update (Zhou et al., 2020). The layer aggregating process is defined as follows:
| (1) |
where is the feature vector of node at the layer, denotes the set of adjacent nodes to the center node, and denotes a set of edges linked to node . The aggregation operator compiles the permutation invariant from the neighborhood nodes’ features to aggregated features, while the update operator computes new node features from the aggregated features by a non-linear transformation (Xu et al., 2018; Li et al., 2019). There are many variants of these two operators. For example, the aggregation functions can include a mean-pooling or a max-pooling aggregator, an attention aggregator, and a variety of other aggregators, while the update function can be an MLP, a gated network, or a convolutional layer (Li et al., 2019). Nevertheless, the receptive field in the traditional GCN layer, such as the graph attention network (GAT) (Veli čkovi ć et al., 2017; Yang et al., 2019), is restricted to 1-hop neighborhoods, which limits their ability to explore more complex functional interactions from broader node features (Wu et al., 2020; Xue et al., 2020).
2.2.3. Graph convolution layer (Normconv)
Two-hop (adjacent neighbors of 1-hop nodes) or multi-hop approaches have also been reported to present an influence in the center ROI by information transfer to 1-hop regions (Seguin et al., 2018; Wu et al., 2020). Traditionally, to obtain 2-hop or multi-hop information, one can use stacked deep GCN layers (Hamilton et al., 2017; Zhang et al., 2018). However, over-smoothing is observed in deep layers and occurs when the weights are convergent in a stationary point where nodes’ representations are unrelated to the input features and result in vanishing gradients (Rong et al., 2019). Thus, instead of building up deeper layers as implemented in literature (Rong et al., 2019), our proposed model aggregates the 1-hop and 2-hop neighbor information in each convolutional layer. The normal graph convolution operation (Normconv) is formulated as:
| (2) |
where contains the weights of neurons in MLP, ‖ denotes the concatenation operator. In particular, MLP is used as an update function, and mean pooling is used as an aggregation function. encodes the 1-hop neighborhood information for each node and encodes the 2-hop neighborhood information by subtracting the 1-hop nodes information from all adjacent information of 1-hop neighboring nodes. By concatenation of these two operators, our GCN layer aggregates and updates 1-hop and 2-hop information simultaneously, which explains how the Normconv component works in our model.
2.2.4. Dynamic edge convolution layer (Edgeconv)
Several recent studies on point cloud segmentation, classification, and generation have shown that dynamic graph convolution on changing graph structure in the training process can capture graph representations more effectively compared to GCNs with a fixed graph structure (Simonovsky and Komodakis, 2017; Valsesia et al., 2018; Wang et al., 2019). The underlying mechanism is that proximity, which is dynamically calculated based on the top- Euclidean distance of nodal features in feature space, captures richer nonlocal information diffusion than the proximity from a fixed input space (Wang et al., 2019). Specifically, this step can be formulated as follow:
| (3) |
where contains a set of edges from the top- nearest nodes to node and denotes a vector of node features. Each node was aggregated and updated using the features of its top- nearest nodes according to the formula (1) and (2). Here, we assume that keeping the top- nearest neighboring node proximity in the adjacency matrix can capture more homogenous brain ROI information features with high sparsity. Another motivation is that the sparsity correlates with the fact that a brain region predominantly interacts with a small number of other regions (Wee et al., 2012; Cassidy et al., 2015). In the Edgeconv component, we calculate the Euclidean distance of node features for every pair of nodes and then retain the closest pairwise nodes as the adjacency matrix coefficients in this layer (Wang et al., 2019). Then the aggregation and update operators are the same defined in the formula (2) of the Normconv layer. Similar to dropout (Srivastava et al., 2014), the dynamic adjacency matrix helps in improving the model generalizability with higher sparseness in the solution space by introducing sparsity in the forward propagation step.
2.2.5. Convolutional readout
Unlike in node classification, where the node representation at the final layer is used for prediction directly, our readout layer generates a subject-level representation from the high dimensional connectome representation followed by the final classification layer. Essentially, the concatenation of max and sum operators over all nodes constitutes a typical readout layer, defined as follow:
| (4) |
is the representative features of all nodes from the convolutional layer. Additionally, we propose a special Edgeconv layer, named ConvReadout, which performs the readout function in a convolution layer by compressing features of each node into one dimension. This readout method is a complement to the typical readout function. As shown in Fig. 1A, the typical readout operator generates one node’s representative features from all the nodes’ features to represent graph information. Our ConvReadout pooling compresses high-dimensional features into a one-dimensional feature for each node by convolution and then represents a graph with one-dimensional features of all nodes, as shown in Fig. 1B. The basic intuition is that the matrix of node features has a node dimension and a feature dimension. The typical readout operator represents a graph in the feature dimension and the convolutional readout operator represents a graph in the node dimension. Extracting information jointly from different dimensions of the same feature extraction may benefit improving classification accuracy. Furthermore, concatenating or adding our readout output with traditional global readout output alleviates the information loss caused by using the traditional global readout operator to compress information from one dimension only. For instance, a CNN-based prediction model embedded with a fused attention module by exploiting both channel and spatial dimensions outperformed one embedded with a one-dimensional attention module (Woo et al., 2018).
Fig. 1.
A comparison between the traditional readout and the convolutional readout. Panel A shows how a typical readout layer works and panel B shows how a convolutional readout works. The number of nodes is denoted by n. Both m and denote the dimension of node features in each layer separately. In our model, n equals m and equals l.
2.2.6. Implementation details
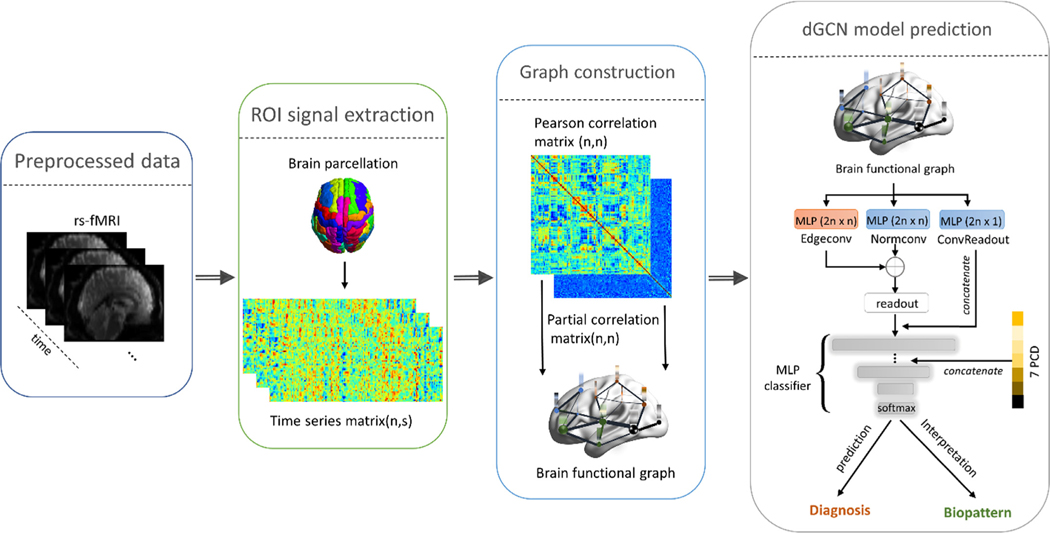
The architecture of our overall workflow is illustrated in Fig. 2. The whole-brain regional time-series signals are extracted from the preprocessed fMRI data, using the anatomical automated labeling (AAL) atlas. In the brain network graph, Pearson’s correlation matrix of regional time series was calculated to form an adjacency matrix and partial correlation coefficients of time series between one ROI and all other ROIs were calculated as node features. The dGCN model was trained to distinguish ADHD patients from HC and identify discriminative and interpretable connectomic biomarkers for better understanding the ADHD-associated brain dysfunctions.
Fig. 2.
A workflow for ADHD diagnosis using our developed dGCN model. The overview of the proposed model is explained in the dGCN model prediction panel. The dimension of node and nodal feature are the same and denoted as n because we use ROI functional partial correlation matrix as nodal features. PCD variables include seven features: age, gender, handedness, IQ measurement, and three Wechsler Intelligence Scale evaluation IQ variables.
The implementation detail of the dGCN model is shown in the right panel of Fig. 2. The combination of Edgeconv layer and Normconv layer was added as a parallel layer, and the nodes’ features learned from the stacked layer ran through a typical readout layer to derive a representative feature vector of the graph. Meanwhile, ConvReadout represented the graph information by aggregating 1-dimensional features in each node. These features were then concatenated with the typical readout features as input for the MLP classifier. Seven PCD features including age, gender, handedness, IQ measurement, and three Wechsler Intelligence Scale evaluation IQ variables were embedded into the second MLP layer after L-2 normalization.
The learning rate in the Adam optimizer was set to 0.01. The batch size was set to 140. The node number and node feature dimension in Fig. 2 were both equal to 116 (#ROIs). In the MLP classifier, dropout (with 0.5 dropout ratio) and batch normalization were used to improve the model generalizability. Furthermore, dropedge with a ratio of 0.3 was used to avoid overfitting in each GCN unit (Rong et al., 2019). We kept the top 32 pairwise distances to construct the adjacency matrix in a dynamic graph convolutional aggregation function. Since the HC group had a larger sample size compared with the ADHD group, the focal loss (Lin et al., 2017): , where , , was introduced to mitigate the imbalanced data. For brain graph construction, the top 20% of Pearson’s correlation coefficients were kept as adjacency matrices to improve the training efficiency as well as to avoid over-smoothing from densely connected graphs (Li and Duncan, 2020). Using the PyTorch package, the models were trained with NVIDIA RTX 2080Ti.
3. Results
3.1. Experimental comparison
To confirm the efficacy of the proposed GCN method, we compared it with other competing approaches, including SVM, logistic regression (LR), MLP, GCN (Kipf and Welling 2016), and GAT (Veli čkovi ć et al., 2017). All models were trained with the same combination of brain functional connectivity features and PCD information. For SVM and LR, recursive feature elimination was adopted to reduce the feature dimensionality and improve model generalizability. The same structure and hyperparameter settings as described in the literature (Chen et al., 2019) were applied to train MLP in our study. Moreover, as common 1-hop deep graph neural networks, GCN (Kipf and Welling 2016; Jiang et al., 2020) and GAT were also included in our model comparison. The same hyperparameter settings in dGCN were used for training GCN and GAT. The 10-fold cross-validation was performed to evaluate the classification performance. Since the fMRI data were collected from four different sites, stratified sampling was used to partition data into 10 folds by the collection site. The metrics used to evaluate model performance were accuracy (ACC), specificity (SPE), sensitivity (SEN), and area under the curve (AUC) of receiver operating characteristic (ROC). The ACC, SPE, and SEN were calculated as follows:
where TP, TN, FP, and FN denote true positive, true negative, false positive, and false negative, respectively.
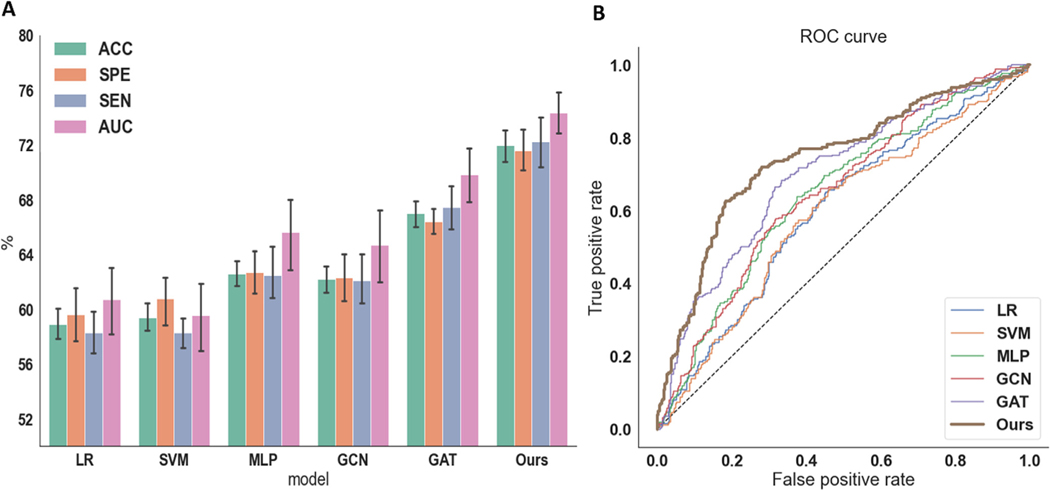
Fig. 3A summarizes the results of ADHD diagnosis for all the compared methods. The ROC curves of each method are depicted in Fig. 3B. The overall results show that deep neural network-based models surpass the traditional machine learning methods. Importantly, our proposed dGCN yields the best results for all the performance metrics (72.0% accuracy, 71.6% specificity, and 72.2% sensitivity).
Fig. 3.
The comparison of accuracy, specificity, sensitivity, and AUC among different methods, including LR, SVM, MLP, GCN, GAT, and our proposed dGCN model. (A) Classification evaluation. (B) ROC curve.
To further assess the generalizability of the dGCN model to unseen data collected from different study sites, a leave-study-site-out analysis was conducted by iteratively using the data from three study sites to train the model, and the data from the left-out site for testing the model (Table 2). The model performance of performing leave-study-site-out is comparable to that of using cross-validation across all sites. The results demonstrated the robustness of our model for unseen data from different study sites.
Table 2.
Classification performance (%) of leave-study-site-out cross-validation.
| Site removed | Accuracy (mean ± std) | Specificity (mean ± std) | Sensitivity (mean ± std) |
|---|---|---|---|
| PK | 72.0 ± 3.1 | 77.7 ± 3.7 | 67.5 ± 2.1 |
| UP | 67.9 ± 2.7 | 73.5 ± 6.3 | 63.3 ± 3.0 |
| NYU | 74.3 ± 3.2 | 70.8 ± 5.0 | 76.2 ± 3.5 |
| KKI | 69.1 ± 2.2 | 65.3 ± 4.2 | 72.4 ± 3.3 |
3.2. Ablation study
We conducted an ablation study to investigate the effect of each GCN block in dGCN on the model performance. As shown in Table 3, each block contributes to enhancing the diagnostic capability of our model. Accuracy drops 2.8% without using the Edgeconv layer while Normconv and ConvReadout account for more than 5% accuracy improvement. Ablation of each GCN block also increases the standard deviation of classification accuracy in cross-validation, which indicates their influence in improving the model stability. We further implemented an ablation study of PCD embedding (see Table 4). The results show that incorporating PCD and functional connectivity features into dGCN effectively increases model accuracy and stability. Results about the effects of 1-hop and 2-hop encoding on model performance were also included in Table 4. Removing either 1-hop or 2-hop encoding from the model decreased its performance, with 1-hop neighboring node information proving to be more critical for better performance. However, keeping only one type of encoding would enlarge the instability of our model.
Table 3.
Ablation study of our dGCN model. The effect of removing each of the dGCN components on the model performance (%) was examined. Here, Accuracy, Specificity, and Sensitivity denote the difference in average accuracy, specificity, and sensitivity between the full dGCN model and other ablation models, respectively. The number of nodes and the dimension of node features are the same and denoted by n.
| Model | Accuracy (mean ± std) | Accuracy (mean) | Specificity (mean ± std) | Specificity (mean) | Sensitivity (mean ± std) | Sensitivity (mean) |
|---|---|---|---|---|---|---|
| dGCN (Full) | 72.0 ± 1.8 | - | 71.6 ± 2.4 | - | 72.2 ± 2.9 | - |
| dGCN without Edgeconv (2n × n) | 69.2 ± 3.9 | 2.8 | 70.0 ± 5.8 | 1.6 | 71.8 ± 7.3 | 0.4 |
| dGCN without Normconv (2n × n) | 66.5 ± 3.2 | 5.5 | 64.3 ± 3.2 | 7.3 | 68.2 ± 5.3 | 4.0 |
| dGCN without ConvReadout (2n × 1) | 67.0 ± 1.9 | 5.0 | 66.1 ± 4.2 | 5.5 | 67.6 ± 2.2 | 4.6 |
Table 4.
Ablation study of PCD embedding and neighboring node effects on dGCN model performance (%). Here, Accuracy, Specificity, Sensitivity denote the difference in average accuracy, specificity, and sensitivity between the full dGCN model and different configurations of the reduced dGCN model.
| Model | Accuracy (mean ± std) | Accuracy (mean) | Specificity (mean ± std) | Specificity (mean) | Sensitivity (mean ± std) | Sensitivity (mean) |
|---|---|---|---|---|---|---|
| dGCN (Full) | 72.0 ± 1.8 | – | 71.6 ± 2.4 | – | 72.2 ± 2.9 | – |
| dGCN (without PCD) | 69.6 ± 2.5 | 2.4 | 67.6 ± 2.7 | 4.0 | 71.1 ± 3.4 | 1.1 |
| dGCN (without FC) | 53.3 ± 3.2 | 29 | 59.6 ± 7.9 | 11.0 | 56.2 ± 6.5 | 16.0 |
| dGCN (without 2-hop encoding) | 67.0 ± 3.9 | 5.0 | 67.8 ± 6.6 | 3.8 | 66.3 ± 5.9 | 5.9 |
| dGCN (without 1-hop encoding) | 62.7 ± 1.9 | 9.3 | 76.8 ± 5.0 | − 5.2 | 51.9 ± 1.7 | 20.3 |
3.3. Interpretation of ADHD diagnostic biomarkers
3.3.1. Most discriminative brain regions and connections
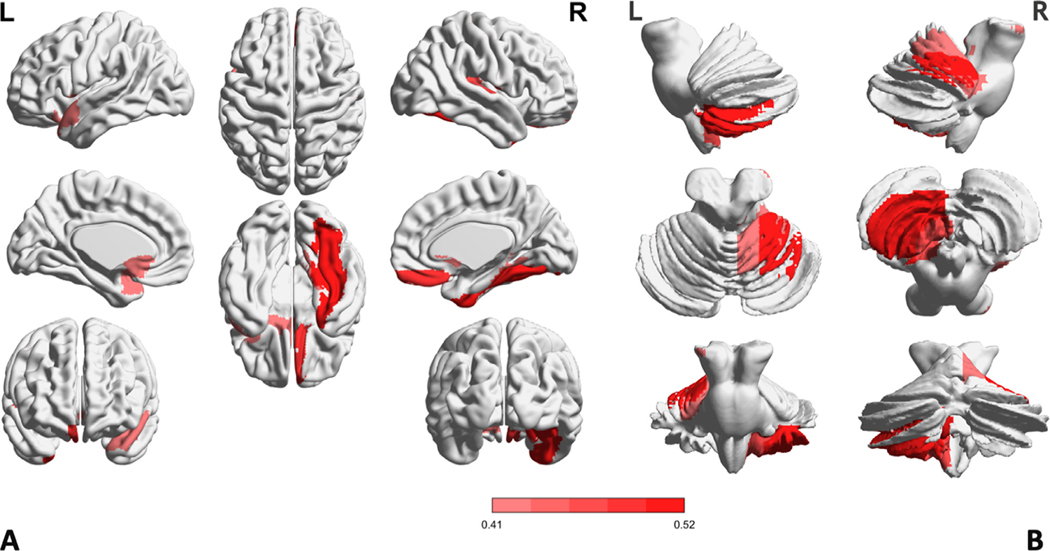
To better understand which brain regions and connections contribute most to the ADHD diagnosis, we investigated the model weights learned from the Edgeconv and Normconv modules, which are important in driving discriminative features. After averaging the weight matrices obtained by these two modules over cross-validation, we further summed the weight matrix along the feature dimension to derive regional weights for visualization of the most discriminative brain regions. As shown in Fig. 4, the 10 ROIs with the largest weights are mainly located in the frontal lobe, occipital lobe, subcortical lobe, temporal lobe, and posterior-fossa (known as the cerebellum in other literature Jiang et al., 2020).
Fig. 4.
Visualization of the top 10 discriminative brain regions. The salient map on the cerebral cortex and subcortex is in panel A, and the salient map on Posterior-Fossa is in panel B.
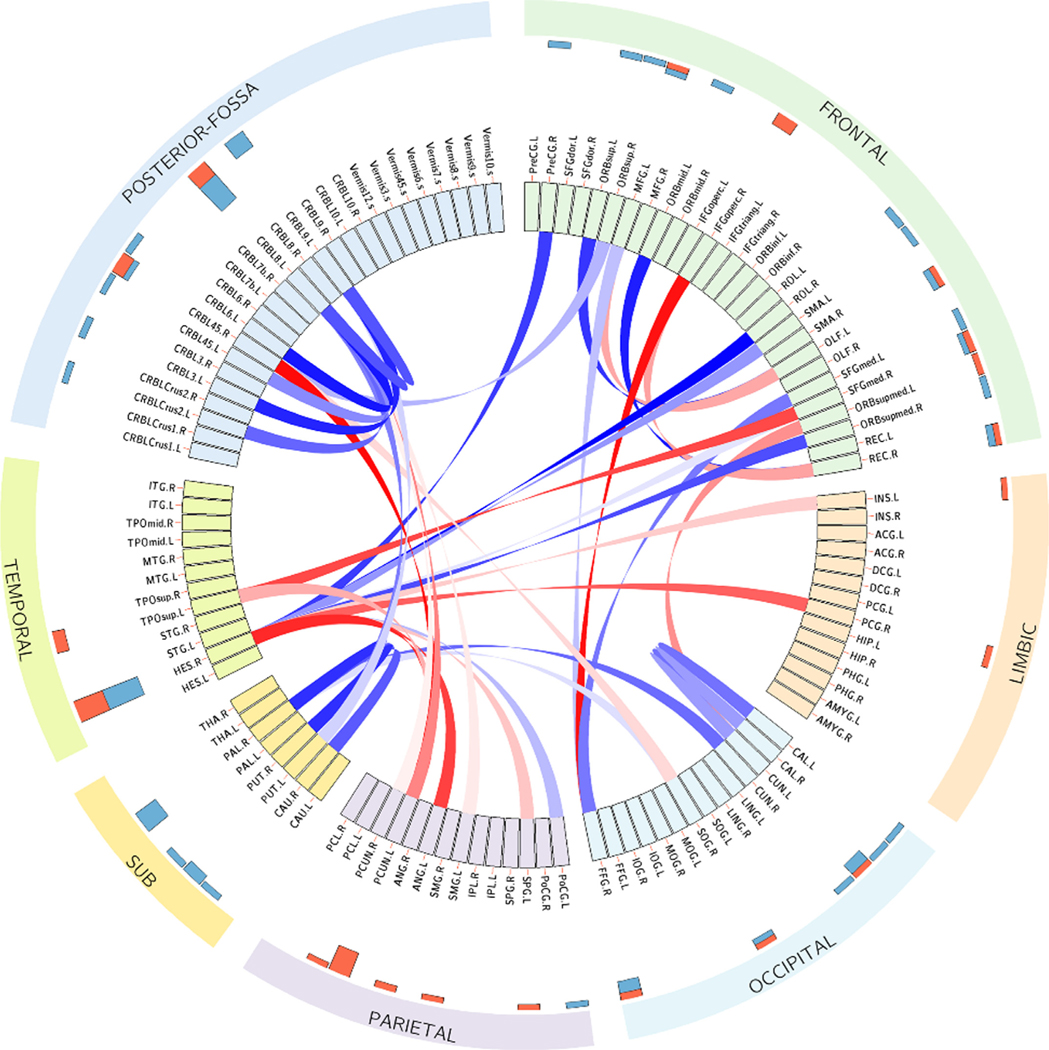
Two-sample t-tests were further applied to investigate the differences in connections corresponding to the top 10 key ROIs between ADHD and HC. Fig. 5 shows the top 40 connections with the most significant differences. The red connections indicate hypo-connectivity (i.e., ADHD < HC), whereas the blue ones are hyper-connectivity (i.e., ADHD > HC). The hyper-connections mainly exist within intra-connections in the frontal lobe, occipital lobe, subcortical lobe, posterior-fossa, and inter-connections in the frontal and temporal lobe, while the hypo-connections are mainly between the frontal, parietal, and temporal lobes. The largest hypo-connectivity occurred in the connection between PCUN. L (Precuneus left) and CRBL45. R (Cerebellum 45 right) ROIs and the largest hyper-connectivity occurred in the connection between ROL.R (Rolandic operculum right)-HES.R (Heschl gyrus right) ROIs.
Fig. 5.
The most discriminative connections were evaluated by two-sample t-tests with false discovery rate (FDR) corrected p-value < 0.05. The hypo and hyper connections are shown in red and blue colors, respectively. The histogram bars at the outer circle show the nodal strengths of values for all ROIs.
3.3.2. Prediction ability of connectomic abnormalities for ADHD symptoms
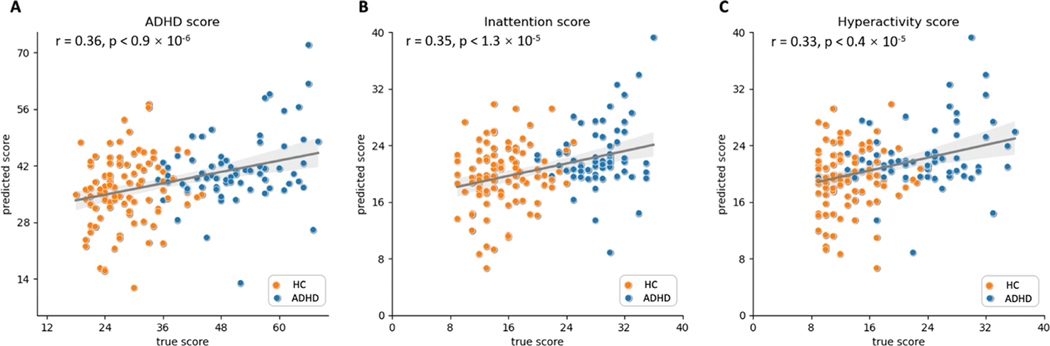
In the ADHD-200 database, the 172 participants recruited at Peking University were assessed with the ADHD Rating Scale IV (ADHD-RS) to measure their symptom severity related to ADHD (Barkley 2011). The ADHD-RS is measured based on 18 questions, half of which are related to inattention, such as how difficult it is for the children to attend tasks or play activities. The remaining nine questions are related to symptoms of hyperactivity and impulsivity. The inattention score is evaluated from the first nine questions, the hyperactivity score is evaluated from the remaining nine questions, and the ADHD score is calculated as a summary of all the questions. A higher score correlates to more severe symptoms. To better understand psychopathology, we further investigated the relationship between the identified connectomic abnormalities and ADHD symptom severity. Nodal strength was calculated by averaging the absolute values of all connectomic features for each of the top 20% discriminative ROIs. A linear regression model was trained with these nodal strength features for predicting ADHD-related symptom severity, with prediction performance evaluated using 10-fold cross-validation. As shown in Fig. 6, we obtained a significant correlation between the symptom severity predicted by the regression model and the observed symptom severity (ADHD score: , Inattention score: , Hyperactivity score: ).
Fig. 6.
Prediction of the three ADHD-RS sub-scale scores based on the average of ROI features corresponding to the 20% largest weights driven by Normconv and Edgeconv modules. (A) ADHD score, (B) inattention score, and (C) hyperactivity score.
3.3.3. Correlation between brain dysfunctions and ADHD score
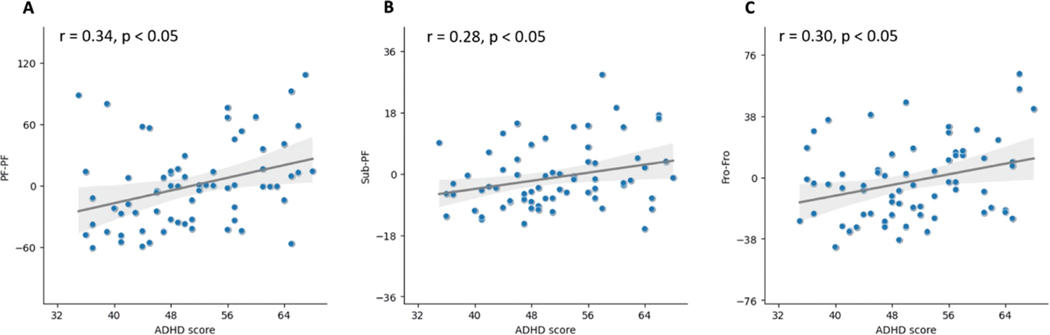
In Fig. 5, we have identified the most significant hyper-connections involving the frontal lobe, occipital lobe, subcortical lobe, and posterior-fossa. To better understand the relationship between the lobe-level abnormalities and ADHD symptom severity, we calculated lobe-to-lobe functional connectivity between all brain lobe pairs and investigated their correlation with the ADHD-RS ADHD subscale score in the ADHD group. As shown in Fig. 7, we observed significant positive correlations between ADHD subscale score and within-PF connectivity (r = 0.34, p < 0.05), within-Fro connectivity (r = 0.30, p < 0.05), and Sub-PF connectivity (r = 0.28, p < 0.05).
Fig. 7.
Correlation between brain lobes connectomic strength and ADHD subscale score. Here, p values are FDR corrected. Fro denotes frontal lobe, Sub is subcortical lobe, and PF is posterior fossa. (A) relationship of functional connectivity within posterior fossa to ADHD score, (B) relationship of functional connectivity between subcortical lobe and posterior fossa to ADHD score, and (C) relationship of functional connectivity within frontal lobe to ADHD score.
4. Discussion
4.1. Advantages of dGCN in brain network analysis
Compared with CNN and other neural network models, GCN has shown great promise in brain functional network analysis due to its superior ability to utilize nodes’ interaction in a topological space (Filip et al., 2020; Zhang and Bellec 2020). The convolution operator of GCN can be designed in either the spatial or spectral domain and the equivalence between the two domains for GCN implementation was theoretically proven (Zhang et al., 2019; Balcilar et al., 2020; Wu et al., 2020b). Recently, GCNs have been increasingly designed in spatial domain (Xu et al., 2018; Chiang et al., 2019) since spatial GCNs are based on a more relaxed version of the graph convolution without the need of computationally expensive eigenvalue decomposition. Our dGCN model was also implemented in spatial domain, which therefore inherited this advantage.
Typically, existing GCN models are trained with a fixed graph and 1-hop neighborhood information for each graph convolutional layer, including the only study so far that adopted a GCN-based classification model (called triplet GCN) for brain network-based ADHD diagnosis (Yao et al., 2019). Training with triplet GCN is time-consuming, and the trained networks are unstable because of the need for a complex sample selection strategy and carefully designed data-pair (triplets) for superior performance. Also, these models either encounter difficulties in convergence or fail to distinguish representative features (Hermans et al., 2017; Yao et al., 2020). An alternative solution to improve the stability of such deep learning models is to train with a large dataset using a large batch size (e.g., more than 1000) (Chen et al., 2020). However, it is infeasible for any current clinical applications given the limited computation resources and sample size. Furthermore, our model is deployed on a graph-level classification task. Compared with the node-level graph classification model in literature (Parisot et al., 2017; Parisot et al., 2018), in which the entire dataset needs to be run through again to test a new subject, our graph-level model can predict a new subject directly without the input of whole dataset.
We proposed a dynamic GCN-based classification model and demonstrated its promising performance in ADHD diagnosis. The first advantage of our model is that it aggregates 1-hop and 2-hop neighborhood node messages to the center node in each convolutional layer. Two-hop neighborhood node information aggregation captures a long-range ROI interaction. In Fig. 3, compared with the 1-hop GCN and GAT model, our model shows significant improvement in ADHD diagnosis. In our ablation experiment, 1-hop encoding contributes more to high accuracy than 2-hop encoding. One possible reason is that 2-hop encoding provides redundant noise for the model. Additionally, Normconv exhibits the largest impact on the model performance. We infer that although all three convolutional components are beneficial to the final classification performance, Normconv was the only module designed to perform the aggregation and update functions, which accounts for the major improvement of model performance. For the ConvReadout layer, the main function is to readout a graph instead of feature aggregation. For the Edgeconv layer, it aims to sparsely aggregate more important node features from the dynamically constructed graph in the feature space. It can be considered as a special regularized Normconv component to increase the model robustness. Training only from the sparse aggregation of the Edgeconv layer is similar to directly using a large dropout ratio, which results in a lower generalization indicated from Table 3. Adding output from Normconv and Edgeconv together should keep the training process of Edgeconv converging in the right direction to alleviate the side effect of regularization. The ablation study of the PCD effect proves the promising boost of including PCD information for ADHD detection, which is consistent with the results reported in other literature (Parisot et al., 2018; Chen et al., 2019).
In recent years, studies have been conducted to explore the roles that different lobes may play in ADHD pathology. An fMRI study of an odd-ball task showed reduced activations in the subcortical lobe in ADHD patients (Rubia et al., 2007). Decreased volume in the frontal cortex and cerebellum has been observed in ADHD patients (Krain and Castellanos, 2006). In a study using both fMRI and dopamine genes, regulation abnormalities of the dopamine D4 receptor were linked to brain functional connectivity in the frontal-striatal-cerebellar loop (Qian et al., 2018). Additionally, because of abnormal development of the cerebellum structure, a range of cognitive deficits, including symptoms of impaired working memory have been observed in the ADHD group (Stoodley and Limperopoulos, 2016; Duan et al., 2021). More gray matter volumes were observed in an ADHD adult and adolescent study, which further indicated the involvement of the cerebellum in ADHD (Duan et al., 2021). In conclusion, our results are consistent with and build on previous results, suggesting that the frontal lobe, subcortical lobe, and cerebellum are likely to be major areas of dysfunctions in ADHD patients.
Furthermore, ADHD could be considered as a default mode network (DMN) disorder (Castellanos and Proal, 2012) since insufficient regulation of DMN to other networks might cause inattentiveness in ADHD (Muroyama et al., 2016). In our study, the important ROIs (shown in Fig. 5) from the frontal, temporal, limbic, and parietal lobes such as the gyrus rectus, temporal pole, superior temporal gyrus, posterior cingulate gyrus, and angular gyrus overlap with the ventromedial prefrontal cortex, temporal pole, posterior cingulate cortex, and posterior inferior parietal lobe of the default mode network. Decreased functional connectivity between dorsal anterior cingulate cortex and posterior cingulate cortex in the DMN network was observed in the ADHD group versus the HC group (Castellanos et al., 2008). Additionally, group-level statistical analysis of value-based decision-making tasks with fMRI revealed that increased DMN suppression is corroborated with the increased DMN signal variance during the decision-making process in ADHD patients (Mowinckel et al., 2017). The different t-value connection patterns of DMN in the two groups of our study might be correlated with those findings. Compared with HC, ADHD patients have decreased connection strength in the posterior cingulate gyrus, angular gyrus, orbital part of inferior frontal gyrus, and temporal pole, but increased connection strength in the gyrus rectus, superior frontal gyrus and other DMN components.
4.2. Limitations and future work
For the graph construction of dGCN, we used ROI-wise correlation coefficients as nodal features. However, such a graph construction strategy ignored the temporal information that is important for characterizing the brain functional dynamics. Increasing studies have suggested that time-varying brain functional dynamics offered unique chronnectomic information for advanced understanding of large-scale network activity in the brain (Allen et al., 2014; Rashid et al., 2018; Li et al., 2020). Extending our dGCN model with temporally dynamic connectome might help improve the quantification of brain dysfunctions.
In the present study, the AAL atlas was used to extract ROI-level connectivity features. However, it has been observed that the anatomical parcellation may cause higher inhomogeneity of extracted time series compared to other functional parcellations (Shen et al., 2013; Gordon et al., 2016; Schaefer et al., 2018). The selection of brain atlas showed a considerable influence in the differentiation of mental disorders such as Alzheimer’s disease, early mild cognitive impairment, and late mild cognitive impairment (Wu et al., 2019). It is worthy of further studies to investigate the classification performance of our model with other functional atlases. Moreover, some existing work has reported that extracting connectivity features from multiple brain atlases increased the diagnostic accuracy of brain disorders (Chen et al., 2019; Khosla et al., 2019). Hence, our future work will also investigate whether a combination of functional connections extracted based on both anatomical and functional parcellations can lead to novel connectomic biomarkers for brain disease studies.
Some prior neuroscientific knowledge might be incorporated into the graph model training for improved graph classification as well as interpretability of the model (Li and Duncan, 2020). For instance, the affiliation of networks and ROIs defined by a specific brain functional parcellation (Schaefer et al., 2018) can be potentially applied to guide the node aggregation process of dGCN via specifically designed biomarker detection pooling and corresponding regularization parameters (Li and Duncan, 2020) for enhancing model learning performance and driving more interpretable biomarkers. In addition, the contribution of identified brain dysfunctions towards ADHD etiology is still underexplored. To understand this association, a larger task-related neuroimaging analysis needs to be launched.
Though the integration of PCD with brain functional connectivity as input for training our model showed improved performance, the used PCD integration strategy is relatively simple. Advanced experiments to explore the intrinsic relationship between phenotypical variables and ADHD are needed, which may drive a more elegant integration of PCD information into our dGCN model for further enhanced diagnosis performance. Our leave-study-site-out cross-validation analysis (Table 2) confirmed the generalizability of the dGCN model to unseen data collected from different study sites of the ADHD-200 dataset. Replication analysis with independent samples collected using different study protocols will provide even stronger evidence for the reproducibility of our results. Our future work will also perform extensive and rigorous analyses using other independent cohorts involving ADHD to replicate the findings of the current study.
5. Conclusions
In this study, we proposed dGCN for the robust quantification of brain connectomic abnormalities in distinguishing ADHD patients from healthy controls. In our model, learning from the dynamic adjacency matrix construction in feature space increases model sparsity, and a new readout layer was proposed to represent a graph from another dimension with an alternative representation. Moreover, a broader ROI functional connection exploration from 2-hop neighborhood nodes in each graph convolutional layer was utilized. Compared with other competing methods, the connectomic biomarkers driven by the proposed model yielded a significant improvement in multiple evaluation metrics for ADHD diagnosis. Our experimental findings suggest that increased functional connectivity from the frontal lobe, subcortical lobe, and cerebellum have a strong correlation with ADHD psychopathology. These promising results prove the strength of our developed dynamic GCN model in providing a brain connectome-based solution for a better understanding of ADHD psychopathology. In summary, our study showed the promise of a novel data-driven quantification of functional connectome abnormalities by leveraging the innovative technique of graph neural networks to improve the prediction of ADHD.
Acknowledgments
This work is in part supported by Lehigh University Internal Grants (FRG, FIG, and Accelator) and Startup Funding. Portions of this research were conducted on Lehigh University’s Research Computing infrastructure partially supported by NSF Award 2019035. Dr. Oathes was funded in part by NIH RF1MH116920 and R01MH111886. Dr. Calhoun was funded in part by NIH R01MH123610.
Footnotes
Declaration of Competing Interest
The authors declare no competing financial interests.
Credit authorship contribution statement
Kanhao Zhao: Conceptualization, Methodology, Software, Writing – original draft, Writing – review & editing. Boris Duka: Writing – review & editing. Hua Xie: Writing – review & editing. Desmond J. Oathes: Writing – review & editing. Vince Calhoun: Writing – review & editing. Yu Zhang: Conceptualization, Methodology, Software, Supervision, Writing – original draft, Writing – review & editing.
Data and code availability
All MRI data used in this study are publicly available at the International Neuroimaging Datasharing Initiative website ( http://preprocessed-connectomes-project.org/adhd200/ ). Codes of the dynamic graph neural networks and brain connectome analyses will be deposited in an open access platform, upon acceptance of this manuscript.
References
- Abrol A, Fu Z, Salman M, Silva R, Du Y, Plis S, Calhoun V, 2021. Deep learning encodes robust discriminative neuroimaging representations to outperform standard machine learning. Nat. Commun 12 (1), 353. doi: 10.1038/s41467-020-20655-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD, 2014. Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex 24 (3), 663–676. doi: 10.1093/cercor/bhs352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balcilar M, Renton G, Héroux P, Gauzere B, Adam S. and Honeine P. (2020). Bridging the gap between spectral and spatial domains in graph neural networks. arXiv preprint arXiv:2003.11702. [Google Scholar]
- Barkley RA, 2011. Barkley Adult ADHD Rating Scale-IV (BAARS-IV). Guilford Press. [Google Scholar]
- Bellec P, Chu C, Chouinard-Decorte F, Benhajali Y, Margulies DS, Craddock RC, 2017. The neuro bureau ADHD-200 preprocessed repository. Neuroimage 144 (Pt B), 275–286. doi: 10.1016/j.neuroimage.2016.06.034. [DOI] [PubMed] [Google Scholar]
- Bessadok A, Mahjoub MA and Rekik I. (2021). Graph neural networks in network neuroscience. arXiv preprint arXiv:2106.03535. [DOI] [PubMed] [Google Scholar]
- Cao M, Yang M, Qin C, Zhu X, Chen Y, Wang J, Liu T, 2021. Using DeepGCN to identify the autism spectrum disorder from multi-site resting-state data. Biomed. Signal Process. Control 70. doi: 10.1016/j.bspc.2021.103015. [DOI] [Google Scholar]
- Cassidy B, Rae C, Solo V, 2015. Brain activity: connectivity, sparsity, and mutual information. IEEE Trans. Med. Imaging 34 (4), 846–860. doi: 10.1109/TMI.2014.2358681. [DOI] [PubMed] [Google Scholar]
- Castellanos FX, Margulies DS, Kelly C, Uddin LQ, Ghaffari M, Kirsch A, Shaw D, Shehzad Z, Di Martino A, Biswal B, et al. , 2008. Cingulate-precuneus interactions: a new locus of dysfunction in adult attention-deficit/hyperactivity disorder. Biol. Psychiatry 63 (3), 332–337. doi: 10.1016/j.biopsych.2007.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castellanos FX, Proal E, 2012. Large-scale brain systems in ADHD: beyond the prefrontal-striatal model. Trends Cogn. Sci 16 (1), 17–26. doi: 10.1016/j.tics.2011.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CP, Keown CL, Jahedi A, Nair A, Pflieger ME, Bailey BA, Muller RA, 2015. Diagnostic classification of intrinsic functional connectivity highlights somatosensory, default mode, and visual regions in autism. Neuroimage Clin. 8, 238–245. doi: 10.1016/j.nicl.2015.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M, Li H, Wang J, Dillman JR, Parikh NA, He L, 2019. A multichannel deep neural network model analyzing multiscale functional brain connectome data for attention deficit hyperactivity disorder detection. Radiol. Artif. Intell 2 (1), e190012. doi: 10.1148/ryai.2019190012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T, Kornblith S, Norouzi M, Hinton G, 2020. A simple framework for contrastive learning of visual representations. In: Proceedings of the International Conference on Machine Learning (ICML). PMLR, pp. 1597–1607. [Google Scholar]
- Chiang WL, Liu X, Si S, Li Y, Bengio S, Hsieh C−.J., 2019. Cluster-GCN: an efficient algorithm for training deep and large graph convolutional networks. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 257–266. [Google Scholar]
- Chin Fatt CR, Jha MK, Cooper CM, Fonzo G, South C, Grannemann B, Carmody T, Greer TL, Kurian B, Fava M, et al. , 2020. Effect of intrinsic patterns of functional brain connectivity in moderating antidepressant treatment response in major depression. Am. J. Psychiatry 177 (2), 143–154. doi: 10.1176/appi.ajp.2019.18070870. [DOI] [PubMed] [Google Scholar]
- Consortium HD, 2012. The ADHD-200 consortium: a model to advance the translational potential of neuroimaging in clinical neuroscience. Front. Syst. Neurosci 6, 62. doi: 10.3389/fnsys.2012.00062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danielson ML, Bitsko RH, Ghandour RM, Holbrook JR, Kogan MD, Blumberg SJ, 2018. Prevalence of parent-reported ADHD diagnosis and associated treatment among U.S. children and adolescents, 2016. J. Clin. Child Adolesc. Psychol 47 (2), 199–212. doi: 10.1080/15374416.2017.1417860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Defferrard M, Bresson X, Vandergheynst P, 2016. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst 29, 3844–3852. [Google Scholar]
- Duan K, Jiang W, Rootes-Murdy K, Schoenmacker GH, Arias-Vasquez A, Buitelaar JK, Hoogman M, Oosterlaan J, Hoekstra PJ, Heslenfeld DJ, et al. , 2021. Gray matter networks associated with attention and working memory deficit in ADHD across adolescence and adulthood. Transl. Psychiatry 11 (1), 184. doi: 10.1038/s41398-021-01301-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faraone SV, Bonvicini C, Scassellati C, 2014. Biomarkers in the diagnosis of ADHD–promising directions. Curr. Psychiatry Rep 16 (11), 497. doi: 10.1007/s11920-014-0497-1. [DOI] [PubMed] [Google Scholar]
- Filip A−C, Azevedo T, Passamonti L, Toschi N, Lio P, 2020. A novel graph attention network architecture for modeling multimodal brain connectivity. In: Proceedings of the 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC). IEEE, pp. 1071–1074. [DOI] [PubMed] [Google Scholar]
- Fonzo GA, Etkin A, Zhang Y, Wu W, Cooper C, Chin-Fatt C, Jha MK, Trombello J, Deckersbach T, Adams P, et al. , 2019. Brain regulation of emotional conflict predicts antidepressant treatment response for depression. Nat. Hum. Behav 3 (12), 1319–1331. doi: 10.1038/s41562-019-0732-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadgil S, Zhao Q, Pfefferbaum A, Sullivan EV, Adeli E, Pohl KM, 2020. Spatio-temporal graph convolution for resting-state fMRI analysis. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI). Springer, pp. 528–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmer J, Schoenholz SS, Riley PF, Vinyals O. and Dahl GE (2017). Neural message passing for quantum chemistry. arXiv preprint arXiv:1704.01212. [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE, 2016. Generation and evaluation of a cortical area parcellation from resting-state correlations. Cereb. Cortex 26 (1), 288–303. doi: 10.1093/cercor/bhu239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton W, Ying Z, Leskovec J, 2017. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. (NIPS) 1024–1034. [Google Scholar]
- Hawco C, Buchanan RW, Calarco N, Mulsant BH, Viviano JD, Dickie EW, Argyelan M, Gold JM, Iacoboni M, DeRosse P, et al. , 2019. Separable and replicable neural strategies during social brain function in people with and without severe mental illness. Am. J. Psychiatry 176 (7), 521–530. doi: 10.1176/appi.ajp.2018.17091020. [DOI] [PubMed] [Google Scholar]
- Hermans A, Beyer L. and Leibe B. (2017). In defense of the triplet loss for person re-identification. arXiv preprint arXiv:1703.07737. [Google Scholar]
- Hoogman M, Muetzel R, Guimaraes JP, Shumskaya E, Mennes M, Zwiers MP, Jahanshad N, Sudre G, Wolfers T, Earl EA, et al. , 2019. Brain imaging of the cortex in ADHD: a coordinated analysis of large-scale clinical and population-based samples. Am. J. Psychiatry 176 (7), 531–542. doi: 10.1176/appi.ajp.2019.18091033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Insel TR, Cuthbert BN, 2015. Brain disorders? Precisely. Science 348 (6234), 499–500. [DOI] [PubMed] [Google Scholar]
- Isallari M, Rekik I, 2021. Brain graph super-resolution using adversarial graph neural network with application to functional brain connectivity. Med. Image Anal 71, 102084. [DOI] [PubMed] [Google Scholar]
- Jiang R, Calhoun VD, Cui Y, Qi S, Zhuo C, Li J, Jung R, Yang J, Du Y, Jiang T, et al. , 2020. Multimodal data revealed different neurobiological correlates of intelligence between males and females. Brain Imaging Behav. 14 (5). doi: 10.1007/s11682-019-00146-z, 1979–1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzman MA, Bilkey TS, Chokka PR, Fallu A, Klassen LJ, 2017. Adult ADHD and comorbid disorders: clinical implications of a dimensional approach. BMC Psychiatry 17 (1), 302. doi: 10.1186/s12888-017-1463-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazi A, Shekarforoush S, Krishna SA, Burwinkel H, Vivar G, Kortüm K, Ahmadi S−A, Albarqouni S, Navab N, 2019. Inceptiongcn: receptive field aware graph convolutional network for disease prediction. In: Proceedings of the International Conference on Information Processing in Medical Imaging. Springer, pp. 73–85. [Google Scholar]
- Khosla M, Jamison K, Kuceyeski A, Sabuncu MR, 2019. Ensemble learning with 3D convolutional neural networks for functional connectome-based prediction. Neuroimage 199, 651–662. doi: 10.1016/j.neuroimage.2019.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kipf TN and Welling M. (2016). Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907. [Google Scholar]
- Krain AL, Castellanos FX, 2006. Brain development and ADHD. Clin. Psychol. Rev 26 (4), 433–444. doi: 10.1016/j.cpr.2006.01.005. [DOI] [PubMed] [Google Scholar]
- Lake EMR, Finn ES, Noble SM, Vanderwal T, Shen X, Rosenberg MD, Spann MN, Chun MM, Scheinost D, Constable RT, 2019. The functional brain organization of an individual allows prediction of measures of social abilities trans-diagnostically in autism and attention-deficit/hyperactivity disorder. Biol. Psychiatry 86 (4), 315–326. doi: 10.1016/j.biopsych.2019.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levie R, Monti F, Bresson X, Bronstein MM, 2019. CayleyNets: graph convolutional neural networks with complex rational spectral filters. IEEE Trans. Signal Process 67 (1), 97–109. doi: 10.1109/tsp.2018.2879624. [DOI] [Google Scholar]
- Li G, Muller M, Thabet A, Ghanem B, 2019. DeepGCNs: can GCNs go as deep as CNNs? In: Proceedings of the IEEE International Conference on Computer Vision (ICCV), pp. 9267–9276. [Google Scholar]
- Li K, Guo L, Nie J, Li G, Liu T, 2009. Review of methods for functional brain connectivity detection using fMRI. Comput. Med. Imaging Graph 33 (2), 131–139. doi: 10.1016/j.compmedimag.2008.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X. and Duncan J. (2020). BrainGNN: interpretable brain graph neural network for fMRI analysis. bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Liu J, Tang Z, Lei B, 2020. Deep spatial-temporal feature fusion from adaptive dynamic functional connectivity for MCI identification. IEEE Trans. Med. Imaging 39 (9), 2818–2830. doi: 10.1109/TMI.2020.2976825. [DOI] [PubMed] [Google Scholar]
- Lin TY, Goyal P, Girshick R, He K, Dollár P, 2017. Focal loss for dense object detection. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 2980–2988. [Google Scholar]
- Liu FT, Ting KM, Zhou Z−H, 2008. Isolation forest. In: Proceedings of the Eighth IEEE International Conference on Data Mining (ICDM). IEEE, pp. 413–422. [Google Scholar]
- Mowinckel AM, Alnaes D, Pedersen ML, Ziegler S, Fredriksen M, Kaufmann T, Sonuga-Barke E, Endestad T, Westlye LT, Biele G, 2017. Increased default-mode variability is related to reduced task-performance and is evident in adults with ADHD. Neuroimage Clin. 16, 369–382. doi: 10.1016/j.nicl.2017.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muroyama A, Seldin L, Lechler T, 2016. Divergent regulation of functionally distinct gamma-tubulin complexes during differentiation. J. Cell Biol 213 (6), 679–692. doi: 10.1083/jcb.201601099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niepert M, Ahmed M, Kutzkov K, 2016. Learning convolutional neural networks for graphs. In: Proceedings of the International Conference on Machine Learning (ICML), pp. 2014–2023. [Google Scholar]
- Parisot S, Ktena SI, Ferrante E, Lee M, Guerrero R, Glocker B, Rueckert D, 2018. Disease prediction using graph convolutional networks: application to autism spectrum disorder and Alzheimer’s disease. Med. Image Anal 48, 117–130. doi: 10.1016/j.media.2018.06.001. [DOI] [PubMed] [Google Scholar]
- Parisot S, Ktena SI, Ferrante E, Lee M, Moreno RG, Glocker B, Rueckert D, 2017. Spectral graph convolutions for population-based disease prediction In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI). Springer, pp. 177–185. [Google Scholar]
- Park HJ, Friston K, 2013. Structural and functional brain networks: from connections to cognition. Science 342 (6158), 1238411. doi: 10.1126/science.1238411. [DOI] [PubMed] [Google Scholar]
- Qian A, Wang X, Liu H, Tao J, Zhou J, Ye Q, Li J, Yang C, Cheng J, Zhao K, et al. , 2018. Dopamine D4 receptor gene associated with the frontal-striatal-cerebellar loop in children with ADHD: a resting-state fMRI study. Neurosci. Bull 34 (3), 497–506. doi: 10.1007/s12264-018-0217-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rashid B, Blanken LME, Muetzel RL, Miller R, Damaraju E, Arbabshirani MR, Erhardt EB, Verhulst FC, van der Lugt A, Jaddoe VWV, et al. , 2018. Connectivity dynamics in typical development and its relationship to autistic traits and autism spectrum disorder. Hum. Brain Mapp 39 (8), 3127–3142. doi: 10.1002/hbm.24064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rong Y, Huang W, Xu T. and Huang J. (2019). Dropedge: towards deep graph convolutional networks on node classification. arXiv preprint arXiv:1907.10903. [Google Scholar]
- Rubia K, Smith AB, Brammer MJ, Taylor E, 2007. Temporal lobe dysfunction in medication-naive boys with attention-deficit/hyperactivity disorder during attention allocation and its relation to response variability. Biol. Psychiatry 62 (9), 999–1006. doi: 10.1016/j.biopsych.2007.02.024. [DOI] [PubMed] [Google Scholar]
- Schaefer A, Kong R, Gordon EM, Laumann TO, Zuo XN, Holmes AJ, Eickhoff SB, Yeo BTT, 2018. Local-global parcellation of the human cerebral cortex from intrinsic functional connectivity MRI. Cereb. Cortex 28 (9), 3095–3114. doi: 10.1093/cercor/bhx179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seguin C, van den Heuvel MP, Zalesky A, 2018. Navigation of brain networks. Proc. Natl. Acad. Sci. U. S. A 115 (24), 6297–6302. doi: 10.1073/pnas.1801351115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Tokoglu F, Papademetris X, Constable RT, 2013. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. Neuroimage 82, 403–415. doi: 10.1016/j.neuroimage.2013.05.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simard PY, Steinkraus D, Platt JC, 2003. Best practices for convolutional neural networks applied to visual document analysis. In: Proceedings of the ICDAR, 3. Citeseer. [Google Scholar]
- Simonovsky M, Komodakis N, 2017. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 3693–3702. [Google Scholar]
- Singh I, Rose N, 2009. Biomarkers in psychiatry. Nature 460 (7252), 202–207. [DOI] [PubMed] [Google Scholar]
- Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R, 2014. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res 15 (1), 1929–1958. [Google Scholar]
- Stoodley CJ, Limperopoulos C, 2016. Structure-function relationships in the developing cerebellum: evidence from early-life cerebellar injury and neurodevelopmental disorders. Semin. Fetal Neonatal Med 21 (5), 356–364. doi: 10.1016/j.siny.2016.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taud H, Mas J, 2018. Multilayer Perceptron (MLP). Geomatic Approaches For Modeling Land Change Scenarios. Springer, pp. 451–455. [Google Scholar]
- Valsesia D, Fracastoro G, Magli E, 2018. Learning localized generative models for 3d point clouds via graph convolution. In: Proceedings of the International Conference on Learning Representations (ICLR). [Google Scholar]
- Veli čkovi ć P, Cucurull G, Casanova A, Romero A, Lio P. and Bengio Y. (2017). Graph attention networks. arXiv preprint arXiv:1710.10903. [Google Scholar]
- Vissers ME, Cohen MX, Geurts HM, 2012. Brain connectivity and high functioning autism: a promising path of research that needs refined models, methodological convergence, and stronger behavioral links. Neurosci. Biobehav. Rev 36 (1), 604–625. doi: 10.1016/j.neubiorev.2011.09.003. [DOI] [PubMed] [Google Scholar]
- Wang Y, Sun Y, Liu Z, Sarma SE, Bronstein MM, Solomon JM, 2019. Dynamic graph CNN for learning on point clouds. ACM Trans. Graph 38 (5), 1–12. doi: 10.1145/3326362. [DOI] [Google Scholar]
- Wee CY, Yap PT, Zhang D, Wang L, Shen D, 2012. Constrained sparse functional connectivity networks for MCI classification. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 212–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolraich ML, Hagan JF, Allan C, Chan E, Davison D, Earls M, Evans SW, Flinn SK, Froehlich T, Frost J, 2019. Clinical practice guideline for the diagnosis, evaluation, and treatment of attention-deficit/hyperactivity disorder in children and adolescents. Pediatrics 144 (4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo S, Park J, Lee JY, Kweon IS, 2018. Cbam: convolutional block attention module. In: Proceedings of the European Conference on Computer Vision (ECCV), pp. 3–19. [Google Scholar]
- Wu D, Li X, Feng J, 2020a. Multi-hops functional connectivity improves individual prediction of fusiform face activation via a graph neural network. Front. Neurosci 14, 596109. doi: 10.3389/fnins.2020.596109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Pan S, Chen F, Long G, Zhang C, Philip SY, 2020b. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw Learn. Syst. 32 (1), 4–24. [DOI] [PubMed] [Google Scholar]
- Wu Z, Xu D, Potter T, Zhang Y Alzheimer’s Disease Neuroimaging, I., 2019. Effects of brain parcellation on the characterization of topological deterioration in Alzheimer’s disease. Front. Aging Neurosci 11, 113. doi: 10.3389/fnagi.2019.00113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu K, Hu W, Leskovec J. and Jegelka S. (2018). How powerful are graph neural networks? arXiv preprint arXiv:1810.00826. [Google Scholar]
- Xue H, Sun XK, Sun WX, 2020. Multi-hop hierarchical graph neural networks. In: Proceedings of the IEEE International Conference on Big Data and Smart Computing (BigComp), pp. 82–89. [Google Scholar]
- Yan S, Xiong Y, Lin D, 2018. Spatial temporal graph convolutional networks for skeleton-based action recognition. In: Proceedings of the AAAI Conference on Artificial Intelligence, p. 32. [Google Scholar]
- Yan W, Calhoun V, Song M, Cui Y, Yan H, Liu S, Fan L, Zuo N, Yang Z, Xu K, et al. , 2019. Discriminating schizophrenia using recurrent neural network applied on time courses of multi-site FMRI data. EBioMedicine 47, 543–552. doi: 10.1016/j.ebiom.2019.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H, Li X, Wu Y, Li S, Lu S, Duncan JS, Gee JC, Gu S, 2019. Interpretable multimodality embedding of cerebral cortex using attention graph network for identifying bipolar disorder. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI). Springer, pp. 799–807. [Google Scholar]
- Yao D, Liu M, Wang M, Lian C, Wei J, Sun L, Sui J, Shen D, 2019. A mutual multi-scale triplet graph convolutional network for classification of brain disorders using functional or structural connectivity. In: Proceedings of the International Workshop on Graph Learning in Medical Imaging. Springer, pp. 70–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao R, Gao C, Xia S, Zhao J, Zhou Y, Hu F, 2020. GAN-based person search via deep complementary classifier with center-constrained Triplet loss. Pattern Recognit. 104 doi: 10.1016/j.patcog.2020.107350. [DOI] [Google Scholar]
- Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roff-man JL, Smoller JW, Zollei L, Polimeni JR, et al. , 2011. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol 106 (3), 1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M, Cui Z, Neumann M, Chen Y, 2018a. An end-to-end deep learning architecture for graph classification. In: Proceedings of the AAAI Conference on Artificial Intelligence, p. 32. [Google Scholar]
- Zhang S, Tong H, Xu J, Maciejewski R, 2019. Graph convolutional networks: a comprehensive review. Comput. Soc. Netw 6 (1). doi: 10.1186/s40649-019-0069-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Chou J, Wang F, 2018b. Integrative analysis of patient health records and neuroimages via memory-based graph convolutional network. In: Proceedings of the IEEE International Conference on Data Mining (ICDM), pp. 767–776. [Google Scholar]
- Zhang X, He L, Chen K, Luo Y, Zhou J, Wang F, 2018c. Multi-view graph convolutional network and its applications on neuroimage analysis for Parkinson’s disease. In: Proceedings of the AMIA Annual Symposium, 2018. American Medical Informatics Association, p. 1147. [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. and Bellec P. (2020). Transferability of brain decoding using graph convolutional networks. bioRxiv. [Google Scholar]
- Zhou J, Cui G, Hu S, Zhang Z, Yang C, Liu Z, Wang L, Li C, Sun M, 2020. Graph neural networks: a review of methods and applications. AI Open 1, 57–81. [Google Scholar]
- Zhu H, Yuan M, Qiu C, Ren Z, Li Y, Wang J, Huang X, Lui S, Gong Q, Zhang W, et al. , 2020. Multivariate classification of earthquake survivors with post-traumatic stress disorder based on large-scale brain networks. Acta Psychiatr. Scand 141 (3), 285–298. doi: 10.1111/acps.13150. [DOI] [PubMed] [Google Scholar]
- Zou L, Zheng J, Miao C, McKeown MJ, Wang ZJ, 2017. 3D CNN based automatic diagnosis of attention deficit hyperactivity disorder using functional and structural MRI. IEEE Access 5, 23626–23636. doi: 10.1109/access.2017.2762703. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All MRI data used in this study are publicly available at the International Neuroimaging Datasharing Initiative website ( http://preprocessed-connectomes-project.org/adhd200/ ). Codes of the dynamic graph neural networks and brain connectome analyses will be deposited in an open access platform, upon acceptance of this manuscript.