Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Oct 2;15(40):47649–47660. doi: 10.1021/acsami.3c07763

Elucidating the Mechanism of Large Phosphate Molecule Intercalation Through Graphene-Substrate Heterointerfaces

Jiayun Liang †, Ke Ma †, Xiao Zhao †,‡, Guanyu Lu §, Jake Riffle ∥, Carmen M Andrei ⊥, Chengye Dong #, Turker Furkan ∇, Siavash Rajabpour ∇, Rajiv Ramanujam Prabhakar ○, Joshua A Robinson #,∇, Vasquez Magdaleno Jr ◆, Quang Thang Trinh , Joel W Ager †,‡, Miquel Salmeron †,‡, Shaul Aloni ††, Joshua D Caldwell §, Shawna Hollen ∥, Hans A Bechtel ‡‡, Nabil D Bassim ⊥,§§, Matthew P Sherburne †, Zakaria Y Al Balushi †,‡,*
PMCID: PMC10571006  PMID: 37782678

Abstract

graphic file with name am3c07763_0007.jpg

Intercalation is the process of inserting chemical species into the heterointerfaces of two-dimensional (2D) layered materials. While much research has focused on the intercalation of metals and small gas molecules into graphene, the intercalation of larger molecules through the basal plane of graphene remains challenging. In this work, we present a new mechanism for intercalating large molecules through monolayer graphene to form confined oxide materials at the graphene-substrate heterointerface. We investigate the intercalation of phosphorus pentoxide (P2O5) molecules directly from the vapor phase and confirm the formation of confined P2O5 at the graphene-substrate heterointerface using various techniques. Density functional theory (DFT) corroborates the experimental results and reveals the intercalation mechanism, whereby P2O5 dissociates into small fragments catalyzed by defects in the graphene that then permeates through lattice defects and reacts at the heterointerface to form P2O5. This process can also be used to form new confined metal phosphates (e.g., 2D InPO4). While the focus of this study is on P2O5 intercalation, the possibility of intercalation from predissociated molecules catalyzed by defects in graphene may exist for other types of molecules as well. This in-depth study advances our understanding of intercalation routes of large molecules via the basal plane of graphene as well as heterointerface chemical reactions leading to the formation of distinctive confined complex oxide compounds.

Keywords: graphene, intercalation, heterointerface, reactions, defects

Introduction

Intercalation is a topotactic insertion process of organic or inorganic chemical species (i.e., atoms, small molecules, etc.) between the interfaces and heterointerfaces of two-dimensional (2D) layered materials. This process is known to form a variety of intercalation compounds, notably in graphite, encompassing a diverse range of intercalants within the host of the 2D layered bulk crystal.1 Intercalation can occur through the exposed side edges of a 2D layered bulk crystal and/or through its basal planes.2 In the latter case, for example, in monolayer to few-layer graphene, the intercalation pathways are typically point defects,3−9 and/or grain boundaries.10 Usually, the intercalation process can occur using a variety of processes, including vapor transport,11 wet-chemical,12−15 and electrochemical16 means. To date, much of the research surrounding the intercalation of monolayer graphene has focused on the intercalation of metals (e.g., Ga, In, Al,17 Bi,18 Fe,19 Sb,20 Gd,21 Pb,22 etc.) and small gas molecules (e.g., CO,23 O224). However, the intercalation of molecules through the basal plane of monolayer graphene that are significantly larger than the lattice parameters of graphene remain challenging. This is because the size and energy barrier for intercalation inhibits the permeation of such large molecules.25,26 The ability to intercalate large molecules could further expand the toolsets for subsurface and heterointerface engineering of 2D layered materials and therefore enrich the material choices available for the fabrication of heterostructures and intercalation compounds used in energy storage, optoelectronics, thermoelectric, catalysis, etc.27−29

Chemical reactions enabled by confinement to the heterointerfaces of 2D layered materials provide a pathway to circumvent the limitation on intercalating large molecules directly through the basal plane. That is, individual chemical species or multiple small fragments of the initial state of the molecule would first intercalate through typically available pathways in the graphene lattice, and then recombine at the heterointerface via chemical reactions. So far, a variety of alloys (Sn1–xGex,30 Fe1–xCox,31 etc.) and compounds (GaN,32−34 AlN,35 MoS2,36 PtSe2,37 Ga2O3,38 etc.) have been formed at graphene-substrate heterointerfaces via chemical reactions. In all of these cases, however, chemical species are individually introduced in a sequential manner when intercalating graphene. This is done to prevent prereactions in the vapor phase between the individual elements prior to intercalation. Such prereactions usually lead to the formation of clusters at defect sites on the graphene surface rather than intercalating through the lattice itself and forming a compound at the heterointerface.

In this work, we report a mechanism of vapor phase intercalation of large molecules through the heterointerface of monolayer graphene to form confined oxide materials underneath graphene with a chemical composition that resembles the initial state of the large intercalant molecule itself. Unlike prior work, where chemical species and/or elements were sequentially introduced into the heterointerface, single molecules were introduced directly into the vapor phase for intercalation through the basal plane. This mechanism was revealed by investigating the intercalation of phosphorus pentoxide (P2O5) molecules directly from the vapor phase to form P2O5 at a graphene-substrate heterointerface. The formation of confined P2O5 was confirmed using a variety of chemical analysis and spectroscopic techniques as well as microscopic surface and cross-sectional imaging. Density functional theory (DFT) was used to corroborate experimental results and to deduce the mechanism for the intercalation of P2O5 molecules through the basal plane of monolayer graphene. First, P2O5 dissociates into small fragments (i.e., Px, Oy, etc.) when interacting with the graphene surface. These small fragments consistently showed lower energy barriers for intercalation through defects commonly observed in the graphene lattice. Once the small fragments intercalate, they react at the heterointerface to form P2O5. We show that the intercalation of P2O5 at the graphene-substrate heterointerface can tune the electronic structure of the graphene overlayer through strain and charge transfer. In addition, we show that this process can also be used in the formation of new confined metal phosphates by intercalating P2O5 into a graphene-substrate heterointerface initially containing a confined 2D indium metal to form InPO4. Although this study focuses on the intercalation of P2O5, the concept of intercalation from predissociated molecules catalyzed by defects in graphene could be possible in other classes of molecules. Ultimately, this study provides an important steppingstone for advancing the understanding of intercalation pathways of large molecules though the basal plane of graphene as well as heterointerface chemical reactions to form unique confined complex oxide compounds.

Results and Discussion

The physical size of phosphorus pentoxide (P2O5) can be deduced from our DFT calculated ground state structure when it is adsorbed onto the surface of pristine monolayer graphene (Figure 1a). This molecule consists of two main phosphorus bonds with oxygen. The P–O single bond (denotated as oxygen bridging) has a bond length of 157–159 pm, and the P=O double bond (denotated as oxygen terminal) has a bond length of 143.2–144.5 pm.39 When the physical size of the molecule is intuitively compared to the lattice parameter of graphene, intercalation through the basal plane appears to be unlikely. Our DFT calculations revealed that the intercalation of P2O5 molecules in its native state through graphene could only occur if large pores, formed by the removal of 9 carbon atoms, were present (see the Supporting Information). The formation of such large pores in graphene is, however, energetically unfavorable.40 In fact, other theoretical studies have predicted large energy barriers for permeation of many atoms and molecules through pristine graphene.25,26 In our case, we experimentally show that it is possible to intercalate P2O5 through monolayer graphene transferred onto germanium substrates without the need for large pores to serve as intercalation pathways. In our studies, germanium was used as a substrate due to the limited solubility41 and low diffusivity42 of phosphorus into germanium, allowing to fully capture and study the formation of P2O5 at graphene-germanium heterointerfaces. To intercalate P2O5, we prepared monolayer graphene on germanium substrates which were then annealed downstream of SiP2O7 at 950°C (see Methods). At such temperatures, the decomposition of SiP2O7 produced an upstream flux where P2O5 is the predominant gas-phase specie, as supported by previously reported experimental and computational studies.43−45 P2O5 then impinges onto the surface of graphene downstream and subsequently intercalates into the heterointerface (Figure 1b). A more detailed discussion of the mechanism is included in the following sections.

Figure 1.

Figure 1

Open in a new tab

Intercalation of P2O5 at the heterointerface of graphene-germanium. (a) Configuration of P2O5 adsorbed onto pristine graphene calculated from DFT. (b) Schematic of intercalation process through the graphene-substrate heterointerface: (i) decomposition of P2O5 into Px and Oy, (ii) intercalation of Px and Oy through graphene and formation of P2O5 at heterointerface via chemical reactions. (c) SEM highlighting the formation of graphene bubbles (white arrows), with an STM image of the graphene lattice on the top surface of the bubble (bottom left inset). (d) SEM-EDS maps of (left) oxygen and (right) phosphorus of the highlighted graphene bubbles in panel (c). (e) STEM-HAADF cross-section image of a graphene bubble with corresponding STEM-EDS maps of the (f) oxygen and (g) phosphorus distribution in the bubble.

As shown in Figure 1c, many bubbles appeared on the surface of graphene after samples were exposed to a flux of P2O5 (white arrows in scanning electron micrograph, SEM). From scanning tunneling microscopy (STM) imaging of the bubble surface (Figure 1c, inset), the characteristic hexagonal lattice of graphene was clear. This suggests that not only was the graphene surface free of large pores but also highlighted that the bubbles themselves were “graphene bubbles” containing subsurface material. Such graphene bubbles are prevalent in many intercalation studies of monolayer to few-layer graphene in the literature.25,46 Upon further inspection of the surface using energy-dispersive spectroscopy (EDS), strong phosphorus and oxygen signals confined to the graphene bubbles were observed (Figure 1d). This implied the formation of phosphorus oxides within the bubbles themselves. The distribution of the phosphorus and oxygen in the graphene bubbles was further corroborated in sample cross sections. In Figure 1e, a representative high-angle annular dark field scanning transmission electron microscope (HAADF-STEM) image of a graphene bubble is shown. The EDS cross-sectional elemental maps of the bubble (Figure 1f,g) also revealed strong oxygen and phosphorus signals. The atomic fractions of oxygen and phosphorus in the graphene bubble were 55.06% and 15.52%, respectively. This elemental distribution was further corroborated within X-ray photoelectron spectroscopy (XPS) depth profiles of the sample, facilitated by repeated ion sputtering (Figure S1). During the ion sputtering process, the graphene surface was first etched. This resulted in a rapid decrease in the C 1s core-level peak intensity (Figure S1a). The peak intensities for the Ge, O, and P core levels increased upon sputtering of graphene (Figure S1b–d), which serves as additional evidence on the confinement of phosphorus oxide at the graphene–germanium substrate heterointerface after samples were exposed to a flux of P2O5.

Chemistry of the Graphene–Substrate Heterointerface

Moreover, the chemical environment of phosphorus oxide within the graphene bubbles was investigated using nano Fourier-transform infrared spectroscopy (nano-FTIR). A near-field white light IR image of a region of the sample containing graphene bubbles, spectrally averaged over ∼610–1400 cm–1, is highlighted in Figure 2a. Spectral points in the range associated with vibrational modes associated with the phosphorus and oxygen functional groups were acquired at 50 nm intervals across a graphene bubble (black arrow). This is plotted in Figure 2b as a near-field phase (φ2) heat map, which is related to the local absorption spectra of the material, and therefore, useful for determining the chemical environment of the intercalant.47,48Figure 2c highlights a comparison between the two nano-FTIR spectra. The top panel (black solid line) is the extracted phase spectrum at the center of the graphene bubble in Figure 2b, while the bottom panel (red solid line) is a spectrum collected from a reference sample of P2O5 using high-resolution synchrotron-based nano-FTIR measurements (see Methods). Evident in Figure 2b and the top panel of Figure 2c are three characteristic IR bands localized to the graphene bubble. These bands were assigned as the P–O–P bending mode (940–970 cm–1), the P–O bridging mode (1060–1125 cm–1), and the P=O terminal oxygen stretching modes (1135–1235 cm–1).49 The intensity of the P=O bond in the heat map (Figure 2b) reached a maximum at the center of the graphene bubble. More importantly, these peaks well matched the P2O5 reference sample in Figure 2c (bottom panel) and therefore supports phosphorus oxide that was confined at the graphene–germanium substrate heterointerface from the cross-section micrograph in Figure 1g was P2O5.

Figure 2.

Figure 2

Open in a new tab

Chemistry at the graphene-germanium heterointerface. (a) Near-field white light IR image in a region of the sample containing large graphene bubbles. The white light IR image is the near-field amplitude (S2) image, which is spectrally averaged over approximately ∼610–1400 cm–1 by setting the interferometer at the white light position. (b) Nano-FTIR spectral heat map acquired at 50 nm intervals along the black solid arrow in panel (a). The graphene bubble region is highlighted with white dashed lines and a dashed arrow. The collected phase channel (φ2) was normalized to that obtained in a silicon sample using the same acquisition parameters. (c) Comparison between extracted nano-FTIR spectrum of a graphene bubble (top panel, black solid line) and spectrum collected from a reference P2O5 sample (bottom panel, red solid line). XPS of C, P, and Ge core levels from graphene on germanium samples (d–f) annealed without an upstream flux of P2O5 (i.e., unintercalated sample) and from graphene on germanium samples (g–i) annealed with an upstream flux of P2O5 (i.e., intercalated sample).

Furthermore, a comparative XPS study between nonintercalated and intercalated samples was also performed to further deduce the chemical bonding information at the graphene-germanium heterointerface. Figure 2d–f are XPS core-level spectra collected from samples that were annealed without an upstream flux of P2O5, while the XPS core levels in Figure 2g–i were from samples annealed downstream to a flux of P2O5 (see Methods). In the nonintercalated samples, the sp3/sp2 carbon ratio, extracted from the C 1s core level, was ∼4% (Figure 2d), and neither phosphorus oxides (Figure 2e) nor germanium oxides (Figure 2f) could be detected in those samples. However, in intercalated samples, the sp3/sp2 carbon ratio increased to ∼7.7% (Figure 2g). Such an increase in sp3-bonded carbon within the nonintercalated samples was likely due to the formation of additional point defects in the graphene lattice. These defects could have resulted from the intercalation process itself or due to the enhanced hybridization of the graphene with the underlying intercalants. Moreover, a strong phosphorus oxide peak, whose binding energy was associated with P2O5 (135 eV, Figure 2h), further corroborated its formation.50 Also, from the Ge 3d core-level, the intercalated P2O5 appeared to oxidize the germanium substrate, resulting in characteristic peaks for GeO and GeO2 that were observed between binding energies of 31–33 eV (Figure 2i). These combined results allude to a strong affinity of oxygen from P2O5 to the underlying germanium substrate and perhaps provides an additional driving force in the intercalation process with the aid of point defect and/or grain boundaries in the graphene lattice as a pathway for intercalation through the basal plane of graphene.8

Mechanism of Large Molecule Intercalation through Graphene

To gain a deeper understanding into the mechanism by which phosphorus pentoxide P2O5 (or molecular formula P4O10) intercalates through the basal plane of graphene, we first examined the adsorptive properties of these molecules on five different graphene systems, consisting of pristine graphene and four graphene lattice defect configurations (Figure 3a, see the Supporting Information). This survey was performed to factor in different interaction parameters of distinct chemical environments on the intercalation process. The configurational space of the adsorptive states (chemisorption vs physisorption) was thoroughly explored by including a multitude of initial interacting geometries for both P2O5 and P4O10 on each of the different graphene lattice defect configurations (Figure 3b). As summarized in Table S1, covalent interactions with graphene occurred exclusively in the chemisorption of P2O5 onto graphene defect sites, whereas in pristine graphene, P2O5 interacted weakly via van der Waals (vdW) forces. In comparison, interactions between the more stable P4O10 molecule and all graphene systems were vdW in nature. In the case of covalent bonding between P2O5 adsorbents and graphene, P atoms consistently demonstrated a higher affinity toward graphene. This is shown by the greater adsorption energy of P2O5 to graphene through the P atom (denoted by P2O5(P) in Figure 3b). In contrast, initial configurations of P2O5 approaching graphene with its O atom (designated by P2O5(O)) either relaxed to drastically different interaction geometries to allow bond formation between carbon and phosphorus or had a much lower total adsorption energy when compared to P2O5(P). The only exception was P2O5(O) chemisorbed to S defects, in which both the atoms of the O and P bonded covalently to the graphene defect site. Such trends can be rationalized by the fulfillment of covalency and increased charge transfer stabilization of carbon atoms at defects when bonding to less electronegative P atoms in P2O5.

Figure 3.

Figure 3

Open in a new tab

Mechanism for intercalation P2O5 through the basal plane of graphene. (a) Top view of the four types of point defects in isolated graphene sheets. (b) Adsorption energy of phosphorus pentoxide on pristine and defective graphene monolayers. Within each PxOy molecule, the atom interacting directly with carbon at the defect site is labeled in parentheses. (c) Calculated energy barrier of bond cleavage for P=O double bond (route 1, labeled as green) and single bond (route 2, labeled as blue) within P2O5 in different local environments. (d) Energy and configurational profile of PO molecule penetrating through defects. (e) Energy barrier of P (blue) and O (red) atoms permeating through defects.

Pristine graphene has been predicted to be impermeable to most gaseous species under nonextreme conditions,25,26,46 and the presence of defects is thus the precondition for P2O5 intercalation. A quantitative description of intercalation through defects is complicated by the competition between diffusion and bonding with carbon atoms at defect sites. This gives rise to three different energy profiles corresponding to distinct pathways.51 To address these complexities, we employed a case-by-case strategy by calculating the penetration barriers for fragments of P2O5 of varied size and chemistry based on calculated and experimental evidence from the literature.45 Based on experimental evidence of P2O5 confinement at the graphene-germanium heterointerface, the intercalation of molecular P2O5 in its entirety was first investigated. Point defects of various sizes were examined, with the largest created by removing 9 adjacent carbon atoms in an isolated graphene sheet (Figure S2). In all scenarios, P2O5 decomposed into fragments solvated by carbon atoms at the defect sites. Notably, the energetic profile of P2O5 permeating through large defects showed a negative reaction coordinate energy curve with small intermediate energy barriers as a result of the bonding of the fragmented P2O5 molecule to the defect site. Despite this negative reaction coordinate energy curve, a barrier of at least 7.7 eV was still present for fragments to desorb from the defect and diffuse into opposite sides of the monolayer graphene (i.e., intercalate). From this, we ascertain that intercalation is only possible from significantly smaller molecular fragments of P2O5. Developed from these findings, we propose a mechanism involving three consecutive steps of realistic energy barriers to intercalate P2O5 through the basal plane of monolayer graphene. First, chemisorbed P2O5 decomposes into atoms or small molecular fragments. The resulting species then intercalate separately through point defects and then react underneath the graphene monolayer to form P2O5 at the confined heterointerface.

Describing such processes with a full network of reaction pathways would require a dedicated theoretical effort and is beyond the scope of this study, but two modes of P–O bond cleavage representing the initial steps of two probable pathways were investigated to exemplify our hypothesis. As illustrated in Figure 3c, route 1 involves cleaving the P=O double bond to remove one terminal oxygen from the molecule, while route 2 describes the fragmentation of P2O5 into PO2 and PO3 by cleaving the single bond between P and bridging O. Energy barriers for both reactions are shown in Figure 3c. Evidently, with the exception of S-defect in route 1, all four types of point defects exhibited catalytic activities toward decomposition of P2O5. These findings were consistent with the results of adsorption state calculations, as covalent interactions and charge transfer between the defects and adsorbed molecules weaken the intramolecular bonds. Having substantiated the possibility of the catalytic dissociation of adsorbed P2O5 at defect sites, we then calculated the energetics of smaller fragments intercalating through point defects. Phosphorus monoxide (PO), the simplest oxide of phosphorus, was chosen as the subject of this study. Given the positive correlation between an intercalant size and the energy barrier required for its permeation through graphene point defects, we postulate that the intercalation of PO provides a baseline for the minimum energy barrier applicable to the diffusion of any potential phosphorus oxide molecules through monolayer graphene. In the focused reaction coordinate diagram (Figure 3d), we present the energy of three key configurations: the adsorbed state, where the PO molecule adsorbs to the defect site; the transition state, where the molecule penetrates halfway through the defect; and the intercalated state, in which PO has permeated through monolayer graphene but has not yet desorbed or reconfigured itself to the lowest-energy absorption geometry. The energy difference between the transition and adsorbed states indicates the minimum energy barrier required for PO molecules to intercalate monolayer graphene. Similar to P2O5, PO could not permeate through pristine graphene or Stone–Wales (SW) defects without the introduction of defects of larger sizes. When penetrating through S- and D-defects, the molecule decomposed into individual atoms with the rate limiting step having an energy barrier as high as 8 eV. On the other hand, PO was surprisingly permeable at Q-defects. It diffused through the Q-defect without further fragmentation, with a barrier of approximately 2 eV, comparable to the energy required to break down chemisorbed P2O5. Finally, to compare atomic phosphorus and oxygen diffusing through the four different types of defects in graphene (Figure 3e), we performed calculations on (4 × 6) graphene supercells and incorporated results for D- and Q-defects from the work by Song et. al.51 Remarkably, while point defects enabled both species to intercalate with reduced energy barriers, the energy barrier for individual atoms to penetrate through D- and Q-defects was higher than those for the PO molecule fragments. This observation reiterates the complexity of the interaction process through graphene point defects that cannot be generalized into a single step process.

Impact of the Intercalants on the Physical Properties of Graphene

Graphene inherits highly delocalized π-electrons. Any modification to the spatial extent of the charge density of these π-electrons or tilt of the π-orbitals leads to significant changes to the physical properties of graphene.52−55 For example, electronegative or electropositive intercalants confined underneath graphene will lead to charge transfer and doping. This in turn influences the spatial extent of the π-electron charge density and thus the Fermi level of graphene. Moreover, intercalants, such as those confined in graphene bubbles, can also lead to straining of the graphene lattice.56−58 This will also change the π-orbital tilt and charge density in graphene, and thus its Fermi level. Therefore, it is expected that the confinement of large P2O5 molecules at the graphene-germanium heterointerface would lead to significant changes to the physical properties of graphene itself. In our case, we show that charge transfer occurs from graphene to P2O5, resulting in a p-type doping of the graphene layer. Raman spectroscopy was used to assess changes in the G and 2D peak positions. In Figure 4a, we compare the Raman spectra between nonintercalated and intercalated samples. After intercalation process, both G and 2D peaks blue-shifted after the intercalation process, resulting from changes in strain and doping of graphene due to intercalation.59,60 Besides the typical G, 2D and D peaks of graphene, a new Raman peak, approximately at 1100 cm–1, was observed (Figure 4a, red solid arrow). This vibrational mode was associated with a 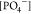Inline graphic unit in the P2O5 cage-like structure, and in our case was activated via charge transfer from graphene to the intercalated P2O5.61 The observation of this vibrational mode in Raman, together with the symmetric stretch of bridging oxygen P–O–P bond (Figure S3), further corroborates the formation of the P2O5 nonplanar cage-like structure at the graphene-substrate heterointerface after intercalation of phosphorus oxide fragments as suggested from our DFT calculations. Furthermore, it is possible to deconvolute the effects of charge transfer and strain on the doping level of graphene by performing a correlation analysis of the G and 2D peak positions between the nonintercalated and intercalated samples (Figure 4b).62 In the intercalated samples, a 12% increase in the hole doping level of graphene was observed when compared to the nonintercalated samples. This was further corroborated by scanning tunneling spectroscopy (STS) dI/dV measurements of the intercalated graphene surface (Figure 4c). The dI/dV curves were collected on the graphene surface in a line scan with a step of ∼1.1 nm. The slope of the dI/dV curve is proportional to the local density of states (LDOS) of the sample at the tunneling site. Two local minima were observed in all dI/dV curves, that is, one at V = 0 which was the phonon scattering gap (green dashed line), and the another at the Dirac point where the LDOS of graphene reaches its minimum (yellow dashed line).63 From Figure 4c, the Dirac point was up-shifted to +425 mV (yellow dashed line) with respect to the Fermi level (V = 0) after intercalation, which indicated that P2O5 led to p-type doping of graphene.

Figure 4.

Figure 4

Open in a new tab

Raman spectra of graphene (a) before (black solid line) and after (red solid line) exposure to an upstream flux of P2O5. (b) Raman 2D versus G peak position of graphene before (black dots) and after (red dots) exposure to an upstream flux of P2O5. (c) STS dI/dV of the intercalated graphene sample. The corresponding phonon scattering gap and Dirac points are highlighted with green dashed line and yellow dashed line, respectively. Spectra are vertically offset for clarity (Tunneling set point = 200 pA, 750 mV).

DFT calculations were also performed to investigate the origins of the observed conductive properties of graphene after intercalation. Given that graphene transferred onto germanium substrates could be subjected to strain,64−66 the impact of possible deformation on the electronic structure of monolayer graphene was studied. Our density of states (DOS) calculations based on (4 × 8) supercells of graphene suggested that the electronic structure near the Fermi level did not undergo significant change, despite an increase in the overall system energy with respect to the increased strain. While compressive and tensile stress led to horizontal stretches and compression of the total DOS, respectively, the overall electronic structure near the Fermi level did not vary (Figure S4). We observed that both pristine and deformed graphenes behaved as semimetals. As a result, strain alone did not significantly contribute to the experimentally observed p-type conductive properties in the Raman and STS measurements. While nonuniform strain and formation of bubbles on the graphene monolayer could cause variations in the distance between graphene and underlying germanium substrate, the impact of the germanium surface on the electronic structure of graphene becomes negligible when the separation reaches ∼2 nm (Figure S5). Notably, even in regions where the graphene monolayer was only a few angstroms from the top layer of the germanium surface atoms, the presence of germanium still does not induce semiconducting behavior in graphene. Similarly, while the exposure to P2O5 caused changes in DOS of graphene far above and below the Fermi level, the overall electronic properties of pristine graphene with adsorbed molecules remained semimetallic, with characteristic converging overlap between the bottom of the conduction band and the peak of valence band (Figure 5a).

Figure 5.

Figure 5

Open in a new tab

Projected DOS of (a) pristine graphene sheet without (black) and with (red and blue) adsorbed phosphorus oxide, (b) graphene with SW- (black), D- (red), and Q-defects (blue) without adsorbed phosphorus oxide. (c) Comparison of p-orbital DOS of graphene with S-defect (black) and with S-defect covalently bound to P atom in chemisorbed P2O5 (red). (d) Differential charge density of P2O5 covalently bound to S-defect. All wireframe isosurfaces denote charge transfer equivalent to 0.001e·Bohr–3. Blue isosurface represents charge loss, and red isosurface indicates charge gain.

Moreover, to elucidate the effect of point defects on altering the bulk conductivity of graphene, the partial DOS of carbon atoms away from the defect sites was also calculated. As shown in Figure 5b, graphene with SW-defects had a conduction band overlapping the valence band at Fermi level, implying semimetallic behaviors as similar to pristine graphene. On the contrary, systems with missing carbon atoms all developed bandgaps and distinct electronic states near the Fermi level. Graphene with S-defects still behaves as a semimetal but develops a gap in its conduction band that is just less than 0.2 eV above the Fermi level. In the case of graphene with D-defects, the bandgap plays an even more noticeable role, as it lies right above the Fermi level, separating the valence band from the conduction band. In systems with Q-defects, the bandgap appears to widen even further, positioning the Fermi level about 0.4 eV above the top of the valence band and 0.7 eV below the bottom of the conduction band. Nevertheless, the enlarged bandgap does not render the system semiconductive. A new, albeit small, state emerges within the band gap and crosses the Fermi level, causing the system to behave more like a metal. Finally, we found that systems whose carbon atoms at defect sites formed covalent bonds to adsorbed P2O5 fragments underwent substantial changes in their electronic structure due to charge transfer between graphene and adsorbed molecules. DOS of carbon atoms in the defected graphene bond to P2O5 is illustrated in Figure S6. In all defected systems, the presence of chemisorbed molecules served to enlarge the bandgap and enhance the states in the bandgap, with P2O5(P) chemisorbed to S-defect being the most notable case (Figure 5c). A summary of these effects is also listed in Table S2. To visualize the loss of electron density in the graphene π-orbitals when P2O5 was covalently bonded to the graphene defect sites, differential charge calculations were employed (Figure 5d). This change in electron charge density is equivalent to hole-doping of the graphene monolayer, which is consistent with our experimental observations.

Synthesis of Metal Phosphates at the Heterointerface

Although phosphorus has limited solubility41 and diffusivity42 into germanium, our XPS analysis of the Ge 3d core-level revealed that the intercalation of P2O5 led to chemical reaction with the germanium substrate. This could have been possible from the intercalated oxygen fragments themselves or the affinity of P2O5(O) to bond with germanium (Figure 2i). To further elucidate other chemical reactions of the intercalated fragments of P2O5 that could take place at graphene-substrate heterointerfaces, we show that this process can also be used to form confined metal phosphates by intercalating P2O5 into a graphene-substrate heterointerface initially containing 2D metals to form indium phosphate as the example in this study (see Methods). Indium phosphate, specifically InPO4, is a wide bandgap insulator (Eg = 4.5 eV)69 with excellent dielectric properties that initially gain interest as a gate material for InP formed via surface oxidation.70−73 However, the formation of dimensionally confined indium phosphates remains largely unexplored, thus impending a more comprehensive understanding of their physical properties and potential applications. In our case, we demonstrated the successful formation of confined indium phosphates by intercalating P2O5 into a graphene-SiC heterointerface initially containing confined mono- to bilayer indium also formed by intercalation.17,74 We identified the composition of the confined indium phosphate at the heterointerface by investigating the In and P core-levels using high-resolution XPS (Figure 6a,b, respectively). In Figure 6a, we compare the core levels of In 3d, before (black solid line) and after (blue solid line) intercalation of P2O5 to the graphene-substrate heterointerface containing 2D indium, to the In 3d core level of a pure In2O3 reference sample (red solid line). In addition to the typical peaks for indium metal (black dashed line), the XPS spectra exhibited new peaks around 445.8 and 453.3 eV in the intercalated sample (blue dashed line). These two new peaks were up-shifted by 1.1 eV from the peak position of the In2O3 reference (red dashed line).75 Furthermore, a strong phosphorus signal was detected in samples intercalated with P2O5 (Figure 6b). Therefore, based on these observations, we can exclude the formation of In2O3 in the P2O5 intercalated samples. Further inspection and comparison of our XPS core-level spectra to previous reported XPS of indium phosphates suggest that the peaks at 445.8 and 453.3 eV are the In 3d core-levels associated with P–O–In 3d3/2 and P–O–In 3d5/2 bonding, respectively. Although the phase of the confined indium phosphate at the graphene-substrate heterointerface was likely in the form of InPO4, In(PO3)3 and other metastable oxide phases could also form at such confined spaces38,67,68 and therefore are important to investigate in future studies.

Figure 6.

Figure 6

Open in a new tab

XPS core levels of (a) In 3d for 2D indium confined at the graphene-SiC heterointerface before (black solid line) and after exposure to P2O5 (blue solid line). The XPS spectra for a pure In2O3 crystal (red solid line) are also included as a reference. The defined range for InPO4 peak positions were evaluated based on data in reference67,68 and is highlighted with a shaded gray region. (b) P 2p for the confined 2D indium after exposure to P2O5.

Conclusions

In summary, we demonstrated that large molecules, such as P2O5, can permeate the basal plane of graphene and intercalate into the heterointerface. This was evident from the strong P and O signals that were detected underneath the graphene surface from spectroscopic measurements (EDS, nano-FTIR, XPS, Raman, and STS) and microscopic cross-sectional imaging and analysis in TEM. Although the physical size of the molecule was larger than that of the graphene lattice, fragments of the molecule could intercalate through typical pathways in the graphene lattice. This was revealed by calculating the penetration barriers for fragments of P2O5 of varied size and chemistry through pristine and defected graphene of different configurations. The complexity of the interaction process of large molecules through the basal plane of graphene cannot be generalized into a single step process. However, a two-step mechanism, based on realistic permeation energy barriers, was proposed for the intercalation of P2O5: (i) P2O5 first dissociated into small fragments (i.e., P, O, etc.) catalyzed by point defects in the graphene lattice; (ii) these fragments once intercalated can chemically react at the confined graphene–substrate heterointerface forming a condensed phase that chemically resembles the initial state of the molecule. It has been shown that the intercalation of P2O5 at the graphene-substrate heterointerface could effectively tune the doping level of graphene via charge transfer. Moreover, the intercalated P2O5 (and/or its fragments) can also act as reactants and further contribute to other interfacial reactions, for example, the conversion of 2D indium into 2D indium phosphate at the heterointerface between graphene and SiC. Although our findings only focus on indium phosphates, our results demonstrate the potential of this approach for the conversion of other metals (e.g., Ga, Al, etc.) and alloys. Furthermore, spatial control over the distribution of defects, such as localized irradiation using plasma processing,76 can promote the selective area intercalation of metals and/or alloys under specific regions of graphene. While the focus of this study is on P2O5 intercalation, the possibility of intercalation from predissociated molecules catalyzed by defects in graphene may exist for other types of molecules as well. This in-depth study advances the comprehension of intercalation routes of large molecules via the basal plane of graphene as well as heterointerface chemical reactions leading to the formation of distinctive confined complex oxide compounds.

Methods

Intercalation of P2O5 at Graphene–Substrate Heterointerfaces

The intercalation process was performed at 1 atm in a single-zone furnace under argon flow. Two kinds of samples were used in this study: transferred CVD graphene (Graphenea) onto cleaned Ge(110) substrates (MTI Corp.) and 2D indium samples intercalated at graphene-SiC(0001) heterointerface, as reported by Rajabpour et al.17 SiP2O7 (Saint-Gobain Inc.) was utilized to produce an upstream flux of P2O5 to the samples. First, the center of the furnace was set to 950 °C at a ramping rate of 55 °C/min (stage I) and then dwelled at 950 °C for 45 min (stage II). In stage II, the measured temperature for the sample and SiP2O7 was 600 and 950 °C, respectively. Samples were then naturally cooled to room temperature under argon flow.

Materials Characterization

SEM and EDS were performed on a Thermo Fisher Scios 2 dual-beam microscope. The cross-sectional samples of graphene bubbles for TEM analysis were prepared using a focused ion beam (FIB) Zeiss NVision 40 FIB-SEM. The target location was extracted from the specimen and attached to a copper FIB grid using a conventional FIB milling and lift-out procedure. The HAADF image and STEM-EDS mappings on the cross-section of graphene bubbles were collected with a Thermo Fisher Scientific Talos 200× operated at 200 kV. HAADF was performed with a spot size less than 1 nm with a convergence semiangle of 10.5 mrad. Furthermore, XPS spectra and depth profiles were carried out in a Thermo-Fisher K-Alpha Plus XPS system and in a Kratos Axis Ultra DLD system using a monochromatic Al Kα source (hν = 1486.6 eV). Raman measurements were performed on a Renishaw inVia system with a 488 nm laser (maximum power at 100 mW). STM was performed in a closed-cycle RHK Pan Scan Freedom SPM system in UHV (∼1 × 10–10 mbar) at a base temperature of 10 K. dI/dV measurements were taken using a built-in digital lock-in amplifier operating at 1.3156 kHz with a 10 mV excitation amplitude. Moreover, nano-FTIR of the graphene bubbles was performed on a commercial scattering-type scanning near-field optical microscope (s-SNOM) setup (Neaspec Inc.), and the collected spectra were normalized to that obtained on a silicon sample using the same acquisition parameters. Nano-FTIR of the P2O5 reference sample was performed on a synchrotron infrared light-based nano-spectroscopy (SINS) setup (Innova, Bruker) (beamline 5.4, Advanced Light Source, Lawrence Berkeley National Laboratory).

First-Principles Calculation

DFT calculations were performed using the generalized gradient approximation (GGA) with the Vienna ab initio simulation package. The projector-augmented-wave (PAW) method was used, and Grimme’s DFT+D2 was applied to better account for the van der Waal’s interaction between graphene monolayer and absorbed species.77 The kinetic energy cutoff was set at 500 eV, and the global convergence criterion for breaking electronic SC-loop was chosen to be 5 × 10–5. A vacuum space of 22 Å was applied on top of the graphene sheet to best model the isolated state of a monolayer. Γ point sampling was used throughout all calculations. For relaxations and nudged elastic band (NEB) calculations, a grid of 5 × 4 × 1 was used. To obtain density of states (DOS), a grid of 9 × 9 × 1 was adopted for best precision. For more information on simulating the reaction mechanism, see the Supporting Information.

Acknowledgments

Z.Y.A. acknowledges the support of this work through the Laboratory Directed Research and Development (LDRD) Program of Lawrence Berkeley National Laboratory under U.S. Department of Energy Contract No. DE-AC02-05CH11231 and the Canadian Institute for Advanced Research (CIFAR) under the Azrieli Global Scholars Program in Quantum Materials. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Some of the XPS analysis was performed under a collaboration with the Liquid Sunlight Alliance, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Fuels from Sunlight Hub under award number DESC0021266. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under no. DE-AC02-05CH11231. J.D.C. gratefully acknowledges support for this work from the Office of Naval Research grant N00014-22-12035. G. L. is supported through Army Research Office Small Business Technology Transfer (W911NF-22-P-0029). J.A.R, C.D., T.F. and S.R. acknowledge the support of the Air Force Office of Scientific Research (AFOSR) through contract FA9550-19-1-0295 and the 2D Crystal Consortium a National Science Foundation Materials Innovation Platform, under cooperative agreement DMR-1539916. M.P.S. acknowledges the support of the National Supercomputing Centre (NSCC) Singapore via the Project ID 13002533 and the support of the nanoQuench project (CHED PCARI IIID-2016-007). Finally, the authors would thank Dr. Hao Chen for providing In2O3 XPS calibration data for this study.

Data Availability Statement

All data needed to evaluate the conclusions in the paper are present in the manuscript and/or the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.3c07763.

  • Additional information including details of graphene transfer process and first-principles calculation, intercalation of P2O5 molecule through a defect of 9 vacant atoms, XPS depth profile for graphene/Ge (110) after exposure to P2O5, projected DOS of carbon atoms in deformed graphene sheet, projected DOS of carbon in defected graphene with P2O5 adsorbed to atoms at defect site (PDF)

Author Contributions

J.L. performed all the intercalation experiments, SEM, SEM-EDS, and Raman characterization. K.M. and M.S. performed and analyzed all the theoretical calculations. C.D., T.F. and S.R. grew the epitaxial graphene and intercalated the indium under the supervision of J.A.R. C.A. and N.B. collected and analyzed all the cross-section STEM-EDS and HAADF results. G.L., J.C., H.B., and J.L. performed and analyzed the nano-FTIR characterization. X.Z., M.S., J.L., R.P., J.A., and S.A. performed and analyzed XPS characterization. J.R. and S.H. performed and analyzed STM and STS measurements. Z.A. conceived the idea and supervised the project. J.L., K.M., and Z.A. wrote the manuscript. All authors discussed, revised, and approved the manuscript.

The authors declare no competing financial interest.

Supplementary Material

am3c07763_si_001.pdf (3.1MB, pdf)

References

  1. Dresselhaus M.; Dresselhaus G. Intercalation Compounds of Graphite. Adv. Phys. 1981, 30, 139–326. 10.1080/00018738100101367. [DOI] [Google Scholar]
  2. Whittingham M. S. Intercalation Chemistry: An Introduction. Intercalation chem. 1982, 1–18. [Google Scholar]
  3. Sutter P.; Sadowski J. T.; Sutter E. A. Chemistry under Cover: Tuning Metal– Graphene Interaction by Reactive Intercalation. J. Am. Chem. Soc. 2010, 132, 8175–8179. 10.1021/ja102398n. [DOI] [PubMed] [Google Scholar]
  4. Jin L.; Fu Q.; Mu R.; Tan D.; Bao X. Pb Intercalation Underneath a Graphene Layer on Ru (0001) and Its Effect on Graphene Oxidation. Phys. Chem. Chem. Phys. 2011, 13, 16655–16660. 10.1039/c1cp21843c. [DOI] [PubMed] [Google Scholar]
  5. Cui Y.; Gao J.; Jin L.; Zhao J.; Tan D.; Fu Q.; Bao X. An Exchange Intercalation Mechanism for the Formation of a Two-Dimensional Si Structure Underneath Graphene. Nano Research 2012, 5, 352–360. 10.1007/s12274-012-0215-4. [DOI] [Google Scholar]
  6. Jin L.; Fu Q.; Yang Y.; Bao X. A Comparative Study of Intercalation Mechanism at Graphene/Ru (0001) Interface. Surface science 2013, 617, 81–86. 10.1016/j.susc.2013.07.008. [DOI] [Google Scholar]
  7. Petrović M.; Šrut Rakić I.; Runte S.; Busse C.; Sadowski J.; Lazić P.; Pletikosić I.; Pan Z.-H.; Milun M.; Pervan P. The Mechanism of Caesium Intercalation of Graphene. Nat. Commun. 2013, 4, 2772. 10.1038/ncomms3772. [DOI] [PubMed] [Google Scholar]
  8. Li G.; Zhou H.; Pan L.; Zhang Y.; Huang L.; Xu W.; Du S.; Ouyang M.; Ferrari A. C.; Gao H.-J. Role of Cooperative Interactions in the Intercalation of Heteroatoms between Graphene and a Metal Substrate. J. Am. Chem. Soc. 2015, 137, 7099–7103. 10.1021/ja5113657. [DOI] [PubMed] [Google Scholar]
  9. Hui J.; Burgess M.; Zhang J.; Rodríguez-López J. Layer Number Dependence of Li+ Intercalation on Few-Layer Graphene and Electrochemical Imaging of Its Solid–Electrolyte Interphase Evolution. ACS Nano 2016, 10, 4248–4257. 10.1021/acsnano.5b07692. [DOI] [PubMed] [Google Scholar]
  10. Xia C.; Watcharinyanon S.; Zakharov A.; Yakimova R.; Hultman L.; Johansson L. I.; Virojanadara C. Si Intercalation/Deintercalation of Graphene on 6h-Sic (0001). Phys. Rev. B 2012, 85, 045418 10.1103/PhysRevB.85.045418. [DOI] [Google Scholar]
  11. Bointon T. H.; Khrapach I.; Yakimova R.; Shytov A. V.; Craciun M. F.; Russo S. Approaching Magnetic Ordering in Graphene Materials by Fecl3 Intercalation. Nano Lett. 2014, 14, 1751–1755. 10.1021/nl4040779. [DOI] [PubMed] [Google Scholar]
  12. Eda G.; Fujita T.; Yamaguchi H.; Voiry D.; Chen M.; Chhowalla M. Coherent Atomic and Electronic Heterostructures of Single-Layer Mos2. ACS Nano 2012, 6, 7311–7317. 10.1021/nn302422x. [DOI] [PubMed] [Google Scholar]
  13. Koski K. J.; Wessells C. D.; Reed B. W.; Cha J. J.; Kong D.; Cui Y. Chemical Intercalation of Zerovalent Metals into 2d Layered Bi2se3 Nanoribbons. J. Am. Chem. Soc. 2012, 134, 13773–13779. 10.1021/ja304925t. [DOI] [PubMed] [Google Scholar]
  14. Kovtyukhova N. I.; Wang Y.; Lv R.; Terrones M.; Crespi V. H.; Mallouk T. E. Reversible Intercalation of Hexagonal Boron Nitride with Brønsted Acids. J. Am. Chem. Soc. 2013, 135, 8372–8381. 10.1021/ja403197h. [DOI] [PubMed] [Google Scholar]
  15. Voiry D.; Salehi M.; Silva R.; Fujita T.; Chen M.; Asefa T.; Shenoy V. B.; Eda G.; Chhowalla M. Conducting Mos2 Nanosheets as Catalysts for Hydrogen Evolution Reaction. Nano Lett. 2013, 13, 6222–6227. 10.1021/nl403661s. [DOI] [PubMed] [Google Scholar]
  16. Ohzuku T.; Iwakoshi Y.; Sawai K. Formation of Lithium-Graphite Intercalation Compounds in Nonaqueous Electrolytes and Their Application as a Negative Electrode for a Lithium Ion (Shuttlecock) Cell. J. Electrochem. Soc. 1993, 140, 2490. 10.1149/1.2220849. [DOI] [Google Scholar]
  17. Rajabpour S.; Vera A.; He W.; Katz B. N.; Koch R. J.; Lassaunière M.; Chen X.; Li C.; Nisi K.; El-Sherif H. Tunable 2d Group-Iii Metal Alloys. Adv. Mater. 2021, 33, 2104265. 10.1002/adma.202104265. [DOI] [PubMed] [Google Scholar]
  18. Warmuth J.; Bruix A.; Michiardi M.; Hänke T.; Bianchi M.; Wiebe J.; Wiesendanger R.; Hammer B.; Hofmann P.; Khajetoorians A. A. Band-Gap Engineering by Bi Intercalation of Graphene on Ir (111). Phys. Rev. B 2016, 93, 165437 10.1103/PhysRevB.93.165437. [DOI] [Google Scholar]
  19. Shen K.; Sun H.; Hu J.; Hu J.; Liang Z.; Li H.; Zhu Z.; Huang Y.; Kong L.; Wang Y. Fabricating Quasi-Free-Standing Graphene on a Sic (0001) Surface by Steerable Intercalation of Iron. J. Phys. Chem. C 2018, 122, 21484–21492. 10.1021/acs.jpcc.8b06789. [DOI] [Google Scholar]
  20. Wolff S.; Roscher S.; Timmermann F.; Daniel M. V.; Speck F.; Wanke M.; Albrecht M.; Seyller T. Quasi-Freestanding Graphene on Sic (0001) by Ar-Mediated Intercalation of Antimony: A Route toward Intercalation of High-Vapor-Pressure Elements. Ann. Phys. 2019, 531, 1900199. 10.1002/andp.201900199. [DOI] [Google Scholar]
  21. Link S.; Forti S.; Stöhr A.; Küster K.; Rösner M.; Hirschmeier D.; Chen C.; Avila J.; Asensio M.; Zakharov A. Introducing Strong Correlation Effects into Graphene by Gadolinium Intercalation. Phys. Rev. B 2019, 100, 121407. 10.1103/PhysRevB.100.121407. [DOI] [Google Scholar]
  22. Klimovskikh I. I.; Otrokov M. M.; Voroshnin V. Y.; Sostina D.; Petaccia L.; Di Santo G.; Thakur S.; Chulkov E. V.; Shikin A. M. Spin–Orbit Coupling Induced Gap in Graphene on Pt (111) with Intercalated Pb Monolayer. ACS Nano 2017, 11, 368–374. 10.1021/acsnano.6b05982. [DOI] [PubMed] [Google Scholar]
  23. Granas E.; Andersen M.; Arman M. A.; Gerber T.; Hammer B. r.; Schnadt J.; Andersen J. N.; Michely T.; Knudsen J. Co Intercalation of Graphene on Ir (111) in the Millibar Regime. J. Phys. Chem. C 2013, 117, 16438–16447. 10.1021/jp4043045. [DOI] [Google Scholar]
  24. Zhang H.; Fu Q.; Cui Y.; Tan D.; Bao X. Growth Mechanism of Graphene on Ru (0001) and O2 Adsorption on the Graphene/Ru (0001) Surface. J. Phys. Chem. C 2009, 113, 8296–8301. 10.1021/jp810514u. [DOI] [Google Scholar]
  25. Leenaerts O.; Partoens B.; Peeters F. Graphene: A Perfect Nanoballoon. Appl. Phys. Lett. 2008, 93, 193107. 10.1063/1.3021413. [DOI] [Google Scholar]
  26. Sun P.; Yang Q.; Kuang W.; Stebunov Y.; Xiong W.; Yu J.; Nair R. R.; Katsnelson M.; Yuan S.; Grigorieva I. Limits on Gas Impermeability of Graphene. Nature 2020, 579, 229–232. 10.1038/s41586-020-2070-x. [DOI] [PubMed] [Google Scholar]
  27. Zhou J.; Lin Z.; Ren H.; Duan X.; Shakir I.; Huang Y.; Duan X. Layered Intercalation Materials. Adv. Mater. 2021, 33, 2004557. 10.1002/adma.202004557. [DOI] [PubMed] [Google Scholar]
  28. Wan J.; Lacey S. D.; Dai J.; Bao W.; Fuhrer M. S.; Hu L. Tuning Two-Dimensional Nanomaterials by Intercalation: Materials, Properties and Applications. Chem. Soc. Rev. 2016, 45, 6742–6765. 10.1039/C5CS00758E. [DOI] [PubMed] [Google Scholar]
  29. Rajapakse M.; Karki B.; Abu U. O.; Pishgar S.; Musa M. R. K.; Riyadh S. S.; Yu M.; Sumanasekera G.; Jasinski J. B. Intercalation as a Versatile Tool for Fabrication, Property Tuning, and Phase Transitions in 2d Materials. npj 2D Mater. Appl. 2021, 5, 30. 10.1038/s41699-021-00211-6. [DOI] [Google Scholar]
  30. Kim H.; Dugerjav O.; Lkhagvasuren A.; Seo J. M. Doping Modulation of Quasi-Free-Standing Monolayer Graphene Formed on Sic (0001) through Sn1-Xgex Intercalation. Carbon 2019, 144, 549–556. 10.1016/j.carbon.2018.12.084. [DOI] [Google Scholar]
  31. Avvisati G.; Gargiani P.; Lizzit D.; Valvidares M.; Lacovig P.; Petrillo C.; Sacchetti F.; Betti M. G. Strong Ferromagnetic Coupling and Tunable Easy Magnetization Directions of Fexco1– X Layer (S) Intercalated under Graphene. Appl. Surf. Sci. 2020, 527, 146599 10.1016/j.apsusc.2020.146599. [DOI] [Google Scholar]
  32. Al Balushi Z. Y.; Wang K.; Ghosh R. K.; Vilá R. A.; Eichfeld S. M.; Caldwell J. D.; Qin X.; Lin Y.-C.; DeSario P. A.; Stone G. Two-Dimensional Gallium Nitride Realized Via Graphene Encapsulation. Nat. mater. 2016, 15, 1166–1171. 10.1038/nmat4742. [DOI] [PubMed] [Google Scholar]
  33. Feldberg N.; Klymov O.; Garro N.; Cros A.; Mollard N.; Okuno H.; Gruart M.; Daudin B. Spontaneous Intercalation of Ga and in Bilayers During Plasma-Assisted Molecular Beam Epitaxy Growth of Gan on Graphene on Sic. Nanotechnology 2019, 30, 375602. 10.1088/1361-6528/ab261f. [DOI] [PubMed] [Google Scholar]
  34. Wang W.; Li Y.; Zheng Y.; Li X.; Huang L.; Li G. Lattice Structure and Bandgap Control of 2d Gan Grown on Graphene/Si Heterostructures. Small 2019, 15, 1802995. 10.1002/smll.201802995. [DOI] [PubMed] [Google Scholar]
  35. Wang W.; Zheng Y.; Li X.; Li Y.; Zhao H.; Huang L.; Yang Z.; Zhang X.; Li G. 2d Aln Layers Sandwiched between Graphene and Si Substrates. Adv. Mater. 2019, 31, 1803448. 10.1002/adma.201803448. [DOI] [PubMed] [Google Scholar]
  36. Michałowski P. P.; Knyps P.; Ciepielewski P.; Caban P. A.; Dumiszewska E.; Kowalski G.; Tokarczyk M.; Baranowski J. M. Growth of Highly Oriented Mos2 Via an Intercalation Process in the Graphene/Sic (0001) System. Phys. Chem. Chem. Phys. 2019, 21, 20641–20646. 10.1039/C9CP03846A. [DOI] [PubMed] [Google Scholar]
  37. Fu J.; Hong M.; Shi J.; Xie C.; Jiang S.; Shang Q.; Zhang Q.; Shi Y.; Huan Y.; Zhang Z. Intercalation-Mediated Synthesis and Interfacial Coupling Effect Exploration of Unconventional Graphene/Ptse2 Vertical Heterostructures. ACS Appl. Mater. Interfaces 2019, 11, 48221–48229. 10.1021/acsami.9b16748. [DOI] [PubMed] [Google Scholar]
  38. Turker F.; Dong C.; Wetherington M. T.; El-Sherif H.; Holoviak S.; Trdinich Z. J.; Lawson E. T.; Krishnan G.; Whittier C.; Sinnott S. B. 2d Oxides Realized Via Confinement Heteroepitaxy. Adv. Funct. Mater. 2023, 33, 2210404. 10.1002/adfm.202210404. [DOI] [Google Scholar]
  39. Hoppe U.; Walter G.; Barz A.; Stachel D.; Hannon A. The Po Bond Lengths in Vitreous Probed by Neutron Diffraction with High Real-Space Resolution. J. Phys.: Condens. Matter 1998, 10, 261. 10.1088/0953-8984/10/2/004. [DOI] [Google Scholar]
  40. Tian W.; Li W.; Yu W.; Liu X. A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation. Micromachines 2017, 8, 163. 10.3390/mi8050163. [DOI] [Google Scholar]
  41. Olesinski R.; Kanani N.; Abbaschian G. The Ge– P (Germanium-Phosphorus) System. Bull. Alloy Phase Diagrams 1985, 6, 262–266. 10.1007/BF02880412. [DOI] [Google Scholar]
  42. Cai Y.; Camacho-Aguilera R.; Bessette J. T.; Kimerling L. C.; Michel J. High Phosphorous Doped Germanium: Dopant Diffusion and Modeling. J. Appl. Phys. 2012, 112, 034509 10.1063/1.4745020. [DOI] [Google Scholar]
  43. Tien T.; Hummel F. The System Sio2-P2o5. J. Am. Ceram. Soc. 1962, 45, 422–424. 10.1111/j.1151-2916.1962.tb11186.x. [DOI] [Google Scholar]
  44. Jones N.; Metz D.; Stach J.; Tressler R. A Solid Planar Source for Phosphorus Diffusion. J. Electrochem. Soc. 1976, 123, 1565. 10.1149/1.2132638. [DOI] [Google Scholar]
  45. Flemish J.; Tressler R. Pxoy Evaporation from Sip2o7 and Its Relationship to Phosphosilicate Glass Films. J. Electrochem. Soc. 1991, 138, 3743. 10.1149/1.2085492. [DOI] [Google Scholar]
  46. Bunch J. S.; Verbridge S. S.; Alden J. S.; Van Der Zande A. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Impermeable Atomic Membranes from Graphene Sheets. Nano Lett. 2008, 8, 2458–2462. 10.1021/nl801457b. [DOI] [PubMed] [Google Scholar]
  47. Huth F.; Govyadinov A.; Amarie S.; Nuansing W.; Keilmann F.; Hillenbrand R. Nano-Ftir Absorption Spectroscopy of Molecular Fingerprints at 20 Nm Spatial Resolution. Nano Lett. 2012, 12, 3973–3978. 10.1021/nl301159v. [DOI] [PubMed] [Google Scholar]
  48. Bechtel H. A.; Muller E. A.; Olmon R. L.; Martin M. C.; Raschke M. B. Ultrabroadband Infrared Nanospectroscopic Imaging. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 7191–7196. 10.1073/pnas.1400502111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Dayanand C.; Bhikshamaiah G.; Tyagaraju V. J.; Salagram M.; Krishna Murthy A. Structural Investigations of Phosphate Glasses: A Detailed Infrared Study of the X(Pbo)-(1– X) P2o5 Vitreous System. J. Mater. Sci. 1996, 31, 1945–1967. 10.1007/BF00356615. [DOI] [Google Scholar]
  50. Wang Y.; Sherwood P. M. Phosphorus Pentoxide (P2o5) by Xps. Surf. Sci. Spectra 2002, 9, 159–165. 10.1116/11.20030115. [DOI] [Google Scholar]
  51. Song B.; Pan L. Penetration of the First-Two-Row Elements through Mono-Layer Graphene. Carbon 2016, 109, 117–123. 10.1016/j.carbon.2016.07.065. [DOI] [Google Scholar]
  52. Sreeprasad T.; Berry V. How Do the Electrical Properties of Graphene Change with Its Functionalization?. small 2013, 9, 341–350. 10.1002/smll.201202196. [DOI] [PubMed] [Google Scholar]
  53. Wu Q.; Wu Y.; Hao Y.; Geng J.; Charlton M.; Chen S.; Ren Y.; Ji H.; Li H.; Boukhvalov D. W. Selective Surface Functionalization at Regions of High Local Curvature in Graphene. Chem. Commun. 2012, 49, 677–679. 10.1039/C2CC36747E. [DOI] [PubMed] [Google Scholar]
  54. Huttmann F.; Martínez-Galera A. J.; Caciuc V.; Atodiresei N.; Schumacher S.; Standop S.; Hamada I.; Wehling T. O.; Blügel S.; Michely T. Tuning the Van Der Waals Interaction of Graphene with Molecules Via Doping. Phys. Rev. Lett. 2015, 115, 236101 10.1103/PhysRevLett.115.236101. [DOI] [PubMed] [Google Scholar]
  55. Banerjee S.; Rappe A. M. Mechanochemical Molecular Migration on Graphene. J. Am. Chem. Soc. 2022, 144, 7181–7188. 10.1021/jacs.1c13193. [DOI] [PubMed] [Google Scholar]
  56. Levy N.; Burke S.; Meaker K.; Panlasigui M.; Zettl A.; Guinea F.; Neto A. C.; Crommie M. F. Strain-Induced Pseudo-Magnetic Fields Greater Than 300 T in Graphene Nanobubbles. Science 2010, 329, 544–547. 10.1126/science.1191700. [DOI] [PubMed] [Google Scholar]
  57. Khestanova E.; Guinea F.; Fumagalli L.; Geim A.; Grigorieva I. Universal Shape and Pressure inside Bubbles Appearing in Van Der Waals Heterostructures. Nat. Commun. 2016, 7, 12587. 10.1038/ncomms12587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Sanchez D. A.; Dai Z.; Lu N. 2d Material Bubbles: Fabrication, Characterization, and Applications. Trends Chem. 2021, 3, 204–217. 10.1016/j.trechm.2020.12.011. [DOI] [Google Scholar]
  59. Ferrari A. C. Raman Spectroscopy of Graphene and Graphite: Disorder, Electron–Phonon Coupling, Doping and Nonadiabatic Effects. Solid State Commun. 2007, 143, 47–57. 10.1016/j.ssc.2007.03.052. [DOI] [Google Scholar]
  60. Ferrari A. C.; Basko D. M. Raman Spectroscopy as a Versatile Tool for Studying the Properties of Graphene. Nat. Nanotechnol. 2013, 8, 235–246. 10.1038/nnano.2013.46. [DOI] [PubMed] [Google Scholar]
  61. Hudgens J. J.; Brow R. K.; Tallant D. R.; Martin S. W. Raman Spectroscopy Study of the Structure of Lithium and Sodium Ultraphosphate Glasses. J. Non-Cryst. Solids 1998, 223, 21–31. 10.1016/S0022-3093(97)00347-5. [DOI] [Google Scholar]
  62. Lee J. E.; Ahn G.; Shim J.; Lee Y. S.; Ryu S. Optical Separation of Mechanical Strain from Charge Doping in Graphene. Nat. Commun. 2012, 3, 1024. 10.1038/ncomms2022. [DOI] [PubMed] [Google Scholar]
  63. Zhang Y.; Brar V. W.; Wang F.; Girit C.; Yayon Y.; Panlasigui M.; Zettl A.; Crommie M. F. Giant Phonon-Induced Conductance in Scanning Tunnelling Spectroscopy of Gate-Tunable Graphene. Nat. Phys. 2008, 4, 627–630. 10.1038/nphys1022. [DOI] [Google Scholar]
  64. Dai J.; Wang D.; Zhang M.; Niu T.; Li A.; Ye M.; Qiao S.; Ding G.; Xie X.; Wang Y. How Graphene Islands Are Unidirectionally Aligned on the Ge (110) Surface. Nano Lett. 2016, 16, 3160–3165. 10.1021/acs.nanolett.6b00486. [DOI] [PubMed] [Google Scholar]
  65. Chen W.; Wang X.; Li S.; Yan C.; He L.; Zhang P.; Yang Y.; Ma D.; Nie J.; Dou R. Robust Atomic-Structure of the 6× 2 Reconstruction Surface of Ge (110) Protected by the Electronically Transparent Graphene Monolayer. Phys. Chem. Chem. Phys. 2020, 22, 22711–22718. 10.1039/D0CP03322G. [DOI] [PubMed] [Google Scholar]
  66. Sutter P.; Hybertsen M.; Sadowski J.; Sutter E. Electronic Structure of Few-Layer Epitaxial Graphene on Ru (0001). Nano Lett. 2009, 9, 2654–2660. 10.1021/nl901040v. [DOI] [PubMed] [Google Scholar]
  67. Hollinger G.; Bergignat E.; Joseph J.; Robach Y. On the Nature of Oxides on Inp Surfaces. J. Vac. Sci. Technol., A 1985, 3, 2082–2088. 10.1116/1.572928. [DOI] [Google Scholar]
  68. Faur M.; Faur M.; Jayne D.; Goradia M.; Goradia C. Xps Investigation of Anodic Oxides Grown on P-Type Inp. Surf. Interface Anal. 1990, 15, 641–650. 10.1002/sia.740151102. [DOI] [Google Scholar]
  69. Wager J.; Wilmsen C.; Kazmerski L. Estimation of the Band Gap of Inpo4. Appl. Phys. Lett. 1983, 42, 589–591. 10.1063/1.94003. [DOI] [Google Scholar]
  70. Torii Y.; Hattori K. On the Electrical Properties of the Inpxoy-Inp Interface. Thin solid films 1991, 202, 29–37. 10.1016/0040-6090(91)90538-9. [DOI] [Google Scholar]
  71. Albanesi E.; Sferco S.; Lefebvre I.; Allan G.; Lannoo M. Electronic Structure of Crystalline Inp Oxides. Solid State Commun. 1993, 86, 27–31. 10.1016/0038-1098(93)90242-F. [DOI] [Google Scholar]
  72. Simon N.; Pascanut C. D.; Santinacci L.; Goncalves A.-M.; Joudrier A.-L.; Etcheberry A. Morphology, Composition and Electrical Properties of Thin Anodic Oxides on Inp. ECS Trans. 2009, 19, 273. 10.1149/1.3120707. [DOI] [Google Scholar]
  73. Ouerdane A.; Bouslama M.; Ghaffour M.; Abdellaoui A.; Hamaida K.; Lounis Z.; Monteil Y.; Berrouachedi N.; Ouhaibi A. Study by Eels and Epes of the Stability of Inpo4/Inp System. Appl. Surf. Sci. 2008, 254, 7394–7400. 10.1016/j.apsusc.2008.05.345. [DOI] [Google Scholar]
  74. Briggs N.; Bersch B.; Wang Y.; Jiang J.; Koch R. J.; Nayir N.; Wang K.; Kolmer M.; Ko W.; De La Fuente Duran A. Atomically Thin Half-Van Der Waals Metals Enabled by Confinement Heteroepitaxy. Nat. mater. 2020, 19, 637–643. 10.1038/s41563-020-0631-x. [DOI] [PubMed] [Google Scholar]
  75. Chen H.; Blatnik M. A.; Ritterhoff C. L.; Sokolović I.; Mirabella F.; Franceschi G.; Riva M.; Schmid M.; Čechal J.; Meyer B. Water Structures Reveal Local Hydrophobicity on the In2o3 (111) Surface. ACS Nano 2022, 16, 21163–21173. 10.1021/acsnano.2c09115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Al Balushi Z. Y.; Miyagi T.; Lin Y.-C.; Wang K.; Calderin L.; Bhimanapati G.; Redwing J. M.; Robinson J. A. The Impact of Graphene Properties on Gan and Aln Nucleation. Surf. Sci. 2015, 634, 81–88. 10.1016/j.susc.2014.11.020. [DOI] [Google Scholar]
  77. Grimme S. Semiempirical Gga-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am3c07763_si_001.pdf (3.1MB, pdf)

Data Availability Statement

All data needed to evaluate the conclusions in the paper are present in the manuscript and/or the Supporting Information.

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES