Abstract
Introduced more than a half-century ago, Granger causality has become a popular tool for analyzing time series data in many application domains, from economics and finance to genomics and neuroscience. Despite this popularity, the validity of this framework for inferring causal relationships among time series has remained the topic of continuous debate. Moreover, while the original definition was general, limitations in computational tools have constrained the applications of Granger causality to primarily simple bivariate vector autoregressive processes. Starting with a review of early developments and debates, this article discusses recent advances that address various shortcomings of the earlier approaches, from models for high-dimensional time series to more recent developments that account for nonlinear and non-Gaussian observations and allow for subsampled and mixed-frequency time series.
Keywords: multivariate time series, vector autoregressive model, graphical models, penalized estimation, deep neural networks, mixed-frequency time series
1. INTRODUCTION
There is a range of applications where the interest is in understanding interactions between a set of time series, including in neuroscience, genomics, econometrics, climate science, and social media analysis. For example, in neuroscience, one may seek to understand whether activity in one brain region correlates with later activity in another region, or to decipher instantaneous correlations between regions—both notions of functional connectivity. In genomics, there is an analogous study of gene regulatory networks. In econometrics, one may be interested in how various macroeconomic indicators predict one another. We also have unprecedented levels of data on people’s actions—including social media posts, purchase histories, and political voting records—and want to understand the dependencies between the actions of these individuals. Modern recording modalities and the ability to store and process large amounts of data have escalated the scale at which we seek to do such analyses.
In many cases, one may seek notions of causal interactions among the time series but be limited to drawing inferences from observational data without opportunities for experimentation and without known mechanistic models for the observed phenomena. In such cases, Granger (1969) put forth a framework leveraging the temporal ordering inherent to time series in hopes of drawing causal statements restricted to the past causing the future. The framework, in reality, assesses whether one series is predictive of another: A series is deemed not to be “causal” of another series if leveraging the history of series does not reduce the variance of the prediction of series . In this review, we distinguish this definition from other standard definitions of causality by referring to it as Granger causality. Although there is a long history of debate about the validity of the Granger causality framework for causal analyses—and justly so—in this review we take the stance that analyzing interactions in time series defined by association has its utility.
Granger causality has traditionally relied on assuming a linear vector autoregressive (VAR) model (Lütkepohl 2005) and considering tests on the VAR coefficients in the bivariate setting. However, in real-world systems involving many time series, considering the relationship between just a pair of series can lead to confounded inferences (e.g., Lütkepohl 1982). Network Granger causality aims to adjust for possible confounders or jointly consider multiple series (Eichler 2007, Basu et al. 2015). There are other important limitations of the linear VAR model underlying standard Granger causal analysis that have precluded its broad utility. Some limiting assumptions include assuming (a) real-valued time series with (b) linear dynamics dependent on (c) a known number of past lagged observations, with (d) observations available at a fixed, discrete sampling rate that matches the time scale of the causal structure of interest. In contrast, modern time series are often messy in ways that break a number of these assumptions, including through nonlinear dynamics and irregular sampling. Recent advances have pushed the envelope on where Granger causality can be applied by loosening these restrictions in a variety of ways. We review some of these advances and set the stage for further developments.
1.1. Outline of Review
In Section 2 we review the history of Granger causality, starting with the original definition and assumptions in Section 2.1 and early approaches for testing in Section 2.2. We then turn to network Granger causality and the issues of lag selection and nonstationary VAR models in Section 3. Finally, in Section 4 we review recent advances that move beyond the standard linear VAR model and consider discrete-valued series (Section 4.1), nonlinear dynamics and interactions (Section 4.2), and series observed at different sampling rates (Section 4.3).
2. THE HISTORY OF GRANGER CAUSALITY
2.1. Definition
In his seminal paper, Granger (1969) proposed a notion of causality based on how well past values of a time series could predict future values of another series . Let be the history of all relevant information up to time and be the optimal prediction of given . Granger defined to be causal for if
| 1. |
where indicates excluding the values of from . That is, the variance of the optimal prediction error of is reduced by including the history of (informally, is causal of if past values of improve the prediction of ). This characterization is clearly based on predictability and does not (directly) point to a causal effect of on improving the prediction of does not mean causes . Nonetheless, assuming causal effects are ordered in time (i.e., cause before effect), Granger argued that, under some assumptions, if can predict , then there must be a mechanistic (i.e., causal) effect; that is, predictability implies causality. We explicitly refer to this definition as Granger causality throughout this review to distinguish it from other formal definitions of causality.
While the definition seems general and does not rely on specific modeling assumptions, Granger’s original argument was based on the identifiability of a unique linear model. Denoting the vector of variables at time by , he considered the linear model
| 2. |
where are lag matrices (coefficients) and , the lag or order, may be finite or infinite. The p-dimensional white noise innovation, or error, term can have a diagonal or nondiagonal covariance matrix .
Granger (1969) pointed out that this model is generally not identifiable (the matrices are not uniquely defined) unless is diagonal. Granger referred to this special case—corresponding to the well-known VAR model (Lütkepohl 2005, p. 427)—as a “simple causal model,” distinguishing it from models with instantaneous causal effects when has nonzero off-diagonal entries. This more general form of Equation 2 is known as a structural vector autoregressive (SVAR) model (Kilian 2013) and can be identified under certain parameter restrictions (Kilian & Lütkepohl 2017). Such SVAR models are further considered in Section 4.3.
The model in Equation 2 is clearly restrictive and does not prove or disprove the presence of causal effects. In particular, there are a number of implicit and explicit restrictive assumptions required for the (S)VAR model to be an appropriate framework for identifying Granger causal relationships:
Continuous-valued series: All series are assumed to have continuous-valued observations. However, many interesting data sources—such as social media posts or health states of an individual—are discrete-valued.
Linearity: The true data generating process, and correspondingly the causal effects of variables on each other, is assumed to be linear. In reality, many real-world processes are nonlinear.
Discrete time: The sampling frequency is assumed to be on a discrete, regular grid matching the true causal time lag. If the data acquisition rate is slower or otherwise irregular, causal effects may not be identifiable. Likewise, the analysis of point processes or other continuous-time processes is precluded.
Known lag: The (linear) dependency on a history of lagged observations is assumed to have a known order. Classically, the order was not estimated and was taken to be uniform across all series.
Stationarity: The statistics of the process are assumed time invariant, whereas many complex processes have evolving relationships (e.g., brain networks vary by stimuli and user activity varies over time and context).
Perfectly observed: The variables need to be observed without measurement errors.
Complete system: All relevant variables are assumed to be observed and included in the analysis—i.e., there are no unmeasured confounders. This is a stringent requirement, especially given that early approaches for Granger causality focused on the bivariate case—that is, they did not account for any potential confounders.
The above requirements were discussed in Granger’s original and follow-up papers (Granger 1969, 1980, 2001) and extensively by other authors (Stokes & Purdon 2017, Maziarz 2015); readers are also directed to the recent review by Glymour et al. (2019). Unfortunately, each of the above requirements is unlikely to hold in practice. These assumptions are also not verifiable and are even more unlikely to hold simultaneously, which is what is required for the identifiability of causal effects. In fact, Granger admitted this limitation and gave examples of cases where causal effects could not be identified or wrong conclusions could be drawn. However, in each case, he presented an argument for why the example did not violate the basic principle, either by giving justifications through an alternative model (Granger 1988) or by adding disclaimers (e.g., the definition cannot be applied to deterministic or perfectly predictable processes).
The debate over the notion of causality introduced by Granger has continued since its introduction. An illustrative example is the commentary by Sheehan & Grieves (1982), who used Granger causality to show that the US gross national product causes sunspots; the rebuttal by Noble & Fields (1983) suggested an alternative model would have led to a different conclusion. Despite its limitations, Granger (1980) and a number of other researchers, including prominent econometricians (Sims 1972, Bernanke & Blinder 1992), have argued that the approach can be used to identify causal effects. Researchers in various applied domains, from neuroscience (Bergmann & Hartwigsen 2021, Reid et al.2019) to environmental sciences (Cox & Popken 2015), have used Granger’s framework to (informally) draw causal conclusions. Other researchers have emphasized the limitations of the approach and have tried to distinguish it as Granger causality or G-causality (Holland 1986, Bressler & Seth 2011).
While limited and not generally informative about causal effects, the notion of Granger causality can lead to useful insights about interactions among random variables observed over time. In the next section, we discuss early approaches for identifying Granger causality and its applications in various domains. In the remaining sections, we discuss approaches that aim to (partially) address some of the limitations of the original Granger causality framework and relax some of the requirements discussed above.
2.2. Early Approaches and Applications
The basic definition (Equation 1) requires that all relevant information is accounted for when testing whether series Granger causes series . However, early methods for identifying Granger causality were limited to bivariate models, ignoring the effect of other variables. In his original paper, Granger (1969) used an argument based on spectral representation, using coherence and phase, to motivate the original definition. Using a bivariate version of the SVAR model (Equation 2) (i.e., with ), he then showed that when is diagonal (i.e., a simple causal model/VAR model), Granger causality corresponds to nonzero entries in the autoregressive coefficients. In particular, for a bivariate model
| 3. |
series is Granger causal for series if and only if for some .
Sims (1972) later gave an alternative definition of Granger causality based on coefficients in a moving average (MA) representation. The characterizations by Granger (1969) and Sims (1972), which have been shown to be equivalent (Chamberlain 1982), can be tested using an F-test comparing two models: the full model, including past values of both and , and the reduced model, including only past values of . Formally,
| 4. |
where and are the residual sum of squares for the full and reduced models with and parameters, respectively. Using this test, is declared Granger causal for if the observed test statistic exceeds the quantile of an F-distribution with and degrees of freedom. Alternatively, one can also use a statistic based on likelihood ratio or Wald statistics (Cromwell & Terraza 1994). A key step in carrying out the testing is to identify the model’s order (or lag), . We discuss the lag selection in Section 3.2. Alternatively, one can also use tests in the spectral domain, using Fourier or wavelet representations (Geweke 1982, Dhamala et al. 2008).
Regardless of testing procedure, Granger causality based on only two variables severely limits the interpretation of the findings: Without adjusting for all relevant covariates, a key assumption of Granger causality is violated. This limitation, which has been well documented (see, e.g., Lütkepohl 1982), is illustrated in Figure 1. Here, data are generated according to the following simple VAR process with three variables and independent and identically distributed (i.i.d.) innovations :
| 5. |
Figure 1.
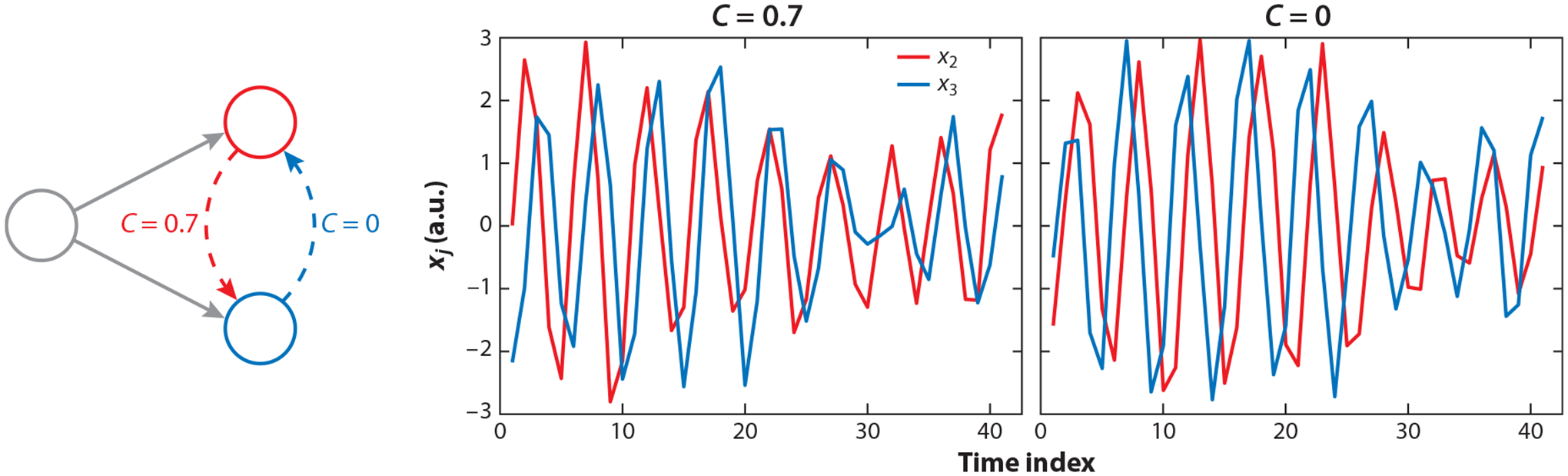
A simple VAR process with three variables generated according to Equation 5. The time series plots (center, right) suggest Granger causal interactions between and in a bivariate analysis excluding . Moreover, the direction of causality is different when and . Bivariate VAR modeling using the vars R package (Pfaff 2008) confirms these observations. Abbreviation: VAR, vector autoregressive.
The two time series plots in Figure 1 correspond to two different VAR models: one with and another with . In the first model, and are affected by values of in lags 1 and 2, respectively. This relationship is reversed in the second model. The patterns of and in the time series plots in Figure 1 clearly suggest that, by ignoring , we may either conclude that is Granger causal for (when ) or that is Granger causal for (when ). This observation is indeed confirmed when we use a test of Granger causality in either case, highlighting the limitation of bivariate tests of Granger causality.
In spite of their limitations, bivariate tests of Granger causality have been widely used in many application areas, from economics (Chiou-Wei et al. 2008) and finance (Hong et al. 2009) to neuroscience (Seth et al. 2015) and meteorology (Mosedale et al. 2006). Similar tests have also been developed for discrete-valued time series (Kontoyiannis & Skoularidou 2016) and for general distributions based on the notion of directed information (Quinn et al. 2015). In the next section, we discuss recent developments that aim to mitigate this limitation by analyzing a potentially large set of variables.
3. NETWORK GRANGER CAUSALITY
The limitations of identifying Granger causality using bivariate models—illustrated in the three-variable example of Figure 1—have long been known and discussed in the literature (e.g., Sims 1980). Needing to account for many variables when identifying Granger causality arises in at least two settings. First, when the goal is to investigate Granger causality between two (or a handful of) endogenous variables and , we need to account for the remaining exogenous variables—targeting the notion of all other relevant information—to prevent identifying incorrect Granger causal relations. This is the setting illustrated in Figure 1 and is common in macroeconomic and econometric studies (Bernanke & Kuttner 2005). Methods based on summaries of exogenous variables, using, e.g., latent factors, have been commonly used to achieve this goal (Bernanke et al. 2005).
In the second setting, which arises naturally in the study of many physical, biological and social systems, the goal is to investigate the relationships among all the variables from a systems perspective. In this case, all variables are endogenous. For instance, when learning gene regulatory networks, all the genes in a given biological pathway are of interest. Similarly, when studying brain connectivity networks, the goal is to interrogate interactions among all regions of interests in the brain. These applications have led to the development of methods for identifying Granger causal relationships among a large set of variables, which can be compactly represented as a network or graph (Eichler 2012) (see Figure 2) and underlie the study of network Granger causality (Basu et al. 2015).
Figure 2.

Illustration of the link between network Granger causality and parameters of SVAR models. (a) Lag matrices and inverse covariance matrix of the innovation, , of an SVAR model. Nonzero entries of and are shaded. (b) Expanded graphical model, which replicates variables over time. (c) Compact graphical model combining all interactions from past lags. In both graphs, Granger causal interactions (solid edges) correspond to nonzero entries in and instantaneous causal effects (dashed undirected edges) correspond to nonzero entries in . Abbreviation: SVAR, structural vector autoregressive.
3.1. Granger Causality Based on Vector Autoregressive Models
In this section we explicitly consider the popular VAR model for Granger causality analysis of multiple variables:
| 6. |
where variables and parameters are defined as in Equation 2.
Proposition 1. Straightforwardly following from the bivariate case (Granger 1969), series is Granger causal for series if and only if for some .
Reading off statements of Granger noncausality from the zeros of the lag matrices is illustrated in Figure 2. The Granger causal relations can also be described via two different graphical models (Eichler 2012): The first is an expanded graph (Figure 2b) with nodes for each time point and edges corresponding to nonzero entries in . This representation is similar to that in dynamic Bayesian networks (Ghahramani 1997). The second graph is a compact representation (Figure 2c), combining edges from different lags of the expanded graph. This latter graph captures the Granger causal relations. In addition, undirected edges indicate instantaneous dependencies captured by nonzero entries in the inverse covariance matrix of the innovations, .
Despite the direct connection between Granger causality and nonzero entries of (Proposition 1), earlier VAR-based approaches used tests of variance similar to those for bivariate models in Equation 4. Moreover, concerned with the increasing number of parameters in the model— parameters for a model with variables—earlier approaches focused on few time series. Bernanke et al. (2005, p. 338) state that “to conserve degrees of freedom, standard VARs rarely employ more than six to eight variables.” While this is a step forward, it is difficult to argue that early moderate-dimensional approaches account for all the relevant information when determining Granger causal relations. Thus, these approaches still do not satisfy the requirements of the definition in Equation 1. This limitation was underscored by Bernanke et al. (2005, p. 338) when stating that “[the] small number of variables is unlikely to span the information sets used by actual central banks.”We consider the challenge of scaling to a large number of series under the two scenarios outlined above: assuming a large set of exogenous series, or that all series are endogenous.
To account for a (potentially large) number of exogenous variables when studying the relationships between a small number of endogenous variables, a well-known approach is the factor-augmented VAR model of Bernanke et al. (2005):
| 7. |
This model is seemingly similar to the VAR model in Equation 6. However, the m-dimensional factors —representing exogenous variables—are unobserved. Bernanke et al. (2005) proposed two estimation procedures for Equation 7 with constraints on the factors: a two-step procedure based on principal components and a direct estimation procedure based on maximum likelihood. Factor models have been used extensively in econometrics (Stock & Watson 2011). Follow-up work has further investigated the estimability of the parameters (Belviso & Milani 2006) and the choice of number of unobserved factors (Ahn & Horenstein 2013, Onatski 2010, Amengual & Watson 2007).
The second scenario involves fitting VAR models with a large number of endogenous variables. Earlier approaches primarily used shrinkage penalties to obtain reasonable estimates in moderate-dimensional VAR models, followed by classical test-based approaches (e.g., the F-test) to infer Granger causality. For instance, motivated by earlier work (Litterman 1986), Leeper et al. (1996) considered a Bayesian approach using a prior shrinking large coefficients or distant lags. Recent work has increasingly focused on directly selecting the nonzero entries of the via sparsity-inducing penalties, often by augmenting the VAR loss function. For the commonly used least squares loss and a general penalty on the coefficient matrices , the general problem can be written as
| 8. |
where denotes the norm and the length of the time series. Fujita et al. (2007) proposed to estimate high-dimensional VARs by using a lasso penalty (Tibshirani 1996):
with a tuning parameter controlling element-wise sparsity in , encouraging many entries to be exactly zero. One can directly deduce from the lasso estimate that is Granger causal for if there exists such that (see Figure 3a). The motivating application for Fujita et al. (2007) was the estimation of gene regulatory networks; based on the particulars of this application, they developed their method for panel data, which often contain observations over a small number of time points, but with repeated measures for multiple subjects. Chudik & Pesaran (2011) considered a very similar estimator (also using a lasso penalty) for economic time series data.
Figure 3.
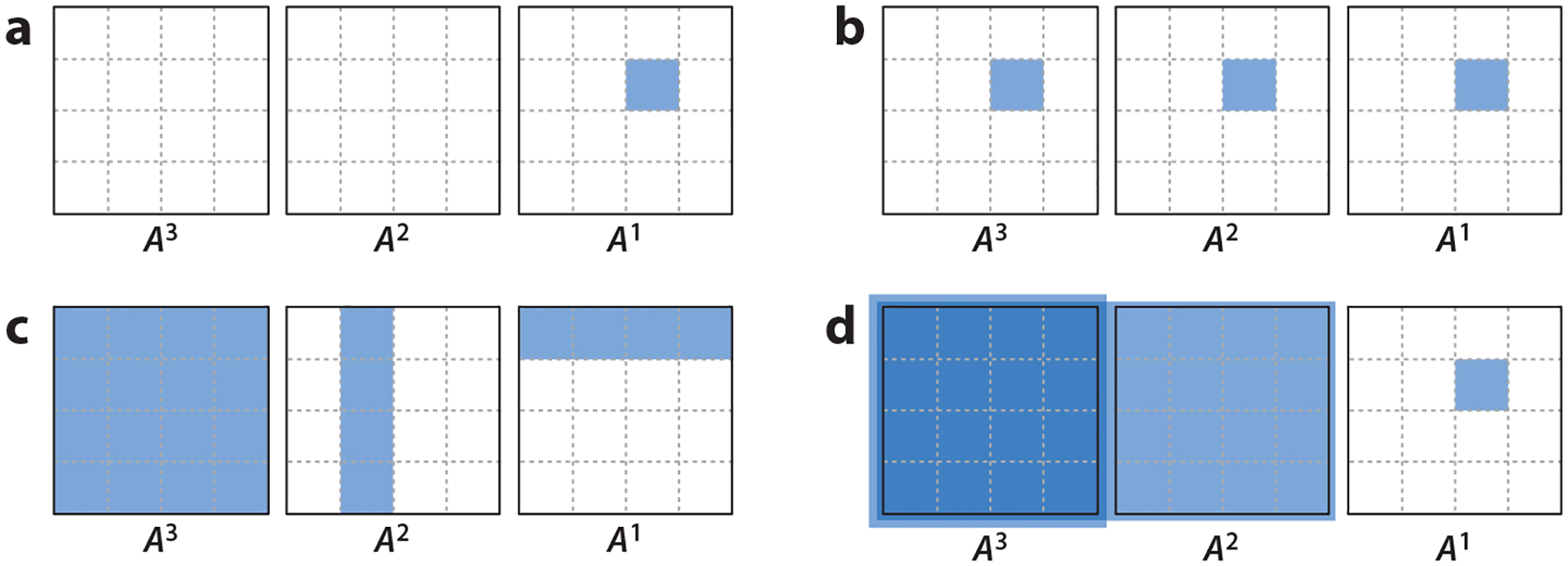
Illustration of different sparsity-inducing penalties for Granger causality estimation based on vector autoregressive (VAR) processes: (a) the lasso penalty applied to each entry of lag matrices (Fujita et al. 2007); (b) the group lasso penalty applied to all lags of the same entry (, ) (Lozano et al. 2009); (c) general group lasso penalty (Basu et al. 2015), applied to groups of related variables or entire lag matrices ; and (d) joint lasso and hierarchical group lasso penalties for inducing sparsity while selecting lags by forcing for larger (Nicholson et al. 2017b).
Lozano et al. (2009) used a group lasso penalty (Yuan & Lin 2006) for aided Granger causality interpretability:
This penalty, which is depicted in Figure 3b, corresponds directly to Granger noncausality from to by enforcing for all . Basu et al. (2015) considered more general group lasso penalties, to group over not only lags but also sets of related variables and even entire matrices (see Figure 3c). The authors also showed that the sparsity pattern resulting from group lasso penalty is only consistent with the truth if the grouped coefficients have similar magnitudes, and that group lasso may only achieve directional consistency; they proposed a thresholded group lasso penalty to consistently learn the sparsity patterns. As illustrated in Figure 4, the resulting estimates can facilitate the interpretation of Granger causal effects in settings with many variables.
Figure 4.
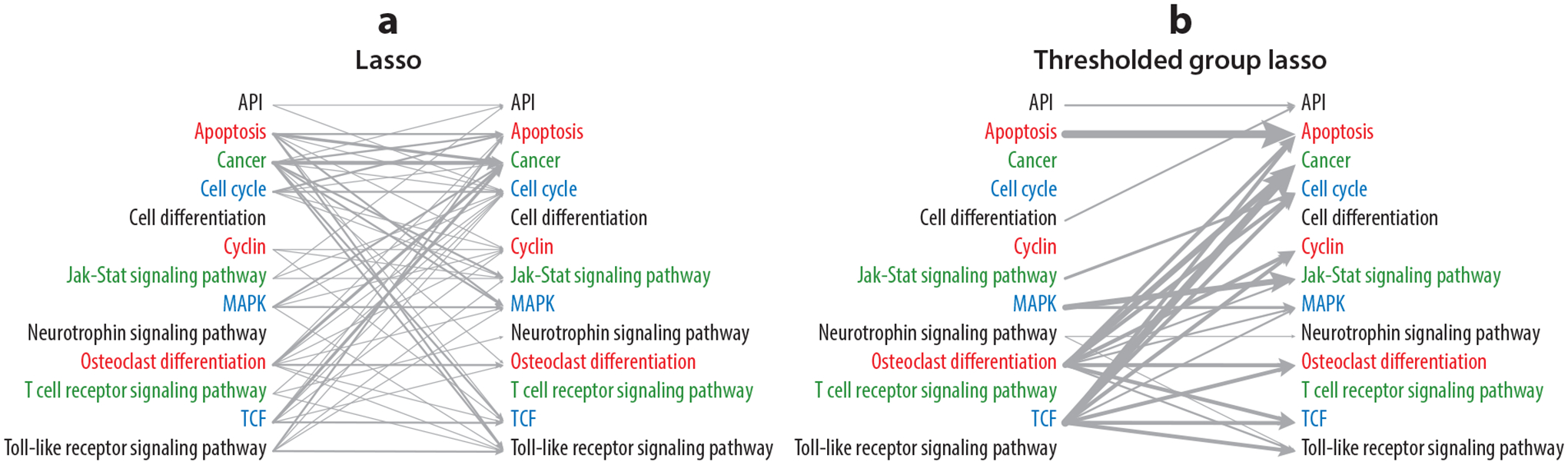
(a) Lasso versus (b) group lasso estimates of T-cell gene regulatory networks (Basu et al. 2015). The terms API, MAPK, and TCF are names of genetic pathways based on information from the Kyoto Encyclopedia of Gene and Genome. Figure adapted with permission from Basu et al. (2015).
The general estimation framework in Equation 8 has been extended to account for dependencies in the inverse covariance of the innovations, (Davis et al. 2016), and to combine the ideas of sparsity and unobserved exogenous variables (Basu et al. 2019). Asymptotic properties of the resulting estimators have also been investigated in high-dimensional settings, where (Song & Bickel 2011, Basu & Michailidis 2015). In particular, Basu & Michailidis (2015) established a connection between the sample size () needed for high-dimensional consistency of the lasso estimate of a VAR process and the eigen-structure of its spectral density matrix. More recent work has developed asymptotically valid inference for the estimated parameters of the VAR process (Neykov et al. 2018, Zheng & Raskutti 2019, Zhu & Liu 2020). Some of these developments have also been implemented in publicly available software packages, including mgm (Haslbeck & Waldorp 2020), bigvar (Nicholson et al. 2017a), and ngc (Etzel & Shojaie 2016).
Bayesian approaches have also been considered as alternatives to regularization methods for analyzing large VAR processes. For instance, George et al. (2008) proposed a Bayesian stochastic search algorithm to identify high-dimensional VAR processes, whereas Bańbura et al. (2010) showed that better performance can be achieved in large models if the tightness of the priors is increased as the model size increases. More recently, Ahelegbey et al. (2016) considered sparsity-inducing priors for high-dimensional VAR processes, Ghosh et al. (2019) established posterior consistency of the Bayesian estimates when using sparsity-inducing priors, and Billio et al. (2019) proposed nonparametric Bayesian priors that cluster the VAR coefficients and induce group-level shrinkage.
3.2. Lag Selection and Nonstationary Vector Autoregressive Models
In classical linear VAR methods, one must explicitly specify the maximum time lag, , when assessing Granger causality. Early approaches often set based on prior knowledge or in ad hoc ways. VARs with different lags may result in different conclusions, further complicating the interpretation of Granger causality. If the specified lag is too short, Granger causal connections at longer lags will be missed, while overfitting may occur if the lag is too large, a problem exacerbated by high-dimensional VAR models.
Regularization-based approaches can be used to systematically estimate the optimal lag from data. To this end, Shojaie & Michailidis (2010) proposed a truncating lasso penalty that shrinks entire coefficient matrices to zero and then sets all following to zero (see Figure 5a). The idea is to scale the penalty for each using data-driven weights calculated based on coefficient matrices in previous lags . Formally, the penalty is given by
where , and for the weights can be compactly written as
with if and if (the convex indicator function). Here, gives the number of nonzero entries of and is a second tuning parameter. Shojaie & Michailidis (2010) show that a block-coordinate descent algorithm converges to a local minimum and establish consistency of this algorithm for selecting the correct Granger causality network in high-dimensional panel data settings. They also propose error-based choices for the two tuning parameters ( and ) that control the type-I and type-II errors in selecting Granger causal effects.
Figure 5.

Illustration of two approaches for lag selection: (a) Assuming a decay assumption—that is, —the lag can be estimated by identifying the first such that . (b) The lag can be estimated without assuming a decay assumption by enforcing entire lag matrices to be zero and setting .
While the decay assumption of Shojaie & Michailidis (2010) may be satisfied in some applications, it may fail in others. To overcome this limitation, Shojaie et al. (2012) proposed an adaptive thresholded lasso penalty that can data-adaptively set entire lag matrices to zero, while allowing others to be nonzero. The effect of this penalty, depicted in Figure 5b, is somewhat similar to the effect of the automatic relevance determination (ARD) priors proposed in the Bayesian nonparametric approach of Fox et al. (2011) for switching dynamic linear models. More specifically, the ARD prior turns off entire blocks of based on the value of their corresponding precision parameters. Another approach for automatic lag selection using regularization, proposed by Nicholson et al. (2017b), is to use a hierarchical group lasso penalty, depicted in Figure 3d. The hierarchical penalty is based on a decay assumption, similar to that in Shojaie & Michailidis (2010), but is convex and can thus lead to more computationally efficient estimation.
The Bayesian nonparametric approach of Fox et al. (2011) addresses another limitation of classical Granger causality methods based on VARs: the assumption of stationarity. Fox et al. (2011) relaxed this assumption by considering a switching VAR model, with lag matrices a function of a latent (switching) variable ; in other words, , where the distribution of depends on . Fox et al. (2011) also consider a switching state-space model allowing the observed data to be a noisy version of the switching VAR process. Nakajima & West (2013) instead propose a method for inducing continuously varying (rather than switching) sparsity in a time-varying VAR model through the use of a latent threshold process. A vectorized form of the time-varying lag matrices is assumed to follow a VAR(1) process with elements thresholded to zero based on a set of latent threshold variables. Nakajima & West (2013) consider a Bayesian approach to inference in this model.
An alternative approach for handling nonstationarity was recently proposed by Safikhani & Shojaie (2020) in the setting of high-dimensional piece-wise VAR processes with many structural break points. To consistently identify the break points and learn the coefficient parameters in each regime, the authors consider a reparameterization based on changes in lag matrices, , and use a combination of lasso penalized estimation and model selection based on the Bayesian information criterion to enforce piece-wise stationarity in estimated lag matrices. Bai et al. (2020) have recently used similar ideas in the case where the lag matrices are a combination of sparse and low-rank components, capturing nonstationary VAR models in the presence of (unobserved) exogenous variables.
4. MORE GENERAL NOTIONS OF GRANGER CAUSALITY
The notion of Granger causality explored so far is suitable for time series that follow linear dynamics. However, many interactions in real-world applications, like neuroscience and genomics, are inherently nonlinear. In these cases, using linear models may lead to inconsistent estimation of Granger causal interactions. Furthermore, classical Granger causality analyses assume real-valued Gaussian time series. This restriction has hindered Granger causality analysis of many important applications involving, for example, count or categorical time series.
To generalize the VAR model of Equation 6, consider a process that, component-wise, can be written as follows:
| 9. |
Here, is a function specifying how the past of all series map to a particular series . Assuming diagonal error covariance, , the linear VAR model is a special case of Equation 9, with a linear function with coefficients given by the ith row of coefficient matrices, . In contrast to standard multivariate forecasting, where a function would jointly model all outputs , this component-wise specification is more immediately amenable to Granger causal analysis. In particular, we can extend the definition of Granger causality to this more expressive class of dynamical models by noting that if the function does not depend on , then is irrelevant in the prediction of series .
Definition 1. Time series is Granger noncausal for time series if and only if for all () and all ,
that is, is invariant to .
Related definitions for specific classes of models have appeared in the literature (see, e.g., Eichler 2012). Note that Equation 9 still assumes additive noise. Definition 1 can be further generalized to statements of conditional independencies modeling arbitrary nonlinear relationships between time series, referred to as strong Granger causality (e.g., Florens & Mouchart 1982). Building on the component-wise process of Equation 9, we further define Granger causality in situations where the series at time are conditionally independent of one another given the past realizations:
| 10. |
Definition 2. Time series is Granger noncausal for time series if and only if ,
| 11. |
In the context of these more general notions of Granger causality, we review in Sections 4.1 and 4.2 recent advances for analyzing multivariate discrete-valued and nonlinear time series, as well as multivariate point processes.
Another implicit assumption of classical Granger causality is that the time series of interest are observed at a regular sampling rate that matches the causal scale. However, due to data integration across heterogeneous sources, many data sets in econometrics, health care, environment monitoring, and neuroscience comprise multiple series sampled at different rates, referred to as mixed-frequency time series. Furthermore, due to the cost or data collection challenges, many series may be sampled at a rate lower than the true causal scale of the underlying process. For example, many econometric indicators, such as gross domestic product (GDP) and housing price data, are recorded at quarterly and monthly scales (Moauro & Savio 2005), but important interactions between these indicators may occur weekly or biweekly (Boot et al. 1967, Stram & Wei 1986, Moauro & Savio 2005). In neuroscience, imaging modalities with high spatial resolution, like functional magnetic resonance imaging, have relatively low temporal resolutions, but many important neuronal processes and interactions happen at finer time scales (Zhou et al. 2014). A causal analysis at a slower time scale than the true causal time scale may miss true interactions and add spurious ones (Boot et al. 1967, Breitung & Swanson 2002, Silvestrini & Veredas 2008, Zhou et al. 2014). In Section 4.3, we review recent approaches to identifying Granger causality in subsampled and mixed-frequency time series (Gong et al. 2015, Tank et al. 2019).
4.1. Discrete-Valued Time Series
A variety of applications give rise to multivariate discrete-valued time series, including count, binary, and categorical data. Examples include voting records of politicians, discrete health states for a patient over time, and action labels for players on a team. Furthermore, even when the raw recording mechanism produces continuous-valued time series, to facilitate downstream analyses, the series may be quantized into a small set of discrete values; examples include weather data from multiple stations (Doshi-Velez et al.2011), wind data (Raftery 1985), stock returns (Nicolau 2014), and sales volume for a collection of products (Ching et al.2002). In these cases, the traditional VAR framework for Granger causal analysis, Equation 6, is inappropriate. In this section, we review recently proposed models, based on the more general framework of Definitions 1 and 2, that infer Granger causality using multivariate, discrete-valued time series.
4.1.1. Categorical time series.
Consider a multivariate categorical time series , and let represent the number of categories that series may take. An order multivariate Markov chain models the transition probability between the categories at lagged times and those at time using a transition probability distribution; under the simplifying assumption of Equation 10,
| 12. |
The component-wise structure of the assumed transition distribution enables estimation and inference to be divided into independent subproblems over each series, . Additionally, Granger noncausality follows Definition 2: Analyzing the transition probability tensor for , does not Granger cause if all subtensors along the mode associated with are equal (see Figure 6).
Figure 6.

(a) Illustration of Granger noncausality in an example with and . Since the tensor represents conditional probabilities, the columns of the front face of the tensor, the vertical axis, must sum to one. Here, is not Granger causal for since each slice of the conditional probability tensor along the mode is equal. (b) Schematic of the mixture transition distribution (MTD) factorization of the conditional probability tensor . Figure adapted with permission from Tank et al. (2021b).
Unfortunately, discovering such invariances (equivalence among subtensors) via, e.g., penalized likelihood proves computationally prohibitive in even moderate dimensions. Instead, Tank et al. (2021b) proposed a more tractable yet still flexible parameterization of the transition probabilities leveraging the mixture transition distribution (MTD) (Raftery 1985, Berchtold & Raftery 2002):
| 13. |
where is a probability vector, is a pairwise transition probability table between and , and is a ()-dimensional probability distribution such that with , . Tank et al. (2021b) showed that the intercept term, , which is not traditionally included in MTD models, is critical for model identifiability and thus Granger causality. The framework of Tank et al. (2021b) is general for higher-order lags, and is presented here for ease of exposition. Additionally, interaction terms can also be included in the MTD decomposition. Figure 6 shows a visualization of the MTD transition probability tensor decomposition.
The MTD model—originally proposed for parsimonious modeling of higher-order Markov chains—has been plagued by a nonconvex objective and unknown identifiability conditions that have limited its utility (Nicolau 2014, Zhu & Ching 2010, Berchtold 2001). Tank et al. (2021b) instead proposed a change-of-variables reparameterization of the MTD that straightforwardly addresses both issues, thus enabling practical application of the MTD model to Granger causality selection. Let denote the vector of intercept probabilities, , and the pairwise transition probability matrix . Let and . Then, the factorization of the conditional probability tensor for the MTD in Equation 13 can be rewritten as
| 14. |
Proposition 2 (Tank et al. 2021b). In the MTD model of Equation 14, following Definition 2, time series is Granger noncausal for time series if and only if the columns of are all equal. Furthermore, all equivalent MTD model parameterizations give the same Granger causality conclusions.
Intuitively, if all columns of are equal, the transition distribution for does not depend on . This result for MTD models is analogous to the general Granger noncausality result for the slices of the conditional probability tensor being constant along the mode being equal. The optimization problem for maximizing log-likelihood can be written as follows. Letting
| 15. |
and including the necessary probability constraints (positivity and summing to one), we have
| 16. |
The problem in Equation 16 is convex since the objective function is a linear function composed with a log function and only involves linear equality and inequality constraints (Boyd & Vandenberghe 2004).
The reparameterization in Equation 14 provides clear intuition for why the MTD model may not be identifiable. Since the probability function is a linear sum of , one may take mass from some and move it to some , or , while keeping the conditional probability tensor constant. These sets of equivalent MTD parameterizations—that yield the same factorized conditional distributions —form a convex set (Tank et al. 2021b). Taken together, the convex reparameterization and this result imply that the convex function given in Equation 16 has no local optima and that the globally optimal solution is given by a convex set of equivalent MTD models. A unique solution can then be identified by constraining the minimal element in each row of (and thus ) to be zero for all (see Figure 7 for an illustration). The intuition for this result is simple: Any excess probability mass on a row of each may be pushed onto the same row of the intercept term without changing the full conditional probability.
Figure 7.

Schematic of identifiability conditions for the (a) MTD and (b) mLTD with and . Identifiability for MTD requires a zero entry in each row of ; for mLTD, the first column and last row must all be zero. In MTD, the columns of each must sum to the same value and must sum to one across all . Abbreviations: mLTD, multinomial logistic transition distribution; MTD, mixture transition distribution. Figure adapted with permission from Tank et al. (2021b).
The above identifiability condition also provides interpretation for the parameters in the MTD model. Specifically, the element denotes the additive increase in probability that is in state given that is in state . Furthermore, the parameters now represent the total amount of probability mass in the full conditional distribution explained by categorical variable , providing an interpretable notion of dependence in categorical time series.
Unfortunately, the set of that satisfy the MTD identifiability constraints is nonconvex since the locations of the zeros are unknown. Tank et al. (2021b) addressed this issue by adding a penalty that biases the solution toward the uniqueness constraints. This regularization also aids convergence of optimization since the maximum likelihood solution without identifiability constraints is not unique. The regularized estimation problem is given by
| 17. |
As Tank et al. (2021b) show, for any and not dependent on and increasing with respect to the absolute value of entries in , the solution to the problem in Equation 17 is contained in the set of identifiable MTD models. Intuitively, by penalizing the entries of the matrices, but not the intercept term, solutions will be biased to having the intercept contain the excess probability mass, rather than the matrices. An entire class of regularizers match the necessary conditions and can be considered.
Proposition 3 (Tank et al. 2021b). Based on the MTD identifiability constraint where each row must have at least one zero element, is Granger noncausal for if and only if (a special case of all columns being equal).
To both enforce the identifiability constraints and select for Granger noncausality, Tank et al. (2021b) explored a set of penalties that encourage some to be zero, while maintaining convexity of the overall objective. These penalties include an penalty on the (with implying ); a group lasso penalty on each (Yuan & Lin 2006); and a group lasso–type penalty that scales with the number of categories per series, , to avoid differentially penalizing series based on their number of categories. To solve the penalized estimation problem, Tank et al. (2021b) developed both projected gradient and Frank–Wolfe algorithms for the MTD model that harness the convex formulation. For the projected gradient optimization, they further developed a Dykstra projection method to quickly project onto the MTD constraint set, allowing the MTD model to scale to much higher dimensions.
4.1.2. Alternative formulation for categorical time series.
Tank et al. (2021b) also proposed a multinomial logistic transition distribution (mLTD) model as an alternative to the MTD:
| 18. |
where and . As with the MTD, interaction terms may be added. Granger causality follows identically to the MTD case in Proposition 2: is Granger noncausal for if and only if the columns of are all equal.
The nonidentifiability of multinomial logistic models is well known, as is the nonidentifiability of generalized linear models with categorical covariates. Combining the standard identifiability restrictions for both settings clarifies that every mLTD has a unique parameterization such that first column and last row of are zero for all and the last element of is zero (Agresti & Kateri 2011) (see Figure 7). Although the mLTD identifiability conditions differ from those of the MTD, Granger noncausality interpretation of the identifiable mLTD mirrors the identifiable MTD in Proposition 3: is Granger noncausal for if and only if (a special case of all columns being equal).
To select for Granger causality in the mLTD model while enforcing identifiability, akin to the MTD case, Tank et al. (2021b) proposed a group lasso penalty on each of the matrices, leading to the following optimization problem:
| 19. |
For two categories, , this problem reduces to sparse logistic regression for binary time series, which was studied by Hall et al. (2016). As in the MTD case, the group lasso penalty shrinks some entirely to zero.
Although the MTD and mLTD are conceptually similar, the parameters of the mLTD are unfortunately harder to interpret. Another alternative formulation one might consider is based on the MTD-probit model of Nicolau (2014); however, this framework is not a natural fit for inferring Granger causality, due to both the nonconvexity of the probit model and the nonconvex constraints on matrices.
4.1.3. Estimating networks of binary and count time series.
The MTD and mLTD models are specifically geared for Granger causal analysis of autoregressive categorical processes. Hall et al. (2016) instead studied a broad class of generalized linear autoregressive (GLAR) models, capturing Bernoulli and log-linear Poisson autoregressive (PAR) models, and focused on the high-dimensional multivariate setting. The GLAR model is specified as
| 20. |
where is an exponential family probability distribution. The formulation in Equation 20 follows a component-wise structure, and from Definition 2 we can decipher that time series does not Granger cause series if and only if .
Hall et al. (2016) considered regularization of constructed row-wise from . They derived statistical guarantees, such as sample complexity bounds and mean-squared error bounds for the sparsity-regularized maximum likelihood estimator, addressing the key challenge of correlations and potential heteroscedasticity in the GLAR observations.
Count data can also be analyzed using autoregressive models with thinning operators of previous counts—so-called integer-valued autoregressive (INAR) processes (McKenzie 2003, Weiß 2018). One example is the Poisson INAR, which performs binomial thinning and adds Poisson innovations. In the univariate case, the process has Poisson margins; in the multivariate case, although a stationary distribution exists, the margins are no longer Poisson unless the thinning matrix is diagonal. Aldor-Noiman et al. (2016) captured dependence between the dimensions of a multivariate count process through the Poisson rate parameters of a multivariate Poisson INAR with diagonal thinning, using multiple shrinkage via a Dirichlet process prior on the rate parameters. The resulting clustering of count time series gives a (strict) notion of Granger noncausality for any pair of series appearing in disjoint clusters.
Another approach is the INGARCH (integer-valued generalized autoregressive conditional heteroskedasticity) model (Weiß 2018), which leverages an autoregressive-like model on the conditional mean and is useful for modeling overdispersed counts. One example is modeling Poisson-distributed counts with a rate parameter defined via the conditional mean process ; other specifications consider binomial or negative binomial conditional distributions. The INGARCH model has connections to both the GLAR of Equation 20 and the popular GARCH model (see, e.g., Bauwens et al.2006). However, the INGARCH model has most commonly been used in low-dimensional settings, often univariate; scaling the model to higherdimensional settings and using it for Granger causality analysis is an open research area, as with the Poisson INAR.
4.1.4. Granger causal interactions in point processes.
A key assumption of the standard Granger causal framework is that observations are on a fixed, discrete-time grid. In Section 4.3, we consider cases where the sampling rate might not match the time scale of the true causal interactions. Here we focus on another important case emerging from irregularly and asynchronously observed time series better modeled via point processes in continuous time.
Inferring Granger causal interactions in the general class of multivariate point processes is often challenging due to the intractability of representing the histories of the processes and their impact on the processes’ evolution. Recent work gained traction by focusing specifically on Hawkes processes, describing self- and mutually-excitatory processes (Zhou et al. 2013, Xu et al. 2016, Eichler et al. 2017). Early applications of Hawkes processes include modeling seismic activity and neural firing patterns, with more recent applications to interactions in social networks and medical event streams. For Granger causality analysis, Eichler et al. (2017) provided straightforward conditions on the link functions of the conditional intensities of the multivariate Hawkes process and derived a nonparametric estimation procedure.
Let be a point process arising from a Hawkes process with conditional intensity functions
| 21. |
where is the baseline intensity and are the link functions with for and . Then, does not Granger cause if and only if for all (Eichler et al. 2017).
Zhou et al. (2013), Xu et al. (2016), and Hansen et al. (2015) recently used sparsity-inducing penalties to infer (high-dimensional) Granger causal networks from Hawkes processes. Motivated by neuroscience applications, Chen et al. (2017a) generalized Hawkes processes to allow for inhibitory interactions, Chen et al. (2017c) proposed a screening approach for efficient estimation of high-dimensional Hawkes process networks, and Wang et al. (2020) developed a high-dimensional inference framework for Hawkes processes. The PAR model version of Equation 20 is also closely related to the continuous-time Hawkes process model and can be used as an alternative to the above approaches.
4.2. Methods for Capturing Interactions in Nonlinear Time Series
Beyond the analysis of discrete-valued time series, as in Section 4.1, there are a range of other scenarios where the relationships between the past of one series and future of another fall outside of the VAR model class of traditional model-based Granger causality analysis. In such cases, model-based methods have been shown to fail in numerous real-world settings (Teräsvirta et al. 2010, Tong 2011, Lusch et al. 2016). One example is time series with heavy tails, which have been modeled using VARs with elliptical errors (Qiu et al. 2015). Another example of particular importance in a number of applications—and one we focus on in this review—is that of nonlinear interactions. Model-free methods, like transfer entropy (Vicente et al. 2011) or directed information (Amblard & Michel 2011), can detect nonlinear dependencies between past and future with minimal assumptions on the predictive relationships. However, these estimators have high variance and require large amounts of data for reliable estimation. These approaches also suffer from curse of dimensionality (Runge et al.2012), making them inappropriate in high-dimensional settings.
Dynamical system representations, often in the form of coupled ordinary differential equations (ODEs), have long been used to capture nonlinear relationship in time series. While ODEs are inherently deterministic, a commonly used approach is to assume that data from the underlying ODEs are contaminated with mean-zero additive noise :
| 22. |
| 23. |
where is a function mapping the current state of all variables to the change in (the derivative ).
While ODE-based approaches for analyzing specific systems use parametric forms, more recent work has focused on system identification using flexible specifications of functions . One such approach, which has been successfully applied to high-dimensional problems, is to consider an additive ODE instead of Equation 22; that is,
| 24. |
For the system in Equation 24, it follows from Definition 1 that is Granger noncausal for if and only if . Using this connection, Henderson & Michailidis (2014) and Wu et al. (2014) developed regularized nonparametric estimation procedures to infer nonzero functions, , and Chen et al. (2017b) addressed the key challenge of estimating the derivative and established the consistency of the network Granger causality estimates.
The ODE-based approaches discussed above offer flexible alternatives to parametric approaches for modeling nonlinear dynamics. However, they are limited to additive interaction mechanisms. A promising alternative is to consider more general dynamics and interactions by leveraging neural networks. Neural networks can represent complex, nonlinear, and nonadditive interactions between inputs and outputs. Indeed, their time series variants, such as autoregressive multilayer perceptrons (MLPs) (Kişi 2004, Billings 2013, Raissi et al. 2018) and recurrent neural networks (RNNs) like long-short term memory networks (LSTMs) (Graves 2012), have shown impressive performance in forecasting multivariate time series given their past (Zhang 2003, Li et al. 2017, Yu et al. 2017).
Consider a nonlinear autoregressive (NAR) model that allows to evolve according to general nonlinear dynamics (Billings 2013), assuming an additive zero mean noise :
| 25. |
In an NAR forecasting setting, there is a long history of modeling using neural networks, via both traditional architectures (Chu et al. 1990, Billings & Chen 1996, Billings 2013) and more recent deep learning techniques (Li et al. 2017, Yu et al. 2017, Tao et al. 2018). These approaches utilize either an MLP with inputs , for some lag , or a recurrent network, like an LSTM, that does not require specifying the lag order.
While these methods have shown impressive predictive performance, they are essentially black-box models and provide little interpretation of the multivariate structural relationships in the series. In the context of Granger causality, due to sharing of hidden layers, it is difficult to specify sufficient conditions on the weights that simultaneously allow series to Granger cause series but not other series for . A second drawback is that jointly modeling a large number of series leads to many network parameters. Thus, these methods require much more data to fit reliably and tend to perform poorly in high-dimensional settings. Finally, a joint network over all for all assumes that each time series depends on the same past lags of other series. However, in practice, each may depend on different past lags of other series. As in the linear methods discussed in Section 3.2, appropriate lag selection is crucial for Granger causality selection in nonlinear approaches—especially in highly parameterized models like neural networks.
With an eye toward inferring Granger causality but simultaneously tackling the sample complexity and lag selection problems, Tank et al. (2021a) proposed a framework leveraging the component-wise model of Equation 9 that disentangles the effects of lagged inputs on individual output series. The method models the component-wise transition functions using neural networks—either via an MLP or RNN like the LSTM—and deploys carefully constructed sparsity-inducing penalties on particular groupings of neural network weights to identify Granger noncausal interactions. One of the penalties—building on the hierarchical group lasso (Kim & Xing 2010, Huang et al. 2011, Nicholson et al. 2017b)—automatically detects both nonlinear Granger causality and the lags of each inferred interaction in the MLP setting. The LSTM-based formulation, in contrast, sidesteps the lag selection problem entirely because the recurrent architecture efficiently models long-range dependencies (Graves 2012). The proposed penalties, depicted together with the methods in Figure 8, also aid in handling limited data in the high-dimensional setting. We review each approach below.
Figure 8.
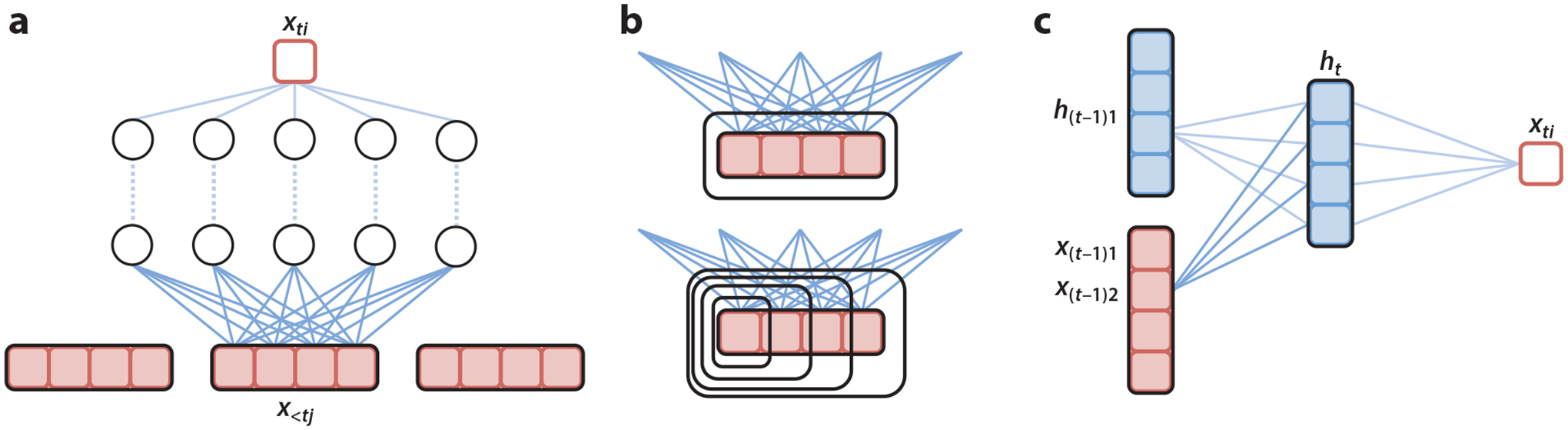
(a) Schematic for cMLPs. If outgoing weights for (dark blue) are penalized to zero, then does not Granger cause . (b) The group lasso penalty jointly penalizes the full set of outgoing weights while the hierarchical version penalizes the nested set of outgoing weights, penalizing higher lags more. (c) Schematic for cLSTM. If outgoing weights to hidden units from an input are zero, then does not Granger cause . Abbreviations: cLSTM, component-wise long-short term memory network; cMLP, component-wise multilayer perceptron. Figure adapted with permission from Tank et al. (2021a).
4.2.1. Multilayer perceptrons.
Define via an MLP with layers and representing the values of lth hidden layer at time . The parameters are given by weights and biases at each layer (with appropriate dimensions for that layer). To draw an analogy with the linear VAR model of Equation 6, we further decompose the weights at the first layer across time lags, . The resulting component-wise MLP (cMLP) is given as (Tank et al. 2021a)
| 26. |
where is an activation function, such as logistic or tanh, and is mean zero white noise. Tank et al. (2021a) use a linear output decoder . However, as the authors mention, other decoders like a logistic, softmax, or Poisson likelihood with exponential link function (McCullagh & Nelder 1989) could be used to model nonlinear Granger causality in multivariate binary (Hall et al. 2016), categorical (Tank et al. 2021b), or positive count time series (Hall et al. 2016). From Equation 26, the Granger noncausality conditions are straightforward to elicit:
Proposition 4 (Tank et al.2021a). In the MLP model of Equation 26, following Definition 1, if the jth column of the first layer weight matrix, , contains zeros for all , then series does not Granger cause series .
By Proposition 4, if the first layer weight matrix, , contains zeros for all , then does not influence the hidden unit and thus the output . Following Definition 1, we see that —which is implicitly defined through the hidden layers of the MLP in Equation 26—is then invariant to . Thus, analogously to the VAR case, one may select for Granger causality by applying a group penalty to the columns of the matrices for each ,
| 27. |
where is a penalty that shrinks the entire set of first layer weights for input series , i.e., , to zero. Three penalties, illustrated in Figure 9, are considered by Tank et al. (2021a): (a) a group lasso penalty over the entire set of outgoing weights across all lags for time series , (the analogue to the group lasso penalty across lags in the VAR case); (b) a novel group sparse group lasso penalty that provides both sparsity across groups (a sparse set of Granger causal time series) and sparsity within groups (a subset of relevant lags); and (c) a hierarchical group lasso penalty to simultaneously select for both Granger causality and the lag order of the interaction.
Figure 9.

Example of group sparsity patterns of cMLP first layer weights with four first layer hidden units () and four input series () with maximum lag . Differing sparsity patterns are shown for the three different structured penalties: (a) group lasso, (b) group sparse group lasso, and (c) hierarchical lasso. Abbreviation: cMLP, component-wise multilayer perceptron.
4.2.2. Recurrent neural networks.
As in the MLP case, it is difficult to disentangle how each series affects the evolution of another series when using a standard RNN. This problem is even more severe in complicated recurrent networks like LSTMs. For a general RNN, the hidden state at time is updated recursively:
| 28. |
where is a nonlinear function that depends on the particular recurrent architecture and are the output weights.
Because LSTMs are effective at modeling complex time dependencies, Tank et al. (2021a) focus on modeling the recurrent function using an LSTM (Graves 2012). The LSTM introduces a second hidden state variable , the cell state, and updates its set of hidden states (, ) recursively as
| 29. |
where ☉ denotes element-wise multiplication. The input (), forget (), and output () gates control how each component of the cell state () is updated and then transferred to the hidden state () used for prediction. The additive form of the cell state update in the LSTM allows it to encode long-range dependencies: Cell states from far in the past may still influence the cell state at time if the forget gates remain close to one. In the context of Granger causality, this flexible architecture can represent long-range, nonlinear dependencies between time series.
Let be the full set of parameters, where and are the full set of first layer weights. In Equation 29, the set of input matrices controls how the past time series affect the hidden representation update and thus the prediction of . Granger noncausality for this component-wise LSTM (cLSTM) follows directly from Definition 1:
Proposition 5 (Tank et al. 2021a). For the cLSTM of Equations 28 and 29, following Definition 1, a sufficient condition for Granger noncausality of a series on a series is that all elements of the jth column of are zero, .
Thus, we may select for Granger causality using a group lasso penalty across columns of and considering
| 30. |
As with the cMLP, for the cLSTM is implicitly defined through the recurrent structure of Equations 28 and 29. For larger , many columns of will be zero, leading to a sparse set of Granger causal connections (see Figure 10). Tank et al. (2021a) optimized the objectives in Equations 27 and 30 (under various choices of penalty) using proximal gradient descent.
Figure 10.
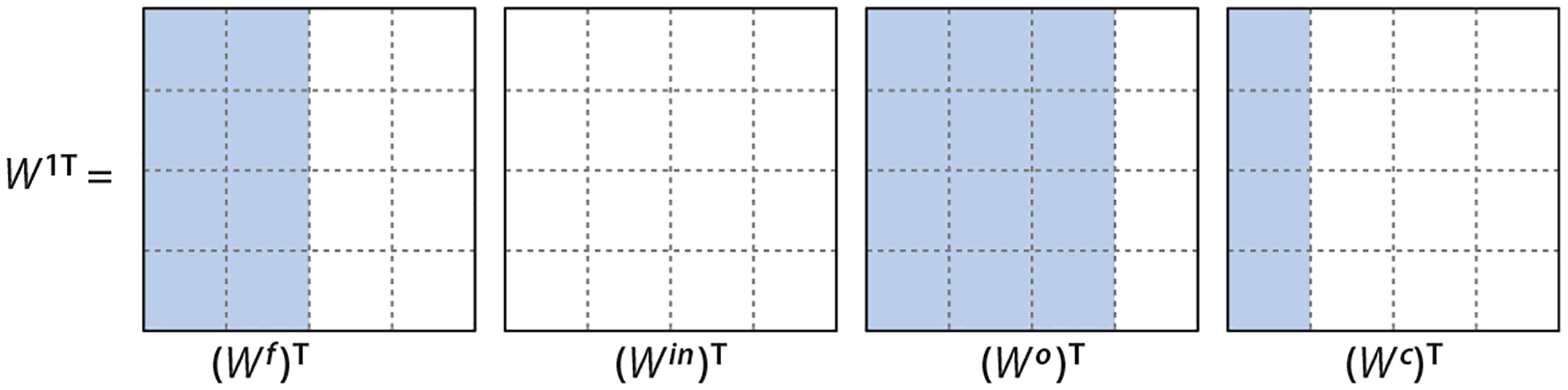
Example of group sparsity patterns in a cLSTM with and . Due to the group lasso penalty on the columns of , the , , , and matrices share the same column sparsity pattern. Abbreviation: cLSTM, component-wise long-short term memory network.
4.3. Subsampled and Mixed-Frequency Time Series
Even if the time series follows a linear VAR (Equation 6), if the process is observed at a sampling rate slower than the true causal scale of the underlying process, as depicted in Figure 11a, a causal analysis rooted at this slower time scale may miss true interactions and add spurious ones (Boot et al. 1967, Breitung & Swanson 2002, Silvestrini & Veredas 2008, Zhou et al. 2014). Mixed-frequency time series also present a challenge to Granger causal analysis. Example scenarios are depicted in Figure 11b–d. The scenario in Figure 11b often arises in econometrics, among other fields, and VAR models are fit at the scale of the least finely sampled time series (see, e.g., Schorfheide & Song 2015). However, for macroeconomic indicators like GDP, the scale of sampling is often determined by practical considerations and may not reflect the true causal dynamics, leading to confounded Granger and instantaneous causality judgments (Breitung & Swanson 2002, Zhou et al. 2014). The scenarios in Figure 11c–d combine subsampled and mixed-frequency settings and their respective challenges.
Figure 11.
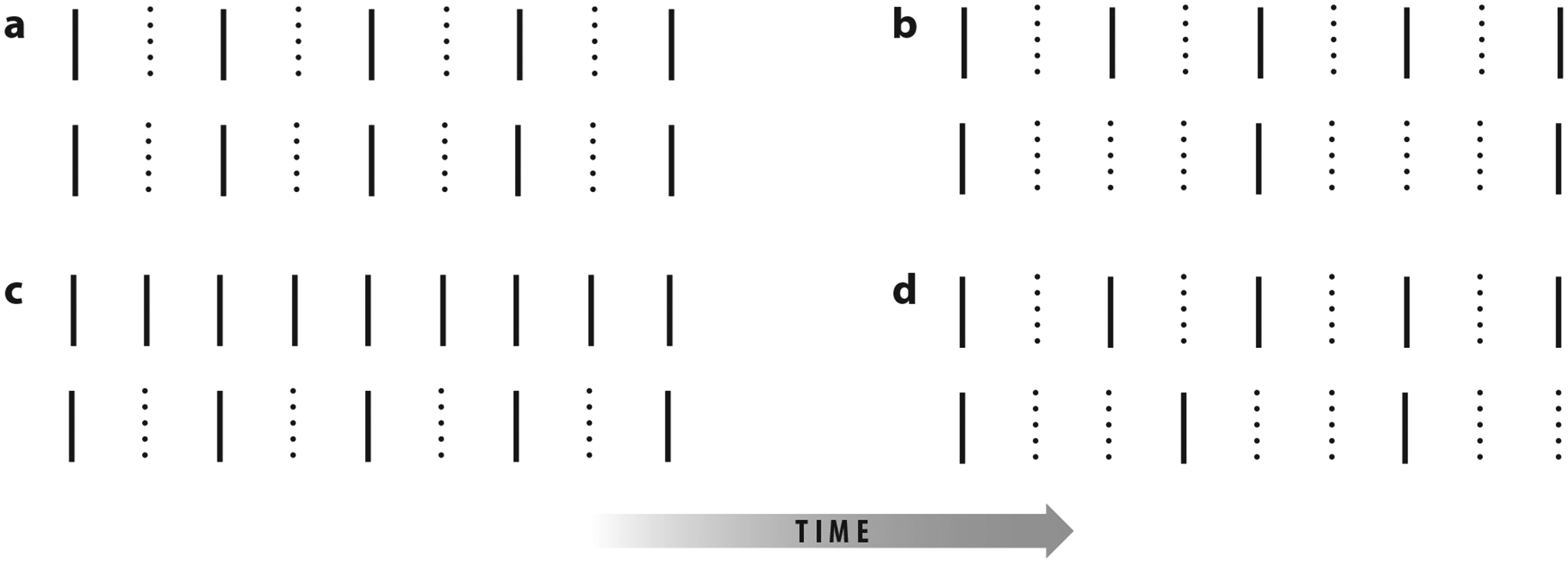
Four types of structured sampling. Black lines indicate observed data and dotted lines indicate missing data. (a) Both series are subsampled. (b) The standard mixed-frequency case, where only the second series is subsampled. (c) A subsampled version of panel b where each series is subsampled at different rates. (d) A subsampled mixed-frequency series that has no common factor across sampling rates and thus is not a subsampled version of panel b. Figure adapted with permission from Tank et al. (2019).
Recently, causal discovery in subsampled time series has been studied with methods in causal structure learning using graphical models (Danks & Plis 2013, Plis et al. 2015, Hyttinen et al. 2016). These methods are model free and automatically infer a sampling rate for causal relations most consistent with the data. For mixed-frequency autoregressive models with no subsampling at the fastest scale (Figure 11b), finding identifiability conditions was an open problem for many years (Chen & Zadrozny 1998). Anderson et al. (2016) recently showed that in the scenario in Figure 11b, a nonstructural autoregressive model is generically identifiable from the first two observed moments, so unidentifiable models make up a set of measure zero of the parameter space (see also Zadrozny 2016). In this section, we instead outline the model-based approach and identifiability conditions explored by Tank et al. (2019) for Granger causality analysis of SVAR models under both subsampling and mixed-frequency settings.
An SVAR (Lütkepohl 2005) allows the dynamics of to follow a combination of instantaneous effects, autoregressive effects, and independent noise. For simplicity, let us consider a lag one SVAR:
| 31. |
where is the structural matrix that determines the instantaneous linear effects, is an autoregressive matrix that specifies the lag one effects conditional on the instantaneous effects, is a white noise process such that for all , and is independent of for all , , , such that . We assume is distributed as . Solving Equation 31 in terms of gives the following lag one SVAR process:
| 32. |
In Equation 32, denotes the lag one linear effect of series on series , and is the structural matrix. The error is known as the shock to series at time , and the element is the linear instantaneous effect of on . The most typical condition is that is lower triangular with ones on the diagonal, implying a known causal ordering of the instantaneous effects. When the errors, , are non-Gaussian, both the causal ordering and instantaneous effects may be inferred directly from the data using techniques from independent component analysis (Hyvärinen et al. 2010). Alternatively, can be directly estimated via maximum likelihood (Lanne et al. 2017).
In the subsampled case, shown in Figure 11a, we observe every time steps, leading to observations, where is the number of subsampled observations. By marginalizing out the unobserved , we obtain the evolution equations
| 33. |
| 34. |
where is the stacked vector of errors for time and the unobserved points between and and . Equation 33 states that the subsampled process is a linear transformation of the past subsampled observations with transition matrix and a weighted sum of the shocks across all unobserved time points. Each shock is weighted by raised to the power of the time lag. Equation 34 appears to take a similar form to the structural process in Equation 31; however, now the vector of shocks, , is of dimension , with special structure on both the structural matrix and the distributions of the elements in . Unfortunately, this representation does not have the interpretation of instantaneous causal effects, as there are now multiple shocks per individual time series. We refer to the full parameterization of the subsampled structural model in Equation 34 as (, , ; ).
A classical analysis based on that does not account for subsampling would incorrectly estimate lagged Granger causal effects in , because does not imply that , and vice versa (Gong et al. 2015). Similarly, estimation of structural interactions may also be biased if subsampling is ignored. This is illustrated in Figure 12, where an analysis based on subsampled data identifies no lagged causal effect between and but a relatively large instantaneous interaction. Tank et al. (2019) provide further details and examples.
Figure 12.
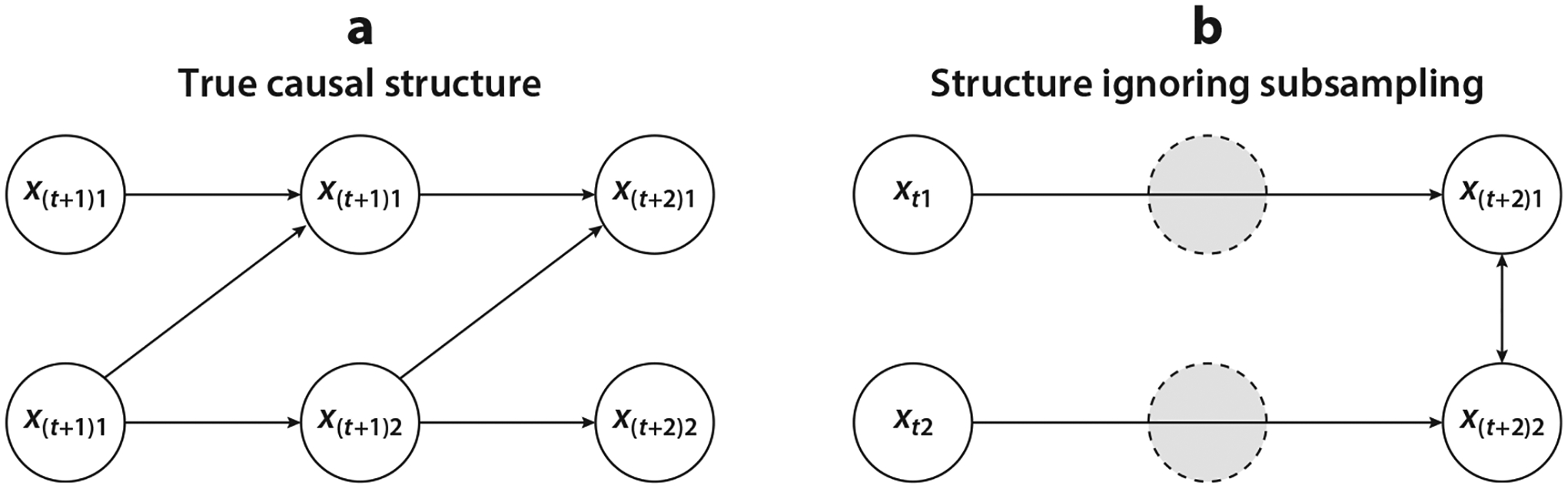
Depiction of how subsampling confounds causal analysis of lagged and instantaneous effects. (a) True causal diagram for regularly sampled data. (b) Estimated causal structure when subsampling is ignored. Figure adapted with permission from Tank et al. (2019).
The mixed-frequency scenarios, Figure 11b–d, are also considered by Tank et al. (2019) and involve defining sampling rates for each series and a set of indicator matrices that select the observed time points from Equation 32. Despite more cumbersome notation, the resulting process follows analogously to the derivation of Equation 34 and can be written as
| 35. |
where are observed lags of the series, is a function of elements of , and follows analogously to the subsampled case using elements of premultiplying elements of . As in the subsampled case, we refer to a parameterization of a mixed-frequency structural model as (, , ; ), where is now a p-vector of sampling rates.
The similar form of Equations 34 and 35 suggests similar identifiability results hold. However, not accounting for subsampling in the mixed-frequency setting (Figure 11c) leads not only to the kind of mistaken inferences discussed above but also to further mistakes unique to the mixed-frequency case (see Tank et al. 2019 for examples).
While both lagged Granger causality and instantaneous structural interactions are confounded by subsampling and mixed-frequency settings, Tank et al. (2019) showed that when accounting for this structure, we may, under some conditions, still estimate the and matrices of the underlying process directly from the subsampled or mixed-frequency data (see Theorem 1). The identifiability of and relies on a set of assumptions outlined below.
Assumption 1. is stationary so that all singular values of have modulus less than one.
Assumption 2. The distributions are distinct for each after rescaling by any nonzero scale factor, their characteristic functions are all analytic or they are all nonvanishing, and none of them has an exponent factor with polynomial of degree at least two.
Assumption 3. All are asymmetric.
Assumption 4. The variance of each is equal to one, i.e., .
Assumption 5. The matrix is full rank.
Theorem 1 (Tank et al. 2019). Suppose that are all non-Gaussian and independent, and the data are generated by Equation 32 with representation (, , ; ). Assume that the process also admits another mixed-frequency subsampling representation . In the pure subsampling case, for all . If Assumptions 1, 2, and 4 hold, then we have the following:
is equal to up to permutation of columns and scaling of columns by 1 or −1; that is, where is a scaled permutation matrix with 1 or −1 elements. This implies
For mixed-frequency only, if is lower triangular with positive diagonals, i.e., the instantaneous interactions follow a directed acyclic graph, and if for all there exists a such that any multiple of is 1 smaller than some multiple of with , then .
If Assumptions 3 and 5 also hold, then .
Theorem 1 demonstrates that identifiability of structural models still holds for mixed-frequency series with subsampling under non-Gaussian errors. The mixed-frequency setting provides additional information to resolve parameter ambiguities in the non-Gaussian setting. Specifically, is identifiable if there is one time step difference between when series and are sampled. This information can be used to resolve sign ambiguities in columns of , which leads to statement 2 in Theorem 1. This result applies directly to the standard mixed-frequency setting (Schorfheide & Song 2015, Anderson et al. 2016), where one series is observed at every time step, as in Figure 11b. It also applies to the case in Figure 11d, since there exist time steps where one series is observed one time step before another series.
In the case of subsampling, if the instantaneous causal effects follow a directed acyclic graph, the structure can be identified without any prior information about causal ordering of the variables.
Corollary 1 (Tank et al.2019). If Assumptions 1,2, and 4 hold and the true structural process corresponds to a directed acyclic graph —that is, it has a lower triangular structural matrix with positive diagonals, and it admits another representation with structural matrix —then . Hence, the structure of is identifiable without prior specification of the causal ordering of .
Together, Theorem 1 and Corollary 1 imply that when the shocks, , are independent and asymmetric, a complete causal diagram of the lagged and the instantaneous effects is fully identifiable from the subsampled time series, .
To estimate Granger causality from subsampled and mixed-frequency time series, Tank et al. (2019) modeled the non-Gaussian errors of the SVAR as a mixture of Gaussian distributions with components. The authors develop an expectation–maximization algorithm for joint estimation of the full set of parameters based only on the observed subsampled and mixed-frequency data . The method is the same for all scenarios in Figure 11a–d.
5. CONCLUSION
In the first part of this article, we briefly reviewed classical approaches to Granger causality, mentioned some of their applications, and discussed their shortcomings. These shortcomings are primarily due to the restrictive (and unattainable) assumptions that are needed in order to infer causal effects from time series data, which was the original premise of Granger causality. They are also due to the limitations of simple approaches that were historically used to investigate Granger causal relations.
In the second part of the article, we discussed recent efforts to relax some of the assumptions made by classical approaches and/or generalize their applicability. These include investigating Granger causal relations among a large set of variables, automatic lag selection, accounting for nonstationarity, developing flexible methods for non-Gaussian and noncontinuous observations, and attempts to account for differences between the true causal time scale and the frequency of the observed data. These recent developments have expanded the application domains of Granger causality and offer new opportunities for investigating interactions among components of complex systems with the goal of gaining a systems perspective to their joint behavior.
In spite of recent progress, there is still much more work to be done in this area. Even when not trying to infer causal effects, we would ideally need flexible nonparametric approaches that handle many observed time series while accounting for unmeasured variables and allowing for nonstationarity. However, despite these limitations, emerging data, especially those obtained from interventions over time and perturbations to the system’s state, offer new opportunities for discovering causal effect of variables on each other. At minimum, these new data and continued developments in this area can help researchers take the first step toward causal inference by restricting the set of possible causal hypotheses. We believe this area will continue to be an active area of research.
ACKNOWLEDGMENTS
This work was supported in part by National Science Foundation (NSF) grant DMS-1722246, National Institutes of Health (NIH) grant R01GM133848, and Air Force Office of Scientific Research (AFOSR) grant FA9550-21-1-0397.
Footnotes
DISCLOSURE STATEMENT
The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- Agresti A, Kateri M. 2011. Categorical data analysis. In International Encyclopedia of Statistical Science, ed. Lovric M, pp. 206–8. Berlin: Springer [Google Scholar]
- Ahelegbey DF, Billio M, Casarin R. 2016. Sparse graphical vector autoregression: a Bayesian approach. Ann. Econ. Stat./Ann. d’Écon. Stat 123–124:333–61 [Google Scholar]
- Ahn SC, Horenstein AR. 2013. Eigenvalue ratio test for the number of factors. Econometrica 81(3):1203–27 [Google Scholar]
- Aldor-Noiman S, Brown LD, Fox EB, Stine RA. 2016. Spatio-temporal low count processes with application to violent crime events. Stat. Sin 26:1587–610 [Google Scholar]
- Amblard PO, Michel OJ. 2011. On directed information theory and Granger causality graphs. J. Comput. Neurosci 30(1):7–16 [DOI] [PubMed] [Google Scholar]
- Amengual D, Watson MW. 2007. Consistent estimation of the number of dynamic factors in a large N and T panel. J. Bus. Econ. Stat 25(1):91–96 [Google Scholar]
- Anderson BD, Deistler M, Felsenstein E, Funovits B, Koelbl L, Zamani M. 2016. Multivariate AR systems and mixed-frequency data: G-identifiability and estimation. Econom. Theory 32(4):793–826 [Google Scholar]
- Bai P, Safikhani A, Michailidis G. 2020. Multiple change points detection in low rank and sparse high dimensional vector autoregressive models. IEEE Trans. Signal Proc 68:3074–89 [Google Scholar]
- Bańbura M, Giannone D, Reichlin L. 2010. Large Bayesian vector auto regressions. J. Appl. Econom 25(1):71–92 [Google Scholar]
- Basu S, Li X, Michailidis G. 2019. Low rank and structured modeling of high-dimensional vector autoregressions. IEEE Trans. Signal Proc 67(5):1207–22 [Google Scholar]
- Basu S, Michailidis G. 2015. Regularized estimation in sparse high-dimensional time series models. Ann. Stat 43(4):1535–67 [Google Scholar]
- Basu S, Shojaie A, Michailidis G. 2015. Network Granger causality with inherent grouping structure. J. Mach. Learn. Res 16(1):417–53 [PMC free article] [PubMed] [Google Scholar]
- Bauwens L, Laurent S, Rombouts JVK. 2006. Multivariate GARCH models: asurvey. J. Appl. Econom 21(1):79–109 [Google Scholar]
- Belviso F, Milani F. 2006. Structural factor-augmented VARs (SFAVARs) and the effects of monetary policy. BE J. Macroecon 6(3):1–46 [Google Scholar]
- Berchtold A 2001. Estimation in the mixture transition distribution model. J. Time Ser. Anal 22(4):379–97 [Google Scholar]
- Berchtold A, Raftery A. 2002. The mixture transition distribution model for high-order Markov chains and non-Gaussian time series. Stat. Sci 17(3):328–56 [Google Scholar]
- Bergmann TO, Hartwigsen G. 2021. Inferring causality from noninvasive brain stimulation in cognitive neuroscience. J. Cogn. Neurosci 33(2):195–225 [DOI] [PubMed] [Google Scholar]
- Bernanke BS, Blinder AS. 1992. The federal funds rate and the channels of monetary transmission. Am. Econ. Rev 82(4):901–21 [Google Scholar]
- Bernanke BS, Boivin J, Eliasz P. 2005. Measuring the effects of monetary policy: a factor-augmented vector autoregressive (FAVAR) approach. Q. J. Econ 120(1):387–422 [Google Scholar]
- Bernanke BS, Kuttner KN. 2005. What explains the stock market’s reaction to Federal Reserve policy? J. Finance 60(3):1221–57 [Google Scholar]
- Billings SA. 2013. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains. New York: Wiley [Google Scholar]
- Billings SA, Chen S. 1996. The determination of multivariable nonlinear models for dynamic systems using neural networks. In Neural Network Systems Techniques and Applications, ed. Leondes C, pp. 231–78. Cambridge, MA: Academic [Google Scholar]
- Billio M, Casarin R, Rossini L. 2019. Bayesian nonparametric sparse VAR models. J. Econom 212(1):97–115 [Google Scholar]
- Boot JC, Feibes W, Lisman JHC. 1967. Further methods of derivation of quarterly figures from annual data. J. R. Stat. Soc. Ser. C 16:65–75 [Google Scholar]
- Boyd S, Vandenberghe L. 2004. Convex Optimization. Cambridge, UK: Cambridge Univ. Press [Google Scholar]
- Breitung J, Swanson NR. 2002. Temporal aggregation and spurious instantaneous causality in multiple time series models. J. Time Ser. Anal 23(6):651–65 [Google Scholar]
- Bressler SL, Seth AK. 2011. Wiener–Granger causality: a well established methodology. Neuroimage 58(2):323–29 [DOI] [PubMed] [Google Scholar]
- Chamberlain G 1982. The general equivalence of Granger and Sims causality. Econometrica 50:569–81 [Google Scholar]
- Chen B, Zadrozny PA. 1998. An extended Yule-Walker method for estimating a vector autoregressive model with mixed-frequency data. Adv. Econom 13:47–74 [Google Scholar]
- Chen S, Shojaie A, Shea-Brown E, Witten D. 2017a. The multivariate Hawkes process in high dimensions: beyond mutual excitation. arXiv: 1707.04928 [stat.ME] [Google Scholar]
- Chen S, Shojaie A, Witten DM. 2017b. Network reconstruction from high-dimensional ordinary differential equations. J. Am. Stat. Assoc 112(520):1697–707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Witten D, Shojaie A. 2017c. Nearly assumptionless screening for the mutually-exciting multivariate Hawkes process. Electron. J. Stat 11(1):1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ching W, Fung ES, Ng MK. 2002. A multivariate Markov chain model for categorical data sequences and its applications in demand predictions. IMA J. Manag. Math 13(3):187–99 [Google Scholar]
- Chiou-Wei SZ, Chen CF, Zhu Z. 2008. Economic growth and energy consumption revisited—evidence from linear and nonlinear Granger causality. Energy Econ 30(6):3063–76 [Google Scholar]
- Chu SR, Shoureshi R, Tenorio M. 1990. Neural networks for system identification. IEEE Control Syst. Mag 10(3):31–35 [Google Scholar]
- Chudik A, Pesaran MH. 2011. Infinite-dimensional VARs and factor models. J. Econom 163(1):4–22 [Google Scholar]
- Cox LATJ, Popken DA. 2015. Has reducing fine particulate matter and ozone caused reduced mortality rates in the United States? Ann. Epidemiol 25(3):162–73 [DOI] [PubMed] [Google Scholar]
- Cromwell JB, Terraza M. 1994. Multivariate Tests for Time Series Models. Thousand Oaks, CA: SAGE [Google Scholar]
- Danks D, Plis S. 2013. Learning causal structure from under sampled time series. Presented at NIPS 2013 Workshop on Causality, Lake Tahoe, NV, Dec. 9 [Google Scholar]
- Davis RA, Zang P, Zheng T. 2016. Sparse vector autoregressive modeling. J. Comput. Graph. Stat 25(4):1077–96 [Google Scholar]
- Dhamala M, Rangarajan G,Ding M. 2008. Estimating Granger causality from Fourier and wavelet transforms of time series data. Phys. Rev. Lett 100(1):018701. [DOI] [PubMed] [Google Scholar]
- Doshi-Velez F, Wingate D, Tenenbaum J, Roy N. 2011. Infinite dynamic Bayesian networks. In ICML’11: Proceedings of the 28th International Conference on Machine Learning, ed. Getoor L, Scheffer T, pp. 913–20. Madison, WI: Omnipress [Google Scholar]
- Eichler M 2007. Granger causality and path diagrams for multivariate time series. J. Econom 137(2):334–53 [Google Scholar]
- Eichler M 2012. Graphical modelling of multivariate time series. Probab. Theory Relat. Fields 153(1–2):233–68 [Google Scholar]
- Eichler M, Dahlhaus R, Dueck J. 2017. Graphical modeling for multivariate Hawkes processes with nonparametric link functions. J. Time Ser. Anal 38(2):225–42 [Google Scholar]
- Etzel N, Shojaie A. 2016. ngc: penalized estimation and visualization for network Granger causality. R Package. https://github.com/shojaie/ngc
- Florens JP, Mouchart M. 1982. A note on noncausality. Econom. J. Econom. Soc 50:583–91 [Google Scholar]
- Fox E, Sudderth EB, Jordan MI, Willsky AS. 2011. Bayesian nonparametric inference of switching dynamic linear models. IEEE Trans. Signal Proc 59(4):1569–85 [Google Scholar]
- Fujita A, Sato JR, Garay-Malpartida HM, Yamaguchi R, Miyano S, et al. 2007. Modeling gene expression regulatory networks with the sparse vector autoregressive model. BMC Syst. Biol 1:39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George EI,Sun D,Ni S. 2008. Bayesian stochastic search for VAR model restrictions. J. Econom 142(1):553–80 [Google Scholar]
- Geweke J 1982. Measurement of linear dependence and feedback between multiple time series. J. Am. Stat. Assoc 77(378):304–13 [Google Scholar]
- Ghahramani Z 1997. Learning dynamic Bayesian networks. In International School on Neural Networks, Initiated by IIASS and EMFCSC, ed. Giles CL, Gori M, pp. 168–97. New York: Springer [Google Scholar]
- Ghosh S, Khare K, Michailidis G. 2019. High-dimensional posterior consistency in Bayesian vector autoregressive models. J. Am. Stat. Assoc 114(526):735–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glymour C, Zhang K, Spirtes P. 2019. Review of causal discovery methods based on graphical models. Front. Genet 10:524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong M, Zhang K, Schölkopf B, Tao D, Geiger P. 2015. Discovering temporal causal relations from subsampled data. Proc. Mach. Learn. Res 37:1898–1906 [Google Scholar]
- Granger CWJ. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37:424–38 [Google Scholar]
- Granger CWJ. 1980. Testing for causality: a personal viewpoint. J. Econ. Dyn. Control 2:329–52 [Google Scholar]
- Granger CWJ. 1988. Some recent development in a concept of causality. J. Econom 39(1–2):199–211 [Google Scholar]
- Granger S 2001. Social engineering fundamentals, part I: hacker tactics. Security Focus, Dec. 18 [Google Scholar]
- Graves A 2012. Supervised Sequence Labelling with Recurrent Neural Networks. New York: Springer [Google Scholar]
- Hall EC, Raskutti G, Willett R. 2016. Inference of high-dimensional autoregressive generalized linear models. arXiv:1605.02693 [stat.ML] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen NR, Reynaud-Bouret P, Rivoirard V, et al. 2015. Lasso and probabilistic inequalities for multivariate point processes. Bernoulli 21(1):83–143 [Google Scholar]
- Haslbeck JM, Waldorp LJ. 2020. mgm: Estimating time-varying mixed graphical models in high-dimensional data. J. Stat. Softw 93(8). 10.18637/jss.v093.i08 [DOI] [Google Scholar]
- Henderson J, Michailidis G. 2014. Network reconstruction using nonparametric additive ODE models. PLOS ONE 9(4):e94003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland PW. 1986. Statistics and causal inference. J. Am. Stat. Assoc 81(396):945–60 [Google Scholar]
- Hong Y, Liu Y, Wang S. 2009. Granger causality in risk and detection of extreme risk spillover between financial markets. J. Econom 150(2):271–87 [Google Scholar]
- Huang J, Zhang T, Metaxas D. 2011. Learning with structured sparsity. J. Mach. Learn. Res 12(Nov.):3371–412 [Google Scholar]
- Hyttinen A, Plis S, Järvisalo M, Eberhardt F, Danks D. 2016. Causal discovery from subsampled time series data by constraint optimization. arXiv:1602.07970 [cs.AI] [PMC free article] [PubMed] [Google Scholar]
- Hyvärinen A, Zhang K, Shimizu S, Hoyer PO. 2010. Estimation of a structural vector autoregression model using non-Gaussianity. J. Mach. Learn. Res 11:1709–31 [Google Scholar]
- Kilian L 2013. Structural vector autoregressions. In Handbook of Research Methods and Applications in Empirical Macroeconomics, ed. Hashimzade N, pp. 515–54. Cheltenham, UK: Edward Elgar [Google Scholar]
- Kilian L, Lütkepohl H. 2017. Structural Vector Autoregressive Analysis. Cambridge, UK: Cambridge Univ. Press [Google Scholar]
- Kim S, Xing EP. 2010. Tree-guided group lasso for multi-task regression with structured sparsity. In ICML’10: Proceedings of the 27th International Conference on Machine Learning, ed. Fürnkranz J, Joachims T, pp. 543–50. Madison, WI: Omnipress [Google Scholar]
- Kişi Ö 2004. River flow modeling using artificial neural networks. J. Hydrol. Eng 9(1):60–63 [Google Scholar]
- Kontoyiannis I, Skoularidou M. 2016. Estimating the directed information and testing for causality. IEEE Trans. Inform. Theory 62(11):6053–67 [Google Scholar]
- Lanne M, Meitz M, Saikkonen P. 2017. Identification and estimation of non-Gaussian structural vector autoregressions. J. Econom 196(2):288–304 [Google Scholar]
- Leeper EM, Sims CA, Zha T, Hall RE, Bernanke BS. 1996. What does monetary policy do? Brookings Pap. Econ. Activ 1996(2):1–78 [Google Scholar]
- Li Y, Yu R, Shahabi C, Liu Y. 2017. Diffusion convolutional recurrent neural network: data-driven traffic forecasting. arXiv:1707.01926 [cs.LG] [Google Scholar]
- Litterman RB. 1986. Forecasting with Bayesian vector autoregressions—five years of experience. J. Bus. Econ. Stat 4(1):25–38 [Google Scholar]
- Lozano AC, Abe N, Liu Y, Rosset S. 2009. Grouped graphical Granger modeling for gene expression regulatory networks discovery. Bioinformatics 25(12):i110–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lusch B, Maia PD, Kutz JN. 2016. Inferring connectivity in networked dynamical systems: challenges using Granger causality. Phys. Rev. E 94(3):032220. [DOI] [PubMed] [Google Scholar]
- Lütkepohl H 1982. Non-causality due to omitted variables. J. Econom 19(2–3):367–78 [Google Scholar]
- Lütkepohl H 2005. New Introduction to Multiple Time Series Analysis. New York: Springer [Google Scholar]
- Maziarz M 2015. A review of the Granger-causality fallacy. J. Philos. Econ 8(2):86–105 [Google Scholar]
- McCullagh P, Nelder JA. 1989. Generalized Linear Models. Boca Raton, FL: Chapman and Hall/CRC [Google Scholar]
- McKenzie E 2003. Discrete variate time series. Handb. Stat 21:573–606 [Google Scholar]
- Moauro F, Savio G. 2005. Temporal disaggregation using multivariate structural time series models. Econom. J 8(2):214–34 [Google Scholar]
- Mosedale TJ, Stephenson DB, Collins M, Mills TC. 2006. Granger causality of coupled climate processes: ocean feedback on the North Atlantic Oscillation. J. Climate 19(7):1182–94 [Google Scholar]
- Nakajima J, West M. 2013. Bayesian analysis of latent threshold dynamic models. J. Bus. Econ. Stat 31(2):151–64 [Google Scholar]
- Neykov M, Ning Y, Liu JS, Liu H, et al. 2018. A unified theory of confidence regions and testing for high-dimensional estimating equations. Stat. Sci 33(3):427–43 [Google Scholar]
- Nicholson W, Matteson D, Bien J. 2017a. BigVAR: tools for modeling sparse high-dimensional multivariate time series. arXiv:1702.07094 [stat.CO] [Google Scholar]
- Nicholson WB, Matteson DS, Bien J. 2017b. VARX-L: structured regularization for large vector autoregressions with exogenous variables. Int. J. Forecast 33(3):627–51 [Google Scholar]
- Nicolau J 2014. A new model for multivariate Markov chains. Scand. J. Stat 41(4):1124–35 [Google Scholar]
- Noble NR, Fields TW. 1983. Sunspots and cycles: comment. South. Econ. J 50:251–54 [Google Scholar]
- Onatski A 2010. Determining the number of factors from empirical distribution of eigenvalues. Rev. Econ. Stat 92(4):1004–16 [Google Scholar]
- Pfaff B 2008. VAR, SVAR and SVEC models: implementation within R package vars. J. Stat. Softw 27(4):1–32 [Google Scholar]
- Plis S, Danks D, Freeman C, Calhoun V. 2015. Rate-agnostic (causal) structure learning. In Advances in Neural Information Processing Systems, ed. Cortes C, Lawrence N, Lee D, Sugiyama M, Garnett R, pp. 3285–93. N.p.: NeurIPS; [PMC free article] [PubMed] [Google Scholar]
- Qiu H, Xu S, Han F, Liu H, Caffo B. 2015. Robust estimation of transition matrices in high dimensional heavy-tailed vector autoregressive processes. JMLR Worksh. Conf. Proc 37:1843–51 [PMC free article] [PubMed] [Google Scholar]
- Quinn CJ, Kiyavash N, Coleman TP. 2015. Directed information graphs. IEEE Trans. Inform. Theory 61(12):6887–909 [Google Scholar]
- Raftery AE. 1985. A model for high-order Markov chains. J. R. Stat. Soc. Ser. B 47(3):528–39 [Google Scholar]
- Raissi M, Perdikaris P, Karniadakis GE. 2018. Multistep neural networks for data-driven discovery of nonlinear dynamical systems. arXiv:1801.01236 [math.DS] [Google Scholar]
- Reid AT, Headley DB, Mill RD, Sanchez-Romero R, Uddin LQ, et al. 2019. Advancing functional connectivity research from association to causation. Nat. Neurosci 22(11):1751–60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Runge J, Heitzig J, Petoukhov V, Kurths J. 2012. Escaping the curse of dimensionality in estimating multivariate transfer entropy. Phys. Rev. Lett 108(25):258701. [DOI] [PubMed] [Google Scholar]
- Safikhani A, Shojaie A. 2020. Joint structural break detection and parameter estimation in high-dimensional nonstationary VAR models. J. Am. Stat. Assoc 10.1080/01621459.2020.1770097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schorfheide F, Song D. 2015. Real-time forecasting with a mixed-frequency VAR. J. Bus. Econ. Stat 33(3):366–80 [Google Scholar]
- Seth AK, Barrett AB, Barnett L. 2015. Granger causality analysis in neuroscience and neuroimaging. J. Neurosci 35(8):3293–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheehan RG, Grieves R. 1982. Sunspots and cycles: a test of causation. South. Econ. J 48:775–77 [Google Scholar]
- Shojaie A, Basu S, Michailidis G. 2012. Adaptive thresholding for reconstructing regulatory networks from time-course gene expression data. Stat. Biosci 4(1):66–83 [Google Scholar]
- Shojaie A, Michailidis G. 2010. Discovering graphical Granger causality using the truncating lasso penalty. Bioinformatics 26(18):i517–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silvestrini A, Veredas D. 2008. Temporal aggregation of univariate and multivariate time series models: A survey. J. Econ. Surv 22(3):458–97 [Google Scholar]
- Sims CA. 1972. Money, income, and causality. Am. Econ. Rev 62(4):540–52 [Google Scholar]
- Sims CA. 1980. Macroeconomics and reality. Econom. J. Econom. Soc 48:1–48 [Google Scholar]
- Song S, Bickel PJ. 2011. Large vector auto regressions. arXiv:1106.3915 [stat.ML] [Google Scholar]
- Stock JH, Watson M. 2011. Dynamic factor models. Oxford Handb Online. 10.1093/oxfordhb/9780195398649.013.0003 [DOI] [Google Scholar]
- Stokes PA, Purdon PL. 2017. A study of problems encountered in Granger causality analysis from a neuroscience perspective. PNAS 114(34):E7063–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stram DO, Wei WW. 1986. A methodological note on the disaggregation of time series totals. J. Time Ser. Anal 7(4):293–302 [Google Scholar]
- Tank A, Covert I, Foti N, Shojaie A, Fox EB. 2021a. Neural Granger causality. IEEE Trans. Pattern Anal. Mach. Intel In press. https://doi.ieeecomputersociety.org/10.1109/TPAMI.2021.3065601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tank A, Fox EB, Shojaie A. 2019. Identifiability and estimation of structural vector autoregressive models for subsampled and mixed-frequency time series. Biometrika 106(2):433–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tank A, Li X, Fox E, Shojaie A. 2021b. The convex mixture distribution: Granger causality for categorical time series. SIAM J. Math. Data Sci 3(1):83–112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao Y, Ma L, Zhang W, Liu J, Liu W, Du Q. 2018. Hierarchical attention-based recurrent highway networks for time series prediction. arXiv:1806.00685 [cs.LG] [Google Scholar]
- Teräsvirta T, Tjøstheim D, Granger CWJ. 2010. Modelling Nonlinear Economic Time Series. Oxford, UK: Oxford Univ. Press [Google Scholar]
- Tibshirani R 1996. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 58(1):267–88 [Google Scholar]
- Tong H 2011. Nonlinear time series analysis. In Encyclopedia of Mathematics. Berlin: EMS. http://encyclopediaofmath.org/index.php?title=Nonlinear_time_series_analysis&oldid=37777 [Google Scholar]
- Vicente R, Wibral M, Lindner M, Pipa G. 2011. Transfer entropy—a model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci 30(1):45–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Kolar M, Shojaie A. 2020. Statistical inference for networks of high-dimensional point processes. arXiv:2007.07448 [stat.ML] [Google Scholar]
- Weiß CH. 2018. An Introduction to Discrete-Valued Time Series. New York: Wiley [Google Scholar]
- Wu H, Lu T, Xue H, Liang H. 2014. Sparse additive ordinary differential equations for dynamic gene regulatory network modeling. J. Am. Stat. Assoc 109(506):700–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu H, Farajtabar M, Zha H. 2016. Learning Granger causality for Hawkes processes. Proc. Mach. Learn. Res 48:1717–26 [Google Scholar]
- Yu R, Zheng S, Anandkumar A, Yue Y. 2017. Long-term forecasting using tensor-train RNNs. arXiv:1711.00073 [cs.LG] [Google Scholar]
- Yuan M, Lin Y. 2006. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B 68(1):49–67 [Google Scholar]
- Zadrozny PA. 2016. Extended Yule-Walker identification of VARMA models with single or mixed-frequency data. J. Econom 193(2):438–46 [Google Scholar]
- Zhang GP. 2003. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 50:159–75 [Google Scholar]
- Zheng L, Raskutti G. 2019. Testing for high-dimensional network parameters in auto-regressive models. Electron. J. Stat 13(2):4977–5043 [Google Scholar]
- Zhou D, Zhang Y, Xiao Y, Cai D. 2014. Analysis of sampling artifacts on the Granger causality analysis for topology extraction of neuronal dynamics. Front. Comput. Neurosci 8:75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou K, Zha H,Song L. 2013. Learning social infectivity in sparse low-rank networks using multi-dimensional Hawkes processes. Proc. Mach. Learn. Res 31:641–49 [Google Scholar]
- Zhu D, Ching W. 2010. A new estimation method for multivariate Markov chain model with application in demand predictions. In BIFE ‘10: Proceedings of the 2010 Third International Conference on Business Intelligence and Financial Engineering, pp. 126–30. Washington, DC: IEEE [Google Scholar]
- Zhu K, Liu H. 2020. Confidence intervals for parameters in high-dimensional sparse vector autoregression. arXiv:2009.09462 [stat.ME] [Google Scholar]


