Abstract
Predictive and reactive behaviors represent two mutually exclusive strategies in a sensorimotor task. Predictive behavior consists in internally estimating timing and features of a target stimulus and relies on a cortical medial frontal system [superior frontal gyrus (SFG)]. Reactive behavior consists in waiting for actual perception of the target stimulus and relies on the lateral frontal cortex [inferior frontal gyrus (IFG)]. We investigated whether SFG-IFG connections by the frontal aslant tract (FAT) can mediate predictive/reactive interactions. In 19 healthy human volunteers, we applied online transcranial magnetic stimulation (TMS) to six spots along the medial and lateral terminations of the FAT, during the set period of a delayed reaction task. Such scenario can be solved using either predictive or reactive strategies. TMS increased the propensity toward reactive behavior if applied to a specific portion of the IFG and increased predictive behavior when applied to a specific SFG spot. The two active spots in the SFG and IFG were directly connected by a sub-bundle of FAT fibers as indicated by diffusion-weighted imaging (DWI) tractography. Since FAT connectivity identifies two distant cortical nodes with opposite functions, we propose that the FAT mediates mutually inhibitory interactions between SFG and IFG to implement a “winner takes all” decisional process. We hypothesize such role of the FAT to be domain-general, whenever competition occurs between internal predictive and external reactive behaviors. Finally, we also show that anatomic connectivity is a powerful factor to explain and predict the spatial distribution of brain stimulation effects.
SIGNIFICANCE STATEMENT We interact with sensory cues adopting two main mutually-exclusive strategies: (1) trying to anticipate the occurrence of the cue or (2) waiting for the GO-signal to be manifest and react to it. Here, we showed, by using noninvasive brain stimulation [transcranial magnetic stimulation (TMS)], that two specific cortical regions in the superior frontal gyrus (SFG) and the inferior frontal gyrus (IFG) have opposite roles in facilitating a predictive or a reactive strategy. Importantly these two very distant regions but with highly interconnected functions are specifically connected by a small white matter bundle, which mediates the direct competition and exclusiveness between predictive and reactive strategies. More generally, implementing anatomic connectivity in TMS studies strongly reduces spatial noise.
Keywords: brain stimulation, frontal aslant tract, motor control, predictive proactive, reactive, tractography
Introduction
Whenever synchronizing our movements to a sensory cue, we can adopt two opposite, mutually exclusive, strategies: a reactive or a predictive strategy (Schmidt, 1968). In the trade-off between speed and accuracy, predictive strategies are faster, but more prone to anticipation errors, while reactive strategies are slower, but more accurate. The reactive strategy consists in waiting for the GO-signal, bottom-up processing its sensory characteristics, and mapping the sensory cue onto a movement commitment. The neural bases of such arbitrary sensorimotor association have been identified, by human imaging studies, in a diffuse network of parietal, premotor and prefrontal regions including the inferior frontal gyrus (IFG), the dorsal premotor region, around the junction between the superior frontal sulcus and the dorsal segment of the precentral sulcus and the regions of the medial wall. The predictive strategy is an internally generated behavior and consists in moving without waiting for the actual sensory information to be available, estimating the time of onset of the GO-signal based on prior knowledge. The neural bases of such top-down process are necessarily different from those of the reactive modality, because, using a predictive strategy, no sensory information is necessary to complete the task. Motivated, internally generated goals are set in the medial prefrontal cortex (MPFC; O’Reilly, 2010; Stuss, 2011) and find a motor outlet in the motor cortices of the medial wall of the hemispheres, i.e., the presupplementary motor area (pre-SMA) and the supplementary motor area (SMA). Unsurprisingly, electrophysiological findings in monkeys indicate in the SMA the presence of neuronal machinery for internal clocking of actions (Shima and Tanji, 2000; Mita et al., 2009). Summing up, predictive behavior is seemingly based on a medial frontal system, anatomically consistent with the orbital cortex and the medial and lateral surfaces of the whole superior frontal gyrus (SFG), while reactive behavior is coded in a lateral frontal system, anatomically consistent with the IFG. In the recent years, a white matter system connecting directly the medial and the lateral frontal regions has been described, that could be a means of direct integration between predictive and reactive behavior. The frontal aslant tract (FAT) is a white matter tract connecting the caudal portion of the SFG (including both its convexity and medial wall) with the ventral premotor cortex and the caudal IFG (Catani et al., 2012). The FAT has been hypothesized to be involved in a series of functions related to language processes, both in the phonological and lexical domain, but also in motor and cognitive functions such as verbal and visuospatial working memory functions, social communication processes, rhythm and music processing, and attentional processes (Serra et al., 2017; Garic et al., 2019; Vallesi and Babcock, 2020; La Corte et al., 2021). We hypothesize that such a variety of functional involvement is supported by an underlying domain-general function that is the coordination between top-down internally generated, predictive behavior with bottom-up, externally triggered actions. To test this hypothesis, we used a task that assess the propensity to adopt either predictive or reactive strategies. In a precued reaction task with a fixed, predictable set-period, participants tend to switch, trial-by-trial between a predictive strategy [identified by very short response times (RTs)] and a reactive strategy (identified by longer RTs). In a previous work we showed that transcranial magnetic stimulation (TMS) applied over the SFG during the SET period induced a preference for predictive behavior, interpreted as a “gain-of-function” of SFG properties (Cattaneo and Parmigiani, 2021). In the present experiment, capitalizing on a model in which IFG and SFG produce two opposing, mutually exclusive behavior, we hypothesized that TMS to the SFG or the IFG should produce a double-dissociation pattern, with SFG stimulation leading to a increased predictive behavior and IFG stimulation leading to increased reactive behavior and. Importantly, we hypothesized that anatomic connectivity by FAT fibers should be a spatial constraint in indicating the specific regions of the SFG and IFG where the double dissociation pattern was to be expected.
Materials and Methods
Behavioral measurement of response times (all experiments)
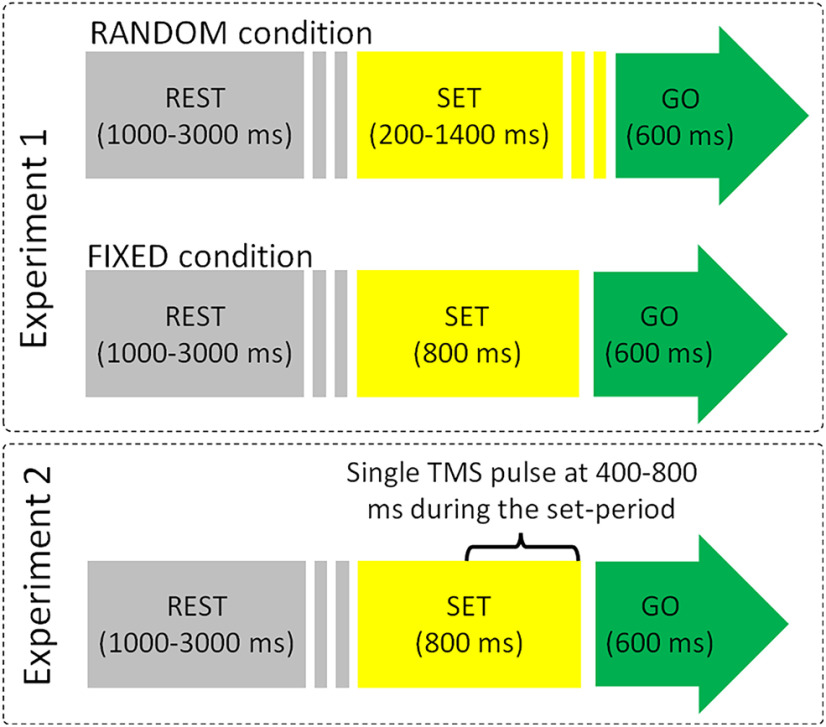
We aimed to exploit here the same task as in Cattaneo and Parmigiani (2021), consisting in a precued simple reaction time, as in a “ready-set-GO” scenario. Subjects were required to place their head on a fixed chinrest for the entire length of the experiment at 60 cm from a 27-inch standard monitor with a refresh rate of 60 Hz, and a keyboard placed in front of them. Stimulus presentation was performed using MATLAB (Psychtoolbox) scripts and delivered by MATLAB v.2018b. The experimental task used in both experiments consisted in a precued GO-task, i.e., a sequence of “rest,” “set-period,” and “GO-signal + response.” The trial structure is illustrated in Figure 1. Participants were warned of the upcoming GO-signal by the set-period, which had a fixed (800 ms) or variable (200–1400 ms) duration in experiment 1 and only a fixed (800 ms) duration in experiment 2. The color of a circle in the center of a white screen informed the Participant of the phase of the trial: gray for rest, yellow for the set-period, and green for the GO-signal. The instruction was to press the spacebar with the right hand as fast as possible on the occurrence of the green dot. Experimental instructions included the information that the duration of the set-period was fixed or variable. Feedback was given when the button was pressed before the GO-signal (false start) in the form of the words “too early” on the screen and when the button was pressed too late “too late” if occurring later than 600 ms from the GO-signal. The whole script for stimulus presentation and TMS triggering is available as supplementary material at: https://osf.io/x76cm/. The gray circle duration (rest phase) varied randomly according to a square-wave function, between 1000 and 3000 ms. In experiment 1 the yellow circle (set-period) varied randomly according to a square-wave function, between 200 and 1400 ms in blocks referred to as RANDOM (see below) or persisted for a constant time duration of 800 ms in blocks referred to as FIXED condition. Conversely, in the TMS Experiment the yellow dot, and hence the set-period, had a fixed duration of 800 ms. The green dot (GO-period) was always presented for 600 ms. Participants wore earphones for the entire duration of both experiments, listening to white noise interspersed with sounds of TMS stimulation, generated by the MATLAB script TAAC-TMS Adaptable Auditory Control (Russo et al., 2022). Before the actual experiment the participants familiarized with the task in a series of at least one practice block, until they reported confidence with the task.
Figure 1.
Schematization of single trials in the two experiments. Upper, RANDOM condition of experiment 1: the duration of the set-period was unpredictable and varied between 200 and 1400 ms. Middle, FIXED condition of experiment 1: the set-period duration is 800 ms in every trial. Lower, TMS was delivered at a random time (square-wave function) comprised between 400 and 800 ms form the beginning of the set-period.
Experiment 1 (behavioral validation of RT distribution)
Experimental design
As stated earlier, we capitalized on the data from Cattaneo and Parmigiani (2021) in which, in a precued RT task, the participants’ responses are seemingly distributed following a bimodal pattern, with a late peak (>200 ms) corresponding to reactive behavior, and an early peak (<100 ms), which cannot possibly be the result of actual perceptual processing of the GO-signal. Indeed, in untrained volunteers minimum RTs with the upper limb, to simple detection tasks are around 200 ms (Woods et al., 2015). To validate and quantitatively demonstrate the actual existence of the predictive behavior, we applied the precued RT task to 20 healthy participants aged 22–49 years (12 females). The experiment consisted in two blocks of 60 trials each. In one block the duration of the set-period (yellow dot) was variable between 200 and 1400 ms (RANDOM block) and in the other block, the set-period was fixed, corresponding to 800 ms (FIXED block). The order of the two blocks was counterbalanced between participants.
Data analysis
Response times (RTs) were considered starting from the GO-signal. Therefore, negative RTs indicated that the button press had occurred before the onset of the GO-signal. Data analysis was aimed at demonstrating that if participants have access to the information on the duration of the set-period, they can produce responses that are anticipatory, of the GO-signal, following a predictive strategy, rather than a reactive strategy. To do so we modeled the distribution of RTs in the two conditions to a function that is the sum of two separate skew-Normal functions, to account for our expectation of a bimodal distribution. To do so we first expressed the distribution of the actual individual RTs by means of Gaussian kernel density estimates (Peter, 1985) using MATLAB’s ‘ksdensity’ function (Fig. 2A,B) and then we plotted the mean value of all kernel estimates to obtain a grand average of all data (Fig. 2A,B, red lines). We then fitted the population data to the sum of two skewed-Normal functions, by means of MATLAB’s ‘curveFitter’ function. Specifically, we adopted the following formula for each of the skewed-Normal distribution (O’Hagan and Leonard, 1976; Azzalini, 1985):
where a is the gain factor for the height of the distribution, m is the mean of the distribution, s is an index of the SD (width) of the distribution and b is the index od skewness (set between −1 and +1). Finally, the goodness of the resulting fit was assessed by the adjusted R2 index. Note that all parameters, a, m, s and b are duplicated as a1, a2, m1, m2, because the fit is performed to the sum of two skewed-Normal curves.
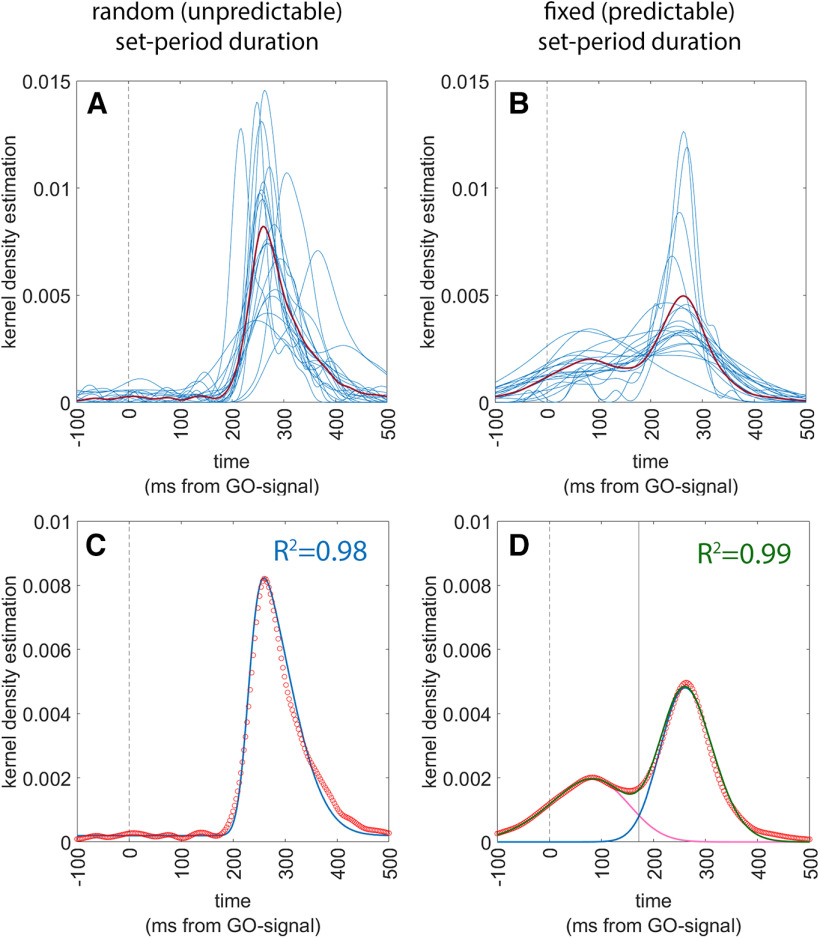
Figure 2.
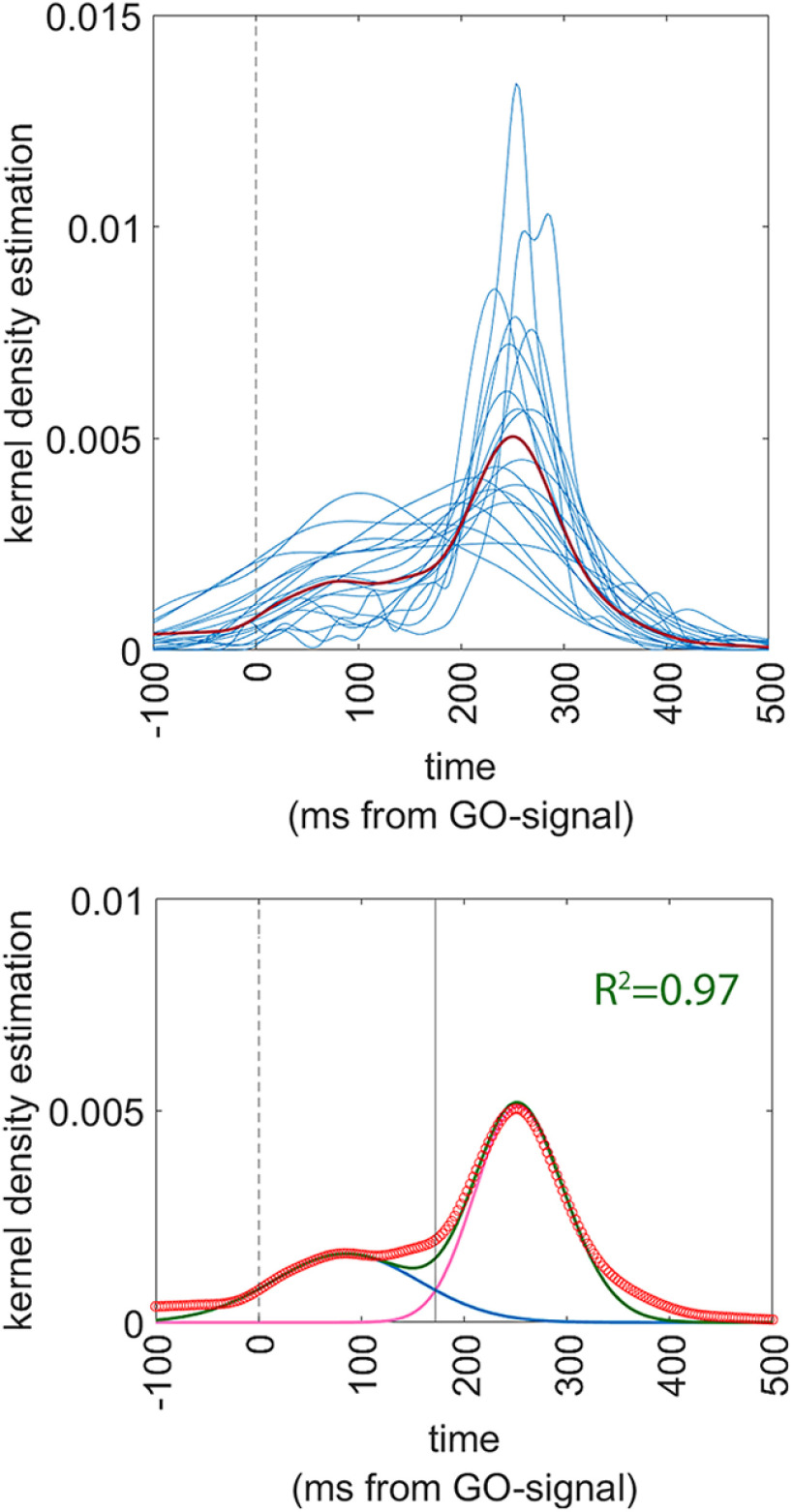
Results of experiment 1. The left panels refer to the RANDOM condition and the right panels refer to the FIXED condition. In all panels, the vertical dashed line indicates t = 0 ms, i.e., the onset of the GO-signal. Upper panels (A and B) show the superimposed individual Gaussian kernel density estimates of the 20 participants (thin blue lines) together with the mean Gaussian kernel density estimate of the whole population (thick red line). Lower panels show a superimposition of the actual data and of the fitting functions, together with an indication of the goodness-of-fit. Actual data are presented as a scatterplot of hollow red circles, indicating the Gaussian kernel density estimates of the population (repeating the data of the thick red line of the upper panels). Fitting skewed-Normal functions are shown as continuous lines. In panel C, the function of a single skewed-Normal function is shown in blue because optimal fitting occurred with a single curve. In panel D, the two skewed-Normal functions required to obtain optimal fitting are shown in purple and blue, and their sum is shown in green. The solid vertical line represents the point of optimal separation between the two distributions (i = 172 ms). The goodness of fit is shown as the R2 value.
Experiment 2 (TMS experiment)
A total of 19 subjects participated in the study (10 females and 9 males aged 22–36 years). The experiment was approved by the local Ethical Committee of the University of Trento (protocol 2020_035) and all participants signed informed consent papers to join the study. Participants were screened for TMS contraindications before the experiment (Wassermann, 1998; Rossi et al., 2009, 2021). All participants were required to join two separate sessions: the first one was an MRI-DTI session and the second one a neuronavigated TMS stimulation session during the performing of a task.
MR imaging
The anatomic images were acquired by a 3T MAGNETOM Prisma (Siemens Healthcare) with a 64-channel head-neck RF receive coil was used to acquire 3D T1-weighted (T1w, multiecho-MPRAGE, 1 mm isotropic), and diffusion-weighted (dMRI) data (2 mm isotropic, TE/TR = 76/4200 ms, shells: b = {0,700,1000,2850} s/mm, 32/64/64 directions. DW imges processing. T1-w images of all the subjects underwent a standard preprocessing. First of all, the raw DICOM T1-w images were converted to NifTI format using dcm2niix software. Then, an AC-PC (anterior-posterior commissures) alignment was performed by means of rigid registration to the MNI152 T1-w template (Avants et al., 2008). The brain mask was estimated using a pretrained 3D U-Net (Ronneberger et al., 2015; Çiçek et al., 2016). The brain mask was used to perform the Bias-Field Correction restricted on the brain voxels, using N4-Bias Field Correction tool (Tustison et al., 2010). Furthermore, the T1-w images were segmented into 6 brain tissue by means of a pretrained 3D-Unet (Amorosino et al., 2020). To support the alignment of structural and diffusion images we computed a synthetic T2-w image using AFNI toolkit (Cox, 1996).
DWI data preprocessing
The preprocessing of the diffusion-weighted imaging (DWI) data were conducted using TORTOISE toolkit (Pierpaoli et al., 2010). With DIFFPREP tool (Okan et al., 2017), we computed the correction for Gibbs ringing, thermal noise, eddy current, and motion distortion. Furthermore, we used DRBUDDI tool to perform the susceptibility induced echoplanar imaging (EPI) distortion correction through diffeomorphic registration (Avants et al., 2008) of the DWIs volumes. DRBUDDI was operated combining both DWI reversed-phase encoding directions (i.e., AP and PA acquisitions) and also the information from an undistorted structural MRI. The DWIs data were also corrected for bias field inhomogeneities (Tustison et al., 2010). The reconstruction of the streamline tractography was performed using MRtrix3 software (Tournier et al., 2012). We performed the multishell, multitissue constrained spherical deconvolution (CSD; lmax = 6; threshold = 0.5) to obtain the WM fiber orientation distribution function (fODF) from the estimation of the response function using the Dhollander method (Dhollander et al., 2016, 2019). Then, we computed the deterministic tractography based on CSD (cutoff 0.001, maximum angle of 75°, step of 0.5 mm) constraining the length of the streamlines between 20 and 250 mm. We initialized the tractography using random seeding of 10̂7 seeds on a WM mask, estimated by thresholding the DTI fractional anisotropy (FA) scalar map with a heuristic value of 0.15. We stopped the tracking by selecting 2*10̂6 streamlines.
Individual FAT dissection and neuronavigation
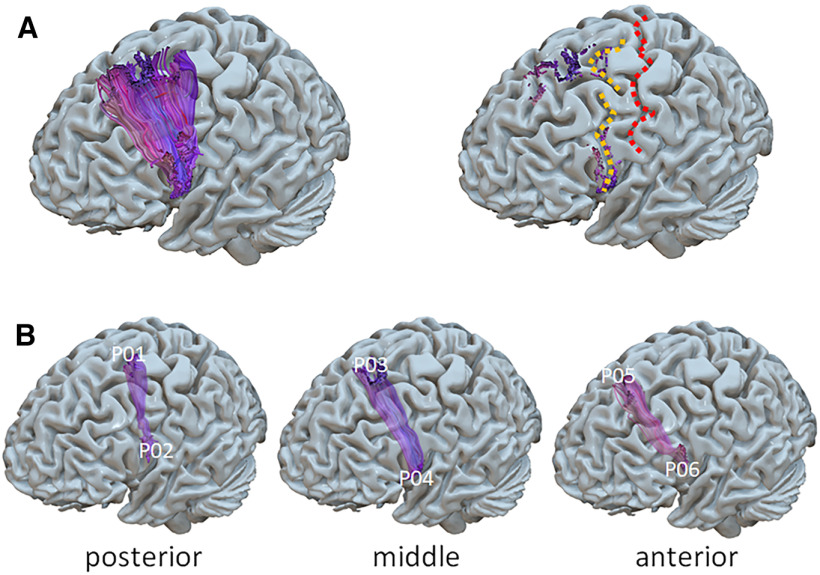
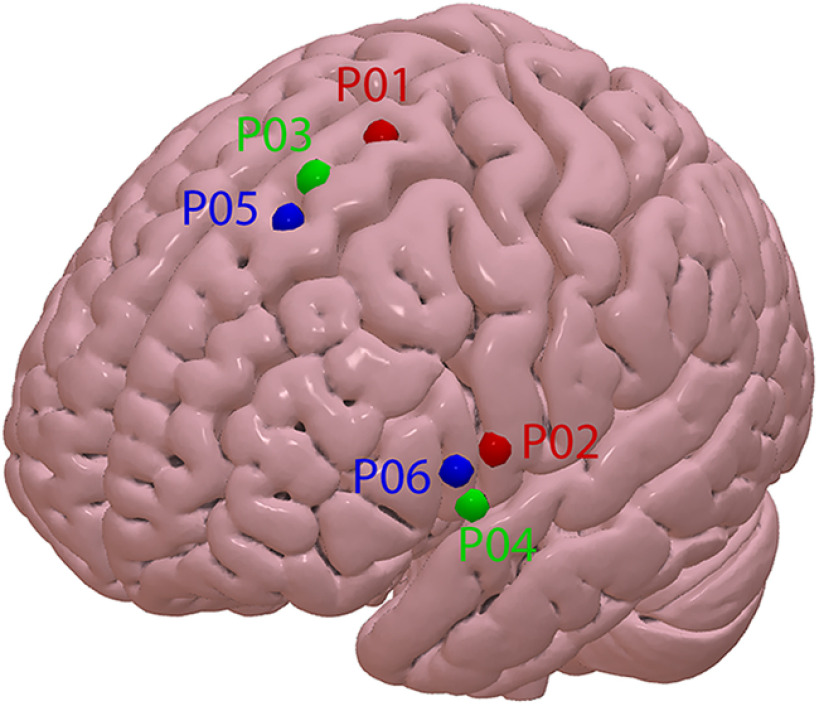
Once the full masked tractogram was obtained, it was processed in TrackVis to dissect the left FAT portion of interest. Note that while there is consensus on the caudal limit of the FAT from the ventral precentral gyrus, the anatomic definition of the FAT lacks a clear rostral border (Varriano et al., 2018). Therefore, a rostral limit was set in the present work to a region of interest i.e., the group of fibers connecting the SFG with the ipsilateral ventral precentral gyrus and IFG-pars opercularis (Fig. 3A). The seed ROIs in the SFG and IFG were set manually, following individual anatomies. False positive tracks were excluded by applying a bandpass length filter (50–90 mm), a x-plane filter, excluding fibers that crossed the midline, a y-plane filter excluding fibers caudal to the central sulcus and finally by means of manual removal on visual inspection using the Tractome toolbox (Porro-Muñoz et al., 2015). The left FATs were then divided into three equal sub-bundles, hereafter named posterior, middle, and anterior (Fig. 3B). The six dorsal and lateral cortical origins of the three sub-bundles were then used as targets for neuronavigated TMS by means of a neuronavigational system (SofTaxic software v.3.4, EMS, Italy connected to a Polaris infrared camera), labeled as points (P) from P01 to P06 with odd points in the dorsal origins and even points in the medial origins. For the purpose of further analysis, the 6 points were treated as three pairs of homologous points, one dorsal and one ventral and each connected by a single sub-bundle (Fig. 3B). To obtain post hoc, population-level, localization of the stimulated spots, the individual brains were then normalized in MNI space and the P01–P06 coordinates were extracted. Table 1 shows all individual coordinates and the mean and SD values. Figure 4 shows the mean coordinates of the six stimulated points. Individual T1-weighd MRs were used for stereotaxic frameless neuronavigation, by means of an optical infrared camera and reflective markers placed on the participant’s head and TMS coil. The rationale for dividing the FAT into three sub-bundles is related to the expected spatial granularity of functional specialization in the SFG and IFG. To use TMS as a mapping tool, we must use a spatial sampling frequency that is adequate to the spatial granularity of the local functional specialization (Cattaneo, 2018). Our previous work on the SFG (Parmigiani et al., 2015, 2018; Parmigiani and Cattaneo, 2018; Lega et al., 2020a,b) shows that local specializations in that region are appropriately sampled with a spatial sampling frequency of one sample every 1.5–2 cm on the cortical surface. The resulting dense grid was therefore made of three spots.
Figure 3.
A, Left panel, The left FAT in a representative participant. Right panel, The central sulcus (in red) and the precentral sulcus (in yellow). B, Division of the left FAT in three sub-bundles and identification of the three pairs of homolog cortical targets for TMS.
Table 1.
Individual coordinates in standard MNI space of the six stimulation spots
| Participant # | P01 (x, y, z) | P02 (x, y, z) | P03 (x, y, z) | P04 (x, y, z) | P05 (x, y, z) | P06 (x, y, z) |
|---|---|---|---|---|---|---|
| 1 | (−14, 9, 75) | (−63, 14, 12) | (−15, 24, 63) | (−56, 17, 0) | (−23, 33, 56) | (−57, 26, 8) |
| 2 | (−20, 6, 75) | (−63, 14, 14) | (−12, 30, 63) | (−60, 15, 2) | (−11, 35, 62) | (−62, 21, 15) |
| 3 | (−17, 3, 75) | (−62, 12, 15) | (−15, 17, 71) | (−57, 15, −2) | (−17, 30, 65) | (−60, 21, 11) |
| 4 | (−17, 9, 72) | (−62, 6, 17) | (−11, 27, 65) | (−59, 12, 0) | (−14, 48, 54) | (−60, 20, 15) |
| 5 | (−12, 6, 75) | (−62, 6, 15) | (−9, 21, 71) | (−60, 14, 3) | (−11, 30, 63) | (−62, 17, 12) |
| 6 | (−23, 15, 71) | (−60, 8, 12) | (−9, 29, 66) | (−59, 14, 3) | (−17, 29, 65) | (−60, 17, 17) |
| 7 | (−24, −9, 78) | (−57, 17, 12) | (−15, 12, 71) | (−57, 17, −2) | (−14, 24, 68) | (−59, 26, 9) |
| 8 | (−12, 6, 75) | (−62, 5, 12) | (−15, 20, 69) | (−60, 12, 6) | (−18, 26, 63) | (−62, 17, 20) |
| 9 | (−20, −2, 77) | (−62, 5, 17) | (−18, 14, 69) | (−60, 12, 5) | (−18, 30, 60) | (−60, 18, 14) |
| 10 | (−23, 12, 72) | (−62, 8, 17) | (−17, 26, 65) | (−60, 12, 2) | (−18, 35, 59) | (−62, 17, 14) |
| 11 | (−20, 2, 75) | (−59, 12, 17) | (−18, 17, 71) | (−59, 15, 2) | (−20, 29, 62) | (−60, 23, 8) |
| 12 | (−15, 5, 74) | (−61, 8, 12) | (−20, 17, 69) | (−62, 11, 0) | (−20, 29, 62) | (−60, 17, 11) |
| 13 | (−14, 3, 78) | (−62, 9, 18) | (−18, 18, 69) | (−63, 9, 5) | (−23, 30, 60) | (−62, 17, 6) |
| 14 | (−15, 2, 77) | (−62, 8, 18) | (−14, 17, 72) | (−60, 14, 3) | (−20, 23, 66) | (−62, 17, 14) |
| 15 | (−20, 9, 74) | (−62, 15, 18) | (−14, 26, 68) | (−60, 15, 5) | (−18, 33, 62) | (−60, 23, 6) |
| 16 | (−18, 2, 77) | (−62, 6, 15) | (−15, 17, 74) | (−62, 12, 6) | (−23, 12, 72) | (−62, 17, 17) |
| 17 | (−21, 2, 75) | (−62, 6, 18) | (−21, 17, 69) | (−60, 12, 3) | (−18, 32, 59) | (−62, 14, 12) |
| 18 | (−14, 8, 71) | (−62, 6, 17) | (−12, 26, 63) | (−60, 9, 0) | (−12, 36, 60) | (−59, 18, 6) |
| 19 | (−12, 12, 75) | (−63, 2, 17) | (−12, 24, 69) | (−60, 14, 2) | (−23, 33, 59) | (−63, 15, 17) |
| Mean | (−17.4, 5.3, 74.8) | (−61.6, 8.8, 15.4) | (−14.7, 21, 68.3) | (−59.7, 13.2, 2.3) | (−17.8, 30.4, 61.9) | (−60.7, 19, 12.2) |
| SD | (3.8, 5.4, 2.1) | (1.4, 4, 2.3) | (3.3, 5.2, 3.2) | (1.7, 2.2, 2.4) | (3.8, 6.8, 4) | (1.5, 3.4, 4.1) |
Figure 4.
Surface render of the MNI-152 template with indication of the average cortical location of each of the six spots.
TMS session
We used a MagPro 100 stimulator, connected to a figure-of-eight TMS coil with 65-mm diameter of each winding (model MagPro MCF-B65). The individual resting motor threshold (rMTh) was assessed in the left hemisphere by stimulating the optimal spot for the visible contraction at rest of the right opponens pollicis muscle (OP). RMTh was assessed as the minimum stimulation intensity that elicits a visible contraction in intrinsic hand muscles with a 50% probability over a series of 10 stimuli. TMS was delivered in one single pulse per trial and the stimulation intensity for the experiment was then set to 120% of the individual rMTh. The coil of the TMS was placed tangentially on the relative left FAT endpoint (i.e., spots P01–P06) selected on the T1 image, with a local error <1.7 mm and single-pulse TMS was delivered at a random time at 400–800 ms from the onset of the set-period. Single-pulse TMS was delivered to the left hemisphere, contralateral to the responding (right) hand. In the attempt to keep the direction of the induced electrical field roughly perpendicular to the main sulci in the stimulated region, we stimulated the SFG with the handle pointing laterally, with a 90° angle to the midline and for the IFG positions we positioned the coil with the handle pointing backwards, parallel to the midline. Sham stimulation was achieved by tilting the coil by 90° to the scalp surface. The position of coil placement on the scalp for sham stimulation was different in each of the three sham blocks. It was on the SFG region in one block, on the IFG region in another block and midway between the two in the third block.
Experimental design
The experiment had a within-subjects design, in which the dependent variable was a measure of the frequency of reactive behavior [the reactive index (RI), see below] and the independent variables were the stimulation sites. We employed a blocked design in which a single stimulation site was targeted in a single block of 40 trials. The order of the six blocks (and therefore of stimulation sites) was randomized between participants. In addition, we ran three extra blocks with sham stimulation, which occurred always at the beginning, in the middle and at the end of the sequence of blocks. This accounted for a total of 40 trials (one block) for each active TMS site, and 120 trials (three blocks) for sham TMS. The behavioral task was performed with a fixed duration of the set-period, corresponding to 800 ms. Participants wore earphones for the entire duration of the experiment, listening to white noise interspersed with sounds of TMS stimulation, generated by the MATLAB script TAAC-TMS Adaptable Auditory Control (Russo et al., 2022)
Data processing
The response time (RT) was calculated as difference between the time of response and the GO-signal and therefore could have both negative and positive values. RT was the main experimental output and index of performance because it allowed to classify trials as product of a reactive strategy or of a predictive strategy.
To verify the assumptions of the present experiment, i.e., that when the set-period is predictable, RTs are distributed bimodally, we performed the same analysis on RT distribution that is described for experiment 1, on the data obtained in the sham condition in the present experiment. Note that in experiment 2, all trials had a fixed, predictable SET-period of 800 ms, identical to the FIXED condition in experiment 1. We validated the RT distribution on trials in the sham condition (because the hypothesis of the present work is that TMS affects the distribution of different strategies) by a curve fitting procedure identical to that used in experiment 1 (see above for the fitted function). As shown in Figure 5 and detailed below in Results, we observed that the RT distribution in the sham trials of experiment 2 was very similar to that in the FIXED condition of experiment 1 (compare Figs. 5 and 2, right panels), with a limit between the two distributions of 172 ms. Therefore, trials were classified according to the response time, as: (1) anticipatory trials (i.e., trials with RT less or equal to 172 ms) and (2) reactive trials (trials with RTs > 172 ms). The choice of analyzing also responses given before the actual GO-signal is that most of these responses are part of the distribution of the reactive trials, as evident from Figures 2 and 5. As a consequence, also responses given before the GO-signal are eloquent of the employment of a predictive strategy. Trials with responses given before TMS were excluded from analysis because they were the result of neural processes unaffected by TMS. The percentage of discarded trials was on average 5.6% of the total (around 2 trials per condition), therefore negligible. We then took into consideration the pool of trials within each single condition (40 trials per each active TMS site) and 120 trials for the sham, and built a ratio called reactive index (RI), by dividing the number of reactive trials by the total number of trials.
Figure 5.
Analysis of distribution of the RTs in the sham condition of experiment 2. The vertical dashed line indicates t = 0 ms, i.e., the onset of the GO-signal. Upper panel shows the superimposed individual Gaussian kernel density estimates of the 19 participants (thin blue lines) together with the mean Gaussian kernel density estimate of the whole population (thick red line). Lower panel shows a superimposition of the actual data and of the fitting functions, together with an indication of the goodness-of-fit. Actual data are presented as a scatterplot of hollow red circles, indicating the Gaussian kernel density estimates of the population (repeating the data of the thick red line of the upper panels). Fitting skewed-Normal functions are shown as continuous lines. The two skewed-Normal functions required to obtain optimal fitting are shown in purple and blue, and their sum is shown in green. The solid vertical line represents the point of optimal separation between the two distributions (t = 172 ms). The goodness of fit is shown as the R2 value.
The RI is distributed between 0 (100% of predictive behavior) and 1 (100% of reactive trials). In this way, the data from all participants were reduced to seven data points per subject: the RI from the six active TMS sites and the RI from the sham condition. Finally, further data reduction was obtained by subtracting the RI from Sham TMS from the 6 RI values of the active TMS spot. The differential RI obtained was a number distributed between −1 and +1 and indicated, if negative, that effective TMS had increased the number of predictive trials compared with Sham and, when positive, that TMS had increased the number of reactive trials compared with Sham. The differential RIs were the actual variable that was used in the statistical analysis.
Statistical analysis
The aim of statistical analysis was to assess whether TMS over a specific site significantly biased the propensity to act with a reactive or a predictive strategy compared with sham TMS. We therefore performed a univariate ANOVA on the RI as dependent variable and with 1 within-subjects factor: TMS (seven levels = sham, P01, P02, P03, P04, P05, and P06). To explore the main effect of the TMS factor, we used six planned comparisons comparing the RI of the sham condition to each of the six active TMS spots by means of t tests for paired samples. We lowered the significance threshold of p = 0.05/6, i.e., to p = 0.008. ANOVA assumptions of normality of data distribution and of similar variance between conditions were verified. The Kolmogorov–Smirnov test showed that all the distributions of the data in each of the six cells of the design were not different from a normal distribution (all p-values > 0.2). Equal variances in the samples were tested by means of Mauchly’s test for sphericity, which did not reject the sphericity assumption (min p-value = 0.6).
Correlation with fractional anisotropy
We analyzed the mean fractional anisotropy (FA) of the FAT to evaluate whether the observed behavior correlates in any way with the anatomic microstructure of the FAT. FA from the frontal lobe white matter has been previously used to assess interindividual variance in white matter connectivity, to explain variability in observed behavioral performance as for example in (Smolker et al., 2015) and, more importantly, FA of the FAT has been shown previously to be predictive of individual behavioral variations (Vallesi and Babcock, 2020). We extracted mean FA from the left FAT in tis middle portion, where its fibers are the most coherent (corresponding to horizontal plane with z = 40) and we correlated it with the RI obtained in the seven conditions of the experimental design (six active TMS and one sham).
Data availability
The whole dataset of anatomic data and the TMS-behavioral data are accessible at the following repository: https://osf.io/x76cm/.
Results
Experiment 1
Results are shown in Figure 2. The optimal fitting was obtained with the following parameters. In the random condition: a1 = 0; a2 = 0.0046; m1 = 0; m2 = 230.1; s1 = 1; s2 = 99.95; sk1 = 0 sk2 = 0.04; the goodness of fit procedure produced a value of R2 of 0.98. For the FIXED condition, the parameters were: a1 = 0.0014; a2 = 0.0037; m1 = 140; m2 = 226; s1 = 150.8; s2 = 92.88; sk1 = −0.011; sk2 = 0.0135; the goodness of fit showed a R2 of 0.99. It is worth noting that the R2 values were extremely high, showing that the fitted functions justified practically all the variance of the data. Second, it should be noted that in the random (unpredictable) condition, the optimal fit was obtained with the parameter a2 set to a null value, therefore transforming the distribution in a unimodal one. The separation point between the early and the late distribution in the FIXED condition corresponded to the value of x (response time) = 172 ms. We assumed based on these data therefore that the early (predictive) trials and the late (reactive) trials were optimally separated by the cutoff value of 172 ms of response time.
Experiment 2
None of the participants reported any significant immediate nor delayed undesired effect of TMS. The results of the evaluation of the distribution of RTs are shown in Figure 5. Specifically, we observed that the function that we applied, based on the sum of two skewed Gaussians, fitted very well the data. The optimal function parameters were: a1 = 0.0041; a2 = 0.00,162; m1 = 224.7; m2 = 85; s1 = 76.5; s2 = 100; sk1 = 0.014; sk2 = 0.0. Goodness of fit showed an R2 of 0.97. We therefore confirmed here, in an independent sample, that predictability of the SET-period allows for two different decisional processes, that produce two different RT distributions. Strikingly, the cutoff value of response times was identical to that in the Behavioral experiment, i.e., x = 172 ms.
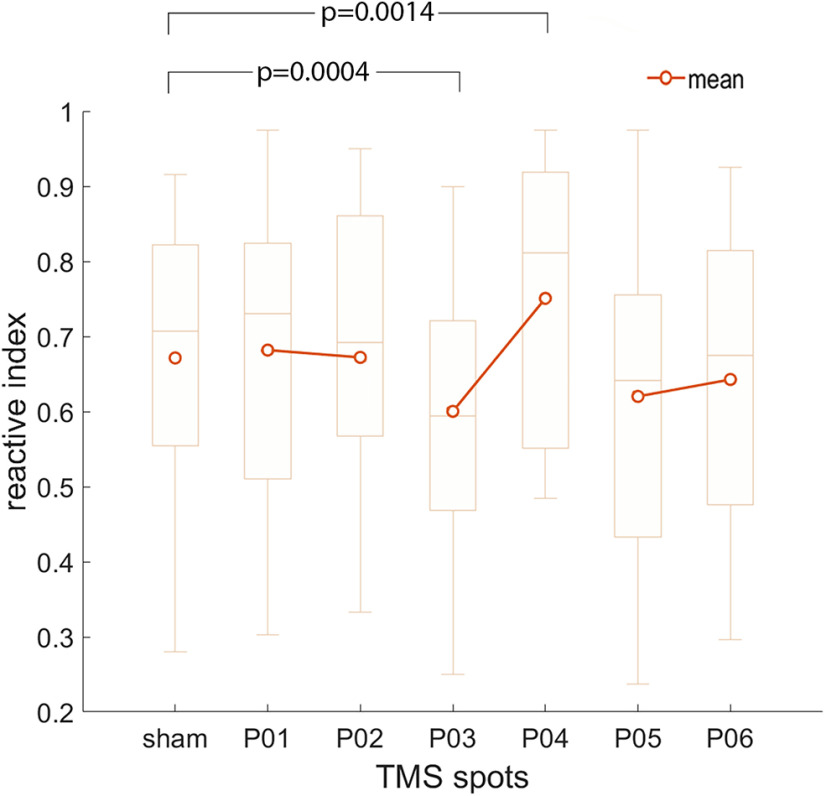
The mean RIs for every participant are presented in Table 2. The results of the ANOVA are illustrated in Figure 6. The one-way ANOVA showed a main effect of the TMS factor [F(6,108) = 5.61, p = 0.00,004; partial η2 = 0.238; observed power (α = 0.05) = 0.996]. Planned comparisons between each of the six active TMS spots with the sham stimulation are summarized in Table 3 and showed that only the mean RI in the P03 and the P04 spots were different from the mean RI of Sham stimulation. In particular, (1) TMS over P03 induced significantly more predictive behavior compared with Sham; and (2) TMS over P04 induced significantly more reactive behavior compared with Sham.
Table 2.
Individual reactivity index (RI) values for the sham condition and for each of the six active TMS conditions
| Participant | Reactivity index (RI) |
Fractional anisotropy (FA) |
||||||
|---|---|---|---|---|---|---|---|---|
| Sham | P01 | P02 | P03 | P04 | P05 | P06 | ||
| #1 | 0.765 | 0.816 | 0.692 | 0.543 | 0.9 | 0.41 | 0.675 | 0.65 |
| #2 | 0.55 | 0.486 | 0.595 | 0.59 | 0.553 | 0.324 | 0.316 | 0.57 |
| #3 | 0.555 | 0.65 | 0.575 | 0.538 | 0.55 | 0.5 | 0.65 | 0.54 |
| #4 | 0.877 | 0.775 | 0.947 | 0.85 | 0.897 | 0.865 | 0.85 | 0.46 |
| #5 | 0.686 | 0.769 | 0.95 | 0.595 | 0.974 | 0.692 | 0.821 | 0.57 |
| #6 | 0.915 | 0.974 | 0.95 | 0.9 | 0.974 | 0.975 | 0.925 | 0.47 |
| #7 | 0.707 | 0.811 | 0.564 | 0.658 | 0.865 | 0.757 | 0.538 | 0.42 |
| #8 | 0.9 | 0.95 | 0.744 | 0.825 | 0.925 | 0.925 | 0.725 | 0.54 |
| #9 | 0.876 | 0.842 | 0.9 | 0.846 | 0.892 | 0.875 | 0.895 | 0.44 |
| #10 | 0.804 | 0.857 | 0.897 | 0.583 | 0.811 | 0.615 | 0.842 | 0.51 |
| #11 | 0.712 | 0.825 | 0.744 | 0.725 | 0.925 | 0.744 | 0.795 | 0.52 |
| #12 | 0.554 | 0.375 | 0.605 | 0.41 | 0.595 | 0.333 | 0.436 | 0.55 |
| #13 | 0.828 | 0.821 | 0.75 | 0.711 | 0.95 | 0.641 | 0.605 | 0.45 |
| #14 | 0.28 | 0.361 | 0.351 | 0.25 | 0.485 | 0.237 | 0.455 | 0.65 |
| #15 | 0.759 | 0.615 | 0.436 | 0.675 | 0.811 | 0.75 | 0.6 | 0.61 |
| #16 | 0.643 | 0.692 | 0.73 | 0.632 | 0.605 | 0.564 | 0.706 | 0.58 |
| #17 | 0.33 | 0.303 | 0.333 | 0.286 | 0.5 | 0.576 | 0.296 | 0.5 |
| #18 | 0.459 | 0.448 | 0.412 | 0.344 | 0.514 | 0.342 | 0.405 | 0.61 |
| #19 | 0.559 | 0.583 | 0.595 | 0.444 | 0.538 | 0.658 | 0.676 | 0.62 |
The last column on the right contains the individual FA values of the left FAT.
Figure 6.
Results of experiment 2. Box-whisker plot indicating mean, median (horizontal segment in the box) first and third quartiles (box extremities) and maximum and minimum values. p-values indicate the significant comparisons between sham and the active TMS spots. Note that only P03 and P04 differed significantly from sham stimulation.
Table 3.
Mean values of the RI for each active stimulation spot and for the sham condition
| TMS spot | Mean | Std. Dv. | t-value | df | P |
|---|---|---|---|---|---|
| P01 | 0.681 | 0.204 | 0.54 | 18 | 0.59 |
| P02 | 0.672 | 0.201 | 0.03 | 18 | 0.98 |
| P03 | 0.600 | 0.191 | −4.32 | 18 | 0.0004 |
| P04 | 0.750 | 0.189 | 3.77 | 18 | 0.001 |
| P05 | 0.620 | 0.219 | −1.60 | 18 | 0.13 |
| P06 | 0.642 | 0.192 | −1.00 | 18 | 0.33 |
| SHAM stimulation | 0.671 | 0.187 | — | — | — |
The t statistics for paired data comparing each active stimulation spot with the sham condition are shown. Significant conditions are highlighted in bold. Note that the threshold for significance has been set to p = 0.05/6, i.e., p = 0.008 to correct for the six multiple comparisons.
The regression analysis on the FA values of the FAT showed that the individual FA value was a valid predictor of the RI index, in all but one (spot P06) of the seven experimental conditions. The results of the analysis and their graphical illustration are found in Table 4 and Figure 7, respectively. These final findings indicated that the behavior that we study is partially predicted by the FA of the FAT; in particular, that the greater the FA, the more the subject has tendency to act with a predictive strategy.
Table 4.
Results of the multiple regression analysis on RI values, with FA as continuous predictor
| Adjusted R2 | df | F | p-value | |
|---|---|---|---|---|
| Sham | 0.207 | 17 | 5.69 | 0.028 |
| P01 | 0.165 | 17 | 4.57 | 0.047 |
| P02 | 0.169 | 17 | 4.65 | 0.045 |
| P03 | 0.305 | 17 | 8.91 | 0.008 |
| P04 | 0.190 | 17 | 5.23 | 0.035 |
| P05 | 0.349 | 17 | 10.64 | 0.005 |
| P06 | 0.050 | 17 | 1.95 | 0.181 |
Figure 7.

Results of the regression analysis using fractional anisotropy (FA) of the FAT as continuous predictor of the individual reactivity index (RI). Refer to Table 4 for statistical parameters.
Discussion
TMS on the SFG promotes predictive behavior and on the IFG promotes reactive behavior
We have investigated the reciprocal role of the SFG and IFG in selecting a predictive or a reactive action strategy. Our specific hypothesis was that the SFG and IFG have reciprocally opposite roles, with the SFG promoting predictive behavior and the IFG promoting reactive behavior and that their interaction is mediated by the FAT. We employed a validated task that simulates a “starting block” scenario that can be solved in every single trial by means of two mutually exclusive strategies: predictive or reactive. TMS delivered during the SET-period to a specific portion of the SFG, induced a bias toward predictive behavior, thus replicating the data from Cattaneo and Parmigiani (2021). The effective TMS spot was P03 (Figs. 3, 4 for the location of TMS spots). Stimulation of the IFG, specifically of the P04 spot, produced behavioral effects opposite to those over P03, i.e., an increase the propensity to perform reactive responses. The polarity of the effects of TMS on behavior can be unpredictable, depending on the interaction between well-controllable stimulation parameters (such as stimulus intensity and timing) with much less controllable subject-dependent parameters (such as state dependency and local anatomy; Silvanto and Muggleton, 2008; Perini et al., 2012). We assume here that TMS had a facilitatory “gain-of-function” effect on behavior as shown in Cattaneo and Parmigiani (2021). Such assumption stems from the comparison of behavioral effects of TMS and previous knowledge on the stimulated brain regions. Specifically, we hypothesize that TMS induced a gain-of-function of the SFG, specifically in the capacity to serve as clock for internal timing of action. In the SFG, several neural signals have been described, that are causally linked to time processing and to timing of action, at the basis of movement based on internally cued anticipatory strategy (Mauk and Buonomano, 2004; Chen et al., 2006; Mita et al., 2009; Casini and Vidal, 2011). Similarly, we hypothesize that TMS induced transient facilitation of IFG, specifically in its capacity to code sensorimotor associations in rule-dependent behavior, that has been suggested in humans (Toni et al., 1999, 2001a,b; Lega et al., 2020a,b) and nonhuman primates (Rizzolatti et al., 2014).
Coexistence of different motor programs and parallel processing of information
We show here that TMS applied during the SET period can induce biases toward one of the two strategies, predictive or reactive. This indicates that up to the actual time of movement, during the SET-period, both strategies are still available and present in parallel channels in the participant’s motor system. If the commitment to one of the strategies was determined earlier on during neural processing, we would not be able to induce a strategy switch with TMS during the SET period. The present data provide evidence in favor of parallel processing of the two possible strategies. Several lines of empirical evidence in human neurophysiology (Michelet et al., 2010; Barchiesi and Cattaneo, 2013; Ubaldi et al., 2015) and human behavior (Van Zoest and Donk, 2006; Barchiesi and Cattaneo, 2015) confirm that top-down control and bottom-up sensorimotor processes seem to coexist up to the very distal phases of action production. The concept of parallel channels in the action system that mediate bottom-up (in this case the reactive strategy) and top-down (the predictive strategy in our protocol), that compete for motor output, is well established in several theoretical models of the action system (Kornblum et al., 1990; Ridderinkhof et al., 2004; Cisek and Kalaska, 2010; McBride et al., 2012).
Anatomical connectivity explains the effects of TMS over distant but interconnected regions
According to our experimental hypothesis, the FAT provides the anatomic substrate for interaction between the SFG and the IFG. Accordingly, we hypothesized that specific sectors of the SFG and the IFG influencing the propensity to act in a predictive or reactive way should be directly connected by FAT fibers. Indeed, we demonstrated that stimulation of two limited portions of cortex produced opposite behavioral effects compared with sham stimulation. The two active regions (P03 and P04) are apparently distant and unrelated and have been identified only by means dense spatial mapping with TMS of the IFG and SFG. However, we show here that coupling different sectors of the SFG and the IFG in terms of homolog regions connected by sub-bundles of the FAT fully explains the variance of the effects of TMS over the two gyri: the only two regions that showed a behavioral effect are directly connected by an anatomic pathway.
A model of FAT function mediating mutual inhibition between SFG and IFG
What is even more striking, is that the effects of TMS on the two FAT terminations were opposite in polarity, i.e., facilitation of predictive behavior on the SFG and facilitation of reactive behavior on IFG. We hypothesize that these two regions act with a mechanism of reciprocal (mutual) inhibition. On the microscale, mutual inhibition is a widely used neural mechanism for selection between competing and mutually exclusive actions, as observed in nonhuman species (Machens et al., 2005; Koyama and Pujala, 2018). Mutual (or lateral) inhibition circuits support winner-takes-all decision processes, making it impossible to elicit two behavioral patterns in response to a certain situation because one excludes the other. Similarly in our study, at the single trial level, the reactive and predictive strategies are mutually incompatible, but participants do not commit to a single strategy forever, but rather tend to choose one strategy over the other on a trial-by-trial basis. Therefore, behavior in single trials is the product a continuous fluctuation of an opaque decision process between the two possible strategies. We show that two opposite biases can be introduced in such decision process, by stimulating two regions of SFG and IFG that are directly mutually interconnected by FAT fibers. We therefore hypothesize that the direct connectivity by FAT fibers mediates reciprocal, mutual inhibition between the SFG and IFG. It is nevertheless important to stress two aspects. The first is that this behavioral phenomenon is specific for the two subregions in the SFG and IFG and is not extended to the whole gyri. While the FAT may connect SFG and IFG along most of their extensions, other behavioral (cognitive) paradigms may unravel other forms of competitive inhibition more anteriorly or posteriorly. Second, direct connectivity by means of the FAT is not the only possible explanation. SFG and IFG could influence each other by means of indirect, subcortical, connections (Aron et al., 2007), as has been suggested for right-lateralized circuits for action inhibition. Similar subcortical connections have also been proposed as integral portions of the FAT circuitry in recent models of FAT function (Dick et al., 2019).
Consistence of the present data with current knowledge on the FAT
We postulate a model for a domain-general function of the posterior FAT, i.e., to directly mediate the interactions between internally generated behavior in the medial frontal cortex and externally triggered behavior in the ventral-lateral frontal cortex. The concept of an all-purpose FAT was first proposed before its actual description as an individual bundle. A white matter connection allowing right SFG-IFG cross-talk has been initially identified by Aron (2007), suggesting these region could inhibit each other directly or through interposition of subthalamic nucleus and hence braking or stopping action. More recently, domain-general theories, proposed a role in motor planning and timing of more or less complex motor sequences, in monitoring and in the interactions between executive control and sensorimotor patterns as proposed among others by Dick et al. (2019). Conversely, specific roles of the FAT have been hypothesized in the language domain, for the left hemisphere. Here, most researches have correlated posterior FAT integrity and function with motor aspects of speech, such as articulation and verbal fluency (Catani et al., 2013; Sierpowska et al., 2015; Kronfeld-Duenias et al., 2016; Cipolotti et al., 2020), although other authors found a relation of FAT structure with lexical decisions and not verbal fluency (Vallesi and Babcock, 2020). The lateralization of the FAT function and the apparent specialization are in our view not in contrast with our model of FAT mediating interactions between internally-timed, predictive behavior and externally-cued, sensory-dependent behavior, because also verbal fluency tasks require strict interaction between timing of word production and the specific articulatory gestures, likely arising from SFG-IFG interactions (Dick et al., 2019).
In conclusion, we show evidence in support of the FAT’s role mediating interactions between predictive and reactive behavior. Specifically, the FAT seems to mediate reciprocal competition between two frontal regions that represent predictive (SFG) and reactive (IFG) strategies. This connectivity system, because of its mutual inhibition organization, supports the selection of actions in a “winner takes all” manner. In addition, we show here for the first time that individual information on anatomic connectivity (tractography) coupled with TMS can significantly improve spatial mapping of cortical functions, by identifying homologous regions. Tractography-guided TMS provides a whole new way to interpret functional brain mapping by means of noninvasive stimulation techniques.
Footnotes
This work was supported by the BIAL Foundation Grant 150/20, entitled “A swing between the inner and the outer worlds: exploring the function of the frontal aslant tract” (to L.C.). We thank Enrica Pierotti for the help in data collection and analysis and Gabriele Amorosino for the valuable help in tractographic analyses.
D. Giampiccolo’s present address: Department of Clinical and Experimental Epilepsy, University College London Queen Square Institute of Neurology, University College London, London WC1N 3BG, United Kingdom and Department of Neurosurgery, National Hospital for Neurology and Neurosurgery, London WC1N 3BG, United Kingdom; and Institute of Neurosciences, Cleveland Clinic London, London W1T 4AJ, United Kingdom.
The authors declare no competing financial interests.
References
- Amorosino G, Peruzzo D, Astolfi P, Redaelli D, Avesani P, Arrigoni F, Olivetti E (2020) Automatic tissue segmentation with deep learning in patients with congenital or acquired distortion of brain anatomy. Lect Notes Comput Sci Subser Lect Notes Artif Intell Lect Notes Bioinforma 12449:13–22. [Google Scholar]
- Aron AR, Behrens TE, Smith S, Frank MJ, Poldrack RA (2007) Triangulating a cognitive control network using diffusion-weighted magnetic resonance imaging (MRI) and functional MRI. J Neurosci 27:3743–3752. 10.1523/JNEUROSCI.0519-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants BB, Epstein CL, Grossman M, Gee JC (2008) Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal 12:26–41. 10.1016/j.media.2007.06.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azzalini A (1985) A class of distributions which includes the normal ones. Scand J Stat 12:171–178. [Google Scholar]
- Barchiesi G, Cattaneo L (2013) Early and late motor responses to action observation. Soc Cogn Affect Neurosci 8:711–719. 10.1093/scan/nss049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barchiesi G, Cattaneo L (2015) Motor resonance meets motor performance. Neuropsychologia 69:93–104. 10.1016/j.neuropsychologia.2015.01.030 [DOI] [PubMed] [Google Scholar]
- Casini L, Vidal F (2011) The SMAs: neural substrate of the temporal accumulator? Front Integr Neurosci 5:35–35. 10.3389/fnint.2011.00035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catani M, Dell’Acqua F, Vergani F, Malik F, Hodge H, Roy P, Valabregue R, Thiebaut de Schotten M (2012) Short frontal lobe connections of the human brain. Cortex 48:273–291. 10.1016/j.cortex.2011.12.001 [DOI] [PubMed] [Google Scholar]
- Catani M, Mesulam MM, Jakobsen E, Malik F, Martersteck A, Wieneke C, Thompson CK, Thiebaut de Schotten M, Dell F, Weintraub S, Rogalski E, Dell’Acqua F, Weintraub S, Rogalski E (2013) A novel frontal pathway underlies verbal fluency in primary progressive aphasia. Brain 136:2619–2628. 10.1093/brain/awt163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattaneo L (2018) Fancies and fallacies of spatial sampling with transcranial magnetic stimulation (TMS). Front Psychol 9:1171–1175. 10.3389/fpsyg.2018.01171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattaneo L, Parmigiani S (2021) Stimulation of different sectors of the human dorsal premotor cortex induces a shift from reactive to predictive action strategies and changes in motor inhibition: a dense transcranial magnetic stimulation (TMS) mapping study. Brain Sci 11:534. 10.3390/brainsci11050534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JL, Zatorre RJ, Penhune VB (2006) Interactions between auditory and dorsal premotor cortex during synchronization to musical rhythms. Neuroimage 32:1771–1781. 10.1016/j.neuroimage.2006.04.207 [DOI] [PubMed] [Google Scholar]
- Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O (2016) 3D U-net: learning dense volumetric segmentation from sparse annotation. Lect Notes Comput Sci Subser Lect Notes Artif Intell Lect Notes Bioinforma 9901:424–432. [Google Scholar]
- Cipolotti L, Molenberghs P, Dominguez J, Smith N, Smirni D, Xu T, Shallice T, Chan E (2020) Fluency and rule breaking behaviour in the frontal cortex. Neuropsychologia 137:107308–107308. 10.1016/j.neuropsychologia.2019.107308 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, Kalaska JF (2010) Neural mechanisms for interacting with a world full of action choices. Annu Rev Neurosci 33:269–298. 10.1146/annurev.neuro.051508.135409 [DOI] [PubMed] [Google Scholar]
- Cox RW (1996) AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res 29:162–173. 10.1006/cbmr.1996.0014 [DOI] [PubMed] [Google Scholar]
- Dhollander T, Raffelt D, Connelly A (2016) Unsupervised 3-tissue response function estimation from single-shell or multi-shell diffusion MR data without a co-registered T1 image. Proc ISMRM Workshop on Breaking the Barriers of Diffusion MRI, Vol 5, Lisbon, Portugal.
- Dhollander T, Mito R, Raffelt D, Connelly A (2019) Improved white matter response function estimation for 3-tissue constrained spherical deconvolution. Proc Intl Soc Mag Reson Med 27:555. [Google Scholar]
- Dick AS, Garic D, Graziano P, Tremblay P (2019) The frontal aslant tract (FAT) and its role in speech, language and executive function. Cortex J Devoted Study Nerv Syst Behav 111:148–163. 10.1016/j.cortex.2018.10.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garic D, Broce I, Graziano P, Mattfeld A, Dick AS (2019) Laterality of the frontal aslant tract (FAT) explains externalizing behaviors through its association with executive function. Dev Sci 22:e12744. 10.1111/desc.12744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kornblum S, Hasbroucq T, Osman A (1990) Dimensional overlap: cognitive basis for stimulus-response compatibility-a model and taxonomy. Psychol Rev 97:253–270. 10.1037/0033-295x.97.2.253 [DOI] [PubMed] [Google Scholar]
- Koyama M, Pujala A (2018) Mutual inhibition of lateral inhibition: a network motif for an elementary computation in the brain. Curr Opin Neurobiol 49:69–74. 10.1016/j.conb.2017.12.019 [DOI] [PubMed] [Google Scholar]
- Kronfeld-Duenias V, Amir O, Ezrati-Vinacour R, Civier O, Ben-Shachar M (2016) The frontal aslant tract underlies speech fluency in persistent developmental stuttering. Brain Struct Funct 221:365–381. 10.1007/s00429-014-0912-8 [DOI] [PubMed] [Google Scholar]
- La Corte E, Eldahaby D, Greco E, Aquino D, Bertolini G, Levi V, Ottenhausen M, Demichelis G, Romito LM, Acerbi F, Broggi M, Schiariti MP, Ferroli P, Bruzzone MG, Serrao G (2021) The frontal aslant tract: a systematic review for neurosurgical applications. Front Neurol 12:641586. 10.3389/fneur.2021.641586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lega C, Chelazzi L, Cattaneo L (2020a) Two distinct systems represent contralateral and ipsilateral sensorimotor processes in the human premotor cortex: a dense TMS mapping study. Cereb Cortex 30:2250–2266. [DOI] [PubMed] [Google Scholar]
- Lega C, Pirruccio M, Bicego M, Parmigiani L, Chelazzi L, Cattaneo L (2020b) The topography of visually-guided grasping in the premotor cortex: a dense-transcranial magnetic stimulation (TMS) mapping study. J Neurosci 40:6790–6800. 10.1523/JNEUROSCI.0560-20.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machens CK, Romo R, Brody CD (2005) Flexible control of mutual inhibition: a neural model of two-interval discrimination. Science 307:1121–1124. 10.1126/science.1104171 [DOI] [PubMed] [Google Scholar]
- Mauk MD, Buonomano DV (2004) The neural basis of temporal processing. Annu Rev Neurosci 27:307–340. 10.1146/annurev.neuro.27.070203.144247 [DOI] [PubMed] [Google Scholar]
- McBride J, Boy F, Husain M, Sumner P (2012) Automatic motor activation in the executive control of action. Front Hum Neurosci 6:82. 10.3389/fnhum.2012.00082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michelet T, Duncan GH, Cisek P (2010) Response competition in the primary motor cortex: corticospinal excitability reflects response replacement during simple decisions. J Neurophysiol 104:119–127. 10.1152/jn.00819.2009 [DOI] [PubMed] [Google Scholar]
- Mita A, Mushiake H, Shima K, Matsuzaka Y, Tanji J (2009) Interval time coding by neurons in the presupplementary and supplementary motor areas. Nat Neurosci 12:502–507. 10.1038/nn.2272 [DOI] [PubMed] [Google Scholar]
- O’Hagan A, Leonard T (1976) Bayes estimation subject to uncertainty about parameter constraints. Biometrika 63:201–203. 10.1093/biomet/63.1.201 [DOI] [Google Scholar]
- Okan M, Nayak A, Jenkins J, Pierpaoli C (2017) TORTOISE v3: improvements and new features of the NIH diffusion MRI processing pipeline. Proc Intl Soc Mag Reson Med 25:3540. [Google Scholar]
- O’Reilly RC (2010) The what and how of prefrontal cortical organization. Trends Neurosci 33:355–361. 10.1016/j.tins.2010.05.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parmigiani S, Cattaneo L (2018) Stimulation of the dorsal premotor cortex, but not of the supplementary motor area proper, impairs the stop function in a STOP signal task. Neuroscience 394:14–22. 10.1016/j.neuroscience.2018.10.005 [DOI] [PubMed] [Google Scholar]
- Parmigiani S, Barchiesi G, Cattaneo L (2015) The dorsal premotor cortex exerts a powerful and specific inhibitory effect on the ipsilateral corticofacial system: a dual-coil transcranial magnetic stimulation study. Exp Brain Res 233:3253–3260. 10.1007/s00221-015-4393-7 [DOI] [PubMed] [Google Scholar]
- Parmigiani S, Zattera B, Barchiesi G, Cattaneo L (2018) Spatial and temporal characteristics of set-related inhibitory and excitatory inputs from the dorsal premotor cortex to the ipsilateral motor cortex assessed by dual-coil transcranial magnetic stimulation. Brain Topogr 31:795–810. 10.1007/s10548-018-0635-x [DOI] [PubMed] [Google Scholar]
- Perini F, Cattaneo L, Carrasco M, Schwarzbach JV (2012) Occipital transcranial magnetic stimulation has an activity-dependent suppressive effect. J Neurosci 32:12361–12365. 10.1523/JNEUROSCI.5864-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter D (1985) Kernel estimation of a distribution function. Commun Stat Theory Methods 14:605–620. 10.1080/03610928508828937 [DOI] [Google Scholar]
- Pierpaoli C, Walker L, Irfanoglu MO, Barnett A, Basser P, Chang L-C, Koay C, Pajevic S, Rohde G, Sarlls J, Wu M (2010) TORTOISE: an integrated software package for processing of diffusion MRI data. Proc Intl Soc Mag Reson Med 18:1597. [Google Scholar]
- Porro-Muñoz D, Olivetti E, Sharmin N, Nguyen TB, Garyfallidis E, Avesani P (2015) Tractome: a visual data mining tool for brain connectivity analysis. Data Min Knowl Disc 29:1258–1279. 10.1007/s10618-015-0408-z [DOI] [Google Scholar]
- Ridderinkhof KR, Van Den Wildenberg WPM, Segalowitz SJ, Carter CS (2004) Neurocognitive mechanisms of cognitive control: the role of prefrontal cortex in action selection, response inhibition, performance monitoring, and reward-based learning. Brain Cogn 56:129–140. 10.1016/j.bandc.2004.09.016 [DOI] [PubMed] [Google Scholar]
- Rizzolatti G, Cattaneo L, Fabbri-Destro M, Rozzi S (2014) Cortical mechanisms underlying the organization of goal-directed actions and mirror neuron-based action understanding. Physiol Rev 94:655–706. 10.1152/physrev.00009.2013 [DOI] [PubMed] [Google Scholar]
- Ronneberger O, Fischer P, Brox T (2015) U-Net: convolutional networks for biomedical image segmentation. Lect Notes Comput Sci Subser Lect Notes Artif Intell Lect Notes Bioinforma 9351:234–241. [Google Scholar]
- Rossi S, Hallett M, Rossini PM, Pascual-Leone A; Safety of TMS Consensus Group (2009) Safety, ethical considerations, and application guidelines for the use of transcranial magnetic stimulation in clinical practice and research. Clin Neurophysiol 120:2008–2039. 10.1016/j.clinph.2009.08.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossi S, et al. (2021) Safety and recommendations for TMS use in healthy subjects and patient populations, with updates on training, ethical and regulatory issues: expert guidelines. Clin Neurophysiol 132:269–306. 10.1016/j.clinph.2020.10.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russo S, Sarasso S, Puglisi GE, Dal Palù D, Pigorini A, Casarotto S, D’Ambrosio S, Astolfi A, Massimini M, Rosanova M, Fecchio M (2022) TAAC - TMS adaptable auditory control: a universal tool to mask TMS clicks. J Neurosci Methods 370:109491–109491. 10.1016/j.jneumeth.2022.109491 [DOI] [PubMed] [Google Scholar]
- Schmidt RA (1968) Anticipation and timing in human motor performance. Psychol Bull 70:631–646. 10.1037/h0026740 [DOI] [Google Scholar]
- Serra L, Gabrielli GB, Tuzzi E, Spanò B, Giulietti G, Failoni V, Marra C, Caltagirone C, Koch G, Cercignani M, Bozzali M (2017) Damage to the frontal aslant tract accounts for visuo-constructive deficits in Alzheimer’s disease. J Alzheimers Dis 60:1015–1024. 10.3233/JAD-170638 [DOI] [PubMed] [Google Scholar]
- Shima K, Tanji J (2000) Neuronal activity in the supplementary and presupplementary motor areas for temporal organization of multiple movements. J Neurophysiol 84:2148–2160. [DOI] [PubMed] [Google Scholar]
- Sierpowska J, Gabarrós A, Fernandez-Coello A, Camins À, Castañer S, Juncadella M, de Diego-Balaguer R, Rodríguez-Fornells A (2015) Morphological derivation overflow as a result of disruption of the left frontal aslant white matter tract. Brain Lang 142:54–64. 10.1016/j.bandl.2015.01.005 [DOI] [PubMed] [Google Scholar]
- Silvanto J, Muggleton NG (2008) New light through old windows: moving beyond the “virtual lesion” approach to transcranial magnetic stimulation. Neuroimage 39:549–552. 10.1016/j.neuroimage.2007.09.008 [DOI] [PubMed] [Google Scholar]
- Smolker HR, Depue BE, Reineberg AE, Orr JM, Banich MT (2015) Individual differences in regional prefrontal gray matter morphometry and fractional anisotropy are associated with different constructs of executive function. Brain Struct Funct 220:1291–1306. 10.1007/s00429-014-0723-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuss DT (2011) Functions of the frontal lobes: relation to executive functions. J Int Neuropsychol Soc 17:759–765. 10.1017/S1355617711000695 [DOI] [PubMed] [Google Scholar]
- Toni I, Schluter ND, Josephs O, Friston K, Passingham RE (1999) Signal-, set- and movement-related activity in the human brain: an event-related fMRI study. Cereb Cortex 9:35–49. 10.1093/cercor/9.1.35 [DOI] [PubMed] [Google Scholar]
- Toni I, Ramnani N, Josephs O, Ashburner J, Passingham RE (2001a) Learning arbitrary visuomotor associations: temporal dynamic of brain activity. Neuroimage 14:1048–1057. 10.1006/nimg.2001.0894 [DOI] [PubMed] [Google Scholar]
- Toni I, Rushworth MFS, Passingham RE (2001b) Neural correlates of visuomotor associations. Spatial rules compared with arbitrary rules. Exp Brain Res 141:359–369. 10.1007/s002210100877 [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Connelly A (2012) MRtrix: diffusion tractography in crossing fiber regions. Int J Imaging Syst Technol 22:53–66. 10.1002/ima.22005 [DOI] [Google Scholar]
- Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC (2010) N4ITK: improved N3 bias correction. IEEE Trans Med Imaging 29:1310–1320. 10.1109/TMI.2010.2046908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ubaldi S, Barchiesi G, Cattaneo L (2015) Bottom-up and top-down visuomotor responses to action observation. Cereb Cortex 25:1032–1041. 10.1093/cercor/bht295 [DOI] [PubMed] [Google Scholar]
- Vallesi A, Babcock L (2020) Asymmetry of the frontal aslant tract is associated with lexical decision. Brain Struct Funct 225:1009–1017. 10.1007/s00429-020-02054-1 [DOI] [PubMed] [Google Scholar]
- Van Zoest W, Donk M (2006) Saccadic target selection as a function of time. Spat Vis 19:61–76. 10.1163/156856806775009205 [DOI] [PubMed] [Google Scholar]
- Varriano F, Pascual-Diaz S, Prats-Galino A (2018) When the FAT goes wide: right extended frontal aslant tract volume predicts performance on working memory tasks in healthy humans. PLoS One 13:e0200786. 10.1371/journal.pone.0200786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wassermann EM (1998) Risk and safety of repetitive transcranial magnetic stimulation: report and suggested guidelines from the International Workshop on the Safety of Repetitive Transcranial Magnetic Stimulation, June 5–7, 1996. Electroencephalogr Clin Neurophysiol 108:1–16. 10.1016/s0168-5597(97)00096-8 [DOI] [PubMed] [Google Scholar]
- Woods DL, Wyma JM, Yund EW, Herron TJ, Reed B (2015) Factors influencing the latency of simple reaction time. Front Hum Neurosci 9:131. 10.3389/fnhum.2015.00131 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The whole dataset of anatomic data and the TMS-behavioral data are accessible at the following repository: https://osf.io/x76cm/.