Abstract
Optimisation of energy efficiency and operational performance as well as assessment of safety levels and emissions of marine operations require detailed information about the acting wave system. It is possible—with an analogy to classical wave buoys—to estimate the directional wave spectrum by processing sensor measurements of wave-induced responses (e.g., motions and structural responses) from a ship. Compared to other sources of wave data (e.g., buoys, satellites, third-generation wave models), estimation concepts using the ship itself as a buoy provide the wave spectrum at the exact spatio-temporal point, potentially increasing accuracy and with minimal associated cost. This paper gives an overview of the technology, discusses associated uncertainties, and highlights new developments made for estimating waves via measured ship responses.
Subject terms: Mechanical engineering, Physical oceanography
Introduction
Measuring ocean waves is of fundamental importance to shipmasters, naval architects, maritime engineers, and ocean scientists alike, since waves are the basic driver of most of the processes of their concern. Here, we note that measuring ocean waves is equivalent to measuring the directional wave spectrum, representing the energy density of the wave components forming the wave system1. Applications dependent on measurements and a characterisation of waves are, e.g.: (a) analysis of wave-structure interactions before/during/after operations, (b) collection of historical data for design and rule specification for offshore structures and ships, (c) preliminary evaluation of offshore sites for renewable energy potential and construction, and (d) assessment of mechanisms of surface-water mixing and air-sea fluxes for understanding weather and climate changes. Examples of use-cases are illustrated in Fig. 1, where the following additional remarks can be added: For the optimal operation of ships sailing in a seaway, real-time, onboard decision support systems can guide the crew to select speed and heading to ensure high levels of safety and performance. For instance, for vessels operating with wind-assisted propulsion, as illustrated in Fig. 1a, it is difficult to decide on a heading where the thrust from wind is maximised while, at the same time, keeping the added resistance from waves minimum. Such a heading selection can be guided by a decision support system if the directional wave spectrum is available. Similarly, decision support systems can warn against the risk of being in dangerous situations, where large motions or parametric roll can lead to loss or damage of cargo2, as illustrated in Fig. 1b. It may also be that an incident, having resulted in container damages and losses, needs further post-voyage investigations, e.g., for reasons of insurance, in which case the in-situ directional wave spectrum must be available. Thus, with the green transition and digitalisation period we are in, soon all vessels need some kind of wave estimation technology for reasons of safety, emission reductions, and inspection. Lastly, it is noted that the development of weather and storms is largely affected by the exchange of energy, momentum, and mass between the atmosphere and the sea, cf. Fig. 1c3. This exchange also influences the carbon budget of the ocean and atmosphere, and thus with a crucial importance to mechanisms related to climate change4,5. At a fundamental level, the exchange between air and sea takes place in the boundary layers over the sea surface, and variations of the surface, characterised by waves, should therefore be measured to enable understanding and modelling of weather and climate.
Figure 1.
Measuring ocean waves. Information about waves is of crucial importance in many applications considered by engineers and ocean scientists.
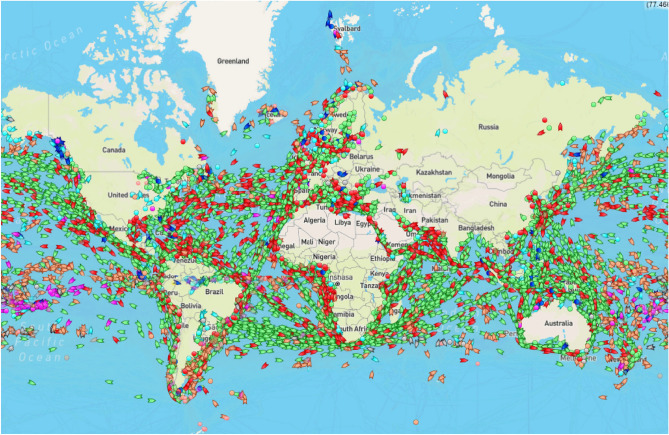
In practice, waves are typically estimated by a buoy, where the buoy’s translational and angular motions, resulting from waves, are the basis for the estimate. By analogy it is possible to use recorded wave-induced motions of a ship to estimate waves. This latter principle, referred to as the wave buoy analogy or ship-as-a-wave-buoy, has been investigated and developed over the past 2-3 decades with a handful of pioneering studies6–10. Generally, the concept is well-understood and produces fair to good results compared to real (“classic”) wave buoys, despite the complexities inherent due to a ship’s large size (length, breadth, draught), relative to the waves we are trying to measure, making a ship behave as a low-pass filter, and since a ship typically advances in the propagating waves. On the other hand, compared to buoys - being deployed in fixed locations, and extremely scarcely located considering the coverage of the oceans - there is an obvious but unexploited potential in using ships as sailing wave buoys. Figure 2 highlights the potential by imagining any ship to be a sailing wave buoy. Hence, accounting for the sheer number (+300,000) of ships in operation, the spatial and temporal coverage considering wave estimation and other environmental data is significant, assuming mechanisms and routines for data sharing.
Figure 2.
Snapshot of vessel positions, as of 27-06-2023 UTC 10:30, from AIS data with colour codes for identification of ship type, noticing that more than 300,000 ships appear. With permission by MarineTraffic (www.marinetraffic.com).
Scope and novelty
This paper gives an overview and presents new developments made at the Department of Civil and Mechanical Engineering, Technical University of Denmark, with selected partners for estimating waves via measured ship responses. Onward, we refer to wave-estimation technologies of this type under the umbrella term the Wave Buoy Analogy (WBA). In the paper, we present new results of a novel framework consisting of a hybrid method11 combining physics-based and machine learning-based wave estimates. Specifically, we introduce an experimental dataset obtained under “controlled conditions” during sea trials, and we show that reasonable wave estimates can be expected using a physics-based method under such favourable conditions. In contrast, for a ship in service, the level of uncertainties associated with operational parameters such as speed and draft can be significant. This motivates the development of a hybrid method, being less sensitive to the aforementioned uncertainties and thus more robust. In concrete terms, the hybrid framework is realised by conditioning the physics-based method on results, i.e. wave estimates, from another source, practically achieved by running a machine learning model concurrently. The hybrid method, as a concept and with its theoretical derivations, has been presented in an earlier paper11 where the machine learning model was trained using data from a wave radar. In the present work, we introduce a new set of results, derived by training the machine learning model instead by the ERA5 database12, to facilitate the conditioning. The advantage in training the machine learning model with ERA5 is that this approach does not require any (extra) hardware on the ship, which for instance is the case if a wave radar should be installed.
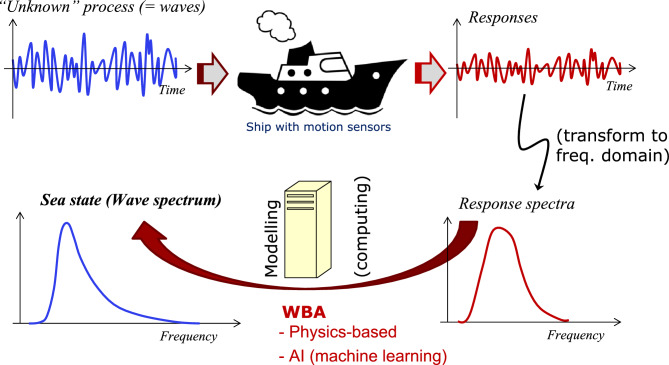
The Wave buoy analogy in a nutshell
Fundamentally, the WBA relies on measuring wave-induced ship responses; say, heave (z), roll (), and pitch (). The principle is sketched in Fig. 3. Introducing the linear time-invariant (LTI) assumption facilitates the use of wave-to-motion transfer functions which leads to what will be referred to as physics-based methods with formulations in both the frequency domain and the time domain. In contrast thereto, purely data-driven approaches exist, relying on machine learning. The main advantage of physics-based methods is that they can provide estimates of the complete directional wave spectrum, where different mathematical strategies13–26 are applied for solving the highly underdetermined equation system describing the physical relationship between the energy densities of waves and the corresponding responses. In machine learning methods27–36, the general relationship between wave parameters and induced responses of a particular ship is learned by comprehensive training with large datasets of measured responses against available sea state information, e.g. from hindcast wave databases. The main advantage of machine learning methods is that transfer functions are not needed, and all uncertainties associated with transfer functions are thus removed. On the other hand, the need for high-quality sensor measurements is emphasised and so is the importance of having accurate (“external”) data used as a proxy for the true wave parameters at the exact spatio-temporal position of the ship. Besides, machine learning methods offer, presently, only wave parameters (not the detailed wave spectrum), although research has been initiated by the international community to relax this restriction, as discussed later.
Figure 3.
Sketch of the wave buoy analogy (WBA), alluding to frequency-domain frameworks.
Hybrid framework
The state of the art literature, as introduced above, demonstrates that machine learning methods, in fact, tend to give better estimates of the wave parameters compared to physics-based methods, when full-scale, operational data from in-service ships is considered. It is thus interesting to compose a hybrid framework, combining results from a machine learning method with the capability of a physics-based method, providing the detailed directional wave spectrum. Such a framework has recently been developed by establishing an algorithm11 that outputs a directional wave spectrum which is conditioned on results from a machine learning method. More specifically, the hybrid framework takes estimated wave parameters from a convolutional neural network32 and uses them as constraints on the directional wave spectrum subsequently computed by a physics-based method8,13. It is noteworthy that the specific physics-based method relies on Bayes’ theorem37, and, in the following, we will refer to it as the Bayesian method.
Results
The potential of a ship as a wave buoy has been confirmed in past studies, as already introduced. However, in the Bayesian method, the motion transfer functions are needed which, in turn, means that the detailed hull geometry as well as knowledge about the exact operational condition (e.g., speed and loading condition) of the ship must be available; otherwise, reliable and accurate motion transfer functions cannot be computed resulting in compromised wave spectrum estimates. Initially, we will therefore introduce two sets of results for underscoring the motivation and relevance of a hybrid framework of the WBA, emphasising that we consider exclusively unconditioned wave spectrum estimates of the Bayesian method in this preliminary assessment. Afterwards, the hybrid framework will itself be assessed using in-service data from a container ship.
Preliminary assessment (unconditioned wave spectrum estimates)
In the preliminary assessment, the first set of results is produced by analysis of dedicated full-scale experimental data obtained during a sea trial campaign using a research vessel of the Norwegian University of Science and Technology (NTNU). The second set of results originates from a container ship which had its wave-induced motions measured during nearly two years of service on a North Atlantic route between Europe and Canada.
Sea trial experiments
Full-scale motion measurements have been collected during sea trials in 2013 with R/V Gunnerus, see Fig. 4. Originally, the sea trials were made to document the effect of a thruster retrofit38, and, as part of this, seakeeping runs were made, where one set of run paths, as illustrated in Fig. 4b, is studied herein. The input to the estimation algorithm, i.e. the Bayesian method, is the measured motion components heave, roll, and pitch, as well as the corresponding transfer functions. The transfer functions have been computed with a 2D strip theory code, ShipX39, using the exact hull geometry and the precise loading condition and speed of the ship during the trial. On each run path, indicated by IDs 03-06, course and engine power were held constant to ensure stationary conditions, and the durations of the single straight-line runs were 25–30 min, meaning that any involved stochastic process, in these periods, is assumed to have a probability distribution that does not change when shifted in time. During the seakeeping tests, the wave spectrum was measured continuously by a free-floating wave buoy (Datawell BV, Waverider SG) deployed in the test area; but without information about the exact distance between the buoy and the individual run path.
Figure 4.
The research vessel Gunnerus is owned and operated by NTNU. Data from a test campaign is studied in the preliminary assessment of the WBA.
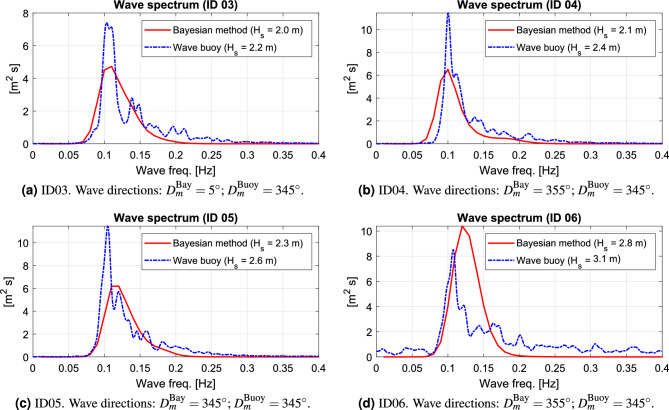
Figure 5 compares wave spectrum estimates by the Bayesian method and corresponding estimates by the wave buoy, noticing that the comparison is made for the point spectra which are integrated versions of the directional wave spectra. The caption of each subplot contains information about the mean wave direction , which indicates the compass direction where the waves come from following the meteorological convention, refer also to Fig. 4b. Moreover, the significant wave height appears in the legend of each subplot.
Figure 5.
Unconditioned Bayesian wave spectrum estimates obtained by analysis of dedicated sea trial experiments with a research vessel, cf. Fig. 4.
Overall, good agreements can be observed from the comparisons in Fig. 5, although Case ID06 stands slightly out compared to the other three cases. In this sense, the main take-away from this initial assessment is that good wave spectrum estimates can be expected, when the WBA is applied under “controlled” conditions. In fact, similar observations have been made in several other studies, where (fully) dedicated experimental datasets, including model tests, are analysed16,18,24,40–43. Note that by controlled conditions should be understood that the detailed hull geometry is available for computation of the transfer functions, and, furthermore, that the uncertainties in operational parameters (i.e., ship speed and loading condition) are small. This means that the computed transfer functions are reliable and (should) provide a realistic match to the real ship’s motion dynamics in waves, within the implicit assumptions (small-amplitude waves) for using transfer functions computed by linear, potential flow strip theory. Nevertheless, roll is a response dominated by nonlinear effects that cannot be captured using transfer functions, where a linear theory is assumed44,45. In this respect, it is noteworthy that the literature7,8 includes discussions about replacing roll with sway in the WBA.
As a final comment, it is important to stress that uncertainties are associated not only with the wave spectra of the WBA but also with those of the wave buoy, although the comparison in Fig. 5 indicates a fair agreement. Furthermore, the inherent randomness, in time and space, of ocean waves means that one never truly compares apples with apples, since the ship and buoy are not exactly at the same position. In other words, speaking about a ground truth makes little sense in this context.
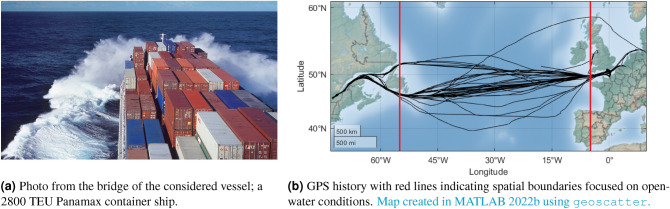
In-service data
The second analysis of this preliminary assessment is made with a dataset from the container ship shown in Fig. 6a, noticing that the analysis considers nearly two years of operational data from service on the North Atlantic, see Fig. 6b. The ship and the complete dataset are thoroughly described in the literature46. For the present study, it suffices to note that the wave-induced accelerations of one angular motion (pitch) and two translational motions (sway, heave), respectively, are simultaneously used as input to the Bayesian estimation method. The particular dataset does not contain information about the ship’s loading condition (i.e., draught and trim) on the voyages, and, due to the nature of the measurements (in-service data), neither has it been attempted to ensure that the vessel’s speed and course are constant during the data recordings used for wave estimation. Yet, transfer functions are needed for the Bayesian method, and a simple solution to account for the missing information with respect to the exact draught is simply to assume a “typical transit draught”46 when computing the transfer functions; even though the ship’s real draught and trim may have been (very) different on many of the studied voyages. Thus, it is appreciated that the transfer functions have been computed from the detailed hull geometry, made available to the authors for the particular purpose, and using a commercial software47. However, the lack of exact knowledge about the operational parameters (draught, trim, speed, course) and their possible fluctuating behavior, at times, clearly introduce large uncertainties in the computed transfer functions.
Figure 6.
In-service data from a container ship has been analysed. In total, 7644 time series samples of 25 minutes duration have been studied.
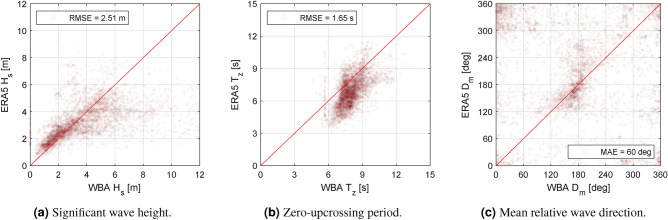
Based on the vessel’s GPS history, reanalysis data (hindcast) of integral wave parameters has been obtained from the ERA5 database12,48. Specifically, ERA5 estimates of significant wave height (), zero-upcrossing period (), and mean wave direction () are studied and used as a means for comparing estimates of the WBA using the Bayesian method, repeating that, initially, unconditioned results are considered.
Figure 7 presents the comparison of estimates by the Bayesian method (’WBA’) against the corresponding estimates from ERA5; in the scatter plots, any perfect agreement is reflected by points located on the line of identity (full red line). To assess quantitatively the deviation between corresponding pairs of estimates, root-mean-squared-errors (RMSE), in dimensional form, are also computed and included for , while the minimum-absolute-error (MAE) is included for , accounting for the directional ambiguity. In short, it is evident from the comparison that significant scatter appears, although the markers for each of the three parameters {, , } to some degree distribute around the line of identity.
Figure 7.
Comparison of integral wave parameters (, , and ) from the ERA5 database and corresponding parameters derived from the unconditioned wave spectrum estimates by the WBA. The legends inform about the root-mean-squared error (RMSE) for and , respectively, and the minimum-absolute error (MAE) for .
Wave spectrum estimates from a hybrid framework
In the hybrid approach, outcomes of a convolutional neural network (CNN) act as constraints on the directional wave spectrum produced by the Bayesian method. The assessment of the hybrid approach is made with the same dataset as presented in the previous subsection focused on in-service data from a container ship. The training of the CNN is based on 80% of the total (filtered) dataset and comprises samples32, while the validation set makes up the remaining 20% of the data, which means that samples are left as unseen data. The reader is reminded that a sample in this context consists of a 25-minute set of MRU (motion response unit) time series and the corresponding ERA5 wave parameters in terms of {, , }.
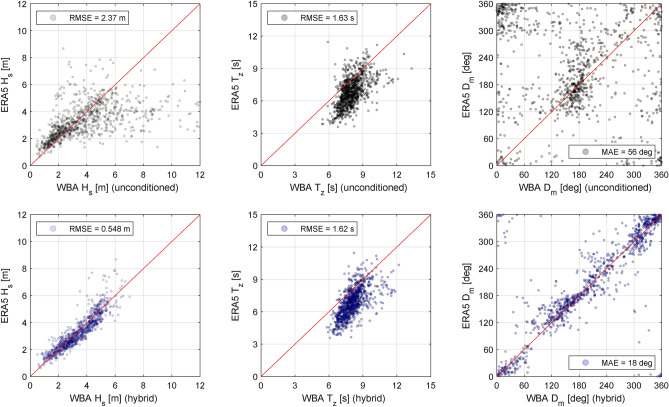
Figure 8 shows the improvement in accuracy by applying the hybrid framework. In the figure, the three top-plots (unconditioned WBA) should be compared against the three bottom-plots (hybrid WBA); noticing that each sub-plot presents the comparison between estimates of ERA5 and the WBA, similar to Fig. 7, in all cases considering samples of the validation data exclusively. The improvements in estimates of significant wave height () and wave direction () are evident. On the other hand, no notable effect appears on the zero-upcrossing period (). The explanation for this observation is that the conditioning of the WBA wave spectrum estimates, using the hybrid framework, is introduced solely through constraints on and , as a deliberate choice for the reason discussed further below. It is important to emphasise that the conditioning of the wave spectrum estimates is made using outcomes of a machine learning method (i.e. the CNN) and not directly the ERA5 parameters themselves. The reason is that for the hybrid framework to be applicable in real-time, the “constraining parameters” must be immediately available, for instance through a pre-trained machine learning method which itself can be formed by earlier offline training with a proxy for the ground truth, like the ERA5 database.
Figure 8.
Integral wave parameters from the ERA5 database against corresponding parameters derived from, respectively, the unconditioned wave spectrum estimates by the WBA (top row) and the conditioned estimates using the hybrid framework of the WBA (bottom row). Left-side plots: , middle plots: , right-side plots: .
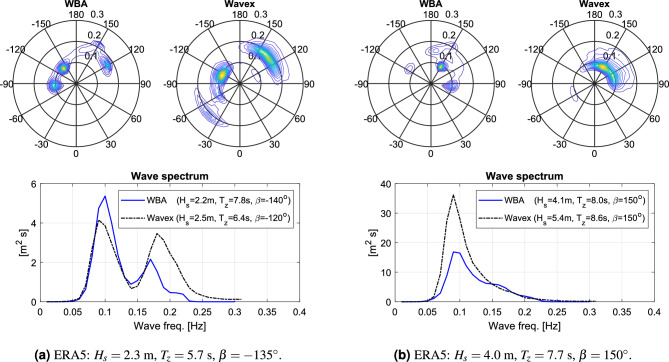
While the assessment of the hybrid framework is made entirely through wave parameters, it is important to stress that many problems of wave-structure interaction require the directional wave spectrum as the fundamental input, not just the wave parameters. Indeed, the proposed hybrid (“machine learning-informed physics-based”) method provides this, as can be seen from two arbitrarily selected samples in Fig. 9. In fact, in the given cases, the WBA spectra are compared with corresponding directional spectra estimated by a wave radar system; noticing that the ship, in the past, was used as a test platform in a research project about hull structure integrity and, for this reason, the ship was also equipped with a wave radar (Wavex by Miros), capable of providing estimates of the onsite directional wave spectrum. In this context, to repeat the general message, it is underlined that wave radars come with uncertainties in their estimates as well. Detailed discussions are beyond the present scope, but particular concerns of wave radars relate to, e.g., the accurate estimation of the significant wave height49 and the effect of rain clutter50.
Figure 9.
Directional wave spectra by the WBA and a wave radar system (Wavex), and with the corresponding point spectra below. In subplots (a) and (b), different time stamps (UTC) are considered (a: 24-09-2007 00:00; b: 06-03-2008 19:00), and the respective sub-captions inform about the corresponding ERA5 wave parameters for the given cases, including the wave encounter angle .
Discussion
Inherently, the use of transfer functions, as in the physics-based variants of the WBA, is associated with several uncertainties. It can be difficult to assign single and general causes for the uncertainties, however, the lack of detailed and exact information with regard to operational conditions (draught, trim, speed, etc.) is a primary source when in-service data is studied. In addition, the complex geometry of a ship hull can lead to difficulties in correctly modelling the physics of the motion dynamics of a ship in waves; especially considering higher and steeper waves. What is more, sometimes the hull geometry is not available to the ship operator, in which case so-called closed-form expressions51,52 can be used as an approximate alternative for the transfer functions. Nevertheless, transfer functions presumably yield a qualitatively correct picture of a ship’s response in waves. A machine learning model, on the other hand, can infer nonlinearities and other unseen tendencies in the data not captured by transfer functions. By forming a hybrid framework, we have therefore tried to include the best from two fundamentally different methods to reach an approach with the potential to emphasise the pros and minimise the cons of the two respective frameworks being merged.
In the assessment using in-service data, wave parameter estimates from the ERA5 database were considered; both for the direct comparison with output of the WBA and for the training of a convolutional neural network, where the ERA5 parameters acted as a proxy for the ground truth. In this sense, the particular database, or a similar database produced by third-generation spectral wave models, can itself be used for making assessments of ship operations, considering aspects of safety as well as performance (fuel consumption analysis, etc.). One disadvantage, however, is that such databases cannot be used for on-board, real-time assessments in the guidance of the shipmaster, since the database is the result of reanalyses made by assimilating the spectral wave model with measured data in offline post-processing. Moreover, reanalysis data will practically never be truly applicable to the exact spatio-temporal position of the ship, due to the fixed resolution of the grid in the reanalysis data. On the other hand, the advantage in training the machine learning model with ERA5 is that this approach does not require additional/extra hardware, noticing that a wave radar system needs a dedicated X-band radar for its functional mode of operation.
In connection with the preceding and with a remark about the practical application, it is imagined that the hybrid method could run by introducing an initial ’training phase’. As an example: At day 0 until, say, day 100, wave spectrum estimates are produced by only the Bayesian method (being solely physics-based). From day 101, enough training data (i.e., recorded motions plus ERA5) has presumably been collected for the machine learning model to produce reliable output, and the hybrid method could start producing results, though with continued training of the machine learning model. On the same note, it is important to mention that a new training phase is needed when/if a new ship is considered. That is, results from one ship cannot be transferred directly to another ship; unless the two ships are identical in their design and with similar operational profiles.
In the hybrid approach, the conditioning of the wave spectrum estimates was made by imposing constraints on and , but not . This is a choice made since the (low-pass) filtering effect of a ship generally implies that high-frequency wave components are not “sensed”, resulting in lost information about the tail of the wave spectrum; with a deteriorating tendency the larger the ship relative to wave length. Consequently, it is thought that it potentially will harm more than it will do good to impose (also) a constraint on , since the estimated conditioned wave spectrum may end up being distorted, or in other ways nonphysical. In fact, the hypothesis was tested and confirmed on a few samples, although not shown herein, but it will take more thorough investigations to make definitive conclusions.
Somewhat related to the previous point, it should be noted that different types of responses exhibit different (low-pass) frequency characteristics. For instance, in relative terms, motion components like heave, roll, and pitch are typically less excited compared to structural hull girder responses such as bending and twisting, when the ship operates in short waves. In other words, the negative effects of a ship’s low-pass filtering characteristics can be diminished by introducing responses not affected by the low-pass behaviour to the same degree as motion components10,19,25. Consequently, designing or selecting the right measurements for improved estimation capabilities would be nice to have as a standard approach, thinking in the direction of a dynamical and automatic selection53,54.
As pointed out earlier, it has little meaning to speak about a ground truth when measuring ocean waves. Nevertheless, in machine learning, a proxy thereof is needed. In this paper, the ERA5 database has been used, without touching the fact that the database represents estimates and is associated with uncertainties itself. In fact, it is possible to include uncertainties in the database from observations, sea surface temperature, and from model-physical parameterisations55. Clearly, it could be interesting to consider this kind of uncertainty in the hybrid method, in an extended and future work, as such an extension could make the WBA even more appealing from a practical-application point of view. In this context, it should be noted that how accurate the wave height, for instance, needs to be, depends on the use-case; in some cases a low accuracy is fine, while in other cases we would like high accuracy. On the same note, it is also interesting to mention that a physics-based version of the WBA, making it possible to include the uncertainty in the transfer functions of the ship, has been developed26. In the future, it appears interesting to investigate possible combinations of that version with the hybrid framework discussed in the present paper.
It is possible to obtain the detailed directional wave spectrum from the ERA5 database. As already noted, research30,33,34 has been initiated for the development of machine learning models capable of reconstructing actual (directional) wave spectra from measured ship responses. The challenge, however, is that wave spectra can be considered as sparse matrices and their prediction is difficult and inefficient. Additionally, larger input/output dimensions lead to a high number of trainable parameters, which makes the models fragile and susceptible to overfitting. Hence, a dimensionality reduction procedure56,57 as pre-processing could be a work-around for increasing model efficiency as well as accuracy, like discussed by one study58. Although the existing studies aimed at predicting the full wave spectrum appear yet as immature, since they consider simulated data only and/or do not assess the model performance on out-of-sample data and thus reflect reduced credibility, it is believed that successful developments will be presented, sooner or later.
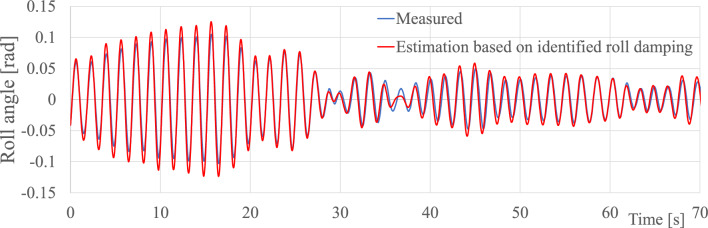
For about two decades, we have investigated concepts for estimating waves via measured ship responses, and the technology provides good estimates of the directional wave spectrum compared to other means. Wave spectra are fundamental inputs to the assessment of many wave-structure interaction problems. However, certain types of problems are dominated by nonlinearities, like the prediction of ship rolling and whipping-induced hull girder vibrations, and, in such cases, actual time series sequences of the surface (wave) elevation are needed. Recently, a method for reconstructing the incident wave profile has been proposed25,43, and, using this method, a framework for nonlinear roll damping identification has been developed59. So far, the framework has been assessed with simulated and model-test data only, see Fig. 10, and further validations with in-service data are thus needed. Another important work for the future will be to investigate the simultaneous use of multiple ships, in a network-based approach, for improved wave estimation and forecasting capabilities over larger geographic regions, with repeated reference to Fig. 2 highlighting the potential in using ships as sailing wave buoys. Initial studies in this direction have commenced60, including related work focused on deriving spatial wave data from a network of buoys and ships61.
Figure 10.
Measured and estimated roll motions in long-crested irregular waves based on model-tests carried out by National Maritime Research Institute (Japan)59. The time axis is in the scale of the model (1:72).
Theory and methods
Wave parameters and statistical metrics
Wave parameters characterising a directional wave spectrum can be derived by integration62. Thus, significant wave height , zero-upcrossing period , and mean wave direction are all derived from the directional wave spectrum ,
| 1 |
| 2 |
| 3 |
where
| 4 |
| 5 |
| 6 |
| 7 |
with as the circular frequency in [rad/s] along the wave direction . Note that the wave encounter angle , providing the wave direction relative to the ship, is directly derived from the mean wave direction and the course of the ship ,
| 8 |
following the convention that head waves is and waves approaching from starboard side and port side, respectively, are indicated by ’+’ and ’’, while following waves is .
To assess quantitatively the deviation between corresponding pairs of wave parameter estimates, root-mean-squared-errors (RMSE), in dimensional form, are computed for , while the minimum-absolute-error (MAE) is computed for , accounting for the directional ambiguity. The expressions follow from:
| 9 |
| 10a |
| 10b |
where y indicates an estimate of the particular parameter in question, i.e. , for sample k considering WBA or ERA5, indicated by indices.
Wave-to-motion transfer functions
In the most basic sense, transfer functions inform how a ship responds to regular (harmonic) waves of unit amplitude. The ship’s linear response in real (irregular) waves can be found by combination (i.e. multiplication) of the transfer functions and the wave spectrum describing the real waves. The interested reader will find several excellent textbooks on the topic44,45,62–64.
Computation of response spectra
To construct the cross spectra, needed as input to the WBA, FFT is performed using the Matlab function cpsd, which is based on Welch’s averaged, modified periodogram method applied on eight sections with 50% overlap, and with each section windowed with a Hamming window65.
The wave buoy analogy (WBA)
Bayesian method
A thorough account of the Bayesian method is given in the literature37,66, and the particular implementation made in this paper considers ships with forward speed8,13. The following contains an introduction to only the most central aspects. From a measured set of responses, corresponding response spectra , , can be computed under the assumption of stationary and ergodic processes. Here, defines the encounter frequency discretised by components. Formally, the directional wave spectrum can be determined from the spectral equation,
| 11 |
where the transfer function is , and the overline denotes the complex conjugate. The intrinsic frequency is [rad/s], and ) [deg] is the wave encounter angle with waves propagating from the compass direction while the compass heading of the ship is . The triangular brackets , with as index, are used to emphasise that evaluation happens for a given frequency of encounter. This requires consideration of the Doppler effect63,67, relating the intrinsic frequency to the encounter frequency (or vice versa) via the wave encounter angle and ship speed, respectively. The expression in the triangular brackets is thus the (theoretically) computed response spectrum converted to the encounter domain. While the formal notation in Eq. (11) excludes details about the actual implementation, the specific literature8,13 includes these, and can be accompanied by a pseudo-algorithm68 for ease of practical implementation. It is noteworthy that ship speed, for matters of fuel performance, will normally be held constant in service conditions, excluding all maneuvering operations, e.g., related to departures and arrivals in harbours. Thus, for most cases in service conditions, the variation in ship speed relative to the average value over, say, 25-30 minutes is insignificant. The Bayesian method solves for the unknown wave spectrum at all discrete pairs of , necessitating regularisation for dealing with the highly under-determined equation system. As such, the method relies on the inclusion of prior information to regularise the solution of the governing equation, cf. equation (11). Specifically, constraints are set on the second order derivative, controlling the smoothness of the mathematical surface describing the directional wave spectrum. In summary, it can be said that the Bayesian method establishes a wave spectrum obtained as a compromise between the agreement between the data and the theoretical prediction, formally controlled by Eq. (11), and the smoothness of the wave spectrum. To “guide” the compromise, an objective criterion (referred to as ABIC) is introduced, as carefully explained in the specific literature8,13.
Convolutional neural network
Neural networks can produce a satisfactory mapping from measured vessel responses to wave parameters. In this paper, the sea state identification, to differentiate from wave spectrum estimation where the entire directional wave spectrum is obtained, builds on an implementation of an Inception model69. Specifically, the identification algorithm32 makes use of response spectra, applied in a multi-task learning (MTL) setting70, for identification of significant wave height, peak period, and wave direction. In MTL, each output is considered as a separate task with its own dedicated branch of fully connected hidden layers and corresponding output layers. Such an architecture is selected to favour physical interdependencies between the wave parameters and improve the model’s generalisation capability71. In the current work, the ship’s speed and draught were not fed into the model; draught was not measured, thus “unknown”, and the speed was relatively constant, varying in the range of 18-20 knots for the vast majority of the data32. In case of more varied operational conditions, however, it will be necessary to refine the neural network, for instance by considering a multi-modal convolutional neural network, which is characterised by several input branches and discussed in greater detail in the literature32.
Hybrid framework
In the hybrid framework11, output ( and ) from the convolutional neural network are considered as physical constraints on the directional wave spectrum to be estimated. This means that additional equations are concatenated to the governing equation system represented by Eq. (11). Specifically, the following equations are considered:
| 12a |
| 12b |
| 12c |
where Eqs. (12b) and (12c) in combination relate to the mean relative wave direction, cf. Eq. (3). It is understood that the wide-tilde, in , is used to indicate the directional wave spectrum to be estimated, whereas the hat-notation on the right-hand side of the equations is used to indicate that the parameters are known from another source; in this case, they are the output from the machine learning model, i.e. the convolutional neural network. Details of the hybrid framework are presented in11.
ERA5 database
Atmospheric reanalyses provide estimations of coherent records of global air-sea-land circulation72–74. Focusing on sea surface conditions, the spatio-temporal development of ocean wave systems can be described by the energy balance equation75–78. Specifically, using third-generation spectral wave models, the time- and position-dependent wave spectrum is computed by integration of the energy balance equation. In addition, observations of wind and waves are assimilated. The ERA5 database12,48 is the result of this type of modelling, and ECMWF (European Centre of Medium-Range Weather Forecasts) has made the reanalysis freely available through EU funding79. In the database, hourly ocean wave data on single levels is available on a regular latitude-longitude grid at resolution, and interpolation to the exact ship position is made accordingly80.
Acknowledgements
The project ADAM4EVE under the framework agreement ’Orient Fond 2021-2025’ between DTU and A/S D/S Orients Fond has covered the Open Access fee. Part of this work has been supported by the Research Council of Norway through the Centres of Excellence funding scheme, project number 223254 NTNU AMOS. The set of sea trials data was made available by the SIMVAL KPN project, financed through grant number 225141/O70 by Rolls-Royce Marine and the Norwegian Research Council.
Author contributions
U.D.N., T.I., and J.J.J. conceived the fundamental concepts. U.D.N. made the numerical implementations. A.H.B. and A.J.S. acquired all data connected to the sea trials with R/V Gunnerus. G.S. acquired the in-service data of the container ship, and Y.S. computed the transfer functions. M.M. provided the ERA5 wave data as well as the machine learning derived results. T.T. conceived the wave profile-reconstructing algorithm and made the implementation of it. Aspects of numerical hydrodynamics, including interpretations of results therefrom have been discussed with H.B.B. R.E.G.M. contributed with conceptions and design related to network-based approaches. U.D.N. wrote the manuscript, all other authors engaged in valuable discussions and provided input and critical revisions.
Data availability
The dataset from R/V Gunnerus is not publicly available due to an agreement between NTNU and Rolls-Royce Marine but is available from the authors on reasonable request.
The in-service data that supports the findings of the hybrid method is available from DNV but restrictions apply to the availability of this data, which was used under license for the current study, and so is not publicly available. Data is however available from the authors upon reasonable request and with permission of DNV.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.St. Denis M, Pierson W. On the motion of ships in confused seas. Trans. SNAME. 1953;61:280–332. [Google Scholar]
- 2.Danish Maritime Accident Investigation Board (DMAIB). Maersk Essen: Marine accident report on loss of cargo. https://dmaib.dk/media/7853/maersk-essen-loss-of-cargo-on-16-january-2021.pdf (2022). Maritime accident report on Maersk Essen’s loss of cargo on 16 January 2021.
- 3.Helmholtz-Zentrum Hereon. Air-Sea Fluxes. (2023). (Accessed 10 June 2023); https://www.hereon.de/institutes/coastal_ocean_dynamics/air_sea_fluxes/index.php.en
- 4.Yousefi K, Veron F, Buckley MP. Turbulent and wave kinetic energy budgets in the airflow over wind-generated surface waves. J. Fluid Mech. 2021;920:55. doi: 10.1017/jfm.2021.377. [DOI] [Google Scholar]
- 5.Smith, A., Callaghan, A. & Bidlot, J. Parameterising CO2 air-sea gas transfer with wave breaking energy dissipation rate, sea state, and wind speed. In EGU General Assembly 2022, 10.5194/egusphere-egu22-7473 (Vienna, Austria, 2022).
- 6.Iseki T, Ohtsu K. Bayesian estimation of directional wave spectra based on ship motions. Control Eng. Pract. 2000;8:215–219. doi: 10.1016/S0967-0661(99)00156-2. [DOI] [Google Scholar]
- 7.Tannuri EA, Sparano JV, Simos AN, Cruz JJD. Estimating directional wave spectrum based on stationary ship motion measurements. Appl. Ocean Res. 2003;25:243–261. doi: 10.1016/j.apor.2004.01.003. [DOI] [Google Scholar]
- 8.Nielsen UD. Estimations of on-site directional wave spectra from measured ship responses. Mar. Struct. 2006;19:33–69. doi: 10.1016/j.marstruc.2006.06.001. [DOI] [Google Scholar]
- 9.Pascoal R, Guedes Soares, C, Sørensen AJ. Ocean Wave Spectral Estimation Using Vessel Wave Frequency Motions. J. Offshore Mech. Arct. Eng. 2007;129:90–96. doi: 10.1115/1.2426986. [DOI] [Google Scholar]
- 10.Nielsen UD. The wave buoy analogy—Estimating high-frequency wave excitations. Appl. Ocean Res. 2008;30:100–106. doi: 10.1016/j.apor.2008.07.002. [DOI] [Google Scholar]
- 11.Nielsen UD, Mittendorf M, Shao Y, Storhaug G. Wave spectrum estimation conditioned on machine learning-based output using the wave buoy analogy. Mar. Struct. 2023;91:103470. doi: 10.1016/j.marstruc.2023.103470. [DOI] [Google Scholar]
- 12.Hersbach et al. ERA5 hourly data on single levels from 1979 to present. https://cds.climate.copernicus.eu (2021). 10.24381/cds.adbb2d47.
- 13.Nielsen UD. Introducing two hyperparameters in Bayesian estimation of wave spectra. Probab. Eng. Mech. 2008;23:84–94. doi: 10.1016/j.probengmech.2007.10.007. [DOI] [Google Scholar]
- 14.Pascoal R, Guedes Soares C. Kalman filtering of vessel motions for ocean wave directional spectrum estimation. Ocean Eng. 2009;36:477–488. doi: 10.1016/j.oceaneng.2009.01.013. [DOI] [Google Scholar]
- 15.Montazeri N, Nielsen UD, Jensen JJ. Estimation of wind sea and swell using shipboard measurements—A refined parametric modelling approach. Appl. Ocean Res. 2016;54:73–86. doi: 10.1016/j.apor.2015.11.004. [DOI] [Google Scholar]
- 16.Pascoal R, Perera LP, Guedes Soares C. Estimation of directional sea spectra from ship motions in sea trials. Ocean Eng. 2017;132:126–137. doi: 10.1016/j.oceaneng.2017.01.020. [DOI] [Google Scholar]
- 17.Brodtkorb AH, Nielsen UD, Sørensen AJ. Sea state estimation using vessel response in dynamic positioning. Appl. Ocean Res. 2018;70:76–86. doi: 10.1016/j.apor.2017.09.005. [DOI] [Google Scholar]
- 18.Nielsen UD, Brodtkorb A, Sørensen A. A brute-force spectral approach for wave estimation using measured vessel motions. Mar. Struct. 2018;60:101–121. doi: 10.1016/j.marstruc.2018.03.011. [DOI] [Google Scholar]
- 19.Chen X, Okada T, Kawamura Y, Mitsuyuki T. Estimation of on-site directional wave spectra using measured hull stresses on a 14,000 TEU large container ships. J. Mar. Sci. Technol. 2020;25:690–706. doi: 10.1007/s00773-019-00673-w. [DOI] [Google Scholar]
- 20.Ren Z, Han X, Verma AS, Dirdal JA, Skjetne R. Sea state estimation based on vessel motion responses: Improved smoothness and robustness using Bézier surface and L1 optimization. Mar. Struct. 2021;76:102904. doi: 10.1016/j.marstruc.2020.102904. [DOI] [Google Scholar]
- 21.Dirdal JA, Skjetne R, Roháč J, Fossen TI. Online wave direction and wave number estimation from surface vessel motions using distributed inertial measurement arrays and phase-time-path-differences. Ocean Eng. 2022;249:110760. doi: 10.1016/j.oceaneng.2022.110760. [DOI] [Google Scholar]
- 22.Brodtkorb AH, Nielsen UD. Automatic sea state estimation with online trust measure based on ship response measurements. Control Eng. Pract. 2023;130:105375. doi: 10.1016/j.conengprac.2022.105375. [DOI] [Google Scholar]
- 23.Kubo, H. et al. Bayesian updating of estimated parameters representing multi-modal directional wave spectrum using measured ship hull stresses. In Proceedings 42nd OMAE (Melbourne, Australia, 2023).
- 24.Zago L, Simos A, Kawano A, Kogishi A. A new vessel motion based method for parametric estimation of the waves encountered by the ship in a seaway. Appl. Ocean Res. 2023;134:103499. doi: 10.1016/j.apor.2023.103499. [DOI] [Google Scholar]
- 25.Takami T, Nielsen UD, Jensen J, Xi C. Estimation of encountered wave elevation sequences based on response measurements in multi-directional seas. Appl. Ocean Res. 2023;135:103570. doi: 10.1016/j.apor.2023.103570. [DOI] [Google Scholar]
- 26.Chen X, Takami T, Oka M, Kawamura Y, Okada T. Stochastic wave spectra estimation (SWSE) based on response surface methodology considering uncertainty in transfer functions of a ship. Mar. Struct. 2023;90:103423. doi: 10.1016/j.marstruc.2023.103423. [DOI] [Google Scholar]
- 27.Duz, B., Mak, B., Hageman, R. & Grasso, N. Real time estimation of local wave characteristics from ship motions using artificial neural networks. In Proceedings of 14th Int’l Symposium on Practical Design of Ships and Other Floating Structures (Yokohama, Japan, 2019).
- 28.Mak, B. & Duz, B. Ship As a Wave Buoy - Estimating Relative Wave Direction From In-Service Ship Motion Measurements Using Machine Learning. In Proceeedings of 38th International Conference on Ocean, Offshore & Arctic Engineering (Glasgow, Scotland, 2019).
- 29.Cheng, X., Li, G., Skulstad, R., Zhang, H. & Chen, S. Spectralseanet: Spectrogram and convolutional network-based sea state estimation. In Proceedings of IECON 2020: The 46th Annual Conference of the IEEE Industrial Electronics Society (2020).
- 30.Scholcz, T. & Mak, B. Ship as a wave buoy - estimating full directional wave spectra from in-service ship motion measurements using deep learning. In Proceedings of 39th International Conference on Ocean, Offshore and Arctic Engineering (Fort Lauderdale, 2020).
- 31.Kawai T, Kawamura Y, Okada T, Mitsuyuki T, Chen X. Sea state estimation using monitoring data by convolutional neural network. J. Mar. Sci. Technol. 2021;26:947–962. doi: 10.1007/s00773-020-00785-8. [DOI] [Google Scholar]
- 32.Mittendorf M, Nielsen UD, Bingham HB, Storhaug G. Sea state identification using machine learning: A comparative study based on in-service data from a container vessel. Mar. Struct. 2022;85:103274. doi: 10.1016/j.marstruc.2022.103274. [DOI] [Google Scholar]
- 33.Han P, Li G, Skjong S, Zhang H. Directional wave spectrum estimation with ship motion responses using adversarial networks. Mar. Struct. 2022;83:103159. doi: 10.1016/j.marstruc.2022.103159. [DOI] [Google Scholar]
- 34.Scholcz, T., Hageman, R., Duz, B. & Mak, B. Consistency assessment of wave directional spectrum predictions from machine learning based ship-as-a-wave-buoy methods. In Proceedings of 41st International Conference on Ocean, Offshore and Arctic Engineering (Hamburg, 2022).
- 35.Bisinotto GA, et al. Sea state estimation based on the motion data of a moored FPSO using neural networks: An evaluation with multiple draft conditions. Ocean Eng. 2023;276:114235. doi: 10.1016/j.oceaneng.2023.114235. [DOI] [Google Scholar]
- 36.Bisinotto, G. A., de Mello, P. C., Cozman, F. G. & Tannuri, E. A. Motion-based Wave inference with neural networks: Transfer learning from numerical simulation to experimental data. In 42nd International Conference on Ocean, Offshore and Arctic Engineering (Melbourne, 2023).
- 37.Akaike H. Likelihood and Bayes procedure. In: Bernado JM, Groot MHD, Lindley DU, Smith AFM, editors. Bayesian Statistics. University Press; 1980. pp. 143–166. [Google Scholar]
- 38.Steen, S., Selvik, Ø. & Hassani, V. Experience with rim-driven azimuthing thrusters on the research ship Gunnerus. In Proceedings of High-Performance Marine Vessels (Cortona, 2016).
- 39.Sintef Ocean. ShipX. http://www.sintef.no/programvare/shipx/. (Accessed 14 June 2023).
- 40.Iseki T, Terada D. Bayesian estimation of directional wave spectra for ship guidance systems. Int. J. Offshore Polar Eng. 2002;12:25–30. [Google Scholar]
- 41.Simos AN, Tannuri EA, Sparano JV, Matos VLF. Estimating wave spectra from the motions of moored vessels: Experimental validation. Appl. Ocean Res. 2010;32:191–208. doi: 10.1016/j.apor.2009.10.004. [DOI] [Google Scholar]
- 42.Brodtkorb, A. H., Nielsen, U. D. & Sørensen, A. J. Online wave estimation using vessel motion measurements. In Proceedings of 11th IFAC Conference on CAMS (Opatija, 2018).
- 43.Takami T, Nielsen UD, Xi C, Jensen J, Oka M. Reconstruction of incident wave profiles based on short-time ship response measurements. Appl. Ocean Res. 2022;123:103183. doi: 10.1016/j.apor.2022.103183. [DOI] [Google Scholar]
- 44.Newman JN. Theory of ship motions. Adv. Appl. Mech. 1978;18:221–283. doi: 10.1016/S0065-2156(08)70268-0. [DOI] [Google Scholar]
- 45.Newman JN. Marine Hydrodynamics. MIT Press; 2017. [Google Scholar]
- 46.Storhaug, G., Moe, E. & Piedras Lopes, T. A. Whipping measurements onboard a midsize container vessel operating in the North Atlantic. In International Symposium on Ship Design and Construction. Marintec, RINA, CMP, and SNAME (2007).
- 47.DNV. Wasim. (Accessed 18 February 2023) https://www.dnv.com/services/linear-and-non-linear-hydrodynamic-analysis-of-vessels-including-forward-speed-wasim-2413 (2023).
- 48.Hersbach H, et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020 doi: 10.1002/qj.3803. [DOI] [Google Scholar]
- 49.Gangeskar R. An algorithm for estimation of wave height from shadowing in x-band radar sea surface images. IEEE Trans. Geosci. Remote Sens. 2014;52:3373–3381. doi: 10.1109/TGRS.2013.2272701. [DOI] [Google Scholar]
- 50.Chen X, Huang W, Zhao C, Tian Y. Rain detection from x-band marine radar images: A support vector machine-based approach. IEEE Trans. Geosci. Remote Sens. 2020;58:2115–2123. doi: 10.1109/TGRS.2019.2953143. [DOI] [Google Scholar]
- 51.Jensen JJ, Mansour AE, Olsen AS. Estimation of ship motions using closed-form expressions. Ocean Eng. 2004;31:61–85. doi: 10.1016/S0029-8018(03)00108-2. [DOI] [Google Scholar]
- 52.Nielsen UD, Mounet REG, Brodtkorb AH. Parameterised transfer functions with associated confidence bands. Appl. Ocean Res. 2022;125:103250. doi: 10.1016/j.apor.2022.103250. [DOI] [Google Scholar]
- 53.Andersen, I. M. V. & Storhaug, G. Dynamic selection of ship responses for estimation of on-site directional wave spectra. In Proceedings of 31st OMAE (Rio de Janeiro, Brazil, 2012).
- 54.Montazeri, N., Nielsen, U. D. & Jensen, J. J. Selection of the optimum combination of responses for wave buoy analogy—an approach based on local sensitivity analysis. In Proceedings of 13th PRADS (Copenhagen, 2016).
- 55.ECMWF. ERA5: uncertainty estimation (Accessed 29 June 2023) https://confluence.ecmwf.int/display/CKB/CDS+dataset+documentation (2023).
- 56.Wang Y, Yao H, Zhao S. Auto-encoder based dimensionality reduction. Neurocomputing. 2016;184:232–242. doi: 10.1016/j.neucom.2015.08.104. [DOI] [Google Scholar]
- 57.Portillo SKN, Parejko JK, Vergara JR, Connolly AJ. Dimensionality reduction of SDSS spectra with variational autoencoders. Astron. J. 2020;160:45. doi: 10.3847/1538-3881/ab9644. [DOI] [Google Scholar]
- 58.Kawamura, Y., Katao, H., Okada, T., Hayakawa, G. & Mitsuyuki, T. Dimensional reduction of directional wave spectrum using autoencoder—toward the development of sea state estimation method using neural network. In Annual Autumn Meeting, Japan Society of Naval Architects and Ocean Engineers, 10.14856/conf.35.0_565 (2022).
- 59.Takami, T., Nielsen, U. D., Jensen, J. J. & Matsui, S. Nonlinear roll damping identification based on onboard ship response measurements. In Proceedings of 10th PAAMES and AMEC (Kyoto, 2023).
- 60.Mounet REG, Nielsen UD, Brodtkorb AH, Tannuri EA, de Mello PC. Simultaneous sea state estimation and transfer function tuning using a network of dynamically positioned ships. Appl. Ocean Res. 2022;129:103367. doi: 10.1016/j.apor.2022.103367. [DOI] [Google Scholar]
- 61.Mounet REG, et al. Deriving spatial wave data from a network of buoys and ships. Ocean Eng. 2023;281:114892. doi: 10.1016/j.oceaneng.2023.114892. [DOI] [Google Scholar]
- 62.Bhattacharyya R. Dynamics of Marine Vehicles. John Wiley & Sons; 1978. [Google Scholar]
- 63.Faltinsen O. Sea Loads on Ships and Offshore Structures. Cambridge University Press; 1990. [Google Scholar]
- 64.Lloyd ARJM. Seakeeping. 2. Ellis Horwood; 1998. [Google Scholar]
- 65.MATLAB R2022b. CPSD—Cross power spectra density. https://se.mathworks.com/help/signal/ref/cpsd.html (accessed 31 August 2023) (2023). MATLAB Documentation.
- 66.Iseki T. Estimation of directional wave spectra using ship motion data. In: Akaike H, editor. The Practice of Time Series Analysis. Springer-Verlag; 1999. pp. 115–130. [Google Scholar]
- 67.Nielsen UD. Transformation of a wave energy spectrum from encounter to absolute domain when observing from an advancing ship. Appl. Ocean Res. 2017;69:160–172. doi: 10.1016/j.apor.2017.10.011. [DOI] [Google Scholar]
- 68.Nielsen UD, Mounet REG, Brodtkorb AH. Tuning of transfer functions for analysis of wave—ship interactions. Mar. Struct. 2021;79:103029. doi: 10.1016/j.marstruc.2021.103029. [DOI] [Google Scholar]
- 69.Szegedy, C., Ioffe, S., Vanhoucke, V. & Alemi, A. A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the thirty-First AAAI conference on artificial intelligence, 4278-4284 (San Francisco, 2017).
- 70.Caruana R. Multi-task learning. Mach. Learn. 1997;28:41–75. doi: 10.1023/A:1007379606734. [DOI] [Google Scholar]
- 71.Ruder, S. An overview of multi-task learning in deep neural networks. 10.48550/arXiv.1706.05098 (2017).
- 72.Uppala SM, et al. The ERA-40 reanalysis. Q. J. R. Meteorol. Soc. 2005;131:2961–3012. doi: 10.1256/qj.04.176. [DOI] [Google Scholar]
- 73.Dee DP, et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011;137:553–597. doi: 10.1002/qj.828. [DOI] [Google Scholar]
- 74.Gommenginger, C., Timmermans, B., Dodet, G. & Bidlot, J. Global wave height trends and variability from new multi-mission satellite altimeter products, reanalyses and wave buoys. In EGU General Assembly 2020, 10.5194/egusphere-egu2020-19804 (Online, 2020).
- 75.Komen G, et al. Dynamics and Modelling of Ocean Waves. Cambridge University Press; 1994. [Google Scholar]
- 76.Tolman H, et al. Development and implementation of wind-generated ocean surface wave models at NCEP. Weather Forecast. 2002;17:311–333. doi: 10.1175/1520-0434(2002)017<0311:DAIOWG>2.0.CO;2. [DOI] [Google Scholar]
- 77.Cavaleri L, et al. Wave modelling–the state of the art (by The WISE Group ) Prog. Oceanogr. 2007;75:603–674. doi: 10.1016/j.pocean.2007.05.005. [DOI] [Google Scholar]
- 78.Ardhuin F, et al. Semiempirical dissipation source functions for ocean waves. Part I: Definition, calibration, and validation. J. Phys. Oceanogr. 2010;40:1917–1941. doi: 10.1175/2010JPO4324.1. [DOI] [Google Scholar]
- 79.Copernicus Climate Change Service Information. ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. (Accessed 21 June 2023) https://cds.climate.copernicus.eu (2020).
- 80.Nielsen UD. Spatio-temporal variation in sea state parameters along virtual ship route paths. J. Oper. Oceanogr. 2021;15:169–186. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The dataset from R/V Gunnerus is not publicly available due to an agreement between NTNU and Rolls-Royce Marine but is available from the authors on reasonable request.
The in-service data that supports the findings of the hybrid method is available from DNV but restrictions apply to the availability of this data, which was used under license for the current study, and so is not publicly available. Data is however available from the authors upon reasonable request and with permission of DNV.