Abstract
The increasing sophistication of mobile and sensing technology has enabled the collection of intensive longitudinal data (ILD) concerning dynamic changes in an individual’s state and context. ILD can be used to develop dynamic theories of behavior change, which in turn, can be used to provide a conceptual framework for the development of just-in-time adaptive intervention (JITAIs) that leverage advances in mobile and sensing technology to determine when and how to intervene. As such, JITAIs hold tremendous potential in addressing major public health concerns such as cigarette smoking, which can recur and arise unexpectedly. In tandem, a growing number of studies have utilized multiple methods to collect data on a particular dynamic construct of interest from the same individual. This approach holds promise in providing investigators with a significantly more detailed view of how a behavior change processes unfold within the same individual than ever before. However, nuanced challenges relating to coarse data, noisy data, and incoherence among data sources are introduced. In this manuscript, we use a mobile health (mHealth) study on smokers motivated to quit (Break Free; R01MD010362) to illustrate these challenges. Practical approaches to integrate multiple data sources are discussed within the greater scientific context of developing dynamic theories of behavior change and JITAIs.
Keywords: Data integration, Data science, Health behavior interventions, Intensive longitudinal data (ILD), Just-in-time adaptive intervention (JITAI), Mobile health (mHealth), Smoking cessation
1. Introduction
The increasing sophistication of mobile and sensing technology has enabled the collection of rich and granular data about an individual’s state and context. Intensive longitudinal data (ILD) has been defined as “sequential measurements on five or more occasions during which a change process is expected to unfold” (Bolger & J.P., 2013). These data can be collected through a variety of methods (ecological momentary assessment [EMA], wearable sensors, etc.). ILD is increasingly used to inform the development of dynamic theories of behavior change, by investigating how behaviors, emotions and other experiences change in daily life. Further, there is growing interest in developing just-in-time adaptive interventions (JITAIs) that leverage ILD about an individual’s state (e.g., mood, behaviors) and context (e.g., location, presence of other people) to match intervention delivery (e.g., the type, timing, intensity) to the rapidly changing needs of individuals in real-world settings (Nahum-Shani et al., 2018).
While sophisticated digital data collection protocols offer tremendous opportunities for behavioral theory development and intervention design, they also involve practical challenges to data curation—defined as “any activity devoted to selecting, organizing, assessing quality, describing, and updating data that result in enhanced quality, trustworthiness, interpretability, and longevity of the data” (Rhee et al., 2006). Many of these challenges relate to the growing use of multiple methods to collect ILD on a particular dynamic construct of interest from the same individual. Examples include measuring medication adherence with smart pill bottles, e-prescribing software, and electronic health records (Toscos et al., 2020); tracking step count with both a small activity tracker worn on the wrist (e.g., Jaw Bone Up Move) and an app installed on the mobile phone (e.g., Google Fit; Klasnja et al., 2016; Klasnja et al., 2019); assessing alcohol use with an ‘active task’ prompting participants to observe and then recall pattern sequences displayed on their mobile phone and a timeline follow-back survey (Rabbi et al., 2018; Rabbi et al., 2017); and measuring psychological distress via button presses performed by participants on a wearable worn on the wrist and corroborated against check-in surveys by study staff (Kleiman et al., 2019). Within the field of smoking cessation, when and how often cigarette smoking occurred was inferred using a smoking detection algorithm (Nakajima et al., 2020; Saleheen et al., 2015), EMAs, and surveys administered during in-person clinic visits (Break Free; R01MD010362).
The use of multiple methods to obtain information from the same individual (i.e., the use of multiple data sources) provides a significantly more detailed view of how a behavior change process unfolds within the same individual than ever before. Indeed, various authors have noted that combining information on the same individual obtained from multiple data sources can enable more accurate inference on a construct of interest, particularly when one data source can be used to supply information that is not present in another, or when measurement error is present in one or more data sources. Yet, to-date, advancements in inferential approaches used to combine information on the same individual obtained from multiple data sources have been developed for and applied to a cross-sectional (i.e., measured at only one occasion) health outcome (He et al., 2014; Lohr & Raghunathan, 2017; Schenker & Raghunathan, 2007; Schenker et al., 2010; Schifeling et al., 2019). However, ILD introduces unique complexities and challenges beyond those presented by cross-sectional data. As such, articulating practical considerations that are necessary to curate ILD from the same individual but obtained from multiple data sources serves as a foundational step towards capitalizing on such information to advance behavioral theory and intervention design. This manuscript highlights practical considerations in curating ILD from multiple sources of data collection. For illustration, we use Break Free – an observational study that sought to examine the influence of intrapersonal and contextual factors on smoking lapse among African American smokers.
2. The motivating study: Break Free – Eliminating tobacco disparities among African Americans
Tobacco use is the leading cause of preventable death and disease and is responsible for nearly one in five deaths in the United States (Mokdad et al., 2004; Samet, 2013). Although rates of tobacco smoking have declined between 1965 and 2018 (42% and 13.7%, respectively; Creamer et al., 2019), about 40 million people in the United States still smoke (Drope et al., 2018). Many smokers have a desire to quit, and over half have attempted to quit for at least a day in the prior 12 months (Ahluwalia et al., 2018; Dube et al., 2009). However, nearly 95% of quit attempts are unsuccessful (Babb et al., 2017), with more than half of smokers experiencing their first lapse (i.e., a smoking event following initial cessation that does not meet definition of relapse [i.e., return to regular smoking following a period of abstinence; Piper et al., 2019)]) within about a week of their quit attempt. Many smokers experience a series of failed quit attempts before achieving long-term smoking cessation success (Hughes et al., 2004; Zhou et al., 2009). Moreover, there are striking inequities in tobacco cessation, with African American being less likely to successfully quit than those in other racial and ethnic groups (Kulak et al., 2016; Stahre et al., 2010). Importantly, there is strong empirical evidence to suggest that smoking lapse is highly predictive of relapse (Garvey et al., 1992; Kenford et al., 1994; Piper et al., 2019) and that states of vulnerability (i.e., conditions that represent high risk) for a lapse and states of receptivity (i.e., conditions representing ability and motivation to engage in) to a specific intervention, may be dynamic. For example, vulnerability to a lapse may occur during moments of distress or when encountering a cue to smoke (e.g., tobacco retail outlet; Watkins et al., 2014) and receptivity to a mobile-based intervention (e.g., recommendation to use medication) may depend on dynamic factors like context (e.g., being around others or alcohol use; Pacek et al., 2018). JITAIs, particularly those designed to be offered to individuals when they are in a state of vulnerability for lapse, and receptive to an intervention, hold promise for smoking cessation. However, existing empirical evidence is often insufficient to inform the selection and adaptation of interventions in a JITAI. For example, it is unclear what constellation of static and dynamic factors represent a state of vulnerability for lapse as well as under what conditions smokers attempting to quit are more receptive to specific intervention options (Nahum-Shani et al., 2021). These gaps motivate studies – such as Break Free – involving ILD on smoking lapse and predictors of lapse in real-time, real world settings (Nahum-Shani et al., in press).
A total of 303 participants were enrolled in the Break Free study. Eligible participants reported smoking at least 3 cigarettes per day (biochemically verified using expired carbon monoxide of 6 parts per million or higher) and were motivated to quit smoking within the next 30 days. All participants were offered approximately 6 weeks of nicotine patch therapy. Those who reported contraindication for the nicotine patch (e.g., heart attack, angina, cardiac arrhythmia, uncontrolled hypertension, skin allergies or chronic skin disease) were not enrolled. Participants were provided with a smartphone and AutoSense sensors (Ertin et al., 2011) for 14 contiguous days (4 days pre-quit through 10 days post-quit). AutoSense consists of a wearable device worn on the left wrist and right wrist, a wearable device worn around the chest, and accompanying smartphone software (mCerebrum). These devices collect a variety of data near-continuously, such as skin and ambient temperatures, electrocardiography, respiration, galvanic skin conductance, wrist acceleration, and wrist orientation (Ertin et al., 2011). Smoking and stress detection algorithms on the smartphone use data from these wearable devices to detect when a participant may have experienced stress or smoking (Nakajima et al., 2020; Saleheen et al., 2015).
The smartphone’s software was designed to deliver 4 Random EMAs per day for 14-days; such EMAs are so-called because their delivery schedule is based on selecting a moment of time from pre-defined contiguous blocks of time (say, 8:00 am – 12:00 pm) according to a uniform probability distribution. In addition, some participants may have also received Event-Contingent EMAs; such EMAs are so-called because their delivery schedule is contingent on smoking and stress algorithms identifying moments of the day when smoking and stress is likely to have occurred. All EMAs asked participants about smoking behavior, urge, mood, and other contextual, interpersonal, and cognitive factors. For simplicity, the remainder of this case study focuses on Random EMAs only. Participants were also asked to self-report smoking abstinence during several in-person clinic visits, such as whether they smoked on the day of the visit, in the last 7 days, and whether there had been a period of time that they had returned to regular smoking following a period of abstinence (i.e., smoked consecutively for 7 days). Further, the smartphone was GPS-enabled and thus collected near-continuous GPS data (every ~3 seconds). Although participants can report contextual information in EMAs (e.g., whether smoking is allowed in their current location), GPS provides real-time spatial mapping at a level of granularity not possible with EMA data alone. Such information may be important for predicting vulnerability to smoking lapse. Taken together, the Break Free study provides snapshots of when and how often cigarette smoking occurred through a combination of EMAs, a smoking detection algorithm, and sensing technology on the smartphone. Table 1 and Figure 1 present the measures in Break Free and the study time frame as it pertains to ILD collection within the 14-day period, respectively.
Table 1.
Available Measures of Lapse in the Break Free Study
| Random EMA (up to 4x per day) | Other (Near-Continuous) |
|---|---|
| Q1. “Since the last assessment, did you smoke any cigarette?” with response options Yes or No. | Smoking detection algorithm providing time stamps (e.g., a timestamp could pertain to 2:00PM on January 4, 2022) at which cigarette smoking was detected. |
| Skip Logic: IF response to Q1=Yes, THEN proceed to Q2 and Q3; ELSE do not proceed to Q2 or Q3. | |
| Q2. “How many cigarettes did you smoke that you did not record?” | |
| Q3. “How long ago did you smoke the first cigarette?” and “How long ago did you smoke the most recent cigarette?” Both of these questions provide response options in terms of the following intervals of time: 0–2 hours, 2–4 hours, 4–6 hours, 6–8 hours, 8–10 hours, 10–12 hours, more than 12 hours |
Figure 1.
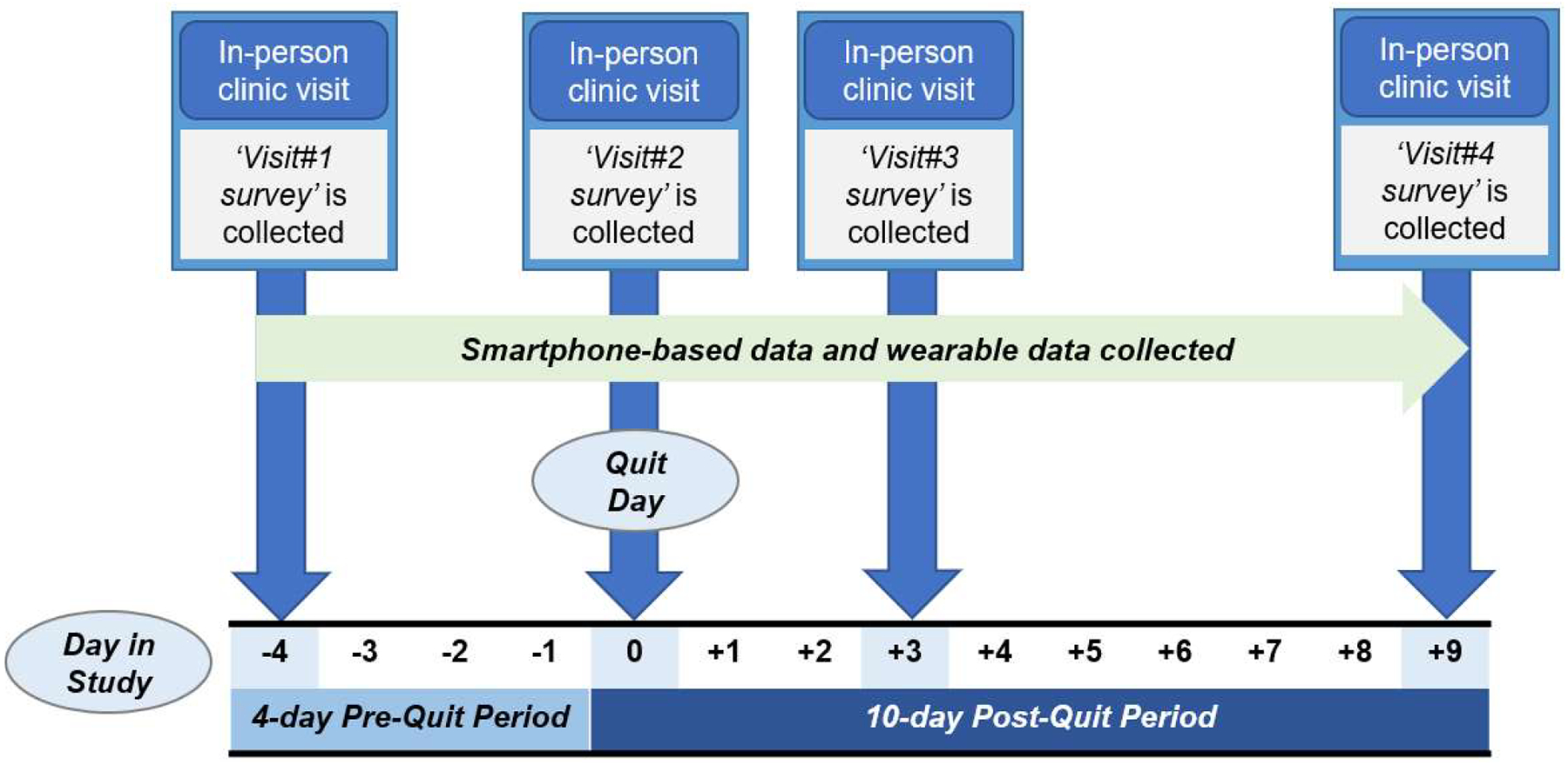
Participant ILD collection period in the Break Free study
3. Case study
Suppose that investigators identify the following scientific question to inform the development of a JITAI for smoking cessation: What combination of stable (e.g., socio-economic status, baseline motivation to quit, etc.) and dynamic factors (e.g., urge, cigarette availability) measured up to time t influence the likelihood of lapse between time t and time t+1 (e.g., cigarette smoking within the next minute, hour, or day from time t)? The length of time between time t and time t+1 is chosen by the investigator, perhaps based on existing empirical evidence and theories of behavior change regarding the timing of a proximal effect of a risk factor on smoking lapse. This scientific question can help investigators identify tailoring variables, or information about when to intervene, to be used in a JITAI targeting the proximal outcome of smoking lapse (Nahum-Shani et al., 2018). However, because multiple data sources in the Break Free study provide information about cigarette smoking, to answer the scientific question, investigators have the opportunity to simultaneously use multiple data sources (i.e., not one at a time, but altogether at the same time) to inform the development of a JITAI. In the remainder of this section, we will describe practical issues investigators need to consider (Section 3.1), and approaches investigators may use to integrate information on the same individual obtained from multiple data sources (Section 3.2). Figures 2 and 3 may be used to supplement examples in Sections 3.1 and 3.2
Figure 2.
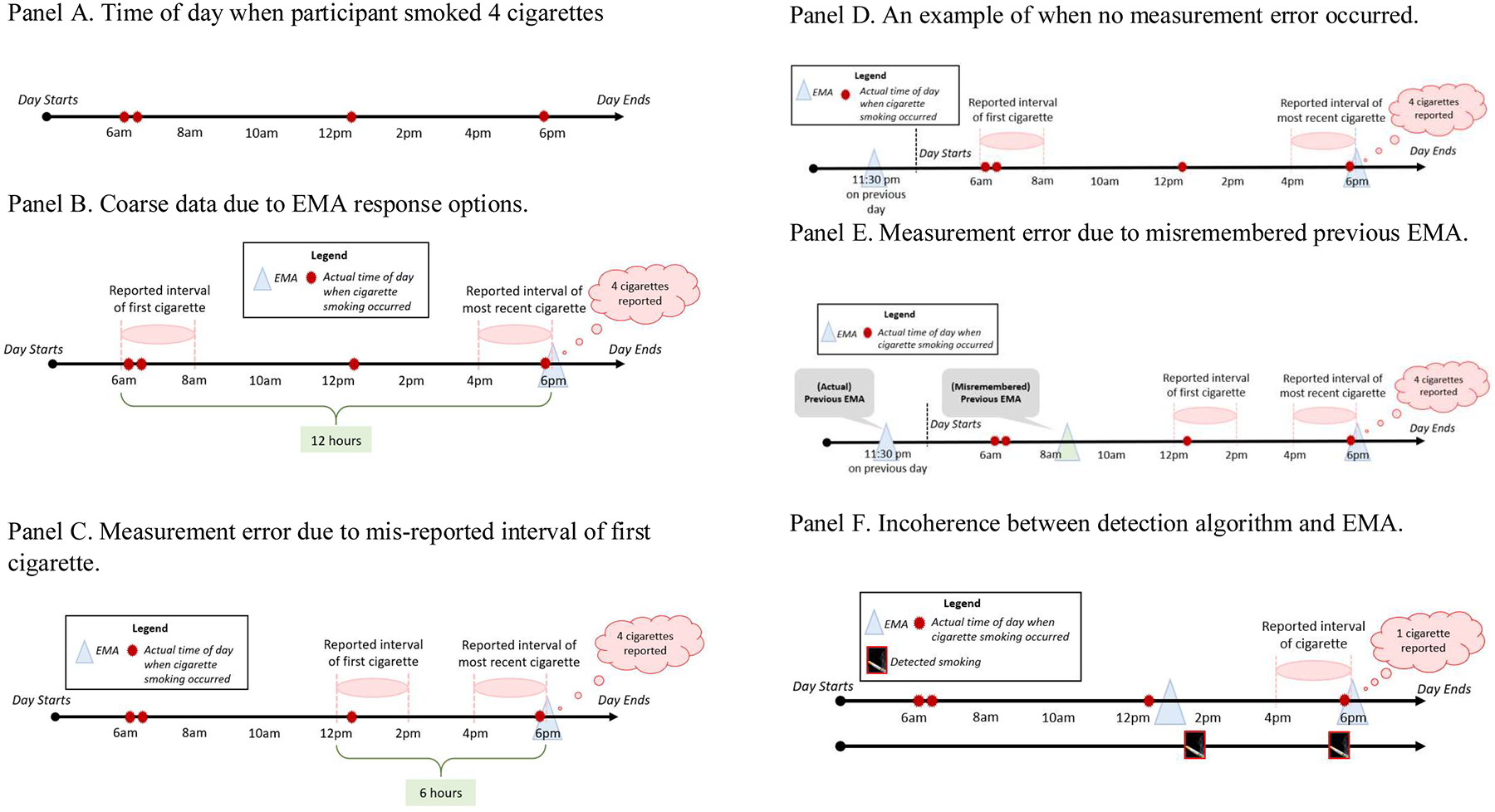
Examples illustrating practical issues to consider in ILD integration
Figure 3.
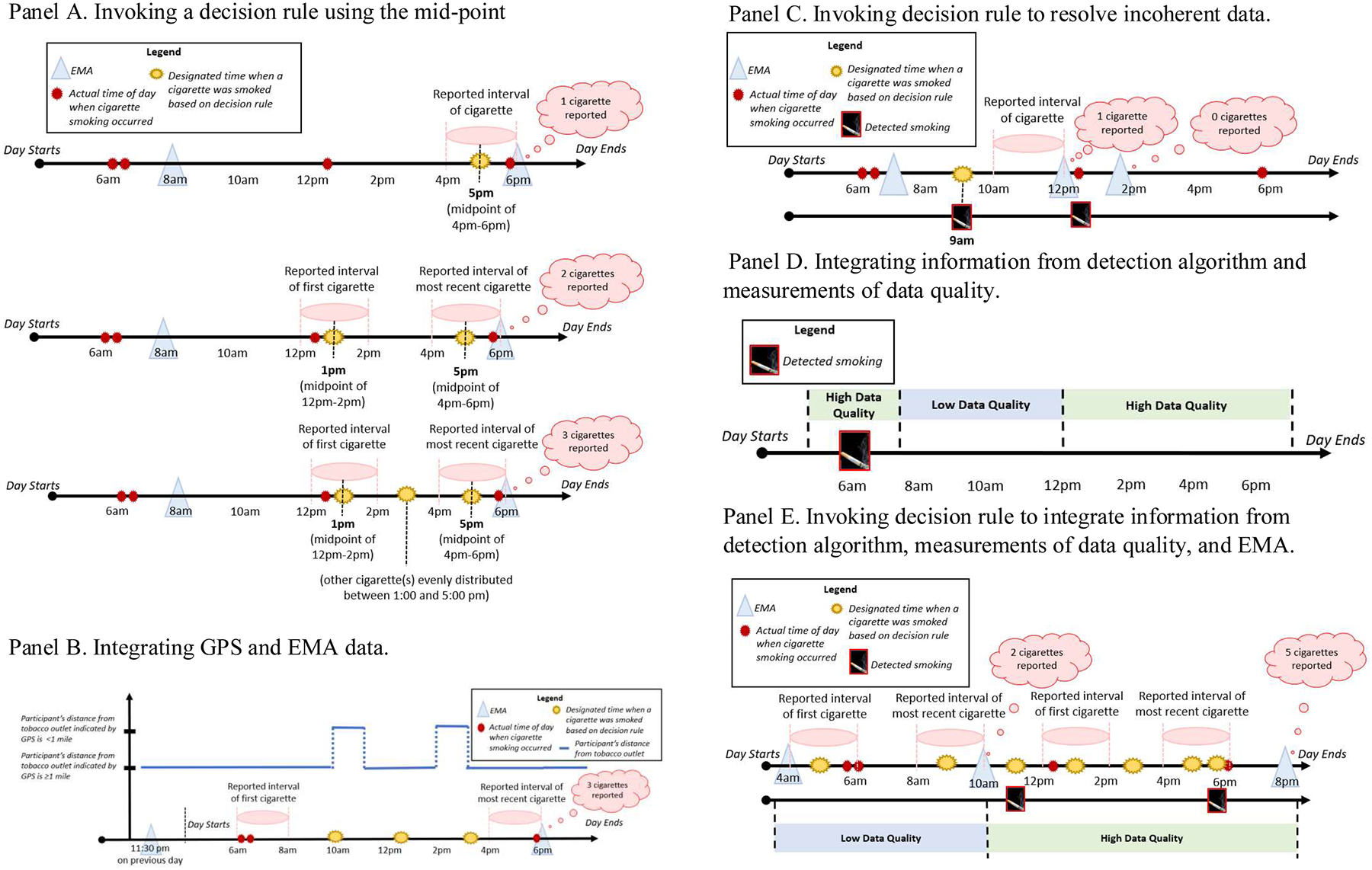
Examples of working to integrate ILD in the presents of coarse, noisy, and incoherent data sources
3.1. Towards ILD Data Integration: Practical Issues to Consider
Studies that collect ILD often involve considerable participant burden. For example, in the Break Free study, participants were prompted to complete up to 40 Random EMAs over 14 days. Over the course of 14 days, they were also asked to wear three pieces of equipment (i.e., wearable devices worn on the left and right wrists and a device worn around the chest) at all times, except when sleeping or showering. Although the use of ILD holds promise in capturing nuanced person-specific changes in stable and dynamic factors (e.g., how risk of lapse might fluctuate over the course of a day for a specific individual), the likelihood of missing data due to participant non-compliance (e.g., non-response to EMA, neglecting to wear the wearable devices) remains a significant and well-documented challenge in mHealth studies (e.g., see Ji et al., 2018; Nelson et al., 2020; Rabbi et al., 2018). However, much less attention has been given to significant challenges that may arise when integrating information on the same individual obtained from multiple data sources. Indeed, issues relating to coarse data, noisy data, and incoherence across data sources, can plague mHealth studies, but there is a dearth of literature on how investigators may deal with these three issues. In what follows, we define coarse, noisy, and incoherent data more precisely and then provide illustrative examples of how these issues can arise in the Break Free study. While we discuss these challenges in the context of the Break Free study, they are relevant to any investigation that focuses on leveraging ILD from multiple data sources to measure how a particular dynamic construct unfolds over time on the same individual.
3.1.1. Measurements of risk of lapse
Table 1 displays the various data sources used to obtain information about cigarette smoking in the Break Free study. Notably, the EMA items concerning cigarette smoking are illustrative of trade-offs faced when designing studies seeking to collect measurements relating to health behaviors that can emerge rapidly and occur at irregularly-spaced bouts, such as cigarette smoking. For example, considerations relating to burden may play a significant role in study design. In the Break Free study, even if participants report to have smoked several cigarettes in an EMA, they are only asked to report when the first and most recent cigarette were smoked in terms of pre-defined intervals of time, relative to the timing of the current EMA (e.g., 0–2 hours ago, 2–4 hours ago, etc.). Although it may appear desirable to ask participants to report the actual time-of-day when they smoked each cigarette, doing so imposes more burden on participants who smoke more heavily than those who to taper their smoking. Further, asking participants to provide information on all occurrences of cigarette smoking is akin to asking participants to engage in self-monitoring (Snyder, 1979). While there is strong evidence showing that self-monitoring can substantially reduce the risk of adverse health outcomes (McBain et al., 2015), self-monitoring every cigarette may not always be feasible in the real-world among individuals undergoing a quit attempt.
To start, suppose we had information about the truth regarding when a participant smoked. Figure 2 panel A shows that they smoked 2 cigarettes after waking (e.g., at approximately 6:05 and 6:15 am), 1 cigarette after lunch (e.g., at approximately 12:35 pm), and 1 cigarette in the afternoon (e.g., at approximately 5:50 pm). Each example presented below is self-contained (with the exception of Example 9, which builds upon concepts described in prior examples).
3.1.2. Coarse Data
Coarse data (Heitjan & Rubin, 1991) are collected when measurements come in the form of a time interval, say [a, b], which contains the time-of-day when the construct of interest (e.g., cigarette smoking) occurred. Example 1 will focus on an EMA at 6:00 pm, during which the participant reported that they smoked 4 cigarettes since the last assessment. Further, they reported to have smoked the first and most recent of these cigarettes 10–12 hours ago and 0–2 hours ago, respectively. Based on their self-reports, the participant smoked 4 cigarettes between 6:00 am – 6:00 pm, but the actual time-of-day when they smoked each individual cigarette is unknown to the investigator (Figure 2 panel B).
3.1.3. Noisy Data
Noisy data can arise when self-reported (e.g., in an EMA) or detected (e.g., via a detection algorithm) values of the construct of interest differ from the actual values. In other words, we say that measurement error has occurred. In the Break Free study, measurement error can occur either when cigarette smoking is not detected by the detection algorithm (i.e., false negatives), or when the detection algorithm erroneously classifies a moment of time as a moment of smoking when smoking did not in fact occur (i.e., false positives). Additionally, measurement error can occur when participants mis-report the time when they smoked. Example 2 (Figure 2 panel C) illustrates this by showing that in an EMA at 6:00 pm, the participant reported to have smoked 4 cigarettes, the first and most recent of the 4 cigarettes 4–6 hours ago and 0–2 hours ago, respectively. In this case, the 4 cigarettes would have been erroneously reported to have occurred between 12:00 pm – 6:00 pm, rather than between 6:00 am and 6:00 pm.
Measurement error may also occur in more subtle ways. Example 3 focuses on two of the four EMAs that were delivered on a particular day. Observe that the EMA items begin with the verbal cue, ‘since the last assessment.’ In this way, the participant is (indirectly) asked to (a) identify which EMA prior to the current EMA they view to be their ‘last assessment’; (b) recall the time of day when their ‘last assessment’ occurred; (c) recall when and how often cigarettes were smoked between their ‘last assessment’ and the current EMA; (d) and finally, report the time when they smoked the first and most recent cigarette (i.e., the first and most recent of the four cigarettes in example 1). In other words, correct reporting in (d) relies on correct antecedent recall of facts surrounding (a) to (c). Suppose that in an EMA at 6:00 pm, the participant reported smoking 4 cigarettes, with the first and most recent occurring 10–12 hours ago and 0–2 hours ago, respectively. If the most recent EMA the participant completed prior to 6:00 pm on the present day was at 11:30 pm yesterday, then there is no measurement error. In other words, the participant correctly reported that (i) they smoked 4 cigarettes between the previous and current EMA; and that (ii) these 4 cigarettes were smoked between 6:00 am – 6:00 pm (Figure 2 panel D).
Now, suppose that the participant misremembered when they completed the previous EMA and thought that it took place at 8:30 am on the current day (rather than at 11:30 pm on the previous day). In this case (Figure 2 panel E), the participant erroneously reported smoking 4 cigarettes between the (misremembered) previous and current EMA, instead of reporting 2 cigarettes only. Further, although the reported time remains correct for 2 of the 4 actual cigarettes smoked (the two cigarettes that were actually smoked between 8:30 am – 6:00 pm), this misremembered interval (i.e., 8:30 am – 6:00 pm) is substantially less coarse than what should have been recalled by the participant had all facts surrounding (a) to (c) been correctly remembered.
3.1.4. Incoherence between Data Sources
Combining information from multiple data sources can enable more accurate inference on a construct of interest (e.g., how risk of lapse might fluctuate over the course of a day) when one data source can be used to supply information that is not present in another, or when measurement error is present in one or more data sources. Example 4 illustrates how information supplied by different data sources can paint an incoherent picture of the construct of interest. Suppose in an EMA at 6:00 pm, the participant reported that they smoked 1 cigarette; further, they reported to have smoked this cigarette 0–2 hours ago (i.e., between 4:00 pm and 6:00 pm). If the most recent EMA the participant completed prior to 6:00 pm on the present day was at 1:00 pm on the same day, it means that no cigarette was reported to have been smoked between 1:00 pm and 4:00 pm. However, the detection algorithm might indicate that smoking occurred at 1:45 pm and 5:50 pm (Figure 2 panel F). In this case, incoherence among data sources is observed. Without making assumptions about the relative validity of each data source or considering additional information, it is unclear how investigators might proceed.
3.2. Towards ILD data integration: Working with ILD, even in the presence of coarse, noisy, and incoherent data sources
The integration of information from multiple data sources can be viewed from within a missing data framework (Lohr & Raghunathan, 2017). ILD from different data sources may supply information about times when smoking occurred that is not present in another data source. One approach to integrating ILD collected from multiple data sources might be to develop multivariate models to impute the value of the desired construct at the time-scale required to answer the pre-specified scientific questions; this is conceptually analogous to integrating cross-sectional data from multiple data sources. However, another approach is through the use of decision rules, which investigators can specify based on practical considerations and existing evidence. Decision rules can express the specific conditions in which a particular value will be designated for the variable of interest, and can be described with IF-THEN statements. A simple example of where a decision rule might be used is in surveys asking individuals to report whether they are currently pregnant; at the same time, the sex of the same individual is available in a national registry (e.g., a census bureau) accessible to researchers conducting the survey. Suppose that individual A reported to be pregnant, but data obtained from a national registry indicates that this individual is a male. In this case, researchers may invoke the rule ‘IF sex = male, THEN pregnant = FALSE; ELSE pregnant=self-reported sex’ when integrating information from the survey and the national registry. In this simple example, the researcher assumes that if data from the survey and national registry are incoherent, then data from the survey is erroneous. In the following examples, we illustrate how decision rules might be used with ILD from studies such as Break Free.
Example 5 focuses on when investigators are using EMAs only to designate the timing of cigarette smoking. Recall that participants reported when they smoked cigarettes in EMAs using the following response options: 0–2 hours, 2–4 hours, 4–6 hours, 6–8 hours, 8–10 hours, 10–12 hours, more than 12 hours1 (Table 1). A Mid-Point Rule may be used to designate the timing of smoking when there is no other available evidence to suggest that smoking may have occurred at a different time. Consider a scenario in which a participant received an EMA at 8:00 am and 6:00 pm on a single day. First, suppose that at 6:00 pm, the participant reported smoking 1 cigarette ‘0-2 hours ago’ (i.e., between 4:00 and 6:00 pm). Investigators may designate the timing of that cigarette to be at the mid-point of the two-hour interval that the participant reported smoking (i.e., 5:00 pm). On the other hand, if the participant reported at 6:00 pm that they smoked 2 cigarettes since the last assessment, and the first was ‘4–6 hours ago’ (i.e., between 12:00 pm – 2:00 pm) and the most recent was ‘0–2 hours ago’ (i.e., between 4:00 pm – 6:00 pm), investigators may designate the time of the first and most recent cigarette to be at the mid-point of the first and most recent two-hour intervals reported (i.e., 1:00 pm and 5:00 pm, respectively). Finally, if the participant reported at 6:00 pm that they smoked more than 2 cigarettes since the last assessment, then the remaining cigarettes (other than the first and most recent) may be evenly distributed between the mid-points of the first and most recent two-hour intervals reported. For example, if the first cigarette was reported to have been smoked ‘4–6 hours ago’ (i.e., between 12:00 – 2:00 pm) and the most recent cigarette was reported to have been smoked ‘0–2 hours ago’ (i.e., between 4:00 – 6:00 pm), the three cigarettes are taken to have occurred at 1:00 pm, 3:00 pm, and 5:00 pm. Our rule designates 3:00 pm as the time when the second of the three cigarettes was smoked because 3:00 pm is at the mid-point of 1:00 pm and 5:00 pm. Figure 3 Panel A displays how the timing of cigarettes would be designated for each of the scenarios above. A decision rule that considers EMA data to designate timing of cigarette smoking is displayed in Table 2, Example 5. However, as we discuss below, a more complex decision rule can be specified by considering available information about the individual’s smoking patterns.
Table 2.
Decision Rules
| Example 5. Decision Rule for EMA data |
| IF number of self-reported cigarettes between the previous and present EMA = 1 |
| THEN cigarette time = the mid-point of the two-hour interval that the participant reported to have smoked. |
| IF number of self-reported cigarettes between the previous and present EMA >1 |
| THEN cigarette times = the mid-point of the two-hour interval reported for the first cigarette and the mid-point of the two-hour interval reported for the most recent cigarette, with any remaining cigarettes reported in EMA distributed evenly between these mid-points. |
| Example 6. Decision Rule for EMA data and GPS |
| IF number of self-reported cigarettes between the previous and present EMA = 1 |
| THEN |
| IF at any time between the previous and present EMA, distance from a tobacco retail outlet between the previous and current EMA< 1 mile, |
| THEN cigarette time = the mid-point starting when the participant was within 1 mile of the outlet and ending when the participant was no longer within 1 mile of the outlet. |
| IF during the entire time between the previous and present EMA, distance from a tobacco retail outlet between the previous and present EMA > 1 mile |
| THEN cigarette time = mid-point of the two-hour interval the participant reported to have smoked. |
| IF number of self-reported cigarettes between the previous and present EMA > 1 |
| THEN |
| IF at any time between the previous and present EMA, distance from a tobacco retail outlet≤ 1 mile, |
| THEN cigarette times = distributed cigarettes evenly starting when the participant was within 1 mile of the outlet and ending when the participant was no longer within 1 mile of the outlet |
| IF during the entire time between the previous and present EMA, distance from a tobacco retail outlet > 1 mile |
| THEN cigarette times = the mid-point of the two-hour interval reportedfor the first cigarette and the mid-point of the two-hour interval reported for the most recent cigarette, with any remaining cigarettes reported in EMA distributed evenly between these mid-points |
| Example 7. Decision Rule for EMA data and Detection Algorithm |
| IF number of cigarettes reported to have been smoked between the previous and present EMA = 0 |
| THEN |
| IF the previous EMA was completed within 4 hours of the current EMA |
| THEN cigarette smoking did not occur between the previous and current EMA. |
| IF the prior EMA was completed more than 4 hours of the current EMA |
| THEN cigarette time = time the detection algorithm detected smoking |
| IF number of cigarettes reported to have been smoked between the previous and present EMA = 1 |
| THEN |
| IF the previous EMA was completed within 4 hours of the current EMA |
| THEN cigarette time = the mid-point of the two-hour interval the participant reported to have smoked. |
| IF the prior EMA was completed more than 4 hours of the current EMA |
| THEN cigarette time = the time the detection algorithm detected smoking |
| IF number of cigarettes reported to have been smoked between the previous and present EMA > 1, |
| THEN |
| IF the prior EMA was completed within 4 hours of the current EMA |
| THEN, cigarette times = the mid-point of the two-hour interval reported for the first cigarette and the mid-point of the two-hour interval reported for the most recent cigarette, with any remaining cigarettes reported in EMA distributed evenly between these mid-points |
| IF the prior EMA was completed more than 4 hours of the current EMA |
| THEN cigarette time(s) = the time the detection algorithm detected smoking. |
| Example 8. Decision Rule for Detection Algorithm and Data Quality |
| IF between two time points (time t and t +1) data quality = high |
| THEN |
| IF the detection algorithm detected cigarette(s) during that time, |
| THEN cigarette time(s) = time the detection algorithm detected smoking; |
| IF the detection algorithm did not detect cigarette smoking during that time, |
| THEN cigarette smoking did not occur. |
| IF between two time points (t and t+ 1) data quality = low |
| THEN it is unknown whether cigarette smoking occurred. |
| Example 9. Decision Rule for EMA data, Detection Algorithm, and Data Quality |
| 1IF between two time points (time t and t + 1) data quality = low |
| THEN, cigarette time(s) = the mid-point of the two-hour interval reported for the first cigarette and the mid-point of the two-hour interval reported for the most recent cigarette, with any remaining cigarettes reported in EMA distributed evenly between these mid-points. |
| IF between two time points (time t and t + 1) data quality = high |
| THEN |
| IF all detected cigarette times lie within the start of the first two-hour interval that the participant reported smoking their first cigarette and the end of the most recent two-hour interval that the participant reported smoking their most recent cigarette |
| THEN cigarette time(s) = time cigarettes are detected, with any remaining cigarettes reported in EMA distributed evenly between the mid-point of the two-hour interval reportedfor the first cigarette and the mid-point of the two-hour interval reportedfor the most recent cigarette. |
| IF any detected smoking times lie either before the start of the first two-hour interval that the participant reported smoking their first cigarette or after the end of the most recent two-hour interval that the participant reported smoking their most recent cigarette |
| THEN |
| IF the prior EMA was completed within 4 hours of the current EMA |
| THEN cigarette time(s) = the mid-point of the two-hour interval reported for the first cigarette and the mid-point of the two-hour interval reported for the most recent cigarette, with any remaining cigarettes reported in EMA distributed evenly between these mid-points, and additionally, any time cigarettes were detected outside these mid-points. |
| IF the prior EMA was completed more than 4 hours of the current EMA |
| THEN cigarette time(s) = time cigarettes are detected, with any remaining cigarettes reported in EMA distributed evenly between the mid-point of the two-hour interval reported for the first cigarette and the mid-point of the two-hour interval reported for the most recent cigarette. |
For simplicity, we only focus on cases when cigarettes reported in EMA > 1. This decision rule can be extended to include scenarios when 0 or 1 cigarette is reported
Example 6 focuses on incorporating additional information about dynamic factors that may influence cigarette smoking. For example, given prior research suggesting that proximity to tobacco retail outlets may serve as a contextual cue to smoke by increasing urge to smoke, information on a participant’s location coinciding with the time period between EMAs may be used to supply information on the time of day when the participant could have smoked (Watkins et al., 2014). Consider a scenario where a participant received an EMA at 6:00 pm and reported that they smoked 3 cigarettes since the previous EMA, which occurred at 11:30 pm on the prior day. They reported that the first cigarette was smoked ‘10–12 hours ago’ (i.e., between 6:00 am – 8:00 am) and that the most recent cigarette was smoked ‘0–2 hours ago’ (i.e., between 4:00 pm – 6:00 pm). A Mid-Point Rule would lead to designating 7:00 am, 12:00 pm, and 5:00 pm as times for each cigarette. However, suppose that that GPS data revealed that the participant was within 1 mile of a tobacco retail outlet between 10:00 am – 11:00 am and 2:00 pm – 3:00 pm. Investigators might leverage time-granular information on proximity to a tobacco retail outlet to supplement information reported in EMA. For example, cigarette times could be evenly distributed between the time frame when the participant was first within close proximity (e.g., within 1 mile of a tobacco outlet) and the time when they were no longer within close proximity to a tobacco retail outlet (e.g., more than 1 mile away from a tobacco outlet). In this example, the designated cigarette times would be 10:00 am, 12:30 pm, and 3:00 pm (see Figure 3, Panel B). We designated 12:30 pm as the time when the second of the three cigarettes were smoked because 12:30 pm is at the mid-point of 10:00 am and 3:00 pm. A decision rule that could be used to consider EMA and GPS data to designate timing of cigarettes smoked is displayed in Table 2, Example 6.
Example 7 focuses on a scenario where EMA and detection algorithm data are available. Suppose that a participant completed 3 EMAs in one day at 7:00 am, 12:00 pm, and 1:45 pm. Suppose that in the EMA at 1:45 pm, the participant reported smoking 0 cigarettes since the last assessment, yet the detection algorithm indicated that smoking occurred at 12:30 pm. Further, suppose that in the EMA at 12:00 pm, the participant reported smoking 1 cigarette ‘0–2 hours ago’ (i.e., between 10:00 am and 12:00 pm), yet the detection algorithm indicated that a cigarette was smoked at 9:00 am. In this scenario, there is incoherence between the detection algorithm and the EMA. Without additional information, it remains unclear how investigators might devise a decision rule to reconcile incoherent information across data sources. One approach to reconcile incoherent information is to consider existing knowledge about the precision of each data source. For example, empirical evidence suggests that the detection algorithm attains a minimal false positive rate of cigarette smoking of 1/6 per day (Nakajima et al., 2020; Saleheen et al., 2015). On the other hand, prior evidence (Shiffman et al., 1997) suggests increased imprecision in self-reported information when individuals are asked to recall occurrences of smoking that occurred more distally compared to more proximally. As such, investigators might weigh the validity of information on cigarette smoking obtained via the detection algorithm versus self-reported in EMA depending on the time between EMAs. In Example 7, the participant is being asked to recall smoking between 7:00 am and 12:00 pm (a 5-hour time frame) and between 12:00 pm and 1:45 pm (a 1 hour and 45-minute time frame). One possibility is that investigators might weigh the validity of the detection algorithm as greater than self-report when there was a 5-hour time frame between EMAs, and thus designate cigarette time to be 9:00 am only (Figure 3 panel C). A decision rule that considers EMA data and detection algorithm data to designate timing of cigarettes smoked is displayed in Table 2, Example 7.
Example 8 focuses on a scenario when information from the detection algorithm and measurements of data quality of data collected from sensors are available. Integration of these data may increase our confidence in the information supplied by the detection algorithm. Suppose the detection algorithm detected that a cigarette was smoked at 6:00 am only. Suppose also that data quality was high between 5:00am and 7:45am, that data quality was low between 7:46 am and 12:00 pm, and that data quality was high between 12:01 pm and 6:30 pm (note that when data quality is low, the detection algorithm would not produce a label output, as if the detection algorithm was ‘paused’). Investigators may then be more confident that a cigarette was likely to have been smoked at 6:00 am, and that no cigarettes were likely to have been smoked between 5:00 am to 5:59 am, between 6:01 am to 7:45 am, or between 12:01 pm and 6:30 pm (i.e., other times with high data quality but no cigarettes were detected). Further, without any additional information (e.g., from EMA) investigators cannot ascertain whether or not any smoking occurred when data quality was low (i.e., between 7:46 am – 12 : 00 pm; Figure 3, panel D). As shown in subsequent examples, additional available data sources (e.g., from EMA) could be integrated with data quality and detection algorithm data to improve our confidence in the designated smoking times. A decision rule that considers data quality and detection algorithm data is displayed in Table 2, Example 8
Example 9 builds upon prior concepts and considers a scenario when an investigator might wish to integrate three or more data sources (e.g., EMA, detection algorithm, and data quality). Suppose a participant answered EMAs at 4:00 am, 10:00 am, and 8:00 pm; further, they reported smoking 2 and 5 cigarettes ‘since the last assessment’ via the 10:00 am and 8:00 pm EMAs, respectively. Further, suppose that data quality was low between 4:00 am and 10:00 am, but high between 10:01 am and 8:00 pm. A decision rule that considers EMA data, detection algorithm data, and data quality is displayed in Table 2, Example 9. Figure 3, Panel E displays the result of applying this rule to the scenario we described in the current example (Example 9). The rule builds on the line of reasoning in Example 8 by solely relying on EMA data when data quality is low. On the other hand, this rule also builds on the line of reasoning in prior examples during times when data quality is high, by (1) considering how investigators may distribute cigarettes differently depending on the time between EMAs (e.g., greater or less than 4 hours); and additionally (2) considering whether there were any detected smoking times before the mid-point of the two-hour interval reported for the first cigarette or after the mid-point of the two-hour interval for the most recent cigarette. Importantly, Example 9 illustrates that rather than removing measurements when there is conflicting information from any given source, integrating information from multiple data sources may improve the precision of the measurement of a construct of interest (in this case, cigarette smoking). This is critical for understanding dynamic mechanisms of change and under what conditions an individual may be vulnerable to smoking and require intervention.
5. Discussion
mHealth studies increasingly utilize multiple types of mobile and sensing technology to collect rich and granular ILD from the same individual over time. This data is vital for gaining a better understanding of how behavior change processes as they unfold in real-time, real-world settings, and plays a key role in the development of JITAIs. However, resource constraints (e.g., even state-of-the-art sensors can yield noisy data) and practical hurdles (e.g., participant burden) present challenges for using study designs that leverage the use of multiple data sources to measure constructs of interest. As our examples show, these considerations go beyond the important issue of missing data (e.g., due to participant non-compliance), to the equally important issues of coarseness, noise, and incoherence among data sources. In this way, the case study and examples herein fill a critical gap in the literature by illustrating how challenges can arise in real studies, and by offering decision rules as a practical starting point that investigators may consider when integrating multiple sources of ILD from mHealth studies. Filling this gap is a foundational first step towards measuring constructs at the level of granularity required to inform dynamic theories of behavior change and to construct interventions that adapt to an individual’s changing needs and context (Collins, 2006; Collins & Graham, 2002; Riley et al., 2015). Indeed, “a major gap that hinders the development of efficacious JITAIs lies in the static nature of existing behavioral and intervention theories and the lack of temporal specificity of theories that are more dynamic in nature” (Nahum-Shani et al., 2018).
The case study described in this manuscript illustrates the use of decision rules to combine information on the same individual obtained from multiple data sources. However, the choice of a final rule requires tapping into expertise from a broad range of disciplines beyond the social, behavioral, and health sciences (e.g., data science, computer science) and gathering consensus among such diverse disciplines. While this process can be challenging and time consuming, it has the potential to improve the reliability and validity of the constructs of interest, particular when data sources complement each other (i.e., when one data source may supply information not present in another source). To improve scientific rigor, investigators may consider using sensitivity testing to explore the robustness of conclusions drawn from the pre-specified data analytic plan, had another decision rule been invoked instead. For instance, investigators could imagine invoking alternative decision rules that are incrementally more “extreme” (or less “extreme”) in one direction up to a point when the conclusion of the initial data analysis is overturned, which is akin to the delta adjustment method in missing data literature (Mallinckrodt et al., 2013). As a concrete sketch, in Example 5, investigators may opt to conduct sensitivity testing to test the robustness of results across designated smoking times using a decision rule implying that (i) cigarettes smoked are clustered around one particular point in time (i.e., one large cluster only); (ii) some cigarettes smoked are clustered around an earlier time while the remaining cigarettes clustered around a later time (i.e., two moderately sized clusters); (iii) cigarettes smoked were evenly distributed (i.e., many small clusters). Each of these could be viewed as alternative but plausible scenarios wherein the robustness of initial results could be tested. The specific scenario(s) in which results of sensitivity testing disagree with the results of the main analysis could prompt further inquiry and motivate future research. To promote rigor and transparency, developing and disseminating documentation to capture these decision rules and their underlying assumptions should also be an integral part of the scientific process (Nahum-Shani et al., 2021; Yap, 2019). Indeed, “good documentation is paramount to effective data use” and enables reproducibility within the scientific community (Vardigan et al., 2008).
This manuscript focused on how investigators can leverage ILD from existing studies, particularly within the mHealth setting. However, the principles illustrated can be applied to the design of new ILD studies, such that they have applications for any study investigating dynamic mechanisms of change, especially those utilizing a digital data collection protocol involving multiple sources of information. Additionally, the examples in this case study, which illustrate issues relating to noise, coarseness, and incoherence between data sources in ILD studies, can be used to guide the development of study designs and procedures to minimize these challenges. For example, investigators may design studies that make it possible for participants to corroborate information collected via sensors (see (Toscos et al., 2020). Even though these features introduce new challenges beyond those presented here, investigators may still build upon principles presented herein to inform the design of new studies.
Finally, when investigators wish to integrate a larger number of data sources, devising decision rules to account for every possible challenge relating to coarseness, noise, and incoherence among data sources may be infeasible. Investigators may need to develop multivariate models to impute the value of the desired construct at the time-scale required to answer their pre-specified scientific questions; as noted earlier, this approach is conceptually analogous to existing work on integrating cross-sectional data from multiple data sources (He et al., 2014; Lohr & Raghunathan, 2017; Schenker & Raghunathan, 2007; Schenker et al., 2010; Schifeling et al., 2019). Extending these approaches to accommodate ILD is an important direction for future research.
Funding.
Research reported in this publication was supported by awards from the National Institute on Drug Abuse (P50DA054039; R01DA039901; National Institute on Minority Health and Health Disparities (R01MD010362), National Cancer Institute (P30CA042014; K99CA252604-01A1; U01CA220437), National Center for Advancing Translational Sciences of the National Institutes of Health (UL1TR002538) and the Huntsman Cancer Foundation
Footnotes
Ethics approval. All Break Free study procedures were approved by the appropriate Institutional Review Board.
Conflicts of interest/competing interests. The authors have no conflicts of interest
In practice, investigators might consider what thresholds to designate the earliest possible cigarette time when “more than 12 hours” is selected by the participant (e.g., a longer interval such as ‘12-24 hours,’ a shorter interval such as “12–14 hours,” or an interval bounded by the most recent EMA prior to the current EMA).
References
- Ahluwalia IB, Smith T, Arrazola RA, Palipudi KM, de Quevedo IG, Prasad VM, … Armour BS (2018). Current Tobacco Smoking, Quit Attempts, and Knowledge About Smoking Risks Among Persons Aged >= 15 Years - Global Adult Tobacco Survey, 28 Countries, 2008–2016. Morbidity and Mortality Weekly Report, 67(38), 1072–1076. 10.15585/mmwr.mm6738a7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babb S, Malarcher A, Schauer G, Asman K, & Jamal A (2017). Quitting Smoking Among Adults - United States, 2000–2015. Mmwr-Morbidity and Mortality Weekly Report, 65(52), 1457–1464. [DOI] [PubMed] [Google Scholar]
- Bolger N, & J.P. L (2013). Intensive Longitudinal Methods. An Introduction to Diary and Experience Sampling Research. The Guilford Press. [Google Scholar]
- Collins LM (2006). Analysis of longitudinal data: the integration of theoretical model, temporal design, and statistical model. Annu Rev Psychol, 57, 505–528. 10.1146/annurev.psych.57.102904.190146 [DOI] [PubMed] [Google Scholar]
- Collins LM, & Graham JW (2002). The effect of the timing and spacing of observations in longitudinal studies of tobacco and other drug use: temporal design considerations. Drug Alcohol Depend, 68 Suppl 1, S85–96. 10.1016/s0376-8716(02)00217-x [DOI] [PubMed] [Google Scholar]
- Creamer MR, Wang TW, Babb S, Cullen KA, Day H, Willis G, … Neff L (2019). Tobacco Product Use and Cessation Indicators Among Adults - United States, 2018. Mmwr-Morbidity and Mortality Weekly Report, 68(45), 1013–1019. 10.15585/mmwr.mm6845a2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drope J, Liber AC, Cahn Z, Stoklosa M, Kennedy R, Douglas CE, & Henson R (2018). Who’s Still Smoking? Disparities in Adult Cigarette Smoking Prevalence in the United States [Article]. Ca-a Cancer Journal for Clinicians, 68(2), 106–115. 10.3322/caac.21444 [DOI] [PubMed] [Google Scholar]
- Dube SR, Asman K, Malarcher A, & Carabollo R (2009). Cigarette Smoking Among Adults and Trends in Smoking Cessation-United States, 2008 (Reprinted from MMWR, vol 58, pg 1227–1232, 2009). Jama-Journal of the American Medical Association, 302(24), 2651–2654. [Google Scholar]
- Ertin E, Stohs N, Kumar S, Raij A, Al’Absi M, & Shah S (2011). AutoSense: Unobtrusively wearable sensor suite for inferring the onset, causality, and consequences of stress in the field. ACM Conference on Embedded Networked Sensor Systems, [Google Scholar]
- Garvey AJ, Bliss RE, Hitchcock JL, Heinold JW, & Rosner B (1992). Predictors of smoking relapse among self-quitters: a report from the Normative Aging Study. Addict Behav, 17(4), 367–377. 10.1016/0306-4603(92)90042-t [DOI] [PubMed] [Google Scholar]
- He Y, Landrum MB, & Zaslavsky AM (2014). Combining information from two data sources with misreporting and incompleteness to assess hospice-use among cancer patients: a multiple imputation approach. Stat Med, 33(21), 3710–3724. 10.1002/sim.6173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitjan DF, & Rubin DB (1991). IGNORABILITY AND COARSE DATA. Annals of Statistics, 19(4), 2244–2253. 10.1214/aos/1176348396 [DOI] [Google Scholar]
- Hughes JR, Keely J, & Naud S (2004). Shape of the relapse curve and long-term abstinence among untreated smokers [Review]. Addiction, 99(1), 29–38. 10.1111/j.1360-0443.2004.00540.x [DOI] [PubMed] [Google Scholar]
- Ji L, Chow SM, Schermerhorn AC, Jacobson NC, & Cummings EM (2018). Handling Missing Data in the Modeling of Intensive Longitudinal Data. Struct Equ Modeling, 25(5), 715–736. 10.1080/10705511.2017.1417046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kenford SL, Fiore MC, Jorenby DE, Smith SS, Wetter D, & Baker TB (1994). Predicting smoking cessation. Who will quit with and without the nicotine patch. Jama, 271(8), 589–594. 10.1001/jama.271.8.589 [DOI] [PubMed] [Google Scholar]
- Klasnja P, Hekler EB, Shiffman S, Boruvka A, Almirall D, Tewari A, & Murphy SA (2016). Micro-Randomized Trials: An experimental design for developing Just-in-Time Adaptive Interventions. Health Psychology, 34(0), 1220–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klasnja P, Smith S, Seewald NJ, Lee A, Hall K, Luers B, … Murphy SA (2019). Efficacy of Contextually Tailored Suggestions for Physical Activity: A Micro-randomized Optimization Trial of HeartSteps. Ann Behav Med, 53(6), 573–582. 10.1093/abm/kay067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleiman E, Millner AJ, Joyce VW, Nash CC, Buonopane RJ, & Nock MK (2019). Using Wearable Physiological Monitors With Suicidal Adolescent Inpatients: Feasibility and Acceptability Study. JMIR Mhealth Uhealth, 0(0), e0. 10.2196/13725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulak JA, Cornelius ME, Fong GT, & Giovino GA (2016). Differences in Quit Attempts and Cigarette Smoking Abstinence Between Whites and African Americans in the United States: Literature Review and Results From the International Tobacco Control US Survey. Nicotine Tob Res, 18 Suppl 1(Suppl 1), S79–87. 10.1093/ntr/ntv228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohr SL, & Raghunathan TE (2017). Combining Survey Data with Other Data Sources. Statistical Science, 32(2), 293–312. 10.1214/16-sts584 [DOI] [Google Scholar]
- Mallinckrodt C, Roger J, Chuang-Stein C, Molenberghs G, Lane PW, O’kelly M, … Thijs H (2013). Missing data: Turning guidance into action. Statistics in Biopharmaceutical Research, 5(4). [Google Scholar]
- McBain H, Shipley M, & Newman S (2015). The impact of self-monitoring in chronic illness on healthcare utilisation: a systematic review of reviews. BMC Health Serv Res, 15, 565. 10.1186/s12913-015-1221-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mokdad AH, Marks JS, Stroup DF, & Gerberding JL (2004). Actual causes of death in the United States, 2000 [Article]. Jama-Journal of the American Medical Association, 291(10), 1238–1245. 10.1001/jama.291.10.1238 [DOI] [PubMed] [Google Scholar]
- Nahum-Shani I, Rabbi M, Yap J, Philyaw-Kotov ML, Klasnja P, Bonar EE, … Walton MA (2021). Translating strategies for promoting engagement in mobile health: A proof-of-concept microrandomized trial. Health Psychol. 10.1037/hea0001101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahum-Shani I, Smith SN, Spring BJ, Collins LM, Witkiewitz K, Tewari A, & Murphy SA (2018). Just-in-Time Adaptive Interventions (JITAIs) in Mobile Health: Key Components and Design Principles for Ongoing Health Behavior Support [Article]. Annals of Behavioral Medicine, 52(6), 446–462. 10.1007/s12160-016-9830-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahum-Shani I, Wetter DW, & Murphy SA (in press). Adapting just-in-time interventions to vulnerability and receptivity: Conceptual and methodological considerations. In Jacobson LMN, & Kowatsch T (Ed.), Digital Therapeutics for Mental Health and Addiction: State of the Science and Vision for the Future. Elsevier. [Google Scholar]
- Nakajima M, Lemieux AM, Fiecas M, Chatterjee S, Sarker H, Saleheen N, … al ‘Absi M (2020). Using novel mobile sensors to assess stress and smoking lapse. International Journal of Psychophysiology, 158, 411–418. 10.1016/j.ijpsycho.2020.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson BW, Low CA, Jacobson N, Areán P, Torous J, & Allen NB (2020). Guidelines for wrist-worn consumer wearable assessment of heart rate in biobehavioral research. NPJ Digit Med, 3, 90. 10.1038/s41746-020-0297-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pacek LR, McClernon FJ, & Bosworth HB (2018). Adherence to Pharmacological Smoking Cessation Interventions: A Literature Review and Synthesis of Correlates and Barriers. Nicotine Tob Res, 20(10), 1163–1172. 10.1093/ntr/ntx210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piper ME, Bullen C, Krishnan-Sarin S, Rigotti NA, Steinberg ML, Streck JM, & Joseph AM (2019). Defining and measuring abstinence in clinical trials of smoking cessation interventions: An updated review. Nicotine & Tobacco Research, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabbi M, Philyaw Kotov M, Cunningham R, Bonar EE, Nahum-Shani I, Klasnja P, … Murphy S (2018). Toward Increasing Engagement in Substance Use Data Collection: Development of the Substance Abuse Research Assistant App and Protocol for a Microrandomized Trial Using Adolescents and Emerging Adults. JMIR Res Protoc, 7(7), e166. 10.2196/resprot.9850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabbi M, Philyaw-Kotov M, Lee J, Mansour A, Dent L, Wang X, … Murphy S (2017). SARA: A Mobile App to Engage Users in Health Data Collection. Proc ACM Int Conf Ubiquitous Comput, 2017, 781–789. 10.1145/3123024.3125611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhee SY, Dickerson J, & Xu D (2006). Bioinformatics and its applications in plant biology. Annu Rev Plant Biol, 57, 335–360. 10.1146/annurev.arplant.56.032604.144103 [DOI] [PubMed] [Google Scholar]
- Riley WT, Serrano KJ, Nilsen W, & Atienza AA (2015). Mobile and Wireless Technologies in Health Behavior and the Potential for Intensively Adaptive Interventions. Curr Opin Psychol, 5, 67–71. 10.1016/j.copsyc.2015.03.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saleheen N, Ali AA, Hossain SM, Sarker H, Chatterjee S, Marlin B, … Kumar S (2015). puffMarker: A Multi-Sensor Approach for Pinpointing the Timing of First Lapse in Smoking Cessation. Proc ACM Int Conf Ubiquitous Comput, 2015, 999–1010. [PMC free article] [PubMed] [Google Scholar]
- Samet JM (2013). Tobacco Smoking The Leading Cause of Preventable Disease Worldwide. Thoracic Surgery Clinics, 23(2), 103–+. 10.1016/j.thorsurg.2013.01.009 [DOI] [PubMed] [Google Scholar]
- Schenker N, & Raghunathan TE (2007). Combining information from multiple surveys to enhance estimation of measures of health. Stat Med, 26(8), 1802–1811. 10.1002/sim.2801 [DOI] [PubMed] [Google Scholar]
- Schenker N, Raghunathan TE, & Bondarenko I (2010). Improving on analyses of self-reported data in a large-scale health survey by using information from an examination-based survey. Stat Med, 29(5), 533–545. 10.1002/sim.3809 [DOI] [PubMed] [Google Scholar]
- Schifeling T, Reiter JP, & Deyoreo M (2019). DATA FUSION FOR CORRECTING MEASUREMENT ERRORS. Journal of Survey Statistics and Methodology, 7(2), 175–200. 10.1093/jssam/smy010 [DOI] [Google Scholar]
- Shiffman S, Hufford M, Hickcox M, Paty JA, Gnys M, & Kassel JD (1997). Remember that? A comparison of real-time versus retrospective recall of smoking lapses. J Consult Clin Psychol, 65(2), 292–300. 10.1037/0022-006x.65.2.292.a [DOI] [PubMed] [Google Scholar]
- Snyder M (1979). Self-monitoring processes. In Advances in experimental and social psychology (Vol. 12, pp. 85–128). Academic Press. [Google Scholar]
- Stahre M, Okuyemi KS, Joseph AM, & Fu SS (2010). Racial/ethnic differences in menthol cigarette smoking, population quit ratios and utilization of evidence-based tobacco cessation treatments. Addiction, 105 Suppl 1, 75–83. 10.1111/j.1360-0443.2010.03200.x [DOI] [PubMed] [Google Scholar]
- Toscos T, Drouin M, Pater JA, Flanagan M, Wagner S, Coupe A, … Mirro MJ (2020). Medication adherence for atrial fibrillation patients: triangulating measures from a smart pill bottle, e-prescribing software, and patient communication through the electronic health record. JAMIA Open, 3(2), 233–242. 10.1093/jamiaopen/ooaa007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vardigan M, Heus P, & Thomas W (2008). Data documentation initiative: Toward a standard for the social sciences. International Journal of Digital Curation, 3(1). [Google Scholar]
- Watkins KL, Regan SD, Nguyen N, Businelle MS, Kendzor DE, Lam C, … Reitzel LR (2014). Advancing Cessation Research by Integrating EMA and Geospatial Methodologies: Associations Between Tobacco Retail Outlets and Real-time Smoking Urges During a Quit Attempt [Article]. Nicotine & Tobacco Research, 16, S93–S101. 10.1093/ntr/ntt135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yap J (2019). jamieyap/SARA v1.0.0
- Zhou XL, Nonnemaker J, Sherrill B, Gilsenan AW, Coste F, & West R (2009). Attempts to quit smoking and relapse: Factors associated with success or failure from the ATTEMPT cohort study. Addictive Behaviors, 34(4), 365–373. 10.1016/j.addbeh.2008.11.013 [DOI] [PubMed] [Google Scholar]


