mtPGS: Leverage multiple correlated traits for accurate polygenic score construction

Summary

Accurate polygenic scores (PGSs) facilitate the genetic prediction of complex traits and aid in the development of personalized medicine. Here, we develop a statistical method called multi-trait assisted PGS (mtPGS), which can construct accurate PGSs for a target trait of interest by leveraging multiple traits relevant to the target trait. Specifically, mtPGS borrows SNP effect size similarity information between the target trait and its relevant traits to improve the effect size estimation on the target trait, thus achieving accurate PGSs. In the process, mtPGS flexibly models the shared genetic architecture between the target and the relevant traits to achieve robust performance, while explicitly accounting for the environmental covariance among them to accommodate different study designs with various sample overlap patterns. In addition, mtPGS uses only summary statistics as input and relies on a deterministic algorithm with several algebraic techniques for scalable computation. We evaluate the performance of mtPGS through comprehensive simulations and applications to 25 traits in the UK Biobank, where in the real data mtPGS achieves an average of 0.90%–52.91% accuracy gain compared to the state-of-the-art PGS methods. Overall, mtPGS represents an accurate, fast, and robust solution for PGS construction in biobank-scale datasets.

Xu et al. propose a statistical method called multi-trait assisted polygenic scores (mtPGS) that constructs accurate polygenic scores for a complex trait of interest by leveraging multiple correlated traits. mtPGS demonstrates enhanced predictive performance in simulations and real applications in the UK Biobank dataset.

Introduction

The polygenic score (PGS) of a complex trait captures an individual’s genetic predisposition for the trait and represents one of the earliest, most stable, and accurately measurable factors underlying the trait.^1,2 A PGS is often calculated as a weighted summation of genotypes across single-nucleotide polymorphisms (SNPs),^3,4,5,6,7 where the SNP effect size estimates serve as the weights. PGSs are commonly referred to as polygenic risk scores (PRSs) when the trait of interest is disease status.^8,9,10 With the abundant availability of genotype and phenotype information collected from large-scale genome-wide association studies (GWASs),^3,4,5 PGSs are becoming increasingly used for genetic prediction of complex traits/diseases,^{11,12,13,14,15,16,17,18,19,20,21,22,23,24,25} disease risk stratification,^3,10,26 pleiotropic association detection,^27,28,29 transcriptome-wide association studies (TWASs),^30,31,32 and Mendelian randomization analysis.^33,34 Accurate construction of PGSs can facilitate disease prevention, improve early intervention, and support the development of personalized treatment.

Many statistical methods have been developed to construct PGSs.^35,36 Different PGS methods often make distinct modeling assumptions on the genetic effect size distribution, use either individual-level GWAS data or summary statistics, and sometimes incorporate external information such as SNP functional annotations.^12,19,36 While most existing PGS methods are univariate in nature and model directly the target complex trait of interest, several multivariate PGS methods have been recently developed to leverage traits that are correlated or relevant to the target trait to facilitate its prediction. Leveraging relevant traits through modeling their genetic correlation with the target trait can facilitate SNP effect size estimation for the target trait and thus improve prediction accuracy. Example multivariate methods that use GWAS individual-level data include the bivariate ridge regression (BVR),³⁷ the multi-trait genomic best linear unbiased prediction (MTGBLUP),³⁸ and the cross-trait penalized regression (CTPR).³⁹ Example multivariate methods that use GWAS summary statistics include weighted multi-trait summary statistic best linear unbiased prediction method (wMT-SBLUP),⁴⁰ multi-trait analysis of GWAS (MTAG),⁴¹ and cross-population and cross-phenotype (XPXP).⁴²

Despite the effectiveness of multivariate PGS modeling, the existing multivariate PGS methods have two important limitations. First, almost all multivariate methods make relatively simple modeling assumptions on the shared genetic architecture between the target trait and the relevant traits. In particular, most methods use a bivariate or multivariate linear mixed model (mvLMM),^43,44 which assumes that all SNPs have non-zero effects and that their effect sizes on the target and relevant traits follow a bivariate or multivariate normal distribution characterized by genetic correlations. Such modeling assumption is not flexible, as a single multivariate normal distribution often cannot effectively capture the SNP effect size distribution across traits and may lead to over-shrinkage of large-effect SNPs and subsequently impede prediction performance. Indeed, recent studies comparing univariate PGS methods found that flexible modeling of the SNP effect size distribution is key to ensure accurate PGSs across a range of traits with distinct genetic architectures.^{12,15,19,45,46} Univariate methods that make flexible modeling assumptions on the genetic architectures, such as DPR,¹² PRS-CS,¹⁵ and DBSLMM,⁴⁵ all outperform standard polygenic models such as best linear unbiased predictor (BLUP) that assumes normality on the SNP effect size distribution. Therefore, it is important to extend the existing multivariate PGS methods toward flexible modeling of the shared genetic architecture to improve PGS accuracy. Such modeling extension, and its application to large-scale biobank datasets such as UK Biobank (UKB),⁴⁷ requires the development of new computationally efficient algorithms. Second, most existing multivariate PGS methods have been primarily focused on modeling the genetic correlation among traits to borrow the SNP effect size similarity information from the relevant traits to improve the PGS for the target trait. However, environmental correlation due to sample overlap is another crucial and indispensable component of the phenotypic correlation.⁴⁴ Many large-scale GWASs, such as UKB, often collect thousands of phenotypes on the same set of individuals.^47,48,49,50 These phenotypes may be correlated with each other due to the shared common environmental exposures. Failing to account for such environmental correlation may lead to reduced PGS performance, especially in datasets where a large proportion of samples have multiple phenotypic measurements. Indeed, a recent study⁴² shows that accounting for the environmental correlation in addition to modeling pleiotropy help improve PGS accuracy.

Here, we present an accurate and scalable multivariate PGS method, which we refer to as the multi-trait assisted PGS (mtPGS), that addresses the above two limitations to effectively leverage multiple correlated traits to predict the target trait of interest. mtPGS makes a flexible modeling assumption on the SNP effect size distribution underneath the shared genetic architecture and explicitly incorporates environmental correlation to aid the prediction of the target trait. mtPGS also takes advantage of a deterministic search algorithm with several algebraic techniques to achieve scalable computation. We illustrate the benefits of mtPGS through comprehensive simulations and applications to 25 traits in the UKB.

Subjects and methods

Method overview

Here, we present an overview of mtPGS, with its technical details provided in the supplemental methods. Our goal is to leverage multiple correlated traits and flexibly model their shared genetic and environmental architecture for accurate genetic prediction on a target trait of interest. To do so, we denote y₀ as an n₀ vector of the target trait that is measured on n₀ samples. We consider M relevant traits and denote y_m as an n_m vector of the m^th trait measured on n_m samples ($m\in \left\{1,\cdots ,M\right\}$). These relevant traits may be obtained in the same study of the target trait or from a separate study with either overlapped or non-overlapped samples. Detailed selection strategy for the relevant traits is described in a later section. We assume that all individuals have their genotypes measured on a common set of p SNPs. We examine the relevant traits one at a time. For each relevant trait in turn, we leverage its shared genetic and/or environmental architecture with the target trait to construct a PGS for the target trait. Afterward, we combine the different PGSs for the target trait constructed based on the different relevant traits into a single PGS as the final PGS. We describe these steps in detail in the following sections.

Bivariate modeling of the target trait and one relevant trait at a time

First, we consider modeling the target trait and one relevant trait jointly through a bivariate modeling framework. Specifically, for the particular trait pair of y₀ and y_m, we separate the individuals into three subgroups, including one subgroup of overlapped individuals and two subgroups of non-overlapped individuals. We denote $n_{ms}\in \left[0,\mathit{min}\left(n_0,n_m\right)\right]$ as the number of overlapping individuals with both y₀ and y_m measured; $n_0^{\ast }=n_0-n_{ms}$ as the number of non-overlapping individuals who were measured only for the target trait y₀; and $n_m^{\ast }=n_m-n_{ms}$ as the number of non-overlapping individuals who were measured only for the relevant trait y_m. For the n_ms overlapped individuals, we denote ${\tilde{\mathit{y}}}_0$, ${\tilde{\mathit{y}}}_m$ as the phenotype vectors of the target trait and the relevant trait, respectively; $\tilde{\mathit{X}}$ as the n_ms by p genotype matrix; and ${\tilde{\mathit{\epsilon }}}_0$, ${\tilde{\mathit{\epsilon }}}_m$ as the vectors of residual errors. For the non-overlapping individuals, we denote ${\mathit{y}}_0^{\ast }$ and ${\mathit{y}}_m^{\ast }$ as the vectors of phenotypic measurements for the $n_0^{\ast }$ and $n_m^{\ast }$ individuals, respectively; ${\mathit{X}}_0^{\ast }$ and ${\mathit{X}}_m^{\ast }$ as the corresponding $n_0^{\ast }$ by p and $n_m^{\ast }$ by p genotype matrices; and ${\mathit{\epsilon }}_0^{\ast }$ and ${\mathit{\epsilon }}_m^{\ast }$ as the corresponding $n_0^{\ast }$ and $n_m^{\ast }$ vectors of residual errors. Within each of the three subgroups of individuals, we center and standardize each phenotype vector and each column of the genotype matrices to have zero mean and unit standard deviation. With these notations, we consider the following three regression models:

$$\begin{array}{c}{\mathit{y}}_0^{\ast }={\mathit{X}}_0^{\ast }{\mathit{\beta }}_0+{\mathit{\epsilon }}_0^{\ast }\text{,}\end{array}$$ (Equation 1)

$$\begin{array}{c}{\mathit{y}}_m^{\ast }={\mathit{X}}_m^{\ast }{\mathit{\beta }}_m+{\mathit{\epsilon }}_m^{\ast }\text{,}\end{array}$$ (Equation 2)

$$\begin{array}{c}\left[{\tilde{\mathit{y}}}_0,{\tilde{\mathit{y}}}_m\right]=\tilde{\mathit{X}}\left[{\mathit{\beta }}_0,{\mathit{\beta }}_m\right]+\left[{\tilde{\mathit{\epsilon }}}_0,{\tilde{\mathit{\epsilon }}}_m\right]\text{,}\end{array}$$ (Equation 3)

where ${\mathit{\beta }}_0$ and ${\mathit{\beta }}_m$ are p-vectors of genotype effect sizes for the two phenotypes, respectively. In the above model, we accommodate both overlapped and non-overlapped individuals through three separate equations to account for distinct sample overlap patterns. The three equations are interconnected by a common set of genetic effect sizes ${\mathit{\beta }}_0$ and ${\mathit{\beta }}_m$, whose similarity characterizes the shared genetic architecture between the traits. To flexibly model the shared genetic architecture between the two traits, we extend the univariate modeling framework of DBSLMM⁴⁵ toward bivariate modeling and assume that the effect sizes of the j^th SNP on the two traits follow a mixture of four bivariate normal distributions,

$$\left(\begin{array}{c}{\beta }_{0j}\\ {\beta }_{mj}\end{array}\right)\sim {\pi }_{11}BN\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{0l}^2& {\rho }_g{\sigma }_{0l}{\sigma }_{ml}\\ {\rho }_g{\sigma }_{0l}{\sigma }_{ml}& {\sigma }_{ml}^2\end{array}\right)\right)+{\pi }_{10}BN\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{0l}^2& {\rho }_g{\sigma }_{0l}{\sigma }_{ms}\\ {\rho }_g{\sigma }_{0l}{\sigma }_{ms}& {\sigma }_{ms}^2\end{array}\right)\right)+{\pi }_{01}BN\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{0s}^2& {\rho }_g{\sigma }_{0s}{\sigma }_{ml}\\ {\rho }_g{\sigma }_{0s}{\sigma }_{ml}& {\sigma }_{ml}^2\end{array}\right)\right)+{\pi }_{00}BN\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{0s}^2& {\rho }_g{\sigma }_{0s}{\sigma }_{ms}\\ {\rho }_g{\sigma }_{0s}{\sigma }_{ms}& {\sigma }_{ms}^2\end{array}\right)\right)\text{,}$$ (Equation 4)

where, with probability ${\pi }_{11}$, the j^th SNP has large effects on both traits; with probability ${\pi }_{10}$ and ${\pi }_{01}$, the j^th SNP has large effect on one trait and small effect on the other; and with probability ${\pi }_{00}$, the j^th SNP has small effects on both traits. Above, BN refers to a bivariate normal distribution; ${\sigma }_{0l}^2$ and ${\sigma }_{ml}^2$ are the variance components of large SNP effect sizes; ${\sigma }_{0s}^2$ and ${\sigma }_{ms}^2$ are the variance components of small SNP effect sizes; and ${\rho }_g$ represents the genetic correlation between the two traits. Our mixture modeling assumption on the effect sizes represents a hybrid between the sparse modeling assumption and polygenic modeling assumption,^19,45 facilitating robust and accurate prediction performance across a range of phenotypes with various underlying genetic architectures. In addition, the mixture of four bivariate normal distributions effectively categorizes SNPs into four groups: SNPs with large effects on both traits, SNPs with large effects on one trait or the other, and SNPs with small effects on both traits. By categorizing SNPs into four groups, mtPGS effectively places different shrinkages on the SNP effect sizes in different groups separately, leading to proper shrinkage of the small effects without over-shrinkage of the large effects.

Besides the genetic effects, we also consider the modeling assumptions on the residual errors, which represent the environmental component underlying the two traits. For the $n_0^{\ast }$ and $n_m^{\ast }$ non-overlapped individuals with only one trait measured, we assume that ${\epsilon }_{0i}^{\ast }$ for the i^th individual follows a normal distribution $N\left(0,{\sigma }_{0e}^2\right)$ while ${\epsilon }_{mj}^{\ast }$ for the j^th individual follows another normal distribution $N\left(0,{\sigma }_{me}^2\right)$. For the n_ms overlapped individuals with both traits measured, we assume that their environmental effects for the i^th individual follow a bivariate normal distribution,

$$\begin{array}{c}\left(\begin{array}{c}{\tilde{\epsilon }}_{0i}\\ {\tilde{\epsilon }}_{mi}\end{array}\right)\sim BN\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{0e}^2& {\rho }_e{\sigma }_{0e}{\sigma }_{me}\\ {\rho }_e{\sigma }_{0e}{\sigma }_{me}& {\sigma }_{me}^2\end{array}\right)\right)\text{,}\end{array}$$ (Equation 5)

where ${\rho }_e$ represents the environmental correlation between the two traits and ${\sigma }_{0e}^2$, ${\sigma }_{me}^2$ are the variance components of the environmental effects for the two traits.

Finally, we note that in the above model, we introduce the genetic and environmental correlation parameters ${\rho }_g$ and ${\rho }_e$ to leverage additional information from the relevant trait to improve the prediction accuracy of the target trait. Specifically, the genetic correlation parameter ${\rho }_g$ allows us to borrow information of the SNP effect size estimates on the relevant trait to help improve the SNP effect estimation on the target trait, thus improving the PGS on the target trait. The environmental correlation ${\rho }_e$ also allows us to effectively control for trait correlation in the overlapped individuals due to the shared environment to facilitate SNP effect size estimation and PGS construction.

Deterministic inference algorithm and use of summary statistics

With the above model, our goal is to obtain the posterior estimates for the effect sizes ${\hat{\mathit{\beta }}}_0$ for the target trait. The effect size estimates would allow us to construct a PGS for the target trait, in the form of

$$s_m={\mathit{x}}^T{\hat{\mathit{\beta }}}_0\text{,}$$

for a new individual with a p-dimensional genotype vector of x, where the subscript m is used to emphasize the fact that the PGS for the target trait is constructed with the help of the m^th relevant trait. Estimating ${\hat{\mathit{\beta }}}_0$, however, is computationally challenging, as the above model requires categorizing each SNP into four distinct categories, which leads to a likelihood with a high dimensional integration that cannot be solved analytically. A standard numerical inference algorithm, such as Markov chain Monte Carlo (MCMC), needs to effectively explore the $4^p$ dimensional space and would inevitably result in heavy computational burden. To ensure scalable computation, we develop an approximate algorithm for inference. We build upon the intuition that we can often obtain a reasonable list of large-effect size SNPs for the target trait through a simple deterministic searching strategy. Specifically, we use the LD clumping and p value thresholding (C+T) procedure implemented in the PLINK software (v.1.90b6.9) to select a set of large-effect SNPs for the target trait. In the C+T procedure, there are three hyper-parameters that need to be specified: LD window size, p value threshold p, and LD threshold r². In mtPGS, we fix the LD window size to be 1,000 kb. For p and r², we tune these two hyper-parameters in the validation set based on four different values of p (1e−5, 1e−6, 1e−7, and 1e−8) and three different values of r² (0.1, 0.2, and 0.25). In the absence of a validation set, we set these hyper-parameters as fixed values (p = 1e−6, r² = 0.2). Because the number of large-effect SNPs is often small (e.g., ranges from 2 to 2,875 in the real data applications), we can treat their effect sizes as fixed effect and fit the following approximate model for inference:

$$\begin{array}{c}{\mathit{y}}_0^{\ast }={\mathit{X}}_{0l}^{\ast }{\mathit{\beta }}_{0l}+{\mathit{X}}_{0s}^{\ast }{\mathit{\beta }}_{0s}+{\mathit{\epsilon }}_0^{\ast }\text{,}\end{array}$$ (Equation 6)

$$\begin{array}{c}{\mathit{y}}_m^{\ast }={\mathit{X}}_{ml}^{\ast }{\mathit{\beta }}_{ml}+{\mathit{X}}_{ms}^{\ast }{\mathit{\beta }}_{ms}+{\mathit{\epsilon }}_m^{\ast }\text{,}\end{array}$$ (Equation 7)

$$\begin{array}{c}\left[{\tilde{\mathit{y}}}_0,{\tilde{\mathit{y}}}_m\right]={\tilde{\mathit{X}}}_l\left[{\mathit{\beta }}_{0l},{\mathit{\beta }}_{ml}\right]+{\tilde{\mathit{X}}}_s\left[{\mathit{\beta }}_{0s},{\mathit{\beta }}_{ms}\right]+\left[{\tilde{\mathit{\epsilon }}}_0,{\tilde{\mathit{\epsilon }}}_m\right]\text{,}\end{array}$$ (Equation 8)

where ${\mathit{\beta }}_{0l}$, ${\mathit{\beta }}_{ml}$ are the p₁ vectors of effect sizes of the large-effect SNPs; ${\mathit{\beta }}_{0s}$, ${\mathit{\beta }}_{ms}$ are the p_s vectors of effect sizes of the small-effect SNPs; ${\mathit{X}}_{0l}^{\ast }$, ${\mathit{X}}_{ml}^{\ast }$ and ${\mathit{X}}_{0s}^{\ast }$, ${\mathit{X}}_{ms}^{\ast }$ are the genotype matrices of the large-effect and small-effect SNPs for the non-overlapping individuals, respectively; and ${\tilde{\mathit{X}}}_l$ and ${\tilde{\mathit{X}}}_s$ are the genotype matrices of the large-effect and small-effect SNPs for the overlapping individuals, respectively. We treat ${\mathit{\beta }}_{0l}$ and ${\mathit{\beta }}_{ml}$ as fixed effects and further assume that $\left[\begin{array}{c}{\mathit{\beta }}_{0s}\\ {\mathit{\beta }}_{ms}\end{array}\right]\sim MVN\left(\mathbf{0},{\mathit{v}}_g\otimes {\mathit{I}}_{p_s}\right)$ and $\left[\begin{array}{c}{\tilde{\mathit{\epsilon }}}_0\\ {\tilde{\mathit{\epsilon }}}_m\end{array}\right]\sim MVN\left(\mathbf{0},{\mathit{v}}_e\otimes {\mathit{I}}_{n_{ms}}\right)$, where MVN denotes the multivariate normal distribution; $\otimes$ denotes the Kronecker product; ${\mathit{v}}_g=\left(\begin{array}{cc}{\sigma }_{0s}^2& {\rho }_g{\sigma }_{0s}{\sigma }_{ms}\\ {\rho }_g{\sigma }_{0s}{\sigma }_{ms}& {\sigma }_{ms}^2\end{array}\right)$ denotes the genetic covariance matrix of the small-effect SNPs; and ${\mathit{v}}_e=\left(\begin{array}{cc}{\sigma }_{0e}^2& {\rho }_e{\sigma }_{0e}{\sigma }_{me}\\ {\rho }_e{\sigma }_{0e}{\sigma }_{me}& {\sigma }_{me}^2\end{array}\right)$ denotes the environmental covariance matrix for the overlapping individuals. With the above approximate model, we can directly obtain the effect size estimates analytically, in the form of

$$\begin{array}{c}\left[\begin{array}{c}{\hat{\mathit{\beta }}}_{0l}\\ {\hat{\mathit{\beta }}}_{ml}\end{array}\right]={\left[\left(n_{ms}{{\hat{\mathit{v}}}_e^{\prime }}^{-1}+\left[\begin{array}{cc}{\hat{\sigma }}_{0e}^{\prime -2}{n}_0^{\ast }& 0\\ 0& {\hat{\sigma }}_{me}^{\prime -2}{n}_m^{\ast }\end{array}\right]\right)\otimes {\mathit{\Sigma }}_{ll}\right]}^{-1}\left[\left({{\hat{\mathit{v}}}_e^{\prime }}^{-1}\otimes {\mathit{I}}_{p_l}\right)\left[\begin{array}{c}{{\tilde{\mathit{X}}}_l}^T{\tilde{\mathit{y}}}_0\\ {{\tilde{\mathit{X}}}_l}^T{\tilde{\mathit{y}}}_m\end{array}\right]+\left[\begin{array}{c}{\hat{\sigma }}_{0e}^{\prime -2}{{\mathit{X}}_{0l}^{\ast }}^T{\mathit{y}}_0^{\ast }\\ {\hat{\sigma }}_{me}^{\prime -2}{{\mathit{X}}_{ml}^{\ast }}^T{\mathit{y}}_m^{\ast }\end{array}\right]\right]\text{,}\end{array}$$ (Equation 9)

$$\begin{array}{c}\left[\begin{array}{c}{\hat{\mathit{\beta }}}_{0s}\\ {\hat{\mathit{\beta }}}_{ms}\end{array}\right]={\left[2{\left({\hat{\mathit{v}}}_g\otimes {\mathit{I}}_{p_s}\right)}^{-1}+\left(\left(n_{ms}{{\hat{\mathit{v}}}_e}^{-1}+\left[\begin{array}{cc}{\hat{\sigma }}_{0e}^{-2}{n}_0^{\ast }& 0\\ 0& {\hat{\sigma }}_{me}^{-2}{n}_m^{\ast }\end{array}\right]\right)\otimes {\mathit{\Sigma }}_{ss}\right)\right]}^{-1}\\ \begin{array}{c}\left[\left({{\hat{\mathit{v}}}_e}^{-1}\otimes {\mathit{I}}_{p_s}\right)\left[\begin{array}{c}{\tilde{\mathit{X}}}_s^T{\tilde{\mathit{y}}}_0-n_{ms}{\mathit{\Sigma }}_{sl}{\hat{\mathit{\beta }}}_{0l}\\ {\tilde{\mathit{X}}}_s^T{\tilde{\mathit{y}}}_m-n_{ms}{\mathit{\Sigma }}_{sl}{\hat{\mathit{\beta }}}_{ml}\end{array}\right]+\left[\begin{array}{c}{\hat{\sigma }}_{0e}^{-2}\left({{\mathit{X}}_{0s}^{\ast }}^T{\mathit{y}}_0^{\ast }-n_0^{\ast }{\mathit{\Sigma }}_{sl}{\hat{\mathit{\beta }}}_{0l}\right)\\ {\hat{\sigma }}_{me}^{-2}\left({{\mathit{X}}_{ms}^{\ast }}^T{\mathit{y}}_m^{\ast }-n_m^{\ast }{\mathit{\Sigma }}_{sl}{\hat{\mathit{\beta }}}_{ml}\right)\end{array}\right]\right]\end{array}\end{array}$$ (Equation 10)

where ${\hat{\mathit{v}}}_e^{\prime }=\left[\begin{array}{cc}{\hat{\sigma }}_{0e}^{\prime 2}& {\hat{\rho }}_e{\hat{\sigma }}_{0e}^{\prime }{\hat{\sigma }}_{me}^{\prime }\\ {\hat{\rho }}_e{\hat{\sigma }}_{0e}^{\prime }{\hat{\sigma }}_{me}^{\prime }& {\hat{\sigma }}_{me}^{\prime 2}\end{array}\right]$, ${\hat{\sigma }}_{0e}^{\prime 2}=1-\frac{p_l}{p}{\hat{h}}_0^2$, ${\hat{\sigma }}_{me}^{\prime 2}=1-\frac{p_l}{p}{\hat{h}}_m^2$, and ${\hat{h}}_0^2$, ${\hat{h}}_m^2$ are the SNP heritability estimates for the target trait and the relevant trait, respectively.

The above estimation form allows us to directly extend mtPGS toward using GWAS summary statistics as input. Specifically, the above estimation form in Equations 9 and 10 contains the LD matrices ${\mathit{\Sigma }}_{ll}$, ${\mathit{\Sigma }}_{sl}$, and ${\mathit{\Sigma }}_{ss}$ as well as linear products such as ${{\mathit{X}}_{0l}^{\ast }}^T{\mathit{y}}_0^{\ast }$ and ${{\mathit{X}}_{0s}^{\ast }}^T{\mathit{y}}_0^{\ast }$. The linear products can be computed based on GWAS marginal Z scores, which, for the j^th SNP and the m^th trait, is in the form of $z_{jm}={\mathit{X}}_{jm}^T{\mathit{y}}_m/\sqrt{n_m}$, where ${\mathit{X}}_{jm}$ represents the j^th column of the genotype matrix ${\mathit{X}}_m$. Therefore, the required GWAS summary statistics include an LD matrix estimated from a reference panel as well as two sets of marginal Z scores from overlapped individuals for the two traits and another two sets of marginal Z scores from non-overlapped individuals for the two traits. In addition, the inference algorithm also works when only two sets of marginal Z scores for the two traits are available as long as the proportion of sample overlap between the two traits is also provided (details in supplemental methods).

Our algorithm effectively extends the scalable algorithm of DBSLMM toward bivariate modeling. In the process, we also adapt four additional procedures to further improve the computational efficiency of the mtPGS algorithm. First, instead of estimating the SNP heritability (${\hat{h}}_0^2$, ${\hat{h}}_m^2$) for the two traits and the genetic (${\hat{\rho }}_g$) and environmental (${\hat{\rho }}_e$) correlations between the two traits in our model, we follow the main idea of DBSLMM⁴⁵ and obtained the estimates of ${\hat{h}}_0^2$, ${\hat{h}}_m^2$, ${\hat{\rho }}_g$, and ${\hat{\rho }}_e$ externally by using GECKO⁴⁴ and treated these estimates as fixed before inferring the other parameters in our model. GECKO is a computational method for estimating both genetic and environmental covariances using GWAS summary statistics. GECKO fits the same linear mixed model used by many other approaches⁵¹ for genetic covariance estimation and relies on a composite likelihood-based algorithm to improve the estimation accuracy of existing method of moments (MoM)-based estimation algorithms while keeping computation in check. Second, we take advantage of the block LD structure of the human genome and follow Berisa et al.⁵² to approximate the LD matrix with a block-diagonal matrix. The block-diagonal approximation to the LD matrix, when further paired with eigen-decomposition on the genetic and environmental covariance matrices, allows us to obtain the SNP effect size estimates in Equations 9 and 10 in each LD block separately. Third, we apply the Woodbury matrix identity for SNP effect size estimation in Equations 9 and 10, which effectively transforms large matrix multiplications into small matrix multiplications. Finally, we leverage the preconditioned conjugate gradient algorithm to solve the linear systems in Equations 9 and 10,⁵³ thus bypassing the computationally expensive matrix inversion for scalable computation. These technical details are provided in the supplemental methods. As a result, the computational complexity of our algorithm scales linearly with respect to the number of SNPs when GWAS summary statistics are available as input, and further scales linearly with respect to the number of individuals when summary statistics are absent.

Combining PGSs from multiple relevant traits

The above two sections have described the details for obtaining the PGS for the target trait using one relevant trait. For a new individual, we obtain the SNP effect size estimates from Equations 9 and 10 and use them to construct the PGS for the target trait of a new individual. We denote the resulting PGS as s_m, as it uses information from the m^th relevant trait. When we have more than one relevant trait, we can combine the PGSs constructed based on all these relevant traits together through a weighted PGS framework. Specifically, we obtain our final PGS for the target trait in the form of

$$s=\sum _{m=1}^M{w_{m}s}_m\text{,}$$

where w_m represents the weight for the m^th PGS. We infer the weights w_m through cross-validation. Specifically, we split the data into three sets: a training set, a validation set, and a test set. We fit our model in the training set, obtain the PGS estimates in the validation set, and further infer the weights in the validation set through a multiple linear regression where the target trait is treated as the outcome and the M PGS values constructed using different relevant traits are treated as the covariates. We finally evaluate the performance of the combined PGSs in the test set. This weighted PGS framework allows us to leverage multiple relevant traits to improve the genetic prediction on the target trait while keeping computation in check.

We refer to our method as the multi-trait assisted PGS (mtPGS). mtPGS is implemented in the mtPGS software, freely available at http://xzlab.org/software.html or https://github.com/xuchang0201/mtPGS.

Compared methods

We compared mtPGS with seven existing summary statistics-based PGS methods: DBSLMM, SBLUP, PRS-CS, MegaPRS, wMT-SBLUP, MTAG, and XPXP. The first four methods are univariate PGS methods that focus only on the target trait, while the last three methods are multivariate PGS methods that can take advantage of multiple relevant traits to construct PGSs for the target trait. All these methods are applied using only GWAS summary statistics and an LD matrix constructed based on a reference panel. We did not include methods such as MTGBLUP and CTPR in comparison as these methods apply only to individual-level data.⁵⁴ To ensure fair comparison across methods, we used the same reference panel of 500 individuals^45,46 randomly sampled from UKB to construct the LD matrix and used this matrix as input for all methods except PRS-CS. For PRS-CS, the software requires using the pre-computed LD matrix available on the software website, which was computed based on European samples in the 1000 Genomes Project phase 3 dataset.

For DBSLMM, we used the deterministic version (v.0.3) for model fitting with default parameter settings. For SBLUP, we used the GCTA software (v.1.93.2beta) to fit the model. In SBLUP, following Maier et al.,⁴⁰ we set the LD window size to 2,000 kb and calculated the input parameter $\lambda$ as $\lambda =M\ast \left(1/h^2-1\right)$, where M is the total number of SNPs used in the analysis and h² is the SNP heritability. For wMT-SBLUP, we used the SMTpred python software for fitting (see web resources). In particular, for each phenotype of the target trait and relevant traits, we first fitted SBLUP to obtain SNP effect size estimates and then computed individual PGS predictors using the “score” function in the PLINK⁵⁵ software. Afterward, we constructed wMT-SBLUP predictors for the target trait using the individual SBLUP predictors of the target trait and relevant traits as input. For PRS-CS, we used the PRS-CS software (v.1.0.0) for model fitting. In PRS-CS, following Ge et al.,¹⁵ we set the hyper-parameter a to the default value of 1 and the hyper-parameter b to the default value of 0.5. For the global shrinkage parameter φ in PRS-CS, due to memory and computational time constraints, we followed Ge et al.¹⁵ and Xiao et al.⁴² and set it to 10⁻² in the simulation studies. In the real data applications, we followed Ge et al.¹⁵ and explored four different choices for φ: 10⁻⁶, 10⁻⁴, 10⁻², and 1. We selected the optimal φ by cross-validations in the validation set. For MegaPRS, we used the LDAK software (v.5.2) for model fitting.⁵⁶ In MegaPRS, following Zabad et al.,⁵⁷ we estimated the per-predictor heritabilities assuming the GCTA model and constructed the PGS by using the BayesR model. We set the LD window size to be 1,000 kb in both simulations and real data applications as suggested by the authors of the method. For MTAG, following Turley et al.⁴¹ and Chung et al.,³⁹ we constructed the PGS by using the multi-trait adjusted summary statistics from MTAG as input for LDpred. Specifically, we first used MTAG to combine summary statistics from GWASs of different traits into multi-trait adjusted summary statistics and then used these summary statistics as input for LDpred to construct a PGS for the target trait. For the LDpred stage of model fitting, we used the LDpred software (v.1.0.11), which requires user specification for two tuning parameters that include the LD radius parameter and the fraction of causal variants parameter $\rho$. For the LD radius parameter, we set it to be the recommended value (m/3,000) in the simulations, with m being the number of SNPs, and set it to be 200 in the real data applications to ensure scalability following Yang et al.⁴⁵ For the fraction of causal variants parameter $\rho$, we used a validation set to tune the parameter $\rho$ in the simulation studies. Specifically, we followed Vilhjálmsson et al.²¹ and Lloyd-Jones et al.¹¹ and explored nine different choices for $\rho$: 1, 0.3, 0.1, 0.03, 0.01, 0.003, 0.001, 0.0003, and 0.0001. The $\rho$ value with the highest prediction R² in the validation set was selected as the optimal fraction parameter. In the real data applications, due to memory and computational time constraints, we set the fraction of causal variants to be 1 following Turley et al.⁴¹ For XPXP, we used the XPXP software for model fitting (see web resources). XPXP is primarily designed for cross-population PGS construction and requires two reference panels for the target and auxiliary population, respectively. Therefore, we partitioned the original UKB reference panel into two equal-sized subsets and supplied them as reference panel inputs for XPXP.

Simulations

We performed comprehensive simulation studies to compare the performance of mtPGS with the other PGS methods. An overview of the simulation settings analyzed in this paper is summarized in Table S1. Specifically, we randomly selected 12,000 individuals with European ancestry from the UKB data (detailed description in the next section). For these individuals, we obtained a total of m = 100,000 SNPs by selecting the first 10,000 SNPs from each of the chromosomes 1 to 10. We first consider the main simulation settings with k = 2 traits. We simulated the two traits on the same set of individuals (i.e., complete-overlap study design), with the first trait being the target trait and the second trait being the relevant trait. In the main simulations, we examined three distinct genetic architectures: polygenic (scenario I), sparse (scenario II), and hybrid (scenario III).

Scenario I is a polygenic scenario, where all SNPs are assumed to have non-zero effects on both traits. We simulated the effect sizes of the i^th SNP on the two traits based on a bivariate normal distribution, with mean zero, variances $h_1^2/m$, $h_2^2/m$, and correlation ${\rho }_g$. In addition, we simulated the environmental effects for the two traits in the j^th individual from another bivariate normal distribution, with mean zero, variances $1-h_1^2$, $1-h_2^2$, and correlation ${\rho }_e$.

Scenario II is a sparse scenario, where we randomly selected 1% of the SNPs to have non-zero effects on at least one trait. We denoted the number of non-zero effect SNPs as p. Among the non-zero effect SNPs, we randomly selected 80% of them to have correlated effects on the two traits, where their effect sizes on the two traits come from a bivariate normal distribution $BN\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}\frac{h_1^2}{p}& \frac{{\rho }_g{h}_1{h}_2}{0.8p}\\ \frac{{\rho }_g{h}_1{h}_2}{0.8p}& \frac{h_2^2}{p}\end{array}\right]\right)$. Here, we set the per-SNP effect size covariance to be $\frac{{\rho }_g{h}_1{h}_2}{0.8p}$ since the genetic covariance ${\rho }_g{h}_1{h}_2$ is contributed by a total of 0.8p SNPs. For the remaining SNPs with uncorrelated effects, we simulated their effect sizes on the two traits from two independent normal distributions, $N\left(0,\frac{h_1^2}{p}\right)$ and $N\left(0,\frac{h_2^2}{p}\right)$, respectively.

Scenario III is a hybrid of the polygenic and sparse scenarios. Here, we assumed that all SNPs have non-zero effects, but their effect sizes come from a mixture of two different distributions. Specifically, we randomly selected 1% of SNPs (denoted as p_l) to have relatively large effects while assigning the remaining SNPs (denoted as p_s) to have small effects. We set the proportion of SNP heritability explained by the large-effect SNPs to be 0.3. In particular, we simulated the effect sizes of each large-effect SNP on the two traits based on a bivariate normal distribution $BN\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\frac{0.3}{p_l}·\left[\begin{array}{cc}{h}_1^2& {\rho }_g{h}_1{h}_2\\ {\rho }_g{h}_1{h}_2& h_2^2\end{array}\right]\right)$. We simulated the effect sizes of each small-effect SNP on the two traits based on another bivariate normal distribution: $BN\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\frac{0.7}{p_s}·\left[\begin{array}{cc}{h}_1^2& {\rho }_g{h}_1{h}_2\\ {\rho }_g{h}_1{h}_2& h_2^2\end{array}\right]\right)$.

For each simulation scenario, we set the heritability of the two traits $h_1^2$, $h_2^2$ to be either 0.25 or 0.5, and we varied the genetic correlation ${\rho }_g$ to be 0.25, 0.5, or 0.75 and environmental correlation ${\rho }_e$ to be 0.1, 0.15, or 0.2, for a total of 36 simulation settings (4 × 3 × 3), with ten simulation replicates per setting. In each simulation replicate, we simulated the SNP effect sizes and environmental effects, and then summed them to obtain the simulated traits. With the simulated data, we divided the samples randomly into a training set of 10,000 individuals, a validation set of 1,000 individuals, and a test set of 1,000 individuals. We fitted the linear regression model implemented in the GEMMA⁴³ software (v.0.98.1) in the training data to compute the marginal Z scores. We also randomly selected 500 individuals from the remaining UKB data and treated them as a reference panel for LD matrix computation. With the marginal Z scores from the training data and the LD matrix from the reference panel, we fitted different PGS methods to obtain SNP effect size estimates. For PGS methods that require parameter tuning (i.e., mtPGS, MegaPRS, and LDpred), we used the validation set to select the optimal tuning parameters. We then evaluated the performance of all methods using R² in the test set. Due to the small sample size and limited number of SNPs in the simulations, it is challenging to obtain accurate estimates of SNP heritability and genetic/environmental correlations. Therefore, following Lloyd-Jones et al.¹¹ and Yang et al.,⁴⁵ we supplied true SNP heritability and genetic/environmental correlations for all PGS methods in the simulations. For each simulation setting, we calculated the mean R² in the test set across the ten replicates as the evaluation metric.

Besides the above simulation settings with completely overlapped samples, we also examined the influence of sample overlap on the predictive performance of different PGS methods. Specifically, we considered two alternative study designs: a non-overlap study design where the two traits are measured on two different sets of individuals and a partial-overlap study design where a fraction of individuals are measured for two traits while the remaining individuals are measured for only one trait. For the non-overlap study design, we randomly selected two sets of n = 10,000 individuals to serve as the training sets for the two traits separately. For the partial-overlap study design, for the training set, we used the same 10,000 individuals in the training set of the complete-overlap study design to simulate the target trait. In addition, we randomly selected 7,000 individuals among them to serve as the common set of individuals with both traits measured. We then randomly selected another 3,000 individuals from UKB and added them to the common set of 7,000 individuals to serve as the training set for the second trait. Therefore, for the training set in the partial-overlap study design, we have a total of 13,000 individuals, with about half of them (7,000) measured for both traits. We used the same validation and test sets for the target trait from the complete-overlap study design for both non-overlap and partial-overlap study designs. For the above two study designs, we set ${\rho }_g$ to be 0.5. We set ${\rho }_e$ to be 0.1 in the partial-overlap study design. For each of these above study designs, we selected the same 100,000 SNPs as in the complete-overlap study design, varied the heritability of both traits to be either 0.25 or 0.5 ($h_1^2=h_2^2=0.25\text{or}0.5)$, and simulated the SNP effect sizes under the three genetic architectures described in the scenarios I–III, for a total of 12 (2 × 6) simulation settings. For each setting in the non-overlap study design, we computed two sets of GWAS summary statistics, one for each trait, to serve as the inputs for PGS methods. For each setting in the partial-overlap study design, we performed two different analyses. In the first analysis, we computed two sets of summary statistics, one for each trait, based on the combined overlapped and non-overlapped individuals from each trait. We then supplied the two sets of summary statistics as inputs for mtPGS and the other PGS methods. We used the Equations 18 and 19 in the supplemental methods for approximate model fitting in mtPGS. In the second analysis, we computed four sets of GWAS summary statistics: two from the overlapped individuals for the two traits, and two from non-overlapped individuals for the two traits. We then supplied the four sets of summary statistics as input for mtPGS and used Equations 9 and 10 for model fitting. We compared the predictive performance of mtPGS in the two different analyses to examine the accuracy of the approximation in Equations 18 and 19 in the supplemental methods. For each simulation setting, we performed ten replicates and calculated the mean R² as the evaluation metric.

Besides the simulation settings with two traits, we also simulated settings with multiple traits to examine whether incorporating multiple relevant traits can further improve the predictive performance of multivariate PGS methods. Specifically, we considered a complete-overlap study design and simulated the number of relevant traits M to be either one, two, or three, with the heritability of all traits set to be 0.5. For settings with more than one relevant trait, we assumed that each relevant trait is genetically correlated with the target trait with ${\rho }_g=0.5$, with the genetic correlation between the relevant traits set to be 0. We further assumed that all traits are environmentally correlated with ${\rho }_e=0.1$. We simulated the SNP effect sizes and environmental effects under the polygenic architecture described in scenario I to obtain the simulated traits. We then computed GWAS summary statistics using GEMMA. For multivariate PGS methods, we fitted prediction models in the training set, tuned hyper-parameters in the validation set, and obtained individual predictors in the test set. For each specific M, we performed ten simulation replicates and calculated the mean R² as the evaluation metric. Besides the main simulations, we also performed additional simulations to examine the influence of the number of traits on mtPGS accuracy and how such influence may vary under different genetic correlations between the target trait and the relevant traits. Specifically, we extended the main simulations by simulating up to ten relevant traits, with the genetic correlation between the target trait and each relevant trait ${\rho }_g$ set to be either 0.1, 0.2, or 0.5. In these additional simulations, we performed mtPGS analysis and evaluated the accuracy of mtPGS under increasing numbers of relevant traits and varying genetic correlation values.

UKB data

We performed simulations and real data applications based on genotype and phenotype data from the UKB.⁴⁷ The UKB recruited 502,618 participants aged 40–69 years from across the United Kingdom between 2006 and 2010. Comprehensive phenotypic and health-related information were accessed for enrolled individuals, and 488,377 individuals were genotyped at ∼800,000 genetic markers using the UK BiLEVE and UK Biobank Axiom Arrays from Affymetrix. Genotype data were imputed using the Haplotype Reference Consortium (HRC) and UK10K + 1000 Genomes Project phase 3 data as reference panels, which resulted in ∼93 million SNPs in total. For the sample quality control (QC) process, we followed the procedures described in the online resources of Neale lab (see web resources). Specifically, we retained individuals (1) who are included in the UKB version 3 imputed genotype data; (2) who are included in the genotype principal component (PC) computation; and (3) who are identified as having White British ancestry by self-reporting “white-British,” “Irish,” or “White” and being within 7 standard deviations away from the first six PCs. We further filtered out individuals (1) who are identified as outliers in heterozygosity and missing rates; (2) who have sex chromosome aneuploidy, defined as putatively carrying abnormal sex chromosome configurations; (3) who are excluded from the kinship inference procedure; (4) who have more than ten putative third-degree relatives in the kinship table; or (5) who withdraw their consent for participating the study. For variant QC, we focused on autosome SNPs in the version 3 imputed genotype data and removed SNPs (1) with missing percentage >5%; (2) with a minor allele frequency (MAF) <0.05; (3) with an INFO score <0.8; (4) with a Hardy-Weinberg equilibrium (HWE) test p value < 10⁻⁷; or (5) that are a duplicated SNP. A total of 361,112 individuals and 6,171,964 SNPs were retained after the above QC steps. Following Bulik-Sullivan et al.⁵¹ and the Neale lab, we further restricted the set of SNPs to those listed in the pre-computed LD scores of European individuals provided by the LDSC website (see web resources), which resulted in 1,119,148 SNPs as the final set for analysis. All QC procedures described above were conducted using the PLINK⁵⁵ software.

Cross-validation in UKB

We performed cross-validations in UKB to evaluate the predictive performances of different PGS methods. Following Maier et al.,⁴⁰ Morrison et al.,⁵⁸ and Yang et al.,⁴⁵ we selected 15 quantitative traits and 10 binary traits with (1) heritability >0.05 based on the Neale lab’s heritability estimation results (see web resources), (2) total sample size >50,000, and (3) number of affected individuals >1,000 for binary traits. The 15 quantitative traits can be categorized into three groups: a group of physical measurements that include standing height (SH), forced vital capacity (FVC), forced expiratory volume in 1 s (FEV1), basal metabolic rate (BMR), systolic blood pressure (SBP), and body mass index (BMI); a group of blood cell traits that include lymphocyte count (LYMPH), platelet count (PLT), platelet distribution width (PDW), neutrophill count (NEUT), red blood cell (erythrocyte) count (RBC), and hemoglobin concentration (HGB); and a group of other quantitative traits that include fluid intelligence score (GF), age at first live birth (AFLB), and birth weight (BW). The ten binary traits are all complex disease traits and include angina (AG), high cholesterol (HCH), hypertension (HTN), type 2 diabetes (T2D), heart attack/myocardial infarction (MI), ulcerative colitis (UC), asthma (AS), cholelithiasis/gall stones (CL), atrial fibrillation (AF), and gout (GO). An overview of the phenotypes analyzed in this paper is summarized in Table S2 for quantitative traits and Table S3 for binary traits.

In the analysis, we first randomly selected 500 individuals from the UKB data to serve as a reference panel for calculating the SNP LD matrix. Afterward, we randomly selected 80% of the remaining individuals as the training set (n = 288,490), 10% as the validation set (n = 36,061), and 10% as the test set (n = 36,061). For each trait in turn, we extracted the corresponding records from the UKB data and constructed the phenotypes based on numeric measurements of quantitative traits and illness coding of binary traits. For the quantitative traits, we focused on the phenotypic values measured during the initial visit among the three assessment center visits for analysis. Due to missing phenotype measurements, the sample size for the quantitative traits ranges from 93,602 to 287,827 in the training set, ranges from 11,602 to 35,985 in the validation set, and ranges from 11,745 to 35,995 in the test set. For the binary traits, we followed Maier et al.⁴⁰ to focus on the disease traits defined by self-reported non-cancer illness coding (data field 20002) instead of the ICD10 code diagnoses to maximize the sample size. For both quantitative and binary traits, we fitted a standard linear regression model in the training data to obtain the marginal Z scores using the GEMMA software. Following the Neale lab (see web resources), all quantitative traits were first adjusted for sex, age, age², genotyping array, and top 20 genotype PCs by regressing the phenotype on these covariates to obtain the phenotype residuals. We then transformed residuals to a standard normal distribution using quantile-quantile normalization and supplied them to GEMMA as phenotypic values. For binary traits, we followed Yang et al.⁴⁵ and directly fitted standard linear regression model using the original binary outcomes for each SNP-phenotype pair by treating sex, age, age², genotyping array, and top 20 genotype PCs as covariates in the GEMMA software to obtain the marginal Z scores. Besides the analyses based on summary statistics generated by linear regression, we also performed sensitivity analyses to evaluate the prediction accuracy of mtPGS for binary traits when summary statistics from logistic regression are used as inputs. Specifically, for each of the ten binary traits in turn, we fitted logistic regression for each SNP-phenotype pair using LDAK software (see web resources) while adjusting for the same set of covariates as in our original linear regression analysis. We then supplied the marginal Z scores from logistic regression to mtPGS for PGS construction and compared the prediction accuracy with results based on linear regression.

With the GWAS summary statistics and the reference panel, we applied different PGS methods to the training data and evaluated their performances in the test data. We examined each of the 25 traits one at a time and treated it as the target trait. For univariate PGS methods, we directly fitted prediction models for the target trait to obtain the SNP effect size estimates. For multivariate PGS methods, we first selected relevant traits for the target trait. Specifically, for each target trait in turn, we examined the remaining 24 traits one at a time and selected those that have statistically significant genetic correlation (p value < 0.05/24) with the target trait to serve as the relevant traits. For the target trait that has no significant genetic correlation with any of the 24 traits, we directly selected the trait with the smallest p value of genetic correlation to serve as the relevant trait. We then modeled the target trait with all selected relevant traits jointly. The number of relevant traits ranges from 1 to 17 for each target trait. For the bivariate modeling stage in mtPGS, the SNP effect size estimates were obtained based on only two sets of summary statistics for each pair of the target trait and relevant trait, as the traits were measured in the same set of UKB participants. The genetic and environmental variance component estimates were obtained using GECKO⁴⁴ with the pre-computed LD scores from the LDSC website. We used the “score” function in PLINK to calculate the PGS in the test data using the estimated SNP effects and evaluated the performance of different PGS methods using R² for quantitative traits and area under the curve (AUC; calculated by R package pROC v.1.18.0) for binary traits.

Besides the main analyses of 25 traits, we also performed two additional analyses to further examine the performance of mtPGS in the UKB. First, we evaluated the additional accuracy gain brought by the step of combining PGSs from multiple relevant traits over the step of pairwise analysis using only one relevant trait for mtPGS. For the pairwise PGS with one relevant trait, we selected the trait with the smallest p value of genetic correlation with the target trait to serve as the relevant trait. Following the selection procedure of relevant traits described previously, we identified more than one relevant trait for 14 target quantitative traits and 6 target binary traits. Therefore, we performed comparisons on these 20 traits. Second, we combined PGSs from the other PGS methods based on the same set of relevant traits using the same linear aggregation method as we did for mtPGS. Specifically, for the univariate PGS methods, we combined the univariate PGS of the target trait with that of each relevant trait. For the multivariate PGS methods, we combined the PGSs of the target trait from pairwise analysis of the target and each relevant trait. In either case, we obtained the weights from the validation set.

Results

Simulations

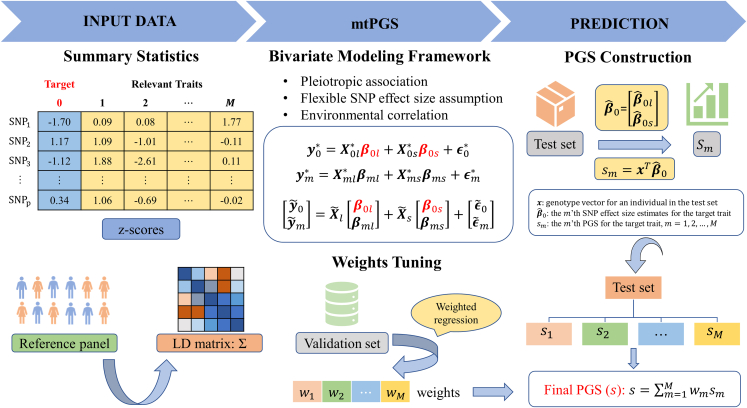
A method schematic of mtPGS is shown in Figure 1, with details provided in the subjects and methods. We performed simulation studies to evaluate the predictive performance of mtPGS and compared it with seven other PGS methods. The seven other methods include four univariate PGS methods (DBSLMM, SBLUP, PRS-CS, and MegaPRS) and three multivariate methods (wMT-SBLUP, MTAG, and XPXP). Simulation and comparison details are provided in the subjects and methods. Briefly, we used the genotypes from UKB to simulate two or more traits on a set of n = 12,000 individuals. We divided these individuals into three sets: a training set (n = 10,000), a validation set (n = 1,000), and a test set (n = 1,000). Among the simulated traits, we treated the first trait as the target trait and the remaining traits as the relevant traits. We then predict the target trait either with (for multivariate PGS methods) or without (for univariate PGS methods) the relevant traits. In the main simulations, we primarily focused on settings with two traits, including one target and one relevant trait, and considered three different genetic architectures underlying the two traits: polygenic (scenario I), sparse (scenario II), and hybrid (scenario III). Each genetic architecture differs in terms of the number of causal SNPs and the SNP effect size distribution. In the main simulations, we varied the SNP heritability ($h_1^2$, $h_2^2$), genetic correlation (${\rho }_g$), and environmental correlation (${\rho }_e$) for the two traits under each genetic architecture, resulting in a total of 108 simulation settings across three scenarios, with ten simulation replicates per setting. Besides the main settings with two traits, we also examined additional settings with more than two traits. An overview of the simulation settings analyzed in this paper is summarized in Table S1. In each simulation setting, we fitted different PGS methods on the training set using summary statistics, tuned hyper-parameters in the validation set if necessary, and evaluated their prediction performance in the test set by computing the mean R² across replicates.

Figure 1.

Schematic of mtPGS

mtPGS performs multi-trait analysis to leverage multiple relevant traits for accurate and scalable PGS construction for a target trait of interest. mtPGS takes input of the GWAS summary statistics for each individual trait (top left) and an LD matrix calculated based on a reference panel (bottom left). mtPGS examines the target trait with the relevant traits one at a time, explicitly models the shared genetic architecture and environmental exposures between the target trait and the relevant trait through a bivariate modeling framework, and constructs a PGS for the target trait by leveraging the relevant trait (top middle). Afterward, mtPGS infers the weights for different PGSs constructed based on different relevant traits in the validation set through a weighted regression model (bottom middle), which allows mtPGS to combine the different PGSs into a single PGS as the final PGS for the target trait of interest (right).

Overall, the simulation results showed that mtPGS achieved improved prediction accuracy across the majority of simulation settings compared to existing PGS methods. Across the 108 main simulation settings, mtPGS was ranked as the most accurate method in 80 settings and was ranked as the second most accurate method in 24 settings (Figures 2 and S1–S17). In the 80 settings where mtPGS was the best, mtPGS achieved an average of 3.65% accuracy gain (median = 3.46%, range = 0.01%–13.53%) over the second-best method. In the 28 settings where mtPGS was not the best, on average, mtPGS was 2.85% less accurate (median = 1.91%, range = 0.14%–10.09%) than the best method. The performance of mtPGS is especially favored in settings where the genetic architecture underlying the traits has a polygenic component (Figure 2B). In particular, mtPGS was ranked as the best method in 33 out of the 36 polygenic settings, 29 (out of 36) hybrid settings, and 18 (out of 36) sparse settings. MegaPRS achieved the second-best prediction performance and was ranked as the best in 21 settings and the second-best in 34 settings. PRS-CS (best in 7 and second in 20) and XPXP (second in 27) also performed well across the simulation settings. DBSLMM was ranked as the second-best in three settings while SBLUP, wMT-SBLUP, and MTAG were neither the best nor the second-best in any of these simulation settings.

Figure 2.

Predictive performance of eight PGS methods in simulations

(A) Jitter plots show the prediction R² across ten simulation replicates for different PGS methods in each of the six simulation settings. Compared methods include mtPGS (light blue), DBSLMM (purple), SBLUP (dark pink), PRS-CS (green), MegaPRS (light pink), wMT-SBLUP (dark blue), MTAG (red), and XPXP (orange). Results are shown for the three scenarios in the complete-overlap study design with the heritability of the target trait $h_1^2=0.25$ (first row) and 0.5 (second row) under the baseline setting (one relevant trait, heritability of relevant trait $h_2^2=0.5$, genetic correlation ${\rho }_g=0.5$, environmental correlation ${\rho }_e=0.1$). Solid line represents the mean R² across ten replicates, with the numerical value also displayed above the line. Best ranking PGS method is denoted with double asterisks and second-best PGS method is denoted with single asterisk.

(B) Pie charts show the proportion of times each PGS method is ranked as the best across simulation settings/replicates for each of the three scenarios in the complete-overlap study design. Each scenario consists of 36 simulation settings, each with ten simulation replicates. The value in each slice represents the number of best-ranking settings for the corresponding PGS method.

One unique feature of mtPGS is its explicit modeling of the genetic correlation between the target trait and the relevant trait, which allows mtPGS to take advantage of the shared genetic architecture between the two traits to enhance PGS accuracy for the target trait. Indeed, the accuracy improvement brought by mtPGS over the other methods becomes more apparent with increasing genetic correlation between the two traits. For example, in the hybrid scenario of the main simulation, with $h_1^2=h_2^2=0.25$ and ${\rho }_e=0.15$, mtPGS was 2.74%, 2.99%, and 4.31% more accurate than the second-best method when ${\rho }_g$ increased from 0.25 to 0.50 and 0.75 (Figures S2, S5, and S8). Across the main simulation settings, the percentage gain brought by mtPGS over the second-best method is also positively correlated with the genetic correlation (Spearman correlation = 0.21; p value = 2.87 × 10⁻²).

Another unique feature of mtPGS is its explicit modeling of the environmental correlation between the target trait and the relevant trait, which allows mtPGS to take advantage of the shared environmental effects in the presence of sample overlap to enhance PGS accuracy. To illustrate such benefits, besides the main simulations with completely overlapped samples, we also considered two additional study designs: a non-overlap study design where the two traits are measured on two different sets of n = 10,000 individuals and a partial-overlap study design where a fraction of the individuals (n = 7,000) were measured for both traits while the remaining individuals (n = 3,000 for each trait) were measured for only one trait. We found that mtPGS achieved robust predictive performance across settings with different study designs. Across the 12 simulation settings under these two study designs, mtPGS was ranked as the most accurate method in 8 settings (4 in non-overlap and 4 in partial-overlap) and was ranked as the second most accurate method in the remaining 4 settings (Figures 3A, S18, and S19). In the 8 simulation settings where mtPGS was the best, mtPGS outperformed the second-best method by an average of 8.24% (median = 5.69%, range = 1.01%–22.72%) in terms of mean R² across the simulation replicates. In the 4 settings where mtPGS was the second-best, mtPGS was on average 3.98% (median = 4.08%, range = 1.85%–5.90%) less accurate than the best method. Notably, in the partial-overlap study design, an approximate version of mtPGS that makes use of two sets of GWAS summary statistics also achieved similar predictive performance as compared to the original version of mtPGS that uses four sets of GWAS summary statistics (Figure S20). In particular, using two sets of summary statistics, mtPGS incurred only an average of 2.76% accuracy loss (median = 2.37%, range = 0.15%–7.83%) across six settings of the partial-overlap study design as compared to using four sets of summary statistics. The relatively stable results suggest that the mtPGS modeling framework is reasonably robust with respect to the input data type in the scenarios with partially overlapped samples.

Figure 3.

Comparison of eight PGS methods in simulation settings with different sample overlap designs and with various numbers of relevant traits

Results are shown for simulation settings under the polygenic scenario.

(A) Jitter plots show the prediction R² across ten replicates for eight PGS methods in non-overlap and partial-overlap study designs with the heritability of the target trait $h_1^2=0.25$ (first row) and 0.5 (second row). Solid line represents the mean R² across ten replicates, with the numerical value also displayed above the line. Best ranking PGS method is denoted with double asterisks, and second-best PGS method is denoted with single asterisk.

(B) Bar plot shows the mean R² for four multivariate PGS methods across ten replicates (y axis) for settings with different number of relevant traits (x axis), with the numerical value also displayed on top of the bar.

A closer look at the simulation results provides us with further insights. First, the performance of different PGS methods were generally improved when $h_1^2$ was increased from 0.25 to 0.5. The increase in performance is typically on the order of approximately 2- to 3-fold improvement for most PGS methods with the only exception of SBLUP. For SBLUP, its performance was much lower than that of the other methods when $h_1^2=0.25$ but became comparable to the other methods when $h_1^2$ increased to 0.5. For example, in the baseline setting (i.e., $h_2^2=0.5$, ${\rho }_g=0.5$, and ${\rho }_e=0.1$) of the hybrid scenario, the mean R² for SBLUP across simulation replicates in the complete-overlap study design was only 0.003 when $h_1^2=0.25$ and was increased to 0.168 when $h_1^2$ was 0.5 (Figure 2A). As a comparison, the mean R² for mtPGS were 0.062 and 0.178 for settings with $h_1^2=0.25$ and 0.5, respectively. Second, the presence of sample overlap does not influence the performance of univariate PGS methods but decreases the performance of some multivariate PGS methods other than mtPGS. For example, in the baseline setting of the sparse scenario, wMT-SBLUP was 4.02% and 14.73% more accurate than the univariate method SBLUP in the non-overlap and partial-overlap study designs, respectively. However, it was 2.01% less accurate than SBLUP in the complete-overlap study design (Figures 2A and S18). The accuracy loss of wMT-SBLUP in settings with sample overlap may be attributed at least in part to its modeling misspecification of the environmental covariance in these settings.

Finally, mtPGS can incorporate more than one relevant trait to facilitate the construction of PGSs for the target trait. To examine the performance of mtPGS in the presence of multiple relevant traits, we simulated one, two, or three relevant traits. In the simulations, the predictive performance of all multivariate PGS methods improved when the number of relevant traits M increased from one to three, though their relative rank does not change (Figure 3B). The improved predictive performance of multivariate PGS methods with increasing number of relevant traits highlight the benefits of leveraging multiple relevant traits to improve the prediction of the target trait. Besides the main simulations, we also examined the influence of the number of traits on mtPGS accuracy and how such influence may vary under different genetic correlations between the target trait and the relevant traits. The results showed that, when ${\rho }_g$ = 0.1 or 0.2, the prediction R² of mtPGS first increased with increasing number of relevant traits and then decreased when more relevant traits were included (Figure S21). However, when ${\rho }_g$ = 0.5, the prediction R² almost increased monotonically with increasing number of relevant traits, which is expected as the relevant traits in the case of ${\rho }_g$ = 0.5 are much more informative than the cases of ${\rho }_g$ = 0.1 or 0.2. Consequently, the benefits of including even ten relevant traits still outweighs the potential bias introduced by the additional modeling parameters in the model in the case of ${\rho }_g$ = 0.5.

Cross-validation in UKB

We evaluated the performance of mtPGS and the other PGS methods by performing cross-validations for 25 traits, including 15 quantitative traits (details in Table S2) and 10 binary traits (details in Table S3), in the UKB. Analysis details are provided in the subjects and methods. Briefly, we focused on 361,112 European-ancestry individuals and a common set of 1,119,148 SNPs. We partitioned the individuals into a training set of 80% individuals, a validation set of 10% individuals, a test set of 10% individuals, and a reference panel of 500 individuals. For multivariate PGS methods, we treated each trait as the target trait and selected the relevant traits among the remaining 24 traits for analysis. The number of the relevant traits used for each target trait ranges from 1 to 17. For each trait in turn, we fitted PGS methods in the training set, tuned hyper-parameters in the validation set, and evaluated their performance in the test set by computing R² for quantitative traits and AUC for binary traits.

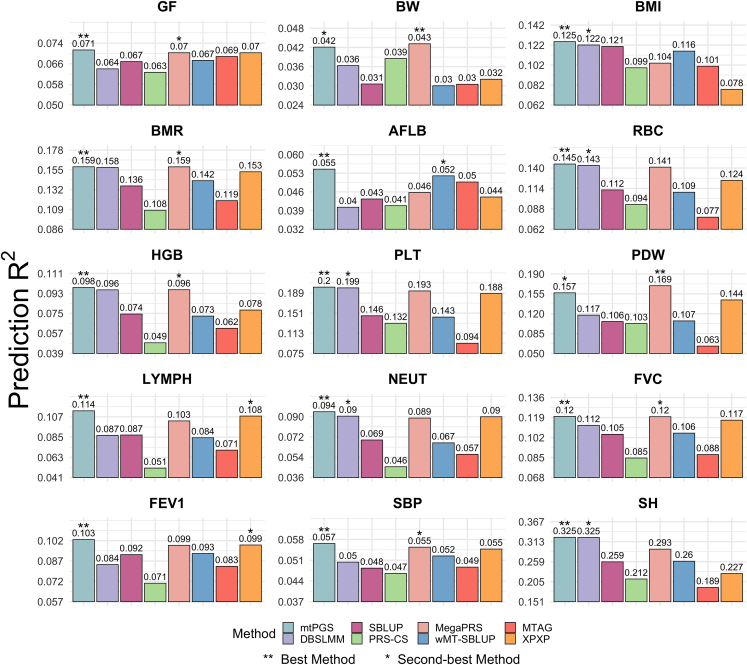
Overall, mtPGS achieved the best performance among all PGS methods across traits. Specifically, mtPGS was ranked as the most accurate for 13 of the 15 quantitative traits (Figure 4) and for 7 of the 10 binary traits (Figure S22). It was also ranked as the second-best method for the remaining 2 quantitative traits and 3 binary traits. In the 20 traits where mtPGS was the best, compared with the second-best method, mtPGS achieved an average accuracy gain of 2.25% (median = 1.99%, range = 0.06%–5.28%) for quantitative traits and 0.89% (median = 0.67%, range = 0.15%–2.43%) for binary traits. In the 5 traits where mtPGS was the second-best, mtPGS was on average 5.23% (median = 5.23%, range = 2.46%–8.00%) less accurate than the best method for quantitative traits and 0.96% (median = 1.33%, range = 0.05%–1.49%) less accurate for binary traits. The performance of mtPGS was followed by MegaPRS (best for 2 quantitative traits; second-best for 5 quantitative traits and 1 binary trait), XPXP (second-best for 2 quantitative traits and 5 binary traits), DBSLMM (second-best for 5 quantitative traits and 1 binary trait), wMT-SBLUP (best for 2 binary traits; second-best for 1 quantitative trait), and PRS-CS (best for 1 binary trait). Both SBLUP and MTAG were neither the best nor the second-best in any of these traits. For quantitative traits, mtPGS on average outperformed DBSLMM, SBLUP, PRS-CS, MegaPRS, wMT-SBLUP, MTAG, and XPXP by 12.00%, 24.83%, 52.15%, 4.98%, 23.85%, 52.91%, and 16.21%, respectively. For binary traits, mtPGS outperformed these methods by an average of 2.56%, 8.73%, 5.06%, 4.32%, 5.06%, 7.89%, and 0.90%, respectively.

Figure 4.

Comparison of eight PGS methods for predicting 15 quantitative traits in UKB

Compared methods include mtPGS (light blue), DBSLMM (purple), SBLUP (dark pink), PRS-CS (green), MegaPRS (light pink), wMT-SBLUP (dark blue), MTAG (red), and XPXP (orange). Title in each panel shows the abbreviation of 15 quantitative traits: fluid intelligence score (GF), birth weight (BW), body mass index (BMI), basal metabolic rate (BMR), age at first live birth (AFLB), red blood cell (erythrocyte) count (RBC), hemoglobin concentration (HGB), platelet count (PLT), platelet distribution width (PDW), lymphocyte count (LYMPH), neutrophill count (NEUT), forced vital capacity (FVC), forced expiratory volume in 1 s (FEV1), systolic blood pressure (SBP), and standing height (SH). Results are shown for the prediction of 15 quantitative traits in the UKB cross-validation, where univariate PGS methods were applied directly for the target trait and multivariate PGS methods were applied by performing multi-trait analysis with relevant traits. The bar plot in each panel shows the prediction R² for each method in the test set, with the numerical value also displayed on top of the bar. Best ranking PGS method is denoted with double asterisks, and second-best PGS method is denoted with single asterisk.

A careful examination of the UKB results provides further insights. First, consistent with previous observations,⁴⁵ the predictive performances of all PGS methods for quantitative traits were positively correlated with their SNP heritability (Pearson correlation ranges from 0.871 to 0.978 for quantitative traits, Figure S23). The correlations of predictive performances and SNP heritability for binary traits are less clear (Pearson correlation ranges from −0.075 to 0.587 for binary traits), likely due to the low disease prevalence in the UKB. Second, the predictive performance of PRS-CS in UKB is much worse than its performance in the simulations (Figures 4 and S22). In particular, PRS-CS became the worst method for 8 out of 15 quantitative traits and for 2 out of 10 binary traits. As a comparison, the performance of mtPGS in UKB is largely consistent with its performance in the simulations. The stable performance of mtPGS in UKB may partially be due to its analytic solutions, which circumvent the convergence issues encountered by MCMC-based PGS methods observed in previous studies.^18,46 Finally, the prediction accuracy of mtPGS for ten binary traits were almost identical whether we used summary statistics based on linear regression or logistic regression, with only an average of 0.01% accuracy loss when using summary statistics based on logistic regression compared to linear regression (Figure S24). The nearly identical results suggest that the mtPGS model fitting is reasonably robust with respect to how the summary statistics are generated.

Besides the main analyses of 25 traits, we also performed two additional analyses to examine the performance of mtPGS in the UKB. First, we evaluated the additional accuracy gain brought by the step of combining PGSs from multiple relevant traits for mtPGS. Here, we focused on the 14 target quantitative traits and 6 target binary traits for which we identified more than one relevant trait. The results showed that the step of combining weighted PGSs improved accuracy on top of the pairwise PGS in 13 out of the 14 quantitative traits and in 5 out of the 6 binary traits, with an average accuracy gain of 4.59% (range = −1.35% to +17.74%) across all 14 quantitative traits and 0.90% (range = −0.26% to +2.90%) across all 6 binary traits (Figure S25). Therefore, the step of combining PGSs from multiple relevant traits provided additional improvement on mtPGS accuracy, with the accuracy gain observed in the real data similar to what was observed in the simulations. Second, we combined PGSs from other PGS methods based on the same set of relevant traits using the same linear aggregation method as we did for mtPGS. The results showed that most PGS methods achieved improved predictive performance when different PGSs were combined using the linear aggregation method (Figures S26 and S27). Specifically, compared to the original univariate or multivariate PGS, the weighted PGS of all methods achieved improved accuracy for the 15 quantitative traits, with the average accuracy gain ranging from 1.52% to 9.73%. In addition, the weighted PGS of all methods, with the only exception of wMT-SBLUP, achieved improved accuracy for the 10 binary traits, with the average accuracy gain ranging from −0.09% to 3.66%. These results dovetail the conclusions from recent studies that weighted linear combination of PGSs can further improve predictive performance for both univariate and multivariate methods.^59,60 Compared to the weighted PGS approach from the other methods, mtPGS still achieved the best performance among all PGS methods across traits. Specifically, for the 15 quantitative traits, mtPGS on average outperformed the four univariate methods DBSLMM, SBLUP, PRS-CS, and MegaPRS by 8.22%, 19.95%, 42.40%, and 3.40%, respectively, and outperformed the three multivariate methods wMT-SBLUP, MTAG, and XPXP by 19.99%, 42.82%, and 5.84%, respectively. For the 10 binary traits, mtPGS on average outperformed the four univariate methods by 1.02%, 4.95%, 4.22%, and 2.12%, respectively, and outperformed the three multivariate methods by 5.14%, 7.52%, and 0.66%, respectively.

Finally, we examined the computing time and memory cost of different PGS methods. mtPGS compares favorably to the other PGS methods with relatively low computing time and memory cost (Table S4).

Discussion

We have presented mtPGS, a PGS method that leverages multiple relevant traits for accurate and scalable PGS construction for a target trait of interest. mtPGS not only flexibly models the shared genetic architecture between the target trait and the relevant traits but also explicitly models their shared environmental architecture, thus achieving accurate and robust prediction performance across a wide range of shared genetic architectures and study designs with distinct sample overlaps. In addition, mtPGS requires only summary statistics for model fitting and relies on a deterministic inference algorithm to achieve scalable computation. We have illustrated the benefits of mtPGS through simulations and applications to 25 UKB traits.

mtPGS flexibly models the shared genetic architecture between the target trait and the relevant traits by categorizing SNPs into different categories based on their effect sizes. Such SNP categorization allows mtPGS to introduce distinct shrinkage on the estimated effect sizes in different SNP categories, achieving proper shrinkage of small effect estimates while avoiding over-shrinkage of large effect estimates. To achieve SNP categorization, mtPGS incorporates a clumping/thresholding-based searching strategy to select SNPs with potentially large effect sizes. While such searching strategy is effective and efficient, we note that more sophisticated selection approaches may improve the accuracy of mtPGS further. For example, instead of applying the clumping/thresholding strategy using the marginal GWAS summary statistics obtained from univariate regression for the target trait, one may apply such strategy to GWAS summary statistics obtained from multivariate regression to improve the detection of large-effect SNPs.⁶¹ In addition, fine-mapping methods such as SuSiE⁶² and FINEMAP⁶³ may also be used to identify SNPs with potentially large effects. As the analytic solution in mtPGS can be obtained for any searching strategy, pairing mtPGS with more powerful searching strategies in the future may lead to improved PGS accuracy.

We have examined the performance of mtPGS in incorporating multiple relevant traits for predicting the target trait of interest. Because mtPGS uses a pairwise modeling framework to incorporate the relevant traits one at a time, there is in principle no limit to the number of relevant traits that can be jointly analyzed using mtPGS. However, selecting the appropriate relevant traits may be necessary to ensure effective selection of informative relevant traits and guarantee subsequent prediction accuracy.^44,51 Selecting appropriate relevant traits can be achieved either based on prior biological knowledge or by performing genetic correlation analysis as done in the present study. With the selected relevant traits, mtPGS relies on the pre-computed genetic and environmental correlation estimates from GECKO, which accounts for the correlated environmental covariance, to model the genetic correlation among traits. Using the pre-computed correlation estimates ensures scalable computation in mtPGS. However, the predictive performance of mtPGS is likely subject to the estimation accuracy of the genetic correlation estimates obtained from GECKO. Consequently, exploring the use of other methods for genetic covariance estimation or exploring the use of local genetic covariance estimation approaches such as SUPERGNOVA⁶⁴ and LAVA⁶⁵ may improve the performance of mtPGS further.

While we have primarily focused on unrelated individuals in both simulations and real data applications in the present study, we acknowledge that individual relatedness can occur in some human GWASs and is especially prevalent in animal breeding programs.⁶⁶ Prediction with PGSs in the presence of related individuals is often carried out based on models that are relevant to or are extensions of linear mixed effect models (LMMs) and best linear unbiased predictors (BLUPs).³⁶ For example, BSLMM is an extension of a LMM and has been widely used for predictions in animal breeding program with heavy individual relatedness as well as related human GWASs.^19,66,67,68 As a multivariate extension of BSLMM, mtPGS models small-effect SNPs to capture the shared polygenic components underlying the traits and thus the individual relatedness. Consequently, mtPGS is expected to capture well the individual relatedness that may be encountered in certain GWASs. Certainly, future efforts are needed to validate this expectation in GWASs with related individuals.

The modeling framework of mtPGS is general and can be extended to incorporate external information such as SNP functional annotations to further improve prediction accuracy. Specifically, we can modify the prior assumption on the effect size of each SNP to be dependent on its functional annotations and then rely on the data to inform us of the contribution from each annotation. Incorporating SNP functional annotations into the prior SNP effect size distribution and inferring their contribution is known to improve prediction performance.^16,69,70 Unfortunately, incorporating SNP functional annotations increases the mtPGS model complexity, making it challenging to obtain an analytic solution for the SNP effect size estimates and thus likely require future development of alternative fitting algorithms.

Data and code availability

The UK Biobank data are from UK Biobank resource under application number 24460. mtPGS is implemented in the mtPGS software, freely available at https://github.com/xuchang0201/mtPGS.

Published: September 15, 2023

Web resources

• DBSLMM, https://github.com/biostat0903/DBSLMM

• GECKO, https://github.com/borangao/GECKO

• GEMMA, http://xzlab.org/software.html

• LDAK, https://dougspeed.com/single-predictor-analysis/

• LDpred, https://github.com/bvilhjal/ldpred

• LDSC, https://github.com/bulik/ldsc

• MegaPRS, https://dougspeed.com/megaprs/

• MTAG, https://github.com/JonJala/mtag

• mtPGS, https://github.com/xuchang0201/mtPGS

• PLINK, https://www.cog-genomics.org/plink/

• PRS-CS: https://github.com/getian107/PRScs

• SBLUP, https://yanglab.westlake.edu.cn/software/gcta/#SBLUP

• UK Biobank-Neale lab, http://www.nealelab.is/uk-biobank

• UK Biobank, https://www.ukbiobank.ac.uk/

• wMT-SBLUP, https://github.com/uqrmaie1/smtpred

• XPXP, https://github.com/YangLabHKUST/XPXP