Demographic modeling of admixed Latin American populations from whole genomes

Summary

Demographic models of Latin American populations often fail to fully capture their complex evolutionary history, which has been shaped by both recent admixture and deeper-in-time demographic events. To address this gap, we used high-coverage whole-genome data from Indigenous American ancestries in present-day Mexico and existing genomes from across Latin America to infer multiple demographic models that capture the impact of different timescales on genetic diversity. Our approach, which combines analyses of allele frequencies and ancestry tract length distributions, represents a significant improvement over current models in predicting patterns of genetic variation in admixed Latin American populations. We jointly modeled the contribution of European, African, East Asian, and Indigenous American ancestries into present-day Latin American populations. We infer that the ancestors of Indigenous Americans and East Asians diverged ∼30 thousand years ago, and we characterize genetic contributions of recent migrations from East and Southeast Asia to Peru and Mexico. Our inferred demographic histories are consistent across different genomic regions and annotations, suggesting that our inferences are robust to the potential effects of linked selection. In conjunction with published distributions of fitness effects for new nonsynonymous mutations in humans, we show in large-scale simulations that our models recover important features of both neutral and deleterious variation. By providing a more realistic framework for understanding the evolutionary history of Latin American populations, our models can help address the historical under-representation of admixed groups in genomics research and can be a valuable resource for future studies of populations with complex admixture and demographic histories.

Drawing from whole-genome data, we infer detailed demographic models for Latin American populations. Our models connect ancient demographic events with recent admixtures, highlighting the often-overlooked Asian migrations in Latin America. These models provide greatly improved accuracy for genomic studies of admixed populations, especially those based on simulations.

Introduction

Genetic diversity among human populations has been shaped by recurrent periods of migration and admixture.¹ Relatively recent admixture across Latin America has resulted in a rich and complex history, shaped by the mixing of ancestries from multiple regions, including Indigenous American, European, and African populations. Each of these populations has its own unique demographic history, both prior to and following their arrival to the continent.^2,3,4 As a result, the genetic composition of Latin American populations depends on both the shared broad-scale history of global human expansion and distinct regional admixture events, leading to patterns of genetic diversity that can vary markedly among Latin American populations and between individuals. However, there is currently a lack of historical models that accurately capture the demographic history and genetic composition of Latin American populations.

Accurate demographic models are essential for investigating a range of evolutionary, epidemiological, and ecological questions, as well as for simulating realistic genetic data.^5,6 But despite the importance of understanding the demographic dynamics of Latin American populations, current models often fail to fully capture the heterogeneity of their genetic diversity. One limitation is that such models do not incorporate the diverse ancestries that have contributed to the genetic makeup of Latin American populations. For example, previous studies have used East Asian populations as a proxy for Indigenous American ancestries,^7,8 despite the genetic divergence between present-day Indigenous American and East Asian individuals due to many thousands of years of isolation and serial founder effects during the peopling of the Americas.^9,10,11,12

Current models are also limited by simplistic admixture histories, which do not accurately reflect the complexity of admixture in Latin American populations.^8,13 Admixture histories in the Americas vary across geographical regions,^4,14 and Latin American populations have experienced admixture events that involved additional populations beyond those typically considered in demographic models. For example, admixture events in Mexico have also involved individuals who descended from East and Southeast Asian populations.¹⁵ This highlights the need for more nuanced models to fully capture the diverse ancestral contributions to the genetic makeup of present-day populations.

The demographic histories of Latin American populations comprise both recent and deeper-in-time processes that shape patterns of genetic diversity.^16,17,18 Inferring demographic models for these cohorts is challenging, as it requires considering multiple historical timescales. At the most recent timescale, admixture between source populations with different present-day genetic ancestries has resulted in a mosaic of genetic ancestry in Latin America. In turn, variation within contributed ancestries has been shaped by the demographic histories of each source population. This deeper-in-time history therefore also contributes to genetic diversity among Latin Americans.¹⁹ To fully capture the intricate histories of these populations, it is therefore essential to consider both of these timescales jointly in demographic inference.

Here, we infer more comprehensive demographic models for multiple cohorts in Latin America that better capture the complex and multifaceted history of these populations. To do this, we employed high-coverage whole-genome sequences from worldwide populations and from across Latin America, including Colombia, Mexico, Peru, and Puerto Rico (Figure 1). We also included 50 recently sequenced individuals of Indigenous ancestries from Mexico, which provide increased resolution to distinguish East Asian and Indigenous American ancestries.^3,20 We integrated demographic inferences at different timescales using the distributions of allele frequencies within and between populations and the numbers and lengths of ancestry tracts within individuals. Using extensive genetic simulations, we show that the resulting models accurately reflect multiple features of genetic variation observed in Latin American cohorts.

Figure 1.

Populations used for demographic reconstruction

(A) Map showing the approximate sampling locations and the population names and codes. Numbers in parentheses denote the number of sampled individuals. Latin American cohorts are marked with a cross.

(B) We used ADMIXTURE (with K = 4) to visualize ancestry proportions of source populations and those from Latin America. The plot reveals substantial variation in ancestry proportions both across populations and among individuals within populations.

Our inferred demographic models can be coupled with models of selection or quantitative traits to explore the joint effects of demography and selection in shaping genomic variation. We demonstrate this application by recovering patterns of variation among missense and nonsense mutations in protein-coding genes. This approach can be extended to model the genetic basis of disease susceptibility and other traits in Latin American cohorts and should serve as a valuable resource for researchers studying evolutionary and medical genomics in Latin American cohorts and other populations with a recent genetic mixture.

Subjects and Methods

Whole-genome data and quality control

We used two high-coverage whole-genome datasets to investigate the demographic dynamics of Latin American populations. The first dataset was the 1000 Genomes Project (1KGP),²¹ which provided 30× high-coverage genomic data from the NYGC that was mapped to the GRCh38 reference genome. We selected reference samples for Africa (AFR), Europe (EUR), and East Asia (EAS) from this dataset; specifically, we used 108 Yorubans from Ibadan Nigeria, 107 Iberians from Spain, and 103 Han Chinese from Beijing, respectively. In addition to these reference samples, we also used data from admixed cohorts within the 1KGP, including 60 Mexicans from Los Angeles (MXL), 104 Puerto Ricans from Puerto Rico (PUR), 94 Colombians from Medellin (CLM), and 85 Peruvians from Lima (PEL), to infer admixture history. The second dataset was from the MX Biobank (MXB) project^3,20 and included 50 high-coverage whole genomes from Indigenous American (AME) descendants in present-day Mexico.

To combine the datasets from the 1KGP MXB projects, we used the CrossMap²² tool to liftover the MXB genomes from the GRCh37 reference genome to the GRCh38 reference genome. Next, we applied two rounds of filters to remove variants that were likely affected by genotyping error or batch effects. The first filter, applied to each source population (AFR, EUR, EAS, and AME) separately, removed variants in Hardy-Weinberg disequilibrium with a p value of 10⁻⁴. The second filter, with a more strict Hardy-Weinberg p value of 0.05, was applied with the purpose of removing potential batch effects. In this case, we applied the second filter to the 50 MXB genomes combined with a set of 29 individuals from the 1KGP (2 MXL and 27 PEL) with the highest proportion of Indigenous American ancestries. In addition to these filters, we also removed variants that were located in masked regions of the genome. After applying these filters, we obtained a combined dataset that was used for all downstream analyses in the study.

Admixture analysis

We used the software package ADMIXTURE v.1.3²³ to estimate individual ancestry proportions based on genome-wide single-nucleotide polymorphism (SNP) data. We applied the following filters to the data: SNPs with a minor allele frequency below 0.05 and SNPs with a Hardy-Weinberg equilibrium test p value below 0.001 were excluded. In addition, we filtered SNPs in linkage disequilibrium with each other using a threshold of r² = 0.1. We ran ADMIXTURE with default parameters, specifying the number of ancestral populations (K) to range from 2 to 6. We conducted an evaluation of the cross-validation error across different K values and found that K = 4 yielded the lowest error.

Demographic inference from allele frequencies

To accurately infer the demographic model, we excluded variants located in CpG sites, which have been shown to have highly variable mutation rates and could potentially bias the results.^24,25 To infer the demographic model, we calculated the folded joint site frequency spectrum (jSFS) for intronic, intergenic, and synonymous variants. The jSFS is the distribution of allele frequencies across multiple populations and can be used to infer demographic parameters such as effective population sizes, divergence times, and migration rates.⁷

We used data from the Yoruba in Ibadan, Nigeria (YRI, as a proxy for African ancestries, AFR), the Iberian population in Spain (IBS, as a proxy for European ancestries, EUR), the Han Chinese in Beijing, China (CHB, as a proxy for East Asian ancestries, EAS), and the Indigenous American population in Mexico (as a proxy for American ancestries, AME) (Figure 1). These or related populations contributed to the genetic makeup of present-day Latin Americans¹⁹ and by using the jSFS, we aimed to identify major demographic events that have influenced their genetic diversity. We classified the variants according to their functional effect with VEP v.102.²⁶ We projected the SFS to 40 haploid copies per population, resulting in a jSFS with four dimensions, one for each of the four populations (AFR, EUR, EAS, and AME). The projection of the jSFS to a smaller sample sizes retains information from the full dataset but reduces the effective sample size so that inference is computationally tractable.

To infer demographic parameters, we used the model moments as our inference engine due to its ability to handle inferences for more than three populations using a diffusion approximation.²⁷ We adopted a two-step approach to infer demographic parameters. In the first step, we inferred a three-population out-of-Africa model (AFR, EUR, and EAS),^7,27 which included 14 parameters such as effective population sizes, split times, and migration rates. In the second step, we included the Indigenous American population as branching out from the ancestors of the East Asian population and inferred three additional parameters: the AME split time from EAS, the bottleneck size, and the population expansion rate (Figure 2A). We performed this same inference for each class of putatively neutral jSFSs (intronic, intergenic, and synonymous). To account for uncertainty in the parameters, we divided the genome into non-overlapping windows of 10 Mb and calculated the jSFS and scaled mutation rates for each window. We generated bootstrap replicates from these windows (n = 288) by sampling with replacement and used a Godambe Information Matrix (GIM) approach²⁸ to estimate parameter uncertainties. Reported confidence intervals from the GIM account for uncertainty due to sampling variance and a finite genome. Uncertainty in estimated mutation rates or average generation time are unaccounted for, so true uncertainty is likely larger than the reported uncertainties using the GIM. However, we expect model and parameter uncertainty to be larger than that of mutation rates and average generation times.

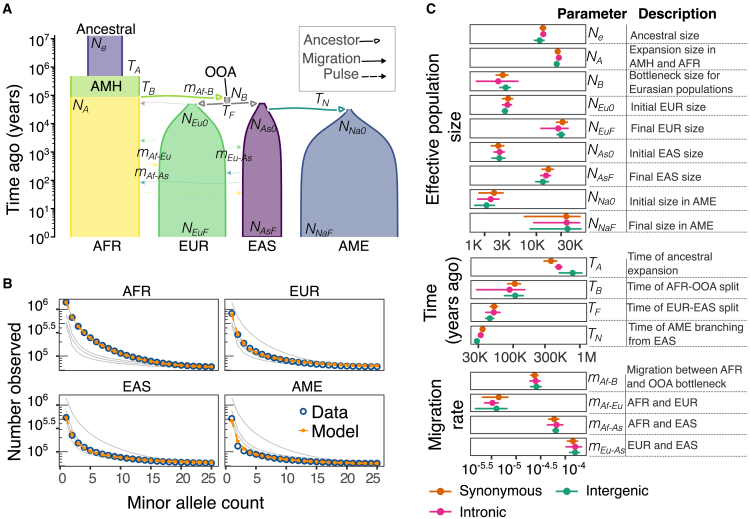
Figure 2.

Inference of continental population history from allele frequencies

(A) Scheme of the inferred model. Widths are proportional to the effective population size, and fonts in italics show the name of the inferred parameters. Abbreviations: anatomically modern humans (AMH) and out-of-Africa (OOA).

(B) Comparison between the folded intronic SFS for the data (blue) and the model’s prediction (orange). Background lines (gray) show the model’s prediction in the rest of the populations.

(C) Comparison of estimated parameters with different sets of SNPs (synonymous, intergenic, and intronic). The error bar denotes the bootstrap confidence intervals (±2 standard deviations). The 95% confidence intervals overlap between annotations for the vast majority of inferred parameters.

Estimation of mutation rates

To convert genetic to physical units (i.e., event times in generations and effective instead of relative population sizes) we required estimates of total mutation rates in retained genomic regions. To estimate this scaled mutation rate, μL, for non-coding (intronic and intergenic) and coding (missense, synonymous, and loss-of-function) regions of the genome, we first subset the genomic coordinates for these regions. For intergenic and intronic regions, we counted the occurrence of each triplet context (excluding CpG contexts) and used the corresponding total mutation rates for each possible mutation for each triplet context, obtained from the gnomAD mutation model,²⁴ to weight the counts. We then summed the weighted counts for all triplets to estimate the scaled mutation rate for non-coding regions. For coding regions, we generated a file with every possible mutation (as bi-allelic SNPs) in the coding regions of the genome and used VEP v.102 tool to predict the consequence of each variant.²⁶ For each consequence (synonymous, missense, or nonsense), we counted the occurrence of each triplet and used the same approach as for non-coding regions to estimate the scaled mutation rate.

Accounting for background selection

Within each of the non-overlapping 10 Mb genomic windows described above, we used estimates of the strength of background selection proposed by McVicker et al.²⁹ to partition data. Within each 10 Mb interval, we computed the weighted mean of McVicker’s B value over that interval. We then stratified windows into four quartiles predicated on the estimated B values. We then executed the same inference process detailed above within each of these quartiles.

Local ancestry inference

We used Gnomix³⁰ to infer the ancestry of specific ancestry segments within the Latin American genomes. We first constructed a reference panel consisting of individuals with known African, European, and Indigenous American ancestries. We selected the Yoruba population (YRI = 108) to represent West African ancestries, the Iberian population in Spain (IBS = 107) and the British in England and Scotland (GBR = 91) for European ancestries, and a combination of MXB Indigenous American samples (n = 50) with 30 1KGP individuals with high Indigenous American ancestries proportions from Peru (PEL = 28) and Mexico (MXL = 2) for Indigenous American ancestries. In addition, we also generated a reference panel including East-Asian ancestry, using the Han Chinese population (CHB = 103) as a reference. We then trained two Gnomix models using these two reference panels, using the default settings which are optimal for whole-genome data and setting the phase parameter to True, in order to re-phase the genomes using the predicted local ancestry. Finally, we used these models to predict the local ancestry in each of the Latin American genomes.

Inference of admixture history

To infer the admixture history, we used the ancestry tract length distribution obtained from the Gnomix output, which we collapsed into haploid ancestry tracts. We analyzed the admixture dynamics independently in each Latin American cohort (MXL, PEL, CLM, and PUR). We evaluated five different admixture models with tracts³¹: ppx_xxp, ppx_xxp_pxx, ccx_xxp, ppx_ccx_xxp, and ppc. The order of each letter in these models corresponds to the order of the source ancestries (AMR, EUR, and AFR), with an underscore indicating a distinct migration event. A “p” represents an ancestry pulse (e.g., xxp is a pulse from AFR ancestry), “c” indicates continuous migration, and “x” indicates no input. We selected these models for analysis because they cover a range of plausible admixture history scenarios and have been previously tested in similar cohorts.^32,33,34,35

To account for the uncertainty in estimated parameters, we generated 100 bootstrap replicates of the ancestry tract distribution by randomly sampling individuals with replacement. For each replicate, we calculated the Bayesian Information Criterion (BIC) to determine the best-fit model. The selected model for each population was based on the BIC as well as agreement with historical evidence when more than one model provide comparable fits to the data. Local ancestry inference identified $\approx 0.5\%$ East Asian ancestry in the MXL and $\approx 1\%$ EAS ancestry in PEL, but $\lesssim 0.2\%$ EAS ancestry in the PUR and CLM cohorts. We therefore explored four-source models for both the MXL and PEL. For the MXL population, we used our best-fit model from the three population inference (the ppx_ccx_xxp model) and added a pulse of East Asian ancestry occurring simultaneously with the African pulse.¹⁵ We optimized this model by exploring the parameter space to find the best fit parameters (modeled as ppxx_ccxx_xxpp, where the fourth population index accounts for EAS-associated migration). For the PEL population, we adapted our best-fit three-population model (ppx_ccx_xxp) to allow for a more recent EAS-associated pulse (modeled as ppxx_ccxx_xxpx_xxxp).

Combining tracts and moments inferences

We integrated our demographic inferences from allele frequencies and tracts into a unified model. To do so, we used demes³⁶ to combine the parameters. In order to account for variations in the generation time, we used a value of 29 years.³⁷ This enabled us to transform the parameters from tracts and moments (e.g., the timing of divergence and admixture events) from generations to years in the past.

Neutral simulations

To ensure the accuracy of our demographic model, we conducted coalescent simulations of neutral genetic sequence data. We used msprime^38,39 to implement the classical coalescent with recombination model (Hudson’s algorithm) for the majority of the simulation, and for the most recent 20 generations we employed the discrete-time Wright-Fisher model,⁴⁰ which better accounts for large sample sizes and genome lengths and provides more accurate patterns of identity-by-descent and ancestry tract variation in admixed populations. To further verify the correctness of our model, we used multiple simulation engines to compare to observed data, including msprime, fwdpy11, and moments. We used tskit for downstream analysis of the simulated genomes.

PCA analysis

We performed a principal component analysis (PCA) on three datasets using the scikit-allel software.⁴¹ The three datasets were (1) observed genotypes, (2) simulated genotypes generated by our model, and (3) simulated genotypes generated by the Browning et al. model.⁸ For the PCA analysis, we excluded all singleton variants. We also performed linkage disequilibrium (LD) pruning by removing variants in high LD (r² > 0.1). The PCA analysis was conducted separately for each dataset.

Computing linkage disequilibrium

We computed linkage disequilibrium (LD) to compare LD decay between data and model predictions. LD was computed as ${\sigma }_d^2=\mathbb{E}\left[D^2\right]/\mathbb{E}\left[p\left(1-p\right)q\left(1-q\right)\right]$, where D is the standard covariance measure of LD, and p and q are allele frequencies at the two loci.⁴² ${\sigma }_d^2$ is closely related to the squared correlation r² but has the advantage that model predictions can be directly computed.^43,44 We binned pairs of intronic and intergenic variants by their recombination distance, using the HapMap genetic map lifted over to GRCh38 coordinates,^45,46 with 18 bins roughly logarithmically spaced between 0 and 1 cM. For each population (YRI, CHB, IBS, AME, and MXL), we computed three LD decay curves: (1) from the real data using software that returns unbiased LD estimates from unphased data,⁴⁷ (2) neutral expectations computed directly from the model parameterization,⁴⁴ and (3) from individual-based simulations including background selection.⁴⁸ These approaches for computing ${\sigma }_d^2$ (instead of r²) allows for unbiased comparisons when sample sizes differ between populations and avoids any biases due to phasing errors.

Forward-in-time simulations

We performed forward simulations using the software fwdpy11 v.0.18.3.^48,49 Our simulations incorporated our inferred demographic model. To ensure the realism of our simulations, we divided the human genome (autosomes only) into windows of 1 Mb and randomly selected 350 of these regions for simulation. We then analyzed the functional annotation of each of these regions, including intergenic, intronic, and coding sequences, and calculated the corresponding mutation rates. To accurately capture the effects of recombination on evolutionary dynamics, we incorporated a human recombination map for GRCh38 obtained from https://github.com/odelaneau/shapeit4/tree/master/maps into our simulations.^45,46 We incorporated distributions of fitness effects (DFEs) for missense and nonsense mutations, in which nonsense mutations were inferred to be more strongly selected against.⁵⁰ To do this, we employed a multiplicative fitness model that allowed us to examine the influence of selective pressures on the genetic diversity of our simulated populations (Figure S8). In comparing between simulations and data, we aggregated data across the 1 Mb regions of the genome that were simulated. The simulation was run for 152,471 generations, corresponding to the recent history of the five modeled populations. Finally, we sampled individuals from each of the five populations at the present time, with sample sizes matching those of our data.

Results

Inferring the deep demographic history through allele frequencies

We used the joint site-frequency spectrum (jSFS) to infer a demographic model for the broad-scale human expansions that resulted in populations representing sources of ancestry of recent admixture in Latin America. Our inferred four-population demographic model builds upon previously inferred models for the out-of-Africa expansion involving AFR, EUR, and EAS populations.^7,17,27 To include the Indigenous American population, we considered models in which their ancestors branched from those of EAS, introducing three additional parameters: the AME split time from EAS, the bottleneck size, and the population expansion rate (Figure 2A). We used moments²⁷ to fit our parameterized models to the observed jSFS for three putative neutral mutation classes—intergenic, intronic, and synonymous variants—which were fit separately.

Our inferred models for deep population history were consistent with the observed SFS for all three mutation classes (Figures 2B, 2C, and S1; Table S1). The estimated 95% confidence intervals for most parameters overlapped across the three sets of SNPs (Figure 2C; Table S1). This consistency across annotations suggests that our inferred models are robust to differences in selective effects (either direct or linked) between mutation classes. We also evaluated alternative models of population size changes in the AME branch, but these models did not provide a better fit to the data (Figure S2). We found that the inferred AME split time was consistent across all tested models, with values ranging from 29,000 to 33,000 years ago.

Because background selection (BGS) is known to bias demographic inference,^51,52 we evaluated the robustness of our inferred demographic model across genomic regions with different inferred strengths of BGS. We partitioned the genome using McVicker’s B values,²⁹ recalculated the jSFS from each subset, and reinferred the same parameterized model using data from regions of low, medium, and high estimates of BGS. As expected, the SFS in each population is skewed toward rare variants in regions experiencing higher BGS (Figure S3). This did not translate to a perceptible difference in our estimated model parameters, except for the inferred ancestral effective population size (Figures S3D and S4). Ancestral N_e (effective population size) was smaller in subsets with stronger BGS, mirroring the decrease in pairwise diversity across subsets (Figure S3C). The consistency of other demographic parameters across B values suggests that our inferred models are not strongly affected by BGS, supporting previous work showing that SFS-based demographic inference is robust to linked selection at levels expected from the genomic architecture in humans.⁵³

While previously reported models have excluded either the Indigenous American population^8,17 or one or more of the other populations (European, African, and East Asian)^7,12 due to methodological limitations, we reconstructed a broad-scale demographic model for global human dispersal that includes the peopling of the Americas. By including all four populations in our analysis, we were able to provide a model that better predicts allele frequencies in each of these groups (Figures 2A and 2B).

Inferring admixture dynamics in Latin American populations

The recent history of Latin American populations involves multiple periods of immigration and extensive gene flow among different Indigenous American, European, and African populations.^4,16,18 Population genetic methods that rely on the jSFS may not be appropriate for resolving such admixture dynamics, as they typically assume a straightforward admixture process involving only a few ancestral populations and lack the necessary resolution to accurately infer the timing of admixture events that occurred relatively recently. However, by analyzing the ancestry tract length distribution (i.e., the distribution of lengths of continuous ancestry segments from each source population in admixed genomes), we inferred admixture models that include up to four ancestral populations and complex migration events.³¹

Using the distribution of ancestry tract lengths, we inferred admixture histories for four cohorts: Mexico (MXL), Puerto Rico (PUR), Colombia (CLM), and Peru (PEL). To calculate the ancestry tract length distribution, we constructed a reference panel of African, European, East Asian, and Indigenous American ancestries to perform local ancestry inference³⁰ (Figure 3A). We treated each population independently, as admixture histories vary between regions in Latin America,^4,14,16 leading to diverse ancestry patterns (Figure 3B). In each population, we used tracts³¹ to test five admixture models including three source populations: AFR, EUR, and AME (Figure S5 and subjects and methods). These models allowed us to explore a variety of admixture scenarios including single pulses of gene flow, multiple pulses, and continuous migration.

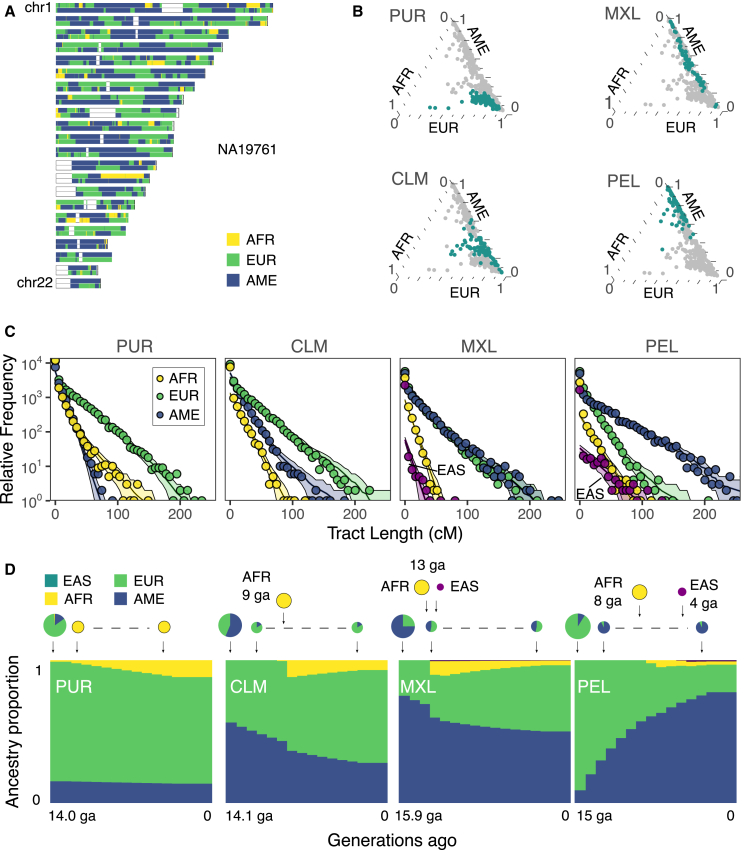
Figure 3.

Inference of admixture history from ancestry tract length distributions

(A) Karyogram with inferred local ancestry tracts (K = 3) in a Mexican individual (MXL).

(B) Ternary plot of ancestry fractions for African, European, and Indigenous American ancestries inferred with ADMIXTURE. Points in blue correspond to the individuals from the population shown, with other populations shown as gray points.

(C) Ancestry tract length distribution of data and best-fit model predictions. Plotted points show the aggregate tract length counts, lines show the maximum-likelihood best-fit tract length distributions for the best model in each population, and shading shows one standard deviation confidence interval, assuming a Poisson distribution of counts per bin.

(D) Scheme of inferred admixture models. Top: pie charts sizes indicate an approximate proportion of migrants in each generation, with the fraction of migrants of each origin in a given generation. The dashed lines connecting the smaller circles denote continuous migration. Bottom: the y axis shows the expected fraction of ancestry in the population over time, and the x axis represents generations ago, 15.9 ga corresponds to c. 1548, and 14 to c. 1604 (1 generation = 29 years).

We used a Bayesian Information Criterion approach (BIC) to compare the fit of these models and select the best-fit model (Figures 3C, 3D, and S6). For Colombia, two of the three-population models provided a good fit to the data based on the BIC: one with a recent discrete admixture event ∼10 generations ago (early 1700s, assuming mean generation times of 29 years), and another that included continuous migration from Indigenous American and European ancestries after an initial admixture event ∼14 generations ago (c. 1600). This second model more closely aligns with known historical events,^54,55 leading us to prefer the model with post-admixture continuous migration. Overall, the models that were selected are consistent with previous studies where admixture histories in Latin America have been explored.^32,33,34

Previous work has identified genetic connections between Mexico and Asia that originated during the Manila galleon trade between the colonial Spanish Philippines and the Pacific port of Acapulco.¹⁵ We identified ∼1% (0.5–1) EAS ancestry among individuals in the MXL cohort using both ADMIXTURE and local ancestry inference (Figure S7). To incorporate this fourth source ancestry, we added an East Asian component to our admixture model for Mexico. We adapted our best-fitting three-population model to include an additional migration pulse from East Asia, occurring at the same time as the African pulse. This choice was motivated by the historical timing of the Manila galleon trade, which coincided with the period of the African slave trade.^56,57 We inferred that this pulse occurred 13 generations ago (early 1600s, Figures 3C and 3D), with initial pulse proportions 0.7% from EAS and 11% from AFR, which is consistent with published estimates.¹⁵

We also identified East Asian-related ancestry in the Peruvian cohort using both ADMIXTURE (0.8%) and local ancestry inference (0.9%). From this, we inferred a four-population admixture model that included an additional migration pulse from EAS. Our findings suggest that an EAS-related migration occurred ∼5 generations ago (mid-1800s) with initial proportion 1.1%. This is considerably more recent than the AFR-related migration, which occurred 8 generations ago (mid- to late 1700s) with initial proportion 5.2%. We did not explore four-source population models for the other cohorts (CLM and PUR), as we observed lower levels of East Asian ancestry in these populations (Figure S7).

Integrating allele frequencies and ancestry tracts: A joint modeling approach for demographic reconstruction in Latin America

We combined our inferences from allele frequencies (Figure 2) and ancestry tracts (Figure 3) to provide a model spanning multiple timescales that shaped genetic diversity in Latin America (Figure 4A). Information from different inference engines (tracts and moments) was integrated using demes,³⁶ a standard format for demographic models in population genetics. In our combined model, we made several assumptions to simplify the analysis and produce a more tractable model. We assumed that the Latin American cohorts (MXL, CLM, PEL, and PUR) are independent of one another and have not experienced recent gene flow between them. We also fixed the effective population sizes (N_e) in admixed populations to a constant value of 20,000 that roughly reflects the present-day N_e in Latin American populations.⁸ We did not infer N_e in these populations because the ancestry tract distribution does not contain information about N_e, and the admixture histories in Latin America are very recent on an evolutionary timescale so that allele frequencies did not fluctuate significantly due to genetic drift.

Figure 4.

Model incorporating both time scales of population history and continental history and admixture dynamics

(A) Visualization of the inferred demographic model. We combined the inferences from allele frequencies and ancestry tracts into a single demographic model. The parameters in red correspond to the parameters estimated from ancestry tracts and the parameters in black were inferred from allele frequencies. The admixed population represents the Mexican population (MXL).

(B) PCA decomposition of genetic data. Left: data chromosome 22; middle: simulation using our inferred model (A); right: simulation using the Browning et al. model. For both models, we simulated a genome of length 50 Mb with msprime. In the data (bottom left) the Indigenous American similarity component is capture by the PC3. This variation is capture in our inferred model (A) but is not present in the simulated genomes from the Browning et al. model,⁸ which uses the East Asian population as a proxy for Indigenous American ancestry.

To validate the accuracy of our joint demographic model, we compared simulated and observed data. We used the coalescent simulator msprime^38,39 to simulate samples for each population under the reconstructed demography (subjects and methods). We compared a principal component analysis (PCA) between the simulated data and observed genotypes on chromosome 22 (Figure 4B). The PCA of simulated individuals closely mirrors those in the observed data (Figure S8), indicating that our model accurately captures broad-scale patterns of genetic diversity in Latin American populations.

PCA uses observed allele frequencies within and between populations, which were also used in the inference of the model. We therefore also examined how well our model captures the decay of linkage disequilibrium (LD) within each population, which was not used in the inference process. Recently admixed populations are expected to show increased LD at distant pairs of loci, while a larger long-term N_e should result in decreased LD. This pattern is observed in the data, with higher long-range LD in the MXL population and lower LD at all distances in the YRI. This pattern is also seen in data simulated under our demographic model, which captured the magnitude of short-range LD and the overall patterns of LD decay (Figure S9A). However, LD decayed faster in our model compared to the data by roughly a factor of 2. This discrepancy does not appear to be due to linked purifying selection, as simulations that included deleterious mutations closely matched neutral model expectations (Figure S9B). Instead, patterns of LD may be more sensitive than allele frequencies to residual population structure within populations, or possible inconsistencies between mutation and recombination clocks could account for the more rapid LD decay in the model.^58,59

To compare to existing models for admixed Latin American populations, we also simulated data under the Browning et al. model of American admixture.^6,8 Using the same simulation and PCA approach, we compared a PCA between this model and real data, finding that our model (Figure 4B) more accurately recapitulates important axes of genetic diversity in Latin American populations. In particular, our model reproduces the variation in Indigenous American ancestries among individuals, as shown by the strong association between the principal component 3 (PC3) and Indigenous American ancestries. In contrast, the Browning et al. model has no association with Indigenous ancestries in PC3, as it uses East Asian ancestry as a proxy for American ancestry.

Simulation of complex demography and selected functional variation

To evaluate the ability of our inferred demographic model to explain patterns of genetic variation under selection, we conducted forward-in-time simulations of non-coding (intergenic and intronic), synonymous, missense, and loss-of-function variants using the fwdpy11 simulation engine.^48,49 We assessed the ability of our demographic model, when combined with inferred models of selection, to explain patterns of genetic variation in different functional categories of the genome.

Missense and loss-of-function (nonsense) mutations are often subject to negative selection because they can have significant impacts on protein function. While non-coding and synonymous variants may be under direct selection due to changes in regulatory elements and codon usage bias,⁶⁰ respectively, here we assumed that they were neutral with respect to selection.^51,61 To simulate selection on nonsynonymous mutations, we incorporated distributions of fitness effects (DFEs) for the two classes of nonsynonymous mutations⁵⁰ (Figure S10; subjects and methods). We simulated a total of 350 Mb of genomic data using our inferred demographic model and spanning various regions of the human genome by sampling from existing recombination maps and genomic annotations (subjects and methods). Due to the computational burden of running forward-in-time simulations, we limited the simulation to only one Latin American population (MXL) jointly with the other source populations (AFR, EUR, EAS, and AME).

We evaluated how well our joint modeling approach matched data from selected mutation classes and assessed any biases within putatively neutral classes due to linked selection. We found that the SFS from simulated data accurately reproduced the SFS from the data for both neutral and selected genetic variation (Figures 5A and S11). Specifically, the SFS fits well for non-coding, synonymous, and missense variants, for which many variants are observed. While there are fewer observed loss-of-function variants, leading to noisier estimates of the SFS, simulated data are largely unbiased across frequency bins (Figure S11). In addition to analyzing the SFS within single populations, we calculated pairwise F_ST between populations. We observed that the simulated F_ST values accurately reproduced those from the observed data (Figure 5B). Together, this modeling approach was able to capture observed patterns of allele frequency variation within and between populations, supporting the utility of our model as a tool for studying complex evolutionary processes in these cohorts through genetic simulations.

Figure 5.

Forward-in-time simulations of functional genetic variation

We simulated a total of 350 independent regions, 1 Mb each, of the human genome by sampling coding annotations and inferred recombination rates.

(A) Comparison between the folded SFS for the data (blue) and the simulation (orange) in different functional categories, summed across all regions. The SFS corresponds to the admixed Mexican population (MXL). Additional populations are shown in Figure S11A.

(B) Box plot of pairwise F_ST values comparing data (n = 350 regions) and simulation (corresponding n = 350 regions). Missense and loss-of-function mutations were combined into a single non-synonymous category.

Discussion

Our study provides comprehensive demographic models for populations in Latin America inferred from high-coverage whole-genome data. These models allow us to examine population dynamics at different time scales, incorporating multiple epochs of demographic history. By inferring a four-population Out-of-Africa model for the deeper demographic history (Figure 2), and using ancestry tract length distributions to infer the recent admixture history in four Latin American cohorts (Figure 3), we were able to create a single model (Figure 4) that jointly captures both allele frequencies and the distribution of ancestry tract lengths. Through extensive simulations, we demonstrated that this model accurately reflects the patterns of genetic diversity present in Latin American populations (Figure 5).

Our inferred demographic models for populations in Latin America represent a significant advance in our ability to accurately account for their evolutionary history in genomic studies. By capturing different aspects of population dynamics, our model provides a powerful tool for studying Latin American populations and understanding the genetic basis of disease in these underrepresented groups.⁶² Populations and individuals with recent genetic admixture are routinely excluded from genomic studies due to concerns over population structure.⁶³ This is due in part to the lack of methods and pipelines to effectively account for shared ancestries and complex demographic histories,^64,65,66 which our study takes steps to address. Past demographic history can also pose a significant challenge to detecting selection, as it can create patterns of genetic diversity that mimic the signatures of selection.^67,68,69 Detailed demographic models are important for controlling for such confounding, allowing for more robust inference of recent selection in Latin American populations. Our models therefore provide a resource for developing and testing methods and pipelines that are specifically tailored to studying admixed populations, improving the accuracy and validity of results obtained from such studies.

Our results reveal a dynamic and multifaceted history. Of note, the inferred AME-EAS split time ranges from 29,000 to 33,000 years ago and it is consistent across all tested models. This suggests that population structure between ancestral groups was already established by this point. This may support the idea of an early migration to the Americas, predating the commonly used time frame of ∼15,000 years ago, or reflect population structure in Siberia, Beringia, and East Asia prior to the expansion into the Americas.^70,71 Importantly, this divergence time does not necessarily pinpoint the exact period of entry into the Americas. Rather, it dates the divergence between the ancestors of Indigenous Americans in Northeast Asia and those of present-day East Asians, and our inferred divergence time aligns with previous estimates.⁷²

Our results also show that the ancestry proportions in Latin American populations have changed over time, with evidence of continuous migration of European and Indigenous ancestries in Mexico, Peru, and Colombia. Similar patterns of changes in ancestry proportions over time have been observed in other admixed populations in the United States.⁷³ This is likely due to both ongoing migrations from Europe to the Americas and migration within the Americas, such as the movement of people from rural to urban areas.^74,75

Recent migration from Asia to the Americas has often been overlooked in genetic studies of Latin American populations. By including data from both East Asian and Indigenous American individuals, we can distinguish between those ancestries in admixed individuals and fit migration models including both sources. We are able to corroborate a previous study that found connections between Southeast Asia and Mexico in the 17th and 18th centuries, associated with the Manila galleon trade.¹⁵ We also find a genetic connection between East Asia and Peru, with admixture occurring in the mid- to late 19th century (Figure 3D). This corresponds with the documented migration of Chinese laborers to Peru during this time period.⁷⁶ Despite high mortality and male-biased migration,⁷⁷ this migration event had lasting contributions to both the cultural and genetic diversity in present-day Peru. Each of these points highlights the importance of considering the heterogeneity of population histories and the historical and cultural interactions of the Americas to understand the demographic history of Latin American populations.

Our models provide valuable insights into the larger-scale demographic history of Latin American populations, but they do not capture all aspects of population history. For example, the arrival of the Spanish in central Mexico led to a significant decline in population size,⁷⁸ which can impact genetic diversity but is not fully captured by our model. With the increasing availability of larger datasets, it will be possible to study more detailed population structure and dynamics using the framework from this study. As we continue to increase the representation of Latin American genomic data, including more whole genomes, we can expect to gain a deeper understanding of the complexity of Latin American population history and to resolve historical processes at finer scales.

Demographic models

The inferred demographic models are provided as supplementary material and in the GitHub repo: https://github.com/santiago1234/mxb-genomes. The model files are in the demes³⁶ format.

• •Model 1 (m1-out-of-africa.yml): four populations out of Africa
• •Model 2 (m2-Mexico-admixture.yml): admixture in Mexico
• •Model 3 (m3-Colombia-admixture.yml): admixture in Colombia
• •Model 4 (m4-Peru-admixture.yml): admixture in Peru
• •Model 5 (m5-PuertoRico-admixture.yml): admixture in Puerto Rico
• •Model 6 (m6-All-admixture.yml): admixture in Latin American populations, combined across models 2–6

Published: September 18, 2023

Web resources

• Code used to process data, infer demographic models, run simulations, and generate visualizations, https://github.com/santiago1234/mxb-genomes

• demes (https://github.com/popsim-consortium/demes-python)

• fwdpy11 (https://molpopgen.github.io/fwdpy11/)

• Gnomix (https://github.com/AI-sandbox/gnomix)

• moments (https://bitbucket.org/simongravel/moments)

• msprime (https://github.com/tskit-dev/msprime)

• tracts (https://github.com/sgravel/tracts)

• tskit (https://github.com/tskit-dev/tskit)

Data and code availability

The 1KGP data^21,79 is publicly available and accessible without restriction. The 50 genomes from the MX-Biobank^3,20 project are deposited in the European Genome-phenoms Archive (EGA) repository, accession number EGAD00001008354.