NNP/MM: Accelerating molecular dynamics simulations with machine learning potentials and molecular mechanics

Abstract

Machine learning potentials have emerged as a means to enhance the accuracy of biomolecular simulations. However, their application is constrained by the significant computational cost arising from the vast number of parameters compared to traditional molecular mechanics. To tackle this issue, we introduce an optimized implementation of the hybrid method (NNP/MM), which combines neural network potentials (NNP) and molecular mechanics (MM). This approach models a portion of the system, such as a small molecule, using NNP while employing MM for the remaining system to boost efficiency. By conducting molecular dynamics (MD) simulations on various protein-ligand complexes and metadynamics (MTD) simulations on a ligand, we showcase the capabilities of our implementation of NNP/MM. It has enabled us to increase the simulation speed by ~5 times and achieve a combined sampling of 1 μs for each complex, marking the longest simulations ever reported for this class of simulation.

Graphical Abstract

Introduction

In the past decade, molecular dynamics (MD) has transitioned from CPU execution to accelerators such as graphical processing units (GPUs). Starting in 2006, CELLMD¹ and subsequently ACEMD² began leveraging GPUs to enhance biomolecular simulations. Numerous other MD codes have either adapted (e.g., AMBER,³ GROMACS,⁴ NAMD⁵) or been initially designed to utilize GPUs (e.g., OpenMM,⁶ HOOMD,⁷ TorchMD⁸). This innovation has improved the cost efficiency of MD simulations by two orders of magnitude.⁹

During the same timeframe, improvements in the accuracy of molecular mechanics (MM) and its force fields (FFs) have not advanced at a comparable pace as the simulation speed. Widely adopted biomolecular FFs, such as AMBER,^10,11 CHARMM,^12,13 and others, offer parameters for proteins and common biomolecules. However, obtaining accurate parameters for novel drug-like molecules remains a challenging task.¹⁴ The recent development of neural network potentials (NNPs) holds promise to address this issue.¹⁵ NNPs leverage the characteristic of neural networks (NNs) as universal approximators, which means they can approximate any function with arbitrary precision relative to the training data. In the context of molecular simulations, NNPs are designed to predict the energy and forces of quantum mechanics (QM) calculations.¹⁶

Recently, numerous NNPs have been proposed (SchNet,¹⁷ TensorMol,¹⁸ AIMNet,¹⁹ PhysNet,²⁰ DimeNet++,²¹ OrbNet,²² PaiNN,²³ SpookyNet,²⁴ NequIP,²⁵ OrbNet Denali,²⁶ TorchMD-NET,²⁷ MACE,²⁸ etc). One of the most used for organic molecules are ANI²⁹ and its derivatives ^30-33 based on a modified Behler-Parrinello (BP) symmetry function.³⁴ For example, the benchmarks of ANI-2x on a set of biaryl fragment, typically found in drug molecules, shows better accuracy than the established general small molecule FFs (CGenFF,^35,36 GAFF,³⁷ OPLS,³⁸ and OpenFF³⁹). The mean absolute error for the entire potential energy profile and rotational barrier heights are 0.5 kcal/mol and 1.0 kcal/mol, respectively,⁴⁰ but it is orders of magnitude faster than its reference QM calculations at the DFT level (ωB97X/6-31G*).³³ However, the BP-type NNPs have several limitations. First, the long-range interactions are not properly accounted for. The NNPs only consider the chemical environment around each atom within a given cut-off distance (5.1 Å for ANI-2x). Second, a limited set of elements is supported (H, C, N, O, F, S, and Cl for ANI-2x). Finally, only neutral molecules can be computed.³³

Despite the current limitations, NNPs are already improving biomolecular simulations. It has demonstrated that the accuracy for drug-like molecules is improved¹⁴ by reparameterizing dihedral angles with ANI-1x.³⁰ Alternatively, the hybrid method of NNP and MM (NNP/MM)⁴¹ allows embedding NNP into a simulation. The main idea of NNP/MM is similar to QM/MM:^42-44 an important region of a system is modeled with a more accurate method, while a less accurate and computationally cheaper one is used for the rest of the system.

Recently, Lahey and Rowley⁴¹ have demonstrated the first application of NNP/MM to protein-ligand complexes. NNP/MM is used to refine binding poses and to compute the conformational free energies. Rufa et al.⁴⁵ have computed the binding free energies of the Tyk2 congeneric ligand benchmark series⁴⁶ using alchemical free energy calculations. Instead of using NNP/MM directly, a non-equilibrium switching scheme has been devised to correct the standard MM calculations to NNP/MM accuracy. It reduces the errors from 1.0 kcal/mol to 0.5 kcal/mol. Vant et al.⁴⁷ have used NNP/MM for the refinement of a protein-ligand complex from cryo-electron microscopy data. The refinement with NNP/MM produces higher-quality models than QM/MM with the semi-empirical PM6 method at a lower computational cost. Xu et al.⁴⁸ have trained a specialized NNP for zinc and used NNP/MM to simulate zinc-containing proteins. The obtained results are in agreement with QM/MM calculations.

A critical limitation for the wider adoption of NNP/MM is the simulation speed. Despite NNP being much faster than QM, it is still slower than MM. For example, Lahey and Rowley⁴¹ and Vant et al.⁴⁷ have reported the simulations speed of 3.4 ns/day and 0.5 ns/day, respectively, on an NVIDIA TITAN Xp GPU. Also, the longest reported simulation is just 20 ns.⁴⁷

In this work, we present an optimized implementation of NNP/MM in ACEMD² based on OpenMM⁶ and PyTorch.⁴⁹ First, the method and relevant optimization strategies are introduced. Second, the capability of software is demonstrated by performing metadynamics (MTD)⁵⁰ simulations of a fragment of erlotinib and molecular dynamics (MD) simulations of four protein-ligand complexes. Finally, the installation and setup of simulations are shown.

Methods

In the NNP/MM approach, a system is partitioned into NNP and MM regions similarly to QM/MM.^42-44 The total potential energy ($V$) consists of three terms:

$$V(\overrightarrow{r})=V_{\text{NNP}}({\overrightarrow{r}}_{\text{NNP}})+V_{\text{MM}}({\overrightarrow{r}}_{\text{MM}})+V_{\text{NNP-MM}}(\overrightarrow{r})$$ (1)

where $V_{\text{NNP}}$ and $V_{\text{MM}}$ are the potential energies of the NNP and MM regions, respectively. $V_{\text{NNP-MM}}$ is a coupling term; $\overrightarrow{r}$, ${\overrightarrow{r}}_{\text{NNP}}$, and ${\overrightarrow{r}}_{\text{MM}}$ are the atomic position of the entire system, NNP region, and MM region, respectively.

It is required that the NNP potential (${\overrightarrow{r}}_{\text{NNP}}$) is a function of the atomic position (${\overrightarrow{r}}_{\text{NNP}}$) and atomic numbers (${\overrightarrow{Z}}_{\text{NNP}}$) of the NNP region. The total charge ($q_{\text{NNP}}$) can be included if necessary:

$$V_{\text{NNP}}({\overrightarrow{r}}_{\text{NNP}})\equiv V_{\text{NNP}}({\overrightarrow{Z}}_{\text{NNP}},{\overrightarrow{r}}_{\text{NNP}},q_{\text{NNP}})$$ (2)

Also, it is required that $V_{\text{NNP}}$ is differentiable with respect to ${\overrightarrow{r}}_{\text{NNP}}$ to compute the atomic forces (${\overrightarrow{F}}_{\text{NNP}}$):

$${\overrightarrow{F}}_{\text{NNP}}=-\nabla V_{\text{NNP}}$$ (3)

In this work, we adapt the coupling term ($V_{\text{NNP-MM}}$) proposed by Lahey and Rowley: ⁴¹

$$V_{\text{NNP-MM}}(\overrightarrow{r})=\sum _i^{N_{\text{NNP}}}\sum _j^{N_{\text{MM}}}(V_C^{i,j}+V_{LJ}^{i,j})$$ (4)

where $V_C^{i,j}=\frac{q_i{q}_j}{4\pi {ϵ}_0{r}_{ij}}$ is the Coulomb potential, $V_{LJ}^{i,j}=4{ϵ}_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{{}^{{}^{{}^{{}^{12}}}}}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{{}^{{}^{{}^{{}^6}}}}\right]$ is the Lennard-Jones potential and $N_{\text{NNP}}$ and $N_{\text{MM}}$ are the number of NNP and MM atoms, respectively; $q_i$ and $q_j$ are the atomic charges; ${ϵ}_{ij}$ and ${\sigma }_{ij}$ are the Lennard-Jones parameters; $r_{ij}$ is the distance between the atoms; and ${ϵ}_0$ is the vacuum permittivity (dielectric constant). In the context of QM/MM, this is known as the mechanical embedding scheme.^43,44

NNP/MM is implemented in ACEMD² using several software components. OpenMM,⁵¹ a GPU-accelerated MD library, is used to compute MM terms and propagate the MD trajectory. OpenMM-Torch, ⁵² an OpenMM plugin, is used to compute the NNP term. It uses PyTorch,⁴⁹ a machine learning framework for NN training and inference on GPUs, to load and execute the NNP on GPU. TorchANI⁵³ is used to create the PyTorch model of ANI-2x.³³ NNPOps,⁵⁴ a library of optimized CUDA kernels for NNP, is used to accelerate critical parts of the computations. Future versions will integrate other NNPs available in TorchMD-NET.^27,55

We have optimized the performance of NNP/MM in three ways. First, all the terms of NNP and MM are computed on a GPU. Neither atomic positions nor atomic forces need to be transferred between the CPU and GPU, as is the case with the original implementation.⁴¹ Second, the featurizer of ANI has been implemented as a custom CUDA kernel and is available in the NNPOps library.⁵⁴ The original featurizer in TorchANI is implemented using only standard PyTorch operations, which are an inefficient way of performing this calculation. Third, the computation is parallelized over the NNs (ANI-2x has an ensemble of 8 NNs) and atoms taking advantage that the same molecule is computed repeatedly. The original implementation in TorchANI computes the NNs sequentially. The original TorchANI version is optimized for batch computing, i.e. many molecules are computed simultaneously, while for MD low-latency computing, i.e. one molecule is computed as fast as possible is necessary. The weights and biases of the atomic NNs are replicated and batched in the same order as the atoms in a molecule, allowing a GPU to efficiently parallelize the calculation for a single molecule. The implementation of the optimized NNs is available in the NNPOps library (https://github.com/openmm/nnpops).

Results and Discussion

Simulations of a fragment

We use metadynamics⁵⁰(MTD) to simulate a fragment (Figure 1) of erlotinib using two models: (1) the conventional MM with GAFF2³⁷ parameters for the fragment; and (2) the NNP/MM where the fragment is modeled with ANI-2x.³³ Lahey and Rowley⁴¹ reported that the fragment has a notable discrepancy between the potential energy surfaces of CGenFF³⁵ and ANI-1ccx.³¹ In this work, we expand the benchmark by computing the free energy surfaces.

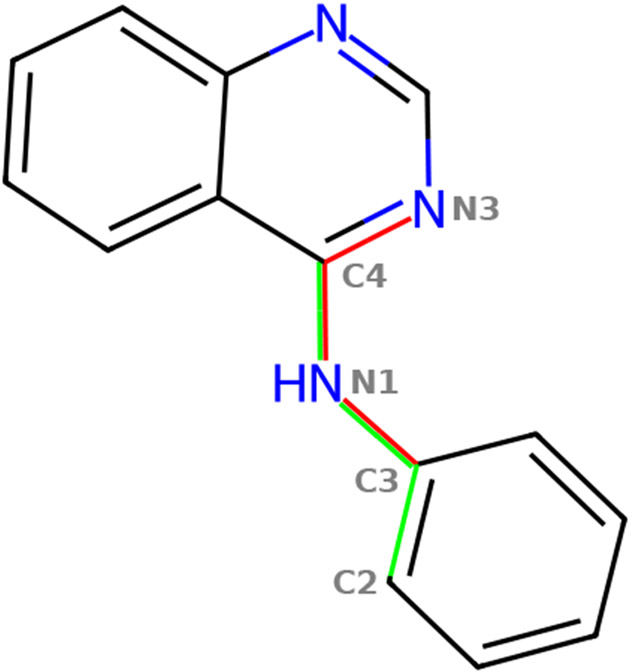
Figure 1:

A fragment of erlotinib. The two dihedral angles used as the collective variable are shown in red and green.

We use the well-tempered MTD⁵⁶ with two dihedral angles (Figure 1) as collective variables. The MTD simulations use the NVT ensemble (T = 310 K), the time step is set to 4.0 fs for the MM simulations, and to 2.0 fs for the NNP/MM simulations because they are unstable with 4.0 fs. For MTD, PLUMED⁵⁷ is used. More details are provided in the supplementary information.

The fragment was simulated for 100 ns with each method. This is sufficient to achieve extensive sampling in the collective variable space. The time series of the dihedral angles (Figure 1) are available in the supplementary information (Figure S1-S2).

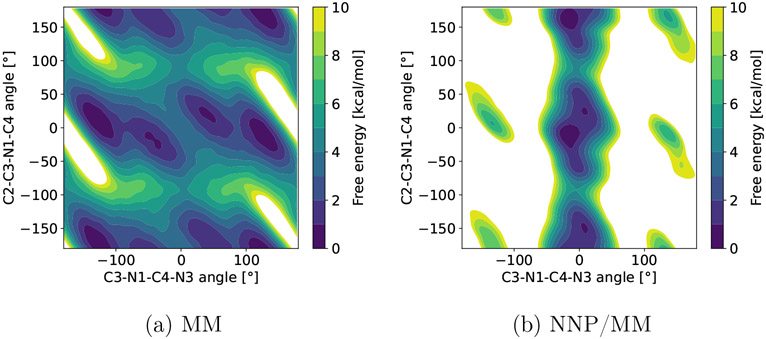
The obtained free energy surfaces (Figure 2) show a significant difference between the models. The dominant conformer of the dihedral angle C3-N1-C4-N3 is predicted by GAFF2 and ANI-2x at ~120° and ~0°, respectively. The fragment has two aromatic rings connected by a conjugated linker, so a planar conformation is expected to be energetically favorable. This is consistent with the potential energy surfaces reported by Lahey and Rowley (see Ref. 41, Figure 3b). Note, the fragment has been chosen for demonstration only and further analysis is beyond the scope of this work.

Figure 2:

Free energy surface of a fragment (Figure 1) of erlotinib computed with MTD using two models MM (a) and NNP/MM (b).

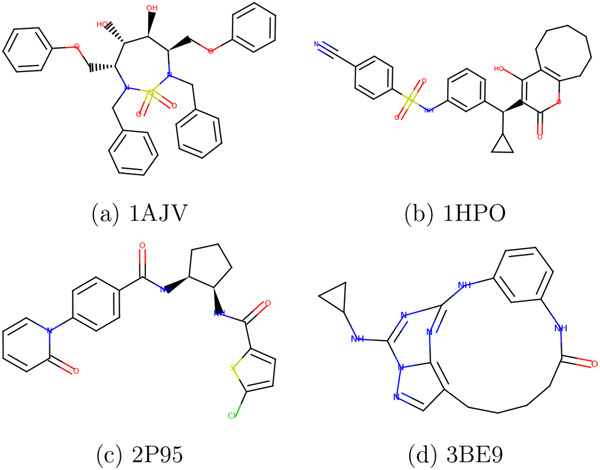
Figure 3:

Ligand structures (a-d) of the selected protein-ligand complexes.

Simulations of protein-ligand complexes

Protein-ligand complexes

We have selected four protein-ligand complexes from PDBbind-2019^58,59 following these criteria. First, the ligand contains only elements supported by ANI-2x (H, C, N, O, F, S, and Cl)³³ and no charged functional groups (amine, carboxylate, etc). Second, the ligand has less than one hundred atoms. Third, the ligand has at least one rotatable bond, and the rotamers energies differ by >3 kcal/mol between GAFF2³⁷ and ANI-2x.³³ We use the Parameterize tool¹⁴ to detect the rotatable bond, scan the dihedral angles of rotatable bonds, and compute the relative rotamer energies. The summary of the protein-ligand complexes is given in Table 1 and the ligand structures are shown in Figure 3. Additionally, the energy profiles of the dihedral angle scan of the ligands are available in the supplementary information (Figure S2-S22).

Table 1:

Summary of protein-ligand complexes.

System	Protein		Ligand		Total atoms
	atoms	residues	atoms	dihedrals
1AJV60	3125	198	75	5	38325
1HPO61	3133	198	64	6	47712
2P95 62	4398	286	50	7	52477
3BE9 63	5451	328	48	2	60412

The protein-ligand complex preparation and equilibration have been carried out with HTMD.⁶⁴ Each complex has been simulated with two different methods: MM, where the ligand is parameterized with GAFF2³⁷ and NNP/MM, where the ligand is modeled with ANI-2x.³³ The protein, in both cases, uses AMBER ff14SB¹¹ FF. The MD simulations use the NVT ensemble (T = 310 K), the time step is set to 4.0 fs for the MM simulations, and to 2.0 fs for the NNP/MM simulations because they are unstable with 4.0 fs. For each combination of a complex and method, 10 independent simulations of 100 ns are performed resulting in the combined sampling of 1 μs. More details are provided in the supplementary information.

Analysis of protein-ligand complexes

All the proteins and ligands maintain their structures in the simulations with both methods (MM and NNP/MM). The protein RMSD fluctuates in the range of 1.8-2.8 Å and the residue RMSF have similar magnitudes when comparing the same protein with both methods. The ligand RMSD fluctuates in the range of 0.2-1.7 Å. In the case of 1AJV and 2P95, there is no significant difference between MM and NNP/MM, but, in the case of 1HPO and 3BE9, the fluctuations are larger by ~0.3 Å for NNP/MM. The time series of protein RMSD, residue RMSF, and ligand RMSD are available in the supplementary information (Figure S23-S34). The difference of the ligand RMSD is expected because, as previous works^14,40,45 indicates, ANI-2x models the dihedral angles more accurately than GAFF. Also, it is important to note that our simulations are 50 times longer than previously reported⁴¹ and have not resulted in any non-physical conformation.

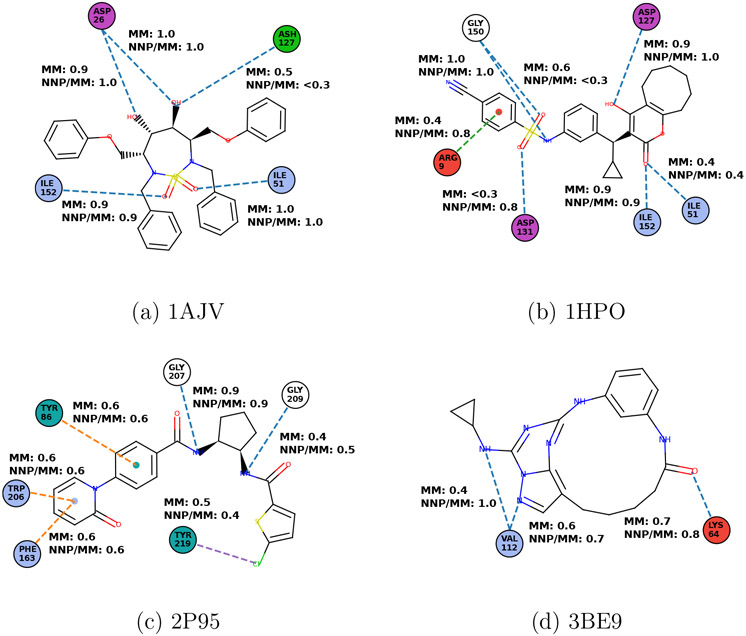
The dominant protein-ligand interactions (Figure 4) qualitatively agree between MM and NNP/MM for all the complexes. The full list of ligand-protein interactions and technical details are available in the supplementary information (Table S1-S8). Note, the protein-ligand systems have been chosen for demonstration only and further analysis is beyond the scope of this work.

Figure 4:

Probabilities of protein-ligand interactions for the different systems and methods (a-d). Protein residues are represented as disks (blue: non-polar, green: polar, red:positively charged, magenta: negatively charged, and dark cyan: aromatic). Interactions are depicted as dashed lines (blue: hydrogen bond, green: cation-π, orange: π-π interaction, and violet: σ-hole). The interactions with probabilities lower than 0.3 are excluded.

Simulation speed

On average, NNPOps⁵⁴ accelerates ANI calculations (energy and forces) 6.5 times (Table 2). The is no strict dependency between the ligand size and the calculation time, which suggests significant overhead is coming from auxiliary operations rather than the computation of NNPs. The overhead mainly comes from PyTorch, which is optimized for batch computing rather than low latency.⁴⁹

Table 2:

Comparison of ANI-2x inference (energy and forces) time (ms) using the original TorchANI and the TorchANI accelerated with NNPOps (TorchANI/NNPOps). The results were obtained with an NVIDIA RTX 4090 GPU.

System	TorchANI	TorchANI/NNPOps	Speed-up
1AJV	11.5	2.17	5.3
1HPO	11.3	1.91	5.9
2P95	13.0	1.54	8.4
3BE9	9.4	1.52	6.2
Average			6.5

Overall NNP/MM is sped up 5.3 times (Table 3) on average when NNPOps⁵⁴ is used. Despite this improvement, NNP/MM is still about an order of magnitude slower than the conventional MM (Table 3), but further optimizations are possible. First, ANI-2x³³ uses an ensemble of 8 NNs. If only one NN could be used, the simulations would be 2.2 times faster on average (Table 3). Second, the time step for the NNP/MM simulations has to be reduced from 4 fs to 2 fs. If the constraint scheme could be adapted to allow 4 fs timestep, the simulations would be 2 times faster. Finally, not all the software components are already fully optimized. For example, the current implementation of OpenMM-Torch (https://github.com/openmm/openmm-torch) performs the NNP and MM calculations on a GPU sequentially, but it would be more efficient to do that concurrently.

Table 3:

Comparison of MD simulation speed (ns/day) of NNP/MM using the original TorchANI, the TorchANI accelerated with NNPOps (TorchANI/NNPOps), and the TorchANI accelerated with NNPOps and just one model of ANI-2x (1 NN). For reference, MM speed is included. The results were obtained with an NVIDIA RTX 4090 GPU.

System	NNP/MM (TorchANI)*	NNP/MM (TorchANI/NNPOps)*	NNP/MM (1 NN)*	MM†
1AJV	12.6	60.1	155	1382
1HPO	13.4	65.9	152	1227
2P95	12.2	73.5	147	1006
3BE9	14.0	74.2	151	995

^*2 fs time step

^†4 fs time step

Extensibility with other NNPs

Our implementation of NNP/MM is agnostic to the NNP model, i.e. it can use any model implemented with PyTorch. As a demonstration, we performed simulations with ANI-1x³⁰ and TorchMD-NET²⁷ trained with the ANI-1 data set.⁶⁵ The simulation speed benchmarks (Table 4) are available just for 3BE9 because both NNPs are limited to 4 elements (H, C, N, and O).

Table 4:

Comparison of MD simulation speed of ANI-1x and TorchMD-NET and their accuracy in mean absolute error (MAE). The results were obtained with an NVIDIA RTX 4090 GPU.

System 3BE9	ANI- 1x*	TorchMD- NET*
speed (ns/day)	127	17.0
accuracy (eV)	0.057	0.010

^*2 fs time step

Software installation and usage

ACEMD can be installed with the Conda package management system.⁶⁶ For dependencies, Conda-forge⁶⁷ is used to ensure compatibility with all major Linux distributions (refer to the ACEMD documentation for details at https://software.acellera.com. The installation command:

$ conda install -c conda-forge \
                -c acellera \
                -c acellera/label/rc \
                acemd=4

For the best performance, it is recommended to have an NVIDIA GPU and its latest drivers installed, but it is possible to run on a CPU only.

The setup of an NNP/MM simulation consists of the following steps. First, a system needs to be prepared for a conventional MM simulation (i.e. initial structure, topology, and force field parameters). Note that the NNP atoms need to be assigned partial charges and Lennard-Jones parameters to compute the coupling term correctly. The system preparation can be easily accomplished with HTMD.^64,68 Second, NNP model files need to be generated with prepare-nnp tool included with ACEMD. It needs the initial structure (e.g. structure.pdb), a selection of the NNP atoms (e.g. "resname MOL"), and a name of NNP

$ prepare-nnp structure.pdb --selection "resname MOL" \
                            --model ANI-2x

The tool generates several files including model.json. Currently, we plan to support the NNP models from TorchANI⁵³ and TorchMD-NET²⁷ but other models will also be supported in the future. Finally, an ACEMD input file needs to be prepared as for a conventional MD simulation (refer to the ACEMD documentation⁶⁹ for details) and needs just one additional line (nnpfile model.json) to enable NNP/MM.

Conclusion

We have showcased an optimized implementation of NNP/MM in ACEMD,² based on OpenMM⁶ and PyTorch,⁴⁹ which delivers simulation speeds of approximately 5 times faster than previously reported. While still slower than classical force fields, the enhanced accuracy of NNPs may justify the increased computational expense (see Rufa et al.⁴⁵). We anticipate this performance gap will continue to shrink in the future. Presently, NNPs have limited applicability due to constraints on charges and elements, but improvements are expected in the near future.

We validated our implementation by conducting metadynamics simulations of an erlotinib fragment and molecular dynamics simulations of four protein-ligand complexes. The fragment simulation results are consistent with prior findings, while the complex simulations exceeded previous durations by over an order of magnitude. These outcomes confirm the effectiveness of our implementation and demonstrate its practical application. Furthermore, NNP/MM can be combined with the enhanced sampling methods (e.g. metadynamics,⁵⁰ replica exchange,⁷⁰ steered molecular dynamics,⁷¹ etc.) and it holds significant potential for alchemical free energy simulations.⁴⁵ It is particularly beneficial for drug discovery efforts, where the simulation of novel molecules is routine but accurate force field parameters may be lacking.