Deciphering viscoelastic cell manipulation in rectangular microchannels

Abstract

Viscoelastic focusing has emerged as a promising method for label-free and passive manipulation of micro and nanoscale bioparticles. However, the design of microfluidic devices for viscoelastic particle focusing requires a thorough comprehensive understanding of the flow condition and operational parameters that lead to the desired behavior of microparticles. While recent advancements have been made, viscoelastic focusing is not fully understood, particularly in straight microchannels with rectangular cross sections. In this work, we delve into inertial, elastic, and viscoelastic focusing of biological cells in rectangular cross-section microchannels. By systematically varying degrees of fluid elasticity and inertia, we investigate the underlying mechanisms behind cell focusing. Our approach involves injecting cells into devices with a fixed, non-unity aspect ratio and capturing their images from two orientations, enabling the extrapolation of cross-sectional equilibrium positions from two dimensional (2D) projections. We characterized the changes in hydrodynamic focusing behaviors of cells based on factors, such as cell size, flow rate, and fluid characteristics. These findings provide insights into the flow characteristics driving changes in equilibrium positions. Furthermore, they indicate that viscoelastic focusing can enhance the detection accuracy in flow cytometry and the sorting resolution for size-based particle sorting applications. By contributing to the advancement of understanding viscoelastic focusing in rectangular microchannels, this work provides valuable insight and design guidelines for the development of devices that harness viscoelastic focusing. The knowledge gained from this study can aid in the advancement of viscoelastic particle manipulation technique and their application in various fields.

I. INTRODUCTION

Hydrodynamic focusing, encompassing both inertial and viscoelastic mechanisms, has attracted attention as a label-free method for particle manipulations with broad applications in biology and industry.^1,2 In both inertial and viscoelastic focusing, injected microparticles laterally migrate within microfluidic channels due to hydrodynamic lift forces until they reach equilibrium positions where all hydrodynamic forces are balanced.^1,2

In inertial focusing, microparticles suspended in Newtonian liquids migrate to their final equilibrium positions through a balance between the wall lift and shear gradient lift forces.^1,3 In the case of straight microchannels, these forces are primarily controlled by channel cross-sectional shape and fold symmetry and fluid flow velocity.^1,3–8 On the other hand, viscoelastic focusing involves suspending microparticles in non-Newtonian fluids where the migration of microparticles is influenced by the combined effects of fluid inertia, elastic forces, shear thinning effects, and secondary flow effects.^2,9–11 Unlike inertial focusing, where the particle equilibrium positions follow the channel's fold symmetry,^3–8 viscoelastic focusing allows control over the number, orientations, and tightness of equilibrium positions independent of the channel's cross-sectional geometry.^12–15 Alterations in the channel's cross-sectional geometry add an extra layer of complexity to this already intricate behavior.^15–17 Moreover, in contrast to inertial focusing, where larger microparticles focus further from the closest channel wall,^3,18,19 viscoelastic focusing exhibits size-dependent focusing behaviors opposite to inertial focusing, where smaller microparticles focus further from the closest channel wall, while larger microparticles occupy positions closer to the wall.^13,20

Commonly cited advantages of viscoelastic focusing over inertial focusing are its ability to manipulate microparticles in the subcellular scale (e.g., exosomes and DNA)^21–23 and a wider dynamic range of flow conditions.² Viscoelastic focusing also exhibits superior resolution in size-based particle sorting applications.^24–26 For example, previous work has shown that viscoelastic focusing in curved and co-flow microchannels can separate microparticles with sub micrometer differences in size,^23–27 which are indistinguishable in inertial focusing. However, to our knowledge, the resolution of size-based sorting using viscoelastic focusing compared to inertial focusing has not been quantitatively investigated in straight microchannels with rectangular cross sections. The investigation of viscoelastic focusing in such devices is of interest due to the inherent sheathless nature, enabling parallelization for throughput enhancement without altering the hydrodynamic conditions experienced by the particle.^4,28,29 Although a few studies have validated the size-based sorting capability of straight devices using binary mixtures containing microparticle with distinct sizes,^13,20 utilizing polydisperse populations would offer a more realistic assessment of the resolutions applicable to biological samples, whose size distribution cannot be precisely controlled prior to the process. Furthermore, it is worth noting that investigations of viscoelastic focusing are often conducted using experimental setups that collect streak images of flowing fluorescent microparticles or stacked images of flowing polystyrene beads.^2,16,30 However, the behavior of polystyrene beads may differ from live cells due to differences in polydispersity and deformability.^5,31 Moreover, streak images may not effectively capture the focusing behaviors of individual cells, especially those that occur infrequently yet exhibit statistical consistency.³⁰ Therefore, an investigation of viscoelastic focusing of viable cells, using data collection methods capable of detecting single-cell level behavior, would enhance our understanding and broaden the applicability of viscoelastic focusing in biological applications.

This study focuses on the lateral migration behavior of a mixture of viable cells in rectangular straight microchannels with inverted aspect ratios but similar dimensions. By flowing cells through rectangular channels with non-unity aspect ratios, we leveraged the dynamic interplay of asymmetric hydrodynamic forces, driven by inertial, elastic, and shear-thinning effects, across the rectangular cross-section due to the reduced fold symmetry when contrasted with square channels. We characterize the flow rate- and cell size-dependent changes in equilibrium position by analyzing high-speed videos recorded at a fixed distance downstream from the inlet (Fig. 1). Custom MATLAB codes were developed to efficiently analyze the large number of frames in these videos while maintaining measurement accuracy. The results demonstrate changes in cell-focusing behavior across the cross-section of the device, and we quantify cell size dependency of both lateral equilibrium position and particle velocity. Additionally, the current work provides insights and guidelines for selecting carrier fluids in microparticle sorting applications and flow cytometry applications, further advancing the field.

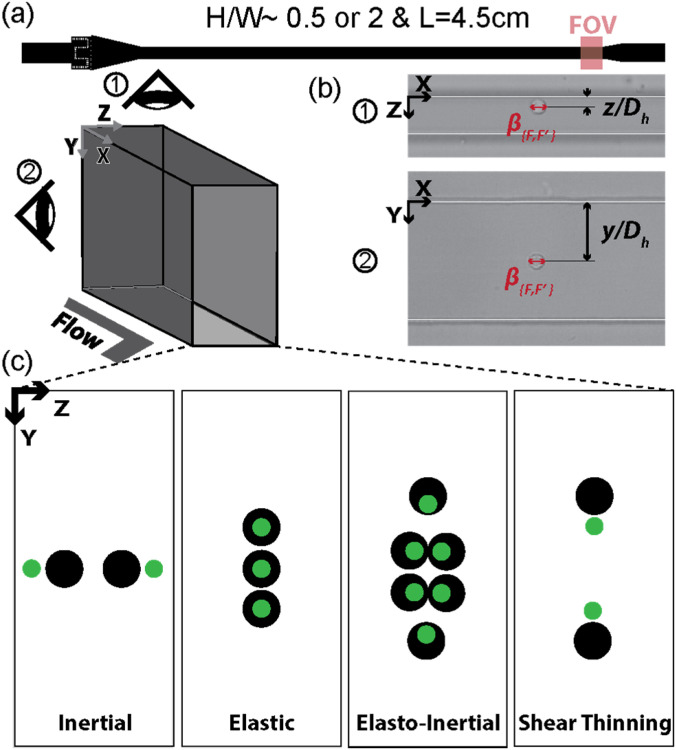
FIG. 1.

Experiment design overview: (a) the schematic depicting the experimental setup. (b) High-speed microscopic images of hydrodynamically focused MIN6 cells in the microchannels with the cross-section of high and low aspect ratios. The high-speed videos were captured at the field of view (FOV) located at 4.5 cm from the inlet. The annotations indicate the dimensionless lateral focusing positions of cells $\frac{y}{D_h}$ and $\frac{z}{D_h}$ and the blockage ratios, $\beta$. (c) The schematics illustrate the cross-sectional cell focusing arrangements under the tested various flow conditions, namely, inertial, elastic dominant, elasto-inertial, and elasto-inertial with strong shear thinning.

II. MATERIALS AND METHODS

A. Microchannel design and fabrication

Straight rectangular microchannels with a low aspect ratio (AR) (H/W ≈ 0.5) and high AR (H/W ≈ 2.0) were fabricated. We utilized devices with similar dimensions but inverted ARs in order to determine cell equilibrium positions across the channel cross-section by observing those in X–Y plane and X–Z plane. Both devices were 4.5 cm long, which was longer than the calculated channel length required to focus cells at their respective equilibrium position. The required channel length was calculated by $\Theta =Wi(L/H){(d_p/H)}^2$ (Refs. 32 and 33), where Wi is the Weissenberg number obtained from experimental measurements. The Weissenberg number is defined as $Wi=\lambda \hspace{0.17em}\gamma \dot{}$. Here, $\lambda$ is the fluid relaxation time, and $\gamma \dot{}$ is the shear rate estimated as $\gamma \dot{}=\frac{2Q}{H{W}^2}=\frac{2V}{W}$.³¹ H is the width of the device (80 μm), $d_p$ is the average diameter of cells obtained from scepter measurements (9.8 μm), $\Theta$ is 1 for particle focusing, and L is the required length of focusing to be calculated. L was 0.4–7.4 mm for 0.05 w/v% PEO solution and 0.17–24.7 mm for 0.2 w/v% PEO solution, implying that cells were expected to be hydrodynamically focused at their respective equilibrium positions near the outlet of our devices (4.5 cm).

Devices were fabricated using standard soft lithography methods. Briefly, the casting mold for our channel was fabricated using a negative photoresist (KMPR 1050, Microchem, USA) with standard photolithography techniques. Microstructures were measured at several points on the mold using a surface profilometer (Keyence VK X100) and stylus profiler (KLA Tencor D-300). Both the low AR and high AR channels had dimensions of 34.5 and 80 μm, respectively (Table S1 in supplementary material). Poly(dimethylsiloxane) (PDMS; Sylgard 184 silicone elastomer kit, Dow Corning, USA) was generated using a 10:1 ratio of PDMS and curing agent. PDMS was degassed and then cured at 60 °C for 24 h. PDMS devices were removed, and inlet and outlet holes were created with a pin vise (Pin vise set A, Syneo). Devices were then bonded to glass slides treated with oxygen plasma (Technics MicroRIE, USA).

B. Microfluidic experimental setup and high-speed imaging

Cell solutions were injected by keeping the solution in a 10 or 1 ml Luer lock syringe (Becton, Dickinson and Company) and connected to devices with Luer-Lock Tip (Becton, Dickinson and Company) and PEEK tubings (1/32” OD, 0.020” ID, IDEX, USA). Solution injection rates were controlled using a standard infuse/withdraw syringe pump (Harvard Apparatus PHD Ultra). To prevent cells from settling, suspended cell solutions were kept vertically, and for solutions in a 10 ml syringe, a small magnetic stir bar was added to the syringe to continuously mix cell solutions.

High-speed videos were acquired near the outlet of the device [Fig. 1(a), ≈4.5 cm from the inlet] using our imaging apparatus, which is capable of visualizing cells traveling at extremely fast velocities (greater than 1 m/s) without motion blur (Fig. S1 in the supplementary material). The setup consists of a high-speed camera (Phantom v2012, Vision Research, Inc) connected to an inverted microscope (Eclipse Ti2, Nikon) with a high-power illumination source (SOLIS-3C, THORLABS). The aperture of the microscope was made smaller to increase the depth of focus of imaging. Videos were recorded at 400–30 000 frames per second, depending on tested flow rates. The location of the focal plane of imaging was manually adjusted using the focusing knob on the microscope.

For low aspect ratio (AR) devices, a video was taken at a single imaging focal plane, and cells flowing both at the focal plane (F) and out of the focal plane (F′) were analyzed (Fig. S2 in the supplementary material). The location of the focal plane was chosen by visually estimating a location where cells were in the focal plane (Fig. S2 in the supplementary material). For high AR devices, high-speed videos were recorded at three imaging focal planes, always less than 15 μm apart centered near the middle of the device (Fig. S2 in the supplementary material). Only cells at the focal plane of imaging (F) were analyzed. The distance between adjacent focal planes was set by using another camera (Photometrics CoolSNAP DYNO) connected to the microscope with associated software (Nikon NIS Elements), which provides quantitative readings of imaging focal plane positions. The focal planes were centered by visually identifying the floor and ceiling of the microchannel.

C. Dimensionless parameters

Reynolds number used in this work was defined as $Re=\frac{\rho v{D}_h}{\mu }$, where $\rho$ is the density of PBS [1.005 584 g/ml at 20 °C (Ref. 34)], $v$ is the average cell flow velocity retrieved from recorded images, $D_h$ is the hydraulic diameter defined as $D_h=\frac{2WH}{W+H}$, and $\mu$ is the dynamic viscosity acquired from the rheometer measurements (Table S2 in the supplementary material). The width (W) and height (H) of the channel are measured to be 34.5 and 80 μm, respectively, by the surface profilometer and stylus profiler. We observed that the polymeric additives, at the tested concentrations, have a negligible effect on the overall density when using the method we employed. Consequently, we adopted the density of PBS, our base buffer, for calculating the Reynolds number across all conditions. In order to visualize cell size dependency of cell velocity, cell speed deviation is calculated as $\Delta V=V-V_{\hspace{0.17em}\beta =0.15}$, where $V$ is the velocity, indicating either non-dimensionalized cell speed, $Re$, or the absolute cell velocity, $v,$ and $V_{\beta =0.15}$ is the cell velocity at β = 0.15 predicted from a linear fit of cell velocity and blockage ratio.

The blockage ratio was defined as ${\beta }_{\{F,F\prime \}}=\frac{a}{D_h}$, where F and F′ indicate whether inertially focused cells are located at the imaging focal plane (bright cells, F) or outside of the imaging plane (dark cells, F′) (Fig. S2 in the supplementary material). It was important to distinctly indicate the dimensionless cell size (i.e., blockage ratio) for cells depending on their equilibrium positions in the direction of imaging because the blurry edges of out-of-focus cells (F′) inevitably yielded larger cell diameter measurements (Sec. SIV and Fig. S3 in the supplementary material). However, we confirmed that the cell position measurements were insensitive to image-crispness; thus, the non-dimensionalized lateral position does not include F (or F′) indices (Fig. S4 in the supplementary material). For low aspect ratio channels, a mean adjusted blockage ratio, β, was calculated to visualize ${\beta }_F$ and ${\beta }_{F\prime }$ on a similar color scale. β was defined as $\beta =\left\{\begin{array}{c}{\beta }_F\\ {\beta }_{F\prime }-({\mu }_{F\prime }-{\mu }_F)\end{array}\right\},$ where ${\mu }_F$ is the average of ${\beta }_F$ and ${\mu }_{F\prime }$ is the average of ${\beta }_{F\prime }$. This could be done because the distribution (Fig. S3 in the supplementary material) and range of β were similar. Note that the recorded range of β values was 0.09–0.35 for F and 0.15–0.42 for F′, which correspond to actual cell diameters of 4.16–17.08 and 7.21–20.09 μm, respectively.

The lateral equilibrium position for cells was calculated as the lateral distance from the channel wall (y or z) divided by the hydraulic diameter, $D_h$. Lateral equilibrium position is defined in terms of hydraulic diameter rather than channel width for comparison of results in low AR and high AR channels. Because lateral equilibrium position was defined by hydraulic diameter rather than channel width, non-dimensionalized location of the channel wall is not equal to one.

The elasticity number, EI, was calculated as $EI=\frac{Wi}{Re},$ where Wi is the Weissenberg number and $Re$ is Reynolds number as previously defined (Fig. S5 in the supplementary material). Q is the volumetric flow rate calculated by $Q=\mathit{HWv}$. Fluid relaxation time for PEO can be estimated using methods outlined by Holzner et al.³¹ EI is defined in terms of Wi rather than Deborah number because Wi is more representative of experimental conditions.³⁵

D. Cell preparation

MIN6 cells (an adherent murine pancreatic beta cell line)³⁶ were kindly provided by Sangwon F. Kim Lab at Johns Hopkins University. Cells were grown in a humidified incubator at 37 °C in a humidified 5% $\mathrm{C}{\mathrm{O}}_2$ environment. Cells were cultured in Dulbecco's modified eagle medium (Gibco, Life Technologies, USA) (D-Glucose: 4.5 g/l, sodium pyruvate: 1 mM, L-glutamine: 4 mM) with additives of 10% FBS (Gibco^®, Life Technologies, USA), 1% 100X penicillin-streptomycin (Sigma-Aldrich Co., USA), 2 mM L-glutamine (Quality Biological 118–084-721EA), 1 mM sodium pyruvate (Gibco^®, Life Technologies, USA), and 0.1% 2-mercaptoethanol (Sigma-Aldrich Co., USA). All MIN6 cells utilized in this study were at passage number lower than 50 and cultured for a minimum of 4 days prior to being harvested for experiments.

Prior to experimentation, cells were dissociated into a single cell suspension by treatment with 0.25% trypsin-EDTA (Gibco, Life Technologies, USA) for 2 min. Trypsin was neutralized using the cell culture medium, and cells were pelleted by centrifugation at 1100 rpm for 10 min. Cells were then resuspended in the desired experimental solution at concentrations of 100 000–150 000 cells/ml. We selected Dulbecco's phosphate buffered saline (PBS) (Gibco, Life Technologies, USA) as the Newtonian base solution (i.e., inertial-only case) to maintain the physiological osmotic pressure of live cells within the fluids. The details on the compositions and preparation processes of the solutions utilized to create non-Newtonian flow conditions are described in Sec. II E. This cell concentration was chosen such that cells in microfluidic channels were always greater than two diameters apart, ensuring minimal cell–cell interactions.³⁷ For cells suspended in PBS, Scepter Handheld Automated Cell counter with Scepter Cell Counter Sensor 40 μm tips were used to assess the size distribution of the cells (Fig. S3 in the supplementary material).

E. Polymer solution preparation and property measurements

Viscoelastic solutions were prepared by dissolving polymeric additives at distinct concentrations. Polyvinylpyrrolidone (PVP), $M_w$ = 360 000 (Sigma-Aldrich Co., USA), at concentrations of 6.8 w/v% in PBS was used to create elastic-only flow condition, and poly(ethylene oxide) (PEO), $M_v$ = 600 000 (Sigma-Aldrich Co., USA), at concentrations of 0.05 and 0.2 w/v% in PBS were used as cell-containing solutions for elasto-inertial and elasto-inertial with the shear thinning effect, respectively. PVP and PEO were selected as polymeric additives because they are biocompatible as FDA approved inactive ingredients for authorized drug³⁸ and widely used in viscoelastic focusing of live cells.^{2,13,17,29,31,32,39–44} Viscoelastic solutions were gently mixed for two days at room temperature to ensure homogeneous solutions. Pure PBS solution, used for Newtonian flow condition, was kept at room temperature for two days to ensure the solution is exposed to similar temperature conditions as viscoelastic solutions. Cell viability tests showed that these tested solutions were not cytotoxic to MIN6 cells (Fig. S6 and Sec. S1 in the supplementary material).

The viscosity of PBS, 0.05 w/v% PEO, 0.2 w/v% PEO, and 6.8 w/v% PVP were measured, using modular compact rheometer (Anton Paar model302) with a cone plate probe with a diameter of 49.980 mm and a cone angle of 0.993 (Anton Paar), and the measurements were 1.04 ± 0.05 cP, 1.28 ± 0.04 cP, 2.43 ± 0.06 cP, and 65.37 ± 7.24 cP, respectively (mean ± standard deviation of the measured viscosity in centipoise, Table S1 in the supplementary material). Shear rates were varied from 400 to 2000 1/s at 20 °C based on previous work by Holzner et al.,³¹ and minimum shear rates required (400 1/s) for accurate measurement of PEO and PBS solution on the rheometer used in this work. PEO solution measurements showed good alignment with theory summarized by Tian et al.⁴⁰ (Sec. S2 in the supplementary material). Rheometer measurements in 0.2 w/v% PEO showed apparent shear thinning behavior not observed in 0.05 w/v% PEO (Fig. S7 in the supplementary material). This finding is consistent with an earlier report, suggesting that higher concentrations of PEO lead to more prominent shear thinning effect.³² This non-trivial increase in the shear thinning characteristics of the PEO solution at higher concentration impacts both viscoelastic and inertial forces and induces cell defocusing toward the channel wall.^13,32 Consequently, we conducted separate investigations involving varying PEO concentration (0.05 and 0.2 w/v%) to isolate and comprehend the distinct influence of the shear thinning effect on the viscoelastic cell focusing phenomenon. The measurements for PVP 6.8 w/v% solution were lower than 90 cP previously reported by Cha et al.⁴³ This was because the rheometer minimum shear rates (400 1/s) used in this work were optimized to PEO and PBS solutions, resulting in a lower readout for PVP solution. Viscosity measurements are further discussed in Sec. S2 in the supplementary material.⁴⁵

F. MATLAB data processing

We developed custom MATLAB codes to facilitate semi-automated image analyses of high-speed videos. These codes enabled the extraction of various measurements, such as cell diameters, focal plane classifications, cell center locations, and channel wall positions, from each video. Our analyses involved processing over 100 000 images per video using a sequence of two successive MATLAB codes. First, a screening code (code 1) was implemented to differentiate frames containing cells from blank frames through background subtraction and thresholding techniques. The background subtraction method involved quantifying the differences between the frame of interest and a background frame without cells (usually the first frame of the video). This process effectively detects pixel indices that potentially correspond to cells, thereby identifying frames with a flowing cell's presence. Subsequently, the detected frames were cropped to isolate cell-containing sections using this information. Then, we employed an edge detection code (code 2), modified from the sample algorithm provided by MathWorks,⁴⁵ to obtain accurate cell position and size from the results of the screening code. This edge detection algorithm significantly influenced the precision of cell position and size determination within images.

Rigorous algorithm optimizations and manual cross-validations were conducted to ensure the reliability of automated detections. As part of our rigorous validation process, we manually cross-verified the detected cell diameters and positions for a randomly selected set of >100 cells per flow condition, and cell sizes were independently validated by comparing them to the independent measurements from a commercial electrical impedance-based cell counter (Scepter 2.0 automated handheld cell counter, MilliporeSigma™, Fig. S3 in the supplementary material).

Given the sensitivity of dimensionless cell positions (i.e., the equilibrium position) to the channel wall detection, we took measures to improve the precision of wall detection, particularly in cases involving irregular shadows near the channel wall. To achieve this, we employed three distinct strategies: (1) calculation using the detected channel wall position, (2) consideration of the overall distribution of cell equilibrium positions relative to the channel core, and (3) utilization of the device's aspect ratio (AR).

Additionally, cell brightness was used to determine whether the detected cells are at the focal plane of imaging (F, bright-cell) or off the focal plane (F′, dark-cell) (Fig. S2 and Sec. S3 in the supplementary material for more details). The acquired measurements were then used to calculate the dimensionless parameters, including Reynolds number, $Re$, blockage ratio (i.e., dimensionless cell size) for cells at the focal plane ( ${\beta }_F$) and outside of focal plane ( ${\beta }_{F\prime }$), and the lateral equilibrium position for cells in the x–y plane, $\frac{y}{D_h},$ or x–z plane $\frac{z}{D_h}$. For PEO solutions, the Reynolds number and average cell velocity are used to calculate elasticity number, EI.

III. RESULTS

A. Inertial force-dominant condition (Newtonian, 10 < Re)

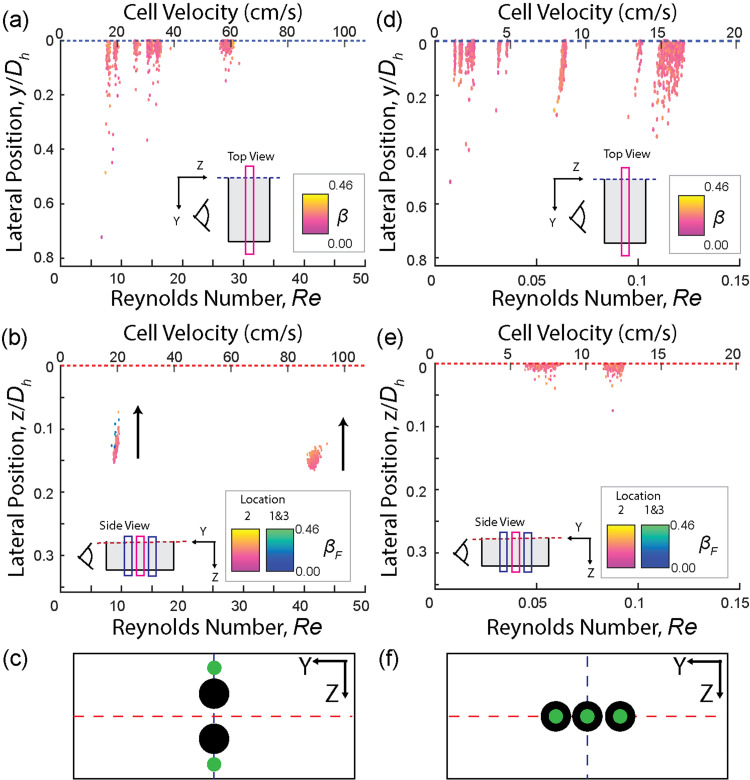
We validated the fluidic and imaging apparatus and analysis methods by evaluating the inertial focusing behaviors of flowing cells suspended in a Newtonian fluid (PBS) through straight rectangular channels and comparing the obtained data to those from previous reports.^3,4,6,46 Cells were injected through two separate channels with inverted aspect ratios (AR ≈ 0.5 or AR ≈ 2) at matched $Re$, such that their inertial focusing equilibrium positions could be extrapolated in the 2D cross-sectional plane (i.e., y–z plane) perpendicular to the injected flow direction (x). In agreement with the literature,^1,3 cells were inertially focused at two parallel focusing streams located at the middle of each long face of the rectangular channel [Figs. 2(a) and 2(c)]. Cell focusing equilibrium positions were independent of cell size (β) in the y direction [Fig. 2(a)], but there exists size dependence in the lateral equilibrium positions of the cells in the z-direction [Fig. 2(b)], where larger cells focus further from the closest channel wall.^3,18,19 Additionally, with increasing $Re$, cell lateral equilibrium positions were distributed more tightly and shifted toward the long-faced wall [Fig. 2(b)].³

FIG. 2.

The lateral focusing positions as a function of the cell flowing speeds (Reynolds number, Re) and color coded by the blockage ratio (β) for purely inertial (PBS, Newtonian) or elastic dominant (6.8 w/v% of PVP in PBS) flow conditions. Note that the lateral position is normalized by hydraulic diameter, (D_h), deviating from the conventional observations that utilize the channel width for Newtonian liquids. The arrows represent an increase in blockage ratio. (a)–(c) Newtonian liquid (PBS) results: cells flown through a (a) low and (b) high aspect ratio channels. (c) Schematic illustrating the focusing behavior in inertial flow conditions, where cells with low and high blockage ratios are color coded in green and black, respectively. (d)–(f) Elastic dominant flow condition (6.8 w/v% of PVP) results: lateral focusing positions of cells in a (d) low and (e) high aspect ratio channel. (f) Schematic illustrating the focusing behavior of cells in elastic dominant flow. Thin boxes within the scatter plots of the cell focusing behaviors indicate the imaging focal plane where the non-dimensionalized cell sizes (β) were obtained. The imaging focal planes were color-coded as pink and dark blue being the focal plane of imaging (F) and off-the focal plane (F′), respectively.

B. Elastic force-dominant condition (non-Newtonian, Re < 1)

We investigated how elastic forces influence the lateral migration of cells without the presence of inertial forces or shear thinning effect by suspending cells in 6.8 w/v% of PVP in PBS solution. PVP exhibits the insignificant shear thinning effect, especially when compared to PEO,⁴⁷ and is highly viscous, allowing for creating elastic force-dominant flow condition with negligible inertial ( $Re$ ≪ 1) and shear thinning effects.^43,48 In agreement with previous reports,^12–14 cells focus at the central plane in the z-direction with a finite focusing width extending in the y-direction of the channel [Figs. 2(d) and 2(f)]. Notably, our analysis method utilizing high-speed images enabled the detection of rare single-cell level behaviors that might have been overlooked in analyses based on time-averaged fluorescent streak images [Fig. 2(d)].

C. Elasto-inertial condition (weakly shear thinning, non-Newtonian, EI = 0.36)

Understanding the combined effects of elasto-inertial forces is essential in comprehending the lateral migration of flowing cells. It goes beyond merely examining the individual influence of inertial force-dominant and elastic force-dominant conditions. These combined forces play a significant role in hydrodynamic manipulations of cells, particularly in cell-focusing behaviors. By considering the interplay between inertial and elastic forces simultaneously, which compete to affect key performance parameters, such as throughput and sorting resolution, we can gain a more comprehensive understanding. This understanding allows us to select the appropriate operational parameters necessary to attain the desired cell-focusing outcome. Ultimately, this knowledge will enable the development of improved strategies for precise and efficient cell manipulation and sorting.

Here, we investigated elasto-inertial focusing with the negligible shear thinning effect by suspending cells in a non-Newtonian weakly shear thinning fluid, 0.05 w/v% of PEO in PBS, instead of using purely elastic solution (6.8 w/v% PVP). This choice was made due to the high viscosity of PVP, leading to device failure at high flow rates. Although 0.05 w/v% PEO was predicted to exhibit a higher shear thinning effect compared to PVP solutions,⁴⁷ our measurement revealed that 0.05 w/v% PEO solution had minimal shear thinning in comparison to 0.2 w/v% PEO (see the rheometer readings in Fig. S7 in the supplementary material) due to the lower concentration of dissolved PEO.³² This selection allowed us to mitigate the shear thinning effect while studying the combined elasto-inertial forces and their impact on cell focusing behaviors.

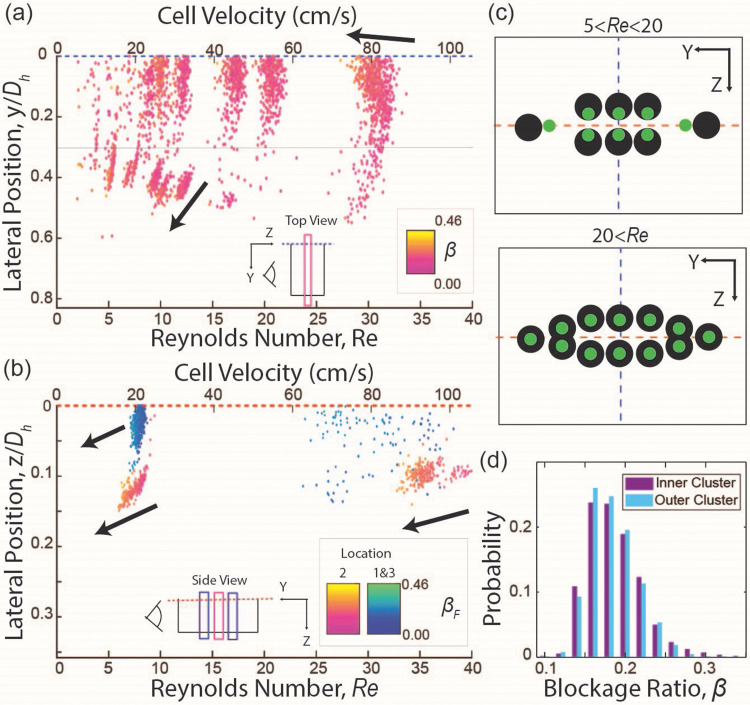
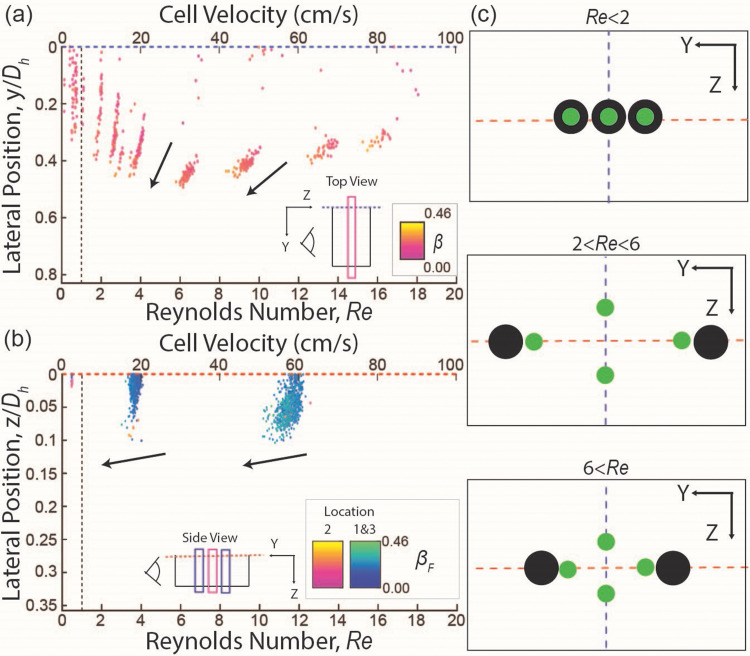
Four equilibrium positions were detected in the cross-section of the device (y–z plane) when $Re<20,$ with each focusing position located at the middle of each face of the channel [Figs. 3(a) and 3(c)]. The focusing streams located at the middle of the short face channel wall ( $0.3<y/D_h$) will be referred to as outer clusters, while cells at the middle of the long face channel wall ( $y/D_h<0.3$) will be classified as cells in inner clusters hereafter [Figs. 3(a) and 3(c)]. Analysis of the overall cell size distribution among cells found in the outer and inner clusters at $5<Re<20$ [Fig. 3(d)] revealed no distinctive differences, suggesting that the two clusters do not represent subpopulations of MIN6 cells with different sizes. While outer clusters form a narrow streamline, the inner clusters occupy a finite focusing width in the y direction, similar to the observed cell focusing behavior from the elastic dominant case [Figs. 3(a) and 3(c)]. Both inner and outer clusters are mirrored across the core of the channel and have cell size-dependent lateral equilibrium positions within each cluster, with smaller cells focusing closer to the core of the channel (Fig. S8 in the supplementary material). Interestingly, both inner and outer clusters exhibit a size dependence in the non-dimensionalized translating velocity of cells, Re, whereby larger cells travel at a slower speed compared to smaller cells at a given bulk fluid flow velocity [Figs. 3, 4, S9(a), and S9(b) in the supplementary material].

FIG. 3.

Results for elasto-inertial flow (0.05 w/v% of PEO in PBS) (a) and (b) lateral focusing position as a function of the cell speeds ( $Re$) and color coded by blockage ratio, (β). (a) Results in a low aspect ratio channel. The gray line at $\frac{y}{D_h}$ = 0.3 represents the cutoff, where cells at 0.3 <  $\frac{y}{D_h}$ are classified as focused in outer clusters, while cells at $\frac{y}{D_h}$ < 0.3 are classified as focused in inner clusters. (b) Results in a high aspect ratio channel. It should be noted that there is a significant spread in the data for locations 1 and 3 at $20<Re$ because of unavoidable variations when centering the focal planes in the y direction. The arrows indicate an increase in the blockage ratio. (c) Schematic illustrating distinct cells focusing behaviors below and above the transition Reynolds number $Re=20$. (d) Histogram of blockage ratio: Probability distribution of blockage ratio for cells focused in the inner cluster and outer cluster in a low aspect ratio channel at $5<Re<15$ was found to be indistinguishable.

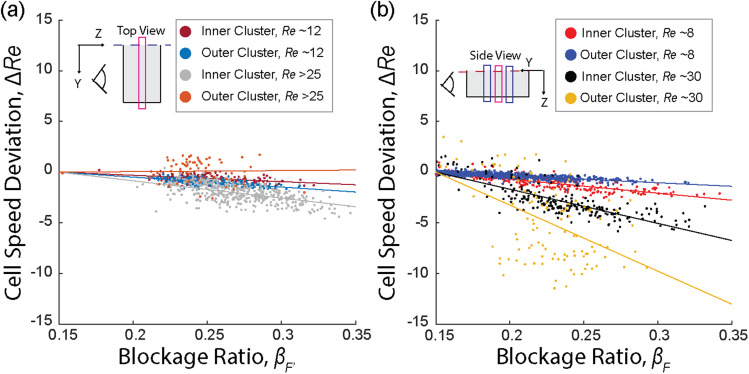
FIG. 4.

Directionality in the size dependency of cell speeds in elasto-inertial flow. (a) Results in a low aspect ratio device: The size-dependent cell speed changes were observed for cells detected outside of the focal plane (cells at F′) in both inner and outer clusters. As the cell size increased, the cell speed decreased with steeper slopes observed at higher $Re$ in the outer cluster compared to the inner cluster. (b) Results in a high aspect ratio device: similar trends are observed, where increasing cell size results in decreasing cell speed. The inner and outer clusters exhibit different rates of decline, with steeper slopes observed in the outer cluster.

As $Re$ exceeds 20, the outer clusters start to defocus, and the cell size-dependency of the lateral positions in these clusters disappears (Figs. 3 and S8 in the supplementary material). On the other hand, the cell size dependency of the lateral position was weakened in inner clusters as indicated by a lower slope magnitude of lateral position vs blockage ratio (Figs. 3 and S8 in the supplementary material). In contrast to the cell size dependency of the lateral position, the cell size-dependent non-dimensionalized cell velocity ( $Re$) is enhanced for the inner clusters in both the y and z directions (Fig. 4), while it is enhanced only in the z direction for the outer clusters. Notably, the cell size-dependent non-dimensionalized cell velocity completely disappears (slope ∼0) in the y direction for outer clusters as $Re$ exceeds 15 (Fig. 4).

D. Effect of shear-thinning on elastic and elasto-inertial conditions (non-Newtonian, EI = 1.7)

In addition to understanding the influence of inertial-only, elastic-only, and inertial-elastic combinations on cell focusing behavior, it is essential to investigate the role of the shear-thinning effect and the interplay between these combined forces in the lateral migration of flowing cells. Such investigations are crucial for selecting parameters that lead to optimum viscoelastic cell manipulation outcomes. In this study, we specifically examined the effect of shear thinning on viscoelastic focusing by suspending cells in a non-Newtonian solution. To achieve a pronounced shear-thinning effect, we utilized a higher concentration of PEO (0.2 w/v%) compared to the concentration we used for evaluating the inertial-elastic combined effect (0.05 w/v%) (Fig. S7 in the supplementary material).

At low flow rates ( $Re<1$), where inertial forces are presumed to be negligible, cells behaved similarly to the purely elastic condition [Figs. 5(a) and 5(c)]. They were focused at the core of the channel with a finite focusing band extending toward the short face channel wall in the y direction. As the flow rate is increased ( $2<Re<6$), the focusing band splits into two bands mirrored over the x–y plane. The distance between these split bands increases with increasing cell velocity ( $Re$), and, within the focusing bands, a clear size-dependency (β vs lateral position) was observed, where smaller cells focus closer to the channel core.

FIG. 5.

Results for purely elastic flow and elasto-inertial flow with strong shear thinning (0.2 w/v% of PEO in PBS) (a) and (b) lateral focusing position as a function of the cell speed, color coded by blockage ratio: (a) results in a low aspect ratio channel, (b) results in a high aspect ratio channel. The arrows indicate an increasing blockage ratio. (c) Schematic illustrating the cell focusing behaviors observed at purely elastic flow ( $Re<1$), elasto-inertial flow at intermediate Reynolds number ( $2<Re<6$), and highly inertial and shear thinning condition ( $6<Re$), where green circles represent smaller cells, and black circle represent larger cells.

With further increases in the flow rate ( $Re>6$), the distance between the two focusing bands decreases, indicating cells are focusing closer to the channel core. However, the size-dependency within bands was still maintained. At these higher flow rates, cells also defocus toward the long face of the channel cross section, resulting in decreased tightness in the z-direction. Similar to the elasto-inertial flow condition, a cell size dependency in non-dimensionalized cell velocity (β vs $Re$) was observed, which became stronger with increased flow velocity [Figs. 7(d), S9, and S11 in the supplementary material]. Additionally, for $2<Re,$ rare occurrences of flowing cells were observed near the middle of the long face channel wall (at y/D_h ∼ 0, z/D_h ∼ 0.1) in both low AR and high AR channels [Figs. 5(a) and 5(b)].

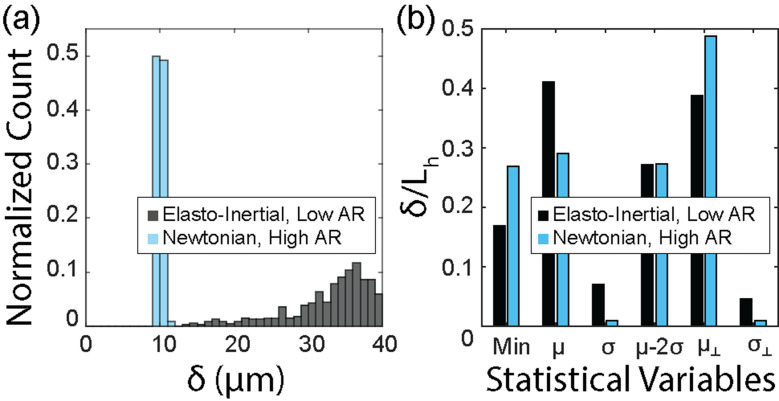
FIG. 7.

Proximity of cell focusing positions to nearest vertical wall in elasto-inertial flow (0.05 w/v% PEO, low AR, 23 < Re) and inertial flow (PBS, high AR, 23 < Re). (a) Histogram illustrating the distance of focused cells from the nearest vertical channel wall. (b) Descriptive statistics of dimensionless distances of focused cell positions from the channel walls. The distance between the channel wall and cell position, δ, was normalized with the characteristic lateral dimension, $L_h$, of the channel. $L_h$ for the high AR and low AR channels was 34.5 and 80 μm, respectively. Here, min, μ, σ, and μ-2σ denote the minimum distance, the mean distance, the standard deviation, and 95% confidence limit of the measurements in the optical detection plane, respectively. The measurements in the plane orthogonal to the optical detection plane are indicated as ⊥.

IV. DISCUSSION

Hydrodynamic focusing, that is the precise manipulations of fluid flow to confine cells in specific spatial regions, plays a pivotal role in advancing the capabilities of flow cytometry and size-based sorting methods. It enables accurate cell analysis and efficient separation based on various biophysical characteristics. In this study, we investigated the distinctive hydrodynamic focusing behaviors of cells observed in rectangular microchannels under three regimes: inertial, elastic, and elasto-inertial flows. Both inertia-only and elastic-only flow conditions can be utilized to focus cells at specific streamlines, confined to a single imaging focal plane. However, as we introduced shear thinning and inertial effects to elastic flow, the interplay between cell size, focusing positions, and flowing speeds became more intricate and complex. This section delves into the implications of these findings, exploring the selection of appropriate flow regimes and device geometries necessary for achieving optimal cell sorting and enhancing cell focusing in flow cytometry applications. Understanding these hydrodynamic behaviors enables us to refine sorting techniques and improve the precision and efficiency of cell analysis.

A. The effects of elastic, shear gradient, and shear thinning on viscoelastic focusing

Our experimental investigation by flowing Newtonian and non-Newtonian fluids through rectangular microchannels with non-unity aspect ratios revealed that the distinctive hydrodynamic focusing patterns can be attributed to the different scaling of the lateral forces responsible for lateral migrations of flowing cells as a function of flow rate ( $Re$). Despite the proportional increase in all hydrodynamic forces involved, including inertial force, elastic force, and shear thinning effect, with increasing flow speed, the elastic force scales with the third power of the flow rate ( $F_e\sim Q^3$), while the inertial lift force scales with the second order of the flow rate ( $F_L\sim Q^2$).^14,49 Moreover, the shear thinning effect adds the complexity of the interplay between the elastic and inertial forces due to non-linear viscosity across the channel cross-section caused by the non-linear velocity gradients of the pressure-driven channel flow.^10,13,14

By testing a wide range of flow rates using fluids with varying degrees of elasticity, inertia, and shear thinning effects, we were able to elucidate the differential influences and directions that these forces induce to achieve the observed hydrodynamic focusing. In a low aspect ratio rectangular microchannel, flowing cell in the elastic dominant regime is focused at the core of the microchannel within a finite width of focusing band confined to a single optical detection plane, z = 0 ( $Re<1$, Fig. 6). This finding agrees with the literature, where particles in elastic dominant flow focus at the center plane where shear is lowest.^12–14

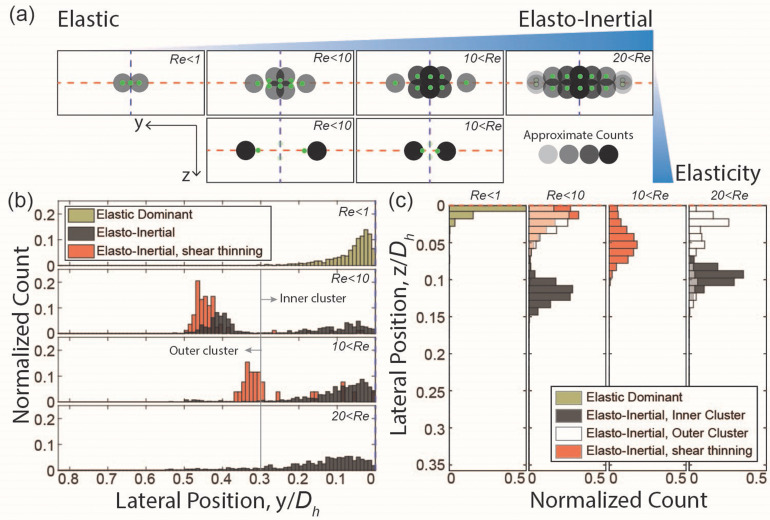
FIG. 6.

Effect of increasing inertia (Re) and elasticity (EI) on cell focusing behavior. (a) Schematic illustrating changes in location, size dependency, and count of cells at each lateral position. (b) and (c) Normalized count of cells as a function of lateral position. (b) Results in a low aspect ratio channel for elastic dominant (6.8 w/v% PVP, Re ≪ 1), elasto-inertial (0.05 w/v% PEO, Re ∼O(10), 15–23, and >23, EI = 0.36), and elasto-inertial with strong shear thinning (0.2 w/v% PEO, Re ∼5–8 and ∼15–20, EI = 1.7) flow conditions. (c) Results for a high aspect ratio channel for elastic dominant (PVP 6.8%, Re ≪ 1), elasto-inertial (0.05 w/v% PEO, Re ∼6 and >25), and elasto-inertial with shear thinning [0.2 w/v%, Re ∼4, and Re ∼ O(10)]. Rare occurrences (<5%) are omitted from data collected for elasto-inertial with shear thinning condition. It is important to note that Re in low AR and high AR channels falls into a similar range, but the absolute values are not identical.

As the inertial force became slightly larger than the elastic force with increasing flow rates beyond $Re=1$ but less than $Re<10$ (i.e., elasto-inertial and viscoelastic inertial regimes), the tightly confined focusing band at the z = 0 plane in the elastic-only regime starts to widen and thicken in both y- and z-directions [Figs. 6(b) and 6(c)]. The increasing magnitude of the inertial force, particularly shear gradient lift force, with increasing flow speed contributes to this outward transition of cell focusing positions from the channel core. This outward transition is preserved only in the y-direction (parallel to the long face of the rectangle) in the fluid with higher polymeric content (i.e., higher viscosity and shear thinning effect), suggesting a higher shear gradient lift force in the z-direction, resulting from sharper velocity gradient, which continues to confine the cell focusing band at z = 0 plane. When the polymeric content is lower, this outward mobility, primarily driven by increasing inertial force in the y-direction, only affects cells already closer to the channel walls, resulting in three cell focusing clusters: one remaining at the channel core and two mirrored at the x–z plane [Figs. 6(b) and 6(c)]. Additionally, in the presence of a stronger elastic force under a similar inertial force magnitude, the symmetrical outward mobility of the focusing band eventually separates the previously single focusing cluster into two mirrored clusters confined to the z = 0 plane. Notably, we observed that smaller cells are slower to respond to this transition, remaining closer to the channel core than larger cells even at higher Re, leading to a size-dependent focusing position within the focusing band (Figs. 3 and 5). This size-dependency of the lateral focusing positions remains unchanged in elasto-inertial flows regardless of the varying degrees of polymeric contents or shear thinning effects.

Beyond the flow rate of $Re=10$, a reversal of the outward movement of the focusing band in the y-direction occurs, resulting in a reduced distance between the outer and inner clusters for the elasto-inertial flow and two mirrored clusters for the viscoelastic inertial flow [Figs. 6(b) and 6(c)]. However, the significant presence of the inertial force prevents the formation of a single focus band confined at z = 0. When the elastic force is sufficiently strong, two mirrored focusing clusters are confined to a single z-plane, maintaining size-dependent focusing (Figs. 3–6). However, when the elastic force is weaker, three focusing clusters exist without size-dependency in lateral positions (Fig. 6). Moreover, beyond $Re=20$, all cells are focused into a band with a finite width and thickness larger than that observed in the elastic-only conditions irrespective of cell sizes.

B. Comparative analysis of flow conditions on hydrodynamic cell focusing

Previous studies have demonstrated the potential of hydrodynamic cell focusing as a means to increase the throughput of flow cytometry applications, achieved through parallelization of straight microchannels and higher fluid flow rates.^4,50–53 In the current work, we investigated multiple flow conditions in microchannels with a non-unity aspect ratio. Among the various flow conditions explored, inertial force dominant (PBS, 10 <  $Re$), elastic force dominant (6.8 w/v% PVP, $Re<1$), and combinations of elasto-inertial forces (0.05 w/v% PEO, $23<Re$) flow conditions ensured that the cell focusing positions were confined within a single imaging focal plane. This confinement is crucial for flow cytometry applications that heavily rely on accurately capturing optical signatures. However, the elastic dominant condition has a fundamental limitation in throughput, where $Re$ cannot be increased beyond one in order to maintain the elastic dominant flow condition. In addition, there are technical limitations where the high viscosity of 6.8 w/v% of PVP in PBS resulted in microdevice failure as flow velocities were increased. Both inertial and elasto-inertial flow conditions showed comparable throughput (cell speed ≈80 cm/s) while tightly focusing cells (Figs. 3 and 4) and do not have the fundamental limitation present in the elastic dominant flow. Furthermore, compared to the inertial flow condition, the elasto-inertial flow condition exhibited cell focusing positions further away from the channel wall, albeit with a wider width of the focusing band (higher standard deviation in the lateral position distributions, Fig. 7). This is often preferable in flow cytometry applications, as close proximity of cells to the channel wall leads to interference in optical signal detections.^54,55

C. Size-dependent focusing behaviors of cells in Newtonian vs viscoelastic inertial flow

We observed size-dependent focusing behaviors in both Newtonian and non-Newtonian inertial flows, revealing distinctive size-dependency directions and orientations influenced by the presence or absence of elastic forces and shear thinning effects. However, when utilizing elasto-inertial flow (specifically, 0.05 w/v% PEO, 5 < Re < 15), the achieved size-dependent focusing ability seemed unsuitable for constructing a simple cell sorting mechanism using bifurcating devices. This is attributed to the radial arrangement of focused particles, where the size of cells progressively increases from the channel's core toward the outer edges. Consequently, the implementation of co-axial devices, which require complex fabrication techniques to create the desired channel geometry, becomes necessary for achieving efficient cell sorting.

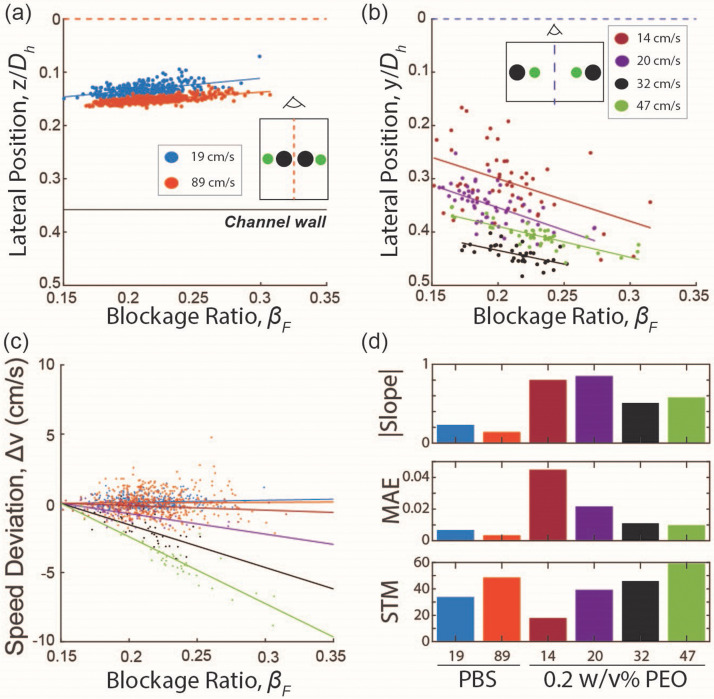
In contrast, size-based sorting using simple microfluidic devices with bifurcating outlets seemed achievable for both Newtonian inertial flow (PBS, 10 < Re) and highly shear-thinning viscoelastic inertial flow (0.2 w/v% PEO, 2 < Re). In Newtonian inertial flow, smaller cells were focused near the channel wall, and their size gradually increased for cells focused closer to the wall of a high aspect ratio channel [Fig. 8(a)]. Conversely, in highly shear-thinning viscoelastic inertial flow, the opposite trend was observed, with larger cells focused near the channel wall and smaller cells positioned closer to the center [Fig. 8(b)]. In addition, in viscoelastic inertial flow, the larger cells focused near the channel walls flowed slower than those smaller counterparts focused near the channel center [Fig. 8(c)]. This observation aligns with the report of Li et al.,⁵⁶ which describes the impact of the shear thinning effect on greater particle-fluid slip velocity for larger cells [Fig. 8(c)].

FIG. 8.

Results for size-dependent focusing behaviors in Newtonian (PBS, high AR) and shear thinning viscoelastic (0.2 w/v% PEO, low AR) liquid, excluding rare occurrences. (a) and (b) Results for lateral position as a function of the blockage ratio in (a) Newtonian liquid at ∼19 cm/s (Re = 10) and ∼89 cm/s (Re = 46) and (b) viscoelastic liquid at 14, 20, 32, and 47 cm/s (Re = 2.5, 4, 6, and 9). (c) Results for the cell speed deviation as a function of the blockage ratio for Newtonian and shear-thinning viscoelastic liquid. The color scheme follows the legend in (a) and (b). (d) Results for the magnitude of the slope, the mean absolute error (MAE), and the magnitude of the slope to MAE ratio (STM) for Newtonian and shear-thinning viscoelastic liquid. The slope is defined as positive for larger cells to be focused closer to the channel center.

We quantified these distinctive and inversing cell-focusing behaviors in Newtonian and viscoelastic inertial flows by determining the slope and mean absolute errors (MAE) of the lateral equilibrium positions, correlated with dimensionless cell size (β) [Figs. 8(a) and 8(b)]. A higher slope magnitude indicates a stronger size dependency while smaller MAE values imply tighter focusing (i.e., a lower probability of overlapping lateral positions of cells with different sizes). Thus, the slope-to-MAE ratio, STM, serves as a metric for predicting the anticipated size-resolution at a given operational flow rate for hydrodynamic label-free cell sorting. As the operational flow rate increases, the focusing tightness increased for both Newtonian and viscoelastic inertial flows, while the magnitude of size-dependency decreased significantly only for viscoelastic inertial flow [Fig. 8(d)]. However, the magnitude of STM was higher for the viscoelastic flow condition for most flow rates owing to a higher magnitude of size-dependency [Fig. 8(d)]. These results indicate that viscoelastic inertial flow would outperform Newtonian inertial flow in terms of anticipated cell sorting resolutions at the optimum flow rate. In contrast, Newtonian inertial flow maintains moderate cell sorting resolutions well beyond the optimum operational flow rate of the viscoelastic inertial flow, suggesting that Newtonian inertial flow is desirable when high throughput of cell sorting is of the highest priority. Overall, our findings suggest that viscoelastic inertial flow is well-suited for cell sorting applications, requiring fine resolutions of size selection with moderate throughput, whereas Newtonian inertial flow is ideal for applications requiring high throughput sorting of cells with relatively large size differences.

V. CONCLUSION

This study presents experimental observations and analyses that advance our understanding of the complex interaction between fluid inertia, elastic forces, and shear thinning effects in hydrodynamic cell focusing using rectangular straight microchannels. Noteworthy phenomena were observed under elasto-inertial flow conditions, where the number and location of focusing positions varied with flow rate. Importantly, we found that, in elasto-inertial conditions, cell focusing positions were further away from the channel wall at higher flow rates compared to inertial focusing. This suggests that elasto-inertial conditions would be preferable for microfluidic flow cytometry applications to minimize optical interference. Moreover, in highly shear-thinning viscoelastic inertial flow, we observed size-dependent focusing behavior of cells, enabling size-based sorting with simple microfluidic devices. Our quantitative analysis predicted superior cell sorting resolution compared to conventional Newtonian devices, although at lower throughput. These findings provide valuable experimental guidelines for the development of microfluidic devices that leverage hydrodynamic focusing. Furthermore, they open possibilities for enhancing current applications of manipulating microparticles in flow. Moving forward, it is imperative for subsequent investigations to delve into the observed phenomena, examining parameters such as microchannel cross-sectional shape and area, cell deformability and shape, polymer aging, molecular weight, and secondary forces. While these factors were held constant in our current study, they undoubtedly merit further exploration in order to comprehensively understand the broader cell focusing dynamics. Furthermore, the development of a computational framework capable of decoupling the distinct contributions of flow characteristics to the observed cell focusing behaviors will undoubtedly enhance the understanding of these phenomena and the ability to control them effectively. By gaining a deeper understanding of these mechanisms, we can further optimize and expand the applications of hydrodynamic focusing techniques.

SUPPLEMENTARY MATERIAL

See the supplementary material for a detailed experimental procedure and supporting results.

AUTHOR DECLARATIONS

Conflict of Interest

S.C.H. benefits financially from royalty payments from Vortex Biosciences, Inc.

Author Contributions

Takayuki Suzuki: Conceptualization (equal); Data curation (equal); Formal analysis (equal); Investigation (equal); Methodology (equal); Project administration (equal); Resources (equal); Software (equal); Validation (equal); Visualization (equal); Writing – original draft (equal); Writing – review & editing (equal). Srivathsan Kalyan: Conceptualization (equal); Investigation (supporting); Writing – review & editing (equal). Cynthia Berlinicke: Conceptualization (equal); Funding acquisition (supporting); Resources (equal); Supervision (equal); Writing – review & editing (equal). Samantha Yoseph: Investigation (supporting). Donald J. Zack: Conceptualization (equal); Funding acquisition (supporting); Resources (equal); Supervision (equal); Writing – review & editing (equal). Soojung Claire Hur: Conceptualization (equal); Funding acquisition (lead); Methodology (equal); Project administration (equal); Resources (equal); Supervision (equal); Writing – original draft (equal); Writing – review & editing (equal).

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.