Multi-task learning for predicting synergistic drug combinations based on auto-encoding multi-relational graphs

Summary

Combinatorial drug therapy is a promising approach for treating complex diseases by combining drugs with synergistic effects. However, predicting effective drug combinations is challenging due to the complexity of biological systems and the limited understanding of pathophysiological mechanisms and drug targets. In this paper, we proposed a computational framework called VGAETF (Variational Graph Autoencoder Tensor Decomposition), which leveraged multi-relational graph to model complex relationships between entities in biological systems and predicted disease-related synergistic drug combinations in an end-to-end manner. In the computational experiments, VGAETF achieved high performances (AUROC [the area under receiver operating characteristic] = 0.9767, AUPR [the area under precision-recall] = 0.9660), outperforming other compared methods. Moreover, case studies further demonstrated the effectiveness of VGAETF in identifying potential disease-related synergistic drug combinations.

Graphical abstract

Highlights

• •An auto-encoding-based computational method for synergistic drug combination prediction
• •Construct a multi-relational graph to model complex relationships between drugs
• •We incorporate multi-task learning to improve the VGAETF’s generalization ability

Health sciences; Medicine; Health technology; Pharmacology

Introduction

Combinatorial drug therapy involves the simultaneous use of two or more compounds to treat a disease, potentially improving therapeutic efficacy through synergistic effects. This approach has gained significant attention and is increasingly utilized in the management and treatment of sophisticated diseases such as cancer, HIV/AIDS,¹ Hepatitis C,² and hypertension.³ Combination therapies offer hope for treating diseases with unmet medical needs. Additionally, drug combinations often involve the use of already approved drugs by the Food and Drug Administration (FDA), which have well-studied toxic properties and side effects. Therefore, patients can safely use these combinations.⁴ Experimental identification of drug combinations with synergistic effects is a time-consuming and costly process, made more difficult by the large amount of potential drug combinations.

Computational methods have emerged as an essential tool for predicting and prioritizing pairs of synergistic drugs. Machine learning algorithms are commonly used to mine potential combination pharmacotherapy from vast amounts of data, providing guidance for clinical trials and reducing costs.⁵ However, it is challenging to extract disease-specific pathophysiological mechanisms and identify drug targets from clinical and laboratory data to predict drug combinations.⁶ To address this issue, researchers have developed innovative approaches that incorporate diverse biological data. For instance, Jiang et al.⁷ predicted synergistic drug combinations for anticancer treatment by building a heterogeneous graph that involves drugs and proteins. Cheng et al.⁸ predicted forecast disease-drug-drug combinations by quantifying the correlations between disease proteins and drug targets in protein interactomes. Li et al.⁹ employed large pre-trained language models, such as generative pre-trained transformer (GPT), to predict the synergistic effects of drug pairs in a few-shot learning scenario. Zhang et al.¹⁰ developed a comprehensive multi-relational graph that incorporates drugs, targets, and enzymes to capture intricate semantic information from diverse entities and utilized drug and cell line embeddings to predict the synergy score of drug combinations. Wu et al.¹¹ improved the deep forest-based method that predicts synergistic drug combinations in cancer cell lines. However, existing prediction approaches rely heavily on pharmacological responses and a thorough comprehension of the genetic and molecular mechanisms of disease, which are often restrictive.¹²

Recently, the embedding of multi-relational graphs has been a valuable tool for drug discovery.¹³ Different from traditional graphs and networks that contain only one type of relationship, the multi-relational graph provides heterogeneous information that comprises multiple entities (e.g., proteins, drugs, and targets) and various types of relationships (e.g., drug-drug interactions or drug-target pairs).¹⁴ Multi-relational graphs utilize nodes to represent entities and edges to represent the relationships between them, providing unstructured semantic relationships between entities.¹⁵ As a result, multi-relational graphs are well-suited for modeling the intricate relationships that exist among entities within biological.¹⁶ By representing biomedical entities as nodes and their relationships as edges in a graph structure, the multi-relational graph is able to learn lower-order representations of entities and relationships simultaneously. This preserves the inherent structure of the multi-relational graph.¹⁷ The learned vectors are used to generate a score for each triplet by a scoring function that gives high scores to true triples and low scores to false ones. This way, the model can infer whether triplets are true or not. Multi-relational graph embedding models include translation-based models like TransE,¹⁸ bilinear models like ComplEx,¹⁹ CP,²⁰ TuckER,²¹ neural network-based models, and graph convolutional networks (GCNs)-based models²² including R-GCN,²³ ComplexGCN,²⁴ etc. Translation-based models treat the relation as a vector that moves the head entity close to the tail entity in an embedding space. The models then obtain a triplet score based on the distance. Bilinear models use multiplicative scoring functions to match the latent semantics of entities and relations, while neural network-based models employ neural network models to learn their interactions. Graph neural networks (GNNs) are used for learning connectivity structure, with the GCN²⁵ acting as a graph encoder.

In this study, we propose VGAETF, an effective framework for predicting disease-related drug combinations by seamlessly integrating drug-oriented and disease-oriented information using multi-relational graph neural networks. We incorporate an auxiliary task of reconstructing the drug-disease relationship matrix and disease-disease relationship matrix to improve the model’s generalization ability. First, we construct a network that involves a drug-disease-drug multi-relational graph, a drug-disease association network, and a disease-disease association network. Second, we then use the variational graph autoencoder to implement a variational inference model that learns the probability distributions of low-dimensional vector representations of drugs. Third, we employ an inner product decoder to learn the representation matrix from disease-resembles-disease and drug-disease relationships and calculate the prediction scores of the triplet facts using tensor decomposition. VGAETF then learns drug and disease features under loss constraints to reveal the underlying structure of drug-disease-drug triplets. Our experimental results show that VGAETF outperforms other compared computational methods in drug combination detection. Furthermore, case studies investigating the effectiveness of VGAETF in predicting drug combinations serve as compelling evidence of its predictive prowess.

Results

The framework of VGAETF

We obtained a dataset from Continuous Drug Combination Database (CDCDB),²⁶ a comprehensive drug combination database containing more than 40,795 drug combinations. We extracted the DrugBank identifiers (IDs) that are related to the FDA Orange Book and the Medical Subject Headings (MeSH) terms that describe the conditions that are treated in the study from our database. The data schema $\left({drug}_i,{disease}_k,{drug}_j\right)$ shows that combining ${drug}_i$ and ${drug}_j$ can treat ${disease}_k$. Among the labeled "Efficacious" drug pairs for one or more diseases, there are a total of 1,105 individual drugs, 1,283 diseases, and 4,709 pairs of drugs. We constructed 59,659 positive samples of drug-disease-drug triplets using this information. In this study, we randomly selected 90% of the positive samples as training data, while reserving the remaining 10% as testing data. Based on the drugs and diseases obtained from the training data, we obtained 26,425 drug-disease associations in the association data. We construct a binary matrix to denote known drug-disease associations in which values of 1 and 0 indicate verified associations and unverified associations between drugs and diseases, respectively. We collate 259 disease-disease associations by Ioannidis, V. et al.²⁷ This dataset contains disease-resembles-disease edges that are based on the co-occurrence of disease terms in PubMed. We also construct a binary matrix that includes two values 1 and 0, denoting validated and unvalidated associations between diseases and diseases, respectively. More details can be found in Table 1.

Table 1.

Statistics of datasets used in this study

Samples	Source	Number
Drugs	Shtar, G. et al.26	1105
Diseases	Shtar, G. et al.26	1283
Training data	Shtar, G. et al.26	53694
Testing data	Shtar, G. et al.26	5965
Drug-disease-drug triplets	Shtar, G. et al.26	59659
Drug-disease associations	Shtar, G. et al.26	26425
Disease-disease associations	Ioannidis, V. et al.27	259

Figure 1 illustrates the structure of VGAETF which follows the popular encoder-decoder framework. We constructed the drug-disease-drug multi-relational graph, the drug-disease association network, and the disease-disease association network. The VGAETF encoder comprising an entity encoder uses the variational graph autoencoder^28,29 to learn the probability distributions of low-dimensional vector representations of drugs. To improve predictive performance, we use an inner product decoder to learn the representation matrix of disease-disease and drug-disease relationships. Including disease-disease relationships can reduce noise and missing data in triplets. Specifically, the learned drug and disease node features are reconstructed into a drug-disease relationship matrix and a disease-disease relationship matrix through an inner product decoder. Therefore, VGAETF employs multi-task learning to deal with the prediction problem of disease-related drug combinations as the primary task and the auxiliary task (i.e., learning disease-disease relationships and drug-disease relationships). The two tasks share the probability distribution of the low-dimensional vector representation learned by the encoder. At this step, VGAETF utilizes the encoder to diffuse the associations and node feature information among the association networks and learn features for drugs and diseases under the constraint of losses.

Figure 1.

Overview of the VGAETF architecture

(A) Construct a drug-disease-drug multi-relational graph, drug-disease association network, and disease-disease association network. For each triplet fact $\left(d_i,r_k,d_j\right)$, we get the corresponding embeddings $z_i$ and $z_j$ of the source node $d_i$ and target node $d_j$ from learned drug features. In addition, we set a trainable diagonal matrix $M_k$ for each edge type $k$. VGAETF learns features for drugs and diseases under the constraint of losses.

(B) VGAETF uses a variational graph autoencoder to implement a variational inference model and learn the probability distributions of drugs $Z_D$.

(C) VGAETF employs the inner product as a decoder to reconstruct the drug-disease association network and the disease-disease association network from the learned latent features and adopts $f\left(s,r,o\right)$ to calculate the prediction scores of the triplet facts.

Experimental setting

We evaluated the performance of the VGAETF model using the area under the receiver operating characteristic (ROC) curve (AUC)³⁰ and the area under the precision/recall curve (AUPRC).³¹ AUC is a binary classification evaluation metric commonly employed in multi-relational graph link prediction, measuring the ability of the model to differentiate between positive and negative samples by computing the area under the curve of the ROC curve. The area under precision-recall (AUPR) is another commonly used evaluation metric, which is especially useful when the positive class is rare or imbalanced, measuring the trade-off between precision and recall by computing the AUPRC. It provides a more informative evaluation of the model performance in the high-recall regime, which is typically more relevant in the context of link prediction in multi-relational graphs.

We implemented the VGAETF models with PyTorch³² and DGL packages.³³ The publicly available source codes were used to implement all baseline methods. The best or default parameters of each method are used. The implementation of TransE, ComplEx, SimplE, and relational graph convolutional network (RGCN) models is provided by the Open Graph Benchmark.³⁴ We use the model implementation of TuckER, ComplexGCN, and knowledge graph embedding-based method for predicting drug combinations (KGE-DC) provided by the authors.

Hyperparameters selection

In this study, we utilized grid search to determine the optimal parameters for our model. Specifically, we initialized the disease embeddings using Xavier initialization³⁵ and optimized the training loss using the Adam solver.³⁶ Various hyperparameters were taken into account in our model. The hyperparameters in the VGAETF model, which include the learning rate, the number of units in hidden layer 1 and hidden layer 2, and the balance factor $\alpha$, were considered. The hyperparameter $\alpha$ balances the contributions of the representation matrices to learn disease-disease relationships and drug-disease relationships in the auxiliary task. To prevent overfitting and improve efficiency, early stopping was implemented during training, and the number of training epochs was fixed at 1,200. The optimal hyperparameters were selected and highlighted in bold in Table 2.

Table 2.

Hyperparameters settings considered for VGAETF, where bolded are the hyperparameters chosen for the model

Hyperparameter	Values considered
Learning rate	0.01; 0.005; 0.001
The number of units in hidden layer 1 (h1)	64; 128; 192; 256; 320; 384;448; 512
The number of units in hidden layer 2 (h2)	64; 128; 192; 256; 320; 384; 448; 512
Balance factor $\alpha$	0.1; 0.2; 0.3; 0.4; 0.5; 0.6; 0.7; 0.8; 0.9

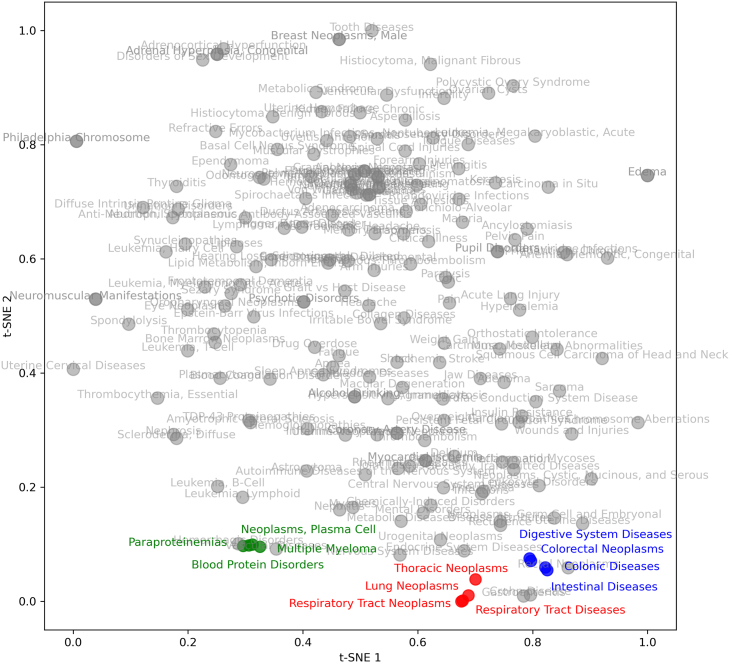
Embedding visualization

Our multi-relational graph embedding models are capable of automatically learning feature vectors for drugs and diseases. To verify the effectiveness of our model, we visualized the disease embedding vectors in a two-dimensional space using t-distributed stochastic neighbor embedding (t-SNE).³⁷ However, due to the potential redundancy and lack of clarity that arises from visualizing and labeling all the nodes, we randomly selected two hundred disease nodes for visualization. By randomly selecting two hundred nodes, we aimed to maintain the representative nature of the dataset. The selection process ensured a diverse sampling from the entire range of diseases, providing an adequate representation of the overall distribution and characteristics. The resulting visualization, shown in Figure 2, reveals the relationships that exist between the embedding vectors of diseases. We observed that diseases that are closely embedded often co-occur in drug combinations, indicating that our model’s learned disease embedding vectors can accurately capture the internal relational structure of diseases within the multi-relational graph of disease-related drug combinations.

Figure 2.

The visualization of disease embedding in VGAETF using the t-SNE package³⁷

From this figure, we can observe that closely embedded diseases often co-occur in drug combinations, suggesting that VGAETF is able to learn disease interconnections in the multi-relational graph of disease-related drug combinations.

For instance, after dimensionality reduction, we found that the diseases of Lung Neoplasms were closely related to Respiratory Tract Diseases, Thoracic Neoplasms, and Respiratory Tract Neoplasms within the two-dimensional space. These three diseases frequently occur in drug combinations together with lung tumors through known triplets. For example, the drug combination of Docetaxel and Pemetrexed, the drug combination of Pembrolizumab and Gemcitabine, and the drug combination of Pemetrexed and Atezolizumab are used to treat these diseases.^38,39,40,41 The findings suggest that our model can effectively manage the intricate relationships inherent in the multi-relational graph of drug combinations related to diseases.

Importance of each component

In this section, a series of studies were conducted to evaluate the contributions of different components to the VGAETF. Specifically, three variants of the VGAETF were implemented, including VGAETF w/o RR, VGAETF w/o DR, and VGAETF w/o DRR. In the VGAETF w/o RR variant, the auxiliary task of reconstructing disease-disease relationship networks was removed. In the VGAETF w/o DR variant, the auxiliary task of reconstructing the drug-disease relationship was removed. Lastly, in the VGAETF w/o DRR variant, both the auxiliary tasks of reconstructing disease-disease relationships and drug-disease relationships were eliminated. These modifications enabled the investigation of the effects of each auxiliary task on the VGAETF’s performance. As shown in Figure 3, VGAETF consistently outperformed the three variants. Specifically, VGAETF w/o RR had slightly higher performance than VGAETF w/o DR with AUPR scores ranging from 0.9626 to 0.9615, while VGAETF w/o DRR had lower performances than VGAETF w/o RR and VGAETF w/o DR, with AUPR scores ranging from 0.9626 to 0.9601, and AUC scores ranging from 0.9746 to 0.9742. These results are consistent with our intuition that understanding the associations between drugs and diseases can provide more comprehensive biological information. Such associations provide valuable information for synergetic drug combination modeling, enabling more accurate prediction of the efficacy of drugs across different diseases and the discovery of new opportunities for drug repurposing, ultimately improving the predictive power of the model.

Figure 3.

The VGAETF ablation experiment compared the performance of VGAETF with three different variants

VGAETF w/o RR did not try to reconstruct the auxiliary task of disease-disease relationships. VGAETF w/o DR did not try to reconstruct the auxiliary task of drug-disease relationships. VGAETF w/o DRR did not do either.

Performance evaluation

Currently, there exist several advanced multi-relational graph embedding techniques for the purpose of predicting triplets in bioinformatics. It should be noted that these models were not developed specifically for drug-disease-drug association prediction. We only used these algorithms for comparative analysis. The baselines we use for comparative analysis include translational distance-based techniques, semantic matching-based techniques, and neural network-based techniques. The details of each method are dicussed here. TransE¹⁸ is a popular multi-relational graph embedding model that represents entities and relations as vectors, aiming to find embeddings that satisfy translation-based scoring functions between head and tail entities. ComplEx¹⁹ extends TransE by representing entities and relations as complex vectors and using the Hermitian dot product to model both symmetric and antisymmetric relations. SimplE⁴² is a simplified version of ComplEx that reduces the number of parameters by using diagonal matrices for relation embeddings and enforcing a sparsity constraint on them. TuckER²¹ combines the Tucker decomposition⁴³ and bilinear forms to model high-order interactions between entities and relations. R-GCN²³ is a GCN that operates on a graph with labeled nodes and relations and utilizes relational graph convolutions to encode node features and learn representations of the graph, and RGCN has also been employed to predict drug combinations (drug-cell line-drug triplet).⁷ ComplexGCN²⁴ extends RGCN by incorporating complex embeddings to handle both real and imaginary parts of relation weights and introduces a novel complex-valued graph convolution operation. KGE-DC¹⁰ constructed a multi-relational graph and combined both drug chemical features and cell line genomic features to learn drug and cell line embeddings to predict the synergy score of drug combinations for cell lines.

To assess the predictive capabilities of VGAETF in comparison with the baselines, a 5-fold cross-validation (CV) was conducted on a randomly selected 90% of the dataset. The remaining 10% of the samples were reserved as an independent test set to prevent overfitting and ensure a realistic assessment of the model’s predictive accuracy. Both VGAETF and the baselines were evaluated on the independent test set to ensure unbiased results. Furthermore, an equivalent number of negative instances were randomly selected from the missing triplets to match the number of positive samples. The entire CV set was used to train all methods, which were subsequently used for predictions on the independent test set to enable objective evaluation.

We compared our model with the seven baseline methods, as depicted in Figure 4. Notably, the obtained results showed that the best AUC and AUPR values of 0.9767 and 0.9660 were achieved using VGAETF, outperforming other computational methods. The superior performance of VGAETF can be attributed to its utilization of the encoder-decoder operation of multi-relational embedding techniques, which incorporates the drug-disease-drug multi-relational graph structure, disease-disease relationship, and drug-disease relationships. The SimplE, KGE-DC, and ComplEx models exhibited remarkable performance, as indicated by their high scores on AUC and the AUPR. Specifically, the SimplE model achieved AUC and AUPR scores of 0.9671 and 0.9557, respectively, highlighting its ability to capture latent representations across various variables. Similarly, the ComplEx model leveraged complex space embeddings to enhance link prediction performance, achieving scores of 0.9397 and 0.9282 for AUC and AUPR, respectively. Furthermore, KGE-DC was instantiated through the integration of a multi-relational graph embedding technique and a neural network and attained an AUC of 0.9717 and an AUPR of 0.9559. These results underscore the efficacy of representing drug-disease-drug interactions as a multi-relational graph, enabling the acquisition of valuable topological insights. Overall, the proposed algorithm employing multi-relational graph embedding directly can yield relatively satisfactory results and exhibit excellent scalability when applied to large-scale datasets.

Figure 4.

Performance of VGAETF as compared with other models

(A) ROC curve and AUC value of the VGAETF model and comparison methods.

(B) Precision/recall curve and AUPRC value of the VGAETF model and comparison methods.

Discussion

To further validate the reliability of VGAETF, we performed detailed case studies on computationally predicted candidate drugs for new anti-hypertension that contain hydrochlorothiazide and new anti-breast cancer that contain trastuzumab. The entire set of drug combinations was used to train the VGAETF model for predicting new anti-hypertension drug pairs that contain hydrochlorothiazide and new anti-breast cancer drug pairs that contain trastuzumab. We masked known triplets of anti-hypertension drug pairs containing hydrochlorothiazide and anti-breast cancer drug pairs containing trastuzumab in our samples, which did not appear in model training. The drug candidates were ranked according to the VGAETF prediction scores for the triplets, and the top 10 scoring candidates are shown in Tables 3 and 4. The rankings of the triplets are based on the predicted scores calculated by the scoring function on embeddings of drugs and diseases, with higher scores corresponding to higher rankings. To indicate the presence of supporting literature, we used the PMID number in PubMed, and "N/A" indicates a lack of confirmation for the association. The results of case studies indicate that our model is indeed able to predict potential disease-related drug combinations.

Table 3.

Top 10 predicted hydrochlorothiazide-containing drug combinations for treating hypertension

Rank	Drug Combination (triplets)	Evidence Source	Evidence type
1	Hydrochlorothiazide-hypertension-Spironolactone	PMID: 363334	Clinical Trial
2	Hydrochlorothiazide-hypertension-Lisinopril	PMID: 27703294	Randomized Controlled Trial
3	Hydrochlorothiazide-hypertension-Labetalol	PMID: 2860990	Clinical Trial
4	Hydrochlorothiazide-hypertension-Aliskiren	PMID: 21122057	Randomized Controlled Trial
5	Hydrochlorothiazide-hypertension-Carvedilol	PMID: 1974505	Clinical Trial
6	Hydrochlorothiazide-hypertension-Valsartan	PMID: 11800062	Clinical Trial
7	Hydrochlorothiazide-hypertension-Eplerenone	PMID: 27651039	Randomized Controlled Trial
8	Hydrochlorothiazide-hypertension-Raltegravir	N/A	N/A
9	Hydrochlorothiazide-hypertension-Amlodipine	PMID: 19470877	Randomized Controlled Trial
10	Hydrochlorothiazide-hypertension-Colchicine	N/A	N/A

Table 4.

Top 10 predicted trastuzumab-containing drug combinations for treating breast cancer

Rank	Drug Combination (triplets)	Evidence Source	Evidence type
1	Trastuzumab-breast cancer-Paclitaxel	PMID: 25564897	Clinical Trial
2	Trastuzumab-breast cancer-Pertuzumab	PMID: 28581356	Clinical Trial
3	Trastuzumab-breast cancer-Capecitabine	PMID: 31825569	Randomized Controlled Trial
4	Trastuzumab-breast cancer-Docetaxel	PMID: 32171426	Clinical Trial
5	Trastuzumab-breast cancer-Gemcitabine	PMID: 12722022	Clinical Trial
6	Trastuzumab-breast cancer-Cyclophosphamide	PMID: 16978400	Clinical Trial
7	Trastuzumab-breast cancer-Cisplatin	N/A	N/A
8	Trastuzumab-breast cancer- Doxorubicin	PMID: 30621698	Clinical Trial
9	Trastuzumab-breast cancer- Fulvestrant	PMID: 34453206	Clinical Trial
10	Trastuzumab-breast cancer-Olaparib	NCT03931551	Clinical trial

Hydrochlorothiazide, a commonly used antihypertensive drug, is a diuretic that lowers blood pressure by reducing the amount of salt and water in the body.⁴⁴ The top 10 predicted candidates for hydrochlorothiazide-containing drug combinations for the treatment of hypertension are listed in Table 3, where eight candidates were supported by clinical studies, such as spironolactone, lisinopril, labetalol, aliskiren, carvedilol, valsartan, eplerenone, and amlodipine.

Hydrochlorothiazide-spironolactone is a potent diuretic combination that effectively treats hypertension by reducing water retention through increased urine output.⁴⁵ Hydrochlorothiazide-lisinopril can produce a synergistic effect, lowering blood pressure more effectively than either drug alone, and improving patient adherence.^46,47 Hydrochlorothiazide-labetalol can be used in combination to achieve better blood pressure control, and labetalol is an alpha-beta blocker that can lower blood pressure by reducing the force of the heart’s contractions and heart rate.⁴⁸ Hydrochlorothiazide-aliskiren can achieve better blood pressure reduction than using either drug alone, especially in obese patients with hypertension, and aliskiren is a hormonal pathway that regulates blood pressure and fluid balance.^49,50 Hydrochlorothiazide-carvedilol can be combined to treat hypertension, and carvedilol is a beta-blocker that can lower heart rate and blood pressure.⁵¹ The combination of hydrochlorothiazide-valsartan has been shown to be effective in the treatment of hypertension, and the advantage of this combination therapy is that it can reduce the dose, thereby reducing adverse reactions.^52,53 The combination of hydrochlorothiazide and eplerenone can produce a synergistic effect, resulting in more effective blood pressure reduction, and eplerenone is an aldosterone receptor antagonist that lowers systolic and diastolic blood pressure.⁵⁴ Combining hydrochlorothiazide with amlodipine has been demonstrated to be effective. Amlodipine, a calcium channel blocker, can lower blood pressure by dilating blood vessels and reducing vascular resistance and pressure.^55,56

To elucidate the mechanism of action of our model in predicting novel drug combinations, we apply GNNExplainer,⁵⁷ a general tool for explaining GNN predictions. We selected the top predicted hydrochlorothiazide-containing drug combinations for treating hypertension in the case study. We used GNNExplainer to identify the most influential nodes in the trained model with respect to the spironolactone central node and analyzed their roles in the prediction. Figure 5 shows the results of the subgraph centered on spironolactone obtained by GNNExplainer. We found a combination of hydrochlorothiazide and spironolactone for treating metabolic syndrome. Additionally, lisinopril with hydrochlorothiazide or spironolactone could be combined to treat cardiovascular diseases (CVDs). Based on the literature on disease comorbidities, hypertension is a significant risk factor for various CVDs, including stroke and heart failure, with CVD being the complication of chronic kidney insufficiency (CKI).⁵⁸ The relationship between hypertension and CKI often coexists in patients, leading to a complex interplay between the two conditions.⁵⁹ Furthermore, the efficacy of hydrochlorothiazide in controlling hypertension has been established. Considering that metabolic syndrome and hypertension frequently coexist, these complex associations may suggest a potential benefit of hydrochlorothiazide and spironolactone in the treatment of hypertension.

Figure 5.

Visualization of the subgraph returned by GNNExplainer for explaining the spironolactone central node.

Table 4 lists the top 10 predicted candidates for trastuzumab-containing drug combinations for breast cancer treatment. Nine of these candidates are supported by clinical studies, including paclitaxel, pertuzumab, capecitabine, docetaxel, gemcitabine, cyclophosphamide, doxorubicin, fulvestrant, and olaparib. The combination of trastuzumab and paclitaxel has been shown to significantly improve survival rates in patients with human epidermal growth factor receptor 2 (HER2)-positive breast cancer.⁶⁰ The trastuzumab-pertuzumab combination is safe and effective in the treatment of HER2-positive early-stage breast cancer.⁶¹ The combination therapy of trastuzumab and capecitabine can produce a synergistic effect in treating breast cancer, resulting in more effective killing of cancer cells.⁶² The combination of trastuzumab and docetaxel has been shown to be effective, improving survival and progression-free survival in patients with HER2-positive breast cancer.⁶³ The trastuzumab-gemcitabine combination shows additive or synergistic antitumor effects in human breast cancer cell lines that overexpress HER2.⁶⁴ The combination therapy of trastuzumab and cyclophosphamide is effective as adjuvant therapy in patients with stage I–III breast cancer.⁶⁵ The combination of doxorubicin and trastuzumab is used to treat early-stage HER2-positive breast cancer, and doxorubicin is a chemotherapy drug that can be used after surgery as adjuvant treatment for breast cancers.⁶⁶ Trastuzumab-fulvestrant demonstrates effectiveness in patients with hormone receptor and HER2-positive metastatic breast cancer, and the combination therapy exhibits moderate clinical efficacy and does not exhibit significant toxicity following standard anti-HER2 treatment.⁶⁷ Trastuzumab-olaparib can be combined to treat HER2-positive breast cancer, primarily by inhibiting the growth and spread of cancer cells through the activity of HER2 and poly (ADP-ribose) polymerase (PARP) proteins.⁶⁸

In this study, we propose a novel computational framework, VGAETF, for predicting disease-associated drug combinations. The VGAETF follows the encoder-decoder framework and employs multi-task learning, where the main task is to predict disease-related drug combinations, while the auxiliary task involves learning the representation matrix of disease-disease and drug-disease relationships. Experimental results show that VGAETF outperforms baseline methods, and case studies focusing on the prediction of novel drug pairs for the treatment of hypertension containing hydrochlorothiazide and new drug pairs for breast cancer treatment containing trastuzumab demonstrate the effectiveness of our model. In our model, we construct a drug-disease-drug multi-relational graph. Multi-relational graphs enable easy modeling of complex relationships between entities in biological systems by representing drugs and diseases as nodes and their associations as edges. Moreover, we show that the multi-task learning of our model helps improve the predictive ability of the model by studying the ablation experiments of three variants of VGAETF. In summary, the proposed VGAETF framework provides a promising approach for predicting disease-related drug combinations, and its effectiveness can be further improved with the incorporation of additional information sources.

Limitations of the study

While VGAETF demonstrates remarkable prediction performance and interpretability, there are certain limitations to consider. Future research endeavors can concentrate on refining negative sampling methods to further improve prediction accuracy. Additionally, exploring transfer learning techniques by pre-training models on extensive and diverse knowledge bases could be beneficial. This would allow fine-tuning of the models specifically for prediction tasks. Moreover, our plans involve incorporating drug metadata into our model to enhance the learning process.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
CDCDB	Shtar, G. et al.26	https://doi.org/10.1038/s41597-022-01360-z
DRKG	Ioannidis, V. et al.27	https://github.com/gnn4dr/DRKG/
Software and algorithms
VGAETF	this study	https://github.com/hhhwy/VGAETF
TransE	Bordes, A. et al.18	https://github.com/snap-stanford/ogb/tree/master
CompIEx	Trouillon, T. et al.19	https://github.com/snap-stanford/ogb/tree/master
SimplE	Kazemi, S. M. and D. Poole42	https://github.com/snap-stanford/ogb/tree/master
TuckER	Balažević, I. et al.21	https://github.com/ibalazevic/TuckER
R-GCN	Schlichtkrull, M. et al.23	https://github.com/snap-stanford/ogb/tree/master
ComplexGCN	Zeb, A. et al.24	https://github.com/Aazeb/ComplexGCN
KGE-DC	Zhang, P. and S. Tu10	https://github.com/yushenshashen/KGE-DC

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Pingjian Ding (dpj@usc.edu.cn).

Materials availability

This study did not generate new unique reagents.

Method details

Preliminaries

The development of synergistic drug combinations may largely be based on the rationale of the treatment of two closely related diseases,⁶⁹ and GNN mostly follows the assumption of learning to assign similar labels to nodes that are closely connected.⁷⁰ Therefore, in this study, we developed a GNN-based method on a multi-relational graph, where two drugs represent entities and diseases represent relationships in the triplets. We explain the disease-related drug combinations prediction task in Figure S1. To predict the disease-related drug combinations, we incorporate additional known triplets associated with the drugs and diseases to learn the embedding vectors for them. Subsequently, these learned vectors are used to generate a score for each drug-disease-drug triplet by the scoring function of tensor decomposition. As shown in Figure S1, in the context of known drug combinations, carvedilol can be combined with spironolactone or pravastatin to treat cardiomyopathies. In the context of drug indication and disease comorbidities, spironolactone and pravastatin can be used for treating high blood pressure and high cholesterol respectively, while hypertension and hyperlipidemia are all risk factors of heart disease. Taken together, spironolactone and pravastatin are intended to be used in combination to treat or prevent diseases (such as heart disease) closely related to hyperlipidemia hypertension, and cardiomyopathies.

Datasets

We obtained a dataset from CDCDB,²⁶ a comprehensive drug combination database containing more than 40,795 drug combinations. We extracted the DrugBank identifiers (IDs) that are related to the FDA Orange Book and the Medical Subject Headings (MeSH) terms that describe the conditions that are treated in the study from our database. The data schema $\left({drug}_i,{disease}_k,{drug}_j\right)$ shows that combining ${drug}_i$ and ${drug}_j$ can treat ${disease}_k$. Among the labeled "Efficacious" drug pairs for one or more diseases, there are a total of 1,105 individual drugs, 1,283 diseases, and 4,709 pairs of drugs. We constructed 59,659 positive samples of drug-disease-drug triplets using this information. In this study, we randomly selected 90% of the positive samples as training data, while reserving the remaining 10% as testing data. Based on the drugs and diseases obtained from the training data, we obtained 26,425 drug-disease associations in the association data. We construct a binary matrix to denote known drug-disease associations that values of 1 and 0 indicate verified associations and unverified associations between drugs and targets, respectively. We collate 259 disease-disease associations from DRKG.²⁷ This dataset contains disease-resembles-disease edges that are based on the co-occurrence of disease terms in PubMed. We also construct a binary matrix that includes two values 1 and 0, denoting validated and unvalidated associations between diseases and diseases, respectively. More details can be found in Table 1.

Description of VGAETF

VGAETF encoder

We follow the encoder approach like VGAE²⁹ to learn the feature representation of the node. We take drug combinations of the drug-disease-drug triplets as the input data for the VGAE encoder. Finally, we can get the low-dimensional representations of drugs as ${\mathrm{Z}}_D\in {\mathbb{R}}^{N\times F}$ where $F$ is the dimension of the final output of the encoder. The drug input features are $X\in {\mathbb{R}}^{N\times N}$ where $N$ is the total number of drugs. The VAE model consists of two parts: encoding and decoding.

The VGAE framework leverages the variational auto-encoder to learn graph-structured data by naturally incorporating node features using GCN. This enables the model to generate interpretable latent representations of undirected graphs based on data distribution. The encoder takes the adjacency matrix $A$ (every node is connected to itself) and the feature matrix $X$ as inputs and uses two GCN layers to obtain a latent variable $z$. The two layers of GCN in VGAE are defined as follows:

$$\text{GCN}\left(\mathrm{X},\mathrm{A}\right)=\tilde{\mathrm{A}}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left(\tilde{\mathrm{A}}\mathrm{X}{\mathrm{W}}_0\right){\mathrm{W}}_1\text{.}$$ (Equation 1)

where ${\mathrm{W}}_0$ and ${\mathrm{W}}_1$ are the trainable weight matrices of the first and second layers. $\tilde{\mathrm{A}}={\mathrm{D}}^{-\frac{1}{2}}\mathrm{A}{\mathrm{D}}^{-\frac{1}{2}}$ is the symmetrically normalized new adjacency matrix with $\mathrm{A}$ added self-connections, and $D$ is the degree matrix of $A$. ${\mathrm{W}}_0$ is shared by ${\text{GCN}}_{\sigma }$ and ${\text{GCN}}_{\mu }$. Specifically, VGAE employs two graph neural networks to fit the $\mu$ and $\sigma$ vectors for each node $i$:

$$\mu ={\text{GCN}}_{\mu }\left(\mathrm{X},\mathrm{A}\right)\text{.}$$ (Equation 2)

$$\mathit{log}\sigma ={\text{GCN}}_{\sigma }\left(\mathrm{X},\mathrm{A}\right)\text{.}$$ (Equation 3)

The latent variable z is then computed as follows:

$$z=\mu +\epsilon \cdot \sigma \text{.}$$ (Equation 4)

where $\epsilon$ follows $N\left(\mathrm{0,1}\right)$. The encoder can also be written as follows:

$$q\left({\mathrm{z}}_i|\mathrm{X},\mathrm{A}\right)={\rm N}\left(z_i|{\mu }_i,\text{diag}\left({{\sigma }_i}^2\right)\right)\text{.}$$ (Equation 5)

VGAETF decoder

We follow the same tensor factorization method as R-GCN²³ to calculate the prediction scores of triplet facts using the final drug representations ${\mathrm{Z}}_D$ learned from the VGAE encoder and a trainable diagonal matrix $M_k$ associated with diseases. Also, we use the inner product as a decoder to learn the representation matrix of disease comorbidities and drug-disease relationships using the node representations of drugs and diseases.

• 1.tensor factorization decoder: For the tensor factorization decoder, $f$ assigns to each triplet $\left(s,r,o\right)$ a score that represents the valid probability of a triplet:

$$f\left(s,r,o\right)=z_s^T{M}_r{z}_o\text{.}$$ (Equation 6)

where the trainable diagonal matrix $M_r$ is specific to the disease type $r$, while $s$ and $o$ refer to the drug entity in the triplet.

• 2.inner product decoder: The decoder computes the reconstructed adjacency matrix by computing the inner product between latent variables $z_i$ and $z_j$ of the nodes, and applying the logistic sigmoid function $\sigma (\cdot )$ as follows:

$$\phi \left(z_i,z_j\right)=\sigma \left(z_i{z_j}^T\right)\text{.}$$ (Equation 7)

Optimization

To account for the lack of negative samples in the known drug-disease-drug triplets, our model generates negative samples during training. We achieve this by randomly corrupting the subject or object of each positive example. The resulting set of negative samples is combined with the real triplets to form the total training set $\mathcal{T}$. We then use cross-entropy loss function⁷¹ to train the model, trying to give a higher probability to seen edges and a lower probability to unseen edges. Our loss function is designed as follows:

$${\mathcal{L}}_1=-\frac{1}{\left|S\right|}\sum _{\left(s,r,o,y\right)\in \mathcal{T}}ylogl\left(f\left(s,r,o\right)\right)+\left(1-y\right)\log \left(1-l\left(f\left(s,r,o\right)\right)\right)\text{.}$$ (Equation 8)

where $\left|S\right|$ is the number of training triplets. The score $f\left(s,r,o\right)$ is normalized between 0 and 1 using the logistic sigmoid function $l\left(x\right)=1/\left(1+\exp \left(-x\right)\right)$. The indicator variable $y$ is set to 1 for positive triplets and 0 for negative ones.

To predict drug combinations using auxiliary information, we optimize our model using a combination of loss functions. Our optimization function, denoted as $\mathcal{L}$, includes the loss function ${\mathcal{L}}_1$, ${\mathcal{L}}_2$ for disease-disease relationships, and ${\mathcal{L}}_3$ for drug-disease relationships. Additionally, $\mathcal{L}$ incorporates the KL divergence⁷² between $q\left(\mathrm{Z}|\mathrm{X},\mathcal{E}\right)$ and $p\left(Z\right)$. KL divergence serves as a regularization term that encourages the learned latent space to follow a predefined prior distribution and prevents overfitting to the training data.⁷³ Formally, ${\mathcal{L}}_2$ and ${\mathcal{L}}_3$ can be defined as:

$${\mathcal{L}}_2=-\frac{1}{\left|RR\right|}\sum _{\left(r_1,r_2\right)\in RR}\log \left(\psi \left(R_{r_1},R_{r_2}\right)\right)$$ (Equation 9)

$${\mathcal{L}}_3=-\frac{1}{\left|DR\right|}\sum _{\left(d,r\right)\in DR}\log \left(\psi \left(D_d,R_r\right)\right)$$ (Equation 10)

where $RR$ stands for all disease pairs in the disease-disease relationship and $DR$ stands for all drug-disease pairs in the drug-disease relationship.

We integrate $\mathcal{L}$ to train the model, i.e.,

$$\mathcal{L}={\mathcal{L}}_1+\left(1-\alpha \right)\cdot {\mathcal{L}}_2+\alpha \cdot {\mathcal{L}}_3-KL\left[q\left(Z|X,\mathcal{E}\right)\Vert p\left(Z\right)\right]$$ (Equation 11)

where $\alpha$ is a hyperparameter that trades off the two loss functions ${\mathcal{L}}_2$ and ${\mathcal{L}}_3$ in the auxiliary task. Our model learns embeddings for drugs and diseases using the Adam optimizer³⁶ to minimize the loss function.

Similar to the calculation process in Chen et al.,⁷⁴ we analyze the computational complexity for two key components of our model. For the training and inference time complexity of the two-layer GCN can be bounded by $O\left(\left|E\right|N+\left|E\right|F+N^3+N^{2}F\right)$, where $\left|\mathrm{E}\right|$ represents the number of edges of the undirected graph. For the decoder, the time complexity is $O\left(\left|\mathcal{T}\right|F+2F\right)$. A complete description of the procedure of VGAETF is presented in Algorithm 1.

Algorithm 1. The complete procedure of VGAETF.

Input: drug-disease-drug multi-relational graph $G=\left(\mathcal{V},\mathcal{E},\mathcal{R}\right)\text{;}$ drug-disease relationship matrix DR; disease-disease relationship matrix RR; train triplets set ${\mathcal{T}}_{train}$; test triplets set ${\mathcal{T}}_{test}$; maximum training epochs T;

Output: triplets prediction probability $f\left(s,r,o\right)$ in ${\mathcal{T}}_{test}$.

• 1.Initialize trainable parameters $\theta =\left\{{X,\mathrm{W}}_0,{\mathrm{W}}_1,M_r\right\}\text{.}$
• 2.t ←1;
• 3.repeat
• 4. Learn drug embedding features ${\mathrm{Z}}_D$ with Equation 5;
• 5. Calculate the triplets prediction probability $f\left(s,r,o\right)$ with Equation 6;
• 6. Reconstruct the representation matrix of drug-disease DR and disease-disease RR with Equation 7;
• 7. Update drug features ${\mathrm{Z}}_D$, disease features ${\mathrm{Z}}_R$ and the parameters of VGAETF by optimizing Equation 11;
• 8.util t > T or Equation 11 is converged;
• 9.return the triplets prediction probability $f\left(s,r,o\right)$ in ${\mathcal{T}}_{test}$ with Equation 6.

Experiments for performance evaluation

We evaluated the performance of the VGAETF model using the area under the receiver operating characteristic (ROC) curve (AUC)³⁰ and the area under the precision/recall curve (AUPRC).³¹ We implemented the VGAETF models with PyTorch³² and DGL packages.³³ The publicly available source codes were used to implement all baseline methods. The best or default parameters of each method are used. The implementation of TransE, ComplEx, SimplE, and RGCN models are provided by the Open Graph Benchmark.³⁴ We use the model implementation of TuckER, KGE-DC, and ComplexGCN provided by the authors. Details are in the key resources table.

In this study, we utilized grid search to determine the optimal parameters for our model. Specifically, we initialized the disease embeddings using Xavier initialization³⁵ and optimized the training loss using the Adam solver.³⁶ Various hyperparameters were taken into account in our model. The hyperparameters in the VGAETF model, which include the learning rate, the number of units in hidden layer 1 and hidden layer 2, and the balance factor $\alpha$, were considered. The hyper-parameter $\alpha$ balances the contributions of the representation matrices to learn disease-disease relationships and drug-disease relationships in the auxiliary task. To prevent overfitting and improve efficiency, early stopping was implemented during training, and the number of training epochs was fixed at 1200. The optimal hyperparameters were selected and highlighted in bold in Table 2.

Published: September 22, 2023

Data and code availability

• •The data reported in this paper is publicly available on GitHub (https://github.com/hhhwy/VGAETF)
• •All original code has been deposited at GitHub and is publicly available as of the date of publication. The DOI is listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request