In Silico Investigation of the Clinical Translatability of Competitive Clearance Glucose-Responsive Insulins

Abstract

The glucose-responsive insulin (GRI) MK-2640 from Merck was a pioneer in its class to enter the clinical stage, having demonstrated promising responsiveness in in vitro and preclinical studies via a novel competitive clearance mechanism (CCM). The smaller pharmacokinetic response in humans motivates the development of new predictive, computational tools that can improve the design of therapeutics such as GRIs. Herein, we develop and use a new computational model, IM³PACT, based on the intersection of human and animal model glucoregulatory systems, to investigate the clinical translatability of CCM GRIs based on existing preclinical and clinical data of MK-2640 and regular human insulin (RHI). Simulated multi-glycemic clamps not only validated the earlier hypothesis of insufficient glucose-responsive clearance capacity in humans but also uncovered an equally important mismatch between the in vivo competitiveness profile and the physiological glycemic range, which was not observed in animals. Removing the inter-species gap increases the glucose-dependent GRI clearance from 13.0% to beyond 20% for humans and up to 33.3% when both factors were corrected. The intrinsic clearance rate, potency, and distribution volume did not apparently compromise the translation. The analysis also confirms a responsive pharmacokinetics local to the liver. By scanning a large design space for CCM GRIs, we found that the mannose receptor physiology in humans remains limiting even for the most optimally designed candidate. Overall, we show that this computational approach is able to extract quantitative and mechanistic information of value from a posteriori analysis of preclinical and clinical data to assist future therapeutic discovery and development.

Glucose-responsive insulin (GRI) analogues are a class of intelligent insulin delivery technology, which supplies a hormonal activity commensurate with local blood-glucose concentrations in a closed-loop, autonomous fashion,^1,2 broadly regarded as “a new horizon in therapeutic technology”.^3,4 In contrast to traditional, open-loop methods for glycemic control, GRIs promise added insurance against hypoglycemia, improved patient compliance, reduced side effects, and optimized, reliable dosing.⁵ Although a closed-loop, pancreas-like regulation may also be achieved with therapies that integrate continuous glucose monitoring and insulin administration,⁶ these sophisticated external devices remain expensive, bulky,¹ and potentially associated with risks of infection, inflammation, and scarring.⁷ The diabetes community’s long-term interest in GRIs has catalyzed a multitude of concepts for glucose responsiveness: these can be roughly classified into insulin-encapsulating polymer carriers with glucose-mediated triggers⁸⁻¹¹ and modified unimolecular insulin with glucose-recognizing motifs.¹²⁻¹⁴ Out of the many GRI constructs showing potential in animal studies,^1,2,15−17 it was Merck’s MK-2640 that marked the milestone as the first GRI to enter clinical trials.¹⁸ Unfortunately, the phase I outcome “revealed insurmountable challenges” for MK-2640’s further development.

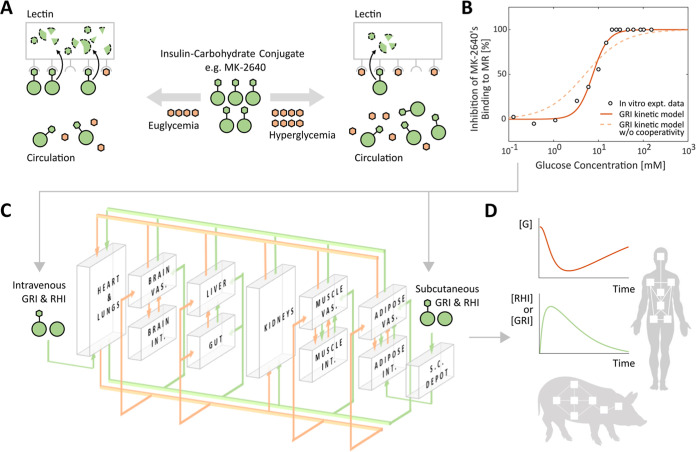
MK-2640 belongs to a family of GRIs whose availabilities in vivo are modulated by a competitive clearance mechanism (CCM) between glucose and the therapeutic molecule.¹⁹⁻²² As illustrated in Figure 1A, these insulin-based constructs contain added carbohydrate moieties, allowing them to be recognized and cleared away by lectins via, in the case of MK-2640, mannose receptors (MRs). The envisioned responsiveness to level of glycemia is a result of the, albeit weak, affinity of glucose for the MR. The competition therefore creates a difference in MK-2640 availability between eu- and hyperglycemia: only in the latter case is the MR-mediated clearance attenuated by glucose competition and the GRI made available to target tissues. CCM is among many mechanisms that rely on a competition between insulin and glucose, which date back to the first GRI system pioneered by Brownlee and Cerami four decades ago.²³ That said, GRIs of the MK-2640 family uniquely modulate insulin availability by enhanced removal at euglycemia, rather than activation at hyperglycemia as in prior technologies.¹⁷

Figure 1.

Overview of the in silico investigation of the competitive clearance GRIs with the IM³PACT modeling platform. (A) Illustration of the glucose-responsive mechanism of MK-2640 and its variants. The carbohydrate-conjugated insulin analogs exemplified by MK-2640 (green) undergo clearance via both the intrinsic insulin receptor (IR) route as well as the additional lectin/mannose receptor (MR) route, with the latter being responsive via the competitive binding of glucose (orange). Consequently, under euglycemia (hyperglycemia), the weak (strong) competition from glucose is designed to allow a high (low) rate of MR-mediated GRI clearance, thus lowering (enhancing) its availability in circulation. Pivotal to the design concept, therefore, is a significant difference in clearance between eu- and hyperglycemia, which was not observed in the clinical clamp studies of MK-2640.¹⁸ The reversible binding processes of the GRI and glucose to MR depicted in the illustration are, respectively, represented by rate constants k_±1 and k_±3, which play important roles in the mechanistic model (eqs 1 and 2). (B) The mechanistic model almost perfectly describes the in vitro assay data of glucose-inhibited MK-2640 binding to MR²¹ but only if the Hill coefficient h_G is incorporated which represents cooperativity. (C,D) IM³PACT couples the mechanistic model of MK-2640 with a physiological model representing the full-body glucoregulation as a network of well-mixed compartments. These compartments consist of the brain, heart and lung, liver, gut, kidneys, muscle, and adipose tissues (C). By solving the equivalent system of differential equations (eqs 7–9), we are able to trace the concentrations of GRI and regular human insulin (RHI) over time, in addition to the blood glucose [G], as they are circulated and metabolized in the body of either humans or minipigs following intravenous or subcutaneous administration (D). Expt., experimental; vas., vascular; int., interstitial; and s.c., subcutaneous.

Merck’s development of competitive-clearance-based GRIs was terminated¹⁷ as the clinical trials reported far less responsiveness in MK-2640 clearance than had been promised by the canine and porcine preclinical evaluations.^18,21 Although suboptimal human pharmacokinetics was attributed to saturation of the MR-mediated clearance capacity.^18,24 However, this mechanism was never proven or quantified. Furthermore, it remained to be answered whether any other distinctions between humans and preclinical animals could have played a role, or whether the rest of the portfolio, reportedly with enhanced potency and undiminished MR affinity,^19,20 might have fared better in a clinical trial. On the modeling front, the Merck team performed thorough model-based meta-analysis,²⁵ interspecies scaling studies,²⁶ and systems pharmacology simulations with the UVa/Padova simulator.²⁷ They established that, whereas the in silico tools were predictive of the clinical pharmacokinetics (PK) and pharmacodynamics (PD) of regular human insulin (RHI), translational modeling based on preclinical data failed to predict the observed PK of MK-2640.^26,28 Although this contrast prompted Kandala et al. to ascribe MK-2640’s underperformance to interspecies differences in MR-specific attributes,²⁶ it remains not well understood (and was not further pursued) whether the critical gap lies with MR distribution, competitive binding, GRI potency, or something else—the central question addressed here.

Although many have characterized the clinical trials as having failed,^18,29 the MK-2640 and RHI data in humans are far from a failure in providing valuable insights into the mechanistic and translational aspects of CCM GRIs. In this study we have compared and contrasted these GRIs’ PK and PD in humans and minipigs by means of an integrated translational modeling platform, with particular focus on the decisive metric of the change in GRI clearance. We designated our platform “GRI Mathematical Model Mapping Performances in Animal and Clinical Trials”, or “IM³PACT”. An expansion of our previous PAMERAH model that mapped rodent- and human physiology,³⁰ IM³PACT couples a mechanistic model of the CCM principle to physiological models of glucoregulatory systems in humans and minipigs, with the minipig being a new addition. As the physiology is modeled as an interconnected network of well-mixed compartments (mathematically, a system of differential equations), our platform is able to track the action of MK-2640 specific to each organ, which concurs with recommendations from Merck’s modeling team. They found that their modified UVa/Padova model had not been designed for capturing the GRI’s hepatic site of action²⁸ and hence was unable to have pictured the dilution of a locally significant PK responsiveness in the systemic pool in humans¹⁸—a potential mechanism confirmed and quantified herein by IM³PACT. By, respectively, transposing minipigs’ key MK-2640 properties onto the human model one at a time, we concluded that unsuccessful clinical translation was not a result of differences in the GRI’s potency, volume of distribution, or intrinsic clearance rate. Rather, the key contributing factors were (i) insufficient clearance capacity via the MR route in humans, as anticipated by Krug et al.;¹⁸ and (ii) incomplete attenuation of MR-mediated elimination under hyperglycemia, meaning only a fraction of the already constrained capacity was utilized. Our study thus establishes in silico diabetes modeling as not only just a tool for GRI design and early-stage screening^30,31 but also an investigative lens through which hypotheses may be falsified/validated, unmeasurable properties quantified, and new insights learned for future GRIs of the CCM family and beyond.

Research Design and Methods

Mechanistic Model of Competitive Clearance GRIs

As with our earlier efforts,³⁰⁻³³ the IM³PACT model comprises two modular components: (i) a mechanistic model describing the glucose responsiveness of the GRI of choice, which is plugged into (ii) a physiological model simulating the circulation and metabolism of glucose, insulin, glucagon, and GRI over time, of humans, rodents, and, as part of the contribution from this research, minipigs. As illustrated in Figure 2, we model the CCM mechanism with the following kinetics analogous to that of competitive enzyme inhibition³⁴

1

2

Figure 2.

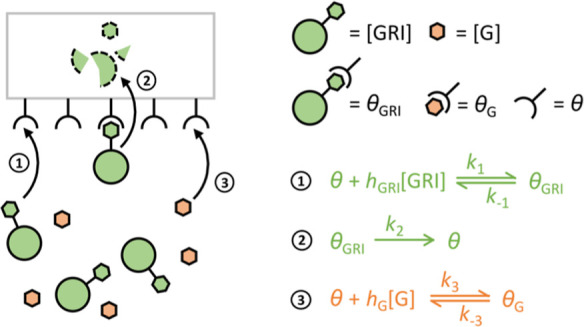
Schematic of the proposed mechanistic model for CCM. Kinetics 1, 2, and 3, respectively, represent the binding of a free GRI to MR, the internalization and elimination of a bound GRI-MR complex, and the competitive binding of glucose to MR.

Equations 1 and 2, respectively, describe the binding of the GRI molecule and glucose to the receptor in charge of competitive GRI clearance, as a function of their concentrations [GRI] and [G]. In the case of MK-2640, θ, θ_G, and θ_GRI denote concentrations of unbound MR sites, those bound to glucose, and those to MK-2640. Their interconversions are dictated by the corresponding rate constants k, of which k₂ in particular captures the irreversible internalization and clearance of the bound GRI, followed by the recycling of receptor θ to the protein surface. Hill coefficients h_GRI and h_G, respectively, indicate the degree of cooperativity³⁵ in the binding of GRI and glucose, their use is further justified below with published experimental data.

Figure 1B shows how a parameterized mechanistic model quantitatively captures the competitive inhibition of MK-2640’s binding to MR with escalating concentrations of glucose, experimentally measured in vitro previously.²¹ Assuming quasi-steady-state and that the internalization and receptor recycling step is rate-limiting, we obtain the following expression for θ (and hence θ_G and θ_GRI) as a function of θ_tot, the time-invariant total number density of MR binding sites

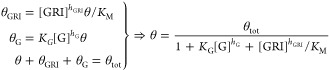3

where K_G = k₃/k_–3 is the glucose binding equilibrium constant and K_M = (k₂ + k_–1)/k₁ is the Michaelis constant.³⁶ The rate of the GRI’s MR-mediated clearance is thus

4

where K_G = k₃/k_–3 lumps together the specific rate of MR-mediated clearance and the local abundance of participating receptors in the liver. The uninhibited rate of clearance, in absence of the competing glucose, would therefore be 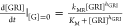. Normalizing eq 4 with this uninhibited rate resulted in the following expression for the glucose-dependent degree of inhibition previously probed with in vitro binding assay

5

with a given MK-2640 concentration of 4 nM, K_M of 3 nM, and h_GRI of 1.5, the experimental data in Figure 1B were fitted almost perfectly to the mechanistic model, yielding a K_G of 0.022 mM^–h and a h_G of 2.537. The latter falls within the typical range of 1–4 for Hill coefficients.³⁷ On the other hand, removal of the glucose Hill coefficient from the mechanistic model results in a far inferior prediction of the inhibitory response (Figure 1B, dashed) regardless of h_GRI and K_G values. Given the lack of binding assay data with varying concentrations of MK-2640 at a fixed [G], h_GRI of 1.5 was instead inferred by fitting with the Krug et al.’s clinical clamp studies of escalating MK-2640 infusion rates,¹⁸ as seen in Supporting Information, Figure S1. The need for a cooperative h_GRI larger than unity is clear, however, even before we attempted to quantitatively fit the model, being (i) evident from the significant initial rise in MK-2640 clearance with increasing concentrations (Supporting Information, Figure S1), and (ii) consistent with literature on insulin-receptor binding.³⁸ Finally, the mechanistic model outputs a half maximal inhibitory concentration (IC₅₀) of 7.5 mM for glucose, which is in good agreement with the 8 mM reported in experiments.

Full-Body Physiological Model of the Glucoregulatory System

The physiological model component of IM³PACT was constructed on the basis of Sorensen-like models³⁹⁻⁴² with a number of added modules and modifications, for instance, accounting for subcutaneous (s.c.) injection kinetics,^31,43,44 intraperitoneal injection kinetics,⁴⁵ and oral glucose absorption following meals.^32,46 Compared to semi-mechanistic parsimonious models of the glucoregulatory system,^47,48 such physiology-based models enable tracking of hormone and metabolite concentrations within each organ and allow therapeutics to take effect locally in their intended compartments, as alluded to earlier.³²Figure 1C illustrates the architecture of IM³PACT’s physiological model, which represents the body as an interconnected network of well-mixed compartments, mathematically equivalent to a system of ordinary differential equations (ODEs) which we solve using well-established numerical methods (ode15s, MATLAB R2020a, the MathWorks, Inc.). Within an arbitrary compartment, the concentrations of a solute [s] in the vascular (subscript “v”) and interstitial spaces (subscript “i”) are, respectively, dictated by

6

7

where V denotes the compartmental volume and Q the arterial blood flowrate through the organ. The characteristic time of transcapillary transport, T, together with the concentration gradient, determines the mass exchange between the vascular and interstitial sub-compartments. For organs with rapid transcapillary equilibrium, only eq 6 remains relevant and is simplified to

8

The local rate of metabolism in the compartment, R, sums up the production and uptake rates as a function of the local concentrations of glucose, insulin, glucagon, and GRI through transfer functions documented in Supporting Information, Table S2. R_v and R_i denote the local rates of metabolism in the vascular and interstitial components, respectively. Of note, in the liver and when the solute s denotes a CCM GRI, a key component of the R term is naturally its receptor-mediated competitive clearance seen in Figures 1A and 2, the rate of which is denoted as R_MRCL

9

per eq 4 of the GRI mechanistic model above, where V, k_MR, [GRI], and [G] are local to the liver compartment. Intravenous (i.v.) boluses are initialized by distributing the dosage to all vascular compartments. On the other hand, a subcutaneous dose enters through a subcutaneous depot where the hexamer–dimer–monomer equilibria are simulated, as discussed in Supporting Information, Table S2.

Model Extension for Minipig Simulation

In contrast to the scarcity of GRI clinical data and the abundance of those in preclinical animals, the vast majority of both the parsimonious and physiology-based simulation platforms to date only model glucoregulation in humans. To facilitate the preclinical-to-clinical translation of GRI therapeutics, our recent publication extended the full-body physiological model to rats and mice with data collected experimentally and extracted from published literature.³⁰ In the present work, using the same workflow, we adapted our model to Yucatan minipigs on which the Merck team performed preclinical MK-2640 studies. Note that while a couple of Merck publications reported murine and canine data of similar CCM analogues, they are derivatives of MK-2640 with modified characteristics.^19,20 A direct cross-comparison between clinical and animal results is therefore only possible with the model extended to minipigs.

The process of cross-species model adaption has been documented in detail in our past report³⁰ and is briefly described here. Instead of numerically scaling down the human parameters by body mass with empirical allometric exponents, systematic measurements of Yucatan minipigs provided anatomical parameters (Supporting Information, Table S1), such as the compartment volumes (V) and hemodynamic flow rates (Q). These experimental measurements were sourced from vendor-provided data sets⁴⁹ as well as research articles.⁵⁰⁻⁵³ Of particular note was a simplified physiology-based model for diabetic Göttingen minipigs by Lunze et al., who determined parameters for the liver, periphery, and plasma compartments.⁴¹ The transfer functions, which describe modulation of each compartment’s metabolic rates by glucose and insulin, were not readily available from literature. Based on sensitivity analyses,^54,55 we identified the most influential of these parameters and subsequently fitted them using data describing use of regular human insulin (RHI) in diabetic and healthy minipigs,¹⁸ further discussed in the Results section. As in the prior adaptation of our model to rodents³⁰ and consistent with other published models,^48,56,57 we performed differentiating parameterization of three parameters for diabetic and healthy minipigs. Following iterative parameterization, we arrived at a final set of model parameters, including those specific to the MK-2640 characteristics (see below), that is self-consistent across RHI and MK-2640 data in minipigs and humans (summarized in Supporting Information, Table S2). All parameter estimations were performed with the standard interior-point optimization algorithm in MATLAB R2020a.

Addressing Key Distinctions between MK-2640 and RHI

Despite observations that (i) the parameterized physiological model is able to simulate the time evolution of glucose-, insulin-, and glucagon concentrations, and (ii) MK-2640 as an insulin-carbohydrate conjugate functions via insulin receptors (as RHI does), it would be inaccurate to simulate each MK-2640 molecule merely as an insulin with added MR-mediated clearance. In addition to the MR-mediated clearance already captured as a part of the above mechanistic model, several key characteristics cause the GRI’s behavior to depart from that of endogenous insulin. We have taken these factors into consideration with corresponding model modifications specific to the CCM GRI as follows:

A signature of MK-2640, and in fact of the other promising CCM GRI candidates investigated preclinically by Merck, is their significantly reduced IR affinity in vitro and potency in vivo.¹⁸⁻²¹ With an IR-binding IC₅₀ in minipigs 19.0-fold larger than RHI (14.6-fold in humans), each MK-2640 molecule is equivalent to just a small fraction of RHI regarding glucoregulation. An effective concentration was therefore used in the model’s transfer functions—the GRI level scaled by the IR IC₅₀ ratio—which is a rigorous result derived from a kinetic model of IR binding and signaling (Supporting Information, Materials Section S2).

In spite of the GRI’s reduced affinity to IR, it was not necessary for a 19-fold increase in dose to achieve a commensurate efficacy as per unit of RHI. In s.c. minipig experiments, for instance, only a 4-to-7-fold increase in dose was used. This is primarily due to a reduction of IR-mediated intrinsic clearance of MK-2640, which is “in inverse proportion to [its] in vitro potency”,¹⁸ a phenomenon commonly observed with sequence-modified insulin analogues.⁵⁸ We incorporated this observation in IM³PACT by introducing a scaling factor Λ_IRC to the liver-, renal-, and periphery compartments, which in each case represents the ratio between intrinsic GRI clearance and the default RHI rate. The quotient of the observed in vivo equivalent dose divided by the IR IC₅₀ ratio (the so-called “in vitro potency”) was used as an initial estimate of Λ_IRC in the parameterization process.

Finally, it was observed among the minipig i.v. bolus data that both RHI and MK-2640 exhibited a biexponential profile of declining plasma concentration with time,²¹ consistent with a classic two-phase model of i.v. PK that describes the distribution of the drug between fast vascular compartments and slowly equilibrating interstitial compartments.^59,60 Nevertheless, the experimentally measured central volumes V_c, defined as the ratio between i.v. dose and onset drug concentration, differ by nearly twofold between RHI and MK-2640 (57 vs 24 mL/kg). Indeed, Kaarsholm and co-workers noted a low steady state volume of distribution in minipigs and dogs.²¹ Mathematically to account for the observed reduction in V_c, we scaled down all the vascular compartments by a factor of Λ_V when a CCM GRI is dosed instead of RHI. In the case of minipigs, Λ_V was computed directly from experimental observations, instead of being fitted, as 24/57 = 0.42.

Results

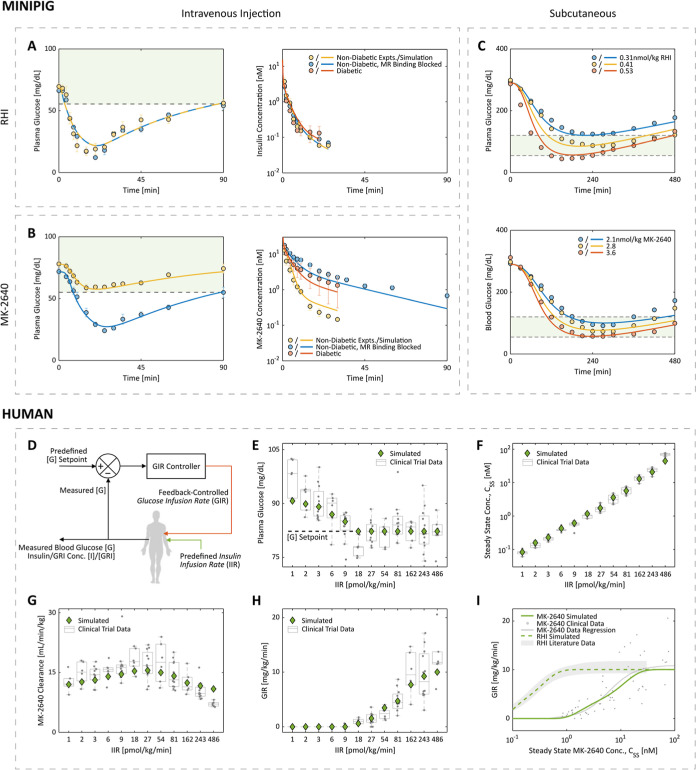
For minipigs, predictions by the parameterized IM³PACT model agreed with the experimental blood glucose and insulin trajectories over time following intravenous (Figure 3A,B) and subcutaneous doses (Figure 3C) of RHI and MK-2640.²¹ Of particular interest are the in vivo measurements of the RHI and MK-2640 concentrations in circulation post i.v. injections (Figure 3A,B, right panels) which were used to (i) validate the vendor-provided and literature values of the compartmental volumes and flow rates and (ii) anchor MK-2640 PK parameters directly. Of note, we mimicked the experimental administration of α-methylmannose (α-MM, a strong MR-binding antagonist) by blocking off the MR-mediated CCM pathway completely (i.e., by enforcing an R_MRCL of 0 regardless of [GRI] and [G] in eq 9). In Figure 3B, the corresponding hypoglycemic episode and sluggish clearance of MK-2640 observed in both the experimental and simulated results clearly demonstrate the PK and PD change brought about by CCM in minipigs. As expected, the addition of α-MM had negligible effects on RHI’s PK and PD (Figure 3A), as suggested by both experiments and simulations.

Figure 3.

IM³PACT is able to quantitatively describe RHI and MK-2640 behaviors in minipigs and humans. (A,B) Experimentally measured concentrations (circles) of blood glucose, RHI, and MK-2640 in minipigs agree with IM³PACT outputs (curves) following an intravenous bolus of 0.17 nmol/kg RHI (A) or 0.35 nmol/kg GRI (B). The experimental MR blockage by α-methylmannose was simulated by shutting off the MR-mediated clearance pathway completely. (C) Similarly, the parameterized mathematical model captures the dose-dependent lowering of blood glucose levels by both RHI (top) and MK-2640 (bottom) post subcutaneous administration. The shadowed areas define the euglycemia range, 55–120 mg/dL, for the minipigs. Circles, minipig in vivo data; curves, simulation. (D) Schematic explaining the principles of glycemic clamps, where the intravenous GIR is feedback controlled to offset a predefined insulin/GRI infusion rate (IIR), such that the blood glucose level is kept at a constant setpoint. (E–I) Simulated results match with clinical results from Merck’s euglycemic (80 mg/dL) trial 1 in terms of measured blood glucose (E), steady-state GRI concentrations (F), clearance rates (G), and GIR (H), thus capturing both MK-2640’s PK and PD in healthy individuals. The agreement between simulated and experimental/literature C_SS-GIR relations for both MK-2640 and RHI means their potency difference is quantitatively represented in IM³PACT. Each of the gray circles in (E–H) represents a single clinical measurement. Experimental results and experimental error bars plotted were digitized from literature reports: ref (21) for panels (A–C); ref (18) for panels (E–I). We refrained from reproducing certain error bars in panels (A–C) and all datapoints below 0.8 nM in panel (I) as their original presentation overlapped significantly with other data or figure elements and could not be faithfully digitized.

Unlike ongoing clinical trials of Novo Nordisk’s investigational GRI, which employed s.c. administration (NCT numbers: NCT04569994 and NCT05134987), clinical studies of MK-2640 used clamps.¹⁸ As illustrated in Figure 3D, in a clamp study^61,62 one varies the real-time i.v. glucose infusion rate (GIR) to counteract the glucose-lowering effect of a predefined insulin infusion rate (IIR) so as to maintain the plasma glucose concentration at a predetermined setpoint. In the case of a GRI, the IIR in turn refers to the infusion rate of the GRI. This design and its output data are shown in Figure 3E for the healthy individuals under a series of euglycemic clamps (“Trial 1”). The steady-state concentrations of RHI or GRI (C_SS) as a function of IIR provide as a PK indicator (Figure 3F), from which the amount of clearance, defined in the clinical trial as IIR/C_SS, can be computed (Figure 3G). As outlined above in Research Design and Methods, the marked increase in MK-2640 at low IIRs served as a justification for the cooperative Hill coefficient h_GRI (see also Supporting Information, Figure S1). The decline in clearance for IIRs larger than 54 pmol/kg/min, or equivalently for C_SS over 5 nM, is a signature of saturating elimination.¹⁸ On the other hand, the steady-state GIR is an indicator of the therapeutic’s PD (Figure 3H). It is apparent in each panel of Figure 3E–H that the IM³PACT-simulated PK and PD properties of MK-2640 in healthy humans match those observed in euglycemic clamp experiments.¹⁸

Comparison of MK-2640’s PD properties to those of RHI is better visualized in Figure 3I wherein GIR is plotted as a function of C_SS. The simulated relations match with the clinical MK-2640 data as well as the RHI correlation summarized from a previous literature meta-analysis.^18,63,64 Krug and colleagues concluded that to arrive at a GIR of 5 mg/kg/min (half of the saturation GIR), the required RHI concentration would be approximately 4% that of MK-2640 due to the latter’s significantly lower potency. Indeed, IM³PACT yields an output value of 4.2%. These results are not far off from the aforementioned IR IC₅₀ ratio, which reflects MK-2640’s weak IR binding affinity (see Research Design and Methods).

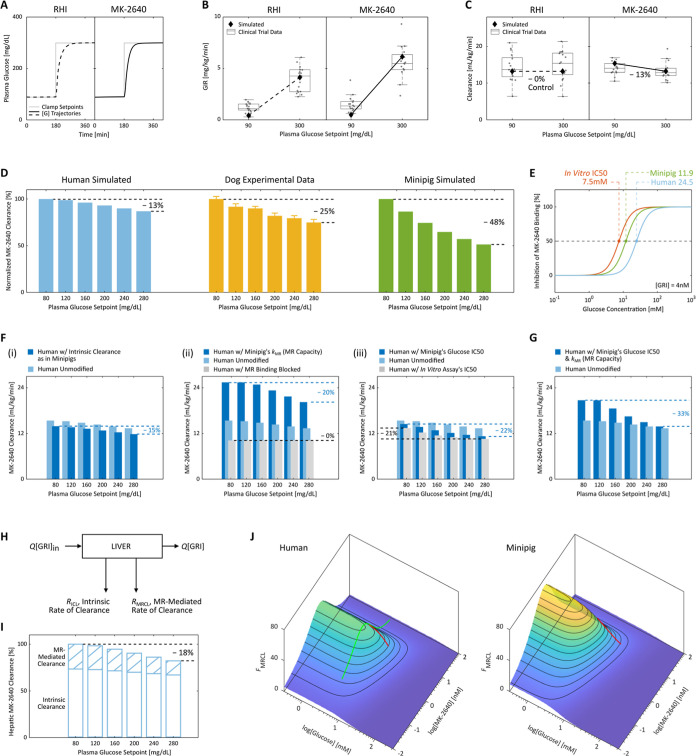
Although trial 1 clamps performed on healthy individuals exhibited unfavorable saturation of clearance at MK-2640 concentrations ≥5 nM, its clinical translation was halted primarily due to the results of a two-stage trial 2, demonstrating negligible benefit for patients with diabetes.¹⁸ As shown in Figure 4A’s simulation results, trial 2 was designed to compare the analog’s PK and PD properties under euglycemic versus hyperglycemic conditions by clamping the patients first at a plasma glucose setpoint of 90 mg/dL for 3 h, followed by clamping at 300 mg/dL for 4 h. Whereas the clinical GIR data (Figure 4B) had suggested a comparatively more significant rise with MK-2640 than with RHI (also captured by our simulations), the reduction in clearance rates (Figure 4C) between clamp levels was underwhelming: Krug et al. reported a 6% difference between geometric means. The present IM³PACT simulations likewise predicted a reduction of 13.0%, also far lower than the reduction observed in the original dog studies: 25.1% promised as reproduced in Figure 4D.^18,21 With IM³PACT, we predicted the outcomes should a diabetic human or minipig undergo the same 6-level clamp protocol as the dogs under a single fixed IIR. With the clearance rates normalized to the 80 mg/dL euglycemic rate for each corresponding species, it is apparent in Figure 4D that while MK-2640’s clearance always drops with higher clamp setpoints, the GRI is significantly less responsive in humans than in dogs or minipigs. We note that the ability to computationally apply an experimental protocol performed on one species to another could prove powerful in reconciling otherwise incomparable literature results, thereby aiding clinical translation.

Figure 4.

Subpar glucose responsiveness of MK-2640 clearance in humans and investigation into the hypothesized causes of the unsuccessful clinical translation. (A–C) In Merck’s clinical trial 2,¹⁸ type 1 diabetic patients were clamped first at 90 mg/dL for 3 h and subsequently at 300 mg/dL for 4 h, with continuous intravenous infusion of either 1.4 pmol/kg/min of RHI (A, left) or 40 pmol/kg/min of MK-2640 (A, right). A glucose-dependent PD response was observed (B), as the GIR increased by 4.1 mg/kg/min for MK-2640 (5.6 in simulation) and only 3.2 mg/kg/min for RHI (3.7 in simulation) between the two setpoints. Despite moderate PD responsiveness, the PK of MK-2640 barely changed (C) with a mere 6% difference in clearance (13% in simulation), which directly contradicted the essence of the design concept. Each gray circle in (B,C) represents a single measurement. (D) We performed a straightforward comparison across species by subjecting our human (blue) and minipig (green) models to the same multi-glycemic clamp protocol previously applied to dogs (yellow). The modulation in clearance was predicted to be 13% in humans between 80 and 280 mg/dL, expectedly close to the clinical trial 2 outcome. In comparison, a 25% change was observed in canine experiments (“∼30%” claimed by Kaarsholm et al.²¹) and 48% in simulated minipigs. Error bars: digitized standard error. (E) Both the parameterized minipig and human models exhibited inhibition curves shifted away from that predicted by the in vitro MR binding assay (also see Figure 1B). This drift caused a 50% increase in MR IC₅₀ for MK-2640 in minipigs and a 2.3-fold increase in humans, meaning reduced competition from glucose. (F) Predicted MK-2640 properties that hindered the clinical translation. (i) If humans hypothetically assume the same extent of MK-2640 elimination as minipigs via the intrinsic IR-mediated route, the clearance change across the glycemic region was predicted to be 15%, not far from the original 13% in panel (D). On the other hand, we found the interspecies differences in MR-mediated clearance capacity (ii) and MR IC₅₀ (iii, representative of the glucose competitiveness) to be strongly correlated with differences in MK-2640 PK. (G) Only the transposition of both factors in panel (F) (ii,iii) from minipigs to humans resulted in a modulation beyond 30%, a threshold critical to MK-2640’s entry into the clinical stage. (H) Schematic of the local mass balance of MK-2640 in the liver. Q, blood flowrate; [GRI]_in and [GRI], local MK-2640 concentrations into and out of the liver compartment. (I) IM³PACT simulations confirmed the Merck team’s hypothesis that the local hepatic MK-2640 PK demonstrates a more salient glucose responsiveness (a change of 18%) than that of the whole body. This improved result, however, still does not compare with the preclinical performances (panel D). (J) A simple proxy metric for the extent of MR-mediated MK-2640 clearance, F_MRCL, can be derived from the liver mass balance in (H). F_MRCL allows direct visualization of the dependence of competitive clearance on local glucose and GRI concentrations, based solely on MK-2640 parameters and the liver physiology without requiring simulation. Green curve, Merck’s clinical trial 1 on non-diabetic individuals (cf. Figure 3G); red curves, trial 2 protocol applied to diabetic humans and minipigs.

We investigated the above disparity in glucose responsiveness by looking for key differences between humans and minipigs, particularly those pertaining to MK-2640’s PK and PD as recommended by Cho and colleagues.²⁸ To this end, Table 1 provides a side-by-side comparison of the relevant parameters in IM³PACT’s human and minipig models. The numerically largest distinction was identified between the k_MR values of MK-2640. The significantly lower k_MR value uncovered in the clinical trials represents a smaller MR-mediated clearance capacity in humans than in minipigs, caused by a lower availability of participating MRs in the compartment (θ_tot, eq 1), a slower elimination of each bound MK-2640 (k₂), or a combination of both in the human body.

Table 1. Interspecies Differences in MK-2640 Properties Hypothesized to Have Contributed to the Unsuccessful Clinical Translation^a.

MK-2640 property	indication	model parameter	human	minipig	dimension
volumetric rate constant of MR-mediated elimination from the liverb	clearance capacity via MR		160.2	606.2	mU/L-min
IR-mediated clearance, as a fraction of RHI	clearance capacity via IR	ΛIRC	90%	60%	[-]
relative affinity to IR, as a fraction of RHI	molecular potency	IR IC50(GRI)/IR IC50(RHI)	4.5%c	5.5%c	[-]
ratio of in vivo MR IC50 to the in vitro assay (7.5 mM)	drift in the most responsive blood glucose range	MR IC50(in vivo)/MR IC50(in vitro)	3.3d	1.5d	[-]
central compartment volume Vc, as a fraction of RHI	deviation of peak post i.v. concentration from RHI	ΛV	85%	42%e	[-]

^aSee the addressing key distinctions between MK-2640 and RHI section for a detailed explanation.

^bSee eqs 4 and 9.

^cBased on the in vitro IR binding assay results reported in Kaarsholm et al.²¹

^dAlso see Figure 4E.

^eCalculated from the reported i.v. bolus data²¹ as analyzed in Research Design and Methods.

Apart from the total MR-mediated clearance capacity, the maximal degree of modulation in MK-2640 clearance is naturally also dependent on the capacity of IR-mediated intrinsic elimination. The latter is characterized in IM³PACT by Λ_IRC, which expresses IR-mediated capacity of MK-2640 clearance as a fraction of its RHI counterpart (see Research Design and Methods). As seen in Table 1, the reduction in IR-mediated clearance is less pronounced in humans (10% vs 26% in minipigs), potentially correlated with the relatively higher affinity to IR. In humans, this larger retention of the intrinsic clearance capacity could have masked a non-negligible modulation in MR-mediated clearance when one examines the total clearance change of trial 2. We verify the validity of this hypothesis below in Discussion.

Orthogonal to k_MR which determines the MR-mediated clearance capacity affordable, the glucose IC₅₀ for MR binding characterizes the actual fraction of that capacity utilized as a function of [G] and [GRI] (see eq 5). In agreement with a prior hypothesis that the in vivo relative binding strengths to MR could have shifted from the in vitro assay,³⁰ we did find the MR IC₅₀ in minipigs and humans to drift upward in each species from the 7.5 mM predicted in vitro, particularly so in humans with a 2.3-fold departure (Table 1 and Figure 4E). As a final insight, the central compartment volume V_c of MK-2640 in humans was similar to that of RHI; this stands in contrast to the minipig ratio of Λ_V = 42% that had been observed in i.v. bolus data (discussed above in Research Design and Methods).

Discussion

Analyzing Root Cause(s) of the Poor Translatability

Interspecies distinction in each of the five MK-2640’s properties can be hypothesized to have contributed to the unsuccessful replication of promising preclinical results in clinical trials. We verified the validity of these potential failure modes in silico by examining simulated clamp outcomes under hypothetical scenarios wherein a given MK-2640 characteristic in minipigs is transposed to humans. For example, Figure 4F(i) showcases a 15.0% reduction in total clearance between euglycemic and hyperglycemic clamp simulations should human IR-mediated clearance of MK-2640 be 60% that of RHI, instead of 90%. Even as this reduced intrinsic clearance did accentuate the glucose-responsive MR contribution, only a 2.0% improvement (above the original 13.0% modulation) does not qualify the Λ_IRC difference as a major contributor to MK-2640’s lack of clinical glucose responsiveness. We likewise demonstrated in Supporting Information, Figure S2 that the GIR’s glucose responsiveness would not meaningfully improve if the human MK-2640 model should adopt the same IR affinity or central compartmental volume of minipigs. Interestingly, in spite of the large disparity in Λ_V across species, an MK-2640 central volume similar to RHI’s would actually enhance the GRI’s response in humans, as the transposition of the porcine Λ_V of 42% further truncated the 13.0% clearance reduction to 8.2% (Supporting Information, Figure S2).

The simulation shown in Figure 4F(ii) suggests that the variation of clearance would be boosted to 20.4% if the human model should assume the MR clearance capacity (k_MR) of minipigs (see Table 1). As expected, a nearly quadrupled value of k_MR raises the total clearance rates at all clamp setpoints, which in turn shifts the partition between glucose-responsive (MR-mediated) and intrinsic (IR-mediated) elimination pathways [Figure 4F(ii)]. If we block MR binding by enforcing a k_MR value of 0, the clearance rate of 10.2 mL/kg/min would be made up solely of IR-mediated MK-2640 removal in the liver, kidney, and periphery. This in turn would predict that with the k_MR of minipigs transposed to the human model, 60.2% of the total clearance at 80 mg/dL would be accounted for by MR. This percentage is much closer to Merck’s canine experiments, which estimated an MR contribution of 80% at euglycemia,²¹ as the unmodified clamp simulations attributed only 33.9% of the total clearance to MR in humans. The significant change in glucose responsiveness brought about by cross-species capacity difference, manifested in the k_MR values, confirms the suspicion of Krug and colleagues: that the “incomplete understanding of quantitative differences across species in [MK-2640’s] clearance capacity complicate predictions of clinical GRI PK and clearance” despite the high sequence conservation of the MR protein itself.¹⁸

The simulations in Figure 4F(iii) investigated the impact of the MR IC₅₀ of MK-2640, which characterizes the range of blood-glucose levels most sensitive to CCM (Table 1). We predicted a modulation beyond 20% if, hypothetically, the MR IC50 in humans would either be the same as in minipigs (22.0%) or as that predicted by the in vivo binding assay (21.3%, see Figure 4E). It is not uncommon for these in vitro assays to deviate from actual in vivo behavior,⁶⁵ sometimes with binding constants differing by orders of magnitude due to changes in receptor presentation, accessibility, and microenvironment.⁶⁶ Although in both minipigs and humans the fractional inhibition curve shifted rightward from the in vitro measurements (Figure 4E), only in the human simulation did the shift impair glucose responsiveness, as the clinical MR IC₅₀ of 24.5 mM was askew of the 80 to 300 mg/dL (4.4–16.7 mM) range wherein clearance modulation is desired. That is, MR-mediated clearance was far from completely switched off at hyperglycemia, and total MR capacity was not fully utilized for glucose responsiveness. Indeed, as shown in the clinical trial 1 data (Figure 3G), the total clearance at high IIRs fell to approximately 10 mL/min/kg after the mannose receptors are saturated. MK-2640 elimination mediated by IR, by deduction, could therefore not exceed 10 mL/min/kg. Similarly, in trial 2 (Figure 4C), the gentle drop in total clearance from 14.0 to 12.8 mL/min/kg in principle left ample room for further reduction at hyperglycemia (>2.8 mL/min/kg), which, if fully utilized, would have translated to a satisfactory 28.6% of change. Supporting Information, Figure S3 provides additional evidence confirming this conclusion, as an i.v. bolus simulation of non-diabetic humans still showed a marked change when α-MM was added, suggesting an active CCM at low blood-glucose concentration (cf. Figure 3B). This result points the lack of PK modulation in humans to MR-mediated clearance remaining significant under hyperglycemic conditions, rather than its insufficiency at euglycemia.

MK-2640 advanced to the clinical stage because of a “30% decrease in clearance observed” in preclinical clamp studies.^18,21 While the mediocre glucose-responsive behavior is predicted to be significantly enhanced when the human IM³PACT model adopts the MR clearance capacity (k_MR) or the MR IC₅₀ as in minipigs, both factors must be combined to surpass the bar as seen in Figure 4G (33.3%). From these observations, we conclude that the underlying reasons for the failure of PK translation are twofold: (i) human mannose receptors are not sufficiently available or rapid for the MR-mediated portion to dominate total clearance, as Krug et al. suggested;¹⁸ and (ii) the concentrations of glucose able to switch on or off the CCM fell out of the clinically relevant glycemic range.

Validating the Hypothesis of a Responsive Local PK

Upon observing the lack of a systemic modulation in MK-2640’s clearance, Krug et al. posited a glucose-responsive PK change confined locally to the hepatic bed and splanchnic tissues.¹⁸ We investigated this hypothesis by focusing on the mass balance of MK-2640 within the liver compartment (Figure 4H)

10

where Q denotes the blood flowrate, [GRI]_in and [GRI] the MK-2640 concentration entering and exiting the liver, and R_ICL the rate of intrinsic clearance mediated by IR. Whereas R_ICL is a function of just [GRI], R_MRCL is dependent on both [GRI] and [G] as dictated by eq 9 derived from MK-2640’s mechanistic model. Hepatic clearance (HCL), the volume of plasma cleared of MK-2640 per unit time in the pharmacological sense, can readily be extracted from the IM³PACT simulations as

11

as presented in Figure 4I. Indeed as Krug and colleagues hypothesized, the hepatic-clearance change between eu- and hyperglycemia is noticeably higher (18%) than that manifested in the systemic pool (13%). Almost the entirety of the responsiveness, as expected, is contributed by MR-mediated clearance—the R_MRCL/[GRI] term—which is 43% lower under hyperglycemic conditions relative to euglycemia. The large discrepancy between 43 and 18% is caused by the dominant contribution from intrinsic IR-mediated clearance, corroborating the above discussion of Figure 4F(ii). The diminished role of MRCL in humans implies that even the improved PK modulation within the liver is only modest in contrast to that previously observed in dogs and minipigs.

Visualizing the Glucose-GRI Landscape for Competitive Clearance

Besides confirming the hypothesis of a hepatic glucose-responsive PK, the local MK-2640 balance within the liver compartment also provides a dimensionless proxy, F_MRCL, for the extent of MR-mediated MK-2640 clearance, the landscape of which over [G] and [GRI] can be analytically mapped without numerical simulation. To begin, eq 10 can be rearranged as

12

where Δ[GRI] is defined as [GRI]_in – [GRI]. F_MRCL is defined as the MR-mediated contribution to Δ[GRI]/[GRI], which in turn represents the overall extent of MK-2640 elimination in the liver. Via the mechanistic model of MK-2640 in eq 10, F_MRCL can be expressed as

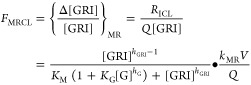13

As shown in Figure 4J, this analytical expression enables the F_MRCL landscape in minipigs and humans to be directly constructed as a function of the local glucose and MK-2640 concentrations. In contrast to the full-body IM³PACT simulations performed in Figure 4F,G,I, the F_MRCL landscapes are independent of specific clamp protocols and so offer a straightforward visualization of the interplay between various levels of glucose and GRI. For example, the green curve traversing the human F_MRCL landscape in Figure 4J represents the escalating-dose clamp study in healthy human volunteers: the glucose concentration was kept constant at 80 mg/dL (4.4 mM), while the MK-2640 concentration varied from 0.08 to 68.62 nM. F_MRCL rises initially at lower GRI levels due to the cooperativity in binding, even more saliently so than in Figure 3G, before reaching a maximum and declining as the MRs are saturated at high GRI concentrations.

The red curves along the F_MRCL surfaces in Figure 4J illustrate the proxy’s utility by proving—in a qualitative but simulation-free manner—the previously identified root causes of the unsuccessful translation. They, respectively, represent the two-stage clamp protocol performed in diabetic humans and minipigs, which revealed PK changes between [G] = 90 and 300 mg/dL (5.0 and 16.7 mM). The interspecies disparity in extent of PK modulation is evident, as F_MRCL shifts by more than 60 in minipigs and by only ca. 30 in humans, hinting that CCM would be significantly less responsive in a clinical context. The first contributing factor is the generally depressed F_MRCL landscape in humans. For instance, the F_MRCL maxima over the selected [G] and [GRI] ranges are 47.2 for humans and 71.0 for minipigs. This is attributed to the lack of clearance capacity by MR in humans relative to preclinical animals, signified by a small k_MR in eq 13 (see also Table 1). Second, while the F_MRCL progression in minipigs appears mostly linear, the noticeable curvature of that in humans marks a gradual descent instead. That is, the most glucose-sensitive linear section of the “S”-shaped response curve (see Figure 4E) is not fully utilized in humans. Both of these factors, directly visualized in the F_MRCL landscapes, agree with conclusions from our earlier quantitative full-body analyses (Figure 4F,G). Although the F_MRCL proxy does not take into consideration the intrinsic clearance rate (i.e., F_ICL in eq 12), it already warns us of the GRI’s diminished responsiveness in humans based on MK-2640 parameters and liver physiology alone, even before running comprehensive IM³PACT simulations.

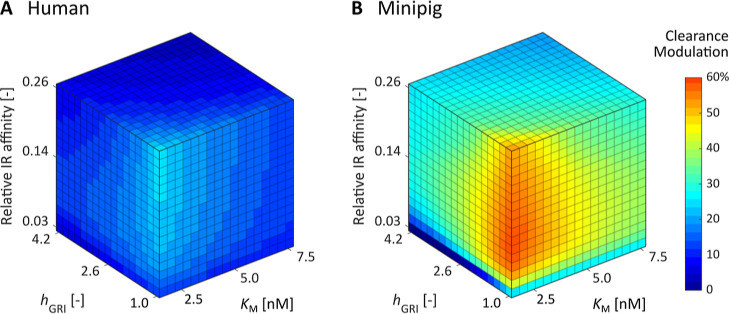
Exploring the GRI Design Space for Better-Performing Candidates

As the pattern of glucose binding to MRs as well as the MR distribution is intrinsic to the relevant physiology, K_G, h_G, and k_MR are not considered design parameters of MK-2640 with room for adjustment. On the other hand, h_GRI, K_M, and the relative IR affinity of a competitive-clearance-based GRI can be customized by, for instance, designing the linker and number of sugar molecules conjugated to the mannosylation site.¹⁹ Following the protocol previously reported,^30,33 we scanned the GRI Design Space, or GRIDS, of MK-2640 in both humans and minipigs to identify the optimal combination of design parameters as well as the performance cap in each species. The objective function plotted in Figure 5A,B represents the change in MK-2640’s clearance between 90 and 300 mg/dL, exactly replicating the clinical trial design in diabetic individuals. For each combination of h_GRI, K_M, and IR affinity, we determined the ratio of MK-2640 and RHI doses corresponding to the half-maximum GIR. Identical to the clinical trial protocol, this “potency ratio” was used as a scaling factor to decide the IIR of the two-stage clamp. Since both the glucose-lowering effect and the intrinsic clearance are mediated by IR-binding, we assumed Λ_IRC scales with the IR affinity accordingly.

Figure 5.

Simulated changes in clearance between eu- and hyperglycemic clamps at 90 and 300 mg/dL for competitive clearance GRI candidates spanning the entire design space. These MK-2640 derivatives are unlikely to be sufficiently responsive in humans (A) even with enhanced potency and optimized MR binding kinetics. In contrast, a much wider range of h_GRI, K_M, and relative IR affinity combinations is predicted to yield glucose-responsive PK in minipigs (B).

The simulation results in Figure 5A,B exhibit a marked contrast: Over the selected parameter ranges, the best performing competitive clearance GRI records only a 24% of PK change in humans, while the optimal GRI candidate in minipigs offers 73%. As shown in Supporting Information, Figure S4, even over a set of expanded parameter ranges, the permitted space corresponding to a responsive clearance modulation of 30% and above is far larger in minipigs than in humans. This means that before we even consider whether the optimal parameter values identified are experimentally practical, the prospect of clinical translation is poor for MR-based competitive clearance GRIs. In other words, we predict that the variants of MK-2640 developed by the Merck team are unlikely to perform well in humans in spite of their enhanced potency.^19,20

Outlook and Summary

The lack of glucose responsiveness revealed in clinical trials halted MK-2640’s development and destabilized confidence in the rest of the CCM GRIs. Nonetheless, many in the field have acknowledged the tremendous value of the clinical data as well as the overall workflow established by the Merck team. The use of mannoside antagonist as a mimic for hyperglycemic conditions, for example, was recognized by Hoeg–Jensen as an innovative development for in vitro investigations.²⁴ The synergy between the iterative experimentation and modeling efforts throughout MK-2640’s development enabled streamlined preclinical and clinical studies as well as improved simulation tools.⁶³ To build on this foundation, we have exploited mechanistic modeling of MK-2640’s glucose responsiveness and translational modeling of the full-body physiology to pinpoint the factors that challenged translation. This approach also promises to provide a basic quantitative understanding of the capacity and action of MRs across species.

Availability of additional experimental data could address the limitations of this study. First, as already discussed, the attribute representative of the overall MR-mediated clearance capacity, k_MR, encompasses both MR availability (θ_tot) as well as its specific rate of MK-2640 internalization (k₂). Decoupling these two degrees-of-freedom would require in vivo or in vitro measurements in addition to existing MR-mediated clearance rates, preferably isolating either the effect of k₂ or θ_tot. MRC1 gene expression data serve as one potential source of information on MR abundance and distribution. Although the expression levels in humans and pigs have been reported, inconsistent protocols render such cross-species comparability uncertain.⁶⁷⁻⁶⁹ Furthermore, RNA and protein expression levels provide only qualitative indicators of MRC1’s activity and are therefore not the best sources for key quantitative information. Second, as Taylor and DiMarchi pointed out, it is of practical value to understand the impacts of inter-individual variability given MK-2640’s reliance on endogenous biological processes.²⁹ While our investigations into population-averaged data and simulations are sufficient in identifying interspecies distinctions central to the GRI’s clinical translation, future iterations of IM³PACT could benefit from population statistics found on systemically measured, individualized RHI and MK-2640 data in both animals and humans,⁷⁰ ideally with a quality that parallels the clinical RHI data set⁷¹ upon which the acclaimed UVa/Padova model was established.^72,73 An informative starting point would be the MK-2640 clinical trial data from 36 healthy and 16 diabetic adults, although only a small subset of experimental results was made accessible and individualized in the publications.¹⁸ The glycemic clamp results were also subject to interferences from external conditions such as algorithms of the GIR feedback controller,⁷⁴ and the steady-state readings may not be as informative to the mathematical model as a time-index concentration portrait.

In summary, we have investigated the clinical translatability of CCM-based GRIs via translational in silico modeling based on preclinical and clinical data of MK-2640 and RHI. To this end, we upgraded upon our previous platform with capabilities of simulating minipigs’ glucoregulatory system as well as mechanistically describing the CCM scheme. The simulation results quantitatively match data from in vitro binding assays, intravenous boluses, subcutaneous injections, and glycemic clamps. Expanding upon hypotheses posited by the experimentalists, we identified and examined potential inter-species distinctions in GRI and mannose-receptor properties that could have compromised the clinical translation of MK-2640. By simulating clinical clamps with these MR properties varied one at a time, we concluded that poor translatability was the consequence of a combination of insufficient clearance capacity in humans and also an in vivo competitiveness profile mismatched with the physiologically relevant glycemic range. Meanwhile, altered IR-mediated clearance, potency, and distribution volume of MK-2640 were found to be minimally relevant to the lack of a responsive PK in the clinic, despite the general relevance of these key parameters to the design of CCM GRIs. We envisage that this study establishes the utility of in silico platforms like IM³PACT not only for design optimization and prediction of translatability,^3,30,33,63 but also for a posteriori analyses of preclinical and clinical data. The latter promises to enable quantitative, mechanistic inferences to be extracted beyond the explicit metrics. Such investigations should be an integral part of a drug-development workflow, regardless of trial outcome, as they channel the maximal value of an experimental study toward future therapeutics meaningful for patients. On a grander scale, IM³PACT builds toward a new paradigm wherein computational tools assume a critical role in all stages of pharmaceutical research and development: from drug design and candidate screening to preclinical testing and clinical development.^3,30,63 Progressing hand-in-hand with experimentation, in silico tools promise to accelerate, de-risk, and optimize the experimental workflow while at the same time improving iteratively via the additional data generated.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsptsci.3c00095.

• Mathematical model setup, mathematical treatment of MK-2640’s reduced IR affinity, simulated plasma glucose response to an intravenous dose of MK-2640 in a non-diabetic human, and simulated changes in clearance between eu- and hyperglycemic clamps at 90 and 300 mg/dL spanning an expanded design space (PDF)

Author Contributions

J.F.Y., X.G., N.A.B., and M.S.S. conceived the mathematical model. J.F.Y., A.D.C., M.A.W., and M.S.S. analyzed the preclinical and clinical data of MK-2640 and generated hypotheses for the failed translation, based on which J.F.Y. constructed the mechanistic model of CCM. J.F.Y. and S.Y. constructed the physiological model on the basis of our previous publication. J.F.Y. performed the parameter estimation based on data A.B.W. organized from the literature. J.F.Y., X.G., S.Y., and G.Z. analyzed the poor translatability of MK-2640 with IM³PACT simulations. J.F.Y. studied the optimal design space of generalized CCM GRIs. J.F.Y., M.A.W., and M.S.S. drafted the manuscript. All authors commented on and edited the manuscript.

This work was supported by National Institutes of Health (1R01DK127761) and Helmsley Charitable Trust (#1902-03727 to MPI team M.S.S., A.C., and M.A.W.). The authors also acknowledge a grant from the Helmsley Charitable Trust to M.S.S. at MIT, no. 2202-05781, for support of IM³PACT development and refinement. M.A.W. was supported in part by the INCITE Scholars program at Indiana University.

The authors declare no competing financial interest.