Reinforcement-based processes actively regulate motor exploration along redundant solution manifolds

Abstract

From a baby’s babbling to a songbird practising a new tune, exploration is critical to motor learning. A hallmark of exploration is the emergence of random walk behaviour along solution manifolds, where successive motor actions are not independent but rather become serially dependent. Such exploratory random walk behaviour is ubiquitous across species' neural firing, gait patterns and reaching behaviour. The past work has suggested that exploratory random walk behaviour arises from an accumulation of movement variability and a lack of error-based corrections. Here, we test a fundamentally different idea—that reinforcement-based processes regulate random walk behaviour to promote continual motor exploration to maximize success. Across three human reaching experiments, we manipulated the size of both the visually displayed target and an unseen reward zone, as well as the probability of reinforcement feedback. Our empirical and modelling results parsimoniously support the notion that exploratory random walk behaviour emerges by utilizing knowledge of movement variability to update intended reach aim towards recently reinforced motor actions. This mechanism leads to active and continuous exploration of the solution manifold, currently thought by prominent theories to arise passively. The ability to continually explore muscle, joint and task redundant solution manifolds is beneficial while acting in uncertain environments, during motor development or when recovering from a neurological disorder to discover and learn new motor actions.

1. Introduction

When pushing a swinging door or grabbing a handrail, there are several potential locations we can place our hand. While such tasks appear simple, the sensorimotor system has the constant challenge of selecting an action from the infinite number of potential solutions along muscle [1–3], joint [4–7] and task redundant dimensions [8–13] (e.g. grabbing a handrail). Past work has highlighted that humans are more variable along such redundant solution manifolds [3,5,6,10,11,14–16], which may reflect an exploratory mechanism that is continually searching for the most successful action [17,18]. Continual exploration may be a beneficial strategy in a dynamic or uncertain environment [19].

Promiscuous songbirds explore by injecting greater levels of variability in the pitch of their tune to attract several mates [20–24]. Likewise, movement variability may facilitate the ability to find the most successful motor action [17,18]. Movement variability has been proposed to arise from stochastic neuromuscular processes [25–27] (‘motor movement variability’), the dorsal premotor cortex during movement preparation [8,28,29] (‘planned movement variability’), and the basal ganglia [18,22,30] (‘exploratory movement variability’). It has been proposed that the sensorimotor system has knowledge of both planned [31] and exploratory [30,32] movement variability, which may arise from separate neural circuits. The role of the basal ganglia provides an explanation for the compromised regulation of exploratory movement variability for those with Parkinson’s disease [30]. It is unclear to what extent the sensorimotor system uses motor, planned, or exploratory movement variability to facilitate exploratory behaviour that promotes success.

Elegant theoretical and empirical work by van Beers et al. [8] suggested that both knowledge of and acting upon planned movement variability lead to exploratory motor behaviour [8,33–35]. They found that participants displayed greater explorative behaviour along the task-redundant dimension compared to the task-relevant dimension. Here, the term exploration captures the idea of increased variability as well as using their variability to traverse a two-dimensional solution space. They quantified exploration using statistical random walks (i.e. lag-1 autocorrelations), where a greater lag-1 autocorrelation is indicative of more exploration. In this context, the term exploration captures not only the presence of movement variability but also the idea that the sensorimotor system is aware of movement variability and allows it to update reach aim to traverse the solution space. Here, greater exploratory random walk behaviour was attributed to passive process that arose from an accumulation of planned movement variability in the task-redundant dimension and not making trial-by-trial corrective actions based on error feedback. A fundamentally different explanation is that reinforcement-based processes may actively regulate the magnitude and structure of movement variability that underlies exploratory random walk behaviour—but this idea has not yet been tested empirically.

Here, we hypothesize that reinforcement-based mechanisms contribute to exploratory random walk behaviour. To test this idea, we manipulated the size of both the visually displayed target and an unseen reward zone, as well as the probability of reinforcement feedback. For all three experiments, we made a priori predictions with a general model. We then found the best-fit model from seven different plausible models, each representing a unique explanation of the mechanisms regulating sensorimotor exploration. Taken together, our empirical and modelling results support the idea that reinforcement-based mechanisms play a critical role in regulating exploratory random walk behaviour.

2. Results

(a) . Experimental design

In Experiments 1 (n = 18), 2 (n = 18) and 3 (n = 18), participants made 500 reaching movements in the horizontal plane (figure 1a). For each trial, participants began their reach in a start position and attempted to stop within a virtually displayed target. They did not have vision of their hand. For each reach, we recorded their final hand position when they stopped within or outside the virtually displayed target.

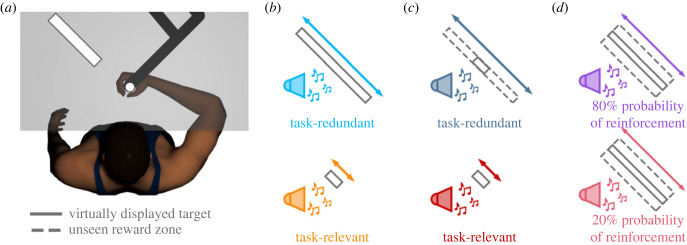
Figure 1.

(a) Experimental apparatus. Participants were told they would receive reinforcement feedback when they successfully stopped within the observed target (dark grey outline). Targets used in (b) Experiment 1, (c) Experiment 2, and (d) Experiment 3. (c,d) Unbeknownst to participants, in Experiment 2 and 3 they received reinforcement feedback when their hand stopped within the unseen reward zone (grey dashed line). (d) In Experiment 3 we manipulated the probability of reinforcement feedback.

For all three experiments, we used a repeated measures experimental design. Participants performed 50 baseline trials, 200 experimental trials, 50 washout trials, and then another 200 experimental trials. Condition order was counterbalanced for the experimental trials. During baseline and washout trials, participants reached towards and attempted to stop within a white circular target. For the first 40 trials of baseline and washout, a small cursor indicated final hand position. Participants received no feedback of their final hand position for the last 10 trials of baseline and washout. Removing feedback for the last 10 trials allowed us to estimate movement variability without the influence of reinforcement feedback or error feedback.

During the experimental trials, participants reached towards and attempted to stop within a rectangular target (figure 1a). The rectangular targets were positioned such that their major and minor axes corresponded to movement extent (i.e. parallel with the reaching movement) and lateral direction (i.e. orthogonal to the reaching movement), respectively. The target dimensions depended on the experimental condition and were scaled according to each participant’s movement variability from their last 10 baseline trials [18]. Scaling target width based on baseline behaviour maintained a relatively constant task difficulty across participants. During the experimental trials, participants were informed that they would receive positive reinforcement when their final hand position was within the target, such that (i) they would hear a pleasant sound, (ii) the target would briefly expand, and (iii) they would earn a small monetary reward. Participants were also informed they would not receive any feedback when they did not stop within the rectangular target.

In Experiment 1, we addressed how reinforcement feedback influences exploration along a redundant solution manifold. In the task-redundant condition, participants reached to a long rectangular target that promoted exploration along the movement extent (figure 1b). In the task-relevant condition, participants reached to a short-rectangular target that discouraged exploration along the movement extent. Here, we predicted greater explorative behaviour along the movement extent in the task-redundant condition compared to the task-relevant condition (see §2c). The goal of Experiment 2 was to control for visual differences in the virtually displayed target size between conditions since past works have shown that a visually larger target leads to greater movement variability [13,36–38]. That is, we wanted to be assured that reinforcement-based processes were leading to greater exploration (lag-1 autocorrelation) rather than greater movement variability due to a larger visually displayed target. Further, this would also allow us to replicate the results from Experiment 1. Participants were shown the short rectangular (task-relevant) target in both conditions (figure 1c). They received reinforcement feedback when their hand stopped inside an unseen reward zone. In the task-relevant condition, the unseen reward zone matched the visually displayed target. Unbeknownst to participants, in the task-redundant condition, they received reinforcement feedback if they stopped anywhere inside a long rectangular, unseen reward zone. Here, we again predicted greater explorative bahaviour along the movement extent of the task-redundant target just as in Experiment 1 (see §2c).

In Experiment 3, we directly manipulated reinforcement feedback to assess how it influences exploration along a redundant solution manifold. Specifically, we manipulated the probability of reinforcement feedback. By manipulating the probability of reinforcement feedback, we were able to simultaneously control for the size of both the visually displayed target and the unseen reward zone. Participants were always shown the task-redundant target. Unbeknownst to the participants, we widened the unseen reward zone in both conditions (figure 1d). Here, we manipulated the probability of receiving reinforcement feedback when participants stopped within the unseen reward zone. Participants performed two conditions, where they either had an 80% or 20% probability of receiving reinforcement feedback. We predict that participants will exhibit greater exploratory random walk behaviour with a higher probability of reinforcement feedback (see §2c).

(b) . A priori model predictions

Only a few models of sensorimotor behaviour that simulate final hand position consider multiple sources of movement variability. Further, these models have varying assumptions on how much knowledge the sensorimotor system has of a particular source of movement variability when updating a motor action [8,18,31,32,39]. Here, we developed a general model (Model 1; equation 1a,b) that consolidated previously proposed models while using a minimal number of assumptions. We used our general model to generate a priori predictions. The general model simulates two-dimensional final reach position (${\mathit{X}}_{\mathit{t}}$) and intended reach aim (${\mathit{X}}_{\mathit{t}}^{\mathbf{a}\mathbf{i}\mathbf{m}}$) according to

$${\mathit{X}}_{\mathit{t}}={\mathit{X}}_{\mathit{t}}^{\mathbf{a}\mathbf{i}\mathbf{m}}+{\mathit{ϵ}}_{\mathit{t}}^{\mathit{m}}+{\mathit{ϵ}}_{\mathit{t}}^{\mathit{p}}+(1-r_{t-1}^e)\hspace{0.17em}{\mathit{ϵ}}_{\mathit{t}}^{\mathit{e}}$$ 1a

$${\mathit{X}}_{\mathit{t}+1}^{\mathbf{a}\mathbf{i}\mathbf{m}}={\mathit{X}}_{\mathit{t}}^{\mathbf{a}\mathbf{i}\mathbf{m}}+r_t^p{\alpha }^p{\mathit{ϵ}}_{\mathit{t}}^{\mathit{p}}+r_t^e{\alpha }^e[(1-r_{t-1}^e){\mathit{ϵ}}_{\mathit{t}}^{\mathit{e}}].$$ 1b

The model incorporates three sources of movement variability (${\mathit{ϵ}}^{\mathit{i}}$): motor (${\mathit{ϵ}}^{\mathit{m}}$), planned (${\mathit{ϵ}}^{\mathit{p}}$), and exploratory (${\mathit{ϵ}}^{\mathit{p}}$). Note that the term planned movement variability refers to the stochastic processes that have been shown to arise in the planning stages of movement [8,28,29]. Exploratory movement variability is added when the previous trial was unsuccessful [18,30,39] ($r_{t-1}^e=0$). If the trial is successful ($r_t^i=1$), reach aim is updated proportionally (α^p, α^e) towards the planned and exploratory movement variability present in movement execution. In the equations, reward outcomes $r_t^p$ and $r_t^e$ are differentiated strictly for notation purposes and refer to the same reward outcome on trial t. Updating towards the previously reinforced motor actions results in a statistical random walk of the final hand positions. This random walk behaviour is qualitatively described as exploration and is quantitatively captured using a lag-1 autocorrelation analysis. A greater lag-1 autocorrelation corresponds to greater exploratory random walk behaviour. Note, while here we focus on sensorimotor exploration, this class of models can and have been used to capture sensorimotor adaptation [8,18,31,32,39].

(c) . Simulating individual behaviour

We first simulated the final hand position of an individual performing the task-redundant and task-relevant conditions from Experiment 1 (figure 2a). Here, we see more exploration, corresponding to a higher lag-1 autocorrelation, along the movement extent of the reach in the task-redundant condition (figure 2b). For this simulated individual, we then quantified the level of exploration along the movement extent for both conditions. A greater lag-1 autocorrelation indicates greater exploration of the solution manifold. Similar to past work [8,9,12,34,40], Model 1 produced greater lag-1 autocorrelation in the task-redundant condition compared to the task-relevant condition along the movement extent of the reach (figure 2c).

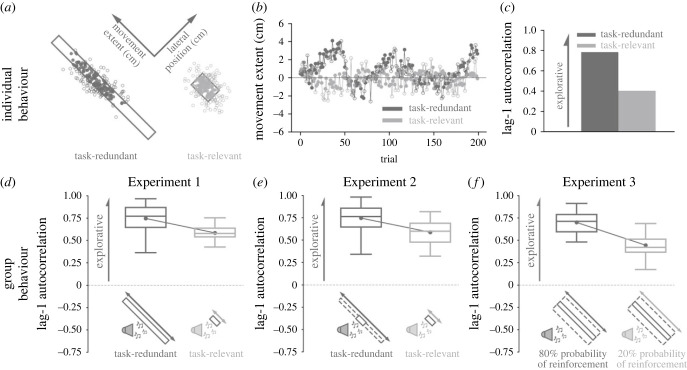
Figure 2.

A priori model predictions. We made theory-driven predictions by simulating (a–c) individual behaviour in Experiment 1 and (d–f) group behaviour in Experiments 1–3 using a model that updates reach aim based on reinforcement feedback while considering different plausible sources of movement variability (equation 1a,b; Model 1). Model parameter values were held constant for all predictions. (a) Successful (filled circle) and unsuccessful (unfilled circle) final hand positions when simulating an individual performing the task-redundant (dark grey) and task-relevant (light grey) conditions in Experiment 1. (b) Corresponding final hand position (y-axis) for each trial (x-axis) along the major axes of the task-redundant and task-relevant targets. Note that there is greater exploration in the task-redundant condition. (c) We quantified exploration by calculating the lag-1 autocorrelation (y-axis) of the trial-by-trial final hand positions along movement extent for each condition (x-axis). Here, a higher lag-1 autocorrelation represents greater exploration along a solution manifold. The model predicts greater lag-1 autocorrelation in the task-redundant condition (dark grey) compared to the task-relevant condition (light grey). (d–f) By using the same parameter values, we simulated 18 participants per condition for the three experiments. (d) For Experiment 1, the model predicted greater lag-1 autocorrelation (y-axis) in the task-redundant condition compared to the task-relevant condition (x-axis). (e) In Experiment 2, the model predicted greater exploration in the task-redundant condition with a large rectangular unseen reward zone compared to the task-relevant condition. (f) In Experiment 3, the model predicted greater exploration in the 80% probability of reinforcement feedback condition relative to the 20% probability of reinforcement feedback condition. Solid circles and connecting lines represent mean lag-1 autocorrelation for each condition. Box and whisker plots display the 25th, 50th and 75th percentiles.

(d) . Simulating group behaviour

To make a priori predictions of group behaviour for Experiments 1, 2 and 3, we used the general model (Model 1) to simulate the final hand position of 18 participants for each condition. For each condition, we calculated the trial-by-trial lag-1 autocorrelation for each participant. This analysis was performed separately along the movement extent and lateral direction of the reach. We used the average lag-1 autocorrelation for each condition as the a priori predictions for each experiment. A priori model predictions of group behaviour for Experiment 1 (figure 2d) show higher lag-1 autocorrelations in the task-redundant condition compared to the task-relevant condition. Similarly, in Experiment 2, the general model (Model 1) predicted greater lag-1 autocorrelation in the task-redundant condition in comparison to the task-relevant condition (figure 2e). In Experiment 3, the a priori model (Model 1) predicted greater lag-1 autocorrelation in the 80% probability of reinforcement condition compared to the 20% probability of reinforcement condition (figure 2f).

(e) . Experiment 1

In Experiment 1, we addressed how reinforcement feedback influences exploration along a task-redundant solution manifold. As a reminder, in the task redundant condition, participants reached to a long rectangular target that was intended to promote exploration along its major axis (figure 1b). In the task-relevant condition, participants reached to a short-rectangular target that discouraged exploration along its major axis.

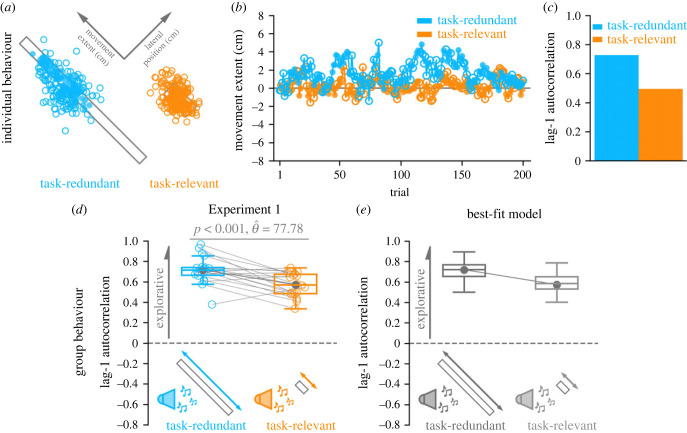
Figure 3a shows final hand positions for an individual participant in both the task-redundant and task-relevant conditions. This particular individual tended to reach towards the upper half of the task-redundant target, but the average final hand position across participants was within 1 cm of the target centre. Note that we would expect final hand positions to cover the entire length of the target given a sufficiently large number of trials. For this participant, we observed greater movement extent exploration of the solution manifold in the task-redundant condition (figure 3b). Conversely, we see less exploration in the task-relevant condition. Greater exploratory behaviour in the task-redundant condition corresponded with a greater lag-1 autocorrelation (figure 3c).

Figure 3.

Experiment 1 results. (a) Successful (filled circle) and unsuccessful (unfilled circle) reaches by an individual participant performing the task-redundant (light blue) and task-relevant (light orange) conditions. (b) Corresponding final hand position coordinates (y-axis) along the movement extent of the task-redundant and task-relevant targets over trials (x-axis). (c) This individual displayed greater lag-1 autocorrelation in the task-redundant condition, matching individual level model predictions (figure 2c). (d) Participants (n = 18) had significantly greater lag-1 autocorrelation (p < 0.001) in the task-redundant condition (light blue) than the task-relevant condition (light orange), suggesting greater exploration of the task-redundant solution manifold. The group level data aligns with predictions of the a priori model (figure 2d). (e) Best-fit model (equation 4a,b; Model 4) according to both Bayesian information criterion (BIC) and Akaike information criterion (AIC) analyses. The best-fit model suggests that participants explored the task-redundant solution manifold by using exploratory movement variability and caching successful actions upon receiving reinforcement feedback. Solid circles and connecting lines represent mean lag-1 autocorrelation for each condition.

At the group level and aligned with our a priori model predictions (figure 2d), we see significantly greater lag-1 autocorrelation (p < 0.001, $\hat{\theta }=77.78$) in the task-redundant condition compared to the task-relevant condition (figure 3d). These results suggest that participants explored the task-redundant dimension by updating their reach aim following positive reinforcement feedback.

Here, we were primarily concerned with movement extent, which corresponded with our experimental manipulation along the major axis of the visually displayed target. Focusing on the movement extent also allowed us to observe behavioural changes induced by failure along the orthogonal lateral position. Thus, focusing on movement extent mitigates spurious artefacts, such as regression to the mean effects that could occur arise along task-relevant dimensions [41]. We also examined lag-1 autocorrelations along the lateral direction that corresponded to the minor axis of the visually displayed targets. We did not see any lag-1 autocorrelation differences between conditions along the lateral direction (electronic supplementary material A, figure SA1).

(f) . Experiment 2

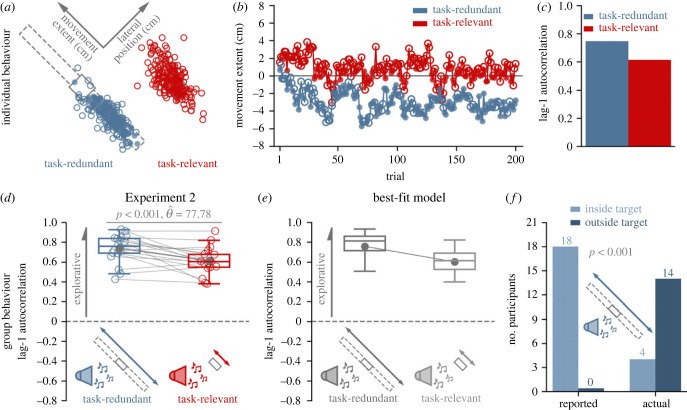
The past work has shown that the distribution of final hand positions can be more variable when reaching to a large target compared to a small target [13,36–38], which could potentially influence exploratory behaviour. The goal of Experiment 2 was to further test the idea that reinforcement feedback drove behaviour and replicate the findings in Experiment 1, while controlling for the visual size of the target. To control visually displayed target size, participants were only shown the short rectangular (task-relevant) target in both conditions. They received reinforcement feedback if they stopped within an unseen reward zone. In the task-relevant condition, the unseen reward zone matched the visually displayed target. Critically, and unbeknownst to participants, in the task-redundant condition, they received reinforcement feedback if they stopped anywhere inside a long rectangular, unseen reward zone (figure 3c).

Aligned with our a priori model predictions (figure 2e), participants displayed significantly greater lag-1 autocorrelation (p < 0.001, $\hat{\theta }=77.78$) along the task-redundant condition compared to the task-relevant condition (figure 4a). These results replicate the finding that reinforcement feedback leads to greater exploratory behaviour along the task-redundant dimension, while also highlighting that the results in Experiment 1 were not due to visual size differences of the virtually displayed target.

Figure 4.

Experiment 2. (a) Successful (filled circle) and unsuccessful (unfilled circle) reaches by an individual participant performing the task-redundant (dark blue) and task-relevant (dark red) conditions. (b) Corresponding final hand position coordinates (y-axis) along the major axis of the task-redundant and task-relevant targets over trials (x-axis). (c) This individual displayed greater lag-1 autocorrelation in the task-redundant condition. (d) Participants (n = 18) displayed significantly greater (p < 0.001) lag-1 autocorrelation (y-axis) in the hidden task-redundant condition (dark blue) compared to the task-relevant condition (dark red), despite observing the same visual target in each condition. The group behaviour aligns with a priori model predictions (figure 2e). (e) Lag-1 autocorrelation (y-axis) for each condition (x-axis) based on simulations by the best-fit model (equation 4a,b, Model 4). (f) To test if they were aware of the long-rectangular reward zone in the task redundant condition (dark blue), participants were asked to mark on a target sheet where they were aiming for the task-redundant condition. All participants reported aiming to a point within the visual target (dark grey bars), but most participants had an average final hand position significantly outside the visual target (light green bars, p < 0.001). These data suggest that updating reach aim towards the most recent successful action may be in part driven by an implicit process (i.e. participants were unaware). Solid circles and connecting lines show mean lag-1 autocorrelation for each condition.

We assessed whether participants were aware of the reward zone manipulation in the task-redundant condition. After the experiment, participants were asked to mark their average final hand position for each condition on a sheet of paper that showed the task-relevant target. All participants reported that they were aiming somewhere within the visually displayed short-rectangular target in the task-redundant condition. As a reminder, in the task-redundant condition, participants saw the task-relevant target but received reinforcement feedback when they stopped within the task-redundant, unseen reward zone (figure 1c).

All 18 participants reported having an average final hand position within the visually displayed target. However, 14 participants had an average final hand position outside the visually displayed target (figure 4c, Fisher’s exact test, p < 0.001). These results suggest participants were unaware of the task-redundant, unseen reward zone and that updating reach aim may, in part, be driven by an implicit process.

(g) . Experiment 3

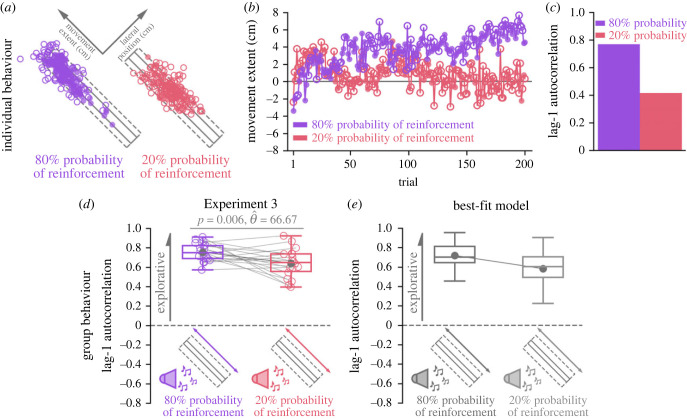
In Experiment 3, we directly manipulated reinforcement feedback to further investigate its role in exploring task-redundant solution manifolds. Specifically, we manipulated the probability of reinforcement feedback. Critically, by manipulating only the probability of reinforcement feedback, we simultaneously controlled for the size of both the visually displayed target and the unseen reward zone. Participants were always shown a task-redundant target (figure 1d). We manipulated the probability that the participants received reinforcement feedback if they stopped within the reward zone. Participants performed an 80% probability of reinforcement feedback condition and a 20% probability of reinforcement conditions.

Aligned with our a priori predictions (figure 2f), participants displayed significantly greater lag-1 autocorrelation (p = 0.006, $\hat{\theta }=66.67$) in the 80% probability condition compared to the 20% probability condition (figure 5a). This result suggests that participants more frequently updated their reach aim when they received a higher probability of reinforcement feedback, which resulted in greater exploration of the solution manifold.

Figure 5.

Experiment 3 results. (a) Successful (filled circle) and unsuccessful (unfilled circle) reaches by an individual participant performing the 80% probability of reinforcement (purple) and 20% probability of reinforcement (pink) conditions. (b) Corresponding final hand position coordinates (y-axis) along the major axis of the target over trials (x-axis). (c) This individual displayed greater lag-1 autocorrelation in the 80% probability of reinforcement condition. (d) Participants (n = 18) displayed greater lag-1 autocorrelations (y-axis) with an 80% probability of receiving reinforcement feedback (purple) compared to a 20% probability of receiving reinforcement feedback (pink). Group behaviour aligned with a priori model predictions (figure 2f). (e) Lag-1 autocorrelations (y-axis) for each condition (x-axis) based on simulations from the best-fit model. This model predicts greater lag-1 autocorrelation for the 80% probability of reinforcement feedback condition (purple) because there were more frequent reach aim updates with a higher probability of positive reinforcement feedback. Solid circles and connecting lines represent mean lag-1 autocorrelation for each condition.

For each of our experiments, we wanted to control for the possibility that the observed lag-1 autocorrelations were the result of unknown stochastic processes rather than the sequential ordering of final hand positions based on reinforcement feedback. To test whether unknown stochastic processes caused the observed lag-1 autocorrelations, we performed a shuffling analysis [12,42] (see electronic supplementary material B). Our analysis suggests that the observed lag-1 autocorrelations are not the result of unknown stochastic processes (shuffled lag-1 ≠ original lag-1, p > 0.05 for all participants).

(h) . Best-fit model

Our general model (Model 1) consolidated previous reinforcement-based reaching models while considering multiple sources of movement variability. This general model did well to generate a priori theory-driven predictions. Yet there are other plausible mechanisms that the sensorimotor system uses to explore a redundant solution manifold. To test this idea, we considered four additional models (Models 2–5) by systematically reducing the number of free parameters from Model 1 (electronic supplementary material, Methods). In addition, we tested two previously proposed reinforcement-based models (Models 6 and 7) in the literature [18,32].

Each model was simultaneously fit to each experimental condition across the three experiments (§4). Specifically, each model was fit to the participant lag-1 autocorrelations in each condition and not the participant’s final hand positions. We used Bayesian information criterion (BIC) and Akaike information criterion (AIC) analyses to compare the fit of each model while penalizing additional free parameters. For both BIC and AIC analyses, a lower score indicates a more plausible model. In agreement, both the BIC and AIC analyses (table 1) supported Model 4 (equation 4a,b) as the best-fit model. The best-fit model (Model 4) simulates final reach position and intended reach aim as follows:

$${\mathit{X}}_{\mathit{t}}={\mathit{X}}_{\mathit{t}}^{\mathbf{a}\mathbf{i}\mathbf{m}}+{\mathit{ϵ}}_{\mathit{t}}^{\mathit{m}}+(1-r_{t-1}^e){\mathit{ϵ}}_{\mathit{t}}^{\mathit{e}}$$ 4a

$${\mathit{X}}_{\mathit{t}+1}^{\mathbf{a}\mathbf{i}\mathbf{m}}={\mathit{X}}_{\mathit{t}}^{\mathbf{a}\mathbf{i}\mathbf{m}}+r_t^e{\alpha }^e[(1-r_{t-1}^e)\hspace{0.17em}{\mathit{ϵ}}_{\mathit{t}}^{\mathit{e}}].$$ 4b

Unlike the general model, the best-fit model (Model 4) does not consider planned movement variability. The model updates its aim towards the next successful final hand position ($r_t^i=1$) following an unsuccessful trial ($r_{t-1}^i=0$). Thus, the best-fit model’s primary mechanism of updating reach aim is to use a cached value of the last known successful action following a miss. This mechanism also makes distinct predictions for the lag-1 autocorrelation conditioned on a successful trial or unsuccessful trial that closely resemble the data (see electronic supplementary material, J). This suggests that the sensorimotor system uses knowledge of exploratory movement variability to update reach aim when behaviour is driven by reinforcement feedback.

Table 1.

Model Selection.

	Model 1	Model 2	Model 3	Model 4	Model 5	Therrien [32]	Cashaback [18]
AIC score	12.41	14.08	15.63	5.62	7.93	8.04	8.04
BIC score	16.29	17.96	19.02	8.05	10.36	10.95	10.47

Using our bootstrapping procedure, we obtained posterior distribution estimates of the model parameters (electronic supplementary material, C). We used the median values of the parameter posterior distributions (α^e = 0.99, σ^mx = 3.93 mm, σ^my = 2.29 mm, σ^ex = 3.40 mm and σ^ey = 2.18 mm) to simulate participant reaching behaviour for Experiment 1 (figure 3e), Experiment 2 (figure 4e) and Experiment 3 (figure 5e). We used this set of parameter values to simulate 18 participants in each experimental condition, holding the parameter values fixed for every simulation. The model did well to capture lag-1 autocorrelations across all three experiments along the movement extent and lateral direction (electronic supplementary material, A, figure SA1).

(i) . Movement variability is greater with failure

Past work has shown that binary reinforcement feedback modulates movement variability [18,30,39,43–46]. An assumption of our models is that an unsuccessful reach leads to an increased amount of exploratory movement variability. To test this assumption, for each condition, we calculated movement variability independently for trials following reinforced and unreinforced reaches. We observed greater movement variability following unreinforced trials compared to positively reinforced trials across all three experiments (p < 0.001 for all experimental conditions; electronic supplementary material, D, figures SD1 and SD2). Increased movement variability following unreinforced trials is shown along the movement extent of the task-redundant target in Experiments 1 and 2 and both conditions of Experiment 3, where there would be limited regression to the mean effects. In total, only 6% of reaches were outside the target bounds in the task redundant dimensions in Experiments 1–3. We ran an additional analysis to control for these 6% of trials potentially causing a regression to the mean. Specifically, in this control analysis, we examined the trial-by-trial movement variability when excluding all participants that had any reaches outside of the target bounds along the movement extent. Again we found significantly greater trial-by-trial movement variability following a miss (p < 0.001 for all comparisons). That is, our results suggest that failure leads to increased trial-by-trial movement variability, independent from regression to the mean effects. We also performed a series of control analyses both with the data and model to gain insight into how the non-stationary nature of final hand positions influence our analysis of trial-by-trial movement variability (see electronic supplementary material, D).

Recent literature has examined the effects of reinforcement (reward) feedback and task success on movement vigour [47,48]. We examined reaction times as a proxy of movement vigour (see electronic supplementary material, E). However, we did not find consistent evidence to suggest that reinforcement feedback modulated reaction times in our experiments.

(j) . The magnitude and structure of movement variability are related and predicted by the best-fit model

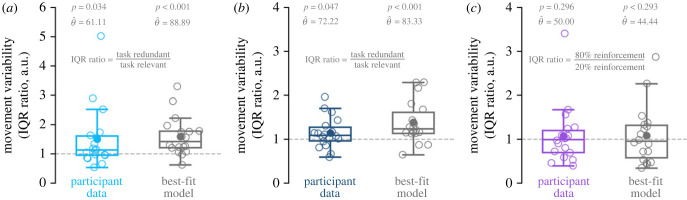
Past studies have quantified exploration by comparing the relative variability between task-redundant and task-relevant dimensions [4–7,11,14] (i.e. ‘uncontrolled manifold’ and ‘orthogonal dimension’). For each condition, we quantified the magnitude of movement variability by calculating the interquartile range (IQR) of participant final hand positions along the movement extent. In Experiment 1 (figure 6a) and Experiment 2 (figure 6b), we took the IQR ratio between the task-redundant and task-relevant for each participant. Past work has extensively used a ratio to quantify the relative movement variability between the task-redundant (termed, uncontrolled manifold) and task-relevant (termed, orthogonal) dimensions [5,7,49–52]. Participants displayed an IQR ratio significantly greater than one in Experiment 1 (p = 0.034) and Experiment 2 (p = 0.047), such that there was a greater magnitude of movement variability in the task-redundant conditions relative to the task-relevant conditions. In Experiment 3 (figure 6c), we took the IQR ratio between the 80 and 20% probability of reinforcement conditions. Participants did not display an IQR ratio greater than one in Experiment 3 (p = 0.296), where the magnitude of movement variability was similar between conditions. The best-fit model captures the observed trends in Experiment 1 (figure 6a, IQR ratio ≠1, p < 0.001), Experiment 2 (figure 6b, IQR ratio ≠1, p < 0.001) and Experiment 3 (figure 6c, IQR ratio ≠1, p = 0.293).

Figure 6.

IQR ratio. (a–c) We calculated the IQR of final hand positions along movement extent for each condition. Here, we show the IQR ratio between conditions (y-axis) for participant data (coloured) and best-fit model simulations (dark grey) for each experiment. Hollow circles represent individual data. Solid circles represent the mean IQR ratio. Box and whisker plots represent 25th, 50th and 75th percentiles. An IQR ratio greater than one (dashed grey line) indicates greater movement variability (a,b) along the task-redundant condition or (c) the 80% probability of reinforcement condition. Participants displayed an IQR ratio greater than one in (a) Experiment 1 (light blue) and (b) Experiment 2 (dark blue). Thus, they had greater variability in their final hand positions during the task-redundant conditions compared to the task-relevant conditions. Participants in (c) Experiment 3 (purple) did not display an IQR ratio significantly greater than one. This suggests that participants showed similar levels of movement variability between the 80 and 20% probability of reinforcement conditions. Our best-fit model (Model 4, dark grey) replicated the observed data in (a) Experiment 1, (b) Experiment 2 and (c) Experiment 3.

Our analysis on the magnitude of movement variability (IQR ratio) shows different results from the structure of movement variability (lag-1 autocorrelation) in Experiment 3, where we see a difference between conditions in lag-1 autocorrelation but not IQR ratio.

Further analysis showed a correlation between the IQR ratio between conditions and the difference in lag-1 autocorrelations between conditions (electronic supplementary material, SF1) for Experiment 1 (ρ = 0.88, p < 0.001), Experiment 2 (ρ = 0.80, p < 0.001) and Experiment 3 (ρ = 0.68, p = 0.002). This suggests that the magnitude (IQR) and trial-by-trial structure (random walk) of movement variability between conditions are related. The best-fit model also captures the relationship between the IQR ratio and the difference in lag-1 autocorrelations between conditions (electronic supplementary material, SF1).

We also repeated this analysis by directly comparing the absolute difference in IQR between conditions, as well as between movement extent and lateral position within each condition. We found that these results trended in the same way as observed in figure 6 but were not significant for Experiments 1 and 2 (p > 0.060 for all comparisons). Since the model makes the same prediction of increased lag-1 autocorrelation along the task-redundant dimension in Experiments 1 and 2, we found the absolute difference in IQR between conditions were significantly different when collapsing across Experiments 1 and 2 (p = 0.042; see electronic supplementary material I).

Taken together, our behavioural and modelling results support the idea that reinforcement-based mechanisms play an important role in driving exploratory behaviour along task-redundant solution manifolds.

3. Discussion

We show that reinforcement feedback regulates sensorimotor exploration along task-redundant solution manifolds. Our finding was robust across a series of experiments where we manipulated the size of both the visually displayed target or unseen reward zone, as well as the probability of reinforcement. Our work suggests that exploratory random walk behaviour arises from utilizing knowledge of movement variability to update intended reach aim when an action is positively reinforced—leading to active and continual exploration of the solution manifold. This mechanism can also explain the common observation of greater spatial movement variability along task-redundant dimensions.

In this article, we aimed to address whether reinforcement feedback contributed to exploratory random walk behaviour. In Experiment 1, we found that participants displayed greater exploratory random walk behaviour along the task-redundant dimension compared to a task-relevant dimension when receiving positive reinforcement feedback that indicated success. Others have reported that a visually larger target leads to greater movement variability [13,36–38]. Thus, to be assured a visually larger target alone was not causing changes in exploratory random walk behaviour, we collected a second experiment. In Experiment 2, we held the visually displayed target size constant and individuals received reinforcement when their final hand position was within a task-relevant or task-redundant reward zone. Replicating the results of Experiment 1, we again found greater exploration in the task-redundant dimension. For the task-redundant condition, we also found that participants were unaware of the large, unseen reward zone relative to the smaller visually displayed target, which may suggest an implicit role of reinforcement-based processes during exploratory behaviour. In Experiment 3, we directly manipulated reinforcement feedback while holding both the visually displayed target and unseen reward zone dimensions constant. Participants exhibited a greater trial by trial, exploratory random walk behaviour with a higher probability of reinforcement feedback. Collectively, these findings support the idea that reinforcement feedback plays an important role in regulating exploratory random walk behaviour.

In a previous study by van Beers et al. [8], participants reached to a long rectangular target and received vectored error-based feedback of their final hand position via a cursor. They also received a numerical reward score that scaled as a function of their distance from the target. They found that participants displayed exploratory behaviour (lag-1 autocorrelation ≈0.55) along the task-redundant dimension of a rectangular target. Conversely, along the task-relevant dimension of the rectangular target they had significantly less exploration (lag-1 autocorrelation ≈0.0), aligning with making corrective actions based on error-based feedback [31,33]. The authors attributed greater explorative behaviour along the task redundant dimension to passively allowing an accumulation of planned movement variability and a lack of error-based corrections. In their model, behaviour was explained by adjusting the error correction term separately for the task-redundant and task-relevant dimensions. An alternate, yet potentially complementary idea, is that exploration along task-redundant solution manifolds is driven by reinforcement-based processes. We recently proposed theoretical work that suggests reinforcement-based processes could also explain exploratory random walk behaviour [18], but this idea had not yet been tested empirically. Aligned with this idea, across our three experiments, we show that reinforcement-based processes contribute to exploratory random walk behaviour along task-redundant dimensions. Interestingly, we observed greater exploration along task-redundant dimensions when behaviour was driven by reinforcement feedback relative to past work that used error feedback [8]. Similar to past adaptation studies [53], an interesting future direction would be to examine the individual roles and interplay between reinforcement-based and error-based processes during sensorimotor exploration.

It has been proposed that the sensorimotor system has knowledge of both planned movement variability that arises in the dorsal premotor cortex [8,28,29] and exploratory movement variability that arises in the basal ganglia [20,22,54]. An accumulation of either of these processes could lead to exploratory random walk behaviour. Critically, however, planned movement variability that is not conditioned on positive reinforcement could not explain the observed differences in Experiment 1–3. For example, Model 5 accumulates planned movement variability every trial regardless of reinforcement feedback and was unable to capture differences between conditions (see electronic supplementary material G). Conversely, models (i.e. Model 1, Model 3, Model 4 [18,32]) that included knowledge of exploratory movement variability to update reach aim conditioned on reinforcement feedback could capture the observed trends. Similar to others, we found greater exploratory movement variability following failure (electronic supplementary material D, figure SD1). Exploratory movement variability has been closely linked to the basal ganglia and the dopaminergic system [22], which scales with reward prediction error in rodents [55]. In humans, those with Parkinson’s disease become unable to regulate movement variability as a function of reinforcement feedback [30]. Parkinson’s disease may be a population of interest to gain causal insight into the influence of reward prediction error and other reinforcement-based processes on sensorimotor exploration.

One of the seven plausible models we considered aligned with the use-dependency hypothesis (Model 5). The use-dependency hypothesis suggests that the sensorimotor system biases a movement to be similar to the previous movement [56,57]. The use-dependency hypothesis also suggests that this behavioural change is not conditioned on reinforcement-based processes. The model proposed by van Beers et al. [8] in some respects resembles the use-dependency hypothesis along the task-redundant dimension. In their model, planned movement variability accumulates along the task-redundant dimension, which biases a movement to be similar to the previous movement. Similarly, our model 5 used planned movement variability, not exploratory movement variability, but failed to capture lag-1 autocorrelation differences between conditions in Experiment 1–3 (see electronic supplementary material G). These model results imply that the differences in exploratory behaviour between conditions is not driven by a use-dependency mechanism. A more parsimonious account of our findings, captured in our general model (Model 1) and the best-fit model (Model 4), is that the sensorimotor system will bias a movement when the previous movement is conditioned on reinforcement feedback. Further, it calls into question whether planned and exploratory movement variability arising in the dorsal premotor cortex and the basal ganglia are unrelated processes. Indeed, the basal ganglia and premotor cortex are known to be linked through a neural loop [58,59]. Beyond performing model comparisons, it is difficult to separate the relative contributions of use dependency and reinforcement-based mechanisms in the current experiment paradigm. For example, use dependency may to some extent contribute to baseline levels of exploratory statistical random walk behaviour. It would be useful to test whether use dependency is conditioned on intrinsic or extrinsic reinforcement-based processes. Nevertheless, our results suggest that a reinforcement-based mechanism is necessary to explain the trends observed across all three experiments.

The primary mechanism by which our best-fit model (Model 4) explores the solution space is by expanding movement variability following an unsuccessful action and using knowledge of that variability to update its reach aim on the next successful action following an unsuccessful action. A prediction following from this mechanism is that lag-1 autocorrelations should not linearly increase as a function of the probability of reinforcement. Rather, lag-1 autocorrelations would peak at some intermediate probability of reinforcement but be lower at be lower at 0% and 100% (electronic supplementary material, figure SH1). This occurs because at 0% probability of reinforcement there are no successful actions to cause an aiming update. Conversely, at 100% probability of reinforcement, there is no additional exploratory movement variability the sensorimotor system has knowledge of to update reach aim. It would be useful for future work to examine multiple probabilities of reinforcement.

After Experiment 2, we asked participants to indicate their average final hand position for each condition. By asking after each condition, we avoided impacting exploration during the experiment through the use of self-reports of trial-by-trial hand positions that have been shown to alter behaviour [60–63]. Our approach is admittedly a weak assessment of implicit processes that may contribute to exploratory behaviour. Holland et al. [43] showed that participants can develop and remove explicit strategies when receiving binary reinforcement feedback in a visuomotor rotation task. However, when participants were asked to remove their explicit strategy during washout, their reach angles did not fully return to baseline levels. Slightly elevated reach angles during washout may to some extent reflect an implicit component of reinforcement-based processes. Our results align with previous work, suggesting participants are unable to localize their hand position using proprioception when receiving only binary reinforcement feedback [64]. In our study, we found similar levels of lag-1 autocorrelations between the task-redundant condition of Experiment 2 and the task-redundant condition of Experiment 1, suggesting that participants were not making corrective actions using proprioception. It would be useful to examine whether there is some level of implicit reinforcement-based processes that contribute to exploratory sensorimotor behaviour.

An observation in the literature is that there is more movement variability along muscle [1–3], joint [4–7], and task [8–13] solution manifolds. This observation has been classically studied in joint space using a dimensionality reduction technique proposed by proponents of the uncontrolled manifold (UCM) hypothesis [7]. The UCM hypothesis posits that humans have increased variability along redundant dimensions that have little impact on task success. This observation can be explained in the context of optimal feedback control, where biological systems tend not to intervene along redundant dimensions because it is energetically costly (termed the ‘minimum intervention principle’) [15]. In other words, the observed increases in movement variability have been previously assumed to occur passively by not intervening. Alternatively, our results show that an increase in variability along task-redundant dimensions may occur from reinforcement-based processes that actively and continually update reach aim towards recently successful motor actions. Here, we analysed both the magnitude (IQR) and trial-by-trial structure (lag-1 autocorrelation) of the movement variability along the movement extent of the reach between conditions. Across Experiments 1–3, we see that the trial-by-trial structure of movement variability (lag-1 autocorrelation) changes depending on unseen reward zone size or the probability of reinforcement feedback. However, the magnitude of movement variability (IQR) only changes with the unseen reward zone size and not the probability of reinforcement feedback, which is predicted by the best-fit model since the available space to explore is the same in both conditions of Experiment 3. While the magnitude of movement variability analysis aligns with both the UCM hypothesis and OFC, neither framework captures changes in the trial-by-trial structure of movement variability. In contrast to past theories, our work suggests that reinforcement-based processes lead to the active and continual exploration of task-redundant solution manifolds.

Past work, including our own, has considered increases in trial-by-trial movement variability following failure as a metric of exploration [18,30,39,65] (electronic supplementary material, D). Likewise, we also considered the distribution of final hand positions (i.e. IQR) across several trials to assess movement variability. Both trial-by-trial and IQR assessments of movement variability only describe a single aspect of the exploratory process. Greater movement variability does not necessarily imply exploration or lead to improved performance. Critically, participants must also have knowledge and act upon movement variability to update their reach aim to increase the likelihood of producing a successful motor action. At the trial level, our model can be thought to explore through exploratory movement variability and exploit through updates in reach aim when an action is reinforced. Across many trials, this process can lead to spatial exploration along a solution manifold with similar level of success. Indeed, it is commonly observed that there is greater movement variability across trials along task-redundant dimensions in joint space [4–7], as well as muscle [1–3] and task space [8–13]. Lag-1 autocorrelation provides a metric to assess whether the sensorimotor system has knowledge of and acts upon movement variability to explore. Collectively our results show that the sensorimotor system modulates movement variability as a function of reinforcement feedback, has knowledge of movement variability and acts upon movement variability to update reach aim following positive reinforcement. Thus, exploration can be considered as a feedback modulated process of expanding and utilizing knowledge of movement variability to actively and continually explore the solution manifold. Future work can be done to control the specific sequence of trial-by-trial reinforcement to better understand the process of utilizing exploratory movement variability to actively explore the solution space.

Exploratory random walk behaviour has been universally seen across species [8,22,34], along neural manifolds [34,66], gait cycles [12,42] and trial-by-trial reaching behaviour [8,9,33,40]. Humans show greater movement variability along muscle [1–3], joint [4–7], and task [8–12] solution manifolds, which to some extent may be driven by reinforcement-based processes continually exploring for the best possible action. Here, we examined exploration of a very simple solution manifold along a two-dimensional solution space. Across three experiments, we showed evidence to suggest that exploratory random walk behaviour arises from utilizing knowledge of exploratory movement variability to update intended reach aim when an action is positively reinforced. This mechanism leads to active and continual exploration that is useful for finding successful motor actions in dynamic or uncertain environments. The ability to explore is also particularly relevant following a musculoskeletal or neurological disorder, where a new set of actions must be discovered and learned to perform everyday, functional tasks.

4. Methods

Please refer to the electronic supplementary material for a detailed description of methods for all experiments.

Ethics

This work was approved by the University of Delaware's International Review Board.

Data accessibility

All data are contained within the manuscript and will be made freely available to the public.

The data are provided in electronic supplementary material [67].

Declaration of AI use

We have not used AI-assisted technologies in creating this article.

Authors' contributions

A.M.R.: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing—original draft and writing—review and editing; J.A.C.: formal analysis, validation, visualization and writing—review and editing; R.L.: validation, visualization and writing—review and editing; S.R.S.: validation, visualization and writing—review and editing; S.G.: supervision and writing—review and editing; J.J.J.: supervision and writing—review and editing; K.K.: supervision, validation and writing—review and editing; M.J.C.: conceptualization, methodology, supervision, visualization, writing—original draft and writing—review and editing; J.G.A.C.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing—original draft and writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

National Institute of Health (NIH U45GM104941) and National Science Foundation (NSF 2146888) grants were awarded to J.G.A.C. Natural Sciences and Engineering Research Council (NSERC) of Canada (RGPIN-2018- 05589) was awarded to M.J.C.