Solar forecasting for a PV-battery powered DC system

Abstract

The photovoltaic (PV) power generation sector has been growing rapidly as a result of the rising need for solar power and the advancement of PV technology. PV Power generation is affected by weather factors such as cloud cover, solar irradiation, temperature, breeze direction and speed, and the amount of rain or snow. As a result, a highly precise PV power predictor is essential to improve security and reliability in the face of financial penalties and ambiguity. Hence, this paper suggests a novel approach to improve the efficiency of PV-battery-powered DC systems by combining solar irradiance prediction using the Long Short-Term Memory (LSTM) algorithm with a power electronic converter design that incorporates a bidirectional port. The LSTM algorithm was employed to predict one week of solar data with a remarkable R² score of 0.96. A steady-state analysis of the proposed Three-Port Converter (TPC) is performed for five different operating modes to guarantee optimal performance. The suggested system's prediction performance was tested using several error metrics such as Mean Absolute Error (MAE), Mean Square Error (MSE), and Root Mean Squared Error (RMSE), which were computed as 0.0318, 0.0027, and 0.0526, respectively. Results from the above error measures show that the suggested approach performs more effectively in estimating solar irradiance. The Adaptive Neural-Fuzzy Interface System (ANFIS) and Incremental Conductance (IC) algorithms are employed for Maximum Power Point Tracking (MPPT) and assessed against various atmospheric conditions. From the MATLAB simulation results, the tracking efficiency of the ANFIS-based MPPT technique is 99.97 %, which is superior to the IC-based MPPT technique. Furthermore, it proved that the suggested approach improves the efficiency of PV-battery-powered DC systems, which is more appropriate for real-world applications such as DC microgrids and Electric Vehicles.

Nomenclature

AC

Alternating Current

ANFIS

Adaptive Neural-Fuzzy Interface System

ARIMA

Auto-Regressive Integrated Moving Average

DC

Direct Current

DISO

Double-Input Single-Output

IC

Incremental Conductance

LSTM

Long Short-Term Memory

MAE

Mean Absolute Error

MLR

Multiple Linear Regression

MPPT

Maximum Power Point Tracking

MSE

Mean Squared Error

PCC

Pearson's Correlation Coefficient

P&O

Perturb and Observe

PV

Photovoltaic

PWM

Pulse Width Modulation

R²

Coefficient of determination

RMSE

Root Mean Square Error

SIDO

Single-Input Double-Output

SISO

Single-Input Single-Output

TPC

Three-Port Converter

1. Introduction

The amount of energy and electricity consumed worldwide continues to rise due to population growth and economic development [1]. In Refs. [[2], [3], [4]], solar power has emerged as a promising alternative to conventional power sources, with advancements in photovoltaic cell technology resulting in improved efficiency, lower costs, and a lighter weight. The accuracy of weather predictions has also improved, enabling the translation of this information into actionable intelligence for the solar industry [5].

In the field of time series forecasting [[6], [7], [8]], various algorithms such as Auto-Regressive Integrated Moving Average (ARIMA), Prophet, Seasonal ARIMA (SARIMA), and LSTM have been employed to forecast irradiance. Among these algorithms, LSTM has shown significant promise due to its ability to forecast long-term and short-term data accurately. This forecasting approach boosts PV system efficiency to 98 % [9]. Multiple Linear Regression (MLR) and Pearson's Correlation Coefficient (PCC) were used in a hybrid machine learning system to test the solar power plant in Germany with capacities ranging from 100 kW to 8,500 kW [10]. A hybrid deep learning procedure is suggested to forecast the energy produced by the hybrid system [11]. To address the difficulty of highly variable renewable energy output, the improved convolutional long-short memory mixture network is suggested for PV energy forecasting [12].

The MPPT [[13], [14], [15]] is a significant factor in enhancing the effectiveness of the PV system, and PV power management systems rely heavily on accurate predictions of solar irradiation. To maximize the output power from PV cells, accurately tracking the system's maximum power point (MPP) is essential. Studies have contrasted the Perturb and Observe (P&O), IC, and ANFIS techniques [[16], [17], [18], [19]]. ANFIS has been found to have less converging time and fewer oscillations while varying solar irradiance, making it a more desirable option.

A comprehensive review was conducted to characterize, assess, and compare the models, majority of the software programmes, and algorithms used to build PV systems over the last eight decades. This review aids in selecting the appropriate PV system design software programme for the user's applications [20].

Traditional AC distribution [[21], [22], [23]] in residential settings can result in extra conversion losses, while a DC distribution system can offer more straightforward, dependable, and effective operation. Moreover, residential DC distribution has certain advantages over residential AC distribution, particularly with the implementation of dispersed generation and storage.

DC microgrids offer greater control and flexibility over the distribution of power and can be designed to operate at different voltage levels, which can increase compatibility with different types of equipment and loads. DC microgrids can offer reduced electromagnetic interference compared to AC microgrids, making them suitable for applications where electromagnetic interference is a concern, such as in medical (pacemakers, MRI machines, or monitoring devices) or aerospace systems.

Non-isolated DC-DC converters have been studied, and it has been found that when compared to non-isolated TPCs, TPCs with partial isolation can obtain significantly greater voltage gain [[24], [25], [26], [27]]. These converters allow for the physical and electrical separation of the input and output circuits, increasing the system's overall efficiency. The physical effects of controlling factors on the hydrodynamic, velocity, and temperature characteristics of induced magnetic fields are discussed [28]. The effects of thermophoresis and Brownian motion are emphasised [29].

The novelty of our research work resides in combining LSTM algorithm-based solar irradiance prediction with a power electronic converter design that incorporates a bidirectional port to improve the efficiency of PV-battery-powered DC systems. The performance outcomes demonstrate that the suggested system has substantial improvement in evaluation metrics such as MAE, MSE, RMSE, and Coefficient of determination (R²).

The significant contributions of this study are summarised as follows:

• 1.The LSTM model is utilized for training on 5 years of data and uses the model to predict 1 week of solar data.
• 2.Designed a three-port DC-DC converter that can accurately predict the DC power for a week, considering the predicted data as input.
• 3.Studied the numerous modes of operation of the designed TPC and performed steady-state analysis to ensure its reliability.
• 4.Adaptive Neural-Fuzzy Interface System (ANFIS) and Incremental Conductance (IC) algorithms are built for Maximum Power Point Tracking (MPPT), and they are tested at different atmospheric conditions.

The rest of the paper is structured as follows: Section II addresses the solar irradiance prediction. Section III describes MPPT techniques. Section IV presents the modes of operation and steady-state analysis. Section V discusses the block diagram and simulation model of the proposed system. Section VI presents the proposed model design. Section VII provides results and discussion. Finally, this paper concludes in Section VIII.

2. Solar irradiance prediction

The solar data for the city of Chennai from 2016 to 2020 has been extracted from the HOMER software. The extracted data has been represented graphically in Fig. 1(a) and (b), which illustrate the solar energy trends over the five-year period. An LSTM model was trained to predict one week's worth of data consisting of 336 data points, with 48 data points collected daily. The model architecture includes four input layers, four dropout layers, and one output layer. The predicted and true data are shown in Fig. 12, and the predicted data was saved into an Excel file. The Spreadsheet Link module in MATLAB is used to export data from Excel files and provide it as input to a PV panel.

Fig. 1.

Solar Irradiation Trends (a) Predicted and Actual Solar Irradiance Values (b) Solar Irradiance trends.

Fig. 12.

Graphical representation of predicted and actual values.

The model's goodness of fit is determined by the coefficient of determination, or R² score, which compares its performance with a simple baseline model that predicts the mean value. The MAE is utilized to calculate the average absolute disparity between the predicted and actual values. The RMSE, a variation of MAE, is found by squaring the average squared deviation from the forecasted value and the real value, which places greater emphasis on significant errors. The MSE measures the mean of the squared discrepancies between the anticipated and real values. All these metrics should be used in combination to assess the overall effectiveness of the model.

3. MPPT techniques

3.1. ANFIS controller

The ANFIS Controller's working procedure is clearly depicted in Fig. 2, which illustrates the steps involved in implementing the controller [19]. The ANFIS learning algorithm is a hybrid approach that combines the gradient descent approach of neural networks with the least squares method of fuzzy systems. This combination allows the ANFIS controller to learn from data and adapt to changing conditions, making it a powerful tool for real-time control and decision-making. Fig. 2 is a helpful visual representation of the ANFIS controller, which can aid in the process of designing, implementing, and fine-tuning the controller for a given application.

Fig. 2.

Flow chart of ANFIS controller.

In this proposed work, a MATLAB code has been developed to train the ANFIS controller by choosing parameters specific to the solar panel, including maximum voltage (V_MPS), open circuit voltage (V_OCS), maximum current (I_MPS), short circuit current (I_SCS), coefficients of voltage (α), and coefficients of temperature (β).

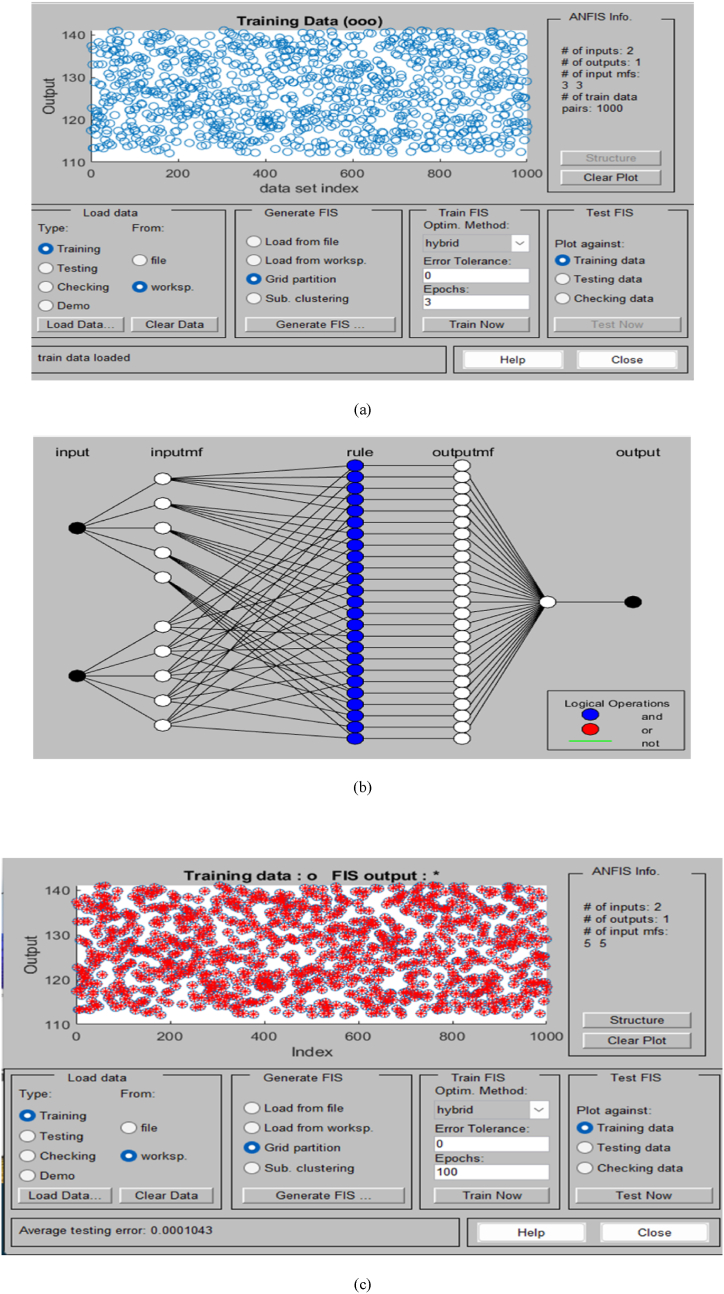
To generate a dataset for training, a for loop is used to randomly generate 1000 samples of temperature (T) and irradiance (G) within predefined ranges (T_min = 15, T_max = 35, and G_min = 0.001, G_max = 1000), as illustrated in Fig. 3(a). The maximum current (I_MP), maximum voltage (V_MP), and maximum power (P_MP) are calculated for each sample [17] using the given formulas:

$${\mathrm{I}}_{\text{MP}}\left(\mathrm{i}\right)={\mathrm{I}}_{\text{MPS}}*(\mathrm{G}/\text{Gs})(1+\left(\mathrm{\alpha }(\mathrm{T}-\text{Ts})\right))$$ (1)

$${\mathrm{V}}_{\text{MP}}\left(\mathrm{i}\right)={\mathrm{V}}_{\text{MPS}}+(\mathrm{\beta }*(\mathrm{T}-\text{Ts}))$$ (2)

$$P_{MP}\left(i\right)=V_{MP}\left(i\right)*I_{MP}\left(i\right)$$ (3)

Fig. 3.

(a) Random 1000 samples of data collected (b) ANFIS model structure (c) The trained data (Red colour) is superimposed with the collected data (Blue colour). (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

The input and output data are stored separately in the input and output matrices, respectively, and combined into a single matrix data, for training the ANFIS controller. For each input, five membership functions with triangular membership types are assigned, and the output of the membership function is set constant. The ANFIS model structure is depicted in Fig. 3(b). Fig. 3(c) illustrates the superimposition of the trained data with the collected data.

3.2. Incremental Conductance controller

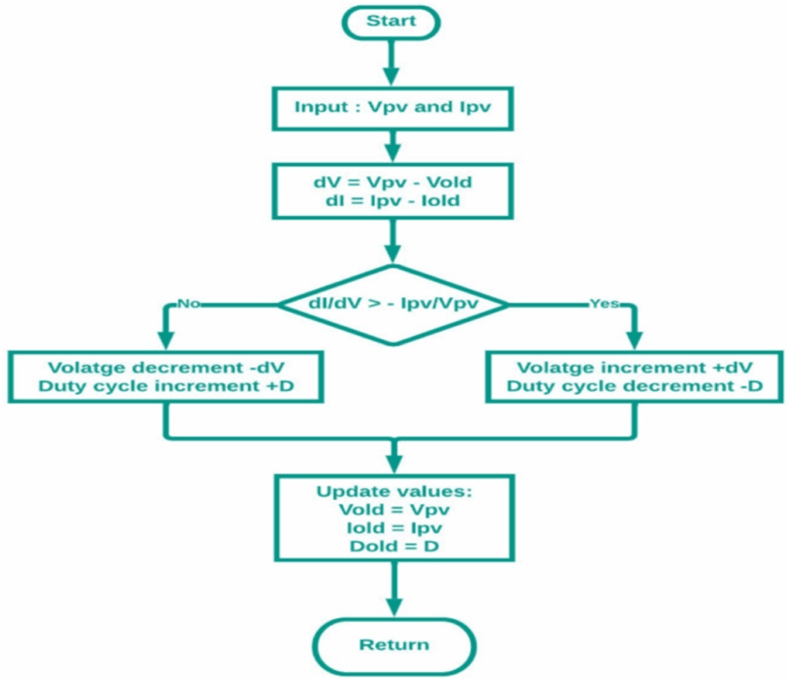
An Incremental conductance controller is an algorithm used in the MPPT technique for photovoltaic systems to monitor the peak power point. It measures the PV panel's output power and compares it to the previous measurement to adjust the system's operating point for maximum power output. The flow chart for IC is depicted in Fig. 4. It is effective in variable conditions where the irradiance and temperature fluctuate [13]. It relies on the fact that the power curve from a PV array of solar panels has a zero slope (dP/dV = 0) at the MPP. It uses the concepts of conductance (I/V) and conductance increment (dI/dV) equality to search for the MPP and adjust the operating point of the system accordingly for maximum power output [14].

Fig. 4.

Flow chart of incremental conductance.

4. Modes of operation and steady state analysis

4.1. Circuit diagram

The solar system with a battery depicted in Fig. 5 can operate in five distinct modes based on the power derived from PV modules, which rely on irradiation and temperature.

Fig. 6.

First Mode (a) State-1 (b) State-2 (c) Current flow graph

(a) State-1 (t0 < t < t1): In Fig. 6(a), C_d gets charged and charges the L_b, S_c is OFF, and the diode D acts in forward bias, and current flows through it, charging the C_c. Now the current charges the C_b, and the current goes through S_b as S_b is ON and S_a is OFF. From S_b, the current flows to L_a, and L_a gets charged, and at t = t1, S_a is ON, S_b is OFF, and S_c is ON, which makes the completion of state 1.

(b) State-2 (t1 < t < t2): In this state, as shown in Fig. 6(b), C_d gets discharged and makes the L_b get discharged; now the diode goes OFF and S_c is ON, and the current flows through it, making the C_c discharged. C_b gets discharged, and the current flows through S_a and charges L_a, completing the steady-state analysis of mode 1 at state 2. The steady-state analysis of mode 1 is shown in Fig. 6(c).

Fig. 7.

Second Mode (a) State-1 (b) State-2 (c) Current flow graph

(a) State-1 (t0 < t < t1): In this state, as shown in Fig. 7(a), C_d gets discharged and makes the L_b get discharged, now the diode goes OFF and S_c is ON and the current flows through it and makes the C_c discharged. From the battery, L_a gets charged, S_a is ON, and S_b is OFF, so the current flows through S_a, and C_b gets discharged, and it completes the steady-state analysis of state 1, making S_a OFF, S_b ON, and S_c OFF at t = t1.

(b) State-2 (t1 < t < t2): In Fig. 7(b), C_d gets charged and charges the L_b, S_c is OFF and the diode D acts in forward bias, and current flows through it charges the C_c. From the battery, L_a gets discharged, which makes the completion of state S_b ON, letting the current get through it and charging the C_b, which makes the completion of State 2. The steady-state analysis of mode 2 is shown in Fig. 7(c).

Fig. 8.

Third Mode (a) State-1 (b) State-2 (c) Current flow graph.

(a) State-1 (t0 < t < t1): In Fig. 8(a), C_d gets charged and charges the L_b, S_c is OFF and the diode D acts in forward bias, and current flows through it charges the C_c. Now the current charges the C_b, and the current goes through S_b as S_b is ON and S_a is OFF. From S_b, the current flows to L_a, and L_a gets discharged, and at t = t1, S_a is ON, S_b is OFF, and S_c is ON, which completes state 1.

(b) State-2 (t1 < t < t2): In Fig. 8(b), C_d gets discharged and the L_b gets discharged; now the diode goes OFF and S_c is ON, and the current flows through it, making the C_c discharged. C_b gets discharged, and the current flows through S_a and charges L_a, completing the steady-state analysis of mode 1 at state 2. The steady-state analysis of mode 3 is shown in Fig. 8(c).

Fig. 9.

Fourth Mode (a) State-1 (b)State-2 (c)Current flow graph

(a) State-1 (t0 < t < t1): From the battery, as shown in Fig. 9(a) L_a gets charged and S_a is ON, S_b is OFF, so current goes through S_a and C_b gets discharged, and at t = t1, the state 1 analysis is completed, making the S_b turn ON.

(b) State-2 (t1 < t < t2): In Fig. 9(b), from the battery L_a gets discharged and S_b is ON, and now the current passes through it, making the charging of C_b and the completion of the steady-state analysis of mode 4 at t = t2. The steady-state analysis of mode 4 is shown in Fig. 9(c).

Fig. 5.

Proposed circuit diagram.

4.2. Modes of operation

• (1)First Mode (PV to Battery & Load)

In the first mode, the battery is charged while the PV panels produce excess power over the load's consumption. The ANFIS-based MPPT controller uses a constant voltage charging approach to ensure that the batteries stay completely charged. In this first mode of operation, the TPC performs like a Single-Input Double-Output (SIDO) converter.

• (2)Second Mode (PV & Battery to Load)

In the second mode, if the amount of energy generated by the PV panels is less than the amount of energy required by the load but the battery is charged completely, then the battery provides reserve power in addition to the PV power. The MPPT algorithm is used to maximize the PV panel's power output, and the battery provides complementary power by operating in the boost mode of the buck/boost bidirectional converter. In this mode of operation, the TPC works like a Double-Input Single-Output (DISO) converter.

• (3)Third Mode (PV to Battery)

In the third mode, if the power supplied by the PV panels exceeds the power required by the demand and the battery is not fully charged, the excess power generated by the PV panels is utilized to energize the battery. The buck mode of the buck/boost bidirectional converter is used to energize the battery during this mode. In this mode of operation, the TPC operates as a Single-Input Single-Output (SISO) converter.

• (4)Fourth Mode (Battery to Load)

In the fourth mode, if there is no power generated by the PV system during the night or on a rainy day, the battery alone discharges to supply power to the load. In this mode, the TPC works as a SISO converter.

• (5)Fifth Mode (Shutdown)

In the fifth and final mode, the entire system is shut down to protect the battery from damage and to protect the load from low voltage if the power supplied by the PV modules is less than the power needed by the demand and the battery is also deeply drained.

5. Block diagram and simulation model of the proposed system

In this proposed system, solar irradiation data is collected and used to train an LSTM model to predict solar data for a week, as shown in Fig. 10. The predicted solar data is then stored in an Excel file and provided as input to the PV panel through a spreadsheet link module.

Fig. 10.

Block Diagram of Proposed model.

The PV module and ANFIS reference model both take irradiance level and operational temperature as inputs. The ANFIS reference model outputs a crisp value of the maximum available voltage from the PV unit at a specific temperature and irradiation level, without any load.

The PI controller and Pulse Width Modulation (PWM) generator are connected in a feedback loop to generate a signal that is directed to the S₃ switch in the PV system. The PI controller compares the reference voltage obtained from the ANFIS reference model with the actual output voltage obtained from the PV unit at a specific temperature and irradiation level. The difference between these two voltages, known as the error voltage, is then fed into the PI controller, which calculates the required output voltage to minimize the error voltage. The output voltage of the PI controller is then directed to the PWM generator.

The PWM signal, which is generated by the PWM generator and has a duty cycle proportional to the required output voltage, is used to control the S_c switch in the PV system, as depicted in Fig. 11. The switch utilizes this signal to regulate the power flow from the PV module to the load, effectively controlling the amount of power delivered to the load.

Fig. 11.

Simulation model of the proposed system.

Additionally, a summing block with input voltages of 220V and the load voltage is connected to the PI controller, which is also connected to the PWM generator. The output signal of the PWM generator is then directed to switch S_a, while its complement is directed to switch S_b.

6. Proposed model design

The PV panel has a power output of 1 kW, with four modules connected in series per string and a single parallel string. This results in an input voltage of 126.56 V (4*31.64 V) for the PV panel. The battery system is made up of ten 12V batteries connected in series, providing a nominal voltage of 120V. The rated capacity of the battery is 40 Ah, with an initial state-of-charge of 50 %. The battery's response time is 30 s.

To design the boost converter, the load resistance is calculated using the output voltage of the load, which is 220V. The maximum output current is determined by using the output power (P) and output voltage (V_out), which are given in equation (4) as follows:

$$I_{outmax}=P/V_{out}$$ (4)

The switching frequency is set to 1 kHz. The ripple inductor current (ΔI_L), is calculated using the formula given in equation (5) as follows:

$$\Delta I_L=0.01I_{outmax}(V_{out}/V_{in})$$ (5)

where, I_outmax is the maximum output current, and V_in is the input voltage.

7. Results and discussion

The suggested system is simulated with the help of MATLAB software. The LSTM algorithm is used to forecast the solar data. Fig. 12 shows the actual and predicted data for a week (25-12-2020 to 31-12-2020) that consists of 336 data points. The effectiveness of a solar prediction model is assessed using commonly used error metrics (like R2 score, MAE, MSE, and RMSE) and the results are depicted in Table 1. The previous research work [15] reported that the RMSE, MSE, and MAE are 0.057, 0.0033, and 0.0413, respectively, while other work [4] reported that the RMSE and R2 values are 3.17 and 0.93, respectively. Table 1 illustrates the considerable enhancements in error metrics (RMSE, MSE, MAE, and R²) of the proposed work compared to the aforementioned reported work. Moreover, it is clear that the higher R² score of 0.9629 indicates a higher degree of accuracy in the forecasting model. On the other hand, the lower MAE, MSE, and RMSE values indicate that the forecasting model works effectively in predicting the solar irradiance. This forecasting process provides useful physical insights into the system's behavior and its dependency on solar irradiation. Further, it facilitates more effective regulation of energy flows, enhancing both charging and discharging efficiency during periods of high and low or no solar irradiation, respectively.

Table 1.

Training data evaluation.

Training Model	R2	MAE	MSE	RMSE
LSTM	0.9629	0.0318	0.0027	0.0526

An ANFIS-based MPPT controller is implemented for a PV system, and its performance is evaluated against that of an IC-based MPPT controller. To test the different atmospheric conditions, three different irradiation levels were examined: low, medium, and high. The low-level ranges from 200 to 400 W/m², the medium-level ranges from 400 to 800 W/m², and the high-level ranges from 800 to 1000 W/m². This changing pattern of irradiation levels is simulated with the help of the signal builder block in MATLAB/Simulink, and it follows a specific pattern that starts at 1000 W/m² and decreases to 800 W/m² at 0.2 s to simulate cloudy weather. The levels then decrease to 600 W/m² at 0.4 s, 400 W/m² at 0.6 s, and 200 W/m² at 0.8 s, and then back up to 1000 W/m² at 0.9 s to depict the clearing of the cloudy region. The voltage, current, and power waveforms of both MPPT techniques (ANFIS and IC-based MPPT techniques) are illustrated in Fig. 13(a) and (b), and Fig. 13(c), respectively. From this, it is clear that the dynamic performance of the ANFIS-based MPPT technique is more stable than that of the IC-based MPPT technique. The convergence and settling times of both techniques (ANFIS and IC-based MPPT techniques) are shown in Table 2, and it shows that the ANFIS-based MPPT technique yields better convergence and settling times than the IC-based MPPT technique. However, it is also observed that the converging times of the ANFIS and IC-based MPPT techniques are almost the same for the 0–0.2 s and 0.8–0.9 s conditions. The short settling time of the ANFIS-based MPPT technique results in lower energy losses compared to the IC-based MPPT technique.

Fig. 13.

(a) Voltage waveforms of ANFIS and IC-based MPPT Techniques (b) Current waveforms of ANFIS and IC-based MPPT Techniques (c) Power waveforms of ANFIS and IC-based MPPT Techniques.

Table 2.

Comparison of converging and settling time of ANFIS and IC-based MPPT techniques.

Time (Seconds)	Converging time (sec)		Settling time (sec)
	ANFIS	IC	ANFIS	IC
0–0.2 (1000 W/m2)	0.0014	0.0014	0.0380	0.0920
0.2–0.4 (800 W/m2)	0.2017	0.2080	0.2168	0.2401
0.4–0.6 (600 W/m2)	0.4017	0.4084	0.4159	0.4461
0.6–0.8 (400 W/m2)	0.6017	0.6082	0.6220	0.6466
0.8–0.9 (200 W/m2)	0.8003	0.8002	0.8096	0.8401
0.9–1 (1000 W/m2)	0.9037	0.9248	0.9105	0.9817

The percentage tracking efficiency of the MPPT algorithm can be calculated [17] as follows:

$$PercentageTrackingEfficiency=(P_{mppt}/P_{pv})*100$$ (6)

Where P_mppt is the power output of the system when the MPPT algorithm is used, and P_pv is the power output of the system without the MPPT algorithm (i.e., using a fixed operating point).

The tracking efficiency of the ANFIS-based MPPT technique is better than that of the IC-based MPPT technique, which is illustrated in Table 3. As a result, the ANFIS-based MPPT technique outperforms the IC-based MPPT technique. Thus, the ANFIS-based MPPT technique is chosen to evaluate the results obtained from the proposed system.

Table 3.

Tracking efficiency of ANFIS and IC-based MPPT technique.

MPPT Technique	Tracking Efficiency
ANFIS	99.97
IC	96.85

The predicted data using LSTM for a week is given as input to the solar PV. During the daytime, the solar irradiation is high, so we can observe the positive voltage, current, and power of the PV panel as depicted in Fig. 14(a). As a result, the PV panel is producing more surplus power than the combined power of the load and the battery; the excess power is used to energize the battery. This results in a reduction in the battery current, and once the power delivered to the battery reaches 500 W, the battery starts charging, resulting in a negative current. Thus, both the first mode (PV to Battery & Load) and the third mode (PV to Battery) are achieved during this phase of operation. When the Battery unit is charging, we can also observe from Fig. 14(b) that the battery SOC increases. Since the amount of energy supplied by the PV panels is less than the amount of energy needed by the load, the battery is energized. As a result, the battery supplies backup power along with the PV power; here, the second mode (PV & Battery to Load) is achieved, as shown in Fig. 14(b). Since the PV unit is not supplying power during the night and only the battery is depleting to power the load, the fourth mode (Battery to Load) is achieved, as shown in Fig. 14(b). Fig. 14(c) indicates that the load voltage is maintained at a range of 219–225V, the current is maintained at a range of 2.27–2.32A, and power is obtained at a range of 497–520W. As a result, the physical insights (such as solar irradiance variability, solar power generation dynamics, battery charging and discharging, energy management) of PV-battery powered DC systems are gained through the proposed approach which leads to improved system performance and energy efficiency.

Fig. 14.

(a) PV panel output voltage, current, and power (b) Battery output voltage, current and SOC (c) DC load output voltage, current and power.

8. Conclusion

Solar energy is one of the cleanest sources of energy, but it faces problems such as low efficiency and power extraction due to variable weather conditions. The conventional MPPT methods have their own set of problems that prevent them from maximising power generation. ANFIS-based MPPT approaches are an effective solution to the problem of poor efficiency in PV systems and overcome the difficulties of conventional MPPT methods. In this work, the PV-battery-powered DC system efficiency is significantly enhanced with the help of the LSTM algorithm and a three-port converter, considering the ANFIS-based MPPT approach. The simulation findings show that the efficacy of the ANFIS-based MPPT technique is superior than that of the IC-based MPPT technique and the LSTM model also exhibited a good R² score of 0.96 for solar prediction. Thus, the suggested system is more suitable for various real-world applications, such as DC microgrids, DC home systems, and solar-powered electric vehicle applications. However, the current study is restricted to simulation aspects; further, it can be validated by experimental results and extended by considering different datasets to predict monthly solar irradiance data.

Data availability statement

No data was used for the research described in the article.

CRediT authorship contribution statement

Iyswarya Annapoorani K: Formal analysis, Project administration, Supervision, Writing – review & editing, Visualization. Rajaguru V: Formal analysis, Investigation, Validation, Writing – original draft, Writing – review & editing. Vedanjali N: Conceptualization, Data curation, Methodology, Resources. Pappula Rajasri: Conceptualization, Data curation, Methodology, Software.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.