Summary
In environmental epidemiology, there is wide interest in creating and using comprehensive indices that can summarize information from different environmental exposures while retaining strong predictive power on a target health outcome. In this context, the present article proposes a model called the constrained groupwise additive index model (CGAIM) to create easy-to-interpret indices predictive of a response variable, from a potentially large list of variables. The CGAIM considers groups of predictors that naturally belong together to yield meaningful indices. It also allows the addition of linear constraints on both the index weights and the form of their relationship with the response variable to represent prior assumptions or operational requirements. We propose an efficient algorithm to estimate the CGAIM, along with index selection and inference procedures. A simulation study shows that the proposed algorithm has good estimation performances, with low bias and variance and is applicable in complex situations with many correlated predictors. It also demonstrates important sensitivity and specificity in index selection, but non-negligible coverage error on constructed confidence intervals. The CGAIM is then illustrated in the construction of heat indices in a health warning system context. We believe the CGAIM could become useful in a wide variety of situations, such as warning systems establishment, and multipollutant or exposome studies.
Keywords: Additive index models, Dimension reduction, Index, Linear constraints, Quadratic programming
1. Introduction
In environmental epidemiology, there is an increasing recognition of the complexity of the mixture of exposure to human health. The number of exposures, be it pollutants, weather variables, or built-environment characteristics can be numerous and interact in a complex fashion to impact human health. The ever-increasing amount of data available allows for complex statistical and machine learning models to be considered. For instance, recent advances such as Bayesian kernel machine regression (Bobb and others, 2015), random forests (Breiman, 2001), or more generally many nonparametric algorithms can achieve impressive predictive power. However, the mentioned models are often referred to as “black boxes” (a recent example is Schmidt, 2020) and are challenging to interpret in practice (e.g., Davalos and others, 2017).
Interpretability of model outputs may be a key component of many real-world applications, especially when they involve decision-making or risk assessment (Rudin, 2019). Public health scientists or decision-makers need clear and easy-to-interpret insights about how the different exposures may impact the given health outcome. Examples include weather-related factors (Chebana and others, 2013; Pappenberger and others, 2015) or air quality indices (Lee and others, 2011; Masselot and others, 2019). The pool of methods used to create indices is currently limited, as many indices are constructed based on previously estimated univariate risks or created based on a literature review (e.g., Monforte and Ragusa, 2018). Another type of study seeking to summarize a large amount of information, exposome-wide association studies, usually focus on linear methods selecting a few number of exposure, thus partly discarding the complexity of the exposure mixture (e.g., Nieuwenhuijsen and others, 2019). Other studies consider index-based methods through the popular weighted quantile sum regression that still relate the created index linearly to the response variable (Keil and others, 2020). Therefore, there is a need for methods able to account for complex mixtures of many variables and provide interpretable indices.
Starting from a pool of exposures 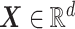 , indices are defined as a small number
, indices are defined as a small number 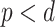 of custom predictors
of custom predictors  that are linear combinations of the original predictors, i.e., of the form
that are linear combinations of the original predictors, i.e., of the form 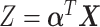 . In this sense, deriving indices
. In this sense, deriving indices 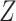 can be seen as a dimension reduction problem. The most famous example of a dimension reduction method is principal component analysis (Jolliffe, 2002). However, in the present work, we are especially interested in a regression context, i.e., in deriving indices related to a response of interest. Methods that are suited for this objective include the single-index model (SIM, e.g., Härdle and others, 1993) in which one index is constructed through the model
can be seen as a dimension reduction problem. The most famous example of a dimension reduction method is principal component analysis (Jolliffe, 2002). However, in the present work, we are especially interested in a regression context, i.e., in deriving indices related to a response of interest. Methods that are suited for this objective include the single-index model (SIM, e.g., Härdle and others, 1993) in which one index is constructed through the model 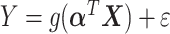 or the projection pursuit regression (PPR, Friedman and Stuetzle, 1981), also known as the additive index model, which extends the SIM in the following fashion:
or the projection pursuit regression (PPR, Friedman and Stuetzle, 1981), also known as the additive index model, which extends the SIM in the following fashion:  . In both models,
. In both models, 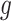 and
and 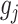 are nonlinear functions representing the relationship between the response
are nonlinear functions representing the relationship between the response  and the constructed index
and the constructed index 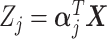 .
.
Although the SIM and PPR models are often used as nonparametric regression models (Wang and Ni, 2008; Yuan and others, 2016; Durocher and others, 2016; Cui and others, 2017), their very general and flexible nature results in a lack of interpretability as well as a tendency to overfit the data (Zhang and others, 2008). The main reasons are: (i) the derived indices include all predictors 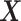 , hence mixing very different variables for which a linear combination makes little sense, (ii) the very general vectors
, hence mixing very different variables for which a linear combination makes little sense, (ii) the very general vectors  do not guarantee interpretability, and (iii) the flexibility of functions
do not guarantee interpretability, and (iii) the flexibility of functions 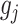 may result in complex functions preventing a clear interpretation of the corresponding index
may result in complex functions preventing a clear interpretation of the corresponding index  .
.
Usually, the predictors at hand can naturally be grouped into variables representing phenomena that jointly impact the response  . For instance, grouped variables can be naturally interacting variables such as several weather, air pollutants, sociodemographic variables as well as lagged variables (Xia and Tong, 2006). Several authors proposed to take advantage of such groupings as a path to improve the interpretability of the derived indices (Li and others, 2010; Guo and others, 2015). This leads to the groupwise additive index model (GAIM) expressed as:
. For instance, grouped variables can be naturally interacting variables such as several weather, air pollutants, sociodemographic variables as well as lagged variables (Xia and Tong, 2006). Several authors proposed to take advantage of such groupings as a path to improve the interpretability of the derived indices (Li and others, 2010; Guo and others, 2015). This leads to the groupwise additive index model (GAIM) expressed as:
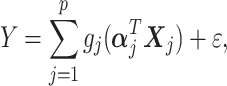 |
(1) |
where the  are subsets of variables of
are subsets of variables of  , i.e.,
, i.e.,  . The GAIM in (1) allows deriving more meaningful indices
. The GAIM in (1) allows deriving more meaningful indices 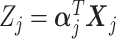 since they are built from subsets of predictors that logically or naturally belong together. It can be seen as a sparser model since only a subset of variables enters a term in (1), noting that sparsity is a key aspect of interpretability (Rudin, 2019).
since they are built from subsets of predictors that logically or naturally belong together. It can be seen as a sparser model since only a subset of variables enters a term in (1), noting that sparsity is a key aspect of interpretability (Rudin, 2019).
Although the GAIM in (1) allows an improvement in the indices interpretability, its flexibility can still result in physically or practically incoherent indices. Thus, it is also of interest to be able to constraint the indices weights 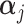 to yield more meaningful indices. Constraints on the weights
to yield more meaningful indices. Constraints on the weights 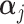 can represent additional information included in the model and reflect the expertise or knowledge specific to a given application context or operational requirements for the created indices. For an index to be useful in practice, it is also highly desirable that it relates to the response
can represent additional information included in the model and reflect the expertise or knowledge specific to a given application context or operational requirements for the created indices. For an index to be useful in practice, it is also highly desirable that it relates to the response 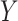 in an easy-to-interpret way. For an air quality index, it is reasonable to expect
in an easy-to-interpret way. For an air quality index, it is reasonable to expect 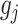 to be monotonically increasing. Similarly, a temperature-related index may impose a convexity constraint on
to be monotonically increasing. Similarly, a temperature-related index may impose a convexity constraint on 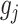 , acknowledging a minimum mortality temperature and increased risks on both sides. A too flexible model for the function
, acknowledging a minimum mortality temperature and increased risks on both sides. A too flexible model for the function 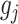 might however give implausible or difficult to interpret indices and therefore limit their usefulness for decision-making. This means that it is also of interest to impose constraints on the shape of the functions
might however give implausible or difficult to interpret indices and therefore limit their usefulness for decision-making. This means that it is also of interest to impose constraints on the shape of the functions 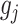 .
.
In the present article, we propose a constrained groupwise additive index model (CGAIM) as a general model that includes all the constraints discussed above. It is a model of the form (1) in which constraints are added on the weights 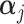 as well as on the functions
as well as on the functions 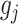 depending on the application. Several authors proposed unconstrained GAIMs based on local linear estimation (Li and others, 2010; Wang and others, 2015; Guo and others, 2015; Wang and Lin, 2017). Fawzi and others (2016) proposed the addition of a few constraints on the weights
depending on the application. Several authors proposed unconstrained GAIMs based on local linear estimation (Li and others, 2010; Wang and others, 2015; Guo and others, 2015; Wang and Lin, 2017). Fawzi and others (2016) proposed the addition of a few constraints on the weights 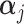 but not on the functions
but not on the functions  . Chen and Samworth (2015) proposed a PPR with shape-constrained functions
. Chen and Samworth (2015) proposed a PPR with shape-constrained functions  , but it is not in a groupwise context. Xia and Tong (2006) and then Kong and others (2010) proposed a GAIM with constraints on both the weights
, but it is not in a groupwise context. Xia and Tong (2006) and then Kong and others (2010) proposed a GAIM with constraints on both the weights 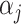 and functions
and functions 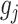 , but limited to monotonicity and without the possibility to add additional covariates such as confounders. Finally, these methods all lack inference procedures to provide uncertainty assessment or test for specific indices of covariates. Such inference results are important for interpretation purposes. We propose here a general model that encompasses all mentioned ones, with the addition of an efficient estimation procedure, as well as index selection and inference.
, but limited to monotonicity and without the possibility to add additional covariates such as confounders. Finally, these methods all lack inference procedures to provide uncertainty assessment or test for specific indices of covariates. Such inference results are important for interpretation purposes. We propose here a general model that encompasses all mentioned ones, with the addition of an efficient estimation procedure, as well as index selection and inference.
2. The CGAIM
In order to present the proposed CGAIM, we rewrite and extend model (1) as:
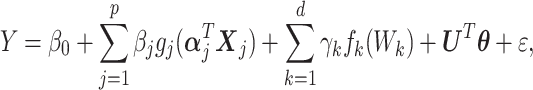 |
(2) |
where  are subsets of all the variables in
are subsets of all the variables in 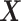 ,
, 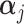 is a vector of weights and
is a vector of weights and 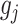 is a nonlinear function. The coefficients
is a nonlinear function. The coefficients 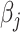 represent the relative importance of each index
represent the relative importance of each index 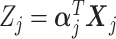 in predicting the response
in predicting the response 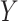 . The constant
. The constant  is the intercept of the model.
is the intercept of the model.
The 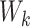 and
and 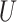 (with dimension
(with dimension  represent additional covariates that are related to
represent additional covariates that are related to 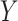 but not entering any index. The formers are nonlinearly related to
but not entering any index. The formers are nonlinearly related to  through
through  with importance
with importance 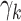 , which are respective counterparts to
, which are respective counterparts to 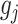 and
and 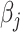 , and the latter are linear. The typical example is confounding variables in environmental epidemiology such as day-of-week or time covariates.
, and the latter are linear. The typical example is confounding variables in environmental epidemiology such as day-of-week or time covariates.
One of the key features of the proposed CGAIM is to allow for any linear constraint on the weights 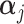 , i.e., constraints of the form
, i.e., constraints of the form  where
where 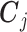 is a
is a 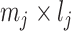 matrix,
matrix, 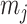 being the number of constraints and
being the number of constraints and 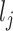 the number of variables in the group
the number of variables in the group  . Linear constraints allow for a large array of constraints. Examples include forcing some or all of the weights in
. Linear constraints allow for a large array of constraints. Examples include forcing some or all of the weights in 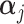 being positive, in which case
being positive, in which case 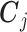 is the identity matrix, and forcing them to be monotonically decreasing, in which case
is the identity matrix, and forcing them to be monotonically decreasing, in which case 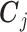 is an
is an 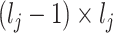 matrix where
matrix where 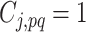 when
when 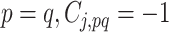 when
when  and
and 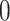 otherwise.
otherwise.
The other key feature of the CGAIM is the possibility to add shape constraints on the functions 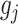 and
and 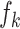 . Shape constraints include monotonicity, convexity, concavity, and combinations of the former (Pya and Wood, 2015). Note that not all functions
. Shape constraints include monotonicity, convexity, concavity, and combinations of the former (Pya and Wood, 2015). Note that not all functions 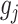 and
and  need to be constrained or have the same shape constraint.
need to be constrained or have the same shape constraint.
For identifiability, we assume that the grouping is chosen before model fitting and that no predictor variable enters two indices, i.e., 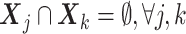 . Regarding the weights
. Regarding the weights 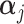 , identifiability can be ensured by the classical unit norm constraint
, identifiability can be ensured by the classical unit norm constraint 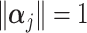 with the first element of
with the first element of 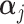 being positive (Yu and Ruppert, 2002; Yuan, 2011). However, we can also take advantage of linear constraints to ensure both identifiability and a better interpretability of the resulting indices. For instance, the constraints
being positive (Yu and Ruppert, 2002; Yuan, 2011). However, we can also take advantage of linear constraints to ensure both identifiability and a better interpretability of the resulting indices. For instance, the constraints  and
and 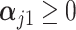 , which represents a weighted average of the variables in
, which represents a weighted average of the variables in  , are enough to ensure identifiability of
, are enough to ensure identifiability of 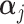 . As estimation of
. As estimation of 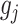 s,
s, 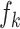 and
and  for fixed
for fixed 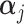 is a generalized additive model (GAM), we consider the classical centering identifiability constraints (Wood, 2004; Yuan, 2011). Finally, since we allow linear covariates in the model, we assume that no function
is a generalized additive model (GAM), we consider the classical centering identifiability constraints (Wood, 2004; Yuan, 2011). Finally, since we allow linear covariates in the model, we assume that no function 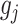 is linear since it could cause identifiability issues in the groupwise context (a formal proof is provided by Fawzi and others, 2016).
is linear since it could cause identifiability issues in the groupwise context (a formal proof is provided by Fawzi and others, 2016).
3. Estimating the CGAIM
In this section, we present an estimation algorithm for the CGAIM based on the general framework of SQP. We first focus on the additive index part of the model for clarity purposes and then extend the estimation to the full model in (2). We also present a generalized cross-validation (GCV) criterion for model selection and two inference procedures.
3.1. Estimation problem
To fit the CGAIM, given observed data 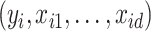 , where
, where 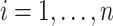 and the
and the 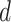 predictor variables are partitioned into
predictor variables are partitioned into 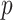 groups, we seek to minimize the squared error over coefficients
groups, we seek to minimize the squared error over coefficients 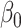 and
and 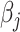 , functions
, functions  and weight vectors
and weight vectors 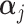 ,
, 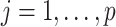 , i.e.:
, i.e.:
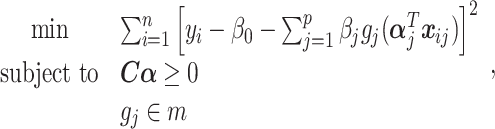 |
(3) |
where  and
and 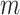 is one of the shape constraints available for
is one of the shape constraints available for 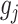 .
.
Since the 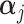 s do not enter linearly in the squared error (3), this is a nonlinear least squares problem which suggests an approach such as a Gauss–Newton algorithm. However, an additional difficulty arises from the constraints of the model, especially those on the
s do not enter linearly in the squared error (3), this is a nonlinear least squares problem which suggests an approach such as a Gauss–Newton algorithm. However, an additional difficulty arises from the constraints of the model, especially those on the 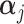 s. It is thus appropriate to consider SQP steps, a general algorithm for nonlinear constrained optimization problems (Boggs and Tolle, 1995). It has been shown to work well in the context of nonlinear least squares (Schittkowski, 1988).
s. It is thus appropriate to consider SQP steps, a general algorithm for nonlinear constrained optimization problems (Boggs and Tolle, 1995). It has been shown to work well in the context of nonlinear least squares (Schittkowski, 1988).
The proposed estimation methods for related models listed in the introduction (Xia and Tong, 2006; Li and others, 2010; Wang and others, 2015) are all based on local regression to minimize the sum of squares (3). However, it can be computationally intensive and makes the inclusion of constraints more difficult due to the high number of local coefficients to estimate. Here, we rather choose an approach based on splines for the function 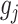 and SQP iterations for the weights
and SQP iterations for the weights 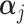 . Note that smoothing splines were shown to have good performances in a PPR context (Roosen and Hastie, 1994).
. Note that smoothing splines were shown to have good performances in a PPR context (Roosen and Hastie, 1994).
3.2. Estimation algorithm
Since the minimization problem (3) is a separable one (Golub and Pereyra, 2003), we propose here to estimate the GAIM with an algorithm that iteratively updates the functions 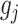 and the weight vectors
and the weight vectors 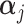 . In the first step, with the
. In the first step, with the 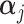 s fixed, we can derive indices values
s fixed, we can derive indices values 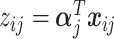 . Estimating the functions
. Estimating the functions  is thus equivalent to estimating a GAM (Hastie and Tibshirani, 1986) using the current
is thus equivalent to estimating a GAM (Hastie and Tibshirani, 1986) using the current 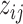 as predictors. In such a model,
as predictors. In such a model, 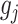 can be efficiently estimated by smoothing splines as detailed by Wood (2017). After estimating the functions
can be efficiently estimated by smoothing splines as detailed by Wood (2017). After estimating the functions 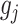 , they are scaled to have norm one, and the coefficients
, they are scaled to have norm one, and the coefficients 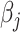 are adjusted accordingly.
are adjusted accordingly.
When shape constraints are considered, different corresponding methods can be considered. Pya and Wood (2015) proposed the shape-constrained additive models (SCAM) that estimates reparametrized P-spline coefficients through an iterative reweighted least squares like algorithm. Meyer (2018) proposed a constrained GAM (CGAM) that uses integrated and convex splines (Ramsay, 1988; Meyer, 2008) with quadratic programming to enforce shape constraints. Finally, Chen and Samworth (2015) proposed the shape-constrained additive regression that estimates nonsmooth shape-constrained functions through maximum likelihood. All these methods allow for monotonicity, convexity, and concavity constraints. Throughout the present article, we consider SCAM as it allows for a more flexible management of functions 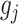 smoothness.
smoothness.
In the second step, with the functions  estimated, we can update the weights
estimated, we can update the weights 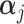 by minimizing the sum of squares function (3) over the
by minimizing the sum of squares function (3) over the 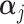 only. Let
only. Let 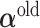 be the current value of
be the current value of  and
and 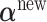 the next value to be computed. The update
the next value to be computed. The update 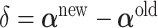 can be conveniently computed by a quadratic program (QP) of the form
can be conveniently computed by a quadratic program (QP) of the form
 |
(4) |
in which 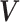 is the matrix containing the partial derivative according to the
is the matrix containing the partial derivative according to the  of the CGAIM equation, i.e., the right-hand side of (2).
of the CGAIM equation, i.e., the right-hand side of (2).  contains
contains 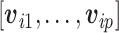 at line
at line  with the vector
with the vector 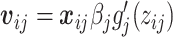 .
.  is the current residual vector that contains
is the current residual vector that contains 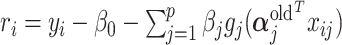 . The objective function in (4) is a quasi-Newton step in which the Hessian part that involves the second derivatives of the CGAIM has been discarded to avoid its computational burden, leaving only the term
. The objective function in (4) is a quasi-Newton step in which the Hessian part that involves the second derivatives of the CGAIM has been discarded to avoid its computational burden, leaving only the term  . Thus, the update
. Thus, the update 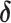 is guaranteed to be in a descent direction. Discarding the second derivative of the model is a distinctive feature of least squares since it is usually negligible compared to the term
is guaranteed to be in a descent direction. Discarding the second derivative of the model is a distinctive feature of least squares since it is usually negligible compared to the term  (Hansen and others, 2013). Note that this is especially true here since both the use of smoothing spline and shape constraints for
(Hansen and others, 2013). Note that this is especially true here since both the use of smoothing spline and shape constraints for 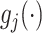 results in smooth functions and thus low second derivatives
results in smooth functions and thus low second derivatives  . Finally, the constraints in (4) ensure that the updated vector
. Finally, the constraints in (4) ensure that the updated vector 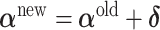 is still in the feasible region. Note that without these constraints, the problem in (4) reduces to a classical Gauss–Newton step for nonlinear least squares (Bates and Watts, 1988).
is still in the feasible region. Note that without these constraints, the problem in (4) reduces to a classical Gauss–Newton step for nonlinear least squares (Bates and Watts, 1988).
The algorithm alternates updating the weights 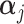 and estimating the functions
and estimating the functions 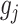 with the current
with the current 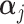 until convergence. Convergence is usually reached when the least squares function (3) does not evolve anymore after updating the
until convergence. Convergence is usually reached when the least squares function (3) does not evolve anymore after updating the  and
and 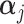 . Note that we can also consider other criteria for convergence such as stopping when the update
. Note that we can also consider other criteria for convergence such as stopping when the update  is very small or the orthogonality convergence criterion of Bates and Watts (1981).
is very small or the orthogonality convergence criterion of Bates and Watts (1981).
To start the algorithm, a constrained linear regression of the 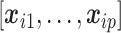 on
on 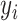 should provide an initial guess
should provide an initial guess  close to the optimal solution (Wang and others, 2015). This constrained linear regression can be implemented as a QP of the form (4) by replacing
close to the optimal solution (Wang and others, 2015). This constrained linear regression can be implemented as a QP of the form (4) by replacing 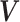 with the design matrix
with the design matrix 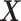 , and
, and 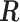 with the response vector
with the response vector 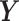 . Alternatively,
. Alternatively, 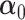 can be initiated randomly, using constrained random number generators (Van den Meersche and others, 2009). Key steps of the estimation procedure are summarized in Algorithm 1.
can be initiated randomly, using constrained random number generators (Van den Meersche and others, 2009). Key steps of the estimation procedure are summarized in Algorithm 1.
Algorithm 1
Constrained GAIM estimation
- 0.
Initialize
either by a QP as in (4) or randomly.
- 1.
Functions
update:
- a.
Estimate the
by a SCAM with
as the response and the
as predictor.
- b.
Scale the estimated
to have unit norm and adjust the coefficients
consequently.
- 2.
Weights
update:
- a.
Compute the update
through the QP (4).
- b.
Set
.
- c.
Scale each
to have unit norm.
- 3.
Iterate steps 1 and 2 until convergence.
3.3. Additional covariates
The integration of the covariates 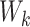 and
and  in the estimation procedure is straightforward since they only intervene in the update of functions
in the estimation procedure is straightforward since they only intervene in the update of functions 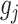 (Step 1 of Algorithm 1). In this step, they are simply added as covariates in the SCAM (or GAM in the unconstrained case), along the current indices
(Step 1 of Algorithm 1). In this step, they are simply added as covariates in the SCAM (or GAM in the unconstrained case), along the current indices 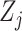 . Shape constraints can be applied on the functions
. Shape constraints can be applied on the functions 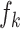 as well. These terms do not intervene in the
as well. These terms do not intervene in the  update step, since they are considered constants with respect to
update step, since they are considered constants with respect to  , which mean that they disappear from the derivative matrix
, which mean that they disappear from the derivative matrix 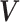 . Finally, note that the coefficients
. Finally, note that the coefficients 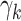 are obtained as the norm of functions
are obtained as the norm of functions  .
.
3.4. Model selection
As the number of indices and covariates grow in the model, it is of interest to select a subset that are the most predictive of the response  . To this end, we propose here a GCV type criterion of the form (Golub and others, 1979):
. To this end, we propose here a GCV type criterion of the form (Golub and others, 1979):
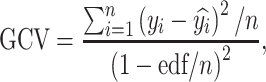 |
(5) |
where the numerator represents the residual error with  the fitted value from the CGAIM, and the denominator is a penalization that depends on the effective degrees of freedom (edf). For a large number of indices
the fitted value from the CGAIM, and the denominator is a penalization that depends on the effective degrees of freedom (edf). For a large number of indices 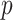 , we can perform the selection as a forward stepwise algorithm in which, at each step, the index minimizing the GCV is added to the model.
, we can perform the selection as a forward stepwise algorithm in which, at each step, the index minimizing the GCV is added to the model.
When a model can be reformulated linearly, the edf term in (5) can be estimated as the trace of the hat matrix, but it is not the case here. Instead, we consider a similar approximation as proposed by Roosen and Hastie (1994) for PPR, i.e.,
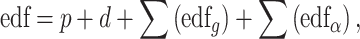 |
(6) |
where  charge one degree of freedom per index and covariate for the coefficients
charge one degree of freedom per index and covariate for the coefficients 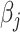 and
and  represent the sum of edfs for each ridge function smoothing, and
represent the sum of edfs for each ridge function smoothing, and  is the sum of edfs for each index weight vector estimation. Estimation of
is the sum of edfs for each index weight vector estimation. Estimation of  is well described in Meyer and Woodroofe (2000) and corresponds to the number of basic functions used in the smooth, to which we subtract the number of active constraints multiplied by a constant usually specified at
is well described in Meyer and Woodroofe (2000) and corresponds to the number of basic functions used in the smooth, to which we subtract the number of active constraints multiplied by a constant usually specified at 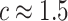 to account for the smoothing penalization (see also Meyer, 2018). Similarly,
to account for the smoothing penalization (see also Meyer, 2018). Similarly, 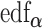 can be estimated as the number of coefficients to which we subtract the number of active constraints (Zhou and Lange, 2013).
can be estimated as the number of coefficients to which we subtract the number of active constraints (Zhou and Lange, 2013).
3.5. Inference
Inference for the ridge functions 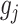 is well described elsewhere (Pya and Wood, 2015; Meyer, 2008) and inference for the coefficients
is well described elsewhere (Pya and Wood, 2015; Meyer, 2008) and inference for the coefficients 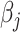 is straightforward as they can be treated like regular regression coefficients using the
is straightforward as they can be treated like regular regression coefficients using the 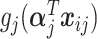 as predictors. Here, we describe inference for the vector of weights
as predictors. Here, we describe inference for the vector of weights 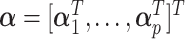 only. If one assumes normality of the residuals, then the transformed vector
only. If one assumes normality of the residuals, then the transformed vector 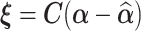 follows a truncated multivariate normal with null mean, covariance matrix
follows a truncated multivariate normal with null mean, covariance matrix 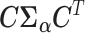 , where
, where 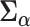 is the covariance matrix of
is the covariance matrix of 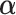 for an unconstrained model, and lower bound
for an unconstrained model, and lower bound 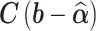 (Geweke, 1996). We can efficiently simulate a large number of vectors
(Geweke, 1996). We can efficiently simulate a large number of vectors 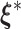 from this truncated multivariate normal, and back-transform them as
from this truncated multivariate normal, and back-transform them as 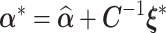 to obtain an estimate of the distribution of the vector
to obtain an estimate of the distribution of the vector 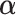 (Botev, 2017). Empirical confidence intervals or other inference can then be obtained from the simulated
(Botev, 2017). Empirical confidence intervals or other inference can then be obtained from the simulated 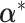 .
.
The unconstrained covariance matrix 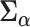 can be obtained through the classical nonlinear least squares approximation
can be obtained through the classical nonlinear least squares approximation  , where
, where 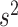 is an estimate of the residual variance of the model (Bates and Watts, 1988). In this instance,
is an estimate of the residual variance of the model (Bates and Watts, 1988). In this instance,  should be estimated using the effective degrees of freedom formula devised in Section 3.4. Note also that since it needs to be inverted, the constraint matrix
should be estimated using the effective degrees of freedom formula devised in Section 3.4. Note also that since it needs to be inverted, the constraint matrix 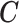 should be a square matrix. If this is not the case, it can be augmented by a matrix
should be a square matrix. If this is not the case, it can be augmented by a matrix 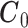 spanning the row null space of
spanning the row null space of  while the vector
while the vector 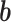 is augmented with
is augmented with 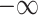 (Tallis, 1965).
(Tallis, 1965).
Without the normality assumption, inference and confidence intervals can be obtained through a bootstrap procedure (DiCiccio and Efron, 1996), with the following procedure. We start by extracting the residuals 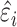 of the CGAIM fit. We then draw from the
of the CGAIM fit. We then draw from the 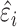 with replacement to obtain a new sample
with replacement to obtain a new sample  that is then added to the fitted values to obtain a new response vector
that is then added to the fitted values to obtain a new response vector 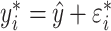 on which the CGAIM can be fitted (Efron and Tibshirani, 1993). We repeat this a large number
on which the CGAIM can be fitted (Efron and Tibshirani, 1993). We repeat this a large number 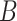 of times to obtain a bootstrap distribution of any parameter from the CGAIM, including the weights
of times to obtain a bootstrap distribution of any parameter from the CGAIM, including the weights 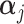 , the ridge functions
, the ridge functions 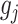 and the coefficients
and the coefficients  .
.
4. Simulation study
In this section, we analyze the performances of the CGAIM on different types of simulated data. We test the ability of the proposed CGAIM to estimate accurately weights 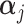 , by comparing it with other methods, its ability to find the most relevant predictors in the context of an important number of exposures, the ability of the GCV criterion to find the correct model and the coverage of the confidence intervals applied as described above.
, by comparing it with other methods, its ability to find the most relevant predictors in the context of an important number of exposures, the ability of the GCV criterion to find the correct model and the coverage of the confidence intervals applied as described above.
4.1. Index estimation
In this setting, three predictor matrices are generated following a multivariate normal distribution of dimension  (
(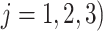 , with null means and covariance matrices having unit diagonal and nondiagonal elements equal to a predefined
, with null means and covariance matrices having unit diagonal and nondiagonal elements equal to a predefined 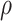 value. The first index is composed of sharply decreasing weights with a log function
value. The first index is composed of sharply decreasing weights with a log function 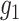 to emulate the effect of air pollution on mortality. The second includes moving average weights with a sigmoid function
to emulate the effect of air pollution on mortality. The second includes moving average weights with a sigmoid function 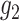 that represent a soft threshold on the index typical of logistic models. The third index represents a classical mortality temperature relationship with weights representing a delayed impact and a U-shaped relationship. The linear predictor is then the sum of the three ridge functions, i.e., with magnitudes
that represent a soft threshold on the index typical of logistic models. The third index represents a classical mortality temperature relationship with weights representing a delayed impact and a U-shaped relationship. The linear predictor is then the sum of the three ridge functions, i.e., with magnitudes  for
for 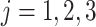 and an intercept
and an intercept  . A large number
. A large number 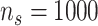 data sets are generated by adding Gaussian white noise to the linear predictor described here. More details on the simulation setup are given in Supplementary material available at Biostatistics online.
data sets are generated by adding Gaussian white noise to the linear predictor described here. More details on the simulation setup are given in Supplementary material available at Biostatistics online.
From the basic mechanism described above, various scenarios are implemented. In these scenarios, we change the sample size of simulated data with  , the correlation between predictor variables with nondiagonal elements of the covariance matrix in
, the correlation between predictor variables with nondiagonal elements of the covariance matrix in 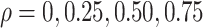 , and the noise level with standard deviations in
, and the noise level with standard deviations in 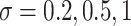 . The unconstrained GAIM and the CGAIM are applied on each of the generated data sets. The CGAIM is applied with the constraints that all weights are positives that
. The unconstrained GAIM and the CGAIM are applied on each of the generated data sets. The CGAIM is applied with the constraints that all weights are positives that  is increasing and
is increasing and 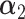 decreasing. The functions
decreasing. The functions 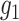 and
and  are constrained to be both monotonically increasing and
are constrained to be both monotonically increasing and 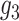 is constrained to be convex. The specific constraints applied to each index are summarized in Table S1 of the Supplementary material available at Biostatistics online. The GAIM is only applied with identifiability constraints, i.e., that non-negativity of the first element of each weight vector
is constrained to be convex. The specific constraints applied to each index are summarized in Table S1 of the Supplementary material available at Biostatistics online. The GAIM is only applied with identifiability constraints, i.e., that non-negativity of the first element of each weight vector  and unit norm for
and unit norm for 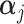 . To test the model with wrongly specified constraints, we fit a mis-specified model (MGAIM) constraining
. To test the model with wrongly specified constraints, we fit a mis-specified model (MGAIM) constraining 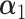 to be decreasing and
to be decreasing and  increasing. For CGAIM and MGAIM, we fix the smoothness of
increasing. For CGAIM and MGAIM, we fix the smoothness of 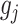 to an equivalent of 10 degrees of freedom. This avoids the computational burden of smoothness optimization in SCAM, while keeping enough flexibility for model fitting.
to an equivalent of 10 degrees of freedom. This avoids the computational burden of smoothness optimization in SCAM, while keeping enough flexibility for model fitting.
Besides the three models described above, three benchmark models are applied on the generated data sets. The first one is the PPR as the most general additive index model available. Comparing the (unconstrained) GAIM to the PPR allows assessing the benefits of defining groups of variables a priori. The second benchmark is the groupwise minimum average variance estimator (gMAVE) of Li and others (2010), as representative of groupwise dimension reduction methods. It allows the evaluation of the estimation method without constraint. Finally, we also apply the functional additive cumulative time series (FACTS) model of Kong and others (2010), that contains a groupwise additive structure and monotonicity constraints on both index weights 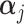 and ridge functions
and ridge functions  . We only apply the monotonicity constraints applied to CGAIM to FACTS, as its extension to other type of constraints in not trivial. The performances are evaluated by comparing the estimated weights
. We only apply the monotonicity constraints applied to CGAIM to FACTS, as its extension to other type of constraints in not trivial. The performances are evaluated by comparing the estimated weights 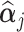 to the true values
to the true values 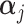 . The quality of estimated
. The quality of estimated 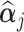 are evaluated using the classical root mean squared errors (RMSE) that aggregates information about both the bias and standard error of the estimators.
are evaluated using the classical root mean squared errors (RMSE) that aggregates information about both the bias and standard error of the estimators.
Figure 1 shows the RMSE for each model for different sample sizes, correlation coefficient between the predictor variables and noise levels. There is overall a clear hierarchy between the compared models, with the GAIM and CGAIM having the lowest errors, the gMAVE having slightly higher errors and being more sensitive to the sample size, and then the FACTS. PPR have overall much higher errors being in addition extremely variable. The methods based on the proposed algorithm on the other hand show important stability with robustness to variation in all explored parameters. As expected, the MGAIM shows low performances because of the mis-specified constraints preventing the model to converge to the true 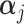 . Note however that it displays very low variance, as it converges towards the best solution within the feasible region (see Supplementary material available at Biostatistics online).
. Note however that it displays very low variance, as it converges towards the best solution within the feasible region (see Supplementary material available at Biostatistics online).
Fig. 1.
Estimated RMSE for different scenarios, varying the sample size (a), the correlation between variables (b), and the noise level (c). Note that the CGAIM and GAIM curves overlap each other at the bottom. Note the log scale.
4.2. Index selection
In this experiment, we evaluate the ability of the GCV criterion (5) to retrieve the correct model. We consider the structure detailed in the previous experiment with 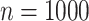 and
and 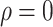 , as well as three noise levels
, as well as three noise levels  and
and 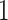 . For each realization, we randomly select
. For each realization, we randomly select 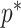 indices
indices 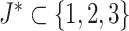 and attribute them a unit coefficient
and attribute them a unit coefficient 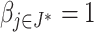 . We attribute
. We attribute  to the remaining indices, thus discarding them from the generated model. At each realization, we choose the best model by GCV and compute the sensitivity and specificity. Sensitivity is defined as the proportion of indices in
to the remaining indices, thus discarding them from the generated model. At each realization, we choose the best model by GCV and compute the sensitivity and specificity. Sensitivity is defined as the proportion of indices in  that are in the model selected by GCV, and specificity the proportion of indices not in
that are in the model selected by GCV, and specificity the proportion of indices not in  that are discarded by the GCV.
that are discarded by the GCV.
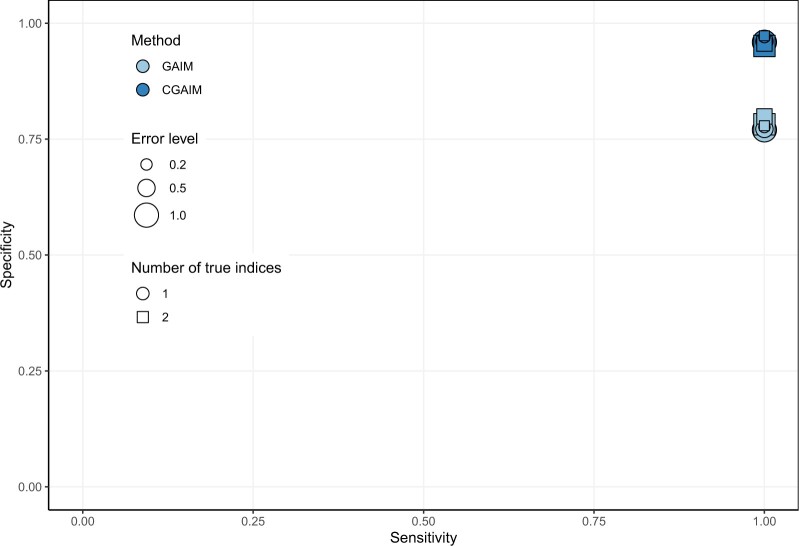
Figure 2 shows the average sensitivity and specificity on 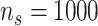 realizations for the two number of non-null indices and various noise levels. Sensitivity is equal to one in all simulations, meaning that the GCV always selects the true indices in the model. Specificity indicates that the GCV select only the true indices most of the time, i.e., around 95
realizations for the two number of non-null indices and various noise levels. Sensitivity is equal to one in all simulations, meaning that the GCV always selects the true indices in the model. Specificity indicates that the GCV select only the true indices most of the time, i.e., around 95 of the time for the CGAIM and around 80
of the time for the CGAIM and around 80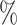 of the time for GAIM. The GAIM might then be prone to slight overfitting, while the constraints in the CGAIM allow achieving more parsimonious models. However, specificity is still high in all cases and is not sensitive to the noise level. The proposed GCV criterion is therefore mostly successful for model selection.
of the time for GAIM. The GAIM might then be prone to slight overfitting, while the constraints in the CGAIM allow achieving more parsimonious models. However, specificity is still high in all cases and is not sensitive to the noise level. The proposed GCV criterion is therefore mostly successful for model selection.
Fig. 2.
Average sensitivity and specificity of index selection computed on the 1000 simulations for various number of true indices and error level.
4.3. Coverage
To evaluate the inference procedures proposed for the CGAIM, we perform simulations to assess the coverage achieved by confidence intervals for the  weights. We generate data sets following the same mechanism described above, with
weights. We generate data sets following the same mechanism described above, with 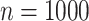 and
and  , as well as three noise levels
, as well as three noise levels 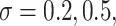 and
and 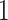 . We then fit a CGAIM model as in the two first experiments and estimate its 95
. We then fit a CGAIM model as in the two first experiments and estimate its 95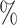 confidence interval using both the normal approximation and residual bootstrap. In both cases, the number of created samples is fixed to
confidence interval using both the normal approximation and residual bootstrap. In both cases, the number of created samples is fixed to  . As the constraints can create some bias, especially for coefficients involved in active constraints, we compute the bias-corrected coverage, as the proportion of confidence intervals containing the average estimated values
. As the constraints can create some bias, especially for coefficients involved in active constraints, we compute the bias-corrected coverage, as the proportion of confidence intervals containing the average estimated values 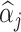 from the simulations (Morris and others, 2019).
from the simulations (Morris and others, 2019).
Figure 3 shows the bias-corrected coverage for both method and the three noise levels. The residual bootstrap shows constant reasonable coverage with values around 96 for all noise levels. In contrast, the normal approximation method is widely affected by the noise level and shows important coverage errors, with major underestimation for the highest noise level. This coverage error can also significantly vary between the various
for all noise levels. In contrast, the normal approximation method is widely affected by the noise level and shows important coverage errors, with major underestimation for the highest noise level. This coverage error can also significantly vary between the various 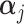 with low coverages for
with low coverages for 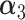 specifically, while the variation between indices is lesser for the residual bootstrap (see Figure S4 of the Supplementary material available at Biostatistics online).
specifically, while the variation between indices is lesser for the residual bootstrap (see Figure S4 of the Supplementary material available at Biostatistics online).
Fig. 3.
Estimated coverage for both inference methods and various noise level. Vertical segments indicate 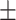 1 standard error of the coverage.
1 standard error of the coverage.
4.4. Exposome
In this experiment, we depart from the structure of the previous experiments and apply the GAIM and CGAIM to estimate the most important predictors in a simulation study typical of exposome studies. We modify the simulation study proposed by Agier and others (2016), using the structure of the HELIX cohort (Robinson and others, 2018). We generate a matrix of 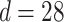 predictors with
predictors with  subjects from the correlation matrix provided in Robinson and others (2018). In each realization, we select
subjects from the correlation matrix provided in Robinson and others (2018). In each realization, we select  predictors
predictors  to have non-null weights, while the remaining predictors are attributed null weights, and have therefore no association with the response. We then generate the response vector through the model
to have non-null weights, while the remaining predictors are attributed null weights, and have therefore no association with the response. We then generate the response vector through the model 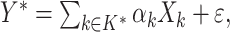 where
where 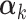 is either -1 or 1 with equal probability to evaluate the ability of the model estimate the direction of the association. Response vectors are then generated such that the
is either -1 or 1 with equal probability to evaluate the ability of the model estimate the direction of the association. Response vectors are then generated such that the 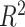 of the model is
of the model is 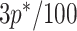 (Agier and others, 2016).
(Agier and others, 2016).
As the correlation matrix used to generate the predictors  represents environmental stressors, five groups naturally arise (Nieuwenhuijsen and others, 2019): climatic (
represents environmental stressors, five groups naturally arise (Nieuwenhuijsen and others, 2019): climatic ( , air pollution (
, air pollution ( , traffic-related (
, traffic-related (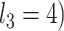 , natural environment (
, natural environment (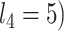 , and built-environment (
, and built-environment (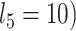 variables. We apply the (unconstrained) GAIM and CGAIM on 1000 realizations of the above-described mechanism with these groups of variables. The CGAIM is applied with the constraints
variables. We apply the (unconstrained) GAIM and CGAIM on 1000 realizations of the above-described mechanism with these groups of variables. The CGAIM is applied with the constraints 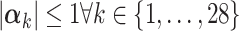 , convexity constraint on
, convexity constraint on  (representing the effect of climate) and increasing monotonicity on other
(representing the effect of climate) and increasing monotonicity on other  (
(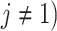 . We then compare the estimated
. We then compare the estimated 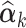 (
(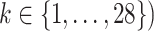 to the true value
to the true value 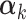 .
.
Figure 4 shows that the 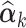 are on average close to the true
are on average close to the true 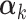 , successfully discriminating null weights but also the direction of non-null weights. They are closer to the true value for the CGAIM compared to GAIM, with also much lower variability in the estimated weights. The difference between estimated and true weights also slightly decreases with the number of non-null weights
, successfully discriminating null weights but also the direction of non-null weights. They are closer to the true value for the CGAIM compared to GAIM, with also much lower variability in the estimated weights. The difference between estimated and true weights also slightly decreases with the number of non-null weights 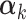 . Therefore, the CGAIM, performs well with many predictors and complex correlation patterns, especially when constraints are considered.
. Therefore, the CGAIM, performs well with many predictors and complex correlation patterns, especially when constraints are considered.
Fig. 4.
Average estimated 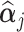 for according to the true value
for according to the true value  . Segments indicate 2.5th and 97.5th percentile of estimated
. Segments indicate 2.5th and 97.5th percentile of estimated 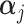 .
.
5. Application
This section presents an example of application in environmental epidemiology in which the CGAIM is used to construct multiple indices representing heat-related mortality risks. A second application on air pollution is presented in Supplementary material available at Biostatistics online. This application considers daily mortality and exposure data spanning the months of June–August for the period 1990–2014 ( from the Metropolitan Area of Montreal in the province of Quebec, Canada, which are described in detail in, e.g., Masselot and others (2018, 2019). Briefly, daily all-cause mortality data are provided by the province of Quebec National Institute of Public Health, while daily temperature and humidity data are extracted from the 1 km
from the Metropolitan Area of Montreal in the province of Quebec, Canada, which are described in detail in, e.g., Masselot and others (2018, 2019). Briefly, daily all-cause mortality data are provided by the province of Quebec National Institute of Public Health, while daily temperature and humidity data are extracted from the 1 km  1 km gridded data set DayMet (Thornton and others, 2021).
1 km gridded data set DayMet (Thornton and others, 2021).
We apply the CGAIM to find optimal weights for temperature indices that represent potentially adverse effects. Indices created include lagged averages of  and
and 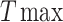 , following the current indices in Montreal (Chebana and others, 2013), and we also include the vapor pressure (
, following the current indices in Montreal (Chebana and others, 2013), and we also include the vapor pressure (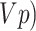 variable to represent humidity, since it is also sometimes considered a determinant of summer mortality (e.g., Barreca, 2012). The objective here is to give an example of the possibilities offered by the CGAIM. Thus, to estimate these indices, the following full model is considered:
variable to represent humidity, since it is also sometimes considered a determinant of summer mortality (e.g., Barreca, 2012). The objective here is to give an example of the possibilities offered by the CGAIM. Thus, to estimate these indices, the following full model is considered:
 |
(7) |
where 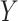 is the all-cause daily mortality,
is the all-cause daily mortality,  ,
,  , and
, and  represent matrices of lags 0, 1, and 2 days of corresponding variables, meaning that the
represent matrices of lags 0, 1, and 2 days of corresponding variables, meaning that the 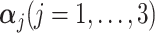 are vectors of length 3. The two additional covariates are the day-of-season and year variables to control for the seasonality, interannual trend, and residual autocorrelation as commonly done in time series study in environmental epidemiology (Bhaskaran and others, 2013).
are vectors of length 3. The two additional covariates are the day-of-season and year variables to control for the seasonality, interannual trend, and residual autocorrelation as commonly done in time series study in environmental epidemiology (Bhaskaran and others, 2013).
We consider a CGAIM and an (unconstrained) GAIM. The CGAIM model includes constraints for positive and decreasing weights with the lag, i.e., 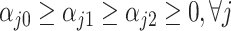 . This is encoded by the following constraint matrix
. This is encoded by the following constraint matrix
 |
(8) |
For the indices to directly represent a measure of heat risk, and because the data are restricted to the hottest months of the year with little exposure to cold, we add the constraint that the relationship 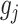 is monotone increasing for all
is monotone increasing for all  . As in the simulation study, we fix the smoothness to the equivalent of 10 degrees of freedom. Confidence intervals are computed through the residual bootstrap.
. As in the simulation study, we fix the smoothness to the equivalent of 10 degrees of freedom. Confidence intervals are computed through the residual bootstrap.
For both the CGAIM and GAIM, we use the GCV criterion (5) to determine the best set of indices to predict summer mortality. Bets models include 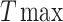 and
and 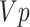 for both the GAIM and CGAIM. Among these two best models, the GCV of the CGAIM one is slightly lower being at 90.2 compared to 90.6 for the GAIM.
for both the GAIM and CGAIM. Among these two best models, the GCV of the CGAIM one is slightly lower being at 90.2 compared to 90.6 for the GAIM.
The indices and their association with mortality are shown in Figure 5. The CGAIM attributes a slightly decreasing weights with lags of 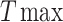 resulting in an index that has a large association with mortality for extreme values, especially above the value 0.9 of the standardized index (around 32
resulting in an index that has a large association with mortality for extreme values, especially above the value 0.9 of the standardized index (around 32 C). Note that this value is slightly below the current
C). Note that this value is slightly below the current 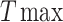 threshold in Montreal. The GAIM attributes a slightly larger weight to lag 2 of
threshold in Montreal. The GAIM attributes a slightly larger weight to lag 2 of 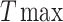 compared to lag 0 and 1, but with larger confidence intervals compared to the CGAIM. The
compared to lag 0 and 1, but with larger confidence intervals compared to the CGAIM. The 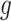 curve is similar to the one of the CGAIM but less smooth. Regarding Vp, the results from the CGAIM is very similar to those of Tmax, the weights roughly spread across lags and with a relationship sharply increasing at highest values of the index. In contrast, the GAIM attributes two opposite weights for lag 0 and 1 of Vp and a null weight for lag 2 with a ridge function oscillating around the zero line. Given the flatness of the ridge function, such a contrast between GAIM or CGAIM could either suggest the influence of unmeasured confounding, or some overfitting from the models. Indeed, evidence regarding the role of humidity in heat-related mortality is overall weak and inconsistent (Armstrong and others, 2019).
curve is similar to the one of the CGAIM but less smooth. Regarding Vp, the results from the CGAIM is very similar to those of Tmax, the weights roughly spread across lags and with a relationship sharply increasing at highest values of the index. In contrast, the GAIM attributes two opposite weights for lag 0 and 1 of Vp and a null weight for lag 2 with a ridge function oscillating around the zero line. Given the flatness of the ridge function, such a contrast between GAIM or CGAIM could either suggest the influence of unmeasured confounding, or some overfitting from the models. Indeed, evidence regarding the role of humidity in heat-related mortality is overall weak and inconsistent (Armstrong and others, 2019).
Fig. 5.
Resulting indices created in Montreal. Top row: weights 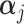 for each selected index; bottom row: functions
for each selected index; bottom row: functions 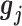 . Indices have been standardized over the range [0–1] for ease of comparison. Each column corresponds to one index. Vertical segments and dotted lines represent block bootstrap 95
. Indices have been standardized over the range [0–1] for ease of comparison. Each column corresponds to one index. Vertical segments and dotted lines represent block bootstrap 95 confidence intervals.
confidence intervals.
6. Discussion
Following the growing need of understanding the impact of mixtures of environmental exposures on human health, the present article proposes a method to construct indices with constraints under the form of a CGAIM. The CGAIM is expected to be of use both for modeling and creating comprehensive indices for public health stakeholders. Its strengths include the possibility to include a high number of predictors  (including lags), include additional prior information from public health experts, and construct multiple indices simultaneously. Compared to previous work on the subject, the key novelties of the work are thus: (i) the possibility to add any linear constraints on the index weights
(including lags), include additional prior information from public health experts, and construct multiple indices simultaneously. Compared to previous work on the subject, the key novelties of the work are thus: (i) the possibility to add any linear constraints on the index weights  , (ii) the inclusion of constrained smoothing in the model to improve the indices usefulness, (iii) a simple and efficient algorithm to estimate the indices, and (iv) a criterion for index selection.
, (ii) the inclusion of constrained smoothing in the model to improve the indices usefulness, (iii) a simple and efficient algorithm to estimate the indices, and (iv) a criterion for index selection.
The constraints allow the proposed model to integrate additional information reflecting prior assumptions about the studied associations as well as integrate operational limitations to constructed indices. Examples of useful prior assumption include constraining indices and function shape to be convex for temperature-related mortality studies, or increasing for air pollution-related mortality studies, for which usual flexible methods may fail (Armstrong and others, 2020). Constraints can also force coefficients towards a specific feasible region to better control for unmeasured confounding causing issues such as the reversal paradox (Nickerson and Brown, 2019). Adding such constraint for prior information, if correctly specified, also results in quicker convergence as shown by the timings reported in Supplementary material available at Biostatistics online. On the other hand, operational constraints force constructed indices to have specific desirable properties. For instance, it is desirable that monitored heat indices reflect two constraints: (i) decreased influence of higher lags to account for increased uncertainty in weather forecasts and (ii) a monotonic association with mortality for ease of interpretation. Such constraints might be desirable even at the expense of more optimal solutions. Although most applications displayed in this article include non-negativity constraints, this is not a specificity of the method, and constraints with negative coefficients are possible, for instance to construct exposure representing differences between variables.
A simulation study shows that the CGAIM can accurately estimate the index weights as well as the index relationship with the response variable compared to other advanced and recent models which is a step further in obtaining representative indices for practical applications. It shows that constraints help the model recover the true coefficient values. The simulation study also shows the model is robust to low sample sizes, highly correlated predictors, low signal-to-noise ratio, and high dimension with complex correlation patterns. The CGAIM is also compared to the PPR to evaluate the benefits of grouping variables, to the gMAVE as well as FACTS algorithms. Comparisons suggest that the CGAIM is more stable than these algorithms. In fact, even without any constraint, the proposed algorithm is efficient and converges quickly to an optimal solution, as shown by the comparison between the GAIM and gMAVE (see Supplementary material available at Biostatistics online for a comparison of computational burden). In addition, simulation studies of Sections 4.2 and 4.3 show that the model can efficiently recover the indices and variables that are the most predictive of the response.
Another strength of the work is in proposing and evaluation two inference procedures, an aspect of multiple index models that is often neglected in multiple index models, except in recently proposed Bayesian methods (McGee and others, 2022). One proposed procedure is based on a normal approximation of constrained nonlinear least squares, and one based on bootstrap resampling. Both methods however display non-negligible coverage error for confidence intervals. The normal approximation can especially widely underestimate the uncertainty. This is mainly related to the covariance matrix constructed from nonlinear least squares that have been shown to significantly underestimate coverage even in far simpler settings (Donaldson and Schnabel, 1987). In contrast, bootstrap-based confidence intervals provide more satisfactory results although Section 4.3 shows that they tend to overestimate uncertainty which is also consistent with previous work on bootstrap confidence intervals (Carpenter and Bithell, 2000). Inference in constrained settings often presents mixed results (Meyer, 2018), and further work is necessary to improve this aspect of the method.
The proposed method assumes that the variables and their grouping is selected a priori, with the idea that in many cases, the researcher has a clear idea of the relevant variables to be included. This assumption is reasonable in many applications in which a natural grouping of variables arises. For instance, in environmental epidemiology, exposure variable can often be grouped into category such as climate, air pollution, or built-environment variables. Common tools to determine which variables to include in a study such as directed acyclic graphs (Greenland and others, 1999) or clustering (Song and Zhu, 2016) can also be used to determine a grouping a priori. When a limited number of concurrent groupings are investigated, the GCV criterion proposed in the present work can be used to decide. However, there may also be a need for a more automated selection procedure and an area for future research is thus to propose a flexible grouping mechanism. This is a difficult problem as the number of possible classifications increases dramatically with the number of variables.
Another limit of the proposed CGAIM is that it is currently restricted to continuous responses. Although this encompasses many situations, including counts when they are large enough such as in the applications above, it is of interest to extend this work to special cases such as logistic regression or survival analysis to increase its applicability. It is thus of interest to develop a generalized version of the CGAIM, in the same fashion as the generalized extension of the PPR (Roosen and Hastie, 1993; Lingj and Liestøl, 1998).
Supplementary Material
Acknowledgments
The authors want to thank the Institut national de santé publique du Québec for access to mortality data. The authors also acknowledge the important role of Jean-Xavier Giroux and Christian Filteau for extracting and managing the data and Anas Koubaa for helping in obtaining preliminary results. Finally, the authors thank the coeditors Professor Dimitris Rizopoulos & Professor Sherri Rose as well as two anonymous referees for their helpful comments and suggestions.
Conflict of Interest: None declared.
Contributor Information
Pierre Masselot, Department of Public Health, Environment and Society, London School of Hygiene & Tropical Medicine, 15-17 Tavistock Place, WC1H 9SH, London, UK.
Fateh Chebana, Centre Eau-Terre-Environnement, Institut National de la Recherche Scientifique, 490, rue de la Couronne, Québec (Québec), G1K 9A9, Canada.
Céline Campagna, Centre Eau-Terre-Environnement, Institut National de la Recherche Scientifique, 490, rue de la Couronne, Québec (Québec), G1K 9A9, Canada and Institut National de Santé Publique du Québec, 945, avenue Wolfe Québec (Québec) G1V 5B3 Canada.
Éric Lavigne, School of Epidemiology and Public Health, University of Ottawa, 600 Peter Morand Crescent, Room 101, Ottawa, Ontario K1G 5Z3, Canada and Air Health Science Division, Health Canada, 269 Laurier Avenue West, Mail Stop 4903B, Ottawa, Ontario K1A0K9 Canada.
Taha B M J Ouarda, Centre Eau-Terre-Environnement, Institut National de la Recherche Scientifique, 490, rue de la Couronne, Québec (Québec), G1K 9A9, Canada.
Pierre Gosselin, Institut National de la Recherche Scientifique, Centre Eau-Terre-Environnement, Québec, Canada, Institut National de Santé Publique du Québec, Québec, Canada, and Ouranos, Montréal, 550 Sherbrooke Ouest, Tour Ouest, 19eme Étage, Montréal (Québec), H3A 1B9, Canada.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org. It includes full details on the data-generating mechanisms and additional results from the simulation study. A second application of the CGAIM to an air pollution index is also presented in Supplementary Materials. An R package cgaim implementing the method is freely available on Github and CRAN. The reproducible code for the simulations and applications is freely available on the first author’s GitHub (https://github.com/PierreMasselot/Paper–2022–Biostatistics–CGAIM).
Funding
The Ouranos consortium (552023); and the Quebec government’s Fonds Vert under the Climate change Action Plan 2013–2020 financial contribution and Mitacs (IT12072).
References
- Agier, L., Portengen, L., Chadeau-Hyam, M., Basagaña X., Giorgis-Allemand, L., Siroux, V., Robinson, O., Vlaanderen, J., González, J. R., Nieuwenhuijsen, M. J., and others. (2016). A systematic comparison of linear regression-based statistical methods to assess exposome-health associations. Environmental Health Perspectives 124, 1848–1856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong, B. G., Gasparrini, A., Tobias, A. and Sera, F. (2020). Sample size issues in time series regressions of counts on environmental exposures. BMC Medical Research Methodology 20, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong, B., Sera, F., Vicedo-Cabrera, A. M., Abrutzky, R., Åsträm, D. O., Bell, M. L., Chen, B.-Y., de Sousa Zanotti Stagliorio Coelho, M., Patricia Matus, C., Dang Tran, N., and others. (2019). The role of humidity in associations of high temperature with mortality: a multiauthor, multicity study. Environmental Health Perspectives 127, 097007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barreca, A. I. (2012). Climate change, humidity, and mortality in the United States. Journal of Environmental Economics and Management 63, 19–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates, D. M. and Watts, D. G. (1981). A relative off set orthogonality convergence criterion for nonlinear least squares. Technometrics 23, 179–183. [Google Scholar]
- Bates, D. M. and Watts, D. G. (1988). Nonlinear Regression Analysis and Its Applications. Wiley. [Google Scholar]
- Bhaskaran, K., Gasparrini, A., Hajat, S., Smeeth, L. and Armstrong, B. (2013). Time series regression studies in environmental epidemiology. International Journal of Epidemiology 42, 1187–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bobb, J. F., Valeri, L., Claus Henn, B., Christiani, D. C., Wright, R. O., Mazumdar, M., Godleski, J. J. and Coull, B. A. (2015). Bayesian kernel machine regression for estimating the health effects of multi-pollutant mixtures. Biostatistics 16, 493–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boggs, P. T. and Tolle, J. W. (1995). Sequential quadratic programming. Acta Numerica 4, 1–51. [Google Scholar]
- Botev, Z. I. (2017). The normal law under linear restrictions: simulation and estimation via minimax tilting. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 79, 125–148. [Google Scholar]
- Breiman, L. (2001). Random forests. Machine Learning 45, 5–32. [Google Scholar]
- Carpenter, J. and Bithell, J. (2000). Bootstrap confidence intervals: when, which, what? A practical guide for medical statisticians. Statistics in Medicine 19, 1141–1164. [DOI] [PubMed] [Google Scholar]
- Chebana, F., Martel, B., Gosselin, P., Giroux, J.-X. and Ouarda, T. B. (2013). A general and flexible methodology to define thresholds for heat health watch and warning systems, applied to the province of Québec (Canada). International Journal of Biometeorology 57, 631–644. [DOI] [PubMed] [Google Scholar]
- Chen, Y. and Samworth, R. J. (2015). Generalized additive and index models with shape constraints. Journal of the Royal Statistical Society: Series B (Statistical Methodology). [Google Scholar]
- Cui, H.-Y., Zhao, Y., Chen, Y.-N., Zhang, X., Wang, X.-Q., Lu, Q., Jia, L.-M. and Wei, Z.-M. (2017). Assessment of phytotoxicity grade during composting based on EEM/PARAFAC combined with projection pursuit regression. Journal of Hazardous Materials 326, 10–17. [DOI] [PubMed] [Google Scholar]
- Davalos, A. D., Luben, T. J., Herring, A. H. and Sacks, J. D. (2017). Current approaches used in epidemiologic studies to examine short-term multipollutant air pollution exposures. Annals of Epidemiology 27, 145-153.e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiCiccio, T. J. and Efron, B. (1996). Bootstrap confidence intervals. Statistical Science 11, 189–212. [Google Scholar]
- Donaldson, J. R. and Schnabel, R. B. (1987). Computational experience with confidence regions and confidence intervals for nonlinear least squares. Technometrics 29, 67–82. [Google Scholar]
- Durocher, M., Chebana, F. and Ouarda, T. B. M. J. (2016). Delineation of homogenous regions using hydrological variables predicted by projection pursuit regression. Hydrology and Earth System Sciences 20, 4717–4729. [Google Scholar]
- Efron, B. and Tibshirani, R. (1993). An introduction to the bootstrap. Chapman & Hall/CRC. [Google Scholar]
- Fawzi, A., Fiot, J., Chen, B., Sinn, M. and Frossard, P. (2016). Structured dimensionality reduction for additive model regression. IEEE Transactions on Knowledge and Data Engineering 28, 1589–1601. [Google Scholar]
- Friedman, J. H. and Stuetzle, W. (1981). Projection pursuit regression. Journal of the American Statistical Association 76, 817–823. [Google Scholar]
- Geweke, J. F. (1996). Bayesian inference for linear models subject to linear inequality constraints. In: Lee, J. C., Johnson, W. O. and Zellner, A. (editors) Modelling and Prediction Honoring Seymour Geisser. New York, NY: Springer. pp. 248–263. [Google Scholar]
- Golub, G. H., Heath, M. and Wahba, G. (1979). Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 21, 215–223. [Google Scholar]
- Golub, G. and Pereyra, V. (2003). Separable nonlinear least squares: the variable projection method and its applications. Inverse Problems 19, R1–R26. [Google Scholar]
- Greenland, S., Pearl, J. and Robins, J. M. (1999). Causal diagrams for epidemiologic research. Epidemiology 10, 37–48. [PubMed] [Google Scholar]
- Guo, Z., Li, L., Lu, W. and Li, B. (2015). Groupwise dimension reduction via envelope method. Journal of the American Statistical Association 110, 1515–1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen, P. C., Pereyra, V. and Scherer, G. (2013). Least squares data fitting with applications. Johns Hopkins University Press. https://orbit.dtu.dk/en/publications/least-squares-data-fitting-with-applications [online; last accessed January24, 2020]. [Google Scholar]
- Härdle, W., Hall, P. and Ichimura, H. (1993). Optimal smoothing in single-index models. The Annals of Statistics 21, 157–178. [Google Scholar]
- Hastie, T. and Tibshirani, R. (1986). Generalized additive models. Statistical Science 1, 297–310. [DOI] [PubMed] [Google Scholar]
- Jolliffe, I. T. (2002). Principal Component Analysis. Springer Science & Business Media. [Google Scholar]
- Keil, A. P., Buckley, J. P., O’Brien, K. M., Ferguson, K. K., Zhao, S. and White, A. J. (2020). A quantile-based g-computation approach to addressing the effects of exposure mixtures. Environmental Health Perspectives 128, 047004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong, E., Tong, H. and Xia, Y. (2010). Statistical modelling of nonlinear long-term cumulative effects. Statistica Sinica 20, 1097–1123. [Google Scholar]
- Lee, D., Ferguson, C. and Scott, E. M. (2011). Constructing representative air quality indicators with measures of uncertainty. Journal of the Royal Statistical Society: Series A (Statistics in Society) 174, 109–126. [Google Scholar]
- Li, L., Li, B. and Zhu, L.-X. (2010). Groupwise dimension reduction. Journal of the American Statistical Association 105, 1188–1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lingjærde, O. and Liestøl, K. (1998). Generalized projection pursuit regression. SIAM Journal on Scientific Computing 20, 844–857. [Google Scholar]
- Masselot, P., Chebana, F., Lavigne, É., Campagna, C., Gosselin, P. and Ouarda, T. B. M. J. (2019). Toward an improved air pollution warning system in Quebec. International Journal of Environmental Research and Public Health 16, 2095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masselot, P., Chebana, F., Ouarda, T. B. M. J., Bélanger, D., St-Hilaire, A. and Gosselin, P. (2018). A new look at weather-related health impacts through functional regression. Scientific Reports 8, 15241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGee, G., Wilson, A., Webster, T. F. and Coull, B. A. (2022). Bayesian multiple index models for environmental mixtures. Biometrics. doi: 10.1111/biom.13569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer, M. C. (2018). A framework for estimation and inference in generalized additive models with shape and order restrictions. Statistical Science 33, 595–614. [Google Scholar]
- Meyer, M. C. (2008). Inference using shape-restricted regression splines. Annals of Applied Statistics 2, 1013–1033. [Google Scholar]
- Meyer, M. and Woodroofe, M. (2000). On the degrees of freedom in shape-restricted regression. The Annals of Statistics 28, 1083–1104. [Google Scholar]
- Monforte, P. and Ragusa, M. A. (2018). Evaluation of the air pollution in a Mediterranean region by the air quality index. Environmental Monitoring and Assessment 190, 625. [DOI] [PubMed] [Google Scholar]
- Morris, T. P., White, I. R. and Crowther, M. J. (2019). Using simulation studies to evaluate statistical methods. Statistics in Medicine 38, 2074–2102. doi: 10.1002/sim.8086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickerson, C. A. and Brown, N. J. L. (2019). Simpson’s Paradox is suppression, but Lord’s Paradox is neither: clarification of and correction to Tu, Gunnell, and Gilthorpe (2008). Emerging Themes in Epidemiology 16, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuijsen, M. J., Agier, L., Basagaña, X., Urquiza, J., Tamayo-Uria, I., Giorgis-Allemand, L., Robinson, O., Siroux, V., Maitre, L., de Castro, M.. and others (2019). Influence of the urban exposome on birth weight. Environmental Health Perspectives 127, 47007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pappenberger, F., Jendritzky, G., Staiger, H., Dutra, E., Di Giuseppe, F., Richardson, D. S. and Cloke, H. L. (2015). Global forecasting of thermal health hazards: the skill of probabilistic predictions of the Universal Thermal Climate Index (UTCI). International Journal of Biometeorology 59, 311–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pya, N. and Wood, S. N. (2015). Shape constrained additive models. Statistics and Computing 25, 543–559. [Google Scholar]
- Ramsay, J. O. (1988). Monotone regression splines in action. Statistical Science 3, 425–441. [Google Scholar]
- Robinson, O., Tamayo, I., de Castro, M., Valentin, A., Giorgis-Allemand, L., Hjertager, K. N., Marit, A. G., Ambros, A., Ballester, F., Bird, P.. and others (2018). The urban exposome during pregnancy and its socioeconomic determinants. Environmental Health Perspectives 126, 077005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roosen, C. B. and Hastie, T. J. (1994). Automatic smoothing spline projection pursuit. Journal of Computational and Graphical Statistics 3, 235–248. [Google Scholar]
- Roosen, C. B. and Hastie, T. J. (1993). Logistic Response Projection BL011214-930806-09TM, AT&T Bell Laboratories, Statistics and Data Analysis Research Department. [Google Scholar]
- Rudin, C. (2019). Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence 1, 206–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schittkowski, K. (1988). Solving constrained nonlinear least squares problems by a general purpose SQP-method. In: Hoffmann, K.-H., Zowe, J., Hiriart-Urruty, J.-B. and Lemarechal, C. (editors), Trends in Mathematical Optimization: 4th French-German Conference on Optimization. Basel: Birkhäuser Basel. pp. 295–309. [Google Scholar]
- Schmidt, C. W. (2020). Into the black box: what can machine learning offer environmental health research? Environmental Health Perspectives 128, 022001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song, S. and Zhu, L. (2016). Group-wise semiparametric modeling: a SCSE approach. Journal of Multivariate Analysis 152, 1–14. [Google Scholar]
- Tallis, G. M. (1965). Plane truncation in normal populations. Journal of the Royal Statistical Society: Series B (Methodological) 27, 301–307. [Google Scholar]
- Thornton, P. E., Shrestha, R., Thornton, M., Kao, S.-C., Wei, Y. and Wilson, B. E. (2021). Gridded daily weather data for North America with comprehensive uncertainty quantification. Scientific Data 8, 190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van den Meersche, K., Soetaert, K. and Van Oevelen, D. (2009). xsample(): an R function for sampling linear inverse problems. Journal of Statistical Software 30, 1–15.21666874 [Google Scholar]
- Wang, K. and Lin, L.(2017). Robust and efficient direction identification for groupwise additive multiple-index models and its applications. TEST 26, 22–45. [Google Scholar]
- Wang, S.-J. and Ni, C.-J. (2008). Application of projection pursuit dynamic cluster model in regional partition of water resources in China. Water Resources Management 22, 1421–1429. [Google Scholar]
- Wang, T., Zhang, J., Liang, H. and Zhu, L. (2015). Estimation of a groupwise additive multiple-index model and its applications. Statistica Sinica 25, 551–566. [Google Scholar]
- Wood, S. N. (2017). Generalized Additive Models: An Introduction with R, 2nd edition. Chapman and Hall/CRC. [Google Scholar]
- Wood, S. N. (2004). Stable and efficient multiple smoothing parameter estimation for generalized additive models. Journal of the American Statistical Association 99, 673–686. [Google Scholar]
- Xia, Y. and Tong, H. (2006). Cumulative effects of air pollution on public health. Statistics in Medicine 25, 3548–3559. [DOI] [PubMed] [Google Scholar]
- Yu, Y. and Ruppert, D. (2002). Penalized spline estimation for partially linear single-index models. Journal of the American Statistical Association 97, 1042–1054. [Google Scholar]
- Yuan, J., Xie, C., Zhang, T., Sun, J., Yuan, X., Yu, S., Zhang, Y., Cao, Y., Yu, X., Yang, X.. and others. (2016). Linear and nonlinear models for predicting fish bioconcentration factors for pesticides. Chemosphere 156, 334–340. [DOI] [PubMed] [Google Scholar]
- Yuan, M. (2011). On the identifiability of additive index models. Statistica Sinica 21, 1901–1911. [Google Scholar]
- Zhang, X., Liang, L., Tang, X. and Shum, H.-Y. (2008). L1 regularized projection pursuit for additive model learning. In: 2008 IEEE Conference on Computer Vision and Pattern Recognition. IEEE. pp. 1–8. [Google Scholar]
- Zhou, H. and Lange, K. (2013). A Path Algorithm for Constrained Estimation. Journal of Computational and Graphical Statistics?: A Joint Publication of American Statistical Association, Institute of Mathematical Statistics, Interface Foundation of North America 22, 261–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.