Computing Geographical Networks Generated by Air‐Mass Movement

Abstract

As air masses move within the troposphere, they transport a multitude of components including gases and particles such as pollen and microorganisms. These movements generate atmospheric highways that connect geographic areas at distant, local, and global scales that particles can ride depending on their aerodynamic properties and their reaction to environmental conditions. In this article we present an approach and an accompanying web application called tropolink for measuring the extent to which distant locations are potentially connected by air‐mass movement. This approach is based on the computation of trajectories of air masses with the HYSPLIT atmospheric transport and dispersion model, and on the computation of connection frequencies, called connectivities, in the purpose of building trajectory‐based geographical networks. It is illustrated for different spatial and temporal scales with three case studies related to plant epidemiology. The web application that we designed allows the user to easily perform intensive computation and mobilize massive archived gridded meteorological data to build weighted directed networks. The analysis of such networks allowed us for example, to describe the potential of invasion of a migratory pest beyond its actual distribution. Our approach could also be used to compute geographical networks generated by air‐mass movement for diverse application domains, for example, to assess long‐term risk of spread from persistent or recurrent sources of pollutants, including wildfire smoke.

Key Points

• The movement of air masses within the troposphere generate air highway connecting distant areas from local to global scales

• Our approach and the accompanying web application tropolink quantifie how distant locations are connected by air‐mass movement

• Our approach can be used to investigate the spread of small biological particles and organisms

1. Introduction

Earth's troposphere is characterized by large‐scale circulation patterns (Schneider, 2006). The movement of air masses in the troposphere transport moisture and particles from natural and anthropogenic sources, such as volcanic ash (Weber et al., 2012), dust (Gonzalez‐Martin et al., 2014), pollen (Kappen & Straka, 1988), and radioactive chemical elements (Masson et al., 2019). The trajectories of some of these particles, when emitted into the atmosphere in massive quantities, can be visualized with satellites (Kellogg & Griffin, 2006). For more inconspicuous particles, large‐scale trajectories must be deduced from indirect ground‐based observations and punctual air samples where those particles are in sufficient concentrations to be detected with current sampling technology (Masson et al., 2019; Schmale & Ross, 2015). This state of the art in tracing and predicting large‐scale trajectories of airborne particles is a considerable handicap, particularly for assessing invasion risk or seasonal dynamics of airborne crop pests and to design surveillance strategies accordingly (Morris et al., 2021; Schmale & Ross, 2015; M. Wang et al., 2021).

Concerning living organisms, windborne long distance dispersal (typically larger than 10 km) has been largely explored for bacteria and fungi (Aylor, 2003, 2017; Barberán et al., 2015; Brown & Hovmøller, 2002; Morris et al., 2008; Soubeyrand et al., 2009), pollen and seeds (Nathan et al., 2011; Williams, 2010; Williams & Barneoud, 2021), aphids (M. Irwin & Thresh, 1988; Isard & Gage, 2001), lepidoptera (Westbrook et al., 2016; Wu et al., 2022), and midges (Aguilar‐Vega et al., 2019). Such small organisms, especially microscopic ones, are not easy to track individually all along their aerial trajectories. However, as illustrated by some of the aforementioned references, they can be spotted in the atmosphere at some specific locations and times, or their origin and flow can be somewhat inferred using genetic data or isotopic profiles. Such information can then be associated to air‐mass trajectories reconstructed with existing software, for example, the HYSPLIT atmospheric transport and dispersion model (Stein et al., 2015), the TAPPAS living organism dispersal model, which is based on HYSPLIT (Durr et al., 2017), and other models providing complementary analysis capabilities (Pretorius et al., 2023; Schmale & Ross, 2015). These software are useful for punctual estimations of dispersal over several days. They can also be used to assess long‐term connectivity between distal areas as recently demonstrated by Pretorius et al. (2023), who identified attracting Lagrangian coherent structures (LCS) for invasive species and bushfire smoke between Australia and New Zealand (LCS resulting in predictable atmospheric pathways for such entities); see also Radici et al. (2022) for an illustration of long‐term and large scale connectivity assessment with HYSPLIT for a fungal plant pathogen. However, these software do not facilitate (for users with moderate programming skills) the analysis of cumulative patterns of recurring atmospheric movements for large spatial networks over extended periods. Estimating long‐term connectivity (e.g., over the entire cultural season of a given crop, or over several years) between many sites is key to understanding the spatial dynamics of populations over large scales (Leyronas et al., 2018), determining the likelihood of an air migration route (Pretorius et al., 2023; Radici et al., 2022; Zadoks, 1967), assessing the capacity of an epidemic to invade a fragmented space (Strona et al., 2017), or identifying sentinel points to be favored within the framework of epidemiological surveillance (Martinetti & Soubeyrand, 2019).

To reach these goals, one of the main challenges remains to be able to work with large networks of sites. The formalism of networks (or graphs) makes it possible to represent both the space through a set of nodes and the flows within this space by considering the links connecting the nodes. This formalism can be used to represent population dynamics or epidemics (Bajardi et al., 2011; Beaunée et al., 2015; Brooks et al., 2008; Hufnagel et al., 2004; Moslonka‐Lefebvre et al., 2011): network nodes may correspond to regions, sites or host units; network links, which may be quantitatively weighted and oriented, may depend on geographical distance (or its derivatives such as resistance and least‐cost distances, McRae, 2006; Picard et al., 2017), on trade flow, or on transport processes over land, air or sea. For airborne organisms, being able to infer a network, whose links would be weighted by the probabilities of atmospheric connection between sites, would offer the possibility of understanding and predicting dynamical spatial processes and species patterns across time, and to design relevant observation and control strategies (Morris et al., 2021). More or less simple frameworks for linking geographical sites using sequences of inferred movement of air masses have been recently proposed (Choufany, Martinetti, Senoussi, et al., 2021; Choufany, Martinetti, Soubeyrand, & Morris, 2021; Radici et al., 2022; M. Wang et al., 2021). The general idea consists of defining some target sites, computing sets of air‐mass trajectories arriving to or departing from these sites (with a software such as HYSPLIT), and calculating the frequency at which these trajectories go through distant sites (which may coincide with other target sites). A spatial tolerance (i.e., a spatial buffer) is generally accounted for in the definition of “go through”; properties of the air masses along their trajectories can be accounted for to weight the trajectories linking two sites (Radici et al., 2022); and properties of windborne particles (typically their mass and shape) can also be considered to assess their ability to stay in the air mass or to be deposited along its trajectory (M. Wang et al., 2021).

Grounded on the proposal made by Choufany, Martinetti, Senoussi, et al. (2021) and Choufany, Martinetti, Soubeyrand, and Morris (2021), on the HYSPLIT model and on gridded meteorological data archives, the new web application tropolink presented in this article allows the construction of geographical networks from trajectories of air masses corresponding to sites and time periods specified by the user. In the name tropolink, “tropo” stands for troposphere, which is the lower layer of the atmosphere (ranging from the ground to 6–18 km, depending on the latitude and the season) and the realm of transportation of organisms that is pertinent to their ecology, evolution and impact on the environment. In addition, “link” evokes the between‐site connectivity that we aim to evaluate. The architecture of tropolink is roughly illustrated by the simplified scheme provided in Figure 1, which describes the input (meteorological data archives, network structure and parameters), the output (air mass trajectories and connectivity matrices) and the mobilized tools (HYSPLIT as well as codes and notebooks for connectivity calculation and output exploration). tropolink allows the user to transparently use massive and global gridded meteorological data and perform intensive computation on a distant computer cluster. It also allows the user to explicitly explore calculated trajectories and connectivity matrices in jupyter notebooks with Python and R environments. The notebooks give a hand to the user to further investigate tropolink output on their own computation system.

Figure 1.

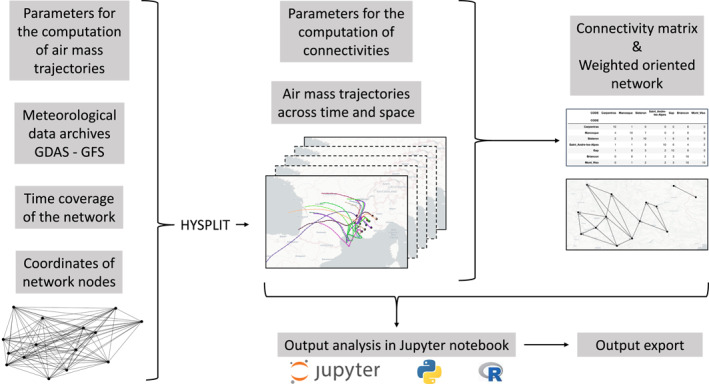
Simplified architecture of tropolink. After providing input parameters, dates, and node locations, HYSPLIT is executed using open meteorological data archives to generate sets of trajectories. Subsequently, connectivities between sites resulting from these trajectory sets can be computed by specifying connectivity parameters. Sets of trajectories and connectivities can then be explored within jupyter notebooks embedded in tropolink and exported for publication and in‐depth analysis.

In the following sections, we briefly describe the theoretical background underlying HYSPLIT and the computation of between‐site connectivity from sets of trajectories. We also present the steps the user must execute when using the web application, illustrate the analysis of trajectories and networks generated by tropolink, from local to continental scales, and discuss further development and usage of the web application. In the illustrations, we show how knowledge of geographical networks of air‐mass movement is pertinent to biological questions concerning the epidemiology of plant diseases and pests. We have chosen to apply tropolink to investigating potential dispersal of four pests, vectors and pathogens for which there is strong evidence for or interrogation about long distance aerial dissemination. The illustrations deal with (a) quantifying tropospheric connectivities between areas of production of sugar beet that are affected by yellows viruses transmitted by aphids, (b) exploring the relationship between tropospheric connectivities between distal populations of a plant pathogen and the epidemiological links between these populations inferred from genomic sequence data, (c) assessing the risk of long‐distance windborne spread of the fall armyworm (Spodoptera frugiperda), a destructive migratory pest that is currently expanding globally, and (d) computing the tropospheric connectivities along the (largely documented) Puccinia pathway in the USA situated at the 97° West longitude, along which wheat stem rust spores spread northward annually (Aylor, 2003).

2. Theoretical Background

From a modeling and mathematical viewpoint, tropolink relies on two main components, the reconstruction of air‐mass trajectories, and the computation of connectivity between network nodes grounded on (possibly large) sets of trajectories. The former component is obtained from the Hybrid Single‐Particle Lagrangian Integrated Trajectory model (HYSPLIT, Draxler & Hess, 1998; Stein et al., 2015) developed by the Air Resources Laboratory of the National Oceanic and Atmospheric Administration. The latter component is based on a recently developed framework for constructing networks from trajectory data (Choufany, Martinetti, Senoussi, et al., 2021). This section sketches the theoretical background of HYSPLIT and trajectory‐based networks. The reader who wants to skip this section only has to know that tropolink generates networks whose nodes are fixed and known and whose edges between nodes are calculated from trajectories of air masses occasionally connecting nodes: the directed edge from node A to node B is weighted by the number (or proportion) of daily trajectories simulated over a specified time period that start from (or arrive to) B and that go through A in a given time interval.

2.1. Reconstruction of Air‐Mass Trajectories

Equations and algorithms underlying HYSPLIT are described by Draxler and Hess (1997, 1998) and Stein et al. (2015) and the following section only presents the main elements of its trajectory compartment. In HYSPLIT, air‐mass trajectories are computed from time integrated advection in a Lagrangian framework, which requires the three‐dimensional velocity field. This input is obtained from gridded outputs of a meteorological model (namely and at least, horizontal wind components, temperature, height or pressure, and pressure at the surface), which are pre‐processed to be used in HYSPLIT. Pre‐processing includes the reconstruction and interpolation of 3D‐wind velocities at any height from the ground to the top layer that is considered using the meteorological model output. Interpolation is performed to re‐map data into a specific terrain‐following vertical coordinate system; See Rolph et al. (2017) who describe how terrain is taken into account, with an illustration in the online HYSPLIT Basic Tutorial: https://www.ready.noaa.gov/documents/Tutorial/html/traj_isob.html.

Once the 3D‐velocity field V = (U, V, W) has been processed and interpolated to the internal model grid, HYSPLIT implements the advection in two stages: the position at time t of an air mass, say P(t), is transformed into a first‐guess position P′(t + Δt) after a duration Δt using the following equation:

$$P^{\prime }(t+\mathrm{\Delta }t)=P(t)+\mathbf{V}(P,t)\mathrm{\Delta }t,$$

then the final value of the position at time t + Δt is given by:

$$P(t+\mathrm{\Delta }t)=P(t)+\frac{1}{2}\left\{\mathbf{V}(P,t)+\mathbf{V}\left(P^{\prime },t+\mathrm{\Delta }t\right)\right\}\mathrm{\Delta }t.$$

The integration time step Δt can vary along the computation of the trajectory and is computed from the requirement that the advection distance per time‐step should be less than 0.75 of the meteorological grid spacing. The variable nature of Δt requires to interpolate V at the positions P(t) and P′(t + Δt), which is performed in a linear way. Trajectories are terminated if they exit the top layer considered in the model, but advection continues along the surface if the trajectories intersect the ground.

2.2. Trajectory‐Based Networks

Spatial and spatio‐temporal networks generated from tropolink have fixed and known nodes typically consisting of fixed‐radius circles around a set of geographical sites as well as directed edges weighted by a connectivity measure grounded on the movement of air masses during the time period of interest. The connectivity measure is derived from the work of Choufany, Martinetti, Senoussi, et al. (2021) as described below.

Consider two spatial domains A and B at the surface of the Earth (i.e., two sets of latitudes‐longitudes) and a period of time T, eventually made of disjoint temporal intervals. Choufany, Martinetti, Senoussi, et al. (2021, Definition 2.3) defines the δ‐lag directed connectivity from A to B over T by:

$${\mathrm{\Psi }}_{\delta ,\nu }^{(2)}(A\to B,T)={\int }_{T\times B}\psi \left(A|s+\delta ,s,x\right)\nu (ds,dx),$$ (1)

where ν(ds, dx) is a probability measure on T × B, δ is a time lag (positive or negative), and ψ is a scalar operator called pointwise connectivity (see Definition 2.2 in Choufany, Martinetti, Senoussi, et al. (2021)). A simple interpretable form of Equation 1 is obtained when ν is the Lebesgue measure ν(ds, dx) = ds × dx, and ψ is the binary function indicating whether the trajectory Γ(s + δ, s, x) of the air mass located at x at time s went through A between s and s + δ. If δ > 0, the trajectory is forward in time (it starts at x at time s and we consider it up to time s + δ > s). If δ < 0, the trajectory is backward in time (it arrives at x at time s and we consider it since time s + δ < s). Hence, Equation 1 becomes:

$${\mathrm{\Psi }}_{\delta ,\nu }^{(2)}(A\to B,T)={\int }_{T\times B}\mathbb{1}(A\cap \mathrm{\Gamma }(s+\delta ,s,x)\ne \varnothing )dsdx,$$ (2)

where $\mathbb{1}(E)=1$ if the event E is true, $\mathbb{1}(E)=0$ otherwise. Equation 2 can be interpreted as the frequency of passage through A of trajectories of duration |δ|. If one approximates this integral by taking only the centroid of B, say ${\overline{x}}_B$, and only one time per day over T, for example, 12:00 UTC (assuming that T is the union of a set of whole days), one obtains the following estimate of Equation 2:

$${\widehat{\mathrm{\Psi }}}_{\delta ,\nu }^{(2)}(A\to B,T)=\frac{|T\Vert B|}{n_T}\sum _{i=1}^{n_T}\mathbb{1}\left(A\cap \mathrm{\Gamma }\left(s_i+\delta ,s_i,{\overline{x}}_B\right)\ne \varnothing \right),$$ (3)

where n _T is the number of days in T, s _i is the unique time taken for the ith day in T, |T|, and |B| are the length and area of T and B, respectively. Hence, Equation 3 is simply the proportion of sampled trajectories intersecting A, multiplied by |T‖B|. In the applications, we set |T‖B| = 1 for facilitating the interpretation of results.

3. Tropolink Workflow

The tropolink workflow can be summarized in four steps illustrated by Figure 2 and detailed in this section. Texts S1 and S2 in Supporting Information S1 respectively give a step‐by‐step description of the use of the application and technical details of its development.

Figure 2.

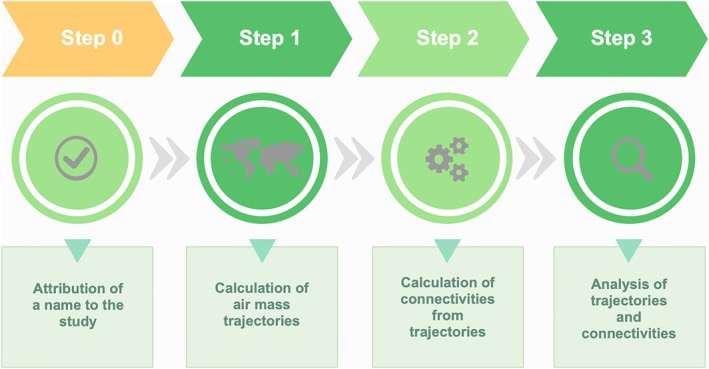
Workflow concept of tropolink.

3.1. Step 0: Attribution of Study Name

As a preliminary step, the user is prompted to give a name and description to the study they want to carry out. The name will be used to identify the set of trajectories to be computed. The name extended by an underscore and a number will be used to identify each connectivity calculation to be carried out based on the aforementioned set of trajectories.

3.2. Step 1: Trajectory Calculation

In step 1, the user provides input information consisting of the set of dates at which trajectories and connectivities have to be computed (T in Section 2.2), the geographical sites forming the nodes of the network (${\overline{x}}_B$ in Section 2.2), and parameters used for HYSPLIT tuning. These input are provided by the user by filling out a form embedded in the web application. In this form, temporal and spatial information can be provided as external files in an application‐specific format (text files with specific characteristics grounded on ISO standards). Popup windows indicate the format to be used for each field‐of‐the‐form/file when necessary.

Concerning the parameters used for HYSPLIT tuning, namely “trajectory duration” (with negative or positive value for backward or forward trajectories, respectively), “starting/arrival hour,” “top of model domain,” and “vertical motion method,” the help page refers the user to the original and complete documentation of HYSPLIT. Once these four parameters are provided, the use of HYSPLIT is transparent: the software and wrapper codes as well as input meteorological data are on distant data storage and computer cluster queried by the web application tropolink. Input meteorological data that are used by tropolink (and HYSPLIT) are global and cover the period from September 2007 to present. They are extracted from the Global Data Assimilation System half‐degree archive from September 2007 to June 2019, and from the Global Forecast System quarter‐degree archive from June 2019 (https://www.ready.noaa.gov/archives.php).

The current version of tropolink uses the version v4.2.0 of HYSPLIT in compliance with its End‐User License Agreement (Draxler & Rolph, 2010; Rolph et al., 2017). This version is installed on a Slurm‐based computer cluster (version 22.05.2) operated with the Debian GNU/Linux 10.03 (Buster) system and administered by the INRAE BioSP research unit.

From a biological perspective, the tuning of trajectory calculations must be performed in a manner that aligns, whenever possible, with the properties or behavior of the organism transported by air mass movements. For example, the typical takeoff time of the insect or particle of interest may serve as the starting point for trajectory calculations. The selected dates for trajectory calculations may coincide with favorable weather conditions for insect or spore takeoff, while the specified locations may correspond to areas featuring high densities of host habitats. Further discussion on this point can be found in Section 5.

3.3. Step 2: Connectivity Calculation

Once trajectories of air masses have been calculated, the user can select the corresponding study, parameterize the connectivity calculation by selecting a type of buffer around nodes and a buffer radius, and run the connectivity calculation. The selection of a buffer around nodes allows the user to specify a spatial tolerance in the computation of the frequency of trajectories arriving at (or departing from) a given node that go through another node or, more precisely, that go through a buffer zone around this node. The buffer can be “circular” (actually, a spherical cap), that is, it contains all points at a geographical distance lower than a specified radius (up to 100 km). It can also correspond to a latitude‐longitude geographical sector centered around the node with half angle to be specified (up to 2°). Moreover, the user can select a subset of dates and locations for which connectivities have to be calculated. The specification of a connectivity calculation can be provided as a json file instead of filling each element of the form.

3.4. Step 3: Jupyter Notebooks

The last step of the tropolink workflow allows the user to perform a first analysis of computed air‐mass trajectories and connectivities in a preconfigured Jupyter environment. The application offers two Jupyter notebooks: the first one is based on a Python kernel; the second one is based on a Python kernel with rpy2 Python package allowing the user to enrich the notebook with R commands. These notebooks show some more or less basic commands to help the users to launch their analyses on their own computer system. In particular, the user can download, in the notebooks, data frames containing trajectory or connectivity data with an easy‐to‐use format in Python or R, plot air mass trajectories with a background map, and display connectivity matrices as oriented networks.

3.5. Additional Features

The application contains a dashboard with a list of the user's studies. This list gives the status of each calculation (in progress, succeeded or failed), it gives access to the specifications for each calculation, which can be downloaded in a json format (for re‐use, modification and sharing), as well as calculation outputs (either trajectories or connectivity matrices).

In addition, tropolink includes a help‐tab complementing information provided by popup windows as well as a tab with credits.

4. Applications

4.1. Estimating Airborne Connectivity Between Areas of Production of Sugar Beet

Here, we present a typical example of estimation of a connectivity matrix that could be used, for instance, as an input for a disease propagation model or in comparative studies of putative influencing factors.

Sugar beet yellowing is caused by several viruses whose main vectors are aphids. Aphids can be transported by air masses over long distances and an important question concerns the contribution of air mass movement to the regional circulation of the aphids and/or the disease with respect to other factors, including more local factors that are known to play a role in aphid and disease dynamics (e.g., see Qi et al. (2004), for the role of winter temperature). Here, we do not address this question beyond the scope of this article, but we aim to assess how spatially heterogeneous the tropospheric connectivity between different production areas of sugar beet is.

Thus, using tropolink, we computed connectivity between 40 production areas, which were identified with a standard hierarchical clustering method (namely the default method implemented in the hclust function in R) applied to the coordinates of 621 sugar beet fields in France; see Figure S1 in Supporting Information S1. These fields, whose locations were provided by ITB (https://www.itbfr.org/) and which were monitored from 2017 to 2021, are considered here to form a representative sample of sugar beet crops in central and northern France. Connectivities between the 40 production areas were inferred from data covering all dates in April from 2013 to 2022, using tropolink with tuning features given by Table 1 and justified in Text S3 in Supporting Information S1.

Table 1.

Specifications of tropolink for Running the Examples About Sugar Beet, Potyvirus, Fall Armyworm (FAW), and Puccinia Pathway

	Sugar beet	Potyvirus	FAW	Puccinia
Dates	Each day of April over 2013–2022	Each day of month m in 2014, for m from January to December	Each day of May–September over 2013–2022	Each day of April–July over 2019–2023
Number of locations	40	27	2,365	20
Longitude extent	(0.3°, 4.4°)	(4.57°, 5.08°)	(−25°, 55°)	−97°
Latitude extent	(46.0°, 51.0°)	(43.63°, 43.73°)	(10°, 50°)	(29°, 48°)
Starting/arrival altitude (m)	500	500	1,000	200
Trajectory duration (hr)	3	−3	12	48
Starting/arrival hour (hr UTC)	14	14	20	17
Top of model domain (m)	10,000	10,000	15,000	10,000
Vertical motion method	Meteorological model's vertical velocity fields
Buffer type	Circular	Circular	Geographic	Circular
Buffer radius	23 km	1 km	0.5°	25 km

The distribution of connectivities shows a large proportion of weak values, most of them corresponding to very distant production areas, and the maximum connectivity is almost 0.4; see Figure 3. Changing the starting altitude of trajectories (either 250 or 750 m instead of 500 m) approximately leads to similar connectivity values. Figure 4 gives an example of forward trajectories obtained for a given date, namely 09 April 2013, and displays the main edges of the network generated by trajectories computed over a set of 300 dates specified in Table 1. When only edges with connectivities larger than 0.15 are shown, we mostly observe diagonal links South‐West–North‐East (SW‐NE) in both directions. We observe a similar pattern when only edges with connectivities larger than 0.05 and lengths larger than 80 km are shown. These observations suggest that an eventual epidemiological dynamics dependent on the tropospheric network may display elongated SW‐NE‐diagonal shapes.

Figure 3.

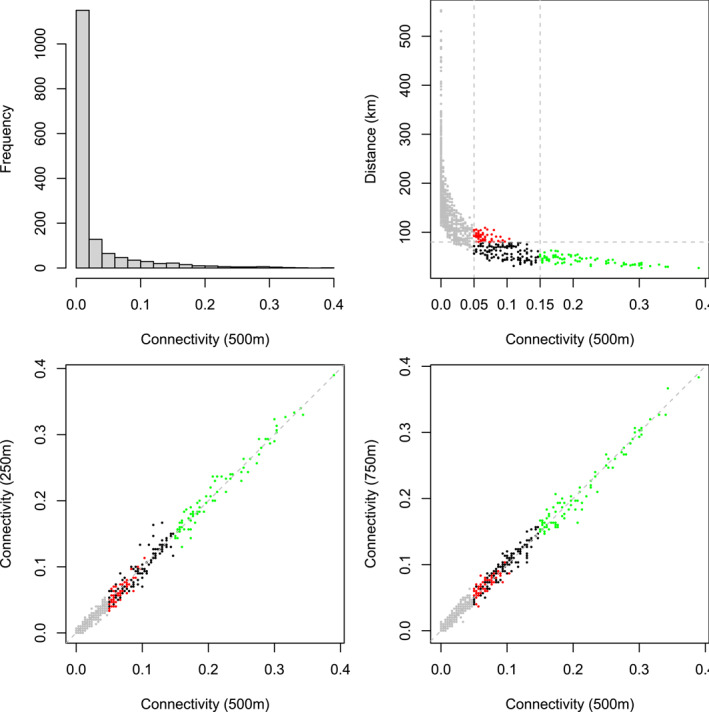
Sugar beet application: Distribution of non‐diagonal connectivities based on trajectories starting at 500 m, say ${\widehat{\mathrm{\Psi }}}_{500}^{(2)}$ (top left); Geographical distance versus ${\widehat{\mathrm{\Psi }}}_{500}^{(2)}$ (top right); ${\widehat{\mathrm{\Psi }}}_{250}^{(2)}$ versus ${\widehat{\mathrm{\Psi }}}_{500}^{(2)}$ (bottom left), and ${\widehat{\mathrm{\Psi }}}_{750}^{(2)}$ versus ${\widehat{\mathrm{\Psi }}}_{500}^{(2)}$ (bottom right). Red points: connectivities in ${\widehat{\mathrm{\Psi }}}_{500}^{(2)}$ larger than 0.05 and geographical distances larger than 80 km; Green points: connectivities larger than 0.15; Black points: connectivities between 0.05 and 0.15 and geographical distances lower than 80 km; and Gray points: connectivities lower than 0.05.

Figure 4.

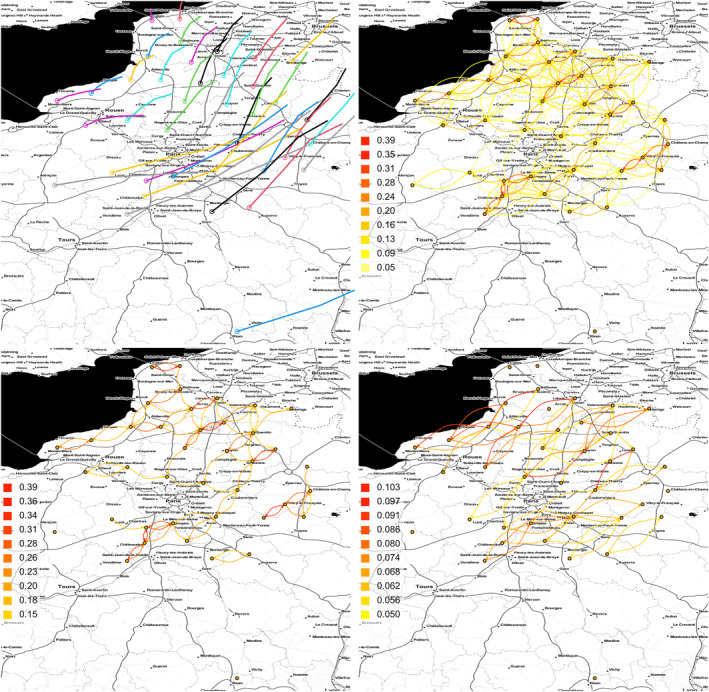
Sugar beet application: trajectories computed on 09 April 2013 (top left); network edges corresponding to connectivities larger than 0.05 (top right), to connectivities larger than 0.15 (bottom left), and to connectivities larger than 0.05 and lengths larger than 80 km (bottom right).

4.2. Investigating Drivers of Epidemiological Links

The second example consists of estimating a connectivity matrix based on air mass movement and assessing whether or not it matches a matrix of epidemiological links grounded on genetic information.

Alamil et al. (2019a) analyzed genomic data to assess epidemiological links within a pathogen metapopulation. The pathogen, a potyvirus, was sampled in 2014 from wild host plants (Tragopogon pratensis) located in 27 patches within a 40 × 10 km area in south‐eastern France. The epidemiological links between the 27 pathogen populations were inferred with the SLAFEEL approach (Alamil et al., 2019a, 2019b) and are displayed in Figure 5, top panel. The potyvirus is transmitted by aphids that, as in the example above, may be transported by wind over relatively long‐distance. Hence, one of the hypotheses possibly underlying the spatial structure of the potyvirus genetics (measured by the epidemiological links inferred with SLAFEEL) is that patches frequently connected by wind contain close genetic variants of this virus. Several other hypotheses have been proposed by Alamil et al. (2019a) including environmental conditions as well as host demography and genetics at the level of each patch. Here, we aim to assess whether or not epidemiological links and tropospheric connectivities coincide, at least partially.

Figure 5.

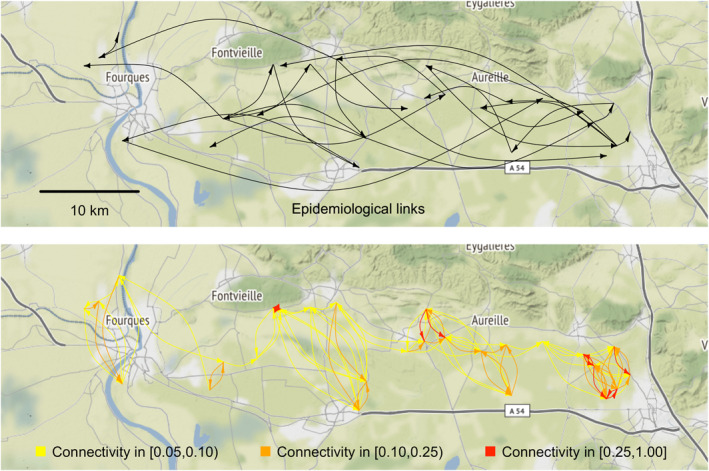
Application of air mass connectivity to potyvirus epidemiology: Epidemiological links between the 27 potyvirus populations inferred by Alamil et al. (2019a) from genomic data (top panel; the links are oriented from the main putative sources for each population), and tropospheric connectivities obtained from tropolink for the whole year 2014 (bottom panel; connectivities lower than 0.05 are not plotted).

In this aim, connectivities were inferred using tropolink applied to the 27 patches. A connectivity matrix was obtained for each month of the year 2014 during which genetic data were collected (tuning features are provided in Table 1 and justified in Text S3 in Supporting Information S1), and a global connectivity matrix was obtained for the whole year 2014. Given the weak spatial resolution of meteorological data at the spatial scale considered here, the trajectories computed by HYSPLIT (and tropolink) mainly provide an indication of the dominant wind direction at each specified date; see Figure S2 in Supporting Information S1.

For the study area considered in this example, we notice a moderate variation of connectivity across the months of the year: the correlation between monthly connectivity matrices (without diagonal terms) ranges between 0.85 and 0.95; Figure S3 in Supporting Information S1 shows how the 12 months of the year are clustered in a relatively consistent manner with respect to the seasons. Figure 5, bottom panel, represents the tropospheric network obtained for the whole year 2014 (only connectivities larger than 0.05 are plotted). To assess the relationship between the matrices of epidemiological links and tropospheric connectivities, we computed the correlation ρ of non‐diagonal terms and we compared it to the correlations ρ* obtained by permuting 10⁴ times the rows of the matrix of epidemiological links (permuting the rows of this matrix means that the vectors of putative sources are switched between the virus populations). This permutation approach allowed us to compute a p‐value given by the proportion of correlations ρ* larger than or equal to ρ. Figure 6 shows that the p‐value is relatively large, either when considering monthly connectivities, whatever the month, or the annual connectivities. P‐values are weaker for June, July, and August, but remain above the classical 0.05 significance level (the network obtained for August leading to the lowest monthly p‐value is shown in Figure S4 in Supporting Information S1). We computed a similar p‐value grounded on the correlation between the matrices of epidemiological links and geographical distances. Here, the p‐value is the proportion of correlations ρ* lower than or equal to ρ (because under the alternative hypothesis, epidemiological links and geographical distances are negatively correlated). The small p‐value (namely 0.02) obtained in this case suggests that epidemiological links and geographical distances are negatively correlated, whereas an eventual relationship between epidemiological links and tropospheric connectivities is not significant based on available data. More data should be collected to test with a larger power an eventual link with air mass connectivities in summer.

Figure 6.

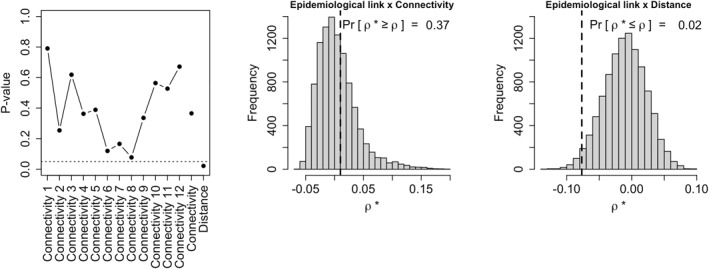
Application of air mass connectivity to potyvirus epidemiology: P‐values for testing the absence of relationship between epidemiological links and either monthly connectivities (from month 1, i.e., January, to month 12, i.e., December), annual connectivities or geographical distances (left); Distribution of the correlation ρ* between permuted epidemiological links and annual connectivities (center), the value ρ obtained without permutation is given by the dashed line; Distribution of the correlation ρ* between permuted epidemiological links and geographical distances (right), the value ρ obtained without permutation is given by the dashed line.

4.3. Assessing the Risk of Long‐Distance Spread of Fall Armyworm

In this example, we compute a connectivity matrix at a larger spatial scale than those considered in the two previous examples, and use it to assess a component of the invasion risk of a crop pest.

The fall armyworm (FAW, S. frugiperda) is a migratory pest insect, which is in a phase of invasion at the global scale, with recently newly colonized territories in Asia and Africa (Early et al., 2018). FAW larvae may be disseminated via the trade of vegetables and fruits, but the adults may also spread with air masses over long distances, typically during nights (Westbrook et al., 2016; Wu et al., 2022). Currently, an important issue concerns the evaluation of the risk of expansion of FAW in northern Africa and Europe. Here, we want to estimate which FAW‐free areas in these regions could be reached given the flight capabilities of FAW and the areas that it presently occupies.

Thus, we computed tropospheric connectivity across a spatial grid covering land at latitudes from Burkina Faso to France (10°–50°N) and longitudes from Cabo Verde to Saudi Arabia (−25°–55°E). Tuning features used to apply tropolink are provided in Table 1 and justified in Text S3 in Supporting Information S1. Typical trajectories at a given date are displayed in Figure S5 in Supporting Information S1. The connectivity matrix and the vector of FAW presence/pseudo‐absence (considered over the same 1°‐resolution) were multiplied (with the matrix product) to estimate a heatmap measuring the risk of long distance dispersal from occupied areas. FAW presence/pseudo‐absence was derived from data extracted from the FAMEWS data base provided by the Food and Agriculture Organization (FAO) and centralizing crowd‐sourcing observations of the fall armyworm (using two sampling approaches: traps and scouting). In this data base, only data with latitudes and longitudes falling within the borders of the indicated countries were kept to build the vector of presence/pseudo‐absence (i.e., >65,000 observations between 01 January 2018 and 10 April 2023; 47% of observed presence for traps, 72% for scouting). FAW is considered to be present in a grid node if at least one observation of FAW was made over the 2018–2023 sampling period; see Figure 7. FAW is considered as absent in the other grid nodes (either without sampling or with sampling but without FAW observation), but this absence is viewed as a pseudo‐absence since FAW might be at densities under the detection threshold in areas covered by the surveillance and might be present in unsampled areas (if Europe is actually considered as FAW‐free, some unsampled territories in Africa and western Asia might be occupied by FAW).

Figure 7.

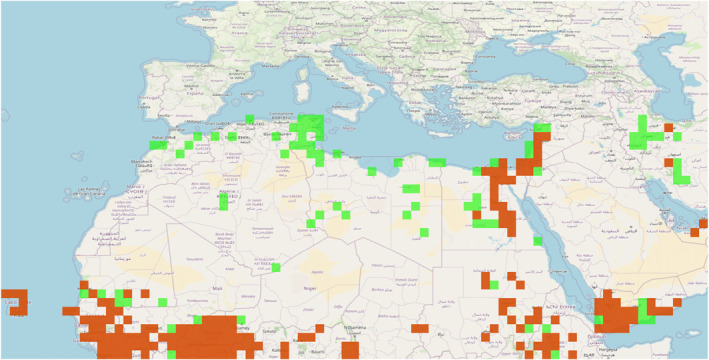
Fall armyworm (FAW) application: Spatial distribution of FAW presence (red grid nodes) and absence (green grid nodes) based on the Food and Agriculture Organization data base with records up to 10 April 2023.

The heatmap that is shown in Figure 8 allows us to identify areas at risk of long‐distance dispersal based on the partial current knowledge of FAW spatial distribution. We observe in particular some connections between already occupied areas, for example, between continental western Africa and Cabo Verde archipelago, and possible migration across seas (e.g., across the eastern Mediterranean and the southern Red Sea).

Figure 8.

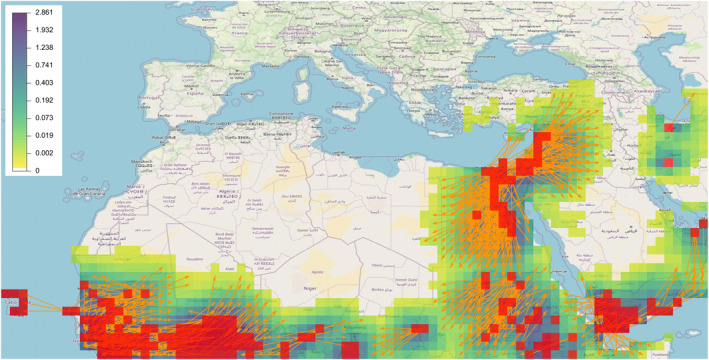
Fall armyworm (FAW) application: Heatmap (color palette from white to purple) corresponding to the matrix product between the connectivity matrix and the vector of FAW presence/pseudo‐absence based on Food and Agriculture Organization (FAO) data. Red grid nodes: areas where FAW is present based on the FAO data base. Orange arrows: Connectivities between distant grid nodes that are larger than 0.001 (connection at least 1 day over 1,000) and longer than 500 km.

4.4. Evaluating Connectivities Along a Recurrent Migration Pathway

In this example, we compute a connectivity matrix to partially characterize a recurrent migration route of an airborne plant pathogen that has already been thoroughly studied.

Several fungus pathways, described as predictable routes for the recolonization of plant fungal pathogens on the basis of host availability, prevailing seasonal winds and favorable weather conditions, have been especially identified in the USA, India, China and Europe (Brown & Hovmøller, 2002). One such pathway has been pinpointed for the stem rust of wheat caused by Puccinia graminis along the 97° West longitude (Aylor, 2003; Hamilton & Stakman, 1967). In this pathway, urediniospores produced by P. graminis lesions overwinter in the southern USA and northern Mexico and are subsequently transported northward from April to July, allowing the infection of progressively planted wheat from Texas to North Dakota (Hamilton & Stakman, 1967). Here, we aim to quantify the prevalence level of northward winds along the 97° West longitude during the observed migration period (thus refining the long‐standing knowledge that northward winds prevail in summer; Ward, 1916).

To accomplish this, we utilize tropolink to calculate tropospheric connectivity among 20 sites displayed in Figure 9, which also shows an example of air‐mass trajectories obtained for a specific date. The parameters used to configure tropolink for this case study are detailed in Table 1, with justifications provided in Text S3 in Supporting Information S1. The resulting connectivity matrix is presented in Figure 9. Notably, this matrix reveals that northward connections occur approximately four times more frequently than southward connections. Indeed, on average, there are 416.5 monthly connections from every sites to northern sites, whereas this average drops to 96.2 for connections to southern sites. Figure S6 in Supporting Information S1 shows that this predominance of northward connections remains consistent when we reduce the buffer radius around the sites used in the connectivity calculation from 25 to 10 km.

Figure 9.

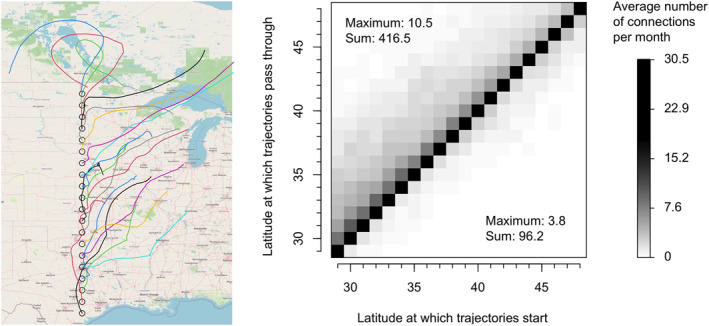
Puccinia pathway application: trajectories computed on 20 June 2020 for sites (circles) located along the 97° West longitude (left) and representation of the connectivity matrix (right). Connectivity is expressed in terms of average number of pairwise connections per month, whose theoretical maximum value is 30.5, that is, the mean number of days per month over the study period. Numbers within the plot on the right‐hand‐side give the maximum and the sum (averaged over 1 month) of northward connections (top left) and southward connections (bottom right).

5. Discussion

The computation of spatial connectivities generated by air‐mass movement and the resulting geographical networks offers new possibilities to test and explore the links between the atmosphere and biological systems with components that are disseminated via the air (Choufany, Martinetti, Senoussi, et al., 2021; Choufany, Martinetti, Soubeyrand, & Morris, 2021; Leyronas et al., 2018; Pretorius et al., 2023; Radici et al., 2022; M. Wang et al., 2021; J. Wang et al., 2023). The tropolink web application precisely contributes to this objective: it facilitates the computation of air mass trajectories and the resulting connectivity matrix for a network of sites, which relies on relatively complex software and massive data for non‐specialist scientists. It should enable users to address a variety of questions related to invasion risks and spatio‐temporal demo‐genetic structures of populations, as well as to handle different spatial and temporal scales and varying numbers of network nodes, as exemplified by the scenarios explored in this article. However, it is important to note that other modeling approaches may be more suitable for describing and predicting the transport of plant pathogens and pests at specific scales, for particular organisms and to test particular hypotheses (Clobert et al., 2012; Jeger et al., 2007; Kenkre & Giuggioli, 2021; Nathan et al., 2011; Schmale & Ross, 2015). The aforementioned examples concern plant pests and diseases, but our approach can be used to generate connectivity data for diverse application domains: for example, the dispersal from identified sources of pollen, dust, radioactive elements, smokes, and other pollutants; see references in the introduction. For such particles, often playing the role of contaminants and xenobiotics, a significant challenge lies in predicting their dispersal locations and magnitudes at various scales (Committee of the Significance of International Transport of Air Pollutants, 2010; Kim et al., 2014; Reisen et al., 2015). In this context, tropolink can be applied to forecast spatial patterns related to long‐term exposure risks, utilizing estimated tropospheric connectivities originating from pollutant sources. We mentioned above the practical aspects of tropolink for the non‐specialist user. In addition, in terms of computation time, if the 40‐cores computer cluster dedicated to tropolink is fully available, a trajectory computation with 30 dates, 40 network nodes distributed in a 500 × 500 km box and 3 hr trajectory duration takes about 3 min. A trajectory computation with around 1,500 dates, 2,300 network nodes distributed in a 5,000 × 5,000 km box and 12 hr trajectory duration takes about 3 hr. The connectivity computation for the latter trajectory study takes about 3 hr 30 min.

Concerning the examples presented above, only preliminary analyses were performed in this article. It would be of particular interest to assess whether the connectivity pattern inferred in the sugar beet application could influence the correlation structure of yellowing disease epidemics in distant production areas, or correlates with the spatial distributions of either the viruses causing the disease or the aphids transmitting the viruses. The latter task could be accomplished by utilizing data generated from long‐term suction trap networks designed to collect migratory aphids (Bell et al., 2015; Lagos‐Kutz et al., 2020). Such an approach could complement current endeavors aimed at modeling and predicting the dynamics of aphids responsible for the spread of sugar beet yellowing disease (Luquet et al., 2023). Furthermore, we could employ the geographical network that we have inferred to design sampling schemes encompassing contrasting situations in terms of connectivity strength. This would allow us to test hypotheses related to aphid transport in relation to their biology with higher statistical power than with a naive sampling scheme. For the potyvirus application, additional data should be collected to increase the power of the test of an eventual relationship between epidemiological links and tropospheric connectivities in summer, as suggested in Section 4.2. Moreover, other measures of epidemiological links between populations derived from genetic distances (Alamil et al., 2022) may be proposed and analyzed with respect to the connectivity patterns provided by tropolink to detect an eventual signature of the inter‐population spread of aphids on the virus dynamics. Regarding the Puccinia pathway, the quantitative information provided by tropolink can allow us to measure how much and where winds prevail over multiple years or for different years. This information can be used to assess whether the annual variations in propagation speed along a pathway, as described by Hamilton and Stakman (1967), are correlated with changes in annual tropospheric connectivity, in addition to fluctuations in host availability and weather conditions. It is also worth exploring whether prevailing winds are a necessary condition or if even minor yet significant winds could be sufficient. This investigation may be pursued by revisiting with tropolink the various plant pathogen pathways reported from around the world (Brown & Hovmøller, 2002; Meyer et al., 2017; Radici et al., 2022; Saubin et al., 2023). For the FAW application, the heatmap is a tool for orientating the surveillance of FAW when one accounts for its natural ability to disperse (note that the surveillance strategy must also depend on other factors, e.g., the risk of introduction with trade of goods). Such a map, crossed with maps of crop sensitivity to FAW larvae and climate‐suitability for FAW (J. Wang et al., 2023), may be used to inform the sampling strategies with the aims of (a) delineating the actual spatial distribution of the pest and (b) enhancing the surveillance in pest‐free areas.

Aim (a) (delineating the actual spatial distribution of the pest) is illustrated by the case of Cyprus and Türkiye: these countries do not use the voluntary FAW monitoring tool provided by FAO, resulting in the absence of FAW observations in the FAMEWS data base. Nevertheless, countries must report presence of invasive pests such as FAW to global and regional plant protection organizations such as the International plant Protection Convention and the European and Mediterranean Plant Protection Organization (EPPO). Thus, a recent map of the EPPO indicates that the pest is present in Cyprus and Türkiye (see Figure S7 in Supporting Information S1): FAW was detected for the first time in early 2023 in the Limassol district, Cyprus (EPPO Reporting Service no. 02/2023, Num. Article: 2023/034), and in 2022 in the Adana province, Türkiye (Pehli̇van & Atakan, 2022). Cyprus and the South of Türkiye are precisely possible arrival points of FAW based on our heatmap, with a possible long‐distance origin from northern Egypt. Hence, our heatmap may be used to orientate surveillance of FAW in the aim of improving the delineation of the FAW distribution based on the voluntary data points provided by countries. Note however that FAW is also present in Canary Islands based on EPPO data (EPPO Reporting Service no. 03/2021 Num. Article: 2021/053), whereas this territory is not highlighted by our heatmap. FAW possibly arrived in Canary Islands with trade of goods (Cock et al., 2017; Plateforme ESV, 2022), via flights of adults during several successive nights (Westbrook et al., 2016), or from an area currently supposed to be FAW‐free but which is not.

Aim (b) (enhancing the surveillance in pest‐free areas) is illustrated by the hypothetical case displayed in Figure 10. In this example, we added nine grid nodes where FAW is present based on EPPO data (namely in Cyprus, Türkiye, and Canary Islands) and two grid nodes where FAW is hypothetically present in Morocco and Tunisia, and we assessed the risk of long distance spread. The inclusion of Morocco and Tunisia is purely hypothetical: FAW has not been reported there through any channel we know of, neither through FAO nor through any regional/global plant protection organization. The presence of FAW in Cyprus and Türkiye increases the risk area in Türkiye and generates a possible dispersal toward the North‐East of the Black Sea. The presence of FAW in Canary Islands generates a risk of dispersal to Western Sahara. In addition, if FAW were present in northern Morocco (resp. northern Tunisia), this would pose a new risk of introduction into southern Spain and Portugal (resp. Italy and Corsica), which should be taken into account to guide surveillance in Europe. Beyond surveillance objectives, the connectivities from occupied areas to pest‐free areas may be used to target likely source populations of FAW and assess the adaptive potential of these populations to the pest‐free areas under focus (Estoup et al., 2016).

Figure 10.

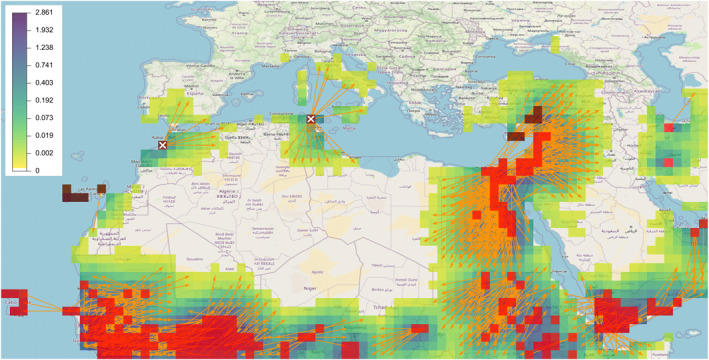
Fall armyworm (FAW) application: Hypothetical heatmap (color palette from white to purple) corresponding to the matrix product between the connectivity matrix and the vector of FAW presence/pseudo‐absence based on Food and Agriculture Organization (FAO) and European and Mediterranean Plant Protection Organization (EPPO) data augmented by two hypothetical grid nodes of FAW presence. Red grid nodes: areas where FAW is present based on the FAO data base. Brown grid nodes: areas where FAW is present based on the EPPO data. Brown grid nodes with white crosses: hypothetical presence of FAW in Morocco and Tunisia, which are actually FAW‐free areas. Orange arrows: Connectivities between distant grid nodes that are larger than 0.001 (connection at least 1 day over 1,000) and longer than 500 km.

In order to advance our ambition of guiding surveillance efforts and enhancing the biosecurity of crops in relation to migrating airborne pathogens and pests, tropolink could contribute to pipelines predicting probable future occupied areas. Such pipelines and accompanying web‐based interactive tools for visualization have already been developed in the USA, particularly for soybean rust (https://soybean.ipmpipe.org/soybeanrust/, Isard et al., 2011) and cucurbit downy mildew (https://cdm.ipmpipe.org/, Ojiambo et al., 2011). Two potential solutions for including tropolink in such pipelines could be explored. First, we can determine the likely locations where an invasive species may be detected if it follows recent air‐mass movements from already occupied areas. This could involve utilizing connectivities calculated by tropolink over the last N days, with the specific value of N depending on the context. Second, we can identify areas that should be monitored in the near future by predicting probable future air‐mass movements from occupied regions. The second solution can be implemented in several ways. One approach is to employ forecast meteorological data sets that HYSPLIT can use instead of archived meteorological data. These forecast data set. allow for predictions ranging from 1 to 10 days, depending on the specific data set used. Alternatively, we can use connectivities calculated from historical data for the relevant period of interest (Choufany, Martinetti, Senoussi, et al., 2021; Choufany, Martinetti, Soubeyrand, & Morris, 2021, shown a certain stability of monthly connectivities across years, suggesting that connectivity is predictable based on past data).

To conclude, we discuss possible improvements of tropolink. This web application is grounded on meteorological data with 0.50°‐resolution in latitude and longitude from September 2007 to June 2019, 0.25° from June 2019. If the resolution of these data may somewhat be considered as insufficient, they present the clear advantage of covering all the regions of the Earth. A future version of tropolink may exploit higher‐resolution data available in certain parts of the world and compatible with HYSPLIT (Hernández‐Ceballos et al., 2014). Concerning the uncertainty in air‐mass trajectories, it can be presently taken into account by considering trajectory ensembles (Rolph et al., 2017), that is to say by noising the initial conditions (i.e., starting/arrival locations, times, and altitudes of trajectories) specified by the user (as we did in a very simple way in the sugar beet application where we computed connectivities for three starting altitudes). For further developing tropolink we may, (a) complement the options consisting of specifying a circular or geographic buffer around network nodes by considering flexible polygons provided by the user (Choufany, Martinetti, Senoussi, et al., 2021). We may also (b) combine variables associated to the computation of air mass trajectories (e.g., the altitude of the air mass along its trajectory, its temperature, its humidity, the level of solar radiation…), land‐use maps, and properties/behaviors of particles/insects (e.g., their shapes, their mass, their behavior with respect to the air mass conditions, their host preferences; Aylor, 2017; Isard & Gage, 2001) for weighting the trajectory contributions to connectivities and especially evaluating the likelihood of particle/insects release and deposition (Choufany, Martinetti, Senoussi, et al., 2021; Radici et al., 2022; M. Wang et al., 2021). We may also (c) generate archives incorporating tropolink specifications and outputs as well as associated metadata for facilitating the sharing of these data on public data repositories, and (d) offer the possibility to the users to share their studies directly within the application (e.g., a user could retrieve a trajectory study from another user and calculate new connectivities), as well as to merge trajectory studies and to split them, in particular to save computation costs. R codes prefiguring some of these perspectives (trajectory ensembles and weighted connectivities) are available in the wiki of the application as vignettes (https://forgemia.inra.fr/tropo-group/tropolink/-/wikis/Examples). We expect that the list of vignettes in the wiki will be enriched by the tropolink user community to share ideas for analyzes in R, Python and any other relevant language.

Conflict of Interest

The authors declare no conflicts of interest relevant to this study.

Supporting information

Supporting Information S1

Richard, H. , Martinetti, D. , Lercier, D. , Fouillat, Y. , Hadi, B. , Elkahky, M. , et al. (2023). Computing geographical networks generated by air‐mass movement. GeoHealth, 7, e2023GH000885. 10.1029/2023GH000885

Data Availability Statement

Trajectory and connectivity data generated for the preparation of this article, as well as the corresponding specifications (node coordinates, dates, and other tropolink options), are available in the public repository Zenodo (Soubeyrand, 2023). Potyvirus genetic data are also available from Zenodo (Alamil et al., 2019b) and FAW data are available from the FAMEWS global platform of the FAO (FAO, 2023).

Software availability statement: The web application tropolink is free but requires a login and a password that can be requested from the software wiki whose link is provided in the reference list (Richard et al., 2023).