Reduced Deep Convolutional Activation Features (R-DeCAF) in Histopathology Images to Improve the Classification Performance for Breast Cancer Diagnosis

Abstract

Breast cancer is the second most common cancer among women worldwide, and the diagnosis by pathologists is a time-consuming procedure and subjective. Computer-aided diagnosis frameworks are utilized to relieve pathologist workload by classifying the data automatically, in which deep convolutional neural networks (CNNs) are effective solutions. The features extracted from the activation layer of pre-trained CNNs are called deep convolutional activation features (DeCAF). In this paper, we have analyzed that all DeCAF features are not necessarily led to higher accuracy in the classification task and dimension reduction plays an important role. We have proposed reduced DeCAF (R-DeCAF) for this purpose, and different dimension reduction methods are applied to achieve an effective combination of features by capturing the essence of DeCAF features. This framework uses pre-trained CNNs such as AlexNet, VGG-16, and VGG-19 as feature extractors in transfer learning mode. The DeCAF features are extracted from the first fully connected layer of the mentioned CNNs, and a support vector machine is used for classification. Among linear and nonlinear dimensionality reduction algorithms, linear approaches such as principal component analysis (PCA) represent a better combination among deep features and lead to higher accuracy in the classification task using a small number of features considering a specific amount of cumulative explained variance (CEV) of features. The proposed method is validated using experimental BreakHis and ICIAR datasets. Comprehensive results show improvement in the classification accuracy up to 4.3% with a feature vector size (FVS) of 23 and CEV equal to 0.15.

Introduction

Breast cancer (BC) is one of the leading causes of mortality in the world, almost observed in women, but it can occur in men too. Diagnosis of BC ordinarily comprises an initial detection by palpation and regular check-ups by ultrasound imaging or mammography and diagnosis of possible malignant tissue growth is tested by breast tissue biopsy [1]. According to the World Health Organization (WHO), BC is affecting a large number of women’s health [2]. Recent studies predict around 27 million new cases of BC by 2030 [3]. Early detection of BC is essential for appropriate treatment and for decreasing the mortality rate. However, BC diagnosis may not be accurate enough as pathologists could only apply visual inspection of samples under microscopes [4, 5]. According to these challenges, computer-aided diagnosis and automatic classification using convolutional neural networks (CNNs) for image classification are active research areas to make a precise diagnosis with less probability of misdiagnosis and a fast detection process.

Current state-of-the-art investigations on BC detection confirm that CNNs are more reliable and faster than the conventional hand-crafted features in the classification task [6]. However, the estimated time to train CNNs might be longer, and it needs expertise to design such networks [6–8]. An applicable solution reported in the literature is referred to as a deep convolutional activation feature (DeCAF) also known as deep features [6, 8, 9]. These approaches reuse pre-trained CNNs to extract deep features and apply them to a classifier for the final decision.

The hand-crafted features in BC histopathological dataset (737 images) have been studied by Filipczuk et al. [10] using circular Hough transform to segment the cell nuclei by circles. Their best result reached 98.51% accuracy utilizing k-nearest neighbor (KNN) as a classifier [10]. However, the region of interest in the virtual slides is not selected automatically and it is a time-consuming process. Additionally, the method cannot guarantee a global optimum, and elliptical segmentation requires a more accurate model which is computationally more demanding. In another work by Sharma and Mehra, hand-crafted features like color, shape, and texture were extracted from the BreakHis dataset and fed to the conventional classifiers such as support vector machine (SVM) and random forest (RF). They reported RF with 1000 trees could achieve 90.33% accuracy for 40 × data [11]. In addition, they have compared the hand-crafted features with deep ones. The accuracy obtained for the classification of the deep features using the VGG-16 network for 40 × data is 93.97%. They have reported that the performance of the hand-crafted features is not satisfactory since it requires deep knowledge about the morphology of cancerous cells and deep features are a preferred alternative. Alhindi et al. compared the local binary patterns (LBP), and the histogram of oriented gradients (HOG) as the hand-crafted features with deep features using the pre-trained VGG-19 for KIMIA Path960 dataset [12]. The highest accuracy is 90.52% for LBP features and the SVM classifier. It is worth mentioning that the feature vector size (FVS) of LBP is equal to 1182 and almost twice the one of the extracted deep features.

To address deep features in histopathological images, Spanhole et al. extracted DeCAF from different fully connected (FC) layers of pre-trained AlexNet with logistic regression classifier to diagnose BC using the BreakHis dataset [6]. The obtained results show that transfer learning is a viable alternative with 84.6% accuracy for 40 × data. Then, Deniz et al. developed a framework to take advantage of two pre-trained CNNs for the binary classification of the BreakHis dataset. They combined DeCAF features from AlexNet and VGG-16 followed by the SVM classifier and reached 84.87% accuracy [8]. In [13], Kumar et al. proposed a variant of VGG-16, wherein all FC layers were removed and evaluated by different classifiers for CMT and BreakHis datasets. The best-reported accuracy is 97.01% for 200 × data from the BreakHis dataset, in which the FVS is 1472.

To overcome the lack of a training dataset, dividing the histopathological image into non-overlapping or random patches and providing them as the input to the pre-trained CNNs for feature extraction has been studied [1, 6, 14]. However, extracting some patches can lead to uncertainty in the classification [15]. To improve the accuracy of the classification, some approaches focused on training CNNs from scratch or fine-tuning the pre-trained CNNs [15–19]. Some of these approaches have reached higher performance while experiencing a time-consuming procedure and arranging hyperparameters precisely. In some cases, training the model or fine-tuning all the layers may not achieve a better performance compared to the transfer learning technique [7, 16, 17]. Additionally, transfer learning hits the spot either encountering the lack of training dataset to train a deep model or adding a few training data to re-train the whole model [13, 14, 16].

Dimension reduction or feature selection of deep features has attracted the attention of researchers recently. Alinsaif et al. applied Infinite Latent Feature Selection (ILFS) method to select top-ranked features from pre-trained CNNs such as ResNet and DenseNet w/wo fine-tuning. The accuracy of binary classification for BreakHis dataset with SVM classifier is reported at 97.96% where FVS is 1300 [16]. Moreover, Gupta et al. proposed extreme gradient boosting (XGboost) to reduce the number of features extracted from ResNet and used information-theoretic measure (ITS) to select the optimal number of layers. The accuracy is reported 97.07 ± 1.18% for 40 × data where FVS is 500, although the accuracy decreased with fewer features [20].

In this study, dimensionality reduction is the main scope to investigate the influence of capturing informative features with a smaller number of features. We have analyzed that all the deep features are not necessarily led to a higher accuracy in the classification task and dimension reduction plays an important role.

Histopathological Database

In this study, we have used two publicly accessible datasets to evaluate the proposed R-DeCAF features. The BreakHis database [21] is a histopathologic BC dataset that was developed in a laboratory (Pathological Anatomy and Cytopathology, Parana, Brazil). This dataset includes microscopic histopathology images of BC and consists of 7909 images of BC tissue taken from 82 patients which is available in 40 × , 100 × , 200 × , and 400 × magnification factors. This dataset includes 2480 benign and 5429 malignant samples with a color image size of 700 × 460. In addition, benign and malignant tumors are divided into subgroups. Samples of this dataset are collected by surgical open biopsy (SOB) method and stained by Hematoxylin and Eosin (H&E) methods. Each image filename includes stored information about the image such as biopsy procedure method, magnification factor, type of cancer and its subtypes, and patient identification. The ICIAR 2018 Grand Challenge dataset is the second dataset that includes 400 H&E-stained histopathology images from BC [22]. It has four groups including normal, benign, in situ carcinoma, and invasive carcinoma, where each group contains 100 breast microscopic images. There is no information about the number of patients for this dataset. In Fig. 1, sample images of benign and malignant tumors from the BreakHis dataset at different magnification factors and sample images from the ICIAR dataset of four categories are shown.

Fig. 1.

a Sample images from the BreakHis database in different magnification factors. The first row belongs to the same slide of the benign tumor and the second row belongs to the same slide of the malignant tumor. b Sample images from the ICIAR dataset of four categories

Methodology

We have proposed R-DeCAF features to capture the essence of the data which causes improvement in the classification task while reducing the computational time due to the fewer features. We have shown that all the features extracted from the pre-trained CNNs cannot be effective in classifying the data. Therefore, reducing the FVS of the extracted deep features to keep informative features and remove unnecessary ones which cause misleading [24] or do not play an important role in the classification, is the primary goal of this study. Moreover, a high dimensional feature vector can dramatically impact the performance of machine learning algorithms to fit data, and generally, this can be referred to as the “curse of dimensionality” [25].

Deep features are extracted from the first FC layer of the pre-trained CNNs (AlexNet, VGG-16, and VGG-19), in which the size of the feature vector is high, i.e., FVS = 4096. The reason for considering the first FC layer; i.e., FC6 is that it provides features more informative for an accurate classification [6, 23]. The weight of the pre-trained CNNs will be kept frozen in transfer learning mode as pre-trained CNNs have been trained by the ImageNet dataset; therefore, freezing the weights trained based on the ImageNet dataset makes the model prepared to use all defined pre-trained weights. Since pre-trained CNNs are trained on a large dataset with a significant number of classes and samples, they can provide large networks with an effective combination of features to classify the data [6, 13]. The advantage of the transfer learning technique is to avoid a time-consuming procedure for training a CNN from scratch [6, 13, 16]. In other words, training and fine-tuning a CNN require a huge amount of data or a medium size of data, respectively. However, transfer learning involves different structures, and it does not need a huge amount of data. Transfer learning is a method to transfer the knowledge learned in one domain to a defined task for classification or feature extraction. Thus, the goal is to transfer the knowledge from natural images to BC histopathological images and simplify the diagnosis process.

To reduce the size of the extracted deep features, different linear and nonlinear dimension reduction methods such as PCA, singular value decomposition (SVD), linear discriminant analysis (LDA), kernel PCA (kPCA), and t-Distributed Stochastic Neighbor Embedding (t-SNE) have been evaluated to generate R-DeCAF features. The architecture of the proposed framework is illustrated in Fig. 2.

Fig. 2.

The diagram of the proposed framework

Pre-trained CNNs

All three defined pre-trained CNNs which are AlexNet, VGG-16, and VGG-19 are studied as the basis of our framework to extract deep features. AlexNet is known to be the primary profound CNN model presented by Krizhevsky et al. [26]. This network contains five convolutional layers and three FC layers where the number of neurons in the last layer is based on the number of classes of the data. The number of neurons in the first and second FC layers is 4096. The VGG-16 and VGG-19 CNNs with more layers are proposed by Simonyan et al. in 2014 [27]. In these two CNNs, small filters of 3 × 3 are used for all the layers to capture fine details in the images and control the number of parameters. VGG-19 has 19 weight layers and VGG-16 has 16 weight layers [27]. It should be mentioned that all the input images are resized to 224 × 224 for the sake of convenience with CNN models in the Pytorch library in this work.

Feature Reduction Algorithms

This study analyzes different dimension reduction methods on DeCAF features categorized into two groups; linear and nonlinear. The former includes PCA, SVD, and LDA, whereas the latter contains kPCA and t-SNE [24, 28]. The PCA method is a linear and unsupervised algorithm, in which new features can be produced by calculating a linear transformation. Eigenvectors and eigenvalues can be computed from the covariance matrix of the data to determine the principal components (PC) of the data. PCA keeps the maximum information of the data in the first PC and continues in descending order because principal directions, and corresponding PCs are considered as the directions of the maximum data variance [24, 25]. SVD is another linear dimension reduction method that is appropriate for sparse data. SVD of a matrix is a factorization of the main matrix into three matrices. In this method, the largest singular values are picked, where the eigenvalues and eigenvectors are in descending order same as in the PCA method. Hence, the input matrix will rebuild in low dimension [24]. LDA is another linear and supervised dimension reduction method that focuses on two critical terms called “scatter between class” and “scatter within a class.” The main aim is to maximize the “scatter between classes” or separability of classes. Therefore, LDA can pick components that separate the data classes in the best way. It should be mentioned that the number of components/features in a reduced dimension can be equal to or smaller than the number of classes-1 [24, 29].

In the group of nonlinear dimension reduction methods, kPCA is one of the popular unsupervised techniques. When the PCA method does not work well and the structure of the data is nonlinear, the kPCA method may perform better. In kPCA, the dimension of the original data can be reduced in a high dimensional space with the advantage of the “kernel trick.” In high-dimensional space decision boundary becomes linear. In this method, the eigenvalues and eigenvectors of the kernel matrix are calculated based on the reduced dimension set of eigenvectors selected in descending order. The product of the original matrix and eigenvectors is calculated to rebuild the new reduced data [25, 28]. The nonlinear and unsupervised t-SNE method is known as a common technique for data exploration and visualization. In this method, data is mapped to a low dimension, such as 2 or 3 dimensions. t-SNE converts the high dimensional Euclidean distances between pairwise data points $x_i,x_j$ into conditional probability $p_{j|i}$ which shows the similarity of the pairwise data points and a similar conditional probability in low dimensional counterparts $y_i,y_j$ of the high dimensional data points $x_i,x_j$ defined by $q_{j|i}$. The conditional probabilities $p_{j|i}$ and $q_{j|i}$ will be equal if the data points $y_i,y_j$ model the similarity between the data points in a high dimensional space [24, 30].

Cumulative Explained Variance (CEV) and the Size of the Features

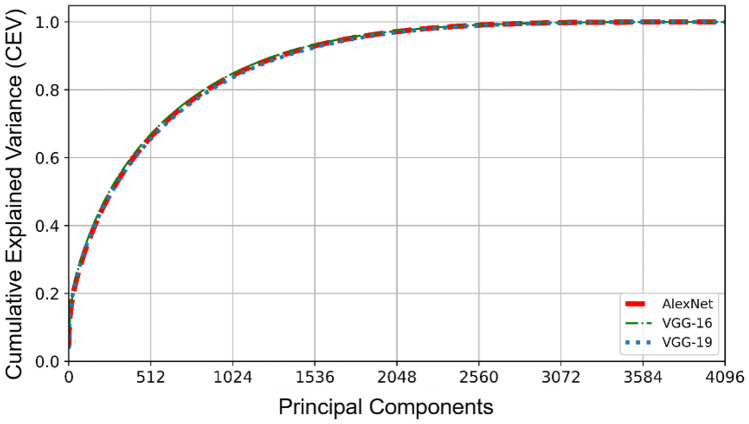
To reduce the size of the features, we have used eigenvalues and the corresponding cumulative explained variance (CEV). Determining the optimal number of PCs is a challenging and critical key to getting an efficient performance and CEV is a way to solve this challenge. CEV is the accumulation of variances to show the summation of variances of the new features, i.e., PCs as the percentage of this accumulated variance by the PC numbers [24]. Figure 3 displays the CEV of DeCAF features extracted from the first FC layer of pre-trained AlexNet, VGG-16, and VGG-19 which is related to the whole magnification data of the BreakHis dataset. As can be seen, approximately with more than 2560 PCs, the CEV has changed insignificantly. In other words, the first 2560 PCs contain 100% of cumulative variances whereas the first 512 PCs cover 67% of the variance of data.

Fig. 3.

CEV of DeCAF features using pre-trained CNNs for the whole magnification data of the BreakHis dataset

It can be concluded that almost half of the transformed features, i.e., PCs, do not have an important role in the classification as a rule of thumb whereas Zhong et al. [9] took advantage of this simple rule. The main reason is because of the high correlation among extracted deep features. To investigate more in detail, we have considered a full range of CEV from 5 to 100%, in which 100% means we have used all PCs obtained from DeCAF features to examine the classification accuracy. Here, the statistical analysis performed on the accuracy obtained for three pre-trained CNNs in 10 different splits of feature vectors into train and test datasets, and Fig. 4 shows the boxplot of these results for the whole magnification data (7909 images) of the BreakHis dataset.

Fig. 4.

The boxplot of the classification accuracy vs Cumulative Explained Variance (CEV) for the whole magnification data of the BreakHis dataset

First, the boxplots of these results show that using CEV less than 100% but more than 15% not only keeps the same performance but also causes improvement in classifying deep features. It may be true that all the improvements are not significant. The main point is that using CEV less than 100% but more than 15% does not make the classification performance worse. Second, the results of Fig. 4 provide more information that we need to feed the classifier with more effective and proper features rather than a large number of features. Therefore, a better accuracy can be achieved with a smaller number of features and the content of features plays a crucial role in the classification task. We have shown by these results that considering a large number of features could not necessarily lead to a higher performance and all DeCAF features extracted from pre-trained AlexNet, VGG-16, and VGG-19 are not compelling and informative in the classification. Figure 4 discloses keeping only 20% to 25% of CEV makes a significant improvement compared to 50% of CEV. These also reduced FVS significantly from 4096 to 63, 103, and 93 for the pre-trained AlexNet, VGG-16, and VGG-19, respectively. More details of this investigation are presented in Table 1, and a p-value is calculated for each case to verify that the improvements are significant.

Table 1.

The classification accuracy (%) of DeCAF and R-DeCAF features using different linear dimension reduction methods on the BreakHis dataset

Framework	Magnification	DeCAF FVS = 4096	R-DeCAF (reduced by linear methods)
			FVS (CEV)	PCA	FVS (CEV)	SVD	LDA
AlexNet (FC6), SVM	40 ×	84.38 ± 1.6	67 (0.25)	88.04 ± 2.1**	67 (0.25)	88.02 ± 2.1**	77.62 ± 1.8**
	100 ×	86.16 ± 1.1	45 (0.20)	89.54 ± 1.0**	45 (0.20)	89.66 ± 0.9**	79.87 ± 2.3**
	200 ×	87.69 ± 1.4	97 (0.30)	90.60 ± 1.4**	135 (0.35)	90.50 ± 1.3**	83.87 ± 1.4**
	400 ×	87.91 ± 1.5	23 (0.15)	91.13 ± 1.4**	23 (0.15)	91.15 ± 1.5**	82.58 ± 1.5**
	Whole mag	85.95 ± 0.7	63 (0.20)	90.24 ± 0.6**	63 (0.20)	90.19 ± 0.5**	71.73 ± 1.1**
VGG-16 (FC6), SVM	40 ×	86.64 ± 2.2	90 (0.30)	89.82 ± 1.7**	90 (0.30)	89.60 ± 1.7*	82.23 ± 0.9**
	100 ×	89.52 ± 1.2	58 (0.25)	91.01 ± 0.7*	206 (0.45)	91.01 ± 1.2*	84.05 ± 1.8**
	200 ×	88.71 ± 0.9	84 (0.30)	90.77 ± 1.4*	56 (0.25)	90.82 ± 1.1*	82.68 ± 0.9**
	400 ×	85.60 ± 1.9	58 (0.25)	88.30 ± 1.3**	58 (0.25)	88.21 ± 1.3*	81.95 ± 1.9**
	Whole mag	87.23 ± 0.8	103 (0.25)	90.49 ± 0.9**	103 (0.25)	90.42 ± 0.8**	73.10 ± 1.0**
VGG-19 (FC6), SVM	40 ×	85.09 ± 1.8	78 (0.30)	87.34 ± 2.0**	51 (0.25)	87.14 ± 1.6**	79.62 ± 1.9**
	100 ×	88.06 ± 1.5	118 (0.35)	90.19 ± 1.3**	118 (0.35)	90.05 ± 1.3*	81.10 ± 1.3**
	200 ×	88.51 ± 1.0	114 (0.35)	89.35 ± 1.2	114 (0.35)	89.60 ± 1.6	82.80 ± 1.3*
	400 ×	86.73 ± 0.8	59 (0.25)	88.60 ± 0.8**	59 (0.25)	88.76 ± 0.9**	82.03 ± 1.9**
	Whole mag	86.67 ± 0.5	93 (0.25)	89.43 ± 0.5**	93 (0.25)	89.37 ± 0.5**	72.03 ± 0.8**

Whole mag. stands for whole magnifications where the images of all magnifications are used; the best results are shown in bold

*p-value_t-test < 0.01,**p-value_t-test < 0.001

Classifier

Here, the SVM algorithm has been selected for the classification as it can handle the high dimensional data and nonlinear classification by using a kernel trick [13]. This technique is used to evaluate the performance of DeCAF and R-DeCAF features in classification tasks to predict whether a sample is benign or malignant. The trained SVM with RBF kernel is considered as the common kernel based on a Grid search among different kernels with the SVM parameter C = 5. The defined dataset is divided into a training set (80%) and a test set (20%). The split method is used, and the results are reported by taking an average of 10 different splits. Comprehensive results are provided by Pytorch and Scikitlearn libraries to validate the proposed method. Since most machine learning algorithms are sensitive to data scaling, in this manner, we apply the Standard Scalar of Scikitlearn library to scale the feature vectors that are extracted.

Results and Discussion

The classification accuracy of DeCAF and R-DeCAF features is summarized in Table 1 by the value of the mean and the standard deviation. The mean differences are also assessed by t-test, and the p-values are reported. The R-DeCAF features are obtained by three linear dimension reduction algorithms, i.e., PCA, SVD, and LDA. First, we have investigated the classification performance using DeCAF features by the three mentioned CNNs in more detail. As you can see in the third column of Table 1, the accuracy of VGG-16 and VGG-19 outperform AlexNet for 40 × , 100 × , and 200 × data of the BreakHis dataset but underperform for 400 × . The reason can be found in both the number of layers and 3 × 3 filters in VGG-16 and VGG-19 networks which can extract more details from images. However, for 400 × data such details from VGG-16 and VGG-19 networks are not necessary as the magnification is higher and the images provide such details. Therefore, AlexNet is a better choice for high-magnification data. It is worth mentioning that the accuracy considering the whole magnification is better for VGG-16 and VGG-19 networks as expected. In addition, the lowest accuracy is observed for 40 × data. This might be because of the region of interest of 40 × data as includes a higher complexity compared with other magnification factors and carries more information which makes accurate data classification more difficult. The magnification factor affects the classification accuracy depending on the complexity level of BC histopathological images.

Second, the classification performance using R-DeCAF features based on different dimension reduction algorithms has been explored further. The results from applying PCA and SVD to generate R-DeCAF features provided almost the same improvement up to 4.3% compared to DeCAF features. For example, the observed accuracy considering pre-trained AlexNet for whole magnification data are 85.95%, 90.24%, and 90.18 for DeCAF features, R-DeCAF features using PCA, and R-DeCAF features using SVD, respectively. Again, we can say that AlexNet is still a better choice for high magnification data even for R-DeCAF features. The results obtained by LDA depict the classification accuracy has been decreased, and this method is not able to capture the essence of data caused by removing informative features. The main reason explaining the low accuracy by LDA is that the number of features of the original dataset is ignored and the obtained dimension (FVS) will be less than the number of classes subtract from one. Therefore, we will have only one feature for binary classification using the LDA technique [24].

To evaluate our proposed method, we have computed the confusion matrix of the classification result for DeCAF and R-DeCAF features. These matrixes are shown in Fig. 5, in which the results were obtained by pre-trained AlexNet for 400 × data (1820 images, 588 benign and 1232 malignant) of the BreakHis dataset. It can be seen that the classification result of R-DeCAF features obtained by PCA outperforms the one of the DeCAF features. In more detail, correctly predicted benign cases increased from 68 to 82%. This is a very impressive result as our proposed method could increase the accuracy in the benign class although the number of data in this class is more limited due to an imbalance in the BreakHis dataset.

Fig. 5.

Confusion matrix for 400 × data from the BreakHis dataset to show the classification result of deep features extracted from pre-trained AlexNet. a DeCAF features and b R-DeCAF features using the PCA algorithm (FVS = 23, CEV = 0.15). 0: benign, 1: malignant

Moreover, we have validated the classification result of DeCAF and R-DeCAF features using other metrics as shown in Table 2. We have reported R-DeCAF features that are reduced by the PCA algorithm as we have observed that the accuracy obtained by PCA outperforms other linear dimension reduction algorithms (see Table 1). Table 2 shows that the precision and F1 score of R-DeCAF features has been improved compared to the ones of DeCAF features; however, recall is different and it has been decreased for R-DeCAF features in some cases.

Table 2.

The classification accuracy, precision, recall, and F1 score (%) of DeCAF and R-DeCAF features (reduced by PCA) on the BreakHis dataset

Framework	Magnification	DeCAF (FVS = 4096)				R-DeCAF (reduced by PCA)
		Accuracy	Precision	Recall	F1	FVS (CEV)	Accuracy	Precision	Recall	F1
AlexNet (FC6), SVM	40 ×	84.38 ± 1.6	85.20 ± 2.1	93.42 ± 1.0	89.10 ± 1.2	67 (0.25)	88.04 ± 2.1	89.61 ± 2.7	94.73 ± 1.5	91.54 ± 1.6
	100 ×	86.16 ± 1.1	85.77 ± 1.5	95.95 ± 0.8	90.57 ± 0.9	45 (0.20)	89.54 ± 1.0	90.05 ± 1.9	95.52 ± 1.3	92.68 ± 0.7
	200 ×	87.69 ± 1.4	87.63 ± 1.5	95.58 ± 1.5	91.42 ± 0.9	97 (0.30)	90.60 ± 1.4	91.11 ± 1.8	95.65 ± 1.3	93.31 ± 1.0
	400 ×	87.91 ± 1.5	87.32 ± 2.1	96.02 ± 1.2	91.44 ± 1.2	23 (0.15)	91.13 ± 1.4	91.31 ± 1.6	95.96 ± 0.9	93.57 ± 1.1
	Whole mag	85.95 ± 0.7	86.98 ± 0.9	93.35 ± 0.6	90.05 ± 0.5	63 (0.20)	90.24 ± 0.6	91.24 ± 0.6	94.78 ± 0.7	92.97 ± 0.5
VGG-16 (FC6), SVM	40 ×	86.64 ± 2.2	88.09 ± 2.7	93.17 ± 1.9	90.53 ± 1.7	90 (0.30)	89.82 ± 1.7	90.43 ± 1.9	95.28 ± 1.8	92.77 ± 1.3
	100 ×	89.52 ± 1.2	89.21 ± 1.4	96.53 ± 1.2	92.72 ± 0.8	58 (0.25)	91.01 ± 0.7	92.15 ± 1.1	95.11 ± 1.5	93.59 ± 0.6
	200 ×	88.71 ± 0.9	89.23 ± 1.5	95.07 ± 1.6	92.04 ± 0.6	84 (0.30)	90.78 ± 1.4	91.03 ± 1.8	96.04 ± 1.1	93.46 ± 1.0
	400 ×	85.60 ± 1.9	85.43 ± 2.2	95.08 ± 1.4	89.98 ± 1.5	58 (0.25)	88.30 ± 1.3	88.92 ± 1.8	95.64 ± 1.4	91.67 ± 1.0
	Whole mag	87.23 ± 0.8	87.86 ± 0.9	94.40 ± 0.6	91.01 ± 0.5	103 (0.25)	90.61 ± 0.9	91.30 ± 0.8	95.18 ± 0.8	93.20 ± 0.7
VGG-19 (FC6), SVM	40 ×	85.09 ± 1.8	86.00 ± 2.4	93.51 ± 1.0	89.58 ± 1.3	78 (0.30)	87.34 ± 2.0	87.01 ± 2.2	95.87 ± 1.3	91.21 ± 1.5
	100 ×	88.06 ± 1.5	87.33 ± 2.0	96.86 ± 0.9	91.84 ± 1.1	118 (0.35)	90.19 ± 1.3	90.60 ± 1.5	95.81 ± 1.0	93.13 ± 1.0
	200 ×	88.51 ± 1.0	88.33 ± 1.0	96.31 ± 0.9	92.14 ± 0.6	114 (0.35)	89.35 ± 1.2	90.10 ± 1.6	95.29 ± 1.2	92.61 ± 0.8
	400 ×	86.73 ± 0.8	86.59 ± 1.5	95.35 ± 1.3	90.74 ± 0.6	59 (0.25)	88.60 ± 0.8	90.27 ± 0.6	93.36 ± 1.4	91.78 ± 0.6
	Whole mag	86.67 ± 0.5	87.39 ± 0.5	94.10 ± 0.7	90.62 ± 0.5	93 (0.25)	89.43 ± 0.5	89.93 ± 0.6	95.22 ± 0.5	92.50 ± 0.4

Whole mag. stands for whole magnifications where the images of all magnifications are used; the best results are shown in bold

Since the BreakHis dataset is imbalanced in which the number of the samples in the malignant class is almost twice the one in the benign class and this ratio is almost the same for different magnifications, we have addressed this issue by reproducing the results of Table 2 based on two more strategies. First, we forced the data to be balanced by randomly selected malignant samples to be the same as the number of benign samples in each magnification factor and SVM is used. Second, we used weighted SVM, and the data is divided into train and test datasets with stratified k-fold (k = 10). We have not provided the whole results for these two strategies here for the sake of saving space. The results of the first strategy were lower compared to the result of Table 2 as we have decreased the number of data to force the dataset to be balanced. The results of the second strategy were close to the results of Table 2, and this means that the effect of the imbalance data of the BreakHis dataset is not crucial as the imbalance ratio of the data is not too high.

In addition, this study evaluates the performance of nonlinear dimension reduction methods, including kPCA and t-SNE described in the “Cumulative Explained Variance (CEV) and the Size of the Features” section. The classification accuracy based on DeCAF and R-DeCAF features is presented in Table 3 by the value of the mean and the standard deviation in addition to FVS. The mean differences are also assessed by t-test, and the p-values are reported. Using the kPCA algorithm, a different number of features has been tested. However, the classification accuracy based on R-DeCAF features is not high enough. So, we have considered the same number of features similar to the PCA method. To apply the t-SNE algorithm, it is highly recommended to first use the PCA method before decreasing the dimension to 2 or 4 features by t-SNE. Therefore, we have reduced FVS in the same step as applying only the PCA method on the feature vectors. Then, t-SNE is implemented to reduce the number of features to 2. As it is clearly shown, nonlinear dimension reduction methods are not effective to capture informative features from DeCAF features and classification accuracy has decreased. However, linear approaches such as PCA could represent a better combination of deep features and lead to higher accuracy in the classification task. Nonlinear dimensionality reduction techniques might be sensitive to the curse of dimensionality and this could be the reason for their improper performance in our study. Hence, these methods are not able to guarantee better performance than linear ones, such as PCA [24, 28]. Moreover, we can consider the presence of more complexity in R-DeCAF features obtained by nonlinear dimension reduction methods which lead to lower classification accuracy.

Table 3.

The classification accuracy (%) of DeCAF and R-DeCAF features using different nonlinear dimension reduction methods on the BreakHis dataset

Framework	Magnification	DeCAF FVS = 4096	R-DeCAF (reduced by nonlinear methods)
			FVS (CEV)	KPCA	PCA + t-SNE
AlexNet (FC6), SVM	40 ×	84.38 ± 1.6	67 (0.25)**	68.45 ± 2.6**	67.77 ± 3.0**
	100 ×	86.16 ± 1.1	45 (0.20)**	69.33 ± 1.9**	69.26 ± 1.9**
	200 ×	87.69 ± 1.4	97 (0.30)**	68.58 ± 1.8**	68.58 ± 1.8**
	400 ×	87.91 ± 1.5	23 (0.15)**	67.46 ± 2.3**	68.85 ± 2.0**
	Whole mag	85.95 ± 0.7	63 (0.20)**	68.15 ± 1.0**	69.41 ± 1.7**
VGG-16 (FC6), SVM	40 ×	86.64 ± 2.2	90 (0.30)**	68.77 ± 2.8**	68.75 ± 3.7**
	100 ×	89.52 ± 1.2	58 (0.25)**	69.11 ± 1.0**	69.66 ± 3.3**
	200 ×	88.71 ± 0.9	84 (0.30)**	68.67 ± 1.5**	68.66 ± 1.5**
	400 ×	85.60 ± 1.9	58 (0.25)**	68.21 ± 2.5**	68.21 ± 2.5**
	Whole mag	87.23 ± 0.8	103 (0.25)**	68.46 ± 0.7**	68.95 ± 1.0**
VGG-19 (FC6), SVM	40 ×	85.09 ± 1.8	78 (0.30)**	68.65 ± 2.2**	69.30 ± 3.9**
	100 ×	88.06 ± 1.5	118 (0.35)**	69.45 ± 2.0**	68.22 ± 4.2**
	200 ×	88.51 ± 1.0	114 (0.35)**	69.95 ± 1.4**	69.73 ± 1.6**
	400 ×	86.73 ± 0 8	59 (0.25)**	68.27 ± 1.9**	67.94 ± 1.6**
	Whole mag	86.67 ± 0.5	93 (0.25)**	68.44 ± 0.9**	67.10 ± 2.8**

Whole mag. stands for whole magnifications where the images of all magnifications are used; the best results are shown in bold

*p-value_t-test < 0.01,**p-value_t-test < 0.001

Based on the analysis that we have done and the results reported in Tables 1 and 3, we can conclude that the accuracy of binary classification for the BreakHis dataset will be enhanced using R-DeCAF features with linear dimension reduction algorithms like PCA and SVD up to 4.3% in different magnification factors. Less probability of overfitting and noise rejection capability of the PCA algorithm and the benefits of sparse data management by the SVD algorithm [24, 31] are the reasons which improve our R-DeCAF features. This is an important finding in which there is a linear combination among deep features which could help us to consider it in modifying networks to perform better.

To investigate the effect of multi-class performance, we have applied DeCAF and R-DeCAF (reduced by PCA) features to the ICIAR dataset which has four classes. Each class contains 100 images which are low for training purposes. The same SVM parameters for the BraekHIS dataset have been applied to this dataset. The results are reported in Table 4; it is worth mentioning that there is a significant reduction in the FVS from 4096 to at most 51 where the classification performance shows a slight improvement. The results show that the R-DeCAf features outperform the D-CAF features in multi-classification as binary classification.

Table 4.

The classification accuracy, precision, recall, and F1 score (%) of DeCAF and R-DeCAF features (reduced by PCA) on the ICIAR dataset (the best results are shown in bold)

Framework	DeCAF (FVS = 4096)				R-DeCAF (reduced by PCA)
	Accuracy	Precision	Recall	F1	FVS (CEV)	Accuracy	Precision	Recall	F1
AlexNet (FC6), SVM	60.75 ± 3.9	61.52 ± 4.0	60.75 ± 3.9	60.44 ± 3.9	24 (0.25)	61.37 ± 4.4	61.62 ± 4.7	61.37 ± 4.4	61.04 ± 4.6
VGG-16 (FC6), SVM	60.75 ± 7.0	61.70 ± 6.8	60.75 ± 7.0	60.80 ± 6.9	51 (0.40)	65.0 ± 4.2	65.38 ± 4.5	65.01 ± 4.2	64.70 ± 4.5
VGG-19 (FC6), SVM	55.87 ± 2.4	57.34 ± 2.5	55.87 ± 2.4	55.82 ± 2.2	38 (0.35)	59.0 ± 3.4	60.02 ± 3.5	59.0 ± 3.4	59.07 ± 3.3

Moreover, we have compared the performance of the proposed framework with the state-of-the-art studies which is summarized in Table 5. In our method, the results of R-DeCAF features obtained by the PCA algorithm have been reported. In the previous works, deep features are extracted from different pre-trained CNNs followed by an SVM classifier as in our case to classify the BreakHis dataset. FVS is also mentioned in Table 5 for a comprehensive analysis and comparison. As we can see, the results obtained from the proposed method have sought to increase the accuracy compared to some approaches. As a case in point, in [8] and [14], the classification of deep features which are extracted from pre-trained CNNs, i.e., AlexNet, VGG-16, and VGG-19 led to lower accuracy in comparison with this study. The higher accuracy obtained by Kumar et al. [13], Gupta et al. [20], and Alinsaif et al. [16] while FVS is not comparable to our case which is almost less than 120. In [13], a global average pooling is applied to five external convolutional layers of all five blocks of VGG-16 and makes a feature vector of 1472 after concatenation. This approach is different from ours where we have just extracted features from one layer (first FC layer). This declares that looking at the features from all layers improves the result. The higher accuracy was reported in [20] where FVS is equal to 500. Although, the accuracy decreased with fewer features. In addition, the authors in [16] could only keep the classification accuracy unchanged by FVS equal to 1300. On the other hand, since we have only analyzed three pre-trained models as feature extractors, we could not examine our proposed concept in the mentioned works [13, 16, 20] in which the CNNs used as feature extractors are different. Moreover, we believe that our proposed method can enhance the performance of transfer learning. In another study based on fine-tuning pre-trained CNNs, the classification accuracy is reported as 80.80% for the 40 × data of the BreakHis dataset [5]. Reducing FVS to less than 120, our proposed method could hit the spot in comparison with previous works and classification accuracy has increased up to 4.3% simultaneously.

Table 5.

Comparison of the classification accuracy obtained from the proposed method and previous methods on the BreakHis dataset

Existing methods	CNN	FVS	Classification accuracy (%)
			40 ×	100 ×	200 ×	400 ×	Whole mag
Bardou et al. [18]	new CNN	2000	90.64	89.58	90.23	75.96	–
Deniz et al. [8]	AlexNet + VGG-16	4096 + 4096	84.87 ± 1.1	89.21 ± 1.4	88.65 ± 2.4	86.75 ± 4.2	–
Gupta et al. [20]	ResNet	500	97.07 ± 1.2	96.10 ± 1.0	94.69 ± 1.2	90.85 ± 2.1	–
Kumar et al. [13]	VGG-16	1472	94.11 ± 1.8	95.12 ± 1.1	97.01 ± 1.1	93.40 ± 1.0	–
Saxena et al. [14]	AlexNet	1526	84.06	87.54	89.40	85.16	–
	VGG-16	3072	86.36	87.77	86.80	84.35	–
	VGG-19	3072	86.64	88.17	85.84	81.67	–
Alinsaif et al. [16]	DenseNet	1300	–	–	–	–	97.96 ± 0.6
Proposed	AlexNet	23–97	88.04 ± 2.1	89.54 ± 1.0	90.60 ± 1.4	91.13 ± 1.4	90.24 ± 0.6
	VGG-16	58–103	89.82 ± 1.7	91.01 ± 0.7	90.77 ± 1.4	88.30 ± 1.3	90.49 ± 0.9
	VGG-19	59–118	87.34 ± 2.0	90.19 ± 1.3	89.35 ± 1.2	88.60 ± 0.8	89.43 ± 0.5

Whole mag. stands for whole magnifications where the images of all magnifications are used

Conclusions

This study proposes R-DeCAF features for BC detection using histopathological images and compares them with DeCAF features. To extract DeCAF features, three different pre-trained CNNs emerged as unsupervised feature extractors. A feature vector from the first FC layer of CNNs with an FVS of 4096 has been extracted. The results show that keeping all DeCAF features extracted from pre-trained AlexNet, VGG-16, and VGG-19 is not effective in the classification task. Thus, various dimension reduction methods on DeCAF features are evaluated to capture informative feature vectors and decrease the computational time too. We reduce the FVS of DeCAF features which is fixed to 4096 by applying appropriate dimension reduction algorithms to generate R-DeCAF features, in which FVS is less than 120 considering about 15% to 35% of CEV which is sufficient and could significantly improve the accuracy up to 4.3% in the best case. Evaluations show that linear dimensionality reduction algorithms could represent an effective combination among deep features and lead to higher accuracy in the classification task, however, nonlinear approaches fail. This is an important finding in which there is a linear combination among deep features which could help us to consider it in modifying networks to perform better. Moreover, PCA performs better among various linear dimension reduction methods. The best-achieved result for 400 × data using pre-trained AlexNet as the feature extractor is 91.13 ± 1.4. It should be noted that data augmentation and particular data preprocessing are not required in the proposed model which is considered a fully automatic model for cancer diagnosis. Moreover, the magnification level of the BreakHis dataset affects the classification accuracy as it depends on the complexity level of histopathological images. The results on the ICIAR dataset also show that the R-DeCAf features outperform the D-CAF features in multi-classification as binary classification. As a future work, modification in deep CNN models based on the PCA algorithm to provide less feature complexity and increase classification accuracy with more reliable and informative features may break this curse. Additionally, examining other pre-trained CNN models to extract deep features and applying this proposed method for performance enhancement will be considered in future work.

Author Contribution

Bahareh Morovati: methodology, software, formal analysis, visualization, and writing—review and editing. Reza Lashgari: writing—review and editing. Mojtaba Hajihasani: software, validation, resources, visualization, and writing—review and editing. Hasti Shabani: conceptualization, formal analysis, investigation, visualization, writing—review and editing, supervision, and project administration.

Declarations

Ethics Approval

This declaration is “not applicable.”

Consent to Participate

This declaration is “not applicable.”

Consent for Publication

This declaration is “not applicable.”

Competing Interests

The authors declare no competing interests.