Multi-parametric optimization of magnetic resonance imaging sequences for magnetic resonance-guided radiotherapy

Abstract

Background and purpose

Magnetic Resonance Imaging (MRI) is widely used in oncology for tumor staging, treatment response assessment, and radiation therapy (RT) planning. This study proposes a framework for automatic optimization of MRI sequences based on pulse sequence parameter sets (SPS) that are directly applied on the scanner, for application in RT planning.

Materials and methods

A phantom with seven in-house fabricated contrasts was used for measurements. The proposed framework employed a derivative-free optimization algorithm to repeatedly update and execute a parametrized sequence on the MR scanner to acquire new data. In each iteration, the mean-square error was calculated based on the clinical application. Two clinically relevant optimization goals were pursued: achieving the same signal and therefore contrast as in a target image, and maximizing the signal difference (contrast) between specified tissue types. The framework was evaluated using two optimization methods: a covariance matrix adaptation evolution strategy (CMA-ES) and a genetic algorithm (GA).

Results

The obtained results demonstrated the potential of the proposed framework for automatic optimization of MRI sequences. Both CMA-ES and GA methods showed promising results in achieving the two optimization goals, however, CMA-ES converged much faster as compared to GA.

Conclusions

The proposed framework enables for automatic optimization of MRI sequences based on SPS that are directly applied on the scanner and it may be used to enhance the quality of MRI images for dedicated applications in MR-guided RT.

1. Introduction

Magnetic Resonance Imaging (MRI) has been integrated into oncology for staging, assessing tumor response, and also for radiation therapy (RT) planning, with the advantages of superior soft-tissue imaging contrast and continuous real-time imaging, which can facilitate tumor and organ-at-risk delineation as well as image registration [1], [2], [3], [4], [5]. The large variety of imaging contrasts in MRI is associated with a large number of different pulse sequence parameter sets (SPS), which have a direct impact on image quality and efficiency of further image processing. Depending on the sequence and the clinical objective, these SPS can consist of up to 30 different parameters (repetition time (TR), echo time (TE), flip angle (FA), bandwidth (BW), turbo factor (TF) and averages, etc.). Each of these parameters directly influences image contrast, image quality, or acquisition time. As many pulse sequences are often not fully optimized to the needs of a specific clinical scenario, additional sequence optimization is often performed manually, which can be cumbersome and time-consuming. Machine learning-based models can help to simplify and automate such tasks, however, to train these models a large amount of data with different SPS needs to be collected and analyzed. Again, manual acquisition of this data at the scanner is a time-consuming procedure that requires repeated human interventions to change the SPS settings, and automation of this acquisition process is preferred. For this, several tools have been presented in literature. “Pulseq” [6] is a high-level, flexible, and hardware-independent open-source framework for the rapid development, representation, and execution of magnetic resonance (MR) sequences. This tool allows users to create customized sequences by applying different schemes of RF pulses and gradients. By utilizing the Pulseq interpreter, these sequences can be exported and executed on a MRI device.

Recently, the self-learning framework ‘MR-zero’ [7], utilizing the Pulseq-tool, has been proposed, which adapts and optimizes MRI sequences based on a Bloch equation simulation. The generated pulse sequence, still requires knowledge of Bloch simulation in order to perform MR sequence optimization. In the more advanced version “MR-double-zero” [8], the “Pulseq” tool is still utilized to remotely control the scanner, however, the optimization directly operates on the acquired imaging data without requiring a Bloch simulation model or any further human interaction. As a prerequisite for implementing clinical sequences with Pulseq, a detailed prior knowledge of the manufacturer pulse schemes with the exact timings of the gradients and RF pulses used in the respective clinical sequence is required. The clinical sequence has then to be built from scratch within Pulseq mimicking as closely as possible the selected sequence.

Just recently, a real-time scanner remote control tool ‘Access-i’ (Siemens Healthineers, Erlangen, Germany) has been introduced, which resolves this problem by allowing the user to access all sequences implemented on the scanner and to change MRI parameters via a script.

This study proposes a framework for automatic optimization of MRI sequences based on SPS that are directly applied on the scanner. Two clinically relevant optimization goals were pursued: i) achieving the same signal and thus contrast as in a target image, and ii) maximizing the signal difference between specified tissue types. Furthermore, the proposed framework is evaluated using two different optimization methods, a covariance matrix adaptation evolution strategy (CMA-ES) and a genetic algorithm (GA). The obtained results demonstrate the potential of the proposed framework for automatic signal difference optimization of MRI sequences, which can improve the application of MRI for application in radiotherapy planning.

2. Material and methods

2.1. Phantom material

Measurements were performed in a cylindrical water phantom equipped with seven in-house fabricated substitutes having different contrasts. The substitutes were kept in place by a PMMA-ring and consisted of different concentrations of agarose (Ag) (AgaroseHEEO Ultra-Quality, Carl RothGmbH&Co. KG, Karlsruhe, Germany), in-house produced nickel-diethylenetriaminepentaacetic acid (Ni-DTPA), and potassium chloride (KCl) (≥99 %, 5 %, Carl RothGmbH&Co. KG, Karlsruhe, Germany). The contrast of Ni-DTPA doped agarose gel was customized to obtain different T1 and T2 relaxation times in MRI by adjusting the concentrations of Ni-DTPA and agarose [9]. Ni-DTPA primarily reduces T1 relaxation time, while a higher concentration of agarose primarily decreases T2 relaxation time. Additionally, KCL is added to adjust the CT value. The substitutes were composed of different concentrations of Ag, Ni, and KCL to create seven different contrasts [10] (see Table 1). As containers, plastic conical centrifuge tubes (50 ml, diameter: 28 m, FalconTM, Thermo Fisher Scientific Inc., Waltham, USA) were used.

Table 1.

Contrast materials providing specific T1 and T2 values at a 1.5 T MRI and 0.35 T MR-Linac. Values as reported in [10].

	Container	#1	#2	#3	#4	#5	#6	#7
1.5 T	T1	420 ± 1	523 ± 1	984 ± 3	1097 ± 4	629 ± 1	876 ± 4	882 ± 2
	T2	67 ± 1	93 ± 2	110 ± 2	46 ± 1	57 ± 1	296 ± 3	107 ± 2
0.35 T	T1	575 ± 4	733 ± 4	1108 ± 4	1155 ± 4	707 ± 4	1106 ± 5	1051 ± 5
	T2	75 ± 5	100 ± 5	119 ± 4	45 ± 1	61 ± 3	311 ± 13	110 ± 5

2.2. Scanner interface

All measurements were performed on a 1.5 T MAGNETOM Sola MR scanner (Siemens Healthineers, Erlangen, Germany) using the 20-channel head coil. To enable the “on-the-run” optimization process, the MR scanner was remotely controlled by Access-i (Siemens Healthineers, Erlangen, Germany). The optimization process was run on a local computer (Intel(R) Core(TM) i5-9400, 2.9 GHz CPU, 6 cores and 16 GB RAM) instead of the host computer of the MRI scanner. By running the optimization process on a separate computer, we were able to optimize the MR sequence parameters based on the acquired images without interfering with the operation of the scanner using an in-house developed Python code. In the next step, optimized SPS are automatically executed, and the optimization loop is terminated if the objective function or parameter values no longer change with respect to a predefined threshold value.

2.3. Optimization process

The SPS was optimized for a 2D turbo spin echo (TSE) sequence with a constant bandwidth of 186 Hz/pixel, resolution of 0.4 × 0.4 mm², slice thickness of 5 mm and turbo factor of 30 with an echo spacing of 11 ms. TE, TR and refocussing FA as main contributors to contrast, were used as optimization parameters and were allowed to vary within a specific range (TE: 12 ms–114 ms, TR: 500 ms –2300 ms and FA: 140°–180°).

The optimization workflow deals with image data obtained for discrete parameter sets directly from the scanner using the Access-i tool. Consequently, gradient-based optimization methods are not applicable since they require a smooth function to calculate the derivatives. We therefore employed two different evolutionary algorithms for evaluation: The genetic algorithm (GA) [11] and the covariance matrix adaptation evolution strategy (CMA-ES) [12]. GA is an evolutionary algorithm that searches for optimal solutions through selection, crossover, and mutation. Through successive iterations, it creates a population of potential solutions, evolves them through crossover and mutation, and selects individuals with the highest objective function values to reproduce the new population and converge to the global optimum solution. In contrast, CMA-ES uses a probabilistic approach that adapts the search distribution using the covariance matrix to focus on promising areas of the search space. This allows efficient convergence to the global optimum solution. Both algorithms were implemented using the Multi-objective Optimization in Python (PyMOO) framework [13]. For GA, we used tournament selection, simulated binary crossover, and polynomial mutation strategies with a default probability of 0.9. For CMA-ES, a sigma value of 0.2 was used. Further, elitism approach was not incorporated into the execution of either algorithm. The workflow was designed to continuously update the SPS and to subsequently execute it on an MR scanner using the Access-i tool, which then results in new image data. In this loop, the signal difference between a predefined regions of interest (ROI) in the substitutes was optimized.

2.4. Clinical use cases

2.4.1. Achieving the same signal as in a target image

Pursuing this goal is reasonable, e.g. if diagnostic MR images are to be included into treatment planning for an 0.35 T MR-Linac, which can exhibit different image signals and thus contrasts between different structures. Using the images from the diagnostic MRI and optimizing the SPS to obtain a similar signal as the MR-Linac may facilitate image processing steps like registration. Also other scenarios, where the target image is acquired at the same device with different sequences or SPS are conceivable.

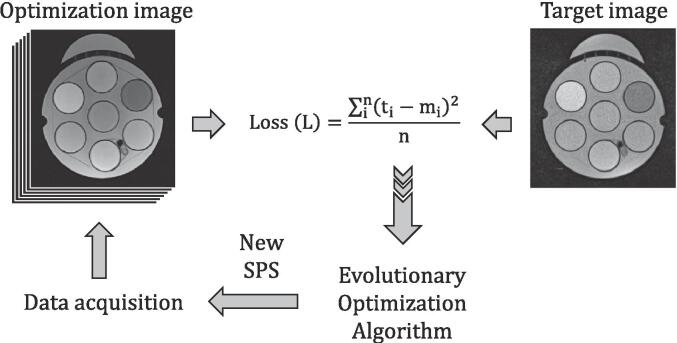
For this, we consider that the scanner generates a signal m_i in substitute i which shall match the signal t_i of the same substitute in the target image acquired under different conditions, without an initial image registration process. The optimization of the SPS involves several steps: First, a set of either predefined or randomly selected parameters is sent to the scanner for data acquisition. Following the acquisition, the substitutes are automatically segmented using region-growing segmentation algorithm [14], [15] and the average signal of each individual ROI m_i is determined. The differences of the signals m_i and t_i determines the mean-square error (MSE) loss function L (Fig. 1), which is sent to the optimizer to update the SPS. Finally, the updated parameters are transferred back to the scanner for the next iteration. This process is repeated until the objective function is below a certain threshold value. Fig. 1 displays the pipeline for ‘on-the-run’ automatic sequence optimization.

Fig. 1.

Flow chart of the proposed “on-the-run” optimization workflow. The optimizer uses the Access-i tool to send the sequence parameters to a real MR scanner, resulting in a set of four MR images (population size of four). These images are then compared to the target to calculate the mean squared error (MSE). The MSE is then fed back to the optimizer to update the sequence parameters until the optimum solution is achieved.

In our experiments, we used a 0.35 T MR-Linac (MRIdian Linac, Viewray Inc., Oakwood, USA) image as a target image (TR = 2000 ms, TE = 35 ms, TF = 15, BW = 202 Hz/pixel, FA = 180° and resolution = 0.78x0.78 mm²). The SPS on the MAGNETOM Sola MR Scanner resulted in optimization image m that is optimized during the process.

2.4.2. Maximizing the signal difference between different tissue types

This use case maximizes the signal difference and thus contrast between specified adjacent tissues to improve the conditions for automated segmentation of tumors and/or organs at risk. For this, we start with a set of either predefined or randomly selected parameters and automatically segment the substitutes in the acquired images. Then, the contrast between neighbouring pairs of substitutes is calculated as the signal difference of m_i and m_j (i < j). As each signal difference in the objective function represents a different clinical objective, this problem can be considered as a multi-objective optimization (MOO) problem. As MOOs are computationally expensive and time-consuming, it is difficult to solve such a problem directly by measurements on the scanner. Therefore, the classical approach of considering a weighted sum of the individual objective functions is applied to arrive at a single objective function [16]:

$$F=\sum _{i,j}{\lambda }_{\mathit{ij}}{\left(m_i-m_j\right)}^{2}withi=1\cdots (n-1),j=(i+1)$$

Where the λ_ij are the weights of the objective functions terms ${\left(m_i-m_j\right)}^2$. To evaluate the performance of the multi-objective optimization algorithm, we conducted experiments with different weighting factors. To begin, we initialized the weights for all containers (λ₁₂, λ₂₃, λ₃₄, λ₄₅, λ₅₆, λ₆₇) to 1 and performed optimization. We then changed the weighting factors λ₃₄ and λ₄₅ to 5, while keeping the other weights (λ₁₂, λ₂₃, λ₅₆, λ₆₇) equal to 1 and evaluated the resulting contrasts.

3. Results

3.1. Achieving the same signal as in a target image

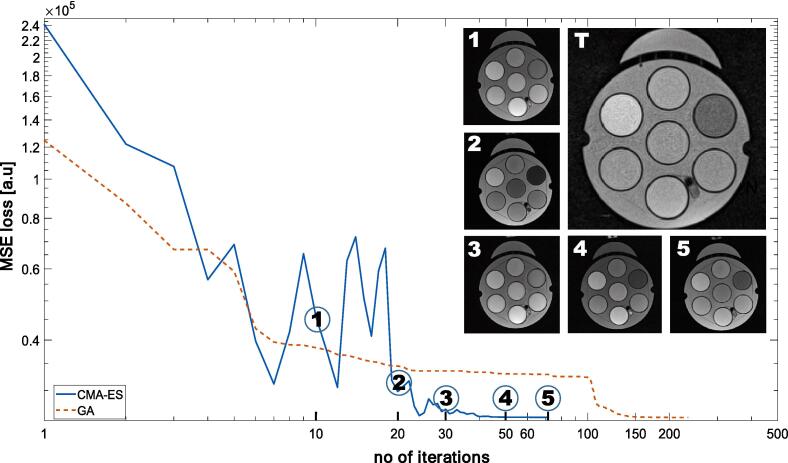
Fig. 2 compares the loss functions for both optimization methods applied in this study. GA needed a larger number of iterations to converge as compared to CMA-ES. Nevertheless, both methods ultimately converged to the same objective function and parameter values (FA: 180°, TE: 50 ms, TR: 2010 ms). For the CMA-ES optimization method, the optimization required 73 iterations (time: ∼2.5 h) to converge, while the GA optimization took 172 iterations (time: ∼4h). The overall experimental duration includes: acquisition time (10–40 s), total number of acquisitions, time required for remotely control MRI using Access-i, and optimization computation, the first two being the limiting factors.

Fig. 2.

A comparison of the MSE loss functions for the GA and CMA-ES optimization methods. Additionally, five images at different iteration numbers (10, 20, 30, 50 and 73) for the CMA-ES method as well as the target image (T) are shown. Note: Images represent one sample image out of a population size of four acquired with various parameter combinations. As a result of the stochastic feature of the GA, the intensity distribution of image 3 is not between image 2 and image 4. In contrast, MSE loss represents the average loss of all four images.

To visualize the progress of the optimization process, the image contrast at 10, 20, 30, 50, and 73 iterations obtained with the CMA-ES method is displayed and compared with the target image (T) acquired at the 0.35 T MR-Linac. The very good agreement between the optimized and the target image indicates successful optimization of the signal distribution. Fig. 3 illustrates the parameters development throughout the optimization process.

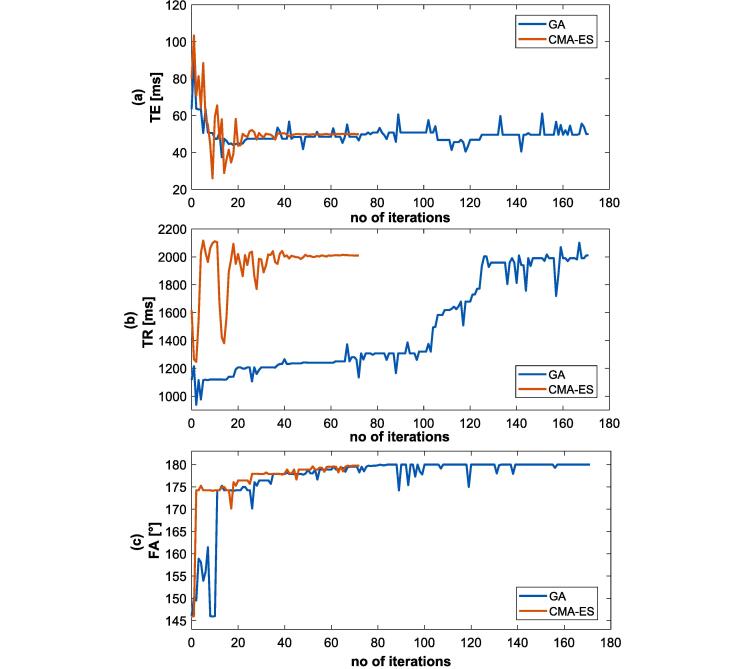
Fig. 3.

Shows the development of TE (a), TR (b) and FA (c) parameters during the optimization process. CMA-ES converges in fewer iterations compared to GA, although both methods results in the same final parameter values.

3.2. Maximizing the signal difference between different tissue types

The CMA-ES and GA methods were also evaluated with respect to maximizing the signal difference between selected substitutes, where CMA-ES required fewer iterations than GA. Therefore, only the final results obtained from CMA-ES are presented. Table 2 presents the results of the optimization method for the two analysed cases. Case 1 (all weights = 1) resulted in rather low contrast between substitutes 3/4 and 4/5, respectively. Case 2 (λ₃₄ = λ₄₅ = 5) markedly improved the contrast between substitutes 3/4 and 4/5, however, on the cost of a decreased contrast between the other substitutes. We found (FA: 173°, TE: 91 ms, TR: 2090 ms) and (FA: 180°, TE: 11 ms, TR: 700 ms) as the optimal parameter values for Case 1 and Case 2, respectively. Fig. 4 further gives a visual representation of these results.

Table 2.

Signal and contrast for the measured substitutes for two different sets of weighting factors.

Container	1		2		3		4		5		6		7
Case 1 (λ12 = λ23 = λ34 = λ45 = λ56 = λ67 = 1)
Signal [a.u]	715.43		232.46		826.68		940.52		894.82		1227.79		494.94
Contrast [a.u]		482.97		594.22		113.84		45.70		332.97		732.85
Case 2 (λ12 = λ23 = λ56 = λ67 = 1, λ34 = λ45 = 5)
Signal [a.u]	688.79		612.78		1030.27		1627.86		1126.77		1095.36		1213.98
Contrast [a.u]		76.01		417.49		569.59		501.09		31.41		118.59

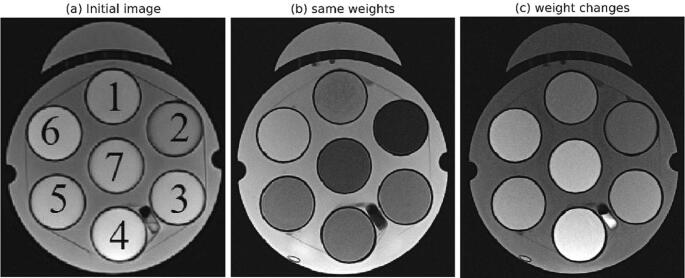
Fig. 4.

Illustration of the impact of the two sets of weighting factors: initial image (a) and image after optimization with λ₁₂ = λ₂₃ = λ₃₄ = λ₄₅ = λ₅₆ = λ₆₇ = 1 (b, case 1) and λ₃₄ and λ₄₅ raised to 5 (c, case 2), respectively.

4. Discussion

In the present study, we demonstrated a proof-of-concept for fully automatic optimization of signal differences in MRI sequences by applying the sequence of SPS directly on the scanner. The optimization was performed for a 2D TSE sequences due to its relatively short acquisition time. We optimized the signal differences by changing the three parameters TR, TE, and FA, however, more parameters could in principle be included.

Furthermore, our study demonstrated how MR sequences can be optimized specifically for application in radiotherapy using two clinical use cases: (i) achieving the same signal as in a target image and (ii) maximizing the signal difference between different tissue types. Use case (i) improves radiotherapy planning in MRgRT, where diagnostic MRI images may be used and registered to images obtained at the MR-Linac [17], [18], [19]. This registration will be facilitated, if the image from the diagnostic MRI is optimized to have the same signal as the target image from the MR-Linac. Use case (ii) on the other hand, is useful to better distinguish adjacent tissue structures and to automatically delineate them for treatment planning.

In this study, we evaluated two optimization algorithms based on evolutionary strategies: GA and CMA-ES. Each iteration of the algorithms runs on a specific population size, determining how many samples have to be acquired and evaluated per iteration. We tested different population sizes, with 2–5 acquisitions and found that a population size of 4 was most suitable for both GA and CMA-ES based on time efficiency. Here, CMA-ES required 73 iterations (resulting in a total of 292 acquisitions), while GA required 172 iterations (resulting in a total of 688 acquisitions).

Furthermore, comparison of the two optimization methods suggests that CMA-ES converges faster and should therefore be preferred over the GA algorithm. It is important to note, however, that the required population size and the number of iterations may differ significantly depending on the number of sequence parameters included in the optimization and the resulting complexity of the objective function. As a proof-of-principle, we only optimized for three sequence parameters in this study. Regarding population size, there is a trade-off between slowing down the optimization by larger population sizes and insufficient diversity if the size is too small.

As an alternative to the employed optimization algorithms, one could also use a discrete gradient descent optimization method [20], a derivative-free approach for solving unconstrained non-smooth optimization problems. This method is based on the concept of discrete gradients, which can approximate the sub-gradients of a wide range of non-smooth functions. Furthermore, this method can improve computational efficiency, as it requires a small population size, therefore requiring a smaller number of image acquisitions. Previous studies [21], [22], [23] have shown that this method is computationally efficient in solving non-smooth optimization problems.

In contrast to the present approach, SPS optimization based on Bloch equations can be performed, which may be faster compared to real acquisition optimization as it does not require a MR device. However, it heavily relies on the knowledge of Bloch simulation to implement a specific sequence and accurate T1 and T2 relaxation times for each tissue, which are not necessarily known. In contrast, our proposed method operates directly on the MR scanner without prior knowledge and simplifies the optimization process and makes it more practical.

In addition, some limitations should be addressed. First, the potential influence of gradient heating and field drifts due to such a long measuring time must be acknowledged, as they may affect image quality and measurement accuracy [24], [25]. Secondly, the phantom was newly prepared following the recipe as described in [10]. However, the T1 and T2 values were not verified again. Thirdly, some MR parameters were not accessible using Access-i, such as echo spacing and echo-train-length/turbo-factor, which also play an important role in contrast formation. Finally, the optimal parameters obtained by using the proposed workflow may be different from clinically used parameters and while the new contrast may be beneficial for a certain application, it may come along with a suboptimal diagnostic image quality.

In this proof-of-principle study, the optimization was performed on a phantom and for clinical implementation, the optimized sequences need also to be tested in-vivo. While phantoms measurements are useful to establish and calibrate an optimized sequence, images may additionally be affected by differences in object size, conductivity and by complex physiological and/or dynamical conditions within the human body. Therefore, the contrast obtained with the optimized SPS has to be validated in humans. As the optimization of the rather simple and fast TSE already took almost 3 h, it may not be feasible to perform the full optimization in-vivo, however, the SPS could be pre-optimized in anthropomorphic phantoms and the obtained SPS may be used as a starting point for further optimization in vivo. This approach may significantly reduce the required optimization times in humans.

Further, more clinical sequences may be integrated into the optimization pipeline, for example, the 3D True Fast Imaging with Steady State Free Precession used for planning at the MRIdian MR-Linac. Finally, further studies have to investigate additional optimization parameters such as contrast-to-noise (CNR), signal-to-noise ratio (SNR) and acquisition time.

In conclusion, the proposed framework for an automatic multi-paratactic optimization of SPS directly on MRI scanner has the potential to enhance the quality of MRI images for specialized purposed in MRgRT. The optimization workflow was established and exemplarily tested for two clinical use cases: (i) achieving the same signal as in a target image, and (ii) maximizing the signal difference between different tissue types. Evaluation of two optimization methods based on evolutionary strategies suggests that CMA-ES is an efficient approach to improve the signal as in a target image or to optimize signal difference between two given tissues. The presented method may be extended by including additional sequence parameters and image quality goals and therefore provides a flexible tool for optimizing MR image sequences for different clinical needs.

CRediT authorship contribution statement

Hafiz Muhammad Fahad: Conceptualization, Methodology, Software, Visualization, Investigation, Writing – original draft. Stefan Dorsch: Conceptualization, Visualization, Writing – original draft. Moritz Zaiss: Validation, Writing – review & editing. Christian P. Karger: Supervision, Validation, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.