Development and validation of a lung graph–based machine learning model to predict acute pulmonary thromboembolism on chest noncontrast computed tomography

Abstract

Background

Computed tomography pulmonary angiography (CTPA) is a first-line noninvasive method to diagnose acute pulmonary thromboembolism (APE); however, whether chest noncontrast CT (NC-CT) could aid in the diagnosis of APE remains unknown. The aim of this study was to build and evaluate a holistic lung graph-based machine learning (HLG-ML) using NC-CT for the diagnosis of APE and to compare its performance with that of radiologists and the YEARS algorithm.

Methods

This study enrolled 178 cases (77 males; age 63.9±16.7 years) who underwent NC-CT and CTPA in the same day from January 2019 to December 2020. Of these patients, 133 (75% of cases; 58 males; age 65.4±15.6 years) were placed into a training group and 45 (25% of cases; 19 males; age 59.6±19.2 years) into a testing group. The other 43 cases (18 males; age 62.8±20.0 years) were used to externally validate the model between January 2021 and March 2022. A HLG was developed with a pulmonary radiomics descriptor derived from NC-CT images. The approach extracted local radiomics features and encoded these local features into a radiomics descriptor as a characterization of global radiomics feature distribution. Subsequently, 8 ML models were trained and compared based on the radiomics descriptor. In the validation group, area under the curves (AUCs) of the HLG-ML model in the diagnosis of APE were compared with those of the 3 radiologists and the YEARS algorithm.

Results

Among the 8 ML models, gradient boosting decision tree demonstrated the best classification performance (AUC =0.772) on the training set. In the testing set, the AUC of gradient boosting decision trees was 0.857 [95% confidence intervals (CIs): 0.699–0.951]. In the validation set, the performance of gradient boosting decision tree (AUC =0.810; 95% CI: 0.669–0.952; Youden index =0.621) outperformed 3 radiologists (AUC =0.508, 95% CI: 0.335–0.681, Youden index =0.016; AUC =0.504, 95% CI: 0.354–0.654, Youden index =0.008; AUC =0.527, 95% CI: 0.363–0.691, Youden index =0.050) and the YEARS algorithm (AUC =0.618; 95% CI: 0.469–0.767; Youden index =0.237).

Conclusions

Compared to all 3 radiologists and the YEARS algorithm, the proposed HLG-based gradient boosting decision tree model achieved a superior performance in the diagnosis of APE on the NC-CT and may thus serve as a valuable tool for physicians in the diagnosis of APE.

Introduction

Venous thromboembolism, which manifests as deep venous thrombosis (DVT) or pulmonary thromboembolism (PE), is globally the third most frequent acute cardiovascular syndrome behind myocardial infarction and stroke (1,2). Clinical probability assessments such as Wells score (3), revised Geneva score (4), and the YEARs algorithm (5) have been developed to predict acute PE (APE); however, the Wells score and the revised Geneva score cannot always be applied to critical patients, as their symptoms and signs are often nonspecific, making it difficult to distinguish APE from other emergencies (6); meanwhile, the YEARs algorithm contains a subjective item, which is highly influenced by the experience of the physician (5).

Computed tomography pulmonary angiography (CTPA) is the first-line noninvasive protocol for detecting and evaluating APE. However, since patients with APE have different clinical manifestations from mild unspecific symptoms and signs to sudden death, CTPA may not be completed upon admission even in the emergency department. Moreover, not every patient is suitable for a CTPA scan, especially those who may have contraindications to contrast agent, renal dysfunction, or high-risk unstable hemodynamic conditions. In addition, increasing use of CTPA has led to the unnecessary risk of increased radiation exposure and contrast medium-induced nephropathy (7). In contrast, chest noncontrast CT (NC-CT) is a convenient and cost-effective examination method which is more often performed for the evaluation of nonspecific chest symptoms. However, the methodology and value of NC-CT in the diagnosis of APE have not been extensively reported.

Radiomics and deep learning (DL) or machine learning (ML) have been used to improve the diagnosis, therapy planning, and prognosis evaluation of tumors (8-13). Radiomic features derived from conventional medical images can provide additional information beyond the scope of visual perception. Recently, Dicente Cid et al. (14) proposed a holistic lung graph (HLG) model that could quantify the tissue texture in the lung parenchyma, merging local and global radiomics of the lungs to classify patients with vascular pathologies. Based on texture analysis on CTPA images, Jimenez-Del-Toro et al. (15) developed a lung graph model to differentiate patients with chronic thromboembolic pulmonary hypertension (CTEPH) from those with PE who did not develop pulmonary hypertension. ML is a field that focuses on the learning aspect of artificial intelligence (AI) by developing algorithms that best represent a set of data and has been widely used in disease diagnosis and evaluation.

To the best of our knowledge, no study has examined the application of HLG-based ML (HLG-ML) model for NC-CT images to diagnose APE. In this study, our objective was thus to develop a HLG model for the extraction, integration, and selection of the holistic pulmonary radiomics descriptors on NC-CT images and then to build an HLG-ML model based on the distribution of radiomics feature rather than pure radiomics feature. Specifically, in this model, diverse local radiomics features are extracted from the lung atlas, forming multiple lung graphs, and each lung graph is encoded into a radiomics descriptor as a marker of global radiomics feature distribution for model building. To illustrate the effectiveness of the HLG-ML model, its performance was compared with that of radiologists and the YEARS algorithm (5).

Methods

Study cohort and design

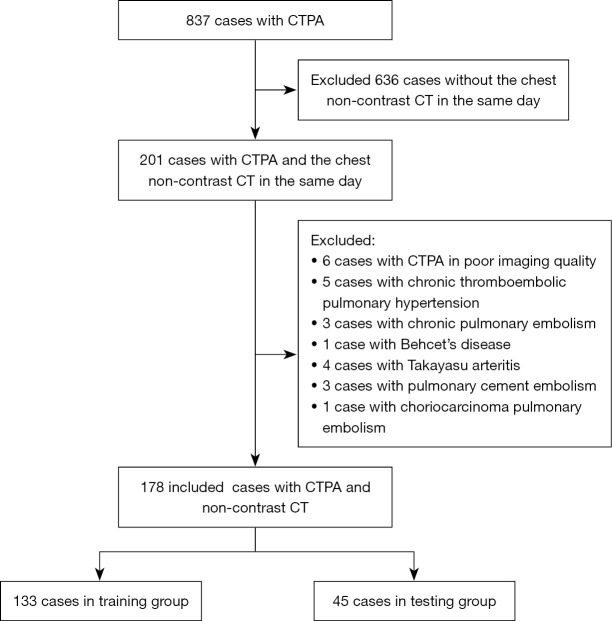
This single-center, retrospective cohort study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by the Institutional Ethics Board of China-Japan Friendship Hospital (No. 2023-KY-070). Individual consent for this retrospective analysis was waived. First, we retrospectively screened patients who underwent CTPA from January 2019 to December 2020 on the Picture Archiving and Communication System (PACS; Carestream Health, Rochester, NY, USA) in our hospital. Second, we included patients who underwent chest NC-CT and CTPA on the same day. Third, among the included cases, 75% and 25% of cases were randomly assigned to a training group and testing group, respectively. Then, patients who underwent chest NC-CT on the same day of CTPA on PACS between January 2021 and March 2022 were placed into a validation group. Subsequently, patients with poor image quality on CTPA (e.g., motion artifacts due to without breath-holding or suboptimal enhancement leading to low contrast enhancement of the pulmonary artery) were excluded. Patients who, according to their electronic medical records, were diagnosed with chronic PE (CPE), CTEPH, nonthrombotic pulmonary embolism, pulmonary arterial sarcoma, or Takayasu arteritis were excluded. In the validation group, the YEARS algorithm (5) was applied to predict the possibility of APE. Figure 1 provides a flowchart detailing how cases in training and testing groups were selected.

Figure 1.

Flowchart of participant selection. CTPA, computed tomography pulmonary angiography; CT, computed tomography.

Chest CT scan

All patients underwent chest NC-CT and CTPA on the same day. Chest NC-CT was obtained in the helical model in the craniocaudal direction with multidetector CT scanners (Aquilion ONE TSX-301C/320, Toshiba, Tokyo, Japan; Brilliance iCT/256, Philips, Amsterdam, The Netherlands). The whole chest was craniocaudally scanned from the lung apex to the lowest hemidiaphragm during a single breath-hold. The scan parameters were as follows: tube voltage 100–120 kVp, tube current 100–300 mAs, section thickness 1.25–2.50 mm, table speed 39.37 mm/s, and gantry rotation time 0.8 s. The mean value of volume CT dose index (CTDI_vol) was 4.51±2.63 mGy, and the dose length product (DLP) was 113.55±61.42 mGy·cm.

CTPA was performed in in the helical model in the craniocaudal direction under the following parameters: tube voltage 100–120 kVp, tube current of 100–300 mAs, section thickness 0.625–1 mm, table speed 39.37 mm/s, gantry rotation time 0.8 s, and reconstruction increment 1–1.25 mm. A soft-tissue reconstruction kernel was used. A mechanical injector was used for intravenous bolus injection of iopromide (370 mg/mL; Ultravist, Bayer, Leverkusen, Germany) at a flow rate of 5.0 mL/s. For optimal intraluminal contrast enhancement, the automatic bolus-tracking technique ensured that the region of interest (ROI) was positioned at the level of the main pulmonary artery with a predefined threshold of 100 Housefield unit (HU), and a fixed delay of 5 seconds was employed for data acquisition. The mean value of CTDI_vol was 9.13±2.01 mGy, and the DLP was 318.07±37.61 mGy·cm.

HLG model based on NC-CT

Region-of-interest segmentation

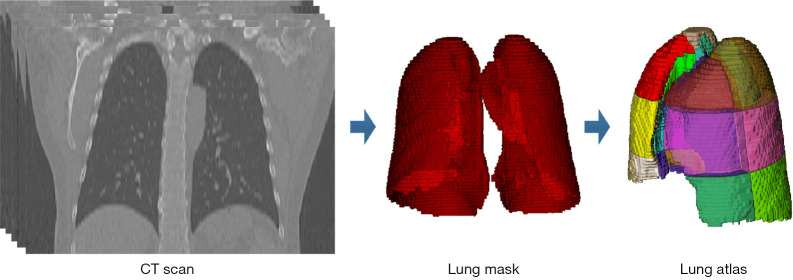
NC-CT images were first preprocessed using isometric sampling with a 1×1×1 mm³ windowing operation, a window level of −600 HU, and a window width of 1,500 HU. Subsequently, a pipeline composed of 2 steps was performed for obtaining a specific artificial lung per patient, which was considered to be the ROI. Initially, lung segmentation was automatically performed with a DL-based segmentation method on InferRead CT Lung (version R3.12.3; Infervision Medical Technology Co., Ltd., Beijing, China) to obtain a lung mask for each piece of NC-CT data. Then, each lung mask was geometrically converted into an atlas containing 36 subregions (14), which was first introduced by Zrimec et al. (16,17). The creation of the lung atlas is shown in Figure 2. In this study, ROI segmentation was implemented using a subregion mask from the atlas to select the voxels within the lung field.

Figure 2.

Creation of the lung atlas. With a sequence of CT slices from a patient, the lung mask was first automatically obtained using the lung segmentation method. The lung atlas was then created by geometrically dividing the lung mask. CT, computed tomography.

Radiomics-based lung graph construction

For each segmented subregion r_i from the lung field, radiomics features were extracted by using PyRadiomics (version 3.0.1; https://pyradiomics.readthedocs.io) in the Python environment (version 3.7.3, Python Software Foundation; https://www.python.org/). During feature extraction, 2 groups of filter operations, Laplacian of Gaussian (LoG) and wavelet decomposition, were applied on each segmented subregion and 7 different classes of radiomics features, including first-order statistics, 3D shape-based features, gray-level cooccurrence matrix (GLCM), gray-level run-length matrix (GLRLM), gray-level size zone matrix (GLSZM), neighboring gray-tone difference matrix (NGTDM), and gray-level dependence matrix (GLDM), were extracted from each copy of the processed and original ROI segmentations. The details of feature extraction using PyRadiomics are available in the literature (18), and a detailed description of each radiomics feature can be found online (https://pyradiomics.readthedocs.io). Overall, 1,004 radiomics features were extracted from each ROI segmentation, which contained 187 first-order statistical features, 14 3D shape features, 253 GLCM features, 176 GLRLM features, 165 GLSZM features, 55 NGTDM features, and 154 GLDM features. For the lung field as a whole, a lung graph for a radiomics feature f_j was defined as the set with N (N≤36) regional feature nodes f_j = {f_j(r₁), f_j(r₂), ..., f_j(r_N)} in this study, and thus 1,004 lung graphs were built.

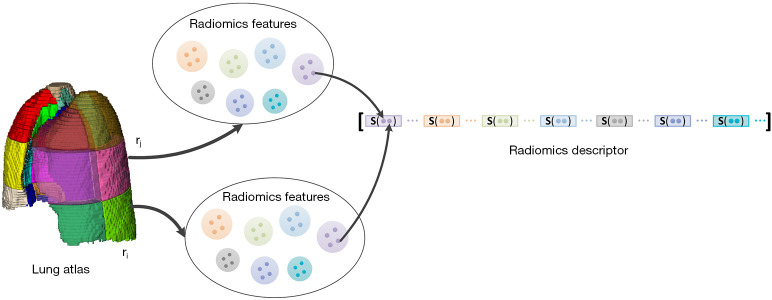
Pulmonary radiomics descriptor integration

With consideration to the data derived from patients who had undergone lung resection, the dimension of such a feature vector was considered to be 36 at most. To directly reflect the distribution of these radiomics features throughout the lung field, 10 common statistics of each feature vector were calculated: maximum value (s₁ = max(fj)), minimum value (s₂ = min(fj)), median value (s₃ = median(fj)), 10th percentile value (s₄ = percentile(f_j,10)), 90th percentile value (s₅ = percentile(f_j,90)), mean value (s₆ = mean(fj)), standard deviation (s₇ = std(fj)), interquartile range (s₈ = percentile(f_j,75)-percentile(f_j,15)), skewness (s₉ = skew(fj)), and kurtosis (s₁₀ = kurt(fj)). The final pulmonary radiomics descriptor vector v was defined as the concatenation of the 10 statistics for each radiomics feature, as follows: v = [s(f₁) || s(f₂) || ... || s(f₁₀₀₄); s = (s₁, s₂, ..., s₁₀)]. This concatenation resulted in the following: $v\in {ℝ}^{10040}$. The construction of the pulmonary radiomics descriptor is shown in Figure 3.

Figure 3.

Construction of the pulmonary radiomics descriptor. Radiomics features were first extracted from each subregion in the lung field. Taking a single radiomics feature as an example, its radiomics feature vector in the lung field was obtained. A cluster of statistics were subsequently calculated for this feature vector. The pulmonary radiomics descriptor was formed from a concatenation of statistics of all feature vectors.

Dimensionality reduction of the pulmonary radiomics descriptor

A large number of features in the pulmonary radiomics descriptor vector might result in an overfitting problem, reducing model robustness. Hence, it was necessary to apply dimensionality reduction to the proposed radiomics descriptor in the training stage. A 3-step workflow for feature dimensionality reduction was adopted in this study. Initially, the Mann-Whitney test was used to conduct a significance analysis for each of the features in the pulmonary radiomics descriptor. These features were ranked according to the P values in ascending order, and the top 1% of the sorting features were retained for subsequent analysis. Subsequently, the Pearson correlation coefficient (r) was calculated between each pair of the remaining features. All pairs of features with |r|>0.85 were filtered, and the feature in each of these pairs with the larger P value from the Mann-Whitney test was removed from the feature set. Finally, least absolute shrinkage and selection operator (LASSO) regression with 5-fold cross-validation was applied to select features with nonzero coefficients from the preserved features for the diagnosis of APE.

ML model development and validation

Using the processed pulmonary radiomics descriptor as input, 8 ML models including Naïve Bayes, logistic regression, k-nearest neighbors, random forest, decision tree, gradient boosting decision tree, support vector machine, and multilayer perceptron were selected and fitted on the training set. Three-fold cross validation was performed on the training set to determine the best hyperparameters for each model and to select the best model. During training, the hyperparameters of each ML model were randomly assigned via grid search (Table S1). The area under the curve (AUC) was selected as the criterion for model performance evaluation. The mean of the AUC values during cross-validation was regarded as the discriminating power of the specific model using the given hyperparameters.

The ML model which demonstrated the best results in the training group (75% of cases) was then applied to the testing group (25% of cases). Thereafter, NC-CT scans of patients between January 2021 and March 2022 were used for model validation. All modeling implementations were conducted in the Python environment (version 3.7.3, Python Software Foundation) based on the scikit-learn package (version 0.21.2; https://scikit-learn.org/).

Diagnostic performance of radiologists

The NC-CT images of each patient in the external group were independently evaluated by 3 chest radiologists with 3 years (reader 1), 5 years (reader 2), and 15 years (reader 3) of experience, respectively, who were blinded to all clinical information and the clinical diagnosis. The diagnosis of the 3 radiologists using NC-CT scans included definite APE and unsure APE.

Statistical analysis

Statistical analyses were performed using SPSS 22.0 (IBM Corp., Armonk, NY, USA) and MedCalc version 20.211 (MedCalc Software Ltd., Ostend, Belgium). The clinical data of the included patients are expressed as the mean ± standard deviation (SD) or median with interquartile range (IQR). Independent samples t test, nonparametric 2-independent samples U test, χ², or Fisher exact test was used to compare the 2 groups. The diagnostic performances of the 3 radiologists and the proposed HLG-ML model were evaluated on the validation set by using AUCs. AUCs were compared using the DeLong Test, and the 95% confidence intervals (CIs) of the AUCs were calculated. Sensitivity and specificity were also calculated. Interobserver consistency among 3 radiologists was evaluated using intraclass correlation coefficient (ICC). All statistical tests were 2-sided, and P values <0.05 were considered significant.

Results

Patient characteristics

The clinical characteristics of all patients are summarized in Table 1. A total of 178 cases (77 males; age 63.9±16.7 years) from January 2019 to December 2020 were randomly grouped into a training set (n=133; 58 males; age 65.4±15.6 years) and a testing set (n=45; 19 males; age 59.6±19.2 years). Table 2 lists the clinical characteristics of patients with APE and those without APE in the training and testing group. The D-dimer level in the APE group was significantly higher than that in the non-APE group (U=1,605.5; P<0.001), while the other clinical metrics were comparable (P>0.05). The other 43 cases (18 males; age 62.8±20.0 years) including 31 patients with APE and 12 patients without APE between January 2021 and March 2022 were used for external validation of the HLG-ML model. In the validation group, gender (χ²=1.944; P=0.163), age (t=–0.030; P=0.967), and body mass index (BMI; t=0.777; P=0.442) between the groups pf patients with APE and without APE were comparable; however, the D-dimer level in patients with APE was higher than that in patients without APE (U=68.5; P=0.001).

Table 1. Clinical characteristics of included patients.

Characteristics	Training group (n=133)	Testing group (n=45)	Validation group (n=43)	P†	P‡	P§
Male/female	58/75	19/26	18/25	0.871	0.774	0.973
Age (years)	65.4±15.6	59.6±19.2	62.8±20.0	0.043*	0.332	0.388
APE (n)	63 (47.3)	23 (51.1)	31 (72.1)	0.609	0.006*	0.009*
BMI (kg/m2)	25.5±4.5	25.5±4.6	24.6±3.9	0.996	0.262	0.418
Temperature (℃)	36.6±0.8	36.7±0.5	36.6±0.3	0.731	0.383	0.278
HR (bpm)	85.0±17.0	91.7±18.1	89.6±14.6	0.059	0.144	0.626
RR (times/min)	20.9±3.8	20.9±3.3	21.3±3.3	0.957	0.757	0.814
SP (mmHg)	126.1±24.7	129.0±19.9	128.0±15.7	0.531	0.677	0.849
DP (mmHg)	76.2±13.7	74.8±13.9	77.6±12.2	0.610	0.504	0.401
Chest pain	31 (23.3)	12 (26.7)	18 (41.9)	0.689	0.018*	0.133
Dyspnea	83 (62.4)	27 (60.0)	31 (72.0)	0.774	0.284	0.232
Hemoptysis	9 (6.8)	2 (4.4)	4 (9.3)	0.576	0.598	0.673
Fever	15 (11.3)	10 (22.2)	6 (14.0)	0.068	0.538	0.315
Syncope	11 (8.3)	2 (4.4)	4 (9.3)	0.394	0.523	0.366
WBC (×109/L)	8.8±4.1	8.3±4.7	9.5±4.1	0.261	0.245	0.467
Percentage of neutrophils (%)	72.2±11.3	73.8±10.7	73.3±12.4	0.193	0.521	0.552
Percentage of lymphocytes (%)	19.3±9.9	17.4±9.1	19.5±10.8	0.277	0.988	0.343
Hemoglobin (g/L)	127.1±22.1	123.6±26.5	125.9±16.7	0.400	0.709	0.630
CRP (mg/L)	17.9 (4.2–52.1)	27.2 (3.7–48.5)	19.5 (4.1–49.3)	0.659	0.787	0.126
D-Dimer (mg/L)	2.2 (1.0–6.7)	2.5 (0.9–7.4)	3.1 (1.2–6.4)	0.961	0.511	0.440
NT-proBNP (pg/mL)	391.0 (88.5–1,600.0)	213.0 (48.3–1,068.5)	324.0 (38.8–1,816.5)	0.185	0.636	0.657

Data are presented as the mean ± standard deviation, median (interquartile range), or number (%). *, P<0.05; ^†, training group and testing group; ^‡, training group and validation group; ^§, testing group and validation group. APE, acute pulmonary thromboembolism; BMI, body mass index; HR, heart rate; RR, respiratory rate; SP, systolic pressure; DP, diastolic pressure; WBC, white blood cell; CRP, C-reactive protein; NT-proBNP, N-terminal prohormone of brain natriuretic peptide.

Table 2. Clinical characteristics of patients with APE and without APE in the training and testing groups.

Clinical data	APE (n=86)	Non-APE (n=92)	χ2/t/U test	P
Male/female	37/49	40/52	χ2=0.004	0.536
Age (years)	63.4±16.8	46.5±16.7	t=0.426	0.67
BMI (kg/m2)	25.2±4.0	25.8±5.1	t=0.639	0.524
Temperature (℃)	36.8±0.6	36.7±0.6	t=0.049	0.961
HR (bpm)	88.6±18.4	84.1±17.3	t=1.446	0.15
RR (times/min)	21.3±4.2	20.3±2.8	t=1.518	0.131
SP (mmHg)	126.0±19.4	127.8±28.2	t=0.435	0.664
DP (mmHg)	75.3±13.2	76.6±14.3	t=0.561	0.575
Chest pain	59 (68.6)	51 (55.4)	χ2=3.266	0.071
Dyspnea	11 (12.8)	14 (15.2)	χ2=0.271	0.641
Hemoptysis	24 (27.9)	19 (20.7)	χ2=1.277	0.258
Fever	8 (9.3)	3 (3.3)	χ2=2.798	0.094
Syncope	7 (8.1)	6 (6.5)	χ2=0.172	0.678
WBC (×109/L)	9.6±4.3	8.5±4.2	t=1.773	0.078
Percentage of neutrophils (%)	73.6±10.2	72.1±11.9	t=0.874	0.383
Percentage of lymphocytes (%)	18.1±9.1	19.5±10.3	t=0.945	0.346
Hemoglobin (g/L)	126.7±24.3	125.8±22.4	t=0.260	0.795
CRP (mg/L)	27.0 (5.7–52.9)	14.2 (3.1–41.7)	U=2,422.5	0.086
D-Dimer (mg/L)	4.8 (2.0–10.7)	1.2 (0.7–2.7)	U=1,605.5	<0.001
NT-proBNP (pg/mL)	390.5 (72.5–1,523.0)	322.0 (92.0–1,568.0)	U=3,213.2	0.931

Data are presented as the mean ± standard deviation, median (interquartile range), or number (%). APE, acute pulmonary thromboembolism; BMI, body mass index; HR, heart rate; RR, respiratory rate; SP, systolic pressure; DP, diastolic pressure; WBC, white blood cell; CRP, C-reactive protein; NT-proBNP, N-terminal prohormone of brain natriuretic peptide.

Pulmonary radiomics descriptor generation and dimensionality reduction

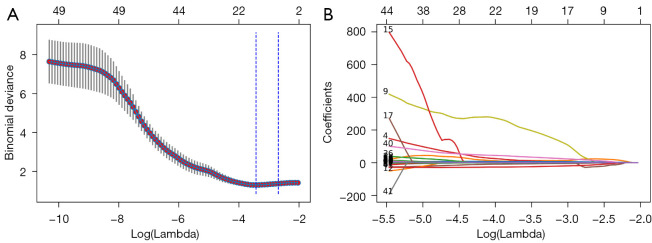
A total of 1,004 radiomics features were successfully extracted from each subregion split from each patient’s NC-CT images, yielding 1,004 multidimensional radiomics-based lung graphs. Following this, the higher-dimensional pulmonary radiomics descriptor vector for each patient was effectively formed. To avoid overfitting, feature dimensionality reduction was conducted on the pulmonary radiomics descriptors. After significance analysis and correlation analysis, 49 features were left in each radiomics descriptor. The P value of each of these features was less than 0.033 in the training set, and |r|<0.85. Subsequently, the remaining candidates in each radiomics descriptor vector were reduced to 19 potential features using LASSO regression (Figure 4). The detailed description of each of the selected features used in the radiomics descriptor vector can be found in Table 3.

Figure 4.

Feature selection via LASSO. (A) The selection of the parameter λ in LASSO through the criteria minimization using 5-fold cross-validation. Plot of a binomial deviance curve with log(λ) on the x-axis. The corresponding λ of the minimum binomial deviation was selected as the optimal value. The selected λ in this experiment was 0.03239994 when log(λ) was –3.42959879. (B) LASSO coefficient distribution of 49 features. LASSO, least absolute shrinkage and selection operator.

Table 3. The selected 19 features in the radiomics descriptor.

Filter operation	Radiomics category	Radiomics feature	Statistics
Wavelet-LLL	GLRLM	Short run low gray level emphasis	10th percentile
Log-sigma-2-0-mm-3D	GLRLM	Run variance	Kurtosis
Wavelet-HHL	GLCM	IMC1	90th percentile
Wavelet-LLL	GLCM	Maximum probability	Skewness
Wavelet-HHH	GLDM	Dependence entropy	Interquartile range
Wavelet-LHH	GLCM	Correlation	Skewness
Wavelet-LLL	GLSZM	Small area low gray level emphasis	10th percentile
Wavelet-LHH	First order	Median	Interquartile range
Log-sigma-2-0-mm-3D	GLSZM	Small area emphasis	Maximum
Wavelet-HHL	GLSZM	Zone entropy	Standard deviation
Wavelet-LHH	GLSZM	Zone entropy	Interquartile range
Wavelet-LHL	GLRLM	Run length non uniformity	Kurtosis
Log-sigma-2-0-mm-3D	GLDM	Large dependence low gray level emphasis	Standard deviation
Wavelet-HHH	GLSZM	High gray level zone emphasis	Interquartile range
Log-sigma-1-0-mm-3D	GLCM	Inverse variance	Interquartile range
Wavelet-LHH	GLCM	Inverse variance	Skewness
Wavelet-HLL	GLRLM	Gray level variance	Kurtosis
Wavelet-LLH	First order	Uniformity	Interquartile range
Log-sigma-2-0-mm-3D	First order	Energy	Skewness

Wavelet-LLL, wavelet-low low low frequency; Wavelet-HHL, wavelet-high high low frequency; Wavelet-HHH, wavelet-high high high frequency; Wavelet-LHH, wavelet-low high high frequency; Wavelet-LHL, wavelet-low high low frequency; Wavelet-HLL, wavelet-high low low frequency; Wavelet-LLH, wavelet-low low high frequency; GLRLM, gray-level run-length matrix; GLCM, gray-level cooccurrence matrix; GLDM, gray-level dependence matrix; GLSZM, gray-level size zone matrix.

Diagnostic performance of the ML model in the training and testing sets

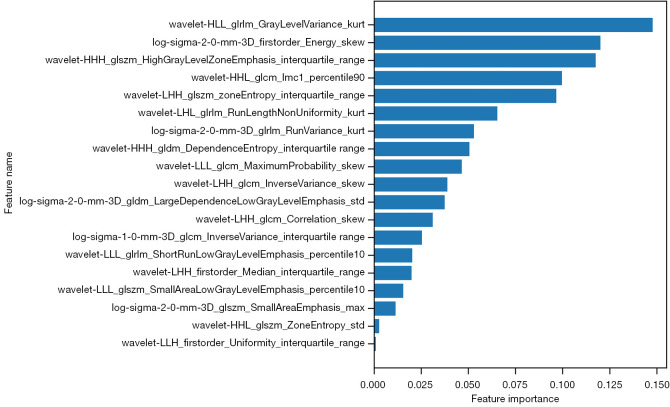
The diagnostic performances of the 8 ML models are summarized in Table 4. Among these models, gradient boosting decision tree yielded the best classification performance in the training set. Thus, the trained gradient boosting decision tree was applied in the testing set. The hyperparameters of the selected gradient boosting decision tree are shown in Table S2. The relative importance of 19 features in this model are shown in Figure 5. The AUC for performance of the HLG-ML model in the testing set was 0.857 (95% CI: 0.699–0.951).

Table 4. AUCs of the 8 ML models in the diagnosis of APE in the training, testing, and validation groups.

ML models	AUCtraining	AUCtesting	AUCvalidation
Gradient boosting decision trees	0.772	0.857	0.810
Naïve Bayes	0.715	0.703	0.727
Decision tree	0.607	0.668	0.642
k-nearest neighbors	0.660	0.641	0.701
Logistic regression	0.746	0.732	0.748
Multilayer perceptron	0.686	0.701	0.677
Random forest	0.763	0.715	0.731
Support vector machine	0.738	0.744	0.735

AUC, area under curve; ML, machine learning; APE, acute pulmonary thromboembolism.

Figure 5.

The importance of each feature in the selected gradient boosting decision trees. Feature importance values are sorted from highest to lowest. The format for each feature name is "Filter Operation_Radiomics Category_Radiomics Feature_Statistics".

External validation of the HLG-ML model, radiologists, and the YEARs algorithm

In the validation group, the ICC of readers 1 and 2, readers 1 and 3, reader 2 and were 0.197 (95% CI: −0.149 to 0.501), −0.031 (95% CI: −0.361 to 0.310), and 0.251 (95% CI: −0.130 to 0.515), respectively. Under the gradient boosting decision trees, the HLG-ML model (AUC =0.810; 95% CI: 0.669–0.952) outperformed the 3 radiologists (Radiologist 1: AUC =0.508, 95% CI: 0.335–0.681; Radiologist 2: AUC =0.504, 95% CI: 0.354–0.654; Radiologist 3: AUC =0.527, 95% CI: 0.363–0.691) and the YEARS algorithm (AUC =0.618; 95% CI: 0.469–0.767) (Figure 6). The HLG-ML model with gradient boosting decision tree (sensitivity =87.1%, 95% CI: 70.2–96.4%; specificity =75.0%, 95% CI: 42.8–94.5%) had better performance compared with the 3 radiologists in terms of sensitivity (51.6%, 95% CI: 33.1–69.8%; 25.8%, 95% CI: 11.9–44.6%; 38.7%, 95% CI: 21.8–57.8%) and specificity (50.0%, 95% CI: 21.1–78.9%; 75.0%, 95% CI: 42.8–94.5%; 66.7%, 95% CI: 34.9–90.1%) (Table 5). Moreover, in a review of the diagnosis provided by the HLG-ML model, 4 cases with segmental or subsegmental APE were missed while 3 cases with multiconsolidation on NC-CT were misdiagnosed.

Figure 6.

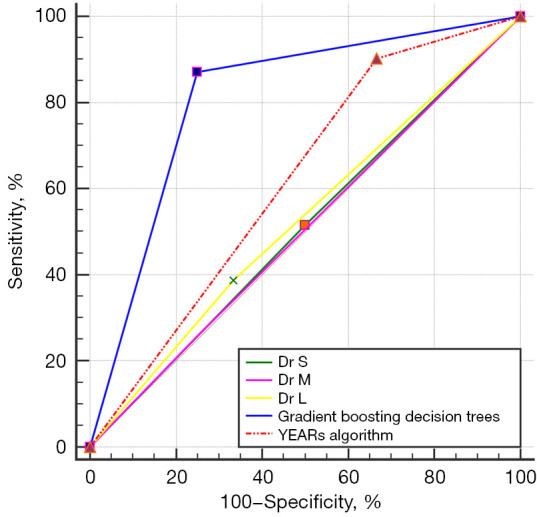
Receiver operating characteristic curves of the proposed holistic lung graph-based machine learning model with gradient boosting decision tree, the 3 radiologists (3-, 5-, and 15-year experience), and the YEARS algorithm.

Table 5. Performances of the HLG-ML model, radiologists, and YEARS algorithm in diagnosing APE in the validation group.

Methods	AUC (95% CI)	Sensitivity (95% CI), %	Specificity (95% CI), %	Youden index
HLG-ML	0.810 (0.669, 0.952)	87.1 (70.2, 96.4)	75.0 (42.8, 94.5)	0.621
Reader 1	0.508 (0.335, 0.681)	51.6 (33.1, 69.8)	50.0 (21.1, 78.9)	0.016
Reader 2	0.504 (0.354, 0.654)	25.8 (11.9, 44.6)	75.0 (42.8, 94.5)	0.008
Reader 3	0.527 (0.363, 0.691)	38.7 (21.8, 57.8)	66.7 (34.9, 90.1)	0.050
YEARS algorithm	0.618 (0.469, 0.767)	90.3 (74.2, 98.0)	33.3 (9.9, 65.1)	0.237

HLG-ML, holistic lung graph-based machine learning; APE, acute pulmonary thromboembolism; AUC, area under the curve; CI, confidence interval.

Discussion

In this study, we developed and validated an HLG-ML model for chest NC-CT to aid in the diagnosis of APE. This HLG-ML model was built with the combination of 3D holistic lung radiomics descriptors and gradient boosting decision tree, and outperformed both the radiologists and YEARS algorithm.

CTPA is the first-line method for detecting APE. In our previous study (19-21), DL based on CTPA was proven to be effective in clot detection and quantitative calculation of clot burden; however, compared with that of NC-CT, the radiation dose of CTPA is higher, and an iodine contrast agent is required. Despite this being the case, no study has yet confirmed whether NC-CT can be used in the diagnosis of APE, although some indirect signs such as subpleural wedge consolidation on NC-CT have been found to indicate APE (22,23). Ehsanbakhsh et al. (24) reported intraluminal signs on NC-CT had a specificity of 98.6% and a sensitivity of 42.5%. These studies were based mainly on the experience of radiologists. Thus, we studied the possibility of detecting APE on NC-CT images using radiomics and an AI algorithm. In this study, all clinical characteristics between the training group and the testing group, except age, were similar. This could ensure the robustness of the model between the training group and the test group. D-dimer was significantly elevated in those with APE patients; however, other clinical characteristics, such as chest pain and hemoptysis, were comparable between the training group and testing group. This confirmed that the symptoms and signs of APE were nonspecific.

Radiomics analysis can be regarded as an objective quantitative biomarker that encodes variations in spatial relationships without relying on subjective interpretations of the images. Cho et al. (25) applied a radiomics approach for glioma grading from pre- and postcontrast T1-weighted, T2-weighted, and fluid-attenuated inversion recovery (FLAIR) magnetic resonance imaging (MRI). After the calculation of 468 radiomics features, 5 were selected for use in a random forest classifier that showed the highest AUC of 0.92 after 5-fold cross-validation. Hawkins et al. (26) developed an ML model of 23 features that yielded a radiomics signature with an AUC of 0.81 for predicting the development of lung cancer in 1 year, which was far superior to volume alone. Coroller et al. (27) used CT radiomic features extracted from primary lung cancer and lymph nodes to predict pathological complete response and gross residual disease after neoadjuvant chemoradiation before surgery. Yang et al. (28) reported the use of radiomics features to predict epidermal growth factor receptor mutation status in patients with non–small cell lung cancer using contrast‑enhanced CT and noncontrast-enhanced CT.

Unlike the above studies (25-28), in which radiomics features were extracted from focal ROIs such as a tumor or lymph nodes or the infarcted area, our research designed whole-lung radiomics descriptors because the distribution of fresh thrombus in the pulmonary artery is heterogeneous and random and because the contrast between fresh thrombus and the pulmonary artery on NC-CT is too poor to discern the thrombus on NC-CT. The HLG-ML model built from 3D local texture descriptors extracted on an atlas-based parcellation enables the merger of local and global radiomics features of the lungs to classify patients with vascular pathologies. Thus, the whole lung on NC-CT was automatically extracted using an automatic lung segmentation algorithm to obtain a lung mask, and then, each lung mask was geometrically converted into an atlas containing the 36 subregions delineated by Dicente Cid et al. (14). From these 36 subregions, 7 different classes of radiomics features were extracted. This step could characterize the entire lung parenchyma using information from local texture regions in the lung and their global correlations; however, a large number of radiomics descriptors may reduce model robustness. Thus, we applied dimensionality reduction to the proposed radiomics descriptor in the training stage, and the remaining candidates in each radiomics descriptor vector were reduced to 19 potential features. To optimize the diagnostic model, we built and compared 8 ML models based on the radiomics descriptor vector. The HLG-ML model with gradient boosting decision tree achieved the best classification performance on the training and testing set. In the validation set, even without any clinical information, the HLG-ML model with gradient boosting decision trees greatly outperformed radiologists, especially in sensitivity and AUC. Meanwhile, although the sensitivity of the YEARS algorithm was higher than that of the HLG-ML model, the AUC, Youden index, and specificity of the HLG-ML model were better than those of the YEARS algorithm.

Technically, compared to the model described by Jimenez-Del-Toro et al. (15), our proposed HLG-ML model has some advantages. First, the conventional operation process of the radiomics method involves target region segmentation, radiomics feature extraction on the target region, feature selection or dimensionality reduction, and ML model construction. Taking our research goal as an example, the process should include lung field segmentation, radiomics feature extraction of the lung, feature selection or dimensionality reduction, and ML model construction. The input of the ML model is the processed radiomics features.

For the graph-based model in our work, radiomic features were extracted in parallel from each of the 36 subregions as opposed to from the whole lung field. Subsequently, the radiomics descriptor was used to explain the distribution of each radiomic feature in the lung field. We referred to this workflow as splitting-integration. Splitting can reduce time consumption on feature extraction as well as the demand for hardware; integration can weaken the impact of this absolute regional division. Even in the absence of certain subregions, the representation of radiomics features in the lung field could also be obtained. Moreover, we divided the lung region into subregions, and a radiomics feature distribution was formed based on the radiomics features extracted from subregions. The ML model is fed statistical descriptive information of the feature distribution, not a single radiomics feature. The amount of information from feature distribution is greater than that from a single feature.

Limitations

To our knowledge, this is the first study to investigate the potential use of the HLG-ML model on NC-CT images for the diagnosis of APE; however, there are several limitations to this research. First, we employed a retrospective, single-center design with a relatively small number of cases, so the robustness of the HLG-ML model is limited by the NC-CT data obtained on 2 CT scanners. More NT-CT data derived from different scanning parameters and multiple centers will optimize and verify the HLG-ML model. Second, although the HLG-ML model showed better performance than did the radiologists and the YEARS algorithm, radiomics features from lung graphs are not explainable, and the current HLG-ML model cannot provide the clot location or burden based on NC-CT, thus limiting its clinical application. DL is a data-driven technique, meaning that its performance improves with larger and more diverse training samples. However, due to the relatively small training sample size employed in our study, the application of DL techniques did not necessarily result in optimal performance. As data on NC-CT continue to accumulate, we aim to assess the potential value of DL in evaluating APE on NC-CT. Third, we excluded cases with CPE, CTEPH and the diseases mimicking APE such as pulmonary tumor embolism, and pulmonary arterial sarcoma; therefore, the differential diagnosis of APE and other diseases mimicking APE with the HLG-ML model need to be examined further. Moreover, we found that the levels of D-dimer in patients with APE were significantly higher than in those without APE. We thus speculate that the combination of the HLG-ML model with clinical and semantic feature analysis might be helpful in accurately diagnosing and evaluating APE. In our future studies, we will build a composite model by combining clinical data, NC-CT, and ML or DL techniques.

Conclusions

An HLG-ML model was developed and validated to predict APE based on NC-CT. This proposed model has the potential to diagnose and assess APE using NC-CT when CTPA is not available.

Supplementary

The article’s supplementary files as

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by institutional ethics board of China-Japan Friendship Hospital (No. 2023-KY-070). Individual consent for this retrospective analysis was waived.