People prefer to predict middle, most likely quantitative outcomes (not extreme ones), but they still over-estimate their likelihood

Abstract

Past work showed a tendency to associate verbal probabilities (e.g., possible, unlikely) with extreme quantitative outcomes, and to over-estimate the outcomes’ probability of occurrence. In the first four experiments (Experiment 1, Experiments 2a–c), we tested whether this “extremity effect” reflects a general preference for extreme (vs central or less extreme) values of a distribution. Participants made predictions based on a frequency distribution in two scenarios. We did not find a preference for extreme outcomes. Instead, most of the participants made a prediction about the middle, most frequent outcome of the distribution (i.e., the modal outcome), but still over-estimated the outcomes’ probabilities. In Experiment 3, we tested whether the over-estimation could be better explained by an “at least”/“at most” reading of the predictions. We found that only a minority of participants interpreted predictions as the lower/upper bounds of an open interval and that these interpretations were not associated with heightened probability estimates. In the final three experiments (Experiments 4a–c), we tested whether participants perceived extreme outcome predictions as more correct, useful and interesting than modal outcome predictions. We found that extreme and modal predictions were considered equally correct, but modal predictions were judged most useful, whereas extreme predictions were judged to be more interesting. Overall, our results indicate that the preference for extreme outcomes is limited to specific verbal probability expressions, whereas the over-estimation of the probability of quantitative outcomes may be more general than anticipated and applies to non-extreme values as well.

Introduction

When people make assertions about uncertain issues, which are abundant in various domains, such as climate, health, politics, and sports, they frequently use words that describe and qualify the strength of their expectations. They say that an increase in global warming is almost certain, that the occurrence of a new pandemic is likely, that it is possible Germany will become the next football World Cup champion, and that it is unlikely that peace will return in the Middle East.

Such phrases are used by experts and lay people alike and have been studied and discussed as verbal probabilities. This is because they seem to serve similar functions in natural language as numeric probabilities do in more formal contexts. Empirical research has shown that, to some extent, verbal and numerical expressions can be coordinated. Although people tend to translate verbal probabilities into a range of numerical probabilities (Budescu & Wallsten, 1995), terms can be consistently ordered (Beyth-Marom, 1982) and people’s interpretations are fairly stable over time (Bryant & Norman, 1980). For example, certain would be appropriate to express probabilities around 90%–100% and likely would be appropriate for probabilities around 60%–80% (e.g., Beyth-Marom, 1982; Theil, 2002). Indeed, scientists in several domains (climate, military intelligence, and health risk) have developed prescriptive guidelines for how verbal probabilities should be converted into numbers and vice versa (European Food Safety Authority, 2017; Intergovernmental Panel on Climate Change [IPCC], 2022; North Atlantic Treaty Organization [NATO], 2016).

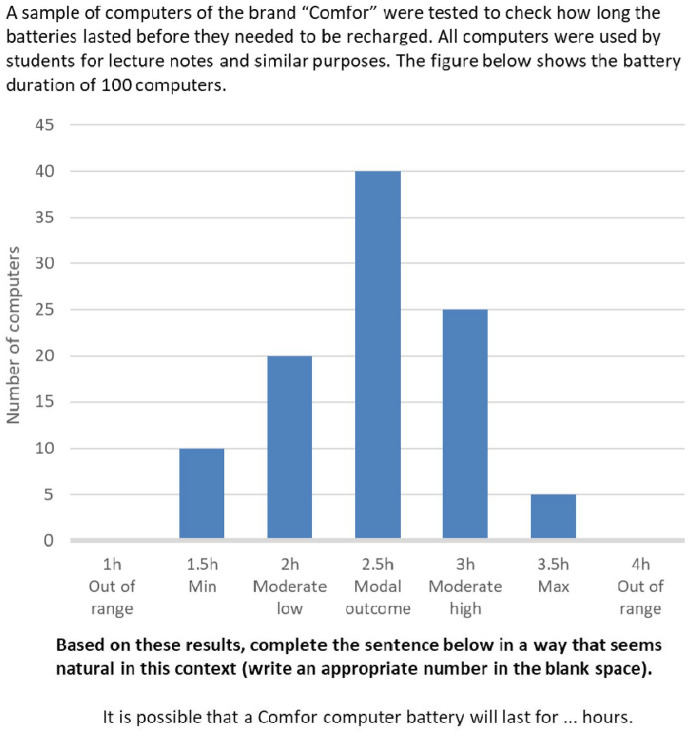
A common but implicit assumption of these translation attempts is that the target events are binary, or dichotomous. For example, a new pandemic is going to occur, or not; Germany will be the next football World Cup champion, or not, and so on. In line with this, it makes sense that a 50% probability is defined as equivalent to an “even chance” as stipulated by the NATO (2016) standards. But verbal probabilities are also used to characterise uncertainty regarding continuous outcomes—which can be measured on a quantitative scale—for example, to predict costs, durations, amounts, or sizes. In that case, recent research using a new methodological approach has shown that people may not choose verbal probabilities to convey a specific probability but rather a location in the distribution of possible outcome values. In the “Which Outcome” approach, studies focus on how people use verbal probabilities to predict continuous outcomes. In a typical task, as shown in Figure 1, participants were given a situation (e.g., we are trying to assess how long computer batteries might last) and were shown the distribution of all actual outcomes. Participants were then asked to select an outcome value to complete a statement featuring a verbal probability expression (e.g., “It is possible that the battery will last for . . . hours”).

Figure 1.

Example of outcome completion task used to demonstrate the extremity preference. Participants most often selected the minimum or maximum outcome value when describing what was certain, unlikely or possible.

The verbal labels of the horizontal axis were not shown to participants.

This approach revealed a preference for extreme outcomes that did not fit with the results obtained by the traditional “translation” approach. For example, possible is typically perceived as meaning a 50% probability, but was used to describe 5%–10% likely outcomes from the top end of the distribution (i.e., the maximal outcome; Juanchich et al., 2013; Teigen et al., 2014). Unlikely is typically used to describe probability values in the 10%–40% range, but people used unlikely to describe outcomes beyond the maximum, which had a probability of occurrence of 0% (Teigen et al., 2013). Similarly, people tended to focus on the 5%–10% likely minimum outcome when predicting what will, or what is certain to happen, despite the fact that those terms convey a probability close to 100% (Teigen et al., 2014; Teigen & Filkuková, 2013). Like possible and unlikely, will and certain were typically associated with extreme outcomes, but this time, the outcome values were picked from the low end of the distribution, designating the minimum outcome that could be expected. This body of findings has been labelled an “extremity effect” (Jenkins et al., 2018), where “middle values are not worth mentioning” (Juanchich et al., 2013).

An important aspect of this extremity preference is its role in communication about uncertain quantities. There appears to be a gap between the way people translate verbal expressions into probabilities and the way they could be perceived by recipients. For example, a speaker might describe a 5% likely (maximum) outcome as possible, but recipients without access to distributions might believe that the outcome referred to has a 50% chance of occurring. Evidence shows that the gap can even be observed within the same individuals taking on the two conversational roles (Juanchich & Sirota, 2017; Teigen et al., 2013; Teigen & Filkuková, 2013). For example, in a climate change study, participants first selected a 10% frequent outcome from a distribution, predicting that a 45 cm sea-level rise was possible, but the same participants subsequently estimated this sea level rise to have a 50% chance of occurring (Juanchich & Sirota, 2017).

The extremity preference seems to be a robust phenomenon replicated across different samples (e.g., British, American, Norwegian), and with different methods of distribution presentation (e.g., graph, table, text; Jenkins et al., 2018; Juanchich et al., 2013). The extremity preference has also been replicated over a variety of contexts, such as daily life events (Juanchich et al., 2013; Teigen et al., 2013, 2014), business project completion time (Løhre & Teigen, 2014), construction cost estimates (Teigen et al., 2019), and natural disasters (Jenkins et al., 2018; Juanchich & Sirota, 2017; Teigen et al., 2018). However, the preference for extreme outcomes may not be independent of the verbal expression being used. Studies showing an extremity preference have mostly concentrated on a limited selection of uncertainty adverbs and adjectives (e.g., unlikely, possible) or modals (e.g., will, can). Studies of some other terms, such as likely and probable, were not associated with extreme outcomes but rather with more moderate (middle) ones, more specifically the peak, or modal value of the distribution (Teigen et al., 2014, 2022b). Interestingly, even in these cases, participants still largely over-estimated the chances of their predicted outcome occurring. Which extreme outcome participants prefer also varies (minimum vs maximum) as a function of the conversational context. Recipients’ conversational goals shape the preference for either end of the distribution (Teigen et al., 2014). For example, when participants spoke to someone considering renting out their flat, the participants selected the highest price a landlord could ask for. However, the preference was reversed when participants addressed someone looking for a place to rent; in that case, most participants selected the lowest possible price a flat could cost (Teigen et al., 2014, Experiment 3). Overall, a large number of studies have demonstrated that participants prefer extreme outcome values when predicting what might happen, but when and why they find extreme values so appealing remains unclear.

A classic suggestion is that people prefer extreme outcomes because they do not understand the frequentistic distribution provided to them. However, the preference for extreme outcomes (and associated probability over-estimation) cannot be simply based on a misunderstanding of the probabilistic information given, since this preference remained the same across numeracy levels (Jenkins et al., 2018). Research also shows that people are able to read and understand a graph showing a frequentistic distribution as proved by correct identification of the frequencies of different outcomes (Teigen et al., 2022b; Study 6). Consistently, in a series of studies on what was likely to happen, education did not predict the preference for a specific outcome, and nor did graph literacy (Teigen et al., 2022b). The extremity preference could be explained by the fact that extreme outcomes might be judged more important and more informative than other values in the distribution “in general.” For instance, athletes will be judged based on their maximal, rather than their average performance. And when people are asked to state their expectations of a product, they seem to lean heavily on “best case” scenarios rather than on more realistic predictions (Tanner & Carlson, 2008). Also, for risks and other negative events, extreme outcomes (e.g., death risks) seem to garner more attention than “normal” outcomes. Indeed, it has been claimed that people show “probability neglect” (Sunstein, 2003) when judging the risks of events with emotionally arousing outcomes, and direct their attention more strongly on maximum but rare outcomes compared with those that are expected. A cancer patient may care more about worst and best case estimates of survival time than average statistics, or in Gould’s apt paraphrase: “The median isn’t the message” (Kirkebøen, 2019).

An alternative account of the extremity preference is that participants do not mean to focus on those outcomes exactly. They might select extreme outcomes as bounds of an implicit range, for example, the computer battery will last (at least) 1.5 hr or (at most) 3.5 hr. Participants did indeed select lower and upper bound markers when those modifiers were explicitly available (Juanchich et al., 2013). For example, they used at least when making minimum predictions of what was certain to happen and at most for maximum predictions of what could possibly happen, (e.g., “It is certain the computer battery will last at least 1.5 hours”). People might therefore select an outcome that implicitly marks the lower or upper bound of an interval of outcomes to be expected, instead of an exact outcome (e.g., “It is certain that the computer will last (at least) 1.5 hours”). When considered as an at least or at most outcome value, the probability associated with the outcomes is greater than when considered as an exact estimate, since it includes the probability of a range of outcomes. In this context, participants’ high probability estimates could therefore be judged as correct. For example, there is indeed a 90%–100% probability that a computer battery would last (at least) 1.5 hr (where 1.5 hr is the lowest duration). Yet, this does not rule out the possibility of miscommunication, since the statement is ambiguous, by explicitly predicting a specific duration, but implicitly suggesting a whole range of outcome values.

Research goal and studies overview

Based on the research on uncertain predictions to date, we propose to tackle three related questions: (1) How general is the preference for extreme outcomes in predictions? (2) To what extent do people over-estimate the probability of their predicted outcome? And (3) what drives the preference for extreme over moderate outcomes?

In the first set of experiments, we tested the extent to which people select extreme outcomes when they are free to produce their own predictions and to what extent they over-estimate the chances of these events. Experiment 1 was a pilot study where participants could select both the probability expression and the outcome that they would “naturally” use to predict an event based on frequentistic information. Based on the extremity preference, we expected to identify a preference for extreme outcomes and an over-estimation of their probability of occurring. In contrast, it turned out that people had a preference for central, most frequent outcomes, but they still over-estimated the chances of occurrence of those outcomes. We tested the robustness of these findings in three experiments where participants selected their answers from a list (Experiment 2a), where the distributions of possible outcomes were skewed (negatively or positively; Experiment 2b) and where participants selected a range of outcomes (Experiment 2c). Experiment 3 assessed whether participants interpreted predictions as exact values or range boundaries (i.e., as “at least” or “at most” values) and how these interpretations impacted participants’ probability estimates. In the last three experiments (Experiments 4a–c), we assessed how people perceive predictions of moderate versus extreme outcomes to determine potential reasons for their preferences. We wanted to determine whether moderate and extreme outcomes are perceived as different with respect to how correct (Experiment 4a), how informative and how useful they appear to be (Experiments 4b–c).

Open science statement

The eight experiments presented here were preregistered. Hypotheses were recorded on AsPredicted prior to running the experiments, along with other key methodological considerations (e.g., sample size target, case exclusion and analyses plans). The pre-registration, along with the data and materials for all the experiments, is available on the Open Science Framework: https://osf.io/v7rpq/.

Experiment 1

Past studies showing a preference for extreme outcomes and probability over-estimation were all based on a similar methodology. In these instances, participants were given incomplete statements that included a verbal probability expression and were asked to fill in an appropriate outcome value, such as “the Jeans is unlikely to shrink by . . . cm” (Jenkins et al., 2018; Juanchich et al., 2013; Juanchich & Sirota, 2017; Teigen et al., 2013, 2014, 2018, 2019). It is therefore unclear whether the choice of extreme outcomes is “natural” and applies to quantitative predictions in general or whether it is triggered by the pre-selected verbal probability expressions. Similarly, when participants over-estimate the chances of their selected outcome this might be limited to a specific task and might not generalise to a situation where participants can freely produce their own probability expressions. In this experiment, we assessed whether the extremity preference and probability over-estimation occurred to the same extent in tasks where participants could select their own probability expressions.

Method

Participants

The sample consisted of 114 British residents recruited by a panel company (Bilendi). Half of the participants were women (50%, 1% non-binary), their highest level of education ranged from primary school (5%) to holding a university degree (69%) with a quarter having a high school certificate (26%). Most were native English speakers (90%, with 10% non-native but fluent). Age ranged from 18 to 76 years old (M = 49.3, SD = 12.7 years).

Design, procedure, and materials

After completing an unrelated task on food perception (Liu et al., 2020), participants read two short scenarios which included a sentence completion task. The first scenario was about how long computer batteries of a hypothetical brand could last (as portrayed in Figure 1) and the second scenario was about how much jeans of a hypothetical brand could shrink after being machine washed (Teigen & Filkuková, 2013). The scenarios were chosen to represent one positive outcome (duration of batteries) and one negative outcome (shrinkage of jeans). The scenarios included a bar chart showing the results of the tests: the duration of 100 batteries (in hours) or the degree of shrinkage (in cm) of 200 pairs of jeans after being thoroughly washed. The computer battery graph is shown in Figure 1. The jeans shrinkage graph was similar, showing seven shrinkage amounts on the horizontal axis ranging from 0.6 to 1.4 cm in increments of 0.2 cm and an approximately normal distribution of frequencies (0, 20, 80 100, 80, 20, and 0). Past work showed that participants from online platforms (like ours) have sufficient levels of numeracy to correctly read the distribution (Teigen et al., 2022b). The vignettes are available on the Open Science Framework. Participants were instructed to complete a sentence with two blank spaces using the text that seemed most natural to them. The two blank spaces were meant to be filled with a probability quantifier and an outcome value as shown in the example below:

It is . . . [probability quantifier] . . . that the battery in a Comfor computer will last for . . . [outcome value] . . . hours.

We expected that participants would mostly express probabilities with verbal phrases (e.g., unlikely, possible, certain), based on the documented preference for words over numbers (Juanchich & Sirota, 2020; Olson & Budescu, 1997; Wallsten et al., 1993), but the space could also contain numbers (e.g., “It is 20% likely that . . .”). The sentence contained an anticipatory dummy subject and associated verb (“It is . . .”), which excluded the use of modals (e.g., can, will) and probabilistic expressions that required an active subject (e.g., to think, to be convinced). There is a debate on what to call expressions that quantify certainty but do not technically refer to a probability term (e.g., it is normal, it is usual). Are these really probability quantifiers? We adopted a broad approach and accepted any phrase from everyday language used to quantify uncertainty as a verbal probability. This is in line with work from the 1980s and 1990s when “classic” probability adjectives were studied together with frequencies or even verbs or modals that quantify uncertainty, e.g., it seems, could be, one must consider (Beyth-Marom, 1982; Reyna, 1981). These words are sometimes used in professional practice, such as the word expected in accounting (Doupnik & Riccio, 2006).

Following the sentence completion task, participants were asked to provide a reason for their answers and gave a numerical estimate of the probability of occurrence of the outcome they had chosen (as a percentage between 0 and 100 on a scale). For the Computer vignette, participants assessed the probability that a computer would actually last for the number of hours that the participants had used in their prediction. For the Jeans vignette, they assessed the probability that a pair of jeans would shrink by the amount they had selected.

Data preparation and coding

The statements given by participants were corrected for minor spelling and grammatical mistakes. Sentences that did not make sense were excluded based on coding by the first author (e.g., “It is 40 that the computer battery will last for 2.5 hours”; “It is medium that the computer will last hours”). On this basis, we discarded 30 phrases in the Computer vignette (26%) and 35 in the Jeans vignette (31%). These sentences were mostly from the same participants, suggesting that those participants had misunderstood the instructions (28 participants were responsible for 80% of the sentences discarded). In the remaining sample of sentences, only one included a numerical probability and it was kept in the sample (“It is 70% likely that the computer will last 2.5 hours or more”). The analyses were hence based on 84 sentences for the Computer scenario and 79 sentences for the Jeans vignette. The outcomes selected by participants were automatically classified in seven bins according to their position in the distribution, as shown in Figure 1. Following on past research, they were classed as follows: out of range below the minimum outcome, minimum, moderate low, peak, moderate high, maximum, or out of range above the maximum (Juanchich et al., 2013; Teigen et al., 2013, 2014). The first two and last two outcome values that formed the tails of the distribution and values beyond those were coded as extreme values, while the other three outcomes were coded as non-extreme. The reasons participants gave to justify their sentences were coded by two research assistants and are reported in the online Supplementary Materials.

Results

Outcome selected

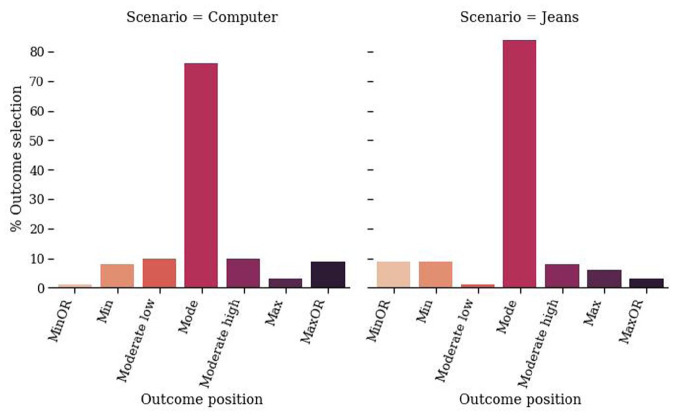
As shown in Figure 2, participants mostly selected middle outcomes that were also the most frequent in the distributions (i.e., the mode). Extreme outcome values were selected in only 15% of the statements (n = 12/78 and n = 11/71 for Computers and Jeans, respectively); binomial tests of extreme versus non-extreme outcomes showed a significant preference for non-extreme values for both the Computer and the Jeans vignettes, χ²(1) = 37.39, p < .001 and χ²(1) = 33.82, p < .001.

Figure 2.

Outcomes selected by participants in the Computer and Jeans vignettes in Experiment 1, showing a preference for middle (modal) outcomes over extreme outcomes in the tails of the distribution (e.g., Min, Max).

Min: minimum outcome with a non-zero frequency; Max: maximum outcome with a non-zero frequency; OR: out of range.

Probability quantifiers

Participants used a wide range of probability phrases in the first part of the sentence. The 84 Computer predictions included 42 different probability quantifiers to predict the duration of a computer battery and of the 79 Jeans predictions, participants used 31 different quantifiers. The most common probability quantifiers are shown in Table 1. In line with their selection of the middle, most frequent outcome, likely, along with expected, probable, and most likely were the most frequent probability quantifiers, followed by terms that characterise the typicality of the outcome (normal, usual, and average). Only a minority of participants selected one of the three verbal probabilities associated with extreme outcomes in past research (unlikely, possible, and certain).

Table 1.

Probability quantifiers most frequently selected in the Computer and Jeans vignettes (in percentages of reports), in Experiments 1 and 2a–c.

Quantifier	Exp. 1		Exp. 2a		Exp. 2b		Exp. 2c
	Comp. (%)	Jeans (%)	Comp. (%)	Jeans (%)	Comp. (%)	Jeans (%)	Comp. (%)	Jeans (%)
Likely	14	20	21	22	30	23	26	27
Expected	11	11	12	12	16	7	21	11
Normal	6	9	5	7	6	1	3	8
Probable	6	8	5	14	14	13	8	9
Usual	6	0	2	2	4	2	4	2
Average	4	6	9	5	–	–	–	–
Certain	4	5	5	3	0	0	2	3
Possible	4	4	6	8	7	18	6	17
Most likely	0	4	19	16	18	25	19	16
Clear	4	0	0	3	0	0	0	0.4
Unlikely	4	0	7	3	4	5	0	1
Noticeable	0	3	3	2	1	1	1	0.4
Inevitable	0	3	2	3	0	0	1	0.4
Known	0	3	2	1	0	0	3	2
Found	2	0	3	2	1	0	3	4

Verbal probabilities in bold were used in previous research demonstrating the extremity effect (e.g., Juanchich & Sirota, 2017; Teigen et al., 2014).

Probability estimates

Participants estimated the probability of occurrence for their chosen outcome to be, on average, 64% in both the Computer and Jeans vignettes (SD = 24 and SD = 22, respectively). These estimates are about twice the statistical probability of the outcome they chose based on the frequencies of the selected outcomes in the distribution, M_computers = 30% (SD = 12) and M_jeans = 29% (SD = 10).

When allowed to pick an outcome and a probability quantifier of their own choice, most participants chose a middle outcome, which was both the average and most frequent outcome in the distribution, and which they described as likely, expected, usual, or normal. Verbal probabilities associated with extreme outcomes in past research were rarely used (e.g., unlikely, possible, and certain). These results suggest that people’s preference for extreme outcomes could be limited to specific and infrequently used quantifiers. However, consistent with past findings, participants had an inflated perception of the likelihood of their predicted outcome. The results must, however, be read with caution, as participants struggled to form a meaningful prediction and about one-quarter of the responses had to be excluded.

We used the results of Experiment 1 to prepare a “natural” list of common verbal probabilities and outcomes to be used in a selection task. We expected that participants would focus their predictions on non-extreme outcomes, but would still over-estimate their probability of occurring. In Experiment 2a, we replicated Experiment 1 and simply limited the alternative responses given to participants. Experiment 2b extended our approach to skewed distribution where the mode differed from the median, to assess whether participants were attracted to an outcome based on its relative frequency or to its location in the distribution. Finally, in Experiment 2c, we asked participants to select a range of outcomes, rather than a single value, to assess whether they would choose a range of values wide enough to indeed be likely.

Experiment 2a

Method

Participants

Overall, 121 American residents from the Amazon Mechanical Turk platform completed the survey. The survey was composed of a few short vignettes, took 5 min to complete and participants were rewarded with US$0.80. In the sample, 39% were women, 31% finished high school, 57% had a college degree (2–4 years), 10% had a master’s degree and 2% a doctoral degree; 13% were unemployed (including students and homemakers), and their ages ranged from 20 to 54 years old (M = 34.37, SD = 8.82 years).

Materials and procedure

The procedure and materials were the same as in Experiment 1. The only difference was that instead of writing their answer in a response box, participants were provided with a drop-down list from which they could select a modifier. The list included the 15 most frequent verbal probabilities produced in Experiment 1 (see Table 1). Similarly, they could select an outcome from a list of nine potential outcomes derived from the values on the horizontal axis of the distribution graphs. This consisted of all the five outcome values with a non-zero frequency along with two values below the lowest value and two values above the highest one. After the sentence completion task, participants were asked to provide reasons for their answers, which were coded by two research assistants (see the online Supplementary Materials). Finally, participants estimated the probabilities of their chosen outcomes on a 0–100 visual analogue scale verbally ranging from 0%: impossible to 100%: certain, by increments of 1. The online questionnaire also included a vignette on the way people perceive framing in food descriptions (Liu et al., 2022).

Results

Outcome selected

As shown in Figure 3, participants mostly selected the modal outcome –the most frequent value in the distribution—which was also the middle outcome. Only about 20% of the participants chose an extreme outcome to describe how long the battery would last and how much the jeans would shrink. Participants chose an extreme outcome less than half of the time for both the Computer (18%) and the Jeans vignettes (23%), χ²(1) = 48.08, p < .001 and χ²(1) = 36.30, p < .001.

Figure 3.

Outcome selected by participants in the Computer and Jeans vignettes, showing a preference for predicting the modal outcome of the distribution over extreme outcomes shown in the tails of the distribution (Experiment 2a, n = 121).

Min: minimum outcome with a non-zero frequency; Max: maximum outcome with a non-zero frequency; OR: out of range.

Verbal probability selection and probability estimates

Participants selected each of the quantifiers provided at least once (except for it is clear in the Computer scenario). The expressions most often selected were likely, most likely, expected, average, and possible in both scenarios (see Table 1). Participants estimated the numeric probability that their selected outcome would occur to be, on average, 67% (SD = 23) in the Computer battery vignette and 61% (SD = 24) in the Jeans shrinkage vignette. This is twice the statistical probabilities of these outcomes in the distributions, and accordingly a large overestimate.

Experiment 2b

Experiments 1 and 2a used normally distributed frequency data where the mode was also the median; hence, it is unclear whether participants selected a value because it was the most frequent or because it was in the middle. In Experiment 2b, we used a skewed distribution to disentangle the preference for the middle outcome from the preference for the most frequent outcome. We expected that participants would select the modal outcome more often than the median and more often than the extreme outcomes. We also hypothesised that participants who selected the verbal probabilities unlikely, possible or certain, would be more likely to select an extreme outcome and would over-estimate its probability more than participants who selected another probability quantifier.

Method

Participants

The study was conducted via the Prolific platform where 84 participants were invited to participate in a 5-min study paying £0.60. The sample consisted of 61% women, 37% men, 1% non-binary, and 1% other. Age ranged from 19 to 60 with a mean age of 34.9 (SD = 10.5). Most participants were native English speakers (96%), with the rest reporting their English proficiency as excellent (67%) or intermediate (33%). Education ranged from high school diploma (17%) to master’s or doctorate degree (26%), with some participants reporting having a college diploma (13%) or a bachelor’s degree (13%).

Design, materials and procedure

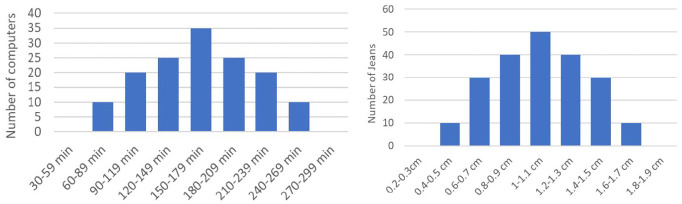
The method was the same as in Experiment 2a, except for the shape of the distributions. For the Computer scenario the distribution was negatively skewed (with 150 batteries tested) and for the Jeans shrinkage scenario, the distribution was positively skewed (with 200 jeans tested), as shown in Figure 4. For the Computer distribution, the modal value (3 hr) was found in 27% of the computers and the median (2.5 hr) in 23% of the computers. For the Jeans scenario, the modal shrinkage (0.8 cm) occurred in 25% of the jeans and the median shrinkage (1 cm) in 20% of the jeans. The task explicitly referred to making a prediction to be clear that participants should concentrate on the future—and probabilities—rather than on describing the frequencies in the graph (e.g., “Based on these results, what is natural to say to predict how long a Comfor computer battery lasts?”). Furthermore, the probability quantifier average was removed from the quantifier list because statements with that term seemed stylistically awkward (e.g., “It is average that the computer battery will last 2.5 hours”).

Figure 4.

Skewed distributions used in the Computer (negative skew) and Jeans scenario (positive skew) in Experiment 2b.

Results

Outcome selection

The distribution of selected outcomes displayed in Figure 5 clearly shows a preference for the most frequent (modal) value, with 70% and 63% of the respondents selecting the mode of the distribution, whereas 16% and 12% selected the midpoint of the distribution. An even smaller number chose extreme values (either lowest or highest values and beyond), but this varied slightly across scenarios with 6% choosing an extreme outcome in the Computer scenario, whereas 15% did so in the Jeans scenario.

Figure 5.

Outcome selected by participants in the Computer and Jeans vignettes, showing a preference for predicting the modal outcome of the (skewed) distribution rather than the middle outcome or extreme outcomes shown in the tails of the distribution (Experiment 2b, n = 84).

Min: minimum outcome with a non-zero frequency; Max: maximum outcome with a non-zero frequency; OR: out of range.

Probability estimates

Participants estimated the probabilities of their selected outcomes to be much higher than the corresponding frequencies of these outcomes in the graph, with M_estimate = 63% (SD = 19) in the Computer vignette and M_estimate = 59% (SD = 23) in the Jeans vignette.

Which probability qualifiers are associated with extreme outcomes?

We tested the hypotheses that the verbal probabilities unlikely, possible, and certain would be more often associated with extreme outcomes compared with the other verbal probabilities and that the probabilities of these extreme outcomes were over-estimated more. We found evidence of a selective preference for extreme outcomes with unlikely, possible, and certain but we did not find evidence that participants over-estimated these probabilities more with those terms relative to other verbal probabilities. In the Computer vignette, 11% of the participants used one of the three quantifiers (n = 9) and 23% did so in the Jeans vignette (n = 17). In both cases, the trio of probability expressions unlikely, possible, and certain was more often associated with extreme outcomes than with moderate outcomes: 44% (vs 1%) in the Computer scenario and 37% (vs 8%) in the Jeans vignette; χ2(1) = 26.68, p < .001, φ = 0.56 and χ²(1) = 10.20, p = .001, φ = 0.35. Despite choosing some extreme outcomes more often when selecting the verbal probabilities unlikely, possible, and certain, participants were not more likely to over-estimate the probability of these outcomes compared with participants who selected other verbal probabilities (e.g., likely, expected). In fact, we observed the opposite. The participants who chose unlikely, possible and certain produced lower probability estimates than people who used other verbal probabilities for the Computer scenario, M = 24.44, SD = 22.49 versus M = 41.04, SD = 17.70, t(82) = 2.58, p = .012, Cohen’s d = 0.91 and for the Jeans vignette, M = 23.41, SD = 27.43 versus M = 42.56, SD = 19.18, t(82) = 3.34, p = .001, Cohen’s d = 0.91. Of course, these figures should be read with caution because of the small number of cases they are based on.

Experiment 2c

In Experiments 1, 2a, and 2b, there was a mismatch in the predictions produced: participants paired a high verbal probability (e.g., likely or expected), with a low-probability outcome (30%–40% likely). This odd association may have been an artefact of the task since none of the outcomes of the distribution had a high probability of occurring; participants could therefore only select an outcome that had a low probability of occurring. For example, in Experiment 2b, the most likely outcome was only 27% likely in the Computer scenario and 23% likely in the Jeans scenario. It is therefore possible that participants selected the most likely outcome in lieu of a likely outcome. This is especially plausible if we consider that some of the participants might not have meant to predict an exact quantity, but instead implicitly predicted the minimum quantity that could be expected (e.g., “It is likely that the computer battery will last (at least) 2 hours”). Participants may have selected a 20%–30% outcome that they qualified as likely because they considered that outcome as the lower bound of a range of possible values. According to this, at least interpretation of the sentence, the corresponding probability of this outcome range is indeed high, since the chances of the computer battery lasting 2 hr or more, add up to 70%. This range of outcomes is actually statistically likely. It is a known phenomenon that stated quantities are not always exact ones but are sometimes communicated and understood as minimum values to be expected (Kennedy, 2013; Mandel, 2014). For example, if one is told: “You need seven answers to pass the test,” they would understand that they need to have at least seven correct answers out of ten, and that more would be okay too. In Experiment 2c, we tested whether participants still preferred to focus on the modal outcome (only) when given the possibility of selecting a range of outcomes, and if that choice could be connected with more accurate probability estimates. The study also assessed participants’ frequency estimates in addition to their probability estimates to test whether participants could make more accurate estimates in the frequency format.

Method

Participants

The study was conducted via the Prolific platform where 225 participants were invited to participate in a 5-min study which paid £0.50. The sample consisted of 71% women, 29% men and 1% non-binary. Age ranged from 18 to 75 with a mean age of 37.9 (SD = 13.88). Most participants were native English speakers (87%). Education ranged from high school diploma (20%) to master’s or doctorate degree (22%), with some participants reporting a college diploma (18%) or a bachelor’s degree (35%).

Materials and procedure

Materials and procedure were similar to that of Experiment 2a, except that we adapted the task so that participants had to complete the sentence with the lower and upper bound of a range based on a graph where each bar corresponded to a range (see Figure 6). This meant that to complete the sentence, participants could choose the modal range or a wider—more likely—range (e.g., “It is . . . . that the battery in a Comfor computer will last between . . . and . . . minutes”). Participants reported their probability estimates that their chosen outcome would occur, as before. Then, on separate pages, participants were asked about the frequency of their chosen outcome based on the distribution figure (“Based on the graph below showing how long a sample of 145 Comfor computer batteries lasted, please assess how many of those computer batteries lasted between [lower bound] and [upper bound] minutes”). Participants gave their frequency answer using a slider that ranged from 0 to the total number of items being tested in that scenario (145 computers and 210 jeans).

Figure 6.

Distribution used in Experiment 2c where outcome bins showed intervals instead of single outcome values. Participants selected a verbal probability term and range to predict how long a computer battery would last and how much some jeans would shrink (e.g., “It is . . . that the battery in a Comfor computer will last between . . . and . . . minutes”).

Results

Probability quantifiers chosen

The top five quantifiers most often selected in the Computer scenario were likely (26%), expected (21%), most likely (19%), probable (8%%), and possible (6%). The top five most selected quantifiers in the Jeans scenario were the same but in a slightly different order: likely (27%), most likely (16%), possible (17%), expected (11%), and probable (9%). In the Computer scenario, 8% of the participants selected a verbal probability term that was shown to be typically associated with an extreme outcome value (i.e., unlikely, possible, certain), and this selection rate increased to 20% in the Jeans scenario, where possible was often chosen and accounted for 17% of the responses.

Outcome range chosen

When we examined the proportion of participants who selected a range that centred only on moderate versus extreme values (min, max, or out of range values), we again found a clear preference for moderate values. Only 1% or 2% of the participants chose a range within the extreme values, while 51% (computer) or 52% (jeans) of the ranges included moderate values only. About 80% of the participants selected ranges that included the modal interval. These ranges were of variable width: 33%–36% selected a range that captured the whole distribution from minimum to maximum values, 25%–30% of the participants selected only the modal interval, and 15%–20% selected ranges that included one or two bins in addition to the modal interval.

Probability and frequency estimates

Our preregistered analysis called for a comparison between participants who had selected an extreme range and those who had selected a moderate range. However, given that, so few participants selected a range within the extremes, conducting the originally planned analysis was not feasible. Instead, we assessed the accuracy of participants’ frequency and probability estimates and their relation to the range chosen.

The full distribution of the frequencies of the ranges chosen by participants (as given by the graph) is depicted in Figure 7 in green, along with how much participants under- or over-estimated the frequency and probability of their selected range (in orange and blue, respectively). Participants selected outcome ranges that had a fairly high objective probability of occurring, with an average of 69% in the Computer vignette (SD = 35) and 75% in the Jeans vignette (SD = 33). As it is shown in the frequency and probability gap rows of Figure 7, on average, participants slightly under-estimated frequencies but over-estimated probabilities of their selected outcome. An analysis of variance (ANOVA) conducted on each scenario and including the three types of outcome judgement as a within-subjects factor (objective frequency, frequency estimates, and probability estimates) supported an overall effect of the type of judgement, F_Computer (1.58, 353.80) = 26.15, p < .001, η ² _p = .11, and F_Jeans (1.49, 333.57) = 8.44, p = .001, η ² _p = .04 (Huynh–Feldt adjusted for sphericity not assumed). The pairwise comparisons between objective frequency and the subjective perceptions show that all the comparisons were statistically significant except for the objective versus subjective probability comparison in the Jeans scenario. ¹

Figure 7.

Differences (“gaps”) between objective frequencies of participants’ chosen ranges (based on the graph) and subjective’ frequency and probability estimates in the Computer and Jeans vignettes.

Negative gap values are under-estimates relative to the objective values shown in the distributions and positive gap values are over-estimates relative to these same objective values. Figure created with the ptitprince library in Python. For each condition, the figure includes a smoothed distribution of the values, a box plot (with interquartile range box, median within the box, whiskers showing the range without outliers and outliers shown using diamonds) and a cloud of dots representing individual data points.

In addition, we explored the relationship between the outcome range frequencies and their subjective frequency and subjective probability. The correlational analyses show that participants’ frequency estimates were fairly attuned to the actual frequencies shown in the graph, with a strong positive relationship (r = .85, p < .001 in the Computer scenario and r = .87, p < .001 in the Jeans scenario). On the other hand, the relationship with the objective frequencies was weaker but still positive for participants’ probability estimates (r = .44, p < .001 and r = .45, p < .001 for the two scenarios, respectively).

Finally, we propose a simple description of the frequency and probability estimates as a function of the three ranges most often chosen (Table 2): the range that included only the modal outcome, the one that included the whole distribution range and the intermediate set of ranges. As shown in Table 2, participants’ frequency perceptions were very accurate when they selected the modal value only, and were slightly under-estimated for the other types of ranges. The accuracy of probability estimates (the gap between subjective and objective values) was more strongly affected by the range selected, with large over-estimates for the modal intervals and under-estimated probabilities for the wider intervals.

Table 2.

Differences between subjective and objective estimates of frequency and probability for three types of ranges selected by participants in Experiment 2c.

Type of range	Computer			Jeans
	% selection (n)	Subj.–Obj. gap		% selection (n)	Subj.–Obj. gap
		Freq.	Proba.		Freq.	Proba.
Modal interval only	30% (67)	+ 0.1%	+ 38%	24% (54)	+ 1.13%	+ 40%
Min to max	33% (75)	−8%	−12%	36% (80)	−15%	−14%
Moderate low to high	16% (37)	−5%	−6%	21% (47)	−0.6%	−10%
Overall	100% (225)	−5%	+ 8%	100% (225)	−3%	+ 4%

Discussion

In three experiments (2a–c), we replicated the results from Experiment 1 showing that people preferred to predict a central rather than a peripheral, extreme outcome. Participants labelled this outcome likely, most likely, or expected and greatly over-estimated its chances of occurrence. In Experiment 2a, this was demonstrated in a more controlled setting using a selection of commonly used quantifiers. The skewed distributions used in Experiment 2b provided evidence that participants preferred the mode of the distribution rather than its middle point. Finally, Experiment 2c showed that when they could select an interval, participants selected ranges that encompassed the central value and almost never chose extreme ranges. Chosen intervals in this experiment were indeed likely on average (p = 70%) and participants’ probability estimates were more accurate for wide ranges than for those that only included modal values. Thus, it may be the case that quantities selected in Experiments 1, 2a, and 2b implicitly represented the bound of a more comprehensive interval that could at least or at most happen instead. Experiment 3 was designed to test this possibility.

Experiment 3

In this experiment, we tested to what extent participants interpret quantitative predictions literally (This is exactly what could happen), or as lower bound predictions (i.e., “This is what could happen at least”) or upper bound predictions (i.e., “This is what could happen at most”). For example, when saying that “the computer battery will likely last 2.5 hours,” they may have meant that the battery would last at least or at most for 2.5 hours. It is well known that quantitative predictions may implicitly focus on at least or at most quantities (e.g., Breheny, 2007; Mandel, 2014). This is, for example, clear in messages, such as “You need to be 18 to buy alcohol” as people easily infer that one should be 18—or older—to be allowed to buy alcohol. The at least and at most interpretations might explain participants’ apparently exaggerated probability estimates. The frequency of a specific modal outcome is fairly low, but the frequency of the outcome at least is actually fairly high because it encompasses the frequency of the mode, plus the frequencies of all the outcomes above the peak. Hence, participants’ probability estimates observed in previous experiments could be more accurate than assumed. In the present experiment, we aimed to test whether indeed participants might view likely outcomes as being outcomes that could happen at least or at most. Participants completed one of two randomly allocated tasks and each task included both the Computer and the Jeans vignettes.

In the modifier selection task, participants received a normally distributed bar graph and a statement about what was likely to happen (e.g., “The computer battery will likely last 2 hours”). Participants were asked which of three interpretations of that statement they found most appropriate: the precise quantity is likely, the likely quantity is what we could expect at least or the quantity is what we could expect at most (e.g., “The computer battery will last for about/at least/at most 2 hours”). We expected that most participants would select the precise interpretation as the most appropriate.

In the probability judgement task, participants received a normally distributed bar graph with three statements about what was likely to happen. One statement centred on the mode, one was concerned with a lower value, and one focused on a higher value. The participants’ task was to select the statement with the highest chance of being true. Participants who interpreted the quantitative statements as at least statements, should select the lower outcome statement as the most likely, whereas those who interpreted statements as at most statements, should select the higher value as more likely. Finally, participants who interpreted the likely quantitative statements as precise predictions should select the modal statement as most likely to be true. We expected that most people would understand quantitative statements to be specifically concerned with the target quantity, and therefore, we hypothesised that most participants would consider that the modal prediction was most likely to come true.

Method

Participants

The survey was conducted via Prolific. A sample of 200 participants completed the survey (median completion: 7 min; £7.71 per hour). Participants were either allocated to the probability task (n = 109) or to the modifier selection task (n = 91). In the sample, 95% of the participants were native English speakers. Of the non-natives, six were experts, three were advanced, and two were intermediate English speakers. The sample included 50% women, 29% men, 0.5% trans men, and 0.5% non-binary. Age ranged from 18 to 81 years with a mean age of 39 years (SD = 14.76). Education ranged from high school diploma (25%) to master’s or doctorate degree (19%), with some participants reporting a college diploma (26%) or a bachelor’s degree (29%).

Materials and procedure

Participants completed either a modifier selection task followed by a probability question or a probability task for both the Computer battery and the Jeans scenarios with a random task allocation and counterbalanced vignette order.

In the modifier selection task, participants were given the same Computer and Jeans scenarios used in Experiment 1 (including the graphs) and read a likely modal prediction for each. In the Computer scenario, they read: Based on these results (shown in the graph), someone said: “It is likely that the battery in a Comfor computer will last for 2.5 hours.” Participants were then asked what the person making that prediction meant:

• The battery of a Comfor computer will likely last for about 2.5 hr.

• The battery of a Comfor computer will likely last for at least 2.5 hr.

• The battery of a Comfor computer will likely last for at most 2.5 hr.

After choosing the statement, participants reported how likely the modal outcome was to occur based on their chosen prediction. What is the probability that a Comfor computer would last for the duration you suggested? The participants were reminded of the predictions they had chosen and provided their judgement on a 0%–100% scale, where 0% was impossible and 100% was certain.

In the probability task, participants were shown the classic vignettes as used in Experiment 1 and were asked which prediction would be the most likely to come true: a prediction describing a low value, a middle value, or a high value, as shown below.

• The battery of a Comfor computer will likely last for 2.5 hr (where 2.5 was the mode of the distribution).

• The battery of a Comfor computer will likely last for 2 hr.

• The battery of a Comfor computer will likely last for 3 hr.

The survey also included an unrelated task presented at the onset of the survey, where participants combined two verbal probability forecasts. The task required participants to estimate the probability of an event that was described as either “not certain” or as having “a chance” to occur by two different forecasters (more details about the method and results are reported in the work of Teigen et al., 2022a).

Results

Modifier selection

In the modifier selection task (n = 91), only a minority selected the predictions that featured the modifiers at least or at most. When a computer battery was described as likely to last for 2.5 hr, 70% of the participants believed that it would last for about that time, and only a few understood the statement as describing a minimum or a maximum duration (at least: 21%, and at most: 9%). Similarly, when jeans were described as likely to shrink by 1 cm, 84% of the participants believed that the jeans would shrink by about that amount and only a minority believed that this described a minimum or maximum to be expected (at least: 10%, and at most: 7%). ²

Interestingly, the selection of the at least and at most interpretations was not consistently associated with a greater probability estimation than the selection of the about interpretation (see Table 3). In the Computer scenario, the probability estimates were higher for participants who selected at least or at most, compared with about, but the difference was not statistically significant, t(89) = 1.74, p = .086, Cohen’s d = 0.40. Furthermore, in the Jeans scenario, the difference was in the opposite direction, with greater probability perception for the about interpretation than for the at least and at most interpretations, but again, the difference was not statistically significant, t(89) = –0.39, p = .697, Cohen’s d = –0.11.

Table 3.

Probability estimates of quantitative predictions in the Computer battery and Jeans vignettes as a function of participants’ interpretations of the outcome as the single bound of an open interval (at least/at most) or as an approximate quantity (about).

Interpretation of the quantitative outcome	Computer		Jeans
	n	M probability (SD)	n	M probability (SD)
At least/at most value	27	65.04 (15.18)	15	59.87 (19.84)
About value	64	58.36 (36)	76	62.26 (22.03)

Probability task

In the probability task (N = 109), 88% of the participants selected the modal outcome prediction as the most likely to be true in the Computer battery vignette, and 95% did so in the Jeans scenario. ³ This shows that a very large majority of the respondents considered that likely referred to the outcome that was specifically mentioned, and did not imply outcomes above or below that point.

Overall, our results support that likely quantities are considered as quantities that are expected—and not as minimum or maximum possible values. The statements were not interpreted as lower bounds in the same way as in some rules (e.g., “You should be 18 to buy alcohol,” “You need to answer correctly 5 of the 10 questions to pass”) where the quantities described are clearly a minimal requirement.

Our results also show that the probability over-estimation was not tied to a particular interpretation, as people who selected the at most, about, and at least interpretations made similar probability estimates. The results support the view that the majority of participants who made likely predictions in Experiments 1–2c were indeed over-estimating the probabilities involved.

In four of our previous experiments (1, 2a, 2b, and 2c), participants consistently chose to predict what was likely and paired that term with the most frequent outcome from the distribution. This is in contrast with past research which found a preference for extreme outcomes for unlikely, certain, and possible predictions (Jenkins et al., 2018; Juanchich et al., 2013; Juanchich & Sirota, 2017; Løhre & Teigen, 2014; Teigen et al., 2013, 2014, 2018, 2019). These two contrasting perspectives are difficult to reconcile and might reflect that both types of statements—those that are concerned with extreme values and those that focus on middle values—have advantages and shortcomings.

Experiment 4a

In the following set of studies, we first tested whether extreme and moderate predictions were judged as correct given a distribution (Experiment 4a) and then assessed how useful and interesting the predictions were (Experiments 4b and c). We compared predictions about central outcomes with statements that are typically used to describe extreme values. We expected that likely statements about middle outcomes as well as unlikely, possible, and will statements about extreme outcomes, would all be considered correct descriptions of a distribution of possible outcomes. However, we expected that participants would perceive the statements differently in terms of usefulness and interest. Building on findings from the work of McKenzie and Amin (2002) showing that bold predictions were considered, under some circumstances, more useful than timid (less extreme) ones, we expected that extreme statements would be considered more useful and interesting.

Method

Participants of Experiments 4a–c

Experiments 4a–c were based on the same online questionnaire completed by 301 participants who were randomly allocated to one of the three experiments. The survey also included two tasks unrelated to the present research question. We filtered out 29 participants who completed the whole survey in less than 3 min (as per our preregistered plans), leaving N = 86, N = 93, and N = 93 for our analyses in Experiments 4a–c, respectively. Participants were aged between 18 and 65 years (M = 37.49, SD = 10.92 years) with 35% being women. Levels of education ranged from 1% with less than high school education to 8% who had a master’s degree or more; 29% had a high school diploma, and 62% had completed a 2- or 4-year college degree.

Design, materials and procedure

Participants received the distributions of computer battery duration and jeans shrinkage as used in Experiments 1 and 2 and evaluated whether each of six predictions seemed correct or not. The predictions included four credible predictions, one middle outcome prediction and three extreme outcomes (a–d) along with two incorrect foil items (e–f) as follows:

1. “It is likely that a Comfor battery will last 2.5 hours” (middle modal outcome);

2. “A Comfor battery will last 1.5 hours” (minimum outcome);

3. “It is possible that a Comfor battery will last 3.5 hours” (maximum outcome);

4. “It is unlikely that a Comfor battery will last 4 hours” (outcome from beyond the range).

5. “A Comfor battery may last 4 hours” (beyond the range outcome);

6. “It is very likely that a Comfor battery will last 3.5 hours” (maximum outcome).

The four predictions corresponded to statements made by participants in Experiments 1–2 and in past studies. We also included two “inappropriate” predictions (e–f) where the probability quantifier did not match the probability of the outcome. These were not commonly found in past research and aimed to ensure that participants did not simply routinely judge all the predictions as correct, and could discriminate between those that were conversationally correct and those that were not appropriate. The predictions were presented in a randomised order to each participant.

Results

Most participants judged statements (a)–(d) to be correct and (e) and (f) to be incorrect, as shown in Table 4. Participants found it acceptable to describe events that were 0% likely as unlikely (statement d), events that were 5%–10% likely as possible (c), and events that were 5%–10% likely as certain by saying “they will happen” (b). Describing the middle outcome as likely was considered to be correct by an even larger majority despite the fact that this value did not occur in more than 40%–50% of the cases. Overall, these results cannot be attributed to a tendency to deem all predictions as correct as the two “inappropriate” predictions were both judged incorrect by most participants (76% and 73%).

Table 4.

Percentages of participants judging predictions to be correct based on a frequency distribution of possible values in two scenarios [95% confidence interval]; Experiment 4a (N = 86).

Prediction	Perceive the prediction as correct
	Computer scenario	Jeans scenario
Moderate outcome prediction
a. Likely + modal outcome	98% [94%, 100%]	92% [85%, 98%]
Extreme outcome predictions
b. Will + minimum outcome	81% [72%, 89%]	64% [54%, 74%]
c. Possible + maximum outcome	84% [75%, 91%]	88% [82%, 94%]
d. Unlikely + beyond range outcome	77% [68%, 85%]	84% [75%, 91%]
Inappropriate predictions
e. May + beyond range outcome	12% [5%, 20%]	15% [8%, 23%]
f. Very likely + maximum outcome	24% [16%, 34%]	27% [18%, 38%]

Experiment 4b

Method

Design, materials and procedure

Participants imagined that they were considering buying a Comfor computer and that they wanted to enquire about the duration of its battery. They then assessed how interesting and useful four predictions that described the duration of Comfor computer batteries were. Note that this time participants were not shown any distributions of possible computer battery durations. The statements were statements (a)–(d) from Experiment 4a (shown in Table 4) and were presented in a randomised order to each participant. Participants were asked to rank the four statements based on how interesting and how useful they were, from first (most interesting/useful) to fourth (least interesting/useful). Participants completed the same procedure for the jeans shrinkage context and the order of the two contexts was randomised.

Results

Participants provided similar ranking of the statements in the Computer and the Jeans scenarios (see Figure 8 with the Computer scenario in the upper panel and the Jeans scenario in the lower panel). As shown in Figure 8, the statement that included will + minimum outcome (b), was ranked most interesting and useful (ranked first and shown in the darkest hue) by about half of the participants, whereas the likely statement (a) was ranked second. The possible + maximum outcome was ranked third, and the unlikely + beyond range statement was considered the least interesting and least useful.

Figure 8.

Participants’ ranks of four probabilistic statements describing the possible duration of Comfor computer batteries and shrinkage of Jeans. The statements were ranked from most (first) to least (fourth) interesting/useful for someone who wanted to purchase the item.

However, participants’ rankings of the statements in this study may not have been driven by their preference for moderate or extreme outcomes. It seems that instead their judgements were mostly driven by the degree of certainty conveyed by the statement. Participants ranked the statement that conveyed the highest degree of certainty (will) as the most useful and interesting and the one that conveyed the lowest degree of certainty (unlikely) as least useful and interesting. In fact, the relationship between ranks of utility and interest and ranks based on probabilistic meaning were the same: “will > likely > possible > unlikely.”

Experiment 4c

In Experiment 4b, participants judged the likely + modal statement as second most useful and interesting and ranked the will + minimum outcome statement in first place. This could be taken as indicating that people find extreme (minimum) outcomes more useful and interesting than modal statements. However, in the statements used in Experiment 4b, the outcome was confounded with the degree of certainty conveyed, so we cannot draw a clear conclusion about what drives the participants’ preferences. The participants seemed to have judged the statements based on the probability they conveyed, and not on whether the outcome was central or extreme. To better assess the participants’ perceptions of extreme versus middle outcome statements, in the next experiment we kept the probability conveyed stable and only changed the outcome, while clearly marking whether the outcome came from the bottom, middle or top of the distribution.

Method

Design, materials and procedure

The materials were the same as in Experiment 4b but included only three statements. Participants read three statements about the minimum, middle, and maximum duration of computer batteries or amount of jeans shrinkage, and were asked to assume that the predictions were correct. These statements all included the modal verb will, together with a relevant modifier (on average, at least, and up to) to mark their position in the distribution and accurately describe the outcome (even if participants were not shown the distribution).

1. A Comfor computer battery will last for 2.5 hr on average (middle outcome);

2. Comfor computer batteries will last for up to 3.5 hr (maximum outcome);

3. Comfor computer batteries will last for at least 1.5 hr (minimum outcome).

Participants ranked the predictions along three dimensions. They assessed how interesting, useful, and cautious the predictions were (on different pages presented in a randomised order to each participant). The most interesting, useful or cautious statements were ranked first and the least interesting, useful, or cautious ones were ranked third.

Results

Figure 9 shows participants’ judgements of how interesting, useful, or cautious the three statements were in the Computer vignette (upper panel) and in the Jeans vignette (lower panel). In terms of interest (leftmost panel), the statement focusing on the maximum outcome (shown in light orange) was more often deemed the most interesting, whereas the statement relating to the lowest possible outcome (shown in pink) was judged the least interesting. The statement about the middle outcome (dark purple) was ranked most often second best. A pairwise Wilcoxon rank test comparing the average rank of the modal prediction to the two extreme predictions showed that the maximum prediction was judged more interesting than the modal one, Z_computer = –2.65, p = .008, Z_jeans = –2.46, p = .014. The minimum prediction was judged less interesting than the modal prediction in the Computer and the Jeans contexts, but the difference was only statistically significant in the Computer context, Z_computer = –5.47, p < .001, Z_jeans = –0.39, p = .697.

Figure 9.

Participants’ ranks of three statements describing the duration of Comfor computer batteries and shrinkage of jeans. The statements were issued with the same degree of certainty, but differed by focusing on the minimum, middle/modal, or the maximum outcome. The statements were ranked from best (first) to worst (third) for someone who wanted to purchase the item (n = 93).

Regarding the statements’ utility, participants did not exhibit a clear pattern of preference. This is shown by the flatter distribution of ranks in the middle panel of Figure 9 where each statement was ranked as being the best (first) by about 30% of the participants. However, because it was ranked second consistently and first sometimes, the statement relating to the modal/middle outcome was on average judged more useful than the extreme minimum statement, Z_computer = 3.14, p = .002, Z_jeans = 2.79, p = .005. The modal/middle outcome statement was also judged more useful than the maximum one, albeit the difference was only statistically significant for the Jeans scenario (and not for the Computer one), Z_jeans = 2.15, p = .032, Z_computer = 1.55, p = .121.

For caution, participants did not find the modal/middle statement more cautious than the two extreme statements (in contrast with our expectations). They actually ranked the minimum and maximum statements as more cautious than the modal/middle prediction in both the Computer and Jeans vignettes, but the mean rank difference was only statistically significant in the Computer vignette: modal/middle versus min: Z_computer = –2.07, p = .039, Z_jeans = 0.68, p = .498, modal/middle versus max: Z_computer = 0.78, p = .436, Z_jeans = 1.82, p = .069. The vignettes also differed in judged cautiousness of minimum and maximum statements. The minimum value was judged the most cautious in the Computer context—where the outcome was positive—whereas the maximum one was judged more cautious in the Jeans shrinkage context—where the outcome was negative. This was probably because “worst case” statements were perceived as more cautious than “best case” statements.

To summarise, the results of Experiment 4a showed that most people considered statements describing the modal outcome of a distribution as likely, to be correct. This was also the case for extreme statements about the minimum or maximum outcomes that could be expected. The results of Experiments 3b and c highlighted why the likely, modal outcome statements commonly produced by participants in Experiments 1 and 2a–c may have been particularly attractive: they appeared as “well rounded” predictions. In the absence of a known distribution, the likely + modal outcome statements were found to be better than the extreme ones (second best for utility, interest and caution). Statements about the maximum outcomes were judged as interesting and useful but less cautious, whereas minimum outcomes were ranked as neither interesting nor useful, but more cautious.

General discussion

To have a fine-grained approach of what might happen in the future, it is useful to focus on how much of an outcome might happen instead of whether or not it might happen (e.g., the sea will likely rise 50 cm vs the sea will likely rise). For instance, being told that climate change is occurring is important but not informative when it comes to guiding the decisions of policy-makers or members of the public. Knowing the magnitude of climate events has more potential in terms of evaluating its threat and making the right decisions. But such predictions are of a probabilistic nature. They may be likely, or unlikely, possible, or uncertain. Past research has shown that many of these “verbal probability expressions” are typically used to describe extremes outcomes near the top or bottom of a distribution (Jenkins et al., 2018; Juanchich et al., 2013; Juanchich & Sirota, 2017; Teigen et al., 2013, 2014, 2018, 2019). These extreme outcomes occur infrequently and hence are formally unlikely, but participants tend to over-estimate their chances of occurring. In our work, we tested whether this “extremity effect” implies (and can be derived from) a general preference for extreme outcomes, while the moderate ones would be considered more trivial and less worthy of being mentioned. But, in our studies, people who were asked to provide their statements freely generated or selected central outcomes more often than extreme ones. They also estimated the predicted values to have a high rather than low probability of occurring—much higher than warranted by the frequencies associated with these outcome values.

Participants do not have a general preference for extreme outcomes when making a quantitative prediction

Our first and most notable finding was that participants did not exhibit a preference for extreme outcomes. On the contrary, they favoured statements about what was normal and average or central in a distribution—far from “not being worth mentioning” as stated in previous research (Juanchich et al., 2013). In four experiments (Experiments 1, 2a–c) we consistently observed that when participants made a quantitative prediction based on a distribution of possible outcomes, they concentrated on the most frequent outcomes of the distribution (the modal outcome values). This does not invalidate the earlier findings of an extremity effect with unlikely, certain, or possible. Instead, it provides a more nuanced understanding of the effect. The extremity preference exists but is limited to a specific group of verbal probability phrases (e.g., unlikely, possible, certain). Importantly, our results show that people do not use this particular terminology often, and so that, naturally tend not to concentrate on extreme outcome values. When choosing their own probability quantifier, participants mostly preferred to call attention to likely or expected outcomes, exemplified by the modal outcome as the most representative value. Thus, the “extremity effect” found with statements about possible and unlikely outcomes is not due to a general preference for extreme outcomes. Some verbal probabilities appear to be “naturally” associated with minimum or maximum possible outcomes, with little consideration for the actual frequencies involved, whereas other quantifiers are associated with the central values of the distribution. It may therefore be misleading to refer to so-called probability words with the term “probability,” since they may actually be used to describe the magnitude of an outcome relative to other possible outcomes, rather than a particular level of probability.

It is also important to note that the outcome selected by participants might vary as a function of their communicative goal. We did not assess this particular possibility in the present experiments, but past research documented the importance of context by showing a reversal of preference for highest to lowest outcome values, depending on the goal of the speaker. For example, the possible price of a house was the highest of the distribution when the speaker talked to a seller, but the lowest when the speaker talked to a buyer (Teigen et al., 2014). The general preference for moderate outcomes we found in our studies might be situationally dependent on participants’ commitment to produce a “correct,” neutral statement, and be shifted towards more extreme values depending on the goal of the speaker or the recipient.

When we sought participants’ evaluations of moderate and extreme predictions (Experiments 4a–c), we found that participants judged what was likely and average to be both interesting and useful in making a decision. Experiments 4b and c together showed that the degree of certainty of a prediction also plays a role in how interesting it is perceived to be. Participants preferred predictions of minimum outcomes that will occur to those that were merely likely, possible, or unlikely to happen (Experiment 4b). However, when predictions were issued with the same degree of certainty, as in Experiment 4c, where will was used in all the statements, maximum outcomes were judged to be more interesting. Minimum outcomes were only considered more useful than maximum ones when they were described with a higher level of certainty (e.g., certain vs possible). Interestingly, with equally certain outcomes, participants seemed to find the maximum outcome more useful and interesting than a minimum or modal one—making, for example, a prediction of maximum possible sea level rise or rainfall most interesting. The asymmetry between the preference for lower or upper bound outcomes may be related to the scalar entailments of numeric quantities, in which large amounts entail smaller ones, but not vice versa (Noveck, 2001; Politzer, 2007) and to the concept of linguistic markedness, whereby dimensions are named after their top rather than their bottom values (Battistella, 1996; Clark & Clark, 1977).

Past work on over-estimation tied that phenomenon to the extremity of the outcome selected. It was assumed that the over-estimation was caused by the infrequency of the outcomes selected by participants, but here we have shown that a similar phenomenon also occurred when participants chose the most frequent outcome of the distribution. Participants largely over-estimated the chances of occurrence of the outcome they had predicted, both when they were extreme (hence rare)—when the most likely outcome was chosen. This is consistent with studies showing that the probability of occurrence of multi-outcome events seems not to be based on their absolute chances, but rather upon how likely they are compared with other events in the distribution (Teigen, 2001; Windschitl & Wells, 1998), and also with more recent work on “likely” interval predictions, where participants mostly failed to select an interval wide enough to be statistically probable (Teigen et al., 2022b).

The over-estimation of numeric probabilities could not be explained by an inability to read the distribution. We found that when choosing an outcome, participants inspected the frequency distributions and were able to identify frequencies quite accurately (Experiment 2c). However, they did not seem to use the numerical information from the graphs to calculate their probability estimates, suggesting two other explanations. First, that they regarded outcome values as interval boundaries rather than exact values, and second, that they did not solve the tasks as “frequentists,” but according to another epistemic or aleatory probability concept where frequency distributions may be informative, but do not yield the p-values of outcomes by definition.

Participants did not use frequencies to guide their probability perceptions

Regarding this latter possibility, participants’ probability estimates may have been based on their choice of probability term instead of based on the frequencies shown in the distribution. In our experiments, participants first made a prediction and then provided a probability estimate for the event they predicted. Their estimates might, accordingly, have been influenced by their choices. So, for instance, when they selected a 40% likely middle outcome and described it as likely, they might have subsequently concluded that, being likely, its probability must be estimated to be around 60%–70%. This could be checked by changing the order of questions, asking for probability estimates first and following up with questions about appropriate verbal statements. The difference in participants’ perceptions of frequency and probabilities (where frequencies were more accurate) raises an interesting applied question and potential application: which one of the two judgements would be more consequential for decisions? And could there be ways of nudging people to think more frequentistically to improve their decisions? Future research could address this possibility, assessing the link between frequency, subjective probability and decision outcome.

Interestingly, Experiment 2c evidences a boundary condition to the probability over-estimation. When asked to produce a range of outcome values, instead of a single value, around one-third of the participants selected the total (complete) range of outcomes. These participants did not over-estimate the chances of their prediction coming true, and even under-estimated it a little. Clearly, it would be impossible to over-estimate the chances of such an outcome to occur, since its probability of occurrence is statistically 100%. An under-estimation of the probability of wide ranges is consistent with research on intervals showing that wider intervals are not necessarily perceived as more likely and actually feel more uncertain than narrower ones (Løhre et al., 2019).

Quantitative estimates as boundaries

When considering the notion of accuracy in probability estimates, it is important to consider how participants construed the task and interpreted the prediction. We have described the notion of probability accuracy based on the expectation that the outcome predicted was exact (albeit rounded), and participants assessed the probability of occurrence of an exact outcome value. However, quantitative predictions could also represent minimal or maximal values to be expected rather than exact values (Breheny, 2007). The knowledge that a numerical value can represent an exact value or the lower/upper bound of an implicit range develops early on in childhood (Musolino, 2004), but it is not always clear to recipients when speakers talk about minimum, maximum or exact values. For example, when reading: “It is certain that 200 of 600 people will be saved,” 60% of the participants believed that at least 200 people would be saved, whereas 30% believed that exactly 200 people would be saved (Mandel, 2014). It is obvious that the interpretation chosen depends on the context, but what exactly in the context triggers that inference is still debated (Breheny, 2007; Mandel, 2014). Experiment 3 showed that, regarding computer battery durations and jeans shrinkages, most people believed that the predictions were exact, focusing specifically on the outcome they had chosen. When describing the likely duration of computer batteries or the amount of jeans shrinkage, we found that only 20% of the participants adopted an at least or at most interpretation. This is consistent with interpretations given to percentages observed in previous studies where a full breakdown of the percentages of alternative outcomes was given (e.g., 200 people will be saved and 400 will die). In that case, most participants adopted an exact interpretation of the quantities while around 24% adopted an at least interpretation and 17% an at most interpretation (Mandel, 2014).

Conclusion

The present studies show that the “extremity effect” that has previously been found for a number of probability quantifiers describing the occurrence of quantitative outcomes cannot be reduced to or described as a generic preference for extreme outcomes. In contrast, most people seem to prefer to predict what is “representative” of the distribution (Teigen et al., 2022b): they describe what is likely, normal, or expected, and tend to concentrate on the middle and most likely outcome of a distribution. Although the peak outcome had a fairly low frequency, participants believed on average that the outcome was quite likely and tended to over-estimate the probability of that outcome.