Discriminant Subgraph Learning from Functional Brain Sensory Data

Abstract

The human brain is a complex system with many functional units interacting with each other. This interacting relationship, known as the functional connectivity network (FCN), is critical for brain functions. To learn the FCN, machine learning algorithms can be built based on brain signals captured by sensing technologies such as EEG and fMRI. In neurological diseases, past research has revealed that the FCN is altered. Also, focusing on a specific disease, some part of the FCN, i.e., a sub-network, can be more susceptible than other parts. However, the current knowledge about disease-specific sub-networks is limited. We propose a novel Discriminant Subgraph Learner (DSL) to identify a functional sub-network that best differentiates patients with a specific disease from healthy controls based on brain sensory data. We develop an integrated optimization framework for DSL to simultaneously learn the FCN of each class and identify the discriminant sub-network. Further, we develop tractable and converging algorithms to solve the optimization. We apply DSL to identify a functional sub-network that best differentiates patients with episodic migraine (EM) from healthy controls based on a fMRI dataset. DSL achieved the best accuracy compared to five state-of-the-art competing algorithms.

1. Introduction

The human brain is a complex system with many functional units interacting with each other. This interacting relationship, known as the functional connectivity network (FCN), is critical for brain functions (Van Den Heuvel and Pol, 2010). To learn the FCN, brain sensory technologies such as EEG, and functional MRI (fMRI) provide relevant data. By applying statistical machine learning algorithms to the data, the FCN can be inferred (Van Den Heuvel and Pol, 2010); (Huang et al., 2012).

The brain is susceptible to various types of diseases and injuries such as migraine, Alzheimer’s disease, and concussion. Past research has revealed that the FCN is altered in patients with these diseases and injuries (Silva et al., 2019). Also, because each type of disease has its specific pathological underpinning and phenotypic presentation, the FCN is altered in different ways for different diseases. Focusing on a specific disease, some part of the FCN, i.e., a sub-network, may be more susceptible than other parts. These findings provide the physiological foundation for the importance of identifying disease-specific sub-networks, which would allow for better detection or classification of the disease.

A motivating example:

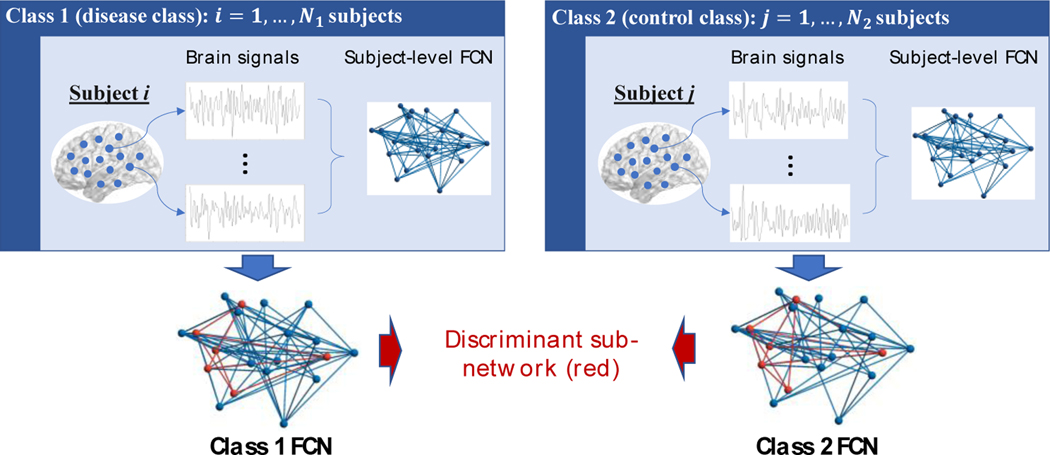
In the study of migraine, past research has revealed that the sub-networks involved in pain processing are likely to be impacted by the disease (Russo et al., 2012). However, the current knowledge about disease-specific sub-networks is quite limited, qualitative, or incomplete (Bogdanov et al., 2017). Fortunately, due to the rapid advance of brain sensory technologies, quantitative data can be collected, which makes it possible to develop machine learning algorithms to identify the sub-networks. For example, fMRI is an imaging technology that allows for collection of dynamic functional activity data from different regions of the brain. Based on the fMRI data, it is possible to identify the disease-specific sub-networks using machine learning. However, the existing machine learning algorithms fall short for providing a suitable solution. While the area of graphical models seems to be conceptually similar to our problem of sub-network identification, graphical modelling algorithms are not designed to find the “discriminant” sub-network that differentiates the patients with migraine from healthy controls. Thus, these algorithms, by design, do not have discrimination or classification capacities. Another related research area is graph classification. However, a fundamental difference between graph classification and our objective is that the former assumes that the graphs are given (i.e., graphs are input to the algorithm), whereas our objective is to learn the discriminant sub-network/subgraph from data (i.e., the subgraph is the output from our algorithm). Due to the limitations of existing methods, we propose a novel Discriminant Subgraph Learner (DSL) to identify the disease-specific sub-network based on brain sensory data, which allows for classification of the disease with high accuracy (Fig. 1).

Figure 1.

Schematic overview of the learning objective of the proposed DSL: DSL simultaneously learns class FCNs and identify the discriminant sub-network from brain sensory data

The basic idea of DSL is briefly introduced here. To capture the variability of the FCN at both the subject and the class levels, we propose a Bayesian hierarchical model, which assumes that the FCN of each subject, represented by the inverse covariance (IC) matrix of the subject’s brain sensory data, shares a common FCN/IC at the class level. Further, we propose an integrated optimization formulation that learns the IC of each class and simultaneously identifies the discriminant subgraph within the IC. The proposed formulation also uses sparsity-inducing penalties to address the challenge of learning ICs from high-dimensional datasets. Further, to provide a tractable solution for the optimization, we develop an iterative algorithm that alternates through subsets of the parameters with convergence guarantee. Additionally, to address the challenge in learning the class-level ICs within the iterative algorithm, we introduce latent variables and develop an Expectation-Maximization (EM) algorithm integrated with Block Coordinate Descent (BCD). The contributions of this paper are summarized as follows:

Contribution to statistical machine learning:

The proposed DSL model interacts with two research areas in machine learning: graphical models and graph classification. However, as explained previously, neither of the existing research areas provides the same capability as DSL. The novel design of DSL includes an integrated optimization formulation that simultaneously achieves two goals: (1) learning the FCN/IC of each class, and (2) identifying the discriminant subgraph within the IC. Additionally, we develop a tractable and converging algorithm to solve the optimization problem of DSL.

Contribution to the application domain:

DSL makes it possible to identify the functional sub-network that best differentiates patients with a certain disease from healthy controls based on functional brain sensory data. Specifically in this paper, we apply DSL to identify a functional sub-network that best differentiates patients with episodic migraine (EM) from controls based on fMRI data. Classification of EM versus controls based on neuroimaging data is a more challenging task than that of chronic migraine (Schwedt et al., 2015). We also compare DSL with four state-of-the-art machine learning algorithms. DSL outperforms all these existing algorithms.

The remainder of this paper is organized as follows: Sec. 2 reviews the related work. Sec. 3 presents the development of the proposed DSL model. Sec. 4 provides simulation experiments. Sec. 5 presents a real-data application. Sec. 6 is the conclusion.

2. Related work

2.1. Graphical models

A graphical model includes nodes to represent variables or features and edges to characterize relationships between the variables. The edges can be undirected or directed. One of the most popular types of undirected graphical models is called Gaussian Graphical Model (GGM), in which the nodes are assumed to follow a multivariate Gaussian distribution. Directed graphical models are also known as Bayesian networks (Jordan and Weiss, 2002). In this paper, our methodological development is based upon GGM. Thus, we focus on reviewing the existing research in GGM in this section.

In a GGM, the weight of the edge between two variables is related to partial covariance or inverse covariance (IC). Therefore, learning a GGM becomes learning the IC matrix from the data. This is a challenging task with high-dimensional features but limited sample sizes. To tackle the challenge, researchers have proposed various formulations that include sparsity-inducing penalties in the IC estimation to control the model complexity. Friedman et al. (Friedman et al., 2007) developed a coordinate descent algorithm for sparse IC estimation under the lasso penalty, known as graphical lasso. Hirose et al. (Hirose, Fujisawa and Sese, 2017) proposed a $\gamma$-lasso to get a robust sparse IC estimation based on $\gamma$-divergence. Huang et al. (Huang et al., 2012) proposed to learn the ICs of multiple tasks using a Bayesian framework that allowed knowledge transfer when learning task-specific ICs.

2.2. Graph classification

Graph classification is a popular research area in recent years due to the emerging graph data in various domains. Graph classification assumes that the graph of each sample is known, instead of having to be learned from data, and aims to use the graphs as input to differentiate between classes.

The existing graph classification methods fall into two general categories: similarity-based and subgraph-feature-based approaches. Similarity-based approaches learn global similarity between each pair of graphs, which is further used by conventional classification algorithms such as SVM for classification of the graphs. Global similarity is measured by graph kernels or graph embedding. Schölkopf, Tsuda and Vert (2003) introduced a unified account of a family of kernels that are defined via label sequences for handling graph data. Other types of kernels have been proposed to measure graph similarity, such as kernels between vertex and/or edge label histograms (Gärtner, Flach and Wrobel, 2003), graphlet kernels (Shervashidze et al., 2009), random walk kernels (Sugiyama and Borgwardt, 2015), and Weisfeiler-Lehman graph kernel (Shervashidze et al., 2011). Graph embedding has also been used for similarity-based approaches. Riesen et al. proposed a graph classification system using Lipschitz embedded graphs (Riesen and Bunke, 2009). One limitation of similarity-based graph classification methods is that the similarity is computed based on the global structure of graphs. However, some sub-structures may not have discriminant power and therefore including them in the computation of graph similarity may negatively affect the classification accuracy. This limitation is better addressed by the other category of graph classification methods based on subgraph features.

The basic idea of subgraph-feature-based approaches is to identify discriminative sub-structures of graphs (a.k.a. subgraphs), and put the subgraphs into a vector-format feature set to which conventional classifiers can be applied. Yan and Han (Yan and Han, 2002) proposed a method called gSpan, which mined frequent subgraphs via a lexicographic order. A LEAP algorithm was developed by Yan et al. (Yan et al., 2008) to exploit correlations between structure similarity and significance similarity by identifying dissimilar graph patterns. Saigo et al. (Saigo et al., 2009) proposed a gBoost method that progressively collects informative patterns and selects subgraphs from the whole subgraph space via a branch-and-bound pattern search algorithm. Vogelstein (Vogelstein et al., 2012) proposed a joint graph/class model to identify class-conditional signals encoded in a subset of edges. Pan et al. (Pan et al., 2015) proposed an MTG algorithm that adopts $l_1$-norm and $l_{21}$-norm regularization under a multitask learning formulation and incrementally selects subgraph features. Thanikaivelan and Gandhi (S. Thanikaivelan and K. Rajiv Gandhi, 2017) considered selecting optimal subgraphs through Principal Component Analysis (PCA) with a combined pruning technique.

2.3. Gaps of the existing research

Neither graphical models nor graph classification algorithms provide a direct solution to our targeted problem. Graphical models learn variable relationships from data, but they do not provide discrimination or classification capacities. Graph classification algorithms aim for classification, but they are under the assumption that the graph of each subject must be given. To solve our problem, one may suggest a two-step approach: 1) applying graphical models to learn the graph (i.e., functional network) of each subject from his/her brain sensory data; 2) applying graph classification algorithms on the learned graphs from 1) for classification. The limitation of the two-step approach is that the uncertainty in learning the graphs in step 1) will propagate to step 2) and affect the classification accuracy. In contrast, DLS integrates the two steps into a single optimization framework, and thus effectively tackling the uncertainty propagation. Our simulation and real-data experiments also demonstrate the advantage of DLS compared with the two-step approach.

3. Development of the proposed discriminant subgraph learner (DSL)

We will provide the model formulation for a two-class classification problem. The proposed model works generally for different types of functional brain sensory data such as EEG and fMRI. We use fMRI here to present the model formulation as this may be a less familiar data type to the readers.

3.1. Mathematical formulation of DSL

The fMRI of each subject is a 4-D object, composed by 3-D brain images taken at a series of n time points. Each brain image includes many voxels as the basic units. At each voxel, the fMRI scan produces a time series measuring the dynamics of functional activity at that location, known as the blood oxygen level dependent (BOLD) signal. When studying a particular disease, it is commonplace to focus on a set of Regions of Interest (ROIs) of the brain related to the disease. Then, the voxel-wise BOLD signals within each ROI can be averaged into a ROI-wise signal. Let $p$ be the number of ROIs. For example, in our case study, $p=33$ corresponding to 33 ROIs based on a meta study of the existing migraine literature (Chong et al., 2017). For each subject $i$ included in the study, let ${\mathbf{x}}_i$ denote the BOLD signals of all the ROIs, i.e., ${\mathbf{x}}_i$ is a $n_i\times p$ matrix with $n_i$ representing the signal length.

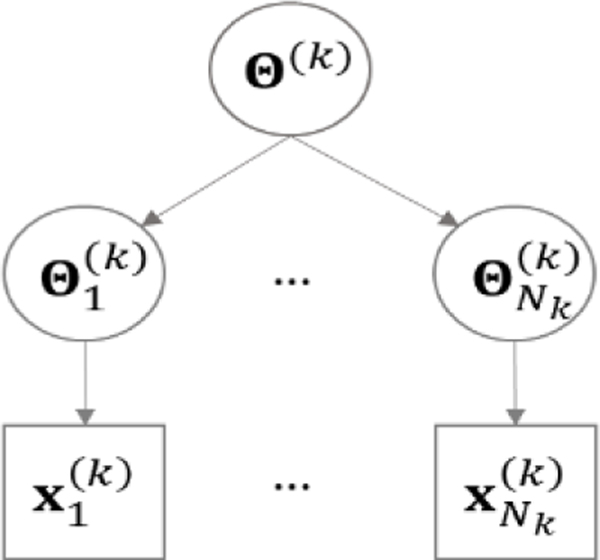
Consider two classes that consist of $N_1$ and $N_2$ subjects, respectively. For example, the two classes can correspond to EM patients and healthy controls, respectively. As the subjects are nested within each class, we propose to use a Bayesian hierarchical model (BHM) to characterize the data generating process (Fig. 2). Focus on class 1. Let ${\mathbf{x}}_i^{\left(1\right)}$ denote the data for subject $i$ in class 1, $i=1,\dots ,N_1$. Recall that ${\mathbf{x}}_i^{\left(1\right)}$ is an $n_i\times p$ matrix, with each row consisting of BOLD measurements for $p$ ROIs at a particular time point. Assume each row of ${\mathbf{x}}_i^{\left(1\right)}$ follows a multivariate Gaussian distribution of ${\mathrm{N}}_p(\mathbf{0},{\mathbf{\Sigma }}_i^{\left(1\right)})$. Let ${\mathbf{\Theta }}_i^{\left(1\right)}\mathrm{ }\triangleq {{\mathbf{\Sigma }}_i^{\left(1\right)}}^{-1}$ be the IC matrix, which has been used in previous research to characterize the functional connectivity among the ROIs (Huang et al., 2012). Further assume the IC matrices of all the subjects in class 1 are generated from a common Wishart distribution, i.e., ${\mathbf{\Theta }}_i^{\left(1\right)}|{\mathbf{\Theta }}^{\left(1\right)}\sim \mathrm{ }\mathrm{W}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{t}\left({\mathbf{\Theta }}^{\left(1\right)},\mathrm{ }h\right)$, $i=1,...,N_1$. ${\mathbf{\Theta }}^{\left(1\right)}$ is the IC matrix of class 1. ${\mathbf{\Theta }}^{\left(1\right)}$ and $h$ are the hyper-parameters of the Wishart distribution, known as the inverse scale matrix and the degree of freedom, respectively.

Figure 2.

BHM for class $k$ ($k=\mathrm{1,\; 2}$)

Based on the proposed BHM in Fig. 2, we can derive the likelihood function of ${\mathbf{\Theta }}^{\left(1\right)}$, $L\left({\mathbf{\Theta }}^{\left(1\right)};{\left\{{\mathbf{x}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}\right)$ as follows:

$$L\left({\mathbf{\Theta }}^{\left(1\right)};{\left\{{\mathbf{x}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}\right)=p\left({\left\{{\mathbf{S}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}|{\mathbf{\Theta }}^{\left(1\right)}\right)=\int p\left({\left\{{\mathbf{S}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}|{\mathbf{\Theta }}^{\left(1\right)},\mathbf{ }{\left\{{\mathbf{\Theta }}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}\right)p\left({\left\{{\mathbf{\Theta }}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}|{\mathbf{\Theta }}^{\left(1\right)}\right)d{\mathbf{\Theta }}_1^{\left(1\right)}\dots d{\mathbf{\Theta }}_{N_1}^{\left(1\right)},$$ (1)

where ${\mathbf{S}}_i^{\left(1\right)}$ is the sample covariance matrix computed from ${\mathbf{x}}_i^{\left(1\right)}$; the first equation is because the likelihood is only relevant to the sample covariance matrices; the second equation is due to the hierarchical structure of the BHM. We can further derive the two probabilities in the integral as follows:

$$p\left({\left\{{\mathbf{S}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}|{\mathbf{\Theta }}^{\left(1\right)},\mathbf{ }{\left\{{\mathbf{\Theta }}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}\right)={\prod }_{i=1}^{N_1}p\left({\mathbf{S}}_i^{\left(1\right)}|{\mathbf{\Theta }}_i^{\left(1\right)}\right)$$ (2)

according to the BHM. A commonly used distribution for a sample covariance matrix is the Wishart distribution, i.e., $n_i{\mathbf{S}}_i^{\left(1\right)}|{\mathbf{\Theta }}_i^{\left(1\right)}\sim \mathrm{W}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{t}(\mathrm{ }{{\mathbf{\Theta }}_i^{\left(1\right)}}^{-1},n_i)$, which has a probability function of

$$p\left({\mathbf{S}}_i^{\left(1\right)}|{\mathbf{\Theta }}_i^{\left(1\right)}\right)\propto {\left|{\mathbf{\Theta }}_i^{\left(1\right)}\right|}^{\frac{n_i}{2}}{e}^{-\mathrm{ }\frac{n_{i}tr\left({\mathbf{\Theta }}_i^{\left(1\right)}{\mathbf{S}}_i^{\left(1\right)}\right)}{2}}.$$ (3)

Furthermore, we can derive the second probability in the integral of (1) as

$$p\left({\left\{{\mathbf{\Theta }}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}|{\mathbf{\Theta }}^{\left(1\right)}\right)={\prod }_{i=1}^{N_1}p\left({\mathbf{\Theta }}_i^{\left(1\right)}|{\mathbf{\Theta }}^{\left(1\right)}\right),$$ (4)

according to the BHM structure. Using a Wishart distribution of ${\mathbf{\Theta }}_i^{\left(1\right)}|{\mathbf{\Theta }}^{\left(1\right)}\sim \mathrm{ }\mathrm{W}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{t}\left({\mathbf{\Theta }}^{\left(1\right)},\mathrm{ }h\right)$ as previously described, we can write the probability function:

$$p\left({\mathbf{\Theta }}_i^{\left(1\right)}|{\mathbf{\Theta }}^{\left(1\right)}\right)\propto {{\left|{\mathbf{\Theta }}^{\left(1\right)}\right|}^{-\frac{h}{2}}\left|{\mathbf{\Theta }}_i^{\left(1\right)}\right|}^{\frac{h-p-1}{2}}\exp \left(-\frac{tr\left({{\mathbf{\Theta }}^{\left(1\right)}}^{-1}{\mathbf{\Theta }}_i^{\left(1\right)}\right)}{2}\right).$$ (5)

Next, inserting (3) and (5) into (1), the likelihood function becomes:

$$L\left({\mathbf{\Theta }}^{\left(1\right)};{\left\{{\mathbf{x}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}\right)\propto \int \{{\prod }_{i=1}^{N_1}{\left|{\mathbf{\Theta }}_i^{\left(1\right)}\right|}^{\frac{n_i}{2}}{e}^{-\frac{n_{i}tr\left({\mathbf{\Theta }}_i^{\left(1\right)}{\mathbf{S}}_i^{\left(1\right)}\right)}{2}}{\prod }_{i=1}^{N_1}{\left|{\mathbf{\Theta }}^{\left(1\right)}\right|}^{-\frac{h}{2}}|\mathrm{ }{\mathbf{\Theta }}_i^{\left(1\right)}\mathrm{ }{\left.\right|}^{\frac{h-p-1}{2}}{e}^{-\mathrm{ }\frac{\mathrm{t}\mathrm{r}\left({{\mathbf{\Theta }}^{\left(1\right)}}^{-1}{\mathbf{\Theta }}_i^{\left(1\right)}\right)}{2}}\}d{\mathbf{\Theta }}_1^{\left(1\right)}\dots d{\mathbf{\Theta }}_{N_1}^{\left(1\right)}$$

$$\propto {\left|{\mathbf{\Theta }}^{\left(1\right)}\right|}^{-\mathrm{ }\frac{N_{1}h}{2}}{\prod }_{i=1}^{N_1}{\left|n_i{\mathbf{S}}_i^{\left(1\right)}+{{\mathbf{\Theta }}^{\left(1\right)}}^{-1}\right|}^{- \frac{n_i+h}{2}}.$$ (6)

In a similar way, we can get the likelihood function of ${\mathbf{\Theta }}^{\left(2\right)}$, $L\left({\mathbf{\Theta }}^{\left(2\right)};{\left\{{\mathbf{x}}_i^{\left(2\right)}\right\}}_{i=1,\dots ,N_2}\right)$.

Furthermore, recall that in this paper we focus on the situation when two classes differ in a sub-matrix (a.k.a. subgraph) in their IC matrices, which only involves a subset of the ROIs. Let $\mathit{C}$ be an indicator matrix, i.e., a $p\times p$ diagonal matrix with 1 or 0 in its diagonal to indicate if an ROI is included in the subgraph or not. $\mathit{C}$ is unknown so it needs to be learned from data. To learn $\mathit{C}$, one approach is to learn the IC matrix of each class, i.e., ${\mathbf{\Theta }}^{\left(1\right)}$ and ${\mathbf{\Theta }}^{\left(2\right)}$, using their respective data, and then compare the learned ICs to identify $\mathit{C}$. The limitation of this sequential approach is that learning of the IC matrix of each class in the first step will affect the identification of $\mathit{C}$ in the second step. When the sample size is limited, it is difficult to learn an accurate IC for each class. Consequently, it will be difficult to identify $\mathit{C}$ accurately. To overcome this limitation, we propose the DSL model to learn $\mathit{C}$, ${\mathbf{\Theta }}^{\left(1\right)}$, ${\mathbf{\Theta }}^{\left(2\right)}$ altogether. DSL aims to solve the optimization problem in (7) that simultaneously balances learning of the IC for each class and identifying the subgraph $\mathit{C}$ that best distinguishes the two classes.

$$\underset{{\mathbf{\Theta }}^{\left(1\right)},{\mathbf{\Theta }}^{\left(2\right)},\mathbf{ }\mathit{C}}{\max }\left\{\begin{array}{c}\stackrel{subgraph\mathrm{ }difference\mathrm{ }between\mathrm{ }classeses}{\overbrace{{\left|\left|{\mathit{C}}^T\left({\mathbf{\Theta }}^{\left(1\right)}-{\mathbf{\Theta }}^{\left(2\right)}\right)\mathit{C}\right|\right|}_1}}+{\mu }_1\stackrel{likelihood\mathrm{ }of\mathrm{ }{\mathbf{\Theta }}^{\left(1\right)}}{\overbrace{L\left({\mathbf{\Theta }}^{\left(1\right)};{\left\{{\mathbf{x}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}\right)}}\\ +{\mu }_2\stackrel{likelihood\mathrm{ }of{\mathbf{ }\mathbf{\Theta }}^{\left(2\right)}}{\overbrace{L\left({\mathbf{\Theta }}^{\left(2\right)};{\left\{{\mathbf{x}}_j^{\left(2\right)}\right\}}_{j=1,\dots ,N_2\mathrm{ }}\right)}}-{\mathrm{\lambda }}_1\stackrel{sparsity\mathrm{ }of{\mathbf{ }\mathbf{\Theta }}^{\left(1\right)}}{\overbrace{{\left|\left|{\mathbf{\Theta }}^{\left(1\right)}\right|\right|}_1}}-{\mathrm{\lambda }}_2{\stackrel{sparsity\mathrm{ }of\mathrm{ }{\mathbf{\Theta }}^{\left(2\right)}}{\overbrace{\left|\left|{\mathbf{\Theta }}^{\left(2\right)}\right|\right|}}}_1\end{array}\right\}$$ (7)

$$\text{s.t.}sum\left(diag\left(\mathit{C}\right)\right)\le K;{\mathbf{\Theta }}^{\left(1\right)}\succ \mathbf{0};{\mathbf{\Theta }}^{\left(2\right)}\succ \mathbf{0}.$$

Specifically, the first term in the objective function of (7) aims to maximize the difference between the submatrices of the IC matrices of the two classes. ${\left|| |\right|}_1$ denotes the $l_1$-norm of the difference. To see the meaning of this term more clearly, consider a simple example of three ROIs and $\mathit{C}=\left[\begin{array}{ccc}1& & \\ & 0& \\ & & 1\end{array}\right]$, i.e., only the first and third ROIs are included in the subgraph. Then the first term in the objective function of (7) becomes ${\left|\left|{\mathit{C}}^T\left({\mathbf{\Theta }}^{\left(1\right)}-{\mathbf{\Theta }}^{\left(2\right)}\right)\mathit{C}\right|\right|}_1={\left|\left|\left[\begin{array}{cc}{\theta }_{11}^{\left(1\right)}& {\theta }_{13}^{\left(1\right)}\\ {\theta }_{31}^{\left(1\right)}& {\theta }_{33}^{\left(1\right)}\end{array}\right]-\left[\begin{array}{cc}{\theta }_{11}^{\left(2\right)}& {\theta }_{13}^{\left(2\right)}\\ {\theta }_{31}^{\left(2\right)}& {\theta }_{33}^{\left(2\right)}\end{array}\right]\right|\right|}_1=\left|{\theta }_{11}^{\left(1\right)}- {\theta }_{11}^{\left(2\right)}\right|+\left|{\theta }_{13}^{\left(1\right)}- {\theta }_{13}^{\left(2\right)}\right|+\left|{\theta }_{31}^{\left(1\right)}- {\theta }_{31}^{\left(2\right)}\right|+\left|{\theta }_{33}^{\left(1\right)}- {\theta }_{33}^{\left(2\right)}\right|$. Furthermore, the second and third terms in the objective function of (7) are the likelihood functions of the class-level ICs, ${\mathbf{\Theta }}^{\left(1\right)}$ and ${\mathbf{\Theta }}^{\left(2\right)}$, given the data in the respective classes. The fourth and fifth terms use two $l_1$ penalties to impose sparsity on the class-level ICs, in order to control the model complexity under limited sample sizes. Essentially, maximizing the five terms simultaneously in the objective function of (7) balances learning of the IC for each class and identifying the subgraph $\mathit{C}$ that best distinguishes the two classes. ${\mu }_1$, ${\mu }_2$ ${\mathrm{\lambda }}_1$, and ${\mathrm{\lambda }}_2$ are tuning parameters to control the trade-off between the different terms. Additionally, there are several constraints in the optimization problem in (7): $sum\left(diag\left(\mathit{C}\right)\right)\le K$ bounds the size of the subgraph by $K$; ${\mathbf{\Theta }}^{\left(1\right)}\succ \mathbf{0}$ and ${\mathbf{\Theta }}^{\left(2\right)}\succ \mathbf{0}$ are to guarantee that the learned IC matrices are valid, i.e., they must be positive definite matrices.

3.2. Optimization algorithm for parameter estimation of DSL

There is no analytical solution for the optimization problem in (7). We propose an Alternating Optimization (AO) algorithm that solves one parameter with the other two parameters fixed and iteratives over the sub-optimizations of the three parameters until convergence. In what follows, we present the sub-optimizations and the methods of solving each one. Furthermore, we summarize the iterative steps over the three sub-optimizations to solve (7) using AO. After presenting the AO algorithm, we discuss its convergence and optimality.

The three sub-optimizations for the three parameters are:

Given ${\mathbf{\Theta }}^{\left(1\right)}$ and ${\mathbf{\Theta }}^{\left(2\right)}$, the sub-optimization with respect to $\mathit{C}$ is:

$${\max }_{\mathit{C}}{\left|\left|{\mathit{C}}^T\left({\mathbf{\Theta }}^{\left(1\right)}-{\mathbf{\Theta }}^{\left(2\right)}\right)\mathit{C}\right|\right|}_1 \text{s.t.}sum\left(diag\left(\mathit{C}\right)\right)\le K;$$ (8)

Given $\mathit{C}$ and ${\mathbf{\Theta }}^{\left(2\right)}$, the sub-optimization with respect ${\mathbf{\Theta }}^{\left(1\right)}$ is:

$$\underset{{\mathbf{\Theta }}^{\left(1\right)}}{\max }\{{\left|\left|{\mathit{C}}^T\left({\mathbf{\Theta }}^{\left(1\right)}-{\mathbf{\Theta }}^{\left(2\right)}\right)\mathit{C}\right|\right|}_1+{\mu }_{1}L\left({\mathbf{\Theta }}^{\left(1\right)};{\left\{{\mathbf{x}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}\right)-{\lambda }_1{\left|\left|{\mathbf{\Theta }}^{\left(1\right)}\right|\right|}_1\};$$ (9)

Given $\mathit{C}$ and ${\mathbf{\Theta }}^{\left(1\right)}$, the sub-optimization with respect ${\mathbf{\Theta }}^{\left(2\right)}$ is:

$$\underset{{\mathbf{\Theta }}^{\left(2\right)}}{\max }\{{\left|\left|{\mathit{C}}^T\left({\mathbf{\Theta }}^{\left(1\right)}-{\mathbf{\Theta }}^{\left(2\right)}\right)\mathit{C}\right|\right|}_1+{\mu }_{2}L\left({\mathbf{\Theta }}^{\left(2\right)};{\left\{{\mathbf{x}}_j^{\left(2\right)}\right\}}_{j=1,\dots ,N_2}\right)-{\lambda }_2{\left|\left|{\mathbf{\Theta }}^{\left(2\right)}\right|\right|}_1\}.$$ (10)

Next, we will discuss how to solve these sub-optimizations:

Solving the optimization in (8)

Let $\mathit{D}\triangleq abs({\mathbf{\Theta }}^{\left(1\right)}-{\mathbf{\Theta }}^{\left(2\right)})$, the absolute difference matrix. Also let $\mathit{c}$ be a vector containing the diagonal elements of $\mathit{C}$, $\mathit{c}={\left(c_1,\dots ,c_p\right)}^T$. Then, (8) is equivalent to a quadratic programming problem below:

$${\max }_{\mathit{c}}{\mathit{c}}^T\mathit{D}\mathit{c}\text{s.t.}{\sum }_{l=1}^p{c}_l\le K;c_l\in \left\{0,1\right\}, l=1,\dots ,p.$$ (11)

This optimization can be solved using a standard quadratic programming solver such as CPLEX.

Solving the optimizations in (9) and (10)

(9) and (10) have the same structure and can be solved in a similar way. It is not hard to see that both optimizations can be converted to the following unified format:

$$\underset{\mathbf{\Theta }}{\max } L\left(\mathbf{\Theta };{\left\{{\mathbf{x}}_i\right\}}_{i=1,\dots ,N}\right)-\lambda {\left|\left|\mathbf{\Theta }\right|\right|}_1+\mu {\left|\left|{\mathit{C}}^T\left(\mathbf{\Theta }-\mathbf{Z}\right)\mathit{C}\right|\right|}_1.$$ (12)

Solving (12) is equivalent to solving (9) if we make $\mathbf{Z}={\mathbf{\Theta }}^{\left(2\right)}$, $\mathbf{\Theta }={\mathbf{\Theta }}^{\left(1\right)}$, $N=N_1$, ${\mathbf{x}}_i={\mathbf{x}}_i^{\left(1\right)}$. Solving (12) is equivalent to solving (10) if we make $\mathbf{Z}={\mathbf{\Theta }}^{\left(1\right)}$, $\mathbf{\Theta }={\mathbf{\Theta }}^{\left(2\right)}$, $N=N_2$, ${\mathbf{x}}_i={\mathbf{x}}_i^{\left(2\right)}$. (12) can be considered as a penalized maximum likelihood estimation. The discussion hereafter will focus on how to solve the optimization in (12).

Using the likelihood function in (6), the optimization becomes

$$\underset{\mathrm{ }\mathbf{\Theta }\mathrm{ }}{\max }\mathrm{ }\{{\left|\mathbf{\Theta }\right|}^{-\mathrm{ }\frac{Nh}{2}}{\prod }_{i=1}^N{\left|n_i{\mathit{S}}_i+{\mathbf{\Theta }}^{-1}\right|}^{-\mathrm{ }\frac{n_i+h}{2}}-\lambda {\left|\left|\mathrm{ }\mathbf{\Theta }\mathrm{ }\right|\right|}_1+\mu {\Vert {\mathit{C}}^T(\mathbf{\Theta }-\mathit{Z})\mathit{C}\Vert }_1\}.$$ (13)

(13) is difficult to solve as it involves determinants of the unknown parameter $\mathbf{\Theta }$. We propose to introduce latent variables and develop an EM algorithm to solve this optimization. EM is a well-known iterative approach to find maximum likelihood estimates of model parameters when it is difficult to obtain maximum likelihood estimates directly (Wu, 1983). The E step finds the expectation of the complete log-likelihood function with respect to the latent variables given observed data and parameter estimates in the current iteration. The M step maximizes the expectation in the E step to update the parameter estimation. The two steps iterate until convergence. Next, we present the EM algorithm developed to solve the optimization in (12). In the proposed EM algorithm, ${{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N},\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}$, and $\mathbf{\Theta }$ are treated as latent variables, observed data, and the parameter to be estimated, respectively. The complete log-likelihood function is:

$$\begin{gathered} \log L\left(\mathbf{\Theta };{{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N},\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}\right)\propto \log p\left({{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N},\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N};\mathbf{\Theta }\right) \\ =\log p\left({\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}|{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N},\mathbf{\Theta }\right)p\left({\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|\mathbf{\Theta }\right) \\ =\log \{{\prod }_{i=1}^N\mathrm{p}\left({\mathit{S}}_i\right|{\mathbf{\Theta }}_i){\prod }_{i=1}^N\mathrm{p}\left({\mathbf{\Theta }}_i\right|\mathbf{\Theta })\} \\ =-\frac{Nh}{2}\log \left|\mathbf{\Theta }\right|+{\sum }_{i=1}^N\frac{n_i+h-p-1}{2}\log \left|{\mathbf{\Theta }}_i\right|-\frac{1}{2}{\sum }_{i=1}^{N}tr\left({\mathbf{\Theta }}_i\right(n_i{\mathit{S}}_i+{\mathbf{\Theta }}^{-1}\left)\right). \end{gathered}$$ (14)

E step

At the $t$-th iteration of the EM algorithm, denote the parameter estimate by ${ }^{\left(t\right)}\mathbf{\Theta }$. Then, the E step is to find the expectation of (14) with respect to the latent variables ${\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}$, given the observed data, ${\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}$, and ${ }^{\left(t\right)}\mathbf{\Theta }$. Denote this expectation by

$$\begin{gathered} Q\left(\mathbf{\Theta }|{ }^{\left(t\right)}\mathbf{\Theta }\right)=E\left[\log L\left(\mathbf{\Theta };{{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N},\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(t\right)}\mathbf{\Theta },{\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}\right)\right] \\ ={\int }_{{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}}\log p\left({\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N},{\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N};\mathbf{\Theta }\right)p\left({\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(t\right)}\mathbf{\Theta },{\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}\right)d{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}. \end{gathered}$$ (15)

The first step of finding the explicit form of $Q\left(\mathbf{\Theta }\right|{ }^{\left(t\right)}\mathbf{\Theta })$ is to find the parametric form of the distribution of ${{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(t\right)}\mathbf{\Theta },\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}$, which is summarized in Proposition 1 below. Please see the proof in Appendix A.

Proposition 1.

The probability distribution of ${{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(t\right)}\mathbf{\Theta },\left\{{\mathit{S}}_i\right\}}_{i=1,\dots ,N}$ is a product of $N$ Wishart distributions, i.e., $Wishart\left({\left(n_i{\mathbf{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)}^{-1},\mathrm{ }{n}_i+h\right),\mathrm{ }i=1,\dots ,N$.

Using the result in Proposition 1, we can further derive the explicit form of $Q\left(\mathbf{\Theta }\right|{ }^{\left(t\right)}\mathbf{\Theta })$, which is given in Proposition 2. Please see the proof in Appendix B.

Proposition 2.

$Q\left(\mathbf{\Theta }\right|{ }^{\left(t\right)}\mathbf{\Theta })$ is proportional to

$$-\mathit{log}\left|\mathbf{\Theta }\right|-\frac{1}{Nh}{\sum }_{i=1}^N\left(n_i+h\right)tr({\mathbf{\Theta }}^{-1}{\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)}^{-1}).$$ (16)

M step

In the M step, we solve an optimization that maximizes the expectation in (17) with two penalties on $\mathbf{\Theta }$ adopted from (12), i.e.,

$${ }^{\left(t+1\right)}\mathbf{\Theta }=\arg \underset{\mathbf{\Theta }\succ 0}{\max }\left\{Q\right(\mathbf{\Theta }\left|{ }^{\left(t\right)}\mathbf{\Theta }\right)-\lambda {\left|\left|\mathrm{ }\mathbf{\Theta }\mathrm{ }\right|\right|}_1+\mu {\left|\left|{\mathit{C}}^T\left(\mathrm{ }\mathbf{\Theta }\mathrm{ }-\mathbf{Z}\right)\mathit{C}\right|\right|}_1\}$$ (17)

Proposition 3 shows an equivalent form of (17) that can be solved more easily. The proof for this proposition is relatively easier and thus skipped due to space limit.

Proposition 3.

The optimization problem in Equation (17) is equivalent to:

$${ }^{\left(t+1\right)}\mathbf{\Theta }=\mathit{arg}\underset{\mathbf{\Theta }\succ 0}{\mathit{min}}\{\mathit{log}\left|\mathbf{\Theta }\right|+tr\left({\mathbf{\Theta }}^{-1}\mathit{H}\left({ }^{\left(t\right)}\mathbf{\Theta }\right)\right)+\mathrm{\lambda }{\left|\left|\mathrm{ }\mathbf{\Theta }\mathrm{ }\right|\right|}_1-\mu {\left|\left|{\mathit{C}}^T\left(\mathbf{\Theta }-\mathbf{Z}\right)\mathit{C}\right|\right|}_1\}\mathrm{ },$$ (18)

where

$$\mathit{H}\left({ }^{\left(t\right)}\mathbf{\Theta }\right)=\frac{1}{Nh}{\sum }_{i=1}^N\left(n_i+h\right){\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)}^{-1}.$$ (19)

(18) is not convex but the sum of a convex and a concave function. In particular, $tr\left({\mathbf{\Theta }}^{-1}\mathit{H}\left({ }^{\left(t\right)}\mathbf{\Theta }\right)\right)+\mathrm{ }\mathrm{\lambda }\left|\right|{\mathbf{\Theta }\left|\right|}_1$ is convex, while $\log \left|\mathbf{\Theta }\right|-\mu {\left|\left|{\mathit{C}}^T\left(\mathbf{\Theta }-\mathbf{Z}\right)\mathit{C}\right|\right|}_1$ is concave. We propose to use a BCD algorithm to solve the optimization in (18). Details of the algorithm are given in Appendix C. Note that we did not explicitly consider the constraint $\mathbf{\Theta }\succ 0$ in the BCD algorithm. Proposition 4 shows that the positive definiteness is automatically guaranteed. Please see the proof in Appendix D.

Proposition 4.

The optimal solution obtained from the BCD algorithm, ${\mathbf{\Theta }}^{\mathbf{*}}$, is positive definite if the initial value, ${ }^{\left(0\right)}\mathbf{\Theta }$, is positive definite.

The initial value of the BCD algorithm can be set to be ${ }^{\left(0\right)}\mathbf{\Theta }=\frac{1}{Nh}{\sum }_{i=1}^N{\mathit{S}}_i^{-1}$, which is positive definite. Then according to Proposition 4, the optimal solution will be positive definite and therefore it is a valid IC matrix. Another reason for choosing the initial values to be ${ }^{\left(0\right)}\mathbf{\Theta }=\frac{1}{Nh}{\sum }_{i=1}^N{\mathit{S}}_i^{-1}$ is that it is an unbiased estimator for $\mathbf{\Theta }$. Because of the Wishart distributions of ${\mathbf{\Theta }}_i|\mathbf{\Theta }$ and $n{\mathit{S}}_i|{\mathbf{\Theta }}_i$, we can get $\widehat{\mathbf{\Theta }}=\frac{1}{Nh}{\sum }_{i=1}^N\widehat{{\mathbf{\Theta }}_i}=\frac{1}{Nh}{\sum }_{i=1}^N{\mathit{S}}_i^{-1}$, which is an unbiased estimator for $\mathbf{\Theta }$.

Finally, the entire procedure for solving the DSL optimization in (7) is summarized as follows:

Algorithm.

for solving the DSL optimization in (7)

Input: ${\left\{{\mathbf{x}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}$ and ${\left\{{\mathbf{x}}_j^{\left(2\right)}\right\}}_{j=1,\dots ,N_2}$; stopping criteria, ${\mathrm{ϵ}}_{\mathrm{A}\mathrm{O}}$, ${\mathrm{ϵ}}_{EM}$; tuning parameters.
Output: solutions for ${\mathbf{\Theta }}^{\left(1\right)},{\mathbf{\Theta }}^{\left(2\right)},\mathit{ }\mathit{C}$.
1.	Compute covariance matrices ${\left\{{\mathbf{S}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}$ and ${\left\{{\mathbf{S}}_j^{\left(2\right)}\right\}}_{j=1,\dots ,N_2}$
2.	Initialize: ${{ }^0\mathbf{\Theta }}^{\left(1\right)};{{ }^0\mathbf{\Theta }}^{\left(2\right)};m\leftarrow 0\mathrm{ };$
3.	Repeat
4.	Compute ${ }^m\mathit{C}$ by solving the quadratic programming in (11);
5.	Compute ${{ }^{m+1}\mathbf{\Theta }}^{\left(1\right)}$ using the proposed EM algorithm:
5.1	Input ${\left\{{\mathit{S}}_i^{\left(1\right)}\right\}}_{i=1,\dots ,N_1}$, ${ }^m\mathit{C},\mathit{ }{{ }^m\mathbf{\Theta }}^{\left(1\right)}$ and ${{ }^m\mathbf{\Theta }}^{\left(2\right)}$
5.2	Initialize ${ }^{\left(0\right)}\mathbf{\Theta }={{ }^m\mathbf{\Theta }}^{\left(1\right)};t\leftarrow 0$;
5.3	Repeat
5.4	E step: derive $Q\left(\mathbf{\Theta }\right|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta })$ using Proposition 2;
5.5	M step: compute ${ }^{\left(t+1\right)}\mathbf{\Theta }$ using BCD;
5.6	$t\leftarrow t+1$
5.7	Until $\left|\left|{ }^{\left(t\right)}\mathbf{\Theta }-{ }^{\left(t+1\right)}\mathbf{\Theta }\right|\right|\le {\mathrm{ϵ}}_{EM}$
5.8	${{ }^{m+1}\mathbf{\Theta }}^{\left(1\right)}\leftarrow { }^{\left(t+1\right)}\mathbf{\Theta }$;
6.	Compute ${{ }^{(m+1)}\mathbf{\Theta }}^{\left(2\right)}$ by following similar steps under 5;
7.	$m\leftarrow m+1$;
8.	until ${\sum }_{v=1}^2\left|\left|{{ }^{m+1}\mathbf{\Theta }}^{\left(v\right)}-{{ }^m\mathbf{\Theta }}^{\left(v\right)}\right|\right|\le {\mathrm{ϵ}}_{\mathrm{A}\mathrm{O}}$

Algorithm convergency

This is an AO algorithm that iteratively solves $\mathit{C}$ and the class-level ICs, ${\mathbf{\Theta }}^{\left(1\right)}$ and ${\mathbf{\Theta }}^{\left(2\right)}$. The sub-optimization of solving $\mathit{C}$ in (8) is a binary quadratic programming problem. According to Lemma 1 in a previous paper (Yuan and Ghanem, 2016), this problem can be transferred to a continuous optimization. The sub-optimizations of ${\mathbf{\Theta }}^{\left(1\right)}$ and ${\mathbf{\Theta }}^{\left(2\right)}$ are solved using EM which is guaranteed to converge to a stationary point based on a previous paper (Wu, 1983). In the M-step, the optimization is solved by BCD whose convergence is presented in Appendix C. Finally, the iterations over the sub-optimizations in the algorithm converge to a first-order stationary point under mild conditions according to a previous paper (Li, Zhu and Tang, 2019). In our experiments, we observed steady increase of the objective function over the iterations and the algorithm converged quickly.

Time complexity

The algorithm iterates over solving $\mathit{C}$ and solving the IC of each class. Solving $\mathit{C}$ is a standard quadratic programming problem, for which the worst-case complexity is $𝓞\left(p^3\right)$. $p$ is the number of variables. Solving the IC uses EM and the M-step is an optimization solved by BCD, for which the worst-case complexity is $𝓞\left(N{p}^3\right)$. N is the sample size. It typically takes 10–15 iterations for the E- and M-step to converge, and takes 3–6 iterations for the AO to converge, which have been consistently observed in our simulation and real-data experiments.

Tuning parameter selection

The tuning parameters of DSL include ${\lambda }_1$, ${\lambda }_2$, ${\mu }_1$, ${\mu }_2$, $h$, and $K$. In practice, we can reasonably set ${\lambda }_1={\lambda }_2$ and ${\mu }_1={\mu }_2$ to impose similar amounts of regularization on the two classes. This reduces the tuning parameters to four. $h$ is hyper-parameter of the Wishart distribution which is not sensitive and only needs to be roughly tuned. To tune the remaining parameters, a grid search can be performed and model training under each combination of parameter settings can be done in parallel. The optimal tuning parameters are those that maximize the cross-validation classification accuracy.

3.3. Classification on new samples

Upon solving the DSL optimization in (7) based on a training dataset, we can use the optimal solutions, i.e., $\widehat{\mathit{C}}$, ${\widehat{\mathbf{\Theta }}}^{\left(1\right)}$, and ${\widehat{\mathbf{\Theta }}}^{\left(2\right)}$, to classy new subjects based on their fMRI data. Specifically, given the fMRI data of a new subject, ${\mathbf{x}}^{*}$, we first compute the sample covariance matrix ${\mathit{S}}^{*}$. Next, we can extract a $q\times q$ sub-matrix of ${\mathit{S}}^{*}$, ${\mathbf{S}}_{sub}^{\mathrm{*}}$, which is the sample covariance matrix of the variables in the subgraph indicated by $\widehat{\mathit{C}}$. In the same way, we can extract the sub-matrices ${\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}$ and ${\widehat{\mathbf{\Theta }}}_{sub}^{\left(2\right)}$ from ${\widehat{\mathbf{\Theta }}}^{\left(1\right)}$, and ${\widehat{\mathbf{\Theta }}}^{\left(2\right)}$. Then, we can use a simple likelihood-based classifier to classify the new subject, i.e., the new subject belongs to class 1 if

$$p\left({\mathbf{S}}_{sub}^{\mathrm{*}}|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}\right)\ge p\left({\mathbf{S}}_{sub}^{\mathrm{*}}|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(2\right)}\right),$$ (20)

The probability function, $p\left({\mathbf{S}}_{sub}^{\mathrm{*}}|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}\right)$, can be computed as:

$$p\left({\mathbf{S}}_{sub}^{\mathrm{*}}|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}\right)=\int f\left({\mathbf{S}}_{sub}^{\mathrm{*}}|{\mathbf{\Theta }}_{sub}^{\mathrm{*}}\right)f\left({\mathbf{\Theta }}_{sub}^{\mathrm{*}}\right|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)})d{\mathbf{\Theta }}_{sub}^{\mathrm{*}},$$ (21)

The key to deriving (21) is to know the distributions of ${\mathbf{S}}_{sub}^{\mathrm{*}}|{\mathbf{\Theta }}_{sub}^{\mathrm{*}}$ and ${\mathbf{\Theta }}_{sub}^{\mathrm{*}}|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}$. To achieve this, we use a nice property of Wishart distributions that the parameterization of Wishart is invariant under marginalization (Dawid, 1981). Specifically, recall that we know $n{\mathit{S}}^{*}|{\mathbf{\Theta }}^{\mathbf{*}}\sim Wishart({{\mathbf{\Theta }}^{\mathbf{*}}}^{-1},n)$ and ${\mathbf{\Theta }}^{\mathbf{*}}|{\widehat{\mathbf{\Theta }}}^{\left(1\right)}\sim Wishart({\widehat{\mathbf{\Theta }}}^{\left(1\right)},h)$. Then, according to the aforementioned property of Wishart distributions, $n{\mathit{S}}_{sub}^{*}\mathrm{ }\mathrm{ }|{\mathbf{\Theta }}_{sub}^{\mathbf{*}}\sim Wishart({{\mathbf{\Theta }}_{sub}^{\mathbf{*}}\mathrm{ }}^{-1},n)$ and ${\mathbf{\Theta }}_{sub}^{\mathbf{*}}\mathrm{ }|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}\sim Wishart({\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)},h)$. Plugging the probability density functions of these Wishart distributions in (21) and through some algebra calculations, we can get:

$$p\left({\mathit{S}}_{sub}^{\mathrm{*}}|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}\right)=\frac{A{\mathrm{\Gamma }}_q\left(\frac{n+h}{2}\right)}{{\mathrm{\Gamma }}_q\left(\frac{n}{2}\right){\mathrm{\Gamma }}_q\left(\frac{h}{2}\right)}{\left|{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}\right|}^{-\frac{h}{2}}{\left|n{\mathit{S}}_{sub}^{\mathrm{*}}+{{\widehat{\mathbf{\Theta }}}_{sub}^{\left(1\right)}}^{-1}\right|}^{-\frac{n+h}{2}},$$ (22)

where $A=n^{\frac{qn}{2}}{\left|{\mathit{S}}_{\mathrm{s}\mathrm{u}\mathrm{b}}^{\mathrm{*}}\right|}^{\frac{n-q-1}{2}}$, and ${\mathrm{\Gamma }}_q\left(x\right)={\pi }^{\frac{q\left(q-1\right)}{4}}{\prod }_{i=1}^q\mathrm{\Gamma }(x+\frac{1-i}{2})$ is the multivariate generalization of the gamma function.

4. SIMULATION STUDY

4.1. Simulation setup

In this section, we assess the performance of DSL using simulation data, in comparison with several competing methods. The data generation process includes five steps:

1. Construct the IC matrix for class 1, ${\mathbf{\Theta }}^{\left(1\right)}$. We generate the entry at the $i$-th row and $j$-th column of ${\mathbf{\Theta }}^{\left(1\right)}$, i.e., ${\theta }_{ij}^{\left(1\right)}$, from a $Uniform\left[-\mathrm{1,1}\right]$ distribution. If $\left|{\theta }_{ij}^{\left(1\right)}\right|<0.5$, set ${\theta }_{ij}^{\left(1\right)}=0$. This is to make the IC matrix sparse.

2. Construct the IC for class 2, ${\mathbf{\Theta }}^{\left(2\right)}$, through the following sub-steps:

   • (2.1)
     Let ${\mathbf{\Theta }}^{\left(2\right)}={\mathbf{\Theta }}^{\left(1\right)}$.
   • (2.2)
     Select a subset of $\omega$ variables that are involved in the discriminate subgraph. Denote the sub-matrix of ${\mathbf{\Theta }}^{\left(2\right)}$ that corresponds to the $\omega$ variables by ${\mathbf{\Theta }}_{sub}^{\left(2\right)}$. Construct $\mathit{C}$ as a diagonal matrix with ones corresponding to the $\omega$ variables and zeros otherwise.
   • (2.3)
     Randomly pick 50% of the non-zero entries in ${\mathbf{\Theta }}_{sub}^{\left(2\right)}$ and change them to be zero. Randomly pick the same number of zero entries in ${\mathbf{\Theta }}_{sub}^{\left(2\right)}$ and change them to be non-zero. Sample each non-zero entry from $Uniform\left(\left[-1,-0.5\right]U\left[\mathrm{0.5,1}\right]\right)$.
   • (2.4)
     For the remaining entries of ${\mathbf{\Theta }}^{\left(2\right)}$ that are not included in ${\mathbf{\Theta }}_{sub}^{\left(2\right)}$, i.e., entries in ${\mathbf{\Theta }}^{\left(2\right)}\backslash {\mathbf{\Theta }}_{sub}^{\left(2\right)}$, resample each positive entry from $Uniform\left[\mathrm{0.5,1}\right]$ and each negative entry from $Uniform\left[-1,-0.5\right]$. The purpose of this sub-step is that although ${\mathbf{\Theta }}^{\left(2\right)}\backslash {\mathbf{\Theta }}_{sub}^{\left(2\right)}$ is not what primarily differentiates class 2 from class 1, we resample its non-zero entries to create a more general case that ${\mathbf{\Theta }}^{\left(2\right)}\backslash {\mathbf{\Theta }}_{sub}^{\left(2\right)}$ is not exactly the same as ${\mathbf{\Theta }}^{\left(1\right)}$ even beyond the discriminate subgraph.

3. Rescale the ${\mathbf{\Theta }}^{\left(1\right)}$ and ${\mathbf{\Theta }}^{\left(2\right)}$ generated in 1) and 2) to ensure that they are positive definite matrices. The rescaling includes first summing the absolute values of off-diagonal entries for each row, then dividing each off-diagonal entry by 1.5 times of the sum, and finally averaging the resulting matrix with its transpose to produce a symmetric matrix.

4. Construct the IC for each subject within class 1, ${\mathbf{\Theta }}_i^{\left(1\right)}$, $i=1,\dots ,N_1$. Sample ${\mathbf{\Theta }}_i^{\left(1\right)}$ from $Wishart({\mathbf{\Theta }}^{\left(1\right)},h)$, where ${\mathbf{\Theta }}^{\left(1\right)}$ is the rescaled IC obtained in step 3). Note that the ${\mathbf{\Theta }}_i^{\left(1\right)}$ sampled in this way is not sparse. We further sparsify ${\mathbf{\Theta }}_i^{\left(1\right)}$ by following a simple and efficient method proposed in (Kuismin and Sillanpää, 2016) that iteratively thresholds the smallest entries in the original non-sparse ${\mathbf{\Theta }}_i^{\left(1\right)}$. This entire process is repeated to construct the IC for each subject within class 2.

5. Generate the data for each subject in class 1, i.e., ${\mathbf{x}}_i^{\left(1\right)}$, $i=1,\dots ,N_1$, from a multivariate Gaussian distribution with zero mean and IC matrix ${\mathbf{\Theta }}_i^{\left(1\right)}$ from step 4). Generate the data for each subject in class 2 in a similar way.

In the first experiment, we generate simulation data of 50 variables and 50 samples in each class. This is a challenging case because the sample size is the same as the number of variables. In addition, we set $\omega =10,15,20,25,30,40,50$ as different sizes of the discriminant subgraph. This simulation setup is comparable to the real-data case study presented in the next section. The real data includes 50 and 49 samples in the two classes, respectively; and a total of 33 ROIs, which is smaller than the 50 variables in the simulation and thus being a relatively easier case. Even though we do not know the size of the subgraph in the real data, the simulation setup includes a wide range of possible sizes ranging from 20% to 100% of the total number of variables. It is reasonable to believe that this range should cover the subgraph size in the real data. In the second experiment, we increase the training sample size to 100, and keep all other settings the same as the first experiment. We use 10-fold cross validation to choose the optimal tuning parameters. Then, the trained model is applied to a separate test set of 50 samples per class to compute the Area Under the Curve (AUC). We repeat this whole process for 30 times and report the average AUC over the 30 simulation runs.

4.2. Competing methods

We compare DSL with a collection of state-of-the-art competing methods. The first competing method is DSL without subgraph selection, referred to as DSL\subgraph. The second to fifth are existing algorithms in graph classification. These algorithms are not directly comparable to our method because they assume that the graphs are known. To make them applicable, we use graphical lasso (Friedman et al., 2007) to learn the IC of each subject. Then, the ICs are used as input to the graph classification algorithms. The following list summarizes the competing methods:

• “DSL\subgraph”: DSL without subgraph selection

• “Vectorized SVM”: Elements of the IC graph for each subject are put into a feature vector. A SVM classifier is built on the feature vector (Friedman, Hastie and Tibshirani, 2001).

• “Similarity-based”: This is one of the two categories of graph classification algorithms reviewed in Section 2. Different kernels have been proposed to measure graph similarity. We choose to report the best accuracy based on four well-studied kernels in the literature: kernels between vertex and/or edge label histograms (Gärtner, Flach and Wrobel, 2003), graphlet kernels (Shervashidze et al., 2009), random walk kernels (Sugiyama and Borgwardt, 2015), and the Weisfeiler-Lehman graph kernel (Shervashidze et al., 2011).

• “gBoost”: Another category of graph classification algorithms is subgraph-feature-based. gBoost is a representative algorithm in this category that has been used as a benchmarking method by other papers (Saigo et al., 2009).

• “MTG”: Another more recent subgraph-feature-based algorithm (Pan et al., 2015).

4.3. Classification accuracies of different methods

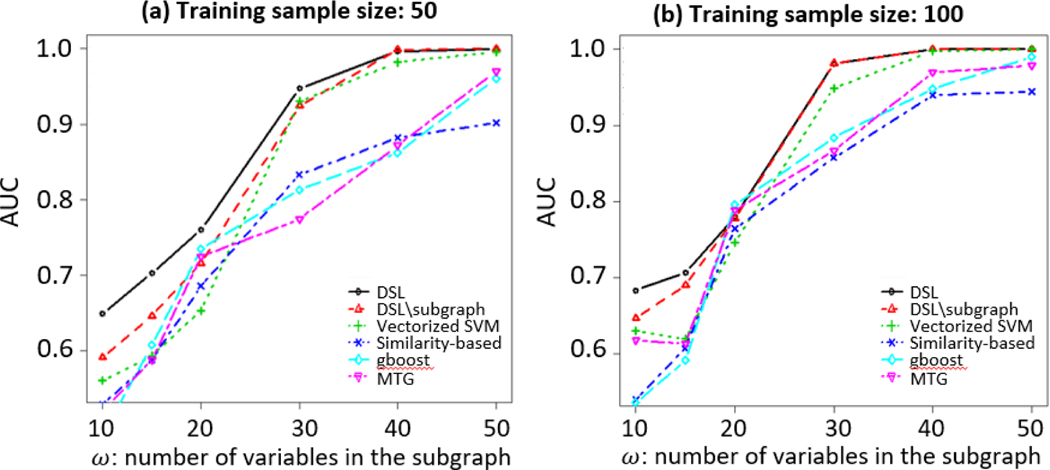
Fig. 3 shows the average AUC performance of DSL and competing methods on test data with respect to different subgraph sizes, under two different training sample sizes: 50 and 100. There are several observations: 1) In general, DSL and DSL\subgraph outperform other competing methods. 2) DSL outperforms DSL\subgraph with a smaller number of variables in the subgraph. This confirms the importance of finding the discriminate subgraph by DSL. 3) With a smaller training sample size, the advantage of DSL over DSL\subgraph is more significant.

Figure 3.

AUCs of DSL and competing methods on a test dataset of 50 samples per class

4.4. Accuracy of DSL in IC estimation and subgraph identification

As the DSL optimization simultaneously estimates the IC of each class and identifies the discriminant subgraph, we use two metrics to evaluate the accuracy of DSL: 1) Structural accuracy of the IC estimation, defined as the accuracy of identifying the truly zero (non-zero) entries in the IC matrix averaged over the two classes; 2) Subgraph identification accuracy, defined as the number of vertices in the true subgraph that are also identified by DSL. These results are summarized in Table 1. There are several observations: (i) In general, the ICs are estimated well, with a higher accuracy at a larger training size, as expected. (ii) The subgraph identification accuracy is better with larger subgraph sizes and with a larger training size. Under a fixed training size, a smaller subgraph size (i.e., a smaller $\omega$) means less difference between the two classes, making it harder to differentiate them. This inherently difficulty hurts the performance of subgraph identification by DSL. As $\omega$ increases, there is more difference between the two classes and naturally the subgraph identification accuracy improves. Looking at Table 1 and Fig. 3 together, the results are consistent in the sense that a larger subgraph size has a higher accuracy for identifying the subgraph by DSL and subsequently a higher AUC in using the identified subgraph for classification.

Table 1.

Accuracy of DSL

$\mathit{\omega }$	Training sample size = 50		Training sample size = 100
	Structural Accuracy of IC estimation	Subgraph identification accuracy	Structural Accuracy of IC estimation	Subgraph identification accuracy
10	0.89	5/10	0.96	6/10
15	0.88	9/15	0.96	10/15
20	0.88	14/20	0.96	17/20
30	0.89	26/30	0.96	28/30
40	0.89	38/40	0.96	39/40
50	0.89	49/50	0.96	50/50

4.5. Computational time

For the most time-consuming case across all the simulation and real-data experiments, i.e., the setting with 50 variables and 100 samples per class, the clock time of training in each parallel thread was around 290 seconds. This task was performed within the R version 4.0.2 environment on a PC with Intel Core i7–10610U 2.30 HGz CPU with 4 cores, 8 logical processors and 16 GB of RAM memory.

5. Real data application

In this section, we present an application of using resting-state fMRI to classify EM and healthy controls. The data of 50 EM patients and 49 age-matched controls were provided by our collaborators at Mayo Clinic Arizona. The dataset is not available to public due to privacy perservation. All migraine patients were diagnosed according to the diagnostic criteria set forth by the International Classification of Headache Disorders (ICHD-II). Patients were excluded if they have neurological diseases other than migraine. Healthy controls were included if they never developed headaches or if they had occasional tension-type headaches with a frequency of less than three tension-type headaches per month.

Imaging was conducted on 3-Tesla Siemens scanners using FDA-approached sequences. Prior to the imaging session, each subject was instructed to stay awake with eyes-closed, known as the resting state. Ten minutes of resting-state fMRI data were collected for each subject. Each fMRI dataset is 4-D, denoted by $(x,y,z,t)$, where $(x,y,z)$ are coordinates for each basic unit (called a voxel) of the 3-D brain image and $t$ is time. In our study, there were a total of $61\times 73\times 61$ voxels in the 3-D brain image and the time series of each voxel contains over 200 time points with some slight difference between subjects. Standard steps of fMRI pre-processing were followed (Chong et al., 2017). We selected 33 ROIs based on findings in the pain and migraine literature. These regions are those consistently shown to participate in pain processing. The 33 ROIs include 16 on each hemisphere and one midline region. Table 2 lists names of the ROIs. The $(x,y,z)$ coordinates for the center of each ROI were also reported. Each ROI was an 8mm sphere drawn around the center coordinates. The average time series over the voxels included in each ROI was computed. The 33 ROI-level time series were used as input data to DSL and competing algorithms.

Table 2.

Names of the ROIs (odd/even numbers represent the right/left hemisphere; 33 is a midline region). Coordinates of the center for each ROI are provided below the name. The ROIs in the subgraph found by DSL are in bold.

1,2	anterior insula (+/−38, 19, −3)	3,4	anterior cingulate cortex (+/−6, 28, 24)	5,6	mid cingulate cortex (+/−10, −7, 46)
7,8	posterior insula (+/−40, −14, 1)	9,10	posterior cingulate cortex (+/−8, −48, 39)	11,12	Thalamus (+/−8, −21, 7)
13,14	primary somatosensory cortex (+/−46, −24, 47)	15,16	dorsolateral prefrontal cortex (+/−40, 39, 24)	17,18	inferior lateral parietal (+/−57, −48, 30)
19,20	ventromedial prefrontal cortex (+/−6, 36, −14)	21,22	second somatosensory cortex (+/−52, −28, 21)	23,24	supplementary motor area (+/−6, 1, 68)
25, 26	temporal pole (+/−41, 10, −32)	27,28	amygdala (+/−22, −1, −22)	29,30	middle temporal gyrus (+/−60, −26, −5)
31,32	Caudate (+/−14, 13, 11)	33	periaqueductal gray matter (−1, −26, −11)

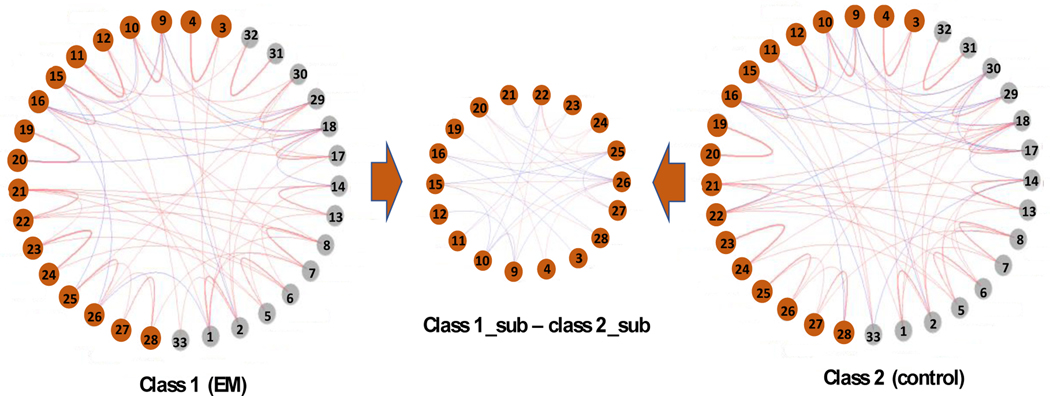
Using the fMRI data of the 33 ROIs, we can compute the sample correlation matrix for each subject, which is used as input to our DSL model. Tuning parameters are selected to maximize the leave-one-out-cross-validated (LOOCV) AUC. The subgraph found by DSL includes 18 ROIs that are highlighted in bold in Table 2. From Table 3, DSL achieves 0.81 AUC, 0.82 sensitivity, and 0.79 specificity, which significantly outperform the competing methods. DSL\subgraph has the second-best AUC (0.72), and its specificity is low (0.59). Other competing methods have even worse AUC. Fig. 4 shows the output from DSL, including the estimated IC matrix of each class converted to partial correlation matrices and the difference between the two classes in terms of the partial correlations of the identified subgraph. Partial correlation matrices have better interpretation than the original IC matrices because their elements are bounded between −1 and 1.

Table 3.

LOOCV accuracy of different methods on migraine data

	AUC	Sensitivity	Specificity
DSL	0.81	0.82	0.79
DSL\subgraph	0.72	0.80	0.59
Vectorized SVM	0.63	0.78	0.51
Similarity-based	0.67	0.68	0.60
gBoost	0.69	0.69	0.66
MTG	0.70	0.68	0.69

Figure 4.

Partial correlation matrices of EM (left) and controls (right) converted from the ICs learned by DSL. Edges with partial correlation magnitude <0.05 are not shown for visual effect. Edges in red/blue represent positive/negative particle correlations. The middle graph shows the difference between the partial correlation matrices of EM and controls on the identified subgraph by DSL (red/blue edges present positive/negative difference.).

Interpretations:

From Fig. 4, we can see that the partial correlation matrix of each class shows strong positive correlations between the left and right hemisphere for the same ROI. This phenomenon has been previously reported for both healthy and diseased brains (Chong et al., 2019). Some of these correlations have no significant difference between the EM and control classes, while some others do. Significant difference is also observed between other ROIs. Furthermore, it is interesting that several ROIs in the subgraph found by DSL are part of well-known functional networks or anatomical regions. For example, the left and right anterior cingulate cortex (3, 4), the left and right posterior cingulate cortex (9, 10) and the bilateral ventromedial are all regions that comprise the default mode network (DMN). This functional network shows synchronous activity when a person is at rest and not actively partaking in an activity. The DMN is involved in self-reflection and mind-wandering (Raichle et al., 2001) and results of several imaging studies have shown abnormal functional connectivity amongst regions of the DMN in patients with migraine (Tessitore et al., 2013) (Faragó et al., 2017) (Yu et al., 2012). Other ROIs that are important in our model include regions of the limbic system such as the left and right amygdala (27, 28), the left and right thalamus (11, 12). In accordance with our results, Hadjikhani et al. found stronger functional connectivity between the thalamus and the amygdala in migraineurs relative to patients with other chronic pain disorders, indicating that aberrant functional connectivity between these regions might be unique to migraine patients (Hadjikhani et al., 2013).

6. Conclusion

We proposed a novel DSL model to learn a sub-network within the FCN that best differentiates patients with a specific disease from healthy controls based on brain sensory data. DSL was demonstrated in an application of identifying a functional sub-network that best differentiates patients with EM from controls based on resting state fMRI data. DSL significantly outperformed competing methods in classification accuracy. There are several limitations of the proposed method. The training time of DSL is relatively slow and efficient optimization solvers can be developed in future research. The current formulation of DSL focuses on binary classification while an extension to more than two classes will address a broader range of problems. Future research may also explore applications of DSL to other neurological diseases and other types of functional brain sensory data.

Appendix A: Proof of Proposition 1

$$\begin{gathered} p\left({{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta },\left\{{\mathbf{S}}_i\right\}}_{i=1,\dots ,N}\right)\propto p\left({\left\{{\mathbf{S}}_i\right\}}_{i=1,\dots ,N}|{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N};{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }\right)p\left({\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }\right) \\ =p\left({\left\{{\mathbf{S}}_i\right\}}_{i=1,\dots ,N}|{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}\right)p\left({\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }\right)={\prod }_{i=1}^{N}p\left({\mathbf{S}}_i\right|{\mathbf{\Theta }}_i){\prod }_{i=1}^{N}p\left({\mathbf{\Theta }}_i\right|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }) \end{gathered}$$ (23)

We have known that $n_i{\mathbf{S}}_i|{\mathbf{\Theta }}_i~Wishart\left({{\mathbf{\Theta }}_i}^{-1},n_i\right)$ and ${\mathbf{\Theta }}_i|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }~Wishart\left({ }^{\left(\mathrm{t}\right)}\mathbf{\Theta },n_i\right)$. Inserting the probability density functions of the two Wishart distributions into Equation (23), we get:

$$\begin{gathered} p\left({{\left\{{\mathbf{\Theta }}_i\right\}}_{i=1,\dots ,N}|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta },\left\{{\mathbf{S}}_i\right\}}_{i=1,\dots ,N}\right) \\ \propto {\prod }_{i=1}^N\frac{|n_i{\mathbf{S}}_i{\left.\mathrm{}\right|}^{\frac{n_i-p-1}{2}}}{2^{n_{i}p}{\left|{\mathbf{\Theta }}_i\right|}^{-\frac{n_i}{2}}{\mathrm{\Gamma }}_p\left(\frac{n_i}{2}\right)}\exp \left(-\frac{1}{2}tr\left(n_i{\mathbf{S}}_i{\mathbf{\Theta }}_i\right)\right){\prod }_{i=1}^N\frac{|{\mathbf{\Theta }}_i{\left.\mathrm{}\right|}^{\frac{h-p-1}{2}}}{2^{hp}{\left|{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }\right|}^{\frac{h}{2}}{\mathrm{\Gamma }}_p\left(\frac{h}{2}\right)}\exp \left(-\frac{1}{2}tr\left({\mathbf{\Theta }}_i{{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }}^{-1}\right)\right) \\ \propto {\prod }_{i=1}^N\left\{\right|{\mathbf{\Theta }}_i{\left.\right|}^{\frac{n_i+h-p-1}{2}}\exp \left(-\frac{1}{2}tr\left({\mathbf{\Theta }}_i(n_i{\mathbf{S}}_i+{{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }}^{-1})\right)\right)\} \end{gathered}$$ (24)

Each term in the product in Eq. (24) is a Wishart distribution with scale matrix ${\left(n_i{\mathbf{S}}_i+{{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }}^{-1}\right)}^{-1}$ and degree of freedom $n_i+h$. ■

Appendix B: Proof of Proposition 2

$$\begin{gathered} \mathit{Q}\left(\mathbf{\Theta }|{ }^{\left(t\right)}\mathbf{\Theta }\right)\propto \int \left\{\right[-\frac{Nh}{2}\log \left|\mathbf{\Theta }\right|+{\sum }_{i=1}^N\frac{n_i+h-\mathrm{p}-1}{2}\log \left|{\mathbf{\Theta }}_i\right| \\ -\frac{1}{2}{\sum }_{i=1}^N\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i\left(n_i{\mathit{S}}_i+{\mathbf{\Theta }}^{-1}\right)\right)\left]\mathrm{ }{\prod }_{i=1}^N|{\mathbf{\Theta }}_i{\left.\mathrm{}\right|}^{\frac{n_i+h-p-1}{2}}{e}^{-\frac{\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i\left(n_i{\mathit{S}}_i+{{ }^{\left(\mathrm{t}\right)}\mathbf{\Theta }}^{-1}\right)\right)}{2}}\right\}d{\mathbf{\Theta }}_1\dots {\mathbf{\Theta }}_N \\ =-\frac{Nh}{2}\log \left|\mathbf{\Theta }\right|{\prod }_{i=1}^N{\mathrm{\Delta }}_i+{\sum }_{i=1}^N{H}_i{\prod }_{j\ne i}{\mathrm{\Delta }}_j-{\sum }_{i=1}^N{G}_i{\prod }_{j\ne i}{\mathrm{\Delta }}_j-{\sum }_{i=1}^N{F}_i\left(\mathbf{\Theta }\right){\prod }_{j\ne i}{\mathrm{\Delta }}_j \\ ={\prod }_{i=1}^N{\mathrm{\Delta }}_i\{-\frac{Nh}{2}\log \left|\mathbf{\Theta }\right|+{\sum }_{i=1}^N\frac{H_i}{{\mathrm{\Delta }}_i}\mathrm{ }-{\sum }_{i=1}^N\frac{G_i}{{\mathrm{\Delta }}_i}-{\sum }_{i=1}^N\frac{F_i\left(\mathbf{\Theta }\right)}{{\mathrm{\Delta }}_i}\}, \end{gathered}$$ (25)

where

$${\mathrm{\Delta }}_i=\int |\mathrm{ }{\mathbf{\Theta }}_i\mathrm{ }{\left.\right|}^{\frac{n_i+h-\mathrm{p}-1}{2}}\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)\right)}{2})d{\mathbf{\Theta }}_i,$$

$${\mathrm{H}}_i=\int \frac{n_i+h-\mathrm{p}-1}{2}\log \left|\mathrm{ }{\mathbf{\Theta }}_i\right|\left|{\mathbf{\Theta }}_i{\left.\right|}^{\frac{n_i+h-\mathrm{p}-1}{2}}\mathrm{e}\mathrm{x}\mathrm{p}\right(-\frac{\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)\right)}{2})d{\mathbf{\Theta }}_i,$$

$${\mathrm{G}}_i=\int \frac{1}{2}\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i{n}_i{\mathit{S}}_i\right)\left|\mathrm{ }{\mathbf{\Theta }}_i{\left.\right|}^{\frac{n_i+h-\mathrm{p}-1}{2}}\mathrm{e}\mathrm{x}\mathrm{p}\right(-\frac{\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)\right)}{2})d{\mathbf{\Theta }}_i,$$

$$F_i\left(\mathbf{\Theta }\right)=\int \frac{1}{2}\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i{\mathbf{\Theta }}^{-1}\right)\left|\mathrm{ }{\mathbf{\Theta }}_i{\left.\right|}^{\frac{n_i+h-\mathrm{p}-1}{2}}\mathrm{e}\mathrm{x}\mathrm{p}\right(-\frac{\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)\right)}{2})d{\mathbf{\Theta }}_i,$$

Since $tr(.)$ is a linear operator, $F_i\left(\mathbf{\Theta }\right)$ can become $F_i\left(\mathbf{\Theta }\right)=\frac{1}{2}tr\left({\mathbf{\Theta }}^{-1}{D}_i\right)$, where $D_i=\int {\mathbf{\Theta }}_i\mathrm{ }\left|{\left.{\mathbf{\Theta }}_i\right|}^{\frac{n_i+h-\mathrm{p}-1}{2}}\mathrm{e}\mathrm{x}\mathrm{p}\right(-\frac{\mathrm{t}\mathrm{r}\left({\mathbf{\Theta }}_i\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)\right)}{2})d{\mathbf{\Theta }}_i$, which is proportional to the mean of a Wishart distribution for ${\mathbf{\Theta }}_i$ with the degrees of freedom $n_i+h$ and scale matrix ${\left(n_i{\mathit{S}}_i+{{ }^{\left(\mathit{t}\right)}\mathbf{\Theta }}^{-1}\right)}^{-1}$. That is, $D_i={\mathrm{\Delta }}_i(n_i+h){\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)}^{-1}$, where ${\mathrm{\Delta }}_i=2^{\frac{(n_i+h)p}{2}}{\pi }^{\frac{p(p-1)}{4}}{\left|n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right|}^{-\frac{n_i+h}{2}}{\prod }_{i=1}^p\mathrm{\Gamma }\left(\frac{1}{2}\left(n_i+h-i+1\right)\right)$ as defined above.

Thus, $\frac{F_i\left(\mathbf{\Theta }\right)}{{\mathrm{\Delta }}_i}=\frac{1}{2}\left(n_i+h\right)tr\left({\mathbf{\Theta }}^{-1}{\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)}^{-1}\right)$.

Remove the constants in (25), we can know that

$$\mathit{Q}\left(\mathbf{\Theta }|{ }^{\left(t\right)}\mathbf{\Theta }\right)\propto -\log \left|\mathbf{\Theta }\right|-\frac{1}{Nh}{\sum }_{i=1}^N\left(n_i+h\right)tr\left({\mathbf{\Theta }}^{-1}{\left(n_i{\mathit{S}}_i+{{ }^{\left(t\right)}\mathbf{\Theta }}^{-1}\right)}^{-1}\right).$$

■

Appendix C: Derivation of the BCD algorithm

For notation simplicity, we re-write (18) into (26), i.e.,

$${\mathbf{\Theta }}^{\mathbf{*}}=\arg \underset{\mathbf{\Theta }\succ 0}{\min }\log \left|\mathbf{\Theta }\right|+tr\left({\mathbf{\Theta }}^{-1}\mathbf{H}\right)+\mathrm{\lambda }\left|\right|{\mathbf{\Theta }\left|\right|}_1-\mu {\left|\left|{\mathit{C}}^T\left(\mathbf{\Theta }-\mathbf{Z}\right)\mathit{C}\right|\right|}_1.$$ (26)

The proposed BCD works by iteratively updating one column and one row of $\mathbf{\Theta }$ at a time while fixing other entries of $\mathbf{\Theta }$. Here, we will only discuss the update on one column/row, i.e., the $j$-th column/row, because all other updates are similar. Specifically, partition $\mathbf{\Theta }$ into:

$$\mathbf{\Theta }=\left(\begin{array}{c}{\mathbf{\Theta }}_{\setminus j\setminus j}{\mathbf{\Theta }}_j\\ {\mathbf{\Theta }}_j^T{\theta }_{jj}\end{array}\right).$$ (27)

Similarly, $\mathbf{H}$, $\mathbf{C}$ and $\mathbf{Z}$ are partitioned in the same way, i.e.,

$$\mathit{H}=\left(\begin{array}{cc}{\mathit{H}}_{\setminus j\setminus j}& {\mathit{H}}_j\\ {\mathit{H}}_j^T& h_{jj}\end{array}\right),C=\left(\begin{array}{cc}{\mathit{C}}_{\setminus j\setminus j}& {\mathit{C}}_j\\ {\mathit{C}}_j^T& c_{jj}\end{array}\right),\text{ and }\mathit{Z}=\left(\begin{array}{cc}{\mathit{Z}}_{\setminus j\setminus j}& {\mathit{Z}}_j\\ {\mathit{Z}}_j^T& z_{jj}\end{array}\right).$$ (28)

Putting the partitioned $\mathbf{\Theta }$ and $\mathbf{H}$ back into (26), the four terms in (26) becomes:

$$\mathrm{l}\mathrm{o}\mathrm{g}\left(\left|\mathbf{\Theta }\right|\right)=\log \left(\alpha \right)+\mathrm{l}\mathrm{o}\mathrm{g}\left(\right|{\mathbf{\Theta }}_{\setminus j\setminus j}\left|\right),$$

$$tr\left({\mathbf{\Theta }}^{-1}\mathit{H}\right)={\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{H}}_{\setminus j\setminus j}+{\alpha }^{-1}{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{{\mathbf{H}}_{\setminus j\setminus j}{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}\mathbf{\Theta }}_j-2{\alpha }^{-1}{{\mathbf{H}}_j^T\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j+h_{jj}{\alpha }^{-1},$$

$${\left|\left|\mathbf{\Theta }\right|\right|}_1=2{\left|\left|{\mathbf{\Theta }}_j\right|\right|}_1+{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j+\alpha +{\left|\left|{\mathbf{\Theta }}_{\setminus j\setminus j}\right|\right|}_1,$$

$${\left|\left|{\mathit{C}}^T\left(\mathbf{\Theta }-\mathbf{Z}\right)\mathit{C}\right|\right|}_1=2{\mathrm{ }c}_{jj}{\left|\left|{\mathbf{C}}_{\setminus j\setminus j}\right({\mathbf{\Theta }}_j-{\mathbf{Z}}_j\left)\right|\right|}_1+{\mathrm{ }c}_{jj}\left|\alpha +{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j-{\mathrm{ }z}_{jj}\right|+{\left|\left|{\mathbf{C}}_{\setminus j\setminus j}({\mathbf{\Theta }}_{\setminus j\setminus j}-{\mathbf{Z}}_{\setminus j\setminus j}){\mathbf{C}}_{\setminus j\setminus j}\right|\right|}_1,$$

where $\alpha ={\theta }_{jj}-{\mathbf{\Theta }}_j^T{{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}\mathbf{\Theta }}_j$. We can know $\alpha >0$ and ${\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j>0$ under the constraint $\mathbf{\Theta }\succ 0$. Therefore, the optimization in (26) becomes:

$$\begin{gathered} \underset{{\mathbf{\Theta }}_j,\alpha \succ 0}{\min }\{\log \left(\alpha \right)+{\alpha }^{-1}{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{{\mathbf{H}}_{\setminus j\setminus j}{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}\mathbf{\Theta }}_j-2{\alpha }^{-1}{{\mathbf{H}}_j^T\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j+h_{jj}{\alpha }^{-1}+2\mathrm{\lambda }{\left|\left|{\mathbf{\Theta }}_j\right|\right|}_1+ \\ \mathrm{\lambda }{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j+\lambda \alpha -2\mu c_{jj}{\left|\left|{\mathbf{C}}_{\setminus j\setminus j}\left({\mathbf{\Theta }}_j-{\mathbf{Z}}_j\right)\right|\right|}_1-\mu c_{jj}\left|\alpha +{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j-{\mathrm{ }z}_{jj}\right|\}. \end{gathered}$$ (29)

${\mathbf{\Theta }}_{\mathrm{j}}$ and $\alpha$ can be solved in alternation. With ${\mathbf{\Theta }}_j$ fixed, (29) becomes a univariate optimization problem:

$$\underset{\mathrm{ }\alpha \succ 0}{\min }\{\log \left(\alpha \right)+{\varphi \alpha }^{-1}+\lambda \alpha -\mu c_{jj}\left|\alpha +{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j-{\mathrm{ }z}_{jj}\right|\},$$ (30)

where

$$\varphi ={\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{{\mathbf{H}}_{\setminus j\setminus j}{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}\mathbf{\Theta }}_j-2{{\mathbf{H}}_j^T\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j+h_{jj}$$ (31)

Furthermore, with $\alpha$ fixed, (29) becomes:

$$\underset{{\mathbf{\Theta }}_j}{\min }\{{\mathbf{\Theta }}_j^{T}A{\mathbf{\Theta }}_j-2{\mathit{d}}^T{\mathbf{\Theta }}_j+2\mathrm{\lambda }{\left|\left|{\mathbf{\Theta }}_j\right|\right|}_1-2\mu {\mathrm{ }c}_{jj}{\left|\left|{\mathbf{C}}_{\setminus j\setminus j}\left({\mathbf{\Theta }}_j-{\mathbf{Z}}_j\right)\right|\right|}_1-\mu c_{jj}\left|{\mathbf{\Theta }}_j^T{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{\Theta }}_j+(\alpha -{\mathrm{ }z}_{jj})\right|\},$$ (32)

where $A={\alpha }^{-1}{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}{\mathbf{H}}_{\setminus j\setminus j}{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}+\mathrm{\lambda }{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}$ and $\mathit{d}={\alpha }^{-1}{{\mathbf{H}}_j^T\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}$. (32) is a unconstrainted non-convex optimization which can be solved efficiently by a coordinate descent algorithm according to (Tseng, 2001) with the coordinate-descent update for each element in vector ${\mathbf{\Theta }}_j$. With estimation for ${\mathbf{\Theta }}_j$ and $\alpha$, we can update ${\theta }_{jj}$ by

$${\theta }_{jj}=\alpha +{\mathbf{\Theta }}_j^T{{\mathbf{\Theta }}_{\setminus j\setminus j}^{-1}\mathbf{\Theta }}_j.$$ (33)

This completes the updating on the $j$-th column/row. Finally, we summarize the proposed BCD algorithm in Algorithm 1.

Algorithm 1.

BCD Algorithm for solving the optimization in (26) in the M-step of the proposed EM framework

Input: ${\mathit{S}}_{\mathrm{i}}$ for each subject, $i=1,\dots ,N$; ${ }^{\left(t\right)}\mathbf{\Theta }$ from the $t$-th EM iteration; $\mathit{C}$ and $\mathbf{Z}$; tuning parameters $\mathrm{\lambda }$, $\mu$, $h$; stopping criterion, ${\mathrm{ϵ}}_{BCD}.$
Output: updated ${ }^{\left(t+1\right)}\mathbf{\Theta }$.
1.	Initialize: ${\mathbf{\Theta }}^0\leftarrow { }^{\left(t\right)}\mathbf{\Theta };k\leftarrow 0\mathrm{ };$
2.	Compute $\mathbf{H}=\mathbf{H}\left({ }^{\left(t\right)}\mathbf{\Theta }\right)$ using Equation (19);
3.	Repeat
4.	Let ${\mathbf{\Theta }}^{k+1}={\mathbf{\Theta }}^k$;
5.	for $j=1$ to $p$ do
6.	Partition ${\mathbf{\Theta }}^{k+1}$, $\mathbf{H}$, $\mathit{C}$ and $\mathbf{Z}$ for $j$-th column/row according to according to (27) - (28), respectively;
7.	Solve the optimization in (29) to get $\alpha$ and ${\mathbf{\Theta }}_j$;
8.	Compute ${\mathrm{\theta }}_{jj}^{k+1}$ using (33) and ${\mathbf{\Theta }}_j^{k+1}={\mathbf{\Theta }}_j$;
9.	Update the $j$-th column/row of ${\mathbf{\Theta }}^{k+1}$ by ${\mathbf{\Theta }}_j^{k+1}\mathrm{ }$ and ${\mathrm{\theta }}_{jj}^{k+1}$;
10.	End for
11.	$k\leftarrow k+1$;
12.	until $\left|\left|{\mathbf{\Theta }}^{k+1}-{\mathbf{\Theta }}^k\right|\right|\le {\mathrm{ϵ}}_{BCD}\mathrm{ }$
13.	${ }^{\left(t+1\right)}\mathbf{\Theta }\leftarrow {\mathbf{\Theta }}^{k+1}$.

Algorithm 1 convergence:

This is a BCD algorithm for solving the optimization in (26), whose 3^rd and 4^th terms are nondifferentiable but separable. Discussion on the convergence of this algorithm can follow from a previous paper (Tseng, 2001). Specifically, although (32) is a unconstrainted non-convex optimization, under the condition of $\mathrm{\lambda }\ge \mu$ the coordinate-descent update for each element in vector ${\mathbf{\Theta }}_j$ has a global minimum. Then, putting (32) and (30) together, we can know that (26) has a unique minimum at each coordinate block, satisfying the conditions of Part C in Theorem 4.1 in the previous paper (Tseng, 2001). This indicates that Algorithm 1 converges to a coordinate-wise minimum point. Furthermore, due to the existence of Gateaux-differentials of (32), we can know that (32) is regular according to Lemma 3.1 in the previous paper (Tseng, 2001). This implies that each coordinate-wise minimum point is a stationary point. In all, when $\mathrm{\lambda }\ge \mu$ i.e., ${\mathrm{\lambda }}_1\ge 1$ and ${\mathrm{\lambda }}_2\ge 1$ in (7), the convergence of Algorithm 1 is guaranteed.

Appendix D: Proof of Proposition 4

Because Algorithm 1 is an iterative algorithm, we only need to prove ${ }^{\left(1\right)}\mathbf{\Theta }$ is positive definite (p.d.) given that ${ }^{\left(0\right)}\mathbf{\Theta }$ is p.d.. If this holds, it will guarantee that the ${\mathbf{\Theta }}^{\mathbf{*}}$ at convergence will be p.d.. To prove the p.d. of ${ }^{\left(1\right)}\mathbf{\Theta }$, we need to prove $\mathbf{\Theta }$ keeps p.d. after the update of each column/row with the initial ${ }^{\left(0\right)}\mathbf{\Theta }$ since BCD algorithm works by iterations.

Let ${\mathbf{\Theta }}^{\left\{1\right\}}$ be the $\mathbf{\Theta }$ obtained after the update on the $1$-th column/row by BCD algorithm with the initial ${\mathbf{\Theta }}^{\left\{0\right\}}={ }^{\left(0\right)}\mathbf{\Theta }$. We only need to prove ${\mathbf{\Theta }}^{\left\{1\right\}}\succ 0$. To prove ${\mathbf{\Theta }}^{\left\{1\right\}}\succ 0$, we will use the property that the determinate of a p.d. matrix must be greater than zero. Using the decomposition in (27) we can write ${\mathbf{\Theta }}^{\left\{1\right\}}$ as:

$$\left|{\mathbf{\Theta }}^{\left\{1\right\}}\right|=\left|{\mathbf{\Theta }}_{\backslash j\backslash j}^{\left\{0\right\}}\right|({\mathrm{\theta }}_{\backslash j\backslash j}^{\left\{1\right\}}-{{\mathbf{\Theta }}^{\left\{1\right\}}}^T{{\mathbf{\Theta }}_{\backslash j\backslash j}^{\left\{0\right\}}}^{-1}{\mathbf{\Theta }}^{\left\{1\right\}})$$ (34)

Then, as long as we can prove $\left|{\mathbf{\Theta }}^{\left\{1\right\}}\right|>0$ we complete the proof of this Theorem. It is obvious that $\left|{\mathbf{\Theta }}_{\backslash j\backslash j}^{\left\{0\right\}}\right|>0$ because ${\mathbf{\Theta }}_{\backslash j\backslash j}^{\left\{0\right\}}$ is the upper-left submatrix of the p.d. matrix ${\mathbf{\Theta }}^{\left\{0\right\}}$. Let ${\alpha }^{\left\{1\right\}}={\mathrm{\theta }}_{\backslash j\backslash j}^{\left\{1\right\}}-.{{\mathbf{\Theta }}^{\left\{1\right\}}}^T{{\mathbf{\Theta }}_{\backslash j\backslash j}^{\left\{0\right\}}}^{-1}{\mathbf{\Theta }}^{\left\{1\right\}}$. According to Equation (30), it is obvious that ${\alpha }^{\left\{1\right\}}>0$. Then we have $\left|{\mathbf{\Theta }}^{\left\{1\right\}}\right|>0$. ■