Effectiveness of hyperbaric chamber ventilation

Abstract

Introduction

Hyperbaric chamber ventilation (HCV) refers to the intentional introduction of fresh gas, whether air, oxygen, or heliox, into a pressurised hyperbaric chamber in order to remove stale or otherwise compromised gas. The minimum required continuous HCV rate is usually determined by mathematical models derived from the contaminant mass balance within a well-stirred compartment. Non-uniform contaminant distribution patterns inside a hyperbaric chamber could emerge and invalidate the predictions of well-stirred models.

Methods

Contaminant distribution was investigated inside a clinical hyperbaric chamber with the aim of comparing well-stirred model predictions with the actual contaminant concentration measurements.

Results

Local ventilation effectiveness inside a clinical hyperbaric chamber may be compromised, leading to higher contaminant concentration values compared to the predictions of a mathematical model with a well-stirred assumption.

Conclusions

A well-stirred assumption in mathematical models is a useful simplification that allows reasonably accurate estimates of HCV requirements. However, local ventilation effectiveness values in a particular hyperbaric chamber might vary, with the potential for hazardous contaminant accumulation in under-ventilated zones.

Introduction

From the moment a clinical hyperbaric chamber is pressurised, the occupants (patients and medical attendants) are physically trapped in a sealed confined space which requires accurate atmosphere control measures to sustain physiological parameters compatible with survival. Hyperbaric chamber ventilation (HCV) refers to the intentional introduction of fresh gas, whether air, oxygen, or heliox, into a pressurised hyperbaric chamber in order to remove stale or otherwise compromised gas. This is different from atmosphere control in closed-loop systems used in some chambers and in saturation for deep-diving operations where refreshing of the internal atmosphere is mainly achieved by targeted removal of waste gases (including carbon dioxide and other products), and metabolised oxygen replacement. Since most clinical hyperbaric chambers use just breathing air as the pressurisation gas, the scope of this study was limited to ventilation of hyperbaric chambers using air.

The primary aim of HCV is maintenance of safe oxygen levels inside the chamber, and removal of hazardous contaminants, mainly carbon dioxide. Excess oxygen inside a hyperbaric chamber increases the fire risk and is thus considered a contaminant. Additionally, HCV can be applied to remove odours and control physical parameters of chamber atmosphere such as temperature and humidity.

HCV is usually applied during the constant pressure phase of a hyperbaric treatment session, but it can also be utilised during compression or decompression. It can also be applied continuously or intermittently. There is a broad diversity of recommendations when it comes to HCV requirements.[ 1]

The current European Standard EN 14931: 2006 primarily addresses HCV requirements in terms of controlling the chamber levels of oxygen, carbon dioxide, impurities in the form of organic compounds, as well as humidity.[ 2] The specified HCV rate of 30 actual litres per minute (ALPM) per person is only stated for a specified duration and as a means of quantifying the minimum required air supply capacity.

In the United States, the NFPA 99: 2021 code requires a minimum HCV rate of 3 cubic feet (84.9 L) per minute (CFM) per occupant not breathing on a built-in breathing system (BIBS), but without specifying pressure and temperature conditions.[ 3] This requirement can be traced back to the 1968 edition (referred to as NFPA 56D-T at that stage), but it was replaced by 3 actual cubic feet per minute (ACFM) (84.9 ALPM) in NFPA 99: 1993 (NFPA 99) and remained so through to the 2005 edition. There were no new editions until 2015, when the 3 CFM requirement was reintroduced. There appeared to be no rationale for this change. The NFPA 99 hyperbaric chapter committee has acknowledged that this flow rate needs further investigation as it does not account for the effect of pressure (personal communication with Francois Burman on 26 November 2022). The determination of an acceptable HCV is based on mitigation of not only excess concentration of contaminants in the chamber atmosphere, but their partial pressure as well.

A more nuanced approach to HCV rate requirement is found in USN Diving Manual Rev 7 of 2016, namely 2 ACFM (56.6 ALPM) per occupant at rest and 4 ACFM (113 ALPM) per active occupant.[ 4] The rationale provided is based on ensuring a carbon dioxide partial pressure of less than 1.5 % surface equivalent value (SEV), and oxygen concentration of less than 25%. The manual emphasises that chamber inlet and exhaust terminal separation is required for optimal chamber ventilation, implying that recommended HCV rates might be inadequate if there is ‘short-circuiting’ of ventilation gas between terminals.

The minimum required continuous HCV rate has been determined by mathematical models with the aim of controlling the levels of metabolically produced carbon dioxide. Such models are typically derived from the contaminant mass balance within a well-stirred single compartment.[ 5 , 6] However, significantly non-uniform contaminant distribution patterns inside a hyperbaric chamber could emerge and invalidate the predictions under this well-stirred assumption. This could pose a hazard, especially in terms of uncontrolled oxygen accumulation (pooling) and the associated risk of fire inside a hyperbaric chamber.

We devised a simple method to investigate the contaminant distribution (specifically oxygen concentration) inside a clinical hyperbaric chamber with the aim of comparing well-stirred model predictions with the actual contaminant concentration measurements. We expressed our findings in terms of relative contaminant removal effectiveness. Mathematical derivation of a well-stirred model of HCV is included. Our findings suggest that local ventilation effectiveness inside a clinical hyperbaric chamber may be compromised leading to higher contaminant concentration values compared to the predictions of a mathematical model with a well-stirred assumption.

Methods

BASIC DERIVATIONS

A glossary containing definitions for mathematical symbols and abbreviations used generally and in the following equations appears at the end of this article Glossary (Page 91) ^{(43.5KB, pdf)} .

A continuity equation can be formulated based on contaminant molar balance during HCV.[ 5]. Equation 1

Equation 1.

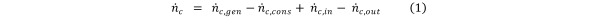
Under standard temperature and pressure conditions (STP), and assuming ideal gas behaviour, the molar amount of contaminant equals the contaminant volume divided by the standard molar volume (the volume occupied by one mole of gas under STP conditions).Equation 2

Equation 2.

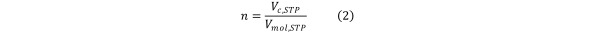
allowing the continuity Equation 1 to be reformulated in terms of contaminant volumes. Equation 3

Equation 3.

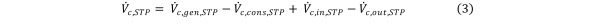
Replacing

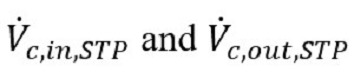
with their equivalent expressions in terms of contaminant concentrations (z) and ventilation flows yields. Equation 4

Equation 4.

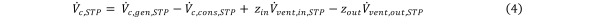
Given that the total volume of the gas in the chamber is constant during constant-pressure HCV, all the volume changes cancel out, i.e., Equation 5

Equation 5.

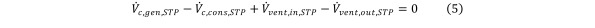
The left-hand side of Eq (4) can thus be expressed in terms of the contaminant concentration change. Also, under perfect mixing assumption, the contaminant concentrations in the chamber and in the exhausted gas are equal. Eq (4) can then be reformulated in the following way: Equation 6

Equation 6.

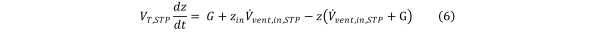
where V_T,STP is the total gas volume in the chamber, defined as:

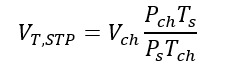
and G is the net contaminant volume gain, i.e.,

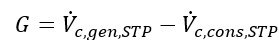
with

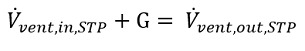
as required by the volume balance of Eq 5.

Solving Eq (6), we obtain the formula for the contaminant concentration in the chamber as a function of time. Equation 7

Equation 7.

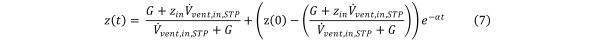
with

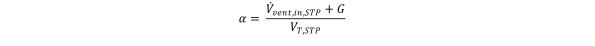
In the limit when t →∞, we observe the following steady state solution: Equation 8

Equation 8.

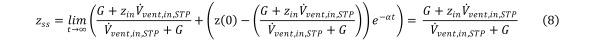
The minimum required HCV inflow rate to maintain a set maximum contaminant concentration indefinitely is thus, Equation 9a

Equation 9a.

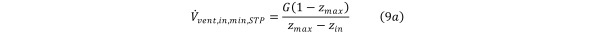
with corresponding HCV outflow, Equation 9b

Equation 9b.

The transient state Eq (7) and the steady state Eq (8) can be modified based on Dalton’s Law that underscores the relationship between the contaminant concentration and the contaminant partial pressure, namely Equation 10

Equation 10.

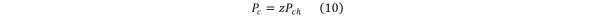
The transient state Eq (7) can then be modified to yield the formula for the partial pressure of the contaminant as a function of time Equation 11a

Equation 11a.

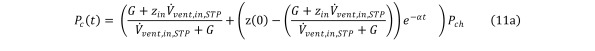
Distributing P_ch yields Equation 11b

Equation 11b.

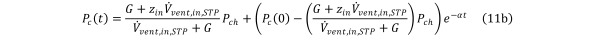
with α remaining the same as in Eq (7).

The steady state Eq (8) becomes modified to govern the minimum HCV rate required to control the partial pressure of the contaminant Equation 12

Equation 12.

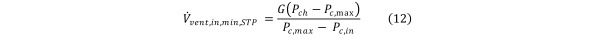
In the absence of contaminant generation or consumption inside the chamber Equation 13

Equation 13.

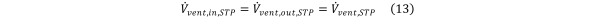
and Eq (6) reduces to Equation 14

Equation 14.

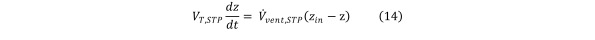
Solving Eq (14) we obtain the formula for the contaminant concentration as a function of time in the absence of contaminant generation or consumption: Equation 15

Equation 15.

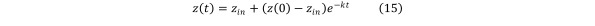
where

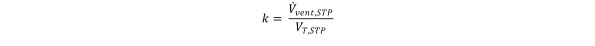
Solving Eq (15) for

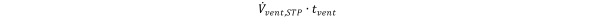
the formula for the required volume of ventilation gas V_vent,STP is obtained as Equation 16

Equation 16.

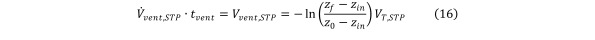
with z₀ ≡ z(0) and z_f being the final contaminant concentration after t = t_vent has elapsed.

EXPERIMENT

Experimental measurements were obtained between 18 July and 19 August 2022, inside a hyperbaric chamber (HAUX-STARCOM 1500/6 MP, Haux Life Support GmbH, Karlsbad, Germany) installed at the Hyperbaric and Tissue Viability Unit located at Gozo General Hospital in Malta.

Oxygen was used as a tracer gas, and oxygen concentrations were measured at 15 sampling points distributed inside the hyperbaric chamber Figure 1. For each sampling point, three separate measurements were obtained at three different chamber pressures with 135 measurements carried out in total. Measurements were obtained under steady state oxygen concentration created by continuous HCV and oxygen injection. Oxygen levels inside the chamber were measured using a portable HAUX–OXYSEARCH analyser.

Figure 1.

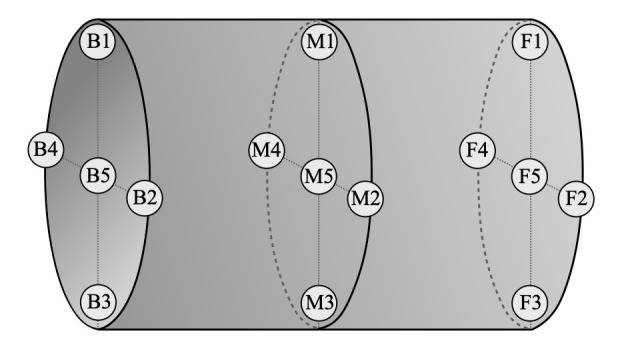
Arrangement of sampling points across the hyperbaric chamber interior

The analyser was spanned using normal atmospheric air on the surface. Oxygen partial pressure values were recorded in mbar and converted to volume concentrations via Dalton’s Law.

Oxygen injection was carried out by the HAUX-FLOW-CONTROL-UNIT at a set actual volume rate. The source was located between sampling points M1 and M4 (Figure 1). The chamber inlet was located in the proximity of point B2, while the chamber outlet was nearest to M3. Due to the fire hazard, an injection rate of 5 ALPM was chosen in conjunction with the set HCV rate of 1100 ALPM to keep oxygen concentration levels in the chamber to below 23.5%3 at all measurement locations upon reaching the oxygen contamination steady state with a set HCV.

To investigate the effect of depth on HCV effectiveness, measurements were obtained at three different hyperbaric chamber (absolute) pressures: 160 kPa, 220 kPa, and 280 kPa. The oxygen concentration values obtained were used to calculate local HCV effectiveness relative to well-stirred model predictions, at each location, using the following expression:

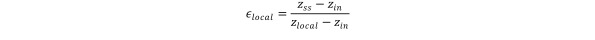
where z_ss represents the steady-state oxygen concentration predicted under well-stirred assumption and computed via Eq (8).

Statistical analysis was performed on results and findings expressed as mean ventilation effectiveness (ε ± 95%) confidence interval for each of the 15 location points at given pressures.

Results

Statistically significant instances of underventilation (ε < 1) were found at all three test pressures (Table 1). At the chamber pressure of 160 kPa, 6 out of 15 points were determined to be underventilated, whereas at 220 kPa and 280 kPa, instances of underventilation were found at 2 out of 15 sampling points. Points F4 and M5 were underventilated at all three chamber pressures (Figure 2). There was a single instance of statistically significant overventilation (ε > 1) at 280 kPa (point F2).

Table 1. Measured mean steady state oxygen concentrations at all sampling points with corresponding ventilation effectiveness values. Statistically significant deviations from well-stirred model marked in bold, also shown in Figure 2; CI – confidence interval .

Point	160 kPa				220 kPa				280 kPa
	ẑss	ε	95% CI Lo	95% CI Hi	ẑss	ε	95% CI Lo	95% CI Hi	ẑss	ε	95% CI Lo	95% CI Hi
F1	0.2115	3.18	-2.29	8.65	0.2133	1.43	-1.14	4.00	0.2113	2.89	0.98	4.81
F2	0.2125	1.49	0.54	2.45	0.2130	1.49	-0.94	3.92	0.2117	2.22	1.03	3.42
F3	0.2131	1.18	0.58	1.77	0.2133	1.25	-0.32	2.82	0.2119	1.98	0.65	3.31
F4	0.2196	0.41	0.04	0.77	0.2202	0.36	0.23	0.48	0.2156	0.65	0.39	0.91
F5	0.2146	0.83	0.15	1.51	0.2153	0.72	0.14	1.29	0.2130	1.22	0.76	1.67
M1	0.2146	0.84	0.13	1.56	0.2144	0.89	-0.01	1.79	0.2129	1.39	0.00	2.77
M2	0.2150	0.75	0.27	1.23	0.2150	0.75	0.24	1.26	0.2137	0.97	0.84	1.10
M3	0.2150	0.72	0.50	0.95	0.2148	0.77	0.28	1.25	0.2137	0.98	0.69	1.27
M4	0.2154	0.67	0.36	0.99	0.2153	0.70	0.30	1.09	0.2140	0.91	0.45	1.36
M5	0.2165	0.57	0.29	0.85	0.2162	0.58	0.51	0.64	0.2149	0.74	0.53	0.95
B1	0.2144	0.83	0.53	1.13	0.2135	1.06	0.49	1.62	0.2126	1.46	0.27	2.64
B2	0.2131	1.18	0.58	1.77	0.2117	3.67	-5.35	12.69	0.2113	3.17	-0.83	7.17
B3	0.2150	0.75	0.27	1.23	0.2139	0.93	0.49	1.36	0.2130	1.26	0.37	2.15
B4	0.2150	0.72	0.50	0.95	0.2141	0.90	0.39	1.42	0.2131	1.18	0.63	1.73
B5	0.2154	0.67	0.36	0.99	0.2150	0.73	0.40	1.07	0.2140	0.91	0.45	1.36

Figure 2.

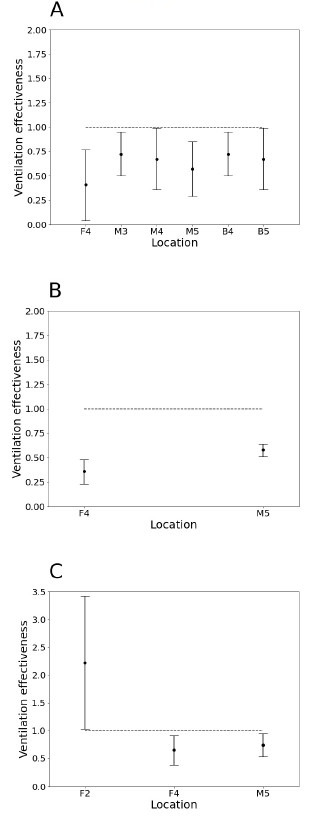
Ventilation effectiveness values (mean ± 95% confidence interval) deviating from well-stirred model predictions at three different hyperbaric chamber pressures, A – 160 kPa, B – 220 kPa and C – 280 kPa

Discussion

The primary measure of HCV is its rate, expressed as standard volume of gas (determined at atmospheric pressure at sea level) exchanged per unit of time. Higher HCV rates facilitate contaminant removal from the chamber atmosphere. However, in reality the same HCV rate can have vastly different effects in the presence of different mixing behaviour of the inflowing air. Ventilation effectiveness is a concept used to address such differences in enclosed space ventilation performance.[ 7 , 8] Factors that could affect ventilation effectiveness of a hyperbaric chamber include chamber geometry, configuration of inlet and exhaust terminals, spatial obstacles, contaminant distribution, the degree of turbulence, and temperature distribution.

Our results indicate that the local ventilation performance of a clinical hyperbaric chamber could be significantly worse than what a well-stirred model would predict. Several sampling points inside the chamber were underventilated (ε < 1) relative to the well-stirred scenario, and the difference found was statistically significant. This was not surprising in the light of our actual experience with HCV. Chamber operators and attendants have long known that stirring the chamber atmosphere manually during HCV tends to facilitate contaminant removal. One study reported that it can take 2.5 times longer to effectively ventilate the chamber if the chamber atmosphere is not manually stirred during ventilation.[ 9]

It is physically possible for a particular region inside a chamber to have a ‘supra-ideal’ ventilation performance (ε > 1) resulting in more effective contaminant removal than what could be achieved by perfect mixing according to a well-stirred model. Indeed, measured HCV performance for the point F2 at 280 kPa exceeded the predictions of the well-stirred model, possibly due to its proximity to the chamber inlet terminal. The same effect occurs by design during local exhaust ventilation (LEV) whereby the contaminant is removed from the atmosphere before it can spread, and it is thus a preferred method of ventilation of hazardous contaminants in industry.[ 10] The LEV concept could be utilised in clinical hyperbaric practice. For example, by positioning a patient with poorly fitted and leaking oxygen mask closer to the chamber’s exhaust terminal, removal of excess oxygen from the chamber atmosphere would most likely be facilitated during HCV.

One might expect that chamber pressure would affect HCV performance due to its effect on gas density, and we observed several instances of increased pressure exhibiting a ventilation effectiveness-enhancing effect, but the overall effect was not strong. However, our data set was obtained by performing measurements on only three separate occasions and on a relatively narrow pressure domain, implying that a study with more statistical power investigating a broader pressure domain might be able to better examine the phenomenon.

Conclusions

A well-stirred assumption in mathematical models is a useful simplification that allows reasonably accurate estimates of HCV requirements. However, local ventilation effectiveness values in a particular hyperbaric chamber might vary, with the potential for hazardous contaminant accumulation in underventilated zones. When the contaminant in question is oxygen, accumulation increases the risk of a catastrophic chamber fire. It is important to bear in mind that in a chamber environment, HCV is never a well-stirred process throughout the chamber and that considerable deviations in local contaminant concentration might exist relative to the values displayed by the chamber’s gas analyser. Efforts should be made to minimise the presence of factors that tend to compromise ventilation effectiveness, such as excessive space partitions or proximity of ventilation terminals. Using more than one oxygen sampling point as well as utilising local exhaust ventilation near the oxygen sources could provide additional safety barriers to hazardous oxygen accumulation. Hyperbaric chamber ventilation effectiveness should be addressed during the design phase prior to chamber manufacture. Thereafter, it should be assessed prior to final certification of the chamber.