A network score-based metric to optimize the quality assurance of automatic radiotherapy target segmentations

Highlights

• •A network score-based metric was proposed as a tool for quality assurance of auto-segmentations.
• •This metric correlated well with clinically relevant distance-based segmentation metrics.
• •The proposed metric showed high capability to detect cases that need review.

Abstract

Background and purpose

Existing methods for quality assurance of the radiotherapy auto-segmentations focus on the correlation between the average model entropy and the Dice Similarity Coefficient (DSC) only. We identified a metric directly derived from the output of the network and correlated it with clinically relevant metrics for contour accuracy.

Materials and Methods

Magnetic Resonance Imaging auto-segmentations were available for the gross tumor volume for cervical cancer brachytherapy (106 segmentations) and for the clinical target volume for rectal cancer external-beam radiotherapy (77 segmentations). The nnU-Net’s output before binarization was taken as a score map. We defined a metric as the mean of the voxels in the score map above a threshold (λ). Comparisons were made with the mean and standard deviation over the score map and with the mean over the entropy map. The DSC, the 95th Hausdorff distance, the mean surface distance (MSD) and the surface DSC were computed for segmentation quality. Correlations between the studied metrics and model quality were assessed with the Pearson correlation coefficient (r). The area under the curve (AUC) was determined for detecting segmentations that require reviewing.

Results

For both tasks, our metric (λ = 0.30) correlated more strongly with the segmentation quality than the mean over the entropy map (for surface DSC, r > 0.65 vs. r < 0.60). The AUC was above 0.84 for detecting MSD values above 2 mm.

Conclusions

Our metric correlated strongly with clinically relevant segmentation metrics and detected segmentations that required reviewing, indicating its potential for automatic quality assurance of radiotherapy target auto-segmentations.

1. Introduction

Target segmentation is a crucial part of the radiotherapy (RT) workflow. In clinical practice, this step is typically done manually by radiation oncologists, which is time consuming and suffers from inter- and intra- observer variability. In particular in online adaptive treatment settings, the time pressure is high because both the patient and the staff involved in the RT treatment are waiting while the segmentations are performed. With the aim of saving time in the clinic, automatic segmentation algorithms based on convolutional neural networks have been investigated for gross tumor volumes (GTVs) in a variety of tumor sites, such as brain [1], [2], head and neck [3], [4], [5], rectum [6] and cervix [7], [8]; and clinical target volumes (CTVs) such as cervical cancer CTV [9] and prostate cancer CTV [10], [11].

Although segmentation algorithms are reaching a reasonable performance [12], [13], [14], they still produce faulty segmentations in some cases. To identify whether automatically generated segmentations are acceptable for clinical use, it is necessary for a clinician to verify them. This limits the time gains of automatic segmentation methods. Therefore, there is a need to recognize automatically in which cases the automatic segmentations need correction. In the context of RT, automatic quality assurance (QA) of the automatic segmentations is a topic of interest nowadays, as showcased in recent reviews [15], [16].

Deep learning networks for auto-segmentation typically predict a score that correlates with the probability that a voxel belongs to the structure to be segmented. Only at the last step, voxel scores are thresholded into a binary segmentation mask. These score maps are often converted into uncertainty maps by applying the entropy operator [17], [18], [19]. It has been shown qualitatively that incorrect areas of the automatic segmentations cover areas of high network entropy [20], [21], [22]. Once an entropy map is computed, the mean over all the voxels [17], [18], [19] is often used as a metric for QA of auto-segmentations. Alternatively, a common approach for QA of auto-segmentations consists of developing machine learning models that directly predict segmentation quality [23], [24].

Up to now, the QA metrics are typically correlated only with the Dice Similarity Coefficient (DSC) [17], [18], [20], [25], [26]. Although DSC is a common metric of segmentation performance, it presents several drawbacks. By construction, it is volume-dependent since it overestimates the performance for large structures. Additionally, it has been shown to correlate poorly with clinically relevant endpoints in RT planning, such as dose/volume metrics [27] and the expected editing time [28]. Distance-based metrics, such as the 95th Hausdorff distance (95th HD), the mean surface distance (MSD) and the surface DSC, suffer less from these drawbacks and are recommended to be reported together with the DSC [28], [29].

We hypothesize that the commonly used entropy operator may overshadow relevant information that is contained in the score maps. The aim of this study was to identify a quality metric that can be generated directly from the output of the network, and which correlates with clinically relevant distance-based metrics. We additionally assessed the capability of the proposed metric to identify automatic segmentations that would need review.

2. Materials and methods

2.1. Data

Two cohorts were retrospectively collected and used in this study. One cohort consisted of a total of 195 histologically proven cervical cancer patients treated in our institution between August 2012 and December 2021. Further details on patient characteristics and their treatment are described in Table S1. The institutional review board approved the study (IRBd20276). Informed consent was waived considering the retrospective design of the study.

A total of 524 separate MRI images of the patients with the brachytherapy applicator in place were included in this work. These images were acquired using a 1.5 T (104 scans) or 3 T (442 scans) Philips MRI scanner. Axial T2-weighted (T2w) turbo spin-echo images were used (TR = [3500–13300 ms], TE = [100–120 ms]) with a pixel spacing of 0.39 mm × 0.39 mm (442 scans) or 0.63 mm × 0.63 mm (104 scans) and a slice thickness of 3 mm. The GTV, as segmented for treatment planning by a radiation oncologist on each available MRI, was available as ground truth.

The other cohort used in this study consisted of a total of 30 patients with intermediate risk or locally advanced rectal cancer treated in our institution. Further details on patient characteristics are described in Table S2. All patients in the study were enrolled in the Momentum prospective registration study (NCT04075305) and gave written informed consent for the retrospective use of their data.

For this cohort, a total of 483 EBRT images were considered. All the fractions were carried out on the Unity MR-Linac (Elekta AB, Stockholm). Axial T2-weighted (T2w) turbo spin-echo images were used (TR = 1300 ms, TE = 128 ms) with a pixel spacing of 0.57 mm × 0.57 mm (349 images) or 0.87 mm × 0.87 mm (134 images) and a slice thickness of 1.20 mm (155 images), 1.8 mm (134 images) or 2.4 mm (194 images). In our institution, the radiation therapists (RTTs) have been trained and certified to segment the CTV for the MRI-guided online adaptive RT workflow of the rectal cancer treatment. Therefore, the CTV used as ground truth was segmented by a RTT on each available MRI for clinical practice. The CTV segmentations were also verified by a radiation oncologist with over 10 years of experience.

2.2. Segmentation framework and training scheme.

In previous studies, we used the nnU-Net framework [30] to segment the cervical cancer GTV [8] and the rectal cancer mesorectum CTV [31]. In the current work, we used a 5-fold cross validation scheme to retrain the networks and assess the robustness of the quality metrics to changes in the training set composition. The training sets were the same as those described in previous articles [8], [31], with 156 patients (418 images) for the cervical cancer cohort and 25 patients (406 images) for the rectal cancer cohort. For both cohorts, the 3D variant of the nnU-Net was used.

2.3. Score map definition

The score map was defined as the voxelwise softmax scores of the last layer of the network of the target segmentation channel before binarization (as depicted in Fig. 1). This strategy was chosen because it can be applied to any trained network without requiring changes to the architecture or training procedure.

Fig. 1.

Workflow of the study design.

The score maps were created for the test sets described in previous studies [8], [31], which included 39 patients (106 images) for the cervical cancer cohort and five patients (77 images) for the rectal cancer cohort. We further subdivided these sets at the scan level into a validation set for parameter optimization and a final test set for evaluating the quality metrics. For the cervical cancer GTV segmentation task, the final validation and test sets each included 53 images. The analyses were done for 52 out of the 53 cases of the test set. The remaining case corresponded to a patient who had her uterus removed which resulted in a variation in anatomy unseen by the trained network. The final validation and test sets for the rectal cancer CTV segmentation task included 39 and 38 images, respectively. Note that the term “score maps” is referred to as “attention maps” in our previous work [8].

2.4. Score-based metrics

We defined a metric (High Score or HiS metric) as the mean of the score map values that were higher than a threshold λ. By thresholding the score map and retaining only the high score voxels, we aimed to remove information that is unimportant for the flagging of potentially incorrect segmentations, as very low values on the score map are expected both in correct and incorrect segmentations.

The mean and the standard deviation (STD) were computed over the non-zero values of the score map to represent the overall score and its variability, respectively. Additionally, the mean over the entropy map was computed for direct comparison with other studies [17], [18], [19], [26].

For each value of λ, the difference in correlation with respect to the performance of the mean over all values of the score map (i.e. λ = 0) was determined. The optimal value of λ was determined empirically as the value at which the HiS correlated best with the MSD in the validation set, in the range (0,0.45) with steps of 0.05. The MSD was chosen to determine the optimal threshold because it is a distance-based metric and therefore more suitable for RT applications (unlike the DSC), it evaluates the whole contour (unlike the 95th HD, which focuses on the gross errors) and it has no hyperparameters (unlike the surface DSC).

2.5. Statistics

The correlation between the metrics and the segmentation performance was assessed with the Pearson correlation coefficient (r) and with the Spearman correlation coefficient. To check the assumption of linearity for Pearson, residual plots were computed. To study the robustness of each metric to the training set composition, the correlations were computed separately for the score maps resulting from each of the five training folds. The mean and the standard deviation of the r were computed over all folds.

To assess the capability of the metrics to distinguish between segmentations that require reviewing and those that can be left unchecked, the area under the curve (AUC) was determined for detecting segmentations that exceeded a specified MSD or 95th HD threshold. The code and additional training details are available in: github.com/RoqueRouteiral/his_qa.

3. Results

For both segmentation tasks and for the four segmentation metrics, the largest improvement of the proposed HiS metric with respect to the mean (Δr) occurred for λ < 0.10, as depicted in Fig. 2. Moreover, for λ > 0.10, Δr remained fairly stable. For the case of the MSD, the largest correlations were found for λ = 0.35 and λ = 0.25 for the cervical and rectal cancer target segmentation tasks, respectively. We took the average between these two values, λ = 0.30, in the subsequent analyses. The computed residual plots (Fig. S1) show that the points were randomly scattered around the horizontal axis, confirming the assumption of linearity between the performance metrics and the HiS.

Fig. 2.

Difference in Pearson correlation coefficient (Δr) with the segmentation metrics between the HiS metric and the mean over the score map as a function of the parameter λ. The bold line is the average Δr among the five folds. The dashed lines represent the Δr for each of the five folds.

Table 1 shows the correlation between the studied metrics and the segmentation quality metrics for the test sets of both cohorts. For the segmentations of the cervical cancer GTV, the HiS achieved a mean r of 0.79 with DSC, −0.60 with 95th HD, −0.66 with MSD and 0.67 with surface DSC. For the segmentations of the rectal cancer CTV, the HiS yielded a mean r of 0.76 with DSC, −0.53 with 95th HD, −0.74 with MSD and 0.62 with surface DSC. For both tasks, the HiS correlated more strongly with the segmentation quality metrics than the rest of the score-based metrics. The only exception was the STD in the case of the cervical cancer task, which correlated as strongly as the HiS and the surface DSC. The HiS also correlated more strongly with all the segmentation metrics for both tasks with the Spearman correlation coefficient (Table S3).

Table 1.

Pearson correlation coefficients (mean ± standard deviation among folds) between the metrics and the segmentation performance metrics. Bold letters indicate the highest correlation among the different metrics.

	DSC	95th HD	MSD	Surface DSC
Cervical cancer cohort
Mean	0.72 ± 0.10	−0.53 ± 0.16	−0.57 ± 0.13	0.60 ± 0.1
STD	0.68 ± 0.06	−0.53 ± 0.14	−0.64 ± 0.13	0.70 ± 0.1
Mean (over entropy map)	0.43 ± 0.14	−0.38 ± 0.09	−0.43 ± 0.11	0.43 ± 0.15
HiS (λ = 0.30)	0.79 ± 0.05	−0.60 ± 0.13	−0.66 ± 0.10	0.67 ± 0.06
Rectal cancer cohort
Mean	0.60 ± 0.03	−0.42 ± 0.10	−0.61 ± 0.06	0.50 ± 0.08
STD	−0.32 ± 0.11	0.22 ± 0.18	0.35 ± 0.15	−0.27 ± 0.17
Mean (over entropy map)	−0.74 ± 0.06	0.47 ± 0.08	0.69 ± 0.07	−0.58 ± 0.09
HiS (λ = 0.30)	0.76 ± 0.08	−0.53 ± 0.07	−0.73 ± 0.09	0.62 ± 0.10

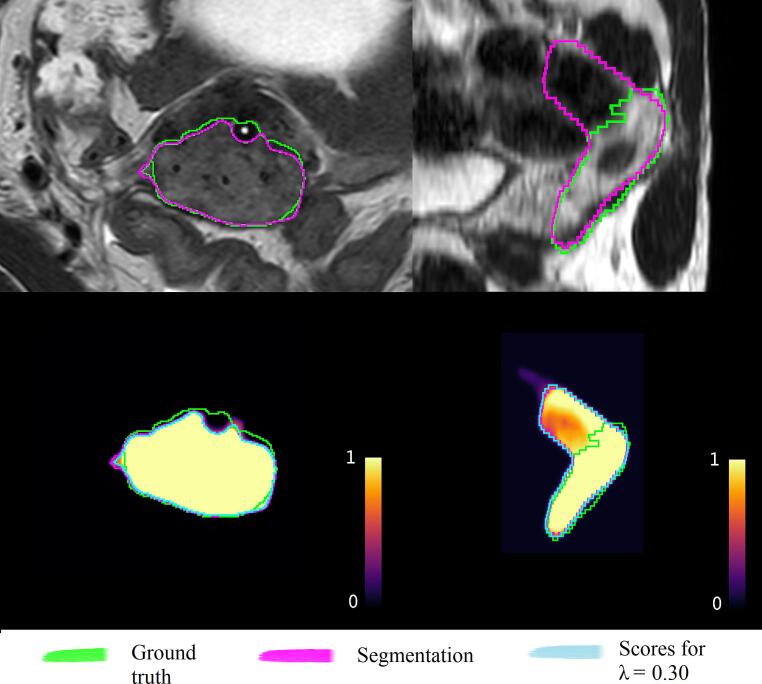
As an illustration, Fig. 3 shows the scatter plots between the HiS metric and the segmentation metrics obtained in one of the five folds of the trained auto-segmentation networks. Note that the range of HiS values is task-dependent and the values are therefore not directly comparable between the two tasks. Fig. 4 illustrates the segmentations and score maps with one example from each auto-segmentation task. For the cervical cancer case (Fig. 4, left), the HiS metric was relatively high for this cohort (HiS = 0.76). Indeed, the segmentation performance was high (MSD = 0.78 mm), with the main error at the location of the applicator channel. For the rectal cancer example (Fig. 4, right), the HiS value was relatively low for this cohort (HiS = 0.89). This case corresponded to a target that was oversegmented by the network, resulting in poor performance (MSD = 3.6 mm), as expected.

Fig. 3.

Scatter plots between the segmentation metrics and the HiS metric for the cervical cancer cohort (top) and the rectal cancer cohort (bottom). The translucent band corresponds to the 95 % confidence interval for the estimated regression, computed via bootstrap.

Fig. 4.

Examples of the segmentations and the correspondent score maps for a cervical cancer case (left, HiS = 0.76) and a rectal cancer case (right, HiS = 0.89). The input images for the segmentation framework, the ground truth segmentation (green) and the automatic segmentation (pink) are depicted on the top row. The corresponding score maps are depicted on the bottom row. The blue line encompasses the voxels for which the score values are higher than λ = 0.3. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

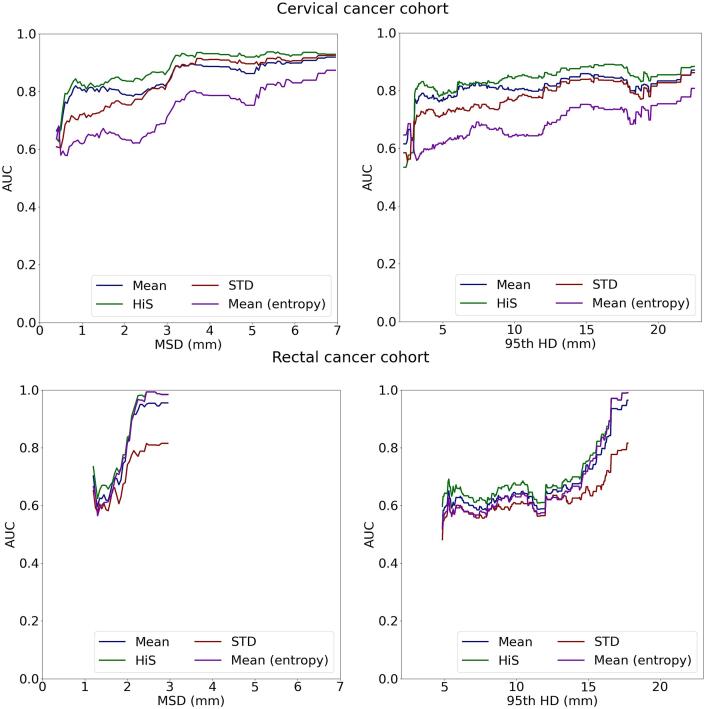
The capability of the studied metrics to detect segmentations that require reviewing is illustrated in Fig. 5, which shows the AUC for detecting segmentations that exceed varying MSD and 95th HD threshold values. The proposed HiS metric achieved higher AUC values than the other baselines metrics for most MSD and 95th HD values, for both auto-segmentation tasks. In particular, for the cervical cancer cohort, the AUC varied between 0.82 and 0.94 for detecting cases for MSD values above 1 mm. For the rectal cancer cohort, the AUC varied between 0.84 and 0.99 for detecting cases with an MSD above 2 mm.

Fig. 5.

AUC for detecting segmentations exceeding a specified MSD (left) or 95th HD (right).

For each task, the AUC was reported between the minimum and maximum values of the obtained MSD and 95th HD over all folds, because the sensitivity and specificity are only defined in these ranges. For the cervical cancer task, these ranges were 0.4 mm to 7.0 mm for the MSD and 2.6 mm to 22.5 mm for the 95th HD. For the rectal cancer task, the ranges were 1.2 to 3.0 mm for the MSD and 4.8 mm to 17.8 mm for the 95th HD.

4. Discussion

In this work we proposed a simple metric based on the network output for automatic QA of auto-segmentations of RT target volumes. This metric averages all score values above a threshold of 0.3. We showed that it correlated strongly with the segmentation performance metrics for two different auto-segmentation tasks. The correlations were strong not only for the DSC but also for the more clinically relevant distance-based metrics. Our proposed metric outperformed the often used mean value of the entire entropy map in the distinction between segmentations that require reviewing and those that can be used without an extra manual check.

The strongest correlations between the proposed metric and the segmentation performance occurred for λ values above 0.1, suggesting that the lowest score values are not very representative of the segmentation performance. Furthermore, it was observed that the choice of λ was not critical for values above 0.2.

Despite the high correlations between the proposed metric and the segmentation quality, similar HiS values corresponded to a large range of values on the segmentation quality metrics, suggesting that the HiS might not always be an accurate surrogate of the segmentation performance. Other works have shown similar behavior in their correlation plots [18], [23]. The aim of this metric, however, is to flag cases that need reviewing, not to predict the segmentation performance. This was demonstrated with the high AUC values achieved by the metric.

Previous studies have qualitatively related the uncertain areas with the segmentation errors [20], [22]. Metrics that show qualitatively where the local edits should be performed could aid clinicians during editing and should therefore be investigated in future work. We speculate that the proposed metric could also be used to select the voxels that are more likely wrong in the segmentation. From our results, we can infer that voxels from the score map that are below the λ = 0.10 threshold did not contribute to the correlation with the segmentation performance. This suggests that those voxels are not relevant for a potential correction. Clinicians could then use this information as an aid to edit the segmentation.

Pearson’s correlation coefficient has been used in previous works to study the correlation between the segmentation performance and QA metrics [25], [26]. Its application assumes linearity between the two variables. Furthermore, outliers can skew its evaluation. To confirm the validity of our results, we computed the Spearman correlation coefficient, which does not assume linearity and is more robust to outliers. The HiS metric still correlated more strongly than the other score-based metrics.

The STD showed strong correlations with the MSD, but only for the cervical cancer GTV segmentation task. For rectal cancer, the correlation was much lower and importantly also changed sign. A similar behavior was observed for the mean over the entropy map, commonly used in literature. This metric showed strong correlations for the rectal cancer segmentation task, but for the cervical cancer GTV the correlations were poor for the segmentation metrics and also changed sign. Therefore, these metrics appear to be less robust for QA. Tumors (like the cervical cancer GTV) are more heterogeneous in size, shape and texture than anatomical structures (like the rectal cancer CTV, or mesorectum). Uncertainties in tumor auto-segmentation networks are likely more prominent than those of auto-segmentation networks of anatomical structures. This may explain the difference in behavior of the metrics across the two tasks. Previous works have mostly focused on segmentation tasks with arguably lower uncertainty, such as the segmentation of anatomical structures [20], [23] or the segmentation of brain tumors [17], [18].

Although most studies propose using the average of the entire entropy map, other works [17], [25] have trained models to automatically predict the DSC coefficient directly from the entropy maps, thereby incorporating the metric definition into the learning task. Learning-based metrics can be more generic than the pre-specified average, but they are also less interpretable and therefore might be less desirable for QA purposes.

Recent literature has focused on other methods for computing the score maps, such as Monte Carlo dropout [17], [18], [32], which averages the scores resulting from multiple instances of the network. We expect our metric to also be applicable to Monte Carlo dropout estimates. However, using the softmax layer outputs eliminates the need for specific architectural or training scheme modifications. Furthermore, it does not require running inference multiple times which could hinder the clinical implementation of the method.

In clinical settings, the clinician could be provided with both the automatic segmentation and its associated HiS score that would serve as a quality metric. Prior to clinical implementation, a pilot study could be set up to assess the time savings achieved by using this tool in a clinical setting. The trade-off between the amount of cases that would not need to be reviewed manually and the missed faulty cases that would require reviewing, should also be assessed.

In conclusion, we identified a simple metric derived directly from the output of the segmentation network that correlated strongly with commonly used segmentation metrics, not only for the case of DSC but also for the more clinically relevant distance-based metrics. The proposed metric was able to flag segmentations that would require review. It is also easy to compute, as it does not require any architecture or training scheme modifications. The proposed metric has potential as a tool for QA of automatic target segmentations.

CRediT authorship contribution statement

Roque Rodríguez Outeiral: Conceptualization, Methodology, Software, Formal analysis, Investigation, Writing – original draft, Visualization. Nicole Ferreira Silvério: Data curation, Resources, Validation. Patrick J. González: Data curation, Resources. Eva E. Schaake: Data curation, Resources. Tomas Janssen: Supervision, Writing – review & editing. Uulke A. van der Heide: Conceptualization, Supervision, Writing – review & editing. Rita Simões: Conceptualization, Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: