Corneal Stress Distribution Evolves from Thickness-Driven in Normal Corneas to Curvature-Driven with Progression in Keratoconus

Abstract

Purpose

To introduce the novel parameter of Corneal Contribution to Stress (CCS) and compare stress distribution patterns between keratoconus (KCN) and normal corneas.

Design

Prospective, observational, cross-sectional study.

Participants

The study included 66 eyes of 40 subjects diagnosed with KCN and 155 left eyes from 155 normal control (NRL) subjects.

Methods

Tomography was obtained to calculate the newly proposed CCS, defined according to the hoop stress formula without intraocular pressure, R/2t, where R is the radius of curvature and t is the thickness. CCS maps were calculated from pachymetry and tangential curvature maps. Custom software identified the 2-mm-diameter zones of greatest curvature (Cspot-max), thinnest pachymetry (Pach-min), greatest stress (CCSmax), and lowest stress (CCSmin). Stress difference (CCSdiff) was calculated as CCSmax – CCSmin. Distances between Cspot-max vs. Pach-min, vs. CCSmax, and vs. CCSmin, as well as between Pach-min vs. CCSmax and vs. CCSmin, were calculated. t tests were performed between cohorts, and paired t tests were performed within cohorts. Univariate linear regression analyses were performed between parameters and distances. The significance threshold was P < 0.05.

Main Outcome Measures

Corneal stress parameters, corneal features of maximum curvature, minimum thickness, and distances between corneal stress parameters and corneal features.

Results

CCSmax was significantly closer to Pach-min (0.79 ± 0.92) and Cspot-max (2.04 ± 0.85) than CCSmin (3.17 ± 0.38, 2.73 ± 1.53, respectively) in NRL, P < 0.0001, whereas CCSmin was significantly closer to Cspot-max (1.35 ± 1.43) than CCSmax (2.52 ± 0.72) in KCN, P < 0.0001. Cspot-max (severity) was significantly related to CCSdiff in KCN (P < 0.0001; R² = 0.5882) with a weak relationship in NRL (P < 0.0080, R² = 0.0451). Cspot-max was significantly related to the distance from Pach-min to CCSmax (P < 0.0001; R² = 0.3737) without significance in NRL (P = 0.8011).

Conclusions

Corneal stress is driven by thickness in NRL, with greatest stress at thinnest pachymetry and greatest curvature. However, maximum stress moves away from thinnest pachymetry with progression in KCN, and minimum stress is associated with maximum curvature. Severity in KCN is significantly related to greater difference between maximum and minimum stress, consistent with the biomechanical cycle of decompensation.

Financial Disclosure(s)

Proprietary or commercial disclosure may be found in the Footnotes and Disclosures at the end of this article.

Keratoconus (KCN) is a progressive ectasia that results in the cornea deforming due to stromal thinning and protrusion. The disease process typically begins during puberty and manifests symptoms of decreased visual acuity, degraded contrast sensitivity, and photophobia by young adulthood. The prevalence of KCN in the United States is increasing and is now estimated at 265 cases per 100,000 individuals.¹ With an increasing case load comes the need for quick and accurate diagnostic testing. Examination of corneal topography maps in conjunction with a careful assessment of the cornea with a slit lamp biomicroscope is a common approach to detect KCN but may be insensitive to early or subclinical disease, in part due to a lack of uniform diagnostic criteria.² Considering the biomechanical parameters of the cornea as an additional variable in the detection of KCN may improve diagnostic accuracy, even for early disease stages.³

Evaluating clinical corneal biomechanics requires a load or perturbation to be applied to the cornea such that the stiffness of its response can be analyzed. The time scale of the biomechanical response can be short, such as a response to an air puff in a single clinic examination, or it can be a much longer, such as corneal biomechanical remodeling in KCN, which occurs over years in response to changing stress distribution throughout the cornea. Both thickness and curvature contribute to corneal stress distribution. Thus, as tomographic curvature and thickness data are changing over time as the disease progresses, the stress distribution is also modified as it tracks these changes. Therefore, data acquired in single clinic examination at any point can be considered a long-time-scale biomechanical response in KCN.

Multiple finite element mechanical models of KCN have been reported in the literature, including patient-specific models in which tomographic data in the form of elevation and thickness serve as inputs to the computer simulation.^4,5 Because the clinical tomographic elevation data are loaded by intraocular pressure (IOP) at the time of acquisition, an unloaded model is first generated, and then IOP is applied in an attempt to recreate the curvature profiles of the original loaded data. These KCN computational models can be used to evaluate responses to various interventions, including intrastromal rings and corneal crosslinking (CXL).^6,7

These computer models are time-consuming to generate and thus, are not practical for monitoring KCN progression in the clinic. Many approaches to automated KCN detection have been reported based on multiple approaches and algorithms. Progression can be monitored with difference maps between time points or using multiple time point displays.⁸ However, thickness and curvature are presented independently in separate maps or separate features in displays, even though they are interdependent in a biomechanical context. Evaluation of changes in thickness and curvature cannot be completed until measurements have been collected across more than one visit, which can become problematic when patients do not return for follow-up appointments.

Therefore, the purpose of the current study is to propose a novel stress distribution map for the clinic that is a function of both curvature and thickness, as well as easy to calculate and interpret. Stress distribution patterns will be compared in KCN and normal corneas, and the relationships between areas of greatest curvature and thinnest pachymetry to areas of highest stress and lowest stress will be analyzed.

Methods

A subset of a larger prospective observational study was generated containing 195 subjects who were imaged with Pentacam Tomography (Oculus). This cohort was composed of 66 eyes from 40 subjects diagnosed with KCN, with fellow eyes considered independent in KCN,9, 10, 11, 12 and 155 left eyes from 155 normal control (NRL) subjects. The protocol was approved by The Ohio State University (OSU) Institutional Review Board and adhered to the principles outlined in the Declaration of Helsinki for research on human subjects. All participants signed informed consent. All subjects with KCN were recruited from OSU ophthalmology practices, as referred from OSU College of Optometry and from community ophthalmologists/optometrists. Healthy participants were recruited from the community to establish an NRL cohort.

Inclusion criteria included a clear cornea; the ability and willingness to comply with the study protocol; age of 18 years or older; and, only for the KCN cohort, a diagnosis of KCN with clinical signs, including at least one of reduced corneal thickness, steepening, Fleischer’s ring, Vogt’s striae, or scissoring. Exclusion criteria for both cohorts included nonintact epithelium; pregnancy; less than 12 weeks postpartum or from cessation of breast feeding; nystagmus; previous ocular surgery, except cataract extraction greater than 3 months prior to date of enrollment; diabetes; systemic disease that causes defects in collagen, such as Marfan’s syndrome; medications that affect biomechanics, such as topical prostaglandin analogs; and, for the NRL cohort, a history of ocular disease or trauma.

All data were collected in a single study visit, which occurred at OSU Havener Eye Institute in Columbus, Ohio. First, demographic data including age, sex, and race were collected. Then measurements of each eye that met study criteria were acquired. Of the devices used in the larger study, only data from the Pentacam are reported for the current subset of subjects. Multiple measurements were acquired on all subjects, with at least 2 of acceptable quality. Examinations were automatically included if the quality assessment made by the device was “OK.” However, for both the NRL and KCN cohorts, some acceptable maps did not receive an “OK” for quality, so each examination was manually evaluated for quality, including the type of error that was reported and the presence of obvious artifact. For example, if a subject in the KCN cohort had 3 examinations with yellow-flagged quality assessments, and 2 seemed similar and the third seemed dissimilar with rapid changes in curvature in a small distance, this third map was excluded for obvious artifact. All included maps were averaged for analysis.

Disease severity in the KCN cohort was assessed using Michael Belin’s ABCD KCN grading system.¹³ In this system, 5 stages are used (0–4) for each of anterior curvature (A), posterior curvature (B), and thinnest pachymetry (C). The anterior curvature has been shown to be similar to the Amsler–Krumeich classification. Distance visual acuity (D) was not recorded in the current data set. The population means of A, B, and C scores were separately calculated, along with the mean of the individual subject average of A, B, and C scores to provide an overall mean stage.

Corneal Contribution to Stress

The formula for hoop stress in a thin-walled sphere, which is acting along the lamellae in the tangential direction, is P × R/2t, where P is internal pressure, R is radius of curvature, and t is wall thickness. To generate the novel parameter of Corneal Contribution to Stress (CCS), IOP was removed from the hoop stress formula for CCS = R/2t to isolate the cornea from the load. This modification of the formula removes the confounding influence of IOP in comparing stress maps over time or between different groups. If it was not removed, these stress maps would be dominated by IOP. In the absence of IOP, CCS exhibits greater stress with either lower thickness in the denominator or flatter curvature (greater R, in mm) in the numerator. CCS was calculated point by point from curvature and thickness maps to generate a “Corneal Contribution to Stress” Map for each subject.

The Cone Location and Magnitude Index (CLMI)¹⁴ was originally designed to detect KCN based on anterior surface data and was improved with its expansion to include posterior surface and pachymetry data with CLMI.X.¹⁵ The algorithm systematically searches over a defined region of interest to identify a 2-mm spot of maximum tangential curvature in diopters (Cspot-max). The Flat Zone Location Magnitude and Index (FLMI) was originally designed to identify the central flattened zone after myopic refractive surgery and is analogous to the CLMI algorithm; however, instead of a maximum, FLMI systematically searches for the minimum 2-mm-diameter spot of lowest curvature.¹⁴ The CLMI and FLMI algorithms were applied to the generated CCS maps to identify the 2-mm-diameter maximum stress zone (CCSmax) and 2-mm-diameter minimum stress zone (CCSmin), respectively. The difference of the average magnitudes of these maximum and minimum zones represents the stress difference (CCSdiff), which quantifies asymmetry in stress distribution. The CLMI algorithm was also applied to the tangential curvature topography maps of all subjects to identify the 2-mm spot of greatest average curvature. The FLMI algorithm was applied to the pachymetry maps of all subjects to identify the 2-mm spot of minimum average pachymetry (Pach-min). Study variables are summarized in Table 1.

Table 1.

Study Variables

Variable	Definition
R	Radius of curvature, mm
t	Thickness, microns (μ)
CCS	Corneal contribution to stress, R/2t, dimensionless
Cspot-max	Magnitude of 2-mm zone of maximum tangential curvature, diopters
Pach-min	Magnitude of 2-mm zone of minimum pachymetry, microns
CCSmax	Magnitude of 2-mm zone of maximum CCS, dimensionless
CCSmin	Magnitude of 2-mm zone of minimum CCS, dimensionless
CCSdiff	Magnitude of CCSmax – CCSmin, dimensionless

The distance between Cspot-max and Pach-min was calculated. To evaluate the location of the greatest curvature and lowest pachymetry relative to maximum and minimum stress, the distance was also calculated between Cspot-max and CCSmax, between Cspot-max and CCSmin, between Pach-min and CCSmax, and between Pach-min and CCSmin.

Statistical Analysis

t tests were performed between cohorts for Cspot-max, Pach-min, CCSmax, CCSmin, and CCSdiff, as well as the calculated distances. Within each cohort, paired t tests were performed between the locations of Cspot-max and CCSmax and between the locations of Cspot-max and CCSmin to determine if the location of maximum curvature was associated with high or low stress. Similar analyses were performed between Pach-min and CCSmax and between Pach-min and CCSmin to determine if the location of minimum pachymetry was associated with high or low stress. Univariate linear regression was performed between Cspot-max, as an indication of KCN severity, and CCSdiff, to investigate the relationship between the asymmetry in max/min stress and the severity of disease in KCN. Regression analysis was also performed between Cspot-max and the distance from Pach-min to CCSmax. The significance threshold was P < 0.05 for all analyses. Receiver operating characteristic (ROC) curves were calculated to evaluate separation of the KCN and NRL cohorts using CCS parameters.

Results

The NRL cohort (43 ± 14 years) was significantly older (P = 0.0006) than the KCN cohort (36 ± 13 years), with 92 females and 63 males in NRL and with 17 females and 23 males in KCN. Self-reported race was tabulated. Most subjects were Caucasian (171), followed by African American (64) and then by Asian (12). There were smaller numbers of Native American (4), Hawaiian (1), more than one race (8), and “not reported” (1).

Table 2 reports the distribution of severity in the KCN cohort using Belin’s ABCD grading system. In the actual scoring of stage, decimal places are not used for individuals, only the whole number. However, we report one decimal place in the population means. In addition to the ABC scores, Table 2 includes simulated keratometry and central corneal thickness for the KCN cohort.

Table 2.

Keratoconus Severity

Parameter	Mean ± SD
Average simulated keratometry (Kavg) in (D)	47.9 ± 5.4
K1 (D)	46.4 ± 5.4
K2 (D)	49.4 ± 5.8
Central corneal thickness, μ	492 ± 48
Belin grade A	2.2 ± 1.5
Belin grade B	2.8 ± 1.4
Belin grade C	1.7 ± 1.0
Average of A, B, and C	2.2 ± 1.2

D = diopter; grade A = Anterior curvature; grade B = posterior curvature; grade C = thinnest corneal pachymetry; SD = standard deviation.

Table 3 reports mean values of study variables. Unsurprisingly, KCN had significantly lower Pach-min and a significantly greater Cspot-max than NRL. KCN also had a shorter distance between Pach-min and Cspot-max than NRL. In stress parameters, KCN had significantly greater CCSmax, CCSmin, and CCSdiff than NRL. Table 4 shows that all distances were significantly different between cohorts. Keratoconus had greater distances from Cspot-max to CCSmax and from Pach-min to CCSmax than NRL. Keratoconus also had shorter distances from Cspot-max to CCSmin and from Pach-min to CCSmin than NRL. In KCN, Cspot-max was significantly closer to CCSmin than CSSmax, whereas in NRL, Cspot-max was significantly closer to CCSmax than CCSmin. Also, in NRL, Pach-min was significantly closer to CCSmax than CCSmin, with no significant difference in KCN.

Table 3.

t Tests of Study Variables

	KCN	NRL	P
Cspot-max, diopters (D)	53.1 ± 6.5 (41.4–74.3)	44.5 ± 1.57 (39.6–49.0)	< 0.0001
Pach-min, microns (μ)	467 ± 57 (319–634)	548 ± 31 (475–621)	< 0.0001
CCSmax, dimensionless	8.82 ± 1.70 (6.50–15.27)	7.06 ± 0.43 (5.93–8.41)	< 0.0001
CCSmin, dimensionless	6.40 ± 0.54 (4.97–7.42)	6.14 ± 0.43 (5.07–7.42)	0.0007
CCSdiff, dimensionless	2.41 ± 1.76 (0.66–9.31)	0.92 ± 0.28 (0.40–2.66)	< 0.0001
Distance of Cspot-max to Pach-min, mm	0.79 ± 0.32 (0.02–1.38)	1.56 ± 0.76 (0.04–3.28)	< 0.0001

CCSdiff = difference between maximum and minimum corneal contribution to stress; CCSmax = maximum zone of corneal contribution to stress; CCSmin = minimum zone of corneal contribution to stress; Cspot-max = maximum zone of tangential curvature; D = diopter; KCN = keratoconus; NRL = normal control; Pach-min = minimum zone of thickness. Data expressed as mean ± standard deviation (range).

Table 4.

Distances between Maximum Curvature, Minimum Pachymetry and Maximum Stress, Minimum Stress

	KCN	NRL	P
Distance of Cspot-max to CCSmax, mm	2.52 ± 0.72 (0.68–5.09)	2.04 ± 0.85 (0.11–4.72)	< 0.0001
Distance of Cspot-max to CCSmin, mm	1.35 ± 1.43 (0.07–5.10)	2.73 ± 1.53 (0.05–5.79)	< 0.0001
P	< 0.0001	< 0.0001
Distance of Pach-min to CCSmax, mm	2.03 ± 0.97 (0.39–5.04)	0.79 ± 0.92 (0.04–3.77)	< 0.0001
Distance of Pach-min to CCSmin, mm	1.88 ± 1.06 (0.09–4.29)	3.17 ± 0.38 (2.02–4.00)	< 0.0001
P	Not significant	< 0.0001

CCSmax = maximum zone of corneal contribution to stress; CCSmin = minimum zone of corneal contribution to stress; Cspot-max = maximum zone of tangential curvature; KCN = keratoconus; NRL = normal control; Pach-min = minimum zone of thickness. Data expressed as mean ± standard deviation (range).

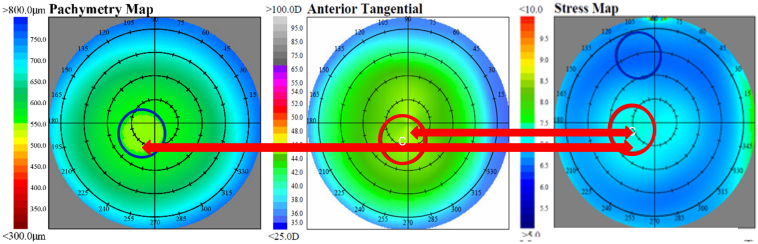
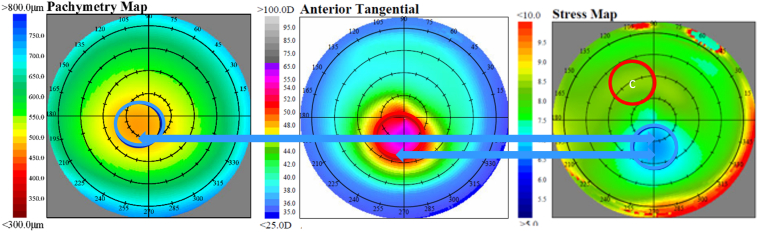
For the purpose of averaging maps to illustrate results, subjects in the KCN cohort were subdivided into a “central” group if the cone center was within the 3-mm-diameter of center on the tangential curvature map or into an “eccentric” group if the cone center was outside of the 3-mm-diameter center. For comparison purposes, subjects in the NRL cohort were subdivided into analogous regions of central or peripheral, based on where the CLMI algorithm located Cspot-max on the tangential curvature map. Figure 1 shows group average maps of pachymetry, tangential curvature, and CCS for the 147 NRL eyes, with the zone of greatest curvature near the map center, as described. This figure illustrates the close association of maximum stress with lowest pachymetry and greatest curvature in NRL. Figure 2 shows group average maps of pachymetry, tangential curvature, and CCS for the 57 eyes with central KCN, and Figure 3 shows group average maps of pachymetry, tangential curvature, and CCS for the 4 eyes with inferior-nasal KCN. These 2 figures illustrate the close association of minimum stress with greatest curvature and lowest pachymetry in KCN. The left eye maps were flipped in all cases to match orientation with the right eye maps to generate an average.

Figure 1.

Average maps of 147 normal control eyes. Blue circles are minimum zones, and red circles are maximum zones. The greatest stress is significantly associated with both thinnest pachymetry and greatest curvature. According to the stress formula, this is consistent with a relationship dominated by thickness and not consistent with curvature. Note the red arrows showing the significantly similar locations of maximum stress (right) to maximum curvature (center) and thinnest pachymetry (left). Note that a white C indicates center of circle.

Figure 2.

Average maps of 57 keratoconus eyes with central cones. Blue circles are minimum zones, and red circles are maximum zones. The lowest stress zone is significantly associated with greatest curvature, which is near the thinnest pachymetry. According to the stress formula, this is consistent with a relationship dominated by curvature and not consistent with thickness. Note the blue arrows showing the significantly similar locations of minimum stress (right) to maximum curvature (center) and the closeness of the minimum stress to thinnest pachymetry (left). Note that a white C indicates center of circle.

Figure 3.

Average maps of 4 keratoconus eyes with inferior-nasal cones. Blue circles are minimum zones, and red circles are maximum zones. The lowest stress zone is significantly associated with greatest curvature, which is near the thinnest pachymetry. According to the stress formula, this is consistent with a relationship dominated by curvature and not thickness. Note the blue arrows showing the significantly similar locations of minimum stress (right) to maximum curvature (center) and the closeness of the minimum stress to thinnest pachymetry (left). Note that a white C indicates center of circle.

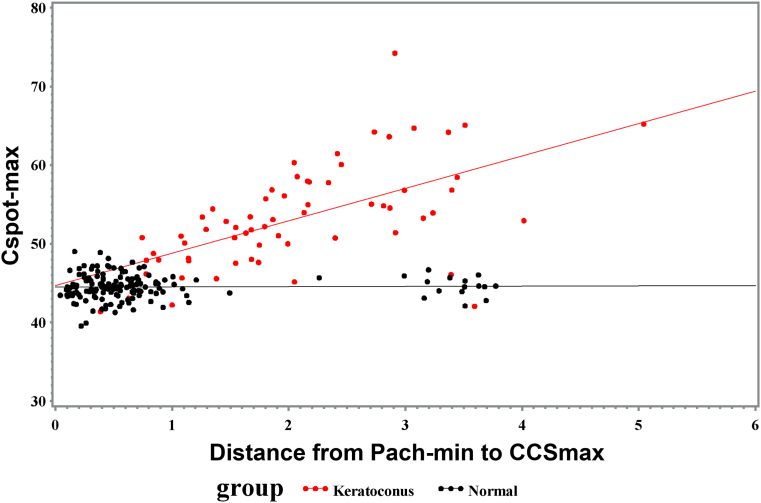
Table 5 reports regression statistics associated with the plots in Figures 4 and 5 for Cspot-max vs. CCSdiff and for Cspot-max vs. the distance from Pach-min to CCSmax, respectively. Both relationships were significant in the KCN cohort. Although Cspot-max vs. CCSdiff was significant in the NRL cohort, the relationship was quite weak (R² = 0.0417). The relationship between Cspot-max and the distance from Pach-min to CCSmax was not significant in the NRL cohort.

Table 5.

Univariate Regression Statistics

	KCN	NRL
Cspot-max (D) vs. CCSdiff (dimensionless)	P < 0.0001; R2 = 0.5882	P = 0.0080; R2 = 0.0451
Cspot-max (D) vs. distance of Pach-min to CCSmax	P < 0.0001; R2 = 0.3737	P = 0.8011; R2 = 0.0004

CCSdiff = difference between maximum and minimum corneal contribution to stress; CCSmax = maximum zone of corneal contribution to stress; Cspot-max = maximum zone of tangential curvature; D = diopter; KCN = keratoconus; NRL = normal control; Pach-min = minimum zone of thickness.

Figure 4.

Linear regression of maximum curvature (Cspot-max) vs. difference between maximum and minimum corneal contribution to stress (CCSdiff) in keratoconus (P < 0.0001; R² = 0.5882) and normal control (P = 0.0080; R² = 0.0451) cohorts.

Figure 5.

Linear regression of maximum curvature (Cspot-max) vs. distance of minimum zone of thickness (Pach-min) to maximum zone of corneal contribution to stress (CCSmax) in keratoconus (P < 0.0001; R² = 0.3737) and normal control (P = 0.8011; R² = 0.0004) cohorts.

The ROC curve calculated for the separation of the KCN cohort from the NRL cohort based only on CCSdiff resulted in an area under the ROC curve of 0.9348. In a stepwise logistic regression with all the CCS parameters, the 3 parameters of CCSmax, the distance of Pach-min to CCSmin, and the distance of Pach-min to CCSmax produced an area under the ROC curve of 0.9511.

Discussion

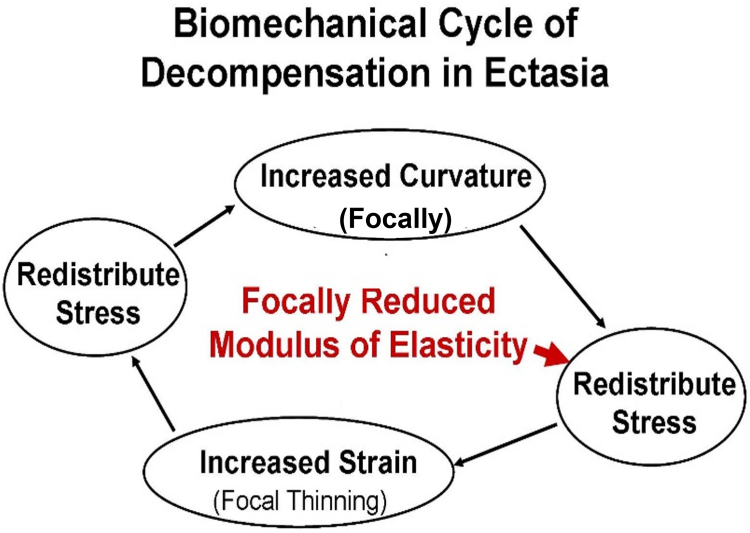
Biomechanical remodeling in KCN over time is demonstrated in the current study by the evolution from maximum stress with thinnest pachymetry (and greatest curvature) in the normal cornea to minimum stress with greatest curvature (and thinnest pachymetry) in KCN. According to the hoop stress formula, higher stress is generated by lower thickness and greater curvature, allowing the conclusion to be drawn regarding the primary driver of stress distribution in healthy corneas as well as in KCN. Namely, corneal thickness dominates the stress distribution in normal corneas, and curvature dominates the stress distribution in KCN. This pattern is consistent with a biomechanical cycle of decompensation in KCN that has been proposed,¹⁶ illustrated in Figure 6. The initiating event for this cycle is focal weakening, which redistributes the stress, leading to greater deformation (focal thinning) in the area of weakening under a consistent IOP load. This further redistributes the stress as the thickness changes, which leads to a compensatory focal increase in curvature in response to oppose the increased stress from thinning, which again redistributes the stress, and the cycle continues. Direct evidence of the asymmetry of corneal properties in KCN has been reported using Brillouin Microscopy, both ex vivo¹⁷ and in vivo.¹⁸ The focal weakness is also consistent with the focal area of lamellar disruption described using x-ray scattering.¹⁹ The current study provides additional evidence for the decompensatory cycle, not only due to the change in the driver of stress distribution with time, but also in the strong relationship between the difference in maximum and minimum stress versus the greatest curvature zone in KCN. In other words, advanced disease is associated with greater asymmetry in stress distribution within the cornea. In addition, greater distance from minimum pachymetry to maximum stress is strongly related to the zone of maximum curvature in KCN, with no relationship in normal corneas. This can be interpreted that as the KCN advances and becomes more severe, the thinnest region of the cornea moves farther and farther away from the area of maximum stress.

Figure 6.

Cycle illustrating the progression of biomechanical decompensation in corneal ectasia.

Detection of early disease in KCN is important for multiple reasons, including providing timely optimal refractive error correction with gas permeable contact lenses, allowing the opportunity for early intervention using CXL,²⁰ and identifying “at risk” corneas, which may not be candidates for refractive surgery or may require surface treatment in refractive surgery rather than an approach that uses a flap or cap with larger percent tissue altered.²¹ Keratoconus detection algorithms are many, with combined tomographic and biomechanical parameters having the highest ROCs.²² However, curvature and thickness are treated as independent parameters in all of the reported approaches. For the first time, curvature and thickness are considered simultaneously in CCS. It may be that combining them in the approximation for CCS will improve detection and monitoring of KCN in the clinic. In addition, all CCS parameters of maximum stress, minimum stress, and difference between maximum and minimum stress are significantly greater in KCN than NRL. The overall stress increases over time in KCN as the cornea thins, so all values are higher. Although the intent of the current study was not KCN screening, the area under the ROC curves presented showed excellent performance for both the single parameter of CCSdiff as well as the 3 CCS parameters combined. However, these values require validation in an independent data set.

The strong relationship between the CCSdiff and maximum curvature, an indication of disease severity, means that CCS may be able to predict progression. The significant association of maximum curvature zone and progression was recently reported at the Association for Research in Vision and Ophthalmology on a 5-year longitudinal data set.²³ One of the critical assessment parameters prior to CXL is to document progression, to prevent the procedure from being performed on a stable cornea. Waiting until this progression is visualized may allow the corneas to thin beyond the minimum thickness threshold allowable for CXL, thus preventing the treatment from being a feasible option for the patient. Moreover, many insurance companies require documentation of progression to cover the cost of treatment. With CCSdiff, the prediction of progression might serve as an adequate indication to proceed with the CXL procedure. This prediction would be especially important in children, who tend to have rapid progression between follow-up visits, so much so that they quickly progress beyond accepted thresholds for CXL. Thus, the necessity to wait for documentation of progression becomes detrimental to their care.

Limitations of this study include using the simple formula of hoop stress for the biomechanically complicated keratoconic cornea to predict stress distribution. However, it has recently been reported using patient-specific finite element models that there is a stress minimum (of the maximum principal component of the stress) in the area of pathology in KCN, consistent with the results of the current study.⁵ This evidence serves as the first step to validate the overall conclusion of minimum stress being associated with maximum curvature in KCN. In addition, even a simple approximation that is devoid of the cumbersome detailed analysis from finite element modeling can be clinically useful in differentiating normal changes in corneal curvature over time from disease progression.

In conclusion, the stress distribution in normal corneas is dominated by thickness, with maximum stress associated with thinnest pachymetry. In KCN, the association breaks down as the disease progresses over time, and the cornea responds biomechanically until the maximum stress is no longer associated with thinnest pachymetry. Rather, the stress distribution in KCN is dominated by curvature with maximum curvature associated with minimum stress. In addition, the difference between maximum and minimum stress is significantly associated with the zone of maximum curvature in KCN, which is consistent with the previously proposed biomechanical cycle of decompensation in KCN and ectasia in general. Further evidence supporting this cyclic decompensation lies in the significant relationship between increasing maximum curvature in KCN and increasing distance between minimum pachymetry and maximum stress. This evolution of the stress distribution pattern, without the confounding influence of IOP, allows the tomographic maps obtained in a single clinic visit to be interpreted as representing long-term biomechanical adaptation. This is applicable to any corneal tomographic device that includes tangential curvature and pachymetry. Future studies are warranted to investigate the use of CCSdiff as a predictor of biomechanical progression in KCN, as well as its detection.

Manuscript no. XOPS-D-23-00052R2.