Can language models be used for real-world urban-delivery route optimization?

Abstract

Language models have contributed to breakthroughs in interdisciplinary research, such as protein design and molecular dynamics understanding. In this study, we reveal that beyond language, representations of other entities, such as human behaviors, that are mappable to learnable sequences can be learned by language models. One compelling example is the real-world delivery route optimization problem. We here propose a novel approach based on the language model to optimize delivery routes on the basis of drivers’ historical experiences. Although a broad range of optimization-based approaches have been designed to optimize delivery routes, they do not capture the implicit knowledge of complex delivery operating environments. The model we propose integrates this knowledge in the route optimization process by learning from driving behaviors in experienced drivers. A real-world delivery route that preserves drivers’ implicit behavioral patterns is first analogized to a sentence in natural language. Through unsupervised learning, we then learn the vector representations of words and infer the drivers’ delivery chains on the basis of the tailored chain-reaction-based algorithm. We also provide insights into the fusion of language models and operations research methods. In our approach, language models are applied to learn drivers’ delivery behaviors and infer new deliveries at the delivery zone level, while the classic traveling salesman problem (TSP) model is embedded into the hybrid framework for intra-zone optimization. Numerical experiments performed on real-world data from Amazon’s delivery service demonstrate that the proposed approach outperforms pure optimization, supporting the effectiveness, efficiency, and extensibility of our model. As a versatile approach, the proposed framework can easily be extended to various disciplines in which the data follow certain grammar rules. We anticipate that our work will serve as a stepping stone toward the understanding and application of language models in tackling interdisciplinary research problems.

Graphical abstract

Public summary

• •Revealing that language models can learn human behavioral sequences.
• •Integrating the implicit knowledge of drivers in the route optimization process.
• •A novel algorithm to optimize delivery routes emulating real-world driving behaviors.
• •Broadening the scope of language models to diverse domains with certain grammar rules.

Introduction

Language models, originally designed to solve problems in computational linguistics, such as speech recognition,^1,2 machine translation,^3,4 and document generation,^5,6 treat human languages as sequences of words governed by specific grammar rules. By following this approach, it was revealed that entities other than languages that are mappable to learnable sequences can also be solved by language models.⁷ For example, protein sequences share many similarities with human language; amino acids can be considered letters, and their multiple combinatorial arrangements can form structures with functions, i.e., words and sentences.^8,9 Similarly, human behaviors are also analogous to human languages. For example, a traveler’s trip chain can be represented as a sentence consisting of departure time, origin and destination coordinates, and travel mode.^10,11 Another typical example is real-world delivery route optimization problem studied in this paper (see the research background section in the supplemental information for details), in which a delivery route is abstracted as a sentence, with its nodes represented by words. The sentence must comply with the grammar rules set up by various real-world constraints, such as an illegal U-turn, road closures for construction, and unpleasant traffic conditions.

In real-world delivery route optimization, the challenges go beyond identifying the shortest path.^{12,13,14,15,16} They encompass intricate real-world constraints to take into account genuine delivery conditions.¹⁷ Easa’s pioneering work introduces the shortest path algorithm incorporating movement prohibitions, hence offering a simpler network representation.¹⁸ However, the dynamic interplay between real-world factors, including traffic, parking, and customer preferences, is often neglected theoretical models. Although manual removal of the complex road segments may be feasible for small networks, it becomes unmanageable on a larger scale. Such divergence often results in drivers equipped with local knowledge deviating from optimized paths. By learning and understanding drivers’ delivery behaviors, the planned routes will be refined to better accommodate complex real-world urban environment.

Motivated by recent interdisciplinary research about language models and grounded in the theoretical foundations of geometric deep learning,¹⁹ in this paper we proposes a novel language-model-based approach to solve real-world urban delivery route optimization problem. The primary function of the language model is to learn and understand drivers’ delivery behaviors, allowing high-fidelity approximations of the real-world delivery routes optimized by drivers. This approach contributes to the development of more efficient and safer routes, as well as improved service quality. A real-world delivery route is analogously defined as a sentence in language, which preserves the implicit knowledge of drivers’ behavioral patterns without involving intensive computations. By learning the behaviors of experienced drivers, the proposed model facilitates the transfer of this knowledge to delivery route planning, which cannot be achieved by using only optimization-based approaches. Instead of performing sequence-to-sequence or step-by-step prediction using supervised learning, we first use unsupervised learning to learn the vector representations of words, and then design a tailored chain-reaction-based algorithm to infer the complete delivery sequence.

This study also provides insights into the fusion of language models and operations research methods. The devised hybrid architecture consists of two parts: the first part uses language model to learn drivers’ delivery behaviors and infer the zone sequence of new deliveries, while the second part uses the classic traveling salesman problem (TSP) model to optimize routing within each zone in the sequence. To validate the effectiveness of the proposed model, we conduct extensive numerical experiments using actual delivery routes. The experimental results show that the proposed method outperforms pure optimization approach. It is worth noting that our approach is not limited to the urban delivery route optimization problem. Adaptations can be seamlessly implemented in interdisciplinary domains, including but not limited to understanding the dynamics of complex stochastic molecular systems^{20,21,22,23,24,25} and protein design,^{9,26,27,28,29} with different features, such as word encoding schemes and sentence definitions.

Results

Real-world delivery routes can be mapped into sentences of language

The fundamental idea behind the proposed framework lies in the analogy that a real-world delivery route can be represented as a sentence in language. This idea stems from the principles of geometric deep learning, particularly the paradigm of “learning on string representations.”¹⁹ In this context, we equate the ID of an element in a route—which can be a node, a delivery stop, or a delivery service zone—to a word in the sentence. The rationale behind this analogy is that the generated sequences, or “sentences,” have two key characteristics: syntax and semantic. Drawing an intellectual connection with molecular strings,³⁰ the syntax aspect dictates that not all combinations of characters result in valid molecules, analogous to how not all sequences of delivery stops form feasible routes, because of real-world limitations. Semantically, the corresponding chemical compounds possess different physicochemical and biological properties depending on how the elements of the string are combined. Likewise, different delivery routes have different efficiencies in route optimization. Hence, the arrangement of delivery stops in our “sentences” carries semantic information about the route’s efficiency. The flowchart of the proposed learning-based model is illustrated in Figure 1.

Figure 1.

Flowchart of the learning-based model

The proposed model consists of three main steps: (1) representing real-world delivery routes as “delivery behavior sentences,” (2) learning delivery behaviors using a machine learning model, and (3) inferring delivery sequences from word vectors.

In the theory of language models, it is widely acknowledged that word sequences with higher occurrence probabilities are more consistent with the grammar criteria.^31,32 Thus, the probability of observing a word sequence can function as an indicator of its grammatical correctness. For instance, assume that we obtain the statistics of a large corpus and find:

$$P\left(\text{join},\text{us},\text{in},\text{building},\mathrm{a},\text{better},\text{world}\right)>P\left(\text{world},\text{better},\mathrm{a},\text{building},\text{in},\text{us},\text{join}\right)\text{.}$$ (Equation 1)

It can be inferred that the sentence “Join us in building a better world” is more grammatically correct. Similarly, the probability of element sequences in the route is used to characterize the driver’s delivery behavior pattern, i.e., the sequences with higher occurrence probabilities are more consistent with the drivers’ behaviors.

In this paper, we focus on Amazon’s delivery service for a better exposition. Detailed descriptions of the dataset are given in the data description section in the supplemental information, as well as in Tables S1–S3. An Amazon delivery route starts from a delivery station (i.e., depot) and then serves several delivery stops, each with a varying number of packages. To facilitate deliveries, Amazon also delineates zone IDs on the basis of the geo-planned area where the stop is located, where each zone contains a varying number of stops. Taking the delivery zone sequence as an example, it is assumed that the statistics of the real-world delivery data show:

$$P\left(D-3.2A,D-3.1A,\dots ,D-2.3C\right)>P\left(D-2.2A,D-3.1A,\dots ,D-2.1B\right)\text{,}$$ (Equation 2)

where “D-3.2A, D-3.1A,…, D-2.1B” are the IDs of the delivery zones in the real-world route. We can infer that zone sequence “D-3.2A, D-3.1A,…, D-2.3C” is closer to the real-world delivery zone sequence.

It should be noted that the words in our approach are not restricted to delivery zone IDs; they can also be fine-grained delivery stop IDs. If we analogize the delivery stop ID to an amino acid, then the use of the delivery zone ID as the word is similar to the three-dimensional (3D) secondary structural element formed by amino acids. We define the main notations used in the paper in Table S4. A real-world delivery route consists of $M$ zones and one delivery station. The delivery station is the starting point of a route, and its index is 0. The zones are labeled with the number $1,\dots ,M$. The real-world delivery behavior sentence is extracted from the delivery route, defined as follows:

$$s=\left(z_0,z_1,\dots ,z_M\right)\text{,}$$ (Equation 3)

where each element of the sentence is a “word” that represents a zone or the delivery station in a route. Each sentence represents a zone sequence, with the order of the words in the sentence being the same as that of the driver’s delivery. The probability that this sentence exists in $\mathcal{H}$ (i.e., a set of zone ID sequence in the training set) is:

$$P\left(z_0,z_1,\dots ,z_M\right)=\prod _{m=0}^{M}P\left(z_m\mid z_0,z_1,\dots ,z_{m-1}\right)\text{,}$$ (Equation 4)

where

$$P\left(z_m\mid z_0,z_1,\dots ,z_{m-1}\right)=\frac{\text{Count}\left(z_0,z_1,\dots ,z_m\right)}{\sum _{z\in D}\text{Count}\left(z_0,z_1,\dots ,z_{m-1},z\right)}\text{,}$$ (Equation 5)

and $z_m$ is the $m$th word in the sentence, and $\text{Count}(·)$ operation indicates the number of occurrences of a subsequence in the training set.

In the actual calculation, the Markov assumption³³ is introduced to further reduce the computational effort, i.e., only the previous $k$ zones are considered when calculating the conditional probabilities in Equation 6.

$$P\left(z_m\mid z_0,z_1,\dots ,z_{m-1}\right)\approx P\left(z_m\mid z_{m-k},\dots ,z_{m-1}\right)\text{.}$$ (Equation 6)

Training the network is equivalent to learning the grammar rules of real-world logistics delivery

We use the Word2Vec approach in natural language processing (NLP)^34,35 to learn vector representations of words in delivery behavior sentences. We construct the delivery behavior sentences on the basis of the actual routes in the dataset, thereby providing an accurate reflection of the real-world delivery behaviors of drivers. To learn the driver’s delivery behavior, our objective is to learn an optimal mapping $\mathcal{F}(·)$ by maximizing the co-occurrence probability of the zones in each delivery behavior sentence.

Word2Vec has two typical modeling ideas, namely continuous bag-of-words (CBOW) and skip-gram.^34,35 Taking the skip-gram structure as an example, the idea is to give a central word and then to predict its context within a certain range, as outlined by the following objective function:

$$\mathcal{L}\left(\theta \right)=\prod _{m=0}^M\prod _{-k\le i\le k,i\ne 0}P\left(z_{m+i}|z_m;\theta \right)\text{,}$$ (Equation 7)

where $\theta$ denotes the parameters to be optimized in the model (e.g., the weight matrix in a neural network), and $z_m$ is the current word. Its negative log likelihood form is generally used as a loss function:

$$\mathcal{L}{\left(\theta \right)}^{\prime }=-\frac{1}{M}\sum _{m=0}^M\sum _{-k\le i\le k,i\ne 0}\log P\left(z_{m+i}\mid z_m;\theta \right)\text{,}$$ (Equation 8)

where

$$P\left(z_{m+i}\mid z_m\right)=\frac{\exp \left(v_{z_{m+i}}^T{v}_{z_m}\right)}{\sum _{z\in D}\exp \left(v_z^T{v}_{z_m}\right)}\text{,}$$ (Equation 9)

and $v_z$ is the word vector corresponding to word $z$, and $D$ is the set of all words.

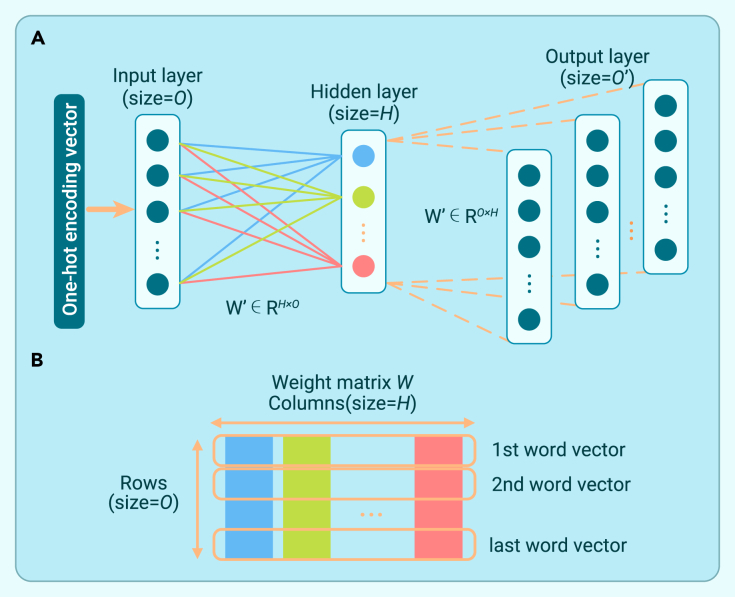
The learning process of optimal mapping $\mathcal{F}(·)$ can be explained by a neural network with a hidden layer. Figure 2A illustrates the neural network, and Table S5 introduces parameters needed for the neural network structure.

Figure 2.

Visualization of the neural network and the associated weight matrix

(A) Structure of the neural network.

(B) Structure of the weight matrix.

The steps of data processing, training, and learning outcomes of the model are as follows.

Step 1. (Encoding) Transform all zone IDs and station IDs in the training set into one-hot encoding vectors.

Step 2. (Constructing samples) Taking skip-gram mode as an example, we need to construct training samples in the form of a “feature-label” pair on the basis of the real-world route sequences. The input feature is the one-hot encoding vector of $z_m$, and the label is formed by concatenating the one-hot encoded vectors of its context.

$$\text{feature}=\text{one}\_\text{hot}\left(z_m\right)\text{.}$$ (Equation 10)

$$\text{label}=\text{concat}\left(\text{one}\_\text{hot}\left(z_{m-k}\right),\dots ,\text{one}\_\text{hot}\left(z_{m-1}\right),\text{one}\_\text{hot}\left(z_{m+1}\right),\dots ,\text{one}\_\text{hot}\left(z_{m+k}\right)\right)\text{.}$$ (Equation 11)

Step 3. (Training) On the basis of the defined loss function, the network weights $W\in {\mathbb{R}}^{H\times O}$ and $W^{\prime }\in {\mathbb{R}}^{O\times H}$ are updated using an optimizer based on the constructed training samples.

Step 4. (Learning outcomes) After training, the learned word vector for the $i$th zone is obtained by multiplying its one-hot encoded vector with the weight matrix $W\in {\mathbb{R}}^{H\times O}$. The matrix structure is shown in Figure 2B.

The complete real-world delivery route can be inferred from the word vector using a tailored chain-reaction-based algorithm

The theoretical foundation of our tailored chain-reaction-based algorithm stem from the notion that functional similarities between entities can be deduced on the basis of their mapping and proximity in the word embedding space.³⁰

By projecting delivery routes to the word embedding space, we aim to infer complete delivery routes on the basis of their proximity and relational mapping in this space. For instance, let us consider an actual route “DES4, D-3.2A,…, D-2.3C” from historical data, where “DSE4” denotes the delivery station, i.e., the starting point of the route. First, we extract the word vectors of station “DSE4.” Given that “DSE4, D-3.2A” co-occurs in historical data, it is inferred that the word vectors of the two elements are similar. Therefore, “D-3.2A” can be identified by finding the zone corresponding to the next most similar vector. From the perspective of the discrete choice model, this operation essentially equates to selecting the zone with the maximized utility.³⁶ In NLP, vector similarity is usually measured using cosine similarity.³⁷ Given the word vectors $v_1$ and $v_2$ for the two zones, respectively, the cosine similarity is defined as follows:

$$\text{similarity}\left(v_1,v_2\right)=\frac{v_1·v_2}{\Vert v_1\Vert \Vert v_2\Vert }\text{.}$$ (Equation 12)

For an unsorted zone ID sequence $s^{+}=\left\{z_0^{+},z_1^{+},\dots ,z_M^{+}\right\}$, where $z_0^{+}$ is the delivery station ID, $z_1^{+},\dots ,z_M^{+}$ are the zone IDs to be sorted, we apply Algorithm 1 to obtain a sorted zone ID sequence from the word vector. Inspired by the basic steps of chain reactions, namely initiation, propagation, and termination,³⁸ the algorithm operates in a similar phased manner. The initiation phase starts with the delivery station, treating it as the initial starting point. The propagation phase then invokes an iterative process that identifies the subsequent delivery zones to be served. The identification relies on finding the word vector most similar to the previous zone. This exploitation of word vector similarity, a by-product of the Word2Vec model trained on historical delivery routes, positions zones frequently and consecutively appearing in historical data in close proximity in the vector space. Essentially, each step in the propagation phase retraces the paths embedded in the word vector space. The algorithm continues its propagation phase until all delivery zones are covered, which marks the termination of the algorithm. The final result is a complete delivery sequence that reflects the historical patterns embedded in the word vectors.

Algorithm 1. Tailored chain-reaction-based algorithm.

Input: Word vector for the delivery station $v_0$, word vector for zone $v_m\in V\setminus \left\{v_0\right\}$, delivery station ID $z_0^{+}$, and zone ID $z_m^{+}\in D^{+}\setminus \left\{z_0^{+}\right\}$.

Output: Zone ID sequence.

1: Initialization: $R\leftarrow \left\{z_0^{+}\right\}$, $S\leftarrow \left\{v_0\right\}$, $r\leftarrow v_0$

2: while $D^{+}-R\ne \varnothing$ do

3: Find $\underset{v_m\in V\setminus S}{\max }similarity\left(r,v_m\right)$

4: Find zone ID $z_m^{+}$ that corresponds to $v_m$, then output $z_m^{+}$

5: $R\leftarrow R\cup \left\{z_m^{+}\right\}$

6: $S\leftarrow S\cup \left\{v_m\right\}$

7: $r\leftarrow v_m$

8: end while

The details of the tailored chain-reaction-based algorithm are elaborated in Algorithm 1.

Fusing language model and operations research method

In Amazon’s package delivery business, a delivery service area is normally divided into zones to facilitate delivery. Figure 3A shows a real-world Amazon delivery route, where the driver completes deliveries in zone “D-3.1A” before proceeding to “D-2.1A,” indicating a tendency to finish one zone before moving to another. Drivers make these decisions on the basis of their knowledge of roadway conditions, infrastructure design, and customer preferences. With extensive experience in delivery in practice, drivers may “reoptimize” the route sequences themselves instead of following the optimal routes provided by the routing system, as the latter may lack consideration of real-world road conditions and drivers’ preferences. Figure 3B displays an optimized delivery route derived from solving the standard TSP that aims at minimizing the travel time. Nevertheless, the optimized route may conflict with drivers’ experience in delivery. In Figure S2, combined with satellite imagery, we present a real-world case showing that delivery routes optimized by the standard TSP model might not be convenient for drivers given actual road conditions. Such kind of knowledge, unfortunately, can hardly be quantified or incorporated by the prevailing route planning system in the industry, resulting in deviated route sequences in practice from the optimal routes.

Figure 3.

Comparison between real-world delivery route and theoretically optimized route

(A) A real-world delivery route of Amazon’s delivery service, where each point represents a delivery stop in the route. Stops within the same delivery service zone share the same color.

(B) A delivery route optimized by the standard TSP model.

(C) Two delivery routes in the same city sharing a common zone subsequence “D-2.1B, D-2.1C, D-2.3C.”

(D) A real-world intra-zone delivery route.

(E) An optimal intra-zone delivery route.

(F) Overview of the real-world delivery route optimization system.

Through the analysis of the actual delivery route data, it is found that a large number of identical subsequences existed in the routing data at the delivery zone level (see Figure 3C), indicating that drivers have an inherent behavioral pattern. However, within each zone, drivers tend to follow the shortest path, as illustrated in Figure 3D. This behavior is theoretically explained by the principle of local optimality.^39,40 The drivers would strive for the shortest path within each zone, essentially optimizing the route locally within each zone.

Motivated by the analysis above, we design a two-step hybrid framework that fuses the language model and operations research method to solve the real-world delivery route optimization problem. In the first step, the language model is used to extract the drivers’ tacit knowledge about optimal delivery patterns, which may not be explicitly incorporated in the traditional delivery routing optimization algorithms. It provides a zone sequence that aligns with drivers’ intuitive preferences. Upon procuring the sequence of zones, the second step treats each zone’s delivery as the classic TSP problem with specific start and end stops (see the method section in the supplemental information). This approach offers a theoretically efficient route that also aligns with the on-ground experiences and preferences of drivers. The general idea of the complete delivery route optimization system is illustrated in Figure 3F.

Comparison of the proposed and traditional optimization model

The real-world data used in our experiments are extracted from Amazon’s delivery service, encompassing critical information such as route information, travel time data, and actual delivery sequence information (see Tables S1–S3).⁴¹ The data contain 6,112 routes from 17 distinct delivery stations scattered across various regions in the United States. We filtered outlier samples and divided the dataset on the basis of the delivery stations, in order to create subsets that align with unique geographical and operational characteristics of each station. To overcome possible limitations imposed by sample size and ensure robust model evaluation, we adopt a leave-one-out cross-validation strategy in our experiments. Detailed statistical information on the dataset is shown in Figures 4A and 4B.

Figure 4.

Performance comparison of different models

(A) Statistics of samples in the data.

(B) Missing rate of zone ID sequences.

(C) Scatterplot showcasing sample errors across different methods.

(D) Error distribution of our method and the optimization approach.

(E) Efficiency metrics of our method and the optimization approach.

(F) Error analysis for 15 delivery stations with different model parameters. Here, $k$ represents the range of contextual information, often termed as window size in NLP.

We use a hybrid evaluation metric to determine the error between the sequences of the model output and the drivers’ high-quality delivery sequences (considered to be the true values). The details of this metric and the sample creation are elaborated in the evaluation metric and sample construction process sections of the supplemental information. Figure 4C illustrates the scatterplots of individual sample errors for both our method and the conventional optimization approach. Figure 4D further shows the error distributions for both methods. Table S6 provides a comparative analysis of the error statistics for the two methods. The proposed approach of generalized sequence modeling shows a clear advantage over the standard TSP model from operations research in terms of both mean error and variance, indicating both the robustness and generalizability of our method. In contrast, the operations research approach, tailored specifically for a single task and dataset, lacks the adaptability needed for broader applications such as protein structure prediction.

Our method decomposes a large-scale route optimization problem into several small-scale route optimization problems. Figure 4E shows a comparison between the computational time of the proposed model and the traditional optimization approach. Although the total number of stops in the route is the same in both solutions, the computational time of our method is much shorter than that of the optimization approach.

The proposed model has several adjustable parameters, and the impact of these parameters on the error is illustrated in Figure 4F and Table S7. Window size has a significant impact on the results and the weighted average error when $k=8$ is much lower than that when $k=1$. From the perspective of feature engineering, $k=8$ implies that the current word, along with eight preceding and eight succeeding words, constitutes a training sample, which contains more information than $k=1$ and leads to better results. However, it should be noted that the length of the zone ID sequence in our study is approximately 20, and there is a bottleneck in improving the model performance by adjusting the window size. This bottleneck manifests itself in the observation that the weighted average error when $k=12$ is larger than that when $k=8$. Despite the benefit of richer information with a larger window, it also introduces more missing values in the training data.

The observed disparity in error between the skip-gram and CBOW models in Figure 4F can be attributed to the distinctions in their underlying architectures. The CBOW model predicts a target word from its context, while skip-gram does the opposite, predicting context words from a target word. This fundamental difference means that skip-gram often ends up with a more detailed representation for less frequent words, as it treats each context-target pair as a new observation. Because of the aforementioned mechanism, skip-gram virtually has more training data, as it learns from multiple context-target pairs for a single center word. In contrast, CBOW aggregates all context words for predicting a single center word, which can sometimes lead to a loss of detailed information. Skip-gram tends to perform better on infrequent words because its emphasis is on predicting contexts for specific target words. On the other hand, CBOW might neglect such words because of its averaging mechanism over contexts.

Performance analysis of the proposed method

In the experiments, an individual model was trained for each delivery station. The errors of corresponding subsets are further analyzed and showcased in Figure 5A. Here, we find that the error is related not only to the quantity of training data but also to the quality of the samples, which we refer to as the matching rate of the samples. See the sample construction process section in the supplemental information for detailed formulas used to calculate this matching rate. The relationship between the number of matched samples (75% match) and the average error is shown in Figures 5B and 5C. It can be found that the average error of the machine learning model decreases as the number of matched samples increases. The potential and practical values of machine learning methods are also revealed relation to the efforts required in algorithm design. Compared with ad hoc approaches, machine learning methods can automatically learn the drivers’ behaviors without extensive expert experience in problem analysis and solution algorithm design for optimization problems.

Figure 5.

Model performance analysis

(A) Prediction error across different delivery stations.

(B) Relationship between the number of matched samples and average error.

(C) Distribution of individual error values.

(D) Relationship between the length of the zone sequence and the average error.

A common challenge in the sequence prediction task resides in the potential rapid escalation of error as the length of the sequence targeted for prediction extends because of weak correlations between inputs and outputs in longer sequences. Figure 5D shows the relationship between the length of the zone sequence and the average error in our model. It is found that the average error fluctuates around 0.04 as the length of the zone sequence increases without an observable tendency to increase.

Conclusion

Our research introduces a pioneering attempt to apply language models, traditionally developed for NLP, to a broader range of tasks. In particular, any tasks involving understanding systems organized by certain grammar rules could potentially benefit from this research. It could be pertinent to fields in which complex systems are typically involved, such as biology, chemistry, and physics. Specifically, we examined the real-world delivery route optimization problem, in which drivers may need to “reoptimize” planned route sequences themselves on the basis of actual scenarios such as road conditions, infrastructure design, and driving preferences rather than strictly following the optimal routes derived from the routing system. In this direction, we have developed a hybrid architecture integrating a language model with an embedded TSP model, seeking to tackle real-world delivery route optimization problems that are challenging to address with merely operations research methods. Numerical experiments were performed on the real-world data from Amazon’s delivery service, and a comparison was made between the proposed method and a pure optimization method. The results shed light on the feasibility, effectiveness, efficiency, and potential adaptability of the proposed method.

The application of the proposed approach can extend far beyond the scope of delivery route optimization. Potential applications span a variety of fields, such as intelligent transportation, smart cities, and autonomous driving.^{42,43,44,45,46,47} As our research progresses, we are optimistic about the broader applicability of this model in tackling complex sequence prediction problems across diverse disciplines. This study serves as a stepping stone toward harnessing the power of language models in practical real-world scenarios, and we look forward to the remarkable advancements that lie ahead.

Materials and methods

See the supplemental information for details.

Published Online: September 29, 2023

Lead contact website

http://www.svm.tsinghua.edu.cn/essay/80/1920.html