Skip to main content
NCBI home page
ACS Nanoscience Au logoLink to ACS Nanoscience Au
. 2023 Jun 14;3(5):375–380. doi: 10.1021/acsnanoscienceau.3c00013

Super-resolution Reflection Microscopy via Absorbance Modulation

Parul Jain †, Claudia Geisler †, Dennis Leitz ‡, Viktor Udachin , Sven Nagorny §, Thea Weingartz §, Jörg Adams ∥, Andreas Schmidt §, Christian Rembe ‡, Alexander Egner †,*
PMCID: PMC10588435  PMID: 37868228

Abstract

graphic file with name ng3c00013_0006.jpg

In recent years, fluorescence microscopy has been revolutionized. Reversible switching of fluorophores has enabled circumventing the limits imposed by diffraction. Thus, resolution down to the molecular scale became possible. However, to the best of our knowledge, the application of the principles underlying super-resolution fluorescence microscopy to reflection microscopy has not been experimentally demonstrated. Here, we present the first evidence that this is indeed possible. A layer of photochromic molecules referred to as the absorbance modulation layer (AML) is applied to a sample under investigation. The AML-coated sample is then sequentially illuminated with a one-dimensional (1D) focal intensity distribution (similar to the transverse laser mode TEM01) at wavelength λ1 = 325 nm to create a subwavelength aperture within the AML, followed by illumination with a Gaussian focal spot at λ2 = 633 nm for high-resolution imaging. Using this method, called absorbance modulation imaging (AMI) in reflection, we demonstrate a 2.4-fold resolution enhancement over the diffraction limit for a numerical aperture (NA) of 0.65 and wavelength (λ) of 633 nm.

Keywords: Nanoscopy, super-resolution, reflection microscopy, absorbance modulation imaging (AMI), absorbance modulation layer (AML)

Introduction and Background

Light microscopy is one of the most commonly used techniques to study tiny structures in the range of around a few hundred nanometers. For examining nontransparent objects such as metals, ceramics, many polymers, semiconductors, or a wide variety of composite materials, this generally involves the detection of the light reflected from the sample surface. Besides intensity, changes in phase or polarization of the back-reflected light can hereby also be used to generate contrast. However, because of light microscopy’s limited resolution due to diffraction, more complex microscopy methods, such as scanning electron microscopy (SEM) or near-field microscopy, are used for structure analysis in the sub-250 nm range.1−5

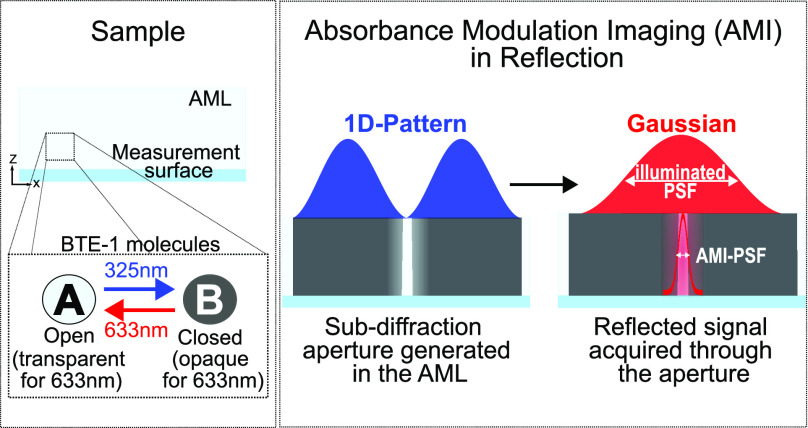
In fluorescence-based light microscopy, stimulated emission depletion (STED) microscopy has overcome the diffraction limit by exploiting the reversible saturable transitions of fluorophores and allows imaging of structures with a resolution of typically a few tens of nanometers.6−9 Absorbance modulation is a modification of the STED principle using photochromic molecules instead of fluorophores. This concept utilizes the fact that some photochromic compounds can be reversibly switched between two isomeric forms with different absorption properties in a light-induced manner.10 It has been already successfully applied in optical lithography11−15 and, as AMI, also in transmission microscopy16 to improve the resolution.

In absorbance modulation, a layer of photochromic molecules is coated on the sample.17 Upon illumination with light of a first (λ1) and a second (λ2) wavelength, respectively, the AML can be reversibly switched to opaque and transparent states for light at λ2. This allows an optically induced near-field aperture for this wavelength to be generated directly above the measurement surface in the AML when it is exposed to a doughnut-shaped point spread function (PSF) at λ1 in conjunction with a Gaussian-shaped PSF at λ2. The size of this aperture depends on the (wavelength-dependent) photophysical properties of the AML and illumination conditions such as spatial intensity distribution and total power. Therefore, it is not limited by diffraction.14,18 Kowarsch et al. have presented a theoretical model of AMI in confocal reflection microscopy and have shown that imaging beyond the diffraction limit should also be feasible in reflection-based light microscopy.19 In this Letter, we prove this concept, to our knowledge for the first time, experimentally.

Integrated Results and Discussion

The principle optical layout of our confocal AMI reflection microscope, shown in Figure 1, is similar to a typical STED setup.20,21 In our implementation, light of two different wavelengths is used. In the following, light at λ1 = 325 nm is termed confinement light, since it induces the AML aperture for light at λ2 = 633 nm. This in turn is called measurement light, since its intensity reflected back from the sample through the AML aperture is detected as the measurement signal. The confinement beam is generated by a titanium–sapphire laser (Ti:Sa) in combination with a third harmonic generator (THG). To minimize the occurrence of nonlinear effects, such as two-photon absorption, the initial temporal pulse length of ∼140 fs is stretched to ∼10 ps using a pulse stretcher (PS) containing a pair of gratings. The characteristic 1D doughnut shape of the PSF is achieved by imprinting a phase pattern on the wavefronts using an appropriate phase mask (1D-PM).22,23 The focal intensity distribution of the confinement laser beam can optionally be realized as a Gaussian by bypassing the phase mask. A continuous wave helium–neon (He–Ne) laser at a wavelength of λ2 = 633 nm is used as the measurement beam. Both beams are combined using a dichroic mirror (DM) and focused on the sample plane using a Schwarzschild objective (SO) with an NA of 0.65. Note that by the use of a Schwarzschild objective the presence of (longitudinal) chromatic aberrations due to the large wavelength difference between λ1 and λ2 is effectively avoided.24,25 Telescopes are used in the individual beam paths to adjust the beam diameters, such that the entrance pupil of the objective is fully illuminated. Additionally, half-wave plates (HWP) and quarter-wave plates (QWP) are utilized to control the polarization state of the respective laser beams. The intensity of the laser beams can be adjusted within several 10 ns by acousto-optical modulators (AOM) installed in the individual beam paths. A piezo stage is used in the microscope to scan the AML-coated sample. The back-reflected light from the sample at λ2 is collected by the same objective, separated from the light at λ1 by the DM, focused onto a detection pinhole (PH), and detected by a low-noise amplified photodiode (Amp-PD). A photomultiplier tube (PMT) after a removable pellicle beamsplitter (PL) can also be used in the microscope for nonconfocal detection of the reflected signal at λ2. Other parameters, e.g., illumination time, movement of the stage, and data acquisition, are coordinated electronically via a National Instruments Data Acquisition (NIDAQ) card in combination with the acquisition software Imspector (Abberior Instruments GmbH, Germany).

Figure 1.

Figure 1

Open in a new tab

Confocal AMI reflection microscope. A titanium–sapphire laser (Ti:Sa) in combination with a third harmonic generator (THG) generates the confinement beam (at λ1 = 325 nm). For optimal absorption within the AML, the generated pulses are then stretched to ∼10 ps by using a pulse stretcher (PS). To generate a Gaussian or 1D doughnut-shaped intensity distribution of the confinement beam in the sample plane (insets), it is possible to switch between two optional beam paths, one of which contains a corresponding phase mask (1D-PM). A continuous wave helium–neon (He–Ne) laser at a wavelength of λ2 = 633 nm is used as the measurement beam. For flexibility, a fiber coupling is used for incorporating the measurement beam into the microscope. The confinement and the measurement beams are combined using a dichroic mirror (DM) and focused on the AML-coated sample, placed on a piezo stage, through the Schwarzschild objective (SO, 52×, NA = 0.65). The back-reflected signal at λ2 is collected by the same objective, separated from the illumination beam path by a beam splitter (BS), focused onto a detection pinhole (PH), and detected by a low-noise amplified photodiode (Amp-PD). For nonconfocal detection at λ2, a pair of a pellicle beamsplitter (PL) and photomultiplier tube (PMT) is also used in the microscope. A spectral filter is placed before the PMT to block the signal at λ1. Telescopes and polarization optics, such as half- and quarter-wave plates (HWPs, QWPs), are used in the respective beam paths to adjust the diameter and polarization state of the laser beams, respectively. Acousto-optic modulators (AOMs) are used to adjust the intensity of the laser beams. Beam-stops are used in the setup to block unwanted laser light. Inset images: PSFs were generated in the sample plane of the microscope with a corresponding phase mask (1D-PM, beam path indicated by solid line) and without a phase mask (beam path indicated by dashed line).

The AML employed in the experiments consists of 1,2-bis(5,5′-dimethyl-2,2-bithiophenyl)perfluorocyclopent-1-ene molecules, referred to as BTE-1, which are mixed with poly(methyl methacrylate) (PMMA) in a weight ratio of 50:50 using anisole as solvent and then spin-coated onto the surface to be investigated.12 For AMI in reflection, a dynamic aperture has to be scanned over the surface; hence, the photochromic molecules within the AML have to undergo numerous switching cycles, ideally without degradation. Therefore, we start by characterizing its fatigue resistance; a 400 nm thick AML is spin-coated onto a chromium mirror and switched several hundred times between opaque and transparent states while detecting the intensity of the reflected signal at measurement wavelength λ2. The PMT and the Amp-PD are used for detecting the reflected signal at λ2 while switching the AML to an opaque and transparent state, respectively. Figure 2 depicts the illumination sequence (Figure 2a) and the cyclic intensity modulation at λ2 due to the change in the absorbance of the AML (Figure 2b). The initial state of the AML is transparent; thus, for the first half of each switching cycle, we illuminate the AML with a power of 1 μW at λ1 and 20 nW at λ2 for 200 ms to switch it to its opaque state. Note that the power at λ2 is chosen such that the changes in the AML transmission can be monitored without significantly affecting the switching process. Then, for the second half of each switching cycle, the AML is illuminated with a power of 1 mW at λ2 for 200 ms to switch it back to its transparent state. For both laser beams, a Gaussian-shaped focus is used. The reflected signal at λ2 changes exponentially, while the AML is switched between its two states (inset in Figure 2b); however, its global minimum (lower gray dashed line in Figure 2b) does not equal zero due to a constant signal offset. This is a consequence of residual reflections at the air–AML interface and an imperfect absorption of the measurement beam by the AML. Moreover, after about 200 cycles, the modulation depth drops to half of the initial (red dashed lines in Figure 2b), suggesting degradation of the AML. This may be caused by several mechanisms, for instance, parasitic side reactions that depend on the molecular structure and experimental conditions.26,27

Figure 2.

Figure 2

Open in a new tab

Switching cycles of BTE-1. (a) A chromium mirror, coated with a 400 nm thick AML, is sequentially illuminated with Gaussian spots at λ1 = 325 nm and λ2 = 633 nm at powers of 1 μW and 1 mW, respectively, for 200 ms each. A Gaussian spot of 20 nW power at λ2 is simultaneously illuminated with light at λ1 to measure the decrease in transparency of the AML. (b) Normalized intensity of the reflected signals at λ2. Gray and red horizontal lines denote full and half modulation depth, respectively. Inset images: Detail of switching cycles 1–6 and 201–206. The first half of each switching cycle (solid line) shows the switching of the AML from its transparent to its opaque state, and the second half (dotted line) represents the AML switching back to its transparent state.

The theoretical model that was used by Kowarsch et al. to study absorbance modulation for reflection microscopy is based on the simultaneous illumination with the measurement and the confinement beam.19 On account of the power ratio between the two beams, the BTE-1 molecules within the AML reach a dynamic equilibrium, generating a subwavelength aperture. However, numerous switching cycles are required to reach this equilibrium, and even then, the individual molecules are constantly being switched on and off. Therefore, to minimize the required switching cycles for image acquisition and hence AML degradation, we implement a sequential illumination scheme (Figure 3a,b). It involves three phases: (i) aperture generation, (ii) data acquisition, and (iii) aperture erasure. The initially transparent AML is first illuminated with the 1D doughnut-shaped confinement beam (at λ1) such that the AML gets opaque for the measurement beam (at λ2) everywhere in the area irradiated by the 1D pattern. Only in the vicinity of the central minimum line of the 1D pattern does the AML remain transparent such that a subwavelength aperture is generated along one dimension. Then, the sample is illuminated with the Gaussian-shaped measurement beam (λ2), and the light transmitted through the aperture and reflected at the sample surface is being detected. Thereby, the aperture is already slightly erased. Finally, the sample is further illuminated with the measurement beam for complete aperture erasure. For high-resolution imaging, this sequence is repeated at different scan positions in the sample, with the scan direction being along the subwavelength extent of the AML aperture (Figure 3c). To reduce AML degradation even further, we additionally optimized its thickness and the light doses involved. The thickness of the AML is increased by a factor of 3 to 1200 nm in order to improve its absorption. Therefore, it is sufficient to apply the confinement beam for only 15 ms at a power of 3 μW, and the measurement beam can be applied at a reduced power of 100 μW for a total of 15 ms. Hence, the light doses for λ1 and λ2 used per cycle are respectively reduced by factors of 4.4 and 133, as compared to the fatigue resistance analysis (Figure 2). While our illumination scheme effectively reduces the number of switching cycles needed to create an aperture in the AML, the currently available switching cycles are insufficient for achieving an isotropic resolution improvement in two dimensions (2D). However, considering the current fatigue resistance of the AML and to perform proof-of-principle experiments of AMI in reflection, we have opted to restrict high-resolution imaging to 1D.

Figure 3.

Figure 3

Open in a new tab

Schematics and timeline of the illumination scheme for AMI in reflection. (a) An xz view of the AML-coated sample. This is first illuminated with a 1D doughnut-shaped confinement beam (at λ1) until an aperture is generated (i). Subsequently, it is illuminated with the Gaussian spot of the measurement beam (at λ2) for a high-resolution measurement through the aperture, generating an effective PSF of subwavelength size (ii). The illumination at λ2 is maintained until the aperture is completely erased (iii). (b) Schematic change in the aperture diameter at λ2 over time due to the change in AML absorption. The dashed vertical lines show the three phases (i), (ii), and (iii) of the illumination scheme. (c) An xy-view of the 1D doughnut PSF and the Gaussian PSF of the confinement and the measurement beam, respectively. The black arrow indicates the scanning direction during imaging.

To demonstrate resolution enhancement for AMI in reflection using our illumination scheme, we image gold nanospheres of 80 nm size on a quartz substrate coated with the AML in the next step. Here, the nanospheres serve as point-like objects for determining the microscope’s effective PSF. First, the sample is imaged with a transparent AML using the measurement laser light (at λ2) only, and the signal is detected by the Amp-PD (Figure 1). Here, the pixel size is 100 × 100 nm, and the pixel dwell time is 10 ms. Figure 4a shows an image of a single nanosphere. Besides the central main peak of the PSF, significant sidelobes can also be observed, which are caused by the inherent partial utilization of the full aperture by Schwarzschild objectives.28,29 Then, a line profile is recorded along the red dashed line shown in Figure 4a (with a 30 nm step size and 15 ms pixel dwell time). According to Figure 4b, the full width at half-maximum (fwhm) of the line profile and thus the diffraction-limited resolution equal 412.3 ± 0.7 nm. Then, the same line is scanned again using the illumination scheme shown in Figure 3. This time, the reflected signal at λ2 is detected per pixel with a time resolution of 10 μs.

Figure 4.

Figure 4

Open in a new tab

Nanosphere measurement. (a) Diffraction-limited 2D image of a single gold nanosphere. (b) Normalized line profile along the red dotted line indicated in (a). The fwhm of the Gaussian fit equals 412.3 ± 0.7 nm. (c) Smoothed AMI measurement at λ2 according to the illumination scheme detailed in Figure 3. The colorbar indicates the recorded signal in arbitrary units. (d) Normalized line profile averaged over times from 50 to 150 μs (green box in (c)) of the raw data. The fwhm of the Gaussian fit equals 169.6 ± 0.7 nm. (e) fwhm of the Gaussian fits to the line profiles of the raw data, each averaged over 100 μs, with respect to time.

Figure 4c shows the time-resolved line profile (step size and measurement time for each step are 30 nm and 15 ms, respectively). The vertical axis corresponds to the scan position, and the horizontal axis shows the measurement time, which comprises phases ii and iii (Figure 3a). The acquired data shown in Figure 4c are smoothed using a moving median filter to minimize the detector noise. The raw measurement data are shown in Supplementary Figure S1. The aperture is smallest for early time points. Therefore, the lowest back-reflected signal is observed here. However, as indicated by the line profile averaged over the times from 50 to 150 μs (green rectangle in Figure 4c) of the raw data as shown in Figure 4d, the resolution amounts to 169.6 ± 0.7 nm, which is about 2.4 times better than the diffraction limit. In Figure 3b, it has been illustrated that as time progresses the aperture size is expected to expand. This correlation explains the observed increase in signal intensity over time, as depicted in Figure 4c. Moreover, this can be directly observed through the increasing fwhm values of the line profiles, which are each averaged over a time period of 100 μs, as shown in Figure 4e. As time progresses, the fwhm approaches the diffraction-limited value.

Finally, we checked whether the reduced fwhm of the effective PSF for AMI in reflection can indeed be utilized to resolve finer structures. Therefore, we coat the AML onto a reflective grating (Supracon AG, Jena, Germany) with a pitch of 500 nm (Figure 5a), which is slightly larger than the diffraction-limited resolution. With purely transmitting AML and using the measurement beam only, the grating structure cannot be resolved in a line scan (Figure 5c) along the red arrow shown in Figure 5a. This changes in case the AMI-imaging scheme is used. The raw measurement data of AMI are shown in Figure 5b, where the grating structure is clearly visible for the early time points. For this measurement, the step size is 30 nm, and the measurement time for each step is 50 ms. Since the light dose of the confinement beam is critical for the aperture generation, a power of 1 μW is chosen, to keep the light dose similar to the one used in the previous measurements on the gold nanosphere. In the line profile averaged over times from 2 to 2.4 ms (green box in Figure 5b), adjacent lines of the grating can be readily discerned. The slight irregularity and shallow modulation depth observed in the resolved grating image are justified due to the coherent nature of our reflection microscope30 and the contributions of the significant sidelobes of the Schwarzschild objective PSF to the signal.

Figure 5.

Figure 5

Open in a new tab

Grating measurement. (a) SEM image of the reflective grating structure (pitch = 500 nm) used for imaging. (b) Raw data acquired via the AMI illumination scheme. The horizontal axis shows the measurement time in milliseconds, and the vertical axis shows the scan positions in μm. The colorbar indicates the recorded signal in arbitrary units. (c) Comparison of the diffraction-limited (red) and high-resolution AMI in reflection (green) line profiles scanned along the red arrow in (a). Both profiles were normalized to their respective maxima.

Concluding Remarks

In summary, we have, to our knowledge, demonstrated the first experimental proof of high-resolution reflection microscopy utilizing absorbance modulation. Currently, the improvement in resolution is 2.4-fold as compared to the diffraction limit and could only be demonstrated in 1D. This is mainly due to the currently still too high degradation of the state-of-the-art AML, which does not provide sufficient cycles for a 2D scan. Consequently, this needs to be improved, e.g., by modification of the polymer used, blending with antifading agents, or the development of improved photochromes. A higher fatigue resistance of the AML would not only allow us to increase the resolution in 2D but also to achieve an overall higher resolution. This is because we are currently also limited in resolution by the achievable signal-to-noise ratio, and a higher AML photostability would allow us to use different illumination schemes for which more signal could be acquired at small aperture sizes. It should also be possible to improve the signal-to-background ratio by using a transmissive objective lens (instead of the used reflective objective), since this suppresses the sidelobes of the PSF more effectively. In this context, a stable photochrome that can be switched at wavelengths greater than 350 nm, ideally greater than 400 nm, would be extremely beneficial, since a large number of excellent achromatic objective lenses and low-cost laser sources, as compared to the Ti:Sa–THG combination used in this study, are readily available. By using a sufficiently chemically inert AML, high-NA immersion objective lenses could then also be used. However, this in turn would require an improved AML in terms of bleaching resistance, and absorption efficiency at the measurement wavelength in its opaque state as the AML would have to be thinner. Thus, there is much opportunity to improve upon the results shown here and to progress super-resolution reflection microscopy toward a powerful method to study the surfaces of opaque materials down to the scale of a few tens of nanometers.

Acknowledgments

This work was supported by the Deutsche Forschungsgemeinschaft (DFG) under a grant to A.E. (412938415), C.R. (412988268), and A.S. (504588119).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnanoscienceau.3c00013.

  • Nanosphere measurement: 1D raw and smoothed AMI measurement at λ2 (PDF)

Author Contributions

CRediT: Parul Jain formal analysis (lead), investigation (lead), visualization (lead), writing-original draft (equal); Claudia Geisler conceptualization (equal), formal analysis (equal), investigation (equal), methodology (equal), supervision (supporting), writing-original draft (supporting), writing-review & editing (supporting); Dennis Leitz investigation (supporting), software (supporting); Viktor Udachin formal analysis (supporting), investigation (supporting); Sven Nagorny formal analysis (supporting), investigation (supporting); Thea Weingartz formal analysis (supporting), investigation (supporting); Joerg Adams conceptualization (supporting), funding acquisition (supporting), methodology (supporting), supervision (supporting), writing-review & editing (supporting); Andreas Schmidt conceptualization (supporting), funding acquisition (supporting), methodology (supporting), supervision (supporting), writing-review & editing (supporting); Christian Rembe conceptualization (equal), funding acquisition (equal), methodology (equal), supervision (supporting), writing-review & editing (equal); Alexander Egner conceptualization (lead), formal analysis (supporting), funding acquisition (lead), investigation (supporting), methodology (lead), supervision (lead), writing-original draft (equal), writing-review & editing (lead).

The authors declare no competing financial interest.

Supplementary Material

ng3c00013_si_001.pdf (5.6MB, pdf)

References

  1. Brandon D.; Kaplan W. D.. Microstructural Characterization of Materials, 2nd ed.; John Wiley & Sons, Ltd, 2008. [Google Scholar]
  2. Leng Y.Materials Characterization: Introduction to Microscopic and Spectroscopic Methods, 1st ed.; JohnWiley & Sons (Asia) Pte Ltd, 2008. [Google Scholar]
  3. Chen X.; Hu D.; Mescall R.; You G.; Basov D. N.; Dai Q.; Liu M. Modern Scattering-Type Scanning Near-Field Optical Microscopy for Advanced Material Research. Adv. Mater. 2019, 31, 1804774. 10.1002/adma.201804774. [DOI] [PubMed] [Google Scholar]
  4. Bandi B.; Slater C.; Farrugia D.; Davis C. Development of Desirable Fine Ferrite Grain Size and Random Second Phase Dual-Phase Steel Microstructures Using Composition and/or Processing Modifications. Metals 2022, 12, 1158. 10.3390/met12071158. [DOI] [Google Scholar]
  5. Shlyakhova G. V.; Bochkareva A. V.; Barannikova S. A.; Zuev L. B.; Martusevich E. V. Microstructure of stainless steel after heat treatment: Data from atomic-force microscopy. Steel Transl. 2017, 47, 99–104. 10.3103/S0967091217020103. [DOI] [Google Scholar]
  6. Hell S. W.; Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. 10.1364/OL.19.000780. [DOI] [PubMed] [Google Scholar]
  7. Klar T. A.; Jakobs S.; Dyba M.; Egner A.; Hell S. W. Fluorescence microscopy with diffraction resolution barrier broken by stimulated emission. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 8206–8210. 10.1073/pnas.97.15.8206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Jacquemet G.; Carisey A. F.; Hamidi H.; Henriques R.; Leterrier C. The cell biologist’s guide to super-resolution microscopy. J. Cell Sci. 2020, 133, 240713. 10.1242/jcs.240713. [DOI] [PubMed] [Google Scholar]
  9. Bond C.; Santiago-Ruiz A. N.; Tang Q.; Lakadamyali M. Technological advances in super-resolution microscopy to study cellular processes. Mol. Cell 2022, 82, 315–332. 10.1016/j.molcel.2021.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Irie M.; Fukaminato T.; Matsuda K.; Kobatake S. Photochromism of Diarylethene Molecules and Crystals: Memories, Switches, and Actuators. Chem. Rev. 2014, 114, 12174–12277. 10.1021/cr500249p. [DOI] [PubMed] [Google Scholar]
  11. Menon R.; Smith H. I. Absorbance-modulation optical lithography. J. Opt. Soc. Am. A 2006, 23, 2290. 10.1364/JOSAA.23.002290. [DOI] [PubMed] [Google Scholar]
  12. Andrew T. L.; Tsai H.-Y.; Menon R. Confining Light to Deep Subwavelength Dimensions to Enable Optical Nanopatterning. Science 2009, 324, 917–921. 10.1126/science.1167704. [DOI] [PubMed] [Google Scholar]
  13. Wei Z.; Bai J.; Xu J.; Wang C.; Yao Y.; Hu N.; Liang Y.; Wang K.; Yang G. Focused laser lithographic system with sub-wavelength resolution based on vortex laser induced opacity of photochromic material. Opt. Lett. 2014, 39, 6707–6710. 10.1364/OL.39.006707. [DOI] [PubMed] [Google Scholar]
  14. Majumder A.; Wan X.; Masid F.; Pollock B. J.; Andrew T. L.; Soppera O.; Menon R. Reverse-absorbance-modulation-optical lithography for optical nanopatterning at low light levels. AIP Adv. 2016, 6, 065312. 10.1063/1.4954178. [DOI] [Google Scholar]
  15. Majumder A.; Bourke L.; Andrew T. L.; Menon R. Superresolution optical nanopatterning at low light intensities using a quantum yield-matched photochrome. OSA Continuum 2019, 2, 1754. 10.1364/OSAC.2.001754. [DOI] [Google Scholar]
  16. Tsai H.-Y.; Thomas S. W.; Menon R. Parallel scanning-optical nanoscopy with optically confined probes. Opt. Express 2010, 18, 16014. 10.1364/OE.18.016014. [DOI] [PubMed] [Google Scholar]
  17. Menon R.; Tsai H.-Y.; Thomas S. W. Far-Field Generation of Localized Light Fields using Absorbance Modulation. Phys. Rev. Lett. 2007, 98, 043905. 10.1103/PhysRevLett.98.043905. [DOI] [PubMed] [Google Scholar]
  18. Pariani G.; Castagna R.; Menon R.; Bertarelli C.; Bianco A. Modeling absorbance-modulation optical lithography in photochromic films. Opt. Lett. 2013, 38, 3024. 10.1364/OL.38.003024. [DOI] [PubMed] [Google Scholar]
  19. Kowarsch R.; Geisler C.; Egner A.; Rembe C. Superresolution reflection microscopy via absorbance modulation: a theoretical study. Opt. Express 2018, 26, 5327. 10.1364/OE.26.005327. [DOI] [PubMed] [Google Scholar]
  20. Willig K. I.; Rizzoli S. O.; Westphal V.; Jahn R.; Hell S. W. STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 2006, 440, 935–939. 10.1038/nature04592. [DOI] [PubMed] [Google Scholar]
  21. Aspelmeier T.; Egner A.; Munk A. Modern Statistical Challenges in High-Resolution Fluorescence Microscopy. Annu. Rev. Stat. Its Appl. 2015, 2, 163–202. 10.1146/annurev-statistics-010814-020343. [DOI] [Google Scholar]
  22. Klar T. A.; Engel E.; Hell S. W. Breaking Abbe’s diffraction resolution limit in fluorescence microscopy with stimulated emission depletion beams of various shapes. Phys. Rev. E 2001, 64, 066613. 10.1103/PhysRevE.64.066613. [DOI] [PubMed] [Google Scholar]
  23. Krüger J.-R.; Keller-Findeisen J.; Geisler C.; Egner A. Tomographic STED microscopy. Biomed. Opt. Express 2020, 11, 3139. 10.1364/BOE.391787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schwarzschild K.Untersuchungen zur geometrischen Optik. II. Theorie der Spiegeltelescope. Astronomische Mitteilungen der Universitaets-Sternwarte zu Goettingen 1905. [Google Scholar]
  25. Liu C.; Wang C.; Liu J.; Tan J. In Elliptical Mirrors: Applications in microscopy; Liu J., Ed.; IOP Publishing, 2018. [Google Scholar]
  26. Nakatani K.; Piard J.; Yu P.; Métivier R. Introduction: Organic Photochromic Molecules. Photochromic Materials: Preparation, Properties and Applications 2016, 1–45. 10.1002/9783527683734.ch1. [DOI] [Google Scholar]
  27. Pariani G.; Quintavalla M.; Colella L.; Oggioni L.; Castagna R.; Ortica F.; Bertarelli C.; Bianco A. New Insight into the Fatigue Resistance of Photochromic 1,2-Diarylethenes. J. Phys. Chem. C 2017, 121, 23592–23598. 10.1021/acs.jpcc.7b04848. [DOI] [Google Scholar]
  28. Horikawa Y. Resolution of annular-pupil optical systems. J. Opt. Soc. Am. A 1994, 11, 1985–1992. 10.1364/JOSAA.11.001985. [DOI] [PubMed] [Google Scholar]
  29. Sheppard C. The use of lenses with annular aperture in scanning optical microscopy. Optik 1977, 48, 329–334. [Google Scholar]
  30. Sheppard C.; Gu M.; Mao X. Q. Three-dimensional coherent transfer functions in fibre optical confocal scanning microscopes. Opt. Commun. 1991, 81, 281–284. 10.1016/0030-4018(91)90616-L. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ng3c00013_si_001.pdf (5.6MB, pdf)

Articles from ACS Nanoscience Au are provided here courtesy of American Chemical Society

RESOURCES