Significance
The three-dimensional spatial distribution of galaxies encodes key cosmological information on the nature of dark energy and the contents of the Universe. Current analyses of the statistical clustering of galaxies successfully extract information on large scales that are well described by analytic models. They, however, struggle on smaller, nonlinear, scales. Here, we present SimBIG, an approach to galaxy clustering analyses that can extract information on nonlinear regimes by exploiting high-fidelity simulations and inference based on machine learning. To demonstrate its advantages, we apply SimBIG to 109,636 galaxies of the BOSS survey and analyze a standard summary statistic of the galaxy distribution. Our constraints are consistent with previous works and substantially improve their precision on select cosmological parameters.
Keywords: cosmology, machine learning, galaxies, simulations
Abstract
We present cosmological constraints from a simulation-based inference (SBI) analysis of galaxy clustering from the SimBIG forward modeling framework. SimBIG leverages the predictive power of high-fidelity simulations and provides an inference framework that can extract cosmological information on small nonlinear scales. In this work, we apply SimBIG to the Baryon Oscillation Spectroscopic Survey (BOSS) CMASS galaxy sample and analyze the power spectrum, , to . We construct 20,000 simulated galaxy samples using our forward model, which is based on 2,000 high-resolution Quijote-body simulations and includes detailed survey realism for a more complete treatment of observational systematics. We then conduct SBI by training normalizing flows using the simulated samples and infer the posterior distribution of CDM cosmological parameters: . We derive significant constraints on and , which are consistent with previous works. Our constraint on is 27% more precise than standard analyses because we exploit additional cosmological information on nonlinear scales beyond the limit of current analytic models, . This improvement is equivalent to the statistical gain expected from a standard analysis of galaxy sample 60% larger than CMASS. While we focus on in this work for validation and comparison to the literature, SimBIG provides a framework for analyzing galaxy clustering using any summary statistic. We expect further improvements on cosmological constraints from subsequent SimBIG analyses of summary statistics beyond .
The three-dimensional spatial distribution of galaxies provides key cosmological information that can be used to constrain the nature of dark matter and dark energy and measure the contents of the Universe. The next generation spectroscopic galaxy surveys, conducted using the Dark Energy Spectroscopic Instrument (DESI; 1, 2, 3), Subaru Prime Focus Spectrograph (PFS; 4, 5), the ESA Euclid satellite mission (6), and the Nancy Gracy Roman Space Telescope (Roman; 7, 8), will probe galaxies over cosmic volumes out to , over 10 Gyrs of cosmic history. Combined with other cosmological probes, they will provide the most stringent tests of the standard CDM cosmological model and potentially lead to discoveries of new physics.
In current analyses, the power spectrum is used as the primary measurement of galaxy clustering (e.g., refs. 9, 10, 11, 12, 13, 14, 15). Furthermore, the analyses are limited to large, linear scales where the impact of nonlinear structure formation is small. These restrictions result from the fact that standard analyses use analytic models based on perturbation theory (PT) of large-scale structure, see refs. 16 and 17 for a review. PT struggles to accurately model scales beyond quasi-linear scales, especially for higher-order clustering statistics (e.g., bispectrum). In the (18) PT analysis, for instance, the authors restrict the power spectrum to and the bispectrum to . In a recent PT analysis, (19) analyzes the bispectrum to ; however, they require 33 extra parameters for the theoretical consistency of their model. PT also cannot be used to model various recently proposed summary statistics, e.g., ref. 20 or to exploit the full galaxy distribution at the field level. While some analyses in real space have analyzed galaxy clustering on smaller scales, e.g., refs. 21–24, they do not simultaneously analyze clustering on large scales.
Another major challenge for current analyses is accurately accounting for observational systematics. Observations suffer from imperfections in, e.g., targeting, imaging, and completeness that can significantly impact the analysis (25, 26). Current analyses account for these effects by applying correction weights to the galaxies. Fiber collisions, for example, prevent galaxy surveys that use fiber-fed spectrographs (e.g., DESI, PFS) from successfully measuring redshifts from galaxies within some angular scale of one another on the focal plane. This significantly biases the power spectrum by more than the amplitude of cosmic variance on scales smaller than (27–29). To correct for this effect, the weights of the “collided” galaxies missed by survey are assigned to their nearest angular neighbors (30, 31). Even for current analyses, these correction weights do not sufficiently correct the measured power spectrum (28). Furthermore, they are only designed and demonstrated for the power spectrum.
Meanwhile, additional cosmological information is available on nonlinear scales and in higher-order statistics. Recent studies have accurately quantified the information content in these regimes using large suites of simulations. (32) and (33) used the Quijote suite of simulations to demonstrate that constraints on cosmological parameters, , improve by a factor of 2 by including nonlinear scales () in power spectrum analyses. Even more improvement comes from including higher-order clustering information in the bispectrum. Similar forecasts for other summary statistics, e.g., marked power spectrum (34, 35), reconstructed power spectrum (36), skew spectra (37), wavelet statistics (38), find consistent improvements from including nonlinear scales and higher-order clustering. Despite the growing evidence of the significant constraining power available in nonlinear scales and higher-order statistics, it cannot be exploited by standard methods with PT.
Robustly exploiting nonlinear and non-Gaussian cosmological information requires a framework that can both accurately model nonlinear structure formation and account for detailed observational systematics. In this work, we present SIMulation-Based Inference of Galaxies (SimBIG), a framework for analyzing galaxy clustering that achieves these requirements by using a forward modeling approach. Instead of analyzing galaxy clustering using analytic models, a forward model approach uses simulations that model the full details of the observations.
In SimBIG, our forward model is based on cosmological -body simulations that accurately model nonlinear structure formation. We also use the halo occupation framework, which provides a compact and flexible prescription for connecting the galaxy distribution to the dark matter distribution. Our forward model also takes advantage of the fact that many observational systematics can be more easily simulated, e.g., refs. 39 and 40 than corrected in the observations. With this forward model, we can rigorously analyze galaxy clustering on nonlinear scales and with higher-order statistics.
To infer the cosmological parameters, our approach does not require sampling the posterior using an assumed analytic likelihood. We instead use simulation-based inference SBI; see ref. 41, for a review. SBI, also known as “likelihood-free inference,” enables accurate Bayesian inference using forward models, e.g., refs. 42–45. Moreover, they leverage neural density estimation from machine learning, e.g., refs. 42 and 46 to more efficiently infer the posterior without sampling or making strong assumptions on the functional form of the likelihood.
In this work, we apply SimBIG to the CMASS galaxy sample observed by the Sloan Digital Sky Survey SDSS-III Baryon Oscillation Spectroscopic Survey (BOSS; 47, 48). With the main goal of demonstrating the accuracy and potential of SimBIG, we use the power spectrum as our summary statistic. We present the cosmological constraints inferred from our analysis and compare them to previous constraints in the literature. In an accompanying paper (49, hereafterH22b), we present our forward model in further detail and the mock challenge that we conduct to rigorously validate the accuracy and precision of SimBIG cosmological constraints.
Simulation-Based Inference of Galaxies SIMBIG
Modern cosmological analyses use Bayesian inference to constrain the posterior distribution of cosmological parameters, , given observation, . In standard galaxy clustering analyses, the posterior is evaluated using Bayes’ rule. The likelihood is assumed to have a Gaussian functional form and evaluated using an analytic PT model.
SBI offers an alternative that requires no assumptions on the form of the likelihood. SBI only requires a forward model—i.e., a simulation that can generate a realization of mock observations, , given set of parameters, . Each realization corresponds to a sample drawn from the likelihood . It uses a training dataset of simulated pairs to estimate the posterior. SBI has already been successfully applied to a wide range of inference problems in astronomy and cosmology (43, 44, 50–55).
In this work, we utilize SBI based on neural density estimation, where a neural network with parameters is trained to estimate . In particular, we use “normalizing flow” models that are capable of accurately estimating complex distributions highly efficiently (56, 57). Below, we briefly describe our forward model and SBI framework.
A. Forward Model.
SBI requires a forward model capable of generating mock observations that are statistically indistinguishable from the observations. We start with high-resolution -body simulations from the Quijote suite (58). These simulations follow the evolution of cold dark matter (CDM) particles in a volume of from to using the TreePM GADGET-III code. They accurately model the clustering of matter down to nonlinear scales beyond (58).
To model the galaxy distribution, we identify gravitationally bound dark matter halos and populate them with galaxies using a flexible halo occupation framework. We identify halos using the ROCKSTAR phase-space-based halo finder (59), which accurately determines the location of halos and resolves their substructure (60). For our simulations, we identify halos with mass down to , depending on the cosmology. We then populate the halos using Halo Occupation Distribution (HOD) models that provide a statistical prescription for populating halos with galaxies based on halo properties such as their mass and concentration. In this work, we use a state-of-the-art HOD model that supplements the standard (61) model with assembly, concentration, and velocity biases. The extra features of our HOD model add additional flexibility that recent works suggest may be necessary to describe galaxy clustering (e.g., refs. 62–64).
Once we have our galaxy distribution in the simulation box, we apply survey realism. We remap the box to a cuboid (65) and then cut out the detailed survey geometry of the BOSS CMASS SGC sample (Materials and Methods). This includes masking for bright stars, centerpost, bad field, and collision priority (25, 26, 48). We apply fiber collisions by first identifying all pairs of galaxies within an angular scale of then, for 60% of the pairs, removing one of the galaxies from the sample. Last, we trim the forward-modeled galaxy catalog to match the redshift range and angular range of the observations.
In this work, we analyze a subvolume of BOSS that spans a relatively narrow redshift range, . Over this range, the number density of the BOSS CMASS galaxy sample does not significantly vary with redshift. We, therefore, use a forward model that is based on -body simulations at a single snapshot and we do not vary the HOD model with redshift. For a different galaxy sample with a significant redshift dependence, the forward model must be modified to account for the redshift dependence.
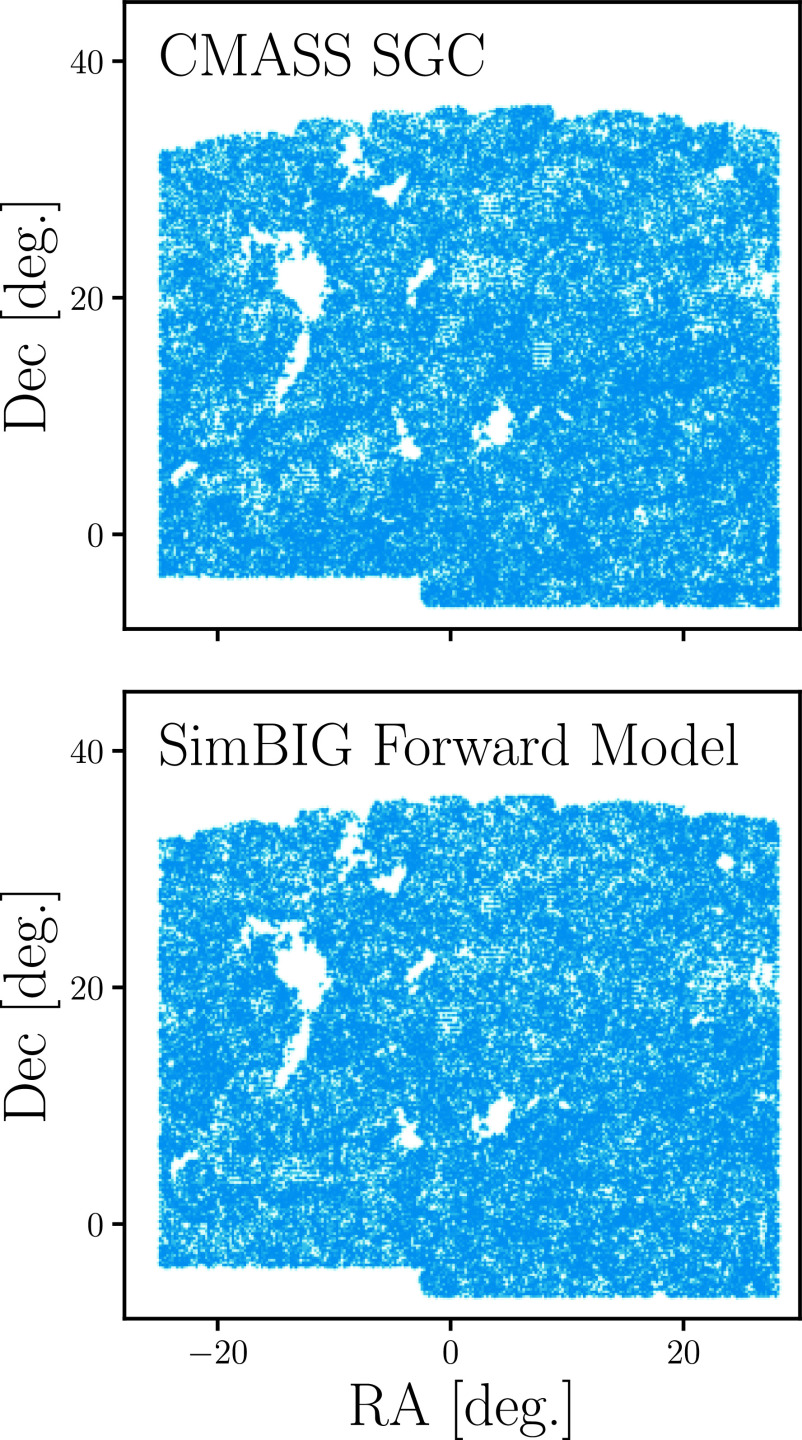
In total, our forward model has 14 parameters. Five CDM cosmological parameters, , that determine the matter distribution and nine HOD parameters that determine the connection between galaxies and halos. For further details on our forward model, we refer readers to H22b. In the Fig. 1, Bottom, we present the 3D spatial distribution of galaxies in our forward model. We present the angular distribution of galaxies in our forward model in Fig. 2. The forward model accurately reproduces the survey geometry and angular footprint of the observed BOSS sample. For additional comparisons of the 3D distributions of galaxies in CMASS and our forward model, we refer readers to  https://youtube.com/playlist?list=PLQk8Faa2x0twK3fgs55ednnHD2vbIzo4z.*
https://youtube.com/playlist?list=PLQk8Faa2x0twK3fgs55ednnHD2vbIzo4z.*
Fig. 1.

The SimBIG forward model produces simulated galaxy samples with the same survey geometry and observational systematics as the observed BOSS CMASS SGC galaxy sample. We present the three-dimensional (3D) distribution of the galaxies from three different viewing angles. The colormap represents the redshift of the galaxies. In the Top set of panels, we present the distribution of galaxies in the CMASS sample. At the Bottom, we present the distribution of a simulated galaxy sample, generated from our forward model. The SimBIG galaxy samples are constructed from Quijote -body dark matter simulations using an HOD model that populates dark matter halos identified using the ROCKSTAR algorithm. The 3D distributions illustrate that our forward model is able to generate galaxy distributions that are difficult to statistically distinguish from observations. For more comparisons of the 3D distributions, we refer readers to  https://youtube.com/playlist?list=PLQk8Faa2x0twK3fgs55ednnHD2vbIzo4z.
https://youtube.com/playlist?list=PLQk8Faa2x0twK3fgs55ednnHD2vbIzo4z.
Fig. 2.
Angular distribution of galaxies from the CMASS sample (Top) and a galaxy sample generated using the SimBIG forward model (Bottom). Comparison of the angular distributions highlights the detailed CMASS angular selection that we include in our forward model to account for observational systematics.
B. Training Dataset for Simulation-Based Inference.
Using our forward model, we construct 20,000 simulated galaxy catalogs. They are constructed from 2,000 Quijote-body simulations, each with 10 different sets of HOD parameters, sampled from a broad prior. The -body simulations are arranged in a Latin Hypercube configuration, which therefore imposes uniform priors on the cosmological parameters that conservatively encompass the Planck cosmological constraints (66).
In principle, SimBIG can be directly applied to the full galaxy catalog if the forward model is capable of accurately modeling observations at all scales. Even with -body simulations, however, this is not the case due to limitations on mass and time resolution and inadequacies of halo occupation models. Instead, we use summary statistics of the galaxy sample, where we can impose cuts, e.g., based on physical scales, to which our forward model is accurate. Since the primary goal of this work is to present and demonstrate the SimBIG framework, we use the most commonly used summary statistic: the galaxy power spectrum multipole, . We also include the average galaxy number density of the sample, .
In this work, we use the redshift-space galaxy power spectrum monopole, quadrupole, and hexadecapole (, and ). We measure , , and for each of the simulated galaxy catalogs using the (67) algorithm. The algorithm accounts for the survey geometry using a random catalog with 4,000,000 randomly positioned objects that have the same radial and angular selection functions as the observed sample. We also include (68) weights with to reduce the variance in measured , as is standard practice. We also impose a conservative limit on the , based on the convergence of matter clustering of the Quijote simulations, see H22b or (58) section 5.2 for further details. We also measure of the BOSS CMASS-SGC galaxy sample with the same algorithm. For the observed we include systematics weights for redshift failures, stellar density, and seeing conditions, which are effects not included in our forward model but shown to be successfully accounted for using the weights (25, 31).
By using , we can compare the constraints inferred using SimBIG with previous constraints, e.g., refs. 12 and 69 as further validation of SimBIG. To be consistent with previous analyses, we include a nuisance parameter, , that is typically included to account for residual shot noise contribution (e.g., refs. 9, 12, 69). In Fig. 3, we present of our forward modeled galaxy catalogs. We randomly select 100 out of the total 20,000 power spectra for clarity. The left, center, and right panels present the monopole, quadrupole, and hexadecapole. Each and measurements serve as in the training dataset for our SBI posterior estimation using normalizing flows.
Fig. 3.

Power spectrum, , measured from the simulated galaxy catalogs constructed using the SimBIG forward model. We present of 100 out of the total 20,000 catalogs for clarity. In each of the panels, we plot the monopole, quadrupole, and hexadecapole of the power spectrum (). For reference, we include measured from the BOSS CMASS SGC galaxy sample (black) with uncertainties estimated from H22b simulations. is the most commonly used summary statistic of galaxy distribution that measures the two-point clustering. We use in this work to showcase and validate the SimBIG framework and make detailed comparisons to previous works in the literature. The of the SimBIG catalogs encompass the BOSS and, thus, provide a sufficiently broad dataset to conduct SBI.
C. Simulation-Based Inference with Normalizing Flows.
Normalizing flow models use an invertible bijective transformation, , to map a complex target distribution to a simple base distribution, , that is fast to evaluate. For SBI, the target distribution is the posterior, , while is typically a multivariate Gaussian. The transformation must be invertible and have a tractable Jacobian so that we can evaluate the target distribution from by change of variables. Since is easy to sample and evaluate, we can also easily sample and evaluate the target distribution. A neural network with parameters is used to provide a highly flexible .
Among the various normalizing flow-based neural density estimators now available in the literature, we use a Masked Autoregressive Flow (MAF; 42). MAF combines normalizing flows with an autoregressive design (70), which is well-suited for estimating conditional probability distributions such as a posterior. A MAF model is built by stacking multiple Masked Autoencoder for Distribution Estimation (MADE; 46) models so that it has the autoregressive structure of MADE models but with additional flexibility to describe complex probability distributions. We use the MAF implementation of the sbi Python package (71, 72).
In training, our goal is to determine the parameters, , of our normalizing flow, , so that it accurately estimates the posterior, . We can formulate this into an optimization problem of minimizing the Kullback–Leibler (KL) divergence between and , which measures the difference between the two distributions.
| [1] |
| [2] |
| [3] |
| [4] |
Eq. 2 follows from the fact that the training dataset is constructed by sampling from with our forward model.
We split the training data into a training and validation set with a 90/10 split, then maximize Eq. 4 over the training set. We use the ADAM optimizer (73) with a learning rate of . We prevent overfitting by stopping the training when the log-likelihood Eq. 4 evaluated on the validation set fails to increase after 20 epochs. We determine the architecture of our normalizing flow through experimentation. Our final trained model has 6 MADE blocks, each with 9 hidden layers and 186 hidden units. For further details on the training procedure, we refer readers to H22b. Once trained, we estimate the posterior of our 5 cosmological, 9 HOD parameters, and 1 nuisance parameter for the BOSS CMASS SGC by sampling our normalizing flow: . and represent the and measurements for the observed BOSS CMASS SGC sample.
1. Results
We present the posterior distribution of the CDM cosmological parameters, , inferred from using SimBIG in Fig. 4. The posterior is inferred from the BOSS down to . The diagonal panels present the marginalized one-dimensional posteriors for each parameter. The other panels present marginalized two-dimensional posteriors of different parameter pairs that highlight parameter degeneracies. We mark the 68 and 95 percentiles of the posteriors with the contours. We infer the posterior of HOD and nuisance parameters; however, we do not include them in the figure for clarity. Among the cosmological parameters, the SimBIG posterior significantly constrains and . This is consistent with previous works that relied on priors from Big Bang nucleosynthesis or cosmic microwave background (CMB) experiments for the other parameters, e.g., refs. 12 and 15. We infer and .
Fig. 4.
(Left) Posterior of cosmological parameters inferred from using SimBIG. In the diagonal panels, we present the marginalized one-dimensional (1D) posterior of each parameter. The other panels present the 2D posteriors that illustrate the degeneracies between two parameters. The contours mark the 68 and 95 percentiles. We accurately analyze down to nonlinear regimes, , by using a simulation-based forward model that includes observational systematics. (Right) We focus on the posteriors of (, ), the parameters that can be most significantly constrained by galaxy clustering alone. We derive and . Our constraints are 27% tighter than the (12) PT constraint (orange).
In the accompanying paper H22b, we present the detailed validation of the SimBIG posterior using a suite of 1,500 test simulations. We construct the test suite using different forward models than the one used for our training data. They are constructed using different -body simulations, halo finders, and HOD models. This is to ensure that the cosmological constraints we derive are independent of the choices and assumptions made in our forward model. Then, we conduct a “mock challenge” where we infer posteriors of the cosmological parameters for each of the test simulations. Since we know the true cosmological parameter values of the test simulations, we can assess both the accuracy and precision of the inferred posteriors.
H22b reveals that SimBIG produces unbiased posteriors. On the other hand, the posteriors are conservative, i.e., they are broader than the true posterior. This is due to the limited number of -body simulations used to construct our training dataset. Although we use 20,000 forward-modeled simulations, they are constructed from 2000 -body simulations with different values of cosmological parameters. This makes our estimate of the KL divergence, Eq. 4 noisy and makes training the SimBIG normalizing flow more challenging. Our constraint on is particularly conservative. Additional -body simulations or improvements to the training would significantly improve the precision of our posteriors.
Despite the fact that they are conservative, the posterior from SimBIG is significantly more precise than constraints from previous works. Mikhail et al. (12) analyzed the of the BOSS CMASS galaxy sample using the PT approach with an analytic model based on effective field theory. For the CMASS SGC sample, with uniform priors on the cosmological parameters, and with , Mikhail et al. (12) inferred . With SimBIG, we improve constraints by 27% over the standard galaxy clustering analysis. We emphasize that this improvement is roughly equivalent to analyzing a galaxy survey 60% larger than the original survey using PT.
Recently, Kobayashi et al. (15) also analyzed the of BOSS CMASS sample but using a theoretical model based on a halo power spectrum emulator. Instead of using a galaxy bias scheme used by PT to connect the galaxy and matter distributions, Kobayashi et al. (15) used halo power spectra predicted by an emulator and a halo occupation framework, similar to the HOD model in our forward model. We note that while the halo power spectrum emulator is trained using simulations, the approach in ref. 15 does not forward model observational systematics. They also make the same assumptions on the form of the likelihood as PT analyses for their inference. For the CMASS SGC sample, with uniform priors on all cosmological parameters, and with , Kobayashi et al.(15) inferred . Kobayashi et al. (15) constraints are tighter than Mikhail et al. (12) PT constraints because the halo occupation model provides a more compact framework for modeling galaxies. Nevertheless, with SimBIG, we improve on their constraints by 13%.
SimBIG produces significantly tighter constraints on because we are able to accurately extract cosmological information available on small, nonlinear, scales. With our forward modeling approach, we can accurately model nonlinear clustering and robustly account for observational systematics down to . In both refs. 12 and 15, they restrict their analysis to due to the limitations of their analyses on smaller scales.
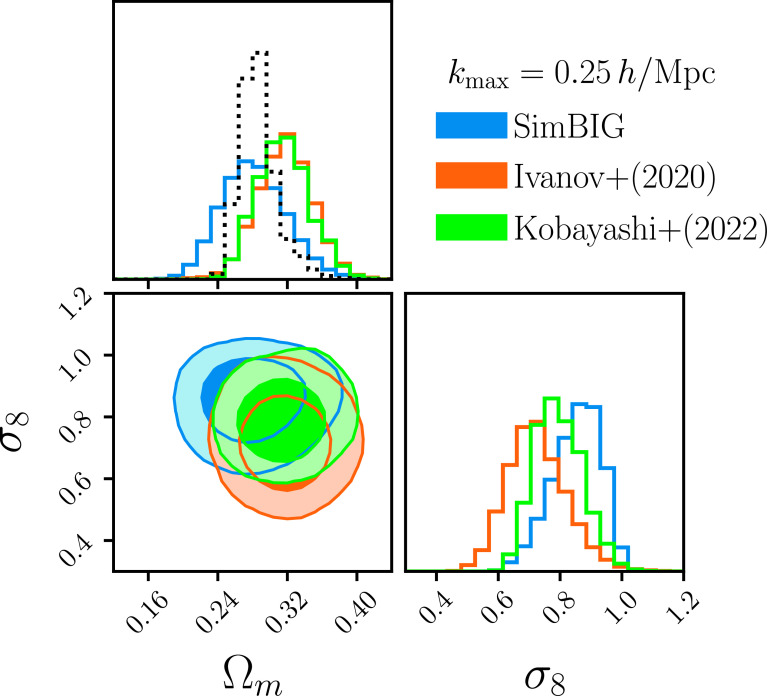
To further verify that our improvement comes from constraining power on small scales, we analyze to using SimBIG. In Fig. 5, we present the SimBIG posterior (blue) along with the posteriors from (12, orange) and (15, green). We focus our comparison on and , the cosmological parameters that can be most competitively constrained with galaxy clustering alone. The contours again represent the 68 and 95 percentiles. We find overall good statistical consistency among the posteriors. For , our places a constraint. This is significantly broader than our constraint and, thus, demonstrates that the constraining power is in fact from nonlinear scales. Furthermore, the precision of the SimBIG constraint is in excellent agreement with the ref. 15 constraint. This serves as further validation of SimBIG, since ref. 15 uses a similar halo occupation framework to model the power spectrum.
Fig. 5.
Comparison of the (, ) posteriors inferred from the CMASS-SGC analysis for from SimBIG (blue), the ref. 12 PT approach (orange), and the ref. 15 emulator approach (green). The contours represent the 68 and 95 percentiles. We find overall good agreement among the posteriors. For , SimBIG infers consistent but broader posterior due to the fact that we use a limited number of simulations. We estimate the expected constraints with more simulations using posterior “recalibration” (black dotted). For , both SimBIG and ref. 15 derive tighter constraints than ref. 12 due to the fact that we use halo occupation instead of a galaxy bias prescription. Meanwhile, the precision of our constraint is in excellent agreement with ref. 15, which uses a similar halo occupation model. The consistency of the posteriors demonstrate that the improvements in the constraints come from additional cosmological information in the nonlinear regime that SimBIG can robustly extract.
For , we infer broader posteriors than refs. 12 and 15. As we discuss above and in H22b, this is due to the fact that the SimBIG normalizing flow is trained using a limited number of simulations. To estimate the expected improvement in the constraints without this limitation, we use the posterior “re-calibration” procedure from ref. 74. The recalibration uses the posteriors inferred for the test simulations and their true parameter values. We calculate the local probability integral transform (75), a diagnostic of the inferred posteriors, and use this quantity to derive a weighting scheme that corrects the posteriors so that it matches the true posterior of the test simulations.
The recalibration uses test simulations, so we do not use it for inference. However, it provides a bound for the SimBIG constraints if we were to have sufficient training simulations. The recalibrated posterior constrains . For reference, we mark the recalibrated constraint (black dotted) in Fig. 5. The recalibrated is in good agreement with both the refs. 12 and 15 constraints. It is significantly tighter than the original SimBIG constraint and illustrates that additional training simulations would significantly improve the precision of the SimBIG constraints.
Based on our posterior, we infer (and for our recalibrated posterior). Multiple recent large-scale structure studies have reported a “ tension” with constraints from ref. 66 CMB analysis. They find significantly lower values of than Planck (23, 76–82). PT analyses of BOSS also infer relatively low values of . Ref. 12, for instance, infers . This tension between constraints from large-scale structure and CMB analyses has motivated a number of works to explore modifications of the standard CDM cosmological model, e.g., refs. 83–86. We do not find a significant tension with the Planck constraints (66). However, given the statistical precision of our constraint, we refrain from more detailed comparison and discussion.
2. Conclusions
We present SimBIG, a forward modeling framework for analyzing galaxy clustering using SBI. As a demonstration of the framework, we apply it to the BOSS CMASS SGC, a galaxy sample at . We analyze the galaxy power spectrum multipoles (), the most commonly used summary statistic of the galaxy spatial distribution, to showcase and validate the SimBIG framework.
SimBIG utilizes a full forward model of the CMASS sample, unlike standard approaches that use analytic models of the summary statistic. The forward model is based on high-resolution Quijote-body simulations that can accurately model the matter distribution on small scales. It uses halo modeling and a state-of-the-art HOD model with assembly, concentration, and velocity biases that provide a flexible mapping between the matter and galaxy distributions. The forward model also includes realistic observational systematics such as survey geometry and fiber collisions. With this forward modeling approach, we can leverage the predictive power of simulations to analyze small, nonlinear, scales as well as higher-order clustering. It also provides a framework to account for systematics for any summary statistic.
Using the forward model, we construct 20,000 simulated CMASS-like samples that span a wide range of cosmological and HOD parameters. We measure and for each of these samples and use the measurements as the training dataset for SBI. To estimate the posterior, we use neural density estimation based on normalizing flows. Using the training dataset, we train our normalizing flows by minimizing the KL divergence between its posterior estimate and the true posterior. Once trained, we apply our normalizing flow to the observed summary statistics to infer the posterior of 5 cosmological, 9 HOD, and 1 nuisance parameter.
Focusing on the cosmological parameters, we derive significant constraints on: and . Our constraints are 27% tighter than the ref. 12 constraints using a standard PT approach on the same galaxy sample. This improvement is roughly equivalent to increasing the volume of the galaxy survey by 60% for a standard PT analysis. The SimBIG constraints are inferred from out to while the PT constraints are limited to . The improvement is driven by the additional cosmological information on nonlinear scales that SimBIG can robustly extract.
We also infer the posterior using SimBIG from with and compare it to posteriors in the literature. In particular, the SimBIG constraint for are in excellent agreement with the constraint from the recent halo model–based emulator analysis of ref. 15. Since they use a similar halo occupation framework as SimBIG, this comparison firmly verifies the robustness of our constraints. The comparison also confirms that the improvement in SimBIG constraints come from the nonlinear regime. In the accompanying H22b, we present additional tests of SimBIG through a mock challenge. The tests use a suite of 1,500 test simulations constructed with different forward models to demonstrate that SimBIG produces unbiased cosmological constraints. H22b also presents further details on our forward model and discusses posterior constraints on HOD parameters.
SimBIG can also extract higher-order cosmological information. Standard galaxy clustering analyses primarily focus on two-point clustering statistics. Analyses of higher-order statistics have been limited to, e.g., the bispectrum (18, 19, 87), and even these analyses extract only limited cosmological information beyond linear scales. In subsequent work, we will use SimBIG to analyze the BOSS CMASS galaxies using higher-order statistics (the bispectrum) and nonstandard observables that contain additional cosmological information: e.g., marked power spectrum, skew spectra, void probability functions, and wavelet- scattering-like statistics. We will also apply SimBIG to analyze field-level summary statistics that capture all the information in the galaxy field using convolutional and graph neural networks.
SimBIG can also be extended to upcoming spectroscopic galaxy surveys observed using DESI, PFS, Euclid, and Roman, which will probe huge cosmic volumes over the next decade. They will produce the largest and most detailed three-dimensional maps of galaxies in the Universe. These surveys are already expected to provide the most precise constraints on cosmological parameters using standard analyses. SimBIG can further exploit the statistical power of these surveys to place even tighter constraints on cosmological parameters and produce the most stringent tests of the standard CDM cosmological model and beyond.
3. Materials and Methods
Observations: SDSS-III BOSS.
In this work, we analyze observations from the Sloan Digital Sky Survey SDSS-III (47, 48) Baryon Oscillation Spectroscopic Survey (BOSS) Data Release 12. In particular, we use the CMASS galaxy sample, which selects high stellar mass Luminous Red Galaxies (LRGs) over the redshift (88). We restrict our analysis to CMASS galaxies in the Southern Galactic Cap (SGC) and impose a redshift cut of and the following angular cuts: and . In upper panels in Fig. 1, we present the three-dimensional distributions of our CMASS SGC galaxy sample at three different viewing angles. We also present the angular distribution of the sample in Fig. 2. In total, our CMASS SGC galaxy sample contains 109,636 galaxies.
Supplementary Material
Appendix 01 (PDF)
In anim_slices_4.mov, we present the projected slices of the galaxy distribution along the radial direction from the point of the view of an observer. The top and bottom panels present the BOSS CMASS and simulated galaxy samples respectively. The right panels highlight the progression of the radial slice for both samples.
In anim_slices_1.mov, we present projected slice of the galaxy distribution along the Z axis for the BOSS CMASS (top) and simulated (bottom) galaxy samples. The panels on the right highlight the progression of the Z slice for both samples.
In anim_3d_rot.mov, we present a rotating view with of the galaxy distribution with the BOSS CMASS and simulated galaxy samples on the left and right panels, respectively. The color indicates galaxy redshift.
Acknowledgments
It is a pleasure to thank Peter Melchior, Uro Seljak, David Spergel, Licia Verde, and Benjamin D. Wandelt for valuable discussions. We also thank Mikhail M. Ivanov and Yosuke Kobayashi for providing us with the posteriors used in the comparison. This work was supported by the AI Accelerator program of the Schmidt Futures Foundation. This work was also supported by NASA ROSES grant 12-EUCLID12-0004 NASA grant 15-WFIRST15-0008. J.H. has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 101025187. A.M.D. acknowledges funding from Tomalla Foundation for Research in Gravity and Boninchi Foundation. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the NSF, and the US Department of Energy Office of Science. The SDSS-III website is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
Author contributions
C.H., M.E., S.H., P.L., E.M., A.M.D., B.R.-S.B., and M.M.A. designed research; C.H. performed research; C.H., M.E., S.H., J.H., P.L., E.M., A.M.D., and B.R.-S.B. contributed new reagents/analytic tools; C.H., M.E., S.H., J.H., P.L., E.M., C.M., A.M.D., and B.R.-S.B. analyzed data; and C.H., M.E., S.H., J.H., P.L., E.M., C.M., A.M.D., and B.R.-S.B. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
Dataset data have been deposited in Zenodo (https://doi.org/10.5281/zenodo.8221749) (89).
Supporting Information
References
- 1.D. Collaboration et al., The DESI experiment. Part I: Science, targeting, and survey design. arXiv [Preprint] (2016). http://arxiv.org/abs/1611.00036 (Accessed 20 July 2021).
- 2.D. Collaboration et al., The DESI experiment. Part II: Instrument design. arXiv [Preprint] (2016). http://arxiv.org/abs/1611.00037 (Accessed 20 July 2021).
- 3.B. Abareshi et al., Overview of the instrumentation for the dark energy spectroscopic instrument. arXiv [Preprint] (2022). https://arxiv.org/abs/2205.10939 (Accessed 26 May 2022).
- 4.Takada M., et al. , Extragalactic science, cosmology, and Galactic archaeology with the Subaru Prime Focus Spectrograph. Publ. Astron. Soc. Japan 66, R1 (2014). [Google Scholar]
- 5.N. Tamura et al., Prime Focus Spectrograph (PFS) for the Subaru telescope: Overview, recent progress, and future perspectives. arXiv [Preprint] (2016). http://arxiv.org/abs/1608.01075 (Accessed 12 April 2021). Ground-based and airborne instrumentation for astronomy VI, vol. 9908, 99081M.
- 6.R. Laureijs et al., Euclid definition study report. arXiv [Preprint] (2011). http://arxiv.org/abs/1110.3193 (Accessed 5 June 2021).
- 7.D. Spergel et al., Wide-field infrarred survey telescope-astrophysics focused telescope assets WFIRST-AFTA 2015 report. arXiv [Preprint] (2015). https://arxiv.org/abs/1503.03757 (Accessed 18 January 2021).
- 8.Wang Y., et al. , The high latitude spectroscopic survey on the Nancy Grace Roman Space Telescope. Astrophys. J. 928, 1 (2022). [Google Scholar]
- 9.Beutler F., et al. , The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Anisotropic galaxy clustering in Fourier space. Mon. Not. R. Astron. Soc. 466, 2242–2260 (2017). [Google Scholar]
- 10.Colas T., d’Amico G., Senatore L., Zhang P., Beutler F., Efficient cosmological analysis of the SDSS/BOSS data from the effective field theory of large-scale structure. J. Cosmol. Astropart. Phys. 2020, 001 (2020). [Google Scholar]
- 11.d’Amico G., et al. , The cosmological analysis of the SDSS/BOSS data from the effective field theory of large-scale structure. J. Cosmol. Astropart. Phys. 2020, 005 (2020). [Google Scholar]
- 12.Ivanov M. M., Simonović M., Zaldarriaga M., Cosmological parameters from the BOSS galaxy power spectrum. J. Cosmol. Astropart. Phys. 2020, 042 (2020). [Google Scholar]
- 13.Chen S. F., White M., DeRose J., Kokron N., Cosmological analysis of three-dimensional BOSS galaxy clustering and Planck CMB lensing cross correlations via Lagrangian perturbation theory. J. Cosmol. Astropart. Phys. 2022, 041 (2022). [Google Scholar]
- 14.S. F. Chen, Z. Vlah, M. White, A new analysis of galaxy 2-point functions in the BOSS survey, including full-shape information and post-reconstruction BAO. J. Cosmol. Astropart. Phys. 2022, 008 (2022).
- 15.Kobayashi Y., Nishimichi T., Takada M., Miyatake H., Full-shape cosmology analysis of the SDSS-III BOSS galaxy power spectrum using an emulator-based halo model: A 5% determination of . Phys. Rev. D 105, 083517 (2022). [Google Scholar]
- 16.Bernardeau F., Colombi S., Gaztanaga E., Scoccimarro R., Large-scale structure of the universe and cosmological perturbation theory. Phys. Rep. 367, 1–248 (2002). [Google Scholar]
- 17.V. Desjacques, D. Jeong, F. Schmidt, Large-scale galaxy bias large-scale galaxy bias. arXiv [Preprint] (2016). http://arxiv.org/abs/1611.09787 (Accessed 1 June 2021).
- 18.Philcox O. H. E., Ivanov M. M., The BOSS DR12 full-shape cosmology: CDM constraints from the large-scale galaxy power spectrum and bispectrum monopole. Phys. Rev. D 105, 043517 (2022). [Google Scholar]
- 19.G. D’Amico, Y. Donath, M. Lewandowski, L. Senatore, P. Zhang, The BOSS bispectrum analysis at one loop from the Effective Field Theory of Large-Scale Structure. arXiv [Preprint] (2022). https://arxiv.org/abs/2206.08327 (Accessed 13 October 2022).
- 20.Naidoo K., Massara E., Lahav O., Cosmology and neutrino mass with the minimum spanning tree. Mon. Not. R. Astron. Soc. 513, 3596–3609 (2022). [Google Scholar]
- 21.Reid B. A., Seo H. J., Leauthaud A., Tinker J. L., White M., A 2.5 per cent measurement of the growth rate from small-scale redshift space clustering of SDSS-III CMASS galaxies. Mon. Not. R. Astron. Soc. 444, 476–502 (2014). [Google Scholar]
- 22.Zhai Z., et al. , The Aemulus project. III. Emulation of the galaxy correlation function. Astrophys. J. 874, 95 (2019). [Google Scholar]
- 23.Lange J. U., et al. , Five per cent measurements of the growth rate from simulation-based modelling of redshift-space clustering in BOSS LOWZ. Mon. Not. R. Astron. Soc. 509, 1779–1804 (2022). [Google Scholar]
- 24.Zhai Z., et al. , The Aemulus Project V: Cosmological constraint from small-scale clustering of BOSS galaxies. Astrophys. J 948, 99 (2023). [Google Scholar]
- 25.Ross A. J., et al. , The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Analysis of potential systematics. Mon. Not. R. Astron. Soc. 424, 564–590 (2012). [Google Scholar]
- 26.Ross A. J., et al. , The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Observational systematics and baryon acoustic oscillations in the correlation function. Mon. Not. R. Astron. Soc. 464, 1168–1191 (2017). [Google Scholar]
- 27.Guo H., Zehavi I., Zheng Z., A new method to correct for fiber collisions in galaxy two-point statistics. Astrophys. J. 756, 127 (2012). [Google Scholar]
- 28.Hahn C., Scoccimarro R., Blanton M. R., Tinker J. L., Rodríguez-Torres S. A., The effect of fiber collisions on the galaxy power spectrum multipoles. Mon. Not. R. Astron. Soc. 467, 1940–1956 (2017). [Google Scholar]
- 29.Bianchi D., et al. , Unbiased clustering estimates with the DESI fibre assignment. Mon. Not. R. Astron. Soc. 481, 2338–2348 (2018). [Google Scholar]
- 30.Zehavi I., et al. , Galaxy clustering in early Sloan digital sky survey redshift data. Astrophys. J. 571, 172–190 (2002). [Google Scholar]
- 31.Anderson L., et al. , The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 441, 24–62 (2014). [Google Scholar]
- 32.Hahn C., Villaescusa-Navarro F., Castorina E., Scoccimarro R., Constraining with the bispectrum. Part I. Breaking parameter degeneracies. J. Cosmol. Astropart. Phys. 03, 040 (2020). [Google Scholar]
- 33.Hahn C., Villaescusa-Navarro F., Constraining M with the bispectrum. Part II. The information content of the galaxy bispectrum monopole. J. Cosmol. Astropart. Phys. 2021, 029 (2021). [Google Scholar]
- 34.Massara E., Villaescusa-Navarro F., Ho S., Dalal N., Spergel D. N., Using the marked power spectrum to detect the signature of neutrinos in large-scale structure. Phys. Rev. Lett. 126, 011301 (2023). [DOI] [PubMed] [Google Scholar]
- 35.Massara E., et al. , Cosmological information in the marked power spectrum of the galaxy field. Astrophys. J. 951, 70 (2023). [Google Scholar]
- 36.Y. Wang et al., Extracting high-order cosmological information in galaxy surveys with power spectra. arXiv [Preprint] (2022). https://arxiv.org/abs/2202.05248 (Accessed 6 June 2022).
- 37.Hou J., Moradinezhad Dizgah A., Hahn C., Massara E., Cosmological information in skew spectra of biased tracers in redshift space. J. Cosmol. Astropart. Phys. 2023, 045 (2023). [Google Scholar]
- 38.M. Eickenberg et al., Wavelet moments for cosmological parameter estimation. arXiv [Preprint] (2022). https://arxiv.org/abs/2204.07646 (Accessed 20 May 2022).
- 39.Rodríguez-Torres S. A., et al. , The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Modelling the clustering and halo occupation distribution of BOSS CMASS galaxies in the Final Data Release. Mon. Not. R. Astron. Soc. 460, 1173–1187 (2016). [Google Scholar]
- 40.Rossi G., et al. , The completed SDSS-IV extended baryon oscillation spectroscopic survey: N-body mock challenge for galaxy clustering measurements. Mon. Not. R. Astron. Soc. 505, 377–407 (2021). [Google Scholar]
- 41.Cranmer K., Brehmer J., Louppe G., The frontier of simulation-based inference. Proc. Natl. Acad. Sci. U.S.A. 117, 30055–30062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.G. Papamakarios, T. Pavlakou, I. Murray, Masked autoregressive flow for density estimation. arXiv [Preprint] (2017). http://arxiv.org/abs/1705.07057.
- 43.Alsing J., Charnock T., Feeney S., Wandelt B., Fast likelihood-free cosmology with neural density estimators and active learning. Mon. Not. R. Astron. Soc. 488, 4440–4458 (2019). [Google Scholar]
- 44.Jeffrey N., Alsing J., Lanusse F., Likelihood-free inference with neural compression of DES SV weak lensing map statistics. Mon. Not. R. Astron. Soc. 501, 954–969 (2021). [Google Scholar]
- 45.L. Tortorelli et al., The PAU survey: Measurement of narrow-band galaxy properties with approximate Bayesian computation. arXiv [Preprint] (2021). http://arxiv.org/abs/2106.02651 (Accessed 13 September 2021).
- 46.M. Germain, K. Gregor, I. Murray, H. Larochelle, “MADE: masked autoencoder for distribution estimation” in Proceedings of 32nd International Conference Machine Learning (2015), vol. 37, pp. 881–889.
- 47.Eisenstein D. J., et al. , SDSS-III: Massive spectroscopic surveys of the distant universe, the milky way, and extra-solar planetary systems. Astron. J. 142, 72 (2011). [Google Scholar]
- 48.Dawson K. S., et al. , The Baryon oscillation spectroscopic survey of SDSS-III. Astron. J. 145, 10 (2013). [Google Scholar]
- 49.C. Hahn et al., SIMBIG: Mock challenge for a forward modeling approach to galaxy clustering. J. Cosmol. Astropart. Phys.2023, 010 (2023).
- 50.Cameron E., Pettitt A. N., Approximate Bayesian computation for astronomical model analysis: A case study in galaxy demographics and morphological transformation at high redshift. Mon. Not. R. Astron. Soc. 425, 44–65 (2012). [Google Scholar]
- 51.Weyant A., Schafer C., Wood-Vasey W. M., Likelihood-free cosmological inference with type Ia Supernovae: Approximate Bayesian computation for a complete treatment of uncertainty. Astrophys. J. 764, 116 (2013). [Google Scholar]
- 52.Hahn C., et al. , Approximate Bayesian computation in large scale structure: Constraining the galaxy-halo connection. Mon. Not. R. Astron. Soc. 469, 2791–2805 (2017). [Google Scholar]
- 53.D. Huppenkothen, M. Bachetti, Accurate X-ray timing in the presence of systematic biases with simulation-based inference. arXiv [Preprint] (2021). https://arxiv.org/abs/2104.03278 (Accessed 29 October 2021).
- 54.Zhang K., et al. , Real-time likelihood-free inference of roman binary microlensing events with amortized neural posterior estimation. Astron. J. 161, 262 (2021). [Google Scholar]
- 55.Hahn C., Melchior P., Accelerated Bayesian SED modeling using amortized neural posterior estimation. Astrophys. J 938, 11 (2022). [Google Scholar]
- 56.Tabak E. G., Vanden-Eijnden E., Density estimation by dual ascent of the log-likelihood. Commun. Math. Sci. 8, 217–233 (2010). [Google Scholar]
- 57.Tabak E. G., Turner C. V., A family of nonparametric density estimation algorithms. Commun. Pure Appl. Math. 66, 145–164 (2013). [Google Scholar]
- 58.Villaescusa-Navarro F., et al. , The Quijote simulations. Astrophys. J. Suppl. Ser. 250, 2 (2020). [Google Scholar]
- 59.Behroozi P. S., Wechsler R. H., Wu H. Y., The ROCKSTAR phase-space temporal halo finder and the velocity offsets of cluster cores. Astrophys. J. 762, 109 (2013). [Google Scholar]
- 60.Knebe A., et al. , Haloes gone MAD: The halo-finder comparison project. Mon. Not. R. Astron. Soc. 415, 2293–2318 (2011). [Google Scholar]
- 61.Zheng Z., Coil A. L., Zehavi I., Galaxy evolution from halo occupation distribution modeling of DEEP2 and SDSS galaxy clustering. Astrophys. J. 667, 760–779 (2007). [Google Scholar]
- 62.A. R. Zentner, A. Hearin, F. C. van den Bosch, J. U. Lange, A. Villarreal, Constraints on assembly bias from galaxy clustering. arXiv [Preprint] (2016). http://arxiv.org/abs/1606.07817 (Accessed 28 April 2021).
- 63.Vakili M., Hahn C., How are galaxies assigned to halos? Searching for assembly bias in the SDSS galaxy clustering Astrophys. J. 872, 115 (2019). [Google Scholar]
- 64.Hadzhiyska B., et al. , Galaxy assembly bias and large-scale distribution: A comparison between IllustrisTNG and a semi-analytic model. Mon. Not. R. Astron. Soc. 508, 698–718 (2021). [Google Scholar]
- 65.Carlson J., White M., Embedding realistic surveys in simulations through volume remapping. Astrophys. J. Suppl. Series 190, 311–314 (2010). [Google Scholar]
- 66.P. Collaboration et al., Planck 2018 results. VI. Cosmological parameters. arXiv [Preprint] (2018). http://arxiv.org/abs/1807.06209 (Accessed 23 July 2021).
- 67.Hand N., Li Y., Slepian Z., Seljak U., An optimal FFT-based anisotropic power spectrum estimator. J. Cosmol. Astro-Particle Phys. 07, 002 (2017). [Google Scholar]
- 68.Feldman H. A., Kaiser N., Peacock J. A., Power spectrum analysis of three-dimensional redshift surveys. Astrophys. J. 426, 23 (1994). [Google Scholar]
- 69.Kobayashi Y., Nishimichi T., Takada M., Miyatake H., Full-shape cosmology analysis of SDSS-III BOSS galaxy power spectrum using emulator-based halo model: A determination of . Phys. Rev. D 105, 083517 (2022). [Google Scholar]
- 70.B. Uria, M. A. Côté, K. Gregor, I. Murray, H. Larochelle, Neural autoregressive distribution estimation. arXiv [Preprint] (2016). http://arxiv.org/abs/1605.02226 (Accessed 27 December 2021).
- 71.D. S. Greenberg, M. Nonnenmacher, J. H. Macke, Automatic posterior transformation for likelihood-free inference. arXiv [Preprint] (2019). https://arxiv.org/abs/1905.07488 (Accessed 14 December 2021).
- 72.Tejero-Cantero A., et al. , Sbi: A toolkit for simulation-based inference. J. Open Source Softw. 5, 2505 (2020). [Google Scholar]
- 73.D. P. Kingma, J. Ba, Adam: A method for stochastic optimization. arXiv [Preprint] (2017). http://arxiv.org/abs/1412.6980 (Accessed 28 December 2021).
- 74.B. Dey et al., “Calibrated Predictive Distributions via Diagnostics for Conditional Coverage” in Proceedings of the Thirty-ninth International Conference on Machine Learning (ICML, Baltimore, MD, 2022).
- 75.D. Zhao, N. Dalmasso, R. Izbicki, A. B. Lee, “Diagnostics for conditional density models and Bayesian inference algorithms” in Proceedings of the Thirty-Seventh Conference on Uncertainty in Artificial Intelligence (PMLR, 2021), pp. 1830–1840.
- 76.Cacciato M., van den Bosch F. C., More S., Mo H., Yang X., Cosmological constraints from a combination of galaxy clustering and lensing—III. Application to SDSS data. Mon. Not. R. Astron. Soc. 430, 767–786 (2013). [Google Scholar]
- 77.Mandelbaum R., et al. , Cosmological parameter constraints from galaxy-galaxy lensing and galaxy clustering with the SDSS DR7. Mon. Not. R. Astron. Soc. 432, 1544–1575 (2013). [Google Scholar]
- 78.A. Leauthaud et al., Lensing is low: Cosmology, galaxy formation or new physics? Mon. Not. R. Astron. Soc.467, 3024–3047 (2017).
- 79.Hikage C., et al. , Cosmology from cosmic shear power spectra with Subaru Hyper Suprime-Cam first-year data. Publ. Astron. Soc. Japan 71, 43 (2019). [Google Scholar]
- 80.M. Asgari et al., KiDS-1000 cosmology: Cosmic shear constraints and comparison between two point statistics. Astron. Astrophys.645, A104 (2021).
- 81.Krolewski A., Ferraro S., White M., Cosmological constraints from unWISE and Planck CMB lensing tomography. J. Cosmol. Astropart. Phys. 2021, 028 (2021). [Google Scholar]
- 82.Amon A., et al. , Dark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to data calibration. Phys. Rev. D 105, 023514 (2022). [Google Scholar]
- 83.Meerburg P. D., Alleviating the tension at low through axion monodromy. Phys. Rev. D 90, 063529 (2014). [Google Scholar]
- 84.Chudaykin A., Gorbunov D., Tkachev I., Dark matter component decaying after recombination: Sensitivity to baryon acoustic oscillation and redshift space distortion probes. Phys. Rev. D 97, 083508 (2018). [Google Scholar]
- 85.Di Valentino E., Melchiorri A., Mena O., Vagnozzi S., Nonminimal dark sector physics and cosmological tensions. Phys. Rev. D 101, 063502 (2020). [Google Scholar]
- 86.Abellán G. F., Murgia R., Poulin V., Lavalle J., Implications of the S8 tension for decaying dark matter with warm decay products. Phys. Rev. D 105, 063525 (2022). [Google Scholar]
- 87.Gil-Marín H., et al. , The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: RSD measurement from the power spectrum and bispectrum of the DR12 BOSS galaxies. Mon. Not. R. Astron. Soc. 465, 1757–1788 (2017). [Google Scholar]
- 88.Reid B., et al. , SDSS-III Baryon Oscillation Spectroscopic Survey Data Release 12: Galaxy target selection and large-scale structure catalogues. Mon. Not. R. Astron. Soc. 455, 1553–1573 (2016). [Google Scholar]
- 89.C. Hahn et al., A forward modeling approach to analyzing galaxy clustering with SimBIG. Zenodo. 10.5281/zenodo.8221749. Deposited 7 August 2023. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
In anim_slices_4.mov, we present the projected slices of the galaxy distribution along the radial direction from the point of the view of an observer. The top and bottom panels present the BOSS CMASS and simulated galaxy samples respectively. The right panels highlight the progression of the radial slice for both samples.
In anim_slices_1.mov, we present projected slice of the galaxy distribution along the Z axis for the BOSS CMASS (top) and simulated (bottom) galaxy samples. The panels on the right highlight the progression of the Z slice for both samples.
In anim_3d_rot.mov, we present a rotating view with of the galaxy distribution with the BOSS CMASS and simulated galaxy samples on the left and right panels, respectively. The color indicates galaxy redshift.
Data Availability Statement
Dataset data have been deposited in Zenodo (https://doi.org/10.5281/zenodo.8221749) (89).