Posterior marginalization accelerates Bayesian inference for dynamical models of biological processes

Summary

Bayesian inference is an important method in the life and natural sciences for learning from data. It provides information about parameter and prediction uncertainties. Yet, generating representative samples from the posterior distribution is often computationally challenging. Here, we present an approach that lowers the computational complexity of sample generation for dynamical models with scaling, offset, and noise parameters. The proposed method is based on the marginalization of the posterior distribution. We provide analytical results for a broad class of problems with conjugate priors and show that the method is suitable for a large number of applications. Subsequently, we demonstrate the benefit of the approach for applications from the field of systems biology. We report an improvement up to 50 times in the effective sample size per unit of time. As the scheme is broadly applicable, it will facilitate Bayesian inference in different research fields.

Graphical abstract

Highlights

• •Bayesian posterior distribution inference for mathematical models can be challenging
• •Our mathematical approach applies marginalization to reduce parameter dimensionality
• •Our method increases the effective sample size per unit of time for all tested models
• •Particularly beneficial for multi-modal posterior problems

Biological sciences; Mathematical biosciences; Systems biology

Introduction

Mathematical models are important tools for understanding and predicting the dynamics of many processes, such as signaling processing in biological systems,^1,2,3 patient progression,^4,5 and epidemics.^6,7 However, the parameters of mathematical models are in general unknown and need to be inferred from experimental data. This is an inherently challenging problem and complicated by the fact that, in addition to the dynamical properties of interest (e.g., rate constants and initial conditions), characteristics of the measurement process may also be unknown. In systems biology, most measurement techniques, including western blotting,⁸ fluorescence microscopy,⁹ and mass spectrometry,¹⁰ are not fully quantitative but provide only relative information. Moreover, there is often an unknown offset and/or noise level.¹¹ Accordingly, unknown observation parameters, such as scaling factors but also offsets and noise levels, have to be estimated along with parameters of the mathematical models.^12,13,14

Bayesian inference is often used to estimate unknown parameters.^15,16,17 A particularly common approach is to employ Markov chain Monte Carlo (MCMC) algorithms, such as (adaptive) Metropolis-Hastings,¹⁸ Hamiltonian Monte Carlo methods,^19,20 and parallel tempering,²¹ to generate representative samples from the posterior distribution. Yet, with increasing number of unknown parameters, the application of MCMC algorithms becomes challenging.²² This is a bottleneck that leaves sampling methods on the edge of computational feasibility. In principle, the challenge can be addressed by reducing the dimensionality of the sampling problem, e.g., by marginalizing over nuisance parameters (as, e.g., demonstrated in cosmology²³). However, there is no generic and broadly applicable framework.

In frequentist inference, a template for the reduction of the dimensionality of parameter estimation problems has been provided.^14,24,25 Here, hierarchical optimization approaches have been developed to determine the maximum likelihood estimate. These methods exploit that the observation parameters can be computed analytically for a given set of model parameters. It has been shown that this benefits the convergence of optimization methods and the computational efficiency, while providing the same results (see, e.g., Loos et al.²⁴). Yet, these concepts cannot be directly translated to Bayesian inference as we are not interested in only optimal point estimates, but in (marginal) posterior distributions over parameters.

In this manuscript, we introduce a generic method for improving sampling efficiency by marginalizing over observation parameters. We provide analytical results for the marginalization over complex posterior distributions for dynamical biological processes—described, e.g., by ordinary differential equations (ODEs)—with a broad class of observation models. The marginalization yields a lower dimensional posterior for MCMC sampling. Samples of the original posterior can be obtained by subsequent sampling of the observation parameters conditioned on the remaining parameters. To illustrate the properties of the proposed approach, we benchmark its performance with a collection of published models, including models for which current available sampling strategies are computationally infeasible. We demonstrate that the proposed method achieves higher sampling efficiencies by reducing the auto-correlation of the samples and increasing the transition probabilities between posterior modes. Indeed, it turns computationally infeasible sampling problems feasible, increasing the set of problems which can be tackled using Bayesian inference.

Results

Many model structures allow for analytical marginalization of parameters and sampling in lower dimensional space

To facilitate Bayesian inference for mathematical models with observation parameters, we developed and implemented a marginalization-based sampling approach (Figure 1). The approach allows for inferring the parameters of mathematical models, such as ODEs and partial differential equation models, from data via observation models with scaling, offset, and noise parameters. For a mathematical model with parameter θ and time- and parameter-dependent states $x\left(t,\theta \right)$, consider the case of a one-dimensional observable with additive Gaussian measurement noise and observation model

$$\overline{y}=\left(s\cdot h\left(x\left(t,\theta \right),\theta \right)+b\right)+ϵ,\text{with}\epsilon \sim \mathcal{N}\left(0,{\sigma }^2\right)$$ (Equation 1)

in which $h\left(x,\theta \right)$ describes the measured quantity, s is the scaling factor ($\in \mathbb{R}$), b is the offset ($\in \mathbb{R}$), and ${\sigma }^2$ is the variance of the measurement noise ($\in {\mathbb{R}}_{+}$). A collection of measurements ${\overline{y}}_k$ at time points $t_k$, with $k=1,\dots ,n_t$, is denoted as data $\mathcal{D}={\left\{\left({\overline{y}}_k,t_k\right)\right\}}_{k=1}^{n_t}$. Following Bayes’ theorem, the posterior distribution of the parameters $\left(\theta ,s,b,{\sigma }^2\right)$ given the data $\mathcal{D}$ is

$$p\left(\theta ,s,b,{\sigma }^2\mid \mathcal{D}\right)=\frac{p\left(\mathcal{D}\mid \theta ,s,b,{\sigma }^2\right)p\left(\theta ,s,b,{\sigma }^2\right)}{p\left(\mathcal{D}\right)}\text{,}$$ (Equation 2)

in which $p\left(\mathcal{D}\mid \theta ,s,b,{\sigma }^2\right)$ denotes the likelihood, $p\left(\theta ,s,b,{\sigma }^2\right)$ denotes the prior distribution, and $p\left(\mathcal{D}\right)$ denotes the marginal probability.

Figure 1.

Standard and marginalization-based Markov chain Monte Carlo sampling

(A) Illustration of the general marginalization concept.

(B) Standard approach.

(C) Marginalization-based approach depicting: (Step 1) the sequential integration of the observation parameters s, b, and ${\sigma }^2$ to evaluate $p\left(\theta \mid \mathcal{D}\right)$, and (Step 2) the (optional) conditional sampling of the marginalized observation parameters.

The standard approach is to use MCMC methods to obtain representative samples from the joint posterior distribution for model parameters θ and observation parameters s, b, and ${\sigma }^2$ (2) for subsequent analysis (Figure 1B). All parameters are sampled jointly, disregarding their nature (Figure 1B); in particular note that the state $x\left(t,\theta \right)$ and the value of the observation map $h\left(x\left(t,\theta \right),\theta \right)$ only depend on θ but not on s, b, or ${\sigma }^2$. This approach is often challenging and even infeasible for models with large datasets since the number of observation parameters can easily exceed the number of model parameters (see, e.g., Bachmann et al. and Raimúndez et al.^26,27).

To simplify the sampling process, we propose a marginalization-based approach, which exploits a decomposition of the sampling problem in two steps (Figure 1C). In Step 1, we consider the marginalization of the posterior distribution (2) with respect to the observation parameters s, b, and ${\sigma }^2$, yielding

$$p\left(\theta \mid \mathcal{D}\right)=\frac{p\left(\mathcal{D}\mid \theta \right)p\left(\theta \right)}{p\left(\mathcal{D}\right)}$$

with $p\left(\mathcal{D}\mid \theta \right)$ as the marginal likelihood given by

$$p\left(\mathcal{D}\mid \theta \right)={\int }_0^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }p\left(\mathcal{D}\mid \theta ,s,b,{\sigma }^2\right)p\left(s,b,{\sigma }^2|\theta \right)\mathrm{d}s\mathrm{d}b\mathrm{d}{\sigma }^2\text{,}$$ (Equation 3)

assuming that the prior can be written as $p\left(\theta ,s,b,{\sigma }^2\right)=p\left(s,b,{\sigma }^2|\theta \right)p\left(\theta \right)$. For various choices of noise models and prior distributions (in particular conjugate priors), this marginal likelihood can be computed in closed form. This is for instance the case for the combination of additive Gaussian noise with a joint prior distribution for s, b, and ${\sigma }^2$,

$$p\left(s,b,{\sigma }^2|\theta \right)=\mathcal{N}\left(s\mid \nu ,{\sigma }^2/\tau \right)\cdot \mathcal{N}\left(b\mid \mu ,{\sigma }^2/\kappa \right)\cdot {\mathrm{\Gamma }}^{-1}\left({\sigma }^2\mid \alpha ,\beta \right)\text{,}$$

in which $\nu ,\mu \in \mathbb{R}$ and $\tau ,\kappa ,\alpha ,\beta \in {\mathbb{R}}_{+}$ denote hyperparameters of the Normal-Inverse-Gamma-distributed joint prior, and ${\mathrm{\Gamma }}^{-1}(\cdot )$ denotes the Inverse-Gamma function. The hyperparameters might depend on θ. Here, we obtain for observations ${\overline{y}}_i$ with $i=1,\dots ,n_t$ the closed-form expression for the marginal likelihood as

$$p\left(\mathcal{D}\mid \theta \right)=\frac{{\left(\beta /C\right)}^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right){\left(2\pi C\right)}^{n_t/2}}\cdot \mathrm{\Gamma }\left(\alpha +\frac{n_t}{2}\right)\cdot \sqrt{\frac{\kappa \tau }{\left(n_t+\kappa \right)\left(\tau +{\sum }_{i=1}^{n_t}{h}_i^2\right)-{\left({\sum }_{i=1}^{n_t}{h}_i\right)}^2}}$$ (Equation 4)

with $h_i:=h\left(x\left(t_i,\theta \right),\theta \right)$ and parameter-dependent constant

$$C:=\beta +\frac{1}{2}\left(\kappa {\mu }^2+\tau {\nu }^2+\sum _{i=1}^{n_t}{\overline{y}}_i^2-\frac{{\left(\kappa \mu +{\sum }_{i=1}^{n_t}{\overline{y}}_i\right)}^2}{n_t+\kappa }-\frac{{\left(\left(\kappa \mu +{\sum }_{i=1}^{n_t}{\overline{y}}_i\right)\left({\sum }_{i=1}^{n_t}{h}_i\right)-\left(n_t+\kappa \right)\left(\tau \nu +{\sum }_{i=1}^{n_t}{h}_i{\overline{y}}_i\right)\right)}^2}{\left(n_t+\kappa \right)\left(\left(n_t+\kappa \right)\left(\tau +{\sum }_{i=1}^{n_t}{h}_i^2\right)-{\left({\sum }_{i=1}^{n_t}{h}_i\right)}^2\right)}\right)\text{.}$$

As the Normal-Inverse-Gamma prior is a conjugate prior for additive Gaussian noise, the marginal likelihood is analytically tractable. There are various other cases, including multiplicative Gaussian noise and even distributions with outliers. For the latter, Laplacian noise has shown to be more robust against measurement outliers.²⁸ Tables S1 and S2 summarize ten practically relevant cases for which we obtained closed-form expressions, and we are certain that many more are possible. For details on the derivation of all individual results (including two cases for Laplace distributed noise), we refer to the supplemental data.

Given the marginalized likelihood function $p\left(\mathcal{D}\mid \theta \right)$ and the prior $p\left(\theta \right)$, the posterior distribution $p\left(\theta \mid \mathcal{D}\right)$ of the parameters of the mathematical model can be sampled using MCMC and related methods. The sampling can be performed in the space of θ, as the observation parameters are implicitly considered (Figure 1C).

The samples of model parameters θ from $p\left(\theta \mid \mathcal{D}\right)$ allow for the assessment of the model properties and its uncertainties. In this regard, there is no difference of sampling the marginalized posterior distribution $p\left(\theta \mid \mathcal{D}\right)$ compared to projecting the full posterior distribution $p\left(\theta ,s,b,{\sigma }^2\mid \mathcal{D}\right)$ onto the θ component. However, tasks like the assessment and plotting of the model-data mismatch also require the posterior of the observation parameters. These can be obtained by sampling from the conditional distribution $p\left(s,b,{\sigma }^2\mid \theta ,\mathcal{D}\right)$. As the observation parameters only influence the observation model (1) and not the calculation of state $x\left(t,\theta \right)$ and observable map $h\left(x,\theta \right)$, the conditional distribution can be expressed in closed form and sampled efficiently. For the aforementioned case, a matching sample of observation parameters for a given model parameter θ can be obtained by drawing from Gamma and Normal distributions:

$${\sigma }^2=1/\lambda \text{with}\lambda \propto \mathrm{\Gamma }\left({\alpha }^{\prime }=\alpha +\frac{n_t}{2},{\beta }^{\prime }=C\right)\text{,}$$

$$b\propto \mathcal{N}\left({\mu }^{\prime }=\frac{\kappa \mu +\left({\sum }_{i=1}^{n_t}{\overline{y}}_i-h_i\right)}{\kappa +n_t},{\lambda }^{\prime }=\lambda \left(n_t+\kappa \right)\right),\text{and}$$

$$s\propto \mathcal{N}\left({\mu }^{\prime }=\frac{\left(\kappa +n_t\right)\left(\tau \nu +{\sum }_{i=1}^{n_t}{h}_i{\overline{y}}_i\right)-\left(\kappa \mu +{\sum }_{i=1}^{n_t}{\overline{y}}_i\right)\left({\sum }_{i=1}^{n_t}{h}_i\right)}{\left(\kappa +n_t\right)\left(\tau +{\sum }_{i=1}^{n_t}{h}_i^2\right)-{\left({\sum }_{i=1}^{n_t}{h}_i\right)}^2},{\lambda }^{\prime }=\lambda \left(\tau +\sum _{i=1}^{n_t}{h}_i^2-\frac{{\left({\sum }_{i=1}^{n_t}{h}_i\right)}^2}{\left(n_t+\kappa \right)}\right)\right)\text{,}$$

with $h_i$ and C being evaluated for model parameter θ. This conditional sampling can be proven to provide the same correlation structure as directly sampling the full posterior distribution. For details on the derivation of the conditional sampling for the observation parameters we refer to the supplemental data. As the conditional sampling can be performed independently and does not require model simulation, it is computationally efficient. For additional observation models see Tables S1 and S2.

In summary, a broad spectrum of parameter estimation problems can be reformulated by performing an analytically tractable marginalization of their observation parameters. Sampling of this lower dimensional posterior distribution for the model parameters θ in combination with conditional sampling for the observation parameters allows the construction of samples from the full posterior distribution. Accordingly, the original sampling problem is decomposed in two sub-problems, of which the conditional sampling is optional.

Marginalization-based approach yields same results at lower computational cost

To compare the performance for the standard and marginalization-based approach, we performed a range of studies using (i) a simple test problem and (ii) published models and datasets.

As a simple test problem we considered a model of a conversion reaction process, $A\rightleftharpoons B$. This process was considered in various other publications^28,29 and can be described using a two-dimensional system of ODEs, with the concentrations of A and B as state variables. Here, we considered that the abundance of B is measured up to an unknown scaling, offset, and noise level. Accordingly, the mathematical model possesses two model parameters, the forward rate A to B, ${\theta }_1$, and the backward rate B to A, ${\theta }_2$, and three observation parameters, the scaling s, the offset b, and the noise variance ${\sigma }^2$ (Table 1). A detailed description of the model is provided in the STAR methods section.

Table 1.

Key numbers and features of the considered toy and benchmark models

Model ID	${\mathit{n}}_{\mathit{\theta }}$	${\mathit{n}}_{\mathit{s}}$	${\mathit{n}}_{\mathit{b}}$	${\mathit{n}}_{\mathit{\sigma }}$	Description	Reference
Toy	2	1	1	1	Conversion reaction	–
M1	13	3	–	–	EGF-AKT pathway	Fujita et al.37
M2	6	3	–	3	STAT5 dimerization	Boehm et al.38
M3	3	1	–	1	mRNA transfection	Leonhardt et al.39
M4	26	31	–	–	Gastric cancer signaling	Villaverde et al.40

The number of unknown model parameters $n_{\theta }$, unknown scaling parameters $n_s$, unknown offset parameters $n_b$, and unknown noise parameters $n_{\sigma }$, which are effectively sampled, are reported.

In the first step, we used the model to assess the correctness of the analytical marginalized likelihood (4) by comparing its agreement with numerical integration of Equation 3. The results show a perfect match for a range of different parameter values (Figure 2A). Yet, the evaluation of the analytical marginalized likelihood was five orders of magnitude faster than the numerical integration (Figure 2B), which highlights the importance of the analytical derivations. In the second step, we performed 100 independent MCMC sampling runs for the standard and marginalization-based approach. The runs employed a state-of-the-art adaptive Metropolis-Hastings method.¹⁸ We found a superior performance of the marginalization-based approach, as the observed effective sample size per unit of time was twice as high as for the standard approach (Figure 2C). This indicates that the marginalization-based approach facilitates already for simple problems the mixing of the MCMC chains and, hence, provides a more efficient exploration of the posterior. Moreover, the model fit for the best sample found (i.e., maximizing the posterior) coincided for both approaches (Figure 2D) as well as the marginal distributions for the model parameters ${\theta }_1$ and ${\theta }_2$ (Figures 2E and 2F), and the conditionally sampled observation parameters (Figures 2G–2I).

Figure 2.

Evaluation of the standard and marginalization-based approach for the toy model

(A) Comparison of analytical vs. numerical integration.

(B) Time comparison of analytical vs. numerical integration.

(C) Effective sample size per unit of time for 100 independent runs.

(D) Model fit of the best sample found during sampling from the standard (orange) and marginalization-based (purple) approach.

(E–I) Parameter marginal posterior distributions computed using a kernel density estimate for the model parameters (E) ${\theta }_1$ and (F) ${\theta }_2$, and the conditionally sampled observation parameters: (G) scaling factor s, (H) offset b, and (I) noise variance ${\sigma }^2$.

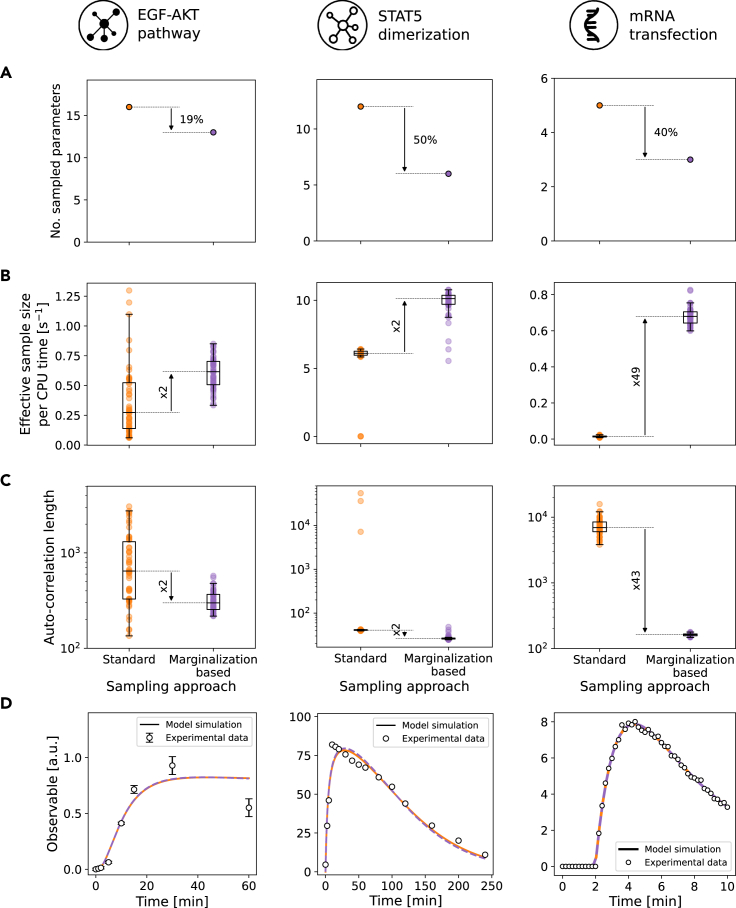
Following the promising results for the test problem, we evaluated the performance of the proposed marginalization-based approach for three already published models and datasets (Table 1 and STAR methods section). The models M1 to M3 describe cellular processes: (M1) epidermal growth factor (EGF)-induced protein kinase B (AKT) signaling; (M2) phosphorylation-dependent STAT5 dimerization; and (M3) mRNA transfection. The numbers of model and observation parameters differ, and so do the observation functions. Accordingly, different closed-form expressions for the marginalized likelihood function are used (Tables S1 and S2). More importantly, the full posterior distributions exhibit different characteristics, ranging for instance from uni- to bimodal.

For the considered application problems, the marginalization of the observation parameters reduced the dimensionality of the sampling problems by up to 50% (ranging from 19% to 50%) (Figure 3A). The validity of the analytical expressions for marginalized likelihoods was again confirmed using numerical integration (Figure S1). To evaluate the impact of this reduction on the sampling efficiency, we performed 50 independent MCMC sampling runs using the parallel tempering algorithm with 10 temperatures.²¹ All the runs were initialized at parameter values maximizing the posterior probability which were found using multi-start optimization.¹² For M1 and M2, these maximum a posteriori (MAP) estimates were unique, while for M3, two MAP estimates were found with identical posterior values. The sampling was run for ${10}^6$ iterations. Further details are provided in the STAR methods section. The high number of iterations allowed all MCMC runs of the standard and marginalized problem to converge according to the Geweke test.³⁰ Yet, the marginalization-based approach achieved a higher effective sample size per unit of computation time than the standard approach (Figure 3B). The improvement was problem dependent and ranged from 2 (M1 and M2) to nearly 50 (M3) times higher efficiency in the marginalization-based approach. As the computation time was similar, the core reason for this is a reduction in the auto-correlation length (Figure 3C). The model fits for the best sample found were identical for both approaches (Figures 3D, S2 and S3) as well as the parameter marginal distributions (Figures S4–S6).

Figure 3.

Evaluation of the standard and marginalization-based approach for the benchmark models

Models M1–M3 are shown from left to right.

(A) Number of sampled parameters.

(B) Effective sample size per unit of time.

(C) Auto-correlation length.

(D) Model fit of the best sample found during sampling. A subset of the experimental data is shown for M1 and M2. Complete datasets and parameter marginal distributions are depicted in Figures S2–S6. A comparison of analytical vs. numerical integration is shown in Figure S1.

In summary, test and application problems demonstrate the acceleration potential of the marginalization-based approach. The improvement was problem specific, with no clear dependence on the degree of dimensionality reduction, but in all cases substantial.

Marginalization-based approach improves transition rates between posterior modes

To understand for which problems the marginalization-based approach is expected to achieve a large acceleration, we considered the model M3. The posterior distribution for M3 is bimodal, and a simple explanation for the acceleration would have been that the bimodality is eliminated. Yet, this is not the case as the bimodality is related to a symmetry in model parameters. Numerical simulations as well as analytical results reveal that the observable trajectory remains unchanged when the mRNA and protein degradation rates are interchanged. As long as the optimal point is not located on the line of equal degradation rates, standard and marginalized posterior are bimodal.

We hypothesized that the large efficiency improvement is related to a lower minimum energy path for the transitions in the marginalized posterior. To assess this, we computed the minimum energy paths³¹ for the standard (Figures 4A and 4B) and marginalized posterior (Figures 4C and 4D) (see details in the STAR methods section). To our surprise, the minimum energy path is almost identical for both approaches (Figure 4E). Hence, there is at least no difference in the minimum energy path.

Figure 4.

Comparison of the minimum energy path for model M3

(A–D) Landscape of the optimized (A and B) posterior and (C and D) marginalized posterior for different fixed values of the model parameters β and δ. The difference with respect to the maximal posterior value is depicted.

(E) Transition coordinates for the minimum energy path.

In order to understand the improvement observed for runs of adaptive parallel tempering methods, we performed 10 runs of a single-chain adaptive Metropolis algorithm¹⁸ with ${10}^6$ iterations for exploring the posterior ($T=1$). We expected this to simplify the interpretation. Yet, the adaptive Metropolis algorithm was essentially unable to transition between the two modes of the posterior, meaning that efficiency improvements could not be assessed with reasonable computation time (see $T=1$ in Figure 5A). To assess the relative complexity of the sampling problem for standard and marginalization-based approach, we repeated the evaluation with the single-chain adaptive Metropolis algorithm for the tempered posterior, keeping the temperature fixed for a specific run. We found that the marginalization-based approach allows already at lower temperatures for transitions between the modes unlike the standard sampling approach (Figures 5A, S8, and S9). For temperatures such as $T=16$, the standard approach showed an average number of only 5 transitions between the modes with many runs only sampling from a single mode (Figures 5B and 5C), while for the marginalization-based approach on average $1.6\times {10}^4$ transitions occurred (Figures 5D and 5E). As the minimum barrier energy is conserved also for higher temperatures (Figure S7), this increase in the transition rate by four orders of magnitude for the same algorithm implies a lower overall complexity of the marginalization-based sampling problem.

Figure 5.

Quantification of the transitions between the posterior modes for different temperatures T for model M3

(A) Number of transitions per ${10}^6$ iterations for a range of temperatures for the standard (orange) and marginalization-based (purple) approach. A total of 10 chains per temperature value are depicted.

(B and D) Marginal distribution computed using a kernel density estimate and (C,E) parameter trace for the model parameter β of a representative chain obtained with the (B,C) standard and (D and E) marginalization-based approach for $T=16$.

(F and G) Direct transitions between the posterior modes of a representative chain along with the minimum energy path obtained with the (F) standard and (G) marginalization-based approach for $T=16$. See also Figures S7–S9.

As the increased transition rate is not caused by an altered energy path, we studied the transition paths. This revealed that the employed single-chain algorithm facilitates jumps over the valley in the objective function (Figures 5F and 5G), meaning that it transitions between high-probability regions around the local optima. These direct transitions appear at a high rate for the marginalization-based approach (Figure 5G), while they rarely happen for the standard approach (Figure 5F). For the latter, most transitions are along low-energy paths with posterior probabilities dropping below the minimum energy path. Accordingly, the transition behavior is for the marginalization-based approach more efficient than for the standard approach.

In summary, the in-depth study of the mRNA transfection model (M3) showed that the marginalization-based approach can achieve substantial accelerations as the structure of the sampling problem is simplified, e.g., by facilitating transitions between modes. The improvements are related to the interplay of sampling approach and problem geometry. In particular for challenging (e.g., multi-modal) problems a much greater improvement could be observed.

Marginalization-based approach enables Bayesian inference for large models

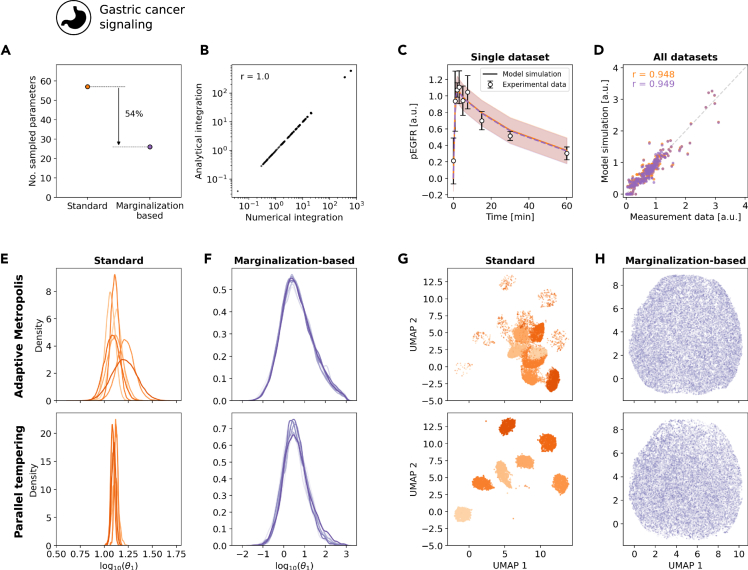
As the marginalization-based approach appeared beneficial for challenging problems, we assessed in a next step whether it enables Bayesian inference for problems for which standard approaches did not provide reproducible results in a reasonable time frame. Specifically, we considered an ODE model for signal transduction in gastric cancer cells (cell line MKN1) that was developed to unravel response and resistance markers.²⁷ This model possesses in total 57 unknown parameters, of which 26 are model parameters and 31 are observation parameters (Table 1, M4).

The application of the marginalization-based approach resulted in a reduction of the dimensionality of the sampling problem by over 50% (Figure 6A). For the 26 model parameters which remain to be sampled, we compared the marginal likelihoods as computed using the previously derived analytical formulas and numerical integration (Figure 6B). The agreement of the results (Pearson correlation $r\approx 1.0$) confirmed the correctness of our analytical integration.

Figure 6.

Convergence of the marginalization-based approach for model M4

(A) Number of sampled parameters.

(B) Scatterplot for the agreement of analytical and numerical integration.

(C and D) Model fit of the best sample found during sampling for, (C) a subset of the experimental data represented as mean +/− standard deviation and (D) the complete dataset in form of a scatterplot, the standard (orange) and marginalization-based approach (purple). (E–H) Results from adaptive Metropolis (top) and parallel tempering (bottom) are shown.

(E and F) Parameter marginal posterior distribution obtained using the (E) standard and (F) marginalization-based approach computed using a kernel density estimate for model parameter ${\theta }_1$.

(G and H) Dimensionality reduction for all samples from all runs for the (G) standard and (H) marginalization-based approach using the UMAP representation. Different shades correspond to individual runs. The UMAPs were constructed using the Python package umap.³² See also Figures S10–S12.

To determine the parameters of the model, we performed sampling using standard and marginalization-based approach. The adaptive Metropolis-Hastings algorithm¹⁸ and the adaptive parallel tempering algorithm²¹ employed in the previous sections were run 10 times with different starting points and random seeds for ${10}^6$ iterations for the adaptive Metropolis-Hastings and ${10}^5$ iterations for the adaptive parallel tempering algorithm. We found that while all runs in the marginalization-based approach (and for both sampling algorithms) successfully finished within a run time limit of 7 days, only 7 out of 10 runs successfully finished for the standard approach for each sampling algorithm. The MAP estimates observed in the different runs provided similar fits (Figures 6C and 6D). In contrast, the marginal distributions of the model parameters differed, with the marginalization-based approach mostly providing broader parameter distributions than the standard approach (Figures 6E and 6F). The assessment of the reproducibility of the marginal distributions revealed a high variability between different runs performed using the standard approach (Figures 6E and S10). On the contrary, for the marginalization-based approach a good agreement between runs was observed (Figures 6F and S11), indicating reproducibility. To verify that the behavior observed for the individual parameters is maintained in the full parameter space, we analyzed the overall agreement of all parameter samples across all runs for the standard and marginalization-based approach by visualizing the samples using the uniform manifold approximation and projection (UMAP) representation.³² We found that the individual runs of the standard approach represent individual clusters in the UMAP (Figure 6G), while the individual runs of the marginalization-based approach were indistinguishable (Figure 6H). This finding was supported by the distribution of the nearest neighbors (Figure S12). This revealed that: (i) in the marginalization-based approach all the individual runs sample from the same distribution and (ii) the standard approach failed for both algorithms considered here.

The study of the model of signal processing in gastric cancer cells revealed that marginalization-based approach allows for reproducible sampling in problems, where the standard approach failed. While for the marginalization-based approach all runs provided consistent results, the standard approach failed to converge within an average central processing unit (CPU) time of 150 h rendering its application impracticable. Furthermore, our study provides improved estimates for the parameters (Figure S13) of important processes of a drug used in clinical practice.

In summary, the application of our marginalization-based approach to Bayesian inference for models with relative measurement data shows consistently that our approach yields the same marginal distributions for the parameters as the standard approach, while being highly more efficient in exploring the parameter space and enabling Bayesian inference of larger models, which was not possible before with the standard approach.

Discussion

Bayesian inference for models of biological processes requires the consideration of parameters of the dynamical systems as well as the measurement process. The unknown scaling factors, offsets, and noise levels often resemble a large fraction of the overall parameters.¹² This complicates sampling and can render the generation of representative samples practically infeasible. Here, we address this challenge by proving that an (analytical) marginalization of the posterior even for dynamical models, for common observation and noise models, and plausible priors. We provide analytical result for additive normal, multiplicative log-normal, and additive Laplace noise for different choices of unknown parameters and priors. This approach allows for the construction of a sample from the full posterior by (i) sampling a marginalized posterior for the parameters of the dynamical systems and (ii) conditional sampling of the observation parameters.

We evaluated the performance of our marginalization-based approach and compared it to the standard approach for four published models, with differences in their complexity. This revealed an increased effective sample size per unit of time, and increased transition probabilities between posterior modes. The marginalization-based approach was for all considered problems more efficient than the standard approach, but—more importantly—it also enabled the assessment of the posterior distribution for larger models for which the standard approach failed to converge in the considered time frame. Interestingly, there was no strong relation between the reduction of the problem dimensionality and the improvement in efficiency. The improvement seems to rather depend in the characteristics of the marginalized posterior and the interplay of these characteristics with the employed sampling algorithm. This is consistent with previous finding for hierarchical optimization,²⁵ where a minimal reduction of the problem dimensionality was shown to substantially improve the conditioning of the optimization problem. Based on our observations we expect the sampling behavior to benefit substantially even from the removal of a small number of parameters, as (i) the likelihood value is often very sensitive to them, which produces narrow rims in the posterior distribution, and as (ii) the removal of a small number of parameters can result in a substantially increased probability to jump between modes. The latter was observed for the model of mRNA transfection. A review of the PEtab benchmark collection³³ showed that 20 out of 30 dynamical models used in systems biology and medicine possess unknown observation parameters. Hence, a large number of modeling projects could profit from the approach.

The approach presented here is not limited to relative measurement data, but also applicable to absolute measurements. As for these, the noise parameters would still have to be inferred (Tables S1 and S2). We provide the detailed derivation in the supplemental data. Accordingly, our approach can be used for combinations of relative and absolute data. Also, it is applicable to different measurement process functions and noise models to the ones considered here. We hypothesize that also an extension to correlated noise is possible, but this remains to be assessed.

The choice of conjugate priors for the marginalized parameters eased the analytical derivation of the marginal posterior. This implies in our case that observable and noise parameters are not independent under the prior. Mostly, this is not a problem since both parameters are related to the measurement process. However, in some cases, there might be known parameters to be independent; therefore, other prior distribution assumptions must be considered. It should be noted that the concept of marginalization is not restricted to integrals that are analytically solvable, but also numerical integration schemes can be considered. However, this would increase the required computation time (as observed in Figure 2B), but very likely the improved mixing properties would be maintained. Whether the improved mixing out-weights the increased computational cost will be problem dependent but might not be unlikely (and would have been the case for the mRNA transfection model (M3)) as the numerical integration over observation parameters will not require numerical simulations of the model. In future research projects this question should be tackled via a comprehensive benchmarking. Similarly, while in this manuscript only cases were presented in which the conditional sampling of observation parameters was straightforward due to the use of conjugate priors, the approach is also applicable if this does not hold. In this case the sampling of the parameters θ is not impaired, but MCMC sampling or rejection sampling might need to be used to obtain sample for the observation parameters.

The proposed method was beneficial in combination with adaptive Metropolis-Hastings and adaptive parallel tempering algorithms. We expect that the same will hold true for sampling algorithms exploiting gradient information, such as Hamilton Monte Carlo sampling.^19,20 As the marginal likelihood is differentiable, merely the derivation and implementation of the gradient are required. The usage of methods which exploit the Riemann geometry of the parameter space of statistical models, e.g., Metropolis-adjusted Langevin algorithm,³⁴ might be slightly more involved. This requires the derivation of the marginalized Fisher information matrix. While we assume that this can be derived in closed form or at least be accurately approximated, the corresponding results are not yet available. Alternatively, automatic differentiation could be employed to obtain gradients.³⁵ The assessment of the impact of posterior marginalization on the performance of these samplers as well as other sampling methods would be highly beneficial but is beyond the scope of this work.

In this study, we focused on the assessment of parameter uncertainties for ODE models. Yet, as the marginalization-based approach provides a complete parameter sample, it facilitates also the evaluation of prediction uncertainties.¹⁶ Accordingly, we expect that it might contribute to resolving reliability problems of Bayes prediction uncertainty analysis encountered in recent studies.³⁶ Furthermore, the proposed approach is not limited to ODEs, but directly applicable for other deterministic models, e.g., partial differential equations.

In summary, the marginalization-based approach provides a new tool for Bayesian inference for models with observation-related parameters. It substantially benefits the efficiency of sampling-based approaches and renders the generation of representative posterior samples for large models possible. As it is agnostic to the structure of the underlying dynamical model, it is widely applicable to mathematical models from different research fields, such as engineering, physics, and ecology.

Limitations of the study

This study has three main limitations. The first limitation is the number of models that were considered in the study. The extrapolation of these results when testing on 4 published models may be not applicable to all models, and behavioral exceptions may occur. However, when selecting our candidate models we tried to cover different degrees of complexities and structures. Similarly, this applies to the sampling algorithms used. Secondly, our approach may be in principle applicable to other model types, such as partial differential equations. While we expect to get similar results, this remains to be evaluated. Lastly, the specification of such a “constrained” observation model is another limitation. Ideally, the approach could be combined with automatic-differentiation schemes to flexibly facilitate the use of multiple observation models.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Code for mathematical modeling, analysis and visualization used in the manuscript	This paper	https://doi.org/10.5281/zenodo.7199473
Software and algorithms
Python version 3.10	Python Software Foundation	https://www.python.org
AMICI (Python package)	Github	https://github.com/AMICI-dev/AMICI
pyPESTO (Python package)	Github	https://github.com/ICB-DCM/pyPESTO
Other
Benchmark PEtab model repository collection	Github	https://github.com/Benchmarking-Initiative/Benchmark-Models-PEtab

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Jan Hasenauer (jan.hasenauer@uni-bonn.de).

Materials availability

This study did not generate new unique reagents.

Method details

Mechanistic modeling of biological systems

We consider models based on ODEs of the form

$$\dot{x}\left(t,\theta \right)=f\left(x\left(t,\theta \right),\theta \right),x\left(t_0,\theta \right)=x_0\left(\theta \right)\text{,}$$

in which the vector field $f:{\mathbb{R}}^{n_x}\times {\mathbb{R}}^{n_{\theta }}\to {\mathbb{R}}^{n_x}$ determines the temporal evolution of the states $x\left(t,\theta \right)\in {\mathbb{R}}^{n_x}$. The unknown model parameters, which are estimated from the measurements, are denoted by $\theta \in {\mathbb{R}}^{n_{\theta }}$. Usually, θ includes reaction rate constants and initial amounts of species. Here, $n_x$ is the total number of modeled species, and $n_{\theta }$ the total number of model parameters. The states $x\left(t,\theta \right)$ and model parameters θ are linked to the observables via the observation map $h:{\mathbb{R}}^{n_x}\times {\mathbb{R}}^{n_{\theta }}\to {\mathbb{R}}^{n_y}$, where $n_y$ is the total number of observables. The observables are the measured properties of the model. Most measurement techniques only provide relative information about the absolute concentrations of interest^8,9 and, frequently, measurements are noise corrupted. Hence, to obtain the measurements $\overline{y}$ (i) the model observables must be rescaled by introducing scaling factors and offsets, and (ii) the model also must capture experimental errors by defining a noise model. Most commonly, independent and additive Gaussian distributed noise models are assumed

$${\overline{y}}_{j,i}=s_{j,i}\cdot h_j\left(x\left(t_i,\theta \right),\theta \right)+b_{j,i}+{\epsilon }_{j,i},\text{with}{\epsilon }_{j,i}\sim \mathcal{N}\left(0,{\sigma }_{j,i}^2\right)\text{,}$$ (Equation 5)

with observable index j, time index i, scaling factors $s\in {\mathbb{R}}^{n_y\times n_t}$, offsets $b\in {\mathbb{R}}^{n_y\times n_t}$, and noise parameters $\sigma \in {\mathbb{R}}^{n_y\times n_t}$. Here, $n_t$ denotes the total number of time points. These parameters are often unknown and, therefore, also need to be estimated along with the unknown model parameters. Other usual noise assumptions include log-normal distributed noise models¹¹ and Laplace distributed noise models.²⁸ In this study, we focus on the case of additive Gaussian noise (5), but implementations for log-normal and Laplace distributed noise models are provided in Tables S1 and S2 and supplemental data.

We denoted the group of all measurements as $\mathcal{D}={\left\{{\overline{y}}_{j,i}\right\}}_{\begin{array}{l}i=\left(1,\dots ,n_t\right)\end{array}}^{j=\left(1,\dots ,n_y\right)}$.

Benchmark models

For the evaluation of the marginalization-based approach, we employed in total five models (one toy model and four published M1–M4) and their corresponding datasets (Table 1).

Toy: Model of a conversion reaction

The conversion reaction model was introduced in²⁸ and describes a reversible chemical reaction, which converts a biochemical species A to a species B with rate ${\theta }_1$, and B to A with rate ${\theta }_2$ (Figure 2). We modified the observation model to include scaling and offsets.For the evaluation of the proposed method, we generated one artificial dataset which is depicted in Figure 2D. For details on the model structure and synthetic data generation we refer to the supplemental data.

M1: Model of EGF-dependent AKT pathway

The model of EGF-dependent AKT pathway has been introduced in³⁷ and possesses in total 16 unknown parameters: 13 model parameters and 3 scaling factors (Table 1, M1). The available experimental data are a total of 144 data points under 6 different experimental conditions for 3 observables. For each data point, the corresponding variance of the measurement noise is provided, therefore it does not need to be estimated. The complete dataset is depicted in Figure S2.

M2: Model of STAT5 dimerization

The model of STAT5 dimerization has been introduced in³⁸ and possesses in total 9 unknown parameters: 6 model parameters and 3 noise parameters. To this model, we have added 3 scaling factors (Table 1, M2), one per observable, for the sake of testing the proposed method. The available experimental data are a total of 48 data points for 3 observables. The complete dataset is depicted in Figure S3.

M3: Model of mRNA transfection

The model for mRNA transfection has been introduced in³⁹ and possesses in total 5 unknown parameters: 3 model parameters, 1 scaling factor, and 1 noise parameter (Table 1, M3). The complete dataset is depicted in Figure 3D. For further details of the model structure we refer to the supplemental data.

M4: Model of gastric cancer signaling

The model for gastric cancer signaling has been introduced in.²⁷ Here, we considered the Cetuximab responder cell line MKN1. The available experimental data for the responder cell line were a total of 303 data points under 106 different experimental conditions for 31 observables. For each data point, the corresponding variance of the measurement noise was provided, therefore it did not need to be estimated.

For all models we used the parameter ranges and prior distributions introduced in the original publications. The priors are mostly uninformative.

Parameter optimization

To determine the maximum a posteriori (MAP) estimates, we minimized the negative log-posterior function. This minimization was performed using multi-start local optimization, an approach which was previously shown to be reliable.^12,40 For local optimization, we used the trust-region optimizer fides.⁴¹ Parameters were ${\log }_{10}$-transformed to improve numerical properties.^40,42,43 We generated 100 starting points for local optimization, except for model M4 for which we used 500 starting points.

Bayesian parameter inference

To perform Bayesian parameter inference, we used MCMC sampling following the pipeline presented in.⁴⁴ Similar to parameter optimization, sampling was performed using ${\log }_{10}$-transformed parameters. The MAP estimates $\left(\hat{\theta },\hat{s},\hat{b},{\hat{\sigma }}^2\right)$ for the full problem (aka without marginalization were used to initialize the MCMC chains⁴⁴: all runs for the standard sampling approach were initialized using the full optimal vector $\left(\hat{\theta },\hat{s},\hat{b},{\hat{\sigma }}^2\right)$ (found using multi-start local optimization); while for all runs for the marginalization-based sampling approach were initialized using the corresponding subset $\hat{\theta }$. Note that for the runs for the marginalization-based sampling approach also the MAP estimate for the marginalized problem could have been used, yet, differences were minor and the chosen approach allowed us to match runs of standard and marginalization-based sampling approach. The parameter posterior distribution was sampled using the adaptive Metropolis¹⁸ and parallel tempering^45,46 algorithms implemented in the Python toolbox pyPESTO.⁴⁷ For the parallel tempering algorithm, we used 10 chains initialized. For all runs of the parallel tempering algorithm, we initialized the first chain – which samples the posterior – with the best optimization result found using multi-start local optimization, the second chain with the second best optimization result, and so on.

Convergence after burn-in was assessed using the Geweke test³⁰ and auto-correlation length using Sokal’s adaptive truncated periodogram-estimator.⁴⁸ Both methods are implemented in pyPESTO and we refer to the respective original publications for technical details. The effective sample size is given by

$$n_{\text{eff}}=\frac{n}{1+2{\sum }_{\tau =1}^{\infty }{\rho }_{\tau }}$$

where n is the number of samples remaining after discarding burn-in period, and ${\rho }_{\tau }$ is the estimated auto-correlation at lag τ.

For all models, the prior hyperparameters for both sampling approaches were the same as used for optimization.

Tempering scheme for the posterior analysis

The posterior for standard and marginalization-based approach were tempered to assess transition characteristics (Figure 5). We used the tempered posteriors

$$p_T\left(\theta ,s,{\sigma }^2\mid \mathcal{D}\right)\propto {\left(p\left(\mathcal{D}\mid \theta ,s,{\sigma }^2\right)p\left(\theta ,s,{\sigma }^2\right)\right)}^{1/T}\text{.}$$

and

$$p_T\left(\theta \mid \mathcal{D}\right)\propto {\left(p\left(\mathcal{D}\mid \theta \right)p\left(\theta \right)\right)}^{1/T}\text{.}$$

with temperature T.

Published: September 28, 2023

Supplemental information

Document S2. Detailed mathematical derivation for all considered marginalization cases

This supplemental data contains a step-to-step guide on how to obtain all marginalization cases considered in the main manuscript and additional ones.

Data and code availability

• •This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
• •All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.