Predicting metabolic fluxes from omics data via machine learning: Moving from knowledge-driven towards data-driven approaches

Abstract

The accurate prediction of phenotypes in microorganisms is a main challenge for systems biology. Genome-scale models (GEMs) are a widely used mathematical formalism for predicting metabolic fluxes using constraint-based modeling methods such as flux balance analysis (FBA). However, they require prior knowledge of the metabolic network of an organism and appropriate objective functions, often hampering the prediction of metabolic fluxes under different conditions. Moreover, the integration of omics data to improve the accuracy of phenotype predictions in different physiological states is still in its infancy. Here, we present a novel approach for predicting fluxes under various conditions. We explore the use of supervised machine learning (ML) models using transcriptomics and/or proteomics data and compare their performance against the standard parsimonious FBA (pFBA) approach using case studies of Escherichia coli organism as an example. Our results show that the proposed omics-based ML approach is promising to predict both internal and external metabolic fluxes with smaller prediction errors in comparison to the pFBA approach. The code, data, and detailed results are available at the project's repository[1].

Graphical abstract

1. Introduction

Metabolic flux prediction is a central challenge in systems biology, with applications ranging from biotechnology to medicine [2], [3], [4]. In the last years, constraint-based modeling (CBM) have become an essential in silico tool to predict and optimize metabolic flux distributions in biological systems by flux balance analysis (FBA). These models rely on a set of constraints and assumptions to simulate the behavior of cell phenotypes, enabling the prediction of metabolic fluxes and cell growth at different conditions [5], [6]. FBA enables the modeling of thousands of biochemical reactions simultaneously captured in the metabolic network reconstruction, which requires prior extensive knowledge of the network and the stoichiometry of the reactions within a particular organism. The impact of genome-scale models (GEMs) in the biotechnology field comes from their essential support in metabolic engineering, namely to optimize production yields [7], [8]. The parsimonious FBA version called pFBA technique was later introduced [9]. FBA aims to maximize a specific objective function, which is usually biomass production and is subject to constraints imposed by the stoichiometry of the metabolic network; pFBA does not seek to maximize any particular objective, it finds a flux distribution that is both feasible and has the smallest possible sum of absolute flux values.

While GEMs have been successful in predicting fluxes and growth rates, they require prior knowledge of the entire metabolic network and the appropriate objective function (they are sensitive to the metabolic objective that is often unknown and likely context-specific) of an organism, limiting their applicability [10]. To overcome some of its shortcomings and improve prediction accuracy there have been successful attempts to integrate GEMs with omics datasets, namely through several context-specific metabolic model extraction algorithms (e.g., iMAT [11], INIT [12] and GIMME [13]). In 2014, Machado et al. [14] performed an extensive comparative study between various FBA-based approaches that integrate transcriptomic or proteomic data against the reference pFBA method. However, the surprisingly equal or poorer prediction performance of these methods when compared to pFBA was found. Moreover, several input preprocessing steps are required to integrate GEMs with large omics datasets. Alternatively, Sánchez et al. [15] incorporated proteomics data to improve GEMs predictions by introducing enzyme kinetic-based constraints, given their known roles in metabolic pathways (GECKO method). Ravi et al. [16] extended FBA with differential gene expression data (deltaFBA approach) to predict metabolic flux differences between conditions. However, the former needs detailed enzyme kinetics and protein abundance data (i.e., experimentally measured turnover numbers) under different conditions. The latter approach requires multiple experimental datasets and does not generate the flux prediction for a given condition (i.e., only produces differences in the fluxes between two conditions).

To compensate for the identified limitations, there have been efforts to integrate two computational frameworks – constraint-based modeling and machine learning (ML) – as pointed out in multiple review studies ([17], [18] and [19]). Vijaykumar et al. [20] introduced a hybrid pipeline combining metabolic modeling with ML to analyze GEMs and refine phenotypic predictions. Culley et al. [21] compared ML-based data integration (combining gene expression profiles with predicted metabolic flux data) to predict yeast cell growth, observing a superior prediction accuracy for multimodal neural networks. Similarly, Magazzu and co-authors [22] explored the role of statistical learning methods against FBA using omics data integration to improve cellular growth rate predictions. More recently, Faure et al. [23] employed hybrid neural-mechanistic modeling which relies on an artificial metabolic network layer encasing the metabolic knowledge while the rest of the network is responsible for learning the FBA constraints by the use of a custom loss function, achieving superior phenotype predictions while also reducing the required training data. Schinn et al. [24] addressed challenges in real-time nutrient control in biotherapeutics manufacturing by integrating statistical models with GEMs, enabling the prediction of amino acid concentrations in culture medium through time.

Recently, with the increased amount of omics data available, data-driven approaches like ML have emerged as a promising alternative to model metabolic functionalities [25], [26], [27]. Their capacity to identify patterns in large datasets, reveals hidden relationships, and learn predictive models from complex omics data has been notable across different domains [28], [29], [30], [31], [32]. Namely, Wytock et al. [33] explored the k-nearest neighbors algorithm to predict bacterial growth rate from gene expression data. Earlier, an Artificial Neural Network was used to predict the fluxes by using mass isotopomer data as the input [34]. Costello and colleagues [35] used a time series perspective of multiomics data and employed regressors to model the dynamic metabolic behavior of a cell. Wu et al. [36] predicted fluxes using an SVM model aided by a constraint programming module, with simple culture variables and detailing the bacterial species. Freischem et al. [37] introduced a novel ML approach that predicts gene essentiality directly from wild-type flux distributions, achieving near state-of-the-art accuracy in identifying essential genes through training binary classifiers on connectivity data from a mass transfer between reactions graph. Although the state-of-art ML methods can disclose some relationships among the omics data, there has not been a supervised ML-based contribution focused on the sole use of transcriptomics and/or proteomics data (with no prior information like stoichiometry) to predict metabolic fluxes.

In this study, we assess the role of state-of-the-art ML models, including Linear Regression, Support Vector Machines, Decision Trees, Random Forests, XGBoost, and Artificial Neural Networks, for predicting metabolic fluxes using transcriptomics and/or proteomics data. Our work consists of a benchmarking analysis that contrasts these models with the conventional pFBA method, underlining the substantial promise of ML techniques in addressing metabolic modeling challenges. Furthermore, the developed omics-based ML models for metabolic flux prediction set this work apart from other related contributions that tackle different predictive challenges [33], [35], [37], [24] or different input data [34], [36], [23].

2. Methods

2.1. Experimental data

The two experimental datasets used in this work were obtained from the literature. Originally published by Ishii et al. [2], the first dataset contains experimental information (transcriptomic, proteomic, and fluxomic data) for the wild-type K12 E. coli culture in chemostat under different dilution rates (D = 0.1, 0.2, 0.4, 0.5, and 0.7 h⁻¹) and for 24 single knockout mutant strains at a D = 0.2 h⁻¹. This dataset contains microarray profiles for 79 genes and proteomics data for 60 proteins of E. coli. Additionally, the dataset also provides information on the standard deviation of the transcriptomic and proteomic measurements. This is one of the largest datasets available with both omic data features (transcriptomic and proteomic) and metabolic fluxes. Therefore, it is the primary case study for training and validating the models under a nested cross-validation process.

The second dataset, published by Holm et al. [3], contains information on E. coli strains growing aerobically in batch cultures. This study produced lower volumes of data, analyzing a wild-type strain and two over-expression mutants, nox (NADH oxidase) and atpAGD (F1-ATPase), to measure transcriptional responses to lowered levels of NADH and ATP. Given the lack of available instances, it is not possible to train an ML model with this dataset. For this reason, it was used as an independent validation set, to assess the generalization ability of the predictors.

2.2. Data preprocessing

All input data are numeric in nature and therefore a standardization process for the raw expression values using the z-score strategy was applied [38]. This involves transforming the features by removing the mean and scaling to unit variance, so the resulting distribution have 0 mean and the standard deviation 1.

Multiple datasets can be used in accordance with the diverse possible feature spaces that will feed the target predictive models. Here, the proteomic, transcriptomic, or a combination of both layers was applied as input. There is also information available on the standard deviation (i.e., experimental uncertainty bounds) associated with the omics measurements which was added to the input. Furthermore, the glucose and oxygen uptake rates were fixed, depending on the test scenario, by appending these fluxes' values to the input. Note that when the fluxes for the uptake rates are fixed they are not considered in the predictive performance metric.

2.3. Models and implementation

Different ML methods to predict metabolic fluxes are tested. The ML algorithms used consist of several widely-used regression models, including Linear Regression (LR) [39], Support Vector Machine (SVM) [40], Decision Tree Regressor (DT) [41], Random Forest (RF) [42], XGBoost Regressor (XGB) [43], and Neural Networks (NN) [44]. The implementations for these models are imported from the Scikit-Learn package (version 1.2.0) [45], with the exception of XGB, which can be found in the xgboost package (version 1.7.5) [43], and the neural networks that were implemented using Tensorflow (version 2.9) [46]. The computations and calculations were performed using Python (version 3.10) [47]. Regarding pFBA, all simulations are done using the COBRApy package (version 0.26.2) [48] with the iAF1260 genome-scale metabolic reconstruction of E. coli [49]. To avoid the influence of random variations or redundancy across FBA simulations the pFBA approach was selected.

All code, data, and results are available in our GitHub repository [1].

2.4. Computational setup

To predict the phenotypes all these ML models are trained and tested in a leave-one-out cross-validation process using the gene expression data and/or protein levels as input (depending on the test scenario), retrieving the average statistics. As for pFBA, considering Ishii's dataset [2], it was used to predict growth rate, 7 secretion fluxes, and 37 intracellular fluxes by the biomass growth objective maximization, given the experimental glucose and oxygen uptake rates as constraints. All the other bounds used the original flux bounds of the metabolic model. In order to simulate the genetic interventions (knockouts), the iAF1260 metabolic network was modified based on each of the respective single-gene deletion before the simulation. Similarly, for the validation in Holm's dataset, pFBA was used to predict growth rate, 1 secretion flux, and 31 intracellular fluxes, given only the experimental glucose rate as a constraint.

The hyperparameters for the majority of the ML models were left at the default values. The only exception is the deep learning approach, which underwent a hyperparameter optimization process that chooses the architectural aspects of the network as well as other relevant parameters like regularization strategy, dropout, and the learning rate (for details, see the GitHub repository [1]).

Moreover, in the case of neural networks, the training and testing process happens in a dual-loop cross-validation process. The outer loop executes in the same leave-one-out fashion that is used across all other models, but within each training iteration, there is an inner loop of cross-validation executing in 5 folds. In each of the 5 training folds, hyperparameter optimization is performed (using a Bayesian approach [50], [51]). The best set of hyperparameters resulting from the search is used to build the neural network that is fitted and evaluated in the outer loop.

2.5. Performance metrics

The prediction performance is measured using the mean absolute error (MAE), where y is the vector of the measured fluxes, $\hat{\mathbf{y}}$ is the vector of the predicted fluxes, and n is the number of measured fluxes,

$$MAE=\frac{1}{n}\sum _{i=1}^n|\widehat{y_i}-y_i|$$ (1)

the root mean squared error (RMSE),

$$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{(\widehat{y_i}-y_i)}^2}$$ (2)

the normalized error (NE),

$$NE=\frac{\Vert \hat{\mathbf{y}}-\mathbf{y}\Vert }{\Vert \hat{\mathbf{y}}\Vert }$$ (3)

and the R²,

$$R^2=1-\frac{{\sum }_{i=1}^n{(\widehat{y_i}-y_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y_i})}^2}.$$ (4)

Additionally, the Wilcoxon signed-rank test is used to obtain statistical guarantees in the comparison of ML models against pFBA [52]. The paired testing handles data without relying on any specific assumptions regarding its distribution. To derive a single p-value from the set of pairwise comparisons, the median p-value approach is considered.

3. Results

The aim of our work was to assess the predictive ability of ML models using transcriptomics/proteomics data and other input variations for estimating metabolic fluxes, comparing them with the standard pFBA method. The performance metrics are averaged firstly across the predicted vector and later across the range of testing instances in the cross-validation process.

3.1. Impact of different inputs on the predictive performance

To assess the influence of each input component (i.e., the type of omics data used as input, uptake rates constrained, and the use of the standard deviation of the omics measurements) in the prediction of metabolic fluxes, we compared the predictive capability of the different models for a variety of conditions and scenarios.

Fig. 1 provides an overview of the results for the best settings per model in the Ishii data [2], using the introduced cross-validation process. Our comparative analysis demonstrated that the best flux predictor was the RF model (NE = 0.261) trained with transcriptomic data (with glucose and O₂ uptake rates fixed), outperforming all the other models and with a p-value < 0.01 against pFBA. Overall, the best configurations from the ML regressors seem to present a normalized error value that is inferior to that of pFBA (NE = 0.381). A more detailed comparison of all the methods and scenarios is given in Table A.1 for Ishii's dataset [2]. For all the comparisons, we found that when the uptake rates are fixed, superior results are achieved across all settings (Table A.1). This outcome is unsurprising due to the relaxation of the problem resulting from the addition of two fluxes to the input data.

Fig. 1.

Comparison of the best regressors in cross-validation (see bold lines in Table A.1) and pFBA, for different prediction scores (including the intracellular, extracellular, and growth fluxes) across all experimental conditions in the E.coli Ishii's dataset. Sorted by increasing normalized error.

The Ishii dataset provides information about two omic layers, transcriptomic and proteomic, but also provides the associated standard deviation of the omics measurements. Taking RF, the best predictor under analysis, Fig. 2 assesses the predictability of each omic layer as input, as well as the impact of including the respective standard deviation of the omics measurements. It can be observed that the prediction error is lower in all settings that do not use the standard deviation, reflecting the benefit of having lower dimensionality in the input. Regarding the impact of the type of omics data, transcriptomics alone seems to improve the flux predictions, outperforming settings where proteomics is used, alone or in combination.

Fig. 2.

Comparison of the performance given by the RF model using different omics (P = Proteomics, T = Transcriptomics, P+T = Proteomics and Transcriptomics), with (left) and without (right) the standard deviation of the omics measurements as input.

3.2. Comparison of intra and extracellular fluxes prediction

In order to illustrate in more detail how the phenotype predictions vary between the best suggested ML model (RF model without standard deviation and including glucose and O₂ uptake rates fixed) and pFBA, we compared the intracellular and extracellular flux predictions. Fig. 3 shows the prediction metrics between intracellular and extracellular fluxes. We noted that intracellular fluxes have noticeably higher absolute prediction errors. However, when the error is normalized, we identified a reduction in the NE values for the intracellular fluxes. This is likely due to the fact that the majority of extracellular fluxes are zero-valued and therefore small deviations from zero will lead to great penalizations in a normalized view. Figs. 3a and 3b further reinforce the performance differences between the RF predictive model and pFBA, since the latter is associated with higher normalized prediction errors in both scenarios. Furthermore, Fig. 3a also strengthens the claim of higher predictive power through transcriptomics data as input, showing decreased predictive error values in both intra and extracellular fluxes.

Fig. 3.

Comparison of the performance between (a) RF model using different omics (P = Proteomics, T = Transcriptomics, P+T = Proteomics and Transcriptomics) as input and (b) pFBA approach for prediction of the intracellular (intra) and extracellular (extra) fluxes.

3.3. Prediction of individual fluxes

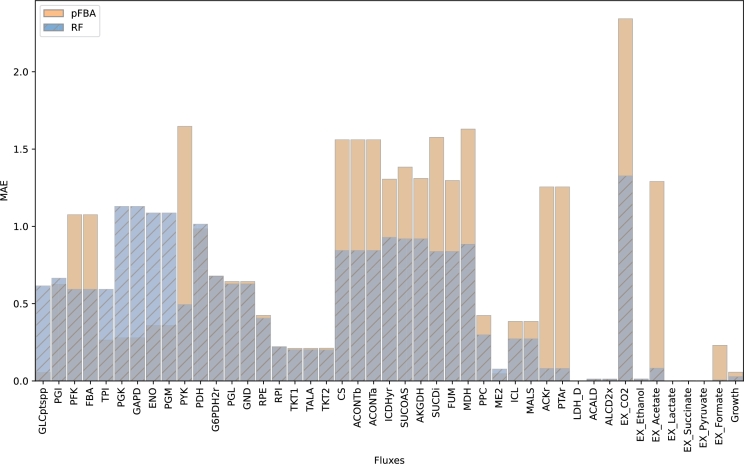
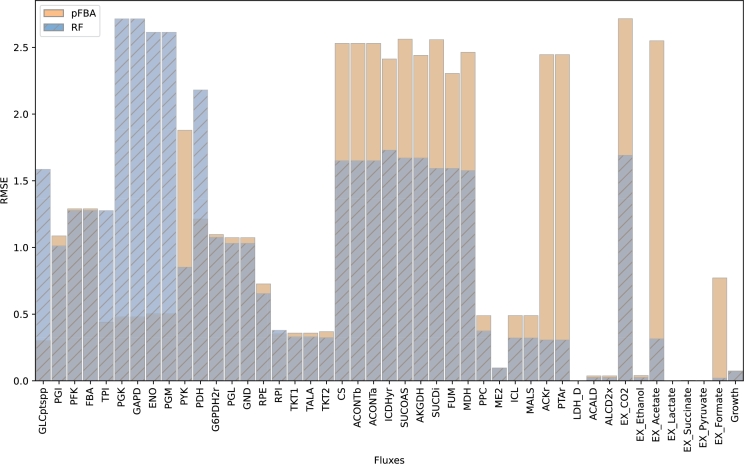
Fig. 4 shows the distributions for the normalized error across metabolic fluxes, for both RFs and pFBA. As previously reported, on average, RFs yield lower error predictions when compared to pFBA. There are 10 fluxes where pFBA performs better than RFs, they roughly coincide in 7 other fluxes (including growth), but RFs outperform pFBA in 28 of the metabolic fluxes, with 4 of those fluxes showing irregularly increased normalized error values from pFBA (i.e., ACKr, PTAr, EX_Acetate, and EX_Formate). Similar distribution plots between the same models for the MAE, RMSE, and R² metrics can be found in appendix (Fig. A.1, Fig. A.2, Fig. A.3, respectively).

Fig. 4.

Average of the normalized error (NE) of RF and pFBA for all reactions in the E.coli Ishii's dataset across different dilution rates and gene knockouts.

Fig. A.1.

Average mean absolute error distributions of RF and pFBA for all reactions in the E.coli Ishii's dataset across different dilution rates and gene knockouts.

Fig. A.2.

Average root mean squared error distributions of RF and pFBA for all reactions in the E.coli Ishii's dataset across different dilution rates and gene knockouts.

Fig. A.3.

Average R² metric distributions of RF and pFBA for all reactions in the E.coli Ishii's dataset across different dilution rates and gene knockouts.

To explore phenotype predictions in scenarios where pFBA estimates are less accurate (i.e., higher dilution rates), caused by sub-optimal cell growth due to overflow mechanisms, we analyze two specific cases in detail. Fig. 5 shows the predictions for each metabolic flux at a dilution rate of 0.5 h⁻¹. The prediction errors for this environmental condition was NE = 0.153 (MAE = 0.529, RMSE = 0.720, R${}^2=0.976$) for RF model and NE = 0.281 (MAE = 0.899, RMSE = 1.321, R${}^2=0.906$) for pFBA, respectively. For most of the fluxes, both the RF model and pFBA perform well and predict values close to the experimentally measured flux value. However, there are a few exceptions where their performance diverges. Namely for the PFK, FBA, PYK, CO2, and acetate fluxes, the RF is close to the experimental value while pFBA yields high error results. On the other hand, for ME2, ICL, MALS, Succinate, and Pyruvate the RF model tends to overestimate flux values. Interestingly, most of the fluxes where the RF fails by slightly overshooting have zero or otherwise very low values. In most of these cases, the fluxes could be accurately predicted by other models, like DTs or XGB. This raises the question of whether increasing the volume of training data would address these challenges, contributing to a stronger ensemble. Since RFs may face hindered generalization capacity, due to their lower variance and higher bias character, especially noticeable in smaller datasets, resulting from each tree in the ensemble using only part of the training data (bootstrapping and subspace selection) and the reduction of used features at each branch split.

Fig. 5.

Comparison between predicted and experimentally measured (true) [2] physiology: intracellular fluxes, extracellular fluxes (mmol/gDW/h), and growth rate (h⁻¹), for D=0.5 h⁻¹ using different models. Details on nomenclature can be found in the metabolic reconstruction model [49]. Models refer to the settings (bold lines) in Table A.1.

A comparison between the predicted and measured fluxes for D = 0.7 h⁻¹ is given in the appendix (Fig. A.4). In this specific dilution setting, both the RF model (MAE = 4.411, RMSE = 6.055, NE = 0.62, R${}^2=0.959$) and pFBA (MAE = 4.214, RMSE = 6.031, NE = 0.618, R${}^2=0.621$) show comparable results. The performance of both models is similarly poor in 10 out of 45 fluxes, with the exception of LDHD and lactate where their results match correctly. On average, across all dilution and knockout settings, the RF model performs the best out of the range of models under assessment, but here they can only outperform pFBA in 21 out of 45 fluxes, while pFBA has better predictive power in 14 out of 45 fluxes comparing to the RF. Interestingly, similarly to what happened at D = 0.5 h⁻¹, for most of the fluxes in which the RF model deteriorates its performance, the DT model appears as a better alternative, outperforming the RF in 34 out of 45 fluxes. Another good candidate would be the XGB model which is on par with DT, outperforming the RF model in 37 out of 45 fluxes.

Fig. A.4.

Comparison between predicted and experimentally measured (true) [2] physiology: intracellular fluxes, extracellular fluxes (mmol/gDW/h), and growth rate (h⁻¹), for D=0.7 h⁻¹ using different models. Details on nomenclature can be found in the metabolic reconstruction model [49]. Models refer to the scenarios (bold lines) in Table A.1.

Finally, the results for the reference dilution rate, D = 0.2 h⁻¹, are also provided in appendix, Fig. A.5. The RF (MAE = 0.118, RMSE = 0.227, NE = 0.105, R${}^2=0.994$) performs significantly better than pFBA at the reference dilution rate (MAE = 0.540, RMSE = 0.763, NE = 0.353, R${}^2=0.856$) on average. The only model able to surpass the predictive power of RF for this specific dilution is XGB (MAE = 0.129, RMSE = 0.188, NE = 0.087, R${}^2=0.995$).

Fig. A.5.

Comparison between predicted and experimentally measured (true) [2] physiology: intracellular fluxes, extracellular fluxes (mmol/gDW/h), and growth rate (h⁻¹), for D=0.2 h⁻¹ using different models. Details on nomenclature can be found in the metabolic reconstruction model [49]. Models refer to the scenarios (bold lines) in Table A.1.

3.4. Generalization to an independent test set

Lastly, to assess the ability of the developed ML models to generalize to experimentally independent data, we applied them to the Holm dataset [3] (composed of three instances/conditions), training with Ishii's data [2]. Table 1 shows the detailed results on the independent validation dataset for the RF predictor and pFBA. Unlike gene knockouts (as in Ishii's data [2]), overexpressions portrayed in Holm's experiments [3] do not alter the network topology. Consequently, this limits pFBA's capacity to accurately predict the phenotypes [14]. For instance, it can be observed that pFBA (in contrast to the RF) does not predict correctly the growth rate and some other intracellular fluxes. However, despite this limitation, the RF model exhibits increased averaged prediction errors compared to pFBA for these cases. This indicates that the generalization ability of the ML models is limited as training observations are scarce.

Table 1.

Error metrics for the RF model with transcriptomics data as input and pFBA on the Holm dataset [3]. The best model is represented in bold and ± indicates the standard deviations.

Model	Uptakes	Deviations	MAE	RMSE	NE	R2
RF	Yes	Yes	3.556 ± 1.283	4.652 ± 1.631	0.492 ± 0.14	0.795 ± 0.066
		No	3.508 ± 1.336	4.527 ± 1.807	0.469 ± 0.12	0.801 ± 0.065
	No	Yes	3.519 ± 1.29	4.595 ± 1.672	0.484 ± 0.135	0.799 ± 0.065
		No	3.557 ± 1.293	4.637 ± 1.669	0.489 ± 0.135	0.794 ± 0.066
pFBA	Yes	N/A	2.157 ± 0.538	2.727 ± 0.558	0.292 ± 0.048	0.912 ± 0.046

Uptakes – glucose uptake rate fixed/constrained or not; Deviations – standard deviation of the omics measurements used or not as input; ‘N/A’ means the option is not available; ‘No’ means the option was not included but may be available in other settings.

To further assess RF's generalization capacity, the learning curves in Fig. 6 assess the changing loss with increasing training set sizes. It is interesting to observe that the NE for the RF model slowly decreases across time, stabilizing after less than 10 training instances (from Ishii's data). When looking at the NE improvements while testing on Holm's data, a clearly steeper trend line is presented. The absence of a stabilizing trend could suggest that the learning process can benefit from additional observations to promote a greater generalization ability. These observations further back the claims for limited generalization on Holm's dataset due to the scarcity of training observations.

Fig. 6.

Normalized error (NE) evolution with increasing training set size, testing on Ishii's and Holm's data.

4. Discussion

This work explores the role of ML methods to predict phenotypes (metabolic fluxes) from transcriptomics and/or proteomics data. The primary objective was to develop a proof-of-concept, rather than proposing a new comprehensive methodology to address the task of flux predictions. Our results point to the competitive performance of ML models compared to pFBA, a state-of-the-art method representative of knowledge-driven approaches for flux distribution prediction. Next, we delve into the broader interpretation and significance of the obtained results, while also addressing limitations and suggesting new avenues for future research.

From the set of ML models tested, we observed that RFs generally show the best predictions in cross-validation (p-value < 0.01 against pFBA). Still, there are specific fluxes for which the predictive performance deteriorates, where other models may outperform. This can either be due to the low amount of training data hindering the completely accurate modeling and/or inherent model limitations. Utilizing an ensemble of predictors to address situations where one model may yield outlying predictions could be a promising next step toward strengthening the predictive ability of ML-based methods. The argument for a less than ideal training data volume is further enforced when considering the good results obtained for the predictions at the reference dilution rate, D = 0.2 h⁻¹, which is the dilution rate used to record the majority of our dataset (25 out of 29 instances). Although the performance deteriorates for higher dilutions, ML models nevertheless remain competitive with pFBA.

However, the same advantage from RFs could not be verified in the independent test set, except in predicting growth rate. This may be indicative of a limited generalization performance but is likely due to the scarcity of training examples, as illustrated in Fig. 6, combined with the added difficulty of Holm's data being generated under different conditions from the training data in Ishii's dataset. Therefore, broader testing using additional case studies is needed to acquire more comprehensive results that may in fact advocate for the use of one specific predictor. Indeed, the potential of ML models as a promising approach (if such omics data are available) is signaled, but it is still unclear how they would perform in other scenarios/conditions, such as different organisms and experimental conditions, which require more extensive training data to enable more reliable testing of their generalization ability.

As highlighted in the introduction section, prior studies have addressed similar challenges using diverse methodologies, different types of inputs, or outputs. In our approach, the core sources of information for metabolic flux predictions can either be transcriptomic or proteomic data sources. However, our results suggest that the use of mRNA data seems generally sufficient to yield good flux predictions. These findings could indicate that for these reactions, the fluxes are controlled at the gene expression level [53]. However, other works found that a combination of both omics yields slightly better results [54], while others point to higher predictive power from proteomics data [55], [56]. In essence, it seems that the two omics contain relevant information for metabolic modeling and it would probably be best to use a combination of both in order to maximize the amount of available information. On the other hand, the inclusion of the standard deviation of the omics measurements as a variable of experimental error was also found to be detrimental to the predictive capacity. Regarding the applications and possible extrapolations, the ML-based modeling of other types of cells/organisms should be achievable given that there are efforts in creating similar datasets (i.e., with both transcriptomic/proteomic and fluxomic data at the same condition/strain).

While our study has shown promising results, the major limitation is the amount of data, due to the scarcity of coordinated transcriptomic and flux profiles, obtained in the same conditions. Also, the omics data used in the learning [2] are limited to the central pathways. Having more data would be important to further assess the models' generalization ability. Nevertheless, a sound cross-validation methodology was adopted to reduce the impact of these limitations, providing the most statistically significant assessment possible, while a small external validation is also presented.

It is also important to delve into the intricacies of model design and constraints, as they play a pivotal role in shaping our findings. We acknowledge the comparison made in our work between ‘structure-naive’ models optimized on experimental data and pFBA. pFBA derives its predictive power from the underlying metabolic stoichiometry and imposed flux constraints rather than direct optimization from experimental data. The lack of generalization observed with some of the machine learning models may extend beyond mere data volume; it is intrinsically tied to the complex landscape of predictive model configurations explored during learning. These models tend to traverse a vast space of plausible configurations, which may not necessarily align with out-of-distribution data, as it is evident in our validation with the Holm's dataset. Therefore, it is imperative to consider not only the data-driven aspects of our study but also the underpinning model design choices and constraints as prior knowledge to guide the learning process. This is precisely the gap that hybrid modeling methodologies (i.e., combined use of CBM and ML) [17], [18], [19], [20], [21], [22] help to fill. However, the full departure from GEMs imposes the aforementioned costs that can only be truly mitigated via more extensive learning processes that can ultimately be carried under the foundations presented in our work.

In the future, it would be relevant to extend this work with more extensive datasets for the same organism. Learning models with more data can improve the predictions and it enables better validation of the approach, which is vital for ensuring generalization. Future work may also complement this study by exploring alternative supervised regression models, using different hyperparameterizations, exploring complex model ensembles, or extending the current principles with constraint programming [36].

GEMs are so well established today that the cost and labor of their use have become marginal, but there are still efforts to create and improve these models, with successive updates promising more complete and accurate metabolic modeling. However, classical GEMs have met their limits with new contributions turning to omics-integrating variants [11], [12], [13], [15], [16], hybrid methods [17], [18], [19], [20], [21], [22], or pure ML-models [26], [27], [33], [34], [35], [36]. We now witness the first efforts to introduce ML-based methods for metabolic modeling which can achieve similar results, or even surpass the performance of pFBA. Furthermore, omics data profiles are being generated faster and more often than ever before. So one can only expect that ML-based methodologies are employed more frequently and with increasingly improved results. This is contrasting to condition-specific GEMs, where the large dimensionality of such data is difficult to handle, need gene-protein-reaction mapping and the selecting of arbitrary thresholds in the gene expression levels can be a problem.

To conclude, the findings presented here motivate the use of ML models for future work in this area, specially to less studied phenotypes/microorganisms. From a temporal perspective, recent contributions are moving towards the fusion of information from pre-acquired metabolic networks and ML [20], [21], [22], [57]. However, pure omics-driven modeling approaches show promise, given the proof of principle presented here. Furthermore, to the best of our knowledge, this is the only study aiming to link transcriptomics/proteomics to metabolic fluxes via supervised ML methods, suggesting that it can be used as a complementary approach (e.g., offer flux constraints/features to reduce the solution space and/or provide an overview of metabolic phenotypes) to the traditional FBA. Currently, this research gap is yet to be fully addressed and there is still room for further contributions, particularly as more omics data will become available.

Funding

This work was supported by the FCT PhD grant to DG (2022.12633.BD), Associate Laboratory for Green Chemistry (LAQV) financed by national funds from FCT/MCTES (UIDB/50006/2020 and UIDP/50006/2020), INESC-ID plurianual (UIDB/50021/2020), and the contract CEECIND/01399/2017 to RSC. The authors also wish to acknowledge the European Union's Horizon BioLaMer project under grant agreement number [101099487].

CRediT authorship contribution statement

Daniel M. Gonçalves: Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft. Rui Henriques: Funding acquisition, Methodology, Supervision, Writing – review & editing. Rafael S. Costa: Conceptualization, Funding acquisition, Methodology, Supervision, Validation, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could influence the work reported in this paper. Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding bodies. Therefore, the authors declare that they have no conflicts of interest.

Appendix A.

Table A.1.

Detailed metrics for all models and scenarios in the Ishii dataset with different inputs. Values in bold represent the best result for each model, ± indicates the standard deviations, and asterisk (*) indicates the best performance overall.

Model	Omics	Uptakes	Deviations	MAE	RMSE	NE	R2	p-value
DT	P	Yes	Yes	0.782 ± 1.142	1.123 ± 1.561	0.438 ± 0.645	0.946 ± 0.058	1.40e-03
			No	1.065 ± 1.518	1.504 ± 2.074	0.571 ± 0.851	0.934 ± 0.066	1.57e-02
		No	Yes	0.982 ± 1.354	1.412 ± 1.867	0.581 ± 0.918	0.952 ± 0.051	4.11e-03
			No	0.741 ± 0.842	1.071 ± 1.203	0.449 ± 0.727	0.944 ± 0.06	4.44e-03
	T	Yes	Yes	0.706 ± 0.941	1.013 ± 1.286	0.338 ± 0.286	0.951 ± 0.048	8.59e-03
			No	0.642 ± 0.905	0.909 ± 1.229	0.306 ± 0.268	0.951 ± 0.059	5.16e-03
		No	Yes	0.793 ± 0.912	1.136 ± 1.237	0.405 ± 0.312	0.957 ± 0.034	5.57e-03
			No	0.729 ± 0.728	1.052 ± 0.999	0.407 ± 0.362	0.941 ± 0.063	6.69e-04
	T+P	Yes	Yes	0.746 ± 0.936	1.076 ± 1.282	0.381 ± 0.364	0.947 ± 0.053	6.45e-03
			No	0.697 ± 0.917	0.992 ± 1.253	0.333 ± 0.271	0.944 ± 0.061	5.99e-03
		No	Yes	0.765 ± 0.937	1.086 ± 1.275	0.381 ± 0.351	0.952 ± 0.061	1.29e-02
			No	0.667 ± 0.692	0.963 ± 0.944	0.361 ± 0.272	0.952 ± 0.04	4.44e-03
LR	P	Yes	Yes	0.69 ± 0.558	1.007 ± 0.753	0.415 ± 0.375	0.903 ± 0.158	1.21e-02
			No	0.686 ± 0.526	0.953 ± 0.688	0.392 ± 0.325	0.908 ± 0.121	7.46e-03
		No	Yes	1.017 ± 0.898	1.442 ± 1.234	0.592 ± 0.587	0.872 ± 0.207	4.31e-02
			No	1.071 ± 0.978	1.483 ± 1.323	0.603 ± 0.587	0.853 ± 0.235	4.55e-02
	T	Yes	Yes	0.691 ± 0.867	0.989 ± 1.198	0.401 ± 0.51	0.936 ± 0.181	1.29e-02
			No	0.653 ± 0.763	0.9 ± 1.038	0.368 ± 0.454	0.913 ± 0.183	5.57e-03
		No	Yes	0.723 ± 0.901	1.034 ± 1.246	0.419 ± 0.529	0.936 ± 0.18	1.29e-02
			No	0.699 ± 0.899	0.961 ± 1.194	0.39 ± 0.508	0.91 ± 0.188	5.57e-03
	T+P	Yes	Yes	0.689 ± 0.86	0.987 ± 1.189	0.401 ± 0.507	0.936 ± 0.181	1.29e-02
			No	0.652 ± 0.763	0.9 ± 1.038	0.368 ± 0.454	0.913 ± 0.183	5.57e-03
		No	Yes	0.723 ± 0.904	1.034 ± 1.248	0.419 ± 0.53	0.936 ± 0.18	1.29e-02
			No	0.699 ± 0.897	0.961 ± 1.193	0.39 ± 0.507	0.91 ± 0.188	5.57e-03
NN	P	Yes	Yes	0.653 ± 0.944	0.937 ± 1.313	0.338 ± 0.335	0.966 ± 0.037	4.13e-05
			No	0.653 ± 0.944	0.937 ± 1.314	0.339 ± 0.342	0.966 ± 0.037	4.13e-05
		No	Yes	0.684 ± 0.931	0.969 ± 1.294	0.361 ± 0.357	0.969 ± 0.037	4.13e-05
			No	0.684 ± 0.93	0.969 ± 1.293	0.361 ± 0.357	0.969 ± 0.037	4.13e-05
	T	Yes	Yes	0.656 ± 0.946	0.94 ± 1.317	0.341 ± 0.347	0.967 ± 0.036	4.13e-05
			No	0.67 ± 0.938	0.968 ± 1.303	0.353 ± 0.346	0.964 ± 0.036	4.13e-05
		No	Yes	0.705 ± 0.931	1.0 ± 1.294	0.375 ± 0.361	0.968 ± 0.036	4.13e-05
			No	0.684 ± 0.93	0.969 ± 1.293	0.361 ± 0.357	0.969 ± 0.037	4.13e-05
	T+P	Yes	Yes	0.656 ± 0.945	0.941 ± 1.314	0.34 ± 0.337	0.967 ± 0.036	4.13e-05
			No	0.652 ± 0.945	0.936 ± 1.314	0.338 ± 0.338	0.967 ± 0.036	4.13e-05
		No	Yes	0.684 ± 0.931	0.969 ± 1.294	0.361 ± 0.357	0.969 ± 0.037	4.13e-05
			No	0.65 ± 0.798	0.922 ± 1.111	0.354 ± 0.355	0.967 ± 0.038	3.63e-05
RF	P	Yes	Yes	0.627 ± 0.822	0.893 ± 1.134	0.355 ± 0.408	0.968 ± 0.039	1.03e-05
			No	0.571 ± 0.826	0.816 ± 1.138	0.324 ± 0.428	0.971 ± 0.038	1.84e-05
		No	Yes	0.733 ± 0.941	1.043 ± 1.3	0.412 ± 0.464	0.97 ± 0.037	2.43e-05
			No	0.672 ± 0.909	0.951 ± 1.255	0.379 ± 0.482	0.97 ± 0.038	1.38e-05
	T	Yes	Yes	0.542 ± 0.823	0.777 ± 1.132	0.282 ± 0.295	0.97 ± 0.038	1.03e-05
			No	0.502 ± 0.777*	0.716 ± 1.067*	0.261 ± 0.299*	0.969 ± 0.038*	7.58e-06*
		No	Yes	0.592 ± 0.814	0.841 ± 1.118	0.316 ± 0.333	0.969 ± 0.037	2.11e-05
			No	0.53 ± 0.803	0.756 ± 1.106	0.283 ± 0.36	0.97 ± 0.036	1.19e-05
	T+P	Yes	Yes	0.542 ± 0.787	0.77 ± 1.081	0.286 ± 0.311	0.97 ± 0.037	8.84e-06
			No	0.507 ± 0.804	0.729 ± 1.105	0.271 ± 0.347	0.97 ± 0.037	7.58e-06
		No	Yes	0.584 ± 0.846	0.829 ± 1.165	0.312 ± 0.362	0.97 ± 0.038	8.84e-06
			No	0.531 ± 0.804	0.758 ± 1.104	0.278 ± 0.316	0.969 ± 0.036	1.03e-05
SVM	P	Yes	Yes	0.589 ± 0.941	0.854 ± 1.304	0.318 ± 0.43	0.971 ± 0.037	3.63e-05
			No	0.567 ± 0.944	0.822 ± 1.307	0.305 ± 0.421	0.971 ± 0.038	1.84e-05
		No	Yes	0.6 ± 0.948	0.87 ± 1.315	0.327 ± 0.465	0.971 ± 0.037	6.84e-05
			No	0.586 ± 0.94	0.852 ± 1.303	0.322 ± 0.466	0.971 ± 0.038	4.13e-05
	T	Yes	Yes	0.613 ± 0.934	0.883 ± 1.293	0.321 ± 0.352	0.971 ± 0.037	2.43e-05
			No	0.597 ± 0.934	0.861 ± 1.296	0.315 ± 0.378	0.969 ± 0.037	2.11e-05
		No	Yes	0.614 ± 0.935	0.885 ± 1.294	0.323 ± 0.355	0.971 ± 0.037	3.63e-05
			No	0.602 ± 0.937	0.869 ± 1.299	0.318 ± 0.384	0.97 ± 0.037	2.43e-05
	T+P	Yes	Yes	0.613 ± 0.934	0.883 ± 1.293	0.321 ± 0.352	0.971 ± 0.037	2.43e-05
			No	0.597 ± 0.934	0.861 ± 1.296	0.315 ± 0.378	0.969 ± 0.037	2.11e-05
		No	Yes	0.614 ± 0.935	0.885 ± 1.294	0.323 ± 0.355	0.971 ± 0.037	3.63e-05
			No	0.602 ± 0.937	0.869 ± 1.299	0.318 ± 0.384	0.97 ± 0.037	2.43e-05
XGB	P	Yes	Yes	1.229 ± 1.558	1.823 ± 2.238	0.724 ± 0.911	0.906 ± 0.09	1.74e-04
			No	1.229 ± 1.558	1.825 ± 2.245	0.725 ± 0.912	0.903 ± 0.089	8.88e-04
		No	Yes	1.33 ± 1.601	1.96 ± 2.295	0.781 ± 0.935	0.905 ± 0.089	4.08e-04
			No	1.381 ± 1.576	2.034 ± 2.255	0.818 ± 0.941	0.899 ± 0.088	2.54e-03
	T	Yes	Yes	0.575 ± 0.703	0.882 ± 0.972	0.316 ± 0.26	0.928 ± 0.083	6.05e-05
			No	0.559 ± 0.693	0.866 ± 0.96	0.314 ± 0.271	0.93 ± 0.074	2.17e-04
		No	Yes	0.664 ± 0.761	0.998 ± 1.057	0.366 ± 0.318	0.924 ± 0.089	8.09e-04
			No	0.647 ± 0.721	0.977 ± 1.008	0.358 ± 0.311	0.925 ± 0.084	8.09e-04
	T+P	Yes	Yes	1.006 ± 1.193	1.647 ± 1.898	0.643 ± 0.745	0.908 ± 0.085	6.84e-05
			No	0.997 ± 1.201	1.635 ± 1.903	0.642 ± 0.748	0.91 ± 0.082	4.99e-04
		No	Yes	1.095 ± 1.174	1.749 ± 1.871	0.686 ± 0.739	0.902 ± 0.09	1.67e-03
			No	1.065 ± 1.172	1.719 ± 1.872	0.671 ± 0.733	0.902 ± 0.095	1.82e-03
pFBA	N/A	Yes	N/A	0.692 ± 0.733	1.058 ± 1.029	0.381 ± 0.185	0.823 ± 0.156	N/A

Omics – P = proteomics, T = transcriptomics, T+P = combination of transcriptomics and proteomics; Uptakes – glucose and O₂ uptake rates fixed/constrained or not; Deviations – standard deviation of the omics measurements used or not as input; ‘N/A’ means the option is not available; ‘No’ means the option was not included but may be available in other settings.