Doping induced phase stabilization and electronic properties of alkaline earth metal doped zirconium (IV) oxide: A first principles study

Abstract

The role of divalent dopant cations such as Ca and Mg in phase stabilization of ZrO₂ has been demonstrated experimentally, with Mg emerging as a crucial dopant ion because of its ability to enhance the photocatalytic properties of ZrO₂. To provide a theoretical basis for these experimental observations, the modifications of the crystal and electronic structure of the monoclinic phase of zirconia, m-ZrO₂, upon doping with Mg have been studied at the atomic level using Density Functional Theory method. Additionally, the effect of dopant ionic radius on the electronic properties has been demonstrated by doping with Ca, which is isoelectronic with Mg. On 6.25 % doping, a structural distortion of the monoclinic crystal structure towards a tetragonal structure is observed. Additionally, the Density of States of doped m-ZrO₂ exhibits the characteristics of t-ZrO₂ in the Zr d orbitals in the unoccupied states and O unoccupied states emerge upon creation of an O vacancy in Mg/Ca doped m-ZrO₂. The calculated band gap of m-ZrO₂ is 3.6 eV. Upon doping there is a shift of the Fermi energy towards the valence band maximum.

1. Introduction

Zirconium oxide (ZrO₂), also known as zirconia, is a wide band gap semi-conductor oxide. It is a polymorphic material with three allotropes at ambient pressures [1,2]. These are the low temperature monoclinic phase (m-ZrO₂), space group P2₁/c [3], also known as baddeleyite and the high temperature tetragonal (t-ZrO₂) and cubic (c-ZrO₂) phases, with transition temperatures of 1478 K and 2650 K respectively [4,5]. ZrO₂ exhibits technologically relevant properties, such as low thermal conductivity, high mechanical strength, high refractive index, optical transparency, high corrosion resistance, high stability at elevated temperatures and catalytic properties [1,3]. Additionally it is non-toxic and has a high porosity [6]. It finds application in improved ceramics, catalysts, solid oxide fuel cells, thermal barriers, oxygen sensors, optical devices [5], medical devices, cutting tools and in nuclear power stations [4]. However, the performance of zirconia in various applications heavily depends on the crystalline structure and phase transformations [7].

The tetragonal and monoclinic zirconia phases are distortions of the high temperature cubic phase. In applications involving thermal cycling, repeated phase transitions occur, accompanied by significant shear deformations, which can result to catastrophic effects such as fracture. Other effects include a change in the stress pattern in grains, which affects the micro hardness. Hence, stabilization of the high temperature phases in order to improve performance through minimization of phase transitions of zirconia continues to be explored [6,7].

To stabilize the high temperature phases of ZrO₂ at low temperatures, researchers have explored techniques such as application of pressure and incorporation of aliovalent dopants. The latter has been explored experimentally by combining single metal oxides with other different metal oxides, so as to introduce defects in the lattice and to reduce agglomeration, which causes a broad distribution of particle size in the nanoparticles [1,3,5,7]. Reduction of agglomeration is desirable because, a decrease in the size of crystallites widens the stability region. This in turn increases the possible applications that the oxide can be put into [8]. Additionally, isovalent isomorphism, such as in the ZrO₂–CeO₂ system and heterovalent isomorphic substitution with divalent alkaline earth and rare earth metals has been reported, with the phase stability showing dependence on factors such as the type and amount of dopant as well as annealing temperature [7].

In addition to phase stabilization, various dopants such as Ni [9] and Mg [5] have been reported to enhance the photocatalytic activity of ZrO₂. Photocatalysis has emerged as one of the preferred technologies for the mitigation against environmental pollution and in applications such as water treatment [10,11]. Among the main factors that influence photocatalytic activity are light absorption ability, separation of photo generated charge carriers and the accessibility to surface active sites. These depend on properties such as the morphology, porosity, crystallinity, and bandgap of the photocatalyst [12]. TiO₂ has been one of the most widely studied photocatalyst, with limitations such as charge recombination being one of its major drawbacks [13,14]. ZrO₂ physico-chemical features are comparable to those of TiO₂ and has been reported to have higher photocatalytic activity than TiO₂ because it is better at stabilizing oxygen vacancies [15].

Of the three phases of zirconia, t-ZrO₂ has demonstrated higher photocatalytic activity compared to c-ZrO₂ and m-ZrO₂ due to its active surface and smaller particle size [5,8]. For instance, tetragonal phase ZrO₂ nanoparticles, with very small particle size were shown to exhibit the best adsorptive capacity for tetracycline [16]. Further, ZrO₂ nanoparticles are playing a crucial role in the field of photocatalysis through modifications such as combination with other visible light active semiconductors in systems such as the ZrO₂ - TiO₂ composite [6] as well as doped systems such as carbon doped t-ZrO₂ [12].

Metal doped zirconia exhibits other interesting properties such as improved oxygen ion conduction in solid oxide fuel cells, which ordinarily require high temperatures to ensure adequate ionic conductivity. The higher temperatures lead to disadvantages such as material degradation and high running costs [1,3,5]. In Mg doped nanocrystalline ZrO₂ thin films, improvement in the photoluminescence intensity has been demonstrated. This has mainly been attributed to the formation of oxygen vacancies [17]. In a theoretical study in which yttrium was used as a dopant in a 2 x 2 x 1 c-ZrO₂ supercell to explain the mechanism of experimentally observed stabilization of zirconia at high temperatures, the synergistic effects of yttrium doping as well as the formation of oxygen vacancies was established [18].

Apart from creation of oxygen vacancies through doping, tuning the electronic band gap and shifting the position of the valence and conduction band, which are responsible for the production of the active species in the photocatalytic process is critical [10]. The energy band gap energies for the ZrO₂ crystalline phases as determined experimentally and from first principles range from 3.04 to 5.8 eV. A red shift of the optical absorption edge has been predicted using Density Functional Theory (DFT) with Ti doping, which is in agreement with experimental observation [19].

Focus on modifications of the low temperature monoclinic zirconia phase, m-ZrO₂, which is dominant in ZrO₂ based catalytic materials, may be beneficial in exposing wider application possibilities of zirconia. A theoretical basis, which provides an atomic level insight on the mechanism behind the observed phase stabilization and electronic structure modifications caused by Mg doping of m-ZrO₂, which has not yet been reported to the best of our knowledge, is necessary. Also, a study on the effect of other alkaline earth dopant metals such as Ca on the electronic properties of m-ZrO₂ would be useful to demonstrate the effect of size of dopant ion on the electronic properties. In this study, an investigation of the incorporation of alkaline earth metal (Mg and Ca) dopants on the structural and electronic properties of the low temperature zirconia phase, m-ZrO_2, has been carried out using DFT. The results contribute to the understanding of the crystal structure – electronic structure properties relation, from an atomic orbital wave functions point of view, that may lead to the prediction of new applications for phase controlled ZrO₂.

2. Computational details

Density Functional Theory (DFT) method based on the Kohn-Sham formalism as implemented by the Quantum ESPRESSO simulation package was used to perform the electronic structure calculations. The Projector Augmented Wave (PAW) approach was used to represent the atomic cores and the Kohn-Sham orbitals of the valence electrons were expanded in plane wave basis sets up to a kinetic energy of 60 Ry. The monoclinic m-ZrO₂ was described by the P2₁/c space group, with 4 Zr and 8 O atoms in its conventional unit cell shown in Fig. 1 (a). To study the structural and electronic properties of the pure and doped m-ZrO₂ systems, 2 x 2 x 1 ZrO₂ supercells consisting of 48 atoms, having the composition Zr₁₆O₃₂, as shown in Fig. 1 (b), were modelled using the Visualization for Electronic Structural Analysis (VESTA) visualization software.

Fig. 1.

a) m-ZrO₂ Unit cell, b) 2 x 2 x 1 m-ZrO₂ supercell.

The calculations to optimize the crystal structure of ZrO₂ and to determine its electronic structure applied the Generalized Gradient Approximation (GGA) with Perdew-Berke-Ernzerhof for solids (PBEsol) parametrization to describe the exchange and correlation in system. A 2 x 2 x 3 Monkhorst-Pack k-point grid for the 2 x 2 x 1 supercells was used for self-consistent field and relaxation calculations, with a convergence threshold on total energy of 10⁻⁸ and 10⁻⁶ Ry respectively. Upon 6.25 % cationic doping, achieved by single cationic substitution, the structures were allowed to relax using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-newton algorithm, until the residual forces were less than 10⁻³ Ry/Bohr, in order to minimize the forces in the system. In addition, the effect of an oxygen vacancy on the electronic structure of m-ZrO₂ and X = (Mg, Ca) doped m-ZrO₂ was studied using a 2 x 2 x 1 supercell with a composition Zr₁₆O₃₁ and Zr₁₅XO₃₁ respectively. The Density of States (DOS) for tetragonal zirconia phase, t-ZrO₂ having space group P4₂/nmc was also determined for comparison. Total energy calculations were performed using the Marzari–Vanderbilt smearing scheme with a Gaussian spreading of 0.05 Ry, while for the DOS calculations, the occupations within the irreducible Brillouin zone were determined using the linear tetrahedron method with Blöechl's corrections. The maximum number of geometric and electronic iterations were set at 100. Where convergence was not achieved within the set number of iterations, as was the case for relaxation calculations, the updated atomic positions were used as input to continue the relaxation calculations. Generally, all calculations begun from scratch.

3. Results and discussion

In this section, the structural and electronic properties of m-ZrO₂ and alkaline earth metal (Mg ^/Ca) doped m-ZrO₂ will be discussed. In addition, the effect of oxygen vacancies on the electronic structures of m-ZrO₂ and doped m-ZrO₂ will be demonstrated. The edge of the valence states next to the Fermi level and the distribution of the Zr unoccupied d states of pure tetragonal ZrO₂ (t-ZrO₂) will also be compared with those of m-ZrO₂ and doped m-ZrO₂.

3.1. Structural properties

Volume optimization was carried out for m-ZrO₂ unit cell, starting with lattice parameters of $a=5.234\mathrm{\AA }.\mathrm{b}=5.268\mathrm{\AA },\mathrm{c}=5.418\mathrm{\AA }$ and $\beta =100.055°$ [21]. Total energy calculations were first carried out for several lattice parameter $a$ values keeping $b/a$ as well as $c/a$ ratios and angle $\beta$ of the unit cell constant. The lattice parameter $a$ corresponding to the unit cell with lowest energy was obtained. The ratios were optimized next in turn, while keeping the rest of the parameters constant in order to find the volume with the lowest energy. The optimized lattice parameters are $a=5.207\AA ,b=5.256\AA ,c=5.424\AA$. These are quite comparable with other theoretical and experimental results as shown in Table 1.

Table 1.

Lattice parameters (a, b and c) of m-ZrO₂ unit cell in comparison with other theoretical and experimental values.

m-ZrO2	a (Å)	b(Å)	c (Å)	Exchange-Correlation/Source
Present work	5.207	5.256	5.424	GGA-PBEsol
Other theoretical results	5.170	5.230	5.340	B3LYP [6]
	5.087	5.175	5.249	LDA [22]
	5.237	5.145	5.355	LDA + U [22]
	5.161	5.231	5.340	GGA-PBE [20]
	5.120	5.160	5.330	GGA [23]
	5.190	5.250	5.350	GGA-PBE [2]
	5.080	5.200	5.220	PP-PW [24]
	5.197	5.243	5.389	GGA-PBE [25]
Experimental results	$5.234$	$5.268$	$5.418$	[21]
	5.145	5.208	5.311	[22]
	5.150	5.210	5.310	[26]
	5.200	5.250	5.410	[23]

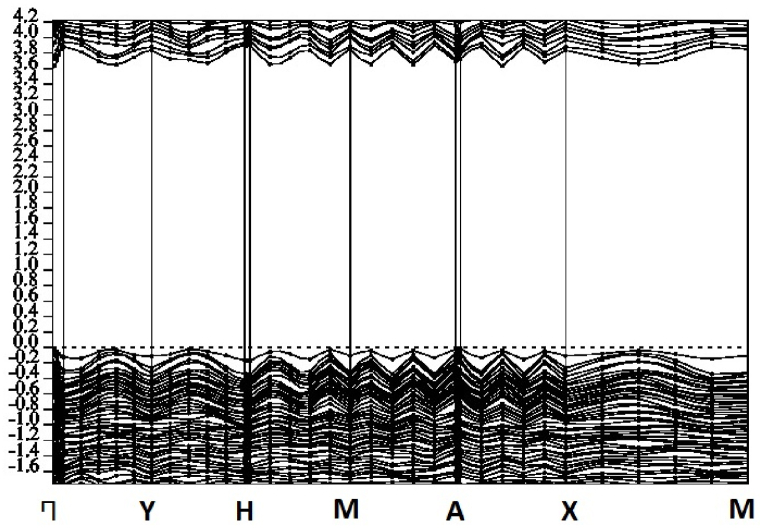
2 x 2 x 1 pure m-ZrO₂ and Mg/Ca doped m-ZrO₂ supercells were then modelled and optimized. The optimization for the $a$ lattice parameter for Mg and Ca doped m-ZrO₂ is shown in Fig. 2 (a), while that of m-ZrO₂ is shown in Fig. 2 (b).

Fig. 2.

Lattice constant $a$ optimization for: a) Mg and Ca doped m-ZrO₂ and b) m-ZrO₂.

The corresponding lattice parameters for the m-ZrO₂ $2x2x1$ supercells are shown in Table 2.

Table 2.

Lattice parameters (a, b and c) of m-ZrO₂ and Mg/Ca doped m-ZrO₂$2x2x1$ supercells.

	a (Å)	b(Å)	$b/a$	c (Å)
m-ZrO2	11.853	10.972	0.926	5.369
Mg doped m-ZrO2	11.642	10.943	0.940	5.310
Ca doped m-ZrO2	11.589	11.009	0.950	5.296

Doping with Mg/Ca causes the $b/a$ ratio to increase from 0.926 in m-ZrO₂ to 0.940 and 0.950 in Mg and Ca doped m-ZrO₂ respectively. It can be seen that the introduction of dopants tends to tetragonalize the monoclinic crystal structure, as the $b/a$ ratio tends towards unity.

A similar effect was predicted for doping m-ZrO₂ with yttrium, in which the lattice parameters changed from $a$ = 10.1788 Å, $b$ = 10.3742 Å to $a$ = 10.2223 Å, $b$ = 10.3765 Å for 3.23 % Y doping and $a$ = 10.2386 Å and $b$ = 10.3711 Å with 6.67 % Y doping [27]. These results offer an explanation as to why Ca doping was previously reported to have a role in increasing the stability of the ZrO₂ mesoporous structure at high calcination temperature for biomedical applications [28] and the role of solutes such as MgO, CaO and Y₂O₃ in lowering the transformation temperature from the tetragonal phase to the cubic phase [23]. They could also explain the experimental observation of the partially stabilized zirconia, containing a tetragonal phase, together with the other two phases, which is formed when the amount of stabilizer is insufficient for the formation of the cubic phase, such as reported for 2–5 mol % of yittria [7].

3.2. Electronic properties

The Total Density of States (TDOS) and Projected Density of States (PDOS) for m-ZrO₂ and t-ZrO₂ are shown in Fig. 3 (a) and (b) respectively.

Fig. 3.

Total Density of States (TDOS) and Projected Density of States (PDOS) for: a)m-ZrO₂ and b) t-ZrO₂.

It can be seen that in both cases, the valence states adjacent to the Fermi level are mainly comprised of the O atom p orbitals, while the lowest energy unoccupied states are predominantly of Zr d character in agreement with the observation made by Milman et al. [1]. In both m-ZrO₂ and t-ZrO_2, the unoccupied states are majorly composed of Zr d orbitals.

However, while the edge of the valence states of the TDOS for m-ZrO₂, just below the Fermi level increases smoothly, the TDOs of t-ZrO₂ increases less smoothly at the edge of the valence states just below the Fermi level as shown in Fig. 3. The enhanced step feature at the edge of the occupied states just below the Fermi level is characteristic of t-ZrO₂ and c-ZrO₂ as described by Li et al. [22].

Another interesting distinction is that an e_g - t_2g split emerges in the Zr d orbitals in the unoccupied states of t-ZrO₂ in the energy region around 5–6 eV as can be seen in Fig. 3 (b), which is not observed in the Zr d orbitals of m-ZrO₂. This feature has been attributed to the symmetry of a cubic or tetragonal crystal structure according to the crystal field theory. The symmetry causes an e_g – t_2g splitting between doubly degenerate and triply degenerate d orbitals, comprised of the lower energy, dx²-dy ² and dz² orbitals and higher energy, dxy, dxz, and dyz orbitals, respectively. This feature is missing for m-ZrO₂ in Fig. 3, in which the Zr d orbitals consist of a single band, in agreement with the explanation offered by Ricca et al. [3].

The TDOS of Mg doped m-ZrO₂ is shown in Fig. 4 (a). As can be seen, it has a similarity at the edge of the valence states below the Fermi level to that of t-ZrO₂ and a split in the Zr d orbitals in the unoccupied states begins to emerge as compared to m-ZrO_2.

Fig. 4.

a) TDOS and PDOS for Mg doped m-ZrO₂ and b) Mg PDOS for Mg doped m-ZrO₂.

The occupation of Mg p states shown in Figue 4 (b), demonstrates the role of the dopant ion in causing the modification at the edge of the TDOS just below the Fermi level. In addition to the Zr d and O p states, the Mg p states also fall within the same enery range and would be involved in hybridization.

A shift in the Fermi level towards the valence band maximum in Mg doped m-ZrO₂ as compared to m-ZrO₂ is evident from the band structure of m-ZrO₂ shown in Fig. 5 (a) and that of Mg doped m-ZrO₂ shown in Fig. 5 (b). This shift could be attributed to charge compensation, considering that a dopant having oxidation state +2 has substituted a Zr⁴⁺ ion.

Fig. 5.

Band structure for a) m-ZrO₂ and b) Mg doped m-ZrO₂.

The calculated band gap of m-ZrO₂ from this work is 3.60 eV, in good agreement with the band gap from other theoretical calculations such as 3.60 eV calculated by Ref. [22] as well as others collated in Table 3.

Table 3.

Band gap energies for m-ZrO₂.

ZrO2	Band gap (eV)
Present work	3.60
Other theoretical results	3.60 [22]
	3.61 [2]
	3.58 [23]
	3.58 [31]
	3.58 [22]
Experimental results	5.80 [32]
	5.68 [31]

The calculated electronic band gaps are however smaller than the experimental values as is expected of standard DFT- PBE methods, which normally underestimate the band gaps of semiconductors, but however offer valuable information when trends in the size of the electronic band gaps upon modification of materials are of interest.

Fig. 6 (a) shows the step feature at the edge of the valence states below the Fermi level in the TDOS of Ca doped m-ZrO₂, which is not surprising, considering the changes observed in the $b/a$ ratio with Ca doping as collated in Table 2. The Ca dopant states occupy higher energies at the edge of the valence states just below the Fermi level as shown in Fig. 6 (b).

Fig. 6.

a) TDOS and PDOS of calcium doped ZrO₂ b) Ca PDOS of Ca doped ZrO₂.

The band structure for Ca doped m-ZrO₂ is shown in Fig. 7, where the Fermi energy shifts towards the valence band maximum as compared to m-ZrO₂ shown in Fig. 5(a).

Fig. 7.

Band structure for Ca doped m-ZrO₂.

So far, the effects of Mg and Ca doping in tetragonalizing the crystal structure and introduction of dopant states at the edge of the valence states below the Fermi level, as well as shifting the Fermi level towards the valence band maximum upon doping, have been demonstrated.

To further compare the effects of Mg/Ca doping of ZrO₂, the formation of oxygen vacancies upon doping is explored. Oxygen vacancies can be formed in doped films during manufacture due to ionic compensation as a result of the charge introduced by a dopant among other factors [29], an effect that has been attributed to improved optical properties. First, the effect of an oxygen vacancy in the electronic structure of m-ZrO₂ is shown in the TDOS and PDOS of the oxygen vacancy defective m-ZrO₂ in Fig. 8 (a) and (b) respectively.

Fig. 8.

a) TDOS for oxygen vacancy defective m-ZrO₂ and b) O p and Zr d PDOS for oxygen vacancy defective m-ZrO₂.

It can be seen that overall, the TDOS shifts to lower energies as compared to perfect m-ZrO₂. In addition, the energy state at around 0.8 eV below the Fermi level is attributed to the Zr d orbitals as shown in Fig. 8 (b) and the narrower electronic gap between the occupied and unoccupied states is between the Zr d orbitals. A similar trend in the TDOS of c-ZrO₂ is reported upon the formation of an oxygen vacancy [18]. It can be deduced just like for TiO₂, which is isoelectronic with ZrO₂, that the oxygen vacancy leaves two excess valence electrons that partially occupy the d orbitals, thereby leading to the emergence of an energy state within a similar energy region below thr Fermi level [30].

Fig. 9 (a) shows that an oxygen vacancy in Mg doped m-ZrO₂ causes the formation of oxygen unoccupied states above the Fermi level, which can be attributed to charge compensation. Fig. 9 (b) clearly demonstrates the emergence of the oxygen unoccupied states at around 0.5 eV above the Fermi level.

Fig. 9.

a) TDOS and PDOS for Zr d, O p and Mg p states for oxygen vacancy defective Mg doped m-ZrO₂ and b) O p states in oxygen vacancy defective Mg doped m-ZrO₂.

The Fermi level falls between the narrow gap between the O p states. This may contribute to the experimentally observed improved photoluminescence intensity due to Mg doping of ZrO₂, stabilization of the tetragonal phase, improved oxygen ion conduction and application in resistive random access memories (RRAMs) [15,17,26]. This result justifies the attribution of the aforementioned experimental observations to the formation of oxygen vacancies in Mg doped zirconia.

The effect of an O vacancy in Ca doped m-ZrO₂ is shown in Fig. 10 (a) and (b).

Fig. 10.

a) TDOS and PDOS for Zr d, O p and Ca p states for oxygen vacancy defective Ca doped m-ZrO₂ and b) O p states in oxygen vacancy defective Ca doped m-ZrO₂.

Just like in the case of Mg doping, the presence of oxygen vacancies in Ca doped m-ZrO₂ causes the formation of oxygen unoccupied states at around 0.5 eV above the Fermi level as shown in Fig. 10 (b). However, unlike the case with Mg dopant, the Ca dopant states dominate the higher energy levels just below the Fermi level and contribute to the unoccupied states within the same region as the O unoccupied states at around 0.5 eV. In addition, Ca and O unoccupied states shift to lower energies and occupy similar energy regions, which would result in increased hybridization between the Ca and O p states. As a result, the Fermi level falls within the narrow gap between the occupied and unoccupied O and Ca p states as shown in Fig. 10, which points to a possibility of the combined effect of the emergence of Ca and O p unoccupied states on experimentally observed activity of Ca doped zirconia.

Therefore, Ca doping is more suitable for stabilization of t-ZrO₂ while Mg doping is recommended in applications where ionic mobility is required. Apart from charge compensation, it is emerging that the ionic radius of the alkaline earth metal dopant is important in the resultant structural and electronic modifications.

4. Conclusion

Doping m-ZrO₂ with Mg/Ca causes structural changes that tend to tetragonalize the crystal structure of m-ZrO₂ from the monoclinic structure by altering the $b/a$ ratio. This effect is reflected in the density of states that bears a similarity with that of t-ZrO₂, an effect that would make doped ZrO₂ suitable for a wider range of applications. Further, the Fermi level shifts towards the valence band maximum, with the introduction of Ca/Mg dopant states, an effect that has been observed in other studies involving doping with main group elements such as sulphur [33]. Of significance is the demonstration of the effect of an oxygen vacancy in the Mg/Ca doped m-ZrO_2, which revealed the emergence of oxygen unoccupied states. The results provide to a large extent, a further understanding of the interplay between crystal structure and electronic structure of zirconia

Funding sources

There are no funding grants to declare.

Data availability statement

Data will be made available on request.

CRediT authorship contribution statement

Jane Kathure Mbae: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing - original draft, Writing - review & editing. Zipporah Wanjiku Muthui: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.