Abstract
High throughput and efficient separation/isolation of nanoparticles such as exosomes remain a challenge owing to their small size. Elasto-inertial approaches have a new potential to be leveraged because of the ability to achieve fine control over the forces that act on extremely small particles. That is, the viscoelasticity of fluid that helps carry biological particles such as extracellular vesicles (EVs) and cells through microfluidic channels can be tailored to optimize how different-sized particles move within the chip. In this contribution, we demonstrate through computational fluid dynamics (CFD) simulations the ability to separate nanoparticles with a size comparable to exosomes from larger spheres with physical properties comparable to cells and larger EVs. Our current design makes use of an efficient flow-focusing geometry at the inlet of the device in which two side channels deliver the sample, while the inner channel injects the sheath flow. Such flow configuration results in an efficient focusing of all the particles near the sidewalls of the channel at the inlet. By dissolving a minute amount of polymer in the sample and sheath fluid, the elastic lift force arises and the initially focused particle adjacent to the wall will gradually migrate towards the center of the channel. This results in larger particles experiencing larger elastic forces, thereby migrating faster toward the center of the channel. By adjusting the size and location of the outlets, nanoparticles comparable to the size of exosomes (30nm to 100nm) will be effectively separated from other particles. Furthermore, the influence of different parameters such as channel geometry, flow rate, and fluid rheology on the separation process is evaluated by computational analysis.
Keywords: microfluidics, computational fluid dynamics, extracellular vesicles, sorting
Graphical Abstract
Separation of nano-sized vesicles and exosomes from cells and other particulates remains a challenge, yet is very much needed for many biomedical applications. This work demonstrates facile separation of nano-sized particles from micron-sized without sample preparation and by use of a simple microfluidic channel. We show that exploitation of viscoelastic fluid flow facilitates precise separation at a high throughput.
II. INTRODUCTION
The isolation and separation of biological particles from heterogeneous mixtures is of paramount importance for many biomedical applications including drug discovery, diagnostics, -omics screening, and personalized medicine, to name a few. Significant engineering efforts have resulted in many chip-based technologies that permit robust separation/isolation of extremely small particles. Despite significant progress, the separation of nanoparticles, in particular exosomes, remains challenging owing to their small size. This study presents a novel microfluidic-based separation approach that demonstrates facile high throughput separation proven by computational fluid dynamics (CFD) simulations. To preface this work, we contrast our findings to the conventional methods for the separation of nanoparticles such as exosomes, discussed below.
Conventional methods for the separation of nanoparticles include ultracentrifugation, size exclusion chromatography, ultrafiltration, and immunoaffinity-based methods. Ultracentrifugation is currently considered the gold standard for exosome separation [1,2]. This method is based on the differences in the sedimentation coefficient of exosomes and other substances in the sample. Ultracentrifugation-based separation techniques can produce large amounts of exosomes. However, they are not suitable for clinical diagnosis due to the time required (>4 h), low recovery rate (5–25%), high cost, and poor repeatability [3–5]. Ultrafiltration is a membrane-based separation technique, which primarily relies on size and molecular weight. This technique is often used in combination with the ultracentrifugation technique where large extracellular vesicles (EVs) and cells are first separated by ultracentrifugation and subsequently, ultrafiltration is used for the purification of exosomes from proteins [6,7]. However, exosome recovery rates can be low owing to issues such as clogging and trapping of particles within the filters [8]. Size exclusion chromatography (SEC) separates particles based on their size, where the separation force is owing to gravitational acceleration. When contrasting ultracentrifugation to size exclusion chromatography, ultracentrifugation is higher in throughput yet lower in yield [9–11]. Thus, it is suggested to use SEC in combination with ultracentrifugation [12]. Immunoaffinity-based methods rely on antigen-antibody affinity to capture exosomes. Various proteins on the membrane of exosomes are ideal biomarkers for the immunoaffinity-based separation of exosomes. Despite the high purity and yield of immunoaffinity-based methods compared to ultracentrifugation [2,13], its application for large-scale exosome separation is inhibited due to several drawbacks such as the requirement of cell-free samples and costly reagents [14–16].
Microfluidic methods, on the other hand, have emerged as powerful tools to address the challenges associated with the aforementioned conventional techniques. The capability of precisely manipulating vast numbers of particles, working with small-volume samples, and integrating with downstream detection tools makes such methods suitable alternatives to be exploited in different medical applications. Among different approaches, inertial microfluidic devices received significant attention for particle separation. The passive nature of such devices significantly increases the portability, simplicity, and durability of such devices when compared to active methods such as those using magnetic fields, acoustic streaming, and electric fields. However, the inertial lift force used in these devices is not strong enough for manipulating submicron particles. The strong dependency of inertial lift force on particle size () results in the deficiency of these devices for separating small particles (less than~3μ).
Using viscoelastic fluids in such devices results in an additional lift force, namely the elastic lift force. The emerging elastic lift force at high flow rates (elasto-inertial flow regime) pushes all the particles toward the center of the channel, which enables precise 3D focusing of particles [17]. Furthermore, the elastic lift force in such devices is dependent on the size of particles, however, proportional to which makes it possible to better manipulate submicron particles [17–19]. Apart from that, the arising elastic lift force in such devices is strongly dependent on the fluid property. Hence, elasto-inertial approaches enable achieving fine control over the forces that act on extremely small particles. That is, the viscoelasticity of fluid that helps carry particles through microfluidic channels can potentially be tailored for high-resolution focusing and separation of micron/submicron particles without the need for an external force at low cost and high versatility. Despite several advantages of elasto-inertial approaches compared to the inertial method, the application of such techniques for efficient isolation of nanoparticles such as extracellular vesicles is still in its infancy. Furthermore, using sophisticated computational techniques is essential to predict the flow field in such devices owing to the inherent complexity of the carrier viscoelastic fluids.
The earliest research on particle migration in viscoelastic fluids was reported by Leshansky et al. [17]. Using a polyacrylic acid (PAA) solution they observed that particle focusing in a rectangular channel was better when using dilute PAA solutions. The influence of shear thinning property on the focusing of particles in a rectangular channel was also conducted by Seo et al.,[18,19] in which a high molecular weight polyethylene oxide (PEO) contributed to shear thinning and degraded the focusing of particles at the center of the channel. Interestingly, by adding a minute amount of polymer (e.g. PEO, PAA, or xanthan gum (XG)) to a Newtonian fluid, the fluid exhibits viscoelastic behaviors. This is in contrast to Newtonian fluid flow in which the shear stresses are the dominant stresses. The existence of long polymer chains in viscoelastic fluids results in the generation of considerable normal stresses. The emerging normal stresses are responsible for an elastic lift force exerted on the particles. The distribution and intensity of elastic forces in such devices not only depend on the flow characteristics but also changes with the fluid properties such as the viscosity of the solvent, polymer molecular weight, and concentration [22,23].
Therefore, following these early studies, different investigators studied the influence of polymer molecular weights, relaxation time, and concentrations. Various reported studies were conducted using straight microchannels, and revealed that particle focusing enhances as the molecular weight and lengths of the polymer decreased [24–26]. Published studies reveal the feasibility of particle focusing/separation for different micron-size particles in slightly different geometries [27][28][29][30]. Apart from these, curved microchannels were employed to enhance the focusing of micron and submicron-size particles [22,31–34]. The Dean drag-induced force in curved channels can potentially enhance the focusing behavior of particles. However, when using viscoelastic fluids, the curvature of the channel generally limits the throughput of the device due to the occurrence of flow instabilities [35].
This work introduces a major advance in elasto-inertial microfluidic separation methods for nano-sized particles. We demonstrate, using computational fluid dynamics (CFD) simulations, unique geometrical conditions that are shown for the first time to enhance submicron particle separation. We incorporate spherical particles that range in size from micron to nano-scale to model heterogeneous samples of cells and extracellular vesicles. The feasibility of achieving high-throughput separation is demonstrated systematically by designing and testing with CFD simulations considering different flow-focusing geometries, identifying the influence of different geometrical parameters and fluid properties, modeling the flow field, and predicting the separation of particles.
III. THEORY AND DEMONSTRATION OF WORKING PRINCIPLE
The theory and demonstration of a novel microfluidic channel that incorporates viscoelastic fluid flow are described herein with a discussion of the varied simulation parameters. It was first conceived that a simple, flow-focusing geometry be simulated with two side inlets and one central inlet. A simple microdevice is ideal for manufacturing, reproducibility, and cost. Thus we simulated two side inlets to deliver the particulate sample (i.e. cell and EV mixture) while the inner channel is used to deliver the sheath fluid. The particulate sample was simulated in the work herein to be dilute and with the particle size ranging from 30 nm-5 μm representing the size of different extracellular vesicles. The sheath and sample fluid are a mixture of a small amount of polymer with phosphate buffered saline to generate viscoelastic properties of the fluid (concentrations noted later).
Fig. 1-a is a schematic of the device. As shown, as the sample encounters the sheath, an initial focusing of all the particles occurs near the sidewalls of the channel at the inlet. However, due to the high shear rate of the carrier viscoelastic fluid, significant elastic stress is generated further along the length of the main channel. This stress is highest at the walls and decreases towards the center of the channel. Hence, the initially focused particles adjacent to the wall experience a stress gradient that exerts a lift force on them. Fig. 1-b shows the contours of typical elastic stress distribution in the cross-section of the main channel. The direction of the exerted elastic lift force on the particles is towards the center of the channel while its magnitude is proportional to their size (). Hence, larger particles experience a greater elastic lift force and migrate faster toward the center of the channel. The different migration speed of particles with different sizes results in a size-based separation of particles as they move toward the outlet of the main channel. By precisely adjusting the size and location of the outlets, particles smaller and larger than a certain size can be separated. This approach effectively results in an efficient focusing of all particles with different sizes near the side walls at the entrance followed by size-based separation of particles in the main channel. However, when applying viscoelastic fluids in this flow regime, elastic instabilities can arise particularly when high flow rates are introduced within flow focusing microchannel. Therefore, the work herein first optimizes the flow-focusing geometry to avoid instabilities at high flow rates. Subsequently, we assess the characteristics of the flow field and exerted forces for different channels and polymer solutions, perform particle tracking, and draw conclusions on how our optimized chip design can accurately and precisely adjust the location and size of the outlets.
Fig. 1.
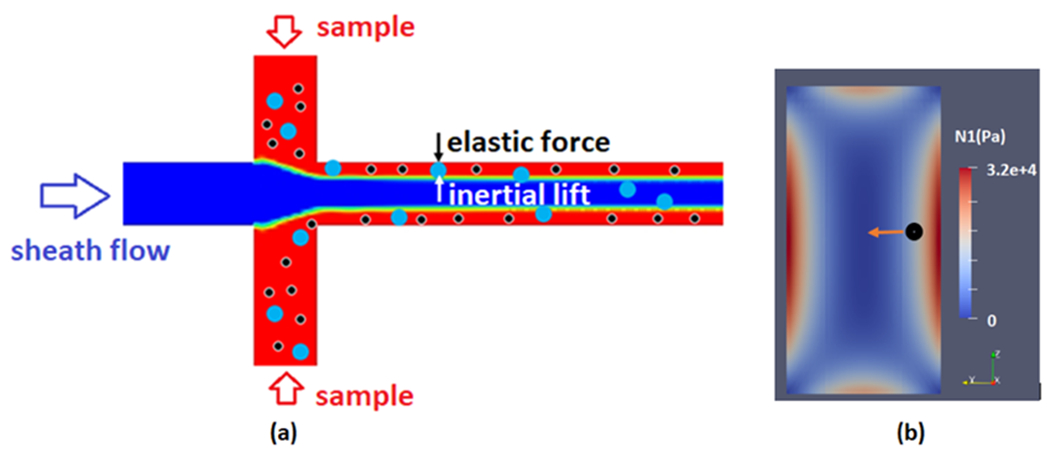
A schematic of the flow focusing geometry and size-based separation of particles (a) and stress distribution in the cross-section of channel (b)
i. Computational approach
CFD simulation was employed to predict the separation of nanoparticles of different sizes in elasto-inertial fluid flow. To this end, governing equations of the flow field are fully resolved to predict the velocity, pressure, elastic stress, and particle trajectories. Such an approach not only reveals the performance of the simulated microfluidic device but also sheds light on the underlying physics necessary for further improvements. The governing equations for viscoelastic fluid flow in the laminar regime are as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The continuity and momentum equations (eq 1,2), contain the velocity u, pressure p, and stress tensor . The stress tensor for viscoelastic fluids is written as the sum of solvent stress and polymer stress (eq 3). The polymer stress in the viscoelastic fluid was taken into account by using Phan-Thien-Tanner (PTT) model (eq 4,5). , and denote the polymer relaxation time, polymer viscosity, and material parameter, respectively. Of note, the PTT model takes into account the finite extensibility of polymers and shear thinning effects [36,37]. Furthermore, previous studies revealed the accuracy of this model in predicting the flow field of viscoelastic fluids [37]. The finite volume method (FVM) was used to numerically solve the transport equations using TransAT 5.6. The pressure velocity coupling in the CFD model was achieved by using the SIMPLEC algorithm. The spatial derivatives were discretized using the HLPA scheme. Furthermore, the Log-conformation tensor (LCT) approach was employed to accurately model the flow field at high Weissenberg numbers.
By adopting the abovementioned numerical approach, the velocity and pressure distribution along with the distribution of polymer stresses are obtained. Using such information, the trajectory of different particles can be simulated by integrating the force balance on particles via a Lagrangian approach. Hence, the following equation is solved for individual particles:
| (6) |
| (7) |
where, , , and indicate the drag force, elastic lift force, and inertial lift force, respectively.
The drag force is quantified as follows:
| (8) |
where, , and indicate the viscosity, particle density, and particle diameter, respectively. Drag coefficient is calculated according to the Morsi-Alexander model [38], and the relative Reynolds number (Re) is defined as follows:
| (9) |
The arising elastic lift force is proportional to the gradient of the first normal stress difference , and particle diameter and calculated as follows:
| (10) |
| (11) |
The inertial lift force is calculated as follows [39]:
| (12) |
3-D numerical simulations were carried out using a uniform mesh with a grid size of . Adoptive time stepping was employed for the transient simulations to ensure the stability of numerical solutions. The adopted Courant number in all the simulations was 0.2.
ii. Fluid Properties
In these simulations, our carrier fluid is assumed to be phosphate buffered saline (PBS). The elasticity of the carrier fluid is adjusted by adding PEOs with different molecular weights and concentrations. Table. 1 shows the property of different solutions examined in this study. The total viscosity of the solution is determined as the summation of solvent viscosity and the polymer viscosity, . The polymer viscosity is calculated as follows [40]:
| (13) |
Table. 1.
Property of PEO solutions with different molecular weights and concentrations.
| c* (Wt%) | c (Wt%) | c/c* | (Pa.s) | λ (s) | |
|---|---|---|---|---|---|
| 300 kDa | 0.3571 | 0.03571 | 0.1 | 0.000105 | 0.000135 |
| 300 kDa | 0.3571 | 0.08927 | 0.25 | 0.000262 | 0.000245 |
| 300 kDa | 0.3571 | 0.1786 | 0.5 | 0.000524 | 0.000385 |
|
| |||||
| 600 kDa | 0.2266 | 0.02266 | 0.1 | 0.000143 | 0.00015 |
| 600 kDa | 0.2266 | 0.05665 | 0.25 | 0.000261 | 0.000274 |
| 600 kDa | 0.2266 | 0.1133 | 0.5 | 0.0005216 | 0.00043 |
|
| |||||
| 1 MDa | 0.1613 | 0.01613 | 0.1 | 0.0001035 | 0.000422 |
| 1 MDa | 0.1613 | 0.04033 | 0.25 | 0.000259 | 0.000765 |
| 1 MDa | 0.1613 | 0.08065 | 0.5 | 0.000517 | 0.0012 |
Where c and are polymer concentration and molecular weight. The effective relaxation time of the polymer solution is determined as follows [40]:
| (14) |
where , and T are Avogadro’s number, Boltzmann constant, and temperature, respectively. The critical overlap concentration is
| (15) |
where is the intrinsic viscosity and calculated as follows:
| (16) |
In viscoelastic flows, the Weissenberg number (Wi) shows the ratio of the elastic force to the viscous force. The Wi number is calculated as follows:
| (17) |
where and are the effective relaxation time and shear rate, respectively. The relative contribution between the inertial and viscous forces is often quantified by using the elasticity number, El, which is defined as the ratio of the Wi number to the Re number.
| (18) |
Finally, based on the aforementioned constraints, we simulated the flow field and trajectory of suspended particles in the microfluidic device shown in Fig. 1-a. It is noteworthy to add that the geometry indicates sample inlets different from sheath inlets. The color-coded figure shows regions within the channel (bird’s eye view) where suspended particles in the sample gradually migrate toward the sheath fluid in the center of the channel. Of note, the rheological properties of sample and sheath fluids are identical and thus interfacial effects are absent.
IV. RESULTS AND DISCUSSION
i. Particle focusing variation with microchip geometry
Our results first include a comparison of differing geometries when observing how particles are focused at the inlet of the main channel. The initial focusing of particles at the entrance of the main channel depends on the flow rate ratios. Moreover, the size-based separation of particles in the main channel requires high total flow rates. This is because the magnitude of the elastic lift force exerted on the particles is dependent on the total flow rate inside the main channel. Hence, to achieve efficient and high-throughput separation, a high sheath flow and total flow rate are required. Yet, by increasing the flow rate, contrary to the Newtonian fluid flow, viscoelastic fluids undergo instabilities associated with the arising normal stresses. Supplementary Fig. S2 shows CFD simulation data indicating the formation of a region of high elastic stress with a flow-focusing geometry that is considered conventional (i.e. standard rectangular sheath and sample inlet channels). Such flow instabilities (color scale of Fig. S2 indicates fluctuating stress throughout the channel) result in undesirable mixing that adversely influences the size-based migration of the particles downstream of the junction, which in turn results in poor separation performance of the device. We then studied how an increase in the width of the sheath inlet and curvature in the geometry influences flow. We simulated streams whereby the sample and sheath flow meet at comparatively low velocities while the total flow rate and the flow rate ratio remained constant. The widths of channels delivering the sheath flow and sample are increased to 230 μm and 50 μm, respectively. Furthermore, the width of the main channel is 30 μm. With curved edges (radius of 100 μm) we also aimed to avoid the formation of high normal stress regions and circulation of flow in the sample close to the corners. Fig. 2-a demonstrates the CFD simulation result that indicates our ability to achieve stable flow and uniform elastic stress distributions at a high velocity (0.7 m/s) in the main channel. With the curved geometry, we investigated how varying flow rate ratios affect the initial focusing of particles at the inlet. The data show that an appropriate focusing of particles can be achieved when the ratio of sheath flow to the sample flow rate is equal to or greater than 5 (supplementary Fig.S2). Fig. 2-b shows the predicted particle trajectories at the flow focusing section for the flow rate ratio of 5. According to the obtained simulation results, for a constant flow rate ratio, the predicted particle trajectories at the inlet are identical for all PEO solutions irrespective of the polymer molecular weights and concentrations. To satisfy the minimum flow rate ratio required for the effective particle focusing the sample and sheath flow rates are chosen to be 42 μL/min (0.035 m/s) and 210 μL/min, (0.076 m/s) respectively.
Fig. 2.
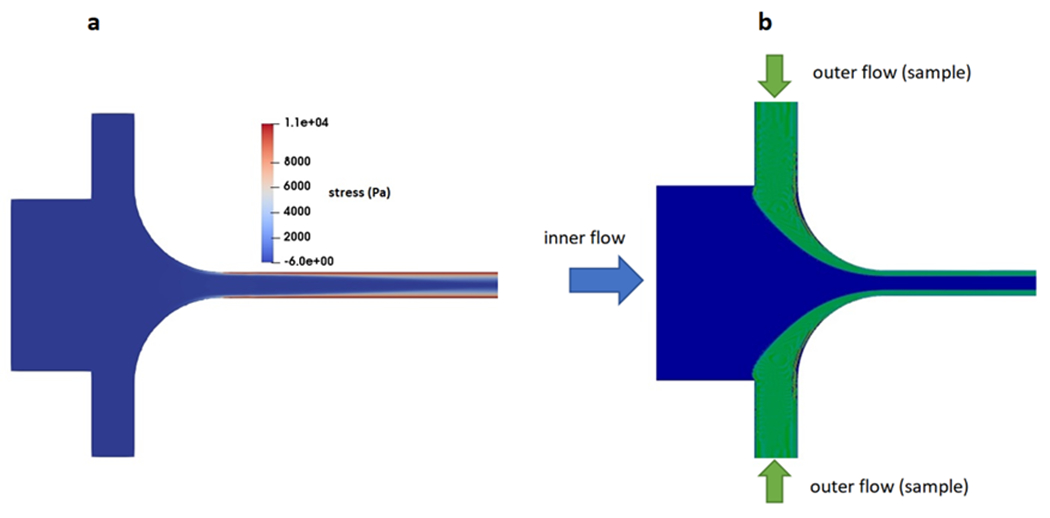
Formation of stable flow and uniform elastic stress distribution (a) and initial focusing of particles (b) in the revised flow focusing geometry for 600kDa PEO solution at total flow rate and flow rate ratio of 252 μL/min and 5.
ii. The influence of channel aspect ratio and fluid Rheology
The elastic stress distribution in the main channel not only depends on the rheology and velocity of the fluid but also on the aspect ratio of the channel. Numerical simulations were performed for channels with different heights while the channel width was kept constant (). According to the CFD simulation results, an increase in channel aspect ratio slightly decreases the maximum elastic stress while resulting in a more uniform distribution of elastic stress (supplementary Fig.S3). An increase in the aspect ratio of the channel ensures that a higher percentage of particles are influenced by the uniform stress region, thereby, increasing the efficiency of particle separation. Moreover, for a constant mean velocity in the channel, increasing the aspect ratio results in a higher flow rate, which in turn, increases the throughput of the particle separation process. In the present study, the width and height of the channel were chosen to be 30 μm and 200 μm, respectively.
Table 1 lists the rheological properties simulated for different PEO solutions. The viscosity and density of solvent (PBS) are 9.98E-4 Pa-s and 1000 kg/m3, respectively. The polymer viscosity and relaxation time were changed by varying the polymer molecular weight and concentration. The maximum PEO concentrations were chosen to be half of the critical overlap concentration, c/c*=0.5. As seen in Table 1, for a constant c/c*=0.5, by increasing the polymer molecular weight from 300 kDa to 1 MDa the relaxation time increases from 0.384 ms to 1.2 ms.
Fig. 3-a shows the distribution of the first normal stress difference at the cross-section of a channel with the width and height of 30 μm and 200 μm and for PEO solutions with different molecular weights. As seen in this figure, for a mean flow velocity of 0.7 m/s dictated by the flow focusing section, an increase in the polymer molecular weight results in an increase in the predicted maximum elastic stress inside the channel. Fig. 3-b illustrates the distribution of first normal stress differences across the width of the channel. As seen, an increase in polymer molecular weight results in a higher first normal stress difference gradient that increases the elastic lift force towards the center of the channel.
Fig 3.
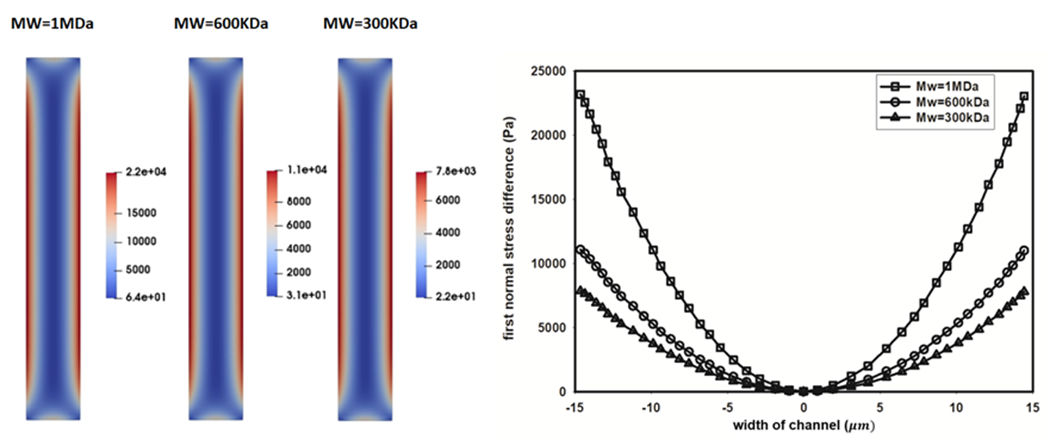
The influence of polymer molecular weight on first normal stress difference (). Contours of predicted in channel section (left), distribution of in the width of the channel (right), V=0.7 m/s, c/c* = 0.5.
iii. Predicting particle trajectories in the channel
After identifying ideal geometric and rheological conditions, we performed final CFD simulations to predict the trajectory of particles and adjust the geometry of the outlet for efficient particle collection. Extracellular vesicles are generally subdivided into exosomes, microvesicles, and apoptotic bodies. We used a range of diameters because of the ranges that exist; i.e. exosome diameters (30-100 nm) are smaller compared to the microvesicles (100-1000 nm) and apoptotic bodies (0.5-3μm) [41]. Initially focused particles at the inlet experience the elastic lift force. The higher elastic lift force exerted on the large particles results in a faster migration of larger particles toward the center of the channel compared to those with small diameters. The trajectory of particles in a certain flow field depends on the shape, density, and size of particles. The density of EVs slightly varies according to their size. Previous studies revealed that an increase in the size of EVs results in an increase in their densities [41]. Table 2 shows the adopted densities for EVs with different sizes. Considering the maximum stress in our microchannel (22 kPa), and Young’s modulus of EVs (26-420MPa) [42] the maximum strain/deformation of EVs remains below 0.001. Hence, all particles were assumed to be spherical.
Table. 2.
Density of particles with different diameters.
| Particle size (nm) | 50 | 100 | 200 | 300 | 500 | 800 |
|---|---|---|---|---|---|---|
| Density (kg/m3) | 1085 | 1160 | 1090 | 1110 | 1130 | 1250 |
We performed a Lagrangian particle tracking simulation to assess the separation performance of particles within the microfluidic device. Due to the high elasticity, we simulated 1MDa as well as 600 kDa PEO solutions as the carrier fluid in the respective CFD simulations. Additionally, to understand the range of possible purities and rate of recovery, we simulated this for five particle size diameters: 50 nm, 100 nm, 200 nm, 300 nm, and 500 nm. The smallest particles (50 nm and 100nm) represent exosomes while larger ones (200 nm, 300 nm, and 500 nm) represent microvesicles. As mentioned previously, our overall objective is to demonstrate a facile way to separate exosomes from larger EVs. Hence, the effective separation of 50 nm and 100 nm particles from those with larger diameters would demonstrate the feasibility of this microfluidic device.
Fig. 4 shows the result of the Lagrangian particle tracking with the 1MDa PEO (c/c*=0.5). The arrows indicate the flow direction toward the outlet of the channel, while the colors indicate the size of the particles. According to Fig. 4-a all particles initially flow near the walls of the channel at the inlet. However, a gradual migration and separation of larger particles toward the center of the channel is observed at a distance of 15 mm downstream from the inlet (Fig. 4-b). Fig. 4-c shows an even further degree of size-based separation at a location of 24 mm downstream from the inlet. Hence, if a chip was designed to collect samples at a location of 24 mm downstream from the sample inlet, particles of size differences with a resolution of 100 nm can be separately sorted. To ensure that such segregation happens for all the injected particles at the inlet, we show a snapshot of the Lagrangian simulation for all particles passing the channel section at 25 mm downstream from the inlet. Fig. 4-d shows the distribution of particles with different sizes when passing the channel cross section 25 mm downstream of the inlet. The Reynolds (Re) and Weissenberg (Wi) numbers for this test were 23.63 and 56, respectively. It is worth mentioning that a previously reported study in the literature revealed the possibility of achieving stable elasto-inertial focusing at comparatively similar Re and Wi numbers [43]. Considering the mean flow velocity of the sample in our simulation, the throughput of the separation process in our microchannel is 45 μL/min.
Fig. 4.
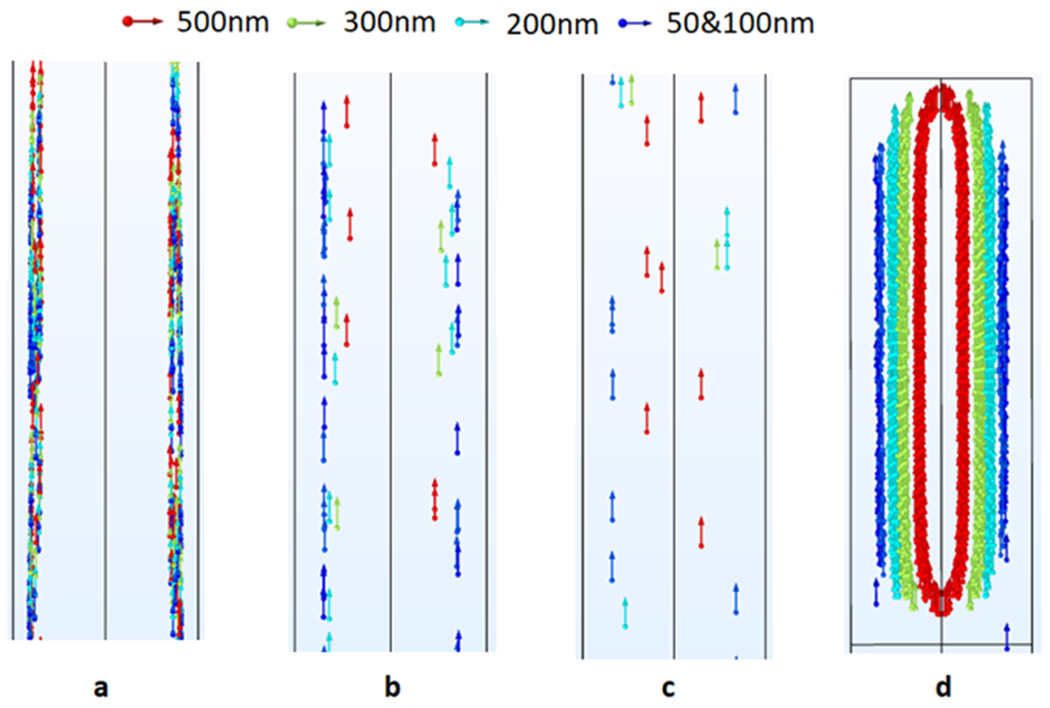
Trajectory of particles suspended in 1MDa PEO solution as moving towards the outlet: (a)1 mm downstream the inlet, (b) 15 mm downstream the inlet, (c) 24 mm downstream the inlet, (d) trapped particles 25 mm from the inlet
Lagrangian particle tracking was also performed for the PEO solution with a molecular weight of 600KDa. However, the obtained results indicate that, due to the lower elastic force exerted on particles, a proper size-based separation cannot be achieved within channel lengths of 25mm (supplementary Fig.S4).
The obtained particle tracking simulation results suggest that using a 1MDa PEO solution as a carrier fluid we can achieve a reasonable separation efficiency 25mm downstream of the inlet. In the present study, we aimed at isolating the particles representing the size of exosomes. Hence, the dimensions of the outlets were adjusted to separate particles with a maximum size of 100 nm from larger ones. Fig. 5-a is a CAD drawing of the dimensions of the microchannel outlet that might be ideal if located 25 mm downstream of the inlet. Fig. 5-b shows the trajectory of particles at the outlet as predicted by a CFD simulation. As seen in Fig. 5-b, particles with diameters larger than 100 nm can be efficiently collected at the inner outlet, while the smaller particles representing the exosomes are collected via outer outlets.
Fig. 5.
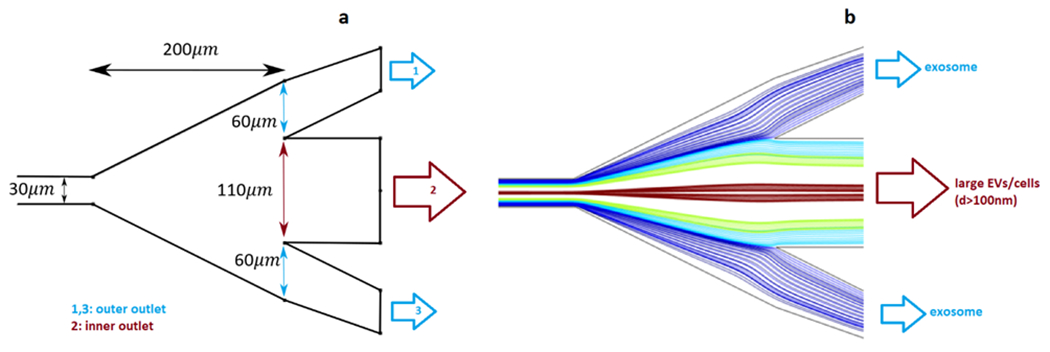
Particle separation at the outlet. (a) geometry and dimensions of the outlet (b) trajectory of particles as predicted by CFD simulation at the outlet.
Finally, Fig. 6 is a CAD representation of the geometry of an ideal microchannel for this simulation. As observed in this figure, sample and sheath fluids are injected via inlet 1 and inlet 2, respectively. The injected sample and sheath fluids meet at the junction with the geometry shown in Fig. 2. Furthermore, the dimensions of diverging section at the outlet are shown in Fig. 5. The dimensions of the curved channels at the inlet and outlet were chosen in a way that tubes with the size of 1/32 inch OD can be safely connected to the microchip to inject the fluids at the inlets and collect the particles at the outlets.
Fig. 6.
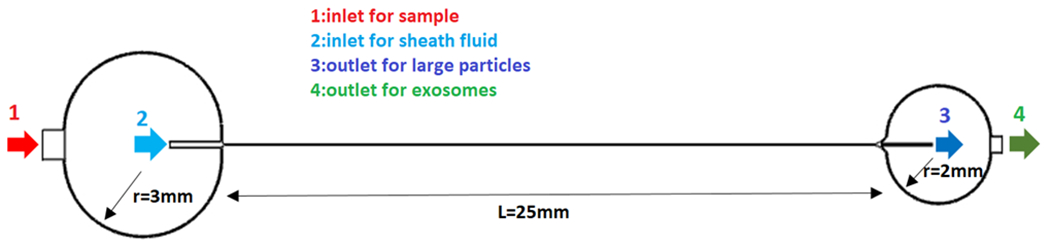
Full design of the microchip showing the inlet and outlet where particles can be collected after separation occurs along the length of the main channel
V. CONCLUSIONS AND FUTURE WORK
A microfluidic chip was designed for the size-based separation of particles representing the size of extracellular vesicles. A detailed computational study consisting of resolving the governing equations of viscoelastic flow-field was employed to avoid uncertainties involved in commonly used empirical models. The microfluidic device in this study makes use of a flow-focusing geometry to initially focus all the particles with different diameters near the side walls of the channel. Then, the elastic lift force is used to gradually separate the initially focused particles based on their sizes. A special design of a flow-focusing section was presented to ensure the stability of flow and efficient particle focusing at high flow rates. The influence of different polymer molecular weights and aspect ratios on the distribution of elastic stress across the channel section was investigated. According to the CFD simulation results an increase in polymer molecular weight and channel aspect ratio results in stronger and more uniform stress distribution, respectively. Finally, Lagrangian particle tracking with a 1MDa PEO solution indicates the possibility of achieving exosome separation at a throughput as high as 45μL/min.
While our simulations suggest a novel approach to separate small particles by exploitation of viscoelastic fluid properties, we note that experimental work must be accomplished for a holistic proof of concept. This will be the focus of future work. However, as a preliminary step towards this goal, we sought out recent experimental approaches reported in the literature that demonstrate the sorting of micron-size particles [44] under similar viscoelastic conditions. We employed a CFD simulation to model the published experimental results of particle separation. A comparison of our CFD simulation result to the published experiment is provided in a supplementary attachment. We find that our CFD model accurately predicts the trajectory of particles with different sizes, which was demonstrated experimentally. It is important to note that the work by Zhang et al. presents the separation of micron-size particles. Whereas the novelty of our work is the separation of nanoparticles, which would not be possible under the experimental conditions (i.e., requires significantly higher elastic stresses, which in turn, provokes the occurrence of elastic instabilities). The chip we design herein can achieve high elastic stresses as well as the throughput important for biomedical applications while preventing the occurrence of elastic instability.
Overall, we present a unique and optimized microfluidic chip, using computational fluid dynamics simulations. The chip, when combined with viscoelastic flow can remarkably facilitate the separation of nano-sized particles at a high purity and throughput. Moreover, the significance of this is that a simple channel can be designed, without the need for over-engineered shapes or external focusing systems. Moreover, several biological fluids (blood, plasma, saliva) have inherent viscoelastic properties [20,21], therefore we envision the possibility of separation of vesicles from samples taken directly from patients without the need for purification or sample preparation.
Supplementary Material
ACKNOWLEDGEMENTS
The work presented in this manuscript was supported by NIH grant # R01GM129859.
REFERENCES
- 1.Yu L-L, Zhu J, Liu J-X, Jiang F, Ni W-K, Qu L-S, Ni R-Z, Lu C-H, Xiao M-B. A comparison of traditional and novel methods for the separation of exosomes from human samples. Biomed Res. Int 2018;2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tauro BJ, Greening DW, Mathias RA, Ji H, Mathivanan S, Scott AM, Simpson RJ. Comparison of ultracentrifugation, density gradient separation, and immunoaffinity capture methods for isolating human colon cancer cell line LIM1863-derived exosomes. Methods 2012;56:293–304. [DOI] [PubMed] [Google Scholar]
- 3.Liga A, Vliegenthart ADB, Oosthuyzen W, Dear JW, Kersaudy-Kerhoas M. Exosome isolation: a microfluidic road-map. Lab Chip 2015;15:2388–2394. [DOI] [PubMed] [Google Scholar]
- 4.Abramowicz A, Widlak P, Pietrowska M. Proteomic analysis of exosomal cargo: the challenge of high purity vesicle isolation. Mol. Biosyst 2016;12:1407–1419. [DOI] [PubMed] [Google Scholar]
- 5.Li A, Zhang T, Zheng M, Liu Y, Chen Z. Exosomal proteins as potential markers of tumor diagnosis. J. Hematol. Oncol 2017;10:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Quintana JF, Makepeace BL, Babayan SA, Ivens A, Pfarr KM, Blaxter M, Debrah A, Wanji S, Ngangyung HF, Bah GS. Extracellular Onchocerca-derived small RNAs in host nodules and blood. Parasit. Vectors 2015;8:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Alvarez ML, Khosroheidari M, Ravi RK, DiStefano JK. Comparison of protein, microRNA, and mRNA yields using different methods of urinary exosome isolation for the discovery of kidney disease biomarkers. Kidney Int. 2012;82:1024–1032. [DOI] [PubMed] [Google Scholar]
- 8.Grant R, Ansa-Addo E, Stratton D, Antwi-Baffour S, Jorfi S, Kholia S, Krige L, Lange S, Inal J. A filtration-based protocol to isolate human plasma membrane-derived vesicles and exosomes from blood plasma. J. Immunol. Methods 2011;371:143–151. [DOI] [PubMed] [Google Scholar]
- 9.Batrakova EV, Kim MS. Using exosomes, naturally-equipped nanocarriers, for drug delivery. J. Control. Release 2015;219:396–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lane RE, Korbie D, Trau M, Hill MM. Optimizing size exclusion chromatography for extracellular vesicle enrichment and proteomic analysis from clinically relevant samples. Proteomics 2019;19:1800156. [DOI] [PubMed] [Google Scholar]
- 11.Takov K, Yellon DM, Davidson SM. Comparison of small extracellular vesicles isolated from plasma by ultracentrifugation or size-exclusion chromatography: yield, purity and functional potential. J. Extracell. vesicles 2019;8:1560809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.An M, Wu J, Zhu J, Lubman DM. Comparison of an optimized ultracentrifugation method versus size-exclusion chromatography for isolation of exosomes from human serum. J. Proteome Res 2018;17:3599–3605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zarovni N, Corrado A, Guazzi P, Zocco D, Lari E, Radano G, Muhhina J, Fondelli C, Gavrilova J, Chiesi A. Integrated isolation and quantitative analysis of exosome shuttled proteins and nucleic acids using immunocapture approaches. Methods 2015;87:46–58. [DOI] [PubMed] [Google Scholar]
- 14.Boriachek K, Islam MN, Möller A, Salomon C, Nguyen N, Hossain MSA, Yamauchi Y, Shiddiky MJA. Biological functions and current advances in isolation and detection strategies for exosome nanovesicles. Small 2018;14:1702153. [DOI] [PubMed] [Google Scholar]
- 15.Zhang M, Jin K, Gao L, Zhang Z, Li F, Zhou F, Zhang L. Methods and technologies for exosome isolation and characterization. Small Methods 2018;2:1800021. [Google Scholar]
- 16.Camussi G, Deregibus M-C, Bruno S, Grange C, Fonsato V, Tetta C. Exosome/microvesicle-mediated epigenetic reprogramming of cells. Am. J. Cancer Res 2011;1:98. [PMC free article] [PubMed] [Google Scholar]
- 17.Leshansky AM, Bransky A, Korin N, Dinnar U. Tunable nonlinear viscoelastic “focusing” in a microfluidic device. Phys. Rev. Lett 2007;98:234501. [DOI] [PubMed] [Google Scholar]
- 18.Seo KW, Byeon HJ, Huh HK, Lee SJ. Particle migration and single-line particle focusing in microscale pipe flow of viscoelastic fluids. RSC Adv. 2014;4:3512–3520. [Google Scholar]
- 19.Seo KW, Kang YJ, Lee SJ. Lateral migration and focusing of microspheres in a microchannel flow of viscoelastic fluids. Phys. Fluids 2014;26:063301. [Google Scholar]
- 20.Brust M, Schaefer C, Doerr R, Pan L, Garcia M, Arratia PE, Wagner C. Rheology of human blood plasma: Viscoelastic versus Newtonian behavior. Phys. Rev. Lett 2013;110:078305. [DOI] [PubMed] [Google Scholar]
- 21.Haward SJ, Odell JA, Berry M, Hall T. Extensional rheology of human saliva. Rheol. acta 2011;50:869–879. [Google Scholar]
- 22.Kwon T, Choi K, Han J. Separation of Ultra-High-Density Cell Suspension via Elasto-Inertial Microfluidics. Small 2021;17:2101880. [DOI] [PubMed] [Google Scholar]
- 23.Xiang N, Zhang X, Dai Q, Cheng J, Chen K, Ni Z. Fundamentals of elasto-inertial particle focusing in curved microfluidic channels. Lab Chip 2016;16:2626–2635. [DOI] [PubMed] [Google Scholar]
- 24.Song HY, Lee SH, Salehiyan R, Hyun K. Relationship between particle focusing and dimensionless numbers in elasto-inertial focusing. Rheol. Acta 2016;55:889–900. [Google Scholar]
- 25.Raffiee AH, Ardekani AM, Dabiri S. Numerical investigation of elasto-inertial particle focusing patterns in viscoelastic microfluidic devices. J. Nonnewton. Fluid Mech 2019;272:104166. [Google Scholar]
- 26.Raoufi MA, Mashhadian A, Niazmand H, Asadnia M, Razmjou A, Warkiani ME. Experimental and numerical study of elasto-inertial focusing in straight channels. Biomicrofluidics 2019;13:034103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yuan D, Zhao Q, Yan S, Tang S-Y, Zhang Y, Yun G, Nguyen N-T, Zhang J, Li M, Li W. Sheathless separation of microalgae from bacteria using a simple straight channel based on viscoelastic microfluidics. Lab Chip 2019;19:2811–2821. [DOI] [PubMed] [Google Scholar]
- 28.Faridi MA, Ramachandraiah H, Banerjee I, Ardabili S, Zelenin S, Russom A. Elasto-inertial microfluidics for bacteria separation from whole blood for sepsis diagnostics. J. Nanobiotechnology 2017;15:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Liu P, Liu H, Semenec L, Yuan D, Yan S, Cain AK, Li M. Length-based separation of Bacillus subtilis bacterial populations by viscoelastic microfluidics. Microsystems Nanoeng. 2022;8:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tian F, Zhang W, Cai L, Li S, Hu G, Cong Y, Liu C, Li T, Sun J. Microfluidic co-flow of Newtonian and viscoelastic fluids for high-resolution separation of microparticles. Lab Chip 2017;17:3078–3085. [DOI] [PubMed] [Google Scholar]
- 31.Raoufi MA, Joushani HAN, Razavi Bazaz S, Ding L, Asadnia M, Ebrahimi Warkiani M. Effects of sample rheology on the equilibrium position of particles and cells within a spiral microfluidic channel. Microfluid. Nanofluidics 2021;25:1–13. [Google Scholar]
- 32.Shiri F, Feng H, Petersen KE, Sant H, Bardi GT, Schroeder LA, Merchant ML, Gale BK, Hood JL. Separation of U87 glioblastoma cell-derived small and medium extracellular vesicles using elasto-inertial flow focusing (a spiral channel). Sci. Rep 2022;12:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Feng H, Jafek AR, Wang B, Brady H, Magda JJ, Gale BK. Viscoelastic particle focusing and separation in a spiral channel. Micromachines 2022;13:361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhou Y, Ma Z, Tayebi M, Ai Y. Submicron particle focusing and exosome sorting by wavy microchannel structures within viscoelastic fluids. Anal. Chem 2019;91:4577–4584. [DOI] [PubMed] [Google Scholar]
- 35.Pakdel P, McKinley GH. Elastic instability and curved streamlines. Phys. Rev. Lett 1996;77:2459. [DOI] [PubMed] [Google Scholar]
- 36.Thien NP, Tanner RI. A new constitutive equation derived from network theory. J. Nonnewton. Fluid Mech 1977;2:353–365. [Google Scholar]
- 37.Alves MA, Oliveira PJ, Pinho FT. Numerical methods for viscoelastic fluid flows. Annu. Rev. Fluid Mech 2021;53:509–541. [Google Scholar]
- 38.Morsi SAJ, Alexander AJ. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech 1972;55:193–208. [Google Scholar]
- 39.Asmolov ES. The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech 1999;381:63–87. [Google Scholar]
- 40.Tirtaatmadja V, McKinley GH, Cooper-White JJ. Drop formation and breakup of low viscosity elastic fluids: Effects of molecular weight and concentration. Phys. fluids 2006;18:043101. [Google Scholar]
- 41.Liangsupree T, Multia E, & Riekkola ML (2021). Modern isolation and separation techniques for extracellular vesicles. Journal of Chromatography A, 1636, 4617730. [DOI] [PubMed] [Google Scholar]
- 42.LeClaire M, Gimzewski J, & Sharma S (2021). A review of the biomechanical properties of single extracellular vesicles. Nano Select, 2(1), 1–15. [Google Scholar]
- 43.Li D, Xuan X. Fluid rheological effects on particle migration in a straight rectangular microchannel. Microfluid. Nanofluidics 2018;22:1–10. [Google Scholar]
- 44.Zhang T, Cain AK, Semenec L, Liu L, Hosokawa Y, Inglis DW, … & Li M. (2023). Microfluidic Separation and Enrichment of Escherichia coli by Size Using Viscoelastic Flows. Analytical Chemistry 2023; 95: 2561–2569 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


