Time-Dependent Diffusion Tensor Imaging and Diffusion Modeling of Age-Related Differences in the Medial Gastrocnemius and Feasibility Study of Correlations to Histopathology

Abstract

Purpose:

Implement STEAM-DTI to model time-dependent diffusion eigenvalues using the Random Permeable Barrier Model (RPBM) to study age-related differences in the medial gastrocnemius muscle (MG). To validate diffusion model-extracted fiber diameter to histological assessment.

Methods:

Diffusion imaging at different diffusion times (Δ) was performed on seven young and six senior participants. Time-dependent diffusion eigenvalues (λ₂(t), λ₃(t), and D_⊥(t), average of λ₂(t), and λ₃(t)) were fit to the RPBM to extract tissue microstructure parameters. Biopsy of the MG tissue for histological assessment was performed on a subset of participants (4 young, 6 senior).

Results:

λ₃(t) was significantly higher in the senior cohort for the range of diffusion times. RPBM fits to λ₂(t) yielded fiber diameters in agreement to those from histology for both cohorts. The senior cohort had lower values of volume fraction of membranes, $\zeta$ in fits to λ₂(t), λ₃(t) and D_⊥(t) (significant for fit to λ₃(t)). Fiber diameter from RPBM fits to that from histology had the highest correlation for the fit to λ₂(t).

Conclusion:

The age-related patterns in λ₂(t) and λ₃(t) could tentatively be explained from RPBM fits; these patterns may potentially arise from a decrease in fiber asymmetry and an increase in permeability with age.

Graphical Abtract

Introduction

Diffusion and diffusion tensor imaging (DTI) have been successfully applied to study microstructural changes in brain tissue in normal and disease states ^1-3. Outside of the brain, diffusion studies have been extended to the heart, skeletal muscle, prostate and kidneys ^4-6. Skeletal muscle diffusion imaging has been established by several groups and is now a fairly mature technology that has also been successfully applied to investigate skeletal muscle disease ^7-14. While indices derived from DTI are sensitive to tissue microstructure, they are not direct measures of tissue microstructure. Models of diffusion in muscle have been proposed that are customized to the geometry and tissue subtypes in skeletal muscle. Karampinos et al. adapted the Kärger bi-compartmental model to skeletal muscle tissue: their paper modeled muscle fibers as cylinders with the endomysium surrounding each muscle fiber completely ¹⁵. Diffusion occurs intracellularly within the muscle fiber and extracellularly in the endomysium. The description of tissue microstructure requires many parameters and the approach by Karampinos et al. attempted to model most of these parameters. However, trying to fit the DTI data to this parameter-rich model leads to problems with degeneracy (lack of unique solutions) and low precision. In order to overcome these deficiencies, a more constrained model with fewer parameters and simplification of the muscle geometry has been proposed, the Random Permeable Barrier Model (RPBM). The RPBM model arose from earlier attempts to characterize the relation between macroscopic diffusion metrics and mesoscopic scale structure that is comparable to the diffusion length ¹⁶. The RPBM model treats muscle as a volume with randomly oriented infinite flat semipermeable membranes and the time dependence of the transverse diffusion coefficient is fit to the model to extract parameters of the tissue microstructure ^17,18. RPBM has been successfully applied to extract tissue parameters in normal muscle and to monitor the effect of exercise on muscle tissue microstructure in normal and in diseased conditions ^18,19. The RPBM model was also recently applied to studying calf muscle atrophy and recovery where atrophy was induced by immobilization of one leg ²⁰. The latter study found that the myofiber diameter was a stronger predictor of atrophy than either anatomical measurements such as cross-sectional area or empirical diffusion parameters. The RPBM model has not yet been applied to cross-sectional human aging studies, for example, to study differences in skeletal muscle microstructure between young and senior human subjects.

DTI indices cannot directly provide information on the microstructure of tissue but models such as RPBM can derive microstructure parameters (such as muscle fiber diameter) from the acquired time-dependent DTI data. However, these model-derived microstructure parameters have to be validated against histology, which is the established reference standard for extracting tissue microstructural information. While histology is the reference standard, it has limitations: it is invasive since a biopsy is required, samples are small and acquired from localized region(s) and repeated measurements are not readily feasible over time. In contrast, diffusion MRI is non-invasive, can be performed repeatedly to track changes over time, and the image field of view can cover the entire muscle(s) instead of being limited to a small region. The RPBM muscle diffusion model-derived muscle fiber size has been compared histology-extracted muscle fiber size in mouse models ²¹ and in humans, to histology results from literature ¹⁸. However, there has been no histological validation of RPBM in human participants based on muscle biopsy on the same subjects.

The objective of this study was to extract, in a cohort of young and senior participants, time-dependent diffusion eigenvalues and microstructural information of calf muscle using diffusion modeling and to correlate these indices to histology-derived parameters. This objective was realized by (i) implementation of an in-house built STEAM-DTI sequence to acquire time-dependent diffusion values and modeling of the time dependence of the transverse diffusion (λ₂(t), λ₃(t) and D_⊥(t)), (ii) testing for significant differences in diffusion eigenvalues at different diffusion times and in model-derived parameters (in regions-of-interest) between young and senior participants, and (iii) exploring correlations between model-derived fiber diameter from fits to (λ₂(t), λ₃(t) and D_⊥(t)) to histology-derived fiber diameter. It should be noted that diffusion modeling was performed on average values in a large region of interest in the medial gastrocnemius rather than on a voxel-by-voxel basis since the SNR was not sufficient for the latter.

Material and Methods

Random permeable barrier model (RPBM) of time-dependent diffusion:

The current paper implements the RPBM model, which is based on treating the muscle as a volume with randomly oriented infinite flat semipermeable membranes ^17,18. The RPBM models the muscle tissue as randomly oriented flat extended permeable membranes that impact diffusion in the fiber cross-section. The assumption is that the sarcolemma membrane is predominantly responsible for restricting the diffusion of water. The time-dependent diffusion coefficient, $D(t)$ that is obtained experimentally from the STEAM-DTI sequence is fit to the RPBM model as proposed in ^17,18:

$$D(t)=\frac{D_0}{2\pi t}\underset{-\infty }{\overset{\infty }{\int }}\frac{d\omega }{(-i\omega {)}^2}\frac{e^{-i\omega t}}{1+\zeta +2z_{\omega }(1-z_{\omega })\left[\sqrt{1+\zeta ∕(1-z_{\omega }{)}^2}-1\right]}$$ (1)

where $t$ is the diffusion time (corresponding to $\Delta$ in the STEAM-DTI sequence in the next section), $\omega$ is frequency, $D(t)$ is the Fourier transform of the dispersive diffusivity $D(\omega )$ ^17,18 and $z_{\omega }=i\sqrt{i\omega \tau }$. The outputs of the RPBM are $D_0$, the free diffusion coefficient, $\zeta$, the effective ‘volume fraction’ occupied by membranes and $\tau$, the characteristic time scale associated with a single membrane. Additional parameters related to the microstructure and diffusion are derived from the following relationships: $\zeta =(S∕V)D_0∕4\kappa$, where $S∕V$ is the surface to volume ratio and $\kappa$ is the membrane permeability and $\tau =l^2∕D_0$ where $l$ is the effective thickness. The effective thickness $l=D_0∕2\kappa$ provides a length scale over which the density gradient is perturbed in the presence of a membrane. The effective thickness: $l$; the membrane permeability: $\kappa$; the surface to volume ratio: $S∕V$ are calculated from $D_0$, $\zeta$ and $\tau$ based on the relationships defined above. The ratio $V∕S$ provides a rough estimate of diffusion barriers since it is a ratio of volume to the surface area of membranes in that volume (diffusion barriers at the sarcolemma surfaces). RPBM provides an accurate estimate of $S∕V$ but the computation of the myofiber diameter as $\mathrm{a}=4∕(S∕V)$ assumes that the fibers are arranged as abutting squares or cubes. The latter is not a realistic assumption for muscle fiber shapes/arrangement and the RPBM model has been shown to consistently underestimate myofiber diameter. Berry et al. experimentally determined that the relationship $\mathrm{a}=6.29∕(S∕V)$ was valid for normal and injured muscle (in-vivo and human subjects) ²². The experimentally determined scale of 6.29 is used in the current study.

Other derived parameters related to the tissue microstructure are the dwell time, ${\tau }_D$, which is defined as the time to traverse the cell of typical dimension, $a$. The dwell time is determined by the size of the cell and the diffusion coefficient: ${\tau }_{{}_D}=a^2∕2D_0$. A time that is related to membrane permeability, called the residence time is defined as the average time spent by the diffusing particle in a cell. This time will depend on the size of the cell as well as on the membrane permeability and is given as: ${\tau }_{{}_k}=a∕(2\kappa )$. The residence time will significantly exceed the dwell time $({\tau }_{{}_R}>>{\tau }_{{}_D})$ in the permeability limited case; i.e., the membrane significantly limits or slows diffusion (very small values of the permeability $\kappa$). This situation also corresponds to $\zeta >>1$; i.e., the effective ‘volume fraction’ occupied by membranes is high and offers a significant barrier to diffusion. For skeletal muscle, the modeling results reported earlier yields $\zeta \sim 1$; this falls into an intermediate permeability case between highly permeable ($\zeta <<1$) to highly restrictive ($\zeta >>1$) ^17,18. It should be noted that in the current paper, Eqn. 1 is applied to fit, in turn, the secondary and tertiary eigenvalues and to the average diffusion in the plane transverse to the muscle fiber, $D_{\perp }(t)$. Prior work using the RPBM model have performed fits only to the average diffusion in the plane transverse to the muscle fiber, $D_{\perp }(t)$. The rationale for the RPBM fits to the secondary and tertiary eigenvalues is given later. Since the fits were performed individually to the secondary and tertiary eigenvalues rather than to the average of the two, the direction of the secondary and tertiary eigenvectors was calculated to verify that these did not change with the diffusion time. It should be noted that noise in the acquired diffusion data can cause these eigenvectors to switch directions.

STEAM-DTI sequence:

The STEAM-DTI was implemented in-house using the design principles detailed in reference ²³. STEAM acquisition gives rise to different spin coherence pathways (other than the desired stimulated echo) that must be dephased. This is accomplished by an appropriate combination of crusher gradients that selectively preserve the spin coherence of the stimulated echo (Supporting Figure 1).

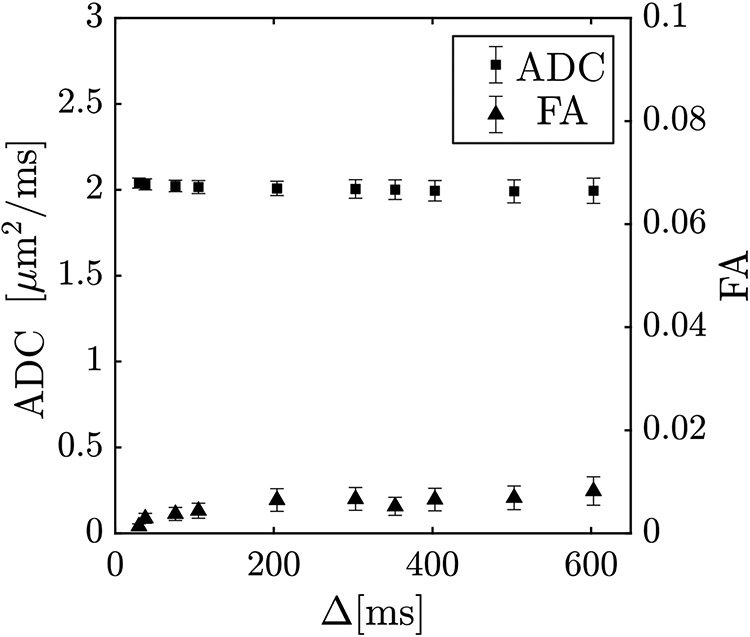
The STEAM-DTI sequence has significant contributions to the b-matrix from cross-terms between diffusion, crusher, and imaging gradients. Supporting Figure 2 is a schematic of the STEAM-DTI pulse sequence implemented for the current study on a 3 T GE scanner (Discovery MR750, GE Medical Systems, WI, USA). The details of all the gradient interactions for the full b-matrix calculation including the timing specifications for the pulse sequence shown in Supporting Figure 2 are provided in the Supporting Background Information. It should be noted that the full b-matrix for STEAM-DTI including the terms from the slice select gradient train for the spectral spatial pulse as well as EPI phase encode and readout trains is not available in the literature. Images were acquired using the custom-built STEAM-EPI DTI sequence shown in Supporting Figure 2. A water selective SPSP RF-pulse was used for selective water excitation. Six non-collinear gradient directions with a nominal b-value of 400 s/mm² were used to map the direction-dependent diffusion at ten values of the mixing time TM (15 ms to 590 ms). ²⁴²⁵The mixing time, TM is the time between the second and third 90° RF pulses when the magnetization is held in the longitudinal direction. The diffusion time, Δ is the time from the start of the first diffusion gradient to the start of its paired rephasing diffusion gradient. Exact values for Δ were extracted from the recorded gradient waveforms. Imaging parameters were: echo time (TE): 32 ms, repetition time (TR): 4000 ms, signal averages (NEX): 2, acquisition matrix size: 80 × 80, field of view (FOV): 200 × 200 mm², 3 slices of 5 mm thickness. Total scan time for ten STEAM-DTI acquisitions was 20 minutes (1 min 56 seconds each). Field maps and localization/ calibration added another 5 minutes to the acquisition. Diffusion data were pre-processed to correct for eddy current and susceptibility induced geometric distortions. B₀ field maps derived from phase maps of gradient echoes acquired at two different echo times were used to correct for susceptibility induced geometric distortions. Diffusion data was pre-processed using the fsl software package ²⁴. After corrections for distortion, the images were denoised by applying the Joint-Rican LMMSE filter ²⁵. These pre-processing steps were performed prior to computing the diffusion tensor and the diffusion eigenvalues (noise pixels determined from the background intensity in the b₀ images were not processed). For the nominal b = 0 images, the b-value varied from 2.4 s/mm² at Δ = 30 ms to 72.8 s/mm² at Δ = 603 ms and for the nominal b = 400 s/mm² images, the b-value varied from 371 s/mm² at Δ = 30 ms to 465 s/mm² at 603 ms, emphasizing the need for full b-matrix calculation (the b-values reported here are the trace of the b-matrix). The main contributions to b₀ are from the crushers gradients and these are dependent on diffusion time and thus an increase in b₀ is seen with Δ. The direction-dependent b-values for the nominal ‘b₀’ images were also accounted for by including those values in the tensor calculation instead of normalizing the diffusion weighted signal intensity by the signal intensity at the nominal ‘b₀’ image. It should be noted that numerical simulation studies have determined b-values of 450 - 500 s/mm² as optimal for muscle tissue diffusion imaging ²⁶ and recent muscle DTI studies routinely use b-values of 450 s/mm^{2 27}. In the current paper, the b-values were set nominally at 400 s/mm² as the interaction of the diffusion and imaging gradients increased b to 472 s/mm² at the longest diffusion times used in the current study. Since the long diffusion times are lower in SNR, the nominal b-value was chosen such that it was close to the optimum b-value at the longer diffusion times rather than the lower diffusion times. Choosing the b-value of 450 s/mm² as the nominal value would have caused the actual b-value to be higher than optimum for the long diffusion time, SNR starved diffusion weighted images. The sequence was validated in a water phantom following the same imaging protocol as described above. ADC values was an average of 2.04 ± 0.03 μm²/ms (ambient temperature: 20 °C) at the lowest diffusion time and remained fairly constant over the rage of diffusion times investigated; this is consistent with a free medium (Figure 1). The ADC value is also close to that reported in the literature for 20 °C ²⁸. FA values were as anticipated for an isotropic, unrestricted medium like water and unaltered as a function of diffusion time Δ (30 ms to 603 ms). The FA values were close to zero across the range of diffusion times (0.001 at Δ = 30 ms to 0.008 at Δ = 603 ms). The small increase of FA at the higher diffusion times may potentially arise from lower SNR of the diffusion weighted images at these times (Figure 1).

Figure 1:

The apparent diffusion coefficient ADC (or mean diffusivity MD) and fractional anisotropy of a water phantom shows ADC remains constant over the range of diffusion times (30 ms to 603 ms) and FA values are close to zero for the same range of diffusion times.

All human imaging studies were performed after IRB approval on a 3 T scanner (Discovery MR750, GE Medical Systems, WI, USA) on eight young (39 ± 13 years, range: 22 to 53 years, 6 male and 2 females) and six senior (72 ± 4 years, range: 65 to 76 years, 4 male and 2 female) participants. Subjects were imaged using a 16-channel knee coil. The RPBM fits were made to the time dependence of λ₂(t), λ₃(t) and D_⊥(t); the values used in the fit were the average over the medial gastrocnemius (MG) muscle segmented from the middle slice. The analysis was limited to the MG muscle since biopsy was only performed on the MG enabling validation of the RPBM model against standard histological analysis. It has been shown in prior studies using the RPBM model that the fits are more robust if $D_0$ is fixed ^17,18. In the current work, $D_0$ was fixed at the average of D_∥(t) evaluated for values of diffusion time greater than 105 ms; beyond this diffusion time of 105 ms there is little time dependent variation of D_∥(t) and averaging over multiple diffusion times provided robustness to noise. Here, it should be noted that the current choice for extracting $D_0$ is based on earlier work by Fieremans et al. ¹⁹. The latter study performed the RPBM fitting with $D_0$ computed from the fit or by fixing $D_0$ and identified that the $D_0$ obtained from the RPBM fit was close to the experimentally determined D_∥(t) at long times. When $D_0$ was fixed at the value of D_∥(t) at long times, the fits of the other two model parameters, $\zeta$ and τ, were more robust. The increase in D_∥ at lower diffusion times is attributed to small-scale intracellular organelles which are likely to slow diffusion isotropically, i.e., decrease D_∥(t) and D_⊥(t) in a similar fashion. Fixing $D_0$ to be D_∥(t) at long diffusion times excludes the isotropic increase in diffusivity at very low diffusion times (< ~100 ms) and the relationship that $D_0$ is equal to the value of D_∥(t) at long diffusion times has been validated ¹⁹. It should be noted that labeling $D_0$ as the free diffusion coefficient is misleading as it would then be expected to be the highest value which is at the lowest diffusion times. However, for the reasons given above, the free diffusion coefficient in the RPBM refers to the diffusion coefficient beyond the isotropic decrease at small diffusion times. $\zeta$ and τ are extracted from the fit to the RPBM model. Other parameters of the RPBM model were computed from these two fitted parameters and $D_0$ extracted from the D_∥(t) data. The Supplementary Information details the parameters that are directly obtained from the RPBM fit, the fixed parameter, and the derived parameters in terms of the direct fit and fixed parameters (Eq. 38-43, Supplementary Information).

Physical Assessment:

Anthropometrics (height, weight and BMI) along with age and physical assessment were recorded for a subset of participants (four young participants and six senior participants from the cohort who were part of the STEAM-DTI MRI acquisition). Physical assessment for muscle strength was made using the following metrics: Hand Grip (left and right hand), Chair stand time, 200 m and 400 m walk time respectively, systolic (SBP) and diastolic (DBP) pre- and post- assessment blood pressure. The chair stand test is the total time taken for the subject to complete 5 stand-ups. In case the subject was not able to complete 5 stand-ups, the time corresponds to the time taken for the number of stands completed.

In addition to the metrics of physical assessment, a frailty score was calculated by tallying up the total score from the responses of the subject to the International Physical Activity Questionnaire (IPAQ) questionnaire ²⁹. All physical assessments were performed by trained professionals at the Exercise and Physical Activity Resource Center (EPARC) at the University of California at San Diego.

Histological assessment:

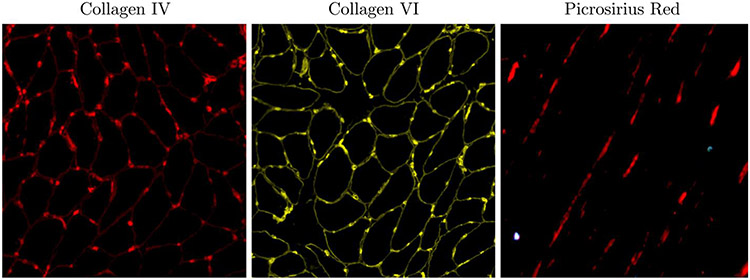
Biopsies were performed with IRB approval on a subset of participants included in the imaging study: 4 of the young participants (39 ± 14 years, range of 22-53 years, 4 male), and all 6 senior participants (72 ± 4 years, range of 65 to 76 years, 4 male and 2 female). Following the physical assessment, muscle biopsies were performed (under local anesthetic) from the gastrocnemius muscle under ultrasound guidance. Biopsies were pinned to cork at resting length and frozen in isopentane cooled in liquid nitrogen. Cross-sections were taken to determine collagens I, III, IV, V, and VI content, whereas longitudinal sections were stained with picrosirius red to determine collagen orientation, ϕ . Collagen fibers, in particular, the fibrillar collagens (Collagens I and III) which are seen at the fascicle level stain with picrosirius red. Since collagen IV surrounds each cell, these images were also used to determine muscle fiber cross-sectional area (f_CSA) and the Feret diameter, (d_F). The muscle fiber diameter reported here is the minimum Feret diameter; this is the routinely reported diameter derived from histology ³⁰. In the rest of the paper, Feret diameter refers to the minimum Feret diameter. Slides were imaged using a Leica DMi8 (Leica Microsystems) inverted microscope using a ×20 objective and processed using the Leica LAS-X software (https://www.cellularimaging.nl/leica-las-x/). Images were analyzed using FIJI software (https://imagej.net/software/fiji/).

Statistical Analysis:

Data are presented as means ± SD. Normality of data was verified visually by histograms and numerically using Shapiro-Wilk’s test ( p > 0.05). Differences in eigenvalues, model-derived parameters, parameters from histological assessment, and physical assessment factors between age groups were then tested for statistical significance using two-tailed t-tests for independent samples. Pearson correlation coefficients were calculated between the fiber diameter obtained from the fits to λ₂(t), λ₃(t), and D_⊥(t), to the fiber diameter from histological analysis. Correlations were considered statistically significant at p < 0.05.

Results

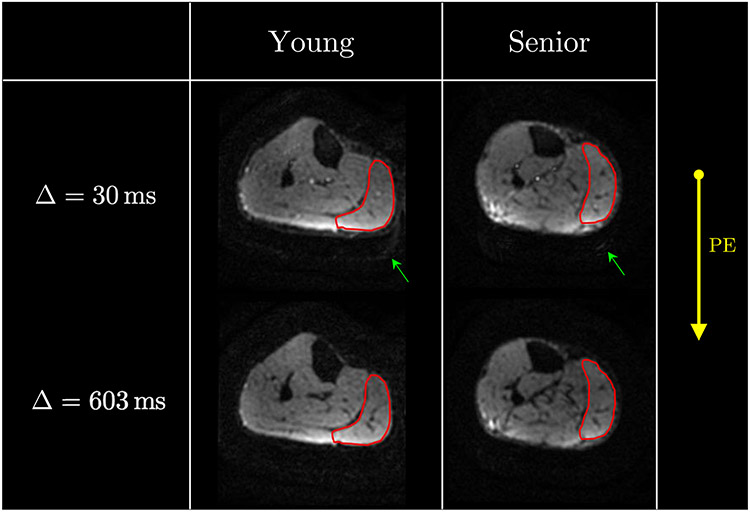
Figure 2 shows the acquired diffusion weighted images at two values of Δ; these images are shown without any mask/background suppression. Effective fat suppression was achieved both due to the spectral-spatial water selective pulse, as well as from the short T₁ of fat and the long mixing times. Excellent fat suppression in the STEAM-DTI is seen at both diffusion times with only a very low signal of fat that is shifted posteriorly at a diffusion time of 30 ms.

Figure 2:

Typical acquired baseline images (nominal b = 0 s/mm²) at diffusion time Δ of 30 ms (top row) and at 603 ms (bottom row) for a young (left column) and a senior (right column) participant. The medial gastrocnemius (MG) muscle is shown contoured in red and images are displayed without any thresholding/masking to illustrate the quality of fat signal suppression. The direction of the phase encode gradient (AP) is shown and fat is anticipated to shift along this direction. Very low signal intensity of the fat image (posteriorly shifted in the background, highlighted with the green arrow) can be visualized in the top left image. The increase in signal at the posterior edge reflects the higher coil sensitivity in that region. Note that each image is individually normalized.

Figure 3 shows representative images of the three eigenvalues (λ₁(t), λ₂(t), and λ₃(t)) at two different values of the diffusion time Δ (shortest and longest), for a young and senior participant, respectively. While calculating the DTI coefficients, a threshold was used to exclude processing of background noise pixels. It should be noted in Figure 3, λ₁(t) in the soleus of the senior subject appears higher at diffusion time of 603 ms than at 30 ms. One potential reason is that with increased amount of connective and adipose tissue in senior subjects, there are many regions of very low intensity in the diffusion weighted images. Voxels containing connective, adipose and muscle tissue will partial volume resulting in signals above the noise threshold (thus, processed to generate the parametric images) but with significantly lower signal intensity than voxels with just muscle tissue. As shown in simulation studies, low SNR leads to incorrect eigenvalues, including increase in λ₁(t) ²⁶. Care was taken to avoid regions of interest in areas with high fat and connective tissue infiltration. Once the three eigenvalue maps were computed, an ROI was defined in the medial gastrocnemius to determine the average diffusion eigenvalues (λ₂(t), λ₃(t) and D_⊥(t)). The lower SNR of the eigenvalue images at long diffusion times is clearly visualized in the images; this arises from the lower SNR of the images acquired at longer diffusion times (the SNR of the b₀ and diffusion-weighted images decreases at longer diffusion times). The eigenvalues averaged separately over the young and senior cohort for the measured diffusion times are shown in Table 1. The SNR of the baseline (nominal b₀ image prior to filtering) averaged over all participants is included in Table 1. Simulation studies have shown that SNR ~20 and SNR ~40 in the baseline images is required for 5% and a 1% accuracy respectively in the diffusion eigenvalues ²⁶. While the SNR of the acquired images in the current study meets the requirements for the computed eigenvalues to have accuracies between 1% and 5%, ROI rather than voxel-based analysis was used here with the expectation that RPBM fitting, and detection of small age-related differences will benefit from the better statistics afforded by ROI rather than voxel-based analysis.

Figure 3:

Diffusion tensor eigenvalue images: λ₁(t), λ₂(t) and λ₃(t) for two different values of the diffusion time, Δ = 30 ms, Δ = 603 ms, for a young (left) and an older (right) participant. Presence of unsuppressed fat is usually visible as intensity artifact bands of subcutaneous fat shifted in the phase encoding direction into the muscle regions. The absence of such bands at low and high mixing times, TM confirms the excellent fat suppression in the STEAM-DTI sequence. The decrease in SNR at longer diffusion can be clearly visualized.

Table 1:

Diffusion eigenvalues for different diffusion times, Δ, averaged over young and senior participants. SNR of the b₀ image for different diffusion times, Δ averaged over all participants.

Δ [ms]	b0 [s/mm2]	SNR	λ1 [ μm2/ms]		λ2 [ μm2/ms]		λ3 [ μm2/ms]
			young	senior	young	senior	young	senior
30	2.4	108	2.26 ± 0.15	2.32 ± 0.17	1.71 ± 0.06	1.64 ± 0.23	1.14 ± 0.09	1.25 ± 0.11
38	3.6	104	2.16 ± 0.14	2.18 ± 0.15	1.47 ± 0.13	1.43 ± 0.22	1.09 ± 0.09†	1.27 ± 0.10†
76	6.0	97	2.00 ± 0.18	2.03 ± 0.13	1.28 ± 0.16	1.27 ± 0.19	0.91 ± 0.09†	1.06 ± 0.13†
105	12.0	95	1.96 ± 0.23	1.99 ± 0.13	1.18 ± 0.16	1.17 ± 0.16	0.82 ± 0.12*	1.02 ± 0.11*
204	24.2	86	1.88 ± 0.24	1.89 ± 0.20	1.13 ± 0.12	1.10 ± 0.10	0.67 ± 0.08*	0.86 ± 0.10*
303	36.3	87	1.81 ± 0.17	1.86 ± 0.19	1.06 ± 0.12	0.98 ± 0.11	0.61 ± 0.06*	0.79 ± 0.06*
353	42.4	84	1.81 ± 0.13	1.83 ± 0.19	1.02 ± 0.11	0.92 ± 0.05	0.64 ± 0.10*	0.84 ± 0.11*
403	48.5	78	1.80 ± 0.15	1.84 ± 0.22	1.03 ± 0.12	0.91 ± 0.10	0.66 ± 0.10†	0.82 ± 0.14†
503	60.7	77	1.80 ± 0.16	1.84 ± 0.21	0.95 ± 0.14	0.88 ± 0.11	0.67 ± 0.11*	0.82 ± 0.06*
603	72.8	60	1.77 ± 0.15	1.86 ± 0.21	0.91 ± 0.15	0.86 ± 0.09	0.66 ± 0.11*	0.80 ± 0.04*

^*Significant difference between young and senior age groups ( p < 0.05)

^†Trend toward a decrease in the senior group ( p < 0.1).

Supporting Figure 3 shows, for one subject, the secondary and tertiary eigenvector color maps at the different diffusion times used in the current study. Eigenvector color maps are relatively uniform except at the longest three diffusion times. The low SNR of the long diffusion time images causes the switch of the secondary and tertiary diffusion eigenvectors as seen in the patchy colormaps at these times. A quantitative analysis in a region of interest (similar to that used for the RPBM analysis) is shown in Supporting Figure 4 (averaged for young and senior groups). A fairly constant value of the projections of the eigenvectors across all diffusion times is seen; this latter finding supports the individual fits of λ₂(t) and λ₂(t) to the RPBM model as proposed in the current study.

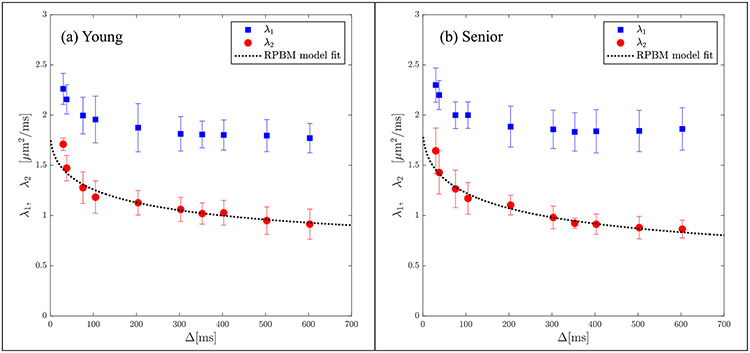
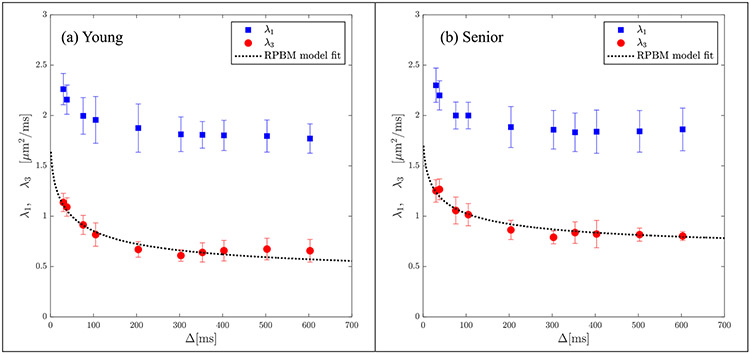
The secondary and tertiary eigenvalues were more strongly dependent on Δ in contrast to the primary eigenvalue (average of 43% decrease in the transverse eigenvalues over the range of experimental diffusion times compared to 21% for the primary eigenvalue). Significant higher values ( p < 0.05) of λ₃(t) was seen in the senior cohort for Δ = 105, 204, 303, 353, 503, 603 ms while a trend to higher values was seen at Δ = 38, 76 and 403 ms ( p < 0.1). Lower values of λ₂(t) in the senior cohort was observed consistently across the range of diffusion times, however, none were significant. Figures 4a and 4b show the results of the model fit to the secondary and tertiary eigenvalues respectively using the corresponding data averaged separately for the young and senior cohorts. Excellent fits to the model were obtained for both cohorts for both eigenvalues and to D_⊥(t), the latter fit is shown in Supporting Figure 5. Plots of the RPBM fit to λ₂(t) for each participant are shown in Supporting Figure 6 (young) and 7 (senior) and residuals of the fits are shown in Supporting Figures 8 (young) and 9 (senior). Corresponding figures for the fit to λ₃(t) are shown in Supporting Figures 10 and 11 (RPBM fits) and Supporting Figures 12 and 13 (residuals). In all the fits to λ₂(t) and to λ₃(t), the residuals have small positive and negative excursions about zero mean; the only exceptions are the fits to λ₂(t) for smaller diffusion times in four young subjects. If the residuals were non-normally distributed, it would mean that the residuals contain structure that is not accounted for in the RPBM model. While not shown here, the individual fits to D_⊥(t) were excellent and the residuals were small and distributed about the zero value. Table 2a and 2b list the model-derived tissue microstructure parameters for young and senior cohorts from λ₂(t) and λ₃(t) respectively. There were no significant differences in any of the RPBM parameters from the fit to λ₂(t). In the RPBM fit to λ₃(t), the senior cohort had significantly lower values of $\zeta$ (volume fraction of membranes) as well as a trend to larger values of the dwell time. Supporting Table 1 shows the RPBM derived values for the fit to D_⊥(t). In the RPBM fit to D_⊥(t), no significant differences were seen between young and senior cohorts in any of the model parameters.

Figure 4a:

Average RPBM model fits of λ₂(t) for the groups of young (a) and senior (b) participants respectively. The points are experimentally determined while the dashed line is the model-derived fit to the eigenvalue.

Figure 4b:

Average RPBM model fits of λ₃(t) for the groups of young (a) and senior (b) participants respectively. The points are experimentally determined while the dashed line is the model-derived fit to the eigenvalue.

Table 2a:

Parameters of tissue microstructure for young and senior participants from the RPBM model fit to λ₂

fit parameters	young	senior
$D_0$ [μm2/ms] free diffusion	1.83 ± 0.16	1.88 ± 0.18
$\zeta$ volume fraction	4.63 ± 3.77	3.06 ± 1.86
$S∕V$ [μm−1] surface to volume ratio	0.10 ± 0.03	0.12 ± 0.03
$\kappa$ [μm/ms] permeability	0.016 ± 0.013	0.024 ± 0.013
$a$ [μm] myofiber diameter	71.64 ± 23.55	54.91 ± 13.91
$l$ [μm] effective thickness	114.60 ± 78.93	58.54 ± 27.05
${\tau }_R$ [ms] residence time	2833.9 ± 1831.1	2942.0 ± 1298.7
${\tau }_D$ [ms] dwell time	2814.4 ± 1359.9	2060.7 ± 889.7

Table 2b:

Parameters of tissue microstructure for young and senior participants from the RPBM model fit to λ₃

fit parameters	young	senior
$D_0$ [μm2/ms] free diffusion	1.83 ± 0.16	1.88 ± 0.18
${\zeta }^{\ast }$* volume fraction	3.75 ± 1.18	2.61 ± 0.39
$S∕V$ [μm−1] surface to volume ratio	0.26 ± 0.06	0.21 ± 0.13
$\kappa$ [μm/ms] permeability	0.03 ± 0.01	0.04 ± 0.03
$a$ [μm] myofiber diameter	16.57 ± 4.11	22.31 ± 8.01
$l$ [μm] effective thickness	30.67 ± 9.59	29.92 ± 13.08
${\tau }_R$ [ms] residence time	292.0 ± 138.3	418.6 ± 282.1
${\tau }_D$ [ms] † dwell time	80.7 ± 39.8	152.4 ± 93.7

^*Significant difference between young and senior age groups ( p < 0.05)

^†Trend towards significant difference between young and senior age groups ( p < 0.1).

Statistical analysis of differences between young and senior cohorts in the biopsy data showed significant lower values in the Feret diameter, d_F ( p < 0.05) and a trend toward lower values in fiber cross-sectional area, f_CSA and higher values in the collagen angle, ϕ ( p < 0.1) with age (Table 3). It should be noted that qualitatively comparing the fiber diameters extracted from the fits to λ₂(t), λ₃(t) and D_⊥(t), the agreement to the histological data is best for the RPBM fit to λ₂(t). Further, the anticipated age-related decrease in fiber diameter seen in histological data (Table 3) is only seen in the fiber diameter extracted from the λ₂(t) data (fiber diameters increased with age on the fits derived from λ₃(t) and D_⊥(t)). Pearson correlation of fiber diameter from the RPBM fits to that obtained from histology (subset of subjects of the imaging study) also showed the highest correlation values to the fit to λ₂(t) though it did not reach significance. The Pearson correlation coefficient (and p values) for the fits are: λ_2: 0.36(0.306), λ₃: 0.35 (0.37), D_⊥: 0.33(0.349).

Table 3:

Parameters extracted from the biopsy analysis in the subgroup of four young and six senior participants.

biopsy measurements	young	senior
Type IV Collagen [AU]	10.91±3.57	13.82±4
Type VI Collagen [AU]	15.28±1.52	14.66 ± 3.19
Fiber cross-sectional area (fCSA)† [μm2]	5575.81±865.19	3882.72±1391.67
Feret’s diameter (dF)* [μm]	63.94 ± 5.77	52.98±6.8
Angle of ECM (ϕ)† [º]	24.00 ± 1.41	32.33 ± 5.16

^*Significant difference between young and senior age groups ( p < 0.05)

^†Trend towards lower diameters and larger angles in the senior cohort ( p < 0.1).

Figure 5 shows the representative histology data for one participant: collagen IV and collagen VI images of the cross-section and picrosirius stained images of longitudinal sections to quantify the collagen angle, ϕ. In physical assessment metrics, significant age-related differences between the young and senior cohorts were found in left hand grip strength (senior participants: lower strength), for 200 m and 400 m walk time (senior participants: longer time), as well as a trend toward higher post-test diastolic blood pressure (Table 4).

Figure 5:

Representative histology images for one participant: collagen IV (also used to quantify fiber CSA and Feret diameter) and collagen VI images of the cross-section and picrosirius stained images of longitudinal sections to quantify ϕ.

Table 4:

Physical assessment metrics measured in the subgroup of four young and six senior participants.

physical assessment metrics	young	senior
Age [years old]	39±13	72±4
Height [cm]	181.7±9	169.2±14.5
Weight [kg]	97.8±28.8	75.1±13.7
BMI [kg/m2]	29.2±6.7	26.6±6
Left hand grip* [kg]	48±7.7	29.3±9.8
Right hand grip [kg]	49.3±9.6	35.2±13.4
Chair stand time [s]	8.3±2.4	9±5
200 m* walk time [s]	113±22.2	191.5±64.1
400 m* walk time [s]	230.8±43.9	400.8±93.5
Pre-test SBP1 [mmHg]	124.5±17.3	145.5±19.1
Pre-test DBP2 [mmHg]	76±5.4	81.8±7.2
Post-test SBP [mmHg]	156.5±17.2	161.5±19.3
Post-test DBP† [mmHg]	74±4.6	83±8.7
2 min post-test SBP [mmHg]	128±21.8	142.2±18.1
2 min post-test DBP† [mmHg]	72.5±4.1	82±7.5
Frailty score	−0.8±0.9	−0.5±0.5

^*Significant difference between young and senior age groups ( p < 0.05)

^†Trend towards higher post-test diastolic blood pressure in senior group ( p < 0.1)

¹Systolic blood pressure,

²Diastolic blood pressure.

DISCUSSION

Physical assessment revealed significant differences between young and senior cohorts in left hand grip (lower in senior) and in the 200 m and 400 m walk time (longer in senior). These findings confirm that there is overall loss of muscle function in the senior cohort that affects the upper and lower extremities. The significantly lower values of the Feret diameter from the histological analysis is in agreement with the well-established fact of age-related muscle atrophy ³¹. The sections that follow include discussion of the age-related differences in (i) diffusion eigenvalues at different diffusion times and (ii) model parameters derived from the fits to λ₂(t), λ₃(t) and D_⊥(t).

At the outset, a justification is provided for fitting the RPBM model to λ₂(t) and λ₃(t) eigenvalues and to D_⊥(t) instead of the more traditional approach of fitting to D_⊥(t) only. In earlier reports, the RPBM model was fitted to D_⊥(t) in order to obtain robust experimental data less sensitive to bias than the individual eigenvalues ^17,18. However, in the current study, the age-related differences in λ₂(t) and λ₃(t) were in opposing directions: λ₂(t) was lower in the senior cohort (though not significantly) while λ₃(t) was significantly higher with age for most of the diffusion times. This differing behavior with age potentially indicates that the two eigenvalues may have a different physiological origin. Further, averaging the secondary and tertiary eigenvalues cancelled/ reduced age-related effects, providing further rationale for fitting the RPBM model separately to λ₂(t) and λ₃(t) rather than to D_⊥(t) only. The fits of D_⊥(t) to the RPBM model is also presented in the current paper to compare to the fits to λ₂(t) and λ₃(t) and to explore if it provides insights different from the fits to λ₂(t) and λ₃(t). One point to note is the decrease in the accuracy of the fit for λ₃(t) (Fig. 4a) and λ₂(t) (Fig. 4b) compared to D_⊥(t) (Supporting Fig. 3). However, even though the RPBM fit to D_⊥(t) is better, the independent fits to λ₂(t) and λ₃(t) were also explored in the current paper since they exhibit different behavior with age and averaging λ₂(t) and λ₃(t) (D_⊥(t)) reduced/eliminated age-related differences.

There were no significant differences in λ₁(t) and in λ₂(t) between the young and senior participants. Previous studies have reported age related changes in skeletal muscle that include changes in muscle fiber cross-sectional area, muscle architecture (fiber length, pennation angle), and in the muscle tissue microstructure, composition and extracellular matrix ³². Age related decrease in either cellular cross-section and/or decrease in fiber length is not anticipated to change the lead eigenvalue since the fiber cross-section does not affect longitudinal diffusion and the fiber length is much longer than diffusion distances. Smaller values of λ₂(t) was seen in the senior cohort though the differences did not reach significance. In contrast to this, significantly longer values of λ₃(t) for a range of diffusion times were observed in the senior cohort compared to the young cohort. While not established experimentally, one model for muscle diffusion postulates that λ₂(t) corresponds to the direction of the longer axis of an elliptical fiber while λ₃(t) corresponds to the direction of the shorter axis of an elliptical fiber ¹⁵. Further, this same model hypothesizes that the morphological asymmetry of the fiber cross-section (elliptical instead of circular fiber cross-section) arises from an asymmetry in deformation of the muscle fiber on contraction. The asymmetry of radial expansion in fiber cross-section has been established in a number dynamic studies of muscle contraction ^33,34. Since the source of the morphological asymmetry arises from deformation asymmetry, it can be extrapolated that with muscle disuse or reduced use (e.g., with age or immobilization), the morphological asymmetry will decrease. This could indicate fiber cross sections tending from elliptical to more circular shapes with age. Indeed, a loss in asymmetry post-suspension (disuse induced by unilateral limb suspension) was found in an earlier exploratory diffusion modeling study of DTI data acquired in subjects before and after limb suspension ³⁵. This latter study used the Karger bi-compartment diffusion model which has several model fit parameters and is not as robust as the RPBM ¹⁵.

RPBM derived fiber diameters were closely matched to the Feret diameter obtained from histology for young and senior participants only for the fit of the model to λ₂(t). The fits to both λ₃(t) and D_⊥(t) gave smaller values of the fiber diameter than the histology derived ones and further, in both fits, the fiber diameter was larger in the senior cohort. The effective ‘volume fraction’, $\zeta$, was lower in the senior cohort for the fits to all three diffusion indices and significant for the fit to λ₃(t). The effective volume fraction provides a measure of how strongly the membranes collectively influence diffusion. The lower values of $\zeta$ in the senior cohort show that in the aged muscle, the membranes do not affect diffusion as much as in the young muscle. This can arise from a decrease in the membrane volume to fiber volume (i.e., larger values of the fiber diameter, a) and/or changes in the permeability (κ) of the tissue. It should be noted that permeability derived from the RPBM model increased in the senior cohorts for fits to λ₂(t) and λ₃(t). It is likely then that changes in both diameter and permeability results in the observed age-related differences in λ₂(t) and λ₃(t).

An age-related increase in permeability will enable water to diffuse more readily across the cell membrane resulting in higher diffusion eigenvalues. A simulation study revealed that diffusion is more sensitive to changes in permeability than to changes in fiber size ³⁶. In the current study, the experimental data from λ₃(t) shows either a trend to increase or a significant increase in the range of diffusion times from 38 ms to 603 ms. This large range of diffusion times over which larger diffusion values were observed potentially indicates that permeability is impaired at senior age. If the longer values of λ₃(t) arise from a change in fiber-diameter then age-related differences in λ₃(t) will be seen at diffusion times, $\Delta$ that result in diffusion lengths (given by $\sqrt{2D_0\cdot \Delta }$ of the order of the fiber diameter and at longer diffusion times. However, λ₃(t) is significantly different between young and old cohorts over the entire range of investigated diffusion times pointing to an origin different from fiber diameter. A 7 T study on mice skeletal muscle from young to adult stages (maturation study) using time-dependent diffusion MRI reported that muscle diffusion was more restricted in adult mice despite the increase in muscle fiber size ³⁷. A potential reason for decrease in the Apparent Diffusion Coefficient (ADC, also referred to as Mean Diffusivity) in the adult mice was postulated to arise from a decrease in membrane permeability in the adult mice. These two studies highlight the potential relative roles of permeability and fiber size in determining diffusion in the fiber cross-section.

In the context of the above discussion, a tentative hypothesis is extended to explain the observed age-related differences with age in λ₂(t) and λ₃(t). The muscle fiber has an elliptical cross-section and λ₂(t) corresponds to diffusion along the long axis of this ellipse and λ₃(t) to short axis of the ellipse. With age, the fiber cross-section becomes less asymmetric (i.e., atrophy is preferentially along λ₂(t) than along the direction of λ₃(t)). One reason advanced for the fiber being elliptical in young subjects is that the deformation during contraction is almost completely along one direction with nearly no deformation in the orthogonal direction leading to morphological asymmetry. However, in senior subjects, disuse or lower activity results in less tissue deformation and the morphological consequence is that the direction of the longer axis is no longer stretched leading to a more symmetric fiber cross-section. Additionally, as seen from the RPBM fits to λ₂(t) and λ₃(t) , permeability is higher in the senior cohort. The increase in permeability will result in an increase in diffusion in the fiber cross-section, i.e., in both λ₂(t) and λ₃(t). The observed differences in λ₂(t) and λ₃(t) between young and senior cohort may potentially be determined from the combination of changes in fiber diameter and permeability. In the case of λ₂(t), in the senior cohort, the fiber diameter in the direction of λ₂(t) has smaller values compared to the younger cohort (presumably from age related muscle disuse). This potentially leads to smaller values of diffusion that is offset by the larger values of diffusion from larger values of permeability in the senior cohort. The net effect is the observed small differences in λ₂(t) between the senior and young cohort (not significant). In the case of λ₃(t), in the senior cohort, fiber diameter potentially has the same value as in the younger cohort and the observed significant larger values of diffusion across all diffusion times is a result of an increase in permeability. This hypothesis was tested by looking at the minimum and maximum Feret diameters. While the minimum Feret diameter was directly measured, the maximum Feret diameter was calculated from the measured fiber cross-sectional area assuming that the muscle fiber has an elliptical cross-section. It should be noted that maximum Feret diameters are prone to inaccuracies arising from the limitations of histology since cryo-sectioning identifies both ‘angulated’ and ‘level’ fibers ³⁰. Assessment of fiber diameter from angulated fibers will result in overestimation; the minimum Feret diameter is used to avoid this error. The average maximum Feret diameter for the young cohort was 110.58 μm ± 7.45 μm and for the old cohort was 83.34 μm ± 8.56 μm (one subject with outlier values was removed from the analysis), the difference was significant (difference between young/senior = 25%, p = 0.0015). Corresponding values for the minimum Feret diameter are shown in Table 3 and the difference and p-values of the difference in young and old cohort was 16% and 0.029 respectively. In addition, the ratio of maximum to minimum Feret diameters was lower in the senior cohort (young ratio: 1.734, senior ratio: 1.635); however, this difference was not significant. While these histology measurements show that muscle fiber reduces along both the long (maximum Feret diameter) and short (minimum Feret diameter) axis, it lends partial support to the RPBM based hypothesis in that histology also indicates that atrophy is more pronounced on the long axis and the fiber is less elliptical with age.

The qualitative comparison of fiber diameters from the RPBM fits to λ₂(t), λ₃(t), and to D_⊥(t) revealed the best match to histology derived Feret diameter was to that obtained from the fit to λ₂(t). In accordance with this qualitative comparison, the Pearson correlation coefficient obtained on a subset of subjects on whom biopsy was performed also yielded the highest correlation for the fiber diameters obtained from the fit to λ₂(t). However, the correlation did not reach significance and was only marginally better than the correlation of fiber diameters from the fits to λ₃(t) and D_⊥(t). The low correlation values for even λ₂(t) may arise from the smaller number of participants in the correlation study; biopsy was performed on all seniors but on only 4/8 young participants of the imaging study. A future study with a larger number of young and senior subjects with both biopsy and imaging may show significant correlations.

While the RPBM model is seeing increased usage, it has not been so far been validated against histology in human studies. Several prior studies have noted the discrepancy between histology derived fiber diameters to RPBM derived fiber diameters: in a rat model of normal skeletal growth, RPBM-derived fiber diameters from in-vivo DTI data did not correlate as well with those derived from histology compared to the RPBM-derived parameters from ex-vivo DTI data ²¹. Model based underestimation of the fiber diameter compared to histology (diameters obtained from prior reports in the literature rather than on the same subject) was also reported in an earlier work ¹⁷. Further, the above-mentioned rat model study found that when comparing the same subject, ex-vivo and histology-derived muscle fiber diameter underestimated this value and could be substantially different from diameters derived from in-vivo DTI data ²¹. A simulation study of DTI in muscle to determine optimal diffusion times compared RPBM-derived muscle fiber diameter to those of the simulation also revealed that RPBM considerably underestimated fiber diameters²². This latter work recommended a scaling factor of 6.29 as opposed to a scale factor of 4 derived using histological data. The current work reveals that fitting separately to λ₂(t) and λ₃(t) provides new physiological insight not available with a fit to D_⊥(t). Further, the fiber diameter extracted from the fit to λ₂(t) (using the scale parameter from Ref. ²²) yielded the best qualitative match and correlation to the histology derived Feret diameter for young and senior cohorts. In contrast, the fits to λ₃(t) and to D_⊥(t) yielded fiber diameters that were underestimated in comparison to histology and importantly, higher values of fiber diameters were seen in the senior compared to the younger cohort. These studies highlight that the RPBM model requires a larger study with validation/ optimization against a histology reference standard. The current study also shows that separate fits to λ₂(t) and λ₃(t) can potentially provide information additional to that obtained from the traditional fit to D_⊥(t) alone. Further, the range of applicability of the model across different muscle conditions (e.g., sarcopenia, dystrophy) remains to be tested.

The limitations of this study are the small sample sizes. However, this was an exploratory study to investigate the feasibility of a study that included time-dependent diffusion, modeling and comparison to histological analysis. Some technical limitations may have arisen from the fairly short STEAM-DTI acquisition used in the current paper (6 diffusion gradient directions, 2 averages) – this was done in order to obtain diffusion eigenvalues at 10 different diffusion times. Further, the RPBM does not model the contribution from perfusion and this will result in an overestimation of $D_0$ and underestimation of $\zeta$ assuming perfusion does not have a dependence on diffusion time. An approximate calculation (7% perfusion fraction, D_perf = 0.1 mm/s²) showed that the perfusion fraction to the total signal attenuation changed from 0.6% at b = 2.4 s/mm² to 0.001% at b = 72.8 s/mm². The decrease in D_∥(t) over the total range of diffusion times used in the current study is ~22%. So, potentially ~0.6% of this decrease can come from reduced perfusion effects at the longer diffusion times but this is still less than 1% effect. However, future studies using nominal values of ~120 s/mm² for the lower b-value may serve to suppress perfusion at all diffusion times to obtain diffusion data free from contributions from perfusion. Other technical limitations may arise from not performing ‘outlier rejection’ since diffusion weighted images of STEAM based sequences are known to have artifacts from signal dropout arising from involuntary incoherent muscular activity ¹⁷. However, a manual check was performed to verify that there was not any significant signal drop out in the images.

In conclusion, this is the first report of time-dependent diffusion eigenvalue differences in the medial gastrocnemius muscle in a cohort of young and senior participants and modeling of the time-dependent diffusion eigenvalues to extract tissue microstructure parameters in the same cohort of participants. Further, the model derived parameters were compared to fiber diameter from a histological analysis of biopsy samples of the MG from the same subjects. The important findings of this study are (i) the tertiary eigenvalue was significantly longer in the senior cohort for a range of diffusion times (105 ms to 603 ms) while the secondary eigenvalue had a small (though not significant) decrease with age; this points to potentially different origins for the secondary and tertiary eigenvalues and the RPBM was thus fit separately to λ₂(t), λ₃(t) and D_⊥(t). (ii) fiber diameter from the fit to λ₂(t) yielded the best qualitative agreement as well as the highest correlation to that from histology in the young and senior cohorts and (iii) $\zeta$, the effective ‘volume fraction’, $\zeta$, which provides a measure of how strongly the membranes collectively influence diffusion was lower in the senior cohort for the fits to all three diffusion indices and also significant for the fit to λ₃(t). It appears from the current study that fits to all three diffusion indices, λ₂(t), λ₃(t) and D_⊥(t), may provide independent insights into tissue microstructure. A tentative hypothesis advanced to explain the age-related differences in λ₂(t) and λ₃(t) was based on a decrease in morphological asymmetry from muscle less use or disuse and an increase in permeability with age, the former effect indicating that muscle function impacts muscle structure opening up an area of future investigation in diffusion modeling. This latter hypothesis was only partially supported by an analysis of minimum and maximum Feret diameters from the histology measurements. Future studies with larger cohorts on whom both time dependent diffusion imaging and histology is acquired will help elucidate in detail muscle fiber microstructural changes with age.

List of abbreviations:

DTI

Diffusion tensor imaging

RPBM

Random Permeable Barrier Model

STEAM

Stimulated Echo Acquisition Mode

SBP

Systolic blood pressure

DBP

Diastolic blood pressure

IPAQ

International Physical Activity Questionnaire

EPARC

Exercise and Physical Activity Resource Center

ECM

Extracellular Matrix