How it feels in a cell

Abstract

Life emerges from thousands of biochemical processes occurring within a shared intracellular environment. We have gained deep insights from in vitro reconstitution of isolated biochemical reactions. However, the reaction medium in test tubes is typically simple and diluted. The cell interior is far more complex: macromolecules occupy more than a third of the space, and energy-consuming processes agitate the cell interior. Here, we review how this crowded, active environment impacts the motion and assembly of macromolecules, with an emphasis on mesoscale particles (10–1000 nm diameter). We describe methods to probe and analyze the biophysical properties of cells and highlight how changes in these properties can impact physiology and signaling, and potentially contribute to aging, and diseases, including cancer and neurodegeneration.

Life in crowded and active environments

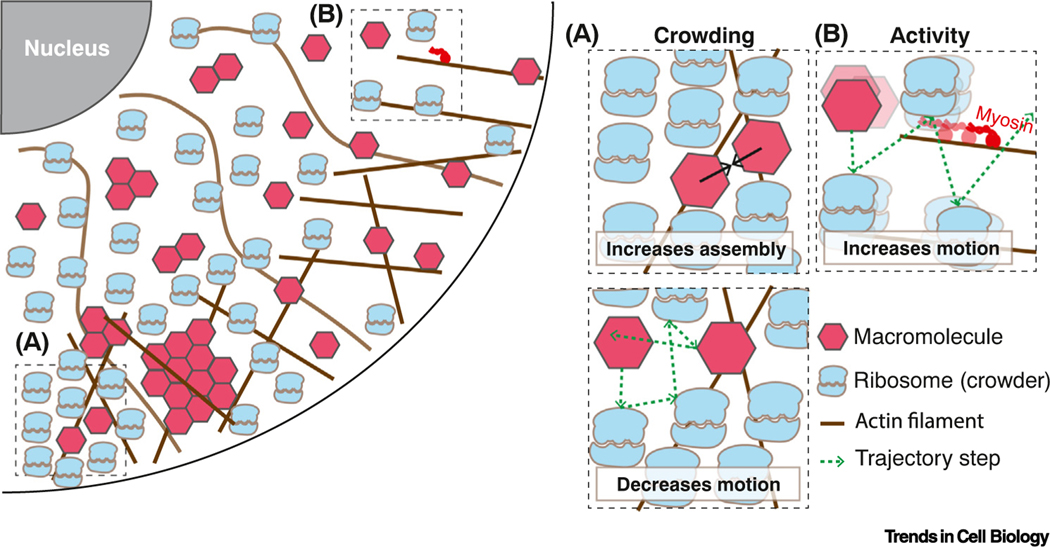
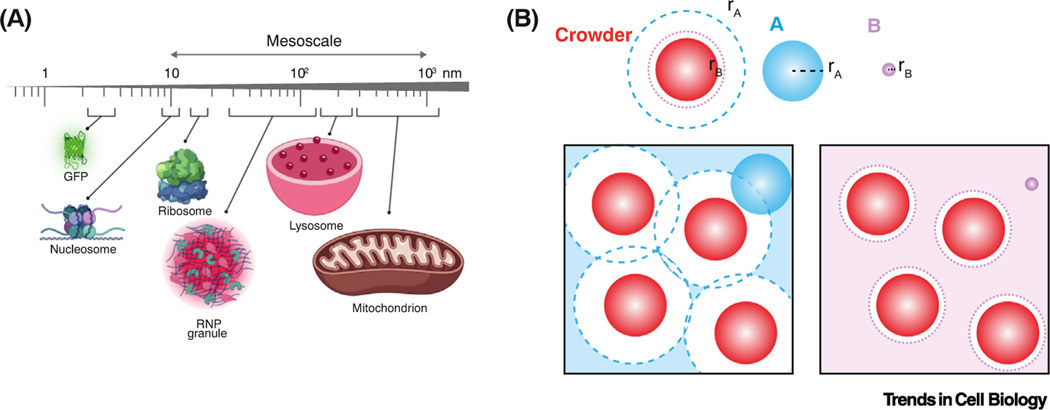
Eukaryotic cells are crowded with a complex mix of macromolecules (see Glossary), membrane-bound organelles, and a dynamic cytoskeleton [1,2]. We will refer to macromolecules (e.g., proteins and RNAs) and macromolecular complexes as particles. The diffusion of particles is decreased by macromolecular crowding but increased by metabolic activity, polymerization and depolymerization (especially of cytoskeletal networks), and the activities of molecular motors, such as myosins, kinesins, and helicases (Figure 1, Key figure). We will explore how this dynamic and crowded environment influences cellular organization and biochemical reactions. For simplicity, we will refer to macromolecular crowding as simply ‘crowding’. In particular, we will focus on crowding by particles of around 10–1000 nm diameter – the cell biological ‘mesoscale’– because a large fraction of the space in the cell, the ‘excluded volume’, is taken up by particles of this size (e.g., nucleosomes are ~10 nm, ribosomes are ~30 nm, mRNA ribonucleoprotein complexes are ~100 nm) (Figure 2A). Most monomeric proteins are in the nanometer (1–5 nm) size range [3–5]. However, many proteins also assemble into mesoscale complexes [6,7]. In addition to protein complexes, pressure filtration and size exclusion experiments suggest that at least 18% of proteins in the Xenopus laevis cytoplasm are organized into mesoscale biomolecular condensates of predominantly 100 nm diameter [8].

Figure 1. The cell interior is crowded and far from thermal equilibrium.

(A) Macromolecular crowding can drive molecular assembly (top) and decrease particle diffusion (bottom). (B) Energy-consuming activities increase particle motion.

Figure 2. Size-scales in cells, and size-dependent volume exclusion.

(A) Diameter of molecules, molecular complexes, and organelles, mesoscale range indicated. (B) Crowders occupying the box limit the volume available to other particles depending on particle size. The center of particle B (lilac) can only occupy positions at least one radius (r_B) away from the crowders (lilac broken circle). A larger particle A (blue) is excluded from a larger volume, also defined by its radius (r_A, blue broken line). The lilac- and blue-shaded regions indicate the accessible volumes for particle A (left) and B (right), respectively. Abbreviation: RNP, ribonucleoprotein.

Crowding agents exclude access to the volume that they occupy in a manner that depends on the size (length scale) of each particle. Particles in a crowded environment can only access gaps that are greater than their diameter (Figure 2B). This means that for particles of similar size or larger than the crowders, the excluded volume can be more than double the actual volume occupied by crowders [9]. So, large particles are far more impacted by crowding than smaller particles. In cells, the restriction of space becomes most apparent for mesoscale particles >30 nm in diameter [10].

However, the cell is not an equilibrium system and intracellular particle diffusion is not as restricted by crowding as predicted by simple models [11]. This is because the cell interior is agitated by the combined effects of molecular motors, enzymatic reactions, ion gradients, cytoskeletal motion; in short, the metabolic activity of the cell. This activity helps to fluidize the cellular interior and increase particle motion. The cell is thus considered ‘active matter’. How is this ‘crowded’ and ‘active’ environment important for biochemical reactions and cell organization?

Crowding can have different impacts on each reaction in the cell. On the one hand, crowding generally disfavors diffusion-limited reactions by decreasing encounter rates [12,13]. On the other hand, crowding can favor molecular assembly [14,15] due to an effect called ‘depletion attraction’ (Box 1).

Box 1. The depletion-attraction force.

Consider particles, let us call them ‘assemblons’, that could assemble or not. In a dilute solution with negligible chemical (enthalpic) interactions, the entropy of the system is maximized (and therefore the system free energy minimized) when the assemblons are evenly mixed, and not assembled together. Thus, it is most favorable to have no assembly, and therefore high entropy.

However, when molecular crowders are added to the system (again, assuming no interactions other than steric constraint), they are excluded from the space around the assemblons (broken line in Figure IA). This excluded space reduces the entropy of the crowders. If the assemblons cluster and assemble, this creates more space for crowders to move, thereby increasing crowder entropy (Figure IB). The number of crowders is generally far larger than the number of assemblons. Therefore, the entropy of the whole system is maximized when the assemblons cluster together because the entropy increase for crowders outweighs the entropy decrease for the assemblons. This is referred to as the entropic depletion-attraction force (Figure IB) [127,128]. The depletion-attraction force was first characterized by Asakura and Oosawa with ‘AO theory’ [129]. Depletion attraction typically leads to a small reduction (a few k_BT) in free energy, but this can be sufficient to stabilize protein structures and facilitate the formation of multimeric protein complexes [127].

Depletion attraction is an entropic effect. The propensity of molecules to assemble depends on the combination of the enthalpic driving force (e.g., bonding interactions) and the entropic effects of the interaction (the effects on disorder). Binding reactions are generally entropically unfavorable, because the reactants become more ordered. However, when two or more components bind one another, they take up less space. In crowded environments, this creates room to move, thereby increasing crowder entropy. Thus, crowders can offset the entropic cost of binding reactions, favoring molecular assembly. This effect is strongest at the mesoscale, where excluded volumes are very high.

Beyond ‘hard-sphere steric constraints’, more complex interactions between crowders and reactants can occur. For example, attractive and repulsive hydrophobic, polar, and charge–charge interactions affect the enthalpic energy landscape. Thus, combined entropic and enthalpic contributions can lead to case-specific effects from crowders in different experimental systems [16,17].

At the larger scale, cell organization can be impacted by crowding. Biomolecular condensation is an extreme example of molecular assembly. Condensates can form through the phenomena of phase separation and percolation transitions [18]. Multivalent interactions can cause particles to spontaneously demix from a solution and condense into a dense phase, where they form complex networks that can be two or three orders of magnitude larger than the original particle, and that coexist with a dilute phase. Subcellular organelles, such as nucleoli [19], p-granules [20], and centrosomes [21], are thought to be phase-separated condensates. As with molecular assembly in general, phase separation is entropically unfavorable, but can be promoted by crowding through the depletion attraction effect [22]. Indeed, phase separation of synthetic systems can be increased by crowding in cells [23].

There are also cases where the depletion-attraction effect can drive phase separation of a single type of particle. A striking example is the spontaneous assembly of rod-like particles into ‘liquid crystals’. This is called isotropic-nematic phase separation. ‘Isotropic’ means that there is no bias in orientation, while ‘nematic’ means that the rods become aligned. In isotropic-nematic phase separation, the rods both act as crowders and form the assembled dense phase. When the rods all line up as a dense liquid crystal, they take up less space, giving more room for the rods in the dilute phase to move. Thus, the rods in the dense phase lose orientational entropy, but this is balanced by a larger increase in entropy of rods in the dilute phase [24]. This effect can cause actin filaments [25] and microtubules (MTs) [26] to spontaneously assemble into liquid crystal ‘tactoids’ (rugby-ball shapes). This liquid crystal mechanism may be crucial for the formation of some metaphase spindles and therefore cell division [26].

In conclusion, crowding slows diffusion but favors molecular assembly. In particular, it can promote phase separation and the creation of membraneless organelles. All cells are both highly crowded and active; they probably evolved this way to accelerate biochemical reactions and favor the formation of higher order structures, thus contributing to cellular organization [9].

What factors affect particle motion inside of cells?

Biological macromolecules undergo many types of motion, including conformational dynamics, rotation, and translational motion. Here, we will simplify and use the term ‘motion’ to refer to the translational motion, or diffusivity of particles. Rapid, directed transport can be achieved by specific molecular systems. For example, in eukaryotic cells, kinesin and dynein motor proteins drive rapid transport along MTs; while myosins drive slower, local cargo transport along the actin network. We will not focus on this type of transport, which is reviewed elsewhere [27,28]. Rather, we will explore how particle size, the presence of crowders, and the non-equilibrium activity of the system affect particle motion.

First, we will inspect the theory of Brownian diffusion and point out where this simple model of diffusion fails to describe the motion of particles in the cell. Brownian motion is driven by the conversion of thermal fluctuations into kinetic energy [29,30]. The Stokes–Einstein equation (Box 2) describes the connection between thermal and kinetic (motion) energy and can be used to predict how particles diffuse. However, the predictions only hold in the relatively simple case of particles of homogeneous size in a homogeneous solvent. The size of solute molecules must be much smaller than that of Brownian particles and there can be no strong enthalpic interactions between particles, or between particles and solutes. However, the cell violates all these assumptions. Therefore, more generalized theories are required.

Box 2. The Stokes–Einstein equation.

The Stokes–Einstein equation was first derived by Einstein in his PhD thesis as the framework for his analyses on Brownian motion and was further elaborated in the 1905 paper that established the theory of Brownian motion [29,30]. For a spherical particle with radius $\mathit{r}$, its diffusion constant $D$ within a viscous fluid (viscosity $\eta$) at temperature $T$ can be expressed as:

$$D=\frac{RT}{N_A}\frac{1}{6\pi \eta r}=\frac{k_{B}T}{6\pi \eta r}$$

where $R$ is the ideal gas constant, $N_A$ is Avogadro’s number, and $k_B$ is the Boltzmann constant.

The Stokes–Einstein equation states that, within a viscous fluid at constant temperature, the diffusion constant of a spherical particle should be inversely proportional to its radius: the larger the particle, the slower its movement. The theory is accurate when the particle’s inertial force is negligible relative to its viscous force (i.e., at low Reynolds number [130]), and the solute molecules are of a homogenous size much smaller than the particle.

This equation uses the underlying assumption of a spherical particle within a fluid of constant viscosity based on Stokes’ law [30]. The model was generalized for more complex fluids and non-spherical particles in the Stokes–Einstein–Sutherland relation [29,37] by replacing radius $\mathit{r}$ and uniform fluid viscosity $\eta$ with the hydrodynamic radius $r_H$ of the particle and the scale-dependent effective viscosity ${\eta }_{eff}$ of the complex fluid.

An alternative way of deriving the Stokes–Einstein equation is through the Langevin equation for a Brownian particle under the assumption of thermal equilibrium, where particle movement is subject to both frictional forces exerted by the viscous medium and fluctuation forces from random collisions with particles in the medium. The strengths of the frictional and fluctuation forces are related through the fluctuation-dissipation theorem [66,131]. The Langevin equation provides a basis to model forces beyond Brownian particle assumptions, in particular enabling description of non-equilibrium conditions [132].

Size

As mentioned earlier, the size of a particle is a key determinant of its motion. Nanoscale particles, such as GFP, and small molecules like metabolites, diffuse in the aqueous phase of the cytosol relatively easily [31,32]. However, once molecular diameter exceeds ~10 nm (i.e., at the mesoscale), diffusion in the cytoplasm becomes substantially lower than predicted by the Stokes–Einstein equation [33] (Figure 2A and Box 2). This is because the majority of cytosolic crowders are around 30–100 nm diameter (ribosomes and polysomes), and so act like ‘molecular sieves’ that slow down particles similar to this size, but allow smaller particles to slip between the gaps. Similar non-linearities exist in the nucleoplasm: small dextrans (up to ~20 nm diameter) diffuse freely, while larger dextrans (around 60 nm diameter) are partially immobilized [34].

It is possible to define a non-uniform ‘effective viscosity’ that increases with particle size to account for these effects; generalizing the Stokes–Einstein equation to the Stokes–Einstein–Sutherland equation can model motion of non-spherical particles in more complex fluids (Box 2) [35–37].

Active matter (non-equilibrium)

The cytoplasm is highly active and out-of-equilibrium. Energy-consuming activities can strongly affect the motion of particles. Increased motion occurs due to constant remodeling of molecular assemblies within the cell, and to the activity of molecular motors. This activity drives fluctuations in the cytosol, increasing molecular diffusivity, and sometimes results in directed motion [38]. For example, MT dynamics increase molecular diffusion within the densely packed metaphase spindle [39].

Hydrodynamic coupling between cytoplasmic particles and molecular motors at the cell periphery can drive flows called ‘cytoplasmic streaming’ [40]. In amoebae of the Chaos group, transport by fluid motion can drive cell motility [41]. The nucleoplasm is agitated by transcription, splicing, DNA replication, and so forth, leading to constant local chromatin remodeling [42]. In addition, every exothermic catabolic reaction releases heat as a byproduct. The heat produced elevates local temperature, increasing the energy and diffusion of particles [43].

Nonequilibrium cell activity is crucial to promote diffusion at the mesoscale. Without ATP, the bacterial cytoplasm changes from a fluid-like to a glass-like solid state for particles >50 nm in diameter [44]. Similar results have been reported upon ATP depletion and carbon starvation in yeasts [45,46]. ATP-dependent processes are also critical for large-scale and coherent motion of chromatin [47].

Overall, these active processes violate the equilibrium assumption of the Stokes–Einstein equation. It is possible to adapt the Stokes–Einstein equation by adding isotropic frequency-independent noise and increased effective temperature [48,49] to model some non-equilibrium processes. However, this approach cannot model nonequilibrium processes that are anisotropic or frequency dependent.

Non-entropic forces

Interactions with the environment (enthalpic forces) can slow particle movement. The most abundant cellular components (ribosomes, DNA, RNA, membranes) have negative surface charge. Therefore, particle surface charge can greatly impact diffusion: negatively charged GFP diffuses 100 times faster than positively charged GFP [50]. Electrostatic interactions are highly dynamic; thermal movements (e.g., diffusion, tumbling) of charged molecules (e.g., proteins, RNAs) can be considered as rapidly moving dipoles that lead to randomly fluctuating electric fields within cells [51]. Weak hydrophobic interactions can also affect particle motion [52]. These electrostatic and hydrophobic interactions can each be modeled as an effective friction [51].

The cell interior has a complex network structure that can be fractal in nature (i.e., boxes within boxes) and is constantly rearranging [53,54]. Particles can be confined within local ‘cages’ that constrain diffusion [55]. Periodic escape from local cages can lead to ‘hop diffusion’. For example, phospholipids diffuse rapidly within small (~230 nm²) compartments confined by transmembrane proteins, before escaping (hopping) to adjacent compartments with a certain probability [56].

The Stokes–Einstein equation is derived from the Langevin equation only considering friction and fluctuation forces for a Brownian particle under thermal equilibrium. The addition of non-entropic forces requires that we either solve a more generalized Langevin equation with an additional force term, or that we model increased ‘effective’ friction and/or fluctuation forces [51].

Viscoelasticity

Cells are also not purely viscous (liquid-like), but rather viscoelastic (a combination of liquid- and solid-like properties). Viscoelasticity is defined by how a material deforms under stress. Elastic materials retain memory of their original shape and restore that shape after deformation because they store deformation energy. Viscous materials do not recover after deformation because deformation energy is dissipated. Viscoelastic materials have both properties depending on the time scales of perturbation; they have a ‘frequency-dependent complex modulus’ composed of an elastic (or storage) modulus and a viscous (or loss) modulus. The ratio between viscous and elastic modulus, also called the loss tangent, indicates whether the material behaves as a viscoelastic fluid (loss tangent >1) or viscoelastic solid (loss tangent <1). Ketchup is a viscoelastic liquid. When the bottle is first inverted, this sauce can be annoyingly solid-like, but with patience it will flow. ‘Silly putty’, is a viscoelastic solid – it can flow very slowly, but will bounce if thrown, or snap if yanked.

The cytoskeleton is a major elastic component in the cytoplasm, and different filament types and networks can confer different viscoelastic properties to the cell. Many cytoskeletal filaments are semiflexible polymers and display a shear-thickening response that causes them to behave as a solid when they experience a large shear force, which may help cells to resist sudden mechanical impacts [57].

Complex combinations of material changes can occur to facilitate certain cell biological processes. Reorganization of the cytoskeletal network can fluidize the cell interior while stiffening the cortex during metaphase [58]. A volume increase concomitantly occurs [59–61], increasing cytosolic particle mobility. Together, these changes are likely to help cells exert forces on confining tissues to enable a more spherical shape, while simultaneously making it easier to move particles and organelles during cell division.

Changes in cellular metabolic state can also promote transitions between viscoelastic fluid and viscoelastic solid states. For example, when ATP is depleted from yeast cells, the cytoplasm changes from a more fluid-like to a more solid-like material state at the mesoscale [45,46]. On the other hand, budding yeast has been found to maintain invariant microviscosity under large ranges of temperature or energy through the phenomenon of ‘viscoadaptation’ [62], by tuning synthesis of the small molecules glycogen and trehalose.

The Stokes–Einstein equation can be generalized and modified to describe viscoelastic systems by replacing the viscosity parameter by a frequency-dependent complex viscoelastic modulus [63–66]. The non-linear size effects mentioned previously can also be accounted for by looking at correlations between the motion of pairs of tracer particles (see later) [67].

How do we measure local biophysical properties inside the cell?

The study of viscoelastic materials is called ‘rheology’, from the Greek ‘rheos’, to flow or stream. Conventional rheology analyzes how external forces deform materials. Various techniques can be used to perturb or deform cells or tissues, including atomic force microscopy (AFM), optical or magnetic tweezers, and pipette suction [68]. Applying oscillatory forces at varying frequency can define the complex viscoelastic modulus. More recently, optogenetic tools have been developed to locally perturb the cell interior. For example, local light-induced RhoA promotes the recruitment of actin and myosin, leading to the local production of forces that then rapidly propagate across the cell [69]. However, these techniques average out heterogeneities and are often difficult at the nano- and mesoscales.

Particle-tracking microrheology (from now on, microrheology) was developed to overcome these limitations [63]. This approach is based on the observation of the motion of tracer particles embedded within materials (Figure 3). Microrheology enables higher throughput characterization of cell properties in complex extracellular environments, such as 3D matrices, and even in live animals (e.g., in the Caenorhabditis elegans embryo [70]). Microrheology has proven to be extremely useful for biological systems and can probe local, subcellular properties. Microrheology can be subdivided into approaches in which the system is either actively perturbed, or passively observed.

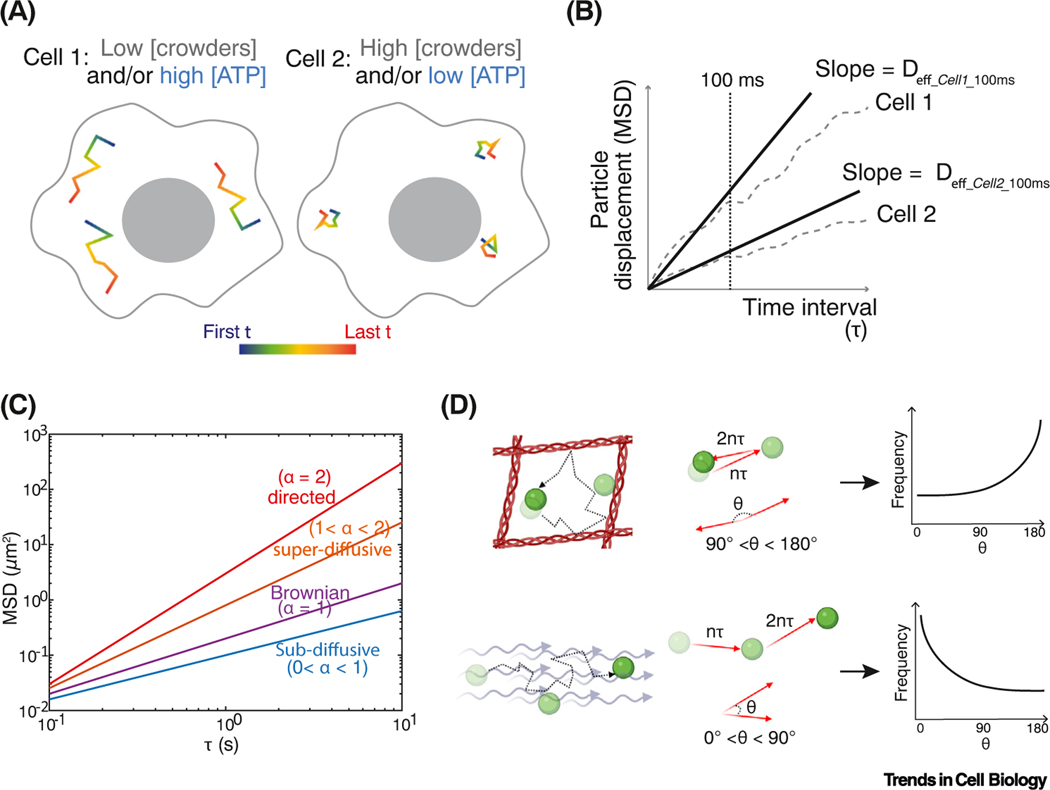
Figure 3. Particle-tracking microrheology and one-point rheology analysis.

(A) Hypothetical trajectories of tracer particles in different intracellular environments. Motion is decreased by high crowding, and increased by ATP-driven agitation. (B) Ensemble and time-averaged mean-squared displacement (MSD) plots of these hypothetical cells. Effective diffusion coefficients (D_eff) are calculated from the slope of MSD as a function of time interval (τ). The cell is crowded, heterogeneous, and structured, giving different effective diffusion coefficients at different time scales. We therefore define an effective diffusion coefficient at a specific time scale, for example, effective diffusivity at 100 ms = D_{eff_100ms}. D_{eff_100ms} is higher for particles in cell 1 than in cell 2. Note: the choice of time scales (broken line) that can be investigated is dependent on the distribution of trajectory lengths that can be experimentally obtained. If the time scale chosen is much longer than the median track length, analysis will be biased to slow-moving particles, which can be misleading. (C) MSD is calculated at each time lag τ from an ensemble of particle trajectories after both time and ensemble averaging. Here, MSD is plotted on a log–log scale where the slope (exponent α) indicates different types of motion. (D) Next step angle bias of particles moving in a confined local region (top) or moving persistently in an active flow (bottom). Next step angle frequency distributions are plotted to the right.

Tracer particles for mesoscale microrheology

Both endogenous and exogenous particles have been used as microrheology probes in vivo [68,71]. Endogenous probes include lipid droplets [72], tagged DNA foci [44,73–76], RNAs and ribonucleoproteins [44,46,73,77], histones and chromatin structures [47], condensates [44,78], and organelles [79]. The advantage of using endogenous probes is that their presence does not perturb the cellular environment. However, it is difficult to control the probe’s size, and there may be significant and regulated interactions with cellular components, making it difficult to interpret the significance of changes in their motion.

The use of exogenous particles overcomes some of these issues, limiting regulated molecular interactions, and allowing precise control of particle size. Synthetic particles include quantum dots [80] and microspheres [81]. However, delivery of exogenous particles into the cell (e.g., microinjection, pinocytosis) can be challenging. Crucially, it is very difficult to introduce exogenous particles into organisms with a cell wall, such as plants, fungi, and bacteria.

New approaches have overcome these limitations making microrheology a more accessible and high-throughput technique. Genetically encoded multimeric nanoparticles (GEMs) are based on scaffold proteins that naturally assemble to form stable protein complexes of a defined shape and size. Fusing the scaffold to fluorescent proteins creates bright tracer particles [23]. Introduction of the gene encoding GEMs creates cells that constantly produce nanoparticles and can therefore be easily analyzed by microrheology. Different scaffolds can yield different sized mesoscale probes. The large number of fluorescent proteins in the multimeric assembly makes these particles bright and reduces photobleaching, allowing rapid imaging rates. Many particles can be tracked simultaneously allowing comparison of different cellular regions. GEMs can also be targeted to different subcellular compartments such as the nucleus [82] and endoplasmic reticulum (ER) [83], enabling comparison of the properties of these different organelles.

Advances in microscopy will increase the power of microrheology approaches. Currently, it is technically difficult to obtain 3D data at millisecond time scales using standard microscope configurations; therefore, track lengths are limited by particles going out of focus in 2D imaging. However, new optical methods such as high-speed, oblique plane light-sheet imaging are beginning to address this problem [84]. These innovations will increase the range of length and time scales available for analysis, opening a deeper understanding of the physical properties of the cell.

Analysis methods for microrheology

The traces of particle motion obtained through passive microrheology can be analyzed in various ways to infer biophysical properties of cells. One-point microrheology calculates the mean-squared displacement (MSD) of each particle trajectory as a function of time lag (τ ) (Figure 3C). For simple Brownian motion, this relationship is linear, and the slope is the diffusion coefficient (D). However, the MSD to tau relationship is not linear in the intracellular environment, but is better approximated with a power law where the particle displacement is proportional to τ^α, where τ represents the time lag and α is the ‘anomalous exponent’. The value of the anomalous exponent, α, describes how the diffusion of particles deviates from Brownian motion: α <1 (subdiffusion) could indicate that particles are subject to enthalpic interactions, that they are within a crowded or confined environment, and/or that they are confined within a viscoelastic material [23,85–87]; α >1 (superdiffusion) indicates that a particle is undergoing directed active transport, such as motor-directed motion, or movement within hydrodynamic flows [79,86].

In addition to MSD, information can be inferred from biases in the angles from one step to the next over a certain time τ [88,89]. We will call this the ‘next step angle’. For Brownian motion, the average of all next step angles is zero; in random motion, there is no directional preference. However, if a particle has persistent motion, for example, directed by molecular motors or driven by intracellular flow, there will be a bias toward next step angles smaller than 90° (Figure 3D). Conversely, if a particle is caged or confined, it will tend to reflect backward, and there will be a greater probability of next step angles closer to 180°. Thus, from the probability distribution of next step angles, we can detect active, directed motion, and confinement. These biases can change at different time scales. For example, particles tend to continue in the same direction at very short time intervals, biasing the distribution to more directed angles [89]. Therefore, it is good practice to compare the next step angle distributions over a range of time lags.

One-point microrheology probes the local environment of tracer particles, analyzing each particle on its own. ‘Two-point microrheology’– analysis of the correlated motion of two particles – is a complementary approach that can reveal non-thermal forces at various length scales, detect local flows, and quantify the amplitude and frequency dependence of non-Brownian stress fluctuations [67,79,90]. A detailed description of this approach would not fit here, but we refer the reader to reviews [90,91].

Biological insights from microrheology

Viscoelasticity

Microrheology has provided important insights into ‘how it feels’ in a cell at the mesoscale. The field has a long history. Starting in the 1950s, Crick and Hughes used active microrheology with micron scale magnetic particles to show that fibroblasts were both viscous and elastic [92]. Hiramoto then discovered that these properties were not constant in time: magnetic bead microrheology probes revealed that the urchin egg cytoplasm was viscoelastic, but that these properties changed during the first mitotic division [93]. This cytoplasmic elasticity helps to organize the cell, for example, restoring the mitotic spindle to its original position if displaced [94,95].

Elastic cytoplasmic behavior changes during cellular differentiation. Microrheology with 1 μm beads showed that terminally differentiated human fibroblasts are viscoelastic, but these cells lost their elastic behavior when they were converted to induced pluripotent stem cells. Likewise, human embryonic stem cells (hESCs) [96] and C. elegans embryonic cells [70] have limited elastic behavior. Mesoscale material properties help determine the mechanical properties of cells. Mechanical cues are critical for cell differentiation [97]. It is possible that low cytoplasmic elasticity could help stem cells sense mechanical forces [98]. On the other hand, increased elasticity (and viscosity) could make cells more mechanically robust. Microrheology using 100 nm particles showed that the cytoplasm of mouse fibroblasts became 25 times more viscous, and four times more elastic when subjected to shear stress [99]. Therefore, elasticity is a crucial parameter that can be tuned to make cells more resistant or compliant to mechanical deformation.

Spatial heterogeneity

The subcellular resolution enabled by microrheology has revealed significant spatial variations in viscoelasticity within cells. The viscoelasticity of the urchin embryo is higher near the nucleus and lower at the cell periphery [93]. Mesoscale microrheology using GEMs revealed significant spatial heterogeneity in cytoplasmic physical properties in the multinucleated fungus Ashbya gossypii with higher crowding around nuclei hyphal tips. This higher crowding may potentiate biomolecular condensate formation in these areas [100]. Microrheology with GEMs also revealed physical heterogeneities both within single cells, and between cells in Schizosaccharomyces pombe yeast cells [82,101]. The causes and consequences of these heterogeneities are largely unknown, but could point to organization of cells at the mesoscale that is more fine-grained than organization by membranes. This is an exciting possibility given the increasing interest in biomolecular condensates and gathering evidence that this dynamic mesoscale structure of the cell is crucial for life.

Subcellular organization

It is now clear that the cell is not a simple, well-mixed colloid, and organization can give useful emergent properties. When Xenopus egg extracts were homogenized to abolish subcellular organization, diffusivity was found to increase as the cytoplasm recovered organization, especially at the mesoscale [102]. This implies that cytoplasmic organization decreases the number of obstacles at the mesoscale.

The nucleus is highly organized at multiple length scales [103] allowing separation of function within the genome. Densely packed heterochromatin is less transcriptionally active but provides mechanical stability by conferring elasticity [104,105]; while more transcriptionally active euchromatin has a more open structure, perhaps allowing more rapid exploration by regulatory factors. Further organization occurs by phase separation of nuclear subcompartments, including the nucleolus [19]. At the mesoscale, GEM nanoparticles targeted to the nucleoplasm (nucGEMs [82]) are constrained to the euchromatic space and are physically excluded from heterochromatin and the nucleolus. Furthermore, mitotic heterochromatin prevents invasion of mesoscale particles from the cytoplasm into the nucleoplasm when the nuclear envelope breaks down at mitosis [106]. Thus, physical restriction of diffusion is likely crucial for both epigenetic control of gene expression, and for maintaining cellular organization.

How does the extracellular environment affect particle motion and assembly?

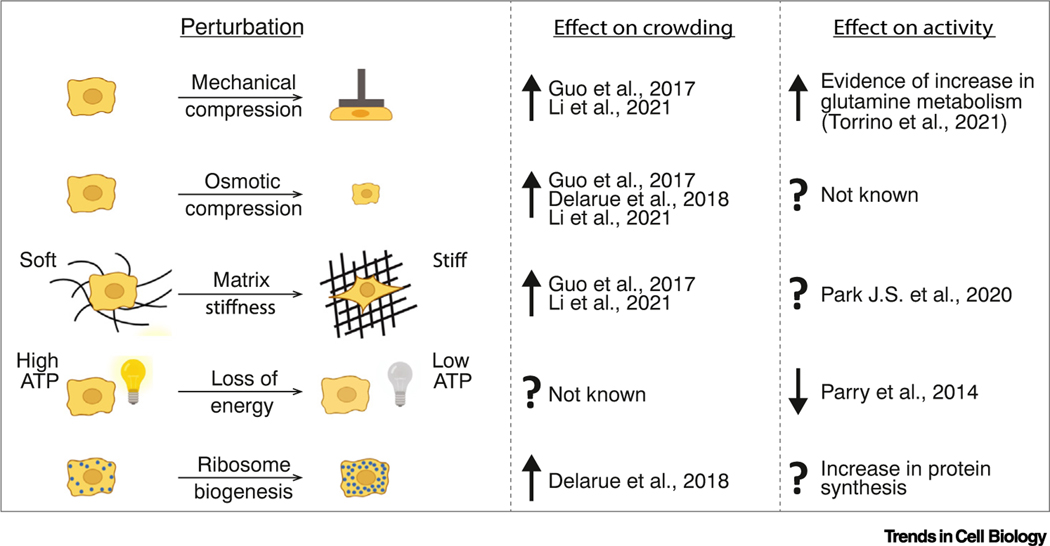
The mesoscale properties of cells are strongly dependent on the environment within which they reside. Cell compression, induced by either mechanical or osmotic force, triggers water efflux, leading to increased molecular crowding and decreased molecular diffusivity (Figure 4) [107]. Cell volume changes also occur in response to substrate stiffness changes [107,108]. Efflux of water occurs in conditions of high substrate stiffness while water influx swells cells on soft substrates. Cell spreading, shear stress, and tensile stress can also result in cell volume decrease [107]. Thus, osmotic and mechanical perturbations cause cells to shrink or swell; these volume changes in turn impact intracellular crowding.

Figure 4. Perturbations that impact crowding and activity.

Examples of how the extracellular environment and the cell state can influence molecular crowding and intracellular non-thermal energy, with references. See [23,44,107,109,126,133].

The molecular consequences of osmotic and mechanically induced crowding changes are myriad, and just beginning to be appreciated. Alteration of crowding in response to different substrate stiffness may influence stem cell differentiation [107]. Increased crowding, in response to stretching, and mechanical and osmotic compression can activate pro-survival Wnt target genes even in the absence of Wnt [109]. Similarly, osmotic pressure triggers phase separation and condensation of the YAP transcription factor leading to changes in genome organization and transcription [110]. Crowding can drive increased kinase activity within synthetic condensates, and Alzheimer’s disease-associated hyperphosphorylation of tau is accelerated by crowding-induced phase separation of this protein [111]. The crucial cell volume regulator, with-no-lysine kinase 1 (WNK1) rapidly forms condensates in response to increased crowding upon hypertonic stress, leading to increased kinase activity and resulting in cell volume recovery [112]. In confined spaces, external pressure stalls volume increase but macromolecules continue to be produced leading to increased crowding and ultimately stalling cell growth [113]. More and more evidence connects mechanical perturbations to cellular signaling networks via changes in the biophysical properties of the cell interior. However, the details of how the intracellular physical environment is sensed remain largely obscure at the molecular scale (see Outstanding questions).

Outstanding questions.

Molecular crowding and non-thermal activity impact molecular motion and assembly. What cellular processes are particularly sensitive to these biophysical factors? Are changes in biophysical properties used to regulate cells?

WNK kinases have been shown to be key sensors of molecular crowding. Do other crowding sensors exist? And are there specific sensors for different cell types or different subcellular compartments?

What are the dominant molecular mechanisms that determine the viscoelastic properties and non-thermal activity of cells at the mesoscale?

How do these properties and mechanisms differ in distinct biological compartments (e.g., in the nucleus, cytoplasm, ER, mitochondria)?

How do intracellular physical properties change in the context of tissues? Do mechanical forces in tissues affect crowding, and if so, does this instruct cell differentiation?

How do stiff, compressive, cancerous tissues impact intracellular crowding and activity?

How does the increased cranial pressure, tissue stiffening, and edema associated with neurodegeneration impact intracellular crowding and activity?

Could changes in intracellular physical properties contribute to aging, cancer, and neurodegeneration?

If physical perturbations are a key part of aging and disease etiology, how could we prevent or reverse these effects?

External nutrient availability and cell–cell signaling can also impact crowding. Inhibition of the growth-regulator target of rapamycin complex 1 (TORC1) pathway leads to decreased ribosomal biogenesis, increased ribosomal degradation through autophagy, and a consequent reduction in cytoplasmic crowding. This decreased crowding increases mesoscale motion, but reduces assembly of a synthetic protein into condensates [23]. Nutrient scarcity is also a key determinant of cytoplasmic fluidity by regulating cellular volume and activity. When budding yeast are starved for glucose, the cytoplasm is initially fluidized [114], but at longer times, cell volume decreases, leading to increased crowding and a glassy cytosol [46]. Starvation also affects cellular activity, leading to decreased molecular motion [44]. Again, the downstream molecular consequences and physiological relevance of these changes are still mostly unknown.

Biophysical perturbations in disease

Many molecular complexes are tuned to dynamically assemble and disassemble. Crowding favors assembly through depletion attraction. Therefore, if the cell becomes too dilute, molecular assembly can be decreased, leading to loss of biochemical function. Indeed, rapid volume swelling can halt mitochondrial enzymatic reactions [115] and cytoplasmic dilution without DNA replication can lead to cellular senescence [116]. Aging is positively correlated with cellular senescence; therefore, understanding how cytoplasmic crowding is regulated might help counteract aging-related diseases.

Conversely, molecular condensation is favored when crowding increases. In extreme stress conditions, excess molecular crowding can reduce the solubility of macromolecules [117]. Aged neural tissues are characterized by malfunction of degradation pathways (e.g., autophagy and proteasome activity) [118]. As a consequence, protein solubility decreases causing an accumulation of insoluble proteins. Aged tissue also has increased extracellular matrix stiffness [119–121] and osmotic and mechanical pressure caused by edema [122]. These physical perturbations can lead to increased crowding in neural cells, which may in turn induce aberrant condensation and protein aggregation [123,124], or tau phosphorylation [111]. Mechanical properties are also highly perturbed in cancer; fibrosis stiffens tumors and confined growth generates compressive stress [125]. The biophysical consequences of these mechanical perturbations are largely unknown. Investigating these phenomena could greatly advance our understanding of both cancer and neurodegeneration.

Concluding remarks

The physical and material properties of the cell interior are a crucial, often overlooked factor in biology. Macromolecular crowding both hinders diffusion and enhances interactions and can profoundly alter biochemical reactions, especially at the mesoscale. Nonequilibrium ‘active matter’ can increase motion and helps prevent glassy states. Advances in techniques like microrheology are beginning to elucidate the general consequences of crowding and active matter for mesoscale molecular biology. However, current techniques still fail to connect length and timescales from nanometers/microseconds to microns/seconds. Improved imaging techniques and new analysis methods will address this deficiency and are likely to better explain nonequilibrium behavior and fractal structures in cells. To understand life, it will be essential to deeply characterize the complex intracellular environment, the reaction crucible within which all biochemistry occurs.

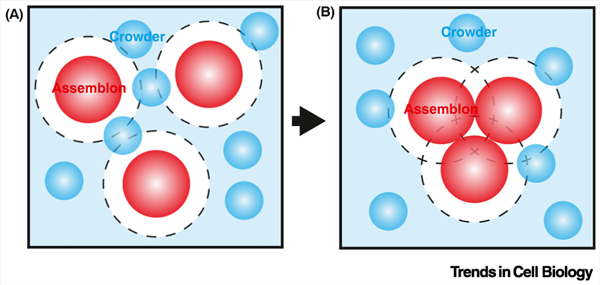
Figure I. Illustration for depletion-attraction force.

(A) Due to steric constraints, crowders (cyan color) cannot access regions (black broken line) around the assemblons (red color). (B) When assemblons cluster, the extra space available to crowders (cyan color) increases the overall entropy of the system. The system tends toward maximum entropy; therefore, crowders favor assembly. This is called the depletion-attraction force.

Highlights.

The cell interior is a highly crowded ‘active material’: ATP-consuming, non-equilibrium activities help fluidize the cell interior. Without metabolic energy, the crowded environment can become ‘glassy’ or solid like.

Molecular crowding reduces particle diffusion, especially at the ‘mesoscale’ (10–1000 nm diameter) but can increase molecular assembly through ‘depletion attraction’.

We can probe molecular crowding and the active matter of the cell interior by observing the motion of tracer particles. This is called ‘microrheology’.

Both internal and external factors influence the biophysical properties of the cell interior: for example, decreased target of rapamycin complex 1 (TORC1) signaling reduces crowding, while mechanical compression increases crowding.

Active control of these properties is crucial for normal physiology; we hypothesize that perturbed molecular crowding or decreased non-equilibrium motion could contribute to diseases like cancer and neurodegeneration.

Glossary

ATP

molecules that provide energy in cells

Active matter

materials that can convert chemical energy (e.g., ATP) into kinetic motion

Brownian diffusion

random particle motion due to collective collisions with fast-moving molecules within the medium

Crowding (macromolecular crowding)

the space taken up by macromolecules

Elastic material

solid material that returns to its original shape after deformation

Enthalpy

in biology (at constant volume and pressure), this is the internal energy of a system. The enthalpy change of a reaction determines if it is favorable. For example, when a favorable bond forms, energy is released as heat and enthalpy decreases

Entropy

measurement of disorder in a system. The second law of thermodynamics states that the total entropy of the universe must increase with time. In biology, entropy can locally decrease, creating order, through the input of energy

Excluded volume

the volume that is inaccessible to a particle in a crowded environment

Hard-sphere steric constraints

when particles are modeled as impenetrable and non-interacting spheres, the ‘steric constraint’ is that particles are not allowed to overlap in space

Liquid crystal

material with properties between a liquid and a solid crystal. For example, rod-shaped particles in a liquid can become locally ordered and aligned but still highly dynamic

Macromolecule

molecules with high molecular weights, for example, DNA, RNA, and proteins

Mesoscale

the ‘in-between’ scale. In this essay, between the nanometer and micrometer scales, that is, 10–1000 nm

Microrheology

the inference of the physical properties of a material from the study of the motion of embedded tracer particles

Out-of-equilibrium

systems that consume energy, or are subject to external forces

Viscous material

liquid material that flows and deforms with no ‘elastic memory’

Viscoelastic material

material with a combination of viscous and elastic properties