Abstract
People have a unique ability to represent other people’s internal thoughts and feelings – their mental states. Mental state knowledge has a rich conceptual structure, organized along key dimensions, such as valence. People use this conceptual structure to guide social interactions. How do people acquire their understanding of this structure? Here we investigate an underexplored contributor to this process: observation of mental state dynamics. Mental states – including both emotions and cognitive states – are not static. Rather, the transitions from one state to another are systematic and predictable. Drawing on prior cognitive science, we hypothesize that these transition dynamics may shape the conceptual structure that people learn to apply to mental states. Across nine behavioral experiments (N = 1439), we tested whether the transition probabilities between mental states causally shape people’s conceptual judgements of those states. In each study, we found that observing frequent transitions between mental states caused people to judge them to be conceptually similar. Computational modeling indicated that people translated mental state dynamics into concepts by embedding the states as points within a geometric space. The closer two states are within this space, the greater the likelihood of transitions between them. In three neural network experiments, we trained artificial neural networks to predict real human mental state dynamics. The networks spontaneously learned the same conceptual dimensions that people use to understand mental states. Together these results indicate that mental state dynamics – and the goal of predicting them – shape the structure of mental state concepts.
Keywords: theory of mind, emotion, concepts, prediction, artificial neural network
People have a powerful ability to represent other people’s internal thoughts and feelings – their mental states. Mental state knowledge has a rich conceptual structure (Cowen & Keltner, 2017; Posner et al., 2005; Russell, 1980; Thornton & Tamir, 2020a). This conceptual structure can be largely summarized using a small set of psychological dimensions. For example, the dimension of valence captures how positive or negative a state is, and this structural dimension reflects people’s understanding of those experiences (Russell, 1980). Certain basic dimensions, such as valence, seem to be widely shared across cultures, though the number and importance of dimensions may vary (Jackson et al., 2019; Russell & Lewicka, 1989; Thornton et al., 2022). This raises a fundamental question: where does this shared structure come from?
Here we investigated the informational origins of people’s mental state concepts. It has long been assumed that this conceptual structure reflects solely the static features of mental states, such as the similar facial expressions stereotypically elicited by surprise and fear. However, mental states – including both emotions and cognitive states – are not static. We thus challenge this assumption: we suggest that static features alone cannot explain the structure of mental state representation. Instead, we propose that a complete account of mental state concepts must also consider how people dynamically transition from one thought or feeling to another. We hypothesize that observation of these transition dynamics shapes the structure of people’s mental state concepts.
What is a mental state concept?
The definition of mental state varies considerably in the affective science and social psychological literatures. Our operational definition of “mental state” is an umbrella term that refers to any hidden state that occupies the mind. By hidden, we mean that mental states must be latent, rather than manifest: one can infer that another person is happy, but not directly sense it in the same way that one could observe the motion of a body in the physical state of running. This definition of mental states includes what are often termed affective states: moods, emotions, and feelings. It also includes cognitive states, such as remembering the past, imagining or planning the future, making decisions, reasoning, or performing mental calculations. Specific instances of a mental state often have propositional content. For example, one might be happy “that their friend got a job” or be thinking “about what to have for lunch”; one could also just feel happy. Although the propositional content of mental states is doubtless important to theory of mind (Saxe & Kanwisher, 2003), here we abstract away from this specific content, and instead focus on the more general context-agnostic conceptualizations of mental states.
A static account of mental state concepts
We propose that mental state dynamics play an important role in shaping the conceptual structure of mental states. However, there is another clear, intuitive account: that mental states concepts are defined by “static features.” Under this static account, each state is associated with a different set of features: the racing heart of excitement, the scrunched face of disgust, the social implications of gratitude, and so forth. People use these features to identify what state another person is in. For instance, people use perceptual features, such as facial expressions and tone of voice, to infer others’ emotions (Zaki et al., 2009): a smiling person is likely feeling happy. People also use behavioral and contextual features to infer others’ states (Barrett et al., 2011; Frijda, 2004); a person throwing punches is likely angry, and a person at a rave is likely excited.
When we think about why people hold the mental state concepts that they do, it is easy to look to these static features for an answer. A pair of states with many features in common – such as joy and gratitude – will be considered conceptually similar, while a pair of states with little in common – such as surprise and sleepiness – will be considered conceptually dissimilar. Indeed, there is evidence that people use static features as a basis for understanding mental state concepts. For example, research on the bodily representation of mental states (Nummenmaa et al., 2018) shows that states that people feel in similar parts of the body (e.g., the head, limbs, or gut) are considered more conceptually similar. In addition, Skerry and Saxe (2015) examined contextual features of states (e.g., Who caused them? Are they associated with safety or danger?) and found that these features likewise shape state representations, measured using neural pattern similarity (Skerry & Saxe, 2015).
A static account of mental state concepts is compatible with both a basic emotions perspective or a constructivist perspective on emotions (Adolphs et al., 2019). From a basic emotions perspectives, emotions are evolutionarily determined responses to specific situations, such as feeling fear in the face of danger (Ekman, 1992). As such, emotions concepts are innate and tied to fixed features. However, one could also arrive at somewhat different static account of mental state concepts from a constructivist perspective (Barrett, 2017b). Constructivists generally eschew the notion that certain static features are deterministically associated with specific states (Barrett et al., 2019; Gendron et al., 2014). For example, one does not smile 100% of the time that one is happy. However, more probabilistic and contextual associations between emotions and features are still argued to be the basis for the formation of emotion concepts. For example, a recent perspective on the cultural evolution of emotions suggests that, over the course of development, people learn about the existence of relatively high-density (i.e., frequently occurring) clusters of affective experiences in certain regions of feature space (Lindquist et al., 2022). The number and locations of these clusters are determined flexibly by culture, but within a culture they eventually come to acquire verbal labels. Under this version of the static account, the proximity in feature space between these labeled clusters of affective experience shape our emotion concepts. However, constructivist accounts can also incorporate dynamics, as we discuss later.
By virtue of its compatibility with both basic and constructivist perspectives, the static account of emotion concepts has come to reflect a widespread default assumption among many psychologists. However, we believe that it is worth questioning this implicit orthodoxy and considering whether dynamic influences on mental state concepts have been overlooked. Importantly, these dynamic and static accounts are not mutually exclusive. Both static features and dynamics could contribute to the conceptual structure of mental states. Indeed, we explore potential complementarity between them in this investigation. Nonetheless, this static account serves as a useful foil against which to compare the dynamic account we propose.
The dynamic account of mental state concepts
Despite the evidence supporting a static account of mental state concepts, we suggest that this account cannot provide a complete explanation for people’s structured knowledge of this domain. Mental states are not static. A mental state does not exist as an isolated event, independent of the other states before or after it. Mental states are dynamic. States ebb and flow over time and transition from one to the next with regularity. Indeed, states are defined in part by the sequence of which they are a part. Confidence followed by sadness seems to us to tell a very different story than confidence followed by joy. Understanding someone’s mental states without considering the sequence in which those states arrived would be as difficult as understanding a sentence without knowing the order of the words. We suggest that these dynamics are key to understanding the structure of mental state concepts.
We propose that the conceptual structure of mental states serves an important goal of the social cognitive system: to make social predictions. Mental states are the hidden movers of the social world. They help people predict which actions a person will take (Frijda, 2004; Hudson et al., 2016): angry people aggress, tired people rest, hungry people eat, and happy people laugh. Mental states also predict other mental states. Experience-sampling studies have demonstrated that people transition between emotions in highly systematic ways (Thornton & Tamir, 2017). For example, someone feeling happy is more likely to next feel relaxed rather than agitated. These dynamics are key to understanding the structure of mental state concepts because state dynamics inform inferences about the social future (Tamir & Thornton, 2018).
The information people take in about states is, by its nature, dynamic: people sample others’ states and experience their own states in a serial manner. In other domains of knowledge, data about dynamics shapes associated concepts. For example, high-level neural representations of objects are shaped by how often they co-occur in people’s natural experience, and not just by their visual features (Bonner & Epstein, 2021). Objects that co-occur frequently are represented by similar patterns of brain activity, even if they look quite different from each other. There is a clear analog in the maxim of Hebbian learning: just as neurons that fire together wire together, representations of objects that appear together come to resemble each other. Similar results have been observed for learning abstract events and motor sequences: transitions between stimuli create event boundaries, shape neural pattern similarity, and give rise to abstract representations of event structure (Kahn et al., 2018; Lynn et al., 2020; Schapiro et al., 2013). Complex networks of associations between such stimuli become manifest in how people predict sequences will unfold. We suggest that the dynamics of mental states may likewise shape the conceptual structure we apply to them. By applying this general learning principle to the specific domain of mental state representation, we may gain new insight into the computational goals of human socio-affective systems, and the information they draw upon.
A growing body of literature suggests that the structure of mental state concepts is at least correlated with – though not necessarily caused by – state dynamics. The more likely one state is to precede or follow another, the more conceptually similar people judge them to be (Thornton & Tamir, 2017). That is, conceptual similarity reflects the temporal relation between each state and the other states that are likely to precede or follow it. This association between transition probability and similarity ratings is whopping: in previous research, we estimated a Spearman rank order correlation of ρ = 0.97 across a sample of hundreds of state pairs (Thornton & Tamir, 2017). This association is high enough that some might consider them the same construct!
How might we account for this close association between mental state transitions and mental state concepts? There are three simple possibilities. First, people may not know the actual transition probabilities between mental states. When asked to judge how likely a state is to follow another, they might instead report their similarity. However, this explanation is inconsistent with existing data showing that people can report emotion transition likelihoods with high accuracy (Thornton & Tamir, 2017). Similarity and experienced transition dynamics seem unlikely to share the same structure by coincidence.
Second, common causes may shape both the transition dynamics and conceptual similarity. For example, heart rate is a key indicator of arousal, an important conceptual dimension of affect (Russell, 1980). Human physiology also constrains how quickly one’s heart rate can change (Borst et al., 1982). This may make it more likely that a person will transition from a high arousal state to another high arousal state than from a high arousal state to a low arousal state. High arousal states thus would have high transition probabilities and high static featural similarity. In this way, the nature of the circulatory system may be a common cause of both static and dynamic features of mental states. If common causes shape both the static and dynamic features of mental states, this would lead to both correlations between these different types of features, and two discrete, albeit correlated, pathways for shaping state concepts. The current work tests whether such common causes are necessary for explaining the correspondence between dynamics and concepts.
The final possible explanation of the correlation between mental state dynamics and concepts is that dynamics causally shape concepts. This point of view is supported by prior neuroimaging research on this topic. In a functional magnetic resonance imaging (fMRI) study of mental state representation, we found that neural representations of mental states systematically resemble the neural representation of likely future states (Thornton, Weaverdyck, et al., 2019). That is, merely thinking of a state like anger reflexively elicits neural activity associated with likely subsequent states, like regret. This relation cannot be explained solely by conceptual similarity because asymmetries in transition probabilities (e.g., tiredness following excitement more than vice versa) were uniquely associated with asymmetric neural representations. That is, the brain spontaneously encodes mental state dynamics over and above any shared variance with conceptual similarity. This result suggests that prediction is the brain’s priority, and that we form concepts as a downstream product of optimizing our representations for mental state prediction.
The conceptual structure of mental states
If mental state dynamics do shape mental state concepts, how are the former translated into the latter? The brain tends to seek out representations of the world that are not only accurate but also efficient (Olshausen & Field, 1996). Representing the transition probability between every pair of mental states might maximize accuracy, but it would be a highly inefficient route to capture mental states dynamics (i.e., due to the size of the transition probability matrix in question). Instead, a geometric representation offers a more parsimonious route: a mind that represents mental states as points within a geometric space, such that transitions are more likely between closer states, has access to a highly efficient representation of state dynamics using just a few conceptual dimensions. Geometric similarity spaces have a long history in psychology (Shepard, 1987), closely tied to need to learn and generalize efficiently. Thus, this proposition represents a logical application of a general cognitive principle to the specific case of mental states.
There is also empirical evidence that the brain employs a geometric approach to represent real-world mental state concepts. A variety of different geometric models have been proposed and tested in this domain. For example, the Circumplex Model (Posner et al., 2005; Russell, 1980), suggests that emotion concepts are organized by two psychological dimensions: valence (pleasant unpleasant) and intensity (high vs. low arousal). More recently, the 3d Mind Model suggests that mental states – inclusive of both affective and cognitive states – are organized by three psychological dimensions (Tamir et al., 2016; Thornton et al., 2022; Thornton & Tamir, 2020a): rationality (vs. emotionality), social impact (the extent to which a state affects other people), and valence (positive vs. negative). The 3d Mind Model also offers a good description of the conceptual structure of mental states, while also predicting their dynamics by encoding transition probability in terms of distance along its dimensions (Thornton, Weaverdyck, et al., 2019; Thornton & Tamir, 2017). These theories offer further grounding for the proposition that people translate the transition dynamics of real-world mental states into a low-dimensional geometric space.
The present investigation
The present investigation had three main goals. First, we tested whether mental state dynamics shape mental state concepts. In nine behavioral studies, participants first observed transitions between mental states, and then judged their conceptual similarity. We expected that states with higher transition probabilities between them would be rated as more conceptually similar. Studies 1a-f introduced participants to state transitions, using novel states with no meaningful static features. This design allowed us to test if state dynamics can play any role in state concepts. In Study 1g, participants observed both reliable state transitions and an orthogonal static feature, allowing us to test if dynamics can play any role in shaping concepts even when competing with a salient static feature.
Second, we sought to understand the mechanism by which people translate mental state dynamics into concepts. We expected that participants would efficiently represent transition probabilities using a low-dimensional geometric state-space. Within this space, closer mental states should be more likely to precede or follow one another in time, and in turn, be judged to be more conceptually similar. Study 1f tested this hypothesis using mental state transitions structured around an easily interpretable geometric structure. In this context, the geometric account made predictions that were clearly distinguished from alternative accounts.
Third, in Study 2a-b, we generalized the findings from Study 1 to a scenario that more closely matches mental state inferences in everyday life. Here, participants had to infer latent states from static features rather than directly observe them, and in which the latent states traversed a continuous rather than discrete state. This allowed us to test the effects of dynamics on mental state concepts in a more naturalistic context.
Finally, in Study 3, we sought to test if real-world mental state dynamics can explain real-world mental state concepts. To this end, we trained artificial neural networks on realistic sequences of mental states. The network was trained specifically with the goal of prediction. The networks used a compressed representation of the current state to predict the next state in a sequence. After training, we compared the representations that the networks had learned to known conceptual dimensions of mental state representation from both the Circumplex and 3d Mind Model. If the artificial neural network spontaneously learned a similar structure, this would indicate that human mental state dynamics – and the goal of predicting them – suffice to explain the real-world structure of mental state concepts.
Study 1
Across Studies 1a-g, we tested the hypothesis that people learn mental state concepts by observing state dynamics. We manipulated mental state dynamics – in the form of transition probabilities – and then tested for corresponding effects on the conceptual structure of those states. These experiments used variations of the same task (Figure 1). Participants played the role of xenopsychologists on a mission to understand the emotions of an alien creature. They first observed the creature experience novel emotions in a sequential learning task, and then rated the conceptual similarity between the emotions. We controlled the statistical regularities of the state sequences they observed, and predicted that it would shape their subsequent conceptual judgements.
Figure 1. Task schematic for Studies 1a-g.
In Part 1, participants viewed a sequence of 50–100 states drawn from a specified transition probability matrix. They were probed during this training phase to predict the next state in the sequence or recall the previous state. In Part 2, participants rated the conceptual similarity between each pair of states.
Studies 1f and 1g also examined the mechanism and robustness of the observed effects, respectively. Study 1f compared several accounts of how dynamics might translate into concepts: (i) a naïve account, in which conceptual similarity perfectly mirrors transition probabilities; (ii) a successor representation account (Dayan, 1993; Momennejad et al., 2017), in which concepts reflect not only the next likely state, but also a weighted combination of more distant future states; and (iii) a geometric account, in which transitions probabilities are encoded by the proximity between states within a low-dimensional space. Study 1g tested whether dynamics would still shape concepts even when they had competition from static features. We paired each alien emotion with a different eye color, creating a different static feature along which people could potentially judge the similarity between these states. We then tested whether the transition dynamics predicted concepts even with such a salient alternative available.
Methods
Overview.
Across all seven experiments in Study 1, participants observed sequence of the mental states of an alien creature. We manipulated the transition probabilities between the alien’s mental states, such that certain states were more or less likely to precede or follow each other. After observing the alien’s states, participants rated the similarities the alien’s states. Our primary prediction in all studies was that transition probabilities would causally shape conceptual similarity, such that states with higher transitions between them would be judged as more similar. The main substantive difference between the different variants of the experimental paradigm across Studies 1a-g was the structure of the transition probability matrices that generated the state sequences that participants observed. These different structures allowed us to ensure the generalizability of our findings, and to test different mechanisms by which transition dynamics might be translated into concepts. The latter was the particular focus of Study 1f, which sought to distinguish between several different computational accounts of this process. Additionally, in Study 1g, we introduced a static feature – eye color – to accompany each alien state. This allowed us to determine whether dynamics would still influence concepts in the presence of a clear alternative.
Transparency and openness.
Of the seven experiments in Study 1, six (b-g) were preregistered on the Open Science Framework (https://osf.io/4m9kw/). Deviations from our preregistered plans are detailed where applicable. For all studies, we report how we determined sample size, all data exclusions, all manipulations, and all measures. All statistical tests were two-tailed. All data and code from this investigation are freely available (Thornton, Vyas, et al., 2019) on the Open Science Framework (https://osf.io/4m9kw/).
Participants.
We recruited a total of 1,012 participants across Studies 1a-g. Eleven participants were excluded due to unanticipated issues with data recording and demographics (see Supplemental Material), leaving 1,001 for analysis. Table 1 reports the distribution of these participants across studies, gender, and age. See Supplementary Materials for additional demographic information. All participants were recruited from Amazon Mechanical Turk using TurkPrime (Litman et al., 2017), with study availability limited to workers from the USA with 95%+ positive feedback. Within Studies 1a-c and separately within Studies 1d-g, participants who had taken part in one of the earlier experiments in a set were excluded. Participants in Studies 1a-c were not prohibited from participating in Studies 1d-g due to the significant time gap between these sets of studies (5+ months) and the different stimuli used. Participants in all studies provided informed consent in a manner approved by Princeton University Institutional Review Board.
Table 1.
Participants breakdown for Studies 1a-g.
| Study | N | Gender | Age | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Women | Men | Other | Not stated | Mean | SD | Minimum | Maximum | ||
| 1a | 20 | 8 | 11 | 1 | 0 | 33.55 | 10.48 | 22 | 55 |
| 1b | 42 | 18 | 24 | 0 | 0 | 36.00 | 10.36 | 21 | 60 |
| 1c | 92 | 34 | 57 | 1 | 0 | 34.32 | 8.94 | 19 | 62 |
| 1d | 213 | 69 | 143 | 0 | 1 | 34.45 | 10.01 | 19 | 73 |
| 1e | 212 | 98 | 112 | 2 | 0 | 35.13 | 10.03 | 20 | 72 |
| 1f | 213 | 86 | 125 | 1 | 1 | 35.30 | 10.69 | 20 | 72 |
| 1g | 209 | 73 | 134 | 1 | 1 | 36.35 | 9.86 | 21 | 70 |
Study 1a was an initial pilot study, and the target sample size was arbitrarily set to 20. The results from Study 1a informed a parametric power analysis which we used to determine the target sample size for Study 1b. We estimated the effect size (Cohen’s d) for this power analysis by correlating transition probabilities and similarity ratings within each participant, Fisher z-transforming them, and dividing the mean by the standard deviation. The power analysis – conducted using the one-sample t-test function from the ‘pwr’ package (Champely et al., 2018) in R (R Core Team, 2015) – targeted 95% power with α = .05. This process was repeated using Study 1b results to estimate sample size for Study 1c, and Study 1c results to estimate the sample size for Study 1d. We retained the target sample size based on the Study 1c data (n = 212) for Studies 1d-g, as similar power analyses based on later studies indicated that this sample size was more than adequate to achieve the desired power. Over the course of Studies 1a-d, we also increased the length of the learning phase of the paradigm and the size of the manipulation in order to improve statistical power (details below).
Experimental Paradigm.
Participants were forwarded from TurkPrime to a custom Javascript-based experiment. After consenting to participate, they were introduced to the study narrative: participants read that they would play the role of a xenopsychologist on an expedition to explore a new world. An advance team had already landed on the planet and identified an interesting alien creature (pictured in the instructions) which they believed to be capable of several different mental states. Participants were instructed that their mission as a xenopsychologist was to understand the alien creature’s mental states so that the expedition could be continued in a manner which was safe – and ideally, beneficial – for both the explorers and the aliens.
The advance team did not yet understand the aliens’ mental states but had labeled them for ease of reference: parpak, bembit, tentum, niznel, fowfas, and gepgin. These labels were 2-syllable nonsense words that we generated to be pronounceable but meaningless. The set listed above was used for Studies 1a-c. We switched the syllables across words to produce a new set for Studies 1d-f. This was repeated to produce another new set for Study 1g.
In Part 1 of the experiment, participants learned about the alien’s states by observing them over time. This observation period constituted the training portion of our experiment (Figure 1). During the training period, participants observed a sequence of 50 (Study 1a) or 100 (Studies 1b-g) mental states. Participants could advance through the sequence at their own pace. The sequence would periodically be interrupted by a probe trial. In Studies 1a-b, the probe trials asked participants to indicate which of the six possible states was least likely to come next in the sequence. In Study 1c, the probe trials asked participants which state had occurred just previously (i.e., 1-back). In Study 1d-g, the probe trials asked participants to indicate which of five states (other than the current one) was most likely to come next in the sequence. Probe trials were presented at regular 10-trial intervals in Studies 1a-b and 1d-g. In Study 1c, the probe trials were randomly distributed within each set of 10 trials, subject to the constraint that there could not be two probe trials in a row.
Due to a programming issue in Studies 1a-c, the state shown after each probe trial was shown twice. In Study 1a, there were 5 probe trials, so as a result of this bug, we showed a sequence of 55 states instead of the planned 50 states. In Study 1b, there were 10 probe trials, so we showed a sequence of 110 states instead of the planned 100 states. Finally, in Study 1c, there were 10 probe trials, so we showed a sequence of 100 states instead of the planned 90 states. This error did not adversely affect our analyses because we modeled only the off-diagonal structure of the transition and similarity matrices, and the error only systematically increased the probability of transitions along the diagonal.
The sequences of states presented in each study were independently randomly sampled from 6 × 6 transition probability matrices (Figure 2 & Figure S2). Studies 1a, 1b, and 1g used a two-cluster structure to approximate the actual structure of emotion transitions observed from experience sampling in previous research (Thornton & Tamir, 2017). Transition probabilities were high (22%, 22%, 40% respectively) within cluster, and low (11%, 11%, and 6.67%) across clusters. Study 1c used a three-cluster structure (within cluster probability = 33% vs. across cluster = 8.3%). Study 1d used a ‘ring’ structure in which states could transition clockwise or counterclockwise with high probability (36.4%) but only crossed the “face” of the clock with low probability (9.1%). This was meant to emulate the structure of the circumplex model of affect (Russell, 1980). Study 1e used a complex structure that approximately orthogonalized transition probabilities from transition profile similarity (see Supplemental Material) with the highest probability being 44% and the lowest non-zero probability being 17%. Study 1f used an asymmetric ring structure, where high probability transitions occurred only in the “clockwise” direction (80%) and lower probabilities for all other transitions (5%). This allowed us to examine asymmetric state transitions and disentangle the successor representation and geometric representation of the state dynamics. In Studies 1a-c, “self” transitions (i.e., repetitions of the same state) were allowed. In Studies 1d-g, states could only transition to other states and repetitions were not allowed. We generally used larger differences between high and low transition probabilities as the experiments progressed in order to maximize effect sizes. Note that, in all studies, the nonsense words were assigned to positions on the transition probability matrix randomly for each participant to avoid any confound that might results from the letter in the words.
Figure 2. Mental state transition probabilities predict similarity ratings.
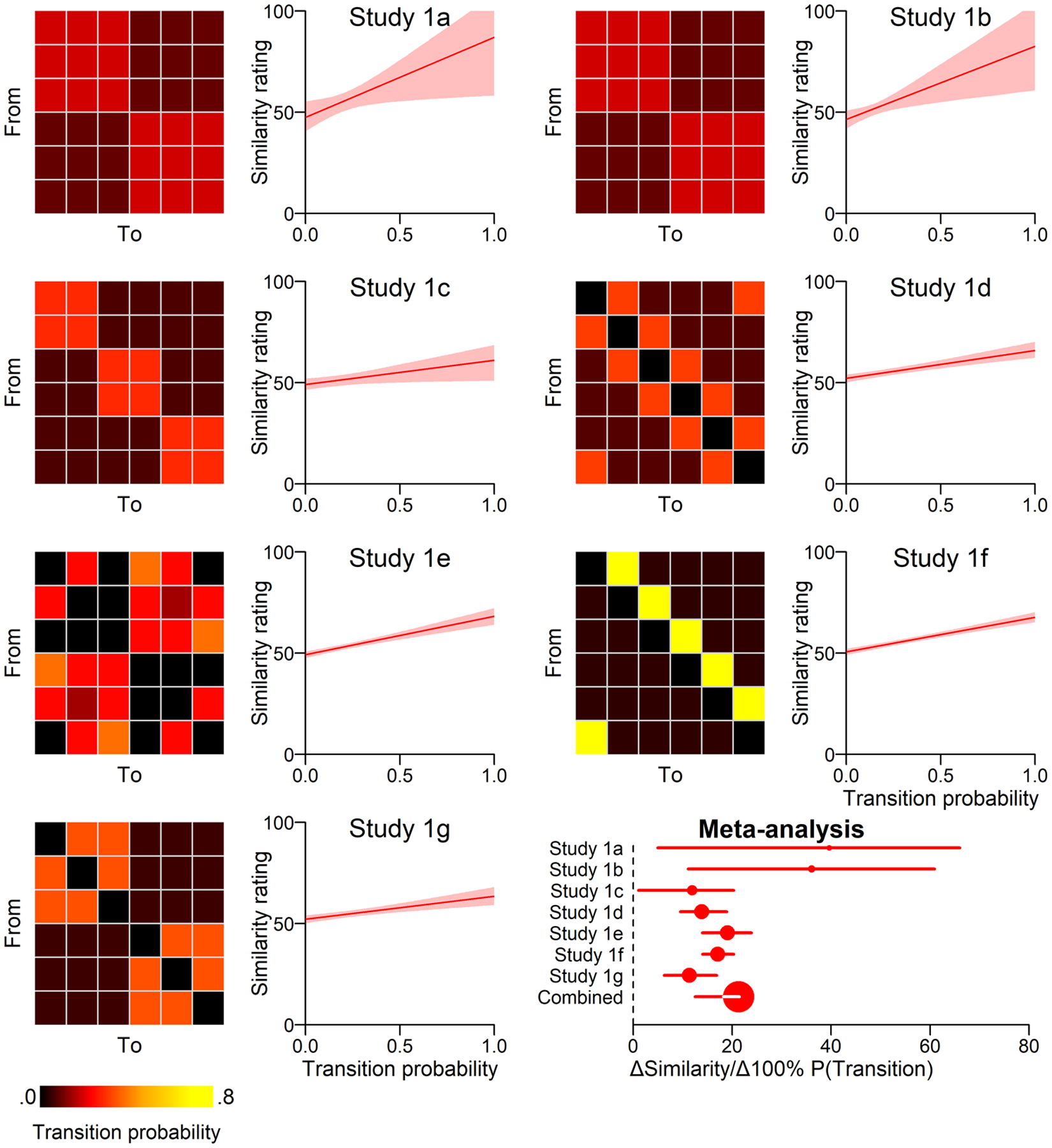
In Studies 1a-g, participants observed a sequence of mental states determined by a predefined transition matrix (heatmaps), and then rated the conceptual similarity between each pair of states. Mental state concepts were significantly predicted by the observed transition probabilities (line graphs) in all studies. Multilevel bootstrapping was used to estimate a meta-analytic effect size and confidence interval (circle radius reflects sample size). The transition probability matrices represent the ideal from which each participant’s sequence was independently sampled; the transitions probabilities each participant observed differed due to random sampling.
Study 1g featured an additional manipulation. Each mental state was paired with an eye color in a drawing of the alien, in addition to the mental state label. The six states fell into two clusters of eye color: reds and blues (Figure 3). We manipulated the shades of reds and blues such that the ratio of within-to-between cluster distance in CIELAB space matched the ratio of within-to-between cluster transition probabilities in the transition probability matrix. The color clusters and the transition clusters contained different sets of states. As a result, the eye color similarity matrix was approximately orthogonal to the transition probability matrix (Figure 3). This allowed us to independently assess the effects of the static feature of eye color and the dynamics of transition probabilities. The eye colors were paired with the state labels throughout training, but not in the subsequent similarity rating phase of the experiment, where participants saw only the labels.
Figure 3. Static and dynamic mental state features jointly shape mental state concepts.
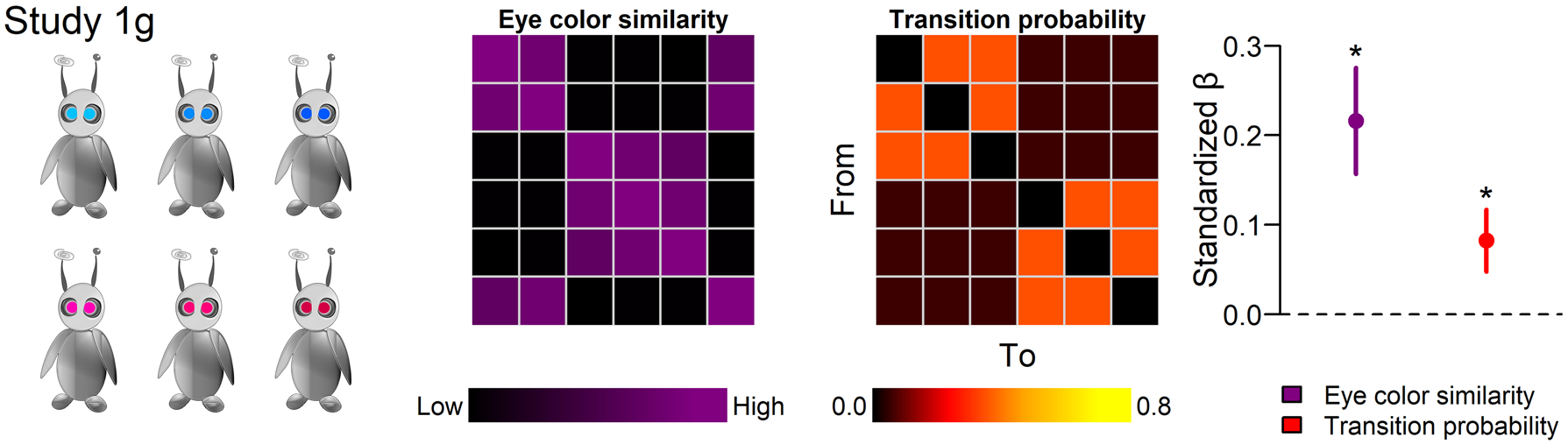
Study 1g manipulated a static feature of mental states (associated eye color) independently of transition dynamics. Heatmaps visualize the competing predictions about state similarity made by eye color and transition probabilities. Both eye color and transition probabilities were statistically significant predictors of similarity judgements, as indicated by standardized betas with confidence intervals in the dot plot.
In Part 2 of the study, after the training phase, participants rated the similarity between pairs of states using a continuous line scale (Figure 1). With six states, there were 15 unique pairs for participants to rate – in random order – in Studies 1a-b. Starting in Study 1c, participants rated both “directions” of similarity (e.g., “How similar is state A to state B?” and “How similar is state B to state A?”) in two blocks, with randomized order within each. This increased the amount of data available for analysis and allowed us to study asymmetric transitions. We never asked participants to rate how similar a state was to itself. Following the similarity rating task, participants reported their demographics and were debriefed.
Statistical analysis.
Effect of dynamics on conceptual structure.
The primary hypothesis examined across all studies was that mental state dynamics causally shape the structure of mental state concepts. To test this hypothesis, we implemented linear mixed effects models that predicted judgements of the conceptual similarity between states, which participants provided, with the transition probabilities between those states, which we manipulated. We computed the transition probabilities that each participant observed and used these as the independent variable in our mixed effects model. Diagonal components of the transition probability matrix, which represent a state recurring after an instance of the same state, were excluded from the model.
In addition to the fixed effect of transition probability, we included a random intercept for subject, and a random slope for transition probability within subject. Study 1 included random effects to account for the nonsense words used to label each mental state. These effects included random intercepts for each of the two states being compared and for the interaction between them. However, we observed that these item effects accounted for zero variance, so they were dropped in subsequent studies.
We ran these linear mixed effects models with the “lme4” package (Bates et al., 2015) in R (R Core Team, 2015). Statistical significance was computed using the Satterthwaite approximation for degrees of freedom implemented in the “lmerTest” package (Kuznetsova et al., 2017). In Studies 1a-d, we preregistered this analysis as our primary confirmatory hypothesis test. Several additional exploratory analyses were also listed (see Supplemental Materials).
Testing the effect of dynamics on geometric representations.
Study 1f examined three potential mechanisms by which mental state dynamics might be translated into mental state concepts. We hypothesized that people translate mental state dynamics into concepts by constructing a geometric representational space. Such a space could be constructed by moving states close to states to which they tend to transition. Proximity within this space would efficiently encode dynamics while also serving as the basis for conceptual judgements. Encoding dynamics via proximity also distinguishes this geometric account from more generic spatial representations, since any matrix can be represented spatially given sufficient dimensions.
The transition probability matrix we used in Study 1f was well suited to testing this geometric account. The matrix could be represented geometrically by a ring structure (i.e., circle), in which transitions were likely around the circle, but not across its face (Figure 4). To quantify the predictions of the geometric account, we computed the Euclidean distances between the six points on this circle which represented the six alien mental states. To aid model convergence and comparison, we amended our registered plans and rescaled these distances to a [0, 1] interval. We then fit a mixed effects model containing this geometric distance predictor as well as the observed transition probabilities (together with random slopes for each predictor within participant, and the participant random intercept, as in all the other mixed effects models). If the geometric predictor in this model was significant, this would corroborate the hypothesis that people translate mental state dynamics into concepts by using the dynamics to construct a low-dimensional representational space.
Figure 4. People use a geometric space to translate state dynamics into concepts.
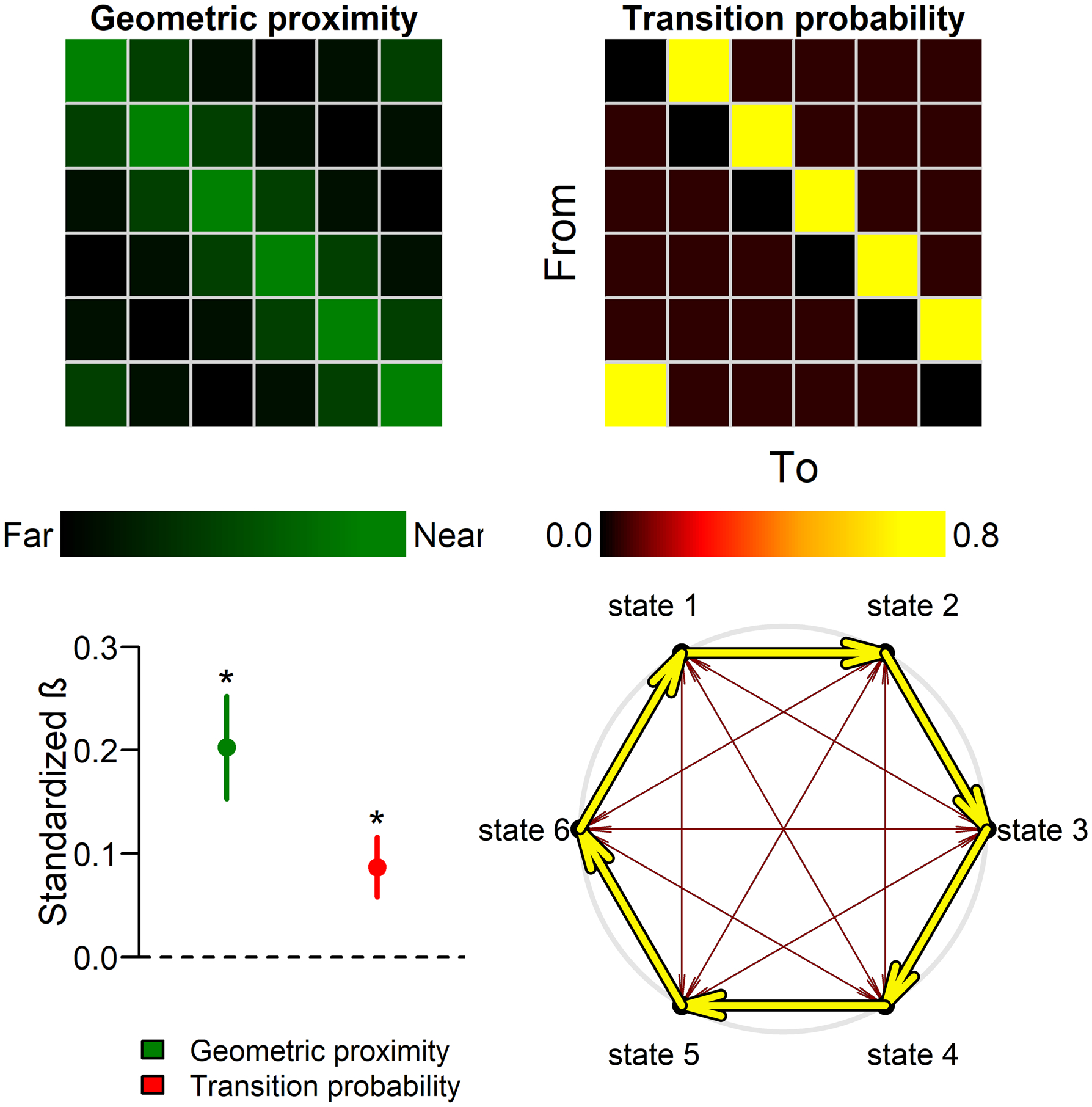
Study 1f tested the hypothesis that dynamics are translated into concepts by embedding states in a geometric space where proximity encodes transition probabilities (bottom right). This model (top left) predicted conceptual similarity more effectively than either the successor representation (not pictured) or the raw transition probabilities (top right).
We also considered two potential alternative models. First, we considered the possibility that participants directly convert transition probabilities into conceptual similarity without any alteration. The analyses described in the previous section – performed for all studies, including 1f – tested whether transition probabilities and conceptual similarity are correlated. Rejection of the null in those analyses would thus corroborate the ‘direct translation’ account (i.e., that there is a direct, linear association between transition probabilities and conceptual similarity). The analysis described in the previous paragraph provides a second test of this direct translation account: if only the transition probabilities, and not the geometric predictor, significantly predicted conceptual similarity, then this would further corroborate the direct translation account. We also conducted a third analysis to test the direct translation account. We hypothesized that this account would fail if participants symmetrized their conceptual similarity judgements. Transition probabilities in this study were highly asymmetric. For example, state A might always precede state B (but never the reverse). The geometric account would predict that participants would judge A similar to B and that they would judge B similar to A. In contrast, the direct translation account would predict asymmetric similarity judgements.
To test for this symmetrizing effect, we mirror reflected the observed transition probabilities across the diagonal of the transition probability matrix. For example, if the original probabilities were p(A → B) = 100% and p(B → A) = 0%, then in the mirror version p(A → B) = 0% and p(B → A) = 100%. This mirror term was included in a mixed effects model alongside the original transition probabilities. We tested each coefficient against zero using the Satterthwaite approximation. If the mirror term was significant, this would indicate that participants were indeed symmetrizing the transitions, and thereby both further support the geometric account and falsify the direct translation account. We compared the mirrored and unmirrored coefficients to each other using bootstrapping. Due to all bootstrapped estimates sharing the same sign, we used percentile bootstrapping rather than the bias-corrected accelerated bootstrapping we had planned. This analysis allowed us to test whether people symmetrized the transitions when they translated them into concepts. We also conducted an exploratory analysis using a different approach to symmetrizing the transition probabilities (see Supplemental Materials).
We planned to test a third account for how dynamics might translate into concepts, the successor representation account (Momennejad et al., 2017). This account proposes that people cache the long-run likelihood of moving from one state to another, rather than just the 1-step transition probabilities. If people used such a representation, we would expect that pairs of states linked together by a third state would be similar to each other, even if there were never any direct transitions between them. For example, if A often led to B, and B often led to C, then the successor representation would predict that people judge A similar to C. However, we found that the optimal successor representation proved to be degenerate: the optimal decay parameter caused the successor representation to converge on the raw transitional probabilities. It was therefore not distinguishable from the direct translation account. As a result, we did not proceed with analyses comparing this account to others (see Supplemental Materials). We did, however, conduct an exploratory analysis in which we tested a symmetrized version of the successor representation, and it performed substantially better (see Supplemental Materials).
Dynamic vs. static effects.
Study 1g tested the independent influence of static and dynamic features on people’s mental state concepts. As described above, we assigned eye colors to the alien’s mental states to create a static feature space for the mental states. We first tested whether this static feature had any effect on mental state concepts. We computed the similarity between the eye colors as the opposite of the distance between the colors. We amended our analysis plans by normalizing this measure to a [0, 1] scale for easier comparison with the transition probabilities. We entered the color similarity into a mixed effects model predicting similarity ratings, with a random intercept for subject and a random slope for color similarity within subject. If the fixed effect of color was significant, this would indicate that this static feature influences the conceptual similarity between states.
Next, we tested whether mental state dynamics still influence mental state concepts when competing with salient static features. We fit a second mixed effects model, in which we included both the eye color similarities and the transition similarities, with corresponding random effects. If the transition similarity predictor in this model was significant, it would indicate that mental state dynamics causally shape mental state concepts even in the presence of a salient static feature. In addition to testing the significance of each coefficient in this model, we compared the standardized coefficients to each other via bootstrapping of linear regressions. These regressions featured the same predictors as the mixed effects model but excluded random effects to accelerate computation. We deviated from our registered plans by using percentile bootstrapping instead of bias-corrected accelerated bootstrapping.
Results
Mental state transitions shape conceptual similarity.
The primary goal of Studies 1a-g was to test for a causal effect of mental state dynamics on mental state concepts. Participants were xenopsychologists on an expedition to understand the emotions of an alien creature. They first observed a sequence of this alien’s mental states, and then rated the conceptual similarity between these states. If mental state dynamics shape mental state concepts, then transition probability should be positively associated with similarity. This is precisely what we observed across all seven experiments (Figure 2 & Figure S3).
In Studies 1a-b, transitions were structure around two clusters of three states each, with high transition probabilities within each cluster, and low transition probabilities across clusters. This structure mimicked the two-cluster structure of emotion transitions observed in human experience sampling data (Thornton & Tamir, 2017). A mixed effects model indicated a statistically significant effect of dynamics on concepts in both Study 1a (b = 39.59, β = .17, t(15.81) = 2.72, p = .015) and Study 1b (b = 36.09, β = .11, t(36.90) = 2.86, p = .0069). Study 1c varied the transition structure, using three clusters of two states instead of two clusters of three. The findings replicated the effects observed in the first two studies (b = 11.93, β = .061, t(86.86) = 2.49, p = .015). Study 1d varied the transition structure again, using a ring-shaped transition structured inspired by the Circumplex Model of affect (Russell, 1980). States had a high probability of transitioning “clockwise” or “counterclockwise” around this ring, but a low probability of transitioning to nonadjacent states across the “face” of the clock. Once again, we observed a significant effect of dynamics on concepts (b = 13.82, β = .090, t(200.25) = 6.06, p = 6.64 × 10−9). In Study 1e, we used a complex transition structure tailored to test a hypothesis regarding second-order transition statistics (see Supplemental Materials; Figure S1). This study also replicated the main effect of dynamics on concepts (b = 19.06, β = .14, t(208.71) = 7.43, p = 2.75 × 10−12). In Study 1f, we returned to the ring structure of Study 1d, this time with the additional constraint that states could only transition “clockwise” with high probability. Again we observed a significant effect of transition probabilities on conceptual similarity judgements (b = 17.08, β = .20, t(213.49) = 10.71, p = 1.07 × 10−21). In Study 1g, participants observed a two-cluster structure of emotion transitions, similar to Studies 1a-b. We again replicated the effect of state dynamics on concepts (b = 11.32, β = .073, t(212.18) = 4.11, p = 5.61 × 10−5).
Together, the results of Studies 1a-g provide unanimous support for the hypothesis that mental state dynamics shape mental state concepts. In all seven experiments, we observed statistically significant effects of transition probabilities on similarity ratings. To precisely estimate the size of this effect, we conducted a post-hoc meta-analysis across studies (Figure 2). This analysis indicated that, on average, changing the transition probability from 0% (impossible transition) to 100% (certain transition) would produce a change in similarity of 21.27 on a 100-point continuous line scale (95% bootstrap CI = [12.40, 21.49]). The high consistency of this effect across seven studies – six of them preregistered – provides strong evidence in favor of a dynamic account of mental state concepts.
Mental state dynamics are represented in a geometric space.
Studies 1a-g support the hypothesis that mental state dynamics shape mental state concepts. Next, we asked how transitions translate into conceptual similarity. Study 1f examined three possible mechanisms explaining how this translation could occur. The first account – suggested by our previous research – was that people translate mental state dynamics into concepts by translating state transition into a low-dimensional geometric space, such that proximity encodes transition probabilities. To test this geometric account, we entered a predictor based on the Euclidean distance between states on a hypothetical ring into a mixed effects model. The results indicated robust support for the geometric account (b = 15.74, β = .25, t(212.00) = 9.98, p = 1.75 × 10−19). Geometric proximity remained a significant predictor when the transition probabilities were included in the model (b = 12.58, β = .20, t(210.90) = 8.06, p = 5.67 × 10−14). This indicates that the geometric account offers unique explanatory power, over and above the transition probabilities themselves (Figure 4). This result does not necessarily mean that participants representational space was 2d – they could have represented the same geometry in higher dimensions – but it does suggest that their representations can be projected onto a 2d manifold. The transitions probabilities also remained a statistically significant predictor, albeit smaller in magnitude (b = 7.26, β = .087, t(234.03) = 5.93, p = 1.07 × 10−8).
The second account we considered was a “direct translation” account in which people would convert transition probabilities directly to similarity ratings without any systematic alteration. Under this account, we would expect similarity ratings to be a direct, linear function of transition probabilities – our default assumption in Studies 1a-e. The primary analyses of all seven studies provided initial support for this account: transition probabilities causally shaped similarity judgements in this manner. However, the asymmetric transition probabilities matrix used in Study 1f permitted a stronger test of this hypothesis. Specifically, we tested whether people symmetrized their similarity judgements relative to the asymmetric transitions. To do so, we entered both the transition probabilities and their mirror reflection into a mixed effects model. We found that both the transitions (b = 20.25, β = .24, t(212.02) = 10.73, p = 9.53 × 10−22) and their mirror image (b = 13.57, β = .163, t(212.74) = 8.00, p = 8.03 × 10−14) were significant predictors of similarity ratings. The statistical significance of the mirror image predictor indicates that people do indeed symmetrize their conceptual similarity judgements relative to the raw transition probabilities. As a result, the similarity judgements do not reflect unaltered transition probabilities, falsifying the direct translation account.
In addition to falsifying the direct translation account, these analyses provide further insight into the geometric account. Euclidean distance is symmetric – just like people’s similarity judgements – so the geometric account performed better in part because it naturally symmetrized the data. However, the symmetrizing was not complete. The raw transition probabilities predicted similarity judgements significantly better than their mirror image (Δb = 6.78, 95% CI = [4.26, 9.24]). This indicates that the conceptual similarity judgements retained some of the asymmetries present in the transition probabilities. This helps to explain why the transition probabilities remained significant – if less important – predictors of similarity when included in a model alongside the geometric distances. Since the geometric account predicted purely symmetric conceptual similarity, it allowed room from the (asymmetric) transition probabilities to explain the residual asymmetry, thereby remaining significant.
Importantly, this symmetrization does not completely explain the success of the geometric account. In an exploratory analysis, we tested the geometric account while controlling for both the raw transition probabilities and their mirror image. Even with the mirror image transitions included, the geometric account remained a significant predictor of similarity (b = 9.45, β = .152, t(197.71) = 3.771, p = .00022). This indicates that geometric account extends beyond the 1-off-diagonals of the transition matrix: in other words, it explains variance in similarity between mental states that are not directly adjacent to one another on the ring, despite the fact that there was no systematic variation in the transition probabilities between nonadjacent states. This provides further, and more specific, evidence for the geometric account.
The third account we considered was the successor representation, which proposes that people cache the long-run likelihood of moving from one state to another, rather than just the 1-step transition probabilities (Dayan, 1993; Momennejad et al., 2017). This account makes asymmetric predictions, but predicts a graded drop-off in the similarity between states in the direction of likely transition around the ring. A decay parameter determines how heavily to weigh near-term vs. far-term transitions when generating a successor representation. We fit this decay parameter to the similarity ratings but found that the optimal value was zero (see Supplemental Materials). This indicates that only the 1-step transitions should be included in the successor representation and not any later steps. As a result, the successor representation was identical to the direct translation account described above. We, therefore, did not test this account separately since the result would have been redundant.
Together, the results of Study 1f support the hypothesis that people efficiently encode mental state dynamics by arranging them within a geometric space. However, it demonstrates that they also retain additional dynamic information – such as asymmetries – that cannot be fully encoded by such a space on its own.
The effect of state dynamics is robust to static features.
Study 1g tested whether dynamics shaped concepts even when forced to compete with a strong signal offered by a static state feature. Study 1g introduced such a competing static feature: alien eye color. Each state was associated with a unique color, in addition to its specific transition profile (Figure 3). The manipulations of transitions and eye color were orthogonal, allowing us to test the independent influence of both dynamic and static features of states on concepts. A mixed effects model containing both predictors revealed indicated significant effects of both transitions (b = 12.64, β = .082, t(210.36) = 4.69, p = 4.98 × 10−6) and eye color (b = 15.35, β = .22, t(208.08) = 7.18, p = 1.19 × 10−11) on similarity judgements. Eye color was a significantly stronger predictor of similarity ratings than transitions (Δβ = .13, 95% CI = [.10, .16]). The results of Study 1g show that dynamic influences on mental state concepts can coexist with even highly salient static features. Static features also had a significant effect, supporting the implicit assumption in the field.
Discussion
Studies 1a-g establish three important findings. First, all seven experiments corroborate the primary hypothesis that mental state dynamics causally shaped the structure of mental state concepts. Second, Study 1f provides insight into the mechanism by which observed dynamics translate into conceptual representations. We found evidence that the mind represents these states using a geometric space, within which more proximal states have high transition probabilities between them. Study 1f does not exhaust all of the possible mechanisms by which people could translate dynamics into concepts, but does at least suggest that conceptual similarity is not purely a linear function of transitions probabilities. Third, Study 1g tested whether the dynamic account of mental state concepts could survive the introduction of salient, reliable static cues to mental state similarity. Such static features are doubtless present in the real world, so it is important to test if they completely override dynamic information. We found that dynamics persisted in influencing mental state concepts, even in the face of this competing static influence (which also shaped conceptual similarity). Together these findings present strong evidence that the way we think about thoughts and feelings may be shaped, at least in part, by how those states typically change over time.
Studies 1a-g all used variants of the same basic experimental paradigm. This paradigm granted us complete experimental control over participants’ experiences with the mental states they learned about. The paradigm included an engaging scenario to increase participant “buy-in,” and included an illustration of the alien that participants were learning about to give them something to imagine. This sort of social-affective framing is common and effective across a wide range of established paradigms. For example, in the false-belief/false-photo task commonly used in fMRI research on theory of mind, the experimental and control conditions are deliberately identical in logical structure, and similar in terms of low-level features such as word lengths (Dodell-Feder et al., 2011; Saxe & Kanwisher, 2003). The only difference between these conditions is the social framing of the false-belief condition, versus the nonsocial framing of the false photo condition. Despite this minimal difference, this task is so reliable that is routinely used as a localizer for social brain regions. More generally, research on anthropomorphism illustrates how readily humans will spontaneously imbue even clearly mindless systems with a human-like mind, in an attempt to achieve a better understand of their environment (Waytz et al., 2010). This established literature thus supports the face validity of the social framing in these studies.
A deeper form of validity was established by the statistical structures we imposed on the task. In Studies 1a-b & g, we created a two-cluster transition probability matrix which closely resembles the true structure of emotion transitions observed from experience sampling (Thornton & Tamir, 2017). In Studies 1d&f, we used a ring-based transition structure which closely resembles the conceptual structure of the Circumplex Model (Russell, 1980). Thus, in addition to the social framing of the task, we also specifically examined the ability of participants to learn concepts from mental state transition structures similar to those that they might actually encounter in their everyday lives.
Despite these efforts toward naturalism, Studies 1a-g lacked many characteristics of perceiving emotions in everyday life. For example, we used arbitrary words and a small number of featureless discrete states to represent the alien’s mental experiences. We presented participants these mental states completely explicitly but in the real world, people’s mental states are rarely so transparent. Rather, people must often use a combination of noisy indicators, such as facial expressions, tone of voice, and context, to infer what others may be thinking or feeling (Barrett et al., 2011; Zaki et al., 2009). Moreover – although the debate over the discrete vs. continuous nature of emotions continues (Barrett et al., 2018; Cowen & Keltner, 2018) – it seems likely that at least some aspects of affective experience are continuous, rather than discrete.
In principle, one could address these problems by running a fully naturalistic version of the Study 1, in which participants observe other people’s emotions change over time. However, people’s prior knowledge and beliefs about emotions make it unlikely that we could manipulate the corresponding concepts through a short statistical learning task. Indeed, it would be worrying if we could substantially alter a person’s concept of happiness in a 20-minute online study. Due to this practical barrier, Studies 2 and 3 adopt different approaches to address these limitations and connect our findings back to the world of actual human thoughts and feelings. Study 2 does this by reintroducing many important features of human mental states into our xenopsychology paradigm. Study 3 complements this by examining real human mental state dynamics, but through the lens of an artificial, rather than human, perceiver.
Study 2
Study 2a – and its preregistered replication, Study 2b – introduced two key elements of real-world human mental states back into a modified version of the statistical learning task from Study 1. First, to better mirror the process of real-world mental state inference, we made the alien’s states latent, rather than directly observable. Specifically, colors of the alien’s eyes became noisy indicators of its hidden mental states. Second, the alien’s latent states became continuous, rather than discrete. That is, the alien’s actual state was represented by numerical coordinates within a continuous state-space, rather than by a discrete word. Within this space, the alien’s emotions wandered nonlinear paths shaped by a combination of pull towards attractors within the space, momentum, and noise.
These modifications to the paradigm allowed Study 2 to achieve three main goals. First, we aimed to replicate the findings from Study 1, showing that transitions between states causally shaped mental state concepts when these more naturalistic elements were reintroduced. Second, we aimed to understand how state concepts come into being in the first place. We tested an account of how discrete state concepts could emerge from observation of the dynamics of a continuous underlying state space. Third, we aimed to understand how dynamic and static features of states complement each other in the development of mental state concepts. We hypothesized that static feature may provide “orientation” (e.g., positive vs. negative valence) to the otherwise orientation-free conceptual space learned through transitions dynamics. Achieving these goals would both strengthen and deepen the insights we arrived at in Study 1.
Methods
Transparency and openness.
Study 2a was a pilot study meant to establish a new behavioral paradigm. Study 2b was a direct replication of Study 2a, and was preregistered on the Open Science Framework (https://osf.io/96twz). Deviations from our preregistered plans are detailed where applicable. For all studies, we report how we determined sample size, all data exclusions, all manipulations, and all measures. All statistical tests were two-tailed. All data and code from these experiments are freely available on the Open Science Framework (https://osf.io/4m9kw/).
Participants.
In Study 2a we targeted the same sample size that we had converged on in Study 1: 212. Ultimately we recruited 207 (74 women and 133 men; mean age = 38.91; age range = 20–71) participants from Amazon Mechanical Turk using TurkPrime (Litman et al., 2017), with study availability limited to workers from the USA with 95%+ positive feedback and who passed TurkPrime’s quality filter.
Based on the results of Study 2a, we conducted a parametric power analysis in R (R Core Team, 2015). This power analysis used the participant-level Pearson correlations between participants’ state similarity judgements and the transitions probabilities they observed. The correlations were Fisherized and then entered into the one-sample t-test function from the ‘pwr’ package (Champely et al., 2018). The results indicated that a sample size of 237 participants would provide greater than 99% power for our primary hypothesis test. An analogous power analysis targeting the correlation between transition probabilities and valence was also conducted, and a sample size of 237 was found to offer greater than 95% power for this hypothesis test as well. We therefore targeted a sample of 240 participants for Study 2b to allow for exclusions.
We ultimately collected a sample of 236 participants from the same pool as Study 2a. Participants from Study 2a were prohibited from participating in Study 2b. After preregistered exclusions (see Supplemental Materials), we were left with a final sample size of 231 (102 women, 124 men, 1 non-binary, 1 other, and 3 preferred not to provide gender; mean age = 40.91; age range = 23–73). See Supplemental Materials for additional demographic information. Participants in both studies provided informed consent in a manner approved by Dartmouth College Committee on the Use of Human Subjects.
Experimental Paradigm.
Participants were forwarded from TurkPrime to a custom Javascript-based experiment. The framing of the experiment was almost identical to that used in Study 1: participants adopted the role of a xenopsychologist on a mission to an alien planet to learn about the mental states of the aliens. Unlike in Study 1, participants in Study 2 were not told in advance the names of the alien’s states, nor how many there were. Rather, they were instructed to pay attention to the alien’s changing eye colors to understand the states that they expressed.
Over the course of the learning phase of the experiment, participants watched 10 1-minute-long videos. Each video was framed as being a recording of the alien over one day. These videos featured the same alien cartoon as in previous studies. Aliens experienced four mental states, each reflected as a location within color space (blue, green, orange, or pink; Figure 5). Participants needed to infer the latent state space model from eye color. The alien’s eye colors changed continuously, albeit noisily, transitioning between the four latent states as described in the stimulus section below.
Figure 5. Illustration of an alien’s state space trajectory.
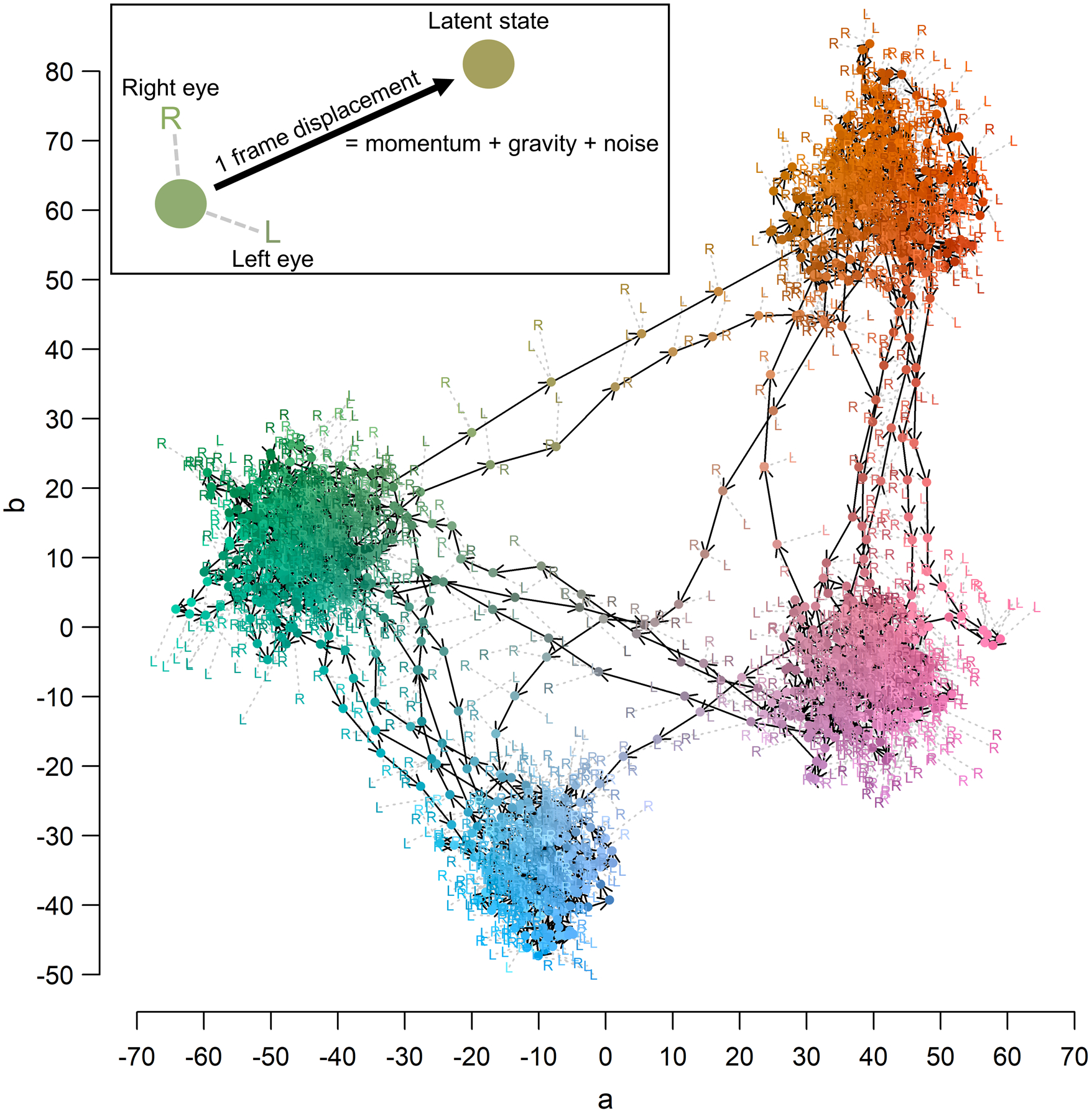
Aliens experienced four mental states, each reflected as a location within color space (blue, green, orange, or pink). States transitioned either to a ‘within cluster’ state (e.g., blue to green) with high probability or to a ‘between cluster’ state (e.g., blue to pink) with low probability. The location of the eye at each time point was determined by a combination of “gravitational” attraction to the currently active state color, momentum along its prior trajectory, and Gaussian noise. Each point in the diagram illustrates the alien’s true latent location in CIELAB space in one frame of one stimulus video. The x- and y-axes represent the a and b parameters of CIELAB space, respectively. Each point is colored as its position in this 3d space. The locations and colors of the “L”s and “R”s reflect the colors of the alien’s left and right eyes, as observed by participants. These colors are noisy indicators of the alien’s true latent position in the state space at the same timepoint (indicated by the circle linked to each “L” and “R” by a dashed grey line). The observable eye colors were semi-randomly displaced from the latent coordinates with their own set of independent dynamics. Arrows indicate the direction of the alien movement in state space from one frame to the next.
After each video, participants completed a probe trial in which they were shown a still frame of the alien in one of the four attractor states, randomly selected. They were asked to select from one of three other still frames – reflecting the other attractor states – to indicate which they though would be most likely to follow the target eye color. Additionally, for all videos after the first, participants were asked to press the “1” key on their keyboard whenever they detected a state change during the video. Due to a data collection error, the response times were only recorded for Study 2a.
After completing the learning phase of the study, participants then completed a post-test to probe how well they learned the latent state space. First, we asked participants to indicate the number of states that the alien had experienced using a free response box. Next, we told participants that – after conferring with their xenopsychologist colleagues – the team had come to the conclusion that the aliens had four different states. We then asked participants to indicate how frequently each of those states occurred with each of the four attractor colors using slider bars. This procedure allowed us to match up the participants’ chosen states to the underlying task states as best possible. Each of the participant’s states was matched with a task state based on the highest rated color (e.g., if the slider bar for “green” was highest on the first state, this would be matched up with green attractor state in the task). Ties were broken based on which of the tied states had the highest second-highest color rating. For example, if two states were both rated as orange 75%, but one state had green 65% as its second highest, and the other had pink 46% as its second highest, then the first state would be matched with the green task state and the second state would be matched with the orange task state.
Using the participant-assigned labels/colors, participants then rated the pairwise similarities between all four states in both directions (i.e., A to B and B to A) using a continuous line scale. On each trial, participants saw the label which they had assigned to the two states in question (e.g., state “X” and state “Y”) and were asked to judge the similarity between them. To help participants remember which state was which, we colored the text of the state names based on which attractor state we had matched with that name using participants color rating judgments. This procedure may have increased the relative impact of the static feature (color) on similarity, relative to the dynamics, because it made color highly salient when making these judgments.
Finally, participants answered several questions designed to test whether they treated them as mental states, per se, or as more domain-general states. First, after participants were told how many states the alien experienced (four), we asked them to provide names for those states using free response boxes. Participants also rated the valence of each of the four states on a line scale from negative to positive. They then matched each of the alien’s states to one of four human states: Content, Relaxed, Rage, and Panic. The matching was performed via a drag-and-drop procedure. Finally, they completed a demographic questionnaire and received debriefing and payment information.
Stimuli.
The primary stimuli in the experiment consisted of videos of a grey cartoon alien (as shown in Figure 3) with varying eye colors (as shown in Figure 5). These videos were generated based upon a 3-dimensional continuous state space model. Within this space, we placed four “attractor” states. Each attractor would be “on” for a period of 3 s, during which it exerted a gravitational pull on the alien’s state. After this period had elapsed, a new attractor state would begin pulling the alien’s state towards it instead, resulting in a transition. The probabilities of these transitions were determined by a predefined transition probability matrix. This transition matrix consisted of two clusters of two attractors each. There was a 60% chance of transition to the other attractor in the same cluster, and a 20% chance of transitioning to either of the other two attractors.
The alien’s latent state traversed the state space in a manner determined by three factors: “gravity” – attraction to whichever of the four attractor states was active, with an effect equal to 10% of the projected distance to that attractor; “momentum” – continuing along its prior trajectory, with an effect proportional to half of its velocity in the previous frame; and 3d Gaussian noise ~N(0,2). After the alien’s states was initialized at one of the four attractor’s coordinates (randomly chosen), its movement through the space proceeded according to these dynamics until the 60 second (1440 frames) duration for each video had elapsed (Figure 5).
The alien’s latent state was not directly observable in the videos. Rather, participants had to infer the latent state from the alien’s eyes, the colors of which provided noisy manifest indicators of its true state. Both the latent state, and these manifest indicators, occupied positions in the same 3-dimensional space. On each frame of the video, the coordinates of each eye were independently, semi-randomly displaced from coordinates of the alien’s latent state. This displacement was governed by its own set of dynamics. These dynamics were similar in concept to the dynamics of the latent state described above, but distinct from them. First, “gravity” attracted the eyes to the latent state, with a forced proportional to 10% of the distance from the eye to the latent state. This gravity force was what kept the eyes bound to the latent state: without it, the eyes would have freely roamed the state space on their own. The gravity force was “unidirectional” (i.e., it attracted the eye to the latent state, but not vice versa). As a result, the latent state influenced the eyes, but the dynamics of the eyes did not influence the trajectory of the latent state. Second, an “inertia” factor provided continuity from one frame to the next: each eye would tend to stay in the same location relative to the true state across frames. Finally, random 3d Gaussian noise ~ N(0, 2) was added. This noise was independent across the two eyes, and also independent of the noise added to the trajectory of the latent state. The eyes were thus completely independent of each other when conditioned upon the latent state. Together, these features meant that representing the alien’s latent state with maximal accuracy requires integrating information over time and over independent information channels. The eyes’ coordinates in the state space were translated into colors to make them directly observable to participants. Specifically, the three dimensions of the state space were translated to the three parameters of the CIELAB color space: L(uminance), a, and b. We used the CIELAB space because it is relatively perceptually uniform compared to other common color spaces such as RGB.
Using the attractor state transition matrix described above, we generated 20 unique sequences of attractor states. We chose locations in the state space for each attractor by selecting four colors from a colorblind-friendly palette, yielding blue: #56B4E9, green: #009E73, orange: #D55E00, and pink: #CC79A7 (Wong, 2011). These attractor colors were randomized with respect to the transition probabilities of the attractors. For example, sometimes blue and green were in the same attractor cluster and had a high transition probability between them, as shown in Figure 5, and sometimes they were in different clusters and had a low transition probability between them. For each of the 20 unique sequences of attractor states, we generated 24 different videos, corresponding to all 24 possible permutations of the attractor colors with respect to the transition probability matrix. During the learning phase of the experiment, each participant saw only 1 of the 24 different permutations of attractor colors and transition probabilities. Within this permutation, they viewed 10 randomly selected videos from the 20 possible. As a result, each participant had a unique experience of the alien’s underlying dynamics. Although the attractor state transitions were identical in each of the 24 variants of the same sequence, the movement of the alien through state space was randomly different in each variant due to the different noise applied to the alien’s latent state trajectory, and the additional noise applied to its eye color displacements. Each frame of the video was rendered as an image based upon the alien illustration (as shown in Figure 3) with edited eye colors. The resulting frame images were rendered into mp4 video files with 500 × 1080 pixel resolution at 24 frames per second using ffmpeg (https://ffmpeg.org/). These videos were then viewed by participants in the experimental paradigm described in the previous section.
Statistical analysis.
Testing dynamic and static influences on conceptual similarity.
To test our primary hypothesis, that mental state transition dynamics shape conceptual similarity, we fit a linear mixed effects model predicting participants’ similarity ratings from the transition probabilities that they had observed in the learning phase. This model included a random intercept for participant, and a random slope for transition probabilities within participant. As in Study 1, we expected higher transition probabilities to predict higher similarity ratings.
We also fit two different variants of this model. In the first variant, we simply substituted the visual similarity between the attractor states in CIELAB space (measured via reverse-coded Euclidean distance) in for the transition probabilities in the initial model. This model allowed us to test the impact of static features (i.e., eye colors) on conceptual similarity, to replicate the results of Study 1g.
In the second variant, we included three additional covariates which we anticipated might impact similarity judgements: the visual similarity between the attractor state colors; how often each color actually co-occurred with each attractor state (there is variability in these co-occurrences due to the noisy, nonlinear dynamics of the alien’s state trajectories); and the typical “times-of-day” (i.e., point within the video) during which state occurred (i.e., the frame-by-state co-occurrence matrix). To make predictions about similarity ratings from each of these three covariates, we took the reverse-coded Euclidean distances between the four attractor states with respect to each variable. The resulting linear mixed effects model contained these three covariates, plus transition probabilities, as fixed effects. The random effects included an intercept for participant, and slopes for transition probability and visual similarity within participant. An additional variant included a learning performance moderated (see Supplemental Materials). We expected that transition probabilities and visual color similarity would both continue to predict conceptual similarity, even when included in the same model as each other and the other covariates.
P-values for each of the coefficients in each of these models, and the valence models described below, were obtained via the Satterthwaite approximation (Bates et al., 2015; Kuznetsova et al., 2017). All numerical variables in these models and the valence models were z-scored prior to being entered into the models. For plotting purposes, we also conducted linear regressions within each participant, predicting their similarity ratings from observed transition probabilities and visual color similarity. These individual fits, their mean, and a bootstrap confidence interval around them are shown in Figure 6B–C.
Figure 6. Primary results from Studies 2a and 2b.
A) The word cloud visualizes the most common free-response labels given to the alien’s mental states, with more frequent words appearing in larger text. Higher transition probabilities predicted higher transition ratings in both Study 2a (B) and Study 2b (C). Thin lines represent participant level regressions between these variables, controlling for visual color similarity. The thick lines represent the mean slope, surrounded by a 95% bootstrap confidence interval. D) Colors reliably predicted valence ratings in Studies 2a and 2b. The distribution of valence is shown via violin plots, with raw ratings ranging from the most positive (+50) to most negative (−50) possible values. The large white circles indicate the median for each color. E) In both studies, outright majorities of participants correctly indicated that the number of states the alien had matched the number of attractors in the state space (four).
Testing the attribution of realistic mental state concepts.
A secondary goal of Study 2 was to assess the extent to which participants were conceptualizing the alien’s mental states as if they were real human mental states. We approached this question in three ways: using valence ratings, forced-choice matching with human states, and free-response labeling of the alien states.
If participants were only conceptualizing the alien’s states as arbitrary statistical objects, rather than mental states, we should not expect to see valence ratings relate coherently to dynamics. In contrast, if participants were thinking about these states as emotions, then we would expect that state with high transition probabilities would also be assigned similar valence ratings. To test this hypothesis, we fit a set of linear mixed effects model identical to those in the previous section, except that the dependent variable was similarity in valence ratings rather than similarity ratings. For this purpose, we computed the absolute difference between the valence rating for each state, sign-flipped these values, and then z-scored them.
Likewise, if participants were thinking about the alien’s states as real mental states, then there should be coherent patterns in how they match the alien’s states with named human states. Specifically, we predicted that pairs of alien states with high transition probabilities between them would be matched with similar pairs of human states, whereas pairs of alien states with low transition probabilities between them would be matched with dissimilar pairs of human states. To test this, we drew upon ratings of the similarity between human states from a prior investigation (Tamir et al., 2016; Thornton et al., 2022). These similarity ratings included judgements of the four states which participants could choose from in the drag-and-drop state matching question in the post-test (i.e., Content, Relaxed, Rage, Panic). We then correlated the transition probabilities between the alien’s states with the similarity ratings of matched human states. The resulting correlation coefficients were Fisher-transformed and entered into a one-sample t-test to determine if the average correlation between alien state dynamics and human state similarity was significantly greater than chance.
Together, the valence and state matching analyses can assess the extent to which participants attributed realistic features to the alien’s mental states. If the hypothesized results obtain, this would indicate that participants are indeed conceptualizing the alien’s states in realistic terms, and increase the external validity of the findings. They would also lend more evidence to support our primary hypothesis that dynamics shape concepts.
Finally, we analyzed participants’ free responses when asked to label the alien’s states. Note that these responses were provided before the forced choice matching, so they could not have been biased by the options we provided. If participants spontaneously labeled the alien’s states using human mental state terms, this would provide a strong indication that they were thinking about them as if they were realistic states. To test this, we manually counted the number of participants who used at least one human mental state word in their free response labels. A response was judged to contain a mental state term if it contained any recognizable English language word for a cognitive or affective state. This analysis was descriptive: we preregistered it but did not specify a precise numerical prediction or inferential procedure.
Testing the complementary role of static features.
In addition to the analysis of valence with respect to dynamics, we conducted a secondary analysis of valence with respect to color. The goal of this analysis was to determine whether participants associated certain colors with positivity or negativity, irrespective of how the colors were aligned with the transition probability matrix for each participant. If so, this would provide an indication of how static features and dynamics might complement each other, such that static features provide the orientation of a conceptual space, and dynamics providing its geometry. To achieve this, we computed all pairwise paired t-tests of the raw valence ratings associated with each of the four eye colors. We controlled for multiple comparisons within this family of tests using the Holm-Bonferroni procedure.
The emergence of discrete states.
Another auxiliary hypothesis examined how conceptualizations of discrete states could emerge from a continuous state space. The alien’s states – both the latent true state, and the eye colors which provided a noisy indication thereof – were continuous in nature. However, we embedded a set of four discrete dynamic attractors within this continuous space. We hypothesized that the presence of these attractors would lead participants to conceptualize of the alien’s states as categorical. Our primary hypothesis was that the plurality of participants would indicate that the alien had the same number of states as the attractors (i.e., four states). Our secondary hypothesis was that most of the other participants would indicate that the alien had 5–10 states. This secondary hypothesis is consistent with participants judging the transitions as states in their own right. Again, these hypotheses were descriptive, and no formal inferential procedure was preregistered.
Results
Dynamic and static influences on conceptual similarity.
As expected, we fully replicated the results from Study 1. Observed transition probabilities significantly predicted ratings of the similarity between the alien’s states (Figure 6B & Figure 6C) in Study 2a (β = .100, t(205.33) = 3.02, p = .002) and Study 2b (β = .092, t(227.14) = 2.82, p = .0052). That is, people learned which states were similar, and which were different, based upon the transition probabilities between those states.
We also found evidence that participants were attuned to other features of the stimuli as well. Specifically, visual color similarity between the states was a significant predictor of similarity in both Study 2a (β = .247, t(206.00) = 4.81, p = 2.98 × 10−6) and Study 2b (β = .28, t(230.00) = 5.71, p = 3.49 × 10−8). Transition probabilities in Study 2a (β = .095, t(208.94) = 2.86, p = .0047) and Study 2b (β = .098, t(229.76) = 3.11, p = .0021) and visual color similarity in Study 2a (β = .22, t(203.48) = 4.28, p = 2.8 × 10−5) and 2b (β = .24, t(227.25) = 5.16, p = .0090) remained statistically significant predictors of rated similarity when entered into the same model alongside the time of day and color co-occurrence covariates. Time of day was not a significant predictor of similarity in Study 2a (β = .012, t(2283.26) = .23, p = .82) nor in Study 2b (β = −.046, t(2558.74) = −.94, p = .35). Color co-occurrence was not a significant predictor of similarity in Study 2a (β = .021, t(2156.08) = 1.21, p = .23) but was in Study 2b (β = .038, t(2403.63) = 2.31, p = .021). These results replicate the outcome of Study 1g, showing that static features influence conceptual similarity alongside dynamic features. They also show that the effect of dynamics survives in the presence of this salient static feature and also when controlling for other potential confounds.
The attribution of realistic mental state concepts.
To determine whether participants conceptualized the alien’s states as real human states or arbitrary statistical objects, we examined the effects of transition dynamics on valence, human state matching, and free response labeling of the alien’s states.
Observed transition probabilities significantly predicted the similarity of valence ratings for the alien’s states in Study 2a (β = .074, t(206.18) = 2.33, p = .021) and Study 2b (β = .062, t(226.62) = 2.12, p = .036). Visual color similarity between the states was also a significant predictor of valence in both Study 2a (β = .14, t(206.00) = 2.69, p = .0078) and Study 2b (β = .16, t(230.00) = 3.29, p = .0012). In a model containing transition probabilities, visual color similarity, time of day, and color co-occurrence, transition probabilities were a marginally significant predictor of valence similarity in Study 2a (β = .063, t(207.17) = 1.91, p = .057) and a significant predictor in Study 2b (β = .068, t(227.30) = 2.33, p = .021). In the same model, visual color similarity predicted valence significantly both in Study 2a (β = .12, t(200.54) = 2.38, p = .018) and 2b (β = .13, t(226.68) = 2.64, p = .0090). In this model, neither time of day in Study 2a (β = .022, t(2305.40) = .46, p = .64) nor Study 2b (β = .034, t(2601.92) = .73, p = .47) nor color co-occurrence in Study 2a (β = .018, t(2106.77) = 1.19, p = .23) nor Study 2b (β = .001, t(2362.57) = .070, p = .94) was a significant predictor of valence similarity. Together, these results indicate that dynamics were indeed a reliable predictor of the valence assigned to the alien’s states, suggesting that participants were attributing to these states the properties of real mental states.
As predicted, there was a statistically significant correlation between the transition probabilities of the alien’s mental states and the rated similarity of the human states that participants matched with the alien’s states in both Study 2a (mean z(r) = .25, t(199) = 3.76, p = .00023) and Study 2b (mean z(r) = .36, t(230) = 5.64, p = 5.01 × 10−8). These results provide further evidence both that transition dynamics are shaping participants’ conceptualization of the alien’s states, and that they are conceptualizing these states as mental states per se, rather than arbitrary objects of statistical learning.
In exploratory analyses, we conducted a version of this analysis featuring visual color similarity instead of transition probabilities. This effect was not significant in Study 2a (mean r = .066, t(199) = 1.79, p = .074) but was in Study 2b (mean z(r) = .073, t(230) = 2.21, p = .028). The transition correlation was significantly greater than the color effect in Study 2a (mean z(r) difference = .19, t(199) = .012, p = .012) and Study 2b (mean z(r) difference = .29, t(230) = 3.81, p = .00018). This indicates that dynamics have a significantly larger impact than static features on how participants matched the alien’s states up with human states.
Finally, we examined the free response labels participants assigned to the alien’s states. In Study 2a, 152 out of 207 participants (73.43%) spontaneously used at least one human mental state term to label the alien’s mental states. In Study 2b, 182 out of 231 participants (79%) spontaneously used at least one human mental state term to label the alien’s mental states. Most of the other common responses in both studies reflected the color of the alien’s eyes (Figure 6A). These results indicate that, even without being prompted to match the alien’s states with human states (as occurred later in the post-test), participants were spontaneously mapping these novel states onto the familiar states of the human mind.
The complementary role of static features.
To assess the potentially complementary roles played by static and dynamic features in shaping mental states concepts, we tested for differences in valence ratings between states with different eye colors. In both Study 2a and Study 2b, we observed the same pattern of valence ratings: blue was rated mostly positively, followed by green, then pink, and finally orange was rated most negative on average (Figure 6D). In Study 2b, all pairwise differences – except the difference between blue and green and the difference between green and pink – were statistically significant (p < .05, corrected). In Study 2b, all pairwise differences between colors were statistically significant (p < .05, corrected). These results suggest that the static feature of color may provide the “orientation” of the alien’s state space (i.e., which pole is positive, and which is negative). In contrast, the dynamics help to shape the geometry of the state space – as described above – but cannot indicate it orientation.
The emergence of discrete states.
In Study 2a, 119 of out 207 participants (57%) correctly identified that the alien had four states (Figure 6E). Most of the rest of the participants (33% of the total) indicated between 5 and 10 states. In Study 2b, 143 of out 231 participants (62%) correctly identified that the alien had four states. As predicted, most of the rest of the participants (34% of the total) indicated between 5 and 10 states. These “errors” are consistent with regarding the transitions between states as states in themselves. These results indicate that the presence of discrete dynamical attractors in a continuous state space can lead people to form predictable numbers of discrete state concepts.
Discussion
The results of Study 2 address several outstanding questions remaining after the experiments of Study 1. First, and most importantly, Study 2 replicates the primary effect observed in Study 1: mental state transition dynamics shape the conceptual structure people ascribe to those states, such that states with higher transition probabilities between them are judged to be more similar. This result obtained in a paradigm that was considerably more complex for participants, requiring them to make noisy inferences of the alien’s hidden mental states. Despite this complication, not only similarity ratings, but also valence ratings and human state matching reflected the state transition dynamics that participants observed. These outcomes add new weight to the evidence corroborating the hypothesis that mental state dynamics shape mental state concepts.
The fact that participants attributed realistic mental state features, such as valence, to the alien’s states – and did so in a manner consistent with their transition dynamics – suggests that they conceptualized as the alien’s states as realistic mental states, and not just arbitrary statistical objects. This interpretation is reinforced by the similar results observed with respect to forced-choice matching between the alien’s states and human mental states, which was also guided by transition dynamics. Moreover, the overwhelming majority of participants spontaneously used human mental state terms to label the alien’s states, suggesting that they were thinking about the alien’s states in these terms even before we explicitly required them to do so. Together, these results increase the external validity of our findings by providing multiple indicators that the results pertain to how people might learn mental state concepts in the real world.
Study 2 also shows how discrete mental state concepts can arise from observations of a continuous state space. Simply because a state space is continuous, does not mean that all locations are equally likely. The presence of attractor states could lead to consistent regularities in the probability density of occupied states over a continuous space. In other words, some locations in state space may be more common than others and maintain a hold on people’s mind over an extended period of time. Even when the state space is continuous, the presence of a discrete number of attractors can lead people to conceptualize the state space in a categorical way. We observed this in participants’ responses, where they indicated that the number of states in the space either matched the number of attractors, or the number of attractors plus the number of transitions between them. This tendency to discretize a continuous state space may reflect internal pressures – such as a cognitive demand to simplify one’s mental model of other minds – or external factors – such as it being easier to communicate using words when states are conceptualized as discrete instead of continuous. Either way, we demonstrate a mechanism by which people may arrive at a discrete conceptualization of others’ mental states, based purely upon observing noisy indicators of their latent states in a continuous state space.
Study 2 provides also deeper insight into the relationship between dynamic and static influences on mental state concepts. We replicate the finding from Study 1g that both dynamic and static features shape similarity judgements. As in Study 1g, the effect of static features (i.e., color space similarity) appears larger. That said, this apparent difference in effect size is ambiguous, and could be attributed to multiple different causes, as previously noted. Moreover, while the effect of static features on similarity ratings is stronger than that of dynamics, the effect of dynamics on human state matching is stronger than that of static features. The effect of dynamics may thus generalize more effectively to the way people think about real world human mental states.
Static features may have the added role of helping to orient the conceptual space learned primarily via transition dynamics. By way of analogy, imagine that you knew all of the airline travel distances between cities on the Earth. With this information, it would be fairly easy to reconstruct an accurate 3d globe (e.g., via a procedure like multidimensional scaling). However, with the distances alone, it would be impossible to tell which direction was “up” and which was “down”. In the case of the globe, this distinction is purely a matter of social convention: north points “up” because global society is dominated by the northern hemisphere. In the case of mental states, the difference in orientation maybe more substantive: it is actually quite important to know whether a mental state is positive or negative in order to predict how someone in that state will behave. The transition dynamics between states may act, in this analogy, much like the airline distances between cities: providing the necessary ingredients to construct an accurate map of the space. The static features may complement this by adding orientation to this geometry. We observed this in Study 2, in that there were systematic differences in how positive or negatively people rated the different alien eye colors, regardless of their positions in the transition probability matrix.
The results of Study 2 start to bridge the gap between the high controlled but less naturalistic experiments of Study 1, and the world of real human mental state dynamics. To help complete this process, in Study 3 we turn even further towards human state dynamics, but abandon the naturalism of our observers. Instead, we seek to understand the prerequisites for forming realistic concepts of human mental states through the eyes of artificial neural networks.
Study 3
Study 3 tested whether mental state dynamics shape mental state concepts by examining how artificial neural networks build representations of mental states from scratch. First, we trained neural networks to predict state transitions based on a large sets of actual human mental state dynamics. We then compared the representations that the network learned to 1d, 2d, and 3d approximations of conceptual structures of these mental states (Russell, 1980; Tamir et al., 2016; Thornton & Tamir, 2020a). If the network’s representations matched the human representations, it would indicate that mental state dynamics are sufficient to explain how people understand those states.
This approach has three key features: First, artificial neural networks start off knowing absolutely nothing beyond what might be implicit in their architecture. Any “experience” a network has results from what is fed into it during training. This means that researchers have complete control over the network’s every experience from “birth” to maturity. This level of control is useful for ruling out confounds. Namely, in Study 3, we provided a network with only mental state dynamics, and not information about static features of the states. This allows us to observe the unique role dynamics play in shaping state concepts. Second, neural networks are fast and patient. They are fast in the sense that they can “experience” a sequence of mental states far more quickly than the participants in Studies 1 or 2 could. They are patient in that they can be trained on extremely long sequences in a single session. In Study 3, we trained a network on hundreds of thousands of mental state transitions in a few minutes. Finally, neural networks are focused – they “care” only about achieving their architect’s specified goal. The programmer describes a certain objective function, and the network attempts to optimize it – and only it. This differs from human participants, who do not temporarily abandon all of their other life goals the moment they begin an experiment. In Study 3, we programmed networks with the singular goal of predicting future states. This allowed us to test whether this high-level goal of prediction, on its own, is sufficient to explain the learning of the predicted mental state representation.
Study 3 considers conceptual structures with 1, 2 and 3 dimensions, to assess whether the neural network can extract the corresponding conceptual structures as reported by human participants. In Study 3a, we consider a 3d neural network representation, and compare it to 3d Mind Model (Thornton & Tamir, 2020a); in Study 3b we consider a 2d neural network representation, and compare it to the Circumplex Model (Russell, 1980); and in Study 3c we consider a 1d neural network representation, and compare it to a unidimensional valence model.
Humans and neural networks operate under different capacity constraints, and it would be difficult to calibrate a neural network to have the same capacity limitations as human. As such, we do not use the neural networks to attempt to estimate the ideal dimensionality of mental state representation, because without an appropriate capacity limitation, the networks would likely prefer a less parsimonious solution than humans.
Methods
Neural network structures.
Three artificial neural networks were trained to predict the next mental state in a sequence of states, using only the identity of the current state. Each network included three primary layers (Figure 7A): an input layer, hidden layer, and output layer.
Figure 7. A neural network learns the 3d Mind Model from dynamics alone.
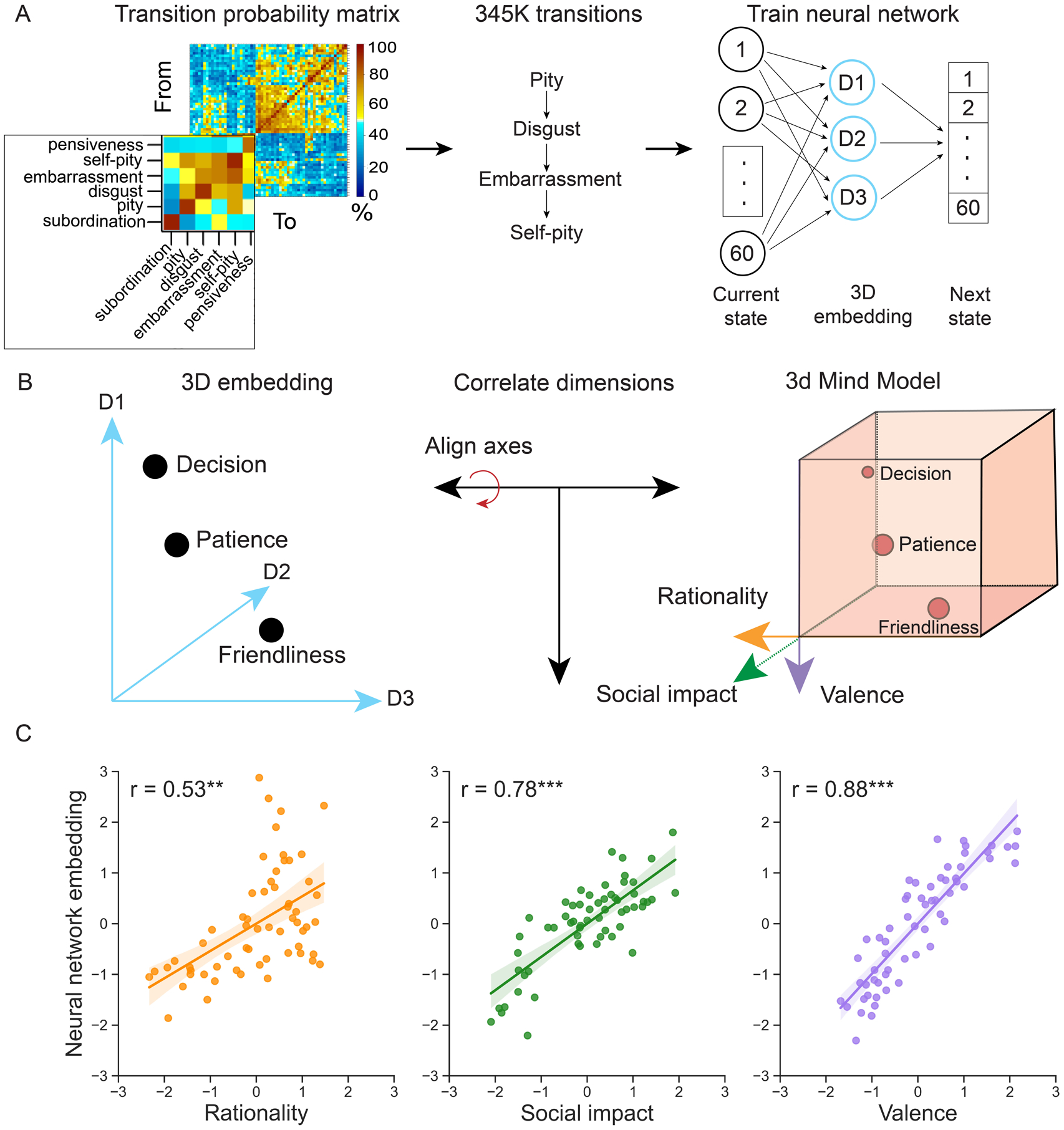
A) Transition probabilities between 60 human mental states were used to generate a sequence of mental states with naturalistic dynamics. This sequence was used to train neural networks in Studies 3a and 3b with a singular goal: to predict the next state from the current state. B) The resulting dimensions learned by the networks were aligned with conceptual structures from the literature, including the 3d including the 3d Mind Model in Study 3a, via cross-validated Procrustes transformations. The aligned dimensions were then correlated with one another to test whether the network had learned a human-like representational space. C) The networks spontaneously learned 1d, 2d, and 3d conceptual spaces. The 3d network in Study 3a recover the conceptual dimensions of rationality, social impact, and valence from the transition dynamics. These results indicate that mental state dynamics – and the goal of predicting them – suffice to explain the structure of mental state concepts.
The input layer represented the identity of the current state. In Studies 3a and 3b the input layer consisted of a length 60 one-hot encoding of 1 of 60 possible mental states. In Study 3c, this layer consisted of just 18 units, to represent the smaller number of states used to train this model. The training data in Study 3c was binary, as in the other studies, but the training data permitted multiple states to co-occur at the same time, so the input vectors were no longer one-hot, but rather multi-hot.
The hidden layer of all three networks compressed the categorical input vector down to a continuous linear representational space. One of our objectives was to demonstrate that the network could recover conceptual spaces of varying dimensionalities, and so the size of this hidden layer varied systematically between networks. In Study 3a the hidden layer was composed of three embedding units; in Study 2b it composed of two embedding units; and in Study 3c it was composed of a single linear activation unit. Adding additional hidden layers with nonlinear activation functions did not improve performance (see Supplementary Materials).
Finally, the output layer of each network was used to predict which mental state was most likely to occur next in the sequence. The numbers of units in the output layers matched the numbers of units in the input layers: 60 for Studies 3a and 3b, and 18 for Study 3c. Since only one state could occur at a time in the transition sequences in Studies 3a and 3b, we used a softmax activation function for the output layers in those studies. Since multiple states could occur at the same time in the training data for Study 3c, we instead used a sigmoid activation function for its output layer.
All neural networks were constructed in Python 3.8.12 (Van Rossum, 2007) using Tensorflow 2.7 (Abadi et al., 2016). The networks were fit using the Adam optimizer with the default learning rate of .001. In Studies 3a and 3b, we used a categorical cross-entropy loss function. In Study 3c we used a binary cross-entropy loss function.
Neural network training.
The training data for the neural networks in Studies 3a and 3b were identical. The data consisted of a sequence of 354,000 mental states. This sequence was generated by a random walk through a transition probability matrix between 60 human mental states (Figure 7A). The random walk was initiated on the most common state (“thought”), and then allowed to walk randomly from there according to an established transition probability matrix, to create the rest of the sequence. The transition probability matrix was generated from average human ratings of the transitions between 60 mental states, collected in a prior investigation (Thornton & Tamir, 2017). These transition ratings were validated against experience sampling data and found to be highly accurate. We used this set of 60 states for these two studies because they are representative of the broader conceptual space of mental states with respect to a wide range of dimensions (Tamir et al., 2016). Recurrences – that is, transitions from a state to itself – were prohibited, and the corresponding cells of the transition probability matrix were set to zero. To create a proper transition probability matrix from the human ratings, the rows of the rating matrix were normalized such that they each summed to one. The length of the sampled sequence was selected to provide the opportunity to observe 100 of each possible transition among the 60 states. The networks in Studies 3a and 3b were trained in a single epoch, with batch size set to 1.
Study 3c used a different training dataset, consisting of actual emotion transitions observed in experience sampling data collected in a previous investigation (Trampe et al., 2015). Consistent with our previous preprocessing of these data, we removed observations with missing data case-wise, and dropped participants with only one emotion report, since these participants could not furnish any transitions (Thornton & Tamir, 2017). The remaining data consisted of 66,492 emotion reports made by 10,739 French and Belgian participants about 18 emotions (9 positive and 9 negative): pride, love, hope, gratitude, joy, satisfaction, awe, amusement, alertness, anxiety, contempt, offense, guilt, disgust, fear, embarrassment, sadness, and anger (Philippot et al., 2003). Participants could report multiple emotions (median = 2 per report). The median participant completed four emotion reports (range: 2–257), with a median separation of 56.8 h (range = 29 s to 432 d). As previously reported, the length of the separation had minimal impact on the structure of the transitions, and we therefore did not consider it when training the neural network on these data (Thornton & Tamir, 2017).
To train the neural network to predict these emotion transitions in Study 3c, we treated each participant was a separate epoch, and set the batch size equal to the number of transitions that the participant had reported. This effectively meant that the network observed each participant’s full set of transitions, and then updated its weights between participants. The training cycled through each participant 10 times, with the participants presented to the network in a different random order on each cycle.
Neural network evaluation.
To assess the accuracy of the networks in Studies 3a and 3b, the fully trained networks were tested on a new sequence of 10,000 states, generated in the same way as the training sequence. Accuracy was calculated as the percentage of correctly predicted transitions. The networks’ accuracies were compared to the maximal possible accuracy, given the nature of the data-generating process. The maximum possible accuracy was calculated based on the transition probability matrix used to generate the training and testing sequences. The most accurate predictions possible for any Markov sequence will always be achieved by guessing the highest probability transition from the current state. For example, if the highest transition probability from “excited” was to “happy” then in the long run, maximum possible accuracy will be achieved by always guessing “happy” when one observes “excited”. To numerically compute the maximum possible accuracy, we averaged the maximum transition probability in each row of the transition probability matrix. Since different states occur with different frequencies, and therefore contribute more or less transitions, we weighted this average by the expected frequencies of each state.
Note that even though this is the maximum possible accuracy for these data, it is not guaranteed to be high in absolute terms. This is because many different state transitions may have similar likelihood, lowering the maximum. Nonetheless, the maximum possible accuracy makes a useful benchmark against which to compare the perform of the artificial neural networks. Because of the compression implied by the small hidden layers of these networks, they do not have sufficient parameters to simply memorize the transition probability matrix and achieve the maximum possible accuracy. How close they come despite the limitation provides insight into the underlying dimensionality of the transitions.
We did not compute the accuracy of the neural network trained in Study 3c because we do not control the data generating process in this case. As such we cannot conclusively estimate the maximum possible accuracy. Since Study 3c also used a different set of states than Studies 3a and 3b, the accuracy cannot be compared to the raw accuracies in those studies either. Due to the lack of comparisons, the accuracy in Study 3c is not interpretable on its own.
The learned structure of mental states.
After each neural network had been trained and tested, we evaluated the representational structure it had learned. We did so by extracting the weights that connected the input layer to the hidden layer. This allowed us to place each of the mental states into a dimensional space: 3d in Study 3a, 2d in Study 3b, and 1d in Study 3c.
Next, we compared each neural network’s dimensional space to a conceptual description of mental states with a matching dimensionality. We compared the 3-dimensional space to the 3d Mind Model; the 2-dimensional space to the Circumplex Model; and the 1-dimensional model to the dimension valence. To determine the location of each mental state on the dimensions of the 3d Mind Model (rationality, social impact, and valence) and the Circumplex Model (valence and arousal) we used human ratings of the 60 states collect in a previous investigation (Tamir et al., 2016). In Study 3c, we instead encoded the 18 emotions using binary values on a single dimension (valence) based on the original design of the experience sampling survey, which entailed 9 positive and 9 negative emotions (Philippot et al., 2003).
The orientation of the representational space learned by the neural networks was arbitrary; the networks had no “incentive” to maximize the interpretability (i.e., simple structure) of its weights. This made it difficult to compare to the 3d Mind Model or Circumplex dimensions. (For example, imagine comparing two maps of the same city when one’s latitude and longitude are rotated with respect to the other.) To address this problem, we aligned the neural network space to 3d Mind Model/Circumplex space using the Procrustes transform. To avoid overfitting this transformation, we fit the transform on 30/60 states, and applied the optimal rotation to the other half. We then correlated the transformed neural network dimensions with the corresponding Circumplex or 3d Mind Model dimensions. The procedure was repeated 10 times with different split-halves to ensure the stability of the results. The results reported in the text represent averages across these iterations. For visualization purposes (Figure 7), it was necessary to apply the Procrustes transform to the complete set of states at once. These results did not substantially overfit relative to the cross-validated results. This was not necessary for Study 3c because the space was unidimensional, so its 1d representation was directly correlated with valence without rotation. In the case of the multidimensional models, we also examined the cross-loadings to determine the extent of 1–1 matching between the network and model.
Results
Study 3 tested whether mental state dynamics – and the goal of predicting mental states – are sufficient to explain mental state concepts. We did so by training a neural network to learn to predict future mental states. This neural network successfully learned to predict future states from current states: at the end of training, the neural networks in Studies 3a and 3b predicted mental state transitions in the validation sequence with accuracies of 2.38% and 2.35%, respectively. Given the transition probability matrix from which the state sequence was generated, chance accuracy was 1.67% (1/60 states). The maximum possible accuracy was 3.02%. The neural networks far exceeded chance performance, and reached 78.75% and 77.76% of the maximum possible accuracy, respectively. This result indicates that a high proportion of the transition structure of human mental states can be described using a relatively low-dimensional space. Note that this low maximum is expected for at least three reasons: i) our definition of accuracy is very strict, in that it requires prediction of the exact state, and near-misses count for nothing, ii) in the real world, people have access to many other forms of information to predict other’s mental state, and iii) real-world inter-mental state dynamics are likely not confined solely to Markovian (i.e., memory-less) dynamics, and so information available here is impoverished.
We next tested whether the neural networks had spontaneously learned to represent mental states using dimensions identified by prior psychological work. Specifically, in Study 3a, we compared the network’s 3d representation to the dimensions of the 3d Mind Model. The network’s dimensions were robustly correlated human judges of where states placed on the conceptual dimensions (Figure 7C): rationality (r = .53, p = .0024), social impact (r = .78, p = 5.36 × 10−8), and valence (r = .88, p = 1.68 × 10−12). In Study 3b, we compared the network’s 2d representation to the dimensions of the Circumplex Model. The network’s dimensions were correlated human judges of where states placed on the conceptual dimensions (Figure 7C): valence (r = .94, p = 4.15 × 10−20), arousal (r = .42, p = .019). The cross-loadings (mis-matched correlations) of the dimensions were considerably higher for the Circumplex Model (rs = .44 and .30) in comparison with the 3d Mind Model (max |r| = .23). This suggests that the 2d network may not be sufficient to capture the full range of states presented in the sequence. This may be due to the presence of cognitive states in addition to affective states: the Circumplex Model was derived to explain only the latter. Finally, in Study 3c, we compared the network’s 1d representation to unidimensional valence, observing a correlation of |r| = .73, p = .00058.
Discussion
Study 3 offers strong evidence that dynamics of real human mental states can explain the conceptual structures that people apply to those states. Neural networks trained to predict mental state transitions spontaneously learned similar conceptual dimensions to those that humans use to understand those states. The networks successfully recovered 3d, 2d, and 1d conceptual representations identified by prior work in psychology. These representational structures allowed the networks to achieve nearly the maximum possible accuracy in their predictions, despite using highly compressed representations. These results suggest that the statistical regularities of real-life mental state dynamics – combined with the goal of predicting those dynamics – may be sufficient to explain the conceptual structure people apply to those mental states. This does not mean that dynamics are the only features that shape how people understand mental states. However, it does mean that other features may not be necessary to explain most of the conceptual structure in this domain, expect insofar as those features are necessary to infer which mental states others are experiencing in the first place. Incorporating static features into training artificial neural networks may provide an avenue for future comparisons of the static and dynamic accounts of mental state concepts.
Study 3 provides important evidence for the external validity and generalizability of our findings, complementing the controlled behavioral experiments in Studies 1 and 2. Study 3 examined a large set of real human mental states, rather than small set of arbitrary states considered in the behavioral studies. We measured the transitions probabilities between these states in two different ways: using human ratings of the transitions in Studies 3a and 3b, a method validated in previous work (Thornton & Tamir, 2017), and using experience sampling to directly measure natural emotion transitions in the field in Study 3c. Across the three experiments in Study 3, we explore conceptual structures with different dimensions and dimensionalities, demonstrating that the neural networks can recover each of those we examine. This indicates that our findings generalize across the different conceptual structures, and are not uniquely tied to one particular model of mental state concepts. That said, some individual dimensions were better captured than others. This may reflect the tendency of artificial neural networks to learn the more important structure in data (i.e., that accounts for more variance in the outcome) before learning finer-grained structure. Finally, Study 3c provides initial evidence for the cross-cultural generalizability of our findings, because the experience-sampling data was collected outside of the United States, in a language other than English.
General Discussion
People rely on a rich conceptual structure to understand each other’s mental states. Here we investigated the origins of this structure: what shapes the way people think about thoughts and feelings? Our results provide a clear answer to this question: mental state dynamics shape mental state concepts. As mental state dynamics unfold, we see mental state concepts follow in tow. Across nine behavioral experiments, the higher the transition probability between a pair of states, the more people inferred that they were conceptually similar. The dynamics were translated into concepts by embedding mental states into a geometric space. In three artificial neural network experiments, networks trained with the sole goal of predicting real-world mental state dynamics spontaneously rediscovered conceptual structures including the 3d Mind Model (Thornton & Tamir, 2020a), Circumplex Model (Russell, 1980), and unidimensional valence. Together these results demonstrate that statistical regularities in mental state dynamics – and the goal of predicting these dynamics – shape the conceptual structure of mental states.
This paper highlights the importance of dynamics to understanding mental state concepts. A more static account of mental state concept begins with the idea that states are associated with certain features – such as physiology, expressions, or stimuli – and that people infer similarity between states based on how many features they share (Ekman, 1992; Nummenmaa et al., 2018; Skerry & Saxe, 2015). We enrich this static view by highlighting the fact that mental states are not static. Instead, the sequence with which mental states unfold contains vital information, like the order of words in a sentence. Anticipating how these sequences of states unfold allows people to make accurate social predictions (Zhao et al., 2018). Indeed, the way people conceptualize mental states appears optimized for this goal of prediction. Considering the transition dynamics between states thus broadens the space of influences on mental state concepts and enriches the static account of the origins of these concepts.
The dynamic and static accounts each offer unique sources of information about mental state concepts. Even when they predict entirely different patterns of conceptual similarity, as in Study 1g and Study 2a-b, people integrate both sources of knowledge to make their ultimate concept judgements. These experiments showed a stronger impact of static features than dynamic ones on similarity ratings. However, this relative strength should be interpreted with caution. We did not tailor the strength of the two signals in this experiment to match the strengths of the static and dynamic signals that humans encounter in the real world. The static features in this experiment were always perfectly reliable – which they are not in real life – while the dynamic information was probabilistic. We also provided a much smaller amount of dynamic information than participants would encounter over years of life. Additionally, in Study 2a-b, we observed a much larger effect of dynamic vs. static features on participants choices about which alien states to match with human states. This suggests that dynamics may provide a more generalizable basis than static features for translating mental state concepts across different agents.
In the real world, the dynamic and static features of mental states are not orthogonal. For example, the dynamics of confusion may lead it to transition frequently to frustration; both confusion and frustration may be expressed with similar static facial movements, like a furrowed brow. If these static and dynamics are highly correlated in the real world, they might reinforce each other to generate a single conceptual structure, rather than compete with each other, as in our experiment. Moreover, the results of Study 2 suggest that static and dynamic features may play complementary roles in shaping mental states concepts: transition dynamics may provide the “geometry” of the conceptual space (i.e., which states are more similar vs. difference) whereas static features may determine the “orientation” of the conceptual space (e.g., which pole of a dimension such as valence is positive vs. negative).
Although the static and dynamic accounts may complement each other, the present results hint that the dynamic account alone may be sufficient to explain the real-world structure of mental state concepts. In Study 3, we trained neural networks to predict naturalistic transitions between mental states. The networks learned 1d, 2d, and 3d representations that closely approximated corresponding conceptual structures used by humans. The fact that the neural network learned these representations spontaneously without access to any static features of these states suggests that statistical regularities in mental state dynamics – and the goal of predicting them – maybe sufficient to explain the fundamental structure of mental state concepts. One need not dismiss the role of static features in mental state concepts on this basis alone. However, taking this deflationary account seriously may prove useful for honing our scientific understanding of static mental state features.
The results of Study 1f may help to explain why dimensional models of mental states – such as the 3d Mind Model (Tamir et al., 2016; Thornton & Tamir, 2020a) and Circumplex Model (Posner et al., 2005; Russell, 1980) – have enjoyed considerable success in affective science. The results indicate that people spontaneously use a geometric space to translate mental state dynamics into concepts. By representing mental states in a geometric space, these theories approximate the way the mind approaches the computational challenge of turning dynamics into concepts.
The present results align with a growing literature on predictive coding (Friston & Kiebel, 2009; Huang & Rao, 2011). This literature suggests that prediction is one of the brain’s primary computational goals, a goal that shapes how the brain represents the world. Rather than reactively representing incoming information, predictive coding argues that the brain actively predicts its inputs, representing the world in terms of likely futures. So far, this theory has primarily been tested within low-level sensory processes like vision and audition (Hohwy et al., 2008; Rao & Ballard, 1999; Vuust et al., 2009) or word acquisition (Saffran et al., 1996). However, we and others have argued that it can also shed light on higher-level processes, like action prediction (Kilner et al., 2007; Thornton & Tamir, 2020b, 2021), emotion (Ruba et al., 2022), and theory of mind (Koster-Hale & Saxe, 2013; Tamir & Thornton, 2018). The present results support this contention, indicating that the goal of prediction may help explain even one of the most abstract domains of cognition: mental state knowledge. In doing so, the present study aligns with recent findings indicating that dynamics, such as co-occurrences and transition probabilities, shape the structure of representations in other domains such as objects (Bonner & Epstein, 2021) and motor sequences (Lynn et al., 2020).
This view is also highly compatible with the constructionist perspective on emotion, which suggests that emotion words are categories learned for the purpose of predicting and interpreting signals from basic affect and context (Barrett, 2017a). The constructionist view focuses more on predicting one’s own state (e.g., to maintain allostasis) while we focus more on predicting others’ states (e.g., to anticipate others’ actions and plan one’s response). Both perspectives clearly recognize the value inherent in predicting minds. That said, constructive accounts are also compatible with a static featural account of mental state concepts, at least at the cultural rather than individual level of analysis (Lindquist et al., 2022). The present findings complement the constructionist perspective by providing a new mechanistic explanation for how and why individual instances of emotion – which are highly variable – are translated into emotion concepts – which are comparatively stable.
The present findings connect affective science to recent computer science research on distributional semantics (Mikolov et al., 2013). Distributional semantic systems such as word embeddings learn to represent the meaning of words by arranging them within high-dimensional vector spaces. The closer two words are in such a space, the more similar they generally are in meaning. The locations of words within this space are dictated by statistical regularities in natural language such as co-occurrences and transition probabilities, in much the same way that representations of mental states in the present investigation are shaped by their transition dynamics. This parallel may hint that linguistic approach to representation learning may generalize well to explaining affective cognition. However, it may also point the way to limitations that may be shared with distributional semantics. For instance, distributional semantics (and artificial neural networks in general) assume a continuously differentiable space of meaning. Although this assumption works fairly well in many cases, there are significant cases in which it fails – such as logical and combinatorial operations. Neural networks can memorize examples of such operations but cannot perform the general rule without help form symbolic systems. This suggests that, in humans, the use of other specialized reasoning systems may be necessary to complement mental state understanding in some instances.
Limitations
Several limitations should contextualize the interpretation of the present results. First, the experimental task used in Study 1 lacked naturalism in several respects, which may undermine the generalizability of these results to real-world contexts. This limitation was necessary to achieve the experimental control we sought, and to avoid interference from people’s existing conceptualization of real mental states. To address this limitation, in Study 2 we reintroduced a number of important naturalistic elements, such as a continuous latent state space which must be inferred from noisy manifest indicators. Additionally, in Study 3 we directly studied real-world mental state dynamics, albeit through the lens of artificial rather than human perceivers. The convergent evidence from these investigations helps to mitigate the lack of naturalism in Study 1.
Second, the experimental samples in Study 1 and Study 2 were composed entirely of US American participants from Amazon Mechanical Turk. These samples are not representative of all US American, or all humans – for instance, they skewed noticeably younger and more male than the US population. Thus, readers should be cautious in extrapolating these results, particularly to cultures substantially different from that of the US. We started to address this concern in Study 3c, in which we relied on a large sample of French and Belgian participants. Although these participants are likewise predominantly Westerners, these data do license broader cross-cultural generalization than reliance upon the Study 1–2 samples alone. More broadly, theories that we consider in Studies 2a&b have also received cross-cultural validation in the previous literature (Russell & Lewicka, 1989; Thornton et al., 2022). For example, the 3d Mind Model has been validated in cross-cultural text analyses across 57 countries, 17 languages, and 2000 years of history (Thornton et al., 2021). The fact that this conceptual structure generalizes across so many cultures – and is spontaneously rediscovered in Study 3 by an artificial system that is not even human – suggests that our present findings may apply widely. Future research should attempt to replicate and extend these findings with more diverse samples. Of particular interest may be the investigation of cultures that place relatively little emphasis on mental states as opposed to other social features, such as actions (Gendron et al., 2014).
Third, as we indicated in the introduction, there are limits to the scope of this investigation. We do not investigate why certain mental state concepts acquire linguistic labels (i.e., words) whereas others do not. We also do not attempt to explain the propositional content of either specific mental states (e.g., what someone is angry about) or mental state concepts (i.e., their dictionary definitions). Based on the limitations of distribution semantic approach for representing the logical structure of language (e.g., negations) or algebraic operations, we suspect that the current approach is ill-suited to explaining propositional mental state information, such as the truth or falsity of a belief. Additionally, we do not touch on the issue of causal, rather than purely predictive, representations of mental states (Ho et al., 2022). These are all important topics, but separate investigations are required to do them justice, and relate them to the present findings.
Fourth, we relied heavily on explicit judgments – particularly of conceptual similarity – throughout Studies 1 and 2. Translating potentially complex mental representations into scalar rating responses is a nontrivial mental operation, and considerable ink has been split on the question of how the requisite calculations are made (Shepard, 1987; Tversky, 1977). We attempted to partially mitigate this issue in Study 2 via the incorporation of other types of responses, such as reaction times and free response items. However, further work on this topic is needed. In this regard, neuroimaging may prove a useful tool for assaying the process of mental state concept formation. Methods such as fMRI could assess the emergence of nascent mental state concepts in real time as they are forming, without the need to disrupt the learning process to solicit behavioral responses. This may allow us to achieve an even more mechanistic understanding of the algorithm underlying the representation learning we have investigated here. This may clarify precisely how operations such as the (partial) symmetrizing of transition probabilities into conceptual similarity judgments actually occurs.
Finally, our investigation of mental state dynamics was limited to a particular type of social dynamics: inter-mental state transition dynamics. There are likely other forms of relevant dynamics, such as co-occurrences, intra-state dynamics, or state-action/action-state dynamics, that likely inform the conceptual representations people form of real-world mental states (Tamir & Thornton, 2018). Such dynamics may also inform other domains of social cognition, and contribute to explaining the conceptual structure of domains such as action or situation representation. Moreover, our investigation was limited to the influence of a particular type of inter-mental state transition dynamics: purely Markovian dynamics. Markovian dynamics mean that the next state depends entirely on the previous state, and not any earlier states. Although Markovian transition dynamics offer a useful first-order approximation of mental state dynamics, we doubt that real-world dynamics are memory-less in this way. Indeed, there is considerable evidence that emotions demonstrate hysteresis (history-dependence) in a way that would violate a Markovian assumption (Goldenberg et al., 2022; Hao, 2017; Sacharin et al., 2012). As we alluded to earlier, confidence followed by sadness seems to tell a very different story from confidence followed by joy, and these different sequences likely make different predictions about people’s future states. To address this issue, in Study 2 we constructed a continuous state space which contained a history-dependent dynamic: emotional momentum (Eldar et al., 2016). Despite this inclusion, we still observed an effect of first-order transition probabilities on conceptual similarity. In future research we hope to incorporate a broader range of dynamic features into the framework established here.
Implications
The results of the present investigation carry significant practical implications. First, they suggest that artificial systems could learn reasonable approximations of the structure of mental state concepts simply by observing state dynamics – they need not experience these states first-hand. Indeed, we provide direct demonstrations of this process in Study 3. This insight outlines a path by which artificial socio-affective systems could learn and use conceptual information about mental states directly from the environment. Second, the present findings also carry significant clinical implications. Many prevalent mental health disorders are characterized by severe social dysfunction (Baron-Cohen, 1997; Couture et al., 2006; Fett et al., 2011). For example, individuals with autism (Sasson et al., 2013), schizophrenia (Kohler et al., 2010), or social anxiety disorder (Hezel & McNally, 2014) often misperceive the mental states of others. If this misperception prevents people from observing typical mental state dynamics, they would be at a distinct disadvantage when predicting others’ future states. Abnormal first-hand experiences with mental states, as experienced by individuals with mood disorders (Cohen & Minor, 2010; Peralta & Cuesta, 1998), might likewise prevent people from learning typical state dynamics, and therefore, concepts. Studying patients’ abilities to experience and track these dynamics may yield insights into ameliorating these deficits. Moreover, neural networks could test potential interventions in silico before expending time and resources on clinical studies.
Conclusion
For decades, research on mental states – particularly emotions – has focused on questions about how these states are organized. Are states organized in terms of continuous dimensions or discrete categories? If dimensions, are there two (Russell, 1980) or three (Tamir et al., 2016; Thornton & Tamir, 2020a)? If categories, are there six (Ekman, 1992), or 27 (Cowen & Keltner, 2017)? Answering these “how” questions is critical to understanding human social and affective life. However, it is also crucial to investigate the origins of this conceptual structure, whatever form it ultimately takes. Why are the states organized in the way they are? Since Darwin, many researchers have sought answers to this question in evolution (Darwin, 1872). However, it is a daunting task to trace the influence of natural selection on complex high-level cognitive functions such as mental state representation. Here we provide an answer based upon a computational analysis: the structure of mental state concepts can be explained by the goal of predicting naturally occurring statistical regularities in mental state dynamics. Although this answer is more proximal than its evolutionary alternative, it can inform the quest for those ultimate answers. It casts light on the computational goal for which the social brain has been optimized by evolution – both biological and cultural – and learning. We hope that in the future, the answer to this why question can also lead us to more precise and fulfilling answers to the question of how the domain of mental states is organized.
Supplementary Material
Acknowledgments
This work was supported by NIMH grant R01MH114904 to D.I.T. The authors declare no conflicts of interest. Data and code are freely available on the Open Science Framework: (https://osf.io/4m9kw/). Author contributions: Conceptualization: M.A.T., and D.I.T; Methodology: M.A.T., M.R., A.V., D.I.T; Software: M.R., A.V., M.A.T.; Validation: M.A.T.; Investigation: M.R., A.V., M.A.T.; Data curation: M.A.T.; Writing - Original Draft: M.A.T.; Writing - Review and Editing: M.A.T., M.R., D.I.T., Visualization: M.A.T., M.R., D.I.T; Supervision: M.A.T., D.I.T; Project Administration: M.A.T. and D.I.T.; Funding acquisition: D.I.T.
References
- Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, Devin M, Ghemawat S, Irving G, & Isard M (2016). Tensorflow: A system for large-scale machine learning. 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), 265–283. [Google Scholar]
- Adolphs R, Mlodinow L, & Barrett LF (2019). What is an emotion? Current Biology, 29(20), R1060–R1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baron-Cohen S (1997). Mindblindness: An essay on autism and theory of mind. MIT press. [Google Scholar]
- Barrett LF (2017a). How emotions are made: The secret life of the brain. Houghton Mifflin Harcourt. [Google Scholar]
- Barrett LF (2017b). The theory of constructed emotion: An active inference account of interoception and categorization. Social Cognitive and Affective Neuroscience, 12(1), 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, Adolphs R, Marsella S, Martinez AM, & Pollak SD (2019). Emotional expressions reconsidered: Challenges to inferring emotion from human facial movements. Psychological Science in the Public Interest, 20(1), 1–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, Khan Z, Dy J, & Brooks D (2018). Nature of emotion categories: Comment on Cowen and Keltner. Trends in Cognitive Sciences, 22(2), 97–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, Mesquita B, & Gendron M (2011). Context in emotion perception. Current Directions in Psychological Science, 20(5), 286–290. [Google Scholar]
- Bates D, Maechler M, Bolker B, Walker S, Christensen RHB, Singmann H, & Dai B (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48. [Google Scholar]
- Bonner MF, & Epstein RA (2021). Object representations in the human brain reflect the co-occurrence statistics of vision and language. Nature Communications, 12(1), 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borst C, Wieling W, Van Brederode JF, Hond A, De Rijk LG, & Dunning AJ (1982). Mechanisms of initial heart rate response to postural change. American Journal of Physiology-Heart and Circulatory Physiology, 243(5), H676–H681. [DOI] [PubMed] [Google Scholar]
- Champely S, Ekstrom C, Dalgaard P, Gill J, Weibelzahl S, Anandkumar A, Ford C, Volcic R, De Rosario H, & De Rosario MH (2018). Package ‘pwr.’ R Package Version, 1–2. [Google Scholar]
- Cohen AS, & Minor KS (2010). Emotional experience in patients with schizophrenia revisited: Meta-analysis of laboratory studies. Schizophrenia Bulletin, 36(1), 143–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couture SM, Penn DL, & Roberts DL (2006). The functional significance of social cognition in schizophrenia: A review. Schizophrenia Bulletin, 32(suppl_1), S44–S63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowen AS, & Keltner D (2017). Self-report captures 27 distinct categories of emotion bridged by continuous gradients. Proceedings of the National Academy of Sciences, 114(38), E7900–E7909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowen AS, & Keltner D (2018). Clarifying the conceptualization, dimensionality, and structure of emotion: Response to Barrett and colleagues. Trends in Cognitive Sciences, 22(4), 274–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darwin C (1872). The expression of the emotions in man and animals (Prodger P, Ed.). Oxford University Press, USA. [Google Scholar]
- Dayan P (1993). Improving generalization for temporal difference learning: The successor representation. Neural Computation, 5(4), 613–624. [Google Scholar]
- Dodell-Feder D, Koster-Hale J, Bedny M, & Saxe R (2011). FMRI item analysis in a theory of mind task. NeuroImage, 55(2), 705–712. [DOI] [PubMed] [Google Scholar]
- Ekman P (1992). An argument for basic emotions. Cognition & Emotion, 6(3–4), 169–200. [Google Scholar]
- Eldar E, Rutledge RB, Dolan RJ, & Niv Y (2016). Mood as representation of momentum. Trends in Cognitive Sciences, 20(1), 15–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fett A-KJ, Viechtbauer W, Penn DL, van Os J, & Krabbendam L (2011). The relationship between neurocognition and social cognition with functional outcomes in schizophrenia: A meta-analysis. Neuroscience & Biobehavioral Reviews, 35(3), 573–588. [DOI] [PubMed] [Google Scholar]
- Frijda NH (2004). Emotions and action. Feelings and Emotions: The Amsterdam Symposium, 158–173. [Google Scholar]
- Friston K, & Kiebel S (2009). Predictive coding under the free-energy principle. Philosophical Transactions of the Royal Society B: Biological Sciences, 364(1521), 1211–1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gendron M, Roberson D, van der Vyver JM, & Barrett LF (2014). Perceptions of emotion from facial expressions are not culturally universal: Evidence from a remote culture. Emotion, 14(2), 251–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldenberg A, Schöne J, Huang Z, Sweeny TD, Ong DC, Brady TF, Robinson MM, Levari D, Zaki J, & Gross JJ (2022). Amplification in the evaluation of multiple emotional expressions over time. Nature Human Behaviour, 6(10), 1408–1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao Y (2017). Dynamic emotion transitions based on emotion hysteresis. 2017 Seventh International Conference on Affective Computing and Intelligent Interaction (ACII), 606–610. [Google Scholar]
- Hezel DM, & McNally RJ (2014). Theory of mind impairments in social anxiety disorder. Behavior Therapy, 45(4), 530–540. [DOI] [PubMed] [Google Scholar]
- Ho MK, Saxe R, & Cushman F (2022). Planning with Theory of Mind. Trends in Cognitive Sciences. [DOI] [PubMed] [Google Scholar]
- Hohwy J, Roepstorff A, & Friston K (2008). Predictive coding explains binocular rivalry: An epistemological review. Cognition, 108(3), 687–701. [DOI] [PubMed] [Google Scholar]
- Huang Y, & Rao RP (2011). Predictive coding. Wiley Interdisciplinary Reviews: Cognitive Science, 2(5), 580–593. [DOI] [PubMed] [Google Scholar]
- Hudson M, Nicholson T, Ellis R, & Bach P (2016). I see what you say: Prior knowledge of other’s goals automatically biases the perception of their actions. Cognition, 146, 245–250. [DOI] [PubMed] [Google Scholar]
- Jackson JC, Watts J, Henry TR, List J-M, Forkel R, Mucha PJ, Greenhill SJ, Gray RD, & Lindquist KA (2019). Emotion semantics show both cultural variation and universal structure. Science, 366(6472), 1517–1522. [DOI] [PubMed] [Google Scholar]
- Kahn AE, Karuza EA, Vettel JM, & Bassett DS (2018). Network constraints on learnability of probabilistic motor sequences. Nature Human Behaviour, 2(12), 936–947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilner JM, Friston KJ, & Frith CD (2007). Predictive coding: An account of the mirror neuron system. Cognitive Processing, 8(3), 159–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohler CG, Walker JB, Martin EA, Healey KM, & Moberg PJ (2010). Facial emotion perception in schizophrenia: A meta-analytic review. Schizophrenia Bulletin, 36(5), 1009–1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koster-Hale J, & Saxe R (2013). Theory of mind: A neural prediction problem. Neuron, 79(5), 836–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuznetsova A, Brockhoff PB, & Christensen RHB (2017). lmerTest package: Tests in linear mixed effects models. Journal of Statistical Software, 82(13). [Google Scholar]
- Lindquist KA, Jackson JC, Leshin J, Satpute AB, & Gendron M (2022). The cultural evolution of emotion. Nature Reviews Psychology, 1–13. [Google Scholar]
- Litman L, Robinson J, & Abberbock T (2017). TurkPrime. com: A versatile crowdsourcing data acquisition platform for the behavioral sciences. Behavior Research Methods, 49(2), 433–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynn CW, Kahn AE, Nyema N, & Bassett DS (2020). Abstract representations of events arise from mental errors in learning and memory. Nature Communications, 11(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikolov T, Chen K, Corrado G, & Dean J (2013). Efficient estimation of word representations in vector space. ArXiv Preprint ArXiv:1301.3781. [Google Scholar]
- Momennejad I, Russek EM, Cheong JH, Botvinick MM, Daw ND, & Gershman SJ (2017). The successor representation in human reinforcement learning. Nature Human Behaviour, 1(9), 680–692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nummenmaa L, Hari R, Hietanen JK, & Glerean E (2018). Maps of subjective feelings. Proceedings of the National Academy of Sciences, 115(37), 9198–9203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshausen B, & Field D (1996). Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, 381(6583), 607–609. [DOI] [PubMed] [Google Scholar]
- Peralta V, & Cuesta MJ (1998). Lack of insight in mood disorders. Journal of Affective Disorders, 49(1), 55–58. [DOI] [PubMed] [Google Scholar]
- Philippot P, Schaefer A, & Herbette G (2003). Consequences of specific processing of emotional information: Impact of general versus specific autobiographical memory priming on emotion elicitation. Emotion, 3(3), 270–283. [DOI] [PubMed] [Google Scholar]
- Posner J, Russell JA, & Peterson BS (2005). The circumplex model of affect: An integrative approach to affective neuroscience, cognitive development, and psychopathology. Development and Psychopathology, 17(03), 715–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. (2015). R: A language and environment for statistical computing. R Foundation for Statistical Computing. [Google Scholar]
- Rao RP, & Ballard DH (1999). Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nature Neuroscience, 2(1), 79–87. [DOI] [PubMed] [Google Scholar]
- Ruba AL, Pollak SD, & Saffran JR (2022). Acquiring complex communicative systems: Statistical learning of language and emotion. Topics in Cognitive Science. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell JA (1980). A circumplex model of affect. Journal of Personality and Social Psychology, 39(6), 1161–1178. [Google Scholar]
- Russell JA, & Lewicka M (1989). A Cross-Cultural Study of a Circumplex Model of Affect. Journal of Personality and Social Psychology, 57(5), 848–856. [Google Scholar]
- Sacharin V, Sander D, & Scherer KR (2012). The perception of changing emotion expressions. Cognition & Emotion, 26(7), 1273–1300. [DOI] [PubMed] [Google Scholar]
- Saffran JR, Aslin RN, & Newport EL (1996). Statistical learning by 8-month-old infants. Science, 274(5294), 1926–1928. [DOI] [PubMed] [Google Scholar]
- Sasson NJ, Nowlin RB, & Pinkham AE (2013). Social cognition, social skill, and the broad autism phenotype. Autism, 17(6), 655–667. [DOI] [PubMed] [Google Scholar]
- Saxe R, & Kanwisher N (2003). People thinking about thinking people: The role of the temporo-parietal junction in “theory of mind.” NeuroImage, 19(4), 1835–1842. [DOI] [PubMed] [Google Scholar]
- Schapiro AC, Rogers TT, Cordova NI, Turk-Browne NB, & Botvinick MM (2013). Neural representations of events arise from temporal community structure. Nature Neuroscience, 16(4), 486–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepard RN (1987). Toward a universal law of generalization for psychological science. Science, 237(4820), 1317–1323. [DOI] [PubMed] [Google Scholar]
- Skerry AE, & Saxe R (2015). Neural representations of emotion are organized around abstract event features. Current Biology, 25(15), 1945–1954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamir DI, & Thornton MA (2018). Modeling the predictive social mind. Trends in Cognitive Sciences, 22(3), 201–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamir DI, Thornton MA, Contreras JM, & Mitchell JP (2016). Neural evidence that three dimensions organize mental state representation: Rationality, social impact, and valence. Proceedings of the National Academy of Sciences, 113(1), 194–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton MA, Reilly BJ, Slingerland E, & Tamir D (2022). The 3d Mind Model characterizes how people understand mental states across modern and historical cultures. Affective Science, 3(1), 93–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton MA, & Tamir DI (2017). Mental models accurately predict emotion transitions. Proceedings of the National Academy of Sciences, 114(23), 5982–5987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton MA, & Tamir DI (2020a). People represent mental states in terms of rationality, social impact, and valence: Validating the 3d Mind Model. Cortex, 125, 44–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton MA, & Tamir DI (2020b). Perceiving actions before they happen: Psychological dimensions scaffold neural action prediction. Social Cognitive and Affective Neuroscience, 16(8), 807–815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton MA, & Tamir DI (2021). Perceptions accurately predict the transitional probabilities between actions. Science Advances, 7(9), eabd4995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton MA, Vyas AD, Rmus M, & Tamir D (2019). Transition dynamics shape mental state concepts. https://osf.io/4m9kw/ [DOI] [PMC free article] [PubMed]
- Thornton MA, Weaverdyck ME, & Tamir DI (2019). The social brain automatically predicts others’ future mental states. Journal of Neuroscience, 39(1), 140–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trampe D, Quoidbach J, & Taquet M (2015). Emotions in Everyday Life. PloS One, 10(12), e0145450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tversky A (1977). Features of similarity. Psychological Review, 84(4), 327–352. [Google Scholar]
- Van Rossum G (2007). Python Programming Language. USENIX Annual Technical Conference, 41, 36. [Google Scholar]
- Vuust P, Ostergaard L, Pallesen KJ, Bailey C, & Roepstorff A (2009). Predictive coding of music–brain responses to rhythmic incongruity. Cortex, 45(1), 80–92. [DOI] [PubMed] [Google Scholar]
- Waytz A, Morewedge CK, Epley N, Monteleone G, Gao JH, & Cacioppo JT (2010). Making sense by making sentient: Effectance motivation increases anthropomorphism. Journal of Personality and Social Psychology, 99(3), 410–435. [DOI] [PubMed] [Google Scholar]
- Wong B (2011). Color blindness. Nature Methods, 8(6), 441. [DOI] [PubMed] [Google Scholar]
- Zaki J, Bolger N, & Ochsner K (2009). Unpacking the informational bases of empathic accuracy. Emotion, 9(4), 478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Z, Thornton MA, & Tamir D (2018). Accurate Emotion Prediction in Dyads and Groups and its Potential Social Benefits. PsyArXiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


