Abstract
The SARS-CoV-2 virus was first detected in December 2019, which prompted many researchers to investigate how the virus spreads. SARS-CoV-2 is mainly transmitted through respiratory droplets. Symptoms of the SARS-CoV-2 virus appear after an incubation period. Moreover, the asymptomatic infected individuals unknowingly spread the virus. Detecting infected people requires daily tests and contact tracing, which are expensive. The early detection of infectious diseases, including COVID-19, can be achieved with wastewater-based epidemiology, which is timely and cost-effective. In this study, we collected wastewater samples from wastewater treatment plants in several cities in North Dakota and then extracted viral RNA copies. We used log-RNA copies in the model to predict the number of infected cases using Quantile Regression (QR) and K-Nearest Neighbor (KNN) Regression. The model's performance was evaluated by comparing the Mean Absolute Percentage Error (MAPE). The QR model performs well in cities where the population is >. In addition, the model predictions were compared with the basic Susceptible-Infected-Recovered (SIR) model which is the golden standard model for infectious diseases.
Keywords: SARS-CoV-2, COVID-19, Quantile regression, K-nearest neighbor regression, Mean absolute percentage error, SIR model
Introduction
The SARS-CoV-2 virus emerged in December 2019 and has severely affected the world. Scientists and researchers have been working tirelessly to understand and combat the virus as it spreads rapidly around the world. One critical aspect of the virus that has garnered much attention is its transmission. Transmission of SARS CoV-2 is thought to be principally through respiratory droplets, although there is growing evidence that airborne transmission may also play a role [1,2]. Some individuals may remain asymptomatic even after the incubation period, posing significant challenges for contact tracing and frequent testing that can be both time-consuming and costly [[3], [4], [5], [6], [7], [8]]. Therefore, early detection and containment of COVID-19 disease is essential for preventing transmission and limiting its spread.
Wastewater-based epidemiology (WBE) has emerged as a promising approach to detecting the presence of infectious agents including SARS-CoV-2, in a cost-effective manner. Wastewater surveillance involves analyzing sewage samples from communities, which can provide information on the prevalence of diseases within that population [9]. The approach has been used in the past to detect outbreaks of diseases such as polio and hepatitis A, and it is now being applied to COVID-19 [[10], [11], [12], [13]]. The virus can be shedded in the feces, urine, blood, and sputum of infected individuals [[14], [15], [16], [17], [18], [19]] and these shedded viral particles can be detected in wastewater samples. Therefore, wastewater surveillance can capture the presence of the SARS-CoV-2 virus even in asymptomatic individuals, enabling early detection of the disease before it spreads further [[20], [21], [22], [23]].
Moreover, wastewater surveillance is a timely and cost-effective method for detecting infectious agents. Traditional methods of testing, such as individual testing or population-wide testing, can be expensive and time-consuming, requiring significant resources. In contrast, wastewater surveillance can provide information on the prevalence of the disease in an entire community at a fraction of the cost of individual testing. The cost of COVID-19 testing can vary based on the type of the test, healthcare provider, and location. Personal tracking tests involve individual testing, where people are tested for COVID-19 using methods such as PCR (polymerase chain reaction) tests, antigen tests, or antibody tests. On average, PCR tests are considered more accurate but may be more expensive than rapid antigen tests. The cost of clinical testing is estimated to be $5.80 per person per year in Latin America and the Caribbean from September 2020 to September 2021 [24].
The cost of wastewater sample analysis can be more cost-effective when considering large populations, as it allows monitoring of a community's infection trends without testing each individual separately. The amount charged can fluctuate relative to the magnitude and regularity of screening, the technology employed, and the research laboratory administering the examination. However, it's considered a more economical approach for tracking COVID-19 in large groups of people. The cost of wastewater testing per person per year is estimated as $0.50 [24]. Thus, researchers and public health entities are increasingly interested in the potential for surveillance of pathogens such as SARS-CoV-2 through routine or episodic testing of wastewater.
Background
SARS CoV-2 has been shown to be reliably shed in the stool of infected patients for up to seven months [25]. A study published by Park et al. [4] investigated gastrointestinal symptoms of COVID-19 patients with mild and asymptomatic symptoms, as well as the shredding of the SARS-CoV-2 virus into their feces. Zhang et al. [26] performed a molecular and serological investigation of COVID-19 patients and found that viral RNA can be detected in anal swabs and blood samples when viral nucleotide has not been detected in oral swabs. Xu et al. [27] clinically investigated the characteristics of pediatric SARS-CoV-2 infection in 10 children and found that there is potential for fecal viral excretion and that testing contaminated water is a viable method for the detection of viral loads. Van Doorn et al. [28] performed a systematic review and meta-analysis of studies based on the fecal-oral transmission of the SARS-CoV-2 virus and found that testing stool samples or anal swabs are more reliable than testing respiratory samples. Additionally, Cheung et al. [29] conducted a systematic review and meta-analysis, and a cohort study and found that stool samples were positive for virus RNA despite negative respiratory samples. Therefore, wastewater surveillance is a good approach to detecting the SARS-CoV-2 virus since it does not rely on the person having symptoms, nor presenting with illness. However, the likelihood of transmission of SARS-CoV-2 virus from sewage-contaminated water or food is very low as reported by Jones et al. [30]. Furthermore, the replicability of SARS-CoV-2 virus is very limited as mentioned by Cerrada-Romero et al. [31].
Furthermore, there are several studies in which wastewater-based epidemiology is used for estimating COVID-19 cases [[32], [33], [34], [35], [36]]. Ahmed et al. [37] collected untreated wastewater samples from one suburban pumping station and two wastewater treatment plant catchments in urban areas in Southeast Queensland and developed a simple equation to estimate positive cases based on the total number of viral RNA copies in wastewater and the number of SARS-CoV-2 RNA copies shed in stool by infected individuals. McMahan et al. [38] implemented a Susceptible-Exposed-Infected-Recovered (SEIR) model to predict the number of infected individuals using the SARS-CoV-2 RNA mass rates in sewage samples. Fazil et al. [39] proposed a stochastic wastewater-based SEIR model, which is similar to the SEIR model proposed by McMahan et al. [38]
Objective
During an outbreak of infectious disease, hospitals need to expand their capacity by adding emergency facilities and increasing medical supplies, staff, and medications. Control measures such as mask mandates, vaccine mandates, social distancing, and business closures are difficult to implement and often controversial. Government and public health authorities must have accurate estimates of disease incidence and prevalence in order to make sound policy decisions. As noted earlier, traditional surveillance methods are severely limited in estimating disease burden when it comes to SARS-CoV-2 transmission due to asymptomatic spread, home testing, and delays in reporting. This study aims to provide further evidence of the utility of wastewater testing for SARS CoV-2 virus to estimate the burden of infection in selected North Dakota populations during key periods of the pandemic, using the K-Nearest Neighbor (KNN) Algorithm [40] and Quantile regression (QR) [41] compared with the Susceptible-Infected-Recovered (SIR) model [42]. By doing so, we can provide an effective method for estimating the number of infected individuals during an outbreak in different populations.
Data collection, viral isolation, and quantification
Wastewater samples were obtained from the intake stream of wastewater treatment plants in various cities in North Dakota. The GLS compact samplers (Teledyne ISCO) were used to collect 24-h composite samples. Subsequently, 250 ml of the composite samples were treated at 60 °C for 30 min and then centrifuged at 4500 g for 10 min at room temperature. The supernatant (100 ml) was collected and HCl was added to adjust the samples to pH 4. Samples were vacuum filtered through 0.45 μm MCE membranes (Millipore Sigma). RNeasy PowerMicrobiome kits (Qiagen) were used to extract total RNA from the membranes. Samples were eluted in 50 μl of elution buffer and 5 μl was used for quantitative real-time PCR (Polymerase Chain Reaction). For PCR reactions, we used N1 primers from the 2019-nCoV RUO kit by Integrated DNA Technologies (IDT), along with the Applied Biosystems TaqPath 1-Step RT-qPCR Master Mix. To construct the standard curve, we employed the 2019-nCoV_N Positive control plasmid from IDT.
Statistical methodology
The primary aim of our research is to estimate the number of COVID-19 cases through the analysis of SARS-CoV-2 RNA copies derived from wastewater samples. To achieve this, we will use a combination of statistical modeling and quantitative analysis. For a selected time, we will employ three distinct models to predict the number of infected cases based on natural logarithm-transformed data of viral RNA copies as the independent variable. These models include the KNN regression model, the QR model, and the basic SIR model. The following section summarizes some basic ideas behind each of the above models.
K-nearest neighbor algorithm (KNN)
KNN algorithm is a supervised machine learning algorithm, which can be used to solve classification and regression problems. The KNN model was first developed by Evelyn Fix and Joseph Hodges in 1951 [40]. In this method, the similarities of the features of k-nearest neighbors are used to predict the outcome variable. The Euclidean distance measure, Manhattan distance, and Minkowski distance methods are commonly used to calculate the similarities of nearest neighbors. Suppose is the predicted target variable value for a given input data point and is the target variable value of the nearest neighbor to the input data point. If is the number of nearest neighbors to consider, then,
| (1) |
To perform KNN regression, first, we need to calculate the distance between the input data point and all the data points in the dataset. Then, using the distance metric, select k-nearest neighbors and use their target variable values to calculate for the input data point. The smaller the k value, the more likely the model will overfit, and the larger the k value, the more likely it will underfit. Therefore, we performed 10-fold cross- validation to select the optimal using the tidymodels package in R. In most of the cities or 11 were observed as optimal . Therefore, we used for all cities for convenience.
Quantile regression (QR)
Quantile regression [41] is a type of regression analysis that models the relationship between the independent variables and the quantile of the dependent variable. Unlike ordinary least-square regression models, QR models need no assumptions. The QR model for the quantile for observation for variables can be written as
| (2) |
The coefficients of the model can be estimated by solving the following minimization problem [43].
| (3) |
Where, and is the error of a single data point. This minimization involves the sum of absolute deviations which places equal weight on all observations regardless of their magnitude. In this study, we used a specific case of QR model where . This corresponds to the median quantile regression estimator, which is robust to outliers in the dependent variable.
Susceptible-infected-recovered (SIR) compartmental model
The SIR model is the first deterministic epidemic model, introduced by Kermack and McKendrick [44]. In this model, the population is divided into three compartments, such as Susceptible (S), Infected (I), and Recovered (I) and we assumed a fixed total population and no new births or deaths. Further, we assumed that all the infected individuals are contagious, and the recovered individuals are immune to the disease. Then, the dynamic of the model compartments can be evaluated using the ordinary differential equations (ODE) as follows.
| (4) |
| (5) |
| (6) |
Where,: Total population,
: Infection Rate - The expected amount of people an infected person infects per day.
: The proportion of infected recovering per day.
Our research aimed to estimate the prevalence of COVID-19 in various cities located in North Dakota State. To achieve this goal, we utilized two distinct modeling techniques, namely KNN regression and QR. In both models, we utilized the natural logarithm-transformed RNA copies as the explanatory variable. We then generated predictions using these models and compared their results with those obtained from the basic SIR model. This comparison allowed us to assess the accuracy and reliability of each approach in estimating the number of SARS-CoV-2 infections in the study population.
By comparing the outcomes of these three models, our study provides valuable insights into the efficacy and accuracy of different modeling techniques in predicting the prevalence of COVID-19 disease in various population groups. This information can help inform public health policies and strategies to manage the ongoing pandemic effectively. Our research has the potential to contribute to efforts aimed at mitigating the spread of the virus and controlling its impact on the affected communities.
Results
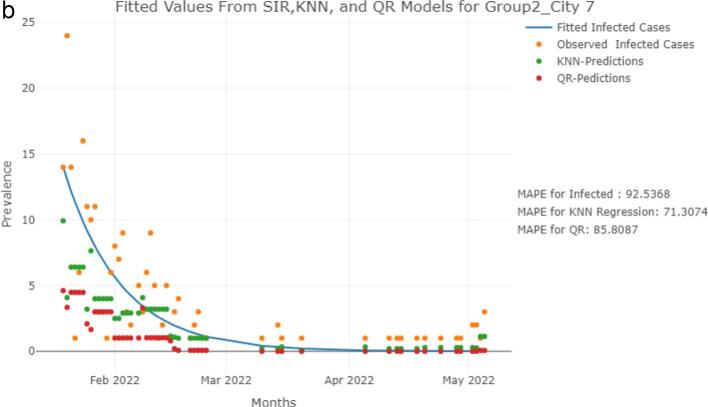
We analyzed a dataset that included variables such as date of data collection, RNA copies, and clinical SARS-CoV-2 infections for various cities in North Dakota. All the analysis were performed using the R software version 4.1.3. The data was collected between January 1st,2021, to May 5th,2022. The prevalence of SARS-CoV-2 infections was predicted for this time frame using KNN regression and QR models with log-transformed RNA copies as explanatory variables. Further, we fitted an SIR model using clinical cases for the period of January 19th, 2022, to May 5th, 2022. We selected only a certain period to fit the SIR model as SIR model is less effective in predicting multiple waves of the virus. We compared these fitted values from SIR model with the KNN and QR models predictions of January 19th, 2022, to May 5th, 2022. Further, we compared the model performance by location, where Group 1 cities have a population and Group 2 cities have a population [45]. The fitted values from the models were compared with the observed counts of SARS-CoV-2 infections and the results are presented in Fig. 1a and Fig. 1b for two specific cities, where Group 1 City 8 has a population and Group 2 City 7 has a population . The model fits for the other cities are provided in the appendix.
Fig. 1.
a. Observed and fitted values comparisons for SIR, KNN, and QR Models for a City in Group 1.
b Observed and fitted values comparisons for SIR, KNN, and QR Models for a City in Group 2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Note: The graphs presented inFig. 1a for a city (population ) and Fig. 1b for a city (population ) depict a comparison between the observed (orange points) and fitted values of SARS-CoV-2 infections, employing three different models, namely SIR (blue line), KNN (green points), and QR (red points). The number of positive cases was estimated using log-RNA copies as the explanatory variable in the KNN and QR models, whereas the observed clinical cases were used to fit the SIR model.
We used mean absolute percentage errors (MAPE) of observed and fitted values to evaluate the performance of the models.
| (7) |
Where, n: Number of observations.
Actual value.
Fitted value.
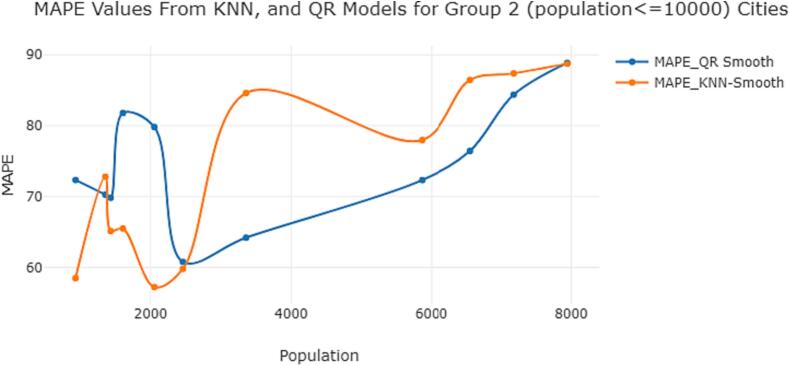
Our results showed that the performance of the models varied between cities, with the SIR model outperforming both KNN and QR models in many cities. In addition, we found that the QR model performed better than the KNN model in Group 1 areas, while the KNN model was effective in predicting the prevalence of COVID-19 in some Group 2 areas. We presented a comparison of the MAPE values of the KNN and QR models in various Group 1 and Group 2 areas of North Dakota. The results are summarized in Table 1 and Fig. 2 for Group 1 areas, and Table 2 and Fig. 3 for Group 2 areas. These comparisons provide insight into the relative performance of the KNN and QR models in predicting the prevalence of COVID-19 cases across different regions of North Dakota. (See Table 3.)
Table 1.
MAPE values of QR and KNN models for Group 1 (population ) cities.
| City | MAPE (QR) | MAPE (KNN) |
|---|---|---|
| City 1 | 94.14 | 127.32 |
| City 2 | 72.73 | 93.82 |
| City 3 | 86.07 | 109.33 |
| City 4 | 94.21 | 107.61 |
| City 5 | 88.52 | 105.85 |
| City 6 | 108.72 | 140.95 |
| City 7 | 90.93 | 116.68 |
| City 8 | 115.69 | 139.52 |
Fig. 2.
MAPE values comparisons for KNN, and QR models for Group 1 (population ) cities. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Note: The graph compares the MAPE values of KNN (orange line) and QR (blue line) models for Group 1 areas.
Table 2.
MAPE values of QR and KNN models for Group 2 (population ) cities.
| City | MAPE (QR) | MAPE (KNN) |
|---|---|---|
| City 1 | 72.34 | 58.50 |
| City 2 | 70.27 | 72.79 |
| City 3 | 69.84 | 65.14 |
| City 4 | 81.80 | 65.49 |
| City 5 | 79.81 | 57.22 |
| City 6 | 60.79 | 59.81 |
| City 7 | 64.21 | 84.61 |
| City 8 | 72.33 | 77.98 |
| City 9 | 76.44 | 86.44 |
| City 10 | 84.39 | 87.39 |
| City 11 | 88.87 | 88.73 |
Fig. 3.
MAPE values comparisons for KNN, and QR models for Group 2 (population ) cities. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Note: The graph compares the MAPE values of KNN (orange line) and QR (blue line) models for Group 2 areas.
Table 3.
Wilcoxon-Sign Rank test results.
| Area | Test Statistics | P-Value |
|---|---|---|
| Group 1 | 0 | 0.007813 |
| Group 2 | 36 | 0.8311 |
The graph presented in Fig. 2 shows that the mean absolute percentage error of the KNN method is consistently higher than that of the QR method for Group 1 areas. Based on this finding, we suggest using the QR model to predict the number of COVID-19 cases in cities with larger populations. This model is likely to provide more accurate predictions compared to the KNN model in such areas, as indicated by its lower MAPE values. By selecting the appropriate modeling technique, we can improve our ability to estimate the prevalence of COVID-19 disease and develop effective strategies to manage its spread in areas with higher populations.
The graph provided in Fig. 3 indicates that the MAPE values obtained from the KNN method are lower for Group 2 areas, particularly when the population size is very small. The graph also illustrates that the QR method performs well for larger populations. Overall, these findings suggest that the choice of modeling technique should be informed by the population size of the study area. In Group 2 areas with smaller populations, the KNN method may provide more accurate predictions. In contrast, for larger populations, the QR method may be a better choice. By carefully selecting the appropriate modeling technique, we can improve the accuracy of our COVID-19 disease predictions and inform effective public health interventions.
In our study, we evaluated the relative performance of QR and KNN models in predicting COVID-19 prevalence in different North Dakota regions. The Wilcoxon-Sign Rank test was applied to compare the MAPE values of QR and KNN models in Group 1 and Group 2 areas. The Wilcoxon-Sign Rank Test is a non-parametric statistical test, used to determine whether two related samples are drawn from populations with the same distribution. As we used the same data in both methods, MAPE values can be considered as matching pairs.
The Wilcoxon signed rank test results indicate that there is no statistically significant difference () in the results obtained from the QR and KNN methods when applied to data from Group 2 areas. However, a significant difference exists between the two methods () when applied to data collected from Group 1 areas.
These findings suggest that the choice of modeling technique should be adapted to the characteristics of the study area. In Group 2 areas, either the QR or KNN method can be used to obtain similar results. However, in Group 1 cities, the QR method may be a more suitable choice for predicting the spread of COVID-19 disease compared to the KNN method. By considering these factors when choosing a modeling approach, we can improve the accuracy of our predictions and inform effective public health interventions.
Discussion
Our analysis was based on data collected from sewage samples and clinical cases observed in several North Dakota cities. The SIR model based on clinical cases, alone predicted the prevalence of COVID-19 cases better than the KNN and QR methods. Using clinical cases alone for surveillance can be expensive and does not always account for asymptomatic cases. Therefore, using wastewater analysis is a more cost-effective and efficient way to determine the prevalence of COVID-19 cases in a community before the disease spreads.
It is worth noting that the KNN and QR methods also used clinical cases as a dependent variable in their models, which may have contributed to some limitations. The number of COVID-19 cases is based on the entire city, while our water treatment plants may not collect wastewater from the entire city. Capturing the required viral loads can also be difficult due to the collected small volume of wastewater samples. This would lead to an underestimation of the number of cases. Despite possible limitations, such as incomplete coverage of sewage in certain areas and lower viral load in smaller sample volumes, our study provides a good estimate of the prevalence of COVID-19 in whole cities using sewage samples.
Overall, our study highlights the potential of wastewater-based analysis as a valuable tool for disease surveillance in communities. This approach requires further development and optimization to address limitations but holds great promise for better surveillance of COVID-19 disease and other infectious diseases in the future.
CRediT authorship contribution statement
Bong-Jin Choi: Methodology, Conceptualization, Formal analysis, Visualization, Writing - original draft, Writing - review & editing. Scott Hoselton: Data curation, Writing - review & editing. Grace N. Njau: Writing – review & editing, Project administration. I.G.C.G. Idamawatta: Visualization, Writing - review & editing. Paul Carson: Writing – review & editing. John McEvoy: Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Support for this project was provided in part by the Centers for Disease Control and Prevention: Epidemiology and Laboratory Capacity for Infectious Diseases, National Initiative to Address COVID-19 Health Disparities Among Populations at High-Risk and Underserved, Including Racial and Ethnic Minority Populations and Rural Communities Cooperative Agreements, and Center for Diagnostic and Therapeutic Strategies in Pancreatic Cancer at the North Dakota State University
Appendix
References
- 1.Jayaweera M., Perera H., Gunawardana B., Manatunge J. Transmission of COVID-19 virus by droplets and aerosols: a critical review on the unresolved dichotomy. Environ Res. Sep. 2020;188:109819. doi: 10.1016/j.envres.2020.109819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhao X., Liu S., Yin Y., Zhang T., Chen Q. Airborne transmission of COVID-19 virus in enclosed spaces: an overview of research methods. Indoor Air. Jun. 2022;32(6):e13056. doi: 10.1111/ina.13056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.J. Tan et al., “Transmission and clinical characteristics of asymptomatic patients with SARS-CoV-2 infection,” Future Virol, p. 10.2217/fvl-2020–0087, doi: 10.2217/fvl-2020-0087. [DOI]
- 4.Bai Y., et al. Presumed asymptomatic carrier transmission of COVID-19. JAMA. Apr. 2020;323(14):1406–1407. doi: 10.1001/jama.2020.2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rothe C., et al. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N Engl J Med. Mar. 2020;382(10):970–971. doi: 10.1056/NEJMc2001468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hu Z., et al. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China. Sci China Life Sci. May 2020;63(5):706–711. doi: 10.1007/s11427-020-1661-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nikolai L.A., Meyer C.G., Kremsner P.G., Velavan T.P. Asymptomatic SARS coronavirus 2 infection: invisible yet invincible. Int J Infect Dis. Nov. 2020;100:112–116. doi: 10.1016/j.ijid.2020.08.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Johansson M.A., et al. SARS-CoV-2 transmission from people without COVID-19 symptoms. JAMA Netw Open. Jan. 2021;4(1):e2035057. doi: 10.1001/jamanetworkopen.2020.35057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.CDC, “National Wastewater Surveillance System,” Centers for Disease Control and Prevention. Accessed: Sep. 01, 2022. [Online]. Available: https://www.cdc.gov/healthywater/surveillance/wastewater-surveillance/wastewater-surveillance.html.
- 10.Berchenko Y., et al. Estimation of polio infection prevalence from environmental surveillance data. Sci Transl Med. Mar. 2017;9(383):eaaf6786. doi: 10.1126/scitranslmed.aaf6786. [DOI] [PubMed] [Google Scholar]
- 11.Anis E., et al. Insidious reintroduction of wild poliovirus into Israel, 2013. Eurosurveillance. Sep. 2013;18(38):20586. doi: 10.2807/1560-7917.ES2013.18.38.20586. [DOI] [PubMed] [Google Scholar]
- 12.Hellmér M., et al. Detection of pathogenic viruses in sewage provided early warnings of hepatitis a virus and norovirus outbreaks. Appl Environ Microbiol. Nov. 2014;80(21):6771–6781. doi: 10.1128/AEM.01981-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.La Rosa G., et al. Surveillance of hepatitis a virus in urban sewages and comparison with cases notified in the course of an outbreak, Italy 2013. BMC Infect Dis. Jul. 2014;14(1):419. doi: 10.1186/1471-2334-14-419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pan Y., Zhang D., Yang P., Poon L.L.M., Wang Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect Dis. Apr. 2020;20(4):411–412. doi: 10.1016/S1473-3099(20)30113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kim J.-M., et al. Detection and isolation of SARS-CoV-2 in serum, urine, and stool specimens of COVID-19 patients from the Republic of Korea. Osong Public Health Res Perspect. Jun. 2020;11(3):112–117. doi: 10.24171/j.phrp.2020.11.3.02. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li X., Zhang S., Shi J., Luby S.P., Jiang G. Uncertainties in estimating SARS-CoV-2 prevalence by wastewater-based epidemiology. Chem Eng J. Jul. 2021;415:129039. doi: 10.1016/j.cej.2021.129039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Peng L., et al. SARS-CoV-2 can be detected in urine, blood, anal swabs, and oropharyngeal swabs specimens. J Med Virol. 2020;92(9):1676–1680. doi: 10.1002/jmv.25936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Crank K., Chen W., Bivins A., Lowry S., Bibby K. Contribution of SARS-CoV-2 RNA shedding routes to RNA loads in wastewater. Sci Total Environ. Feb. 2022;806:150376. doi: 10.1016/j.scitotenv.2021.150376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li X., et al. SARS-CoV-2 shedding sources in wastewater and implications for wastewater-based epidemiology. J Hazard Mater. Jun. 2022;432:128667. doi: 10.1016/j.jhazmat.2022.128667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kumar M., Joshi M., Patel A.K., Joshi C.G. Unravelling the early warning capability of wastewater surveillance for COVID-19: a temporal study on SARS-CoV-2 RNA detection and need for the escalation. Environ Res. May 2021;196:110946. doi: 10.1016/j.envres.2021.110946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kumar M., et al. Lead time of early warning by wastewater surveillance for COVID-19: geographical variations and impacting factors. Chem Eng J. Aug. 2022;441:135936. doi: 10.1016/j.cej.2022.135936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Medema G., Heijnen L., Elsinga G., Italiaander R., Brouwer A. Presence of SARS-Coronavirus-2 RNA in sewage and correlation with reported COVID-19 prevalence in the early stage of the epidemic in the Netherlands. Environ Sci Technol Lett. Jul. 2020;7(7):511–516. doi: 10.1021/acs.estlett.0c00357. [DOI] [PubMed] [Google Scholar]
- 23.Randazzo W., Truchado P., Cuevas-Ferrando E., Simón P., Allende A., Sánchez G. SARS-CoV-2 RNA in wastewater anticipated COVID-19 occurrence in a low prevalence area. Water Res. Aug. 2020;181:115942. doi: 10.1016/j.watres.2020.115942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Manuel D., Amadei C.A., Campbell J.R., Brault J.-M., Veillard J. World Bank; Washington, DC: Jan. 2022. Strengthening public health surveillance through wastewater testing: An essential investment for the COVID-19 pandemic and future health threats. Accessed: Aug. 31, 2022. [Online]. Available: https://openknowledge.worldbank.org/handle/10986/36852. [Google Scholar]
- 25.Natarajan A., et al. Gastrointestinal symptoms and fecal shedding of SARS-CoV-2 RNA suggest prolonged gastrointestinal infection. Med. Jun. 2022;3(6) doi: 10.1016/j.medj.2022.04.001. pp. 371–387.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang W., et al. Molecular and serological investigation of 2019-nCoV infected patients: implication of multiple shedding routes. Emerg Microbes Infect. 2020;9(1):386–389. doi: 10.1080/22221751.2020.1729071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Xu Y., et al. Characteristics of pediatric SARS-CoV-2 infection and potential evidence for persistent fecal viral shedding. Nat Med. Apr. 2020;26(4) doi: 10.1038/s41591-020-0817-4. Art no 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.van Doorn A.S., Meijer B., Frampton C.M.A., Barclay M.L., de Boer N.K.H. Systematic review with meta-analysis: SARS-CoV-2 stool testing and the potential for faecal-oral transmission. Aliment Pharmacol Ther. 2020;52(8):1276–1288. doi: 10.1111/apt.16036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cheung K.S., et al. Gastrointestinal manifestations of SARS-CoV-2 infection and virus load in fecal samples from a Hong Kong cohort: systematic review and meta-analysis. Gastroenterology. Jul. 2020;159(1):81–95. doi: 10.1053/j.gastro.2020.03.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jones D.L., et al. Shedding of SARS-CoV-2 in feces and urine and its potential role in person-to-person transmission and the environment-based spread of COVID-19. Sci Total Environ. Dec. 2020;749:141364. doi: 10.1016/j.scitotenv.2020.141364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cerrada-Romero C., et al. Excretion and viability of SARS-CoV-2 in feces and its association with the clinical outcome of COVID-19. Sci Rep. May 2022;12(1) doi: 10.1038/s41598-022-11439-7. Art. no. 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vallejo J.A., et al. Modeling the number of people infected with SARS-COV-2 from wastewater viral load in Northwest Spain. Sci Total Environ. Mar. 2022;811:152334. doi: 10.1016/j.scitotenv.2021.152334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Robotto A., et al. Wastewater-based SARS-CoV-2 environmental monitoring for Piedmont, Italy. Environ Res. Jan. 2022;203:111901. doi: 10.1016/j.envres.2021.111901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Matheri A.N., Belaid M., Njenga C.K., Ngila J.C. Water and wastewater digital surveillance for monitoring and early detection of the COVID-19 hotspot: industry 4.0. Int J Environ Sci Technol. Feb 2022 doi: 10.1007/s13762-022-03982-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jiang G., et al. Artificial neural network-based estimation of COVID-19 case numbers and effective reproduction rate using wastewater-based epidemiology. Water Res. Jun. 2022;218:118451. doi: 10.1016/j.watres.2022.118451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.La Rosa G., et al. First detection of SARS-CoV-2 in untreated wastewaters in Italy. Sci Total Environ. Sep. 2020;736:139652. doi: 10.1016/j.scitotenv.2020.139652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ahmed W., et al. First confirmed detection of SARS-CoV-2 in untreated wastewater in Australia: a proof of concept for the wastewater surveillance of COVID-19 in the community. Sci Total Environ. Aug. 2020;728:138764. doi: 10.1016/j.scitotenv.2020.138764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McMahan C.S., et al. COVID-19 wastewater epidemiology: a model to estimate infected populations. Lancet Planet Health. Dec. 2021;5(12):e874–e881. doi: 10.1016/S2542-5196(21)00230-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fazli M., Sklar S., Porter M.D., French B.A., Shakeri H. Oct. 20, 2021. Wastewater-Based Epidemiological Modeling for Continuous Surveillance of COVID-19 Outbreak. medRxiv, p. 2021.10.19.21265221. [DOI] [Google Scholar]
- 40.Silverman B.W., Jones M.C. E. Fix and J.L. Hodges (1951): an important contribution to nonparametric discriminant analysis and density estimation: commentary on Fix and Hodges (1951) Int Stat Rev. 1989;57(3):233–238. doi: 10.2307/1403796. [DOI] [Google Scholar]
- 41.Koenker R., Bassett G. Regression quantiles. Econometrica. 1978;46(1):33–50. doi: 10.2307/1913643. [DOI] [Google Scholar]
- 42.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc Royal Soc London Series A, Contain Papers Math Phys Char. 1927;115(772):700–721. [Google Scholar]
- 43.Rodriguez R.N. 2017. Five Things You Should Know about Quantile Regression. Accessed: Sep. 12, 2023. [Online]. Available: https://www.semanticscholar.org/paper/Five-Things-You-Should-Know-about-Quantile-Rodriguez/7e824688e34f6010ee203c86643b17ccbd9acf90. [Google Scholar]
- 44.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc Royal Soc London Series A, Contain Papers Math Phys Character. 1927;115(772):700–721. [Google Scholar]
- 45.U. C. Bureau, “City and Town Population Totals: 2020-2021,” Censusgov Accessed: Apr 28, 2023. [Online]. Available: https://www.census.gov/data/tables/time-series/demo/popest/2020s-total-cities-and-towns.html.