Abstract

Viable alternatives to scarce and expensive noble-metal-based catalysts are transition-metal carbides such as Mo and W carbides. It has been shown that these are active and selective catalysts in the hydrodeoxygenation of renewable lipid-based feedstocks. However, the reaction mechanism and the structure–activity relationship of these transition-metal carbides have not yet been fully clarified. In this work, the reaction mechanism of butyric acid hydrodeoxygenation (HDO) over molybdenum carbide (Mo2C) has been studied comprehensively by means of density functional theory coupled with microkinetic modeling. We identified the rate-determining step to be butanol dissociation: C4H9*OH + * → C4H9* + *OH. Then we further explored the possibility to facilitate this step upon heteroatom doping and found that Zr- and Nb-doped Mo2C are the most promising catalysts with enhanced HDO catalytic activity. Linear-scaling relationships were established between the electronic and geometrical descriptors of the dopants and the catalytic performance of various doped Mo2C catalysts. It was demonstrated that descriptors such as dopants’ d-band filling and atomic radius play key roles in governing the catalytic activity. This fundamental understanding delivers practical strategies for the rational design of Mo2C-based transition-metal carbide catalysts with improved HDO performance.
Keywords: molybdenum carbide, hydrodeoxygenation, heteroatom doping, linear-scaling relationships, descriptors
1. Introduction
The catalysis community is facing two grand challenges: (1) tackling over-reliance on nonrenewable fossil-based resources for materials, chemicals, and fuel production; (2) design and discovery of efficient catalysts based on earth-abundant elements. These two challenges need to be addressed together.1−3 The use of biomass as feedstock together with abundant transition-metal carbide based catalysts is therefore an integrated approach that can address both of these challenges.4
Traditionally, platinum-group metals (PGMs) are well-known for their high catalytic activity and stability while catalyzing a wide range of reactions involved in biomass valorization.5−8 However, PGMs are scarce, hence expensive, and susceptible to deactivation by impurities such as sulfur-based compounds (SOx) and nitrogen-based compounds (NOx) present in the feedstocks.9−11 Therefore, much work has been done to find viable alternative catalysts to PGMs, of which transition-metal carbides (TMCs),12−18 especially molybdenum carbide (Mo2C)19−25 and tungsten carbide (W2C),23−26 are most promising because they exhibit PGM-like properties due to their comparable electronic structures.
TMCs are synthesized by introducing C atoms in the transition metal’s lattice. Electronic structure studies showed that the valence s-p electrons from the C atoms combine with the s-p-d electrons from the transition metal, providing the TMCs with catalytic properties similar to those of PGMs.14,16,27−30 Also, it has been reported that the activity of a bulk transition-metal catalyst is largely governed by the presence of either a high or, in contrast, a specific low density of d electrons close to the Fermi level (EF).27,28 In the case of PGMs, the EF is present in a region where a high density of d-electrons is present, while the EF lies in the region of a low density of d electrons in the case of bulk TMs. However, in the case of TMCs, EF lies in the region of the intermediate level of d-electron states. Thus, the electronic structure of TMCs resembles that of PGMs, and as a result TMCs gain PGM-like catalytic properties. Furthermore, TMCs show resistance to deactivation by impurities in the bulk11,24 and are also a popular choice because of their mechanical hardness, thermal stability, and conductivity.12
Experimentally, TMCs have been shown to be active for reactions such as hydrogenation, hydrodeoxygenation, isomerization, methanation, etc.19−25,31 For instance, Oyama et al.14 reported that in reforming n-hexane at 670 K, a tungsten carbide (β-W2C) catalyst shows yields close to that of Pt/SiO2 (8.6% vs 11.6%), and β-W2C exhibits even better selectivity for isomerization products compared to that of Pt/SiO2 (71% vs 60%) for the same reaction. Stellwagen et al.23 performed experiments determining the activity and selectivity differences in W2C and Mo2C supported on carbon nanofibers for a stearic acid hydrodeoxygenation reaction. They observed that W2C catalysts were selective for alkene products, while Mo2C catalysts were selective toward oxygenates. The obtained alkenes and oxygenates are platform chemicals for synthesizing a wide range of value-added products. Interestingly, in contrast to W2C and Mo2C, conversion of stearic acid using PGMs such as Pd and Pt catalysts primarily yields heptadecane via a decarboxylation pathway, which shows that TMCs favor different mechanisms.32
Although the catalytic performance of TMCs has been investigated by experiments, an understanding of the underlying mechanisms and the intrinsic nature of active sites in many of the aforementioned reactions is still quite challenging. Density functional theory (DFT) has been used to identify the nature of active sites at the atomic level. For example, Shi et al. studied the structure and stability of different facets of the orthorhombic Mo2C using DFT. These authors took into consideration different facets such as (001), (010), (110), (100), (110), (101), (011), and (111) with all possible surface terminations (Mo; C; Mo/C) and found that the (011) facet with the mixed termination (Mo/C) is the most stable surface, followed by the (101) facet with mixed termination (Mo/C).33 Also, Wang et al. studied the CO adsorption equilibrium over (001), (101), and (201) facets of hexagonal Mo2C catalyst using DFT. These authors provided phase diagrams showing that a stable CO coverage can be obtained by tuning the temperature (T) and partial pressure (p) of CO for different facets of Mo2C.34 Additionally, these authors showed that the stability of a particular Mo2C facet can be tuned as a function of carbon chemical potential and the differences in surface termination (Mo vs Mo/C) explicitly influence the CO activation mechanism.35 Furthermore, DFT has been used to study reaction mechanisms over different Mo2C catalysts: e.g., Ren et al. showed that Mo2C is a highly selective catalyst for conversion of biomass-derived oxygenate to unsaturated hydrocarbons as it selectively cleaves C–O bonds and not C–C bonds.21 Shi et al.36 studied the HDO reaction mechanism of butyric acid to butane over a hexagonal Mo2C (101) surface within the DFT framework. The stepwise reaction mechanism was provided, and butanol dissociation was identified as the rate-determining step (RDS). These authors also studied water formation on Mo2C (001) and Mo2C (101) facets and established that the barrier for water formation is sensitive to the choice of the active Mo2C facet. Oliveira et al.37 also studied the HDO reaction mechanism of acrylic acid over orthorhombic Mo2C (001) within the DFT framework. Their proposed mechanism led to the conclusion that an alkane and water should be the main products, in line with experimental observations by Sousa et al.38 Another conclusion was that TMCs predominantly attack the C=O bonds as shown by Ren et al.21 as well, while PGMs favor activating C=C scission. Moreover, Wang et al. explored the change in adsorption energies of CO, H2, H2O, and CO2 over a stable hexagonal Mo2C (101) catalyst upon doping with metals such as Fe, Co, Ni, Cu, Pt, and Pd. These authors observed a strong influence of loading (0% vs 25% vs 50%) on the adsorption energies due to change in the electronic structure upon doping, which results in strong electron transfer from the metal to the surface in the case of transition metals, while this effect is less prominent in the case of Pt and Pd.39 These computational studies provided a fundamental basis for exploring the intrinsic nature of other promising Mo2C-based catalysts for the HDO reaction and established that butyric acid is a good model for investigating the HDO reaction mechanisms.
On the other hand, even though the catalytic activity and reaction mechanism of Mo2C catalysts are known to some degree from previous experimental and theoretical investigations, it is still not clear what the structure–activity relationships are. Many strategies have been proposed in the literature to understand such relationships, and most of them are based on the Sabatier principle40 and Brønsted–Evans–Polanyi (BEP)41,42 principle.43−45 For instance, Michaelides et al.46 performed ab initio calculations to determine a linear scaling relationship between the activation energies and reaction enthalpies for a broad range of surface-catalyzed reactions. Nørskov et al. have implemented the Sabatier and BEP principles in their works47−51 and developed a model, i.e., the Hammer–Nørskov model,52 to demonstrate that trends in adsorption energies over transition metals are governed by interactions between an adsorbate’s valences states and a metal’s d states. More recently, Gong et al.53−55 have used similar approaches in their studies for screening catalysts by means of interpretable intrinsic descriptors of activity. For example, these authors used a multidimensional approach in studying the redox activity of vanadium oxides upon doping.53 They showed that the p-band center is the most crucial descriptor governing the activity, and other descriptors emerging from the coordination environment such as an unoccupied d-band center and s- and d-band fillings also play important roles in tuning the oxygen activity.Such structure–activity relationships shed light on the intrinsic laws governing the external catalytic activities and provide an efficient approach for catalysts screening.
In the current study, we investigated the mechanism of all reaction steps involved in the hydrodeoxygenation (HDO) of the butyric acid reaction over the orthorhombic Mo2C (101) surface by DFT, to provide a detailed insight into the formation of oxygenates, alkenes, and alkanes. Even though the HDO mechanism of butyric acid has previously been studied over hexagonal Mo2C (101) catalyst,36 it was interesting to see how the most stable orthorhombic Mo2C catalyst promotes the HDO reaction. Hence, we used a stable corrugated orthorhombic Mo2C (101) catalyst.56 Throughout the text we refer to the orthorhombic phase of Mo2C as β-Mo2C. Butyric acid has been used as a model compound to mimic the nature of long-chain fatty acids derived from the biobased feedstock.36 The results obtained using DFT were then used as an input for a microkinetic model to derive surface coverages and degree of rate control (DRC) coefficients. DRC analysis showed that butanol dissociation is the RDS to which the overall rate of the reaction is the most sensitive. Subsequently, we doped the Mo site involved in this RDS with a range of transition metals to tune the activity of β-Mo2C. In addition, the key descriptors governing the structure–activity relationships of the doped β-Mo2C catalysts were identified. By analyzing the structure–activity relationships, we identified that dopants’ d-band filling and atomic radius are the two most relevant descriptors correlating well with the activity of doped β-Mo2C catalysts.
2. Computational Details
All the DFT57,58 calculations were performed with the Vienna ab initio Simulation Package (VASP.5.4.4 and VASP.6.2.1).59,60 The generalized gradient approximation (GGA) with PBE exchange and correlation functional was used to account for the exchange-correlation energy.61 The electron–ion interactions were described using the projected augmented wave (PAW) method and the plane-wave (PW) basis set.59,60 The convergence criterion for energy calculation and structure relaxation was set to an SCF threshold of 10–5 eV and a maximum force threshold of 0.05 eV/Å. Γ-centered k-meshes with sizes of 6 × 6 × 6 and 2 × 2 × 1 were used for sampling the Brillouin zone in the case of bulk and slab models, respectively. Gaussian-type smearing with a width of 0.05 eV was applied for the electronic energy density of states. To identify the transition states, the climbing-image nudged elastic band (CI-NEB) method62,63 was used, and frequency analysis was performed to confirm that there was only one imaginary frequency along the reaction coordinate. Dipole corrections were applied in the vacuum (z) direction. For CI-NEB calculations, a maximum force threshold of 0.10 eV/Å was implemented. The vdW interactions were described by the DFT-D3BJ method developed by Grimme et al.64,65
To study the catalytic activity of Mo2C toward HDO of butyric acid, we choose the orthorhombic (β) phase of Mo2C. From experimental phase diagrams, β-Mo2C has been concluded to be the most stable phase of Mo2C.33,66 X-ray diffraction (XRD) and DFT studies have also confirmed that β-Mo2C is the most stable phase.67−69 Low Miller index (100, 001) surfaces of β-Mo2C have been used for theoretical studies because of their high activities for hydrogenation reactions; however, they are less likely to dominate the surface area of as-synthesized β-Mo2C catalysts as predicted by Tacey et al.36,37,56 Therefore, in this work, we use the (101) catalytic surface as it has a more corrugated structure, making it a more dynamic catalytic surface and fetching unique catalytic properties.56 Additionally, the reactivity is explicitly dependent on the species present on the surface. In the case of β-Mo2C (101), the surface can have either one of Mo and C species or it can have both Mo and C species aka mixed-termination. It has been reported that mixed termination (Mo–C–Mo) enhances the stability of the catalytic surface but, at the same time, also provides a ridged structure which explicitly influences the reactivity of the surface.56 Hence, we considered using a mixed-terminated β-Mo2C (101) catalytic surface in this study.
The bulk structure of β-Mo2C was fully relaxed, and we obtained the lattice parameters a = 4.75 Å, b = 5.23 Å, and c = 6.05 Å, which are in good agreement with the experimentally reported values (a = 4.74 Å, b = 5.21 Å, c = 6.03 Å).67 From the optimized bulk, we cleaved a (101) surface and built a unit cell with a thickness of nine atomic layers (three stoichiometric layers of Mo2C), as shown in Figures S1 and S2 in the Supporting Information. A vacuum distance of 15 Å in the z direction was introduced to minimize interaction with the periodic images. After relaxing the atoms in the unit cell, we created a supercell of size 2 × 3 × 1, which was deemed to be a big enough surface for the HDO reaction. The bottom six atomic layers of the supercell were fixed to reduce the computational cost of the calculations and mimic the bulk.
The adsorption energies (Eads), reaction energies (ΔE), and activation barriers (Ea) were calculated as follows:
| 1 |
| 2 |
| 3 |
Here, Eslab+reactant is the total energy of the slab with a reactant adsorbed on it, Eslab is the total energy of the clean slab, Ereactant and Eproduct are the total energies of the reactant and product of each elementary reaction step, respectively, and Etransition state is the total energy of the transition state (TS). The zero-point energies have been corrected for all of the adsorption and desorption steps.
For descriptor identification, Bader charge analysis was done using code written by Henkelman et al.70 and the electronic structure parameters such as M (d-band center), NM (p-band center), M (d-band filling), and NM (p-band filling) derived from the density of states (DOS) were calculated using the Python pymatgen package.71
X-band filling (X = s, p, d) was calculated as
| 4 |
Here, ε means energy and ρ(ε) means the density of states.
The unoccupied d-band center was calculated as
| 5 |
The doping formation energies were calculated to estimate the stability of the doped Mo2C systems under Mo2C synthesis conditions.14,24 Since Mo2C catalysts are synthesized by performing carburization with CH4 and H2,30 we considered the possibility of doping heteroatom as follows:
The formation Gibbs free energies (ΔG) of doped Mo2-xMxC were calculated as follows:
| 6 |
Here, GMo2-xMxC is the Gibbs free energy of the slab upon doping with a hetero metal atom (M), GMo2C is the Gibbs free energy of the clean slab/pristine Mo2C, GMOy is the Gibbs free energy of the bulk of the most stable oxide phase of M at 600–700 °C, GMoO3 is the Gibbs free energy of the bulk of the most stable oxide phase of Mo at 600–700 °C, GH2 is the Gibbs free energy of H2, and GH2O is the Gibbs free energy of H2O.
In this method, the vibrational and PV contributions of solids were neglected and the Gibbs free energies of Mo2C and Mo2–xMxC solids were approximated as their respective electronic energies computed by DFT, considering that the temperature has a negligible influence on the systematic energy. The chemical potential of the gas-phase compounds H2 and H2O depends on the experimental temperature (T) and their corresponding partial pressures (p). We assume that it complies with the ideal gas law and that the chemical potential of gas-phase H2 and H2O at the reference state of 0 K is μH2(0K) = EH2 and μH2O(0K) = EH2O, respectively. At arbitrary T and p, they can then be written as
| 7 |
| 8 |
And thus, the formation Gibbs free energies (ΔG) can be written as
| 9 |
The MKMCXX package72 was used for the microkinetic modeling (MKM) simulations.73 MKM is a tool used to identify the critical intermediates and rate-determining elementary reactions. The chemokinetic network was modeled using a set of ordinary differential equations involving rate constants, surface coverages, and partial pressures of gas-phase species. Time integration of the differential equations was conducted using the linear multistep backward differential formula method with a relative and absolute tolerance of 10–8. The DFT results including the elementary reaction steps, forward/backward barriers, and forward/backward prefactors are provided in section S2 of the Supporting Information.
The rate constant (k) of an elementary reaction step is given as
| 10 |
where Q⧧ and Q are the partition functions of the activated complex and its corresponding initial state, respectively, and ΔEa is the activation energy.
To identify the steps that control the butyric acid consumption rate and the product distribution, we performed the degree of rate control (DRC) analysis, as developed by Kozuch and Shaik74,75 and popularized by Campbell.76
The DRC coefficient is defined as
| 11 |
3. Results and Discussion
3.1. HDO Reaction Mechanism of Butyric Acid over β-Mo2C (101) Surface
The overall balanced equation for the HDO reaction mechanism is
All elementary reaction steps are summarized in section 2 of the Supporting Information. In Tables S1 and S2, the reaction pathways and energetics for dissociation of H2 on the β-Mo2C (101) catalytic surface are summarized based on the DFT mechanism study. In this section the whole mechanism will be discussed as follows: (1) butyric acid to butanal; (2) butanal to butanol; (3) butanol to 2-butene; (4) 2-butene to butane.
3.1.1. Butyric Acid to Butanal
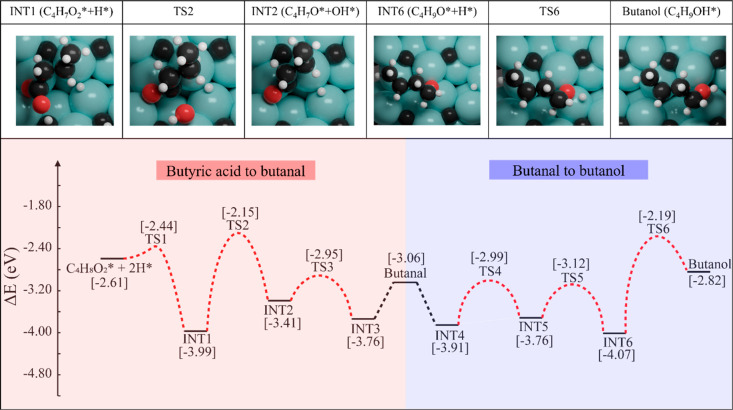
The reaction energy diagram is shown in Figure 1. As reported in the literature,36 butyric acid prefers to be adsorbed on the surface via metal (surface)–oxygen (reactant) interactions with an Eads value of −0.80 eV. Upon reactant adsorption, the H from the C–OH bond tends to exothermically dissociate and stabilize on the surface, as shown in Figure 1, INT1. Subsequently, breaking of the C–O bond and forming the OH group on the surface take place simultaneously, which requires an activation energy (Ea) of 1.84 eV, and this process (Figure 1, INT1 → INT2) is endothermic in nature (ΔE = 0.58 eV). The next step is hydrogenation of the C atom of the carbonyl group, which can be achieved with an activation barrier of 0.46 eV. The resulting product, butanal, is stable on the surface due to strong metal–carbon (reactant) and carbon (surface)–carbon (reactant) interactions, and its desorption from the surface is difficult (ΔE = 3.17 eV). The OH group on the surface can interact with H on the surface to form H2O (Tables S3 and S4).
Figure 1.
Reaction energy profile for the formation of butanal and butanol from butyric acid over the (101) surface of β-Mo2C. The local geometries of intermediates and transition states of the key reaction steps are highlighted on top.
3.1.2. Butanal to Butanol
To convert butanal to butanol, the first step (Figure 1, INT4 → INT5) is the hydrogenation of the terminal C (Ea = 0.92 eV; ΔE = 0.15 eV) and subsequent hydrogenation (Figure 1 INT6 → INT7) of O (Ea = 1.88 eV; ΔE = 1.25 eV). The hydrogenation order cannot be the other way around, as the resulting intermediate is unstable. Also, hydrogenation of O on the surface is a kinetically demanding process (Ea = 1.41 eV, ΔE = 0.55 eV) as reported in Tables S3 and S4, which is consistent with a previous report36 in the literature. The barrier for butanol desorption from the surface is 3.00 eV.
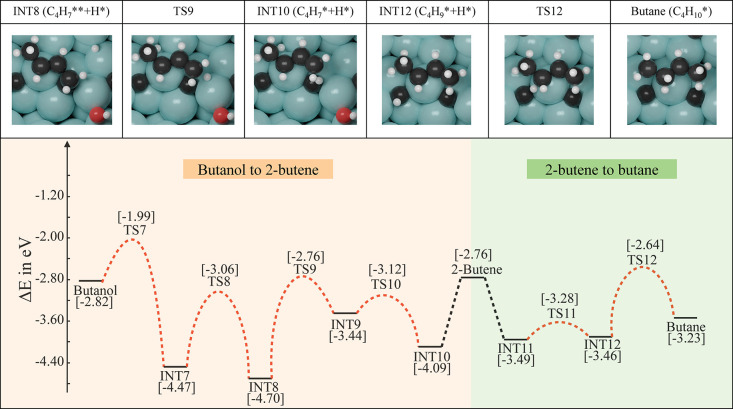
3.1.3. Butanol to 2-Butene
For the conversion of butanol to butene, pathways for both 1-butene and 2-butene formation were considered; however, we were unable to locate a transition state for the formation of 1-butene. The reaction energy diagram of butanol to 2-butene is shown in Figure 2. In the first step, activation of the C–OH bond in butanol takes place, which is kinetically and thermodynamically favorable (Ea = 0.83 eV; ΔE = −1.65 eV). Interestingly, the barrier for C–OH bond activation we obtained is significantly smaller than that reported by Shi et al.,36 i.e., 1.50 eV. This could be because that surface C atoms facilitate C–OH bond activation, while in ref (36) only Mo atoms are present on the surface. The obtained C4H9* (INT7) species is stable on the surface. In the next step, C4H9* undergoes dehydrogenation to produce a precursor, C4H7** (INT8), for 2-butene formation. This process involves H-transfer from C2 to the surface (Ea = 1.41 eV; ΔE = −0.13 eV), which also triggers H-transfer from C3 to the surface, as it was being stabilized by C3 from the reactant and Mo from the surface. This further stabilizes INT8 because of the strong C–C interaction between Creactant and Csurface. To push the reaction forward, the C1–Csurface bond cleavage was triggered by the diffusion of an H atom to Csurface (Figure 2, INT8 → INT9), which is kinetically difficult and thermodynamically endothermic (Ea = 1.94 eV; ΔE = 1.26 eV). The final step is hydrogenation of C1 to form 2-butene (Figure 2, INT9 → INT10). This step needs to overcome a barrier of 0.32 eV, and the reaction energy is −0.65 eV. The desorption barrier for 2-butene from the surface is 2.25 eV.
Figure 2.
Reaction energy profile for the formation of 2-butene and butane from butanol over the (101) surface of β-Mo2C. The local geometries of intermediates and transition states of the key reaction steps are highlighted on top.
3.1.4. 2-Butene to Butane
The final step in the HDO of butyric acid is the formation of butane. The C=C bond of 2-butene can be hydrogenated via a two-step mechanism. The 2-butene intermediate (INT11) is very stable on the surface (Eads = −2.76 eV). To promote the hydrogenation reaction (INT11 → INT12), surface H* needs to be activated. First, a one-step dual hydrogenation was considered. However, the 2-butene species resists hydrogenation by one of the H atoms because of its high stability. Hence, the hydrogenation steps were carried out via a two-step mechanism. C2 was first hydrogenated (Ea = 0.21 eV; ΔE = 0.03 eV; INT11 → INT12) followed by C3 hydrogenation (Ea = 0.82 eV; ΔE = 0.23 eV; INT12 → butane).
3.2. Microkinetic Modeling Based on DFT Results
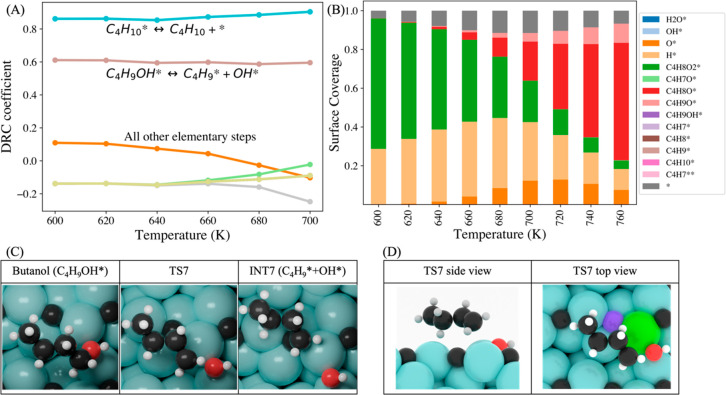
To further unravel the rate-determining step under experimental reaction conditions (T = 623 K, pH2 = 30 bar),24 MKM was performed, and the results are presented in Figure 3A,B. From the DRC analysis (Figure 3A), we could see that the overall reaction rate is the most sensitive to butanol dissociation and butane desorption elementary steps. As DFT-D3 is known to overestimate the binding energies of the reactants on the solid surface,64,77 the butanol dissociation elementary step is assigned to be the RDS, and the local geometries are highlighted in Figure 3C. It is important to highlight here that butanol dissociation was reported to be the RDS in the work of Shi et al.36 as well, in which they studied the HDO reaction of butyric acid over a hexagonal Mo2C (101) surface. From our DFT and MKM results, it is found that the (101) facet of the orthorhombic Mo2C with mixed surface termination is more active than the (101) facet of the hexagonal Mo2C with only Mo sites on the surface. The activation barrier for breaking the C–OH bond of butanol is 0.83 eV in our case, much lower than that over the hexagonal Mo2C (101) surface (Ea = 1.50 eV).36 Moreover, the surface coverage analysis (Figure 3B) as a function of T reveals that as the reaction moves forward, the coverage of oxygen on the surface is increasing, which hints toward the plausible reaction route to molybdenum oxycarbide formation during the reaction. This is consistent with the observation that water formation on the β-Mo2C (101) surface is kinetically (Ea = 1.37 eV) and thermodynamically (ΔE = 1.00 eV) unfavorable (Tables S3 and S4). Instead, the OH groups produced on the surface during the reaction can further dissociate to produce an O species on the surface, which could eventually lead to the formation of molybdenum oxycarbide (Ea = 0.86 eV; ΔE = −0.55 eV). Also, reaction orders of the reactants, i.e., butyric acid (C4H8O2) and gas-phase hydrogen (H2), are calculated as a function of T (section S8 in the Supporting Information). Figure S5 shows that at higher temperatures the hydrogen is easily accessible for the reaction; hence, increasing the concentration of H2 in the reaction could potentially speed up the reaction, while the reaction order of butyric acid is not very sensitive to the temperature. Selectivity analysis is shown in Figure S6. It is demonstrated that for all four products, i.e., butanal, butanol, 2-butene, and butane, butene is the main product over the surface of β-Mo2C (101) throughout the simulated reaction temperatures.
Figure 3.
(A) DRC coefficients for all the elementary reaction steps as a function of temperature. (B) Surface coverage as a function of temperature. (C) Local geometries of the rate-determining step identified by DRC analysis. (D) Side and top views of the transition state of the RDS with active sites for heteroatom doping highlighted (green, Mo active site for metal doping; purple, C active site for nonmetal doping).
2.3. Heteroatom Doping and Descriptor–Activity Relationship
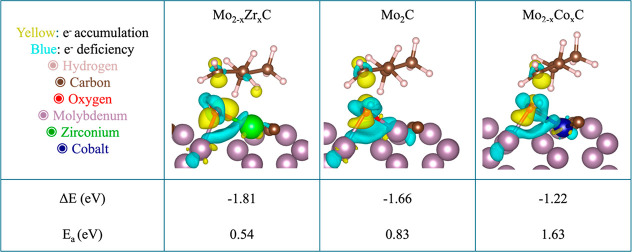
Based on the MKM result, i.e., butanol dissociation (C4H9*OH + * → C4H9* + *OH) is the RDS in HDO of butyric acid to butane (see above and Figure 3A), we then explored ways to improve the activity of Mo2C for butanol dissociation. From the transition state calculation, it is evident that the kinetic barrier of butanol dissociation mostly depends on how well the Mo active site (Figure 3D, green) can stabilize the OH group and how well the C active site (Figure 3D, purple) can stabilize the C4H9* group. Hence, we modified the property of the metal (M) and nonmetal (NM) actives sites in the pristine Mo2C surface by heteroatom doping, as previously demonstrated by Wang et al. and Jiang et al.39,53 In this study, the doped catalysts are representative of a single-atom catalyst model with a low loading of dopants. It is therefore assumed that the heteroatom dopant sites are highly dispersed in the matrix of Mo2C, and dopants do not change the main crystal structure of Mo2C. The M active site was doped by a series of transition metals (M = Ti, V, Cr, Fe, Co, Ni, Pt, Nb, Zr, W) where the OH group adsorbs, and the NM active sites by other main-group elements (NM = B, N, O, S) were examined. The doping of the NM active site did not change the barrier for RDS significantly (Figure S4), but doping of the M active site resulted in a wide range of barriers for the RDS (Figure 4A). The barrier of RDS on the pristine Mo2C surface is 0.83 eV, as discussed in section 3.1. Upon doping with Zr, the barrier of RDS can be reduced to 0.54 eV, while, upon doping with Co, it was increased to 1.63 eV. It was found that doping with Zr, Nb, V, and W enhances the activity of the Mo2C surface, whereas doping with Ti, Cr, Fe, Co, Ni, and Pt inhibits the activity of the Mo2C surface. To further extract the intrinsic properties of dopants governing the activity, electronic properties such as the Fermi level (EF), Bader charge (M), Bader charge (NM), M (d-band center), NM (p-band center), M (d-band filling), and NM (p-band filling) of all the doped surfaces were studied, and the relationships between the electronic and geometric descriptors and the activation barriers for RDS (C–OH cleavage) were interrogated (Figure S3). With such a study, we aimed to establish structure–activity relationships by correlating the physical and/or chemical descriptors with the C–OH bond cleavage barrier. It was found that the reaction follows the BEP principle; i.e., the activation energy is inversely proportional to the reaction enthalpy (Figure 4A). Interestingly, the intrinsic geometric descriptor of the atomic radius of dopants has a good correlation with the activation barrier of C–OH bond cleavage (Figure 4B). Metal dopants with larger radii exhibit higher activity for C–OH bond breaking, suggesting that a flexible coordination environment plays a key role in tuning the barrier of the RDS. The other two relevant descriptors identified are M (d-band filling) and NM (p-band filling), as shown in Figure 4C,D. Furthermore, we did a multilinear regression78 using the Python scikit-learn(79) package for the hitherto mentioned most-promising descriptors and all other electronic and geometric data (Figure S3). It was shown that ΔE, M (d-band filling), NM (p-band filling), and the radius of M have good linear-scaling relationships with the activation barriers (Figure 4 and Figure S3).
Figure 4.
Linear-scaling relationships of descriptors: (A) reaction energy, ΔE; (B) atomic radius of the dopant; (C) d-band filling of the dopant; (D) p-band filling of surface C with the reaction barriers of the RDS.
Here, M (d-band filling) is the fractional occupation of the d-band of the doped active M site, while NM (p-band filling) is the fractional occupation of the p-band of the doped active NM site. Figure 4C shows that it is relatively easier to break the C–OH bond if the d-band of the doped M site is emptier compared to the d-band of the Mo active site in the pristine Mo2C catalyst. On the other hand, Figure 4D shows that it is relatively easier to break the C–OH bond if the p-band of the NM site is fuller compared to the p-band of the C active site adjacent to the Mo active site in the pristine Mo2C catalyst. It can be inferred that electrons are being transferred from the M (d-band) → C (p-band). This is similar to an observation by Wang et al., where they observe strong electron transfer from the dopant metal to the surface.39 This charge transfer makes the M (d-band) more accessible to stabilize the −OH group by accepting electrons from the O (p-band). To obtain a physical picture of this charge transfer process, a charge density difference analysis was performed (Figure 5), as described in section S6 in the Supporting Information. It can be seen that electron transfer from the O (p-band) → M (d-band) is the most significant for the Mo2–xZrxC catalyst because the d-band of Zr is emptier, and hence the activation barrier is lower. However, in the case of Mo2-xCoxC, the d-band of Co is relatively full (Figure 4C); therefore, O (p-band) → M (d-band) electron transfer is not favorable, which is reflected by a larger Ea compared to that of the pristine Mo2C catalyst. It is worth mentioning that improving the barrier of the RDS by means of heteroatom doping could cause an imbalance in the overall reaction and shift the RDS to another elementary step. Therefore, further calculations would be needed to verify if the RDS is shifted.
Figure 5.
Charge density difference analysis of the proposed Mo2–xZrxC (best), pristine Mo2C, and Mo2–xCoxC (worst) catalysts. Isosurface value: 0.0074.
2.4. Formation Gibbs Free Energy of Doped Mo2–xMxC
After we identified the most-promising dopants (M = Zr, Nb, V, Ti, W) for enhancing the activity of pristine Mo2C, we further calculated the formation Gibbs free energy (ΔG) as described in section 2, eqs 6–9, and Jiang et al.’s work53 to evaluate the thermodynamic facility of forming these doped Mo2C under experimental Mo2C synthesis conditions.14,24Figure 6 demonstrates the formation Gibbs free energy as a function of the chemical potentials of H2 and H2O. It is indicated that Nb- and V-doped Mo2C are the most facile doped catalysts to synthesize, while the synthesis of Ti- and Zr-doped Mo2C is the least feasible under the typical experimental carburization conditions. Contrastingly, synthesis of W-doped Mo2C is independent of the chemical concentration of H2 and H2O. From these results it is speculated that even though DFT predicts the lowest barrier for RDS (0.54 eV) in the case of Mo2–xZrxC, its synthesis under typical Mo2C synthesis conditions could be quite challenging. On the other hand, Mo2–xNbxC is not only relatively much easier to form compared to Mo2–xZrxC, but also can enhance the activity of the Mo2C catalytic surface as well (barrier for RDS: 0.58 eV) and hence is a good candidate for experimental validation. Overall, it is concluded that Mo2–xZrxC and Mo2–xNbxC are the two most-promising catalysts for enhancing the activity of Mo2C for HDO reactions.
Figure 6.
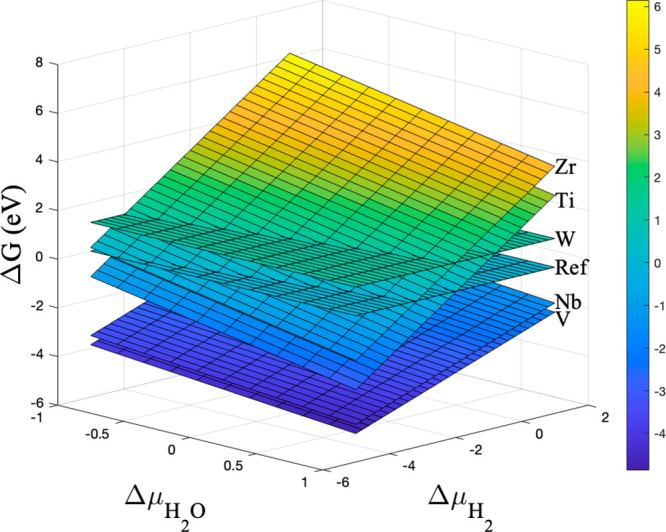
Formation Gibbs free energy of doped Mo2C as a function of the H2 and H2O chemical potentials.
4. Conclusions
In this work, the comprehensive HDO reaction mechanism of butyric acid over the β-Mo2C (101) catalytic surface has been studied by means of DFT. Combining the DFT results with MKM, it is identified that C–OH activation during the butanol dissociation is the rate-determining step for the HDO of butyric acid. It is found that water dissociation on the surface of Mo2C is favorable, which could contribute to molybdenum oxycarbide formation during the reaction. The insights into the rate-determining step were then exploited by fine-tuning the activity of Mo2C by means of heteroatom doping. The results indicate that Mo2C catalytic surfaces upon doping with Zr and Nb have significantly lower activation barriers toward C–OH bond dissociation compared to the pristine Mo2C surface. Moreover, the doping data was further analyzed using multilinear regression to unravel the most important descriptors, and it is established that generic geometric (dopants’ atomic radius) and electronic (dopants’ d-band filling) descriptors play a key role in governing the activity of the doped Mo2C catalysts.
Acknowledgments
The authors acknowledge the Dutch Organization for Scientific Research (NWO) for access to the Dutch national e-infrastructure (grants EINF-750, EINF-3542, and EINF-4916) and Marlene Führer (Wageningen University) for highly fruitful discussions.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscatal.3c03728.
Atomic models used for DFT calculations, elementary reaction steps with forward and backward barriers (and prefactors) used for MKM simulations, calculations for H2 dissociative adsorption and H2O formation/dissociation, charge density difference analysis, correlation heat map for potential descriptors of reactivity, and the rest of the MKM results (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Kalz K. F.; Kraehnert R.; Dvoyashkin M.; Dittmeyer R.; Glaser R.; Krewer U.; Reuter K.; Grunwaldt J. D. Future Challenges in Heterogeneous Catalysis: Understanding Catalysts under Dynamic Reaction Conditions. ChemCatChem. 2017, 9 (1), 17–29. 10.1002/cctc.201600996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanzafame P.; Perathoner S.; Centi G.; Gross S.; Hensen E. J. M. Grand challenges for catalysis in the Science and Technology Roadmap on Catalysis for Europe: moving ahead for a sustainable future. Catal. Sci. Technol. 2017, 7 (22), 5182–5194. 10.1039/C7CY01067B. [DOI] [Google Scholar]
- Toniato A.; Vaucher A. C.; Laino T. Grand challenges on accelerating discovery in catalysis. Catal. Today 2022, 387, 140–142. 10.1016/j.cattod.2021.10.001. [DOI] [Google Scholar]
- Smith K. J. Metal carbides, phosphides, and nitrides for biomass conversion. Curr. Opin Green Sustain Chem. 2020, 22, 47–53. 10.1016/j.cogsc.2019.11.008. [DOI] [Google Scholar]
- Mondelli C.; Gozaydin G.; Yan N.; Perez-Ramirez J. Biomass valorisation over metal-based solid catalysts from nanoparticles to single atoms. Chem. Soc. Rev. 2020, 49 (12), 3764–3782. 10.1039/D0CS00130A. [DOI] [PubMed] [Google Scholar]
- Corma A.; Iborra S.; Velty A. Chemical routes for the transformation of biomass into chemicals. Chem. Rev. 2007, 107 (6), 2411–2502. 10.1021/cr050989d. [DOI] [PubMed] [Google Scholar]
- Yun Y. S.; Berdugo-Diaz C. E.; Flaherty D. W. Advances in Understanding the Selective Hydrogenolysis of Biomass Derivatives. ACS Catal. 2021, 11 (17), 11193–11232. 10.1021/acscatal.1c02866. [DOI] [Google Scholar]
- Sudarsanam P.; Zhong R.; Van den Bosch S.; Coman S. M.; Parvulescu V. I.; Sels B. F. Functionalised heterogeneous catalysts for sustainable biomass valorisation. Chem. Soc. Rev. 2018, 47 (22), 8349–8402. 10.1039/C8CS00410B. [DOI] [PubMed] [Google Scholar]
- TopsÃ̧e H.; Massoth F. E.; Clausen B. S.. Hydrotreating catalysis; Springer: 1996. [Google Scholar]
- Şenol O. İ.; Ryymin E. M.; Viljava T. R.; Krause A. O. I. Reactions of methyl heptanoate hydrodeoxygenation on sulphided catalysts. J. Mol. Catal. A Chem. 2007, 268 (1–2), 1–8. 10.1016/j.molcata.2006.12.006. [DOI] [Google Scholar]
- Breysse M.; Djega-Mariadassou G.; Pessayre S.; Geantet C.; Vrinat M.; Perot G.; Lemaire M. Deep desulfurization: reactions, catalysts and technological challenges. Catal. Today 2003, 84 (3–4), 129–138. 10.1016/S0920-5861(03)00266-9. [DOI] [Google Scholar]
- Chen J. G. Carbide and Nitride Overlayers on Early Transition Metal Surfaces: Preparation, Characterization, and Reactivities. Chem. Rev. 1996, 96 (4), 1477–1498. 10.1021/cr950232u. [DOI] [PubMed] [Google Scholar]
- Hugosson H. W.; Jansson U.; Johansson B.; Eriksson O. Phase stability diagrams of transition metal carbides, a theoretical study. Chem. Phys. Lett. 2001, 333 (6), 444–450. 10.1016/S0009-2614(00)01414-7. [DOI] [Google Scholar]
- Oyama S. T. Preparation and Catalytic Properties of Transition-Metal Carbides and Nitrides. Catal. Today 1992, 15 (2), 179–200. 10.1016/0920-5861(92)80175-M. [DOI] [Google Scholar]
- Chen P. R.; Ye J. S.; Wang H.; Ouyang L. Z.; Zhu M. Recent progress of transition metal carbides/nitrides for electrocatalytic water splitting. J. Alloys Compd. 2021, 883, 160833. 10.1016/j.jallcom.2021.160833. [DOI] [Google Scholar]
- Tackett B. M.; Sheng W. C.; Chen J. G. G. Opportunities and Challenges in Utilizing Metal-Modified Transition Metal Carbides as Low-Cost Electrocatalysts. Joule 2017, 1 (2), 253–263. 10.1016/j.joule.2017.07.002. [DOI] [Google Scholar]
- Führer M.; van Haasterecht T.; Bitter J. H. Catalytic performance of carbon-supported mixed MoW carbides for the deoxygenation of stearic acid. Catal. Today 2023, 418, 114108. 10.1016/j.cattod.2023.114108. [DOI] [Google Scholar]
- Souza Macedo L.; Stellwagen D. R.; Teixeira da Silva V.; Bitter J. H. Stability of Transition-metal Carbides in Liquid Phase Reactions Relevant for Biomass-Based Conversion. ChemCatChem. 2015, 7 (18), 2816–2823. 10.1002/cctc.201500566. [DOI] [Google Scholar]
- Agrawal K.; Roldan A.; Kishore N.; Logsdail A. J. Dehydrogenation and dehydration of formic acid over orthorhombic molybdenum carbide. Catal. Today 2022, 384–386, 197–208. 10.1016/j.cattod.2021.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar A.; Bhan A. Oxygen content as a variable to control product selectivity in hydrodeoxygenation reactions on molybdenum carbide catalysts. Chem. Eng. Sci. 2019, 197, 371–378. 10.1016/j.ces.2018.12.027. [DOI] [Google Scholar]
- Ren H.; Yu W.; Salciccioli M.; Chen Y.; Huang Y.; Xiong K.; Vlachos D. G.; Chen J. G. Selective hydrodeoxygenation of biomass-derived oxygenates to unsaturated hydrocarbons using molybdenum carbide catalysts. ChemSusChem 2013, 6 (5), 798–801. 10.1002/cssc.201200991. [DOI] [PubMed] [Google Scholar]
- Sullivan M. M.; Bhan A. Acetone Hydrodeoxygenation over Bifunctional Metallic-Acidic Molybdenum Carbide Catalysts. ACS Catal. 2016, 6 (2), 1145–1152. 10.1021/acscatal.5b02656. [DOI] [Google Scholar]
- Stellwagen D. R.; Bitter J. H. Structure-performance relations of molybdenum- and tungsten carbide catalysts for deoxygenation. Green Chem. 2015, 17 (1), 582–593. 10.1039/C4GC01831A. [DOI] [Google Scholar]
- Führer M.; van Haasterecht T.; Bitter J. H. Molybdenum and tungsten carbides can shine too. Catal. Sci. Technol. 2020, 10 (18), 6089–6097. 10.1039/D0CY01420F. [DOI] [Google Scholar]
- Fuhrer M.; van Haasterecht T.; Bitter J. H. Cinnamaldehyde hydrogenation over carbon supported molybdenum and tungsten carbide catalysts. Chem. Commun. (Camb) 2022, 58 (98), 13608–13611. 10.1039/D2CC05322E. [DOI] [PubMed] [Google Scholar]
- Gosselink R. W.; Stellwagen D. R.; Bitter J. H. Tungsten-based catalysts for selective deoxygenation. Angew. Chem., Int. Ed. Engl. 2013, 52 (19), 5089–5092. 10.1002/anie.201209809. [DOI] [PubMed] [Google Scholar]
- Bennett L. H.; Cuthill J. R.; McAlister A. J.; Erickson N. E.; Watson R. E. Electronic structure and catalytic behavior of tungsten carbide. Science 1974, 184 (4136), 563–565. 10.1126/science.184.4136.563. [DOI] [PubMed] [Google Scholar]
- Levy R. B.; Boudart M. Platinum-like behavior of tungsten carbide in surface catalysis. Science 1973, 181 (4099), 547–549. 10.1126/science.181.4099.547. [DOI] [PubMed] [Google Scholar]
- Deng Y.; Ge Y.; Xu M.; Yu Q.; Xiao D.; Yao S.; Ma D. Molybdenum Carbide: Controlling the Geometric and Electronic Structure of Noble Metals for the Activation of O-H and C-H Bonds. Acc. Chem. Res. 2019, 52 (12), 3372–3383. 10.1021/acs.accounts.9b00182. [DOI] [PubMed] [Google Scholar]
- Lee J. S.; Oyama S. T.; Boudart M. Molybdenum Carbide Catalysts.1. Synthesis of Unsupported Powders. J. Catal. 1987, 106 (1), 125–133. 10.1016/0021-9517(87)90218-1. [DOI] [Google Scholar]
- Wang H. Y.; Diao Y. A.; Gao Z. R.; Smith K. J.; Guo X. W.; Ma D.; Shi C. H2 Production from Methane Reforming over Molybdenum Carbide Catalysts: From Surface Properties and Reaction Mechanism to Catalyst Development. ACS Catal. 2022, 12 (24), 15501–15528. 10.1021/acscatal.2c04619. [DOI] [Google Scholar]
- Snåre M.; Kubičková I.; Mäki-Arvela P.; Eränen K.; Murzin D. Y. Heterogeneous Catalytic Deoxygenation of Stearic Acid for Production of Biodiesel. Ind. Eng. Chem. Res. 2006, 45 (16), 5708–5715. 10.1021/ie060334i. [DOI] [Google Scholar]
- Shi X.-R.; Wang S.-G.; Wang H.; Deng C.-M.; Qin Z.; Wang J. Structure and stability of β-Mo2C bulk and surfaces: A density functional theory study. Surf. Sci. 2009, 603 (6), 852–859. 10.1016/j.susc.2009.01.041. [DOI] [Google Scholar]
- Wang T.; Wang S.; Li Y.-W.; Wang J.; Jiao H. Adsorption Equilibria of CO Coverage on β-Mo2C Surfaces. J. Phy Chem. C 2012, 116 (10), 6340–6348. 10.1021/jp300422g. [DOI] [Google Scholar]
- Wang T.; Luo Q.; Li Y.-W.; Wang J.; Beller M.; Jiao H. Stable surface terminations of orthorhombic Mo2C catalysts and their CO activation mechanisms. App Catal. A: Gen 2014, 478, 146–156. 10.1016/j.apcata.2014.03.042. [DOI] [Google Scholar]
- Shi Y.; Yang Y.; Li Y. W.; Jiao H. J. Theoretical study about Mo2C(101)-catalyzed hydrodeoxygenation of butyric acid to butane for biomass conversion. Catal. Sci. Technol. 2016, 6 (13), 4923–4936. 10.1039/C5CY02008E. [DOI] [Google Scholar]
- Oliveira R. R.; Rocha A. B. Acrylic acid hydrodeoxygenation reaction mechanism over molybdenum carbide studied by DFT calculations. J. Mol. Model 2019, 25 (10), 309. 10.1007/s00894-019-4186-1. [DOI] [PubMed] [Google Scholar]
- Sousa L. A.; Zotin J. L.; da Silva V. T. Hydrotreatment of sunflower oil using supported molybdenum carbide. Appl. Catal. A: Gen 2012, 449, 105–111. 10.1016/j.apcata.2012.09.030. [DOI] [Google Scholar]
- Wang F.; Tian X.; Jiao H. Adsorption of CO, H2, H2O, and CO2 on Fe-, Co-, Ni-, Cu-, Pd-, and Pt-Doped Mo2C(101) Surfaces. J. Phy Chem. C 2021, 125 (21), 11419–11431. 10.1021/acs.jpcc.1c03372. [DOI] [Google Scholar]
- Ooka H.; Huang J.; Exner K. S. The Sabatier Principle in Electrocatalysis: Basics, Limitations, and Extensions. Front Energy Res. 2021, 9, 1. 10.3389/fenrg.2021.654460. [DOI] [Google Scholar]
- Bronsted J. N. Acid and Basic Catalysis. Chem. Rev. 1928, 5 (3), 231–338. 10.1021/cr60019a001. [DOI] [Google Scholar]
- Evans M. G.; Polanyi M. Inertia and driving force of chemical reactions. Trans Faraday Soc. 1938, 34 (0), 11–24. 10.1039/tf9383400011. [DOI] [Google Scholar]
- Bligaard T.; Norskov J. K.; Dahl S.; Matthiesen J.; Christensen C. H.; Sehested J. The Bronsted-Evans-Polanyi relation and the volcano curve in heterogeneous catalysis. J. Catal. 2004, 224 (1), 206–217. 10.1016/j.jcat.2004.02.034. [DOI] [Google Scholar]
- Logadottir A.; Rod T. H.; Norskov J. K.; Hammer B.; Dahl S.; Jacobsen C. J. H. The Bronsted-Evans-Polanyi relation and the volcano plot for ammonia synthesis over transition metal catalysts. J. Catal. 2001, 197 (2), 229–231. 10.1006/jcat.2000.3087. [DOI] [Google Scholar]
- Yan W. Q.; Zhu Y. A.; Zhou X. G.; Yuan W. K. Rational design of heterogeneous catalysts by breaking and rebuilding scaling relations. Chin J. Chem. Eng. 2022, 41, 22–28. 10.1016/j.cjche.2021.10.025. [DOI] [Google Scholar]
- Michaelides A.; Liu Z. P.; Zhang C. J.; Alavi A.; King D. A.; Hu P. Identification of general linear relationships between activation energies and enthalpy changes for dissociation reactions at surfaces. J. Am. Chem. Soc. 2003, 125 (13), 3704–3705. 10.1021/ja027366r. [DOI] [PubMed] [Google Scholar]
- Latimer A. A.; Kulkarni A. R.; Aljama H.; Montoya J. H.; Yoo J. S.; Tsai C.; Abild-Pedersen F.; Studt F.; Norskov J. K. Understanding trends in C-H bond activation in heterogeneous catalysis. Nat. Mater. 2017, 16 (2), 225–229. 10.1038/nmat4760. [DOI] [PubMed] [Google Scholar]
- Hammer B.; Morikawa Y.; Norskov J. K. CO chemisorption at metal surfaces and overlayers. Phys. Rev. Lett. 1996, 76 (12), 2141–2144. 10.1103/PhysRevLett.76.2141. [DOI] [PubMed] [Google Scholar]
- Lausche A. C.; Medford A. J.; Khan T. S.; Xu Y.; Bligaard T.; Abild-Pedersen F.; Norskov J. K.; Studt F. On the effect of coverage-dependent adsorbate-adsorbate interactions for CO methanation on transition metal surfaces. J. Catal. 2013, 307, 275–282. 10.1016/j.jcat.2013.08.002. [DOI] [Google Scholar]
- Norskov J. K.; Bligaard T.; Rossmeisl J.; Christensen C. H. Towards the computational design of solid catalysts. Nat. Chem. 2009, 1 (1), 37–46. 10.1038/nchem.121. [DOI] [PubMed] [Google Scholar]
- Anand M.; Rohr B.; Statt M. J.; Norskov J. K. Scaling Relationships and Volcano Plots in Homogeneous Catalysis. J. Phys. Chem. Lett. 2020, 11 (20), 8518–8526. 10.1021/acs.jpclett.0c01991. [DOI] [PubMed] [Google Scholar]
- Hammer B.; Nørskov J. K. Theoretical Surf Sci and catalysis—calculations and concepts. Adv. Catal. 2000, 45, 71–129. 10.1016/S0360-0564(02)45013-4. [DOI] [Google Scholar]
- Jiang C.; Song H.; Sun G.; Chang X.; Zhen S.; Wu S.; Zhao Z. J.; Gong J. Data-Driven Interpretable Descriptors for the Structure-Activity Relationship of Surface Lattice Oxygen on Doped Vanadium Oxides. Angew. Chem., Int. Ed. Engl. 2022, 61 (35), e202206758 10.1002/anie.202206758. [DOI] [PubMed] [Google Scholar]
- Lin X.; Wang Y.; Chang X.; Zhen S.; Zhao Z. J.; Gong J. High-Throughput Screening of Electrocatalysts for Nitrogen Reduction Reactions Accelerated by Interpretable Intrinsic Descriptor. Angew. Chem., Int. Ed. Engl. 2023, 62, e202300122 10.1002/anie.202300122. [DOI] [PubMed] [Google Scholar]
- Chang X.; Zhao Z. J.; Lu Z.; Chen S.; Luo R.; Zha S.; Li L.; Sun G.; Pei C.; Gong J. Designing single-site alloy catalysts using a degree-of-isolation descriptor. Nat. Nanotechnol 2023, 18 (6), 611–616. 10.1038/s41565-023-01344-z. [DOI] [PubMed] [Google Scholar]
- Tacey S. A.; Jankousky M.; Farberow C. A. Assessing the role of surface carbon on the surface stability and reactivity of β-Mo2C catalysts. Appl. Surf. Sci. 2022, 593, 153415. 10.1016/j.apsusc.2022.153415. [DOI] [Google Scholar]
- Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. B 1964, 136 (3b), B864. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140 (4a), A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Kresse G.; Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6 (1), 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [Google Scholar]
- Kresse G.; Furthmuller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens Matter 1996, 54 (16), 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77 (18), 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Uberuaga B. P.; Jonsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phy 2000, 113 (22), 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
- Henkelman G.; Jonsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phy 2000, 113 (22), 9978–9985. 10.1063/1.1323224. [DOI] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132 (15), 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32 (7), 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Parthé E.; Sadogopan V. The structure of dimolybdenum carbide by neutron diffraction technique. Acta Crystallogr. 1963, 16 (3), 202–205. 10.1107/S0365110X63000487. [DOI] [Google Scholar]
- Haines J.; Leger J. M.; Chateau C.; Lowther J. E. Experimental and theoretical investigation of Mo2C at high pressure. J. Phys.: Condens. Matter 2001, 13 (11), 2447–2454. 10.1088/0953-8984/13/11/303. [DOI] [Google Scholar]
- Politi J. R.; Vines F.; Rodriguez J. A.; Illas F. Atomic and electronic structure of molybdenum carbide phases: bulk and low Miller-index surfaces. Phys. Chem. Chem. Phys. 2013, 15 (30), 12617–12625. 10.1039/c3cp51389k. [DOI] [PubMed] [Google Scholar]
- Page K.; Li J.; Savinelli R.; Szumila H. N.; Zhang J.; Stalick J. K.; Proffen T.; Scott S. L.; Seshadri R. Reciprocal-space and real-space neutron investigation of nanostructured Mo2C and WC. Solid State Sci. 2008, 10 (11), 1499–1510. 10.1016/j.solidstatesciences.2008.03.018. [DOI] [Google Scholar]
- Henkelman G.; Arnaldsson A.; Jonsson H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36 (3), 354–360. 10.1016/j.commatsci.2005.04.010. [DOI] [Google Scholar]
- Ong S. P.; Richards W. D.; Jain A.; Hautier G.; Kocher M.; Cholia S.; Gunter D.; Chevrier V. L.; Persson K. A.; Ceder G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. 10.1016/j.commatsci.2012.10.028. [DOI] [Google Scholar]
- Filot I. A. W.; Van Santen R. A.; Hensen E. J. M. The optimally performing Fischer–Tropsch catalyst. Angew. Chem. Int. Ed 2014, 53, 12746–12750. 10.1002/anie.201406521. [DOI] [PubMed] [Google Scholar]
- Motagamwala A. H.; Dumesic J. A. Microkinetic Modeling: a tool for rational catalyst design. Chem. Rev. 2021, 121 (2), 1049–1076. 10.1021/acs.chemrev.0c00394. [DOI] [PubMed] [Google Scholar]
- Kozuch S.; Shaik S. A combined kinetic-quantum mechanical model for assessment of catalytic cycles: application to cross-coupling and Heck reactions. J. Am. Chem. Soc. 2006, 128 (10), 3355–3365. 10.1021/ja0559146. [DOI] [PubMed] [Google Scholar]
- Kozuch S.; Shaik S. Kinetic-quantum chemical model for catalytic cycles: the Haber-Bosch process and the effect of reagent concentration. J. Phys. Chem. A 2008, 112 (26), 6032–6041. 10.1021/jp8004772. [DOI] [PubMed] [Google Scholar]
- Campbell C. T. The Degree of Rate Control: A Powerful Tool for Catalysis Research. ACS Catal. 2017, 7 (4), 2770–2779. 10.1021/acscatal.7b00115. [DOI] [Google Scholar]
- Araujo R. B.; Rodrigues G. L. S.; Dos Santos E. C.; Pettersson L. G. M. Adsorption energies on transition metal surfaces: towards an accurate and balanced description. Nat. Commun. 2022, 13 (1), 6853. 10.1038/s41467-022-34507-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marill K. A. Advanced statistics: linear regression, part II: multiple linear regression. Acad. Emerg Med. 2004, 11 (1), 94–102. 10.1197/j.aem.2003.09.006. [DOI] [PubMed] [Google Scholar]
- Bisong E.Introduction to Scikit-learn. In Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners; Bisong E., Ed.; Apress: 2019; pp 215–229. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.