Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Oct 8;63(20):6183–6191. doi: 10.1021/acs.jcim.3c01153

AmberTools

David A Case †, Hasan Metin Aktulga ‡, Kellon Belfon §, David S Cerutti ∥, G Andrés Cisneros ⊥, Vinícius Wilian D Cruzeiro #, Negin Forouzesh ∇, Timothy J Giese ○, Andreas W Götz ◆, Holger Gohlke ⊙,◒, Saeed Izadi ◓, Koushik Kasavajhala ⊖, Mehmet C Kaymak ‡, Edward King ⦶, Tom Kurtzman ◇,⊡, Tai-Sung Lee ○, Pengfei Li ◨, Jian Liu ◧, Tyler Luchko ⬒, Ray Luo ⦶, Madushanka Manathunga ⬓, Matias R Machado ⬕, Hai Minh Nguyen †, Kurt A O’Hearn ‡, Alexey V Onufriev ⬔, Feng Pan ◩, Sergio Pantano ⬕, Ruxi Qi ◪, Ali Rahnamoun ‡, Ali Risheh ∇, Stephan Schott-Verdugo ◒, Akhil Shajan ⬓, Jason Swails △, Junmei Wang ▲, Haixin Wei ⦶, Xiongwu Wu ▽, Yongxian Wu ⦶, Shi Zhang ○, Shiji Zhao ⦶,▼, Qiang Zhu ⦶, Thomas E Cheatham III ◮, Daniel R Roe ◭, Adrian Roitberg ⧩, Carlos Simmerling ⊖, Darrin M York ○, Maria C Nagan ⧨,*, Kenneth M Merz Jr ⬓,*
PMCID: PMC10598796  NIHMSID: NIHMS1940356  PMID: 37805934

Abstract

graphic file with name ci3c01153_0003.jpg

AmberTools is a free and open-source collection of programs used to set up, run, and analyze molecular simulations. The newer features contained within AmberTools23 are briefly described in this Application note.

Introduction

The present status of the Amber (Assisted Model Building and Energy Refinement) suite of programs has been the product of decades of effort from a broad range of research groups, starting with the group of the late Peter Kollman in the early 1980s.1 Amber contains tools for energy minimization (EM), molecular dynamics (MD) simulations, free energy (FE) calculations, potential of mean force (PMF) capabilities, and all the needed tools to set up the modeling effort. The software stack has been reviewed in the past,2−4 and the manual contains detailed descriptions of all the algorithms in Amber as well as a full list of contributors to Amber over the years (see https://ambermd.org). Besides the actual code, Amber is used to describe a series of highly regarded force fields5 for proteins,6−12 carbohydrates,13,14 nucleic acids,7,8,15 and lipids.16 The present Application Note will only describe the latest additions to the open-source AmberTools23 and as such is not meant to give a thorough exposition of all the methods and capabilities of AmberTools and Amber.

Overview of Amber and AmberTools

Amber and AmberTools form a collection of programs that are designed to work together to facilitate system setup, MD simulations, and trajectory analysis for biomolecules. It is useful to note that the Amber force fields mentioned above can be used in a variety of molecular dynamics codes outside of AmberTools and Amber. The Amber code is updated in even-numbered years, and it uniquely includes the base MD code known as pmemd, which offers parallel and graphics processing unit (GPU)-accelerated versions of the MD codes along with some free-energy-based methods not implemented in AmberTools. Analogous MD function is available in sander in AmberTools. AmberTools is distributed under an open-source license, primarily the GNU General Public License, with some portions covered by other compatible open-source licenses. The Amber force fields are in the public domain and are distributed with AmberTools. The pmemd code is distributed as source code but has a separate license that contains restrictions on use and redistribution; there is no license fee for noncommerical use of pmemd. Full details on licensing and distribution can be found at https://ambermd.org.

Typical Workflow

The basic workflow for AmberTools is shown in the accompanying (see Figure 1), and it describes preparation, simulation, and analysis steps. Preparation starts at the top, since all MD simulations require some sort of starting three-dimensional (3D) structure, which for biomolecules is usually in the form of a PDB-format file; AmberTools has some model-building capabilities (e.g., PACKMOL-Memgen, see below), but other codes are generally used if experimental structures are not available. The prepareforleap step, which is recent and still under development, carries out tasks to map components in the input file to Amber nomenclature (especially useful for carbohydrates), add hydrogens, identify cross-links, assign histidine protonation states, and similar tasks. Next is the LEaP program, which is a workhorse program that connects the nascent structure to Amber’s built-in force fields for proteins, nucleic acids, carbohydrates, lipids, and common solvents and to bespoke force fields for other components like ligands and cofactors that can be created by programs like antechamber and mdgx (for general organic molecules) and pyMSMT (for metal ions). The LEaP code creates two files: an “inpcrd” file that has complete three-dimensional coordinates and a “prmtop” file that contains all other information needed for force field-based analyses of the system. The latter file can be examined and edited via parmed, which can also export similar files in the GROMACS or CHARMM format.

Figure 1.

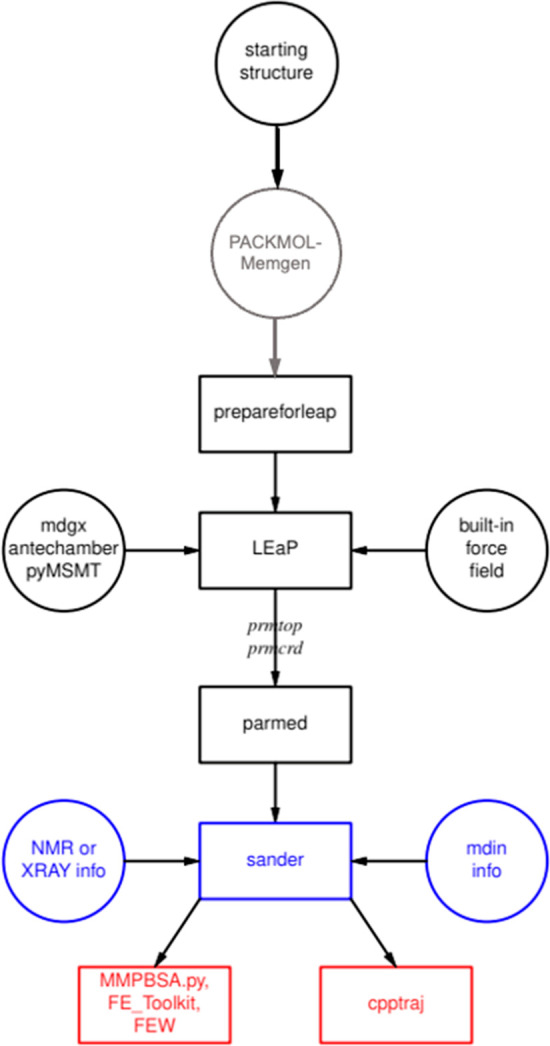
Figure 1

Open in a new tab

Common workflow in AmberTools. Flow went from top to bottom. Black boxes are for preparation, gray indicates an optional preparation step specific for membrane systems, blue for simulation, and red for analysis.

The simulation phase is primarily the province of sander or pmemd. The “mdin” file contains a large number of parameters that control the type and length of the simulation to be carried out, the integration method, the use of a QM/MM (quantum mechanics/molecular mechanics) model, specification of enhanced-sampling and thermodynamic integration methods, and the like. Restraints on the system, often from NMR or X-ray data but more recently from cryogenic electron microscopy (cryoEM) and other sorts of integrative modeling, can also be input at this point.

Snapshots of conformations are generally stored at regular intervals during a simulation and then serve as input for an analysis phase. The cpptraj program is the workhorse code here, providing geometric and energetic analyses, clustering algorithms, and many other routines. Three other codes, MMPBSA.py, FE_Toolkit, and FEW (Free Energy Workflow)17 are devoted to estimating free energy changes. More complete descriptions of all of this, including a full list of programs, encompassing nearly 1000 pages of text, are in the Amber23 Reference Manual.

AmberTools23 Updates

We have a number of significant new features for AmberTools23 which include automated building of membrane-protein–lipid-bilayer systems, enhancements to the polarizable Gaussian multipole method, extensions to the Poisson-Boltzmann surface area (PBSA) method, enhanced free energy capabilities, enhanced QM and QM/MM capabilities, and a significant upgrade of the Amber Web site and tutorials. Each of these additions is summarized below.

1. Polarizable Gaussian Multipole Model in the SANDER Program

The polarizable Gaussian Multipole (pGM) model is a next-generation induced-dipole polarizable model aiming to balance accuracy and efficiency for molecular simulations of biomolecular systems.18−22 We recently developed a new framework for efficient computation of analytical atomic gradient for the pGM model.18 The pGM virial for constant pressure molecular dynamics simulations was also implemented in previous releases of Amber.19 The accuracy and robustness of the pGM model have also been validated on various molecular properties.20−22 In the AmberTools23 release, we further optimized the induced-dipole iteration algorithm. Specifically, we introduced maximum relative error as the convergence criterion to ensure energy conservation in molecular dynamics simulations. We also designed and implemented multiorder extrapolation (MOE) and local preconditioning conjugate gradient (LPCG) schemes to accelerate the induced-dipole iteration.23 Given the new developments, MD simulations with the pGM model are able to achieve a similar level of energy conservation as those with the point charge additive models, within 2–3 induction iterations.

2. New Features in the PBSA Program

MM/PB(GB)SA24 is an end-point method for calculating the free energies of molecules in implicit solvent, i.e., Poisson–Boltzmann (PB) and generalized Born (GB). Solvation interactions, especially solvent-mediated dielectric screening and Debye–Hückel screening, are essential determinants of the structure and function of biomolecules. Several efficient finite-difference numerical solvers, both linear25−27 and nonlinear,28 are implemented in pbsa for various applications of the Poisson–Boltzmann method. The GPU support of those solvers is also implemented in pbsa.cuda.29−31 In the 2023 release, improvements to the pbsa program include the integration of the Machine-Learned Solvent Excluded Surface (MLSES) model,32 which provides a highly efficient and differentiable molecular surface for continuum solvation modeling of biomolecules. Various options for the MLSES model have been implemented, allowing users to optimize performance on both central processing unit (CPU) and GPU platforms using Fortran, the CUDA kernel, and LibTorch. This flexibility enables users to choose the best-suited hardware and software environments for their needs. Additionally, an MBAR/PBSA strategy has been developed combining the PBSA continuum solvent model with the Multistate Bennet Acceptance Ratio (MBAR) approach. This coupling allows for more accurate modeling of electronic polarization, leading to improved accuracy in absolute binding free energy simulations of highly charged ligands.33

To date, the GB model in AmberTools could be specified with the following “igb” values: 1,34 2,35 5,36 7, and 8.37 In 2017, an accurate yet efficient grid-based surface GB model was introduced38 which is currently available in AmberTools as a stand-alone application named GBNSR6 ($AMBERHOME/bin/gbnsr6).39 GBNSR6 calculates the solvation free energy of an input structure on a single snapshot. In AmberTools23, GBNSR6 has been integrated into MMPBSA.py(40) such that it runs over multiple snapshots extracted from the trajectories of protein, ligand, and complex structures. To run this model, “igb = 66” is now available in MMPBSA.py. All input parameters of the stand-alone GBNSR6 program can be modified through the MMPBSA.py input file.

3. PyRESP and PyRESP_GEN

Accurate modeling of electrostatic and polarization effects is crucial in molecular simulations. Many polarizable force fields have been developed to account for these important effects. Among these models, the polarizable Gaussian Multipole (pGM) model has emerged as a self-consistent approach in handling both short-range and long-range interactions.18−23 We have recently developed the PyRESP program41 for electrostatic parametrizations for point charge additive models and induced-dipole models, including the pGM model. By performing least-squares fittings to electrostatic potentials surrounding molecules, the PyRESP program extends functionalities of the ancestor RESP program that only perform parametrizations for point charge additive models.42 However, the process of generating input files for PyRESP is tedious and error-prone. In the AmberTools23 release, we implemented a flexible and user-friendly program, PyRESP_GEN,82 to minimize the user’s efforts to set up a PyRESP run. In addition, we also optimized the restraint weights for the pGM models with and without permanent dipoles. For the pGM-perm model, the optimal strategy for electrostatic potential fitting is also proposed.

4. 3D-RISM

The 3D reference interaction site model (3D-RISM) of molecular solvation43 is an implicit solvent model that calculates equilibrium density distributions and thermodynamics of explicit solvent models. The implementation in AmberTools permits MD, energy minimization, and trajectory analysis through sander, while rism3d.snglpnt provides standalone trajectory analysis.44 Recently, periodic boundaries were introduced, allowing application to crystal structure refinement and other periodic systems.45 In addition, computational scaling for open boundaries was improved via treecode summation for electrostatic interactions, providing a 2–4 times speedup for typical proteins and enabling application to large biomolecular complexes with more than 1 million atoms.46

5. LibTorch Interface to Amber

We introduced a LibTorch interface to the 2023 release of AmberTools, which is a cutting-edge C++ runtime library developed by the PyTorch team.47 This library enables flexible tensor computations and dynamic deep neural network modeling. Amber now provides two options for enabling the LibTorch library: a built-in mode and a user-installed mode. With the LibTorch integration, the pbsa program supports both CPU and GPU environments, making it highly versatile. Additionally, user instructions and tutorials have been provided for configuring the LibTorch library, making it more accessible to researchers and developers working in Amber and AmberTools.

6. Free Energy

Free energy methods have been a mainstay of Amber for decades.48,49 Besides our existing free energy technology base this latest release of AmberTools includes a collection of new software tools for the robust analysis of free energy simulations (FE-ToolKit)50,51 as well as workflow tools for production free energy simulation setup and analysis (ProFESSA)52 using the GPU-accelerated Amber free energy engine with enhanced sampling features. This software is part of the Amber Drug Discovery Boost package.53

6.1. FE-ToolKit

The FE-ToolKit contains two main utilities: edgembar(51) for analysis of alchemical free energy simulations (e.g., such as those used for prediction of ligand-protein absolute and relative binding free energies in drug discovery54) and ndfes(50) for analysis of multidimensional free energy profiles (e.g., such as those used for prediction of minimum free energy pathways in studies of enzyme mechanisms55,56).

6.2. Edgembar

The edgembar program performs analysis of alchemical free energy simulations using the multistate Bennett acceptance ratio (MBAR) method,57 the Bennett acceptance ratio (BAR) method,58 exponential averaging,59 thermodynamic integration,60 or combinations of these approaches. Alchemical free energy simulations often calculate a network of relative free energy differences between two environments. For example, ligand binding applications in drug discovery use a network of alchemical transformations between ligands, termed a “thermodynamic graph”, where each ligand represents a “node” in the graph and each “edge” represents an alchemical transformation between ligands bound to their target relative to that in aqueous solution. Given the alchemical simulation outputs from the independent trials in both environments, edgembar will perform a “network-wide” free energy analysis,51 including the imposition of cycle closure and, optionally, experimental constraints. The analysis produces a comprehensive report of the results, including uncertainties and warnings. The report identifies potential problems with simulations that may require further attention. The issues include: a lack of convergence, the analysis of too few statistically independent samples, poor phase space overlap between adjacent alchemical states,61 and poor reweighting entropy.62

6.3. Ndfes

The ndfes program evaluates multidimensional free energy surfaces from umbrella sampling.50 The analysis can be performed with the variational free energy profile (vFEP) method,63,64 MBAR,57 the weighted thermodynamic perturbation method (wTP),65 and the generalized weighted thermodynamic perturbation method (gwTP).66 The wTP and gwTP methods estimate the free energy surface of an expensive target-level of theory from the sampling performed with inexpensive reference potentials.66 The estimation of ab initio QM/MM free energy surfaces in condensed-phase environments has become more practical in the latest version of AmberTools with the combined introduction of the GPU-accelerated QUICK software67 and ndfes analysis program.

6.4. ProFESSA

The ProFESSA workflow52 uses the GPU-accelerated AMBER free energy engine. The workflow establishes a flexible, end-to-end pipeline for performing alchemical free energy simulations that brings to bear technologies including new smoothstep softcore potentials and optimized alchemical transformation pathways,68 the alchemical enhanced sampling (ACES) method,69 and a network-wide free energy analysis51 with optional imposition of cycle closure and experimental constraints implemented in FE-ToolKit.

7. Quantum Mechanical/Molecular Mechanical Methods

Amber has had a long tradition of QM/MM methods and implementations,70 with the most recent additions being the QUICK/sander QM/MM implementation in AmberTools23.67,71−73QUICK/sander has been extensively updated, and its performance has been significantly improved. QUICK, as distributed with AmberTools23, can also be used as a standalone QM program for single point calculations or geometry optimizations.

7.1. Performance Improvements/AMD Implementation

With the second-generation electron repulsion integral code and other performance enhancements recently introduced into QUICK,67,71−73 higher ps/day can be obtained in QM/MM simulations.73 For instance, with respect to AmberTools21,74 up to 2× speedups have been observed for benchmark simulations with different QM regions of photoactive yellow protein on NVIDIA V100 GPU.73 Furthermore, support for AMD GPUs has been enabled. Users can now make use of AMD data center cards such as MI50, MI100, MI200, and MI250 for simulations. According to benchmark studies, the performance on the MI100 is similar to that of NVIDIA V100.73 The implementation runs properly on MI200 and MI250 cards; however, the performance is not yet optimized for these cards. The recommended AMD GPU for the current version is MI100. An optimized version for MI2XX will be available to users in the next AmberTools release.

7.2. Long-Range Electrostatics

For the treatment of long-range electrostatics in QM/MM, the ambient-potential composite Ewald method (CEw) developed by Giese and York75 has been integrated. The performance penalty for turning on CEw in the GPU version is <25% for Hartree–Fock (HF) and <10% for density functional theory (DFT) in comparison to standard QM/MM with 8 Å electrostatic cutoff. This allows users to carry out more accurate simulations at a slightly higher computational cost.

7.3. Dispersion

Among other minor features introduced into QUICK, dispersion corrections in DFT and data exporting capability into Molden format are notable. Grimme’s dispersion corrections (D2, D3 with different damping)76 can be used in QM/MM with appropriate functionals. Users can also export Cartesian coordinates, molecular orbitals, etc. of the QM region into Molden format for visualization purposes.

8. Automated Building of Membrane-Protein–Lipid-Bilayer Systems

PACKMOL-Memgen is a simple-to-use command line implementation of a generalized workflow for the automated building of membrane-protein–lipid-bilayer systems based on open-source tools including Packmol, memembed, pdbremix, and AmberTools.77 It allows for setting up multiple configurations of a system in a user-friendly and efficient manner, which can serve as starting configurations in MD simulations under periodic boundary conditions. Since its introduction, support was added for additional lipid headgroups and to include solutes in the water or membrane phase and generate curved membrane surfaces or double bilayer systems. Additionally, SIRAH78 coarse-graining routines can be used, and non-membrane systems (water or mixed-solvent simulations) can now be set up.79 In the AmberTools23 release, PACKMOL-Memgen now handles all Amber-supported ions and the OPC3 water model as well as allows generating HMR systems, providing control for pmemd.cuda, and using pdb2pqr for protonating the protein.

9. mdgx

The mdgx program, which began as a denovo reimplementation of the basic features needed for molecular dynamics and stayed in service for its uncommon capability of storing multiple topologies and coordinate sets in the space of a single runtime instance, has gained two noteworthy features. First, it can postprocess Amber topology files to add pmemd-compatible representations of the GROMACS virtual sites.80 While mdgx itself can perform limited MD simulations with such models, the performant pmemd GPU implementation can now incorporate massless sites into its free energy methods. Virtual sites require parameters to be useful, but the mdgx program itself has tools for fitting their charges as well as bonded parameters in the context of these extra monopoles. Virtual site force fields are a logical extension of popular fixed-charge models, entailing incremental updates to the dynamics engine and incremental increases in the cost of the simulations. Second, through its ability to calculate multiple systems at once, mdgx has an exploratory feature for running simple implicit solvent dynamics on many replicas of different topologies on one GPU. By running independent trajectories on each GPU multiprocessor, mdgx scales simulations of small peptides and drug molecules to modern GPUs with tens of times the throughput of other GPU MD implementations when tasked with small systems. This capability has been applied to docked pose refinement.81

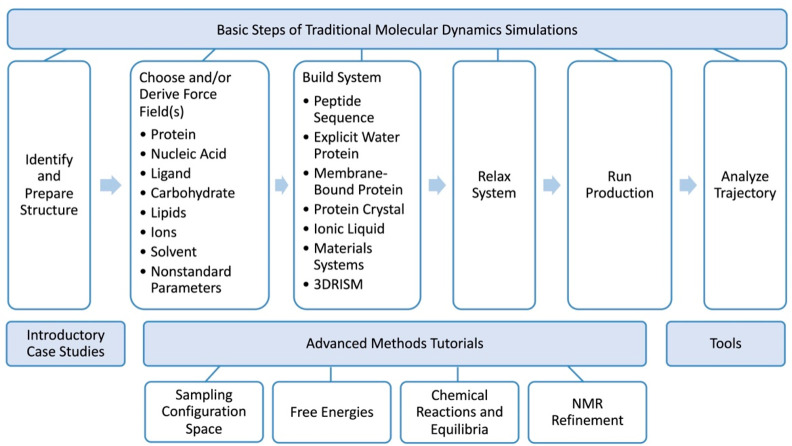
10. The Amber Web Site and Tutorials

The Amber Web site (https://ambermd.org) supports the user community with new release information, manuals, tutorials, and information on force fields. Users are directed to the most recent manual version to learn about technical usage and appropriate literature references to communicate best practices in the field. The Amber tutorials have also been reorganized and span topics ranging from initial system setup to advanced methods (Figure 2). A tutorial overview page guides new users through the process of building, running, and analyzing a system and points them to key initial case studies. The recent tutorials overall are more modular, and learning objectives are given. New tutorial development has focused on building different system types and tutorials for creating stable systems through relaxation of system positions for both explicit and implicit solvent as well as a tutorial covering advanced thermodynamic integration methods such as using smoothstep softcore potentials,68 enhanced sampling for softcore ligand energies, and methods such as ACES.69

Figure 2.

Figure 2

Open in a new tab

Overview of the Amber Tutorials. Tutorials are modular, cover the basic steps of a typical molecular dynamics simulation, introductory case studies, advanced methods, and some tools that are commonly employed by Amber users.

Modeling software is not useful without compatible force fields. Included in the release of AmberTools are the force fields developed by the Amber community. The main force fields page contains a list of recommended force fields, and each type of molecule/ion has a separate page outlining nuances in choosing an appropriate force field.

Conclusions

The most significant additions to AmberTools23 are briefly summarized. AmberTools is freely available at https://ambermd.org. Full details on licensing, distribution, and hardware supported can be found at https://ambermd.org.

Acknowledgments

The authors are grateful for the financial support provided by the National Institutes of Health (Nos. GM62248 and GM107485 to DMY; GM130367 to RL; GM130641 to KMM and HMA; NIH U2COD026506 to KMM; GM108583 to GAC; GM149874 to TSL; GM144596 to AO; GM107104 and GM135136 to CS; NHLBI Z01 HL001051-23 to DRR; GM147673 to JW; No. GM146633 to NF; and R35GM144089 to TK), the National Science Foundation (2209718 to DMY; 2209717 to KMM, HMA, and AWG; NSF OAC1835144 to KMM and AWG; OAC-2117247 to GAC; CHE-2050541 to MCN; CHE-2018427 to MCN and TL; CHE-2102668 to TL; CTMC-1665159 to CS; CHE-1955260 to JW; CHE-2216858 to NF), Loyola University Chicago (start-up funds to PL), the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) (Project CRC 1208 (No. 267205415) to HG (subproject A03)), FOCEM (MERCOSUR Structural Convergence Fund) COF 03/11 to SP, National Natural Science Foundation of China (NSFC-22225304 to JL), and Intel oneAPI Center of Excellence program to AWG. We also thank NVIDIA, AMD, and Intel for technical guidance and support.

Data Availability Statement

The AmberTools suite is free of charge, and its components are mostly released under the GNU General Public License (GPL). Please see https://ambermd.org for licensing and distribution.

The authors declare no competing financial interest.

References

  1. Weiner P. K.; Kollman P. A. AMBER: Assisted model building with energy refinement. A general program for modeling molecules and their interactions. J. Comput. Chem. 1981, 2, 287–303. 10.1002/jcc.540020311. [DOI] [Google Scholar]
  2. Case D. A.; Cheatham T. E. 3rd; Darden T.; Gohlke H.; Luo R.; Merz K. M. Jr.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Pearlman D.; Case D. A.; Caldwell J.; Ross W. S.; Cheatham T. E. II; DeBolt S.; Ferguson D.; Seibel G.; Kollman P. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 1995, 91, 1–41. 10.1016/0010-4655(95)00041-D. [DOI] [Google Scholar]
  4. Salomon-Ferrer R.; Case D. A.; Walker R. C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. 10.1002/wcms.1121. [DOI] [Google Scholar]
  5. Ponder J. W.; Case D. A. Force fields for protein simulations. Adv. Protein Chem. 2003, 66, 27–85. 10.1016/S0065-3233(03)66002-X. [DOI] [PubMed] [Google Scholar]
  6. Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins 2006, 65, 712–725. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Weiner S. J.; Kollman P. A.; Case D. A.; Singh U. C.; Ghio C.; Alagona G.; Profeta S.; Weiner P. A New Force Field for Molecular Mechanical Simulation of Nucleic Acids and Proteins. J. Am. Chem. Soc. 1984, 106, 765–784. 10.1021/ja00315a051. [DOI] [Google Scholar]
  8. Weiner S. J.; Kollman P. A.; Nguyen D. T.; Case D. A. An All Atom Force Field for Simulations of Proteins and Nucleic Acids. J. Comput. Chem. 1986, 7, 230–252. 10.1002/jcc.540070216. [DOI] [PubMed] [Google Scholar]
  9. Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M. Jr.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. 10.1021/ja00124a002. [DOI] [Google Scholar]
  10. Wang J. M.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  11. Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Tian C.; Kasavajhala K.; Belfon K. A. A.; Raguette L.; Huang H.; Migues A. N.; Bickel J.; Wang Y.; Pincay J.; Wu Q.; Simmerling C. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. 10.1021/acs.jctc.9b00591. [DOI] [PubMed] [Google Scholar]
  13. Kirschner K. N.; Yongye A. B.; Tschampel S. M.; Gonzalez-Outeirino J.; Daniels C. R.; Foley B. L.; Woods R. J. GLYCAM06: a generalizable biomolecular force field. Carbohydrates. J. Comput. Chem. 2008, 29, 622–655. 10.1002/jcc.20820. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Tessier M. B.; Demarco M. L.; Yongye A. B.; Woods R. J. Extension of the GLYCAM06 Biomolecular Force Field to Lipids, Lipid Bilayers and Glycolipids. Mol. Simul. 2008, 34, 349–363. 10.1080/08927020701710890. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Cheatham T. E. 3rd; Case D. A. Twenty-five years of nucleic acid simulations. Biopolymers 2013, 99, 969–977. 10.1002/bip.22331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dickson C. J.; Walker R. C.; Gould I. R. Lipid21: Complex Lipid Membrane Simulations with AMBER. J. Chem. Theory Comput. 2022, 18, 1726–1736. 10.1021/acs.jctc.1c01217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Homeyer N.; Gohlke H. FEW: a workflow tool for free energy calculations of ligand binding. J. Comput. Chem. 2013, 34, 965–973. 10.1002/jcc.23218. [DOI] [PubMed] [Google Scholar]
  18. Wei H.; Qi R.; Wang J.; Cieplak P.; Duan Y.; Luo R. Efficient formulation of polarizable Gaussian multipole electrostatics for biomolecular simulations. J. Chem. Phys. 2020, 153, 114116 10.1063/5.0019560. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wei H.; Cieplak P.; Duan Y.; Luo R. Stress tensor and constant pressure simulation for polarizable Gaussian multipole model. J. Chem. Phys. 2022, 156, 114114 10.1063/5.0082548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Wang J.; Cieplak P.; Luo R.; Duan Y. Development of Polarizable Gaussian Model for Molecular Mechanical Calculations I: Atomic Polarizability Parameterization To Reproduce ab Initio Anisotropy. J. Chem. Theory Comput. 2019, 15, 1146–1158. 10.1021/acs.jctc.8b00603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Zhao S.; Wei H.; Cieplak P.; Duan Y.; Luo R. Accurate Reproduction of Quantum Mechanical Many-Body Interactions in Peptide Main-Chain Hydrogen-Bonding Oligomers by the Polarizable Gaussian Multipole Model. J. Chem. Theory Comput. 2022, 18, 6172–6188. 10.1021/acs.jctc.2c00710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Zhao S.; Cieplak P.; Duan Y.; Luo R. Transferability of the Electrostatic Parameters of the Polarizable Gaussian Multipole Model. J. Chem. Theory Comput. 2023, 19, 924–941. 10.1021/acs.jctc.2c01048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Huang Z.; Zhao S.; Cieplak P.; Duan Y.; Luo R.; Wei H. Optimal Scheme to Achieve Energy Conservation in Induced Dipole Models. J. Chem. Theory Comput. 2023, 19, 5047–5057. 10.1021/acs.jctc.3c00226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Wang E.; Sun H.; Wang J.; Wang Z.; Liu H.; Zhang J. Z. H.; Hou T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. 10.1021/acs.chemrev.9b00055. [DOI] [PubMed] [Google Scholar]
  25. Luo R.; David L.; Gilson M. K. Accelerated Poisson-Boltzmann calculations for static and dynamic systems. J. Comput. Chem. 2002, 23, 1244–1253. 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
  26. Wang J.; Luo R. Assessment of Linear Finite-Difference Poisson-Boltzmann Solvers. J. Comput. Chem. 2010, 31, 1689–1698. 10.1002/jcc.21456. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Wang J.; Cai Q.; Xiang Y.; Luo R. Reducing Grid Dependence in Finite-Difference Poisson–Boltzmann Calculations. J. Chem. Theory Comput. 2012, 8, 2741–2751. 10.1021/ct300341d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Cai Q.; Hsieh M.-J.; Wang J.; Luo R. Performance of Nonlinear Finite-Difference Poisson-Boltzmann Solvers. J. Chem. Theory Comput. 2010, 6, 203–211. 10.1021/ct900381r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Qi R.; Botello-Smith W. M.; Luo R. Acceleration of Linear Finite-Difference Poisson–Boltzmann Methods on Graphics Processing Units. J. Chem. Theory Comput. 2017, 13, 3378–3387. 10.1021/acs.jctc.7b00336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Qi R.; Luo R. Robustness and Efficiency of Poisson–Boltzmann Modeling on Graphics Processing Units. J. Chem. Inf. Model. 2019, 59, 409–420. 10.1021/acs.jcim.8b00761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wei H.; Luo R.; Qi R. An efficient second-order poisson–boltzmann method. J. Comput. Chem. 2019, 40, 1257–1269. 10.1002/jcc.25783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wei H.; Zhao Z.; Luo R. Machine-Learned Molecular Surface and Its Application to Implicit Solvent Simulations. J. Chem. Theory Comput. 2021, 17, 6214–6224. 10.1021/acs.jctc.1c00492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. King E.; Qi R.; Li H.; Luo R.; Aitchison E. Estimating the roles of protonation and electronic polarization in absolute binding affinity simulations. J. Chem. Theory Comput. 2021, 17, 2541–2555. 10.1021/acs.jctc.0c01305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hawkins G. D.; Cramer C. J.; Truhlar D. G. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 1996, 100, 19824–19839. 10.1021/jp961710n. [DOI] [Google Scholar]
  35. Onufriev A.; Case D. A.; Bashford D. Modification of the generalized Born model suitable for macromolecules. J. Phys. Chem. B 2000, 104, 3712–3720. 10.1021/jp994072s. [DOI] [Google Scholar]
  36. Onufriev A.; Bashford D.; Case D. A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
  37. Mongan J.; Simmerling C.; McCammon J. A.; Case D. A.; Onufriev A. Generalized Born model with a simple, robust molecular volume correction. J. Chem. Theory Comput. 2007, 3, 156–169. 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Forouzesh N.; Izadi S.; Onufriev A. V. Grid-Based Surface Generalized Born Model for Calculation of Electrostatic Binding Free Energies. J. Chem. Inf. Model. 2017, 57, 2505–2513. 10.1021/acs.jcim.7b00192. [DOI] [PubMed] [Google Scholar]
  39. Forouzesh N.; Mukhopadhyay A.; Watson L. T.; Onufriev A. V. Multidimensional Global Optimization and Robustness Analysis in the Context of Protein-Ligand Binding. J. Chem. Theory Comput. 2020, 16, 4669–4684. 10.1021/acs.jctc.0c00142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Miller B. R. 3rd; McGee T. D. Jr.; Swails J. M.; Homeyer N.; Gohlke H.; Roitberg A. E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
  41. Zhao S.; Wei H.; Cieplak P.; Duan Y.; Luo R. PyRESP: A Program for Electrostatic Parameterizations of Additive and Induced Dipole Polarizable Force Fields. J. Chem. Theory Comput. 2022, 18, 3654–3670. 10.1021/acs.jctc.2c00230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
  43. Kovalenko A.; Hirata F. A molecular theory of liquid interfaces. Phys. Chem. Chem. Phys. 2005, 7, 1785–1793. 10.1039/b416615a. [DOI] [PubMed] [Google Scholar]
  44. Luchko T.; Gusarov S.; Roe D. R.; Simmerling C.; Case D. A.; Tuszynski J.; Kovalenko A. Three-dimensional molecular theory of solvation coupled with molecular dynamics in Amber. J. Chem. Theory Comput. 2010, 6, 607–624. 10.1021/ct900460m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Gray J. G.; Giambasu G. M.; Case D. A.; Luchko T. Integral equation models for solvent in macromolecular crystals. J. Chem. Phys. 2022, 156, 014801 10.1063/5.0070869. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wilson L.; Krasny R.; Luchko T. Accelerating the 3D reference interaction site model theory of molecular solvation with treecode summation and cut-offs. J. Comput. Chem. 2022, 43, 1251–1270. 10.1002/jcc.26889. [DOI] [PubMed] [Google Scholar]
  47. Paszke A.; Gross S.; Chintala S.; Chanan G.; Yang E.; DeVito Z.; Lin Z.; Desmaison A.; Antiga L.; Lerer A.. Automatic differentiation in pytorch. In Conference on Neural Information Processing Systems ;2017.
  48. Kollman P. Free-Energy Calculations - Applications to Chemical and Biochemical Phenomena. Chem. Rev. 1993, 93, 2395–2417. 10.1021/cr00023a004. [DOI] [Google Scholar]
  49. Song L. F.; Merz K. M. Jr. Evolution of Alchemical Free Energy Methods in Drug Discovery. J. Chem. Inf. Model. 2020, 60, 5308–5318. 10.1021/acs.jcim.0c00547. [DOI] [PubMed] [Google Scholar]
  50. Giese T. J.; Ekesan S.; York D. M. Extension of the Variational Free Energy Profile and Multistate Bennett Acceptance Ratio Methods for High-Dimensional Potential of Mean Force Profile Analysis. J. Phys. Chem. A 2021, 125, 4216–4232. 10.1021/acs.jpca.1c00736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Giese T. J.; York D. M. Variational Method for Networkwide Analysis of Relative Ligand Binding Free Energies with Loop Closure and Experimental Constraints. J. Chem. Theory Comput. 2021, 17, 1326–1336. 10.1021/acs.jctc.0c01219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Ganguly A.; Tsai H. C.; Fernandez-Pendas M.; Lee T. S.; Giese T. J.; York D. M. AMBER Drug Discovery Boost Tools: Automated Workflow for Production Free-Energy Simulation Setup and Analysis (ProFESSA). J. Chem. Inf. Model. 2022, 62, 6069–6083. 10.1021/acs.jcim.2c00879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Lee T.-S.; Tsai H.-C.; Ganguly A.; Giese T. J.; York D. M.. Efficient and Automated Methods for Accurate Prediction of Protein-Ligand Binding Affinities in AMBER Drug Discovery Boost. In Free Energy Methods in Drug Discovery: Current State and Future Directions , ACS Symposium Series; Armacost K. A., Thompson D. C., Eds.; ACS, 2021; Vol. 1397, pp 161–204. 10.1021/bk-2021-1397.ch007 [DOI] [Google Scholar]
  54. Cournia Z.; Chipot C.; Roux B.; York D. M.; Sherman W.. Free Energy Methods in Drug Discovery—Introduction. In Free Energy Methods in Drug Discovery: Current State and Future Directions , ACS Symposium Series; Armacost K. A., Thompson D. C., Eds.; ACS, 2021; Vol. 1397, pp 1–38. 10.1021/bk-2021-1397.ch001 [DOI] [Google Scholar]
  55. Gaines C. S.; Giese T. J.; York D. M. Cleaning Up Mechanistic Debris Generated by Twister Ribozymes Using Computational RNA Enzymology. ACS Catal. 2019, 9, 5803–5815. 10.1021/acscatal.9b01155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Ganguly A.; Weissman B. P.; Giese T. J.; Li N. S.; Hoshika S.; Rao S.; Benner S. A.; Piccirilli J. A.; York D. M. Confluence of theory and experiment reveals the catalytic mechanism of the Varkud satellite ribozyme. Nat. Chem. 2020, 12, 193–201. 10.1038/s41557-019-0391-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Shirts M. R.; Chodera J. D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Bennett C. H. Efficient estimation of free energy differences from Monte Carlo data. J. Chem. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
  59. Zwanzig R. W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420. 10.1063/1.1740409. [DOI] [Google Scholar]
  60. Kirkwood J. G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
  61. Giese T. J.; York D. M. Development of a Robust Indirect Approach for MM --> QM Free Energy Calculations That Combines Force-Matched Reference Potential and Bennett’s Acceptance Ratio Methods. J. Chem. Theory Comput. 2019, 15, 5543–5562. 10.1021/acs.jctc.9b00401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Wang M.; Li P.; Jia X.; Liu W.; Shao Y.; Hu W.; Zheng J.; Brooks B. R.; Mei Y. Efficient Strategy for the Calculation of Solvation Free Energies in Water and Chloroform at the Quantum Mechanical/Molecular Mechanical Level. J. Chem. Inf. Model. 2017, 57, 2476–2489. 10.1021/acs.jcim.7b00001. [DOI] [PubMed] [Google Scholar]
  63. Lee T. S.; Radak B. K.; Pabis A.; York D. M. A New Maximum Likelihood Approach for Free Energy Profile Construction from Molecular Simulations. J. Chem. Theory Comput. 2013, 9, 153–164. 10.1021/ct300703z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Lee T. S.; Radak B. K.; Huang M.; Wong K. Y.; York D. M. Roadmaps through free energy landscapes calculated using the multi-dimensional vFEP approach. J. Chem. Theory Comput. 2014, 10, 24–34. 10.1021/ct400691f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Li P.; Jia X.; Pan X.; Shao Y.; Mei Y. Accelerated Computation of Free Energy Profile at ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semi-Empirical Reference Potential. I. Weighted Thermodynamics Perturbation. J. Chem. Theory Comput. 2018, 14, 5583–5596. 10.1021/acs.jctc.8b00571. [DOI] [PubMed] [Google Scholar]
  66. Giese T. J.; Zeng J.; York D. M. Multireference Generalization of the Weighted Thermodynamic Perturbation Method. J. Phys. Chem. A 2022, 126, 8519–8533. 10.1021/acs.jpca.2c06201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Cruzeiro V. W. D.; Manathunga M.; Merz K. M. Jr.; Götz A. W. Open-Source Multi-GPU-Accelerated QM/MM Simulations with AMBER and QUICK. J. Chem. Inf. Model. 2021, 61, 2109–2115. 10.1021/acs.jcim.1c00169. [DOI] [PubMed] [Google Scholar]
  68. Tsai H. C.; Lee T. S.; Ganguly A.; Giese T. J.; Ebert M. C.; Labute P.; Merz K. M.; York D. M. AMBER Free Energy Tools: A New Framework for the Design of Optimized Alchemical Transformation Pathways. J. Chem. Theory Comput. 2023, 19, 640. 10.1021/acs.jctc.2c00725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Lee T. S.; Tsai H. C.; Ganguly A.; York D. M. ACES: Optimized Alchemically Enhanced Sampling. J. Chem. Theory Comput. 2023, 19, 472–487. 10.1021/acs.jctc.2c00697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Götz A. W.; Clark M. A.; Walker R. C. An extensible interface for QM/MM molecular dynamics simulations with AMBER. J. Comput. Chem. 2014, 35, 95–108. 10.1002/jcc.23444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Manathunga M.; Jin C.; Cruzeiro V. W. D.; Miao Y.; Mu D.; Arumugam K.; Keipert K.; Aktulga H. M.; Merz K. M. Jr.; Götz A. W. Harnessing the Power of Multi-GPU Acceleration into the Quantum Interaction Computational Kernel Program. J. Chem. Theory Comput. 2021, 17, 3955–3966. 10.1021/acs.jctc.1c00145. [DOI] [PubMed] [Google Scholar]
  72. Manathunga M.; Miao Y.; Mu D.; Götz A. W.; Merz K. M. Jr. Parallel Implementation of Density Functional Theory Methods in the Quantum Interaction Computational Kernel Program. J. Chem. Theory Comput. 2020, 16, 4315–4326. 10.1021/acs.jctc.0c00290. [DOI] [PubMed] [Google Scholar]
  73. Manathunga M.; Aktulga H. M.; Götz A. W.; Merz K. M. Jr. Quantum Mechanics/Molecular Mechanics Simulations on NVIDIA and AMD Graphics Processing Units. J. Chem. Inf. Model. 2023, 63, 711–717. 10.1021/acs.jcim.2c01505. [DOI] [PubMed] [Google Scholar]
  74. Case D. A.; Atulga H. M.; Belfon K.; Ben-Shalom I. Y.; Brozell S. R.; Cerutti D. S.; Cheatham T. E. II; Cisneros G. A.; Cruzeiro V. W. D.; Darden T. A.; Duke R. E.; Giambasu G. M.; Gilson M. K.; Gohlke H.; Goetz A. W.; Harris R.; Izadi S.; Izamailov S. A.; Jin C.; Kasavajhala K.; Kaymak M. C.; King E.; Kovalenko A.; Kurtzman T.; Lee T. S.; LeGrand S.; Li P.; Lin C.; Liu J.; Luchko T.; Luo R.; Machado M.; Man V.; Manathunga M.; Merz K. M.; Miao Y.; Mikhailovskiii O.; Monard G.; Nguyen H.; O’Hearn K. A.; Onufriev A.; Pan F.; Pantano S.; Qi R.; Ranhnamoun A.; Roe D. R.; Roitberg A.; Sagui C.; Schott-Verdugo S.; Shen J.; Simmerling C. L.; Skrynnikov N. R.; Smith J.; Swails J.; Walker R. C.; Wang J.; Wei H.; Wolf R. M.; Wu X.; Xue Y.; York D. M.; Zhao S.; Kollman P. A.. Amber 2021 ;University of California: San Francisco, CA, 2021.
  75. Giese T. J.; York D. M. Ambient-Potential Composite Ewald Method for ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation. J. Chem. Theory Comput. 2016, 12, 2611–2632. 10.1021/acs.jctc.6b00198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Grimme S.; Hansen A.; Brandenburg J. G.; Bannwarth C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. 10.1021/acs.chemrev.5b00533. [DOI] [PubMed] [Google Scholar]
  77. Schott-Verdugo S.; Gohlke H. PACKMOL-Memgen: A Simple-To-Use, Generalized Workflow for Membrane-Protein-Lipid-Bilayer System Building. J. Chem. Inf. Model. 2019, 59, 2522–2528. 10.1021/acs.jcim.9b00269. [DOI] [PubMed] [Google Scholar]
  78. Klein F.; Sonora M.; Helene Santos L.; Nazareno Frigini E.; Ballesteros-Casallas A.; Rodrigo Machado M.; Pantano S. The SIRAH force field: A suite for simulations of complex biological systems at the coarse-grained and multiscale levels. J. Struct. Biol. 2023, 215, 107985 10.1016/j.jsb.2023.107985. [DOI] [PubMed] [Google Scholar]
  79. Barrera E. E.; Pantano S.. Simulating Transmembrane Proteins with the Coarse-Grained SIRAH Force Field: Tips and Tricks for Setting Up and Running in AMBER. In A Practical Guide to Recent Advances in Multiscale Modeling and Simulation of Biomolecules ;Wang Y., Zhou R., Eds.; AIP Publishing LLC, 2023. [Google Scholar]
  80. Larsson P.; Kneiszl R. C.; Marklund E. G. MkVsites: A tool for creating GROMACS virtual sites parameters to increase performance in all-atom molecular dynamics simulations. J. Comput. Chem. 2020, 41, 1564–1569. 10.1002/jcc.26198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Hsu D. J.; Davidson R. B.; Sedova A.; Glaser J. tinyIFD: A High-Throughput Binding Pose Refinement Workflow Through Induced-Fit Ligand Docking. J. Chem. Inf. Model. 2023, 63, 3438–3447. 10.1021/acs.jcim.2c01530. [DOI] [PubMed] [Google Scholar]
  82. Zhu Q.; Wu Y.; Zhao S.; Cieplak P.; Duan Y.; Luo R. Streamlining and Optimizing Strategies of Electrostatic Parameterization. Journal of Chemical Theory and Computation 2023, 19 (18), 6353–6365. 10.1021/acs.jctc.3c00659. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The AmberTools suite is free of charge, and its components are mostly released under the GNU General Public License (GPL). Please see https://ambermd.org for licensing and distribution.

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES