Electric Double Layer Effects in Electrocatalysis: Insights from Ab Initio Simulation and Hierarchical Continuum Modeling

Abstract

Structures of the electric double layer (EDL) at electrocatalytic interfaces, which are modulated by the material properties, the electrolyte characteristics (e.g., the pH, the types and concentrations of ions), and the electrode potential, play crucial roles in the reaction kinetics. Understanding the EDL effects in electrocatalysis has attracted substantial research interest in recent years. However, the intrinsic relationships between the specific EDL structures and electrocatalytic kinetics remain poorly understood, especially on the atomic scale. In this Perspective, we briefly review the recent advances in deciphering the EDL effects mainly in hydrogen and oxygen electrocatalysis through a multiscale approach, spanning from the atomistic scale simulated by ab initio methods to the macroscale by a hierarchical approach. We highlight the importance of resolving the local reaction environment, especially the local hydrogen bond network, in understanding EDL effects. Finally, some of the remaining challenges are outlined, and an outlook for future developments in these exciting frontiers is provided.

1. Introduction

Electrocatalytic reactions invariably occur within the electric double layer (EDL), which is formed between an electronic conductor, most often a metal, and an ionic conductor, namely, an electrolyte solution. Therefore, the structures of interfacial EDLs greatly determine the thermodynamics, kinetics, and product selectivity of electrocatalytic reactions (e.g., hydrogen evolution/oxidation reaction, oxygen evolution/reduction reaction, CO₂ reduction reaction), which have been collectively referred to as the EDL effects.¹⁻³ Resolving the EDL structure and linking it with the electrocatalytic performance have been a lasting research theme in electrocatalysis, because it is not only of fundamental importance but also of practical significance to the innovation of sustainable energy conversion and storage technologies, such as fuel cells, water electrolyzes and so on.^4,5

The classical Gouy–Chapman–Stern (GCS) model has been used to describe the EDL structure on mercury-like electrodes in the absence of specifically adsorbed species.⁶ Frumkin and co-workers and later Fawcett and co-workers contributed tremendously to understanding EDL effects on outer-sphere electron transfer kinetics.⁷⁻¹⁰ Since electrocatalytic reactions modify the EDL structure in a nontrivial way, it is unsurprising that the GCS model is insufficient for exploring the EDL effects in electrocatalysis. Luckily, thanks to the development of ab initio simulation and in situ spectroscopic techniques, we have seen a giant leap in understanding the EDL structure beyond the overall GCS picture, where molecular details are averaged out.

Over the past few decades, various electrochemical in situ spectroscopy technologies, e.g., the surface-enhanced Raman scattering/infrared reflection adsorption (SERS/SEIRA),¹¹⁻¹⁹ sum-frequency generation (SFG),²⁰⁻²³ and ambient pressure X-ray photoelectron spectroscopy (AP-XPS),²⁴⁻²⁷ have been employed to gain atomistic insights into the EDL structure and further understand its roles in electrocatalysis. However, distinguishing between the spectroscopic signals of the EDL and the bulk phases is still challenging. Equally challenging is the interpretation of the obtained spectra, which is a fight against uncertainties. Because of these challenges and uncertainties, these studies “could only show compatibility with the classic GCS theory and did not have sufficient resolution to investigate the deviations due to the molecular structure”, as commented by Magnussen and Groß.²⁸

Theoretical studies, spanning from the ab initio molecular dynamics (AIMD) simulations to the continuum models, are valuable to dissect the complex EDL effects in electrocatalysis.²⁹⁻³⁴ By explicitly modeling the ions and solvents, AIMD can well obtain the atomistic picture of the EDL and the fundamental properties of electrochemical interfaces. Continuum models are particularly helpful in understanding the local reaction environment in the EDL that is determined together by mass transport, electrostatic interactions, and interfacial reactions. In addition, continuum models complement AIMD by setting up the proper initial configuration of the EDL corresponding to a certain operation condition.³⁵ However, there still exist many challenges to be addressed in the future to reach a better and more elaborate understanding of the EDL roles. For example, the configuration (compositions and sizes) of explicit electrochemical interface models in the ab initio simulation studies are still fairly simplified compared to the real systems due to the high computational cost. Current AIMD simulations for complicated electrochemical interfaces and processes are still restricted to the constant charge framework due to the lack of an advanced and highly efficient constant potential scheme. As for continuum models, important molecular structures, such as the hydrogen bond network, are yet to be incorporated, in addition to the long-standing issue of proper parametrization. In this Perspective, we first provide an overview of the roles of the EDL in electrocatalysis, focusing on the ubiquitous pH, cation, and anion effects on electrocatalytic reactions. We then sketch recent efforts to decipher the EDL effects in electrocatalysis through AIMD simulations and hierarchical continuum approaches. Finally, brief concluding remarks and an outlook are presented at the end of this Perspective.

2. Overview of the Electrolyte Effects and Potential EDL Origins

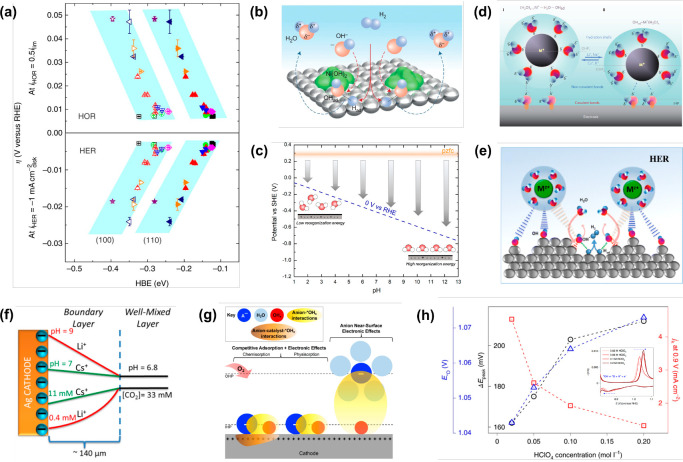
It is well-known that the nature of the electrolyte (e.g., the pH, the concentration, and identity of cation/anion) plays important roles in affecting the electrocatalytic activity.^36,37 However, such electrolyte effects remain inadequately understood so far. As shown in Figure 1, during an electrocatalytic reaction, various adsorbed species including reactants, products, intermediate spectators, and specifically adsorbed ions, often accumulate on the electrode surface, forming the inner Helmholtz plane (IHP).^38,39 Alterations in the composition and quantity of these adsorbates not only affect the electronic structures of the catalyst but also influence the charge state of the electrode surface and the strength of interfacial electric field. Consequently, this will lead to changes in the concentrations, arrangements, and configurations of solvent molecules and counterions that hold the opposite charge of the electrode and situate at the outer Helmholtz plane (OHP). Such modifications to the EDL structures will not only considerably impact the number of active sites and the adsorption energetics of reaction intermediates but also modulate the kinetics of the proton-coupled electron transfer (PCET) process between interfacial solvent molecules and surface intermediates. Therefore, the electrolyte effects, including pH, cation, and anion effects, can exert substantial influence on the activity and product selectivity of electrocatalytic reactions.

Figure 1.

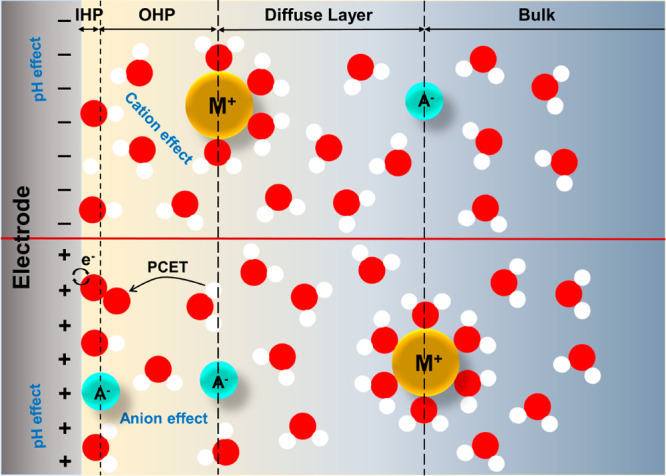
Schematic of the EDL structures on negatively (upper panel) and positively (lower panel) charged electrodes and typical electrolyte effects in electrocatalysis.

The kinetic pH effect is one of the most extensively studied electrolyte effects and is commonly observed in various electrocatalytic reactions.⁴⁰⁻⁴² The essence of altering the electrolyte pH is changing the electrode surface charge density, which will further influence the type and coverage of adsorbed species, the strength of the interfacial electric field, the configuration of solvent molecules, and the local concentrations of anions or cations in the EDL, eventually significantly impacting the thermodynamics and kinetics of electrocatalytic reactions. Numerous studies have demonstrated that the rate and selectivity of proton-involving electrocatalytic reactions are greatly affected by the electrolyte pH. For example, under acidic conditions, the kinetics of hydrogen evolution and oxidation reactions (HER/HOR) is 2–3 orders of magnitude higher than that under alkaline solutions.⁴³⁻⁴⁵ To explain the pH effect in hydrogen electrocatalysis, Yan et al. and Markovic et al. proposed the hydrogen binding energy (HBE) theory and the bifunctional mechanism, respectively (Figure 2a,b). Yan et al. believed that stronger hydrogen binding energy under alkaline conditions would lead to a higher activation energy barrier and proposed that HBE could be used as the sole descriptor for HER/HOR kinetics.⁴⁶⁻⁴⁹ On the other hand, Markovic et al. suggested that the slower kinetics in alkaline conditions can be attributed to the higher activation barrier caused by water dissociation/formation.⁵⁰ In contrast, Koper and Feliu et al. re-examined the interfacial double layer microenvironment and proposed that the highly negative charge on the electrode surface under alkaline conditions could induce a strong electric field at the electrode/electrolyte interface.^51,52 Thus, as shown in Figure 2c, the strong interfacial electric field will rigidify the interfacial water molecules and increase their reorganization energy as species cross the EDL, ultimately resulting in sluggish HER/HOR kinetics.^53,54 In contrast to hydrogen electrocatalysis, the oxygen reduction reaction (ORR) often exhibits superior activity in alkaline media, particularly on metal–nitrogen–carbon (M–N-C) catalysts, which show 7–10 times better ORR activity in alkaline compared to acid conditions.^55,56 Mukerjee et al. attributed this activity disparity to different electron transfer mechanisms, suggesting that the specifically adsorbed hydroxyl species under alkaline conditions could promote inner-sphere electron transfer reactions and thereby lead to a four-electron pathway. However, under acidic conditions, the ORR undergoes an outer-sphere electron transfer mechanism, mainly contributing to the two-electron H₂O₂ formation.^55,57 Additionally, from the perspective of catalyst stability, Jaouen et al. proposed that protonation of N atoms on the catalyst surface and subsequent anion binding in acidic media lead to catalyst deactivation and the decreased activity.^58,59 Furthermore, changes in electrolyte pH can also affect the types of frequently occupied oxygenated species on metal atoms, thereby forming new reaction active centers with modulated electronic structure and further affecting the ORR kinetics.^60,61 Regarding the CO₂ reduction reaction (CO₂RR), adjusting the electrolyte pH influences not only the reaction kinetics but also the product selectivity, especially on copper-based catalysts.⁶²⁻⁶⁶ Therefore, the complete understanding of the pH effect is crucial for advanced electrocatalytic research and has attracted extensive research interest recently.

Figure 2.

(a–c) Current theories for the pH effect of HER/HOR. (a) HBE theory. Adapted with permission from ref (46). Copyright 2015 Springer Nature. (b) Bifunctional theory. Adapted with permission from ref (50). Copyright 2013 Springer Nature. (c) Interfacial microenvironment theory. Adapted from ref (53). Copyright 2020 American Chemical Society. (d–f) Current explanations for the cation effect in electrocatalysis. (d) Site-blocking theory. Adapted with permission from ref (67). Copyright 2009 Springer Nature. (e) Noncovalent interaction model. Adapted with permission from ref (70). Copyright 2012 Springer Nature. (f) Local pH theory. Adapted from ref (71). Copyright 2016 American Chemical Society. (g, h) Current explanations for the anion effect of ORR. (g) Schematic of the anion effects on the ORR performance. Adapted with permission from ref (81). Copyright 2021 Wiley-VCH Verlag GmbH & Co. (h) Kinetic descriptor for the effect of nonspecifically adsorbed anions on ORR. Adapted with permission from ref (85). Copyright 2022 Springer Nature.

Compared to the pH effect, the cation effect on the electrocatalytic kinetics is often attributed to the strength of noncovalent interactions between hydrated cations in the EDL and *OH or OH^– species.⁶⁷⁻⁶⁹ Markovic et al. showed that for the HOR, ORR, and methanol oxidation, the reaction rates follow the order of Cs⁺ > K⁺ > Na⁺ > Li⁺ at the potential range from 0.8 to 1.0 V vs the reversible hydrogen electrode (RHE). For such activity trend, they proposed that as the radius of the alkali metal cation increases, the charge density of the ion gradually decreases, resulting in different solvation properties. As shown in Figure 2d, cations with weak solvation abilities, such as K⁺ and Cs⁺, will maintain a complete solvation configuration, remaining distant from the *OH on the electrode surface and leading to the formation of a (H₂O)_xM⁺···H₂O···*OH structure (M⁺ represents the metal cations). In contrast, cations with strong solvation abilities, such as Li⁺ and Ba²⁺, will partially lose their solvation water molecules and come closer to *OH, forming a (H₂O)_xM⁺···*OH structure. These noncovalent interactions gradually strengthen as the cation radius decreases, thereby increasing the thermodynamic stability of *OH on the electrode surface. Consequently, *OH strongly occupies and blocks the surface active sites, resulting in a significant decrease in the HOR, ORR and methanol oxidation kinetics. In contrast, for HER, it is proposed that the cations can promote the dissociation of interfacial water molecules by stabilizing the *OH/OH^– products, thus leading to kinetics following the order of Cs⁺ < K⁺ < Na⁺ < Li⁺ (Figure 2e).⁷⁰ Similarly, the CO₂RR follows the same activity trend as ORR, and one mainstream explanation is that the pK_a values for hydrolysis of hydrated cations exhibit distinct values, thereby resulting in varying local pH near the electrode and the distinction in the concentration of dissolved CO₂ (Figure 2f).^71,72 Additionally, it is reported that larger cations such as Cs⁺ and Ba²⁺ can better stabilize the *CO₂^– intermediate and promote its conversion to the *COOH intermediate.⁷³⁻⁷⁵ These phenomena and explanations highlight the significant influence of cations on the electrocatalytic kinetics, which is mainly attributed to the noncovalent interactions between cations in EDL and reaction species. However, it should be pointed out that Shao-Horn et al. and Jia et al. have reported the opposite cation effects for HOR around 0.05 V vs RHE, namely, K⁺ < Na⁺ < Li⁺.^76,77 For this, Shao-Horn et al. proposed an interfacial mechanism to understand such cation effects well in HER/HOR.

The electrocatalytic kinetics can also be significantly affected by the presence of anions in the EDL (Figure 2g).⁷⁸ In the case of HER/HOR in acid media, the reactivity is almost not influenced by the change of anion species.^79,80 This may be due to the electrode surface being usually much more negatively charged during HER/HOR, repelling anions in the outer Helmholtz layer and diminishing the specific adsorption of anions on the electrode surface. In addition, it is well-known that the HOR/HER activity on Pt in acid is usually limited by the mass transport of H₂, thus leading to the fact that the dependence of HOR/HER activity on the identity of anion species in acid cannot be observed. But it is not strong evidence for the lack of anion effect in HER/HOR, especially as the electrolyte pH rises. For the ORR on Pt-based catalysts, the activity in different electrolytes follows the order of HClO₄ > HNO₃ > H₂SO₄ > HCl. This can be easily attributed to the specific adsorption of anions such as Cl^–, SO₄^2–, and NO₃^–, which could readily and firmly occupy most of the reaction sites at the ORR relevant electrode potential, eventually hindering the adsorption of oxygen molecules and significantly decreasing the activity.⁸¹⁻⁸³ In the case of ClO₄^–, Attard et al. observed a gradual decrease in the ORR kinetics with increasing HClO₄ concentration, and attributed it to the involvement of ClO₄^– specific adsorption that competes with *OH for surface sites.⁸⁴ However, Koper et al. proposed that the ClO₄^– in the EDL does not undergo specific adsorption but rather influences the reversibility of *O ↔ *OH conversion through noncovalent interactions with *OH species, which could serve as a kinetic descriptor for ORR (Figure 2h).⁸⁵ When it comes to the CO₂RR, it should be noted that the CO₂RR shows higher activity in H₂PO₄^2– and HCO₃^– solutions compared to HClO₄ solution at the same concentration. The prevailing explanation is that anions such as HCO₃^– can act as proton donors, thereby altering the local pH near the electrode and promoting the CO₂RR.⁸⁶⁻⁸⁸

It can be seen that the above-discussed models and theories for understanding the effects of electrolyte nature on electrocatalysis were mainly from the perspective of the adsorption thermodynamics of surface intermediates or the covalent/noncovalent interactions between interfacial reaction species and electrolyte components. Beyond this, it should be noted that the interfacial EDL structures are also greatly modulated by the pH and the concentration and identity of the cations or anions. Therefore, understanding various electrolyte effects from the perspective of the interfacial EDL structure should be taken more seriously, especially at the atomic–molecular level rather than merely focusing on the energetics of surface reaction steps. Still, this faces tremendous challenges due to the extreme complexity and elusiveness of electrocatalytic interfaces. In this regard, advanced ab initio simulations can provide a significant way to precisely dissect the interfacial EDL atomic structure and its microscopic relationships with the reaction mechanism and kinetics. Section 3 focuses on recent AIMD studies on electrocatalytic EDL effects.

3. Ab Initio Simulations of the EDL Effects

The AIMD simulation, as is well-known, not only can provide a quantum chemical treatment for the interwoven electronic interactions between the electrode and various electrolyte compositions but also can capture the dynamic characteristics of liquid electrolyte at certain temperatures and enable statistical analysis.^89,90 Moreover, with ever-increasing computer power and the development of efficient first-principles algorithms in recent years, AIMD studies of complex electrocatalytic interfaces and processes have been largely affordable. Consequently, as we can see there has been a surge of AIMD simulations recently bringing about novel insights into the EDL effects in electrocatalysis.^30,91,92 Such efforts mainly centered around three aspects: (i) faithfully determining the fundamental properties of the EDL, e.g., the potential of zero charge (PZC), the surface charge relation, and the differential double layer capacitance, and meanwhile understanding their molecular origins, which is the fundamentally critical starting point for understanding the EDL effects; (ii) directly giving out the atomic structure features of EDL and the thermodynamics and kinetics of reaction steps under the various electrocatalytic conditions comparable to experimental values, which offer researchers the opportunity to intuitively capture the possible relationships between multiple EDL factors and electrocatalytic performances; and (iii) extracting the vibrational spectra of arbitrary interfacial species through the Fourier transform of the velocity autocorrelation function, which can guide the analysis of in situ experimental vibration spectra and further provide validation of the proposed EDL roles through the comparisons between experimental and computational spectroscopies. In the following, several recent advancements in the above three aspects are specifically reviewed.

3.1. Ab Initio Understanding of the Fundamental EDL Properties

A comprehensive and profound knowledge of the fundamental properties of the EDL, especially the PZC including the potential of zero free charge (PZFC) and the potential of zero total charge (PZTC), the surface charge relation, and the differential capacitance, is the cornerstone to understand EDL effects in electrocatalysis.⁹³⁻⁹⁵ This is because, based on these fundamental EDL parameters, the charge state and density on the electrode surface, which control the EDL structures and the electrocatalytic kinetics, can be easily evaluated. However, the experimental determination of these fundamental properties of the EDL is fairly burdensome, because it requires not only satisfactory preparation of single crystal electrodes but also precise and standard characterization approaches, which thus results in difficulty obtaining the fundamental EDL parameters for a series of practical systems of interest.⁹⁶⁻⁹⁸ In contrast, it is relatively simple and convenient to get the PZC values, the surface charge relation, and the differential double-layer capacitance and further understand their formation mechanisms through AIMD simulations.⁹⁹⁻¹⁰¹ More notably, these computational electrochemical properties of the EDL are often very consistent with the corresponding experimental results, demonstrating the accuracy and reliability of the ab initio simulations.

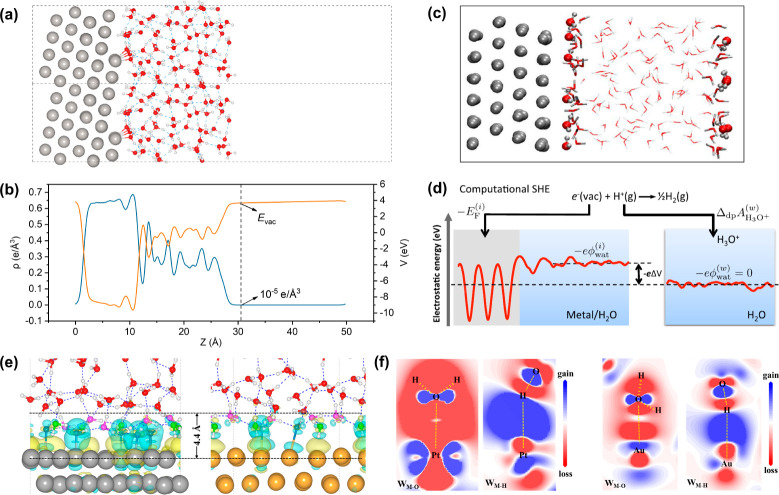
As the most fundamental concept in electrochemistry, the acquisition of the PZC has recently attracted widespread interest in ab initio simulation studies, especially obtaining the PZFC by modeling the clean electrode surface covered by an ion-free water film. Typically, the PZC is calculated by the work function method,^29,102 in which a vacuum layer has to be introduced in the electrode/water interface model to obtain the vacuum level (Figure 3a). Due to the existence of a water/vacuum interface in such a model, it has been argued that the water film should be thick enough to ensure the accurate simulation of the bulk liquid water region and the EDL. In this regard, our research group and Sakong et al. suggested that a thickness of ∼1.5–2.0 nm for the water layer is often sufficient.^103,104 On the other hand, due to the asymmetry and the limited z-axis dimension of the explicit electrode/water/vacuum interface model, the planar-averaged electrostatic potential curve in the vacuum region is usually inclined, which brings great uncertainty to the acquisition of the vacuum level. In principle, the vacuum level should be the electrostatic potential value at the position where the electron density is absolute 0, which, however, is not certain due to the constant decay of the electron density. For this, our group employed the cutoff method (Figure 3b), in which the vacuum level is determined as the electrostatic potential at the position where the cutoff value of electron density is chosen as 10^–5 e Å^–3.¹⁰⁵ In this way, as listed in Table 1, we have obtained the PZFC of several metal single crystal surfaces, as 0.27 V for Pt(100), 0.21 V for Pt(111), −0.11 V for Pt(110), −0.15 V for Pd(111), and 0.57 V for Au(111) versus the standard hydrogen electrode (SHE), all agreeing well with the corresponding experimental values. Notably, we can capture the imperceptible change trend of the PZFC for the three kinds of Pt low-index facets by using the cutoff method, namely, Pt(100) > Pt(111) > Pt(110), which is also completely consistent with the experimental trend. These current results unequivocally demonstrate the accuracy and credibility of the cutoff method in calculating the PZC of electrochemical interfaces.

Figure 3.

(a, b) Asymmetric metal/water interface model and the corresponding cutoff method to obtain the vacuum level for PZC calculation. Adapted with permission from ref (105). Copyright 2022 AIP Publishing. (c, d) Symmetrical metal/water interface model and the corresponding cSHE method to calculate PZC. Adapted with permission from ref (99). Copyright 2017 American Physical Society. (e, f) Three-dimensional and two-dimensional charge redistributions at Pt(111)/water and Au(111)/water interfaces. Adapted from ref (103). Copyright 2021 American Chemical Society.

Table 1. Summary of the Calculated PZC (PZC_theory) and the Experimental PZC (PZC_exp) for Several Metal Surfaces^a.

surface	method	PZCtheory vs SHE (V)	PZCexp vs SHE (V)
Pt(100)	cut-off	0.27	0.21–0.37106−109
	cSHE	–0.1099
Pt(111)	cut-off	0.21105	0.19–0.3495,106−108,110,111
	cSHE	0.2099
	hybrid	0.23103
Pt(110)	cut-off	–0.11105	0.06–0.22106−108,112
Pd(111)	cut-off	–0.15	0.10–0.30106−108,113
	cSHE	–0.5099
Au(111)	cut-off	0.57	0.47–0.53106−108,114,115
	cSHE	0.5099
	hybrid	0.52103

^aA value of 4.44 eV is used as the absolute potential energy of the SHE.

In addition, the combination of the implicit solvation model based on the Poisson–Boltzmann equation with the explicit electrode/water/vacuum interface model is an effective way to avoid the inclined electrostatic potential curve, because the implicit solvation model can screen any net dipole interaction between the asymmetric surfaces, thereby providing a reference electrostatic potential in the bulk of the implicit electrolyte to easily calculate the work function or PZC.^103,116,117 Interestingly, taking Pt(111)/water and Au(111)/water interfaces as examples, our research group found that the hybrid scheme (explicit + implicit model) can give almost the same PZFC values (0.23 V for Pt(111) and 0.52 V for Au(111) vs SHE) as those calculated by the cutoff method (Table 1). However, when the thickness of the explicit solvent layer is kept sufficient (above 1.5 nm), it is certain that the introduction of the implicit model will greatly increase the computational cost. Meanwhile, Gauthier et al. has reported that the usage of current implicit solvation models in electrochemical interface still comes with a number of open challenges, especially leading to the unphysical placement of ionic countercharge into the explicit electrolyte layer and then some uncertainty.¹¹⁸ Therefore, it can be seen that the calculations of work function or PZC for electrochemical interfaces based on the cutoff method is relatively facile and low-cost.

Apart from the typical work function method, the computational standard hydrogen electrode (cSHE) method has also been developed by Cheng and Sprik in recent years to calculate the PZC of electrochemical interfaces.^99,119,120 In the cSHE method, the vacuum layer in the electrochemical interface model is not required, and the whole interface model is symmetrical (Figure 3c). Then, taking the deprotonation free energy of a solvated hydronium ion in a pure water model as reference, the PZC can be calculated directly after obtaining the Fermi energy of the electrode/water interface and the average electrostatic potential of the bulk water phase in the interface model (Figure 3d). The cSHE approach can avoid treating the water/vacuum interface and introducing the experimentally estimated SHE potential that has an uncertainty on the order of ∼0.5 V. Based on the cSHE concept, Le et al.⁹⁹ calculated the PZFC of a series of metal electrodes (Table 1), which can also reproduce well the experimental values. Furthermore, one of the exciting things is that the PZFC values for some metal/water interfaces (e.g., Pt(111), Au(111)) calculated through the cutoff method are very close to those derived from the cSHE method. Such results seem to be different from the study by Bramley et al., which argued that the work function method usually yields PZC values that are ∼0.2 V lower than those derived from the cSHE method.¹⁰² Certainly, it is necessary to calculate the PZC of more electrode/water systems based on the cutoff method in the near future, to further verify the universality of the above conclusions.

In addition to the determination of the PZC value, understanding the nature and establishment mechanism of PZC has also been a lasting focus in electrochemistry and surface science.^121,122 A long-standing puzzle is why the PZC of a metal electrode in aqueous solution is significantly lower than the value calculated from the work function of the metal electrode in vacuum. In this regard, combining AIMD simulation and density functional theory (DFT) calculation, Le et al., Sakong et al., and Duan et al. reported that the dominant contribution of the difference between PZC and work function is the charge redistribution/transfer between the interfacial water molecules and the metal surface.^99,104,123 Furthermore, our research group has provided more detailed insights through the careful investigation of the atomic and electronic structures of the Pt(111)/water and Au(111)/water interfaces.¹⁰³ We showed that at both metal/water interfaces, only the chemisorbed O-down water molecules (W_M–O) and the H-down water molecules (W_M–H) within 4.4 Å away from the metal surface (Figure 3e) contribute to the charge redistributions, thus resulting the lowering of the metal work function at interfaces with water. Specifically, the nearest W_M–O significantly lowers the metal work function, by pushing the spilled electrons back into the metal skeleton and by transferring the electrons to the metal surface through coordination bonds, while the second nearest W_M–H slightly elevates the metal work function through the covalent metal–H chemical interaction (Figure 3f).

In recent years, AIMD simulations have also shined brilliantly in revealing and understanding the surface charge relation and the differential capacitance behavior of electrocatalytic interfaces because they are key properties for characterizing the EDL.¹²⁴ Undoubtedly, this requires modeling the electrified electrode/electrolyte interface, which is a challenging task because of the extreme complexity of the electrochemical interface. Currently, there are two mainstream manners to electrify the electrode surface, namely varying the electron number of the interface and inserting explicit counterions into the electrolyte film.^125,126 The former manner often needs additional counter charge compensation strategies to avoid a net charge in the periodic supercell, which mainly includes the homogeneous background charge method,^127,128 continuum dielectric method,¹²⁹ implicit solvent method based on Poisson–Boltzmann equation,^130−132 and solvated jellium method.¹³³ By contrast, the latter manner does not require any additional computational setup. However, these two methods have advantages and drawbacks. The main advantage of the former manner is that we can continuously adjust the surface charge density on the working electrode and the electrode potential by introducing fractional charge, while such an interface model based on this manner lacks explicit electrolyte ions, which leads to variation of the effective potential of an electron across the explicit electrolyte region seriously deviating from the scenario at a real electrocatalytic interface. The second manner is exactly the opposite, in which the distribution of explicit counterions in the vicinity of the charged electrode surface can provide a reasonable representation for the real EDL, especially for almost all experimental electrocatalytic systems with high electrolyte concentrations. Due to the discreteness of the number of explicit counterions, it is hard to continuously control the electrode potential to an arbitrary value comparable to experimental potential merely by varying the inserted counterion number. It is apparent that the efficient and nice combination between these two methods is of great significance for electrochemical interface simulation, which unfortunately remains a huge challenge at present. No matter how, it must be recognized that the existence of explicit counterions is essential to the elucidation and understanding of the surface charge relation and the differential capacitance behavior of electrocatalytic interfaces through ab initio simulation. In other words, we can temporarily tolerate the discontinuous adjustment of the electrode potential, but we cannot ignore the lack of interaction of the counterion with the electrode and solvent and its influence on the potential and species distributions, which is fatal to the accurate understanding of the fundamental electrochemical properties of the EDL. This point is also indispensable for further simulating the electrocatalytic reaction process and understanding the complex EDL effects in electrocatalysis.

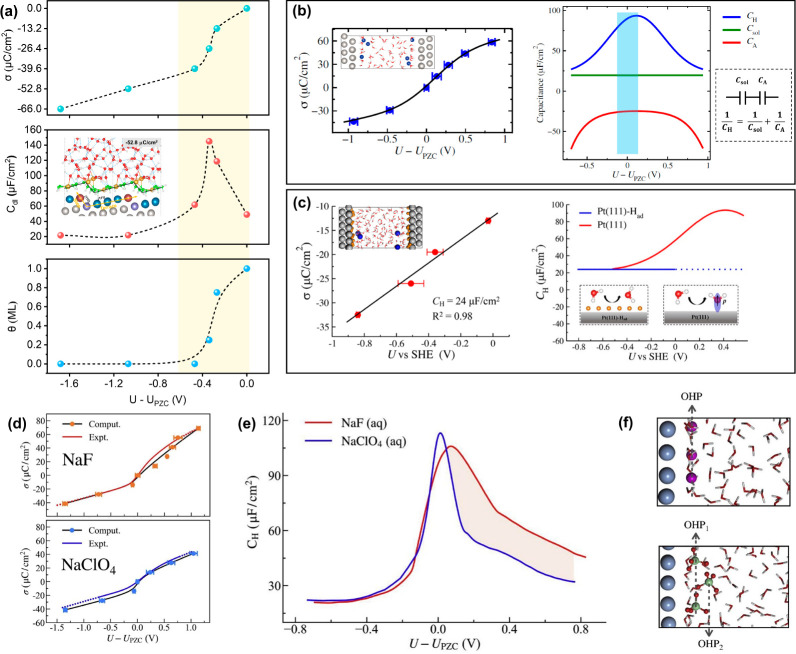
Based on the explicit counterion insertion manner, our research group has revealed the charge–potential relation and the differential capacitance behavior of the EDL at stepped Pt(553)/water interface and their formation mechanisms through AIMD simulations.¹⁰⁵ It exhibits an S-shaped charge–potential relation around the PZC, whereas a linear charge–potential relation occurs at potentials away from the PZC (Figure 4a). This thus leads to a typical bell-shaped differential capacitance behavior, which reaches a maximum of 145 μF/cm² near the PZC and then decays to a constant value of ∼20 μF/cm² as the surface charge density becomes negative enough. It is further found that toward negative potentials, the surface coverage of the O-down water chemisorbed on the step Pt atoms displays the same change trend as the charge–potential curve, namely including an S-shaped part and another linear part. It indicates that the surface charge relation and differential capacitance behavior of the stepped Pt(553)/water interface are jointly controlled by the chemisorption of water and EDL charging. Similarly, Le et al. have also well reproduced the bell-shaped differential Helmholtz capacitance (C_H) of the Pt(111)/water interface through ab initio simulation with explicit ion insertion (Figure 4b) and decomposed it into two components in series, viz. the solvent dielectric capacitance (C_sol) and the water chemisorption capacitance (C_A).¹³⁴ It is demonstrated that the C_sol induced by the usual dielectric response of solvent in the Helmholtz layer is a constant value of ∼20 μF/cm², while the C_A due to water chemisorption is negative and attains a maximum around the PZC. Therefore, connecting the C_sol and C_A will give rise to the bell-shaped profile of C_H.

Figure 4.

(a–c) AIMD-simulated surface charge relations and the differential capacitance behaviors for different electrodes. (a) Pt(553) electrode. Adapted with permission from ref (105). Copyright 2022 AIP Publishing. (b) Pt(111) electrode. Adapted with permission from ref (134). Copyright 2020 AAAS. (c) Pt(111)-H_ad electrode. Insets are the corresponding interface models. Adapted from ref (135). Copyright 2021 American Chemical Society. (d–f) AIMD-revealed anion effect in the surface charge relation and Helmholtz capacitance behavior of Ag(111). Adapted with permission from ref (136). Copyright 2022 Elsevier.

Furthermore, it is encouraging that the subtle effects of surface adsorbed species and electrolyte anions on the charge relation and capacitive behavior of the EDL can also be captured and understood by ab initio simulations. Le et al. have performed a series of AIMD calculations for the electrified Pt(111)–H_ad/water interfaces at saturation coverage of adsorbed hydrogen (H_ad) corresponding to the typical hydrogen evolution reaction conditions.¹³⁵ They revealed that the saturated hydrogen adsorption at the Pt(111)/water interface altered the charge–potential relationship from an S-shape to a straight line (Figure 4c), thus resulting in the transformation of the interfacial capacitance behavior from the bell-shaped curve to a constant value of ∼24 μF/cm², agreeing well with the experimental measurements under the same conditions.⁹⁷ Such an effect of H_ad for the Pt(111) electrode is ascribed to the complete inhibition of water chemisorption by H_ad species, thus removing the negative capacitive response owing to water adsorption/desorption processes at the interface. In contrast, our research group found that the effect of H_ad on the charge–potential relation and interfacial capacitance behavior of the stepped Pt(553) surface can be almost negligible.¹⁰⁵ This is mainly due to the spatial separation between H_ad on the terrace sites and water adsorbed on the step sites, which brings about a much lower inhibition effect on water chemisorption. As for the electrolyte anion effect on the charge relation and capacitive behavior of the EDL, Li et al. took the Ag(111) electrode as the model system because it has a wide double-layer potential window and then simulated the Ag(111)/NaF solution and Ag(111)/NaClO₄ solution interfaces.¹³⁶ The results showed that although the charging curves as well as the difference capacitance behaviors of Ag(111) in both NaF and NaClO₄ solutions exhibit similar shapes (viz. the S-shape and bell-shape, respectively), the difference capacitance curve for F^– is distinctly broader than that for ClO₄^– at positive potentials versus PZC (Figure 4d,e). Such an anion effect has been attributed to the disparate EDL microstructures in different solutions (Figure 4f). Compared to the small F^– ion, the ClO₄^– with larger ionic radius not only increases the width of the compact Helmholtz layer but also considerably reduces the water content in the double layer and even forms a second Helmholtz plane at very positive potentials, thereby giving rise to a narrower shape of differential capacitance.

To sum up, we have demonstrated the great advantages of ab initio simulations in capturing and understanding the fundamental properties of the EDL, and there has been notable progress that has been made so far. These valuable, comprehensive, and deep insights into the electrochemical interfaces are quite crucial to uncover the EDL effects in electrocatalysis and meantime will provide innovative guidance for the molecular level control of electrochemical interfaces to further improve electrocatalytic performance. Finally, it needs to be emphasized again that the explicit treatment of all components of the electrochemical interfaces at the quantum mechanical level is the prerequisite for a fundamental understanding of the EDL structures and properties.

3.2. Ab Initio Correlations between EDL Structures and Electrocatalytic Kinetics

In recent years, there has been a visible increase in investigations applying the ab initio simulation means to model the electrocatalytic reactions at electrode/electrolyte interfaces, which have provided several new insights into the atomic-scale reaction mechanism and the “structure–function” relationships between EDL microstructure characteristics and electrocatalytic kinetics.^134−142 Nevertheless, it is fair to say that the research field is still in its infancy. In addition, due to the considerable complexity of the electrocatalytic process, its ab initio simulation is very demanding and needs special care to ensure the reliability of the simulated results and opinions. Thereinto, the most important point is to construct and determine a fairly complete and self-consistent atomistic model of electrocatalytic interface, in which the adsorption state/configuration on the electrode surface, the liquid electrolyte composition, and the electrode potential must be explicitly and aptly considered as far as possible according to the target experimental conditions. Otherwise, for the ab initio simulation of electrocatalytic reactions, it is easy to obtain unreliable conclusions due to the inappropriate inputs.

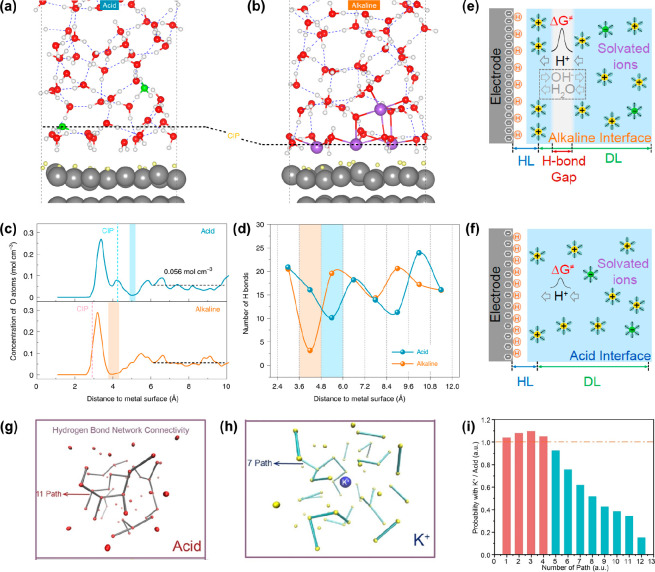
Abiding by the above principles, our research group has simulated the acid and alkaline interface structures and elementary reaction steps under hydrogen electrocatalysis (HER/HOR) conditions on a Pt(111) single crystal electrode combining the AIMD means and the slow-growth enhanced free-energy sampling approach, to understand the underlying origin of the pH-dependent HER/HOR kinetics.¹⁴³ We mimicked the acid and alkaline properties of the EDL by introducing H₃O⁺ and Na⁺ cations, respectively, in the vicinity of the electrode surface and then controlled the electrode potentials into the corresponding experimental hydrogen electrocatalytic potentials by tailoring the number of inserted cation (Figure 5a,b). These simulation methods/operations for electrocatalytic reactions are based on the equation U_RHE = (⌀ – ⌀_SHE)/e + 0.059pH, in which ⌀ and ⌀_SHE are the work functions of the electrocatalytic interface and the standard hydrogen electrode, respectively, and the pH is defined as the corresponding experimental value. Currently, due to the limitation of AIMD computational cost, the electrocatalytic models still need to be simplified, and especially the concept of electrolyte bulk concentration for a such small model size is meaningless. In the constructed EDL models under hydrogen electrocatalysis conditions, the Gouy–Chapman diffusion layers have been omitted and only the compact Helmholtz layers were modeled. This simplification can be considered reasonable, because the realistic electrolytes (0.1 M HClO₄ and NaOH) often possess fairly high concentration. In addition, the hydrogen adsorption intermediate was also introduced to describe the surface adsorption state under the hydrogen electrocatalysis potentials. On the basis of such “electrode potential–EDL properties–surface adsorption” self-consistent electrocatalytic models, we determined that compared to the acid interface, there is a wider and more severe gap zone (marked by the shaded area) of water distribution above the closest ion plane (CIP) at alkaline interfaces (Figure 5c). This correspondingly led to frustrated connectivity of the H-bond networks in the alkaline EDL (Figure 5d). Such an EDL structural feature was universal at simulated Pt(100)/electrolyte and Pt(553)/electrolyte interfaces. It is well documented that hydrogen electrocatalysis essentially involves a hydrogen transfer (HT) process, via the Volmer and/or Heyrovsky reaction, which consists of roughly two HT steps in series, namely, the HT between the electrode surface and the interfacial species closest to it and the HT between the bulk solvent and the closest interfacial species through the H-bond networks in the EDL. Therefore, it is imaginable that the great discontinuity of H-bond networks in alkaline EDL would inhibit the hydrogen electrocatalytic reactions (Figure 5e,f). Furthermore, combined with the slow-growth simulation, we proved that the HT process between the electrode surface and the interfacial water reactant in alkaline conditions has a lower free energy barrier than that in acid conditions, which confirms the key role of the HT from bulk to the interface in determining the hydrogen electrocatalytic kinetics. Thus, we proposed that it is the significantly different connectivity of hydrogen-bond networks in acid and alkaline EDLs that causes the large kinetic pH effect in hydrogen electrocatalysis. To further support this opinion, we have also simulated the Pt₃Ru(111)/electrolyte and caffeine-modified Pt(111)/electrolyte interfaces under alkaline conditions because these two catalysts have been reported to greatly increase the alkaline hydrogen electrocatalytic activity. It is found that both the adsorbed OH species on the oxophilic Ru sites of the Pt₃Ru(111) electrode and the caffeine molecule on the Pt(111) electrode could distinctly improve the connectivity of water and H-bond networks in the alkaline EDL and thereby resulted in higher reaction kinetics. It is clear from this work that the ab initio simulations have great advantages and potential in revealing the molecular-scale mechanisms of electrocatalytic EDL effects.

Figure 5.

(a, b) AIMD-simulated EDL structures under acid and alkaline hydrogen electrocatalytic conditions on Pt(111). (c, d) Comparison of the water distributions and H-bond number distributions. (e, f) Schematic of the correlations between the AIMD-simulated EDL structure features and the overall hydrogen electrocatalytic kinetics. Panels a–f are adapted with permission from ref (143). Copyright 2022 Springer Nature. (g, h) Evaluation of the H-bond network connectivity through the graph theory approach for the acid solutions without and with K⁺. (i) Relative probabilities of path number of hydrogen bonds in acid solution with K⁺ compared to pure acid solution. Panels g–i are adapted with permission from ref (144). Copyright 2023 Wiley-VCH Verlag GmbH & Co.

The proposed H-bond network connectivity mechanism has also been used to understand the cation effect in hydrogen electrocatalytic kinetics. Recently, Li et al. found that on Au and Pt microelectrodes in 0.1 M trifluoromethanesulfonic acid (HOTf), the diffusion-limited current of HER was suppressed greatly as KOTf was added to the solution, which means that the proton transfer rate in the EDL was much lowered by the existence of K⁺ cations.¹⁴⁴ Combined with the ab initio path integral molecular dynamics simulation and the graph theory approach, they have simulated the proton diffusion in the acid solutions without and with K⁺ and evaluated the connectivity of H-bond networks (Figure 5g,h). It was found that the connectivity of the water and H-bond network was much lower in the solution with K⁺ (Figure 5i), which would suppress the concerted hopping and thereby decrease the proton mobility in the EDL. Similarly, Huang et al. have also reported that the structure-breaking cation Cs⁺ could expel the interfacial water molecules and destroy the interfacial H-bond network, which would significantly cause sluggish proton transfer in the Volmer and/or Heyrovsky steps.⁷⁶ The importance of interfacial hydrogen-bonding networks for reaction kinetics has been continuously emphasized very recently, which is greatly advancing the fundamental understanding of modern electrocatalysis.^145,146

Apart from the simple hydrogen electrocatalytic reactions, the ab initio simulation is also gradually being applied to study the complex multielectron multiproton transfer reactions (such as the ORR/OER, CO₂RR, and CO reduction), mainly focusing on determining the entire reaction pathway at the electrochemical interface, obtaining the energetics along the reaction process, and determining the key interfacial EDL factors that affect the reaction performance.^147−151 In this regard, the main challenge is that the multielectron multiproton transfer reaction not only involves more elementary steps but also has many possible products and corresponding reaction mechanisms. More importantly, the existence of various reaction intermediates will produce extremely complex surface adsorption structures, and meanwhile, the surface adsorption structure is often potential-dependent. Due to its key role in affecting the electrocatalytic performance and mechanism and even the EDL features, the determination of surface adsorption structure should be given attention first in the simulation of complex electrocatalytic reactions.^152,153 This will greatly increase the cost and difficulty of ab initio simulation but is worthwhile to ensure the accuracy of the simulation results.

For the ab initio simulations of electrocatalysis, another thing that needs to be mentioned is that a large part of the current research is based on the constant charge scheme, which is inconsistent with the actual constant potential condition. If the lateral cell dimensions of electrochemical interfaces are large enough, the change of electron density on the electrode surface over the course of an elementary reaction can be ignored, at which the constant charge simulation can be equivalent to the constant potential condition.^154,155 However, such a method is largely out of reach for the current computational cost affordability. For limited cell dimensions, a fairly handy “charge-extrapolation” method developed by Chan and Nørskov is often used now to correct the energy change in constant charge simulation.^156,157 Another alternative and desirable method is to simulate the electrocatalytic systems under the framework of the grand-canonical ensemble, in which the electron number of the system is taken as a variate and needs to be adjusted automatically along the whole reaction process to maintain a constant electrode potential. As we mentioned above, this approach requires a charge compensation scheme to keep the model charge neutral. Bonnet et al. pioneeringly connected the electrochemical interface to a fictitious potentiostat, which allowed the exchange of electronic charge at a preset electrode potential.¹⁵⁸ Recently, combining with the VASPsol to balance the net charge, Liu et al. implemented this potentiostat strategy to perform ab initio simulation for oxygen reduction electrocatalysis on cobalt–nitrogen–carbon and boron-doped carbon catalysts, which provided an insightful interpretation for selective production of hydrogen peroxide.¹⁵⁹ Furthermore, Bouzid et al. developed the constant Fermi-level molecular dynamics method based on the fictitious potentiostat method, which could reproduce well the capacitive behavior, PZC value, and interfacial water orientation transformation of a Pt(111)/water interface compared to the experimental measurements.^160,161 Unfortunately, the ab initio constant potential simulation on the basis of the potentiostat concept has not been used commonly in electrocatalysis, due to its high computational cost and the lack of algorithm integration in mainstream DFT software. In this regard, Xia et al. developed a new fully converged constant potential (FCP) algorithm based on Newton’s method and a polynomial fitting, which could overcome the numerical instability and efficiently converge to the preset electrochemical potential.¹⁶² More importantly, it is external to the self-consistent field (SCF) calculations, thus being flexible to combine with various computational codes. On the other hand, Wippermann et al. have proposed a canonical thermopotentiostat approach regarding the electric field as the control parameter, which can avoid the treatment of charged systems and be easily implemented into the existing AIMD packages.^163,164 Similarly, Luan et al. further developed the electric field controlling constant potential (EFC-CP) method to approximately realize constant potential simulation by applying a self-adaptive electric field on a charge neutral system.¹⁶⁵ It is expected that these methods can be widely applied, benchmarked, and even further improved in the near future to greatly facilitate the accurate understanding of EDL effects in electrocatalysis and obtain the reaction thermodynamic and kinetic parameters.

3.3. Ab Initio Vibrational Spectroscopy for Understanding Electrocatalytic EDL Effects

As mentioned above, various in situ electrochemical vibrational spectroscopy technologies currently play incomparable roles in dissecting the EDL structures at the molecular level and understanding its effects on electrocatalytic performance. Still, they face several enormous challenges, especially the accurate analysis and assignment of experimental spectral signals. In this regard, computational vibrational spectroscopy by means of dynamic AIMD simulations, which can be given by the Fourier transformation of the velocity autocorrelation functions along the AIMD trajectories and termed as power spectrum (also known as the vibrational density of states, VDOS),¹⁶⁶ can be well applied to assist the experimental spectral analysis. Compared to the harmonic spectra calculated from the static approach based on harmonic approximation, the advantages of the AIMD-derived VDOS analysis is that it can consider the anharmonicity effect, which is particularly crucial for electrocatalytic systems that involve bond formation and breaking.^167,168 In addition, the thermal effect, the electric field, and the interaction with surrounding species can also be well considered in AIMD simulations, which are necessary to capture more realistic vibrational spectroscopy characteristics of simulated electrocatalytic interfaces for comparison with the in situ experimental spectra.

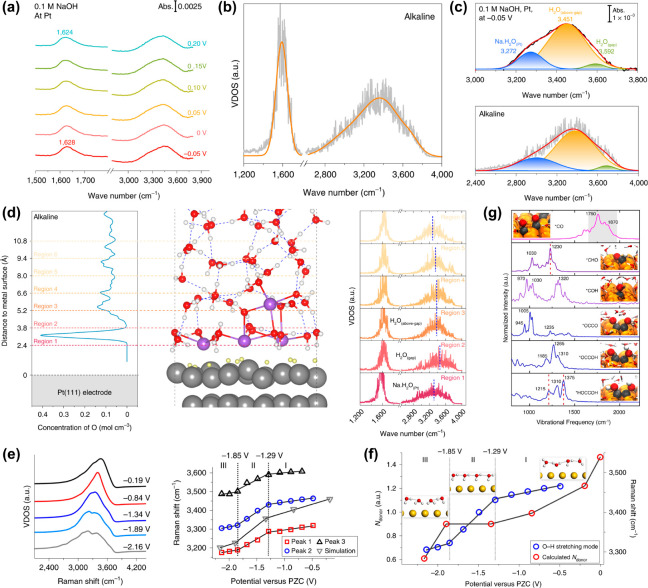
Recently, our research group has combined the computational VDOS approach and in situ surface-enhanced infrared absorption spectroscopy (SEIRAS), to verify the proposed H-bonding network connectivity mechanism for the kinetic pH effect of hydrogen electrocatalysis on Pt.¹⁴³ Taking the alkaline hydrogen electrocatalytic interface as an example (Figure 6a,b), it can be seen that the O–H stretching band in the computational VDOS of the interfacial water molecules within ∼6.6 Å of the electrode surface was fairly consistent with the experimental spectrum, both exhibiting a broad and symmetric shape. However, once the water molecules further from electrode surface (>6.6 Å) were taken into account in the calculation of VDOS, the shape of the O–H stretching peak would gradually deviate from the experimental spectrum. This not only means that the in situ SEIRAS signals were mainly derived from the interfacial water but also shows that the computational vibrational spectroscopy extracted from a reasonable electrocatalytic interface model can well reproduce the experimental results. Furthermore, the deconvolutions of both experimental and computational O–H stretching vibrational spectra possessed the same feature, namely, including three components (Figure 6c). According to the traditional H-bonding number rule, these three components from high frequency to low frequency will be assigned to the isolated water, 2-coordinated hydrogen-bonded water, and 4-coordinated hydrogen-bonded water, respectively. By contrast, we have assigned these three components to the interfacial water molecules in the H-bonding gap region (H₂O_(gap)), above the gap region (H₂O_(above-gap)), and nearest to the electrode surface (Na·H₂O_(Pt)), respectively, with the assistance of the detailed layer-by-layer VDOS analysis (Figure 6d), which provided a rational verification for the simulated EDL structural features under alkaline hydrogen electrocatalytic conditions and thus the proposed interfacial mechanism of the pH effect. Similarly, the computational VDOS analysis has also been united with the in situ Raman spectroscopy, to elucidate the potential-dependent orientation and H-bonding network of interfacial water.¹⁶⁹ It was reported that the O–H stretching frequency of water in the calculated VDOS exhibited the same potential dependence as the experimental Raman frequency (Figure 6e). That is, the frequency gradually decreased while sweeping to negative potentials, and the Stark tuning rate underwent two transitions, which thus revealed the continuous transition of the orientation and H-bonding network structure of the interfacial water molecule from “parallel” to “one-H-down” and then to “two-H-down” (Figure 6f). From the above, one can see the combination between experimental and computational vibrational spectra can provide a compelling avenue for exploring electrochemical interface structures and understanding EDL effects more accurately.

Figure 6.

(a, b) In situ SEIRAS spectra and computational VDOS for alkaline hydrogen electrocatalytic interface on Pt. (c) Deconvolutions of the experimental and computational O–H stretching peaks. (d) Layer-by-layer VDOS analysis of water at alkaline hydrogen electrocatalytic interface on Pt. Panels a–d are adapted with permission from ref (143). Copyright 2022 Springer Nature. (e) Calculated VDOS of interfacial water on Au and the corresponding peak frequencies at different potentials. (f) H-bonding network structure analysis of interfacial water as a function of potential. Panels e and f are adapted with permission from ref (169). Copyright 2019 Springer Nature. (g) VDOS of several reaction intermediates in the CO reduction on Cu(100). Adapted with permission from ref (171). Copyright 2022 National Academy of Sciences.

Another advantage of the integration of computational VDOS with in situ spectroscopy is to accurately identify the surface reaction intermediates (Figure 6g), especially for the multiproton multielectron reactions (e.g., CO₂ reduction, N₂ reduction). In this regard, Cheng et al. and Shao et al. have provided representative works.^170,171 Through the VDOS calculation, the vibrational features of arbitrary possible intermediate species at various reaction conditions can be obtained and then compared with the experimental spectral signals, eventually determining the actual intermediates and electrocatalytic mechanism.

4. Hierarchical Continuum Modeling of the EDL Effects

As discussed above, ab initio simulation can well obtain the atomistic pictures of the EDL and thereby seek out the correlation between a certain EDL feature and electrocatalytic kinetics. However, it is still hard to provide specific and quantitative contributions of various interfacial factors in deciding the electrocatalytic performance. By contrast, the theoretical model descriptions can offer a fairly comprehensive consideration of various reaction factors and then isolate the role and quantify the contribution of a single specific variable in electrocatalysis. In other words, a proper examination of the impact of EDL effects on electrocatalytic reactions necessitates a comprehensive analysis encompassing various aspects. This includes the mechanism of the electrocatalytic reaction, the behavior of surface charging, considering the influence of adsorbates, and the mass transport phenomena occurring within the electrolyte solution. These considerations should extend from the atomistic reaction zone to the microscopic non-electroneutral environment in the EDL, and further to the macroscopic electroneutral electrolyte solution. Given the involvement of multiple physical phenomena and scales, the problem exceeds the capabilities of any single theoretical or computational approach. Consequently, adopting a hierarchical methodology appears to be the sole feasible approach in the foreseeable future to effectively manage the intricate couplings among processes occurring across a wide spectrum of time constants and lengths, as commented by Exner and Bonnefont.^172,173

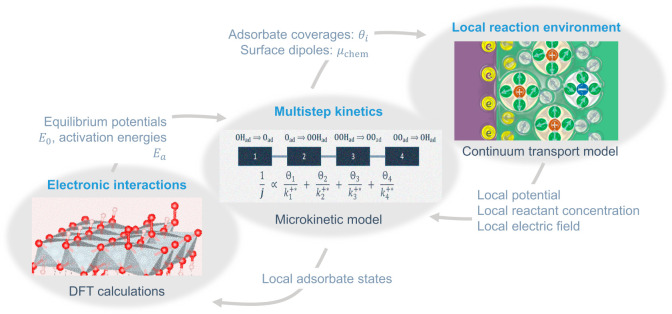
Recent years have witnessed the popularization of such hierarchical models. Figure 7 shows the model framework developed by Huang and co-workers.^174−177 On the atomistic scale, the reaction mechanism is determined from density functional theory (DFT) calculations. On the macroscopic scale, the continuum transport model that considers the microscopic non-electroneutral EDL describes the local reaction conditions, including the concentration of reactant(s) and the electric field in the reaction zone. Between these scales, the microkinetic model bridges the DFT calculations and the continuum transport model. The bridge has three functions. First, it describes the reaction considering the coupling between different elementary reaction steps without designating any priori RDS; see a critical analysis on potential determining step and RDS in a previous report.¹⁷⁸ Second, it merges the local reaction conditions provided by the continuum transport model and energetic parameters of elementary steps determined from the DFT calculations. Third, it provides the coverage amounts of adsorbates as a function of electrode potential that are crucial inputs for setting up the interface configurations in the DFT calculations and boundary conditions in the continuum transport model. The three models are interrelated and should be solved in a self-consistent manner.

Figure 7.

Hierarchical approach to model the EDL effects on electrocatalytic reactions. The approach integrates DFT calculations to determine the reaction mechanism on the atomistic scale, a continuum transport model to describe the local reaction conditions on the macroscopic scale, and a microkinetic model between them to treat the coupled multistep electron transfer kinetics.

Currently, DFT calculations are usually performed using the computational hydrogen electrode method,¹⁷⁹ and the reaction barriers of the elementary steps are seldom computed. We are glad to see that constant-potential DFT calculations of the reaction mechanism are emerging.^{133,145−165,180−182} The electron transfer kinetics are usually described using the Butler–Volmer equation. Modern electron transfer theories are rarely used, probably due to the many parameters involved in these theories. Nevertheless, a few works have underscored the importance of the metal electronic structure and solvent dynamics that are not explicitly considered in the Butler–Volmer equation.^174,183 The continuum transport model usually involves the Poisson–Nernst–Planck theory with various levels of modifications considering ion size and bulk reactions.

The model framework has been applied to several electrocatalytic reactions, including ORR,^175,177 oxygen evolution reaction (OER),¹⁸⁴ formic acid oxidation reaction (FAOR),^176,185 hydrogen peroxide redox reaction (HPRR),¹⁸⁶ and CO₂RR.¹⁸⁷ Below, we take two recent examples to illustrate the main aspects of the hierarchical approach.

The OER activity has been revealed to vary among the electrolyte cations. Specifically, many catalysts, including nickel- and cobalt-based oxides, are more active in CsOH than LiOH.^188,189Figure 8a shows the experimental data of the OER at NiOOH in 0.1 M MOH (M = Li, Na, Cs). Recently, using the hierarchical modeling approach, Huang et al. revealed that the cation dependency of the OER activity is closely related to the local reaction environment in the EDL.¹⁸⁴ Based on the work function calculated from DFT, the NiOOH catalyst has a potential of zero charge of 1.93 V_RHE at a pH of 13. Therefore, the NiOOH catalyst is negatively charged in the potential region relevant for the OER, e.g., 1.6–1.9 V vs RHE. Consistent with our analysis, the point of zero charge of Ni(OH)₂ is reported to be ∼11; namely, the solid will be negatively charged at pH > 11 under open circuit conditions.

Figure 8.

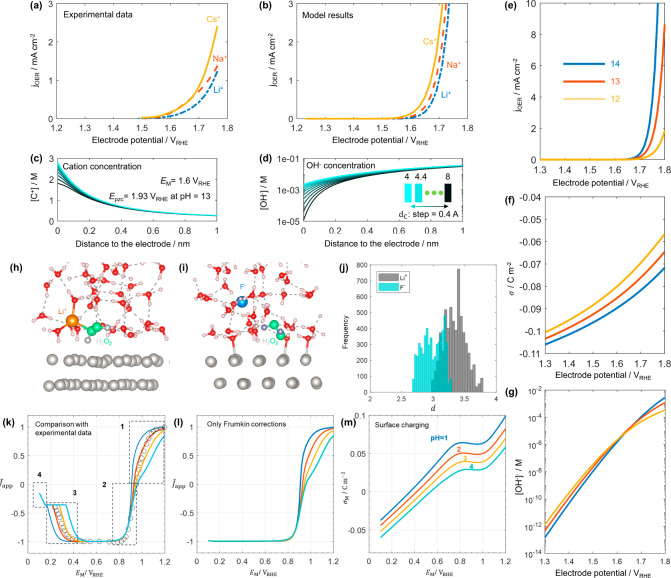
(a–d) Theoretical description of the cation effects in OER: (a) experimental polarization curves reported by Michael et al.¹⁸⁹ and (b) model-derived polarization curves of the OER at NiOOH in 0.1 M MOH (M = Li, Na, Cs) solution; (c) cation concentration near the electrode surface with the effective cation diameter d_c varying between 4 and 8 Å with a step of 0.4 Å; (d) concentration of hydroxyl anions at the electrode potential of 1.6 V_RHE. (e–g) Theoretical description of the pH effect in the OER: (e) model-derived polarization curves of the OER in x M LiOH (x = 1, 0.1, 0.01), with maintaining a constant total ionic strength of 1 M; (f) relationship between surface charging at the three pH levels; (g) concentration of OH^– at the reaction plane as a function of electrode potential for the three pH levels. Panels a–g are adapted with permission from ref (184). Copyright 2021 American Chemical Society. (h–m) Theoretical description of the surface charge effect in HPRR: (h, i) configurations of charged Pt(111)–water interfaces containing a single H₂O₂ molecule in water, in which panel h displays the negatively charged Pt(111) surface with one Li⁺ cation in water and panel i shows the positively charged Pt(111) surface with one F^– anion in water; (j) histograms depicting the medium distance between the two oxygen atoms of the H₂O₂ molecule and the outermost layer of Pt atoms; (k) model-derived polarization curves at four different pH levels, along with the experimental polarization curve (indicated by circles) for pH = 2; (l) model-derived polarization curves considering only Frumkin corrections; (m) surface charging behaviors calculated at four pH levels. Panels h–m are adapted with permission from ref (186). Copyright 2022 Elsevier.

As the electrode surface is negatively charged, cations accumulate within the EDL, as shown in Figure 8c. Different lines denote cations of different diameters in the range between 4 and 8 Å. The cation concentration is lower for bigger cations, signifying the overcrowding of cations within the EDL. Due to the intensified steric repulsion of bigger cations, the concentration of hydroxyl anion, [OH^–], decreases more in the EDL (Figure 8d). Since the hydroxyl anion is the reactant of the OER, a lower concentration of hydroxyl anion renders a lower OER activity, regardless of the detailed reaction mechanism. This explains why the OER activity is lower in LiOH than CsOH, considering that solvated Li⁺ is bigger than solvated Cs⁺.¹⁹⁰ The model-simulated polarization curves are shown in Figure 8b, which agree well with the experimental data in Figure 8a.

The pH effects of the OER can be interpreted also from the cation overcrowding phenomena.¹⁸⁴ Many OER catalysts are more active in more alkaline solutions on the RHE scale; see Figure 8e–g. This pH dependency on the RHE scale is widely taken as a clue of decoupled proton–electron transfer, since the thermodynamics of a concerted proton–electron transfer is pH independent on the RHE scale. Such a thermodynamic view does not consider the pH-dependent local reaction conditions in the EDL. On the RHE scale, the electrode surface is more negatively charged when the solution pH is higher, as shown in Figure 8f. As a result, the effect of cation overcrowding becomes more prominent at higher pH levels, causing a decrease in hydroxyl anion concentration at potentials below 1.6 V_RHE, despite the overall higher bulk OH^– concentration at higher pH levels (Figure 8g). With an increasing electrode potential, the surface charge becomes less negative, mitigating the cation overcrowding effect and leading to higher OH^– concentrations for elevated pH levels at potentials above 1.6 V_RHE. Since the activity of OER is constrained by the OH^– concentration influenced by the cation overcrowding effect, it exhibits an increase with rising pH levels at potentials above 1.6 V_RHE, as depicted in Figure 8e. That is, at high electrode potentials, the pH effect of the OER arises from the OH^– concentration, because the cation overcrowding effect is mitigated and only has a minor impact on the OER activity.

The hierarchical approach has also been employed to understand the influence of surface charge on H₂O₂ redox reactions on Pt(111).¹⁸⁶ As shown in Figure 8h–j, AIMD simulations reveal a statistical trend wherein the O–O bond of the hydrogen peroxide molecule (the reactant) is located at a greater distance from the platinum surface under negative surface charge conditions, simulated by introducing a lithium ion in the water layer (Figure 8h), as compared to the positive surface charge condition simulated by introducing a fluorine anion in the water layer (Figure 8i). Since the electronic interaction strength diminishes exponentially with distance, we anticipate a higher activation barrier for breaking the oxygen–oxygen bond of hydrogen peroxide, consequently leading to the anomalous experimental observation of suppressed reduction current with decreasing electrode potential (Figure 8k). Based on this premise, a microkinetic double-layer model was employed to offer a comprehensive interpretation of the polarization curves for this system. At potentials below 0.2 V_RHE, the convergence of polarization curves across various pH levels into a single curve can be attributed to the site-blocking effect of hydrogen adsorption, which approaches thermodynamic equilibrium and remains pH-independent on the RHE scale. In the potential range 0.2–0.6 V_RHE, the suppression of HPRR is caused by the negative surface charge (Figure 8m). Our AIMD simulations reveal that the negative surface charge on Pt(111) repels the O–O bond of H₂O₂ further from the electrode surface, resulting in a higher activation barrier for its cleavage. This surface charge effect explains why the suppression occurs at higher potentials for higher pH values and is more pronounced in the presence of smaller effective cations. The benchmark model, which considers Frumkin effects but neglects this surface charge effect, fails to reproduce the pH-dependent suppression of the HPRR in this region (Figure 8l). Moving into the potential range of 0.6–0.9 V_RHE, the net reduction current becomes nearly pH-independent due to the rapid kinetics of OH_ad adsorption on Pt(111). Under equilibrium conditions, the HPOR should be pH-independent on the RHE scale since both elementary steps of the HPOR involve proton-coupled electron transfer. The reduction in net oxidation current at potentials above 0.9 V_RHE and at higher pH values provides evidence of the significance of nonequilibrium microkinetics in this regime.

The role of the interfacial solvent environment has not been adequately considered in previous works. Part of the reason is that previous works have employed the phenomenological Butler–Volmer equation to describe electron transfer kinetics, in which the solvent environment plays no explicit role.^177,190 Nevertheless, advanced electron transfer theories have already pointed out the central importance of the solvent environment in electron transfer reactions.^191−193 In particular, there was a wave of joint experimental and theoretical research activities on the dynamic solvent effects in the 1980s and 1990s.^194,195 However, such advanced electron transfer theories are seldom employed to describe electrocatalytic reactions, indicating that a gap between the research field of chemical physics and electrocatalysis must be bridged.

The solvent environment affects both energetic (the activation barrier, ΔG_a) and dynamic (the barrier crossing frequency ν_n) factors in the expression for the rate of electron transfer. In the homogeneous electron transfer process, the orientational configuration of the solvent molecules is exclusively determined by the charge state of the reactant. In contrast, for the interfacial electron transfer process, the orientational configuration of the solvent molecules is also influenced by the excess free charge on the electrode surface.¹⁹⁶ Consequently, the difference on the axis of the solvent coordinate between the oxidant and reductant states is smaller for interfacial electron transfer than for homogeneous electron transfer. It is then implied that the solvent reorganization energy λ shall decrease as the reactant approaches the interface, which has been confirmed in recent experimental and computational works.^197,198 In addition, molecular dynamic simulations have shown that when water molecules in the first layer are strongly bound by the metal, the hydrogen-bonding network and the solvation structure of the solute are frustrated.¹⁹⁹ Such effects are believed to exert a significant impact on the electron transfer kinetics.²⁰⁰

5. Conclusion and Outlook

In summary, we have briefly reviewed the recent progress in understanding the EDL effects in electrocatalysis through ab initio simulations and hierarchical continuum models. In terms of ab initio modeling for electrocatalytic interface structure and process, the efforts have provided several novel atomistic insights into the fundamental properties of EDL and the relationships between the EDL atomic structure characteristics and electrocatalytic performance. This would tremendously facilitate the further development of modern electrochemical science and trigger a transition in the strategies for improving electrocatalytic performance from the design of the catalyst’s composition and electronic structures to the regulation of the interfacial EDL structures. In addition, the integration between the ab initio simulation and the electrochemical in situ spectroscopy technologies bridged by computational spectroscopy offered an exciting research paradigm to accurately obtain the molecular-level pictures of electrochemical EDL structures and reaction pathways, which is fairly significant to further uncover the mechanisms of various EDL effects in electrocatalysis and will attract more interest in the near future. The hierarchical modeling approach integrates three key elements of a proper undertaking of deciphering electrocatalysis, namely quantum-mechanical DFT calculations to determine the reaction mechanism on the atomistic scale, a continuum EDL model to describe the local reaction conditions, and a microkinetic model between them to treat the coupled multistep electron transfer kinetics. Such theoretical models have been demonstrated as an effective and quantitative avenue to manage the intricate couplings among various interfacial processes, highlighting the key role of the local reaction environment in determining the electrocatalytic activity.

Although some significant progress based on ab initio simulations and hierarchical continuum models has been made to dissect the EDL effects in electrocatalysis, it is fair to say that both fields are still quickly developing and face several great challenges and limitations. A small step forward in addressing these challenges will provide important opportunities for a deep understanding of the electrocatalytic EDL effects.

For the ab initio simulation of EDL effects, first, it has been mentioned that almost all current simulations of the electrocatalytic interface structure and process are limited to the constant charge scheme, which is completely inconsistent with the constant potential conditions along real electrocatalytic reactions. Therefore, the development of efficient and user-friendly constant potential algorithms will always be the main theme pursued by ab initio simulation research for electrocatalysis. In addition, it is noted that when developing the constant potential approach, the choice and setup of the charge compensation scheme should be compatible with the explicit consideration of solutes (e.g., cations, anions) in interfacial models, which has been highlighted as a prerequisite for meaningful electrocatalytic interface simulations. Second, current electrocatalytic interface models are still very simplified compared with the realistic systems. In the interface models with extremely limited sizes, we generally cannot consider the factor of electrolyte concentration and ignore the diffusion layer. Meanwhile, the time scale of ab initio simulation for the electrocatalytic system is currently limited to tens of picoseconds. In this regard, developing molecular simulation methods based on machine-learning potential is a promising approach to distinctly enhance the spatial and temporal scales in electrocatalytic research. Such machine-learning potential-based simulation methods are especially important to enable the investigation of EDL effects in more complex reactions, such as the electrocatalytic coupling system and the electrocatalytic transformation of biomass/organic molecules. Recently, several advances have been made.^201−204 Third, the ab initio simulation results of dynamic interfaces are mainly verified by the comparison between computational vibration spectroscopy and experimental vibration spectroscopy at present. However, the combination between them is largely qualitative, and the computational spectral peaks tend to have larger widths.^143,169 This may be due to the differential spectrum processing of experimental spectroscopy, the rationality of the simulated interface model and reaction condition settings, or the effectiveness of current vibrational spectroscopy calculation methods. Therefore, we need to make more efforts to achieve a closer match and even a reasonable quantitative comparison between the computational and experimental spectroscopy, which will greatly facilitate the accurate dissection of the electrocatalytic interface.

For the hierarchical continuum modeling of EDL effects, incorporation of atomistic and molecular structure obtained from AIMD into the hierarchical framework is a unqualified need. In the reviewed hierarchical models, the interfacial EDL was treated at the mean field level, which could omit crucial short-range correlations and atomistic scale details of the EDL. In addition, it is very important to conduct parameter identifiability and sensitivity analysis of these hierarchical models that are heavy parameters.

Author Contributions

CRediT: Peng Li conceptualization, writing-original draft, writing-review & editing; Yuzhou Jiao writing-original draft, writing-review & editing; Jun Huang conceptualization, writing-original draft, writing-review & editing; Shengli Chen conceptualization, supervision, writing-original draft, writing-review & editing.

The authors declare no competing financial interest.