基于非线性高阶特征和超图卷积神经网络的阿尔茨海默症分类

Abstract

阿尔茨海默症（AD）是一种不可逆转的大脑神经退化性疾病，会损害患者记忆力和认知能力。因此，AD诊断具有重要意义。大脑感兴趣区域（ROI）之间往往是多个区域以非线性的方式协同交互，充分利用此类非线性高阶交互特征有助于提高AD诊断分类的准确性。为此，提出基于非线性高阶特征提取和三维超图神经网络相结合的AD计算机辅助诊断框架。首先针对ROI数据使用基于径向基函数核的支持向量机回归模型训练出基估计器，再通过基于基估计器的递归特征消除算法提取功能性磁共振成像（fMRI）数据中的非线性高阶特征，进而将特征构造成超图，最后基于fMRI数据的四维时空特性搭建超图卷积神经网络模型来进行分类。阿尔茨海默症神经影像倡议（ADNI）数据库上的实验结果表明，所提框架在AD/正常对照（NC）分类任务上的效果相较于Hyper Graph Convolutional Network（HyperGCN）框架提高了8%，相较于传统二维线性特征提取方法提高了12%。综上，本文框架在AD分类效果上较主流深度学习方法有所提升，可为AD计算机辅助诊断提供有效依据。

0. 引言

阿尔茨海默症（Alzheimer’s Disease，AD）是一类不可逆的大脑神经退行性疾病^[1]。如今全世界有5 500万人患有AD，该疾病被认为是导致死亡的第七大原因^[2]。由于AD的不可治愈性，文献[3]指出应当转变治疗思路，重点关注AD的预防及诊断，因此AD诊断的准确性和高效性日益重要。

研究表明，AD病情与脑功能连接网络和结构的拓扑变化有关^[4-5]，而在神经影像技术中，功能性磁共振成像（functional magnetic resonance imaging，fMRI）数据因为具备较高的时空分辨率，能较地好记录脑功能连接网络结构的变化信息，所以常被研究者用于构建大脑功能连接网络。主要方法是利用fMRI表达出来的各体素上的血氧水平依赖（blood oxygenation level dependent，BOLD）信号时间序列计算出大脑区域两两之间的功能关联性，以此构造出脑功能连接网络。接着，采用机器学习或深度学习的方法，从中学习和筛选出对AD发展各阶段更为敏感而有效的特征，以期帮助提高AD诊断的准确性和可靠性。例如，Ju等^[6]基于fMRI数据构造脑功能连接网络，利用自编码器提取高级特征，并用Softmax分类器完成分类。Wee等^[7]基于扩散张量成像技术和fMRI数据构建脑功能连接网络，使用多核支持向量机（support vector machine，SVM）区分正常对照组（normal control，NC）和AD患者组。类似地，Li等^[8]利用脑功能连接网络训练学习稀疏自编码器（sparse auto encoder，SAE），再使用Softmax分类器进行分类。Eslami等^[9]基于脑功能连接网络，通过自编码器获取有效的特征，使用单层感知机来分类。上述方法在提取fMRI数据特征及构建脑功能连接网络的研究上做出了重要贡献，然而往往无法同时利用多个脑区之间的非线性交互特征及多个脑区协同作用时的多元高阶特征，忽略了大脑作为非线性动态系统的本质^[10]。

研究表明，大脑活动是由多个脑区协同非线性作用来完成的，大脑的非线性高阶特征需要一种合适的数据结构来进行存储，才能有效利用其特性提升AD诊断分类性能。大脑的脑功能连接网络本质上是一种图结构类型，而图神经网络（graph neural network，GNN）在众多图结构数据中展现了强大的特征提取和学习能力^[11]，因此现有研究工作主要利用GNN对基于fMRI影像的脑功能连接网络进行分析。Wen等^[12]提出了一种基于先验脑结构学习的多视图图卷积网络，通过不同阈值构建多个脑功能连接网络，建立共享图嵌入层来学习不同脑功能连接网络的特征。该模型可以有效学习感兴趣区域（region of interest，ROI）在不同阈值的特征，但无法利用多个脑区间的交互特征。Li等^[13]基于fMRI影像特征提出一种脑图神经网络，为不同图节点动态赋权重，并通过池化层对节点聚类。上述方法往往使用普通邻接图结构，将脑区抽象为图节点，脑区间的特征抽象为带权边，然而普通图结构只能存储相邻脑区之间的二元特征，无法存储多个脑区之间的多元高阶特征。

因此，为了存储多个脑区之间的非线性多元高阶相关关系，本文提出基于非线性高阶特征和超图卷积神经网络的AD分类框架。首先对fMRI源数据进行预处理并提取出BOLD信号，再针对BOLD信号中的ROI数据，使用基于径向基函数（radial basis function，RBF）核的支持向量回归模型（support vector regression，SVR）训练出基估计器，通过基于基估计器的递归特征消除算法（recursive feature elimination，RFE）提取fMRI数据中的非线性高阶特征，进而构造超图，最后基于fMRI数据的四维时空特性搭建超图卷积神经网络模型来完成分类任务。

1. 实验方法

1.1. 整体流程

本文的目标是构造基于fMRI数据对AD进行辅助诊断分类的框架，如图1所示。本框架主要分为数据处理、超图构造、多模态数据构造和分类模型搭建四个部分。为了有效利用fMRI图像中各个脑区之间的非线性高阶相关关系，本框架首先对fMRI数据进行预处理并提取BOLD信号，随后使用非线性高阶特征提取算法挑选出多个关键脑区之间的非线性高阶相关关系并构造成超图，接着将超图中节点和边信息与BOLD信号构造成多模态数据，最后搭建针对性的三维超图卷积神经网络——fMRI HyperGraph Neural Network（FHyperGNN）模型来完成分类任务。

图 1.

Overall framework

整体框架

1.2. 数据处理

源fMRI数据需要经过预处理、脑图谱建模和BOLD信号提取才能转换成可在深度神经网络中进行训练的数据。首先将源fMRI数据进行预处理。本文使用DPARSF^[14]（Data Processing Assistant for Resting-State fMRI）工具箱和spm12软件包进行预处理，fMRI图像预处理包含以下几个步骤：图像格式转换、去除初始时间点、时间片校正、头动校正、空间标准化、去线性漂移、协变量回归、低频滤波和空间平滑等。其中，时间片校正步骤中，fMRI图像按照3 s的时间间隔分割成140个时间片段；去除初始时间点步骤中，删除前10个时间片，取后续的130个时间片；低频滤波步骤中，选择滤波频段为0.01～0.1 Hz频段；其他步骤调用库函数，选择默认参数即可。

随后对fMRI数据进行脑图谱建模。Automated Anatomical Labeling（AAL）^[15]图谱是应用最广泛的脑图谱，提供了可靠的“功能”集群定位，具有良好的解剖学解释性，可以识别大脑的功能变化。该图谱共有116个脑区，前90个为大脑脑区，其余为小脑脑区，本文主要基于AAL图谱的大脑区域对fMRI进行建模研究。

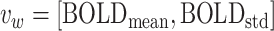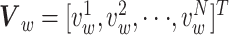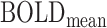最后进行BOLD信号的提取。提取每个ROI的BOLD信号的平均值和标准差作为该ROI的特征 ^[16]，所有的ROI特征构成ROI特征矩阵 。其中， 和 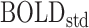分别表示当前ROI的BOLD信号的平均值和标准差，其具体计算公式如式(1)、(2)所示。

设某个ROI的BOLD信号为 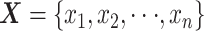，n为该ROI内部的BOLD信号个数，则有：

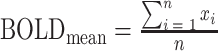1

2

1.3. 构造超图

在神经影像学领域，图论广泛应用于大脑连通性分析，简单图中，一条边只连接两个相关的节点，仅能表征脑区之间的成对关系。实际上，大脑活动往往包括多个脑区之间的协同作用，各个脑区之间存在高阶关系，这种非线性高阶相关关系无法用简单图表示。因此，本文使用超图来表征节点之间的非线性高阶相关关系，根据数据处理得到的结果，使用非线性高阶方法来构造超图。

一般来说，超图是一种扩展图，其一条边（称为超边）可以连接多个节点^[17]。而简单图是一种特殊的超图，每个超边只包含两个节点。超图样例如图2所示。

图 2.

Example of a hyper-graph

超图样例

SVR是一种非参数回归方法^[18]。本文采用RBF核作为支持向量回归模型的核函数（RBF-SVR），该核函数能够在复杂的非线性模型中表现出极强的性能，具有显著的优势^[19]。本文使用RBF-SVR模型来对fMRI数据进行拟合，实现对fMRI数据中各个脑区之间的非线性作用关系的提取。

RFE算法^[20]是一种特征筛选算法，常被用于筛去弱相关关系。本文通过基于RBF-SVR模型的RFE算法来计算多个脑区之间的非线性高阶相关关系，并以此构造超边，多个超边最终组成超图。

具体来说，在构造超边时，使用目标ROI的BOLD信号时间序列值作为标签，其他ROI的BOLD信号时间序列值作为训练数据来训练RBF-SVR模型，训练完成的RBF-SVR模型作为RFE算法的估计器，使RFE算法可以筛选出对目标ROI拟合效果最好的数个ROI，并依此构造一条基于该ROI的超边。重复对N个ROI都执行此操作，即可得到N条超边，这N条超边则构成一幅关于当前fMRI样本数据的超图。

构造完成的超图中，每一条超边都表征一种非线性高阶相关关系。例如，人的记忆行为往往涉及多个ROI协同非线性作用，此类高阶非线性交互特征可能被某条超边记录下来，而AD患者关于此类记忆行为的特征可能偏弱，从而影响模型分类结果。此类超图即可存储基于RBF-SVR模型的RFE算法筛选出的，多个ROI之间的非线性高阶相关关系。

超图中，每个ROI会有一条与之唯一对应的超边，该超边上，与当前ROI有强相关关系的多个ROI会被置1，其余ROI位置则置0，该条超边即可表征大脑中基于此ROI的多个ROI之间的强相关关系。因此，该超图可反馈多个ROI之间复杂的非线性高阶相关关系，超图中的每一条超边都表征该超边对应的ROI与其他多个ROI的非线性高阶交互特征。

1.4. 构造多模态数据

在神经网络训练中，使用多种模态的数据可以有效提高模型的鲁棒性^[21]。本文将BOLD时间序列进行均匀随机去噪，并将每个样本的时间序列数据和超图数据合并成一个多模态数据集作为模型输入。

1.5. 搭建FHyperGNN模型

主流超图算法如DHGNN^[22]和HyperGCN^[23]，其基本思想是将全部样本构造成一张超图，并基于样本间相关性来进行分类。本文提出的FHyperGNN模型以单个fMRI样本为单位构造超图，其超边集为样本内各个脑区之间的非线性多元相关关系，通过这种样本内部脑区之间的非线性多元相关关系来进行分类。同时，由于fMRI数据是一种四维数据，在一个时间段的连续采集过程中，患者可能轻微晃动头部，导致数据噪点增多，从而干扰模型对正常脑区信号的读取。为了减轻此类干扰，提高FHyperGNN模型泛化能力，引入了正则化方法去噪，从而提高fMRI分类任务的准确度。

FHyperGNN模型结构如图3所示。多模态数据首先经过一系列FHyperGNN块，进行非线性高阶特征学习，随后进行正则化并进入Dropout层丢弃部分特征，防止训练过程中出现过拟合现象。最后进入Linear层并使用Softmax激活函数完成分类任务。

图 3.

Network architecture of FHyperGNN

FHyperGNN网络结构

2. 数据与实验设置

2.1. 数据集介绍

本文研究所采用的数据来自阿尔茨海默症神经影像倡议（Alzheimer’s Disease Neuroimaging Initiative，ADNI）数据库。ADNI数据库公开提供一系列测试对象的fMRI、基因数据以及其他生物标记和相关诊断信息，成为研究AD的一套比较标准的研究数据^[24]。

本文实验数据采用了从ADNI数据库下载的66个受试者（31名AD、35名NC）的226例fMRI影像，每个受试者可能有多例fMRI影像。该数据包括了被试的影像信息、性别、年龄、简易智力状态检查量表和临床失智评分量表评分等基本信息，所有数据均由仪器Philips Medical Systems扫描获取，扫描层为48层，层厚为3.3 mm，重复时间TR=3 s，回波时间TE = 30 ms，翻转角度FA = 8°，共140个Volume，即140个时间点。具体信息如表1所示。

表 1. The dataset used in this study.

本研究使用的数据集

受试者分组	影像数量	男/女	年/岁	简易智力状态检查量表	临床失智评分量表
AD（N=31）	97	14/17	75.27 ± 6.17	20.84 ± 4.24	0.875 ± 0.43
NC（N=35）	129	15/20	75.79 ± 6.90	29.14 ± 1.41	0.044 ± 0.14

2.2. 参数设置及评价指标

本文采用五折交叉验证的方法，为了避免数据泄露，将数据集按照受试者水平随机分为五个子集，来自同一受试者的fMRI影像只会出现在同一个子集内，训练集、测试集和验证集的比例分别为3∶1∶1。

训练时，训练批量大小设置为64，Epoch为200，使用Adam优化器^[25]进行参数更新。实验采用分类准确率（accuracy，ACC）、受试者操作特征（receiver operating characteristic，ROC）曲线下面积（area under curve，AUC）、马修斯相关系数（Matthews correlation coefficient，MCC）三种分类指标衡量模型性能。

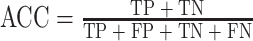3

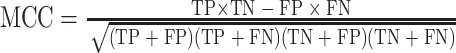4

公式(3)、(4)中的TP、TN、FP和FN分别代表真阳性数量、真阴性数量、假阳性数量和假阴性数量。

2.3. 对比试验

为了验证本文方法的有效性，将提出的网络模型与下列方法做对比。所有的比较实验均在本文的数据集上进行，均采用五折交叉验证方法，以减少因数据集划分对实验结果的影响。

（1）Pearson

传统的构建脑功能连接网络的方法是使用皮尔逊相关的方法计算 ROI 间的连接强度，即感兴趣区域i和感兴趣区域j的连接强度，连接强度计算方法如公式（5）所示：

5

（2）ST-GCN^[26]

ST-GCN方法在时空图的背景下构造函数连通网络，采用时空图卷积神经网络学习数据中的时空信息，学习图中功能连接的重要性。

（3）MVS-GCN^[12]

MVS-GCN方法以图形神经网络为基础，通过不同的阈值构建多个脑功能连接网络，建立一个共享的图嵌入层来学习每个脑功能连接的特征。

（4）BrainGNN^[13]

BrainGNN模型利用拓扑和功能信息来构造ROI图卷积层，是一个基于图神经网络的端到端fMRI预测框架。

（5）二阶线性超图^[17] + FHyperGNN。该方法将一个ROI的时间序列由其他的ROI稀疏表示，这些稀疏表示的ROI作为一条超边加入到超图中，并计算超图的节点聚类系数。

（6）高阶非线性超图 + HyperGCN^[23]

HyperGCN是一种基于属性超图的SSL图卷积网络框架。使用K-近邻算法线性构造超图，将数据集所有样本构造成一张超图，借此找出各样本之间的相关性，通过此类相关性来进行辅助分类。

3. 实验结果分析

表2是基于fMRI图像的AD/NC分类任务中，各类方法的分类性能。可以看到FHyperGNN模型的得分较高的同时，标准差相对较低，表明模型的稳定性较强，在fMRI数据上的分类鲁棒性要优于其他方法模型。

表 2. Comparison of various methods on the ADNI dataset.

各种方法在ADNI数据集上的比较

方法	ACC	AUC	MCC
Pearson	0.62 ± 0.07	0.67 ± 0.10	0.25 ± 0.15
ST-GCN	0.67 ± 0.04	0.69 ± 0.16	0.39 ± 0.06
MVS-GCN	0.71 ± 0.09	0.70 ± 0.10	0.45 ± 0.18
BrainGNN	0.62 ± 0.03	0.62 ± 0.10	0.23 ± 0.07
二阶线性超图 + FHyperGNN	0.67 ± 0.01	0.69 ± 0.16	0.39 ± 0.19
高阶非线性超图 + HyperGCN	0.69 ± 0.07	0.71 ± 0.08	0.44 ± 0.09
高阶非线性超图 + FHyperGNN	0.75 ± 0.06	0.75 ± 0.08	0.48 ± 0.09

本文使用的fMRI数据特征提取方法与传统的皮尔逊相关系数方法相比，分类准确率提高了21%，与ST-GCN、BrainGNN和MVS-GCN等模型相比，分类准确率都有不同程度的提高，说明本文使用基于RBF-SVR的递归消除算法提取特征，并通过超图存储非线性高阶脑功能连接网络的方法是有效的。

本文框架与二阶线性超图方法相比，分类准确率提高了12%，二者对比结果直观体现出非线性高阶特征对于分类的重要性。相较于流行的超图模型HyperGCN，本文模型的分类准确率提高了9%。在数据复杂度高、样本个体庞大的fMRI数据集中，相较于学习不同样本之间的相关性，关注样本内部不同ROI之间的非线性高阶相关关系往往是更优选择。

本文模型表现出较好效果的同时，有效抑制了过拟合现象。模型训练过程中的ACC值及LOSS值变化如图4所示。

图 4.

The ACC value and LOSS value of the training process

模型训练过程的ACC值及LOSS值

4. 结论

为了提高fMRI数据下AD计算机辅助诊断的准确性，本文提出一种基于非线性高阶特征和三维超图卷积神经网络的AD分类框架。该框架使用基于RBF核的SVR模型来辅助提取fMRI数据中各个脑区之间的非线性关系，并基于RFE算法来提取多个脑区之间的高阶相关关系。随后将提取出的非线性高阶相关关系构造成超图，并搭建了针对性的超图神经网络模型——FHyperGNN来完成分类任务。本文提出一个能高效利用fMRI影像中多个ROI之间非线性多元相关关系的AD分类框架。与如今主流的基于fMRI数据的AD分类方法对比，本框架在fMRI数据特征提取和基于fMRI数据的分类任务上效果有所提高，能够更好地应用于AD计算机辅助诊断中。

然而，这项研究仍存在一定的局限性。例如在RFE算法构造超图时，未能更好地利用fMRI数据中的时序信息；fMRI数据中关于各个脑区的空间分布信息也可能对分类任务有正向作用。此外，还可以开展可解释性研究，从而寻找AD的生物标志物等。在今后的研究中，将针对上述局限性开展进一步的研究。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：罗百荣主要负责数据记录与分析、算法程序与设计以及论文撰写；曾安、潘丹主要负责实验流程、协调沟通、计划安排、提供实验指导以及论文审阅修订，容华斌主要负责实验指导，张小波、林靖、杨洋和刘军主要负责论文审阅修订。

Funding Statement

国家自然科学基金项目（61976058）；广州市科技计划项目（202103000034，202206010007，202002020090）；广东省科技计划项目（2021A1515012300，2019A050510041，2021B0101220006）；云南省重大科技专项（202102AA100012）